Assessing the Perturbing Effects of Drugs on Lipid Bilayers Using Gramicidin Channel-Based In Silico and In Vitro Assays

Abstract

Partitioning of bioactive molecules, including drugs, into cell membranes may produce indiscriminate changes in membrane protein function. As a guide to safe drug development, it therefore becomes important to be able to predict the bilayer-perturbing potency of hydrophobic/amphiphilic drugs candidates. Toward this end, we exploited gramicidin channels as molecular force probes and developed in silico and in vitro assays to measure drugs’ bilayer-modifying potency. We examined eight drug-like molecules that were found to enhance or suppress gramicidin channel function in a thick 1,2-dierucoyl-sn-glycero-3-phosphocholine (DC_22:1PC) but not in thin 1,2-dioleoyl-sn-glycero-3-phosphocholine (DC_18:1PC) lipid bilayer. The mechanism underlying this difference was attributable to the changes in gramicidin dimerization free energy by drug-induced perturbations of lipid bilayer physical properties and bilayer–gramicidin interactions. The combined in silico and in vitro approaches, which allow for predicting the perturbing effects of drug candidates on membrane protein function, have implications for preclinical drug safety assessment.

Introduction

Amphiphilic small molecules tend to accumulate in cell membranes at the membrane/solution interface^1,2 where they potentially cause deleterious changes in membrane protein function by modulating the cell membrane’s physicochemical properties. The molecular basis for the bilayer-mediated changes in membrane protein function is that first, membrane-embedded/spanning proteins perturb the adjacent lipid packing,^3,4 which will incur energetic penalty due to bilayer deformation, and second, membrane proteins’ functional cycles tend to involve conformational transition between, e.g., inactivated (I) and activated (A) states. The free energy change for the protein conformational transition between states I and A (ΔG_total^I → A) will be the sum of energetic contributions from rearrangements within the protein (ΔG_protein) and changes in lipid packing/deformation around the protein (ΔG_bilayer^I → A). ΔG_bilayer, and therefore, ΔG_total^I → A will vary with changes in bilayer physical properties (such as thickness, curvature, and elasticity).

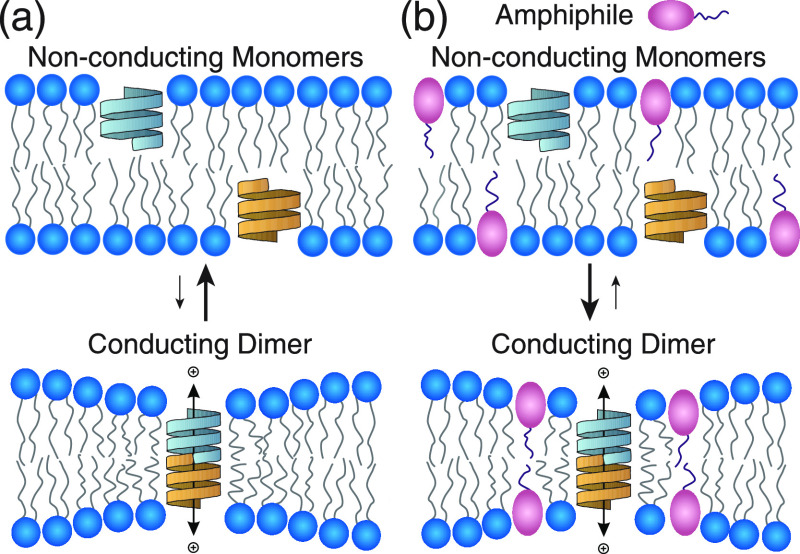
Partitioning of amphiphilic drug molecules into cell membranes may indiscriminately alter the function of a number of proteins by perturbing ΔG_bilayer^I → A. Therefore, as a guide to safe drug development, it becomes important to assess the lipid bilayer perturbing effects of drug candidates. To this end, we developed an in vitro model system using gramicidin channels as molecular force probes for changing bilayer properties.⁵⁻¹⁰ Gramicidin channels have a well-characterized structure and function and thus have become powerful model membrane proteins.^8,9,11−22 In experiments, the function of gramicidin channels can be quantified by the rate of ion movement across lipid bilayers, which is determined by the number of conducting channels at thermodynamic equilibrium. Conducting gramicidin channels form by the transmembrane dimerization of non-conducting subunits that reside in the two bilayer leaflets (Figure 1).

Figure 1.

Gramicidin channel function. (a) Cation conducting β^6.3-helical gramicidin A (gA) channels form by transmembrane dimerization of two non-conducting gA monomer subunits. (b) When amphiphiles (drugs) are added to the aqueous phase and partition into the bilayer, it will alter physical properties and thereby shift the gramicidin monomer ↔ dimer equilibrium, usually toward the dimer.

The monomer ↔ dimer equilibrium can be described as:

1

where M and D denotes the monomer and the dimer, k_B is Boltzmann’s constant, and T is the temperature in Kelvin. When amphiphilic drugs partition into the lipid bilayer, they will alter lipid bilayer properties, which will produce a change in the ΔG_bilayer^M → D (and maybe the ΔG_protein). Numerous studies have shown how small molecules alter gramicidin channel function, and the changes in function of integral membrane proteins can be predicted by changes in gramicidin function.^1,5−10

Here, we pursue this question by estimating the drug-induced shifts in the equilibrium distribution between gramicidin monomers and dimers in lipid bilayers by computing the potential of mean force (PMF) for the gramicidin monomer ↔ dimer transition.⁴ Mapping the PMF for the gramicidin monomer ↔ dimer transition in lipid bilayers, however, is difficult with atomistic molecular dynamics (MD) simulations. The slow translational/rotational diffusion and the structural plasticity of gramicidin monomers in lipid bilayers pose challenges to the convergence of atomistic MD simulations,⁴ which motivated us to develop a computationally more feasible approach based on the coarse-grained (CG) Martini framework.²³ The Martini force field has been widely used to investigate membrane protein dimerization, aggregation, and channel gating.²⁴⁻²⁸

Simulating processes such as the hydrogen bond promoted trans-bilayer gramicidin dimerization with the Martini force field, however, is not trivial because hydrogen bond interactions are included only implicitly in the Martini force field. We therefore developed a Martini-compatible CG model for gramicidin A (gA), which is the major component of the naturally occurring gramicidin D (gD). The CG gA model was validated against 112 μs all-atom (AA) replica-exchange umbrella sampling (REUS) simulations.²⁹ Then, using the CG models, we performed 2.52 ms REUS simulations to investigate the effects of eight biologically active drug-like molecules (called drugs hereafter)—capsaicin, cholesterol, cyclohexane, dodecylphosphocholine (FC12), hexaethylene glycol monododecyl ether (C12E6), octanol, Triton X-100, and resveratrol—on the PMF for gA monomer ↔ dimer transition in two lipid bilayers with different thicknesses: 1,2-dioleoyl-sn-glycero-3-phosphocholine (DC_18:1PC) and 1,2-dierucoyl-sn-glycero-3-phosphocholine (DC_22:1PC). Except for resveratrol, which has a promiscuity score, or pScore, of 265, as evaluated using Badapple (http://pasilla.health.unm.edu/tomcat/badapple/badapple),³⁰ the chosen drugs do not have the characteristics of pan assay interference compounds (PAINS).^31,32

The PMF results were compared with results obtained from the in vitro gramicidin channel-based fluorescence quench experiments, which quantitatively characterize the equilibrium number for gA channels. Good agreement was achieved between the simulations and the experiments, suggesting that the molecular mechanism underlying the drug-induced changes in gramicidin channel ion conducting function can be well captured with CG models. The simulations unveiled that the tested drug molecules shift the gA dimer versus monomer equilibrium by non-specifically perturbing the lipid–gA interactions, and the perturbing effects are more pronounced in the thick bilayer than in the thin bilayer. These simulation and experimental approaches, and the unveiled molecular mechanism, open up for an approach to identify PAINS-like molecules,^4,31,32 which are promiscuous modifiers of membrane protein function, and for safety assessment in drug design and development.

Results and Discussions

Evaluation of the Coarse-Grained Models

The gA channel’s ion-conducting rate reflects the equilibrium number of gA channels formed in the lipid bilayer. For a specific gA:lipid number ratio, the equilibrium number of gA channels is determined by the free energy difference between the monomeric and the dimeric gA states in the lipid bilayer (ΔG^M ↔ D).³³ In simulations, the perturbing effects of drugs on the gA channel’s function can thus be assessed by calculating the drug-induced change in ΔG^M ↔ D (or ΔΔG^M ↔ D|_Drug). Before we calculated ΔΔG^M ↔ D|_Drug with the CG models (see the Supporting Information for the development of the CG gA model and Figure S1 for the CG mapping schemes for the drugs), we first evaluated the developed CG model for the gA channel in which the hydrogen bond interactions at the formyl-N-termini were treated implicitly. We did AA- and CG-unbiased MD simulations to probe the structural stability of the gA channel embedded in the thick DC_22:1PC bilayer. In both AA and CG simulations, the two gA subunits remained associated throughout a 2 μs MD simulation, though the CG gA channel was found to be more flexible than the AA gA channel, as shown in Figure S2.

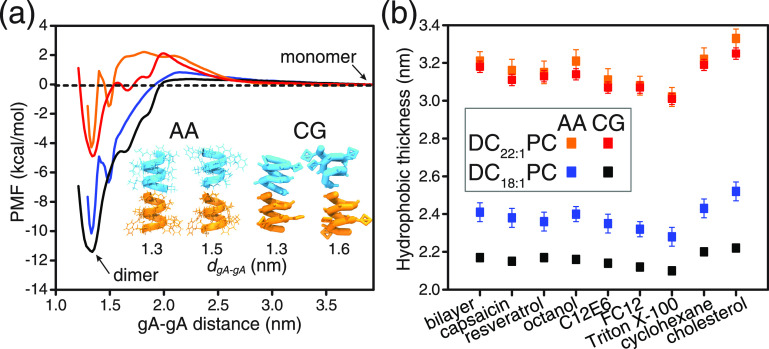
We further evaluated the CG gA model by comparing the AA and CG PMF profiles for the gA monomer ↔ dimer transition in the DC_18:1PC and DC_22:1PC bilayers. As shown in Figure 2a, the CG model predicts the ΔG^M ↔ D to be −11.4 and −4.9 kcal/mol in the DC_18:1PC and DC_22:1PC bilayers, similar to the −10.2 and −4.3 kcal/mol calculated with the AA model. On closer inspection, the AA PMF profiles exhibit two “V”-shaped local free energy minima at ∼1.3 and ∼1.5 nm along the gA–gA center-of-mass distance (d_gA–gA) reaction coordinate. These two free energy minima denote two different metastable gA dimer configurations formed during the AA-REUS simulations, as illustrated by the snapshots in Figure 2a. At d_gA–gA ≈ 1.3 nm, the two gA monomers can form a maximum number of six hydrogen bonds at the formyl-N-terminal interface, which is the canonical structure.³⁴ At d_gA–gA ≈ 1.5 nm, the two monomers have rotated relative to each other by two amino acid positions and can only form a maximum of four hydrogen bonds (see Figure S3); this may be a transition state on the reaction coordinate between the non-conducting monomers and conducting dimers. In the CG PMF profiles, there is a free energy minimum at d_gA–gA ≈ 1.3 nm, and the associated CG gA dimer configuration resembles the AA six-hydrogen-bond channel structure. The CG PMF profiles also exhibit a kink at d_gA–gA ≈ 1.6 nm where the two CG gA monomers have rotated relative to each other in a way similar to the atomistic four-hydrogen-bond channel. To evaluate the finite-size effect on the PMF, we also calculated the PMF using a larger-sized DC_22:1PC bilayer system (1000 lipids). The PMF result obtained from the larger bilayer system is close to that obtained from the smaller system (Figure S4).

Figure 2.

(a) PMF profiles for gA monomer ↔ dimer transition in the DC_18:1PC and DC_22:1PC bilayers (orange: AA-DC_22:1PC; red: CG-DC_22:1PC; blue: AA-DC_18:1PC; black: CG-DC_18:1PC). The reaction coordinate is the center-of-mass distance between the two gA monomers. In the AA simulations, the center-of-mass of the gA monomer is defined using all Cα atoms of the monomer; in the CG simulations, the center of mass of the monomer is defined using all backbone beads of the monomer. In the AA-REUS simulations, two structurally different dimers are obtained at gA–gA distances of ∼1.3 and ∼1.5 nm. At d_gA–gA ≈ 1.3 nm, the two subunits can form a maximum number of six hydrogen bonds, while at d_gA–gA ≈ 1.5 nm, the two subunits can only form a maximum number of four hydrogen bonds due to the relative rotation between the two monomers. The two different gA dimer structures are also observed in the CG-REUS simulations, and the derived CG PMF profiles exhibit a free energy minimum at d_gA–gA = 1.3 nm and a kink at d_gA–gA = 1.6 nm. (b) Effects of the tested drugs on the hydrophobic thickness of DC_18:1PC and DC_22:1PC bilayers. The methods used to calculate the bilayer’s hydrophobic thickness are illustrated in Figure S1. For the DC_18:1PC bilayer, the calculated hydrophobic thickness values using the AA and the CG models deviate by ∼0.2 nm. This discrepancy can be attributed to the four-carbon mapping scheme of the CG building blocks, as illustrated in Figure S1. The error bars for AA and CG simulations are ±0.05 and ± 0.03 kcal/mol, respectively.

The CG models for the eight drugs are from previous works,^23,35−37 and here, we investigated the effects of the drugs on the hydrophobic thickness of DC_18:1PC and DC_22:1PC bilayers (Figure 2b). The AA and CG simulation results show good agreement predicting that Triton X-100, FC12, C12E6, resveratrol, capsaicin, and octanol decrease the hydrophobic thickness of the two bilayers, whereas cholesterol and cyclohexane tend to increase the bilayer thickness. The CG models thus reproduce the effects of drugs on ΔG^M ↔ D, and the existence of two different gA dimer configurations as observed in the AA simulations.

Effects of Bilayer-Embedded Drugs on ΔG^M ↔ D

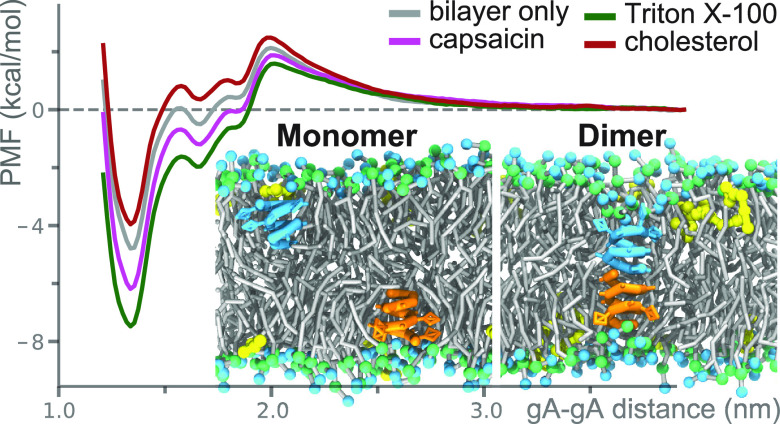
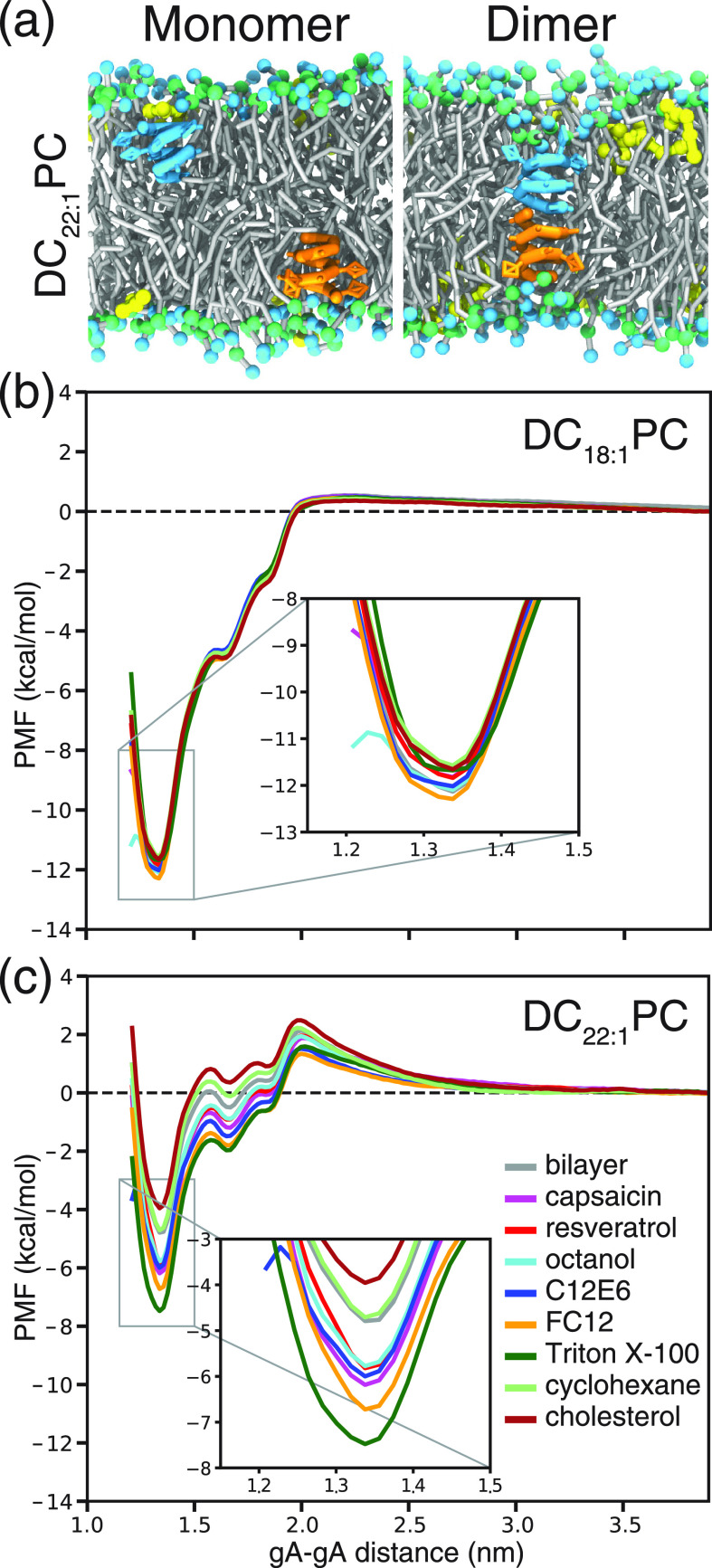
Using the CG models, we ran a total of 2.52 ms REUS simulations to predict the effects of bilayer-embedded drugs on ΔG^M ↔ D. Figure 3a illustrates the gA monomer and dimer states in the lipid bilayer with embedded drugs (drug:lipid number ratio = 0.084). Figure 3b,c shows the PMF profiles for gA monomer ↔ dimer transition in DC_18:1PC and DC_22:1PC bilayers incorporated with different drugs. The PMF profiles in Figure 3b show that the eight drugs have virtually no effect on ΔG^M ↔ D in the thin DC_18:1PC bilayers (the ΔΔG^M ↔ D|_Drug values are ≤0.5 kcal/mol, see Table 1). In the thick DC_22:1PC bilayer, the drugs cause more pronounced changes in ΔG^M ↔ D. Resveratrol, octanol, capsaicin, C12E6, FC12, and Triton X-100 decrease ΔG^M ↔ D between ∼1.0 and ∼2.7 kcal/mol (Figure 3c and Table 1), indicating that these six molecules tend to shift the gA monomer ↔ dimer equilibrium toward the conducting dimers. Cholesterol, in contrast, increases ΔG^M ↔ D by ∼0.8 kcal/mol, indicating that this bilayer-condensing/thickening molecule shifts the monomer ↔ dimer equilibrium toward the non-conducting monomers. Cyclohexane increases ΔG^M ↔ D by only ∼0.1 kcal/mol.

Figure 3.

Effects of drugs on gA monomer ↔ dimer transition. (a) Snapshots for two gA monomers (colored cyan and orange) and the dimeric channel in the DC_22:1PC bilayer doped with capsaicin (colored yellow). Effects of different drugs on the PMF for gA monomer ↔ dimer transition in (b) DC_18:1PC and (c) DC_22:1PC bilayers. All of the CG PMF profiles are well converged (see Supporting Information) and the error bars are within 0.05 kcal/mol.

Table 1. Summary of ΔG^M ↔ D and ΔΔG^M ↔ D|_Drug Predicted with the CG-REUS Simulations and the Fluorescence Quench Experiments (Unit: kcal/mol)^a.

	simulations			simulations		experiments
DC18:1PC	ΔGM ↔ D	ΔΔGM ↔ D|Drug	DC22:1PC	ΔGM ↔ D	ΔΔGM ↔ D|Drug	ΔΔGM ↔ D|Drug
bilayer only	–12.1	0	bilayer only	–4.8	0	0*	0**
capsaicin	–11.8	0.3	capsaicin	–6.2	–1.4	–0.6*	–0.5**
resveratrol	–11.8	0.3	resveratrol	–5.8	–1.0	–1.8*	–1.7**
octanol	–12.1	0.0	octanol	–5.8	–1.0	–0.3*	–0.4**
C12E6	–12.0	0.1	C12E6	–6.0	–1.2	–1.5*	–1.4**
FC12	–12.3	–0.2	FC12	–6.7	–1.9	–0.5*	–0.5**
Triton X-100	–11.7	0.4	Triton X-100	–7.5	–2.7	–1.6*	–1.5**
cyclohexane	–11.6	0.5	cyclohexane	–4.7	0.1	0.0*	0.0**
cholesterol	–11.7	0.4	cholesterol	–4.0	0.8	NA	+2.5**

^a*, Experiments with gD. ^**, Experiments with gA

Fluorescence Quench Experiments

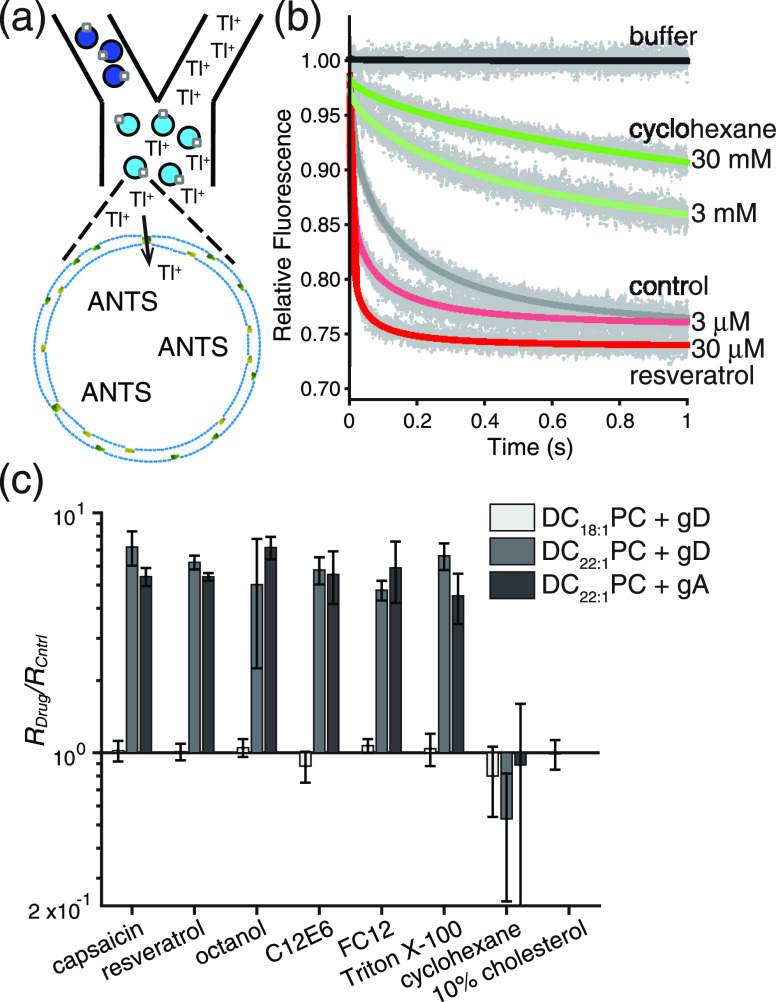
To verify the CG simulation results, we did fluorescence quench experiments to quantify the eight drug molecules’ perturbing effects on the activity of gramicidin channels embedded in the DC_18:1PC and DC_22:1PC bilayers (see Supporting Information, Methods for details). In these experiments, we used both synthesized gA and the naturally occurring mixture of gramicidin A, B, and C (gD), the same mixture we used in previous studies.^{5−7,16,38−40}Figure 4a shows a schematic illustration of the fluorescence quench assay. ANTs that encapsulated large unilamellar vesicles (LUVs) were quenched using a gramicidin permeable quencher (Tl⁺), and drug-induced changes in the channel activity (quencher influx) were captured using a stopped-flow spectrofluorometer. Figure 4b shows representative fluorescence quench traces induced by the bilayer-thinning/softening resveratrol and the bilayer-thickening/stiffening cyclohexane.

Figure 4.

Effects of drugs on the gramicidin monomer ↔ dimer equilibrium. (a) Schematic description of the stopped-flow fluorescence quench experiments: gramicidin permeable Tl⁺ quenches the LUV encapsulated fluorophore ANTS. (b) Representative fluorescence quench traces in DC_22:1PC LUVs doped with gD. (c) Effects of drugs on the fluorescence quench rates (gramicidin monomer ↔ dimer equilibrium) in DC_18:1PC LUVs doped with gD (light gray), DC_22:1PC LUVs doped with gD (dark gray), and DC_22:1PC LUVs doped with gA (black). The aqueous drug concentrations were 100, 30, 1800, 10, 300, 30, and 30,000 μM for capsaicin, resveratrol, octanol, C12E6, FC12, Triton X-100, and cyclohexane, respectively, and the estimated molar ratios of the drugs in the bilayers were 0.32, 0.02, 0.48, 0.04, 0.21, 0.04, and 0.93, respectively; cholesterol was added at a molar ratio of cholesterol:lipid of 1:10 when preparing the LUVs. Mean ± S.D. n = 3–4.

Figure 4c shows the drug-induced changes in fluorescence quench rate (R_Drug/R_Cntrl) in DC_18:1PC (gD:lipid = 1:40,000) and DC_22:1PC (gD:lipid = 1:2000 and gA:lipid = 1:2000) LUVs mixed with different drugs. It is found that the tested drugs produced little change in R_Drug/R_Cntrl in the thin DC_18:1PC bilayer and even in the DC_20:1PC LUVs (see Figure S5). In the DC_22:1PC LUVs, however, the R_Drug/R_Cntrl values are markedly increased or decreased depending upon the drug species. Drugs that thin/soften the bilayer (e.g., capsaicin, resveratrol, octanol, C12E6, FC12, and Triton X-100) shift the gramicidin monomer ↔ dimer equilibrium toward the dimer state in the DC_22:1PC LUVs, and thus the number of conducting gramicidin dimers/channels (and the fluorescence quench rate) is increased by these drugs. By contrast, drugs that thicken/stiffen the bilayer (e.g., cholesterol and cyclohexane) shift the gramicidin monomer ↔ dimer equilibrium toward the monomer state. Adding 10 mol % cholesterol to the DC_22:1PC LUVs effectively precludes the formation of conducting channels.

We further investigated the effect of drug concentration (except cholesterol) on the gramicidin channel activity (Figure S6) using both gD (gD:lipid = 1:2000) and gA (gA:lipid = 1:6000) (gA is a more potent channel former in DC_22:1PC LUVs than gD).⁴ For the six bilayer-thinning/softening drugs, the corresponding R_Drug/R_Cntrl value measured with both gA and gD increased with increasing drug concentration. Increased cyclohexane concentration, in contrast, decreased R_Drug/R_Cntrl. For cholesterol, we tested DC_22:1PC LUVs doped with 10 mol % cholesterol (Figure S6) at varying gD:lipid molar ratios between 1:200 and 1:2000. We observed channel formation only when the gD:lipid molar ratio is larger than 1:400, suggesting that ∼10 times as much gD is needed in order to achieve the same channel activity as we observed in cholesterol-free DC_22:1PC LUVs.

Using the aqueous concentration as a reference, Figure S6 shows that the six bilayer-thinning/softening drugs’ bilayer-modifying potency follows the order of C12E6 > Triton X-100 > resveratrol > capsaicin > FC12 > octanol. For comparison with the MD simulations, we also estimated the six drugs’ mole fraction in the bilayer, m_D, using their calculated octanol/water partition coefficient ALogP⁴¹ (Table S3). The results (Figure S7) show that the bilayer-modifying potency per molecule in the membrane varies by one to two orders of magnitude, and the six drugs can be categorized into two groups: a group of potent modifiers, Triton X-100, C12E6, and resveratrol, where R_Drug/R_Cntrl > 3 at an estimated m_D = 0.01; and a group of weaker bilayer modifiers, FC12, octanol, and capsaicin, where R_Drug/R_Cntrl reaches 3 only at an estimated m_D > 0.15.

The drug-induced changes in R_Drug/R_Cntrl in the DC_22:1PC LUVs, where the concentration of non-conducting gramicidin monomers is much higher than the concentration of conducting gramicidin dimers, allow us to estimate ΔΔG^M ↔ D|_Drug (see Supporting Information, Methods). For comparison between the experimental and CG simulation estimates, we note that R_Drug/R_Cntrl increases as an approximately linear function of drug concentration,^6,42 and we used the results adjusted for m_D (Figure S7) to estimate what R_Drug/R_Cntrl would be at a drug:lipid ratio = 0.084, the ratio used in the CG simulations, and used this estimate for R_Drug/R_Cntrl to calculate ΔΔG^M ↔ D|_Drug. The cholesterol-induced changes in ΔG^M ↔ D (ΔΔG^M ↔ D|_Chol) could similarly be estimated from the gramicidin:lipid molar ratios that were needed to give approximately equal quench rates in cholesterol-free and cholesterol-containing LUVs (Figure S6). The ΔΔG^M ↔ D|_Drug values determined in DC_22:1PC LUVs prepared with gA or gD are summarized in Table 1. There is good overall agreement between the simulation and experimental results. The differences reflect, at least in part, a combination of uncertainties about the actual drug partition coefficients into the bilayer and approximations in the CG model.

Drugs Perturb Gramicidin Channel Function by Modulating Lipid Bilayer–Gramicidin Interactions

The results obtained from the CG-REUS simulations and the fluorescence quench experiments are in overall agreement: first, the eight tested drugs produce marked changes in gA channel functions only in the thick DC_22:1PC bilayer, and second, capsaicin, resveratrol, octanol, C12E6, FC12, Triton X-100 shift the gA monomer ↔ dimer equilibrium toward the conducting dimers, whereas cyclohexane and cholesterol tend to shift the equilibrium toward the non-conducting monomers.

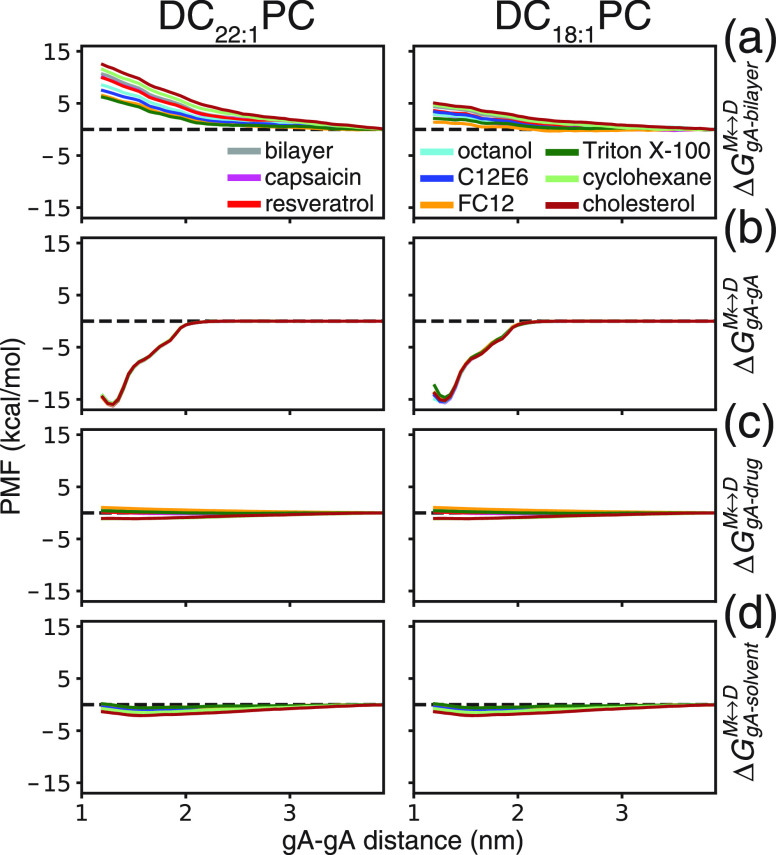
To elucidate the molecular mechanism underlying the simulation and experimental results, we used the force integration approach^12,43 to decompose the simulation derived PMF into four independent energetic contributions: the gA–lipid bilayer interactions, the gA–gA interactions, the gA–drug interactions, and the gA–solvent (water and ions) interactions (see Supporting Information). The ΔG^M ↔ D can then be estimated by

2

The resultant decomposed PMF profiles are shown in Figure 5, and the associated ΔG_gA – gA^M ↔ D, ΔG_{gA – bilayer}, ΔG_{gA – solvent}^M ↔ D, and ΔG_{gA – drug} values are summarized in Table S2.

Figure 5.

Decomposition of the PMF profiles into energetic contributions associated with (a) gA–lipid bilayer, (b) gA–gA, (c) gA–drug, and (d) gA–solvent interactions in both DC_22:1PC and DC_18:1PC bilayers. The decomposed PMF profiles do not contain the Jacobian correction term for the free energy, but this correction term is important to reconcile the PMF obtained with different methods (see Figures S10 and S11 for the differences between WHAM, force integration (FI) and decomposed force integration (DFI) approaches).

Figure 5a shows the contributions of the lipid bilayer–gA interactions to the PMF. The PMF values increase as the two gA monomers approach each other in the two lipid bilayers, indicating that the gA–lipids interactions/packing exert an energetic barrier that inhibits the gA monomer → dimer transition. In the thick DC_22:1PC bilayer, the ΔG_{gA – bilayer}^M ↔ D was 9.6 kcal/mol in the absence of drugs; in the presence of drugs, ΔG_{gA – bilayer} ranged between 5.5 and 11.5 kcal/mol depending on the drug species. Capsaicin, resveratrol, octanol, C12E6, FC12, and Triton X-100 reduced ΔG_{gA – bilayer}^M ↔ D, whereas cyclohexane and cholesterol increased ΔG_{gA – bilayer}. In the thin DC_18:1PC bilayer, ΔG_{gA – bilayer}^M ↔ D was 4.1 kcal/mol in the absence of drugs; in the presence of drugs, ΔG_{gA – bilayer} ranged between 1.3 and 4.7 kcal/mol depending on the drug species. Again, capsaicin, resveratrol, octanol, C12E6, FC12, and Triton X-100 decreased ΔG_{gA – bilayer}^M ↔ D, whereas cyclohexane and cholesterol produced an increase. Figure 5b shows the contributions of the gA–gA interactions to the PMF. The profiles are almost indistinguishable in the two lipid bilayers, and they are not significantly affected by the presence of the drugs. As the two gA monomers approach each other, the PMF values remain constant until the gA–gA distance reaches at ∼2 nm, where the PMF begins to decrease. The results support the notion that favorable short-range polar gA–gA interactions provide the driving force for gA dimerization. The ΔG_gA – gA values show that the gA–gA interactions are strong enough to overcome the lipid bilayer imposed energetic barrier even in the thick DC_22:1PC bilayer. Figure 5c shows the contributions of the gA–drug interactions to the PMF. The ΔG_{gA – drug}^M ↔ D values are in the range of −1.4 to 0.7 kcal/mol in the two bilayers incorporated with different drugs. These values are small compared to the energetic contributions from gA–lipid bilayer and gA–gA interactions, indicating that specific drug–gA interactions do not account for the changes in gA channel function. Likewise, the energetic contributions from the gA–solvent interactions are negligible (Figure 4d).

The PMF decomposition analysis indicates that drug molecules mainly affect the gA channel functions by altering gA–lipid bilayer interactions. Figure S8 shows how the ΔΔG^M ↔ D|_Drug values (Figure 3 and Table 1) are well correlated with the changes in ΔG_{gA – bilayer}^M ↔ D (i.e., ΔΔG_{gA – bilayer}) in the thick DC_22:1PC bilayer, indicating that ΔΔG^M ↔ D|_Drug is a good approximation for the drug’s bilayer modifying potency as sensed by gA (ΔΔG_bilayer^M ↔ D|_Drug); whereas the correlation is poor in the thinner DC_18:1PC bilayer. For the drugs tested here, their effects on gA function or, equivalently, ΔΔG^M ↔ D|_Drug, also correlate well with the drug-induced changes in bilayer thickness (Figure S9), which are associated with changes in other bilayer physicochemical properties, such as area per lipid, lipid tail ordering, curvature, and elasticity.

Bilayer-Perturbing Molecules versus PAINS

As previously noted, some so-called PAINS turn out to be bilayer active.^31,32 The converse need not be true, a molecule that is bilayer active is unlikely to make it masquerade as hits in protein-based high-throughput screens unless its chemical characteristics satisfy the criteria for being a PAIN—as evaluated, for example, using Badapple.³⁰ Yet, bilayer-active molecules are likely to masquerade as hits in cell-based screens because the changes in bilayer properties that we measure as changes in the gramicidin monomer ↔ dimer equilibrium will produce changes in the function of many other membrane proteins,³³ which are likely to lead to changes in overall cell function that may make the molecule appear to be a hit. As noted elsewhere,⁴⁴ modest changes in bilayer properties may lead to desired poly-pharmacology; more extreme changes in bilayer properties, however, are likely to lead to frank toxicity. That is, bilayer-active molecules constitute a novel class of cell-based assay interference compounds (CAINS).

Conclusions

We have developed a combined computational and experimental approach to predict the perturbing activities of drug-like molecules on membrane protein function. The gramicidin channel was selected as the model membrane protein because: first, the structural and functional properties of gA channels are well established; second, the free energy for gA monomer ↔ dimer transition, which underlies the channel’s ion-conducting functions, is approachable with REUS simulations; and third, the gramicidin channels have proven to be experimental probes for changes in bilayer properties. Even for the 15 amino acid-long gA, however, free energy calculations of gA dimerization in the heterogeneous lipid-drug environment are plagued by a sampling convergence problem with atomistic models and thus require extensive computational resources. The sampling problem can be mitigated with the CG models without losing important thermodynamic information. Our CG simulations and experimental results consistently showed that the lipid bilayer’s intrinsic physical properties, such as thickness, influence the drugs’ perturbing actions on the gA channel’s function. The tested drugs enhance or suppress the ion channel’s function by altering the bilayer environment and bilayer–protein interactions, which are more sensitive to subtle thickness/elasticity changes in the thicker DC_22:1PC bilayer. Drugs may promiscuously alter the functions of many other membrane proteins through a similar bilayer associated mechanism.¹ When designing or testing new drugs, their potency of modifying membrane protein function should be assessed and compared to dosage to improved drug safety.

Experimental Section

Coarse-Grained Simulations

The CG gA model was developed based on the framework of the Martini force field (see the Supporting Information for details).^23,45 Unbiased CG MD simulations were first done to equilibrate the gA channel structure in the DC_18:1PC and DC_22:1PC lipid bilayers. The starting structures for gA channels embedded in the two bilayers doped with different drug molecules were constructed with the insane program.⁴⁶ The simulation systems contain 190 lipids (95 lipids in each leaflet), 16 drug molecules (eight in each leaflet, for a drug:lipid molar ratio of 0.084), and one gA channel. For each system, 2 μs CG MD simulations were performed in the semi-isotropic ensemble at 310.15 K and 1 bar. Unbiased CG MD simulations were also done to investigate the drugs’ effects on the bilayer’s hydrophobic thickness. This was done by removing the gA channel from the 18 systems followed by 2 μs CG MD simulation. Using the CG models, we also performed REUS simulations²⁹ to investigate the effects of eight drugs on the PMF for gA monomer ↔ dimer transition in the DC_18:1PC and DC_22:1PC lipid bilayers. In the REUS simulations, a sequence of umbrella windows is created to span the entire range of a pre-defined collective variable (CV). Then, during the REUS simulations, a biasing potential is imposed to each umbrella window to restrain the CV to fluctuate around a target CV. In our case, the biasing potential was harmonic, i.e.,

3

where ξ is the target and ξ_i the instantaneous value of the CV, k is the umbrella spring constant, and i is the index number for the umbrella window. The total potential energy of umbrella window i is determined as the sum of the force field-based potential energy and the imposed harmonic biasing potential. During the REUS simulations, two neighboring umbrella windows i and j can exchange their configurations with the replica exchange probability determined by the Metropolis criterion,

4

with

5

where 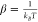(k_B is the Boltzmann constant) and V^ex is the biasing potential energy obtained after the configurations of the two neighboring windows are swapped. The PMF for the gA monomer ↔ dimer transition was derived with the weighted histogram analysis method (WHAM) approach.⁴⁷ The PMF profiles were also derived with the force integration approach,⁴³ with the harmonic force for umbrella window i derived as

6

We used the center-of-mass distance between the two gA monomers as the CV and 56 umbrella windows with the CVs ranging between 1.20 and 3.95 nm were created. The CG REUS simulations were run using GROMACS 2018⁴⁸ patched with PLUMED2.4.2.⁴⁹ For each window, we ran 2.5 μs MD simulations, and the total amount of CG REUS simulation time was 2.52 ms. The exchange between neighboring windows was attempted every 100 ps. The umbrella spring constant was 5500 kJ/mol/nm².

All-Atom Simulations

To calibrate and validate the CG models, we ran unbiased AA MD simulations of the gA channel embedded in pure DC_18:1PC and DC_22:1PC bilayers. The starting configurations for the AA MD simulations were constructed using the CHARMM-GUI scripts.⁵⁰ Each simulation system contains 200 lipids (100 lipids in each leaflet) and one gA channel. The simulation systems were hydrated, containing 12,000–14,000 TIP3P water and 0.15 M KCl. Each system was equilibrated for 2 μs. Using the equilibrated systems, we ran 112 μs AA REUS simulations to probe the PMF for the gA monomer ↔ dimer transition in the pure DC_18:1PC and DC_22:1PC bilayers. To improve the convergence of the AA REUS simulations, each of the 56 umbrella sampling windows was simulated for up to 1 μs. The CV was the COM distance between the two gA monomers. Exchange between two neighboring windows was attempted every 100 ps. The umbrella spring constant was 5500 kJ/mol/nm² and the 1d-WHAM program from Grossfield (http://membrane.urmc.rochester.edu/content/wham/)⁵¹ was used to derive the PMF profiles. To investigate the effects of different drugs on the lipid bilayer’s hydrophobic thickness, we ran unbiased AA MD simulations of DC_18:1PC and DC_22:1PC bilayers doped with the eight different drugs. The simulation system contains 200 lipids and 20 drug molecules (10 molecules in each leaflet). Each of the 16 systems was simulated for 500 ns. The CHARMM36 force field was used to model the gA channel and lipids.^52,53 The drugs were modeled with the CHARMM general force field,⁵⁴ and the force field parameters for gA formyl and ethanolamine groups were from published work.¹¹

For other AA and CG simulation methods and parameters, see the Supporting Information. In total, we have run 120 μs AA simulations and 2.59 ms CG simulations.

Gramicidin Fluorescence Quench Assay

We quantified the gramicidin channel activity using a fluorescence quench assay,^6,55 which is based on the quenching of a water-soluble intravesicular fluorophore 8-aminonaphthalene-1,3,6-trisulfonate (ANTS) by the gramicidin channel-permeating monovalent cation thallium (Tl⁺). DC_22:1PC in chloroform (25 mg/mL, > 99%), DC_20:1PC in chloroform (10 mg/mL, > 99%), DC_18:1PC in chloroform (25 mg/mL, > 99%), and cholesterol (ovine wool, in powder form, > 98%) were from Avanti Polar Lipids (Alabaster, AL). [Val¹] gramicidin A (gA, ≥ 99.9% by HPLC) was a generous gift from Roger E. Koeppe II (University of Arkansas). The naturally occurring mixture of the linear gramicidins from Bacillus brevis (gramicidin D, or gD, after René Dubos,⁵⁶ 100%) was from Sigma-Aldrich. Thallium nitrate (TlNO₃, 99.9%), sodium nitrate (NaNO₃, ≥ 99%), 4-(2-hydroxyethyl) piperazine-1-ethanesulfonic acid (HEPES, ≥ 99.5%), capsaicin (≥ 95%), resveratrol (≥ 99%), octanol (≥ 99%), Triton X-100 (≥ 99%), and cyclohexane (99.5%) were from Sigma-Aldrich Co. C12E6 (≥ 99%) and FC12 (≥ 95%) were from Anatrace (Maumee, OH). Methanol (≥ 99.8%) and chloroform (≥ 99.8%) were from VWR (Radnor, PA) (St. Louis, MO). The disodium salt of 8-aminonaphthalene-1,3,6-trisulfonic acid (ANTS, 95%) was from Invitrogen (Eugene, OR). Cholesterol was dissolved into chloroform at 4 mg/mL. The gramicidin mixture (gD) and the pure gA were dissolved to 500 μg/mL in methanol and stored at −40 °C. All materials were used without further purification. Stock solutions of buffers and quenchers were prepared using Millipore Milli-Q deionized water Millipore Sigma (Burlington, MA); the pH was adjusted to 7 using NaOH and HNO₃. The standard buffer was 140 mM NaNO₃ plus 10 mM HEPES; the quench buffer was 50 mM TlNO₃ plus 94 mM NaNO₃ and 10 mM HEPES. The ANTS-buffer was made with 25 mM ANTS, 100 mM NaNO₃, and 10 mM HEPES, and stored in the dark. All chemicals were used as supplied with a purity of ≥95% (each indicated above) as determined by vendor, except a gA purity of ≥99.9% that was determined by HPLC.

The ANTS-loaded large unilamellar vesicles (LUVs) were prepared using different gramicidin:lipid mole ratios (1:40,000 for DC_18:1PC, and 1:2000 for DC_22:1PC) by mixing the lipids with the respective gramicidin stock solution at the given molar ratio; the cholesterol experiments were done by adding cholesterol at various cholesterol:lipid ratios before forming the LUVs. The lipid–gramicidin mixture then was dried under nitrogen and further dried overnight in vacuum. The lipid was rehydrated with ANTS buffer in the dark; the volume of the ANTS buffer was adjusted to give a lipid concentration of 10 mM. The sample was equilibrated at room temperature for 3 h and sonicated for 1 min. After six freeze–thaw cycles, the gramicidin:lipid suspension was extruded 21 times with an Avanti mini-extruder using a 0.1 μm polycarbonate filter to form LUVs. Extravesicular ANTS was removed with a 2.5 mL PD-10 desalting column (GE Healthcare, Piscataway, NJ), and the solution was covered and stored in the dark at 12.5 °C. The LUV size distribution was determined using dynamic light scattering with a Litesizer 500 (Anton Paar, Austria); the average diameter was around 130 nm, and the samples were monodisperse as determined by the polydispersity index (PDI), which was ≤0.10, with little variation among the tested vesicle types (DC_18:1PC, DC_22:1PC, and Chol: DC_18:1PC).

The time course of the Tl⁺-induced quench of the ANTS fluorescence was measured at 25 °C using an SX-20 stopped-flow spectrofluorometer (Applied Photophysics, Leatherhead, UK) with an instrumental dead time of ∼1.5 ms and a 5000 points/s sampling rate. The ANTS excitation wavelength was 352 nm, and the emitted light was recorded above 450 nm using a high pass filter (Applied Photophysics). Each LUV sample was incubated at 25 °C in the dark for at least 10 min before the quench rate was measured. The gramicidin channel activity was quantified by first measuring the fluorescence in the absence of a quencher (Tl⁺) and then measuring the time course of fluorescence quench when mixing the LUVs with the Tl⁺-containing quench solution. Due to the unavoidable variation in LUV volumes (and surface areas and surface densities of conducting channels), the time course of fluorescence quench cannot be described by single exponential decays. To analyze the quench traces, we therefore described the time course using a so-called stretched exponential,⁵⁷ which is an efficient way to describe the sum of exponential decays with time constants and weights that reflects the distribution of vesicle sizes and the number of conducting channels in the vesicle membrane:

7

where F(t) denotes the ANTS fluorescence intensity of at time t, F(0) and F(∞) are the initial and final fluorescence values, respectively, β (0 < β ≤ 1) accounts for the dispersity of the vesicle population, and τ₀ is a parameter with unit of time. F(0), F(∞), β, and τ₀ were determined from a nonlinear least squares fit of eq 7 to the first 200 ms of the quench curve, and the quench rate was defined as⁵⁵

8

evaluated at t = 2 ms. The drug-induced changes in the relative rate (R_Drug/R_Cntrl) was defined as:

9

where the subscripts “Cntrl” and “Drug” denote the rates in the absence and presence of the drug.

Glossary

Abbreviations Used

MD

molecular dynamics

CG

coarse-grained

AA

all-atom

PMF

potential of mean force

REUS

replica-exchange umbrella sampling

DC_18:1PC

1,2-dioleoyl-sn-glycero-3-phosphocholine

DC_20:1PC

1,2-dieicosenoyl-sn-glycero-3-phosphocholine

DC_22:1PC

1,2-dierucoyl-sn-glycero-3-phosphocholine

C12E6

hexaethylene glycol monododecyl ether

FC12

dodecylphosphocholine

LUVs

large unilamellar vesicles

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jmedchem.0c00958.

• Supplementary methods providing details on gA CG development, simulation setup, and estimation of the changes in bilayer deformation energy; 12 additional figures; and four tables (PDF)

• Molecular formula SMILE strings for the tested compounds is also provided (CSV)

Author Contributions

D.S, W.F.D.B., and H.I.I. designed the simulations; D.S performed and analyzed the simulations; T.A.P. and O.S.A. designed and performed the experiments; D.S, W.F.D.B., T.A.P., O.S.A., M.H., S.H., F.Z, F.C.L., and H.I.I. wrote the manuscript.

The authors declare no competing financial interest.