Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 29;124(42):9420–9427. doi: 10.1021/acs.jpcb.0c08126

Observation of Ultrafast Coherence Transfer and Degenerate States with Polarization-Controlled Two-Dimensional Electronic Spectroscopy

Andy S Sardjan †, Floris P Westerman †, Jennifer P Ogilvie ‡, Thomas L C Jansen †,*
PMCID: PMC7586392  PMID: 32990439

Abstract

graphic file with name jp0c08126_0009.jpg

Optical spectroscopy is a powerful tool to interrogate quantum states of matter. We present simulation results for the cross-polarized two-dimensional electronic spectra of the light-harvesting system LH2 of purple bacteria. We identify a spectral feature on the diagonal, which we assign to ultrafast coherence transfer between degenerate states. The implication for the interpretation of previous experiments on different systems and the potential use of this feature are discussed. In particular, we foresee that this kind of feature will be useful for identifying mixed degenerate states and for identifying the origin of symmetry breaking disorder in systems like LH2. Furthermore, this may help identify both vibrational and electronic states in biological systems such as proteins and solid-state materials such as hybrid perovskites.

Introduction

Coherent multidimensional spectroscopies (CMDS) are powerful tools to unravel optical, structural, and dynamical properties of matter.1−8 Examples include the determination of protein structures,9 unraveling the tumbling motion of organic cations in hybrid perovskites,10 and the determination of relaxation pathways in natural light-harvesting systems.11−17 Since the early development of CMDS techniques, it was realized that polarization control provides a crucial handle to suppress unwanted signals,18,19 highlight specific properties,20−22 and simplify the interpretation of spectra.23 One of the polarization schemes proposed was the cross-polarized sequence applicable in two-dimensional infrared (2DIR)20 and two-dimensional electronic spectroscopy (2DES).24 This technique was designed to eliminate diagonal peaks and expose the cross-peaks needed for determining structure. Despite several successes,20,24−28 the cross-polarized sequence has received limited attention due to the difficulty of interpreting the resulting spectra and the inherent low intensity of the signals. Here, we will simulate the cross-polarized 2DES spectra for the light-harvesting complex LH2 and demonstrate that the spectra contain a persistent feature originating from ultrafast coherence transfer, which can be used as a signature of mixed degenerate states in the system. That is, degenerate states involving the same chromophores will be visible, while accidental degenerate states will not give rise to the observed signature.

The cross-polarization scheme illustrated in Figure 1 was originally demonstrated to suppress the 2DIR signal of isolated vibrations in isotropic media.20 This also implies that the individual ground-state bleach, stimulated emission, and excited-state absorption signals are suppressed for an isolated vibrational or electronic state. If the transition dipole of the transition is further fixed in space, the suppression is perfect, resulting in zero 2DIR/ES signal from isolated states. Still, weak diagonal ground-state bleach signals were observed in experiments and simulations.26 As stated above, we will here demonstrate that such signals can arise due to ultrafast coherence transfer.

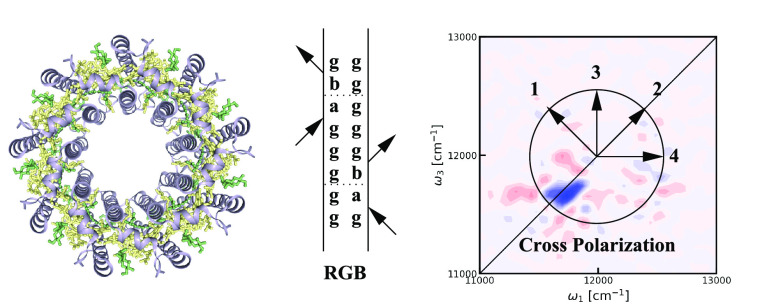
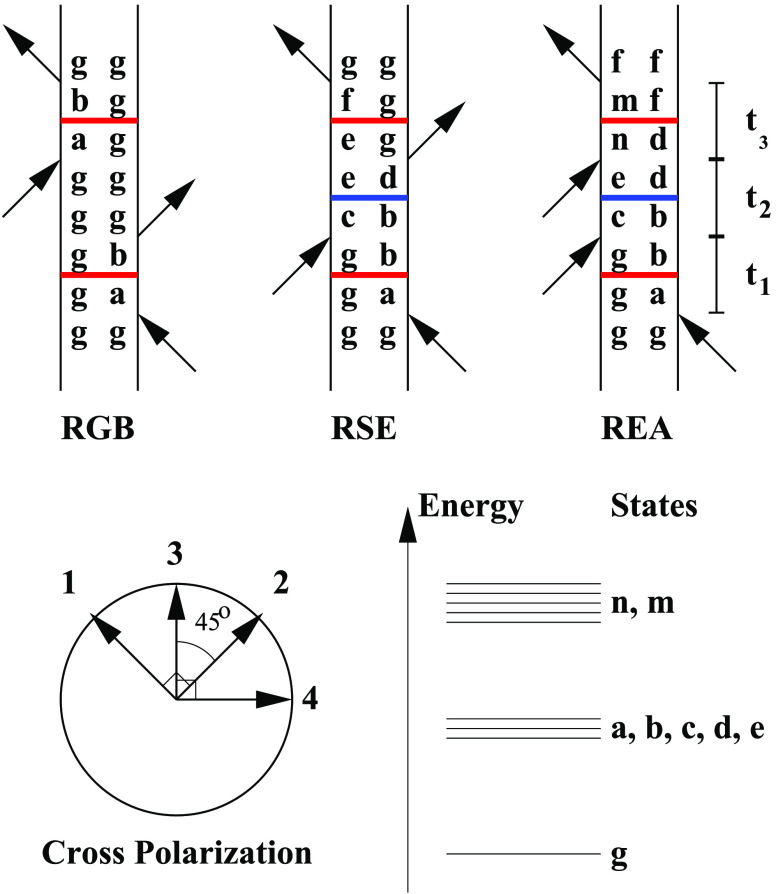
Figure 1.

Figure 1

Open in a new tab

Top: illustration of the rephasing ground-state bleach (RGB), rephasing stimulated emission (RSE), and rephasing excited-state absorption (REA) double-sided Feynman diagrams. The letter g signifies the ground state, letters a–e represent different single excited states, and the letters n and m represent double excited states. The two coherence times are labeled t1 and t3, while the population time is labeled t2. The change of letter during these times illustrates the possibility for the quantum state to change. The horizontal blue lines indicate potential population transfer, while horizontal red lines indicate potential coherence transfer. Bottom left: the angles between the four polarization vectors in the cross-polarization experiment is illustrated. The arrows show the polarization of each collinear beam with the time order given by the added numbers. Bottom right: labeling of the different energy levels is illustrated.

Shortly after the first coherent two-dimensional spectra7,29 were published, ultrafast coherence transfer was reported.30 This was followed up by a few reports for different two-dimensional techniques.31−33 The process of coherence transfer is illustrated in the double-sided Feynman diagrams in Figure 1. During the coherence times (t1 and t3) the system is in a coherence between two states separated by an energy comparable to the energy of the laser photons. While a coherence may initially be generated between, for example, the ground state and the state a, the process of coherence transfer arising from the bath induced mixing of quantum states in the system may lead to a coherence between the ground state and the state b. During the population time, both coherence transfer and population transfer may take place. The coherence times are often quite short, suppressing coherence transfer during these time delays. Therefore, coherence transfer pathways are often neglected in the modeling and interpretation of two-dimensional spectra.34

In the remainder of this paper, we will first describe the methods used to simulate the two-dimensional electronic spectra of the LH2 system. Then we will present the results for different polarization directions and population times and analyze the origin of the spectral features. Finally, we will draw our conclusions.

Methods

The LH2 system was treated by considering each of the 27 bacteriochlorophyll molecules as a two-level electronic system representing the ground and the Qy state of each molecule. The structure of the system was taken from the protein database (pdb) structure named 1kzu.35 The two-level systems were coupled using the transition-dipole coupling scheme. This allows the system to be described by a time-dependent Frenkel exciton Hamiltonian

graphic file with name jp0c08126_m001.jpg 1

Here, i and j label the 27 bacteriochlorophylls, bi† and bi are the Paulionic creation and annihilation operators, and E⃗(t) is the external electric field. The time-dependent energy gap for each molecule is given by ϵi(t), while the transition-dipole moment vector is μi. The coupling between different molecules is given by Jij. A transition dipole strength was set to 5.001 D, and this transition dipole is located on the magnesium atom and directed from the nitrogen denoted NB in the pdb structure to the nitrogen denoted ND in the pdb structure. The structure and resulting transition dipoles and couplings were assumed fixed throughout the simulations. The chromophores in LH2 are arranged in two rings. One ring contains 18 bacteriochlorophyll molecules and is termed B850 for its absorption at 850 nm. The other ring of nine bacteriochlorophyll molecules absorbs light at 800 nm and is termed B800.

The average energy of the B850 chromophores was set to 12255 cm–1 while the energy of the B800 chromophores was set to 12495 cm–1. The dynamic disorder was modeled with overdamped Brownian motion with a standard deviation of the fluctuation of 320 cm–1 for the B850 chromophores and 141 cm–1 for the B800 chromophores. For both types of chromophores, the correlation time was set to 150 fs. These parameters are slightly adjusted for better agreement with the linear absorption as compared to the values used previously.36 The coupling was obtained by using the transition dipole coupling model. In this way, a 600 ps long trajectory of the Hamiltonian is created where the off-diagonal elements are constant as the location and orientation of the chromophores are fixed as defined by the pdb structure. The diagonal elements, on the other hand, are fluctuating, reflecting the effect of the bath dynamics on the excitation frequencies of the individual chromophores. The python script used to generate the Hamiltonian is available on github.37

The 2DES spectra were calculated by using the Numerical Integration of the Schrödinger Equation (NISE) scheme,38,39 which essentially uses the classical path approximation to calculate the four-point transition dipole response functions governing the 2DES signal. For the present simulations an improved implementation was done explicitly by using coupled two-level systems instead of three-level systems with large anharmonicity effectively moving overtone peaks out of the observation window. In this method, the quantum system is propagated by solving the time-dependent Schrödinger equation for short (3 fs) time intervals assuming that the Hamiltonian, including the effect of the bath fluctuations, can be considered constant during each interval. This procedure accounts for nonadiabatic transitions during all time delays and therefore includes both population transfer and coherence transfer processes as driven by the bath fluctuations. The most important approximation of this scheme is that the bath is independent of the system’s degrees of freedom, and a detailed balance is not recovered.40 For the spectral properties studied here this limitation is not important.

Furthermore, the code was parallelized by using a hybrid MPI and OpenMP approach. The calculation can be split up in large, independent chunks of work: different starting positions for averaging along the trajectory as well as the 21 different box polarizations21 for each starting position. By use of MPI, each of these chunks is distributed to different nodes. Each chunk of work consists of long-running loops iterating over t1; these loops were parallelized by using OpenMP to make use of the multiple cores in a node. In essence, the time-dependent Hamiltonian trajectory is used to calculate the response function through propagating the electronic wave function from numerous starting points along the trajectory and evaluating the average. More details are provided in recent reviews.2,41 The calculations were performed by using the same setting as in our previous study of F-2DES and 2DES with parallel polarization.36 The most important simulation details are summarized in the following. The coherence times (t1 and t3) were varied from 0 to 192 fs in 3 fs steps. The waiting times were varied from 0 fs to 2 ps. A 300 fs exponential apodization function was used to suppress numerical noise. The spectral were calculated by averaging over 3998 realizations of the disorder in the diagonal energies. These realizations were equally spaced along the generated Hamiltonian trajectory.

Results and Discussion

The calculated 2DES spectra at zero waiting time for the parallel, perpendicular, and cross-polarization are shown in Figure 2. For the parallel and perpendicular polarization clear bleach signals are observed at the diagonal around 11700 cm–1 (the B850 band) and around 12500 cm–1 (the B800 band). Above the diagonal B850 band a clear excited-state absorption feature is observed. No obvious cross-peaks are observed between the two bands. These general trends are in good agreement with both previous simulations and experiments. The biggest difference between the parallel and perpendicular polarization spectra is that the intensity of the parallel spectrum is about 3 times larger than that of the perpendicular one. This is not visible in Figure 2 due to the individual scaling of the contour lines. The cross-polarization spectrum is very different. The intensity is about 50 times lower, which also results in a worse signal-to-noise ratio. The spectrum consists of three peaks all located in the B850 region. No clear peaks are observed in the B800 region. The interpretation of the cross-polarization spectrum is complex, but essentially this choice of polarization is thought to eliminate all diagonal peaks, leaving only cross-peaks in the spectra. As the B850 band essentially originates from 18 coupled chromophores, the observed peaks should consist of cross-peaks between the resulting collective excitations. In a simplified manner, the spectrum can be seen as two peak pairs: one at the position of the diagonal peak of the parallel spectrum and another peak pair at the position of the excited-state absorption peak. This kind of structure arises as the peaks are dominated by coherent excitations of collective excited states26 which result in peaks that are expected to acquire a complex phase with waiting time determined by the energy difference between the involved states. In other words, we expect that these peaks are oscillating signatures of electronic coherences between the collective excited states in the B850 band. As the excitations in the B800 band are much more localized,40,42 it is not surprising that peaks in that spectral region are too weak to be observed.

Figure 2.

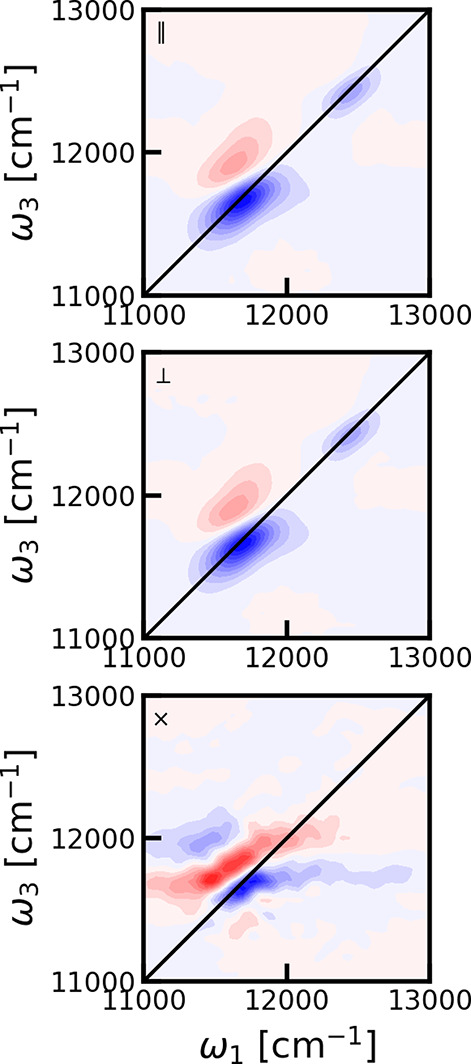
Figure 2

Open in a new tab

2DES spectra for LH2 at waiting time zero for parallel (||, top), perpendicular (⊥, middle), and cross (×, bottom) polarization. Contour lines as plotted at 10% levels of the maximum of the individual 2DES spectrum. Red contours represent the absorption signal, while blue contours represent bleach.

The cross-polarization 2DES spectra were calculated for different waiting times. In Figure 3 the spectra are shown for representative choices of these. We observe that the peak intensity rapidly decreases with waiting time, and from around 72 fs the spectrum is dominated by a single sharp diagonal bleach feature. This bleach peak is very persistent and is even clearly visible above the numerical noise level after 2 ps. The observation of this persistent constant amplitude peak was unexpected. In the papers, where this polarization configuration was first proposed, it was found that diagonal peaks should be eliminated.20 From symmetry considerations, as worked out in detail in refs (20) and (21), the signal from individual chromophores should completely vanish and no ground-state bleach signal should be present, at least as long as the identity of the excited states was preserved during the coherence times. We would, therefore, expect that the signals should oscillate and rapidly decay as they should originate from stimulated emission or excited-state absorption diagrams involving electronic coherences. The same data are shown in Figure 4 where the data are normalized for each individual waiting time. This reveals that there is no significant diagonal peak at the B800 peak position.

Figure 3.

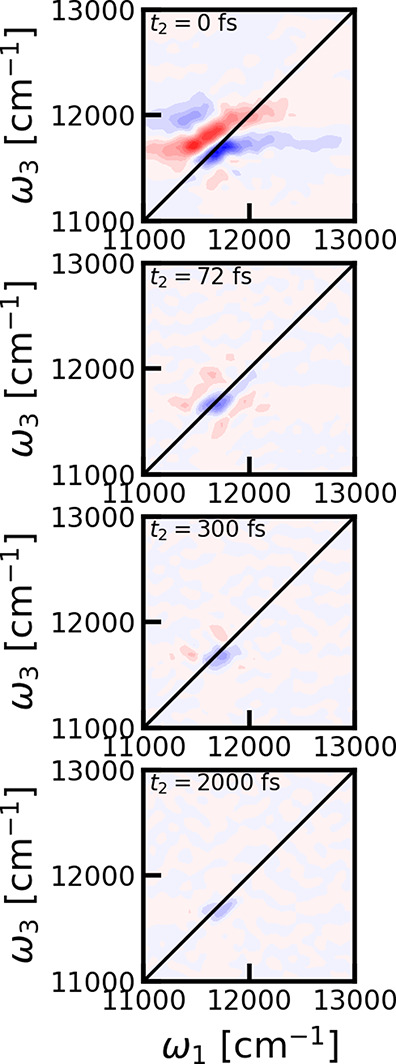
Figure 3

Open in a new tab

Cross-polarized 2DES spectra for LH2 for different waiting times. From top to bottom: 0, 72, 300, and 2000 fs. Contour lines as plotted at 10% levels of the maximum of the 2DES spectrum at 0 fs waiting time.

Figure 4.

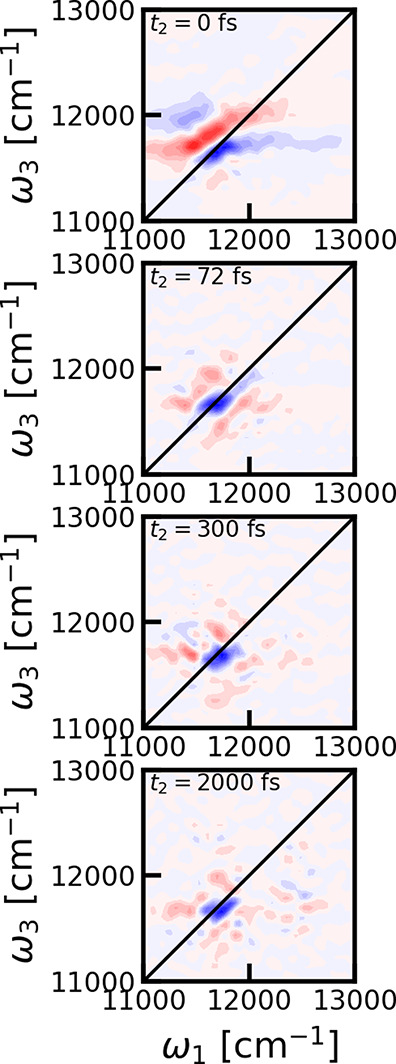
Figure 4

Open in a new tab

Cross-polarized 2DES spectra for LH2 for different waiting times. From top to bottom: 0, 72, 300, and 2000 fs (same as Figure 3). Contour lines as plotted at 10% levels of the maximum of the 2DES spectrum for each individual waiting time.

The origin of the persistent peak was analyzed by separating the 2DES cross-polarized spectrum at 300 fs in the ground-state bleach, stimulated emission, and excited-state contributions as shown in Figure 5. Interestingly, the stimulated emission signal is not distinguishable from the numerical noise, while the excited-state absorption has a small absorptive contribution at the location of the persistent peak feature. The strongest signal is seen in the ground-state bleach contribution, which was expected to be efficiently suppressed by the cross-polarization scheme. We did find that stimulated emission contributes to the signal at shorter times; however, that signal is dominated by short-lived rapidly oscillating electronic coherences between the B800 and B850 states. The absence of a stimulated emission peak rules out a simple interpretation that the peak arises from an electronic coherence during the population time between two degenerate states, whose energies are correlated on a 300 fs time scale. The ground-state bleach signal at 300 fs is round, and any frequency memory has been lost during the population time. It is therefore expected that no further dynamics will take place and this signal will persist, decaying with the 1 ns lifetime43 of the electronic excitation.

Figure 5.

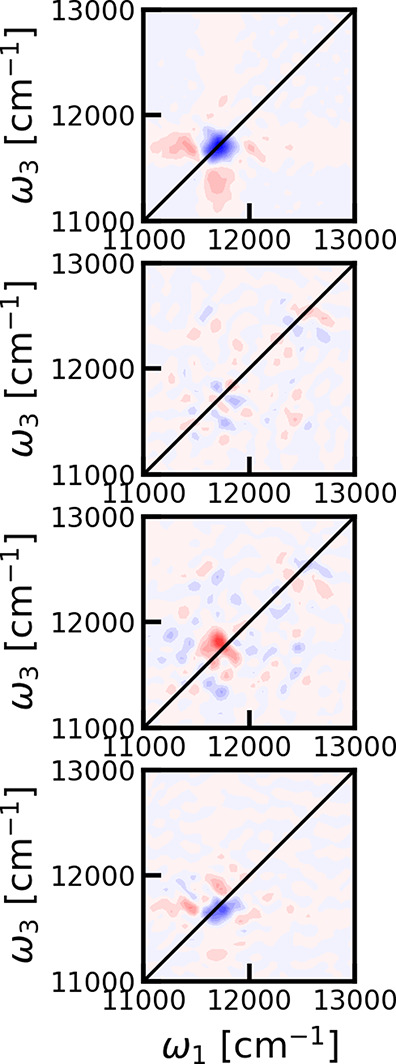
Figure 5

Open in a new tab

Decomposition of the two-dimensional cross-polarization spectra at 300 fs. From top to bottom: ground-state bleach, stimulated emission, excited-state absorption, and the full two-dimensional electronic spectrum. Contour lines as plotted at 10% levels of the maximum of the ground-state bleach spectrum.

We proceed by examining diagonal cuts in the cross-polarization 2DES spectrum at population time 300 fs in Figure 6. The cuts through the cross-polarization spectra were scaled by a factor of 50 to bring them to the same scale as the parallel polarization cuts. From the presented cuts we observed that there is indeed only a persistent signal at the B850 peak position and nothing at the B800 peak position. The peaks seen in the diagonal cuts through the parallel polarization 2DES spectra are narrower than the corresponding peaks in the calculated absorption spectrum. Still, the persistent peak in the cross-polarization spectrum is even narrower. This could suggest that states in a narrower range of energies are responsible for this feature or that an interference involving contributions with the opposite sign contributes to the signal.

Figure 6.

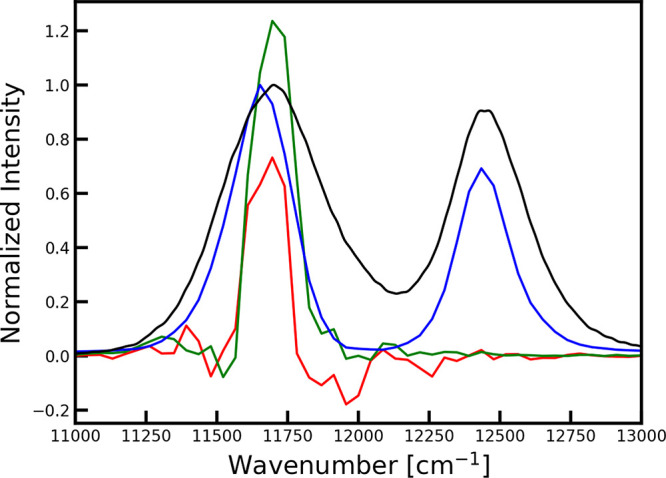
Figure 6

Open in a new tab

Comparison of diagonal cuts of the two-dimensional cross-polarization spectrum at 300 fs (red), the ground-state bleach contribution to the cross-polarization spectrum at 300 fs (green), and the two-dimensional parallel polarization spectrum at 300 fs (blue) with the linear absorption spectrum (black). The cross-polarization data are scaled by a factor of 50 compared to the parallel polarization data, while the linear absorption spectrum is scaled to match the peak height of the parallel polarization data.

The time evolution of the signals at the B850 peak position is shown in Figure 7. The normal parallel polarization 2DES signal is scaled with a factor of 0.02. The parallel polarization signal initially decays to about one-third of the initial value as excitation is redistributed over the chromophores. The ground-state bleach, stimulated emission, and excited-state absorption signal contributions to the cross-polarization signal are essentially flat over the whole time range except at very early times (<500 fs). The ground-state bleach signal is negative and about twice the magnitude of the excited-state absorption signal. The stimulated emission signal is close to zero except at very early times, where oscillations are observed due to electronic coherences. The variations after ∼300 fs in the cross-polarization signal are attributed to numerical noise resulting from the numerical average over numerous disorder realizations, which is enhanced as the cross-polarization spectra are calculated as differences between signals.21,26 The cross-polarization at the B850 diagonal point is thus about 50 times weaker than the parallel polarization signal. In previous experiments, cross-polarization signals 20 times weaker than the parallel polarization were resolved, and suppression of a parallel polarization contributions by a factor 125 has previously been reported.26

Figure 7.

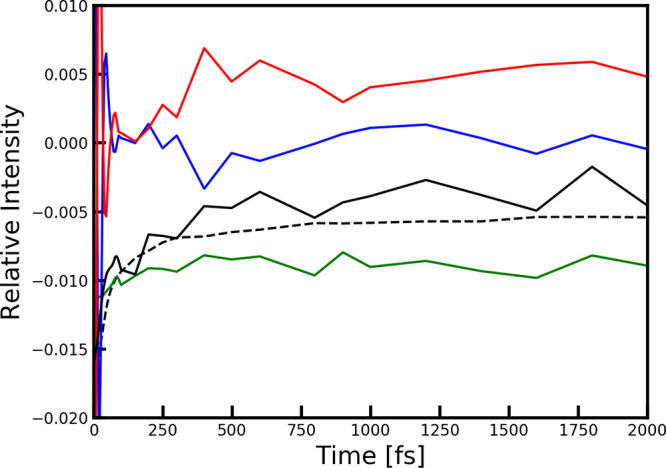
Figure 7

Open in a new tab

Comparison of the intensity of different spectral components at the position of the B850 peak (ω1 = ω3 = 12434 cm–1). In dashed black the overall intensity of the parallel polarization signal is shown scaled with a factor 0.02 for comparison. The stimulated emission contribution is shown in blue, the excited-state absorption contribution is shown in red, and the ground-state bleach contribution to the cross-polarization signal is shown in green. The full cross-polarization signal is shown in black. All intensities are plotted relative to the parallel signal intensity at waiting time zero.

The anisotropy was obtained from the simulation data near the diagonal B850 and B800 peak using the relation 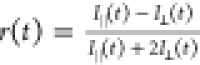Inline graphic, where I∥(t) and I⊥(t) are the intensities at population time t = t2 at the given spectral location for experiments with parallel and perpendicular laser pulse polarization, respectively. This is a measure of the loss of the orientational correlation of the transition dipole connected with the underlying transitions. In this case, the value starts close to 0.4, indicating perfect correlation and decays to 0.1 as the transition dipole is distributed over a circle in the plane of the aggregate. The experimental decay was reconstructed from the exponential decay constants reported in refs (44 and 45), demonstrating good agreement with the present simulation. The decay time of 60 fs in the B850 band is much faster than the 383 fs decay time in the B800 band, reflecting the weaker coupling between the nine chromophores in the B800 ring than that found for the more closely packed 18 chromophores in the B850 ring. The fast anisotropy decay indicates that the eigenstates in the B850 band exhibit either rapid nonadiabatic mixing or fast population transfer, and the transition dipole direction for the bright eigenstates loses orientational correlation in the plane spanned by the transition dipoles on the fast 60 fs time scale, more than 6 times faster than the same process in the B800 band. The anisotropy decay is compared with the absolute value linear response function connected with the chromophores contributing to a particular band: RBXXX(t) = |∑α=x,y,z⟨μα(t)U(t,0)PBXXXμα(0)⟩|, where μα(t) is the transition dipole moment and U(t,0) is the time evolution operator. PBXXX is a projection matrix that selects the chromophores contributing to each band. Thus, its elements are zero except on the diagonal, where they take a value of one for chromophores contributing to the B800 or B850 band. The dephasing time given by the decay of the response function essentially determines the width of the given peak in the absorption spectrum. The fast anisotropy decay observed for the B850 band means that the transition dipole moments of the B850 bright eigenstates lose their orientational identity. For ring structures like the B850 ring, it is well-known that for symmetry reasons the excited states dominating the absorption band are a set of degenerate states denoted the k = ±1 states. The transition dipoles of these two states are perpendicular to each other. The disorder in the system breaks the degeneracy slightly and efficiently mixes the two states. In the two-dimensional spectra, this takes place as a coherence transfer process during the coherence times. As the anisotropy decay and the dephasing time of the B850 states are comparable, the coherence transfer is efficient enough to scramble the transition-dipole directions during the coherence times. This is much weaker for the B800 band as the anisotropy decay is significantly slower than the dephasing time.

We can now understand why there is a persistent ground-state bleach B850 signal for the cross-polarization as the polarization is in essence scrambled by coherence transfer during the t1 and t3 time periods, which destroys the suppression of the diagonal peak. For the B800 band, the coherence transfer is too slow to produce a visible cross-polarization peak. The stimulated emission peak, on the other hand, disappears at long time delays as coherence and population transfer during the population time induce strong interference between signals from the two dominant eigenstates. The excited-state absorption signal is still nonzero at longer times, and as seen in Figure 6, roughly half of the ground-state bleach signal is canceled by the excited-state contribution.

Figure 8.

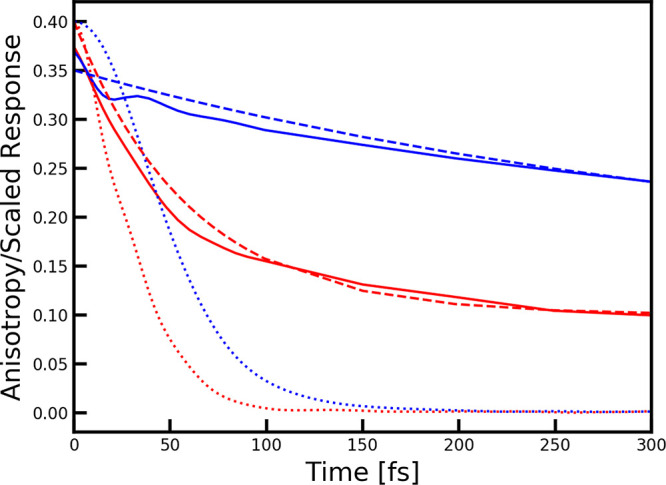
Figure 8

Open in a new tab

Comparison of the anisotropy decay as a function of waiting time extracted from the calculated 2DES spectra for LH2 at the position of the B850 peak (ω1 = 11739 cm–1 and ω3 = 11653 cm–1) (red) and the B800 peak (ω1 = ω3 = 12434 cm–1) (blue) and the scaled absolute value linear response function (dotted lines) as defined for the two types of chromophores in the text. Anisotropy decay reconstructed from the experimental 2DES data of ref (44) at the B850 (red dashed) and B800 (blue dashed) peak positions are shown for comparison.

The persistent ground-state bleach feature identified in this paper will likely be even more prominent in fluorescence detected two-dimensional electronic spectra (F-2DES)46,47 as these spectra tend to be dominated by ground-state bleach and stimulated emission signals.36,48−50 The same coherence transfer mechanism observed here is the likely explanation for the weak ground-state bleach signals in the cross-polarization experiments and theory signals observed for the Fenna–Matthews–Olson complex, where polarization was used to suppress ground-state vibrational coherences.26 When studying electronic coherences in this way, there is therefore a need to consider ground-state vibrational signals arising from coherence transfer processes.

In this study, we neglected the potential presence of strongly coupled vibrational modes. Such modes are known to contribute to electronic spectra including two-dimensional electronic spectra.51−53 Vibronic effects could potentially affect the predicted cross-polarization spectra. However, we would only expect them to affect the presence of the observed persistent peak if they break the symmetry, resulting in the mixed degenerate states.

In this study, we assumed the perfect symmetry of the LH2 system reported in the X-ray crystal structure. However, single-molecule experiments54 suggest that this symmetry is in practice broken by a C2 symmetry perturbation. Potentially, such perturbations will modify the persistent ground-state bleach feature observed in the ensemble cross-polarization two-dimensional spectra. Such experiments may thus provide a great handle on studying symmetry breaking in both LH2 and other systems, which otherwise require the use of single-molecule spectroscopy for detection.

Conclusions

In summary, we modeled the population time-resolved two-dimensional electronic spectra of the LH2 light-harvesting system using different laser polarization schemes. The calculated anisotropy decay reproduced recent experimental results very well. In the cross-polarization data, an unexpected persistent ground-state bleach feature was observed, which was assigned to coherence transfer resulting in the mixing of the two degenerate states with the strongest transition dipoles. This feature was only observed for the B850 band and not for the B800 band. This can be understood as this feature requires the mixing of the degenerate exciton states on a time scale faster or comparable to the dephasing time of the involved exciton states. The coupling between the closely packed molecules in the B850 ring is much larger than the coupling in the less densely packed B800 ring, and therefore the coherence transfer is much faster in the B850 ring as also reflected in the faster anisotropy decay.

The cross-polarization 2D spectra are more challenging to obtain due to the inherently weak signals compared to the conventional parallel and perpendicular polarization spectra. However, in the cross-polarized spectrum, the sharply defined peak enables determination of the peak position of the degenerate pair more sensitively than in the conventional polarization spectra. This sharp feature may also be very sensitive to symmetry breaking.

The feature observed here for the cross-polarization two-dimensional electronic spectra of LH2 can also be expected to be found in other systems with degenerate states as well as in two-dimensional infrared and fluorescence detected two-dimensional spectroscopies. A few examples can be found in the infrared spectra of the asymmetric NH bend of alkylammonium ions (such as methylammonium), the amide I spectrum of α-helices,55 the electronic spectra of thiangulene derivatives,56 and the spectra of natural57 and artificial58 tubular aggregates. Furthermore, the observed feature may explain weak ground-state bleach features reported in the cross-polarization two-dimensional electronic spectra of the Fenna–Matthews–Olson complex.26

Acknowledgments

J.P.O. gratefully acknowledges the support of the National Science Foundation through Grant #PHY -1914608. T.L.C.J., F.P.W., and A.S.S. thank the Center for Information Technology of the University of Groningen for their support and for providing access to the Peregrine high performance computing cluster. Ariba Javed and Vivek Tiwari are kindly acknowledged for fruitful discussions.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Yoshitaka Tanimura Festschrift”.

References

  1. Tanimura Y.; Mukamel S. Two-dimensional femtosecond vibrational spectroscopy of liquids. J. Chem. Phys. 1993, 99, 9496. 10.1063/1.465484. [DOI] [Google Scholar]
  2. Jansen T. L. C.; Knoester J. Waiting Time Dynamics in Two-Dimensional Infrared Spectroscopy. Acc. Chem. Res. 2009, 42, 1405–1411. 10.1021/ar900025a. [DOI] [PubMed] [Google Scholar]
  3. Cho M. Coherent two-dimensional optical spectroscopy. Chem. Rev. 2008, 108, 1331. 10.1021/cr078377b. [DOI] [PubMed] [Google Scholar]
  4. Jonas D. M. Two-dimensional femtosecond spectroscopy. Annu. Rev. Phys. Chem. 2003, 54, 425. 10.1146/annurev.physchem.54.011002.103907. [DOI] [PubMed] [Google Scholar]
  5. Hochstrasser R. M. Two-dimensional spectroscopy at infrared and optical frequencies. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 14190. 10.1073/pnas.0704079104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wright J. C. Multiresonant Coherent Multidimensional Spectroscopy. Annu. Rev. Phys. Chem. 2011, 62, 209–230. 10.1146/annurev-physchem-032210-103551. [DOI] [PubMed] [Google Scholar]
  7. Hybl J. D.; Albrecht A. W.; Faeder S. M. G.; Jonas D. M. Two-Dimensional Electronic Spectroscopy. Chem. Phys. Lett. 1998, 297, 307–313. 10.1016/S0009-2614(98)01140-3. [DOI] [Google Scholar]
  8. Hamm P.; Lim M.; DeGrado W. F.; Hochstrasser R. M. The two-dimensional IR nonlinear spectroscopy of a cyclic penta-peptide in relation to its three-dimensional structure. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 2036–2041. 10.1073/pnas.96.5.2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Manor J.; Mukherjee P.; Lin Y.-S.; Leonov H.; Skinner J. L.; Zanni M. T.; Arkin I. T. Gating Mechanism of the Influenza A M2 Channel Revealed by 1D and 2D IR Spectroscopies. Structure 2009, 17, 247–254. 10.1016/j.str.2008.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bakulin A. A.; Selig O.; Bakker H. J.; Rezus Y.; Müller C.; Lovrincic R.; Sun Z.; Chen Z.; Walsh A.; Frost J.; et al. Real-Time Observation of Organic Cation Reorientation in Methylammonium Lead Iodide Perovskites. J. Phys. Chem. Lett. 2015, 6, 3663–3669. 10.1021/acs.jpclett.5b01555. [DOI] [PubMed] [Google Scholar]
  11. Brixner T.; Stenger J.; Vaswani H. M.; Cho M.; Blankenship R. E.; Fleming G. R. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 2005, 434, 625. 10.1038/nature03429. [DOI] [PubMed] [Google Scholar]
  12. Collini E.; Wong C. Y.; Wilk K. E.; Curmi P. M. G.; Brumer P.; Scholes G. D. Coherently Wired Light-Harvesting in Photosynthetic Marine Algae at Ambiant Temperature. Nature 2010, 463, 644. 10.1038/nature08811. [DOI] [PubMed] [Google Scholar]
  13. Dostál J.; Mančal T.; Augulis R.; Vácha F.; Pšenčik J.; Zigmantas D. Two-Dimensional Electronic Spectroscopy Reveals Ultrafast Energy Diffusion in Chlorosomes. J. Am. Chem. Soc. 2012, 134, 11611–11617. 10.1021/ja3025627. [DOI] [PubMed] [Google Scholar]
  14. Lewis K. L. M.; Ogilvie J. P. Probing Photosynthetic Energy and Charge Transfer with Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2012, 3, 503–510. 10.1021/jz201592v. [DOI] [PubMed] [Google Scholar]
  15. Wells K. L.; Lambrev P. H.; Zhang Z.; Garab G.; Tan H.-S. Pathways of energy transfer in LHCII revealed by room-temperature 2D electronic spectroscopy. Phys. Chem. Chem. Phys. 2014, 16, 11640–11646. 10.1039/C4CP00876F. [DOI] [PubMed] [Google Scholar]
  16. Ferretti M.; Hendrikx R.; Romero E.; Southall J.; Cogdell R. J.; Novoderezhkin V. I.; Scholes G. D.; van Grondelle R. Dark States in the Light-Harvesting complex 2 Revealed by Two-dimensional Electronic Spectroscopy. Sci. Rep. 2016, 6, 20834. 10.1038/srep20834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Do T. N.; Huerta-Viga A.; Akhtar P.; Nguyen H. L.; Nowakowski P. J.; Khyasudeen M. F.; Lambrev P. H.; Tan H.-S. Revealing the excitation energy transfer network of Light-Harvesting Complex II by a phenomenological analysis of two-dimensional electronic spectra at 77 K. J. Chem. Phys. 2019, 151, 205101. 10.1063/1.5125744. [DOI] [PubMed] [Google Scholar]
  18. Jansen T. L. C.; Snijders J. G.; Duppen K. Interaction induced effects in the nonlinear Raman response of liquid CS2: a finite field nonequilibrium molecular dynamics approach. J. Chem. Phys. 2001, 114, 10910. 10.1063/1.1374959. [DOI] [Google Scholar]
  19. Kubarych K.; Milne C. J.; Miller R. J. D. Heterodyne detected fifth-order Raman response if liquid CS2:’Dutch Cross’ polarization. Chem. Phys. Lett. 2003, 369, 635. 10.1016/S0009-2614(03)00039-3. [DOI] [Google Scholar]
  20. Zanni M. T.; Ge N.-H.; Kim Y. S.; Hochstrasser R. M. Two-dimensional IR spectroscopy can be designed to eliminate the diagonal peaks and expose only the crosspeaks needed for structure determination. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 11265. 10.1073/pnas.201412998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hochstrasser R. M. Two-Dimensional IR-Spectroscopy: Polarization Anisotropy Effects. Chem. Phys. 2001, 266, 273–284. 10.1016/S0301-0104(01)00232-4. [DOI] [Google Scholar]
  22. Ham S.; Hahn S.; Lee C.; Kim T.-K.; Kwak K.; Cho M. Amide I modes of alpha-helical polypeptide in liquid water: Conformational fluctuation, phase correlation and linear and nonlinear vibrational spectra. J. Phys. Chem. B 2004, 108, 9333. 10.1021/jp048678e. [DOI] [Google Scholar]
  23. Tokmakoff A. Orientational correlation functions and polarization selectivity for nonlinear spectroscopy of isotropic media. II. Fifth order. J. Chem. Phys. 1996, 105, 13. 10.1063/1.471859. [DOI] [Google Scholar]
  24. Schlau-Cohen G. S.; Ishizaki A.; Calhoun T. R.; Ginsberg N. S.; Ballottari M.; Bassi R.; Fleming G. R. Elucidation of the timescales and origins of quantum electronic coherence in LHCII. Nat. Chem. 2012, 4, 389–395. 10.1038/nchem.1303. [DOI] [PubMed] [Google Scholar]
  25. Westenhoff S.; Palecek D.; Edlund P.; Smith P.; Zigmantas D. Coherent Picosecond Exciton Dynamics in a Photosynthetic Reaction Center. J. Am. Chem. Soc. 2012, 134, 16484–16487. 10.1021/ja3065478. [DOI] [PubMed] [Google Scholar]
  26. Thyrhaug E.; Tempelaar R.; Alcocer M. J. P.; Žídek K.; Bína D.; Knoester J.; Jansen T. L. C.; Zigmantas D. Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex. Nat. Chem. 2018, 10, 780–786. 10.1038/s41557-018-0060-5. [DOI] [PubMed] [Google Scholar]
  27. Maekawa H.; Formaggio F.; Toniolo C.; Ge N. H. Onset of 310-helical secondary structure in Aib Oligopeptides probed by coherent 2D IR spectroscopy. J. Am. Chem. Soc. 2008, 130, 6556. 10.1021/ja8007165. [DOI] [PubMed] [Google Scholar]
  28. Sengupta N.; Maekawa H.; Zhuang W.; Toniolo C.; Mukamel S.; Tobias D. J.; Ge N. H. Sensitivity of 2D IR Spectra to Peptide Helicity: A Concerted Experimental and Simulation Study of an Octapeptide. J. Phys. Chem. B 2009, 113, 12037–12049. 10.1021/jp901504r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hamm P.; Lim M. H.; Hochstrasser R. M. Structure of the Amide I Band of Peptides Measured by Femtosecond Nonlinear-Infrared Spectroscopy. J. Phys. Chem. B 1998, 102, 6123–6138. 10.1021/jp9813286. [DOI] [Google Scholar]
  30. Khalil M.; Demirdöven N.; Tokmakoff A. Vibrational coherence transfer characterized with Fourier-transform 2D IR spectroscopy. J. Chem. Phys. 2004, 121, 362. 10.1063/1.1756870. [DOI] [PubMed] [Google Scholar]
  31. Nee M. J.; Baiz C. R.; Anna J. M.; McCanne R.; Kubarych K. J. Multilevel vibrational coherence transfer and wavepacket dynamics probed with multidimensional IR spectroscopy. J. Chem. Phys. 2008, 129, 084503. 10.1063/1.2969900. [DOI] [PubMed] [Google Scholar]
  32. Baiz C. R.; Kubarych K. J.; Geva E. Molecular Theory and Simulation of Coherence Transfer in Metal Carbonyls and Its Signature on Multidimensional Infrared Spectra. J. Phys. Chem. B 2011, 115, 5322–5339. 10.1021/jp109357d. [DOI] [PubMed] [Google Scholar]
  33. Pakoulev A. V.; Rickard M. A.; Mathew N. A.; Kornau K. M.; Wright J. C. Frequency-Domain Time-Resolved Four Wave Mixing Spectroscopy of Vibrational Coherence Transfer with Single-Color Excitation. J. Phys. Chem. A 2008, 112, 6320–6329. 10.1021/jp711014h. [DOI] [PubMed] [Google Scholar]
  34. Read E. L.; Engel G. S.; Calhoun T. R.; Mancal T.; Ahn T. K.; Blankenship R. E.; Fleming G. R. Cross-peak-specific two-dimensional electronic spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 14203–14208. 10.1073/pnas.0701201104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Prince S.; Papiz M.; Freer A.; McDermott G.; Hawthornthwaite-Lawless A.; Cogdell R.; Isaacs N. Apoprotein structure in the LH2 complex from Rhodopseudomonas acidophila strain 10050: modular assembly and protein pigment interactions. J. Mol. Biol. 1997, 268, 412–423. 10.1006/jmbi.1997.0966. [DOI] [PubMed] [Google Scholar]
  36. Kunsel T.; Tiwari V.; Matutes Y. A.; Gardiner A. T.; Cogdell R. J.; Ogilvie J. P.; Jansen T. L. C. Simulating Fluorescence-Detected Two-Dimensional Electronic Spectroscopy of Multichromophoric Systems. J. Phys. Chem. B 2019, 123, 394–406. 10.1021/acs.jpcb.8b10176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. https://github.com/lacourjansenlab/LH2_Hamiltonian.
  38. https://github.com/GHlacour/NISE_2017.
  39. Liang C.; Jansen T. L. C. An Efficient N3-Scaling Propagation Scheme for Simulating Two-Dimensional Infrared and Visible Spectra. J. Chem. Theory Comput. 2012, 8, 1706–1713. 10.1021/ct300045c. [DOI] [PubMed] [Google Scholar]
  40. van der Vegte C. P.; Prajapati J. D.; Kleinekathöfer U.; Knoester J.; Jansen T. L. C. Atomistic Modeling of Two-Dimensional Electronic Spectra and Excited-State Dynamics for a Light Harvesting 2 Complex. J. Phys. Chem. B 2015, 119, 1302–1313. 10.1021/jp509247p. [DOI] [PubMed] [Google Scholar]
  41. Jansen T. L. C.; Saito S.; Jeon J.; Cho M. Theory of coherent two-dimensional vibrational spectroscopy. J. Chem. Phys. 2019, 150, 100901. 10.1063/1.5083966. [DOI] [PubMed] [Google Scholar]
  42. Trinkunas G.; Herek J. L.; Polívka T.; Sundström V.; Pullerits T. Exciton Delocalization Probed by Excitation Annihilation in the Light-Harvesting Antenna LH2. Phys. Rev. Lett. 2001, 86, 4167–4170. 10.1103/PhysRevLett.86.4167. [DOI] [PubMed] [Google Scholar]
  43. Monshouwer R.; Abrahamsson M.; van Mourik F.; van Grondelle R. Superradiance and Exciton Delocalization in Bacterial Photosynthetic Light-Harvesting Systems. J. Phys. Chem. B 1997, 101, 7241–7248. 10.1021/jp963377t. [DOI] [Google Scholar]
  44. Massey S. C.; Ting P.-C.; Yeh S.-H.; Dahlberg P. D.; Sohail S. H.; Allodi M. A.; Martin E. C.; Kais S.; Hunter C. N.; Engel G. S. Orientational Dynamics of Transition Dipoles and Exciton Relaxation in LH2 from Ultrafast Two-Dimensional Anisotropy. J. Phys. Chem. Lett. 2019, 10, 270–277. 10.1021/acs.jpclett.8b03223. [DOI] [PubMed] [Google Scholar]
  45. Jimenez R.; Dikshit S. N.; Bradforth S. E.; Fleming G. R. Electronic Excitation Transfer in the LH2 Complex ofRhodobacter sphaeroides. J. Phys. Chem. 1996, 100, 6825–6834. 10.1021/jp953074j. [DOI] [Google Scholar]
  46. Tekavec P. F.; Lott G. A.; Marcus A. H. Fluorescence-detected two-dimensional electronic coherence spectroscopy by acousto-optic phase modulation. J. Chem. Phys. 2007, 127, 214307. 10.1063/1.2800560. [DOI] [PubMed] [Google Scholar]
  47. Tiwari V.; Matutes Y. A.; Gardiner A. T.; Jansen T. L. C.; Cogdell R. J.; Ogilvie J. P. Spatially-resolved fluorescence-detected two-dimensional electronic spectroscopy probes varying excitonic structure in photosynthetic bacteria. Nat. Commun. 2018, 9, 4219. 10.1038/s41467-018-06619-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Maly P.; Mancal T. Signatures of Exciton Delocalization and Exciton-Exciton Annihilation in Fluorescence-Detected Two-Dimensional Coherent Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 5654–5659. 10.1021/acs.jpclett.8b02271. [DOI] [PubMed] [Google Scholar]
  49. Kühn O.; Mančal T.; Pullerits T. Interpreting Fluorescence Detected Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2020, 11, 838–842. 10.1021/acs.jpclett.9b03851. [DOI] [PubMed] [Google Scholar]
  50. Schröter M.; Pullerits T.; Kühn O. Using fluorescence detected two-dimensional spectroscopy to investigate initial exciton delocalization between coupled chromophores. J. Chem. Phys. 2018, 149, 114107. 10.1063/1.5046645. [DOI] [PubMed] [Google Scholar]
  51. Halpin A.; Johnson P. J. M.; Tempelaar R.; Murphy R. S.; Knoester J.; Jansen T. L. C.; Miller R. J. D. Two-Dimensional Spectroscopy of a Molecular Dimer Unveils the Effects of Vibronic Coupling on Exciton Coherences. Nat. Chem. 2014, 6, 196–201. 10.1038/nchem.1834. [DOI] [PubMed] [Google Scholar]
  52. Tiwari V.; Peters W. K.; Jonas D. M. Electronic Resonance with Anticorrelated Pigment Vibrations Drives Photosynthetic Energy Transfer Outside the Adiabatic Framework. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 1203–1208. 10.1073/pnas.1211157110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Butkus V.; Zigmantas D.; Valkunas L.; Abramavicius D. Vibrational vs. electronic coherences in 2D spectrum of molecular systems. Chem. Phys. Lett. 2012, 545, 40–43. 10.1016/j.cplett.2012.07.014. [DOI] [Google Scholar]
  54. Matsushita M.; Ketelaars M.; van Oijen A. M.; Köhler J.; Aartsma T. J.; Schmidt J. Spectrosopy on the B850 Band of Individual Light-Harvesting 2 Complexes of Rhodopsudomonas Acidophila II. Exciton States of an Elliptically Deformed Ring Aggregate. Biophys. J. 2001, 80, 1604–1614. 10.1016/S0006-3495(01)76133-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Woutersen S.; Hamm P. Time-Resolved Two-Dimensional Vibrational Spectroscopy of a Short Alpha-Helix in Water. J. Chem. Phys. 2001, 115, 7737–7743. 10.1063/1.1407842. [DOI] [Google Scholar]
  56. Haedler A. T.; Kreger K.; Issac A.; Wittmann B.; Kivala M.; Hammer N.; Köhler J.; Schmidt H.-W.; Hildner R. Long-range energy transport in single supramolecular nanofibres at room temperature. Nature 2015, 523, 196–199. 10.1038/nature14570. [DOI] [PubMed] [Google Scholar]
  57. Dostál J.; Mančal T.; Vácha F.; Pšenčík J.; Zigmantas D. Unraveling the nature of coherent beatings in chlorosomes. J. Chem. Phys. 2014, 140, 115103. 10.1063/1.4868557. [DOI] [PubMed] [Google Scholar]
  58. Milota F.; Prokhorenko V. I.; Mancal T.; von Berlepsch H.; Bixner O.; Kauffmann H. F.; Hauer J. Vibronic and Vibrational Coherences in Two-Dimensional Electronic Spectra of Supramolecular J-Aggregates. J. Phys. Chem. A 2013, 117, 6007–6014. 10.1021/jp3119605. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES