Handling missing predictor values when validating and applying a prediction model to new patients

Abstract

Missing data present challenges for development and real‐world application of clinical prediction models. While these challenges have received considerable attention in the development setting, there is only sparse research on the handling of missing data in applied settings. The main unique feature of handling missing data in these settings is that missing data methods have to be performed for a single new individual, precluding direct application of mainstay methods used during model development. Correspondingly, we propose that it is desirable to perform model validation using missing data methods that transfer to practice in single new patients. This article compares existing and new methods to account for missing data for a new individual in the context of prediction. These methods are based on (i) submodels based on observed data only, (ii) marginalization over the missing variables, or (iii) imputation based on fully conditional specification (also known as chained equations). They were compared in an internal validation setting to highlight the use of missing data methods that transfer to practice while validating a model. As a reference, they were compared to the use of multiple imputation by chained equations in a set of test patients, because this has been used in validation studies in the past. The methods were evaluated in a simulation study where performance was measured by means of optimism corrected C‐statistic and mean squared prediction error. Furthermore, they were applied in data from a large Dutch cohort of prophylactic implantable cardioverter defibrillator patients.

1. INTRODUCTION

An increasing number of prediction models are published in support of clinical decision‐making. Well‐known examples in the cardiovascular domain are the QRISK3 model (predicting risk of heart attack and stroke) ¹ and the Seattle Heart Failure ² model. Recently, several guidelines were published on how to perform and report prediction modeling, ³ , ⁴ , ⁵ generally involving (i) model development, (ii) validation, and (iii) real‐world application. Missing data are a key issue in each of these stages. Especially the handling of missing data at the time of model development has been an active research area and multiple imputation has arisen as a general‐purpose tool to account for missing data. ⁶ , ⁷ Assuming missingness at random, multiple imputation methods allow for the use of all available data (avoiding selection bias and loss of statistical power) and at the same time account for uncertainty with respect to the missing data. ⁶ , ⁸ , ⁹ While missing data during the model development stage have attracted much attention, there is a scarcity of research on how to account for missing data during validation and real‐world application of prediction models. We propose that the methods by which missing data are handled should be an integral part of prediction model development, and be transferable to any new data, be it to validation data or new individual cases.

Starting with the validation setting, prediction model validation has received considerable attention. ¹⁰ , ¹¹ , ¹² Its main goal is to provide empirical evidence of model performance beyond the data used for its development, ideally across different (but related) settings and populations. ¹³ As for prediction model development studies, validation data are usually affected by missing values. We propose that the correct way of handling missing values in validation data depends on the intended use of the to‐be‐validated model. More specifically, it depends on whether one intends to allow for missing data during model application in practice. To make the underlying rationale more clear, let us consider the use of imputation as applied independently in a set of validation data. ¹⁴ , ¹⁵ , ¹⁶ Use of this this strategy requires estimation of the necessary imputation models in the validation set, and thereby uses information that is not readily available in practice when a single new patient presents with missing values. That is, it uses information from other new patients (in the validation set) and in practice patients present individually. The main consequence is that the validation study approximates model performance for those with complete data. This could be in line with the intended use of the model, but the implied performance estimate is expected to be optimistic when allowing for missing data in real‐life application. Also, validation performance becomes a mixture of prediction model performance and a local procedure to handle missing data. If the goal is to allow for missing data in practice, one ideally assesses prediction model performance and a transferable missing data method at the same time. Here we focus on this latter goal.

When applying previously developed prediction models in new, individual patients, accounting for missing values is not straightforward. As described above, a prediction model ideally has an intergrated missing data method that can be used for new individual patients. However, in practice most models do not allow for missing data at all, or do so by means of methods that have been shown to be problematic. Examples of prediction modelsthat enforce valid values for all predictors include implementations of the classic Framingham model (eg, on mdcalc.com ¹⁷ ) and the before‐mentioned Seattle Heart Failure model. ² , ¹⁸ Alternatively, some models allow for missing data on a limited set of variables and use simple imputation procedures. For example, the well‐known QRISK3 model uses the average value from the development study for a measure of deprivation when geographical region is unknown (ie, mean imputation), it uses a conditional average based on ethnicity, age, and sex for missing values of Cholesterol/HDL ratio, blood pressure and BMI (ie, conditional mean imputation), and it uses zero imputation when the SD of the last two blood pressure readings is missing. ¹⁹ Each of these methods has been shown to have issues in the context of model development, ⁶ but there is no clear guidance on missing data problems in the model application stage.

As an example of the possible mismatch between model validation and model application in practice, QRISK3 validation removed all patients with unknown geographical region and used multiple imputation by chained equations to handle remaining missingness. ²⁰ This validation does not contain any information on those with missing region and reflects performance for otherwise complete data, while the application allows for missing predictors. We have not been able to find an example in which missing data were allowed in practice and where missing data was handled consistently between validation and application.

In this paper, we propose that validation, whether internal or external, should handle missing data in a way that only depends on the development data and is applicable when making predictions for new individual patients. Therefore, the proposal specifically relates to prediction models that intend to allow for missing data in practice. This implies the need for missing data methods that transfer to real‐life application. We consider six strategies to address missing values in individual patients when calculating a risk prediction. We compare them with the before mentioned use of (independent) multiple imputation and do so in an internal validation setting. Our work builds on methods developed and described by Marshall et al ²¹ and Janssen et al. ²² We will describe their suggestions, present new methods, and describe all methods in a realistic setting including missing data in the model development stage. The various methods will be illustrated with simulated data and data from an ongoing project on the prediction of mortality after primary therapy with an implantation cardioverter defibrillator (ICD) in heart failure patients at risk for cardiac arrhythmia and death (the DO‐IT Registry). ²³

2. METHODS

We consider prediction models with expectation of the form E[y_i| x_i] = g⁻¹(x_ib), where y_i is the outcome of patient i, x_i is the vector with values of the set of prediction variables, b is the associated vector of regression weights, and g⁻¹(⋅) is an (inverse) link‐function. We here focus on the binary case, and discuss extensions to cope with censored outcomes in the applied example section.

When applying a prediction model in individual patients, several approaches can be considered to account for missing predictor values. For ease of exposition, it helps to introduce some notation. First, define x_i as the partition (x_io, x_im) where x_io is the vector of observed predictors and x_im is the vector of unobserved predictors for individual i. Analagously, define b as the partition (b_o, b_m) where b_o and b_m represent the vectors of weights of the observed and unobserved predictor variables respectively. The model of interest can then be written as E[y_i| x_io, x_im] = g⁻¹(x_iob_o + x_imb_m) and cannot be evaluated directly due to the missing x_im. Several apporaches can be taken to arrive at predictions for a new individual conditional on his or her observed data only. The approaches described in the current paper can be separated into three groups based on the underlying theory. These will be shortly summarized in order to give a quick overview of the methods. To simplify notation, the i subscripts will be omitted in further equations.

The first group of methods aims to find a submodel of the original model based on the observed covariates only. That is, the aim is to find

$$E[y|x_o]=g^{-1}(x_o{\check{b}}_o),$$

where ${\check{b}}_o$ represent the vector of weights for a model conditional on the observed data only. Such a model is directly applicable for prediction purposes. The challenge for these submodel methods is to estimate ${\check{b}}_o$. The second group of methods integrates over the unobserved data to arrive at the predictions of interest. That is, the full model E[y| x_o, x_m] is integrated over the conditional distribution g(x_o| x_m) as follows

$$E[y|x_o]=\int E[y|x_o,x_m]g(x_m|x_o)\partial x_m,$$

where g(x_m| x_o) describes the distribution of the unobserved data given the observed data. This marginalization over the unobserved data retains the original full model coefficients. The challenge for this group of methods is to estimate g(x_m| x_o). The third group of methods aims to impute the missing covariates to enable use of the original full model, as in

$$E[y|x_o,{\widehat{x}}_m]=g^{-1}(x_o{b}_o+{\widehat{x}}_m{b}_m),$$

where ${\widehat{x}}_m$ contains the imputed values for the unobserved covariates. Here, the challenge lies in identification of the imputation models. All imputation methods that we considered were based on chained equations, also known as fully conditional specification. ⁶ , ²⁴ Imputation methods that have been shown to have issues in previous research have not been evaluated, and will not be covered in detail. These include zero imputation, mean imputation, and conditional mean imputation. ⁶

The methods to be described in the following sections are submodels directly estimated in the development data (method 1) and submodels based on the one‐step‐sweep (method 2), marginalization over the unobserved predictors (method 3) and marginalization over both the unobserved predictors and the outcome (method 4), single imputation based on chained equations (method 5) and multiple imputation based on chained equations (method 6). Each of these methods can be applied to new individual patients and therefore applies to both validation and application of prediction models. In addition, since it has been used in practice for validation purposes, the independent use of multiple imputation in the validation set (method 7) will be evaluated. Note, however, that this use of multiple imputation does not extend to new individual patients, since in that case there is not enough data to independently estimate the imputation models. Regarding terminology, development data is used to refer to the data on which the prediction model was originally developed. Training and test data were reserved for the description of internal validation procedures to describe splitting of the development data. Importantly, note that the outcome value is always missing during model application. While it is commonly available in internal and external validation settings, the information in the observed outcomes should never be used when interest is in evaluation of model performance in real‐life settings.

2.1. Submodel methods

The submodel approaches described by Janssen et al ²² refer to the development of Marshall et al. ²¹ As described above, the underlying idea is to find the necessary submodels to cope with missing data in the application setting (ie, submodels based on only the observed data). The most straightforward way to do so is to fit all necessary submodels in the development data. For a two variables example, this implies that not only the full prediction model E[y| x₁, x₂] = g⁻¹(x₁b₁ + x₂b₂) is fitted and reported, but also the submodels $E[y{x}_1]=g^{-1}(x_1{\check{b}}_1)$ and $E[y{x}_2]=g^{-1}(x_2{\check{b}}_2)$. The prediction for a new person with a missing x₂ value is then calculated using the $E[y{x}_1]=g^{-1}(x_1{\check{b}}_1)$ submodel. It is not difficult to estimate the submodels in the development data, but if the number of predictor variables (say, k) is large and all of them may be missing, then the number of submodels may be very large: with k predictor variables there are 2^k submodels. If k = 15, the number of submodels is already 32,768 and this is not rare: both the before‐mentioned QRISK3 and Seattle Heart Failure model have k ≥ 15. This direct estimation of the 2^k submodels was the first of the implemented methods. To avoid estimation of a large number of submodels, Marshall et al ²¹ suggested to approximate $\check{b}$ based on the weights b of the full prediction model and their varience‐covarience matrix only. Note that b may include an intercept and the design matrix a correspondig unity column. The approximation starts from the assumption that the full model estimate b has a multivariate normal distribution with true mean b and covariance matrix S. Hence, by simply reporting the regression coefficients b of the full prediction model and its variance‐covariance matrix S, predictions can be made for new patients, regardless of whether they are affected by missing values. Note that the estimates of b and S may also be pooled estimates over multiply imputed development data. Either way, predictions are only based on the development data and do not require imputation in the new individual. Using the above described partition of b as (b_o, b_m), and accordingly partitioning covariance matrix S as $\left(\begin{array}{cc}{S}_{\mathit{oo}}& S_{\mathit{om}}\\ S_{\mathit{mo}}& S_{\mathit{mm}}\end{array}\right)$, the conditional distribution of the weights of the nonmissing predictor variables given the weights of the missing predictor variables is normal with approximate mean calculated with the sweeping operation as ${\check{b}}_o=b_o-S_{\mathit{om}}{S}_{\mathit{mm}}^{-1}{b}_m$. For instance, again using the two variable example of full model E[y| x₁, x₂] = g⁻¹(x₁b₁ + x₂b₂), then for a patient with missing x₂, his/her prediction will be based on $E[y{x}_1]=g^{-1}(x_1{\check{b}}_1)$ with ${\check{b}}_1=b_1-S_{12}(1/S_{22})b_2$, where the right‐hand side contains full model parameter estimates and b₁ is the estimated parameter for predictor x₁, S₁₂ is the covariance between b₁ and b₂, and S₂₂ is the variance of b₂. Interestingly, for the logistic model, predictions based on these submodels correspond one‐to‐one to procedures that impute x_m with the best linear predictor based on x_o, weighted by the binomial variance in the development data. ²¹

2.2. Marginalization methods: Integrating over the unknown values

As described above, an alternative approach arises when we partition the vector of covariate values too, and estimate E[y| x_o] as follows:

$$E[y|x_o]=\int E[y|x_o,x_m]g(x_m|x_o)\partial x_m.$$

All required conditional distributions can be estimated in the development data, but with large numbers of predictor variables the number of conditional distributions would again be extremely large. For this reason, we propose to estimate the joint distribution of x = (x_o, x_m) in the development study, and to derive the required conditional distributions from this joint distribution. This is especially attractive when x follows the multivariate normal distribution with mean μ and covariance matrix ∑. When we partition μ as (μ_o, μ_m) and ∑ accordingly as $\left(\begin{array}{cc}{\mathrm{\sum }}_{\mathit{oo}}& {\mathrm{\sum }}_{\mathit{om}}\\ {\mathrm{\sum }}_{\mathit{mo}}& {\mathrm{\sum }}_{\mathit{mm}}\end{array}\right)$ then the conditional distribution g(x_m| x_o) has mean ${\mu }_m+{\mathrm{\sum }}_{\mathit{mo}}{\mathrm{\sum }}_{\mathit{oo}}^{-1}(x_o-{\mu }_o)$ and covariance ${\mathrm{\sum }}_{\mathit{mm}}-{\mathrm{\sum }}_{\mathit{mo}}{\mathrm{\sum }}_{\mathit{oo}}^{-1}{\mathrm{\sum }}_{\mathit{om}}$.

In most situations, the vector x will consist of both categorical and quantitative variables and the joint distribution will therefore almost certainly be nonnormal. We hypothesize, however, that the normal distribution is close enough to the true joint distribution. If that is the case, then the following approach will approximate E[y| x_o] to any desired degree of precision. Alternatives may involve nonparametric distributions estimated with multivariate splines ²⁵ or copula models. ²⁶ , ²⁷

The mean μ and covariance matrix ∑ can be estimated in the development data. These μ and ∑ are then used for a new person i with missing data to derive the conditional distribution g(x_im| x_io). We then draw a number of random vectors ${\stackrel{\sim }{x}}_{\mathit{im}1},\dots ,{\stackrel{\sim }{x}}_{\mathit{imj}},\dots ,{\stackrel{\sim }{x}}_{\mathit{im},\mathit{\text{ndraws}}}$from this distribution. Concatenating ${\stackrel{\sim }{x}}_{\mathit{ij}}=(x_{\mathit{io}}{\stackrel{\sim }{x}}_{\mathit{imj}})$ one may calculate $E[y_i{x}_{\mathit{io}}{\stackrel{\sim }{x}}_{\mathit{imj}}]$ and average over the n draws:

$$E[y_i|x_{\mathit{io}}]=\sum _{j=1}^{n\text{draws}}E[y|x_{\mathit{io}},{\stackrel{\sim }{x}}_{\mathit{imj}}]\frac{g({\stackrel{\sim }{x}}_{\mathit{imj}}|x_{\mathit{io}})}{{\sum }_{r=1}^{n\text{draws}}g({\stackrel{\sim }{x}}_{\mathit{imr}}|x_{\mathit{io}})}.$$

This Monte Carlo integration approximates the integral of interest over g(x_m| x_o) and was implemented as method 3. It is based on available predictor variables and the estimated normal approximation of the joint distribution of predictors in the development data. Note that integration over g(x_m| x_o) is not the same as evaluation of the full prediction model at (x_o, E[g(x_m| x_o)]).

For use of multiple imputation in model development, it has been recognized that imputation of missing x_m may also depend on y. Consequently, imputations are derived from the conditional distribution g(x_m| x_o, y). ⁶ If the parameters of this imputation model were known, the model could also be used to impute missing x_m given (x_o, y) in a new patient. This model is, however, depending on the outcome variable y which is in principal not available for a new patient. One could use the entire chained‐equations‐imputation‐model from the development data and impute y too, but here we examine the possibility to integrate out y from the imputation model. This is essentially an extension of method 3 that also integrates over the outcome. In this method, we therefore use the conditional distribution g(x_m| x_o) that is obtained by integrating out y:

$$g(x_m|x_o)=\int g(x_m|x_o,y)h(y|x_o)\partial y.$$

If y is a binary outcome this simplifies to

$$g(x_m|x_o)=g(x_m|x_o,y=1)\mathrm{h}(\mathrm{y}=1|{\mathrm{x}}_o)+g(x_m|x_o,y=0)\mathrm{h}(\mathrm{y}=0|{\mathrm{x}}_o),$$

which nicely illustrates that g(x_m| x_o) is obtained by averaging g(x_m| x_o, y) for every possible value that y may have, but weighted with the probability that y has that particular value.

Notice that h(y| x_o) is a submodel of the full prediction model and this suggests an algorithm which is a combination of methods 1 and 2. Thus, we estimate the joint distributions g(x ∣ y = 0) and g(x| y = 1) in the development data and we approximate h(y| x_o) using Marshall et al's ²¹ suggestion (as in method 1). For a new person i with missing values of covariates in the vector x_im, we first sample a number of outcomes y_i1, …, y_ij, …, y_{i, ndraws} from h(y| x_o) and given the sampled values y_ij (j = 1, …, ndraws), we sample ${\stackrel{\sim }{x}}_{\mathit{imj}}$ from g(x_im| x_io, y = y_ij), and j = 1, …, ndraws. As with method 2, the joint distribution g(x| y = y) will usually not be normal, but for the current application we approximate g(x| y = y) with the multivariate normal distribution. As above, alternatives may involve nonparametric distributions estimated with multivariate splines or copula models.

2.3. Imputation methods

As described above, the main goal is to find imputations such that one can arrive at proper predictions based on the full original model. That is, the original set of regression weights (b_o, b_m) is applied to a combination of the observed and imputed values $(x_o{\widehat{x}}_m)$ as in

$$E[y|x_o,{\widehat{x}}_m]=g^{-1}(x_o{b}_o+{\widehat{x}}_m{b}_m).$$

The mainstay method for multiple imputation during model development is multiple imputation by chained equations, also known as fully conditional specification. ⁶ , ⁸ , ²⁴ These names refer to the typical specification where each variable has its own imputation model conditional on all the other variables (ie, for the outcome given all of the x variables, for x₁ given the outcome and all other x variables, …). That is, they are fully conditioned (on all other variables) and chained in the sense that all variables are used as both predictor and outcome. The main advantage of imputation by chained equation resides in the great flexibility that is available for the specification of each of these models, which can take any form.

It has previously been suggested that these fully conditional imputation models, as developed for missing data in the development dataset, can also be used to impute missing data in new patients. ²² From a methodological viewpoint, it is perfectly valid to use the previously fitted imputation model(s) in a new patient; the prediction and imputation model are considered as a unit. Although it is theoretically possible to extract the fully conditional imputation models from the development data, common software packages do not store the estimated parameters of the imputation models (eg, packages like mice in R ⁸ ; for an overview of available free and commercial statistical software for multiple imputation see Nguyen et al ⁷ ). To the best of our knowledge, only the Amelia package in R ²⁸ (which assumes multivariate normality on the complete data) provides multiple imputation model parameters. This makes application of the imputation models to data of new patients difficult. Moreover, if the fully conditional models were available, they could not be used directly when multiple missing values are present in the new individual. This is because a fully conditional model can only be used for imputation when all predictors are known. Importantly, note that this is always the case in practice, since the outcome is always missing and is also one of the predictors in the fully conditional imputation models for any x variable.

Two separate approaches can be taken to overcome these technical aspects. First, as proposed by Janssen et al, ²² one can simply stack the new patient below the original development data, and impute all patients together. A second possibility is to fit the required fully conditional models on the imputed development data and use these models to impute missing values in the new individual. These two methods were implemented as our methods 5 and 6, respectively.

Use of the stacked imputation procedure (method 5) solves two problems. First, it does not require the imputation model parameters to be available, and second, it naturally copes with multiple missing values in the new individual. However, is also poses two new problems. First, rerunning the imputation process over the combination of the entire development data and the new patient is a considerable computational burden to arrive at a single prediction. Second, a more theoretical issue is that simultaneous imputation of the development data and the new case allows sharing of information between them, while one would prefer to separate them for validation purposes. That is, the imputation model is reestimated while it should theoretically be fixed as part of the prediction model. While this issue may only be theoretical for a single patient, the issue is clearer when predictions for an entire validation set are required: the imputation models will be highly influenced by the validation data. To cope with these issues, we propose to derive the imputed development data before stacking. In this way, the imputed sets can be stored for later use (thus avoid the computational burden of the imputation process in the development data) and the imputation models are not affected by the new individual. The latter relates to the fact that updating of the imputation models only makes use of cases with observed outcomes (outcomes of the imputation models that is), ⁶ and the new patient is thus always omitted for the necessary imputation models (ie, those for which the new individual has missing values). A further issue shortly mentioned above is that imputation models used at the time of model development are based on all variables in the analysis, including the outcome variable y. The outcome variable y is, however, missing per definition for new patients. Therefore, the chained equation approaches will automatically impute y for the new patient. This value can simply be discarded though. The most important downside of this approach is that the original development data need to be available for every new prediction (also see Box 1 for each method's requirements). Besides computational, storage, and network issues relating to the online availability of data, limitations due to privacy regulation and data sharing limitations may form the most pressing issue for many datasets.

Box 1. Specification of information that needs to be accessed for implementation of the missing data methods.

Each of the methods to handle missing data when applying a prediction model in new patients requires additional summary statistics and or data beyond the prediction model itself. This box enlists these requirements in addition to the full prediction model parameter vector b.

Data requirements.

Method

1 ‐ Estimation of all submodels: requires estimated regression coefficients for all (possibly 2^k) submodels of the prediction model of interest.

2 ‐ Submodels by means of the one‐step‐sweep: only requires the estimated regression coefficients and the variance‐covariance matrix of developed prediction model of interest.

3 ‐ Marginalize over missing x variables: requires estimated means, and their variance‐covariance matrix, for all variables in the development dataset that are used in the prediction model of interest.

4 ‐ Marginalize over missing x variables and the outcome: requirements are those for methods 2 and 3 combined, where the latter are needed conditional on the outcome.

5 ‐ Stacked multiple imputation: requires the entire development dataset.

6 ‐ Imputation by fixed chained equations: requires the vector of parameter estimates for each of the fully conditional models as derived in the development dataset, as well as the mean of each variable in the development data.

7 ‐ Independent imputation by chained equations: requires a set of test cases and can therefore not be used in case of a single new patient. This method was included for comparison in the validation setting where a set of test cases is available.

Note .

In case of missing data in the development dataset, multiple imputation can be used and pooled estimates can be derived for each of the required pieces of information using Rubin's rules (eg, pooled model parameter estimates, variable means and variance‐covariance matrices).

To avoid the need for availability of the development data, we propose to derive the fully conditional model for each variable in the multiply imputed development data (method 6). This summarizes all the required information from the development dataset for the future imputation process, and at the same time copes with the computational burden occurring with straightforward stacked imputation (since the imputation models are directly available and do not have to be re‐estimated). Additionally, no tricks are required to avoid sharing of information between development data and on or more new cases. Also, as for stacked imputation, there is great flexibility in the possible classes of models that can be used. For the current application, linear models were used for continuous variables and logistic models were used for dummy coded variables. However, many more classes are conceivable and have been used successfully in multiple imputation (eg, Poisson regression, multinomial regression, multilevel models). ⁶ Due to estimation of the full conditional models in multiply imputed development data, the models adequately reflect the available information accounting for missing data (assuming missingness at random). Imputations for a new case can be derived iteratively in a small number of iterations. Starting from imputation of the missing x variables with the marginal means as estimated in the development data, one iterates over the full conditional models as in standard chained equation procedures. A key difference though, is that the imputation models remain fixed. First, the outcome is predicted based on the observed x variables and initial imputations for missing x variables. Second, the imputation of the first missing x variable is updated based on its fully conditional model and the current state of the data, and so on over all other missing variables and repeated until convergence to the most likely imputations given the observed data (usually in <5 iterations for 10e‐6 tolerance on the predicted outcome). Note that predicted probabilities are used in the iterative process and not the most likely binary class. Also, note that this method is essentially a simplification of traditional imputation by chained equations with the stochastic components removed. Therefore, it inherits the same theoretical limitations with respect to the relatively weak theoretical underpinnings and assessment of its value will mainly have to come from empirical evidence. ²⁴

2.4. Independent multiple imputation by chained equations for sets of patients

Lastly, while not applicable in a new patient, presence of an entire validation set allows for standard multiple imputation by chained equations as commonly used during model development. As described above, this is also the way in which the QRISK3 model was validated. A key feature of this method is that is does not allow the development data to influence validation data. However, there are at least two issues. First, the imputation method applied during validation cannot be applied in practice to new patients (hence explaining the different practical solutions implemented in for instance the QRISK3). This is only of interest when only the performance for complete cases is of interest and the model is not to be applied in cases with missing data. Second, the imputation models are allowed to vary between the development and validation set, and consequently obscure performance evaluation in the validation set when transportability of the imputation procedure is of interest. Considering these issues, this method was only evaluated as a reference since it has been used in practice, but it does not satisfy our main goal under evaluation: application of a prediction model in a (possibly single) new case with missing data. If the latter is the goal of interest, we argue that it follows directly that this method should not be used for validation purposes.

2.5. Implementation requirements

The information that is required to be able to perform these different procedures varies across the methods and ranges from just the prediction model and the variance covariance matrix of its parameters to the entire development dataset. A summary of these requirements per method is available in Box 1.

3. SIMULATION

3.1. Setup

The setup of the simulation study in shown in Figure 1. To study the performance of the six methods we simulated data of N = 1000 persons with values on six predictor variables x = (x₁, x₂, …, x₆) and a binary outcome y. Values for x were sampled from the multivariate normal distribution with mean zero and variance 1 and a positive correlation of 0.3. Covariates x₂ and x₅ were dichotomized (equal or below vs above zero), and covariates x₃ and x₆ were log‐squared according to log(0.01 + x²) causing their distributions to be (left) skewed. Covariates x₁ and x₄ were not transformed. After these transformations, all continuous covariates were standardized again to have mean zero and variance 1. The binary outcome variable was modeled using a logit‐link function.

FIGURE 1.

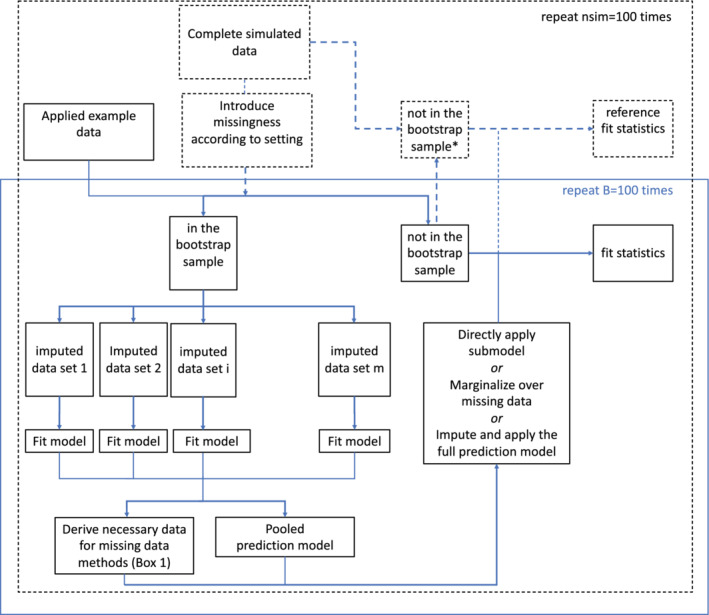
The flow of both the simulation study and applied example are shown. Parts relating only to the simulation study are shown with dashed lines. The applied example included 100 bootstrap sample evaluations. * note that within each simulation iteration these are the same cases as the out‐of‐bag sample with missing data, but with fully observed information  [Colour figure can be viewed at wileyonlinelibrary.com]

Given the sampled (transformed) values for x, the probability of outcome‐value y = 1 was calculated per person using the logit‐function log(Odds(y = 1)) = α + xβ, where β was chosen as (0.8, 0.9, 1.0, 0, 0, 0) and α such that the relative frequency of y = 1 was about 30%. Given the associated probabilities Pr(y = 1| x), values for y were sampled from the Bernoulli distribution. This simulation design led to a prediction model with a c‐statistic of about 0.8.

Next, we created missing data using eight scenarios. Scenarios one, two, three, and four use a completely random process with (i) 5% missing data for all variables, (ii) 20% missing data for all variables, (iii) 20% missing data for all variables except x₁ which had 50% missing data, and (iv) 50% missing data for all variables. Scenarios five, six, seven, and eight use a missing at random process where the missingness on variable x_j depended on the observed values of y and the other observed covariates. Percentages of missing data follow the same sequence as for the missing completely at random settings. The missingness models were logistic and details are given in Table 1.

TABLE 1.

Missingness models to create missing values in the simulated data

Scenario	% Missing Data (%)	Which Covariates	Missingness Generating Mechanism	Missingness Model
1 MCAR	5	all x	Rij∼rbinom(0.05) i = 1, , , . , N; j = 1…, 6
2 MCAR	20	all x	Rij∼rbinom(0.20) i = 1, , , . , N; j = 1…, 6
3 MCAR*	20‐50	x1	Ri1∼rbinom(0.50) Rij∼rbinom(0.20) (j = 2, …, 6) i = 1, , , . , N
4 MCAR	50	all x	Rij∼rbinom(0.50) i = 1, , , . , N; j = 1…, 6
5 MAR	5	all x	Rij∼rbinom(π ij) i = 1, , , . , N; j = 1…, 6	log(πij) = α + β1x−j + β2y α = logit(0.025); β 1 = β 2 = 0.5
6 MAR	20	all x	Rij∼rbinom(π ij) i = 1, , , . , N; j = 1…, 6	log(πij) = α + β1x−j + β2y α = logit(0.2); β1 = β2 = 0.5
7 MAR*	20‐50	x1	Ri1∼rbinom(πi1) Rij∼rbinom(${\pi }_{ij}$ (j = 2, …, 6) i = 1, , , . , N	log(πi1) = α + β1x−1 + β2y α = logit(0.5); β1 = β2 = 2.5 log(${\pi }_{ij}$) as defined in row 6
8 MAR	50	all x	Rij∼rbinom(πij) i = 1, , , . , N; j = 1…, 6	log(πij) = α + β1x−j + β2y α = logit(0.5); β1 = β2 = 0.5

Abbreviations: MAR, missing at random; MCAR, missing completely at random.

Notes: R_ij = 1 indicates that the value of covariate j in person i is missing; x^−j is the covariate vector excluding covariate j. *) Scenario 3 and 7 start from 2 and 6 respectively as implemented for all variables but x_1, and consequently add the process for scenarios 4 and 8 respectively to create missing data in x₁.

Given the simulated data (after introduction of missingness), a bootstrap sample was drawn with replacements and sample size equal to the full dataset. Standard multiple imputation by chained equations with m = 5 imputed datasets was used within the bootstrap sample. ⁹ Both the pooled full (logistic) prediction model and the necessary requirements for each missing data method (see Box 1) were derived from the imputed bootstrap data. Where appropriate, these required estimates were pooled using Rubin's rules. For instance, the estimated mean and variance‐covariance matrix of the variables requires for the one‐step‐sweep submodel method were pooled across imputations. Based on the pooled prediction model of interest and the missing data method requirements, all that needs to be estimated in the bootstrap sample is available and was applied to the out‐of‐bag (OOB) cases one by one. That is, predictions were derived for the OOB samples one by one by means of each of the missing data methods for individuals under evaluation. This one‐by‐one application was in line with the intended goal of the missing data methods: to provide methods that apply in practice to new individuals.

Prediction performance for these OOB cases was summarized by means of the c‐statistic (as a measure of discriminative performance) and root mean squared prediction error (rMSPE). Predictions based on multiple imputation methods were averaged. The c‐statistic could be obtained directly based on the predicted values and the observed outcomes. The rMSPE was obtained based on the predicted values and the known simulated event probabilities for the OOB cases. Also, we obtained “reference” performance measures based on complete OOB data (as shown in Figure 1). To do so, complete data was obtained for those in the OOB sample (from earlier steps in the data simulation), and the pooled prediction model was applied. This reference performance therefore corresponds to model performance in absence of missing data during model application, but already accounting for the decrease in prediction model performance caused by incomplete development data. Note that this reference is expected to be unachievable (some information is always unrecoverably lost due to missing data).

As a further comparison, independent multiple imputation in the OOB cases was evaluated (method 7). Performance measures were derived as for the methods applying to individual cases. Also, to illustrate the effect of including the outcome when performing missing data methods during model application, both stacked imputation (method 5) and independent multiple imputation (method 7) were evaluated without deleting the outcome in the OOB samples.

3.2. Simulation results

With respect to processing times, Figure S1 shows the distribution of maximum individual prediction times (including application of the missing data method) for each OOB sample. As expected, stacked imputation takes longest with up to 8 seconds of processing time. However, all other methods derived predictions in less than half a second; more precisely, less than 0.3 seconds for the 2^k submodels and the marginalization approaches and less than 0.06 seconds for the one‐step‐sweep and fixed chained equations. These processing times illustrate applicability in practice with respect to speed of the evaluated methods, and of those besides stacked imputation in particular.

Results for discriminative performance are shown in Figure 2 and Table S1. Mean reference performance in complete OOB samples was a C‐statistic around 0.78 to 0.79 across missing data settings. This illustrates that standard multiple imputation by chained equations handled missing data well in the model development part of the evaluation (ie, there was only a small decline in performance when the amount of missing data during model development increased). With respect to the missing data methods under evaluation, Figure 2 shows that all methods came close to model performance under complete OOB data in settings with only 5% missing data. However, discrepancies began to appear when the amount of missing data increased. The one‐step‐sweep submodel results (method 2) were clearly less discriminative than the others. On the contrary, the approaches failing to omit the outcome information (5y and 7y) showed optimistic performance. In this case, optimistic equals discrimination that seem better than as evaluated for complete cases (ie, cases without missing data). This clearly illustrates the need for omission of outcome information in the test set(s) of an interval validation procedures. Of the remaining methods, the 2^k submodels (method 1) and fixed chained equations (method 6) performed best and were closely followed by stacked multiple imputation (method 5). In most runs, they even performed better than independent multiple imputation in the test set (method 7). This is expected to relate to the relatively small sample size of the test data (OOB samples) with respect to the training data (bootstrap sample), which always has a ratio of approximately 1 to 1.7. Both marginalization methods (methods 3 and 4) had intermediate performance.

FIGURE 2.

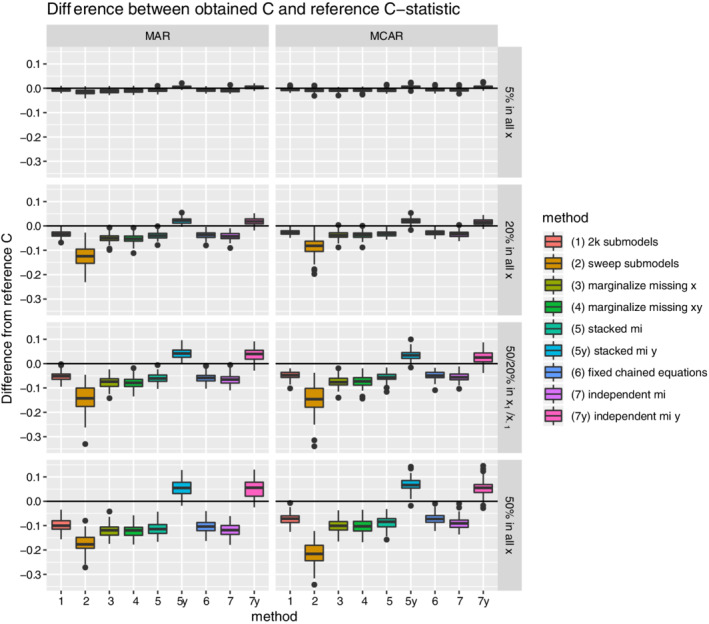
Boxplots for the difference between the estimated out‐of‐bag C‐statistic and reference C‐statistic (as derived under complete out‐of‐bag data) are shown per missing data method and missing data setting. Each simulation iteration renders an observation.  [Colour figure can be viewed at wileyonlinelibrary.com]

Root mean squared prediction error results are shown in Figure 3. In general, performance declines as the amount of missing data increases. The comparative performance of the methods with respect to prediction error was very similar to the pattern for discriminative performance. The best‐performing methods are the 2^k submodel method (method 1), the fixed chained equations (method 6), and the two methods making use of the outcome information not available in practice (method 5y and 7y) that were just included for purpose of illustration.

FIGURE 3.

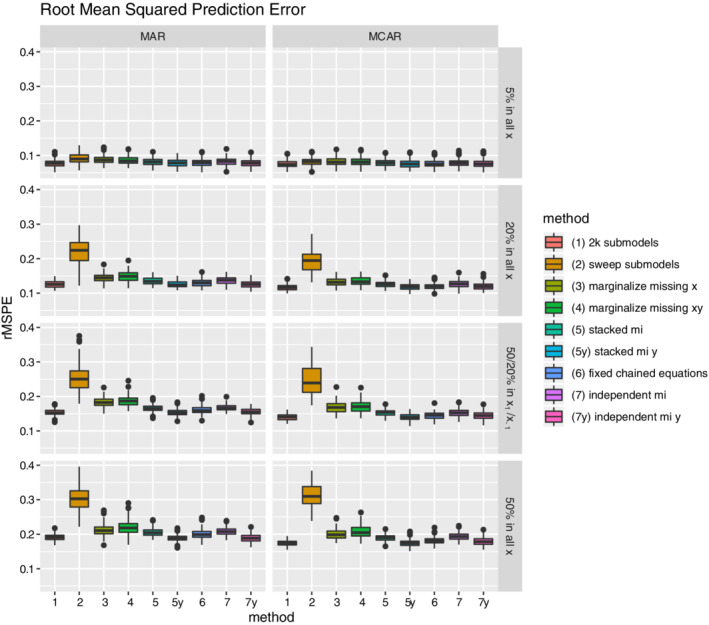
Boxplots for the average root mean squared prediction error (rMSPE) per missing data method and missing data setting. Each simulation iteration renders an observation.  [Colour figure can be viewed at wileyonlinelibrary.com]

Beyond discriminative performance, prediction error, and processing times, Figure S2 illustrates the associations between predicted probabilities derived from each of the applied methods to a those with missing data in a test set (ie, OOB sample). Predicted probabilities are shown for each of the eight simulated missing data scenarios for the first simulation run. As shown, both marginalization approaches have a high correspondence across settings. The same holds for predictions based on the 2^k submodels (method 1) and those based on the fixed chained equations approach (method 6).

4. ICD STUDY

4.1. Setup

As an empirical example, we describe the results of each of the seven methods to deal with missing data in persons in test sets with data from the DO‐IT registry. In the study alongside this registry, prediction models are developed to help decision‐making on implantation of cardioverter defibrillators (ICD) in primary prevention patients at risk for cardiac arrhythmia and death. This registry included 1433 patients between September 2014 and June 2016 from all Dutch ICD implanting hospitals. ²³ Only patients with a primary indication according to the Dutch national guidelines for ICD therapy were included. Patients were followed for occurrence of appropriate ICD therapy (defibrillator shock or antitachycardia pacing for ventricular tachyarrhythmias) or all cause death. At the date of implantation, a set of 45 patient characteristics was gathered including biographic, clinical, and biochemical risk factors of arrhythmia and sudden death. These included binary variables (such as sex), categorical variables (such as classes of mitral insufficiency), and continuous variables such as age, weight, NTproBNP and eGFR levels, and QRS duration. Some of the continuous variables showed extremely skewed distributions.

The primary goal of the project was to develop a joint prediction model for appropriate ICD therapy and death with the total set of patient characteristics. Survival time was censored in 92% of the sample. Details are available in van Barreveld et al. ²³ For the current paper, we focus only on the prediction model for all cause death. We chose to analyze these data with a Cox regression model, and therefore used a log‐log link function. We used the algorithm specified in Figure 1 for internal validation. In the imputation sets of the bootstrap training samples we performed Cox regression with Akaike Information Criterion‐based backward selection of the 45 predictor variables. Each predictor that was selected in at least half of the imputations was selected in the final model. Instead of backward selection one could use lasso or another penalization approach to select the relevant variables; the optimal choice of algorithm for our data falls outside the scope of the current paper.

Inevitably, there were missing values in the set of patient characteristics. Averaged over the sample of patients and the set of characteristics, the percentage of missing values was 4.6%. However, some variables had a much higher percentage missingness, with the highest percentages for the level of NTproBNP (60.0%) and BUN (blood urea nitrogen) (20.7%). NTproBNP also showed to be one of the most important predictor variables.

In order to apply the methods in this survival setting with a censored outcome, several extensions were necessary for method 4 (marginalization over x and y) and the imputations methods. These will be described here in the context of the internal validation setting of the application study. To cope with the censored outcome, we calculated martingale residuals for each person in the training sets using the Kaplan‐Meier survival curve and used these residuals in the imputation models in the training sets.

For the imputation methods, the martingale residuals were included in the imputation models instead of the outcome and time‐to‐event. Instead of full conditional models for the event indicator and time‐to‐event, a linear full conditional model with the martingale residual as the outcome was used. Accordingly, the martingale residual was also used as a predictor in the full conditional models for the covariates. While improvements have been proposed, ²⁹ this was not the subject of the current study.

While these relatively simple changes suffice for the imputation methods, the extension required for method 4 is more involved. The martingale residual of person i with event or censoring at t_i has expectation zero but is usually very skewed. We nevertheless approximated the distribution of (x_i, mr_i) with the multivariate normal distribution with mean (μ_x, μ_mr) and partitioned covariance matrix

that was estimated in the training sets (and pooled over imputations).

Now consider persons with missing values on covariates x_m and observed values on covariates x_o. We partitioned the vector (x, mr) as (x_o, mr, x_m) with partitioned

mean and covariance matrix (μ_o, μ_mr, μ_m) and $\left(\begin{array}{ccc}{\mathrm{\sum }}_{\mathit{oo}}& {\mathrm{\sum }}_{o,\mathit{mr}}& {\mathrm{\sum }}_{o,m}\\ {\mathrm{\sum }}_{\mathit{mr},o}& {\mathrm{\sum }}_{\mathit{mr}}& {\mathrm{\sum }}_{\mathit{mr},m}\\ {\mathrm{\sum }}_{m,o}& {\mathrm{\sum }}_{m,\mathit{mr}}& {\mathrm{\sum }}_{\mathit{mm}}\end{array}\right)$.

We next approximated the distribution of (x_o, mr) negating x_m (as with method 2) with the multivariate normal distribution with mean $({\bar{\mu }}_o{\bar{\mu }}_{\mathit{mr}})=({\mu }_o{\mu }_{\mathit{mr}})-{\mathrm{\sum }}_{(o\mathit{mr}),m}{\mathrm{\sum }}_{\mathit{mm}}^{-1}{\mu }_m$ and variance ${\mathrm{\sum }^{‾}}_{(o\mathit{mr})\mid m}={\mathrm{\sum }}_{(o\mathit{mr})}-{\mathrm{\sum }}_{(o\mathit{mr}),m}{\mathrm{\sum }}_{\mathit{mm}}^{-1}{\mathrm{\sum }}_{m,(o\mathit{mr})}$, where ${\mathrm{\sum }}_{(o\mathit{mr})}=\left(\begin{array}{cc}{\mathrm{\sum }}_{\mathit{oo}}& {\mathrm{\sum }}_{o,\mathit{mr}}\\ {\mathrm{\sum }}_{\mathit{mr},o}& {\mathrm{\sum }}_{\mathit{mr}}\end{array}\right)$ and ${\mathrm{\sum }}_{(o\mathit{mr}),m}=\left(\begin{array}{c}{\mathrm{\sum }}_{o,m}\\ {\mathrm{\sum }}_{\mathit{mr},m}\end{array}\right)$.

In person i with missing x_im values and observed values x_io, the mean and variance of the distribution of mr_i given x_io was next calculated as ${\stackrel{=}{\mu }}_{\mathit{mr}}={\bar{\mu }}_{\mathit{mr}}-{\mathrm{\sum }^{‾}}_{\mathit{mr},o\mid m}{\mathrm{\sum }^{‾}}_{o\mid m}^{-1}(x_{\mathit{io}}-{\bar{\mu }}_o)$ and ${\mathrm{\sum }^{=}}_{\mathit{mr}\mid o}={\mathrm{\sum }^{‾}}_{\mathit{mr}\mid m}-{\mathrm{\sum }^{‾}}_{\mathit{mr},o\mid m}{\mathrm{\sum }^{‾}}_{o\mid m}^{-1}{\mathrm{\sum }^{‾}}_{o,\mathit{mr}\mid m}$, where ${\mathrm{\sum }^{‾}}_{o\mid m}$, ${\mathrm{\sum }^{‾}}_{\mathit{mr},o\mid m}$, ${\mathrm{\sum }^{‾}}_{o,\mathit{mr}\mid m}$ and ${\mathrm{\sum }^{‾}}_{\mathit{mr}\mid m}$ are the submatrices of ${\mathrm{\sum }^{‾}}_{(o\mathit{mr})\mid m}$. We then sampled mr_i a couple of times (ndraws times) from the normal distribution with mean ${\stackrel{=}{\mu }}_{\mathit{mr}}$ and variance ${\mathrm{\sum }^{=}}_{\mathit{mr}\mid o}$: mr_i1, …, mr_ij, …, mr_{i, ndraws}.

Given the sampled value of the martingale residual mr_ij, the mean and variance of the conditional distribution (x_m| x_io, mr_i = mr_ij) were calculated in a similar fashion as described under method 3 and we then sampled a couple of values x_m from this distribution: x_im1, …, x_imj, …, x_{im, ndraws}. Given the sampled values for x_m and given the observed values for x_io, the linear predictor of the Cox regression model was calculated for patient i and averaged over the sampled values for x_m.

4.2. Application results

The apparent results and the internal validation results based on these survival extensions were as follows. The median number of predictor variables that were selected in the 100 bootstrap training sets was 8 (IQR 7‐10). Almost all predictor variables were selected at least once, but only age, weight, mitral insufficiency category, use of diuretics, blood sodium, blood urea nitrogen, ACE inhibitor or AT‐II antagonist use, and NTproBNP were selected more than 40% of the time. The average apparent C‐statistic calculated in the 100 bootstrap samples was 0.827 (SD 0.023) and the average c‐statistics over the 100 OOB samples are shown in Table 2. All methods showed very similar results, with the patterns of differences among methods was similar to the simulations: the corrected C‐statistic for the one‐step‐sweep submodels was relatively low and that for methods failing to ignore the outcome was relatively high. Given the relatively low proportion of missing data in the applied example, these relatively similar results across methods were expected and are in line with the simulation study results.

TABLE 2.

Prediction performance statistics for the applied example

Method	Mean (OOB) C (SD) in the test sets a
2k submodels	0.747 (0.034)
One‐step‐sweep submodel	0.736 (0.041)
Marginalization over missing x variables	0.747 (0.034)
Marginalization over missing x and y	0.747 (0.034)
Stacked multiple imputation	0.747 (0.034)
Stacked multiple imputation with y	0.764 (0.033)
Fixed chained equations	0.748 (0.033)
Independent multiple imputation	0.746 (0.034)
Independent multiple imputation with y	0.756 (0.034)

^aMean over 100 out‐of‐bag (OOB) samples.

5. CONCLUSION

With implementation of a prediction model there is a choice to make on whether missing values of predictor variables are accepted for a patient who wants to know his/her likelihood of some future outcome. If one chooses not to accept missing values in new patients, we think that validation of the prediction model should be done with test sets without missing data, or using independent multiple imputation in the test data (method 7). We focused on the setting where one wants to allow for missing data during model application in practice, and therefore in model validation as well. We propose to only use missing data methods in validation that can also be used in practice in single new patients, and have considered several ways of dealing with missing values for new patient when applying or validating a prediction model.

With respect to the accuracy of predictions for new individual patients in case of missing data, use of the 2^k submodels (method 1) and use of fixed chained equations (method 6) were best in terms of corrected C‐statistic and root mean squared prediction error, with only small mutual differences. Both methods abide by our two main principles: (i) the imputations should only depend on the model development data, and (ii) they should be applicable in new individual patients. Furthermore, predicted event probabilities as derived by both methods for new individuals with missing data were very highly correlated across missing data settings. However, the methods are very different in nature. The 2^k submodels method uses a different prediction model for each missing data pattern, whereas the same full prediction model is used on imputed data when applying fixed chained equations.

Of the remaining methods, marginalizing over the missing data (methods 3 and 4) and use of stacked multiple imputation (method 5) showed intermediate performance with respect to the above described methods. Submodels based on the one‐step‐sweep (method 2) did not perform well. Importantly, our evaluation of imputation methods that fail to ignore available data on the outcome in the test set showed over‐optimistic performance estimates. This also holds for use of independent multiple imputation in the test data. It is therefore key to omit outcome data in the test set when validation a model for use in practice. Interestingly, independent multiple imputation in the test set was included to show reference performance, but it was outperformed by both methods 1 (2^k submodels) and 6 (fixed chained equations).

Lastly, the difference between the evaluated methods was small in the applied example, which had an average percentage of missing data of 4.6%. These results were as expected when looking at the simulation study results for a relatively low proportion of missing data, and the performance pattern across methods was similar as well. Therefore, the difference between the methods will only start to have a larger impact on the results when the proportion of missing data increases.

6. DISCUSSION

We have evaluated two submodel methods, two marginalization methods, and two imputation methods to derive predictions for new individuals with missing data. Several of these methods show promising results, with the best performance for estimation of separate submodels based on observed covariates only (2^k submodels) and an imputation approach based on fixed chained equations. Also, computation times were extremely fast for these two methods.

A key feature of all of the evaluated approaches was that they were only based on the prediction model development data. Therefore, both the prediction model of interest and the requirements for the method to handle missing data in future individuals can be considered as a unit. We have proposed to also use these methods when validating a prediction model that is intended to cope with missing data in practice (in contrast to independent use of multiple imputation in the validation set). To the best of our knowledge, the notion that both the prediction model and the missing data method for use in practice should be used during model validation has not been fully recognized.

Beyond these key messages, the differences among the evaluated methods are worth some discussion. Starting with the theoretical basis, both the submodel methods and marginalization methods have a firm theoretical grounding. The submodels based on observed data only are an obvious reflection of all the available information. While our implementation of the estimation of submodels leans on the missing at random assumption (due to being estimated in multiply imputed data that was imputed under that assumption), this is not strictly necessary. Mercaldo and Blume have recently implemented a pattern‐mixture variant that does not need this assumption. ³⁰ The downside is that the submodels used in their approach are more difficult and sometimes impossible to estimate. The great computational, storage, and reporting savings achieved by the one‐step‐sweep submodels are achieved by additional assumptions, among which the multivariate normality of prediction model coefficients. These assumptions led to a decrease in performance offsetting the benefits.

The marginalization approaches, marginalizing over the missing data, are effectively just another way to arrive at the submodel of interest by integrating out the unknown covariates. The main limiting factor for these methods is not in their theoretical basis, but in the implementation that assumed multivariate normality of the data. If the multivariate distribution of the data could be properly reflected, these methods should retain all relevant information.

The story is somewhat different for the imputation approaches which all make use of chained equations. There has long been a lack of strong theoretical grounding for the use of imputation by means of chained equations. Citing from an overview article on imputation using chained equations by White et al ²⁴ : “justification of the multiple imputation by chained equations procedure has rested on empirical studies rather than theoretical arguments”. Nonetheless, advances have been made recently and this literature is nicely summarized in the second edition of van Buuren's monograph on missing data (Sections 4.5 and 4.6). ³¹ Here we highlight two key references. First, Hughes et al provided conditions (compatibility and noninformative margins) on the conditional models under which chained equation based imputations are draws from the joint distribution of interest (finite‐sample results). ³² Second, Liu et al provided asymptotic results showing that compatibility alone is sufficient as sample size tends to infinity. ³³ In practice though, model compatibility is difficult to check. In fact, citing Liu et al ³³ : “it is precisely when a joint model is difficult to obtain that iterative imputation is preferred.” Regardless of the difficulty of checking these theoretical properties in practice, imputation by means of chained equations has been used effectively in many areas. ³¹ The main benefit of the chained equations resides in the great amount of flexibility in model specification. Basically, any model can be used, thus avoiding the possibly problematic assumption of multivariate normality. With respect to the fixed chained equations, note that they are essentially a simplified version of the standard chained equations implementations where all stochastic elements are removed: the imputation model parameters remain fixed. Also, note that it is relatively straightforward to extend the use of fixed chained equations to allow for multiple imputations. Instead of using the point estimates for the imputation model coefficients, one can sample coefficients from the estimated multivariate normal distribution of imputation model coefficients and thereby propagate their uncertainty. The main rationale for use of single imputation in the current implementation of fixed chained equations related to the interest in point predictions, which do not require propagation ofuncertainty.

Beyond theoretical aspects, more practical aspects are often limiting factors in practice. These primarily relate to processing speed and data availability. For instance, use of stacked imputation as originally proposed by Janssen et al ²² is computationally very expensive, because each new prediction requires imputation of the entire development data. Possibly even more important is that the development data has to be available at the time of prediction, which is often not possible due to privacy regulations. Currently, we are developing prediction models for mortality of metastatic cancers using training data of the Dutch cancer registry and test data of the Belgium cancer registry. Both datasets cannot leave their respective countries making this virtually impossible. All other methods can be performed based on summaries of the development data, as shown in Box 1. Nonetheless, these summaries can be quite extensive (such as 2^k submodels). Modern computers and mobile apps can easily store and process this amount of information however.

Following the need for missing data methods applicable in practice, we have proposed that prediction model validation should also be based on these methods. The main reason for doing so is when one wants to allow for missing data in practice. If that is not the case, then use of standard multiple imputation in development and validation data separately would provide an estimate of performance when all variables are observed. Besides the intended use of the prediction model, a brief discussion of the similarity between the internal and external validation setting is of interest. We propose that they are handled in the same way, using missing data methods that transfer to practice in the validation data (whether hold‐out sample, cross‐validation hold‐out fold, OOB samples, or truly external data). An alternative to our implementation of internal validation would be to impute first and cross‐validate or bootstrap later. However, in case of internal validation and use of multiple imputation, it is preferable to let the bootstrap evaluations reflect the uncertainty in estimation of the imputation models. ¹⁶ We think this argument extends to other missing data methods.

6.1. Study limitations

We did not evaluate the possible use of auxiliary variables that are not included in the prediction model, but that might provide information about missing variables. If these auxiliary variables are available at the time of model developments and application, they could be envisioned to improve imputation procedures. Also, we have evaluated performance based on point predictions, but did not touch upon their uncertainty. Furthermore, since we have evaluated an internal validation setting, we have not evaluated generalizability to other settings. Just as prediction models may need updating in new populations, the required data for each of the missing data methods may also need updating for those settings. In that sense, they are just additional models and have to be treated accordingly. Lastly, the evaluated methods all assume missingness at random. When there is a strong suspicion that missing data may be missing not at random, the above described method by Mercaldo and Blume may be of interest. ³⁰

Summarizing, the allowance for missing data when applying a prediction model to new individuals requires specific missing data methods that differ from the model development setting. We have proposed and evaluated such approaches and have shown good performance of a submodel method basing predictions on observed data only and an imputation method based on fixed chained equations. Both are feasible in practice and the choice should be made based on aspects beyond accuracy and computational burden, such as the desire for a single prediction model (as for fixed chained equations) or lack of the need for imputation (as for the submodel methods). Moreover, we have emphasized the need to use missing data methods that translate to practice during prediction model validation.

Supporting information

Table S1 Prediction performance statistics for the simulated data

Figure S1 The distribution of maximum individual prediction time per OOB sample is shown per missing data method and missing data setting. Each observation is the maximum processing time to derive a prediction for an individual in an OOB sample including implementation of the missing data method.

Figure S2: (A‐H) The relation between the predicted event probabilities for those out of bag samples with missing data. Scatterplots for relation between predicted probabilities across the implemented methods are shown below the diagonal; their correlation is shown above the diagonal. Each subfigure shows results for a specific missing data setting as labeled in the subfigure titles. Predictions are shown for the first (OOB) bootstrap sample.

Supporting Information

Hoogland J, van Barreveld M, Debray TPA, et al. Handling missing predictor values when validating and applying a prediction model to new patients. Statistics in Medicine. 2020;39:3591–3607. 10.1002/sim.8682

DATA ACCESSIBILITY

Data for the applied example (DO‐IT Registry) are not available for sharing since they are part of an ongoing study and contain privacy sensitive data according to the General Data Protection Regulation. Scripts to perform the simulation study, including data generation and analysis, are available for sharing.

DATA AVAILABILITY STATEMENT

Data for the applied example (DO‐IT Registry) are not available for sharing since they are part of an ongoing study and contain privacy sensitive data according to the General Data Protection Regulation. Scripts to perform the simulation study, including data generation and analysis, are available for sharing.