Kilohertz retinal FF-SS-OCT and flood imaging with hardware-based adaptive optics

Abstract

A retinal imaging system was designed for full-field (FF) swept-source (SS) optical coherence tomography (OCT) with cellular resolution. The system incorporates a real-time adaptive optics (AO) subsystem and a very high-speed CMOS sensor, and is capable of acquiring volumetric images of the retina at rates up to 1 kHz. While digital aberration correction (DAC) is an attractive potential alternative to AO, it has not yet been shown to provide resolution allowing visualization of cones in the fovea, where early detection of functional deficits is most critical. Here we demonstrate that FF-SS-OCT with hardware AO permits resolution of foveal cones, imaged at eccentricities of 1° and 2°, with volume rates adequate to measure light-evoked changes in photoreceptors. With the reference arm blocked, the system can operate as a kilohertz AO flood illumination fundus camera with adjustable temporal coherence and is expected to allow measurement of light-evoked changes caused by common path interference in photoreceptor outer segments (OS). In this paper, we describe the system’s optical design, characterize its performance, and demonstrate its ability to produce images of the human photoreceptor mosaic.

1. Introduction

Adaptive optics (AO) has transformed the capabilities of retinal imaging modalities such as flood illumination (FI) fundus camera, scanning light ophthalmoscopy (SLO), and optical coherence tomography (OCT), by permitting correction of optical aberrations introduced by the ocular media of the eye. The resulting diffraction-limited imaging through a dilated pupil yields resolution sufficient for seeing most photoreceptors in the retina [1–3] and has allowed measurement of retinal structure [4–6] and function [7–12] at the cellular level.

Over the past few years a number of investigators have demonstrated full-field (FF), swept-source (SS) optical coherence tomography (OCT) systems implemented with high-speed CMOS detectors, capable of effective A-scan rates substantially higher than traditional flying-spot confocal OCT [13–15]. Some have also demonstrated that the phase of the OCT signal can be used to estimate and correct blur caused by optical aberrations [16,17], which is especially valuable in FF-SS-OCT where optical aberrations do not affect the number of photons detected since pinholes are not used in this imaging modality [18]. This approach, termed computational adaptive optics or digital aberration correction (DAC), has been used to improve the visibility of peripheral cone photoreceptors, but has not yet been shown to resolve the smaller and more tightly packed foveal cones, whose visualization in the near-infrared (NIR) requires diffraction-limited imaging through a $\sim$ 7 mm pupil.

In this work, we describe a FF-SS-OCT system equipped with a hardware AO subsystem designed to provide cellular resolution imaging of the human retina in vivo. The system has a number of interesting features. First, by combining AO with FF-SS-OCT, the system is able to resolve foveal cones, which may permit future studies of optoretinographic (ORG) responses much like those measured in peripheral cones using DAC [19], or line field OCT with hardware AO [20]. Second, with the reference arm blocked, the system can be operated as a very high speed (kHz+) AO flood illumination fundus camera capable of measuring light-evoked responses through common-path interference [7,21–24]. These common-path effects have proven difficult to quantify in single cells without a priori knowledge of the underlying changes. However, recent elucidation of the latter using phase-sensitive AO-OCT in cones [8] and rods [12], including the initial rapid contraction [9,25], may permit a more informed approach, especially in conjunction with high-speed imaging and fine control over the source coherence.

2. Experimental setup

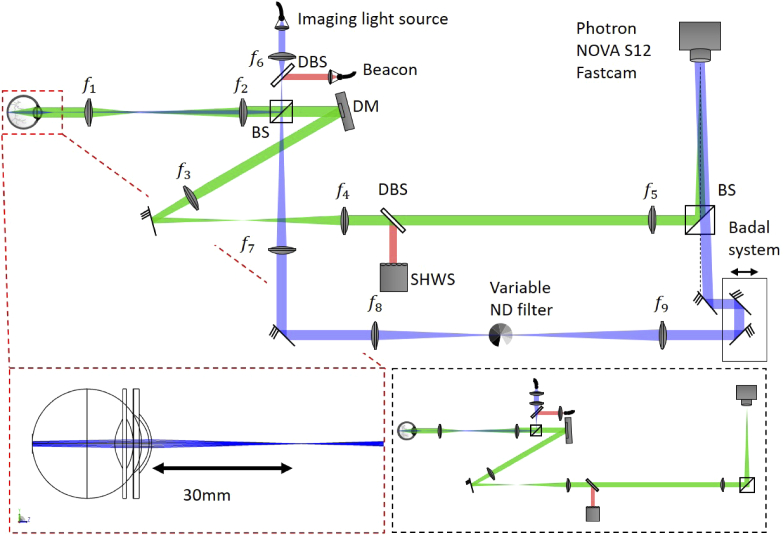
The imaging system operating in AO-FF-SS-OCT configuration consisted of a Mach-Zehnder interferometer with tunable light source (BS-840-2-HP, Superlum, Cork, Ireland) with an 800 nm to 875 nm tuning range with sweep speeds between 100 nm/s to 100 000 nm/s (Fig. 1). The light was split into sample and reference arms with a 20/80 beam splitter. In the sample arm, light was focused 3 cm in front of the subjects’s cornea, illuminating a 2° field-of-view (FOV) on the retina with a converging (but not focused) beam with a power of 3 mW measured at the cornea, deemed safe for retinal and corneal continuous exposure by the 2014 ANSI standard (up to 30 000 s) [26]. The backscattered light by the retina was imaged onto a high-speed 2D CMOS sensor (FASTCAM NOVA S-12, Photron, Tokyo, Japan) allowing frame rates between 2 fps and 1 000 000 fps over regions of interest between $1024\times 1024$ and $128\times 16$ pixels. The optical system was designed for imaging through a dilated 6.75 mm pupil, yielding a lateral resolution of 2.6 µm in the eye. To achieve sufficiently high lateral sampling by the camera’s 20 µm pixels, a magnification between the retina and sensor of approximately 20x was chosen, accomplished with a series of three 4f telescopes ($f_1=100$ mm, $f_2=200$ mm, $f_3=300$ mm, $f_4=200$ mm, $f_5=500$ mm). The sample channel also incorporated a hardware AO subsystem incorporating a superluminescent diode (SLD) beacon (IPSDM0701-C, Inphenix, Livermore CA, USA) with 755 nm center wavelength and full-width-half-maximum (FWHM) bandwidth of 30 nm, a deformable mirror (DM) (DM-97-15, ALPAO, Montbonnot-Saint-Martin, France) and custom-built Shack-Hartmann wavefront sensor (SHWS). The pupil sizes at DM and SHWS were respectively ${\mathrm{\Phi }}_{DM}=13.5$ mm and ${\mathrm{\Phi }}_{SHWS}=9$ mm. The SHWS consisted of a CMOS camera (acA2040-90um, Basler, Ahrensburg, Germany) and microlens array (MLA300-14AR-M, Thorlabs, Newton NJ, USA). The beacon’s collimated beam was 3 mm in diameter and had a power of 100 µW, measured at the cornea. Accounting for the fact that the beacon was focused on the retina, the simultaneous illumination from two sources was in accordance with the laser safety standards [26]. The AO system was operated in closed-loop with a gain of 0.3 and rate of 30 Hz, using open source software developed in Python/Cython by our lab [27]. Wavefront slopes were measured relative to reference coordinates generated by a planar wavefront propagated through the non-common path. Diffraction-limited imaging (residual wavefront error RMS ${\sigma }_W\le 61$ nm - Maréchal criterion) $\lambda /14$ was achieved in all subjects. The beam transmitted at the first BS forms the reference arm. It is expanded and collimated and hits the camera with an angle of $\approx 1^{\circ }$ with respect to the sample arm. The advantages of this off-axis approach will be treated in section 3.1. At the reference arm there is still a variable ND filter used to adjust its power according to the frame exposure time of the camera for different OCT volume rates, avoiding saturation of the CMOS sensor. OCT signal processing was done in Python and MATLAB.

Fig. 1.

Schematic of the AO-FF-SS-OCT setup (not to scale). BS: beam splitter; DBS: dichroic beam splitters; DM: deformable mirror; SHWS: Shack-Hartmann wavefront sensor; $f_{1-9}$: achromatic doublet lenses ($f_1=100\mathrm{m}\mathrm{m}$, $f_2=200\mathrm{m}\mathrm{m}$, $f_3=300\mathrm{m}\mathrm{m}$, $f_4=200\mathrm{m}\mathrm{m}$, $f_5=500\mathrm{m}\mathrm{m}$, $f_6=100\mathrm{m}\mathrm{m}$, $f_7=500\mathrm{m}\mathrm{m}$, $f_8=500\mathrm{m}\mathrm{m}$, $f_9=750\mathrm{m}\mathrm{m}$). The dashed red line box shows the Zemax optical design of the Maxwellian illumination with its beam focused 3 cm away of the cornea. The dashed black box presents the system operating as a AO-FI camera.

By blocking the interferometer reference arm, the setup can also be operated as an AO-FI camera, supporting future studies of light-evoked modulations of common-path interference in the OS. Previous demonstrations have required AO to prevent washout of the responses of neighboring cells due to optical blur, and because in the absence of the reference arm the phase of the backscattered light is not measured, DAC is unlikely to be of use. Previous work demonstrated that the magnitude of the response was modulated by the coherence length of the illuminating light [7]. Here, the coherence length can be adjusted by altering the sweep range of the source in conjunction with the frame rate of the camera. Further adjustments may be possible in post-processing by incoherently summing frames over known spectral bandwidths. In the present work, in order to ensure all frames had identical spectral content, we required at least one full sweep of 50 nm per frame, which limited us to a maximum frame rate of 2000 fps. Halving the bandwidth would allow us to double the frame rate to 4000 fps, notwithstanding losses in contrast due to shorter exposure times. Still higher imaging rates could be achieved by illuminating with a fixed-spectrum broadband source.

3. Signal processing

3.1. Off-axis demodulation and filtering

A single OCT volume began with the acquisition of a series of 500 images, $I(x,y,\lambda )$, saved during a single sweep of the source (adjusted to $825-875$ nm). Each image in the series is a coherent sum of the object $O$ and reference $R$ fields, which vary spatially ($x,y$) and with respect to wavelength $\lambda$:

$$I(x,y,\lambda )\propto |R(x,y,\lambda )+O(x,y,\lambda ){|}^2.$$ (1)

Expanding this product reveals the two auto-correlation terms and the two cross-correlation terms:

$$\begin{array}{rl}I(x,y,\lambda )=& |R(x,y,\lambda ){|}^2+|O(x,y,\lambda ){|}^2\\ & +R{(x,y,\lambda )}^{\ast }O(x,y,\lambda )\\ & +O{(x,y,\lambda )}^{\ast }R(x,y,\lambda ).\end{array}$$ (2)

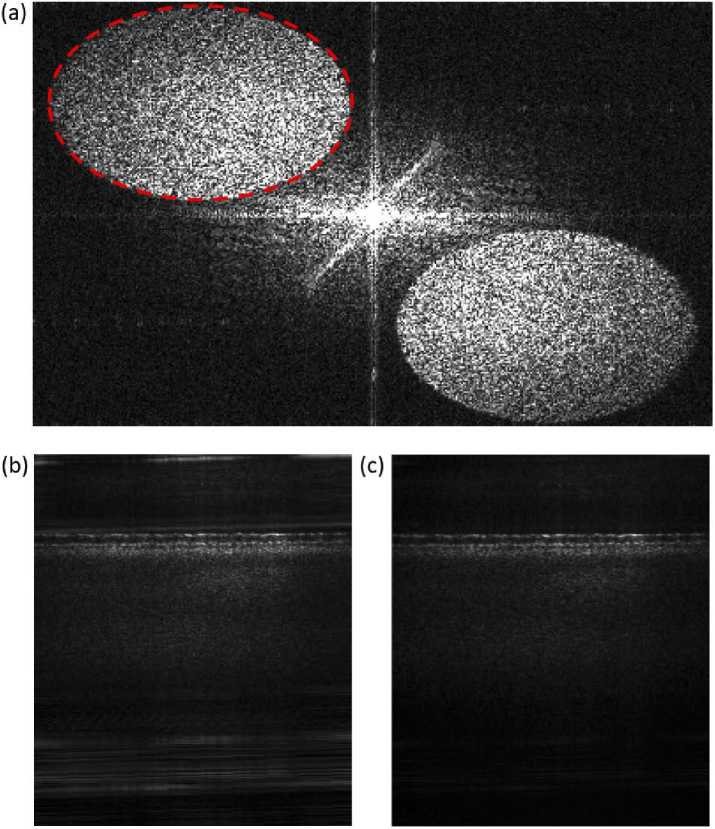
The reference beam was designed to be off-axis relative to the sample arm, by $\approx 1^{\circ }$, in order to create a carrier frequency. By spatially filtering the 2D Fourier transform with respect to the x- and y-coordinates of each camera frame, this approach aims to rejects the DC and auto-correlation components and selects just one of the cross-correlation components [28,29], resulting in a filtered spectral stack $I_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}$. Doing so accomplishes two goals: first, it removes common path artifacts; second, by selecting only one of the complex conjugate cross-correlation pair, imaging depth is extended [29]. Increasing the off-axis angle improves the separation of terms, and thus the rejection of common path artifacts. However, this angle is limited by the pixel size of the camera, since the camera must sample the carrier frequency with at least two pixels per cycle. For wavelength $\lambda$ and pixel size $x_{px}$, the maximum off-axis angle is given by ${\theta }_{max}=\arcsin [\lambda /(2x_{px})]$. Our pixel size of 20 µm and minimum wavelength of 825 nm yields a maximum angle of $\approx {1.2}^{\circ }$. With this angle, the complete suppression of the auto-correlation terms would limit the pupil size to ≈2.6 mm, representing a significant reduction of lateral resolution from 2.6 µm to 6.7 µm. However, since the spectral strength of autocorrelation noise rapidly decreases with increasing spatial frequencies, a significant noise suppression is already achieved with this lower carrier frequency and pupil size 6.75 mm (Fig. 2).

Fig. 2.

Fourier transform of the intensity interference pattern on the camera for single exposure (i.e., a single 0.1 nm bandwidth within the sweep range). Fringe introduced by the off-axis reference beam shifts the signal (dashed red ellipse) and its complex conjugate term into opposite quadrants in the Fourier space. Here, signal and complex conjugate terms appear elliptical due to the non-square ROI ($384\times 240$ pixels); (b) B-scan without off-axis filtering. Many artifacts can be seen, including some very close to the retinal structure; (c) B-scan after filtering in the Fourier space. Although the numerical aperture of the system and limited angle at the carrier frequency does not allow complete separation of cross and autocorrelation terms, a significant noise suppression is achieved by this method.

Because the source’s sweep speed is constant with respect to $\lambda$, after spatial filtering $I_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}$ was resampled to be uniform with respect to wavenumber $k=2\pi /\lambda$, using linear interpolation, and yielding a $k$-stack of images, $I_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}(x,y,k)$.

3.2. Short-time Fourier transformation dechirping

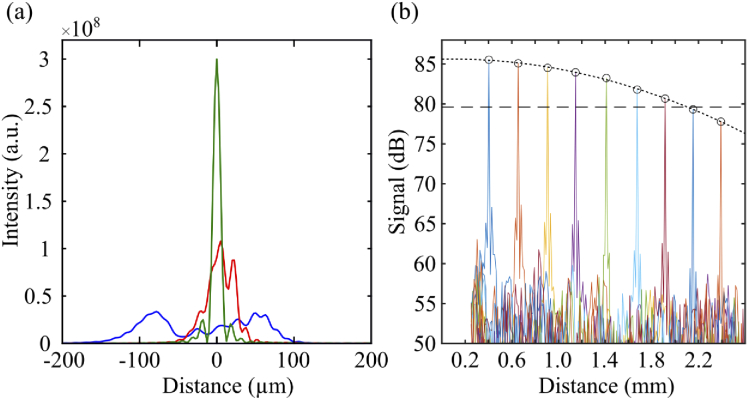
In FD-OCT, dispersion mismatch between sample and reference arm is commonly compensated in post-processing by adding $k$-dependent phase shifts, defined as a third-order polynomial, to the measured spectral fringe $I(x,y,k)$ [30]. As with previous reports of slow-sweeping SS-OCT systems [31], the chirp in our measurements was insufficiently corrected by this approach. After correction of third-order chirp, the axial profile of images of a model eye with a mirror in the retinal plane remained broader than expected (see Fig. 4(a)), and also continued to vary considerably across measurements. This suggested that higher-order chirp was present, possibly due to vibrations causing path length difference variations between reference and sample arms during single wavelength sweep (i.e., acquisition of a single OCT volume) see Fig. 3(a).

Fig. 4.

(a) Axial point spread function in air after no dechirping (blue), correction using a 3rd-order phase polynomial (red) and correction using the STFT dechirping approach (green); (b) Sensitivity roll-off of the OCT system was 6 dB over 2.1 mm.

Fig. 3.

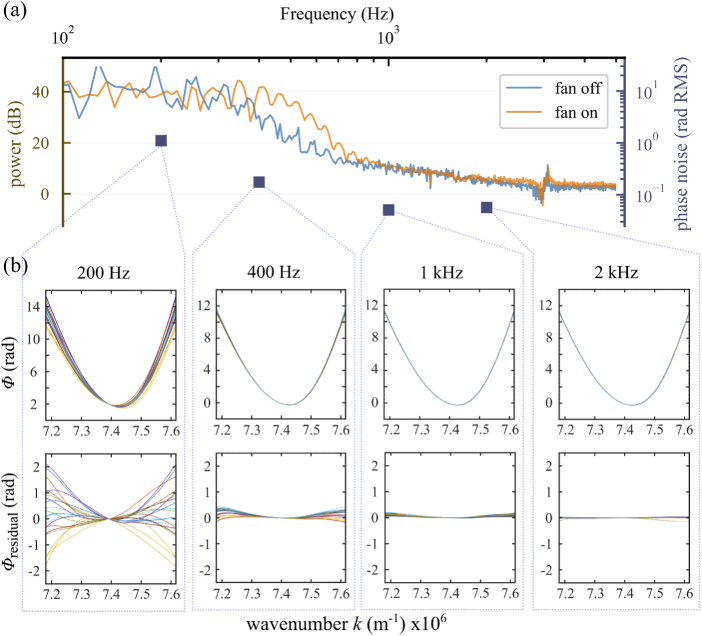
Spectral analysis of system vibrations. (a) Power spectrum of fluctuations in the off-axis carrier fringe (possibly due to system vibrations) measured with model eye (consisting of a lens and a mirror positioned at its back focal plane) in the sample channel, with the camera fan on and off; blue squares show the standard deviation of chirp (${\sigma }_{\varphi (k)}$) measured over 20 volumes acquired at selected rates within the frequency range. It is apparent that increasing volume rates reduces chirp, and that this reduction qualitatively follows the power spectrum. (b) (top) Phase correction ($\varphi (k)$) for 20 volumes acquired with the AO-FF-SS-OCT at different volume rates (specified at the top of each plot) and calculated numerically using the STFT dechirping approach; the characteristic curve suggests a constant component due to deterministic nonlinearity in the sweep. (bottom) The average $\varphi (k)$ at 2 kHz was used as a proxy for the constant chirp component and subtracted from each phase correction curve to visualize the residual chirp caused, for example, by system vibrations or noise in the source. This illustrates the importance of applying high order corrections for $k$-stack dechirping, correcting volumes individually, and the potential advantage of higher volume rates.

To correct chirp in our acquired data, a method based on short-time Fourier transformation (STFT) [31,32] was employed. In this approach, the $k$-stack $I_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}(x,y,k)$ is multiplied by each of a series of boxcar windows of width $8.7\times {10}^4{\mathrm{m}}^{-1}$, centered about the wavenumber corresponding to a frame in the $k$-stack. The windowed $k$-stack was Fourier transformed in the $k$ dimension and, in the resulting series of low-resolution volumes, the chirp manifested as apparent axial motion of the sample $\mathrm{\Delta }z=z-z_0$, where $z_0$ is the average sample position in the series. Under these conditions, the phase correction is then given by:

$$\varphi (k)=\int \mathrm{\Delta }zdk,$$ (3)

which was used to calculate the corrected $k$-stack:

$$I\prime (x,y,k)=I_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}(x,y,k)\times e^{i\varphi (k)}.$$ (4)

4. System characterization

Here, the main aspects of the AO-FF-SS-OCT system are presented. We describe the impacts of higher-order chirp on the acquired OCT signal, the importance of STFT dechirping to correct random changes in the optical path length in each acquired volume, and the advantage of this method over the commonly used polynomial dechirping. Sensitivity roll-off was also measured. Furthermore, we compared the theoretical and experimentally computed values for sensitivity to axial displacement between two scatterers in the sample (or, equivalently, sensitivity to phase shifts). This parameter will be important to characterize the system’s capability to measure ORG responses.

4.1. Spectral analysis of system vibrations

The high volume acquisition speed achieved in FF-SS-OCT systems is due to massive parallelization of A-scan acquisition rather than high sweep rates. The relatively slow sweep rate makes the system vulnerable to artifacts caused by system vibrations and motion of the sample. The AO system and associated magnification requirement necessitate two additional telescopes in the sample channel, which may exacerbate these artifacts by increasing the system’s footprint.

Random changes in the optical path length (OPL) of either arm of the Mach-Zehnder interferometer affect the acquired signal. Their impacts depend on their frequency content, and fall into different regimes, regardless of the specific implemented frequencies. Above the sensor frame rate they cause unrecoverable fringe washout. Below the volume acquisition rate (or sweep rate) they result in bulk motion, which can be corrected using registration, histogram-based bulk motion correction [33], or, in phase-based ORG applications, by monitoring relative phase differences within the image [19,34]. Between these two regimes, however, OPL noise causes time-varying phase shifts within the $k$-stack (chirp) analogous to that caused by dispersion mismatch [30] and, in principle, numerically correctable, as described in §3.2. For our 200 Hz volume rate experiments, these regimes are >100 kHz (100 000 fps), <200 Hz, and [200 Hz,100 kHz], respectively.

In point-scanning swept-source systems with sweep rates ≥100 kHz and scanning point- or line-illumination [20] spectrometer-based systems, the high-frequency regime is typically neglected, but the OPL fluctuations between the scan rate and volume rate are encoded as spatially varying phase noise. Parallelization in our system guarantees, in principle, that OPL fluctuations are spatially constant.

To characterize system vibrations, we placed a model eye–consisting of a lens and a mirror positioned at its back focal plane–in the sample channel, parked the source at 825 nm, collected images at 1 000 000 fps, and computed the temporal power spectrum of the resulting carrier fringe. System vibrations are illustrated in Fig. 3(a). The power at frequencies above 2 kHz is almost flat, which suggests that the impact of fringe washout above this value is negligible and little can be gained in fringe contrast in single frames of the $k$-stack by further reducing the single frame integration time. At high frame rates the camera operates with reduced ROI (h $\times$ v pixels) so this plateau in the power spectrum also suggests that the tradeoff between FOV and volume rate may be unfavorable at volume rates higher than 1 kHz. The power spectrum shows that most of the power lies at frequencies $\lesssim$1 kHz, which would have negligible effect on the phase stability of typical scanning flying spot SS-OCT systems operating at 100 kHz to 400 kHz sweep rates but would cause significant chirp for swept sources operating at 200 Hz to 1000 Hz, and illustrates the importance of a robust method of reducing chirp, either numerically or by increasing the system’s speed.

To test the effect of increased $k$-stack acquisition speed on the need for numerical dechirping, we acquired series of 20 volumes of the model eye at sweep rates of 200 Hz, 400 Hz, 1 kHz, and 2 kHz. STFT dechirping was performed to determine the correction phasor $e^{i\varphi (k)}$ as described in Eq. (3). $\varphi (k)$ was used to visualize the chirp at various volume rates, shown in Fig. 3(b). The blue squares in Fig. 3(a) show the standard deviation of the dechirping phasor ${\sigma }_{\varphi (k)}$ as a function of volume acquisition rate. To facilitate comparison with the power spectrum in Fig. 3(a), we plotted these in log scale. As expected, the standard deviation falls with increasing volume rate, and qualitatively resembles the vibrational power spectrum.

4.2. Characterization of OCT system performance

To characterize OCT performance, images of a model eye with a mirror in the sample arm were acquired at 100 000 fps (ROI $384\times 240$ px), with the source sweeping at 10 000 nm/s, resulting in volume rate of 200 Hz and effective A-scan rate of 18.4 MHz. A neutral density filter (ND=$1.0$) was placed in front of the mirror, and OCT volumes were acquired. From these, the signal-to-noise ratio (SNR) was estimated by dividing the peak reflectivity of the mirror by the standard deviation of a region in the image that appeared to be free of both signal and coherent artifacts. With a resulting SNR of $134.5$, the sensitivity of the system was estimated to be ≈63 dB. Sensitivity roll-off was also measured by axially translating the mirror in the sample arm, using a calibrated translation stage showing an OCT signal drop of 6 dB approximately 2.1 mm from the zero path length (Fig. 4(b)).

The axial resolution ($\mathrm{\Delta }z$) was estimated experimentally by measuring the full width at half-maximum (FWHM) of the point spread function (PSF) with a mirror in the sample arm. Three versions of the corresponding OCT image were computed–without dechirping, with 3rd-order polynomial dechirping, and using the STFT approach. As shown in Fig. 4(a), when using the STFT approach, $\mathrm{\Delta }z=$ 10.1 µm in air, close to the theoretically expected by the coherence length of the light source, given by the DC component of the Fourier transform of the spectral interferogram (Eq. (2)), which was $l_c=9.9$ µm. The corresponding resolution in the retina ($n=1.38$) was $\mathrm{\Delta }z=$7.3 µm. As shown in the same figure, the FWHM PSF for the uncorrected and 3rd-order-corrected PSFs were significantly higher. While it is evident that the STFT approach improves the PSF by measuring and correcting chirp, its precision is presumably limited both by finite oversampling of the boxcar-filtered images and shot noise. Thus, residual chirp is likely present, which may have an impact on phase sensitivity, as described in §4.3 below.

4.3. Sensitivity to axial displacement

The intended application of the system is to measure tissue deformations much smaller than the system’s axial resolution, which manifest as phase shifts. As reported in early in vivo phase sensitive OCT work [34], when using relative phase differences between two reflective surfaces within the volume, the optical path measurement is immune to axial motion artifacts and other sources of OPL instability.

The theoretical lower limit on phase-based displacement sensitivity for a single scattering object is dictated by shot noise, and can be computed from the SNR of the image of that scatterer [35]:

$$\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}}\approx \frac{{\lambda }_0}{4n\pi }\sqrt{\frac{1}{\text{SNR}}}.$$ (5)

For the axial component of the relative displacement between two scatterers, the uncertainty is compounded and given by:

$$\begin{array}{rl}\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }}& =\sqrt{{(\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},1})}^2+{(\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},2})}^2}\\ & \approx \frac{{\lambda }_0}{4n\pi }\sqrt{\frac{1}{{\text{SNR}}_1}+\frac{1}{{\text{SNR}}_2}},\end{array}$$ (6)

where $\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},n}$ is the displacement sensitivity of the $n^{\mathrm{t}\mathrm{h}}$ scatterer.

To characterize the displacement sensitivity of our system and the relative contributions of different noise sources, a series of OCT images were collected using a glass cover slip, which contained two reflections originating from both surfaces. The reflected light was attenuated by tilting cover glass to avoid saturation of the CMOS camera.

The SNR of each surface was calculated as described above, and a corresponding value of $\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }}$ was calculated using Eq. (6). The reflections originating from the two surfaces of the cover slip had SNRs of $129.0$ and $59.6$, corresponding to a theoretical displacement sensitivity limit of 7.3 nm.

An empirical estimate of displacement sensitivity $\delta x_{\mathrm{e}\mathrm{x}\mathrm{p}}$ was also made by computing the standard deviation of the phase difference between the two cover glass interfaces, ${\sigma }_{\mathrm{\Delta }\varphi }$, across 1000 volumes acquired over 5 s:

$$\delta x_{\mathrm{e}\mathrm{x}\mathrm{p}}\approx \frac{{\lambda }_0}{4n\pi }{\sigma }_{\mathrm{\Delta }\varphi },$$ (7)

resulting in $\delta x_{\mathrm{e}\mathrm{x}\mathrm{p}}=$9.9 nm.

This allowed us to estimate the phase noise contributed by the instrument using:

$$\delta x_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}}=\sqrt{{(\delta x_{\mathrm{e}\mathrm{x}\mathrm{p}})}^2-{(\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }})}^2}.$$ (8)

The difference between experimentally measured and theoretically predicted displacement sensitivity (Eq. (8)) was 6.7 nm, which could be due to uncorrected chirp, phase instability in the source, or synchronization between the source and camera, or it may indicate that the OCT system is not shot noise limited. It is important to emphasize though that the displacement sensitivity is not a fixed parameter of the system but rather is dependent on the SNR of the object whose displacement is to be measured.

Table 1 summarizes the significant characteristics of the system and data acquisition settings during imaging.

Table 1. Specifications of the AO-FF-SS-OCT system.

Imaging source bandwidth	825 nm to 875 nm
Wavefront beacon bandwidth	740 nm to 770 nm
Lateral resolution (in the retina)	2.6 µm
Axial resolution (in the retina)	7.3 µm
Volume rate	200 Hz to 1000 Hz
Measured system sensitivity	63 dB @ 200 Hz
A-scan rate (effective)	8.2 MHz to 18.4 MHz
Sensitivity roll-off (6 dB)	2.1 mm

5. Human imaging

5.1. Human imaging protocol

Three subjects, free of known retinal disease, were imaged in the temporal (T) retina at 1° and 2°. Eyes were dilated and cyclopleged using topical drops of phenylephrine (2.5 %) and tropicamide (1.0 %). A bite bar and a forehead rest were employed to position and stabilize the subject’s pupil during imaging. Subject fixation was guided with a calibrated target. OCT reference arm length was adjusted by translating a Badal system and using real-time B-scan images, prior to acquisition of series of $k$-stacks. With closed-loop AO correction, all images were diffraction-limited by the Maréchal criterion, with an expected lateral resolution at the retina of approximately 2.6 µm. Optimal focus for photoreceptor imaging was achieved by adding defocus to the SHWS reference coordinates in closed-loop, while visually inspecting areal images or B-scans in the cases of flood and OCT imaging, respectively. The images from the best subject are presented here. All procedures were in accordance with the Declaration of Helsinki and approved by the University of California Davis Institutional Review Board.

5.2. OCT imaging of photoreceptors

For retinal imaging with OCT, after $k$-mapping, dechirping, and Fourier transformation, the volumes were segmented axially and the photoreceptor inner segment - outer segment junction (IS/OS) and cone outer segment tip (COST) layers were identified, aerially projected, registered, and averaged. 40 projections were averaged to produce each en face OCT image.

B-scans from volumetric images of the retina, acquired at 200 Hz, revealed a pair of bright, periodically punctuated and correlated bands in the outer retina, believed to originate from the IS/OS and COST [36,37]. B-scans are shown in Fig. 5(c and d). Their appearance was consistent with what is observed in similar scanning AO-OCT images. En face projections of the IS/OS and COST revealed the cone mosaic, as shown in Fig. 5(e and f), and bear resemblance to AO-SLO images of the cone mosaic, as well as en face projections produced by point-scanning AO-OCT systems. It is notable, however, that due to parallel acquisition of the whole volume, the en face shown here are free from the image warp often visible in images from scanning systems.

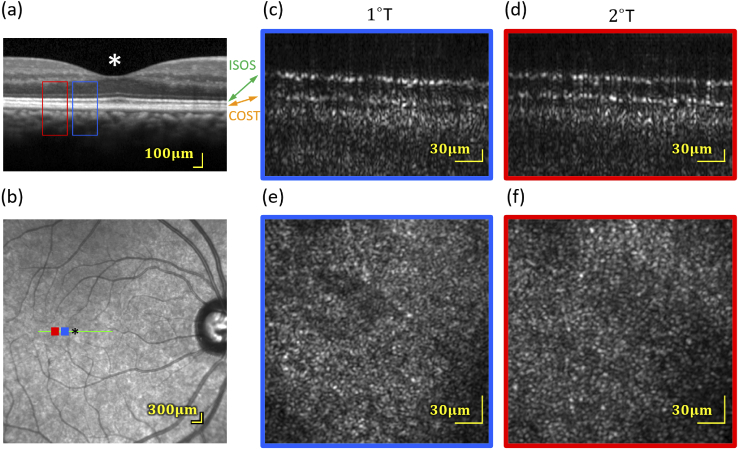
Fig. 5.

(a and b) Spectralis OCT and SLO scans indicating the areas that were imaged with the AO-FF-SS-OCT. (c and d) amplitude B-scans (averaged over four lateral B-scans in a single volume) from 1° and 2° in one subject, from volumes acquired at 200 Hz. Only the outer retina is shown. At both eccentricities, two bright bands are visible, originating from the IS/OS and COST. Each has the characteristic periodic pattern of the photoreceptor mosaic. The dark region separating them is the cone OS, visibly longer at 1° than 2°. (e and f) Corresponding en face projections through the cones (average of 40 motion-corrected volumes). Analysis of the IS/OS and COST band SNRs implies a sensitivity to light-evoked deformation of 7.3 nm.

5.3. High-speed flood-illuminated fundus imaging of photoreceptors

As described in §2, blocking the reference channel permits the system to be used for high-speed (kHz) AO-FI imaging, with temporal coherence adjustable via the sweep range of the laser and integration time of the camera. This mode of operation permits measurement of stimulus-evoked changes in coherent en face reflectivity of photoreceptors [7], which has been shown to be a quantifiable and reproducible effect [24]. In this mode, the source was set to sweep between 825 nm and 875 nm at sweep rate of 100 000 nm/s.

Images of the cone mosaic were successfully collected at 1 kHz (Fig. 6) at 1° and 2°. Cones were laterally resolved in these retinal images. The contrast of the cones is not as high as in comparable AO-SLO images of cone mosaic. This is presumably due, in parts, to the lack of confocality and the significantly lower integration time. The radially averaged power spectra were computed for both images, showing peaks at $\approx 0.18\mu {\mathrm{m}}^{-1}$ and $\approx 0.14\mu {\mathrm{m}}^{-1}$ respectively, corresponding to a periodicity of 5.6 µm and 7.1 µm respectively–within the range of the expected cone spacing at the imaged eccentricities [38,39]. The cones in the foveal center were not well resolved in any subject.

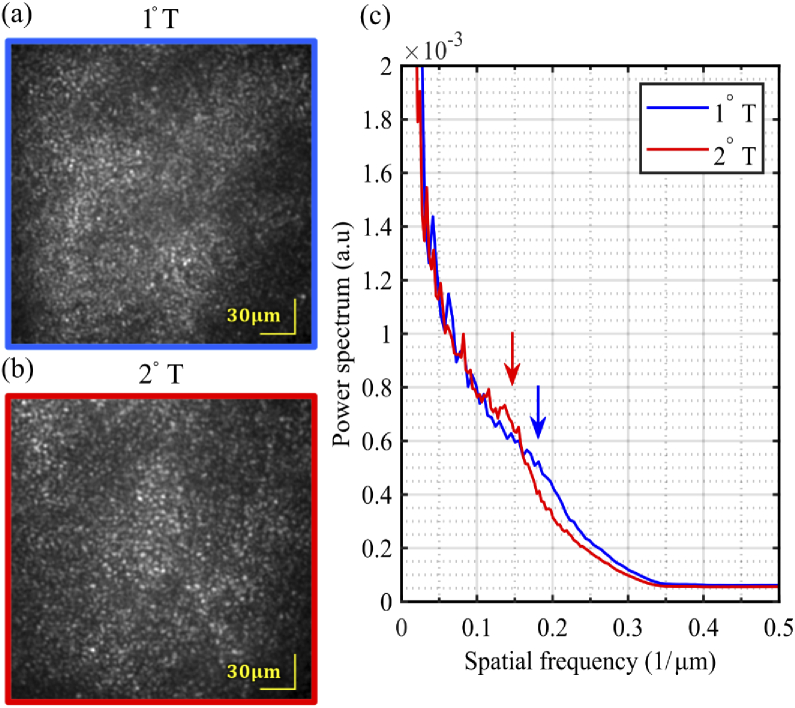
Fig. 6.

Images of photoreceptors mosaic (1000 registered and averaged frames) from one subject, at two foveal eccentricities–(a) 1° temporal and (b) 2° temporal–acquired in flood illumination mode at 1 kHz with closed-loop AO correction. Both show the characteristic hexagonally tiled cone mosaic, with the cones more tightly packed closer to the fovea. (c) Average radial profile of the cone mosaic at 1°T and 2°T. The arrows show the periodicity of each cone mosaic.

5.4. Modal filtering of closed-loop correction

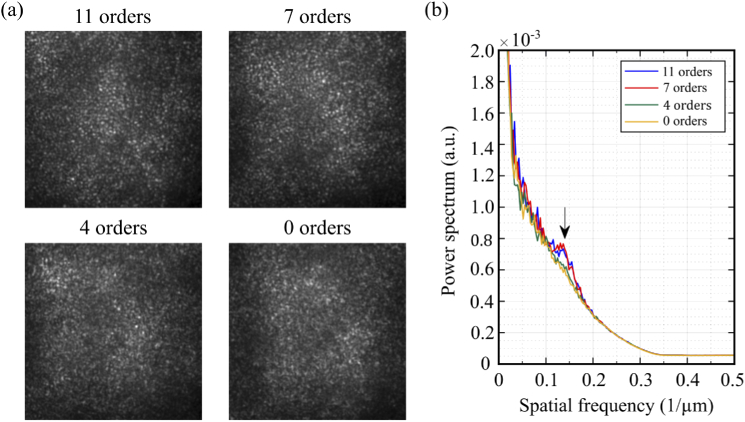
Low order DAC correction has been used to image peripheral photoreceptors using FF-SS-OCT [18]. To estimate the minimal aberration order required to resolve foveal cones, we imaged the photoreceptor mosaic at 2°T, with the AO correction restricted to certain Zernike coefficient order. This was done by first calculating Zernike coefficients $c$ using $c=D^{+}\cdot s$, where $D$ a rectangular matrix containing $x$ and $y$ partial derivatives of each Zernike polynomial up to the 11th order (75 Zernike polynomials, excluding tip, tilt and piston) at the centers of each subaperture, $D^{+}$ is its pseudo-inverse, and $s$ is the corresponding set of measured $x$ and $y$ slopes. Next, coefficients in $c$ above the desired order $n$ were zeroed (${\hat{c}}_n$) and the filtered slopes ${\hat{s}}_n$ were calculated using ${\hat{s}}_n=D\cdot {\hat{c}}_n$. Mirror commands were generated by multiplying $\hat{s}$ by the AO system’s control matrix.

When filtering closed-loop correction by Zernike modes, we observed that residual error increased with a reduction of the number of modes (35–50 nm for $n=11$ ($75$ Zernike modes); 70–80 nm for $n=7$ ($33$ Zernike modes); 120–140 nm for $n=4$ ($12$ Zernike modes); and 950–1020 nm for $n=0$ (without AO correction). The impact of this residual error on resolution can be seen in the areal images and at the radially averaged power spectra of the images shown in Fig. 7. With 7 radial orders or higher a peak showing the cone mosaic periodicity can be observed at $\approx 0.14\mu {\mathrm{m}}^{-1}$. This peak, however, does not appear when $n\le 4$. The structures seen on areal images for correction up to n=4 represent random speckle field created by interference between multiple reflectors within the blurred PSF [40]. This result exhibits an advantage of the hardware AO approach with respect to DAC, considering that the latter may be limited by computational tractability, being unfit to calculate high order wavefront aberrations in a reasonable amount of time [28].

Fig. 7.

(a) Areal fundus camera images of cone mosaic at 2°T showing the system performance with adaptive optics operating with different Zernike orders; (b) Average radial profile of the cone mosaic shows that the cone mosaic could only be clearly identified (black arrow) using AO correction with higher Zernike modes.

5.5. Kilohertz OCT imaging

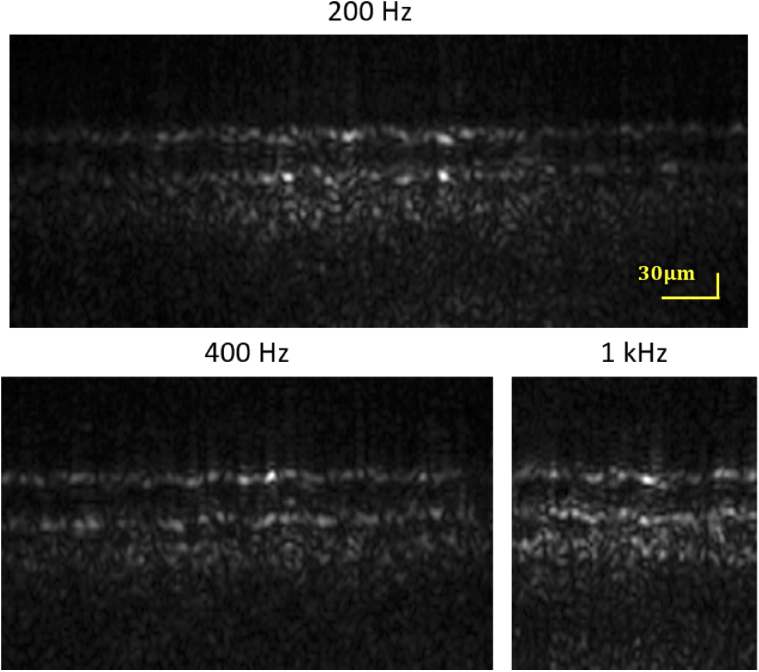
Preliminary evidence suggests that in the ORG, OS elongation velocity increases with increasing stimulus dose [8,12]. Because OS elongation manifests as phase changes that are wrapped into $[0,2\pi )$, the speed requirements of ORG measurements are dictated, in part, by the desired stimulus levels. We sought to characterize the impact of increasing the OCT volume rate on field of view (FOV), SNR, and displacement sensitivity. To do this, we acquired AO-corrected OCT volumes at rates of 200 Hz, 400 Hz, and 1000 Hz with power in the reference arm adjusted by a variable ND filter to minimize the drop of integrated energy by the increasing camera’s frame rate. The IS/OS and COST layers were segmented, and from these ${\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{I}\mathrm{S}/\mathrm{O}\mathrm{S}}$ and ${\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{C}\mathrm{O}\mathrm{S}\mathrm{T}}$ were calculated as described above. Applying Eq. (6) allowed us to compute theoretical relative displacement sensitivity $\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }}$ for each of the volume rates. Representative B-scans acquired at various volume rates are shown in Fig. 8, and resulting values of SNR and $\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }}$ are shown in Table 2. At 200 Hz and 400 Hz the integrated energy per pixel were comparable (1:0.98) and, as a result, the displacement sensitivity was not significantly impacted by the volume rate. At 1000 Hz the camera exposure time was only $2\mu$s and the integrated energy per pixel could no longer be compensated by the variable ND filter, showing a drop of $23\mathrm{\%}$ with respect to OCT volumes at 200 Hz. That was reflected in the lower displacement sensitivity. However, the three-dimensional structure of the photoreceptors was visible at all volume acquisition rates, and the displacement sensitivity ranged from 7.3 nm to 9.2 nm is sufficient for ORG measurements with bleaching levels lower than 1.8 % [8].

Fig. 8.

B-scans at $2^{\circ }$T using different volume rates. IS/OS and COST bands are visible at all three rates. Analysis of the bands’ SNRs revealed displacement sensitivities between 7.3 nm to 9.2 nm, sufficient to detect photoreceptor responses to bleaches of as little as 1.8$\mathrm{\%}$ of pigment in cones and 0.007$\mathrm{\%}$ in rods.

Table 2. Tradeoffs between volume rate and displacement sensitivity.

Frame rate (fps)	Sweeping speed (nm/s)	Volume rate (Hz)	FOV a (px)	A-scan rate (MHz)	${\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{I}\mathrm{S}/\mathrm{O}\mathrm{S}}$	${\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{C}\mathrm{O}\mathrm{S}\mathrm{T}}$	$\delta x_{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r},\mathrm{\Delta }}$ (nm)
100 000	10 000	200	$384\times 240$	18.4	$80.8$	$103.8$	7.3 nm
200 000	20 000	400	$256\times 128$	13.1	$110.8$	$63.6$	7.7 nm
500 000	50 000	1000	$128\times 64$	8.2	$58.9$	$55.5$	9.2 nm

^aOne pixel is equal to 1 µm at the retina.

6. Discussion

FF-SS-OCT offers an intriguing alternative to traditional raster scanning (flying spot) OCT systems, despite some key advantages of these more traditional approaches. In scanning systems, field of view and sampling density can be adjusted by changing scan angles and scanner speed, without any alteration to the optics. Additionally, confocality of fiber-based scanning systems confers an inherently lower noise floor and improved sensitivity and SNR.

However, FF-SS-OCT possesses several key advantages as well. Because it requires no pupil conjugate plane(s) for scanners, its optical design is simpler than that of corresponding scanning systems. Moreover, since all parts of the retinal FOV are imaged simultaneously, it is immune to the image warp caused by eye movements in scanning systems. While most high-speed swept-source lasers operate at $>1$ µm, slower tunable sources are available at shorter wavelengths, conferring advantages in both axial and lateral resolution. Finally, due to the state of the art in high-speed swept sources and high-speed CMOS sensors, FF-SS-OCT at present permits substantially higher volume rates than scanning systems.

In FF-SS-OCT, no light from the sample is rejected by a pinhole or fiber tip when the PSF is degraded by aberrations; it all arrives at the sensor. In flood illumination imaging, this yields little benefit, as noise in the stray light degrades the image SNR. However in the case of OCT, where the phase of the light is measured and can be computationally altered, the possibility exists to reshape the PSF numerically and recover diffraction-limited resolution. Traditional scanning systems may utilize DAC, but in addition to light lost when coupling back, these systems also suffer from an ambiguity between aberration and axial eye movement in determining the origins of phase shifts. To overcome the shortcoming of photon loss a previous work have implemented a combined hardware and computational wavefront correction in a scanning system, showing further improvement of image sharpness in images corrected using hardware AO [41].

DAC is an inverse problem requiring substantial computation, and correction sufficient to resolve foveal cones has not yet been demonstrated in FF-SS-OCT. However, several investigators have implemented ways to constrain the problem and improve its tractability [17,42,43]. Nevertheless, the SNR of the OCT image likely imposes a limit on the precision with which we can compute the complex pupil function, and without an analysis of noise propagation in these computations we cannot determine DAC’s theoretical resolution limit.

The primary application for the system described in this paper is acquisition of optoretinograms (ORGs) of photoreceptors [19] and other retinal neurons [44]. While the ORG is an emerging and rapidly developing tool, at present it requires cellular resolution. In the immediate future we are interested in studying the impacts of retinal disease on photoreceptor function, especially in foveal cones, where such diseases have the greatest impact on quality of life, and rods, which are often impacted first. For ORGs of these, hardware AO confers the required resolution.

A related method is FF time-domain (TD) OCT using white light [45], which sidesteps entirely the impact of aberrations on resolution (but not sensitivity) by employing high spatial coherence to filter the photons misplaced by optical aberrations. Phase perturbations manifesting in speckle have been used to visualize subcellular dynamics in tissue explants and the human cornea [46], and may represent a complementary retinal imaging modality, especially when equipped with axial eye tracking [47]. DAC has also been employed in line-scanning TD-OCT, which mitigates the contributions of axial motion to the phase of the interference fringe [48]. In FF-SS-OCT, spatial coherence manifests as cross-talk, and approaches have been demonstrated to mitigate this source of noise [49,50].

Another key requirement for current ORG methods is sensitivity to displacements in the retina orders of magnitude smaller than the axial resolution currently offered by OCT. The derivation for displacement sensitivity was described in the context of spectral domain phase microscopy [35], and here we have described how to apply the principle to the ORG, where bulk motion of the retina requires measurement of phase differences instead of absolute phase. We have shown that the system will be able to detect changes of <10 nm in the OS, sufficient for detecting responses to stimuli that bleach less than 1.8 % of cone photopigment or as little as 0.007 % of rod photopigment. In applications where we would like to detect dysfunction, this sensitivity permits us to detect deviations in the expected amplitude of responses to bright stimuli as small as 5 % cone photopigment bleach level [8], which suggests it could be a useful probe of photoreceptor dysfunction.

Displacement sensitivity depends on the SNR of the objects whose displacements need to be measured, and the SNR of these depends on the sensitivity of the system. We found that one of the key limitations to the AO-FF-SS-OCT system’s sensitivity was chirp in the spectral fringe, likely the result of vibrations. We have demonstrated a way to numerically remove this chirp and improve the system’s axial PSF and sensitivity using the STFT, although future work includes establishing a theoretical limit for our system’s sensitivity and developing additional computational methods to improve it. We have also shown that increasing the system’s volume acquisition rate (by reducing its FOV and increasing the camera’s frame rate and light source sweep speed) reduces the amount of chirp present in the spectral fringe. This may be a useful alternative to numerical dechirping when real-time feedback on image quality is required. It may also be a complement to numerical dechirping, but one which sidesteps the bottlenecks imposed by the image SNR and computational tractability. While the fastest retinal volumes we acquired (1 kHz) required a very small field of view ($\sim 128$ µm × 64 µm), this still permits imaging of between 500 and 300 cones simultaneously, at eccentricities of 1° to 2°, respectively, enough to study the fundamental properties of the ORG and establish ORG norms.

In addition to limiting the FOV, high speed OCT imaging also requires shorter integration times on the sensor and subsequently lower spectral fringe contrast, which reduces the system’s sensitivity and its images’ SNR. One of the consequences of reduced SNR is poorer displacement sensitivity, although this reduction can be attenuated by increasing the power in the reference arm, as can be seen in the values computed from retinal images acquired at different volume acquisition rates.

The tradeoff between displacement sensitivity and speed may be fortuitous, though. The minimum volume rate required for measuring the ORG is dictated by the initial velocity of the elongation phase. In previous work [8] we observed elongation velocities as high as 3 µm⋅s⁻¹, corresponding to 50 rad⋅s⁻¹ or $8\mathrm{w}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{s}\cdot {\mathrm{s}}^{-1}$, to flashes that bleached 70$\mathrm{\%}$ of cone photopigment. These require, minimally, volume rates of 16 Hz to avoid $2\pi$ phase wrapping ambiguities, but higher sampling rates offer a better safeguard against them. The initial elongation rates in response to flashes bleaching 1.8$\mathrm{\%}$ were approximately 30 times slower, and could be successfully imaged with correspondingly slower volume rates. This means that the responses to dim stimuli, close to the noise floor, can be measured at lower rates with correspondingly higher SNR, while responses to bright stimuli can be measured with higher speeds since the subsequent lower SNR is less of a factor.

In this work we have described a retinal imaging system incorporating FF-SS-OCT and hardware AO. The system provides sufficient axial and lateral resolution for resolving foveal cone photoreceptors–which have not yet been visualized using FF-SS-OCT with DAC–and sufficient displacement sensitivity (<10 nm) to measure optoretinographic responses to dim stimuli. The system can double as a flood illumination fundus camera with imaging rates of at least 1 kHz. Future plans include implementing Powell lenses in the imaging light source to convert the beam from Gaussian to top-hat, improving the uniformity of illumination without compromising the power at the sample and reference arms, incorporation of a DMD-based visible stimulus channel and AO subsystem with higher speed and dynamic range, comparisons of AO and DAC approaches to aberration correction, and investigations of ORG changes in patients with diseases of the retina.

Funding

National Eye Institute10.13039/100000053 (R00-EY-026068, R01-EY-026556).

Disclosures

RSJ and RJZ have patents related to AO-OCT. DV and KVV declare no conflicts of interest.