Full-field spectral-domain optical interferometry for snapshot three-dimensional microscopy

Abstract

Prevalent techniques in label-free linear optical microscopy are either confined to imaging in two dimensions or rely on scanning, both of which restrict their applications in imaging subtle biological dynamics. In this paper, we present the theoretical basis along with demonstrations supporting that full-field spectral-domain interferometry can be used for imaging samples in 3D with no moving parts in a single shot. Consequently, we propose a novel optical imaging modality that combines low-coherence interferometry with hyperspectral imaging using a light-emitting diode and an image mapping spectrometer, called Snapshot optical coherence microscopy (OCM). Having first proved the feasibility of Snapshot OCM through theoretical modeling and a comprehensive simulation, we demonstrate an implementation of the technique using off-the-shelf components capable of capturing an entire volume in 5 ms. The performance of Snapshot OCM, when imaging optical targets, shows its capability to axially localize and section images over an axial range of ±10 µm, while maintaining a transverse resolution of 0.8 µm, an axial resolution of 1.4 µm, and a sensitivity of up to 80 dB. Additionally, its performance in imaging weakly scattering live cells shows its capability to not only localize the cells in a densely populated culture but also to generate detailed phase profiles of the structures at each depth for long durations. Consolidating the advantages of several widespread optical microscopy modalities, Snapshot OCM has the potential to be a versatile imaging technique for a broad range of applications.

1. Introduction

Designing a versatile microscopy technique for biosciences requires the engineer to make some critical choices to maximize its functionalities, such as three-dimensional imaging, speed, resolution, contrast, and field-of-view, while minimizing the compromises made. These choices can be perceived as a series of theoretical and practical decisions, each to ensure that all of the features of the microscope can be retained. Some of these theoretical decisions include the choice between confocal and widefield imaging [1,2], the mechanism for axial sectioning [3–6], the excitation source, and the detector.

The goal of this paper is to design and demonstrate a novel optical microscopy technique for 3D imaging of sample dynamics label-free. To enable this, we examine both the theoretical and the practical choices involved in its design. Among the different label-free approaches, scattering is observed in any sample with a non-uniform refractive index and an optimal choice to ensure the versatility of the microscopy setup [7]. The second choice is between widefield imaging and point-scanning confocal microscopy (PSCM). While PSCM enhances the image contrast by rejecting any out-of-focus light, the ease of implementing widefield imaging and the stability it affords for tracking dynamic changes make it more optimal for applications in bioimaging [1]. It is well-known that PSCM requires scanning mirrors to position a focal region that imparts a considerable optical intensity on the sample at each point, and proves particularly advantageous in 3D layered samples such as biological tissues, particularly with the optical sectioning ability of the confocal geometry. On the other hand, widefield imaging is favorable in its ease of implementation, its lower photo-exposure on the sample, and its ability to create a snapshot of spatially co-registered sample dynamics at every time point through parallel detection of multiple lateral pixels. Widefield imaging is commonly utilized in techniques such as Quantitative Phase Imaging (QPI) or Differential Interference Contrast (DIC) microscopy for imaging thin, transparent, and sparse samples [8]. However, these techniques are usually implemented in transmission mode and the performance of widefield imaging in these contexts for observing 3D samples is poor due to the lack of axial sectioning.

As an alternative to confocal axial sectioning, coherence gating can be used to enable axial sectioning in widefield imaging. This principle is utilized in techniques such as full-field optical coherence microscopy (FF-OCM) to achieve isotropic sub-micron resolution [9,10]. While traditional FF-OCM requires a physically modulated reference arm, variants such as the off-axis FF-OCM [11], which uses a spatially modulated reference arm with a diffraction grating, or single-shot FF-OCM [12,13], which acquires four phases simultaneously by stepping the phase using a combination of waveplates and geometrical phase shifts, require no moving parts for imaging within a plane. Since coherence gating requires an interferometric setup, the complex-valued scattered field from the sample can be measured instead of the real-valued intensity. One of the major challenges to widefield imaging, particularly in the reflection mode such as that in FF-OCM, is the increased presence of signal-degrading speckles arising from coherent cross-talk. Mathematically, one must perform three measurements along three orthogonal axes for discerning the 3D information. Since the information along $x$ and $y$ is known through widefield imaging or PSCM, an additional measurement must be performed along $z$ (e.g. FF-OCM [14] or time-domain OCM [15]), the wavelength, $\lambda$ (e.g. spectral-domain OCM (SD-OCM) [16]), or at different incident angles, $\theta$ (e.g. digital holography [17,18]). Among these, a hyperspectral camera can measure the scattered field in $x$, $y$, and $\lambda$. In fact, hyperspectral cameras have been previously used for light field imaging at larger spatial scales [19].

In this paper, we present a novel optical microscopy technique for full-field 3D low coherence interferometry with no moving parts, designed based on simple principles using well-characterized commercially available components, and called Snapshot OCM. Using a broadband light-emitting diode (LED) as the source and a hyperspectral camera as the detector, Snapshot OCM can measure the 3D complex-valued scattered optical field from the sample with micron-scale transverse and axial resolutions. Practically, an LED has several advantages over other broadband sources such as superluminescent diodes or mode-locked lasers for full-field imaging. Firstly, LEDs are low-cost components that also consume low power [20]. Secondly, LED-based illumination can be designed to be spatially incoherent; since signal-degrading speckles arising from coherent cross talk are a major problem in full-field imaging, a spatially incoherent light source can drastically reduce them [21–23]. While there are several configurations of commercially available hyperspectral cameras, we have used the image mapping spectrometer (IMS)-based hyperspectral camera as an example for both simulation and practical demonstrations [24]. Previous attempts for tomographic imaging using hyperspectral cameras have proven successful for imaging samples with spatial resolutions of tens of microns [25]. In the next section, we present a comprehensive simulation of the entire setup to verify the principles of Snapshot OCM and have demonstrated its various features including 0.8 µm transverse resolution and 1.4 µm axial resolution, 3D full-field imaging with no moving parts, the ability to detect subtle refractive index gradients in biological samples, and the ability to generate highly detailed phase profiles of non-sparse samples in three dimensions.

It is critical to note that each of the imaging modalities mentioned above has been widely utilized for clinical and research applications. Hence, using commercially available and thoroughly characterized technologies and components to develop our optical setup makes Snapshot OCM easily adaptable to various environments and versatile applications. Moreover, Snapshot OCM can be seen as a natural progression from FF-OCM techniques without any movable parts, extending its capabilities to 3D imaging, and offering spectral detection as a supplementary contrast mechanism. By offering unique advantages over other comparable techniques, Snapshot OCM can fill critical gaps in optical microscopy.

2. Theoretical feasibility of Snapshot OCM

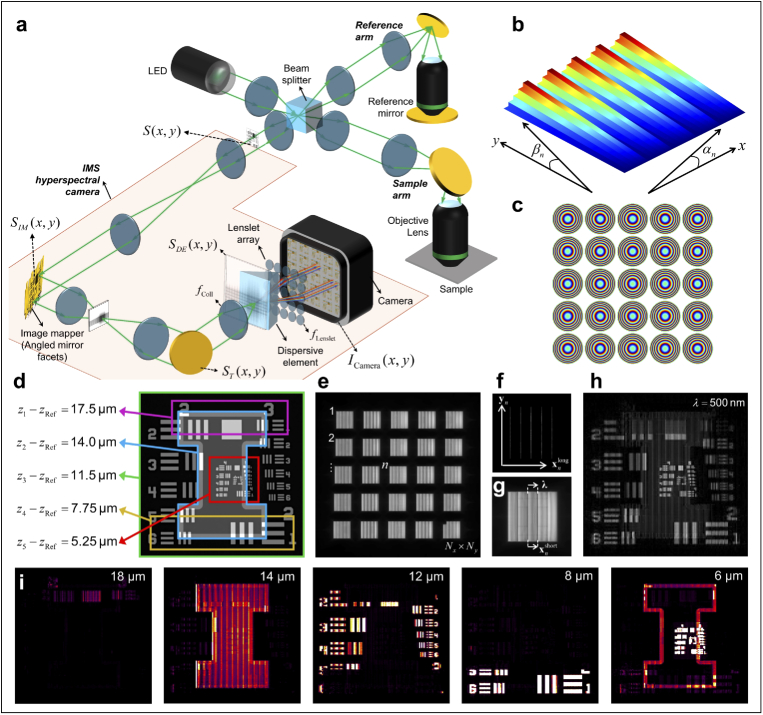
Since the concept of 3D snapshot tomography is previously under explored, it raises the necessity to establish its theoretical feasibility. Figure 1(a) shows the schematic representation of our Snapshot OCM setup. While the excitation, sample, and reference arms are typical of an FF-OCM setup, the detection arm is an IMS hyperspectral camera. Briefly, an IMS hyperspectral camera consists of an image mapper, a dispersion element, and a lenslet array that relays the image to a camera with a large format sensor. We simulated the image formation in our setup in three dimensions, $x$, $y$, and $z$, where the direction of propagation of light is $z$. Firstly, we assume that the interference pattern at the entrance of the camera, $S(x,y)$, is the interference between the signal from the sample arm and the reference arm. After the first translation of $S$ to the image mapper, which consists of a stack of angled mirror facets, the image mapper splits the image, $S_{\mathrm{I}\mathrm{M}}(x,y)$, into a stack of $N$ slices along $x$, where each slice is deflected in $x$ and $y$ directions by angles ${\alpha }_n$ and ${\beta }_n$, respectively, and $n$ ranges from 1 to $N$. Assuming that the lenslet array consists of $N_x$ lenses along $x$ and $N_y$ lenses along $y$, we define ${\alpha }_n\in \{1,2,\dots ,N_x\}\times {\theta }_x$ and ${\beta }_n\in \{1,2,\dots ,N_y\}\times {\theta }_y$. This ensures that these slices are remapped into different locations on the camera, divided into $N_x\times N_y$ blocks with $\frac{N}{N_x\times N_y}$ slices per block. Adjacent image slices within a single block are separated by a distance $\mathrm{\Delta }x$ along $x$. After passing through a dispersive element (a prism or a diffraction grating), each slice is dispersed along $x$ for spectroscopic measurements. Finally, the lenslet array maps this onto the camera, where the image formed is discretized such that each slice spans $Y$ pixels along $y$ and the spectrum of each slice is dispersed over $M$ pixels. From this raw image, each point in the object can be recovered to form a discrete 3D data cube, $I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}(\mathbf{x},\mathbf{y},\mathit{\lambda })$, of size $N\times Y\times M$ using 4 coordinates: the block number corresponding to the lenslet, $\mathbf{n}\in \{1,2,\dots ,N_x\times N_y\}$, the $y$ coordinate in each block, ${\mathbf{y}}_n$, the $x$ coordinate for the slice at $\lambda ={\lambda }_c$ (where ${\lambda }_c$ is the central wavelength), ${\mathbf{x}}_n^{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}$, and the wavelength of the slice spread along the $x$ direction, ${\mathbf{x}}_n^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}=f_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}(\mathit{\lambda })$ (where $f_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}(\mathit{\lambda })$ is the function of the dispersion element). Under ideal conditions, both $\mathbf{x}=\{{\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_N\}$ and $\mathbf{y}=\{{\mathrm{y}}_1,{\mathrm{y}}_2,\dots ,{\mathrm{y}}_Y\}$ can be assumed to be linear, and $\mathit{\lambda }=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_M\}=f_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{-1}(\{{\mathrm{x}}_{n,1}^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}},{\mathrm{x}}_{n,2}^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}},\dots ,{\mathrm{x}}_{n,M}^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}\})$, where ${\lambda }_{\frac{M}{2}}={\lambda }_c$ and ${\lambda }_M-{\lambda }_1=\mathrm{\Delta }\lambda$. While the vectors ${\mathbf{x}}_n^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}$ and ${\mathbf{x}}_n^{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}$ help in orienting oneself to the image captured at the camera plane, the reconstructed data cube, $I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}$, is in the same spatial dimensions and orientation as the object plane i.e. $(\mathbf{x},\mathbf{y},\mathit{\lambda })$. A schematic illustration of the mechanism of an IMS hyperspectral camera is shown in Supplementary Fig. S1. The calibration and reconstruction algorithms are described in detail in Cui et al. [26].

Fig. 1.

(a) Schematic representation of Snapshot OCM using an LED as light source and an IMS-based hyperspectral camera as a detector. The areas shaded orange denote the camera. The optical path lengths of the sample and the reference arms are assumed to be nearly equal. (b) The image mapper simulated as a pure phase function. The surface plot of the phase is shown here after unwrapping along $y$. Note that the angles ${\alpha }_n$ and ${\beta }_n$ are usually very similar; however, since the size of each slice along $y$ is significantly longer than its size along $x$, the range of phase for the same tilt is significantly larger in $y$ than in $x$. Therefore, the tilt of each slice along $x$ appears negligible. (c) The phase of the simulated lenslet array. (d) The simulated 3D object where the different features are highlighted with borders of different colors to indicate their axial displacements with respect to the reference arm. (e) The simulated image on the camera after illumination with a broadband light source. Each block represents the image formed after a lenslet, the adjacent numbers indicate the address of the lenslet array. (f) Representative image on the camera for monochromatic illumination from a single lenslet to illustrate the effect of image slicing, the gap between two adjacent slices, and the addressing schema. (g) Representative image on the camera for broadband illumination from a single lenslet to illustrate the effect of the dispersive element in filling the gaps between adjacent slices and the addressing schema that is relevant for reconstruction. (h) $|I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}(x,y,\lambda =\text{500 nm})|$ reconstructed from the image in (e). (i)  Filmstrip of $|E_{\mathrm{O}\mathrm{C}\mathrm{M}}|$ at different depths in the Snapshot OCM volume that has the closest match to the depths in (d). The numbers at the top right corner of each frame indicates its location in $z$.

The reconstructed data cube is expressed in terms of the optical field from the sample and reference arms as

$$I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}(\mathbf{x},\mathbf{y},\mathit{\lambda })=\mathrm{\Re }\left(\begin{array}{l}|S_{\mathrm{R}\mathrm{e}\mathrm{f}}(\mathbf{x},\mathbf{y},\mathit{\lambda }){|}^2\\ +{\int }_z|S_{\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}(\mathbf{x},\mathbf{y},\mathit{\lambda },z){|}^2\\ +\begin{array}{c}{\int }_z{S}_{\mathrm{R}\mathrm{e}\mathrm{f}}(\mathbf{x},\mathbf{y},\mathit{\lambda })S_{\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}(\mathbf{x},\mathbf{y},\mathit{\lambda },z)\\ e^{j\frac{4\pi }{\mathit{\lambda }}(z-z_{\mathrm{R}\mathrm{e}\mathrm{f}})}\end{array}\end{array}\right),$$ (1)

where $S_{\mathrm{R}\mathrm{e}\mathrm{f}}$ is the optical field from the reference arm, $S_{\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}(z)$ is the scattered field from the sample from a depth of $z$, and $z_{\mathrm{R}\mathrm{e}\mathrm{f}}$ is the optical path length of the reference arm. Given $I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}$ and an incoherent background $I_{\mathrm{B}\mathrm{a}\mathrm{c}\mathrm{k}}=|S_{\mathrm{R}\mathrm{e}\mathrm{f}}{|}^2$ after neglecting the self-interference of the scattered signal from the sample, the 3D reconstructed complex-valued field in the $(x,y,z)$ domain, $|E_{\mathrm{O}\mathrm{C}\mathrm{M}}|$, can be estimated using the non-uniform discrete Fourier transform (NUDFT) [27]. While SD-OCM traditionally employs resampling the spectral data to be linear in $k$ through interpolation followed by an inverse Fourier transform, the limited number of spectral samples in Snapshot OCM led to the choice of NUDFT as the method for OCM reconstruction in this paper. We define a row vector for wavenumbers, $\mathbf{k}=\{k_1,k_2,\dots ,k_M\}=\frac{2\pi }{\mathit{\lambda }}$, which need not be linear, and a vector of axial coordinates, $\mathbf{z}=\{z_1,z_2,\dots ,z_M\}$, linearly spaced between $-\frac{1}{2}{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $\frac{1}{2}{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, where $z_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is approximately the half coherence length of a beam centered at ${\lambda }_c$ with a bandwidth of $\frac{\mathrm{\Delta }\lambda }{M}$. The details of the effects of $\mathrm{\Delta }\lambda$ and $M$ on the axial resolution and axial range of Snapshot OCM are illustrated in Supplementary Fig. S2 and are discussed in Supplement 1 ^{(41.5MB, pdf)} . $E_{\mathrm{O}\mathrm{C}\mathrm{M}}(\mathbf{x},\mathbf{y},\mathbf{z})$ is given by

$$E_{\mathrm{O}\mathrm{C}\mathrm{M}}(\mathbf{x},\mathbf{y},\mathbf{z})=\sum _{i=1}^M(I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}(\mathbf{x},\mathbf{y},k_i)-I_{\mathrm{B}\mathrm{a}\mathrm{c}\mathrm{k}}(\mathbf{x},\mathbf{y},k_i))e^{j2k_i\mathbf{z}}$$ (2)

We simulated this setup using Fresnel free-space propagation vectors, a phase-only image mapper (Fig. 1(b)), parabolic phase functions to represent ideal lenses and the lenslet array (Fig. 1(c)), and a dispersion element whose angle of dispersion is linearly related to $\lambda$ in MATLAB (Mathworks Inc., Natick, MA, USA). An object was simulated as an USAF target overlaid on the "block I-logo" of the University of Illinois, as seen in Fig. 1(d), where different parts of the object are displaced by arbitrary distances in $z$ using the phase function, $e^{j\frac{2\pi }{\lambda }(2z)}$. This simulates a 3D object in space, without any defocus. The complete set of equations describing the simulation are provided in Supplement 1 ^{(41.5MB, pdf)} . When simulated for the conditions $N_x=N_y=5$, $N=125$, ${\lambda }_c=500\mathrm{n}\mathrm{m}$, 500 pixels along $y$, and $\mathrm{\Delta }\lambda =150\mathrm{n}\mathrm{m}$ corresponding to 90 spectral samples, the simulated image at the camera is shown in Fig. 1(e), where the distribution of image slices between the lenslets and the dispersion for the various wavelengths of incident light can be observed. By carefully choosing the angle of dispersion for the dispersive element, the length of the vector ${\mathbf{x}}_n^{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}$ can be set as ${\mathbf{x}}_{n,2}^{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}-{\mathbf{x}}_{n,1}^{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}$ for a given light source. Figure 1(f,g) elucidate the coordinate system, and the difference between a monochromatic and a broadband image for an arbitrary block formed on the camera. Figure 1(h) shows the reconstructed data cube from the image in Fig. 1(e) at 500 nm, where there are artifacts observed in the images due to slicing, even under ideal simulation conditions. Additionally, there is also an apparent loss to the image resolution due to the discretization as a consequence of slicing. Furthermore, the contrast in the image is not only due to the features present in the object, but also due to the position of different parts of the image in $z$. While, it is impossible to localize the axial positions of each feature based on the images in the $(x,y,\lambda )$ domain, observing the 3D image in the $(x,y,z)$ domain, as shown in Fig. 1(i), can localize each feature to its appropriate axial location. The transverse spatial resolution of the images remains unchanged from its spectral-domain counterpart after NUDFT across all depths. The theoretical axial resolution for the simulated beam, as defined by the bandwidth of the source, was 1.67 µm, whereas $\mathbf{z}$ was set to be a linearly spaced vector of 40 elements between $-$19 µm and 20 µm. Therefore, each feature, which is theoretically infinitesimally thin, is seen in approximately 3 pixels along $z$ in the reconstructed images. Additionally, the artifacts in the image due to slicing are also apparent in the reconstructed $(x,y,z)$ domain images. Moreover, there is a roll-off to the image intensity, i.e., the features are placed farther away from the zero optical path difference (OPD) location, typically observed in SD-OCM. Furthermore, for the optical planes closer to 0 OPD, the brightest image features from DC component of the signal, i.e. the outline from the "block I-logo" and parts of the USAF target, are visible. These artifacts can be reduced in the practical implementation of Snapshot OCM by acquiring a background containing the respective self-interference of both the sample and reference signals with the overall OPD beyond than the axial range of imaging.

While the detailed analysis of these results is presented in Section 5, these results from simulation clearly prove the theoretical feasibility of Snapshot OCM; with a hyperspectral camera and a broad-band light source, 3D information from the sample could be accurately recovered using full-field imaging with no moving parts. As the next step, we implemented Snapshot OCM practically to evaluate its performance and observe its capabilities in imaging biological specimen.

3. Experimental evaluation of Snapshot OCM

The Snapshot OCM setup was sourced by a mounted LED centered at 565 nm and expected to generate a bandwidth of 104 nm. (M565L3, Thorlabs, Inc., Newton, NJ, USA). The hyperspectral camera was assembled by Rebellion Photonics, Inc. (Houston, TX, USA), with a $5\times 8$ lenslet array and 12 image slices per lenslet. The detector used in the hyperspectral camera was a 12-bit 12 MP CCD camera (B4822M, Imperx, Inc, Boca Raton, FL, USA) with a maximum frame rate of 3.3 Hz. The same water immersion objective lens (LUMPLFLN40XW, Olympus Corporation, Waltham, MA, USA) with a numerical aperture of 0.8 was used in both the sample and reference arms. The LED was operated at its rated maximum current of 1 A. The incident power on the sample was less than 25 mW and the exposure time of the camera was adjusted between 2 ms and 5 ms such that it was always operated near saturation. The background for each volume was taken by moving the reference arm well beyond the axial range of the setup from peak interference.

Data was acquired using a custom LabVIEW software (National Instruments Corporation, Austin, TX, USA). Real-time display was implemented using a CUDA-based program with accelerated computing on a graphical processing unit (GeForce RTX 2080 Ti, NVIDIA Corporation, Santa Clara, CA, USA) to reconstruct and display both $I_{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}}$ and $E_{\mathrm{O}\mathrm{C}\mathrm{M}}$ after NUDFT. The raw data was later processed in MATLAB with additional steps to correct the wavefront and dispersion mismatch errors between the sample and the reference arms. The wavefront error was modelled as a transversely variant second-order polynomial phase function which was applied to the Fourier transform of $E_{\mathrm{O}\mathrm{C}\mathrm{M}}$ in the $(x,y,k)$ domain. Similarly, the dispersion mismatch was modelled as a fourth order transversely invariant function of $k$. The images corrected for these errors, $E_{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}}$, can be described as

$$E_{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}}(x,y,z)={\mathfrak{F}}_{k\to z}^{-1}\left(\begin{array}{l}{e}^{jk({\gamma }_0+{\gamma }_{1}x+{\gamma }_{2}y+{\gamma }_3{(x-x_c)}^2+{\gamma }_4{(y-y_c)}^2)}\\ \cdot e^{j({\alpha }_4{k}^4+{\alpha }_3{k}^3+{\alpha }_2{k}^2+{\alpha }_{1}k+{\alpha }_0)}\\ \cdot {\mathfrak{F}}_{z\to k}(E_{\mathrm{O}\mathrm{C}\mathrm{M}}(x,y,z))\end{array}\right)$$ (3)

where $\mathfrak{F}$ is the Fourier transform, and ${\gamma }_{0-4}$, $x_c$, and $y_c$ are tuned manually based on the visual response from the phase of the OCM images to ensure a flat phase profile in the empty regions. Similarly, ${\alpha }_{0-4}$ were tuned to minimize the axial resolution of the reconstructed Snapshot OCM cross-section images.

Theoretically, the axial resolution and the axial range for the camera are 1.27 µm and $\pm$12 µm, respectively. However, since the measured effective bandwidth of the LED is approximately 150 nm (see Supplement 1 ^{(41.5MB, pdf)} ), the expected axial resolution is 1.42 µm (see Supplementary Fig.S3). Additionally, due to the nonlinearity of the dispersion element used in the camera, the images were reconstructed to span an axial distance of $\pm$10 µm in air over 40 pixels. The detailed explanation for these calculations are presented in Supplement 1 ^{(41.5MB, pdf)} . While, one of the blocks the simulated camera images shown in Fig. 1(e) has a part of its features cut-off due to the edge effects of Fourier transform and Fresnel propagation, similar effects were not observed in the images acquired from the IMS hyperspectral camera (Supplementary Fig. S4).

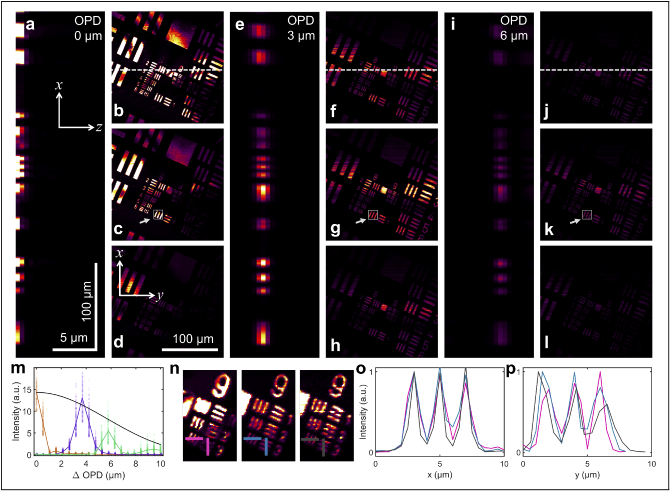
A reflective USAF target was used as the sample and was placed at different optical path differences (OPD), by moving the reference mirror. Figure 2(a,e,i) show the cross-sectional ($x$-$z$) view of the USAF target after reconstruction in the time domain, after cropping out the complex conjugate. The reflective target appears to span 3 pixels along $z$ for each OPD, corresponding to 1.5 µm, which matches closely with the theoretical axial resolution. When the OPD is close to 0, spatial interference of the sample and reference beams induces artifacts to the reconstructed en face ($x$-$y$) images for the three axial locations of highest intensity (Fig. 2(b-d)). In contrast, while there is a decrease to the overall image intensity when the OPD is approximately 3 µm, observed both in the cross-sectional (Fig. 2(e)) and en face images (Fig. 2(f-h), the artifacts due to spatial interference are absent, and all the original features of the object are preserved. This drop in intensity seen in the color scale of the en face and cross-sectional images at each depth matches closely with the theoretical roll-off of sensitivity with depth calculated from Eq. (3) in [28] (Fig. 2(m)) for the regions-of-interest indicated. The peak signal-to-noise ratio (SNR), calculated as the ratio of the 99^th to the 1^st quantile of $|E_{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}}|$ for the depth with maximum intensity, drops from 80 dB to 70 dB, and then to 64 dB when the OPD is 0 µm, 3 µm, and 6 µm, respectively. This decrease in SNR is more pronounced as the images are placed farther away from the position of 0 OPD, as seen in the en face images for an OPD of 6 µm shown in Fig. 2(j-l). However, when the color scale is normalized, as seen in Fig. 2(n), the images at the three different OPDs retain all the features in the object. In fact, the smallest grouping on the target is still visible and resolvable for all OPDs. The transverse resolution can be calculated based on the graphs shown in Fig. 2(o,p), plotted along the lines shown in Fig. 2(n), along both $x$ and $y$, and is approximately 0.8 µm, showing that the effect of slicing the images and reconstructing them later does not affect the optical resolution of the reconstructed images. Overall, these results show that Snapshot OCM can enable 3D imaging and axial localization for the entire imaging range. Having evaluated the performance of Snapshot OCM on standard imaging targets, we demonstrated its performance on biological samples.

Fig. 2.

(a) Cross section of a Snapshot OCM volume of an USAF target placed at 0 OPD in the $x$-$z$ plane through the ${300}^{\mathrm{t}\mathrm{h}}$ pixel in $y$ (along the white dotted line in (b)). (b-d) Corresponding en face images from a Snapshot OCM volume of an USAF target placed at 0 OPD at the three consecutive depths of maximum intensity in the cross-sectional images shown in (a). (e) Cross-section of a Snapshot OCM volume of an USAF target placed at an OPD of approximately 3 µm through the ${300}^{\mathrm{t}\mathrm{h}}$ pixel in $y$ (along the white dotted line in (f)). (f-h) Corresponding en face images from a Snapshot OCM volume of an USAF target placed at OPD of approximately 3 µm at the three consecutive depths of maximum intensity in the cross-sectional images shown in (e). (i) Cross-section of a Snapshot OCM volume of an USAF target placed at an OPD of approximately 6 µm through the ${300}^{\mathrm{t}\mathrm{h}}$ pixel in $y$ (along the white dotted line in (j)). The legend for the axes and the scale bars also correspond to the other cross sectional images in (a) and (e). (j-l) Corresponding en face images from a Snapshot OCM volume of an USAF target placed at OPD of approximately 6 µm at the three consecutive depths of maximum intensity in the cross-section images shown in (i). The legend for the axes and the scale bars also correspond to the other en face images in (b-d) and (f-h). (m) Graph that depicts the variation of image intensity ($|E_{\mathrm{O}\mathrm{C}\mathrm{M}}{|}^2$) at different $z$ locations for region of interest indicated in (c), (g), and (k) from three Snapshot OCM volumes of the USAF targets at different OPDs. The solid line indicates the median intensity at each depth while the points show the distribution of all the raw values. The colors gold, purple, and green correspond to OPDs of 0, 3, and 6 µm, respectively. The black line is the theoretical roll-off of sensitivity with depth [28] normalized to the maximum intensity at 0 OPD. (n) Zoomed-in and intensity-normalized en face images of the smallest bars in the USAF target at the same locations in $z$ as that of (c), (g), and (k). The horizontal and vertical lines show the slices along which the graphs in (o) and (p) are plotted to calculate the transverse resolution. (o) The intensity of the structures along the horizontal lines in (n), where the color of the plot corresponds to the color of the corresponding line, i.e. pink, blue, and gray correspond to OPDs of 0, 3, and 6 µm, respectively. (p) The intensity of the structures along the vertical lines in (n), where the color of the plot corresponds to the color of the corresponding line, i.e. pink, blue, and gray correspond to OPDs of 0, 3, and 6 µm, respectively.

4. Demonstration of Snapshot OCM on biological samples

To demonstrate the performance of Snapshot OCM for biological applications, we imaged a concentrated cluster of mouse renal mesangial cells cultured on a flat surface. Secondary cultures of SV40 MES 13 mouse mesangial cells (CRL-1927, American Type Culture Collection, Manassas, VA, USA) were plated on a 35-mm Petri dish with a cell adherent coating and grown in Iscove’s Modified Dulbecco’s Medium with no phenol red (21056023, Thermo Fisher Scientific, Waltham, MA, USA), supplemented with 10% v/v fetal bovine serum (16140071, Thermo Fisher Scientific, Waltham, MA, USA) and Penicillin-Streptomycin-Glutamine (10378016, Thermo Fisher Scientific, Waltham, MA, USA) for 30 hours in an incubator at 37°C in an environment with 95% air and 5% CO2. The cells were imaged at room temperature within 10 minutes of being taken out of the incubator.

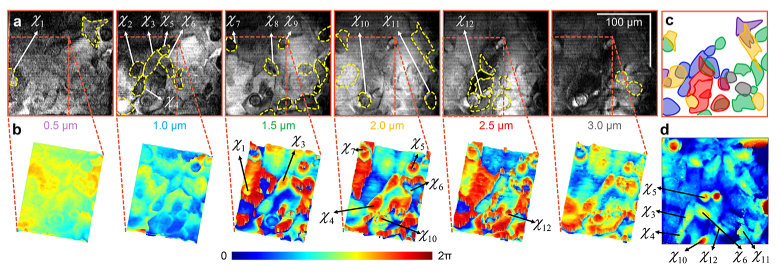
Figure 3(a) shows a stack of en face images of the magnitude of the scattered field at the depths indicated below each panel. A few cells and features were manually annotated, based on both positive and negative contrasts. Since these cells were grown on a partially reflective glass surface, the bulk of the interference pattern was formed not due to the scattering from the cells themselves, but from the light reflected off the glass surface after passing through the cells, as illustrated in Supplementary Fig. S5. While the glass surface is only theoretically 0.3% as reflective as the USAF target (Fig. 2), the peak SNR of the Snapshot OCM images shown is sufficiently high, at 40 dB. Therefore, based on the differences between the refractive index of the cells compared to that of the surrounding culture media, the cells appear axially displaced. While previous studies on full-field and spectral-domain OCM have used physical darkfield apertures to filter the backreflections from the glass surface [29–31], we chose to use computational darkfield filters instead if needed during post-processing to maximize signal collection during imaging. These segmentations are collated and shown in Fig. 3(c), where the colors of the cells correspond to the depths from which they were segmented. However, some of the features are apparent at more than one depth due to the axial length of the objects and the axial resolution of our setup; for instance, the cell marked ${\chi }_{10}$ is visible across all depths and its shape and profile can be tracked along these depths independently. While it appears to have a rounded shape between 2-3 µm, it has a distinctly hollow shape between 0.5-1.5 µm. A traditional FF-OCM image was acquired by splitting a part of the detection arm with a beam splitter cube and capturing the interference pattern with an independent camera. Images acquired at four phase differences between the sample and the reference arm close to 0 OPD were combined to generate a single phase image. Compared to the standard FF-OCM phase image shown in Fig. 3(d), the contrast between different structures in the sample is markedly better for the Snapshot OCM images. Particularly, the magnitude of the Snapshot OCM images has sharp boundaries between features and better contrast compared to a gradual gradient between the different features in the magnitude of the traditional FF-OCM images (Supplementary Fig. S6). Since the traditional FF-OCM images were taken with an independent camera, the image appears distorted transversely compared to the Snapshot OCM images. This could be attributed to differences in the wavefront errors in the optics in the two detection paths.

Fig. 3.

(a) Stack of the magnitude of en face Snapshot OCM images of mouse mesangial cells cultured densely on a flat surface at contiguous series of depths. The exact axial locations in microns are indicated below each frame. The dotted yellow lines highlight a few structures that were manually annotated based on the contrast due to changes in intensity at each depth. Particular structures of interest are labelled ${\chi }_1$-${\chi }_{12}$ at different depths. Scale bar: 100 µm. (b) Surface plot of the phase of the Snapshot OCM images for the same depths corresponding to a zoomed-in region in the intensity images in (a). The phase profiles of the structures of interest in (a) are marked with the same labels. The intensity and phase images of the cells in (a) and (b) were median filtered with a 5$\times$2 and a 4$\times$4 window, respectively, to enhance visualization. (c) An overlay of the different annotated structures in (a). The color of each structure corresponds to the color of the font that indicates the axial locations of frames in (a). (d) Phase of a traditional FF-OCM image of the same sample acquired with an independent camera. The structures of interest are marked with the same labels in (a) and (b).

Although the contrast between different features is more apparent in the magnitude of the Snapshot OCM images, additional details about the shape and structure of the cells can be observed in the phase of the Snapshot OCM images shown in Fig. 3(b). Highly detailed profiles of the cells marked ${\chi }_1$, ${\chi }_{3-7}$, ${\chi }_{10}$, and ${\chi }_{12}$ are visible. These profiles encode information about the axial locations, profiles, and the orientations of the cells. For instance, by tracking the phase of cells ${\chi }_3$ and ${\chi }_4$ across the different depths and assuming that the cells have equal refractive indices, it is apparent that ${\chi }_3$ is slightly closer to 0 OPD than ${\chi }_4$. Additionally, the shapes of cells ${\chi }_3$ and ${\chi }_4$ are significantly different from those of ${\chi }_5$ and ${\chi }_{10}$ between 1.5 and 3.0 µm. In fact, overall, there are two distinct cell populations observed throughout the cultures, rounded (${\chi }_5$, ${\chi }_7$, ${\chi }_9$, ${\chi }_{10}$, and ${\chi }_{12}$) and fibroblast-like (${\chi }_1$, ${\chi }_3$, ${\chi }_4$, ${\chi }_6$, and ${\chi }_8$). This is expected for the mouse renal mesangial cell-line used here, which is myofibroblast-like. However, since the phase is cumulatively modified across these depths, the differentiation of the phase between two depths can decouple this effect and provide a detailed 3D model of the cell similar to QPI, as seen in Supplementary Fig. S7. Nonetheless, the phase profiles in OCM cannot be directly and generally translated to physical distances since the physical distance of the optical path is unknown in Snapshot OCM compared to QPI, although application-specific assumptions can help interpret the phase of OCM signals to physical quantities derived from QPI. The cross-sectional and en face Snapshot OCM images of the SV40 cells along the $x$-$y$, $x$-$z$, and $y$-$z$ planes at different locations are shown in Supplementary Fig. S8. These results demonstrate that Snapshot OCM has the unique capability of being able to localize and generate detailed spatial profiles of extended clustered biological features though full-field spectral domain imaging. In particular, we have shown our setup to be not only low cost and implemented using off-the-shelf components, but also that its resolution and axial range are optimal for imaging dense cell cultures in 3D.

Next, we imaged the dynamic response of NIH 3T3 mouse fibroblasts (CRL-1658, American Type Culture Collection, Manassas, VA, USA) to Paclitaxel, a microtubule stabilizer. Typically, fibroblasts cells tend to extend protrusions based on mechanical and chemical cues and form a network. On the other hand, Paclitaxel disrupts the cellular structures, thereby inducing collapse of these networks. Figure 4 shows the complex-valued scattered field from a culture of fibroblasts on a flat surface, following the protocols previously described for the SV40 cells, at two different depths 2 µm apart, at two different time points 30 minutes apart. Paclitaxel solution was prepared by dissolving 9 mg of powdered Paclitaxel (T7402, Sigma Aldrich, St. Louis, MO, USA) in 1 mL of complete culture media at 37°C on the day of the experiments. This solution was later added to the fibroblasts, originally containing 2 mL of complete culture media 30 s after the start of imaging (00:00:30). By observing the magnitude of the scattered field in Fig. 4, especially the regions highlighted in green, pink, and yellow, there is a distinct change apparent to the cellular morphology between the instances 00:08:00 and 00:38:00. Notably, the cell highlighted in green retracts its protrusion. By correlating these changes to the phase of the scattered field, it is apparent that contracting of this cell also causes relaxation of features along the vicinity of the cell, indicating that Paclitaxel induced changes not just to the individual cells but to the overall network. These subtle changes to the network dynamics are also visible in the regions highlighted in cyan and in white. These changes can be observed more continuously and holistically in Visualization 1 ^{(16.5MB, mp4)} , that displays the magnitude and phase of the scattered field at six different depths captured continuously at 1 volume per second for 40 minutes. The effects of the diffusion of Paclitaxel through the culture is apparent between 00:00:30 and 00:06:00, where there are drastic dynamic changes observed both to the magnitude and phase of the scattered field. After that, the overall phase of the culture remains stable, and the subtle changes induced by the effect of Paclitaxel to the fibroblasts can be seen. These results highlight that Snapshot OCM has the spatial and temporal stability for dynamic imaging of biological samples over long periods of time. Section 5 highlights the advantages of Snapshot OCM in comparison with other optical imaging techniques, elucidates the benefits and limitations of the current iteration of our system, and discusses application-driven solutions to design future Snapshot OCM setups.

Fig. 4.

Magnitude (grayscale) and phase (blue-red color map) of the scattered field from NIH 3T3 fibroblasts imaged using Snapshot OCM, displayed at depths 2.5 µm and 4.5 µm from 0 OPD at two instances in time 30 minutes apart. A 3$\times$3-pixel computational darkfield filter was added to generate the magnitude images to improve their contrast. Paclitaxel was added at time 00:00:30 at a final concentration of 3 mg/mL. Differences to the cellular morphology between the two instances at each depth are highlighted in the magnitude images, and differences to the overall network are highlighted in the phase images. The different colors (green, pink, cyan, yellow, and white) are indicative of different cells/spatial locations of interest. A computational 3$\times$3 pixel dark-field filter was added to the transverse Fourier domain at every depth to generate images of the magnitude of the scattered field. Scale bar: 100 µm.

5. Discussion

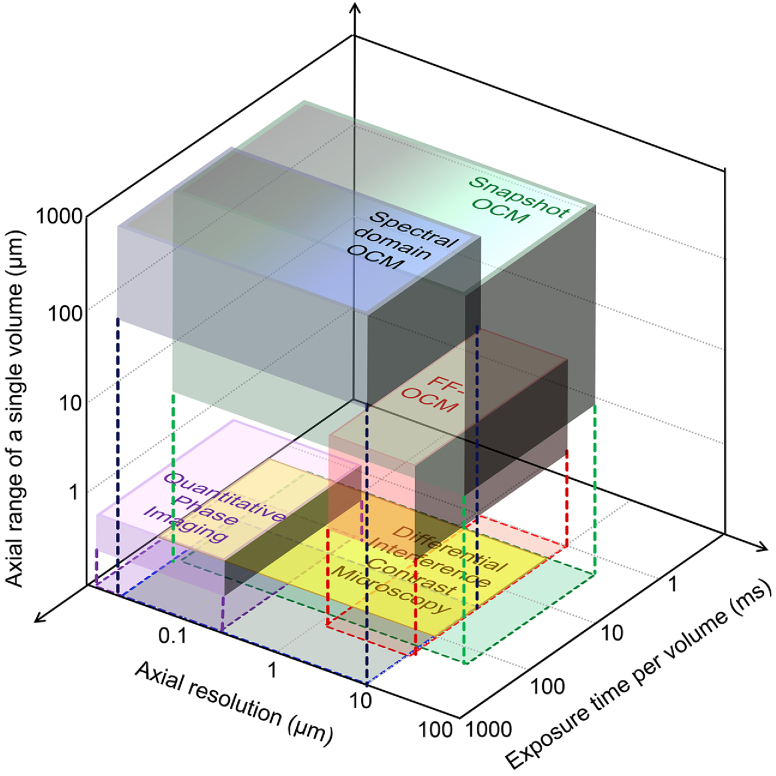
In this paper, we began with the goal of imaging biological sample dynamics in 3D. Following the logical choices made in the design of prevalent microscopy techniques such as DIC microscopy, QPI, FF-OCM, and SD- OCM, we theorized that full-field spectral-domain interferometry can be the optimal choice for 3D imaging. Having designed and demonstrated this novel microscopy modality through a Snapshot OCM setup, it is important to quantitatively compare our setup with these existing modalities. Firstly, the results show that Snapshot OCM does not cause any degradation to the transverse resolution of the overall optical setup. While there is some degradation to the image quality due to a smaller number of slices during simulation (Fig. 1(i)), when implemented practically with 480 slices in the image mapper, these effects are not observed and an isotropic resolution of approximately 1 µm is achieved (Fig. 2–4). Figure 5 shows the comparison between these different techniques based on their axial range covered in every volume, their ability to resolve features along $z$, and the exposure time per volume [32–41]. In this illustration, the exposure time required per volume was set to be the acquisition time for a single volume. Among these, brightfield microscopy and DIC microscopy are ideally designed for extremely thin samples, therefore have no axial range in the conventional sense. Additionally, these modalities are typically used in the transmission mode; therefore, the samples must be relatively transparent [8,38]. This essentially restricts the biological samples that can be imaged to sparse cell cultures and extremely thin fixed tissue slices. While these techniques are simple to implement in any environment, they provide no information about the axial profiles of the sample. While QPI is also restricted to imaging thin samples, the recovered phase is directly related to the refractive index and the physical sizes of the sample. However, when the product of the refractive index and the axial distance is greater than $\frac{\lambda }{4\pi }$, it creates phase wrapping, thereby restricting the axial range of imaging to a few hundred nanometers. Techniques such as gradient light interference microscopy (GLIM) have sought to extend the axial range of QPI by switching between two aperture sizes that alternatively provide quantitative phase information and qualitative tomograms [42]. Nonetheless, GLIM requires the acquisition of multiple independent frames to reconstruct a single volume. Similarly, Descloux et al. presented a technique for partially coherent quantitative phase imaging by Fourier filtering an image obtained on two independent cameras and a multi-plane prism [43]. While capable of imaging sample dynamics by retrieving the phase in the 3D Fourier domain, the technique relies on transmission mode and the axial volume of the technique is restricted to a couple of microns which cannot be extended without scanning.

Fig. 5.

Illustrative comparison of the capabilities of different optical imaging modalities based on their axial resolution, exposure time per volume, and the axial range covered by a single volume. Although QPI does not have an axial range in the traditional sense, the reconstructed phase does correspond to the axial profiles of the samples. Similarly, although the axial resolution of SD-OCM and Snapshot OCM is limited to a few microns based on the intensity images alone, the darker areas are included because the axial profiles due to a few tens of nanometers could be recovered from the phase of the images. The transparent rectangles represent the footprint of the 3D objects on the 2D plane and the dotted lines help orient location of each 3D object in space.

Among the coherence-gated techniques, the axial range and axial resolution are equal for FF-OCM since it generates images only along one $x$-$y$ plane. It can be argued that FF-OCM can acquire volumetric data by axial scanning. However, this was ignored since it involves not the manipulation of the optical beam but rather physical displacement of the sample, the reference mirror, or the objective lens. Additionally, both traditional methods of QPI and FF-OCM need multiple frames acquired at different locations of the reference arm to reconstruct a single complete image. Therefore, these techniques require a larger duration of photo exposure on the sample. Off-axis variants of QPI and FF-OCM overcome these limitations, usually with a small decrease to the transverse spatial resolution. Nonetheless, they are restricted to an axial range of a few microns. While each of these techniques has been implemented with cameras that can image up to a few hundred frames per second [44], they are typically used for video-rate imaging. Additionally, the images are captured over a bright background, unlike fluorescence imaging, thereby reducing the need for long exposure times. In contrast to the other techniques discussed, SD-OCM generates 3D images through 2D raster scanning. However, raster scanning intrinsically requires longer exposure times. SD-OCM setups typically report volumetric rates of 1-10 Hz, although a few specialized setups have demonstrated volume rates of up to 100 Hz [39]. The maximum total exposure per volume for Snapshot OCM can be calculated as $\frac{25\text{mW}}{{(0.2\text{mm})}^2}\cdot 5\text{ms}=3.125{\text{mJ mm}}^{-2}$. Comparatively, assuming a spot size of 1 µm, a line scan rate of 1 MHz for an SD-OCM setup, and an incident power of 1.25 mW (significantly lower than the incident power used for MHz-OCT systems [45]), the total exposure per volume required to achieve the same sampling as the Snapshot OCM setup implemented in this paper can be calculated as $\frac{1.25\text{mW}}{{(0.001\text{mm})}^2}\cdot 1\text{ µs}\cdot 448\cdot 480=0.27\times {10}^6{\text{mJ mm}}^{-2}$. This is 5 orders of magnitude greater than the exposure for Snapshot OCM. Also, compared to an LED, expensive light sources such as broadband lasers or superluminescent diodes are needed for the implementation of SD-OCM. Due to the ability of SD-OCM to image features up to a few millimeters deep with an axial resolution of a few microns, it has found several clinical applications for in vivo imaging. Nonetheless, as seen in Fig. 5, it is evident that there exists a large gap in technologies that Snapshot OCM can fill. As seen in Supplementary Fig. S2 and discussed in Supplement 1 ^{(41.5MB, pdf)} , the axial resolution and axial range of imaging can be varied over a large scale by changing $N$, $M$, and $\mathrm{\Delta }\lambda$. Just like SD-OCM, Snapshot OCM images represent the complex-valued scattered optical field rather than the real-valued intensity, although both are available for analysis. Figures 2–4 show that Snapshot OCM can not only image reflective samples with high sensitivity of 80 dB, but also weakly scattering samples such as cells and submerged flat glass surfaces with a sufficiently high sensitivity of 40 dB. Similar signal-to-noise ratios and sensitivity values have been previously reported for similar FF-OCM techniques, albeit for much longer exposure times [9,46]. Additionally, the intensity images provide good contrast and enable axial localization of different structures in the sample (Fig. 3(a)), while the phase provides detailed axial profiles of each depth (Fig. 3(b)). Furthermore, spectral-domain coherence imaging has been proven to be more sensitive than their time-domain counterparts. As seen in Fig. 4 and Visualization 1 ^{(16.5MB, mp4)} , Snapshot OCM can track the dynamics in biological samples by imaging both the magnitude and phase of the scattered fields for long duration.

Snapshot OCM is challenged by both the disadvantages of full-field imaging and the inherent limitations of using a hyperspectral camera. One of the critical challenges in full-field interferometry is the mismatch between the wavefronts and dispersions of the sample and reference arms in non-common path geometries [47]. The two most common wavefront mismatch errors observed were tilt and Petzval field curvature. These cause features on the same plane in the object appear axially shifted and the image response function is spatially invariant, making localization difficult. However, these errors were corrected computationally since Snapshot OCM generates the complex-valued optical field rather than real-valued intensity. Therefore, as seen in Supplementary Fig. S9, the wavefront mismatch can be interpolated as a parabolic function, and the image can be resampled along $k$ for the results shown in Figs. 2–4. Similarly, the contrast of the images can be improved in post-processing through computational darkfield filters as seen in Fig. 4. Another critical disadvantage of full-field imaging in reflection mode is the presence of signal-degrading speckle patterns due to coherent cross-talk. Coherent gating comparatively reduces the presence of speckle due to multiple scattering. Similarly, Spatial light modulators and deformable mirrors have been previously used to overcome these limitation of widefield/full-field imaging [48,49]. However, by using an LED as a light source, the effects of spatial interference can be reduced significantly [21,22].

Apart from the disadvantages of full-field interferometry, using a hyperspectral camera presents its own set of unique challenges. Firstly, compared to SD-OCM which typically takes 500-2000 spectral samples, Snapshot OCM takes a limited number of samples since the number of pixels between two monochromatic slices at the camera plane is limited. Typically, to reconstruct SD-OCM volumes, the raw data is interpolated along a polynomial curve to ensure that the spectral sampling is linear along $k$, followed by an inverse fast Fourier transform. However, the limited number of spectral sample points in Snapshot OCM causes large errors in resampling; therefore, the images are reconstructed using NUDFT. Secondly, the “stripe“ artifacts due to slicing the images that were observed during the simulation (Fig. 1) were also apparent in our implementation of Snapshot OCM, particularly in the images shown in Fig. 3(a). This artifact is a consequence of image slicing using the image mapper for hyperspectral imaging, where each image slice encounters different aberrations and attenuations on the way to the camera plane. While the steps to reduce these artifacts described by Cui et al. [26] were implemented here, these artifacts nonetheless persist causing some distortions to the image features. As seen in Supplementary Fig. S10, without median filtering, these artifacts severely affect the phase of the reconstructed Snapshot OCM images. One reason for these artifacts could be our method of reconstruction using a look-up table, where the discretization effects are not considered. For instance, the footprint of each color in each slice on the camera is assumed to be exactly one pixel wide, which does not hold true if the camera plane is even slightly tilted. Therefore, although computationally intensive, reconstructing the data cube through solving an inverse problem could mitigate the discretization issues, thereby eliminating the stripe artifacts. Since the inverse matrix is expected to be relatively sparse, a combination of computational methods and GPU-based acceleration can help with the practical implementation of this reconstruction method.

The IMS-based hyperspectral cameras used to obtain the results in Fig. 2–4 were initially built in 2010, mainly for applications in fluorescence imaging [50,51]. This had several consequences for our results. Firstly, while the exposure time per volume for the results in Fig. 2 and Fig. 3 was 2 ms and 5 ms, respectively, the maximum frame rate of the 12 megapixel (MP) detector is 3.3 Hz. However, modern 12 MP cameras can achieve frame rates of 330 Hz. Therefore, by replacing the camera with a modern one, samples can be imaged sustainably at hundreds of frames per second with similar exposure times. This would be critical for imaging biological dynamics at different time scales. Secondly, the bandwidth of the current detector is approximately 250 nm spread over 40 spectral bins using a highly nonlinear dispersion element. Consequently, the axial range of our setup is approximately 10 µm, which was optimal for imaging cells cultured on a flat surface. For tissue imaging, particularly for ophthalmic imaging, the axial range must be expanded to 150-200 µm. This can be achieved by a fundamental redesign of the setup by replacing the dispersion element to reduce the bandwidth of the camera to less than 100 nm and switching to a camera with a larger sensor format to increase the number of spectral bins (Supplementary Fig. S2). Of course, this implies a need to acquire tens of megapixels per volume to maintain similar transverse sampling as our current setup. Currently, there are 50-60 MP sensors available on the market capable of frame rates of 10-20 Hz. Additionally, the next generation camera for Snapshot OCM can be designed to operate optimally under bright conditions by choosing a sensor with larger full-well capacity. This could improve the overall sensitivity of the setup and enable us to image the direct backscattering from tissues rather than relying on the reflection from the cover glass surface. This can expand Snapshot OCM to a plethora of biological applications for imaging 3D extended live samples for capturing their dynamics, and such camera redesign is currently underway.

In summary, in this paper, we presented a setup for 3D imaging of samples using no movable parts called Snapshot OCM, that uses full-field spectral-domain interferometry. We proved its theoretical feasibility through a comprehensive simulation of an IMS-based hyperspectral camera. Additionally, we explored the key differences between traditional SD-OCM techniques and Snapshot OCM to redesign the image reconstruction methods. After implementing Snapshot OCM with off-the-shelf components, we evaluated its performance on imaging USAF targets placed at different optical path lengths and proved that Snapshot OCM is capable of 3D imaging with micron-scale transverse and axial resolution. Finally, we demonstrated the performance of Snapshot OCM for biological imaging where it was not only able to contrast and axially localize densely populated cells in culture but was able to generate detailed phase profiles of structures at every depth in 3D for long durations. By updating the IMS hyperspectral camera with faster detectors and tailoring the spectral performance to the sample characteristics, Snapshot OCM will have the potential to fill critical gaps in optical imaging techniques for 3D biological imaging applications.

Funding

Air Force Office of Scientific Research10.13039/100000181 (FA9550-17-1-0387); National Institutes of Health10.13039/100000002 (R01EY029397); National Science Foundation10.13039/100000001 (CBET 18-41539).

Disclosures

The authors declare no conflicts of interest.

See Supplement 1 ^{(41.5MB, pdf)} for supporting content.