Abstract
The auto-fluorescent coenzymes reduced nicotinamide dinucleotide (NADH) and oxidized flavin adenine dinucleotide (FAD) allow label-free detection of cellular metabolism. The optical redox ratio, which is traditionally computed as the ratio of NADH and FAD intensities, allows quantification of cell redox state. In addition to multiple formulations of the optical redox ratio from NADH and FAD intensity measurements, a fluorescence lifetime redox ratio (FLIRR) based on the fractions of protein-bound NADH and FAD was developed to overcome the limitations of experimental factors that influence fluorescence intensity measurements. In this paper, we compare fluorescence-intensity computations of the optical redox ratio with the fluorescence lifetime redox ratio for quiescent and activated T cells. Fluorescence lifetime images of NAD(P)H and FAD of T cells were acquired with a two-photon fluorescence lifetime microscope. Metabolic perturbation experiments, including inhibition of glycolysis, oxidative phosphorylation, glutaminolysis, and fatty acid synthesis revealed differences between the intensity and lifetime redox ratios. Statistical analysis reveals that the FLIRR has a lower standard deviation and skewness (two-tail T-test, P value = 0.05) than the intensity redox ratio. Correlation analysis revealed a weak relationship between FLIRR and intensity redox ratio for individual cells, with a stronger correlation identified for activated T cells (Linear regression, R-value = 0.450) than quiescent T cells (R-value = 0.172). Altogether, the results demonstrate that while both the fluorescence lifetime and intensity redox ratios resolve metabolic perturbations in T cells, the endpoints are influenced by different metabolic processes.
1. Introduction
Optical imaging reveals biochemical, morphological, and metabolic information of cells and tissues. Imaging of the endogenous fluorophores reduced nicotinamide adenine dinucleotide (NADH) and flavin adenine dinucleotide (FAD) provides a label-free tool to study cell metabolism [1]. The metabolic coenzyme NADH is an electron acceptor in glycolysis and electron donor in oxidative phosphorylation, while FAD is the principle electron acceptor in oxidative phosphorylation [2]. The reduced form of NAD, NADH, is fluorescent, while the oxidized form, NAD+, is not [3]. In contrast, the oxidized form of FAD is fluorescent, while the reduced form, FADH2 is not [3]. Since NADH and FAD each represent a different redox state, quantification of these signals is a useful tool to assess cell and tissue redox state [4]. In measurements of cells and tissues, the fluorescence emissions of NADH and its phosphorylated form NADPH are indistinguishable, so NAD(P)H is often used to represent their combined signals [5].
The optical redox ratio relates the fluorescence intensities of NAD(P)H and FAD, and provides an optical measurement of the redox state of a cell [6]. The optical redox ratio is often used for label-free detection of changes in cell or tissue metabolism due to the functions of NADH and FAD as coenzymes of metabolic reactions [1]. Multiple definitions of the optical redox ratio are reported in the literature. The first formula, FAD intensity divided by NAD(P)H intensity (FAD/NAD(P)H) was proposed by Britton Chance in 1979 [3]. Over the years, additional intensity-based formulas including NAD(P)H/FAD, NAD(P)H/(FAD + NAD(P)H), and FAD/(FAD + NAD(P)H) have been reported [7–10]. The optical redox ratio is used to identify different metabolic states between normal and cancerous tissues, to identify anti-cancer drug response, and to stratify different cell states including activation of immune cells and differentiation of stem cells [7,8,11–13].
In addition to the fluorescence intensity-based computations of the optical redox ratio, a fluorescence lifetime redox ratio (FLIRR) can be computed from the fluorescence lifetime of NAD(P)H and FAD [14–16]. The fluorescence lifetime of a given fluorophore is the time between the absorption of an excitation photon and the release of the emission photon prior to the relaxation to the ground electronic state. The fluorescence lifetime is picoseconds to nanoseconds in duration and dependent on both the chemical structure of that molecule as well as the surrounding microenvironment of the fluorophore [17]. Within cells, NAD(P)H and FAD can each exist in two confirmations, protein-bound or free. NAD(P)H has a short lifetime in the free configuration, and a longer lifetime in the bound condition [18]. FAD has a short bound lifetime and longer free lifetime [4,19]. Time-domain fluorescence lifetime imaging (FLIM) allows detection of the fluorescence intensity decay as a function of time after the excitation event at each pixel [17]. Fluorescence lifetimes are computed by deconvolution of the system response and fitting the fluorescence to a two-component exponential decay model, [Eq. (1)], where I (t) is the fluorescence intensity as a function of time t, τ1 and τ2 are the short and long lifetimes, respectively, α1 and α2 are the fractional components of the short and long lifetimes, respectively (i.e. if I(t) is normalized to 1, α1 + α2 = 1), and C accounts for background noise [17,20].
The fluorescence lifetime redox ratio (FLIRR) is defined as the fractional contribution of bound NAD(P)H (α2) divided by the fractional component of bound FAD (α1) [14–16]. Wallrabe et al. defined the FLIRR thusly to report changes in metabolism due to their reasoning that during oxidative phosphorylation, bound NAD(P)H increases because it is converted to NAD+ by the enzyme NADH dehydrogenase, and bound FAD decreases through the activities of the enzyme succinate dehydrogenase [14]. The FLIRR overcomes several experimental limitations of fluorescence intensity imaging. Fluorescence intensity measurements are influenced by laser power, detector gain, light scattering, and the concentration of the fluorophore; however, fluorescence lifetimes are independent of these experimental factors. Therefore, the FLIRR may provide redox and metabolic information in settings where these factors are difficult to control such as experiments across multiple days and 3-dimensional imaging of organoids or in vivo tissues [21]. The changes in FLIRR due to metabolic perturbations in prostate cells are consistent with the changes observed in the intensity-based redox ratio (FAD/NAD(P)H) for CoCl2 treatment, glucose challenge, and doxorubicin treatment, all perturbations that increased the FLIRR and intensity-based redox ratio [14,21].
The correlation between the intensity and lifetime redox ratios is unreported across a range of metabolic states. This comparison is needed to support the hypothesis that the FLIRR and intensity redox ratio are equivalent metrics of cellular metabolism. The advantages of lifetime measurements make the FLIRR an attractive metric of cellular metabolism for applications where fluorescence intensity studies are limited. However, it is important to understand the relationship between these optical metrics so that they can be used and interpreted appropriately in label-free imaging studies of cell metabolism. The goal of this paper is to evaluate both the intensity and lifetime optical redox ratios to detect metabolic perturbations in quiescent and activated T cells. To compare optical redox ratio definitions, we used a dataset of NAD(P)H and FAD fluorescence lifetime images of quiescent and activated T cells treated with metabolic inhibitors, rotenone with antimycin A(R + AA, inhibit electron transport chain and oxidative phosphorylation, respectively), 2-deoxy-d-glucose (2DG, glycolysis inhibitor), 5-(Tetradecyloxy)-2-furoic acid (TOFA, fatty acid synthesis inhibitor), and Bis-2-(5-phenylacetamido-1,3,4-thiadiazol-2-yl) ethyl sulfide) (BPTES, glutaminolysis inhibitor) [12]. Quiescent and activated T cells utilize different metabolic pathways. Activated T cells use aerobic glycolysis and glutaminolysis while quiescent T cells are dependent on oxidative phosphorylation [22–26]. Therefore, this dataset allows direct comparison of fluorescence lifetime and intensity redox ratio definitions across a variety of metabolic states and perturbations. This investigation will improve our understanding of the similarities and differences between the intensity and lifetime redox ratios to optimize the usage of these non-invasive endpoints of cellular metabolism in research and translational studies.
2. Methods
2.1. Autofluorescence lifetime imaging of T cells
The NAD(P)H and FAD fluorescence lifetime images from the T cell metabolic inhibitor experiment of quiescent and activated T cells published in Walsh et al. [12] were provided by AJ Walsh and MC Skala. No new images were acquired for this study. The methods summarized here are covered in full detail in Walsh et al. [12].
Peripheral blood was drawn from a healthy donor (n = 1 donor, 1 blood draw) in accordance with approval by the Institutional Review Board of the University of Wisconsin-Madison (#2018-0103) and after informed consent was obtained from the donor. CD3+ cells (T cells) were isolated from the blood and a portion were activated with a tetrameric antibody against CD2, CD3, and CD28 (StemCell Technologies). After 48 hours, both activated and quiescent cells were plated for five experimental groups: control, rotenone (1 μM, 10 minute incubation) with antimycin A (1 μM, 10 minute incubation), 2DG (50 mM, 10 minute incubation), TOFA (50 μg/ml, 1 hour incubation) and BPTES (20 μM, 1 hour incubation). NAD(P)H and FAD fluorescence lifetime images of T cells were acquired sequentially. Fluorescence lifetime decays were analyzed to extract images of fluorescence lifetime components. Images were segmented into cells, including nucleus and cytoplasm regions using an automated image segmentation algorithm previously described [12,27].
This study used the image set consisting of five different parameters (I0 - fluorescence intensity; α1 - fraction of free NAD(P)H, bounded fraction of FAD; α2 -bounded fraction of NAD(P)H, free fraction of FAD; τ1-shorter fluorescence lifetime; τ2-longer fluorescence lifetime) for both NAD(P)H and FAD based on biexponential models of fluorescent lifetime decay curve, Eq. (1).
2.2. Image processing procedure
In this paper, image processing was performed using MATLAB. First, an FAD intensity threshold (pixels < 120) was set to exclude segmented regions of noise. In addition, we checked every image manually to ensure the cells that were identified by the software were real cells instead of debris or noise. The cells with an average NAD(P)H τ1 value less than 50 ps were identified as red blood cells [28] and were excluded from the analysis. The number of cells in each group is shown in Table 1.
Table 1. Number of cells in each group.
| Group | Cell status | Number of cells |
|---|---|---|
| Control | Activated | 258 |
| Quiescent | 262 | |
| Rotenone + Antimycin A | Activated | 277 |
| Quiescent | 205 | |
| 2DG | Activated | 148 |
| Quiescent | 430 | |
| TOFA | Activated | 243 |
| Quiescent | 275 | |
| BPTES | Activated | 241 |
| Quiescent | 339 |
The redox ratio of each cell was calculated in two ways: at the pixel-level and at the cell-level. For the pixel average method, the redox ratio was calculated on a pixel-basis from the NAD(P)H and FAD fluorescence intensity images. Then, all pixels of the cytoplasm of each cell were averaged for a single redox ratio value for the cell. For the cell average method, the redox ratio was calculated on a cell-basis: the pixel values of NAD(P)H and FAD fluorescence intensities in a cell were summed separately and then the ratio of the summed intensities was acquired as the redox ratio for the cell. To compare the pixel average method with the cell average method, we ensured the same pixels were used for each method. Based on these two methods, we calculated four different definitions of redox ratios for each cell: FAD intensity divided by NAD(P)H intensity (FAD/NAD(P)H), NAD(P)H intensity divided by the sum of FAD and NAD(P)H intensity [NAD(P)H/(FAD + NAD(P)H)], FAD intensity divided by the sum of FAD and NAD(P)H intensity [FAD/(FAD + NAD(P)H)], and NAD(P)H protein bounded fraction divided by FAD protein bounded fraction (NAD(P)H α2/FAD α1) [14,15,21].
2.3. Mitochondria segmentation
To compare the redox ratio of mitochondria and non-mitochondria cytosol compartments within T cells, mitochondria masks were obtained from the NAD(P)H intensity images. Because the NAD(P)H concentration is higher in mitochondria than the surrounding cytosol, the bright, punctate areas of NAD(P)H fluorescence intensity images correspond with mitochondria [16]. In this study, we created mitochondria masks from the brightest 20% of pixels in each cell’s cytoplasm. The 20% threshold was selected to capture the pixels with the greatest NAD(P)H signal which correspond to mitochondria [16]. The 20% threshold was selected by visual inspection of the images across different threshold values. This threshold method to identify mitochondria within NADH images has been used previously [14,16]. We calculated the four different redox ratios [FAD/NAD(P)H, NAD(P)H/(FAD + NAD(P)H), FAD/(FAD + NAD(P)H), and NAD(P)H α2/FAD α1] for the mitochondria areas based on the pixel average and cell average methods for each cell using the mitochondria masks.
2.4. Statistical analysis
In this paper, we assessed the data distribution characteristics for each redox ratio definition by calculating the standard deviation and skewness of the histogram of redox ratio values for each T cell experimental group. A two-sided student’s t-test (α-value = 0.05) was used to assess statistical differences between means of endpoint values (redox ratio, standard deviation, skewness, R value) between T cell groups. Similarly, a two-sided student’s t-test (α-value = 0.05) was used to assess statistical significance between mean redox ratio values of control and inhibitor treated T cells within the quiescent or activated T cell sets. Linear regression analysis was used to evaluate the correlation between the different redox ratio definitions, between NAD(P)H α2 and FLIRR, and between NAD(P)H α2 and FAD/NAD(P)H.
3. Results
3.1. Pixel and cell level computations of optical redox ratio are equivalent
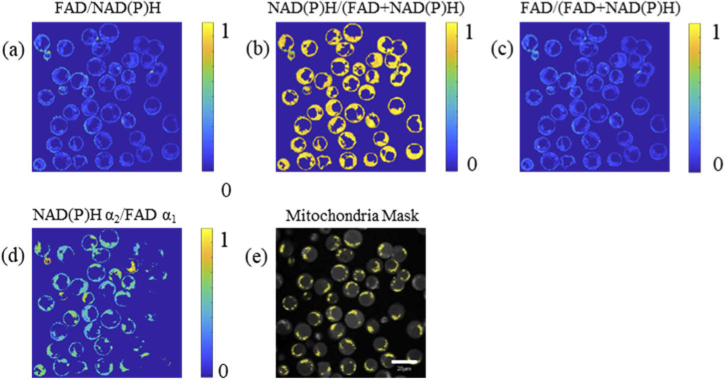
In the autofluorescence images of NAD(P)H and FAD, T cells are circular (Fig. 1). The cell nuclei are darker than the cytoplasm because NAD(P)H is mainly located in the cytosol and mitochondria, and FAD is primarily located in mitochondria. In the redox ratio images (Fig. 1(a)(b)(c)(d)), only cytosol regions are included in the redox ratio calculations. In the mitochondria mask images, the yellow areas in the T cells were labeled as the mitochondria based on the NAD(P)H fluorescence intensity images (Fig. 1(e)).
Fig. 1.
Representative images of the optical redox ratio of activated control T cells. The redox ratio is calculated at the pixel level by (a) FAD/NAD(P)H intensity, (b) NAD(P)H/(FAD + NAD(P)H) intensity, (c) FAD/(FAD + NAD(P)H) intensity, and (d) NAD(P)H α2/FAD α1. Redox ratios are normalized to the maximum value. (e) Corresponding mitochondria mask (yellow areas) of the T cells. Scale bar = 20 μm
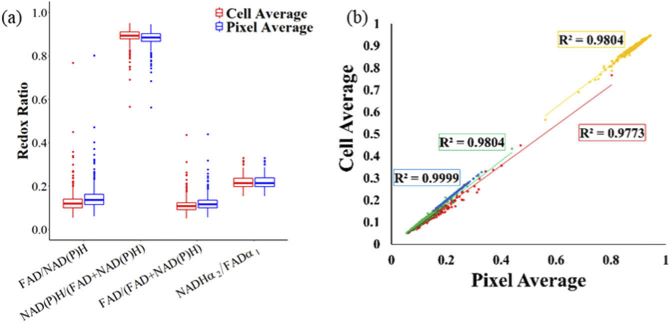
To compare the effect of calculating the optical redox ratio at the pixel or cell level, each definition of redox ratio was obtained by computing the ratio at the pixel or cell level. No statistical differences were found between the pixel average and the cell average method for any redox ratio definition or T cell group (Fig. 2(a)). Additionally, the values for each cell computed by the pixel and cell average methods are highly correlated (R value > 0.95, confidence value = 95%, Fig. 2(b))
Fig. 2.
Cellular redox ratios computed at the pixel level and cell level are equivalent. (a) Redox ratios computed at the pixel level and cell level for activated control T cells. (b) Correlation between pixel-average and cell-average redox ratio for activated control T cells. Red = FAD/NAD(P)H, Yellow = NAD(P)H/(FAD + NAD(P)H), Green = FAD/(FAD + NAD(P)H), Blue = NAD(P)H α2/FAD α1
3.2. FLIRR measurements are more uniform than intensity redox ratio measurements
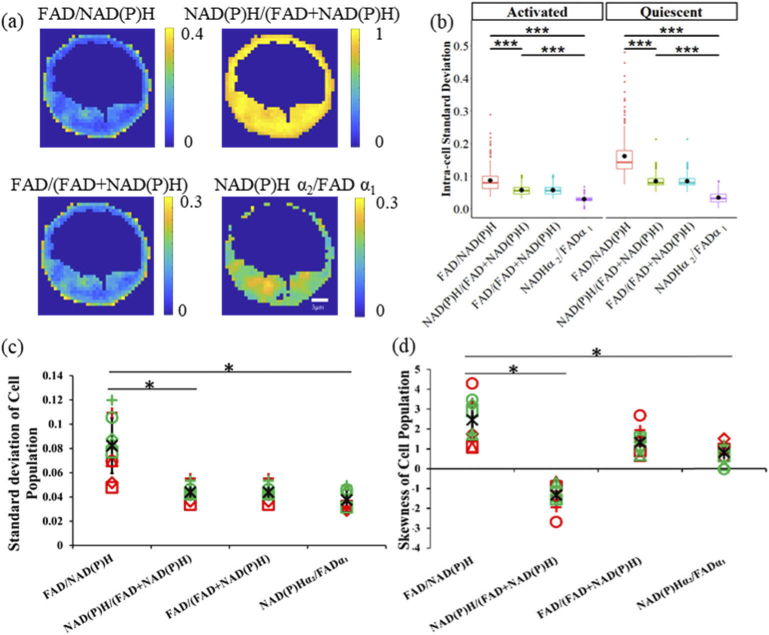
The spatial heterogeneity of redox ratios within a typical cell is shown in Fig. 3(a), and the intensity redox ratios have higher intracellular standard deviations than the fluorescence lifetime redox ratio (two-tail T test, P-value = 0.05, Fig. 3 (b)). To assess the statistical characteristics of the different optical redox ratio definitions, we compared the standard deviation and histogram skewness of each T cell experimental group. The results (Fig. 3 (c)(d)) show that the standard deviation of FAD/NAD(P)H is the highest (two-tail T test, P-value = 0.05, Fig. 3 (c)). FAD/NAD(P)H also has the highest skewness value (two-tail T test, P-value = 0.05, Fig. 3 (d)). The FAD/(FAD + NAD(P)H) and NAD(P)H/(FAD + NAD(P)H) ratios have the same standard deviations and the same skewness values, but with opposite signs(Fig. 3 (c)(d)). The FLIRR has the most normal distribution with the smallest standard deviation and skewness values as compared with the intensity-based optical redox ratios (two-tail T test, P-value = 0.05, Fig. 3 (c)(d)).
Fig. 3.
Distribution characteristics of optical redox ratios, (a) FAD/NAD(P)H, NAD(P)H/(FAD + NAD(P)H), FAD/(FAD + NAD(P)H), and NAD(P)Hα1 /FAD α1 redox ratio images of a representative cell (control, activated T cell) demonstrate intracellular heterogeneity. (b) Intra-cellular standard deviation of different redox ratios for activated and quiescent control T-cells. (c) Intra-population standard deviation of different redox ratios (d) Intra-population skewness of different redox ratios. Black * represents the mean of all T cell groups, red symbols represent activated T cells, green symbols represent quiescent T cells, circles for control, squares for rotentone + antimycin A, triangles for TOFA, and + for BPTES. * p < 0.05, two-tail T test.
3.3. FLIRR does not correlate with the intensity redox ratio
To determine whether the FLIRR correlates with the intensity-based optical redox ratio, we used linear regression to evaluate the correlation between each definition of redox ratio at the cell level for each T cell group. The linear regression results (Table 2) show that all intensity-based definitions of optical redox ratio (FAD/NAD(P)H, NAD(P)H/(FAD + NAD(P)H), FAD/(FAD + NAD(P)H)) are highly correlated (R > 0.95). The R values between each intensity-based optical redox ratio and the FLIRR range from 0.08-0.6, with a mean R value of 0.311. Higher R correlation values for the comparison between intensity-based optical redox ratios and FLIRR were found for activated T cells (mean R value = 0.450) than for quiescent T cells (mean R value = 0.172).
Table 2. Different Redox Ratios Relationship Table a .
| Cell Dish | R value | Cell Status | RR1- RR2 | RR1-RR3 | RR2-RR3 | RR1-FLIRR | RR2-FLIRR | RR3-FLIRR |
| Control | Activated | 0.987 | 0.987 | 1 | 0.431 | 0.435 | 0.435 | |
| Quiescent | 0.966 | 0.966 | 1 | 0.082 | 0.006 | 0.006 | ||
| R + AA | Activated | 0.995 | 0.995 | 1 | 0.518 | 0.518 | 0.518 | |
| Quiescent | 0.977 | 0.977 | 1 | 0.202 | 0.251 | 0.251 | ||
| 2DG | Activated | 0.988 | 0.988 | 1 | 0.520 | 0.527 | 0.527 | |
| Quiescent | 0.967 | 0.967 | 1 | 0.086 | 0.169 | 0.169 | ||
| TOFA | Activated | 0.986 | 0.986 | 1 | 0.453 | 0.446 | 0.446 | |
| Quiescent | 0.955 | 0.955 | 1 | 0.124 | 0.200 | 0.200 | ||
| BPTES | Activated | 0.968 | 0.968 | 1 | 0.299 | 0.347 | 0.347 | |
| Quiescent | 0.950 | 0.950 | 1 | 0.267 | 0.332 | 0.332 | ||
RR1: FAD/NAD(P)H, RR2: NAD(P)H/(FAD + NAD(P)H), RR3: FAD/(FAD + NAD(P)H), FLIRR: NAD(P)H α2/FAD α1. R + AA: Rotenone + Antimycin A, 2DG: 2-deoxy-d-glucose, TOFA: 5-(Tetradecyloxy)-2-furoic acid, BPTES: Bis-2-(5-phenylacetamido-1,3,4-thiadiazol-2-yl) ethyl sulfide.
3.4. Metabolic inhibition alters the redox ratio of T cells
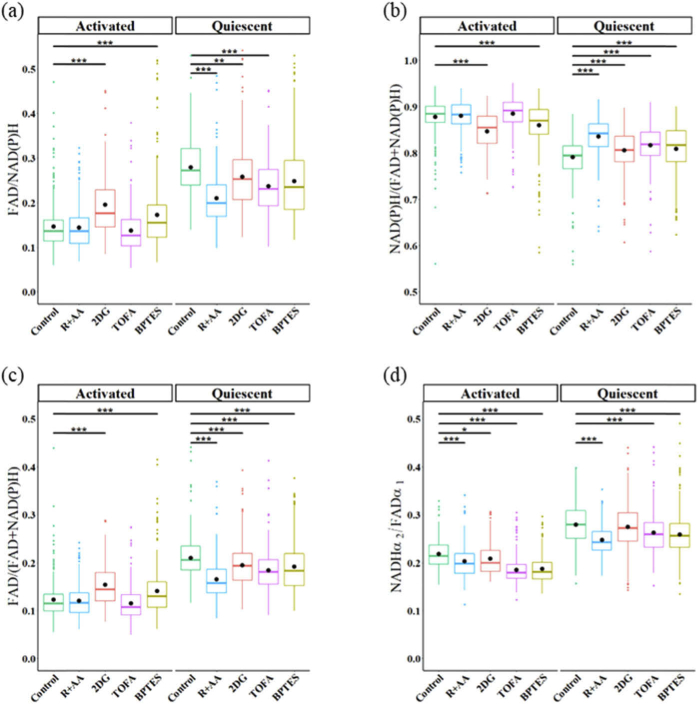
We used the response of T cells to metabolic inhibitors to determine whether the intensity based optical redox ratios and FLIRR are sensitive to metabolic perturbations of T cells. FAD/NAD(P)H, NAD(P)H/(FAD + NAD(P)H), FAD/(FAD + NAD(P)H), and NAD(P)H α2/FAD α1 of quiescent and activated T cells were computed for control, rotenone + Antimycin A (R + AA), 2DG, TOFA, and BPTES treated T cells (Fig. 4(a)(b)(c)(d)). 2DG and BPTES-treated activated T cells have increased FAD/NAD(P)H and FAD/(FAD + NAD(P)H) ratios (and a decreased NAD(P)H/(FAD + NAD(P)H) ratio) as compared to control activated T cells (Fig. 4(a)(b)(c)). R + AA, 2DG and TOFA treatment decreased the FAD/NAD(P)H and FAD/(FAD + NAD(P)H) ratios (and increased the NAD(P)H/(FAD + NAD(P)H) ratio) of quiescent T cells as compared to control quiescent T cells (Fig. 4(a)(b)(c)). BPTES-treated quiescent T cells have a reduced FAD/(FAD + NAD(P)H) ratio and increased NAD(P)H/(FAD + NAD(P)H) ratio as compared to control quiescent T cells (Fig. 4(b)(c)). The FLIRR of activated T cells is decreased for R + AA, 2DG, TOFA, and BPTES treated cells as compared with activated control T cells (Fig. 4(d)). Similarly, the FLIRR is decreased in quiescent T cells with R + AA, TOFA, and BPTES treatment (Fig. 4(d)). The metabolic perturbation of T cell results are summarized in Table 3.
Fig. 4.
Comparison of redox ratio calculations for quiescent and activated T cells treated with metabolic inhibitors. (a) FAD/NAD(P)H (b) NAD(P)H/(FAD + NAD(P)H) (c) FAD/(FAD + NAD(P)H) (d) NAD(P)H α2/FAD α1. R + AA: Rotenone + Antimycin A, 2DG: 2-deoxy-d-glucose, TOFA: 5-(Tetradecyloxy)-2-furoic acid, BPTES: Bis-2-(5-phenylacetamido-1,3,4-thiadiazol-2-yl) ethyl sulfide. * p < 0.05, ** p < 0.01, ***p < 0.001 for two-sided Student’s t-test with Bonferroni correction for multiple comparisons.
Table 3. Metabolic Inhibitor-Induced Changes in Redox Ratios of Quiescent and Activated T cells a .
| Definition Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Activation Status | A | Q | A | Q | A | Q | A | Q |
| Rotenone + Antimycin A | — | ↓ | — | ↑ | — | ↓ | ↓ | ↓ |
| 2DG | ↑ | ↓ | ↓ | ↑ | ↑ | ↓ | ↓ | — |
| TOFA | — | ↓ | — | ↑ | — | ↓ | ↓ | ↓ |
| BPTES | ↑ | — | ↓ | ↑ | ↑ | ↓ | ↓ | ↓ |
2DG: 2-deoxy-d-glucose, TOFA: 5-(Tetradecyloxy)-2-furoic acid, BPTES: Bis-2-(5-phenylacetamido-1,3,4-thiadiazol-2-yl) ethyl sulfide; A: Activated; Q: Quiescent. FLIRR trends inconsistent with intensity-based redox ratios denoted with shading.
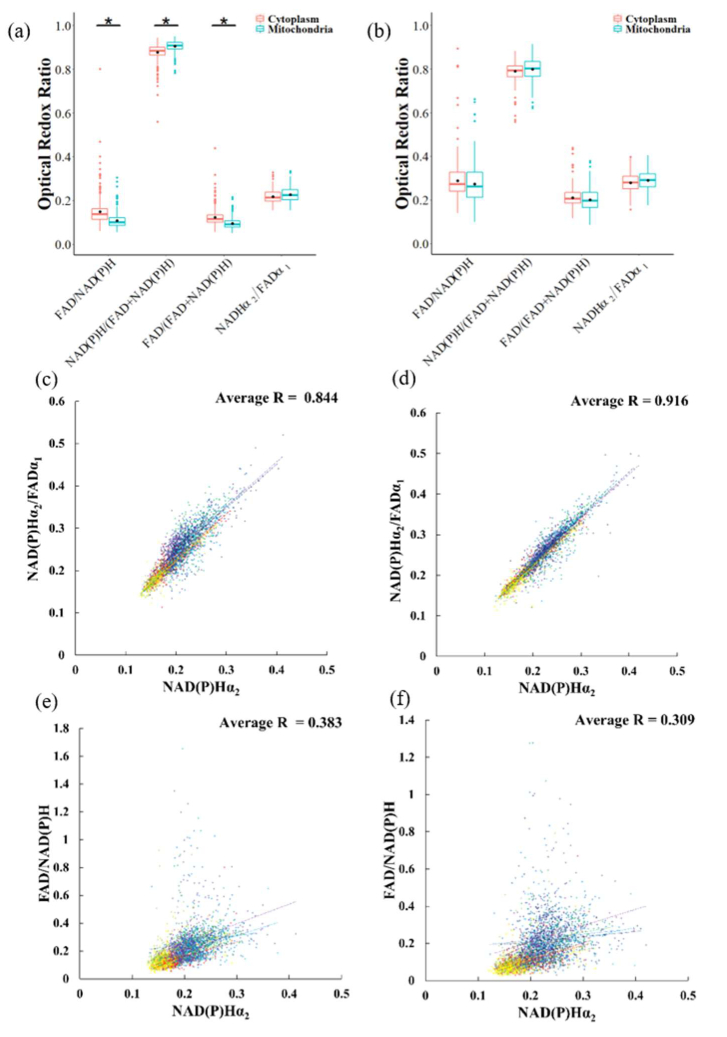
3.5. Intensity redox ratios identify different metabolic states between the mitochondria and the cytoplasm
According to previous studies of cancer cells [15,29], an increase in FLIRR correlates with an increase in the NAD(P)H enzyme-bound fraction, α2, and this relationship is different between mitochondria and cytoplasm pixels. Therefore, we compared the redox ratio of the mitochondria with the redox ratio values of the cytoplasm of activated and quiescent T cells for each redox ratio definition. Activated T cells have higher FAD/NAD(P)H and FAD/(FAD + NAD(P)H) redox ratios in the cytoplasm than in the mitochondria areas (two-tail T-test, P value = 0.05, Fig. 5(a)(b)).
Fig. 5.
Comparison of redox ratios between mitochondria and cytoplasm pixels of T cells. Redox ratios of mitochondria and cytoplasm pixels of (a) activated control T cells and (b) quiescent control T cells. (c) Correlation between NAD(P)H α2 and FLIRR in the cytoplasm and (d) in the mitochondria (e) Correlation between NAD(P)H α2 and FAD/NAD(P)H in the cytoplasm and (f) in the mitochondria. In (c-f) each color represents a T cell group. (dark red = activated control, red = activated rotenone + antimycin A, orange = activated 2DG, yellow = activated TOFA, light green = activated BPTES, green = quiescent control, light blue = quiescent rotenone + antimycin A, blue = quiescent 2DG, dark blue = quiescent TOFA, purple = quiescent BPTES).
We used linear regression to describe the relationship between the FLIRR and NAD(P)H α2 of mitochondria pixels and the cytoplasm. The scatter plots (Fig. 5(c)(d)) show a linear relationship between the FLIRR and NAD(P)H α2. Moreover, a stronger linear relationship (R-value of 0.91 vs 0.84) is observed between the FLIRR and NAD(P)H α2 for mitochondria than for the cytoplasm. However, linear regression reveals only a weak relationship between NAD(P)H α2 and the intensity redox ratio (FAD/NAD(P)H); R = 0.383 for cytoplasm, R = 0.309 for mitochondria (Fig. 5(e)(f)).
4. Discussion
Due to the roles of NAD(P)H and FAD as metabolic coenzymes, the fluorescence redox ratio detects metabolic shifts in cells [3,14]. Simplistic interpretations of the intensity redox ratio focus on NADH and FAD utilization in glycolysis and oxidative phosphorylation: increased glycolysis increases NADH concentration (reduces FAD-numerator redox ratios) and increased oxidative phosphorylation increases FAD and reduces NADH concentrations (increased FAD-numerator redox ratios). However, additional metabolic pathways including fatty acid oxidation/synthesis and glutaminolysis use NAD(P)H and FAD as cofactors [30]. NADH is produced in the reaction of glutamate to α-ketoglutarate [30]. NADH is consumed and FAD produced in the conversion of Acetyl CoA to Acyl-CoA in the synthesis of fatty acids [30]. The FLIRR is computed from the ratio of bound NAD(P)H to bound FAD, the metabolic-basis of which are difficult to interpret. Upon activation, T cell metabolism shifts from tricarboxylic acid oxidation of glucose and β-oxidation of fatty acids to glycolysis and glutaminolysis [22–26]. Therefore, we evaluated fluorescence intensity and lifetime computations of the redox ratio in quiescent and activated T cells.
The intensity redox ratio resolves metabolic perturbations in quiescent and activated T cells (Fig. 4, Table 3). As expected due to the dependence of quiescent T cells on oxidative phosphorylation and fatty acid oxidation [22–26], inhibition of oxidative phosphorylation/ETC and fatty acid oxidation reduced the FAD-numerator intensity optical redox ratios of quiescent T cells, as compared to control quiescent T cells, but had no effect on the intensity redox ratios of activated T cells. Inhibition of glycolysis and glutaminolysis increased the FAD-numerator intensity redox ratios as compared to the corresponding redox ratios of the control activated T cells, as expected due to the dependence of activated T cells on glycolysis and glutaminolysis [22–26]. Interestingly, glycolysis inhibition of quiescent cells decreased the FAD-numerator intensity redox ratios. Due to the reliance of quiescent T cells on TCA and fatty acid oxidation, quiescent T cells replace the lost TCA fuel source from glycolysis (pyruvate) with increased fatty acid oxidation [31], which would result in increased NADH and reduced FAD, yielding a reduced FAD-numerator redox ratio. Likewise, the decrease in the redox ratio FAD/(FAD + NAD(P)H) of quiescent cells due to BPTES inhibition of glutaminolysis suggests compensation through an increase in fatty acid oxidation or reduced TCA utilization. Since our additional preprocessing filtering steps resulted in a smaller dataset of T cells included in the final analysis than those included in Walsh et al. [12], the quiescent T cells treated with BPTES demonstrate here an increased NAD(P)H/(FAD+ NAD(P)H) ratio which is not consistent with the result reported in Walsh et al [12].
Nearly equivalent results were obtained for all intensity redox ratio definitions. Metabolic perturbation results were consistent across the different intensity redox ratios (Table 3), except for BPTES treated quiescent T cells. The BPTES reduction of the FAD-numerator redox ratio was statistically significant for the normalized redox ratio (FAD/(FAD + NAD(P)H)) but not the redox ratio computation FAD/NAD(P)H. This difference is likely attributed to the reduced standard deviation and skewness of the normalized redox ratio distribution (Fig. 3(c)(d)) which increase the power of the statistical analysis. Cell-level correlation analysis also revealed a high correlation between intensity redox ratio measurements (R > 0.95; Table 2). Either normalized ratio, FAD/(FAD + NAD(P)H) or NAD(P)H/(FAD + NAD(P)H) is preferred, since these computations normalize the ratio value between 0 and 1 and have a distribution with a lower standard deviation and skewness as compared with FAD/NAD(P)H(Fig. 3(c)(d)). No differences were found between redox ratios with NAD(P)H or FAD in the numerator other than the expected inversion. Computations of each redox ratio at the cell and pixel levels were equivalent (Fig. 2). The ability of the intensity redox ratio to detect a variety of metabolic perturbations provides a label-free tool for comparative analysis of cell metabolism [32–34].
The FLIRR measurement is computed as the ratio of the fraction of bound NAD(P)H to the fraction of bound FAD (NAD(P)H α2 / FAD α1) [14,15,21]. In the electron transport chain (ETC), NADH donates an electron and is converted to NAD+ by the enzyme NADH dehydrogenase (Complex I) and FADH2 is converted to FAD by the enzyme succinate dehydrogenase (Complex II) [1]. Reduced oxidative phosphorylation leads to a reduced FLIRR through decreased NAD(P)H α2 and increased FAD α1 [14,15,21]. Increased oxidative metabolism by glucose challenge, CoCl2 and doxorubicin increased the FLIRR of prostate cancer cells [14]. Similarly, the FLIRR of both quiescent and activated T cells decreased with oxidative phosphorylation and ETC inhibition (Fig. 4(d), Table 3).
The FLIRR also detects inhibition of glycolysis, fatty acid oxidation, and glutaminolysis in T cells. The FLIRR decreased with inhibition of glycolysis in activated T cells but was unchanged in quiescent T cells with glycolysis inhibition (Fig. 4(d), Table 3), reflecting the increased dependence of activated T cells on glycolysis as compared with quiescent T cells [25] Furthermore, the FLIRR of both activated and quiescent T cells decreased with glutaminolysis and fatty acid synthesis inhibition (Fig. 4(d), Table 3). A decreased FLIRR suggests an increase in bound FAD, a decrease in bound NAD(P)H, or both. The decrease in FLIRR due to glutaminolysis inhibition may reflect decreased NADH binding to malate dehydrogenase due to BPTES inhibition of the glutaminolysis pathway. Likewise, the reduced FLIRR due to inhibition of acetyl-CoA carboxylase 1 by TOFA is consistent with reduced NADH binding and increased FAD binding following inhibition of the fatty acid oxidation pathway [30]. Altogether, the consistent decrease in FLIRR, regardless of the specific pathway inhibited, suggests that the FLIRR detects decreased metabolism but is not sensitive to specific metabolic pathway utilization.
The FLIRR exhibits less intra- and inter- cellular heterogeneity than the intensity redox ratio (Fig. 3). The lifetime fractions of NAD(P)H and FAD are between 0% and 100% at each pixel, while the fluorescence intensities of NAD(P)H and FAD range from 50 to 1500 in this experiment. Therefore, the range of possible FLIRR values is smaller than the range of intensity-based optical redox ratio values. The distribution data of FLIRR shows a lower standard deviation (Fig. 3(c)) and a lower skewness value (Fig. 3(d)) than the intensity redox ratios. This difference is attributed to the limited range of the α values. Additionally, spatial binning is used to analyze the FLIM data, which reduces the spatial resolution (Fig. 3(a)(b)) contributing to the lower spatial heterogeneity of FLIRR as compared to the intensity redox ratios [35]. Confounding factors including laser power, detector gain, inner filter effects, and photobleaching that influence fluorescence intensity measurements can promote a higher variability of the intensity optical redox ratio. Conversely, the fluorescence lifetime is independent of absolute photon counts and unaffected by the variability of these factors.
FLIRR and intensity redox ratios are not correlated for T cells. The results of linear regression analysis between the FLIRR and intensity redox ratio for individual cells revealed a low correlation coefficient (Table 2). Additionally, the metabolic inhibitors induced changes in intensity redox ratios that were not consistently replicated by the FLIRR (Table 3). Rotenone + Antimycin A and 2DG induced opposite changes in the intensity redox ratio (oxidative phosphorylation inhibition of quiescent T cells and glycolysis inhibition of activated T cells). However, all metabolic perturbations resulted in a decreased FLIRR of both quiescent and activated T cells, except for glycolysis inhibition of quiescent T cells which induced no change from control quiescent T cells. These differences suggest the lifetime and intensity redox ratios report different information about cellular metabolism. The consistent decrease in FLIRR observed regardless of initial metabolic state or metabolic pathway inhibition suggests that the FLIRR may be responsive to general metabolic flux and insensitive to specific metabolic pathway utilization. The greater correlation between intensity redox ratio and FLIRR for activated T cells (R = 0.450) than quiescent T cells (R = 0.172) also supports this hypothesis that the FLIRR is influenced by metabolic flux or capacity because activated T cells have increased metabolic demands than quiescent T cells [25]. Although the relationship between NAD(P)H intensity and α1 can be described by the Michaelis-Menten reaction kinetics equation for solutions of coenzyme-enzyme pairs, the complexity of a cell environment and multitude of potential binding partners with unique reaction parameters obscure the relationship between intensity and α1 [36–39].
Analysis of the intensity redox ratio and FLIRR for cytoplasm and mitochondria pixels reveals additional differences between these endpoints. The difference in intensity redox ratios between cytoplasm and mitochondria pixels of activated T cells (Fig. 5(a)) is not replicated in the FLIRR (Fig. 5(b)), suggesting an inability of the FLIRR to distinguish signals from glycolysis and oxidative metabolism or this is an artifact of the limited dynamic range of the FLIRR, due to the 0-100 range of the α values. The FLIRR is mainly driven by changes of the NAD(P)H enzyme-bound fraction α2 and displays a linear relationship with NAD(P)H α2 (Fig. 5(c)(d)) which is stronger for mitochondria pixels than cytoplasm pixels. However, the intensity redox ratio is not correlated with NADH α2 (Fig. 5(e)(f)). Metabolic FAD is confined to the mitochondria, yet the reduced correlation between FLIRR and NAD(P)H α2 of cytoplasm pixels compared to the mitochondria pixels suggests a non-metabolic FAD contributes to the FLIRR measurements of cytoplasm pixels. During the synthesis of FAD from cytosolic riboflavin, FAD is synthesized inside mitochondria and exported into the cytosol [40,41]. Therefore, the FAD in cytosolic areas, which is not used in mitochondria metabolic activities, may alter the relationship between the FLIRR and NAD(P)H α2. Additionally, riboflavin, the precursor of FAD, may contribute fluorescence emission in non-mitochondria pixels [42,43]. Other compounds in the cytoplasm which are related to riboflavin such as alloxazine, lumichrome, and lumiflavin may also contribute to the fluorescence signal of FAD [44].
5. Conclusion
In this paper, we analyzed different definitions of optical redox ratio computed from NAD(P)H and FAD fluorescence intensity and lifetime measurements for activated and quiescent T cells. The FLIRR exhibits less inter- and intra- cellular heterogeneity, and FLIRR measurements across populations of T cells have more normal distributions as compared with the conventional intensity redox ratios. However, linear regression analysis demonstrated only a weak relationship between the FLIRR and intensity redox ratios for individual cells, suggesting that the FLIRR and intensity redox ratio are not correlated endpoints of cellular metabolism. Metabolic perturbation experiments revealed only decreased FLIRR due to pathway inhibition while the intensity redox ratios increased or decreased depending on metabolic pathway utilization. Comparative analysis of redox ratios of cytoplasm pixels and mitochondria pixels suggest a non-metabolic contribution of FAD or other fluorescent flavins in the cytoplasm contribute to the FLIRR. When selecting a redox ratio computation, our results indicate that normalized formulations of the intensity redox ratio (FAD/(NAD(P)H + FAD) or NAD(P)H/(NAD(P)H + FAD) should be used since these computations normalize the ratio value between 0 and 1 and have a distribution with a lower standard deviation and skewness. Additionally, the results suggest the FLIRR is a useful metric of cellular metabolism, and may be more appropriate for 3D tissues and in vivo measurements due to the advantages of fluorescence lifetime measurements over intensity measurements. However, the FLIRR is not a substitution for the optical redox ratio and should be interpreted appropriately as a separate variable. Altogether the results demonstrate that while both the fluorescence lifetime and intensity redox ratios resolve metabolic perturbations in T cells, the endpoints are not correlated at either a cell or population level and report different responses to metabolic perturbations within T cells.
Acknowledgements
The authors would like to thank Melissa C. Skala for providing the database of T cell fluorescence lifetime images.
Funding
Texas A and M University10.13039/100007904 (Start Up Funds); Air Force Office of Scientific Research10.13039/100000181 (FA9550-20-1-0078).
Disclosures
The authors declare no conflicts of interest.
References
- 1.Georgakoudi I., Quinn K. P., “Optical imaging using endogenous contrast to assess metabolic state,” Annu. Rev. Biomed. Eng. 14(1), 351–367 (2012). 10.1146/annurev-bioeng-071811-150108 [DOI] [PubMed] [Google Scholar]
- 2.Walsh A. J., Poole K. M., Duvall C. L., Skala M. C., “Ex vivo optical metabolic measurements from cultured tissue reflect in vivo tissue status,” J. Biomed. Opt. 17(11), 116015 (2012). 10.1117/1.JBO.17.11.116015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chance B., Schoener B., Oshino R., Itshak F., Nakase Y., “Oxidation-Reduction Ratio Studies of Mitochondria in Freeze-trapped Samples,” THE JOURNAL OF BIOLOGICAL CHEMISTRY. 254(10), 4764–4771 (1979). [PubMed] [Google Scholar]
- 4.Kolenc O. I., Quinn K. P., “Evaluating Cell Metabolism Through Autofluorescence Imaging of NAD(P)H and FAD,” Antioxid. Redox Signaling 30(6), 875–889 (2019). 10.1089/ars.2017.7451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Huang S., Heikal A. A., Webb W. W., “Two-Photon Fluorescence Spectroscopy and Microscopy of NAD(P)H and Flavoprotein,” Biophys. J. 82(5), 2811–2825 (2002). 10.1016/S0006-3495(02)75621-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Varone A., Xylas J., Quinn K. P., Pouli D., Sridharan G., McLaughlin-Drubin M. E., Alonzo C., Lee K., Munger K., Georgakoudi I., “Endogenous two-photon fluorescence imaging elucidates metabolic changes related to enhanced glycolysis and glutamine consumption in precancerous epithelial tissues,” Cancer Res. 74(11), 3067–3075 (2014). 10.1158/0008-5472.CAN-13-2713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ostrander J. H., McMahon C. M., Lem S., Millon S. R., Brown J. Q., Seewaldt V. L., Ramanujam N., “Optical redox ratio differentiates breast cancer cell lines based on estrogen receptor status,” Cancer Res. 70(11), 4759–4766 (2010). 10.1158/0008-5472.CAN-09-2572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Palmer S., Litvinova K., Rafailov E. U., Nabi G., “Detection of urinary bladder cancer cells using redox ratio and double excitation wavelengths autofluorescence,” Biomed. Opt. Express 6(3), 977–986 (2015). 10.1364/BOE.6.000977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pena A.-M., Boulade M., Brizion S., Tissot N., Bornschlögl T., Galey J.-B., Bernerd F., Planel E., “Multiphoton FLIM imaging of NADH and FAD to analyze cellular metabolic activity of reconstructed human skin in response to UVA light,” SPIE BiOS. 10882, 9 (2019). 10.1117/12.2508858 [DOI] [Google Scholar]
- 10.Alhallak K., Rebello L. G., Muldoon T. J., Quinn K. P., Rajaram N., “Optical redox ratio identifies metastatic potential-dependent changes in breast cancer cell metabolism,” Biomed. Opt. Express 7(11), 4364–4374 (2016). 10.1364/BOE.7.004364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Skala M. C., Riching K. M., Gendron-Fitzpatrick A., Eickhoff J., Eliceiri K. W., White J. G., Ramanujam N., “In vivo multiphoton microscopy of NADH and FAD redox states, fluorescence lifetimes, and cellular morphology in precancerous epithelia,” Proc. Natl. Acad. Sci. U. S. A. 104(49), 19494–19499 (2007). 10.1073/pnas.0708425104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walsh A. J., Mueller K., Jones I., Walsh C. M., Piscopo N., Niemi N. M., Pagliarini D. J., Saha K., Skala M. C., “Label-free Method for Classification of T cell Activation,” Nature Biomedical Engineering 10.1038/s41551-020-0592-z (2019). [DOI] [PMC free article] [PubMed]
- 13.Rice W. L., Kaplan D. L., Georgakoudi I., “Two-photon microscopy for non-invasive, quantitative monitoring of stem cell differentiation,” PLoS One 5(4), e10075 (2010). 10.1371/journal.pone.0010075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wallrabe H., Svindrych Z., Alam S. R., Siller K. H., Wang T., Kashatus D., Hu S., Periasamy A., “Segmented cell analyses to measure redox states of autofluorescent NAD(P)H, FAD & Trp in cancer cells by FLIM,” Sci. Rep. 8(1), 79 (2018). 10.1038/s41598-017-18634-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cao R., Wallrabe H., Siller K., Rehman Alam S., “Single-cell redox states analyzed by fluorescence lifetime metrics and tryptophan FRET interaction with NAD(P)H,” Cytometry, Part A 95(1), 110–121 (2019). 10.1002/cyto.a.23711 [DOI] [PubMed] [Google Scholar]
- 16.Alam S. R., Wallrabe H., Svindrych Z., Chaudhary A. K., Christopher K. G., Chandra D., Periasamy A., “Investigation of Mitochondrial Metabolic Response to Doxorubicin in Prostate Cancer Cells: An NADH, FAD and Tryptophan FLIM Assay,” Sci. Rep. 7(1), 10451 (2017). 10.1038/s41598-017-10856-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lakowicz J.R., Principles Of Fluorescence Spectroscopy, (Springer US; 2006), Chap. 3. [Google Scholar]
- 18.Lakowicz J. R., Szmacinski H., Nowaczyk K., Johnson M. L., “Fluorescence lifetime imaging of free and protein-bound NADH,” Proc. Natl. Acad. Sci. 89(4), 1271–1275 (1992). 10.1073/pnas.89.4.1271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nakashima N., Yoshihara S. K., Tanaka F., Yagi K., “Picosecond fluorescence lifetime of the coenzyme of D-amino acid oxidase,” The Journal of Biological Chemistry 255(June.10), 5261–5263 (1980). [PubMed] [Google Scholar]
- 20.Ghukasyan Vladimir V., Heikal Ahmed A., Natural Biomarkers for Cellular Metabolism: Biology, Techniques, and Applications. (CRC Press, 2015), pp. 77–80. [Google Scholar]
- 21.Cao R., Wallrabe H., Siller K., Periasamy A., “Optimization of FLIM imaging, fitting and analysis for auto-fluorescent NAD(P)H and FAD in cells and tissues”. Methods and Applications in Fluorescence (2020). [DOI] [PubMed]
- 22.Wang R., Green D. R., “Metabolic checkpoints in activated T cells,” Nat. Immunol. 13(10), 907–915 (2012). 10.1038/ni.2386 [DOI] [PubMed] [Google Scholar]
- 23.Wang R., Dillon C. P., Shi L. Z., Milasta S., Carter R., Finkelstein D., McCormick L. L., Fitzgerald P., Chi H., Munger J., Green D. R., “The transcription factor Myc controls metabolic reprogramming upon T lymphocyte activation,” Immunity 35(6), 871–882 (2011). 10.1016/j.immuni.2011.09.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Frauwirth K. A., Harris M. H., Rathmell J. C., Riley J. L., Parry R. V., Plas D. R., Elstrom R. L., June C. H., Thompson C. B., “The CD28 Signaling Pathway Regulates Glucose Metabolism,” Immunity 16(6), 769–777 (2002). 10.1016/S1074-7613(02)00323-0 [DOI] [PubMed] [Google Scholar]
- 25.Chang C.-H., Curtis J. D., Leonard J., Maggi B., Faubert B., Villarino A. V., O’Sullivan D., Huang S. C.-C., Windt G. J. W. v. d., Blagih J., Qiu J., Weber J. D., Pearce E. J., Jones R. G., Pearce E. L., “Posttranscriptional control of T cell effector function by aerobic glycolysis,” Cell 153(6), 1239–1251 (2013). 10.1016/j.cell.2013.05.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Michalek R. D., Gerriets V. A., Jacobs S. R., Macintyre A. N., MacIver N. J., Mason E. F., Sullivan S. A., Nichols A. G., Rathmell J. C., “Cutting edge: distinct glycolytic and lipid oxidative metabolic programs are essential for effector and regulatory CD4+ T cell subsets,” J. Immunol. 186(6), 3299–3303 (2011). 10.4049/jimmunol.1003613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Walsh A. J., Sharick J. T., Skala M. C., Beier H. T., “Temporal binning of time-correlated single photon counting data improves exponential decay fits and imaging speed,” Biomed. Opt. Express 7(4), 1385–1399 (2016). 10.1364/BOE.7.001385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sun Q., Zheng W., Wang J., Luo Y., Qu J. Y., “Mechanism of two-photon excited hemoglobin fluorescence emission,” J. Biomed. Opt. 20(10), 105014 (2015). 10.1117/1.JBO.20.10.105014 [DOI] [PubMed] [Google Scholar]
- 29.Lukina M.M., Dudenkova V.V., Ignatova N.I., Druzhkova I.N., “Metabolic cofactors NAD(P)H and FAD as potential indicators of cancer cell response to chemotherapy with paclitaxel,” Biochim. Biophys. Acta, Gen. Subj. 1862(8), 1693–1700 (2018). 10.1016/j.bbagen.2018.04.021 [DOI] [PubMed] [Google Scholar]
- 30.Liu Z., Pouli D., Alonzo C. A., Varone A., Karaliota S., Quinn K. P., Münger K., Karalis K. P., Georgakoudi I., “Mapping metabolic changes by noninvasive, multiparametric, high-resolution imaging using endogenous contrast,” Sci. Adv. 4(3), eaap9302 (2018). 10.1126/sciadv.aap9302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Patsoukis N., Bardhan K., Chatterjee P., Sari D., Liu B., Bell L. N., Karoly E. D., Freeman G. J., Petkova V., Seth P., Li L., Boussiotis V. A., “PD-1 alters T-cell metabolic reprogramming by inhibiting glycolysis and promoting lipolysis and fatty acid oxidation,” Nat. Commun. 6(1), 6692 (2015). 10.1038/ncomms7692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Heaster T. M., Walsh A. J., Zhao Y., Hiebert S. W., Skala M. C., “Autofluorescence imaging identifies tumor cell-cycle status on a single-cell level,” J. Biophotonics 11(1), e201600276 (2018). 10.1002/jbio.201600276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mokrý M., Gál P., Vidinský B., Kusnír J., Dubayova K., Mozes S., Sabo J., “In vivo monitoring the changes of interstitial pH and FADNADH ratio by fluorescence,” J. Biophotonics 82(3), 793–797 (2006). 10.1562/2005-09-08-RA-678 [DOI] [PubMed] [Google Scholar]
- 34.Walsh A. J., Cook R. S., Manning H. C., Hicks D. J., Lafontant A., Arteaga C. L., Skala M. C., “Optical metabolic imaging identifies glycolytic levels, subtypes, and early-treatment response in breast cancer,” Cancer Res. 73(20), 6164–6174 (2013). 10.1158/0008-5472.CAN-13-0527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Walsh A. J., Beier H. T., “Temporal and spatial binning of TCSPC data to improve signal-to-noise ratio and imaging speed,” Proc. SPIE 9712, 97120R (2016). 10.1117/12.2208880 [DOI] [Google Scholar]
- 36.Yu Q., Heikal A. A., “Two-photon autofluorescence dynamics imaging reveals sensitivity of intracellular NADH concentration and conformation to cell physiology at the single-cell level,” J. Photochem. Photobiol., B 95(1), 46–57 (2009). 10.1016/j.jphotobiol.2008.12.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu C., Webb W. W., “Measurement of two-photon excitation cross sections ofmolecular fluorophores with data from 690 to 1050 nm,” J. Opt. Soc. Am. B 13(3), 481–491 (1996). 10.1364/JOSAB.13.000481 [DOI] [Google Scholar]
- 38.Yi M., Liu Q., “Michaelis–Menten mechanism for single-enzyme and multi-enzyme system under stochastic noise and spatial diffusion,” Phys. A 389(18), 3791–3803 (2010). 10.1016/j.physa.2010.05.041 [DOI] [Google Scholar]
- 39.Sharick J. T., Favreau P. F., Gillette A. A., Sdao S. M., Merrins M. J., Skala M. C., “Protein-bound NAD(P)H Lifetime is Sensitive to Multiple Fates of Glucose Carbon,” Sci. Rep. 8(1), 5456 (2018). 10.1038/s41598-018-23691-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bafunno V., Giancaspero T. A., Brizio C., Bufano D., Passarella S., Boles E., Barile M., “Riboflavin uptake and FAD synthesis in Saccharomyces cerevisiae mitochondria: involvement of the Flx1p carrier in FAD export,” J. Biol. Chem. 279(1), 95–102 (2004). 10.1074/jbc.M308230200 [DOI] [PubMed] [Google Scholar]
- 41.Giancaspero T. A., Locato V., de Pinto M. C., De Gara L., Barile M., “The occurrence of riboflavin kinase and FAD synthetase ensures FAD synthesis in tobacco mitochondria and maintenance of cellular redox status,” FEBS J. 276(1), 219–231 (2009). 10.1111/j.1742-4658.2008.06775.x [DOI] [PubMed] [Google Scholar]
- 42.Barile M., Brizio C., Valenti D., Virgilio C. D., Passarella S., “The riboflavin FAD cycle in rat liver mitochondria,” Eur. J. Biochem. 267(15), 4888–4900 (2000). 10.1046/j.1432-1327.2000.01552.x [DOI] [PubMed] [Google Scholar]
- 43.Huhner J., Ingles-Prieto A., Neususs C., Lammerhofer M., Janovjak H., “Quantification of riboflavin, flavin mononucleotide, and flavin adenine dinucleotide in mammalian model cells by CE with LED-induced fluorescence detection,” Electrophoresis 36(4), 518–525 (2015). 10.1002/elps.201400451 [DOI] [PubMed] [Google Scholar]
- 44.Masae T., Yoichi I., Jun-ichi N., Hiromasa I., “Low-frequency vibrational modes of riboflavin and related compounds,” Chem. Phys. Lett. 401(4-6), 475–482 (2005). 10.1016/j.cplett.2004.11.108 [DOI] [Google Scholar]