Fast in vivo multiphoton light-sheet microscopy with optimal pulse frequency

Abstract

Improving the imaging speed of multiphoton microscopy is an active research field. Among recent strategies, light-sheet illumination holds distinctive advantages for achieving fast imaging in vivo. However, photoperturbation in multiphoton light-sheet microscopy remains poorly investigated. We show here that the heart beat rate of zebrafish embryos is a sensitive probe of linear and nonlinear photoperturbations. By analyzing its behavior with respect to laser power, pulse frequency and wavelength, we derive guidelines to find the best balance between signal and photoperturbation. We then demonstrate one order-of-magnitude signal enhancement over previous implementations by optimizing the laser pulse frequency. These results open new opportunities for fast live tissue imaging.

1. Introduction

Multiphoton microscopy has demonstrated unique advantages for deep and live tissue imaging [1]. However, the acquisition speed of standard point-scanning two-photon-excited fluorescence (2PEF) microscopy is generally bounded to a µs per pixel due to signal limitations resulting from fluorophore photophysics [2]. This limit sets important constraints for investigating fast biological phenomena or for multiscale imaging [3]. Improving the speed of multiphoton microscopy is therefore an active field of research [4–9]. Among the strategies developed to improve the acquisition speed in multiphoton fluorescence imaging, light-sheet illumination exhibits distinctive advantages [4], with applications in cell biology [10], neurosciences [11], developmental biology [12], or organoid research [13]. Light-sheet illumination involves reduced average power and peak intensity [4] compared to other approaches based on a collinear arrangement of illumination and detection such as multifocal point-scanning [5] or scanless wide field illumination [9]. Indeed, the parallelization of the illumination in an orthogonal geometry such as in light-sheet imaging is done along the light propagation direction, requiring a single excitation beam to excite many pixels. In addition, the low-aperture focusing used to generate the light-sheet results in reduced laser peak intensity at the sample for the same detected signal, without compromising optical sectioning nor axial resolution [4,14]. Finally, the parallelization of the illumination results in long pixel dwell times and therefore in higher signal levels compared to fast scanning approaches [8]. These characteristics are expected to set different photoperturbation-related constraints in multiphoton light-sheet microscopy compared to fast collinear geometry approaches.

When optimizing a live fluorescence assay, it is essential to characterize the mechanisms and thresholds of photoperturbations at stake during imaging [15]. Knowledge of the dependence of perturbations on illumination parameters can then be used to balance the level of signal and of unwanted effects. In linear imaging techniques using continuous wave lasers, signal and perturbations are generally simply proportional to the excitation power or can be modulated by optimizing the spatial duty cycle of the illumination pattern [16]. In multiphoton imaging relying on pulsed excitation, additional illumination parameters can be adjusted to mitigate photoperturbations. Indeed, when the dominant perturbation process has a different nonlinear order than the signal, the signal-to-photoperturbation ratio can be increased by adjusting the laser duty cycle $\tau /T$ either through the laser pulse frequency (or repetition rate) $f=1/T$ [17], or through the pulse duration $\tau$ [18]. For instance, when the dominating perturbation process has an order higher than two, increasing the laser pulse frequency is an efficient strategy for increasing two-photon excited fluorescence (2PEF) while keeping photoperturbation at a constant level [17]. In standard multiphoton microscopy, various perturbation mechanisms have been investigated such as linear absorption and photothermal effects [5,19], fluorophore saturation [20], fluorophore photobleaching [21,22], or nonlinear photochemical phenomena [17,18,23,24].

In multiphoton light-sheet microscopy, adjusting the laser pulse frequency remains an attractive yet unexplored strategy to balance signal and photoperturbation. Indeed, most multiphoton light-sheet microscopes described so far [4,10–13,25–32] were implemented using a mode-locked Ti:sapphire laser at $f$∼80 Mhz, which is the most commonly used laser source in multitphoton microscopy. However, this choice is questionable and may not take full advantage of light-sheet illumination and its orthogonal geometry. A better understanding of the experimental parameters governing linear and nonlinear photoperturbation involved in the specific illumination conditions used in multiphoton light-sheet illumination is therefore necessary to bring this imaging modality to its full potential.

In this study, we devised a systematic experimental workflow to assess the nature and level of photoperturbations induced during imaging of the beating heart in live zebrafish embryos with multiphoton light-sheet microscopy (or 2P-SPIM, two-photon single-plane illumination microscopy). We found that monitoring the instantaneous heart beat rate (HBR) is a sensitive probe of both heating and higher-order-multiphoton induced perturbations. We identified the level and nonlinear order of photoperturbations during live imaging as a function of laser mean power, pulse frequency, and wavelength. This analysis enabled us to derive guidelines for determining which pulse frequency provides the optimal balance between signal, linear and nonlinear photoperturbation. In turn, we achieved high-speed in vivo two-photon imaging with an order-of-magnitude signal increase compared to previous reports using light-sheet illumination.

2. Results

2.1. Two- and three-photon excited fluorescence increases with lower pulse frequency in multiphoton light-sheet microcopy

In multiphoton microscopy, the order n of any optical process OP_n dictates how it is linked to the laser illumination intensity I, since $O{P}_n\sim I^n$. It can then be shown that OP_n, depends on the laser pulse frequency f (or period T=1/f), the pulse duration τ, and the mean power P_mean as follows

$$O{P}_n\sim {\left(\frac{T}{\tau }\right)}^{n-1}{P_{mean}}^n$$ (1)

As a consequence, nonlinear signals used in multiphoton light-sheet microscopy, such as 2-photon excited fluorescence (2PEF [4,25,28,29]), second harmonic generation (SHG [33]) or 3-photon excited fluorescence (3PEF [30]) can be enhanced by increasing T while keeping P_mean constant. Such enhancement has been established for point-scanning multiphoton imaging [17], but has not yet been demonstrated in the case of light-sheet illumination. Using 2P-SPIM imaging zebrafish embryos expressing mCherry fluorescent proteins, KTP nanocrystals [33], and fluorospheres embedded in a gel (see section Material and methods and Table S1 in Supplement 1 ^{(1.7MB, pdf)} ), we confirmed that both 2PEF and SHG signals depend linearly on T (n = 2, Fig. 1(a)-(b), Table S2 in Supplement 1 ^{(1.7MB, pdf)} ) and that 3PEF signals depend quadratically on T (n = 3, Fig. 1(c)). Hence, by decreasing the laser pulse frequency from 80 to 1 MHz at a constant mean power, 2PEF/SHG and 3PEF signals can be increased by a factor 80 and 6400, respectively. Reaching such enhancement factors is however potentially limited by the onset of higher-order unwanted effects caused by pulses of high energy E_pulse and peak power P_peak. In the case of live imaging of zebrafish embryos, we did not observe any saturation of mCherry fluorophore using P_mean = 100 mW and T up to 0.2 µs (f = 4.4 MHz), corresponding to E_pulse = 28 nJ (Fig. 1(a)). This value is one-to-two orders of magnitude higher than the saturating E_pulse estimated in point-scanning multiphoton microscopy [20]. Such a difference can be explained by the low illumination focusing used in 2P-SPIM. Indeed, given mCherry two-photon cross section [34] and a 0.1 illumination numerical aperture, the saturating E_pulse should be ∼200 nJ according to [20]. While the fluorophore saturation was not limiting, we however observed tissue damage when using higher T and E_pulse. As a consequence, it appears that the signal enhancement obtained by tuning the laser pulse frequency is limited by photopertubations, and that optimizing illumination parameters P_mean and T requires their systematic investigation.

Fig. 1.

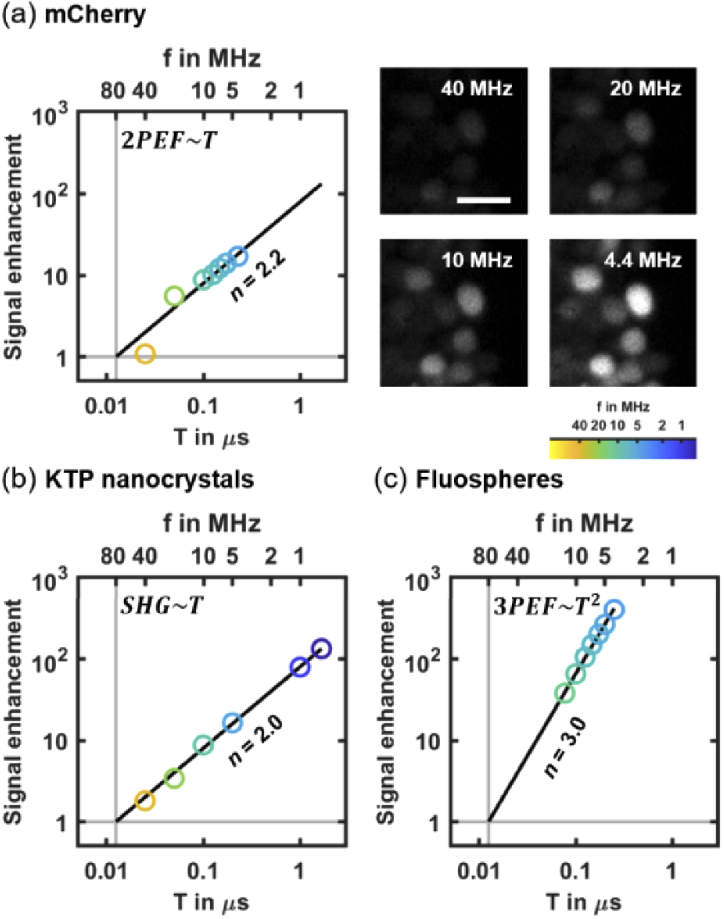
Signal enhancement in multiphoton light-sheet microscopy by decreasing the laser pulse frequency f (i.e. by increasing its period T) at constant mean power P_mean in the case of 2PEF (a), SHG (b), and 3PEF (c). (a) Linear increase in 2PEF signal (left) from mCherry labeled zebrafish embryos imaged at 168 frames per second with P_mean = 100 mW (N = 3 embryos). Representative images (right) of mCherry labeled cell nuclei used for signal quantification at f = 4.4, 10, 20 and 40 MHz using the same pixel gray scale. Scale bar is 10 µm (b) Linear increase in SHG signals from KTP nanocrystals (N = 500 nanocrystals). (c) Quadratic increase of 3PEF signals from blue fluorescent microspheres (N = 30 microspheres). 2PEF, 3PEF and SHG signals were normalized to the signals at f = 80 MHz (vertical gray lines). The order n of each optical process is retrieved from a linear fit of logarithmic scaled data (indicated with black lines). Detailed results of linear fits are given in Table S2 in Supplement 1 ^{(1.7MB, pdf)} .

2.2. Investigation of linear perturbation and nonlinear photodamage in vivo using zebrafish heart beating as a reporter

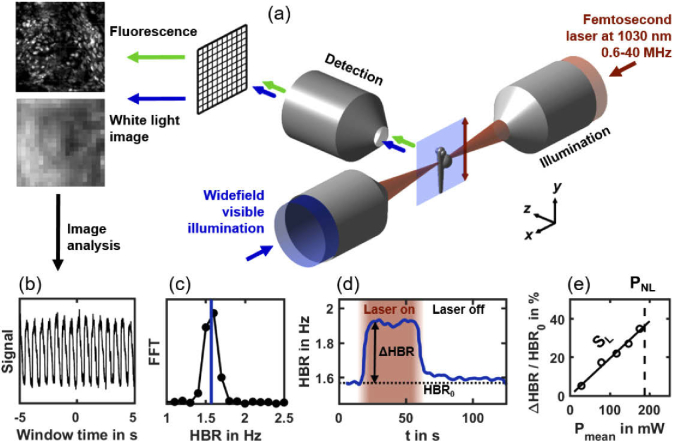
To systematically investigate the invasiveness of 2P-SPIM in vivo imaging depending on illumination parameters, such as laser pulse frequency f or laser mean power P_mean, we designed an experimental workflow using heart dynamics as a reporter of photoperturbation (Fig. 2, Visualization 1 ^{(3.4MB, mp4)} and Visualization 2 ^{(3.8MB, mp4)} and Material and methods). We imaged hearts of zebrafish embryos, using both white-light illumination and 2PEF imaging, during illumination using a femtosecond laser with tunable pulse frequency in the 1-40 MHz range (Fig. 2(a)). White-light illumination generates images of the heart of sufficient quality to quantify the instantaneous heart beat rate (HBR) even when the femtosecond laser was switched off or when using unlabeled embryos (Fig. 2(b)-(c), Visualization 1 ^{(3.4MB, mp4)} ). We kept all imaging parameters constant, except P_mean and f = 1/T. During a typical 130s-experiment (Fig. 2(d)), the HBR baseline HBR₀ was first recorded with the laser switched off. The laser was then turned on during ∼40 s and an increase in HBR was observed and quantified when stabilized. Finally, the laser was switched off to follow the HBR recovery (Fig. 2(d)). We then plotted the relative variation of heart beat rate (ΔHBR/HBR₀) as a function of the laser mean power P_mean (Fig. 2(e)) for different embryos with a fixed pulse frequency f. From this graph, we extracted two critical parameters: (i) the linear slope (S_L) characterizing the relative increase in HBR and (ii) the mean power threshold (P_NL) at which we started to observe nonlinear photodamage, such as irreversible arrhythmia, beating arrest or bubble formation (Visualization 2 ^{(3.8MB, mp4)} ). These two parameters will be used in the next sections to characterize linear and nonlinear invasive effects during 2P-SPIM imaging. We found that this approach was a fast, reproducible and quantitative investigation of optically-induced disruptions. It was also very sensitive and allowed us to detect very small variations of the HBR, down to 0.02 Hz or 1% of relative variation.

Fig. 2.

Experimental workflow to quantify linear perturbation and nonlinear photodamage using zebrafish heart beat rate (HBR) as a reporter. (a) 2P-SPIM setup with two illumination modes: a tunable pulse frequency femtosecond laser at 1030 nm wavelength (shown in red) is scanned to generate a light-sheet over the embryo, and wide field white light illumination (shown in blue). Either fluorescence (green arrows) or white light (blue arrows) images are acquired. (b) Periodic intensity fluctuations extracted from white light images correspond to the beating of the heart. (c) Instantaneous HBR is estimated using a ten second windowed Fourier transform of that signal with sub-time point accuracy (blue line). (d) The instantaneous HBR is measured along time, and increases by ΔHBR compared to the baseline HBR₀ when the fish is exposed to femtosecond laser illumination (in red). (e) At a given laser pulse frequency, the relative ΔHBR is proportional to the laser mean power P_mean with a slope S_L. P_mean is increased up to a power threshold P_NL over which nonlinear photodamage occur estimated from image observation and HBR arrhythmia (Visualization 2 ^{(3.8MB, mp4)} ).

2.3. Linear absorption at low mean power result in limited heating and reversible increase in HBR

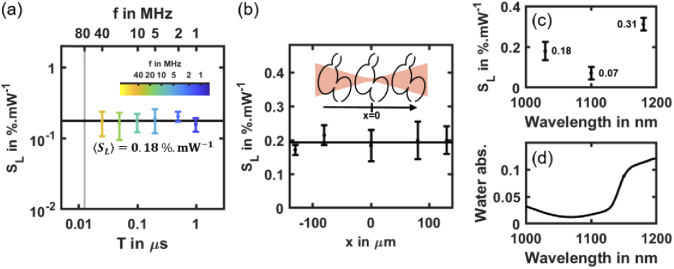
When increasing the laser mean power, with all other imaging parameters remaining constant, the first effect we observed was a linear increase in HBR (Fig. 2(e)). To demonstrate that this effect was due to a reversible linear absorption of the laser light, we conducted several experiments. First, we measured the slope S_L as defined above and showed that it does not depends on the laser pulse frequency (Fig. 3(a), and Table S2 in Supplement 1 ^{(1.7MB, pdf)} ), which characterized an optical process of order n = 1. We verified experimentally that, as expected for a linear effect, S_L does not depends on the position of the focus when moving it away from the center of the heart but keeping the heart within the illumination cone (Fig. 3(b)). In addition, we observed that this perturbation was reversible: the HBR systematically returned to its base level within a few tens of seconds after illumination stopped (Fig. 2(d)).

Fig. 3.

Linear effect at low mean power may be related to water absorption and tissue heating. (a) Linear slope S_L of the HBR relative variation of mCherry labeled zebrafish hearts (N = 27 embryos) depending on the laser pulse frequency f = 1/T. Black line indicates mean value < S_L> = 0.177 ± 0.017%.mW^-1). (b) S_L as a function of the relative position of the fish heart and illumination beam focus in the x-direction at f = 10 MHz (N = 3 embryos per position). Black line indicates mean S_L value. (c) S_L at f = 80 MHz depending laser wavelength. (d) Water absorption spectrum in the 1000-1200 nm wavelength range.

To examine whether this effect was mediated by the fluorophore, we performed the same experiment in unlabeled embryos (Fig. S1a in Supplement 1 ^{(1.7MB, pdf)} ) and in embryos labeled with a different fluorophore (Fig. S1c in Supplement 1 ^{(1.7MB, pdf)} ). We measured similar S_L values in both cases, validating that HBR increase is not mediated by labeling. Finally, to test whether this effect was mediated by water absorption, we repeated the experiments at different wavelengths using a tunable 80 MHz laser source. We found that S_L does depend on laser wavelength and follows the same variation as water absorption in the 1000-1200 nm range (Fig. 3(d)). This result suggests that water absorption might be involved and could induce a local heating of the specimen when the laser is on. Since the HBR is known to linearly depend on the temperature in the zebrafish embryo [35,36], S_L can be related to a change in local temperature. We measured an HBR variation of ∼0.29 Hz/°C (Fig. S2 in Supplement 1 ^{(1.7MB, pdf)} ) and S_L remains close to 20% per 100 mW when illuminating embryos with f = 1-40 MHz and λ = 1030 nm. As a consequence, we obtain a typical temperature increase of 1.4°C per 100 mW. Such measurement is consistent with recently reported heating measurements in the mouse brain using point-scanning multiphoton microscopy [5,19]. Together, these results demonstrate that the first detectable disruption when imaging the zebrafish heart with 2P-SPIM is reversible and due to linear absorption of the laser light. They also suggest that this linear effect is not mediated by the fluorophore and could be due to water absorption. Using an illumination of P_mean = 70 mW at λ = 1030 nm would then result in a typical temperature increase of ∼1°C and a limited and reversible HBR increase of ∼0.3 Hz, which remains within physiological conditions for zebrafish embryos. More generally, it appears that adjusting the laser pulse frequency at a constant mean power is an effective strategy to enhance the signal while keeping linear heating at a constant level.

2.4. Scaling law of highly nonlinear photodamage

When increasing further the laser mean power, with all other imaging parameters being held constant, we observed strong and irreversible tissue photodamage at a given power threshold P_NL as defined above (Fig. 2(e)). To demonstrate that this effect was due to a nonlinear photodamage mechanism, we measured P_NL at different laser pulse frequencies. Unlike in the case of S_L and linear heating due to water absorption, P_NL strongly depends on T (Fig. 4(a)), and decreases from 320 mW at 20 MHz to 30 mW at 1 MHz (Table S1 in Supplement 1 ^{(1.7MB, pdf)} ). This dependence on T is expected from a nonlinear optical process according to Eq. (1). To estimate the scaling law and the order n of this perturbation mechanism, we performed a linear fit on P_NL(T) plotted in logarithmic scale (Fig. 4(a)). According to Eq. (1), the threshold P_NL should scale as $\log P_{NL}\sim \frac{1-n}{n}\log T$. We found n = 5.8 (Table S2 in Supplement 1 ^{(1.7MB, pdf)} for details) with a good reproducibility of the experiment from one embryo to the other considering the high nonlinearity of the optical effect. To confirm the nonlinear nature of these perturbations, we measured P_NL at f = 10 MHz for different positions of the heart relative to the beam focus along the illumination axis and keeping the heart within the illumination cone. Unlike in the case of S_L and a linear effect, we observed a lower photodamage threshold P_NL when the laser beam was focused at the center of the heart (Fig. 4(b)). Its variation could be fitted to the intensity profile along the illumination axis of a Gaussian beam of 0.05 numerical aperture (black line in Fig. 4(b)), which is close to the actual numerical aperture of the 2P-SPIM setup. Such behavior is expected from a nonlinear optical process that is sensitive to the local intensity. To test whether the observed nonlinear photodamage were mediated by the fluorophore, we measured P_NL(T) and estimated n in unlabeled embryos (Fig. S1b in Supplement 1 ^{(1.7MB, pdf)} ) and in embryos labeled with a different fluorophore (Fig. S1d in Supplement 1 ^{(1.7MB, pdf)} ). We found similar values for P_NL and the order n, which was close to 5 (n = 4.8 and 4.9, respectively; Table S2 in Supplement 1 ^{(1.7MB, pdf)} ). If photodamage had been sensitive to the fluorophore, we would have obtained significantly higher values of P_NL and n in the case of unlabeled embryos. Together, these results demonstrate that increasing the signal in 2P-SPIM by increasing the average power or decreasing the laser pulse frequency is limited by irreversible highly nonlinear photodamage with an order close to n = 5, which are not mediated by the fluorophore.

Fig. 4.

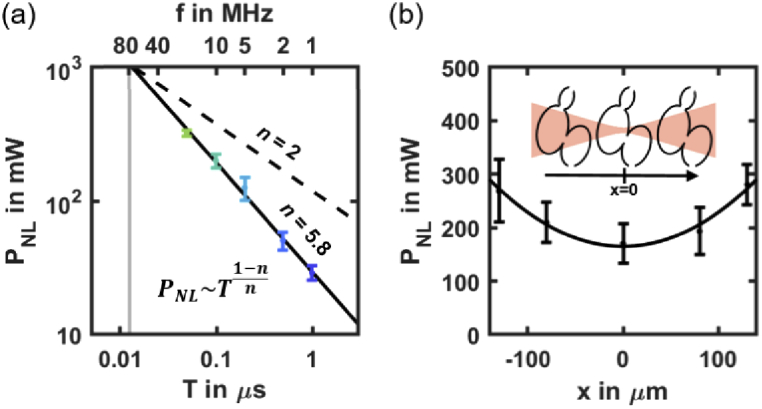
Scaling law of nonlinear photodamage. (a) Nonlinear photodamage threshold P_NL in mCherry labeled zebrafish hearts (N = 21 embryos) depending on the laser pulse frequency f = 1/T. Black line shows the result of the scaling law fitted on logarithmic scaled data. The P_NL (T) follows a scaling law of order n∼5.8 (see Table S2 in Supplement 1 ^{(1.7MB, pdf)} for details). Black dashed line indicates a scaling low of order n = 2 to show how it deviates from 2PEF signal. (b) P_NL as a function of the relative position of the heart and illumination beam focus at f = 10 MHz (N = 3 embryos per position). Black line indicates the result of a Gaussian fit. Error bars indicate standard deviation.

2.5. Photobleaching of mCherry at 1030 nm using 2PSPIM is a nonlinear process

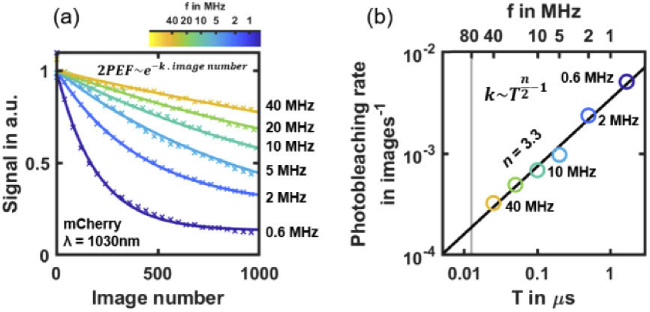
The last unwanted photoinduced effect we analyzed in this study is fluorophore photobleaching. We measured the photobleaching rate of mCherry at 1030 nm wavelength when tuning the laser pulse frequency (Fig. 5). To be relevant to experimental applications, this measurement was performed at a constant starting 2PEF signal level by adjusting the laser power P_mean to compensate for the variation in T (see Table S2 in Supplement 1 ^{(1.7MB, pdf)} for details). It results in $P_{mean}\sim T^{-\frac{1}{2}}$ according to (1). At f = 40 MHz (yellow line in Fig. 5(a)), very low photobleaching is observed, which confirms previously reported experiments at f = 80 MHz [37]. However, we showed the photobleaching rate increases with T. Since $P_{mean}\sim T^{-\frac{1}{2}}$, photobleaching of order n should scale as $T^{\frac{n}{2}-1}$. Hence, we estimated the order of the mCherry photobleaching rate to be n = 3.3 (Table S2 in Supplement 1 ^{(1.7MB, pdf)} ), which is consistent with previous investigations of photobleaching in multiphoton microscopy [21]. In the following section, we will consider the photobleaching observed at f=0.6 MHz (dark blue line in Fig. 5(a)) as the experimental threshold. It corresponds to a 50% signal decay after ∼150 images or ∼1s of acquisition.

Fig. 5.

Scaling law of mCherry photobleaching at 1030 nm wavelength using 2P-SPIM. (a) mCherry 2PEF signal decay during 2P-SPIM imaging depending on the number of acquired images at different laser pulse frequency f (from 0.6 to 40 MHz). Mean power is adjusted depending on f to start with the same 2PEF signal level at each experiment (N = 3 embryos per condition). Solid lines indicate exponential fits used to estimate the photobleaching rate. (b) Photobleaching rate depending on laser pulse frequency f. These logarithmic scaled data are used to perform a linear fit (black line) and estimate the n-order of the photobleaching rate.

2.6. Balancing signal and photoperturbation to optimize live 2P-SPIM imaging of the zebrafish heart

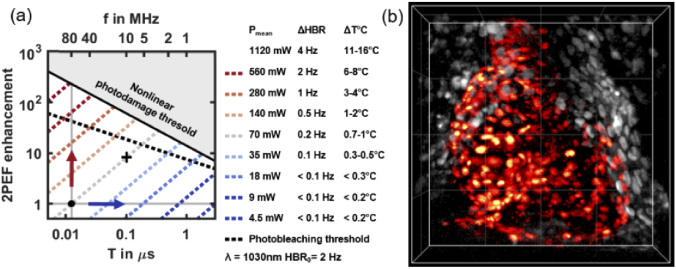
To select the optimal laser pulse frequency and enhance signal during 2P-SPIM imaging, we used our characterization of heating, highly nonlinear photodamage and photobleaching. We represented in a single graph a model of how they limit signal enhancement when adjusting the laser pulse period T (or frequency f = 1/T) and mean power P_mean (Fig. 6(a)). The signal enhancement is defined as the 2PEF signal normalized to the signal obtained in typical 2P-SPIM imaging conditions (f₀ = 1/T₀ = 80 MHz and P₀ = 70 mW), as previously reported [37]. In this graph, a constant photoperturbation is represented by a straight line whose slope depends on its order. The position of this line and the sign of its slope is critical to optimize the laser pulse frequency and to balance signal and photoperturbation, as explained in section Material and methods.

Fig. 6.

Optimized 2P-SPIM imaging of the zebrafish heart at 10 MHz pulse frequency. (a) 2PEF signal enhancement graph used to select the optimal laser pulse frequency. Signal enhancement corresponds to $\frac{T{P_{mean}}^2}{T_0{P_0}^2}$ with T₀ = 1/f₀ = 1/80 MHz and P₀ = 70 mW, the reference 2P-SPIM imaging conditions (black dot). Solid and dashed black lines correspond to the nonlinear photodamage $\frac{T{P_{NL}}^2}{T_0{P_0}^2}$ and the photobleaching thresholds, respectively. Dashed blue-to-red lines corresponds to line of constant mean power and constant linear effect (variation of heart beat rate ΔHBR and of temperature ΔT°C). (b) 2P-SPIM imaging of the beating heart in histone mCherry-labeled zebrafish embryo at 3 days post-fertilization. 4D imaging at 168 frames per second using f = 10 MHz and P_mean = 70 mW (black cross in a) with 200 × 200 × 100 µm or 500 × 500 × 100 voxels field-of-view and one heart cycle of 75 frames. 4D reconstruction using post-acquisition time synchronization as previousy described [37,39]. 3-D rendering and manual heart segmentation (red cells) performed with Imaris. Ventral view with anterior up. Grid spacing 50 µm.

Starting from previously reported imaging conditions of 2P-SPIM imaging of the beating heart (black dot in Fig. 6(a), at f₀ and P₀), several strategies are possible. First, the signal can be increased at f= 80 MHz by increasing the mean power, that is following the vertical line on the graph (Fig. 6(a), red arrow). In this case, a >200-fold signal enhancement can be obtained before reaching nonlinear photodamage at P_mean>1W. However, large mean powers will induce heating beyond physiological conditions. Our analysis shows that at f= 80 MHz, photothermal effects are the limiting factor in 2P-SPIM, which is different to point-scanning multiphoton microscopy [16,17,22] and calls for a different optimization approach. It can be explained by the low illumination NA used in 2P-SPIM.

A second possibility would be to reduce f down to the 1 MHz range at constant 2PEF signal by following a horizontal line on the graph (Fig. 6(a), blue arrow). The graph shows that a constant signal with lower heating can be obtained while reducing the mean power below 10 mW. However, in this regime, the nonlinear photodamage threshold is very low and prevents signal enhancement. In addition, photobleaching at low laser pulse frequencies as reported above for mCherry could be limiting depending on the fluorophore properties.

To optimize heart imaging, we therefore followed an intermediate path. We kept P_mean constant at P₀ = 70 mW (light gray dashed line in Fig. 6(a)). We then decreased f and increased the signal while ensuring that heating was less than 1°C therefore keeping the HBR in physiological conditions (less than 0.2 Hz variation). By using f = 10 MHz (black cross in Fig. 6(a)), P_mean remained one order of magnitude below the nonlinear photodamage threshold and we obtained a one order-of-magnitude increase in 2PEF signal. Such signal was sufficient to image the beating heart at the fastest speed of the camera (168 frames per second, corresponding to 42 MHz pixel rate, and, after 3D reconstruction, to 4.2 GHz voxel rate), without significant photobleaching (Fig. 6(b), Visualization 3 ^{(8.3MB, mp4)} ). Indeed, we measured less than 10% signal loss after 75 frames (corresponding here to one heart cycle). As expected, recording the same beating heart using f = 40 MHz and f = 10 MHz at constant mean power (Visualization 4 ^{(1.7MB, mp4)} ) results in a 4 fold increase in 2PEF signal. Finally, by recording a smaller volume, we could capture the outflow tract valve dynamics at 488 frames per second with a good axial resolution (Visualization 5 ^{(4.6MB, mp4)} ). These valves are among the deepest and most dynamic structures in the beating heart [38].

3. Discussion

In this study, we established that live imaging of mCherry-labeled zebrafish embryonic heart using 2P-SPIM is significantly optimized by decreasing the laser pulse frequency from 80 to ∼10 MHz. This strategy increases the signal by 8-fold without inducing additional heating nor reaching nonlinear photodamage thresholds or significant photobleaching rates. Hence, we achieved high-speed multiphoton imaging in vivo while maintaining both low laser average power and peak intensity. Indeed, the mean laser power (P_mean = 70 mW) was at least one order of magnitude lower than used in other parallelized techniques using multifocal point-scanning [5] or wide-field illumination [40], which limits thermal effect. In addition, the laser peak intensity (I_peak = 0.1 TW.cm²) was maintained below typical values used in standard multiphoton point-scanning microscopy, and one-to-two orders of magnitude below the values used in recent development of fast multiphoton microscopy [5,8]. Our study also provides guidelines to further optimize 2P-SPIM imaging. For instance, increasing the laser wavelength from 1030 to the 1100 nm range would drastically reduce linear absorption and heating (Fig. 3(c)). By using the same reasoning, and assuming that the level and order of nonlinear photodamage are similar, the optimal laser pulse frequency would then be in the range of 20-30 MHz with P_mean∼180 mW, resulting in a 2- to 3-fold additional increase of 2PEF signal at constant thermal effects. In addition, mCherry excitation would be enhanced at 1100 nm, with potentially lower photobleaching. However, laser sources with such parameters delivering sufficient mean power are not yet common.

To adjust the laser duty cycle $\frac{\tau }{T}$ (Eq. (1)), one could also reduce the laser pulse width $\tau$ and potentially obtain similar results than increasing T. In this study, we decided to adjust the laser pulse frequency, since using sub-50 fs pulses in multiphoton microscopy brings additional dispersion issues. While decreasing $\tau$ would theoretically have the same effect on signal as increasing T, the change in photoperturbation induced by a shorter pulse may be different and would require further investigations.

We anticipate the benefit demonstrated in this work can be obtained for any implementation of 2P-SPIM, including using Bessel [10,27,29] or Airy [31,32] beams instead of Gaussian beams, as long as the laser peak intensity remains lower than in the point-scanning case. The nonlinear photodamage threshold involved in 2P-SPIM using different beam shapes would however require further investigations.

To assess photoperturbations, we devised a strategy using zebrafish embryo HBR as a reporter. This approach is convenient for several reasons. First, HBR quantification is instantaneous, can be monitored over time and does not require any specific labeling strategy or manipulation of live specimen. In addition, we have shown it reports both on reversible effects such as heating and on irreversible nonlinear photodamage by identifying arrhythmia or cardiac tissue damage. To further investigate photoperturbations or apply this work to different organisms, many other reporters could be used, including the monitoring of reactive oxygen species, cell cycle, cytoskeletal dynamics, metabolism, or cell apoptosis [15].

This study mainly focused on 2PEF signals. However, a similar signal enhancement strategy can be applied to other nonlinear contrast mechanisms, such as SHG (Fig. 1(b)) or 3PEF (Fig. 1(c) and Fig. S3 in Supplement 1 ^{(1.7MB, pdf)} ), taking into account some subtleties. In the case of multiphoton light sheet imaging of SHG nanocrystals [33], the signal is not limited by saturation or photobleaching and the illumination wavelength can be freely adjusted to minimized water absorption since these probes are achromatic. Additionally, the higher the order of the signal, the stronger its enhancement will be by adjusting the pulse frequency. A quadratic signal enhancement is obtained in the case of 3PEF, corresponding to 64-fold more signal at f = 10 MHz (Fig. S3 in Supplement 1 ^{(1.7MB, pdf)} ) compared to previously reported 3P-SPIM at f = 80 MHz [30].

More generally, to take full advantage of light-sheet illumination we demonstrated the laser pulse frequency needs to be optimized compared to current implementations of 2P-SPIM. As a word of caution, it should be noted that several results of this study may be application-specific, such as the photobleaching scaling law of mCherry or the photodamage threshold in zebrafish cardiac tissue. In addition, other experimental parameters may have critical impact on photoperturbations, such as the laser wavelength or the illumination scan speed. However, our study confirmed several general guiding rules. First, unlike in standard point-scanning microscopy, in the case of 2P-SPIM at f = 80 MHz, live imaging is not limited by fluorophore saturation or nonlinear photodamage, but by a dominating linear effect, which is likely heating by water absorption. This comes from the lower illumination NA and laser peak intensities used in 2P-SPIM compared to point-scanning techniques. Together, our results suggest f = 80 MHz is not adapted to 2P-SPIM imaging and that decreasing f to enhance 2PEF signals is a better strategy than simply increasing the laser power. Then, nonlinear photodamage and photobleaching limits how low f can be. Finally, laser pulse frequency below 80 MHz and above 1 MHz should be used. Ideally, a laser source providing tunability in both wavelength (900-1200 nm) and pulse frequency (typically 1-40 MHz) would be ideal to optimize live 2P-SPIM imaging.

4. Conclusion

In conclusion, we investigated photoperturbations in live 2P-SPIM imaging by tuning the laser pulse frequency instead of the mean power. By using zebrafish heart beating as a rapid and sensitive experimental reporter, we identified and characterized different photoperturbation processes, specifically a reversible linear effect, likely due to water absorption and heating, and an irreversible nonlinear process of nonlinear order ∼5. None of these perturbations were mediated by the fluorophore. In addition, we characterized the scaling law of a fluorophore photobleaching rate. We established that the limiting parameters in 2P-SPIM differ from the ones previously reported using point-scanning multiphoton microscopy [17,18] and call for a different optimization strategy. Finally, we used these results to balance signal and photoperturbation in live 2P-SPIM imaging of the zebrafish heart: optimizing the laser pulse frequency, we obtained an 8-fold increase in 2PEF signal without inducing additional heating nor reaching nonlinear photodamage thresholds. Such optimization allowed us to image the zebrafish beating heart at the highest camera speed, and with improved signal-to-noise ratio compared to previously reported [37]. Hence, we achieved high-speed multiphoton imaging in vivo up to 0.5 kHz frame rate while maintaining both low laser average power and peak intensity. More generally, these results show that f = 80 MHz is not adapted to 2P-SPIM imaging since it can cause significant linear absorption and heating. In addition, to enhance 2PEF signals, lowering f appears as a better strategy than increasing the laser power. However, reaching the 1 MHz range may expose to nonlinear photodamage and fluorophore photobleaching. In conclusion, it appears that a femtosecond laser source tunable in both wavelength (900-1200 nm) and pulse frequency (1-40 MHz) would be ideal in 2P-SPIM to optimize live imaging conditions. The significant signal improvement obtained by optimizing the laser pulse frequency will undoubtedly extend the range of application of live 2P-SPIM imaging, with faster acquisition or stronger signal-to-noise ratio.

5. Material and methods

5.1. Multiphoton light-sheet microscopy

Multiphoton light-sheet microscopy (2P-SPIM) was performed using a custom-built optical set-up (Fig. 2(a)). The illumination arm was composed of an Ytterbium fiber femtosecond laser (Satsuma, Amplitude) producing pulse trains at 1030 nm wavelength, with 290-310 fs pulse duration and 0.6-40 MHz tunable frequency. Fast control of the illumination power was obtained with either an electro-optic modulator (EOM, Conoptics) or the laser built-in acousto-optic modulator, with additional wave plates and polarization beam splitters to tune the power modulation range. A shutter (Thorlabs) was used to completely block the laser. The illumination beam propagating in the x-direction (Fig. 2(a)) was focused on the sample by a low numerical aperture (NA) water immersion objective (10× 0.30 NA, Nikon). Illumination beam divergence was controlled with a telescope so as to achieve an effective illumination NA of ∼0.09, corresponding to a Gaussian beam waist w₀ of ∼3.6 µm (light-sheet thickness) and an axial resolution of ∼3 µm of two-photon excited fluorescence signal. A pair of galvanometer mirrors produces on the one hand the illumination light sheet by vertical scanning of the beam in the y-direction synchronously with the camera read-out, and on the other hand the displacement in z of the light-sheet to perform volume imaging. The white light illumination was performed with a LED desk lamp focused onto the sample with a 10× 0.30 NA objective (Nikon) from the opposite side to that used for laser illumination. The detection arm was composed of a high NA water immersion objective (16× 0.80 NA, Nikon) collecting fluorescence orthogonally to the light-sheet plane. The z-position of the detection objective was moved in synchrony with the z-scanning of the light-sheet by using a piezo stage. A short-pass 800 nm filter was used to detect signal only in the visible range. A tube lens was used to image the illuminated plane onto a sCMOS camera (Flash 4.0, Hamamatsu) with a pixel size of 0.4 µm. The camera line detection was synchronized with the illumination y-scanning. The Sample was maintained in chamber filled with water solution and positioned from the top of the chamber with a combination of a motorized stage (MP285, Sutter Instrument) for translation in X, Y and Z directions, and a rotation stage for rotation about the Y axis. The sample was mounted in agarose using a glass capillary tube. Its spatial position was controlled by the combination of a rotation stage about the y-axis and a three-way motorized stage (MP285, Sutter Instrument), positioned over a water-filled chamber. All peripheral devices, including laser illumination power using the EOM, shutter, galvanometer mirrors, piezo-stage, camera, and motorized sample stage, were controlled and synchronized using custom-written LabVIEW (National Instruments) software. Image acquisition was performed at maximum imaging speed. It was determined by the vertical size (y-direction) of the field of view, with a camera line detection set to its minimum (9.8 µs), corresponding to the imaging speed of 168 frames per second for a 500 pixels field of view in the y-direction. In this case, each image was illuminated and detected in 4.9 ms, with 1.1 ms additional delay between images, during which the laser was switched off. The camera detection time per pixel was set to 490 µs. As a consequence, the signal per pixel was limited by the pixel illumination time during a y-scan, corresponding to ∼73 µs/pixel. $P_{mean}$ is the mean power at the sample during imaging taking into account the laser switching off between images. To estimate $S_L$depending on the illumination wavelength (Fig. 3(c)), another home-built microscope was used as described in [37].

5.2. Sample preparation for imaging

The following zebrafish lines were provided by AMAGEN zebrafish facility at CNRS Gif-sur-Yvette (UMS 3504 CNRS / UMS 1374 INRA): casper, casper crossed with Tg(ubi:H2B-mCherry) and casper crossed Tg(actb1:nls-TagRFP) (ama008632Tg on zfin.org). Both transgenic lines provide ubiquitous labeling of cell nuclei. Embryos were either obtained from AMAGEN or from the Ecole polytechnique zebrafish facility. Eggs were raised in the dark at 28°C for three to five days. For imaging, embryos were anaesthetized with 0.01% (100 mg/L) Tricaine (MS-222, Sigma Aldrich) and embedded in 1% (10 g/L) low melting point agarose (Sigma Aldrich) as previously described [4]. Imaging was performed at room temperature (20-23°C) in the imaging chamber filled with 0.01% Tricaine solution. All experiments were performed with zebrafish embryos at 4-5 days post-fertilization unless specified and before independent feeding larval forms, which complied with the European directive 2010/63/UE. KTP nanocrystals were prepared and mounted for imaging as previously described [30]. Blue FluoSpheres (350/440, Thermofisher F8815) were diluted at a ratio of 1:1000 in agarose.

5.3. Image analysis and reconstruction

Image processing and analyses were performed using Fiji [41] and Matlab (The MathWorks Inc.). To estimate the signal level (Fig. 1), cell nuclei or point sources were segmented using an intensity threshold and the signal averaged from all segmented pixels. 4D reconstructions (Fig. 6(b) and Visualization 3 ^{(8.3MB, mp4)} , Visualization 4 ^{(1.7MB, mp4)} , and Visualization 5 ^{(4.6MB, mp4)} ) were performed using post-acquisition time synchronization of beating heart images [37,39]. A 3 × 3 median filter was applied to images before 4D reconstruction. 4D rendering and manual heart segmentation were performed using Imaris (Bitplane). For display of images in Fig. 6(b) and Visualization 3 ^{(8.3MB, mp4)} , the pixel histogram was linearly stretched and gamma adjusted (value of 2). To generate Visualization 4 ^{(1.7MB, mp4)} , the same linear stretch of pixel histograms was applied to both imaging datasets. For Visualization 5 ^{(4.6MB, mp4)} , a five timepoint median filter was applied, the pixel histogram linearly stretched and gamma adjusted (value of 1.8).

5.4. Heart beat rate analysis and definition of $S_L$and $P_{NL}$

To estimate $S_L$and $P_{NL}$, the heart beat rate (HBR) was quantified depending on the illumination parameters. In each experiment described in Fig. 2, the heart was imaged at 168 fps using white light illumination and time series of 22 000 images (500 × 500 binned by a factor 20). The first 3000 images (18 s of acquisition) were used to quantify the HBR baseline (HBR₀). Then, during 10000 images (from acquisition time 18 to 77 s), the femtosecond laser was switched on at a given mean power $P_{mean}$ and period T and the embryo was illuminated as during 2P-SPIM imaging. The ΔHBR variation was quantified during this time. Finally, during the last 12000 frames (from acquisition time 77 to 131 s), the femtosecond laser was switched off to follow the HBR returning to the baseline when the HBR variation was reversible. The instantaneous HBR was estimated using custom-made scripts written in Matlab (The MathWorks Inc.) as follows. A 10 second time-windowed fast Fourier transform (FFT) of the temporal signal from each pixel was performed (Fig. 2(b)-(c)). To obtain the instantaneous HBR, the 30 best pixels were selected based on their FFT signal-to-noise measure, defined as the ratio of the FFT maximum over the time window divided by the mean value of the FFT. Instantaneous HBR value at each pixel was estimated with sub-timepoint accuracy using a three-point interpolation (Fig. 2(c), Visualization 1 ^{(3.4MB, mp4)} ). The mean HBR value from the 30 selected pixels at each time point was then estimated and plotted depending on time as in Fig. 2(d). ΔHBR relative variation was defined as HBR-HBR₀, the difference between the HBR after and before switching the laser on. Finally, this experiment was repeated on the same embryo at a given laser pulse frequency f using an increasing $P_{mean}$. The reversible nature of the laser induced effect were verified by observing the HBR returning to the same HBR₀ at the beginning of each measurement (Visualization 2 ^{(3.8MB, mp4)} ). $P_{mean}$ was increased up to the observation of irreversible photodamage such as heart arrhythmia or bubble formation (Visualization 2 ^{(3.8MB, mp4)} ). The threshold $P_{NL}$ was then defined as the mean between the highest $P_{mean}$ used without irreversible photodamage and the $P_{mean}$ inducing them. Finally, $S_L$was defined as the slope of the linear regression of ΔHBR/HBR₀ depending on $P_{mean}$ at a given laser period T (Fig. 2(e)). Such measurements were also performed depending on the illumination beam x-position within the heart (Fig. 3(b) and 4(c)) and on the illumination wavelength (Fig. 3(c)). Unless specified, all incertitude in this manuscript corresponds to 90% confidence intervals.

5.5. Photobleaching analysis

To quantify photobleaching depending on the laser period T, zebrafish embryo expressing mCherry were imaged in the tail region to avoid artefact due to cell motion. A different area was imaged in each condition. The photobleaching experiments were performed at constant fluorescent signal levels by adjusting $P_{mean}$ to keep $T.{P_{mean}}^2$ constant. Due to the Gaussian profile of the illumination in the x-direction, photobleaching is stronger at the center of the field of view. We then selected the center part of the image (40 µm large in the x-direction) to analyze the 2PEF signal decay. Finally, to optimize the exponential decay fit of the experimental data using scripts written in Matlab (The MathWorks Inc.), we analyzed 1000 images for f = 0.6-2 MHz (fast decay), and 5000 images for f = 5-40 MHz (slow decay). The photobleaching rate k is then defined as the decay rate of an exponential fit:

$$2PEFsignal(imagenumber)\sim \text{A}+\text{B}\ast e^{-k.imagenumber}$$

5.6. Signal enhancement graph

To balance signal and photoperturbation, we plotted on the single graph how the 2PEF and 3PEF signal enhancement (Fig. 6(a) and Fig. S3 in Supplement 1 ^{(1.7MB, pdf)} , respectively) is limited by unwanted processes (heating, highly nonlinear photodamage and photobleaching). In such a graph, the n_S-order signal enhancement $S_{n_S}$ is plotted in logarithmic scale depending on the laser pulse period T. We then have:

$$S_{n_S}(T,P_{mean})=\frac{T^{n_S-1}{P_{mean}}^{n_S}}{{T_0}^{n_S-1}{P_0}^{n_S}}$$

with T₀ = 1/80 MHz and P₀ = 70 mW, corresponding to typical laser parameters currently used in multiphoton light-sheet microscopes. In this graph, a line of constant $P_{mean}$ has a slope of $n_S-1$. In the case of 2PEF or 3PEF signals, lines of constant $P_{mean}$ have a slope of 1 ($n_S=2$, blue-to-red color dashed lines in Fig. 6(a)) or 2 ($n_S=3$, blue-to-red color dashed lines in Fig. S3 in Supplement 1 ^{(1.7MB, pdf)} ).

In the case of a n_P-order photoperturbation, with a power threshold $P_{th}$(T), we have:

$$P_{th}(T)={\left(\frac{T}{T_0}\right)}^{\frac{1-n_P}{n_P}}{P}_{th}(T_0)$$

and

$$S_{n_S}(T,P_{th})={\left(\frac{T}{T_0}\right)}^{\frac{n_S}{n_P}-1}{\left(\frac{P_{th}(T_0)}{P_0}\right)}^{n_S}$$

As a consequence, a line of constant photoperturbation has a slope of $\frac{n_S}{n_P}-1$ in this graph. The sign of this slope is critical to balance the signal and the photoperturbation and depends on their relative order.

In the case of 2PEF signal ($n_S=2$, Fig. 6(a)), a line of constant n_p-order photoperturbation has a slope of $\frac{2}{n_P}-1$. This slope is positive and equal to one in the case of a linear effect such as heating ($n_P=1$). Hence, lines of constant linear effect (blue-to-red color dashed lines in Fig. 6(a)) correspond to lines of constant P_mean and to specific linear variation of HBR and of temperature, as estimated from our experimental investigation. In the case of $n_P>2$, such as for photobleaching or nonlinear photodamage, the slope is negative (solid and dashed black lines in Fig. 6(a), for P_NL, and photobleaching threshold, respectively). For instance, the nonlinear photodamage threshold P_NL ($n_P=5.8$) reported in section 2.4 follows a line:

$$S_2(T,P_{NL})={\left(\frac{T}{T_0}\right)}^{\frac{2}{5.8}-1}{\left(\frac{P_{NL}(T_0)}{P_0}\right)}^{5.8},$$

with P_NL(T₀)∼1100 mW is estimated from our experimental fit.

These unwanted processes have an order that is different from 2. As a consequence, adjusting the laser parameters has differential impact on signal of order 2 and on unwanted effects. In general, a reduction of photoperturbation of order $n_P<2$ (respectively $n_P>2$), is obtained by increasing (respectively decreasing) T = 1/f. In our graph, this is highlighted by positive (respectively negative) slopes of lines of constant photoperturbation. For instance, since highly nonlinear photoperturbations ($n_P>2$) were often reported as the limiting factor in point-scanning multiphoton microscopy [17,18,23], it was proposed to increase f above 80 MHz to mitigate them [17]. Here, we observed the opposite behavior during live 2P-SPIM imaging. Indeed, the first observable effect is linear and is likely due to heating by water absorption, which calls for a different optimization approach.

Funding

Agence Nationale de la Recherche10.13039/501100001665 (ANR-11-EQPX-0029, ANR-15-CE13-0015); Fondation pour la Recherche Médicale10.13039/501100002915 (DEI201512440).

Disclosures

The authors declare no conflicts of interest related to this article.

See Supplement 1 ^{(1.7MB, pdf)} for supporting content (Fig. S1-3, Table S1-2, and Visualization legends).