Comparison of four nonlinear growth models in Creole chickens of Mexico

Abstract

Animal growth is a complex and dynamic process that involves physiological and morphological changes from hatching to maturity. It is defined as the increase in body size per time unit. Mathematical functions, called growth models, have been used to explain growth patterns. The aim of this study was to compare the Gompertz-Laird, logistic, Richards, and Von Bertalanffy growth models to determine which best fits the data of the Creole chickens (CC). Three hundred forty-seven CC were individually weighed from hatching until 177 D of age. Birds were fed a starter diet (0–18 D of age; 19% crude protein (CP) and 3,000 kcal of ME/kg) and grower diet (19–177 D of age; 18% CP and 2,800 kcal of ME/kg). Data were analyzed using PROC NLIN to fit the nonlinear growth curve. The coefficient of determination (R²), Akaike information criteria (AIC), and Bayesian information criteria (BIC) were used to compare the goodness of fit of the models. The Von Bertalanffy (R²: 0.9382, 0.9415; AIC: 2,224.1, 2,424.8; BIC: 2,233.5, 2,434.3, for females and males, respectively) was the model that best explained growth of the birds. On the other hand, both the Gompertz-Laird and logistic models overestimated hatching BW and underestimated the final BW of CC. Females reached age of maximum growth faster than males. The asymptotic weight was higher in males (3,011 g) than in females (2,011 g). Body weight at inflection point was 892 g at 64 D of age for males and 596 g at 54 D for females. In conclusion, the best fit of the data was obtained with the Von Bertalanffy growth model; the information is intended to serve as the basis for utilizing CC.

Introduction

The production of Creole chickens (CC) in rural communities of Mexico provide households livelihood security, animal protein, and economic income. However, the body weight (BW) of CC is about 3 times lower than that of commercial breeds (Segura-Correa et al., 2004, Okeno et al., 2012). Body weight of local chickens (LC) is an important economic trait for farmers. This characteristic is heritable, and therefore, it could be improved through breeding programs (Osei-Amponsah et al., 2013). Creole chickens in Mexico had their origin mainly from European birds brought to Mexico by the Spanish conquerors in the 16th century (Segura-Correa et al., 2004); however, the population of CC cannot be organized in differentiated genetic subpopulations so that the CC of Mexico can be considered a unique mix of genetics (Gorla et al., 2017). Animal growth is a complex physiological and morphological process from hatching to maturity. It is defined as the increase in BW and organ size per unit of time or age (Yang et al., 2006, Kaplan and Gürcan, 2018). Animal growth has been summarized using mathematical equations or growth curves that result in mathematical parameters that are biologically interpretable (Tzeng and Becker, 1981, Aggrey, 2002, Yang et al., 2006). In addition, mathematical growth functions can be used to predict daily energy, protein, and mineral dietary requirements; suitable slaughter age; and age of sexual maturity (Darmani-Kuhi et al., 2010, Nahashon et al., 2010, Kebreab et al., 2011, Kaplan and Gürcan, 2018). Some researchers have studied the growth of LC using Gompertz, logistic, Richards (Norris et al., 2007, Olawoyin, 2007, Magothe et al., 2010, Rizzi et al., 2013, Osei-Amponsah et al., 2014), and Von Bertalanffy models (Yang et al., 2006, Ngeno et al., 2010, Zhao et al., 2015). These nonlinear models describe growth of LC, but each one has different characteristics and limitations (Norris et al., 2007). For this reason, it is very important to choose the model that best describes the growth pattern. In Mexico, no research has been carried out to describe the growth pattern of CC, and much less have programs aimed to improve local poultry genetic resources been developed. Therefore, the aim of this study was to compare the Gompertz-Laird, logistic, Richards, and Von Bertalanffy growth models to identify the one that best describes the CC growth pattern.

Materials and methods

Study Sites

This study was conducted at the experimental chicken house at the Colegio de Postgraduados, Campus Campeche, Mexico. Chickens were raised under natural environmental condition (light, temperature, and humidity). Environmental temperatures range from 18.0°C to 30.0°C; rains are abundant during the summer (June to September), and total annual precipitation is 1,600 mm (INEGI, 2014). The study period lasted 177 D (from December 2016 to June 2017).

Chickens and Environmental Conditions

A total of 24 Creole cocks and 76 Creole hens were randomly collected from the backyards of rural communities of Campeche State. The chickens had color plumage varieties: brown, yellow, and silver with black edge plumage. Chickens had naked neck; frizzled, had feathered shank; were rumples; were dwarf; and had normally fully feathers. Chickens were pedigree-mated by artificial insemination (sex ratio 1 cock: 3 hens), and 427 chicks were hatched. Chicks were given ad libitum access to feed and water. The feeding program was divided into 2 phases: a starter diet (from hatching until 18 D of age) containing 19.0% crude protein (CP) and 3,000 kcal ME/kg and a grower diet (19–177 D of age) containing 18.0% CP and 2,800 kcal ME/kg (Table 1). All birds were individually weighed at hatch. Birds were weighed every third day until 57 D of age; subsequently, they were weighed every 14 D until 177 D of age. All procedures were performed in accordance with the guide for care and use of experimental animals approved by the General Academic Council of the Colegio de Postgraduados.

Table 1.

Composition of experimental diets of Creole chickens.

Ingredient (%)	Starter	Grower
Corn	64.20	61.92
Soybean meal	30.78	28.95
Soybean oil	0.87	-
Calcium carbonate	1.40	1.40
Orthophosphate	1.46	1.49
L-Lysine	-	0.05
DL-Methionine	0.09	0.10
L-Threonine	0.09	0.12
Choline chloride	0.21	0.21
Vitamin-mineral premix1	0.60	0.60
Sodium chloride	0.30	0.30
Sand2	-	4.86
Calculate level (%)
Metabolizable energy, kcal/kg of diet	3,000	2,800
Crude protein	19.00	18.00
Calcium	0.85	0.85
Available P	0.40	0.40
Methionine	0.41	0.41
Methionine + cystine	0.75	0.73
Lysine	1.02	1.00
Sodium	0.17	0.16

Abbreviations: kcal, kilocalories; kg, kilogram.

¹Provided the following per kilogram of diet: retinyl acetate, 9,000 IU; cholecalciferol, 2,500 IU; Dl-α-tocopheryl acetate, 20 IU; menadione sodium bisulfite complex, 3.0 mg; riboflavin, 8.0 mg; cobalamin, 0.015 mg; pantothenic acid, 10 mg; niacin, 40 mg; folic acid, 0.5 mg; choline, 300 mg; biotin, 0.055 mg, thiamine, 2.0 mg. Minerals: iron, 65.0 mg; zinc, 100 mg manganese, 100 mg; copper, 9.0 mg; selenium, 0.3 mg; iodo, 0.9 mg.

²Sand was used as an inert filler in diet.

Growth Models

Four growth models were chosen to describe the growth pattern of CC: Gompertz-Laird, Richards, Von Bertalanffy, and logistic.

Gompertz-Laird Model

The following equation describes the Gompertz-Laird growth curve:

$$W_t=W_0\exp \left[\left(L/K\right)\left(1-\text{exp}-\mathit{Kt}\right)\right]$$

where $W_t$ is the BW of chicken at time t, $W_0$ is the hatching BW (g), $\exp$is the exponential, L is the initial growth rate (g/D), and K is the rate of exponential decay of the initial specific growth rate or maturation rate (g/D).

Age of maximum growth (ti) (D) and asymptotic weight ($W_A$) (g) were estimated as follows: $\mathit{ti}=\left(1/K\right)\text{log}\left(L/k\right)$ and $W_A=W_0\text{exp}\left(L/K\right)$ (Laird et al., 1965, Aggrey, 2002).

Richards Model

The following equation describes the Richards growth model:

$$W_t=W_A{\left[1-\left(1-m\right)\text{exp}\left[-K\left(t-\mathit{ti}\right)/m^{m/\left(1-m\right)}\right]\right]}^{1/\left(1-m\right)}$$

where $W_t$ is the BW of chicken at time t, $W_A$ is the asymptotic BW (g), exp is the exponential, K is the maximum relative growth (g/D), ti is the age of maximum growth (D), and m is a shape parameter, with the property that $m^{1/\left(1-m\right)}$ is relative weight at ti (Richards, 1959, Aggrey, 2002).

Von Bertalanffy Model

The Von Bertalanffy model has been used to describe the growth of indigenous chicken (Yang et al., 2006, Ngeno et al., 2010, Adenaike et al., 2017) using the equation:

$$W_t=W_A\ast {\left(1-B\ast \exp {}^{\left(-K\ast t\right)}\right)}^3$$

where $W_t$ is the BW of chicken at time t, $W_A$ is the asymptotic BW (g), $\exp$is the exponential, K is the maximum relative growth (g/D), and B is the integration constant. Age of maximum growth (ti) (D) and BW at age of maximum growth ($W_I$) (g) were estimated as follows: $ti=\ln \left(3B\right)/k$ and $W_I=W_A\ast 8/27$ (Goshu and Koya, 2013).

Logistic Model

To estimate the expected BW at specific age, the following equation describes the logistic growth model:

$$W_t=W_A/\left[1+\text{exp}-K\left(t-ti\right)\right]$$

where $W_t$ is the BW of chicken at time t, $W_A$ is the asymptotic BW (g), $\exp$is the exponential, K is the exponential growth rate (g/D), and ti is the age of maximum growth (D) (Robertson, 1923, Aggrey, 2002).

Statistical Analysis

The models were fitted to the data using the PROC NLIN of SAS Institute Inc. (2011; version 9.3, Cary, NC). The Marquardt iterative procedure was used to find the values of the model parameters that minimize the sums of the squared deviations between observed and fitted values.

Goodness-of-Fit Criteria

Three criteria were used to compare the goodness of fit of the models: 1) Coefficient determination: $R^2=1-\left(\mathit{SSE}/\mathit{SST}\right)$; 2) Akaike’ information criterion: $\mathit{AIC}=n\ast \ln \left(\mathit{SSE}/n\right)+2k$; and 3) Bayesian information criterion: $\mathit{BIC}=n\ast \ln \left(\mathit{SSE}/n\right)+k\ast \ln \left(n\right)$, where SSE is the sum of squares of errors, SST is the total sum of squares, n is the number of observations, k is the number of parameters, and $\ln$ is the natural logarithm. The preferred model is the one with the smallest AIC and BIC values (Narinc et al., 2013), and the coefficient of determination values must be similar or close to 1.

Result

Overall means and standard deviations of BW of CC are presented in Table 2. The Gompertz-Laird model predicted an average hatching BW that was higher than the observed weight for females and males (51.1 vs. 36.5 g and 53.5 vs. 37.2 g, respectively). The initial growth rate of females (0.0751 g/D) was lower than that of males (0.0765 g/D). On the other hand, pullets had a faster rate of decay or maturation rate for BW than cockerels (Table 3).

Table 2.

Means and standard deviations for body weight at different ages of Creole chickens.

Age (D)	Body weight (g)
	Male (n = 177)1	Female (n = 170)1
0	37.2 ± 4.7	36.5 ± 5.2
3	51.9 ± 8.3	49.9 ± 7.7
6	63.3 ± 9.6	60.5 ± 9.5
9	81.2 ± 14.9	76.1 ± 13.4
12	101.9 ± 17.6	95.5 ± 16.1
15	130.9 ± 24.2	121.4 ± 21.5
18	163.0 ± 30.3	150.8 ± 25.8
21	196.7 ± 38.8	181.6 ± 33.2
24	228.0 ± 43.3	207.7 ± 35.0
27	259.7 ± 49.5	232.9 ± 40.5
30	303.1 ± 59.2	270.1 ± 46.5
33	342.9 ± 68.2	304.0 ± 51.3
36	390.0 ± 78.4	348.9 ± 59.7
39	433.3 ± 86.7	382.4 ± 68.3
42	487.8 ± 94.1	428.1 ± 75.5
45	543.9 ± 108.7	468.8 ± 84.2
48	582.8 ± 116.0	500.5 ± 87.8
51	645.6 ± 126.6	549.9 ± 95.3
54	697.3 ± 133.1	594.3 ± 103.3
57	768.5 ± 148.6	644.5 ± 113.1
72	1,051.4 ± 203.8	850.1 ± 151.4
87	1,292.9 ± 241.8	1,023.2 ± 174.0
102	1,542.8 ± 268.6	1,191.3 ± 209.3
117	1,787.7 ± 323.1	1,323.4 ± 209.6
132	1,992.4 ± 342.2	1,445.0 ± 244.1
147	2,141.9 ± 364.5	1,524.9 ± 257.8
162	2,268.3 ± 377.3	1,641.5 ± 298.1
177	2,409.2 ± 410.7	1,749.3 ± 306.6

Abbreviation: n, sample size.

¹Only 347 Creole chickens reached the end of the study. The percentage of mortality was 19.0%.

Table 3.

Parameters for Creole chickens predicted by growth models.

Model	Male (n = 177)1	Female (n = 170)1
Gompertz-Laird
Hatching BW (W0)	53.5	51.1
Initial growth rate (L)	0.0765	0.0751
Rate of decay or maturation rate (K)	0.0195	0.0210
Age of maximum growth (ti)	69.8	60.8
Asymptotic weight (WA)	2,683.1	1,839.1
Richards
Maximum relative growth (K)	0.0065	0.0068
Age of maximum growth (ti)	66.3	54.4
Asymptotic weight (WA)	2,875.1	2,012.8
Shape parameter (m)	0.7752	0.6651
Von Bertalanffy
Maximum relative growth (K)	0.0137	0.0152
Age of maximum growth (ti)	64.3	54.4
BW at age of maximum growth (WI)	892.2	596.0
Asymptotic weight (WA)	3,011.3	2,011.6
Integration constant (B)	0.8040	0.7628
Logistic
Exponential growth rate (K)	0.0367	0.0380
Age of maximum growth (ti)	80.9	72.4
Asymptotic weight (WA)	2,356.9	1,652.3

W₀ = g; L = g/D; K = g/D; ti = D; W_A = g; W_I = g; n = sample size.

¹Only 347 Creole chickens reached the end of the study. The percentage of mortality was 19.0%.

The maximum relative growth predicted by the Richards and Von Bertalanffy models and the exponential growth rate predicted by the Logistic model were higher in females than in males (Table 3).

Hens reached age of maximum growth faster than cocks for all the models. The difference between sexes was 9.0, 8.5, 11.9, and 9.9 D for Gompertz-Laird, logistic, Richards, and Von Bertalanffy models, respectively (Table 3).

The lowest predicted asymptotic weight in hens and cocks (1,652.3 and 2,356.9 g, respectively) was obtained using the logistic model, whereas the highest asymptotic weight was estimated using the Richards model for hens (2,012.8 g) and using the Von Bertalanffy model for cocks (3,011.3 g) (Table 3).

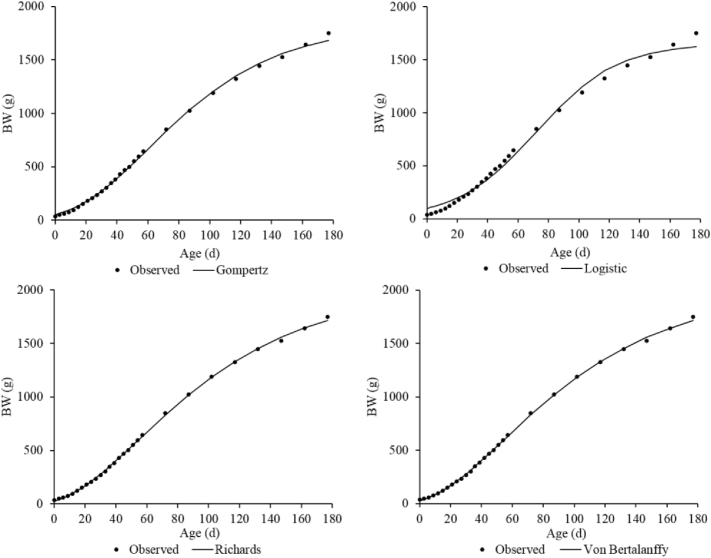
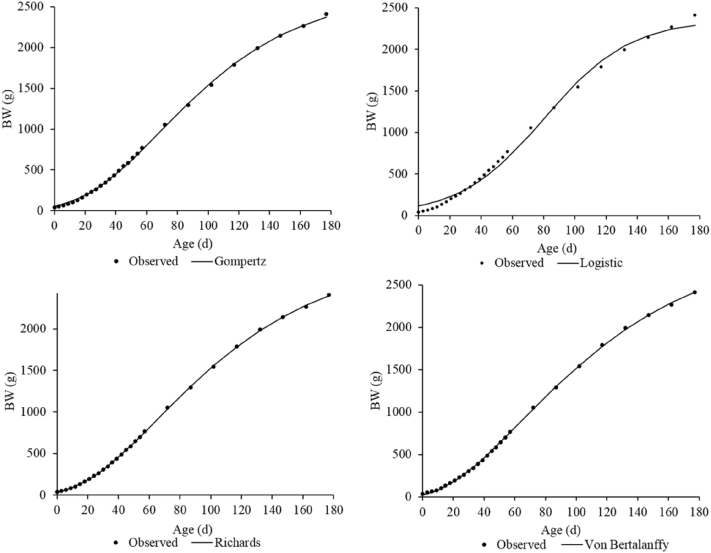
Based on the 3 goodness-of-fit criteria (R², AIC, and BIC), the Von Bertalanffy model produced the best fit of the data (Table 4) for female and males (Figures 1 and 2, respectively).

Table 4.

Goodness-of-fit criteria for the studied growth models.

Sex	Model1	R2	AIC	BIC
Male	Gompertz-Laird	0.9412	2,425.5	2,435.0
	Logistic	0.9360	2,440.9	2,450.4
	Richards	0.9415	2,426.5	2,439.2
	Von Bertalanffy	0.9415	2,424.8	2,434.3
Female	Gompertz-Laird	0.9374	2,226.2	2,235.6
	Logistic	0.9305	2,243.9	2,253.3
	Richards	0.9382	2,226.1	2,238.6
	Von Bertalanffy	0.9382	2,224.1	2,233.5

Abbreviations: AIC, Akaike information criterion; BIC, Bayesian information criterion; R², coefficient of determination.

¹The preferred model is the one with the smallest AIC and BIC values, and the coefficient of determination values must be similar or close to 1.

Figure 1.

Growth curve for females predicted by four growth models in comparison with the observed data.

Figure 2.

Growth curve for males predicted by four growth models in comparison with the observed data.

Discussion

Growth parameters provided information about age and weight of maximum growth, growth rate, and asymptotic weight in animals. Hatching BW predicted by the Gompertz-Laird model for females and males (51.1 and 53.5 g, respectively) was 3.6 and 8.9 g higher than those reported by Aggrey (2002) for unselected random mating Athens Canadian chicken populations (47.7 g for females and 44.6 g for males).

The Gompertz-Laird growth function usually overestimates hatching BW to improve fitting the data to the model. Barbato (1991) suggested that hatching BW should be measured and not used as an estimated parameter of the model. The results agree with those reported by Magothe et al. (2010) in Kenya, who observed that the Gompertz-Laird model overestimated hatching BW in indigenous chickens.

The initial growth rate was lower in females than in males. Mignon-Grasteau (1999) found a similar pattern: females had a slow initial growth rate (0.0979 g/D); however, the growth values obtained by this author for unselected chickens were better than those reported in the present study. In contrast, the initial growth rate obtained by Magothe et al. (2010) for mixed-sex indigenous chickens (0.0599 g/D) was lower than the average obtained for both sexes of CC (0.0758 g/D). Results of our study show that the maturation rate was not in line with findings reported by Aggrey (2002), who reported a maturation rate of 0.0216 g/D for females and 0.0224 g/D for males in an unselected chicken population. Similarly, in Nigeria, Adenaike et al. (2017) reported a maturation rate of 0.1712 g/D and 0.1685 g/D in naked-neck and normal-feathered chickens, respectively. Moreover, they mentioned that a low maturation rate indicates delayed maturity and a high value indicates accelerated maturity. On the other hand, Mignon-Grasteau (1999) found that the maturation rate was high for females compared with males, based on the Gompertz-Laird growth model; this result is in line with those obtained for CC using the same model.

The maximum relative growth and exponential growth rate predicted in this research were close to the values reported by Narinc et al. (2010) in slow-growing broilers using the Von Bertalanffy model and Rizzi et al. (2013) in local Italian chickens using the logistic model. Nevertheless, they were lower than those obtained with fast-growing chickens (Ross PM3) reported by Topal and Bolukbasi (2008) (females = 0.091 and males = 0.098 for Von Bertalanffy model; females = 0.781 and males = 0.744 for Logistic model). The fact that relative growth is slower in CC than in fast-growing chickens is explained by the lack of a genetic improvement program, poor nutrition, and deficient sanitary management.

Age of maximum growth predicted by the logistic model for CC is in agreement with that reported by Osei-Amponsah et al. (2014) in Ghanaian LC and Yang et al. (2006) in Jinghai yellow chickens. On the other hand, Aggrey (2002) reported lower values for age of maximum growth in unselected females using the Gompertz-Laird, Richards, and logistic models. This finding confirms that males reach the age of maximum growth later than females. The BW at the age of maximum growth predicted by the Von Bertalanffy model was 596.0 g for females and 892.2 g for males. However, Zhao et al. (2015) indicate that indigenous chickens in China had lower values for BW at age of maximum growth using the same model.

In general, the males had greater asymptotic weight than the females for all the models. In a study conducted in Spain with Castellana Negra male chickens, Miguel et al. (2008) estimated an asymptotic weight of 2,660.9 g using the Gompertz-Laird model. This result is close to that obtained in our research for CC males (2,683.1 g). In addition, Rizzi et al. (2013) reported an asymptotic weight of 2,046.0 g for female Italian LC using the Richards model, which agrees with our findings for CC females (2,012.8 g).

In line with our results, Yang et al., 2006, Ngeno et al., 2010, and Adenaike et al. (2017) observed that the Von Bertalanffy growth model was the best-fitting model for describing growth of LC. On the other hand, Rizzi et al. (2013) and Osei-Amponsah et al. (2014) found that the Richards model produced the best fit of the data for LC, while Zhao et al. (2015) found that the Gompertz-Laird model was the best to describe the growth pattern of Chinese indigenous chickens.

In conclusion, based on the goodness-of-fit criteria (R², AIC, and BIC), the best fit of the data was obtained with the Von Bertalanffy model for both sexes. Knowledge of the growth characteristics of both CC sexes could help define feeding programs to meet nutritional needs from hatching to age of maximum growth, reproduction programs, and marketing strategies. Finally, more research to estimate genetic parameters of growth curve parameters of CC is recommended to allow selection based on growth characteristics.