Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jan 29;92(5):3896–3903. doi: 10.1021/acs.analchem.9b05397

Hydrodynamic Solvent Coupling Effects in Quartz Crystal Microbalance Measurements of Nanoparticle Deposition Kinetics

Zbigniew Adamczyk 1,*, Marta Sadowska 1
PMCID: PMC7588021  PMID: 31994383

Abstract

graphic file with name ac9b05397_0006.jpg

Hydrodynamic coupling effects pertinent to quartz crystal microbalance (QCM) investigation of nanoparticle adsorption kinetics were evaluated using atomic force microscopy and the theoretical modeling. Monodisperse polymer particles of the size between 26 and 140 nm and the density of 1.05 g cm–3 were used. The ζ-potential of particles was opposite to the substrate ζ-potential that promoted their irreversible adsorption on the silica sensor. The experimental kinetic data were interpreted in terms of theoretical calculations derived from the hybrid random sequential adsorption model. This allowed us to determine the amount of hydrodynamically coupled solvent (electrolyte) for the absolute particle coverage range up to 0.5. The coupling function representing the ratio of the solvent to the particle volumes was also determined and used to explicitly calculate the solvent level in particle monolayers. It is shown that the solvent level abruptly increases with the particle coverage attaining values comparable with the particle size. One can expect that these results can serve as useful reference data for the interpretation of protein adsorption kinetics on rough surfaces where the presence of stagnant solvent is inevitable.

Controlling macromolecules, especially protein adsorption at solid substrates, is necessary for their separation and purification by chromatography and filtration, for enzyme immobilization on various biosensors, and for performing immunological assays (ELISA) or latex agglutination tests. On the other hand, undesired protein adsorption can exert adverse effects leading to artificial organ and implant failure plaque formation, inflammatory response, blocking of sensors, fouling of ultrafiltration units, etc. Therefore, protein adsorption processes were extensively studied by a variety of experimental techniques such as ellipsometry and reflectometry,1−5 lightmode waveguide spectroscopy (OWLS),3,6−10 total internal reflectance fluorescence (TIRF),11,12 surface plasmon resonance (SPR),13,14 and electrokinetic methods.15,16 However, these techniques exhibit some limitations; for example, they require protein molecule labeling, there are special requirements for the substrate (transparent or nonconductive), the protein coverage is indirectly calculated (ellipsometry, reflectometry, OWLS) assuming empirical models of the monolayer, and the sensitivity of the measurements is not satisfactory for the low-coverage range.17−20

These disadvantages can be partially eliminated applying the quartz crystal microbalance (QCM) technique that enables versatile, real-time studies of protein adsorption and desorption kinetics on various substrates in liquid phases under flow conditions.3−6,13,21−29 Because of exceptional sensitivity, this method is also used to study the kinetics of nanoparticle and microparticle deposition on various substrates.30−36

However, a quantitative interpretation of results derived from QCM measurements is complicated by the fact that the primary signal, i.e., the oscillation frequency shift, depends on both the adsorbed solute (molecules or particles) mass and the hydrodynamically coupled (trapped) solvent mass. The latter depends on the solute size, shape, its orientation on the surface, monolayer coverage, and oscillation frequency.23,24,34−40 Other complicating factors are the particle mechanical compliance (stiffness) and the contact zone strength, which may enable particle oscillatory, rolling, or sliding motions. These aspects were thoroughly analyzed applying the finite element modeling23−25,30,39 and some phenomenological approaches.4,5,25

It is also shown that the substrate roughness of the characteristic dimensions comparable with protein molecule size significantly affects the adsorption kinetics measured by QCM, especially at the low-coverage range.29,40

In order to experimentally determine the significance of these effects it is necessary to acquire the adsorption kinetics for the same solute/interface system using complementary experimental techniques. This was done ex situ using various techniques such as ellipsometry,3 SPR,14 OWLS,3,7 atomic force microscopy (AFM), and X-ray photoelectron spectroscopy (XPS).29 The ratio of the wet and the dry masses derived in this way gives the water factor that can be used as a scaling parameter for converting the QCM data to the dry mass.

In refs (4, 5, 13, 22, and 25) some ingenious QCM-D cell designs were developed in order to simultaneously monitor in situ the dry mass of adsorbed proteins using reflectometry, ellipsometry, and SPR measurements. In this way, hydration of streptavidin, avidin, and other bioparticles was determined as a function of adsorption time13 or the protein coverage.4,5,25 It was shown that the amount of coupled solvent monotonically decreased with protein overage, which was interpreted in terms of several phenomenological models.

An alternative, less laborious method was applied in refs (26, 28, and 29), where the amount of coupled water (hydration degree) in the adsorbed protein layer is calculated as the difference between the wet QCM mass and the dry mass derived from the solution of the continuity (mass transfer) equation. The bulk mass transfer rate constant used in these calculations can be derived either ab initio via the numerical solution of the Navier–Stokes equation32 or more conveniently from calibrating experiments involving metal nanoparticles characterized by a large density.41−43 However, the measurements involving such dense nanoparticles do not allow one to precisely determine the volume of the coupled solvent, which is a parameter of primary significance.

Given the deficiency of systematic investigations, the main goal of this work is to quantitatively determine the QCM hydration functions for nanoparticles using theoretical modeling combined with direct AFM microscope imaging. Monodisperse polymer particles of a spherical shape, well-controlled surface properties, and a large stability are used in our measurements, which facilitates their irreversible adsorption at negatively charged silica sensors. Because their density is comparable with the solvent (electrolyte) density, and they do not exhibit specific hydration effects, a precise determination of the dynamic hydration effects, in particular, the coupled water level in particle monolayers, becomes feasible. It is expected that the acquired results can be exploited as useful reference systems for a quantitative interpretation of protein adsorption/desorption processes, especially on rough surfaces where the presence of stagnant water films is inevitable.

Experimental Section

Materials and Methods

All chemical reagents such as sodium chloride, sodium hydroxide, and hydrochloric acid were commercial products of Sigma-Aldrich and were used without additional purification. Ultrapure water was obtained using the Milli-Q Elix and Simplicity 185 purification system from Millipore.

The stock suspensions of positively charged amidine and negatively charged sulfate polystyrene microparticles (latexes) were supplied by Invitrogen. These suspensions of a concentration determined by densitometry and the dry mass method were diluted to the desired concentration, typically 10–100 mg L–1, before each adsorption kinetic measurement. The ionic strength of the suspensions was adjusted by the addition of a NaCl solution, and the pH was regulated by the addition of hydrochloric acid solutions.

The diffusion coefficient of microparticles was determined by the dynamic light scattering (DLS) using the Zetasizer Nano ZS instrument from Malvern. The hydrodynamic diameter was calculated using the Stokes–Einstein relationship.

The particle size distribution was independently determine by laser diffractometry using the LS 13 320 Beckman Coulter device, which furnishes precise size distribution (albeit for particle sizes above 40 nm) and by ambient air AFM imaging using the NT-MDT Solver BIO device with the SMENA SFC050L scanning head.

The electrophoretic mobility of particles was measured using the laser doppler velocimetry (LDV) technique using the same apparatus. The ζ-potential was calculated using the Henry formula.

Quartz/silicon dioxide (SiO2) sensors used in the experiments were supplied by Q-Sense, Gothenburg, Sweden. Before every measurement, the sensors were cleaned in a mixture of 96% sulfuric acid (H2SO4), hydrogen peroxide (30%), and ultrapure water in volume ratio 1:1:1 for 3 min. Afterward, the sensor was rinsed by deionized water at 80 °C for 30 min and dried out in a stream of nitrogen gas. The roughness of sensors was examined by semicontact mode AFM imaging carried out under ambient conditions. It was confirmed that the sensors exhibited the root-mean-square (rms) roughness below 1 nm.

Methods

The QCM measurements were carried out according to the standard procedure described in refs (26 and 39). First, a stable baseline for the pure electrolyte (NaCl) of controlled ionic strength and pH was obtained. After the stabilization of the baseline, a particle suspension of controlled concentration was flushed through the cell at a fixed flow rate. After a prescribed time, the desorption run was initiated where pure electrolyte solution of the same pH and ionic strength was flushed through the cell. This procedure was modified in the case of negatively charged particles. In order to promote their adsorption of the negatively charged sensor, a supporting monolayer of the cationic polyelectrolyte (PAH) was adsorbed under in situ conditions according to the previously described method41,42 Three–five separate QCM experiments were performed for each particle type in order to increase the measurement precision.

The adsorbed particle mass per unit area (coverage), hereafter referred to as the wet mass (coverage), was calculated from the Sauerbrey equation:44

graphic file with name ac9b05397_m001.jpg

where Δm is the mass per unit area (coverage) change, Δf is the frequency change, no is the overtone number, and CQ is the mass (coverage) sensitivity constant equal to 0.177 mg m–2 Hz–1 for the 5 MHz AT-cut quartz sensor.

The deposition kinetics of particles on sensors was determined using the AFM method using the procedure described in refs (41−43). Accordingly, the QCM adsorption runs were stopped after discrete time intervals and the sensors were removed from the suspension and imaged under ambient conditions by AFM using the NT-MDT Solver BIO device with the SMENA SFC050L scanning head. The number of particles per a unit area (typically one square micrometer), denoted hereafter by N, was determined by a direct counting of over a few equal-sized areas randomly chosen over the sensor with the total number of particles exceeding 2000. This provides a relative precision of these measurements at more than 95%. Using the known values of the surface concentration N the absolute (dimensionless) coverage of particles was calculated as Θ = NSg, where Sg is the characteristic cross section of the particles.

Results and Discussion

Bulk Particle and Substrate Characteristics

Initially, basic physicochemical characteristics of particles comprising their size, electrophoretic mobility, and ζ-potential were acquired. Four suspensions were used in our investigations having the DLS particle diameter dp equal to 26, 39, 67, and 140 nm, referred to later on as the A20, L40, A70, and A140, respectively (see Table S1). These particle monolayers on the QCM sensor acquired by AFM are shown in Figure S1.

It should also be mentioned that the particle suspensions were stable over the time period significantly exceeding the time of the typical QCM experiments. This was confirmed in separate experiments via the DLS measurements where the particle size distribution was monitored as a function of the storage time.

The ζ-potential of the particles was derived from the LDV measurements, where their electrophoretic mobility was directly measured for various pHs. The mobility was converted to the ζ-potential using the Henry formula. One can infer from Table S1 that the A20, A70, and A140 particles exhibit at pH 4 and ionic strength of 0.01 M a large and positive ζ-potential, equal to 71, 74, and 79 mV, respectively, whereas the L40 particles exhibited a negative ζ-potential equal to −82 and −90 mV for pH of 4 and 5.7 (ionic strength 0.01 M), respectively.

In order to properly interpret the adsorption kinetic measurements it is also necessary to know the physicochemical characteristics of the silica substrate. Since it is not feasible to directly determine the ζ-potential of the silica sensor, thorough measurements were performed for oxidized Si/SiO2 wafers by applying the streaming potential measurements.10 It was determined that the ζ-potential of the bare (unmodified) substrate was equal to −20 and −45 mV at pH 4 and 7.4, respectively (for I = 10–2 M NaCl). In the case of PAH-modified substrate, the ζ-potential was equal 40 mV for this pH range.

Kinetics of Particle Deposition: QCM Measurements

One should emphasize that the use of polymer nanoparticles in the QCM studies is advantageous because of their spherical shape, low dispersity degree, and the density almost matching the solvent density. Moreover, the large absolute values of the ζ-potential of particles (opposite to the sensor ζ-potential) enhance their ability to form a strong contact with the substrate surface. Also, a precise determination of the particle coverage on the sensor is facilitated via direct AFM imaging as above-described.

A primary QCM kinetic run performed for the A20 particles is shown in Figure 1 as the dependence of Δf/no and the dissipation to frequency change ratio ΔD/(−Δf/no) on the adsorption time (analogous runs for other particles are presented in Figure S2).

Figure 1.

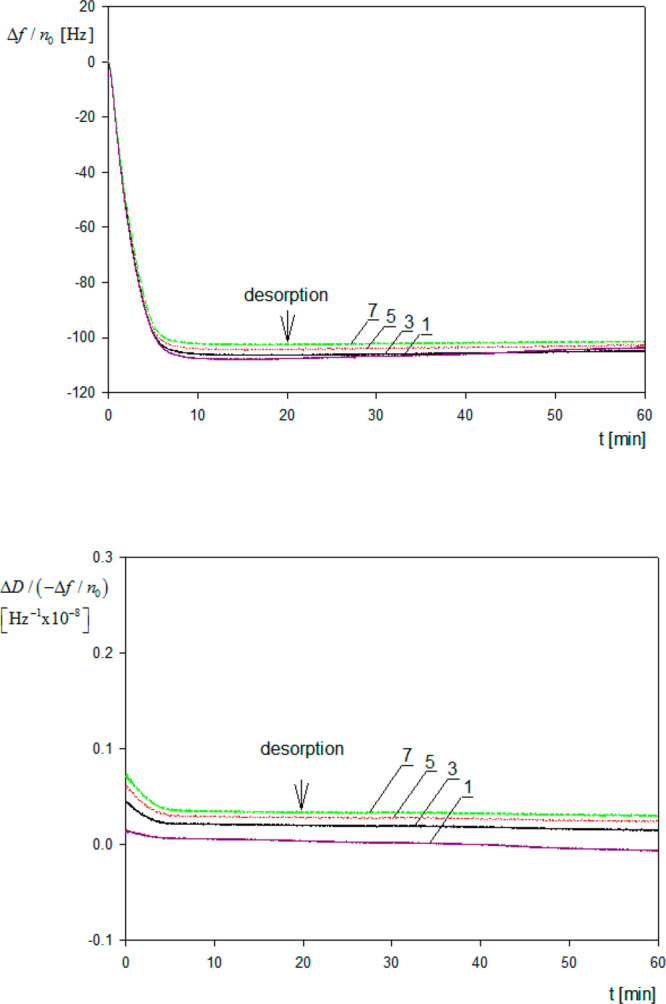
Figure 1

Open in a new tab

Primary adsorption runs for polymer particles derived from QCM measurements and expressed in terms of the frequency change Δf/no and the ratio of dissipation to frequency change ΔD/(−Δf/no) for various overtones 1, 3, 5, 7; silica sensor, ionic strength 0.01 M, pH 4, volumetric flow rate 2.5 × 10–3 cm3 s–1, A20 particle suspension, bulk concentration 10 mg L–1, pH 4.

One can observe that Δf/no abruptly decreases, attaining a stationary value at the time of ca. 10 min. After the stabilization of the signal the desorption run was initiated by flushing pure electrolyte with the same flow rate, ionic strength, and pH. It is seen in Figure 1 that the change in Δf/no was minor, which suggests a negligible desorption of the particles. It should also be mentioned that the ratio of the dissipation to frequency change ΔD/(−Δf/no) did not exceed 1 × 10–9 Hz–1 both for the adsorption and desorption runs. Hence, the experimental kinetic run for the A20 particles is fully analogous to the previously observed one for protein molecule adsorption.26,28

An analogous behavior was also observed for larger particles (see Figure S2), where the values of −Δf/no monotonically decreased with the overtone number. For example, for the A70 particles the ratio of −Δf/no for the seventh and the first overtone at low particle coverage range was equal to ca. 0.80. In accordance what was suggested in refs (23, 34, and 35) one can attribute this behavior to purely hydrodynamic effect rather than to increased dissipation due to particle, rocking, or sliding motion. In order to confirm this hypothesis, the interaction energy of particles with the substrate surface is calculated using the DLVO interaction potential consisting of the electrostatic double layer and van der Waals contributions, both being attractive in our system. Calculations presented in the Supporting Information confirm that the DLVO energy varies between −48 and −280 kT (where k is the Boltzmann constant and T is the absolute temperature) for the A20 and A140 particles, respectively (calculated for ionic strength of 0.01 M). This gives the desorption time equal to 3 × 1015 s (Supporting Information) for the A20 particles, which is infinite from a practical point of view, confirming the irreversibility of particle adsorption. Additionally, using the DLVO potential, the contact force for various particle sizes was calculated and compared with hydrodynamic shearing and inertia forces due to the oscillatory motion of the sensor. It is shown that these forces are considerably smaller than the contact force for the entire range of the particle size studied in this work. However, because the DLVO force scales up as particle size, whereas the inertia force scales up as the cube of the particle size, one can expect that it may become significant for micrometer-sized particle of a larger density, which was experimentally confirmed in ref (39).

The dependence of −Δf/no on the overtone number was systematically studied by Gillissen et al.34,35 performing three-dimensional modeling of flow around spherical and spheroidal particles firmly attached to an oscillating interface using the lattice Boltzmann algorithm. It was shown that −Δf/no linearly increased with the scaled penetration depth (hydrodynamic boundary layer thickness) defined as

graphic file with name ac9b05397_m002.jpg 1

where δh is the flow penetration depth, ap = dp/2 is the particle radius, v is the kinematic viscosity of the fluid, ω = 2πfno is the angular velocity, and f is the fundamental oscillation frequency of the sensor.

Therefore, these results indicate that, for a fixed particle size, −Δf/no linearly decreases with the square root of the overtone number. These theoretical calculations were experimentally confirmed using suspensions of unilamellar vesicles of the size 56–114 nm adsorbing on titania-modified QCM sensors. However, these results are only valid for a single particle attached to the substrate, i.e., in the limit of their negligible coverage.

In this work the primary results shown in Figure 1 as the dependence of −Δf/no on the adsorption time are converted to the coverage expressed in milligrams per square meter and denoted by ΓQ (one should observe that ΓQ = 0.01Δm, where Δm is expressed in the commonly used unit of nanograms per square centimeter).4,5,7,14,22 As seen in Figure 2, the deposition kinetics derived from QCM is characterized by an abrupt, quasi-linear increase in the coverage with the time, and then a saturation at stationary plateau value, which did not change upon desorption where pure electrolyte flow was initiated.

Figure 2.

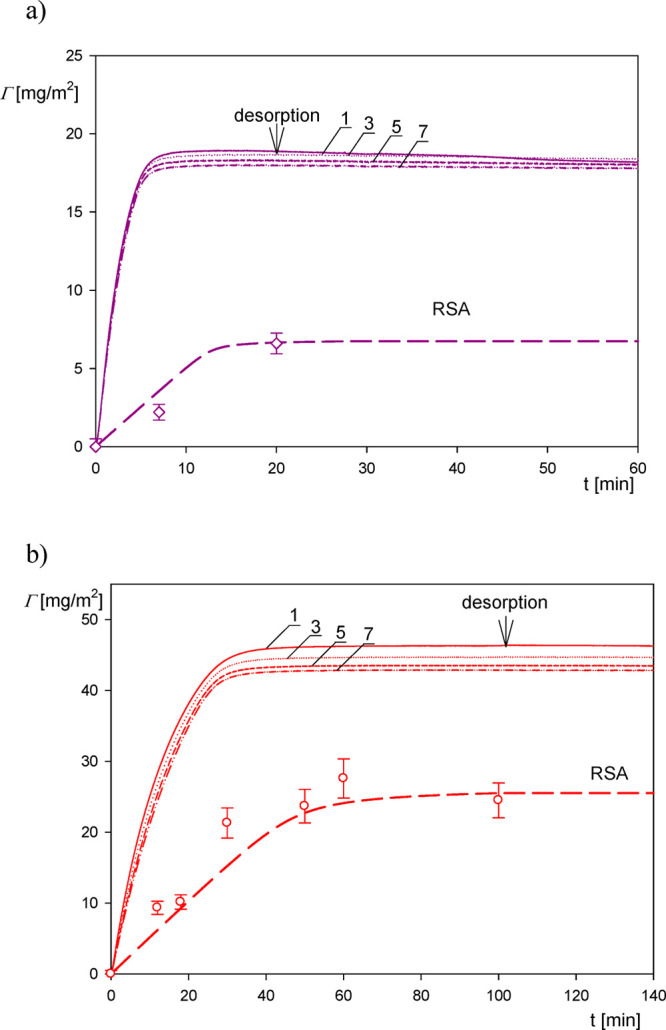
Figure 2

Open in a new tab

Kinetics of particle deposition derived from QCM-D measurements using the Sauerbrey equation for various overtones (solid lines denoted by 1, 3, 5, 7); silica sensor, pH 4, volumetric flow rate 2.5 × 10–3 cm3 s–1. (a) A20 particle suspension; the bulk concentration is 10 mg L–1. (b) A70 suspension; the bulk concentration is 20 mg L–1. The points represent the experimental dry mass derived from AFM, and the dashed lines denote the theoretical dry mass results derived from the RSA model.

The QCM results presented in Figure 2 are compared with theoretical calculations derived from the hybrid random sequential (RSA) approach,46 which directly yields the particle adsorption kinetics in the form of the dry mass versus the adsorption time dependencies. The validity of this model for a quantitative interpretation of nanoparticle adsorption kinetics on various substrates was previously confirmed in refs (41−43), and (47). It was also applied to acquire hydration functions from the QCM adsorption kinetic measurements for fibrinogen26 and human serum albumin28,29 on the silica and gold sensors.

As shown in the Supporting Information, using this approach, the coverage of adsorbed solute can be expressed in the following form:

graphic file with name ac9b05397_m003.jpg 2

where Γ is the time-dependent coverage, Γ0 is the initial coverage, Γ′ is the dummy integration variable, ka and kd are the kinetic adsorption and desorption constants, kc is the mass transfer constant, B(Γd) is the surface blocking function, and cb is the mass concentration of particles in the bulk.

The adsorption and desorption constants occurring in eq 2 can be calculated using empirically accessible parameters such as the particle and the substrate ζ-potentials, particle size, flow rate, etc. On the other hand, the blocking function is acquired from the Monte Carlo modeling (Supporting Information).

Using these parameters, the adsorption kinetics of particles was calculated from eq 2 using efficient numerical integration algorithms, and it is shown in Figure 2 as dashed lines. One can observe that for the A20 particles the QCM wet mass is considerably larger than the theoretical results with the ΓQ/Γ ratio attaining ca. 10 for short times. However, for longer times where the coverages attain saturation (maximum) values, the Γ/ΓQ ratio significantly decreases to ca. 3. It is interesting to mention that our results are analogous to those previously reported by Bingen et al.5 where the wet and the dry coverages were simultaneously determined by QCM and reflectometry. The ΓQ/Γ ratios reported in ref (5) in the limit of low coverage were equal to 11, 6, and 5 for the mosaic virus (CPMV) (whose shape was approximated by a spherical particle of the diameter equal to 28 nm), streptavidin, and avidin, respectively.

The validity of the theoretical results presented in Figure 2 was checked by direct AFM determination of the particle coverage. Accordingly, in these measurements, the QCM run was stopped after a defined time interval and the sensor was thoroughly examined using AFM imaging. This allowed us to precisely determine the average number of particles per unit area and, in consequence, the absolute coverage Θ, which is connected with the mass coverage through the following relationship:

graphic file with name ac9b05397_m004.jpg 3

where mp = 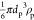Inline graphic is the mass of a single particle and ρp is the particle density.

One can observe in Figure 2 that the AFM-derived experimental results agree with the RSA theoretical data, which validates the use of this model for predicting the adsorption kinetics.

It should also be mentioned that the absolute coverage is a universal variable allowing us to quantitatively analyze the hydrodynamic coupling of particle monolayers by defining appropriate functions of the particle coverage (Supporting Information). Primarily, it is useful to define the commonly used function H, which represents the ratio of the coupled solvent mass to the QCM wet mass:

graphic file with name ac9b05397_m006.jpg 4

Another useful function is defined as the ratio of the coupled solvent volume to the particle volume:

graphic file with name ac9b05397_m007.jpg 5

where vs is the coupled solvent volume, vp is the particle volume, and ρs is the solvent (water) density.

It should be mentioned that, in contrast to H, the v̅ function (also denoted as Hv, φv(5,40)) is more universal because it does not depend on the particle and solvent densities.

The dependence of the hydration function calculated using the QCM measurements on the coverage Θ of particles is shown in Figure 3. As seen, in the limit of zero coverage, the extrapolated values of the hydration function are equal to 0.9 ± 0.02 and 0.85 ± 0.02 for the A20 and A70 particles, respectively. These values correlate with those previously reported by Bingen et al.,5 which were equal to 0.89, 0.8, and 0.8 for the CPMV (virus), streptavidin, and avidin, respectively. Also, Gillissen et al.34 predicted in the limit of negligible coverage the value of 0.9 for 30 nm diameter liposomes adsorbing on titania.

Figure 3.

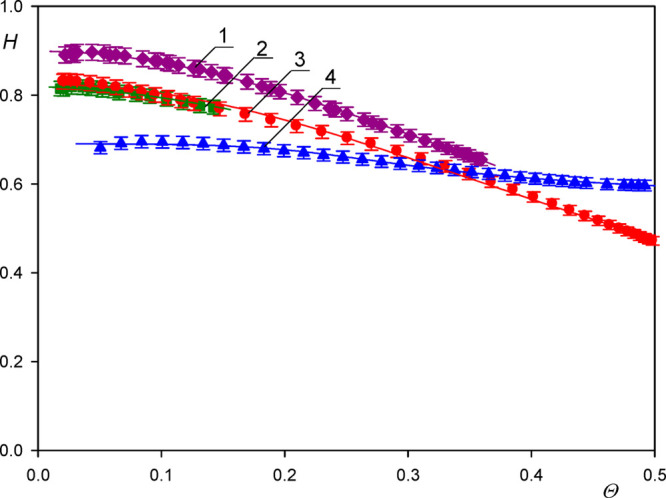
Figure 3

Open in a new tab

Dependence of the function 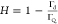Inline graphic on the dry coverage of particles Θ determined for various particle sizes; silica sensor, pH 4, ionic strength 0.01 M; for calculating the QCM coverage, the first overtone was used. 1, A20; 2, L40; 3, A70; 4, A140 suspension. The points show the experimental values calculated from eq 4; the lines represent fits of experimental data.

For larger coverages the hydration function monotonically decrease in a quasi-parabolic manner attaining the value of 0.60 for Θ = 0.4. Such a behavior was previously observed in ref (26) for side-on adsorption of fibrinogen adsorption and for human serum albumin,28 although in the latter case the initial and the minimum values of the hydration function were markedly lower.

On the other hand, as seen in Figure 3, for the largest A140 particles, the extrapolated zero coverage hydration function was markedly lower and equal to 0.72 ± 0.03.

However, one should remember that this coupling function is specific because it depends on the density of adsorbing solutes (particles or protein molecules) that may obscure a comparison among various systems studied in the literature. In this respect, the v̅ function is more universal because it is only controlled by hydrodynamic coupling; thus in consequence, it only depends (for a fixed oscillation frequency) on the particle coverage, size, and shape. The v̅ function calculated using the data presented in Figure 4 in the limit of low coverage is equal to 9.5 ± 1, 6.0 ± 0.5, and 3.0 ± 0.5 for the A20 (where δh/ap = 18), A70 (where δh/ap = 6.5), and A140 particles (where δh/ap = 3.4), respectively. This decreasing trend in the v̅ function with the particle size (the δh/ap parameter) was theoretically predicted by Gillissen et al. and interpreted as solely due to the hydrodynamic coupling forces.

Figure 4.

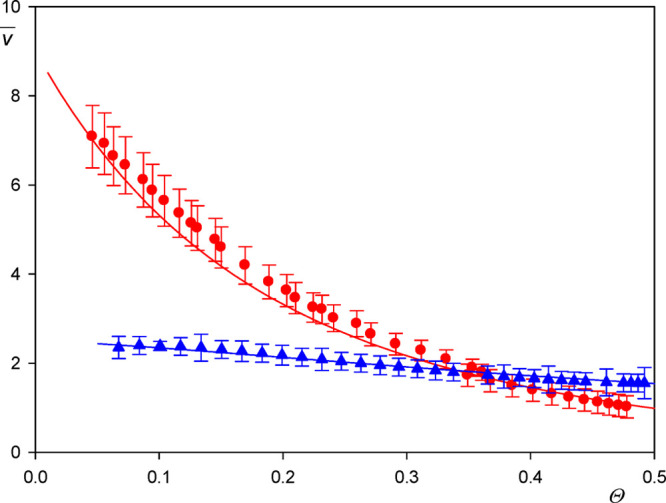
Figure 4

Open in a new tab

Dependence of the hydration function v̅ (averaged over the A20, L40, and A70 suspensions and various overtones) (red points) on the dry coverage of particles Θ; silica sensor, pH 4 and 5.7, ionic strength 0.01 M. The solid line denotes the theoretical results calculated from the fitting function given by eq 6. The blue points show the results obtained for the A140 particles, where results for the first overtone are presented.

It is interesting to compare these results with previously reported data, although they are rather scarce. Reimhult et al.13 obtained for streptavidin in the limit of low coverage (short times) v̅ of ca. 9.0, whereas Bingen et al.5 obtained ca. 9.0 and ca. 6.0 for streptavidin and avidin, respectively. However, it should be mentioned that the experimental data pertinent to the v̅ function obtained from experiments in the limit of low coverage may be charged by a significant error because of the nonstationary transport conditions in the cell, the sensor roughness, and irregular protein molecule shape deviating from the spherical shape.

The v̅ function for the entire range of particle coverage (averaged over the A20, L40, and A70 suspensions and various overtones 1–7) is graphically shown in Figure 4. One can observe that it decreases to 3.0 for Θ = 0.25 and 1.5 for Θ = 0.40. This correlates well with the results reported by Bingen et al.,5 who obtained 1.6 and 1.4 for avidin and streptavidin, respectively (in the limit of the maximum coverage), and Macakova et al.,40 who reported the value of 1.34 ± 0.26 for dodecyltrimethylammonium bromide (DTAB) spherical micelle monolayers on silica sensors.

The experimental v̅ function shown in Figure 4 can be adequately interpolated by the following expression (see Figure 4):

graphic file with name ac9b05397_m008.jpg 6

where Cv = 10.

The analytical form of the v̅ function given by eq 6 is useful for calculating the coupled solvent level in the particle monolayer. It is a parameter of essential significance for the interpretation of the QCM results pertinent to rough surface or multilayer adsorption of particles and proteins. It is shown that the scaled coupled solvent level can be calculated from the following equation (Supporting Information):

graphic file with name ac9b05397_m009.jpg 7

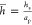where Inline graphic and hs is the dimensional solvent level.

Equation 7 has the following real root:

graphic file with name ac9b05397_m011.jpg 8

where Q and q are functions of the particle coverage alone given by

graphic file with name ac9b05397_m012.jpg 9

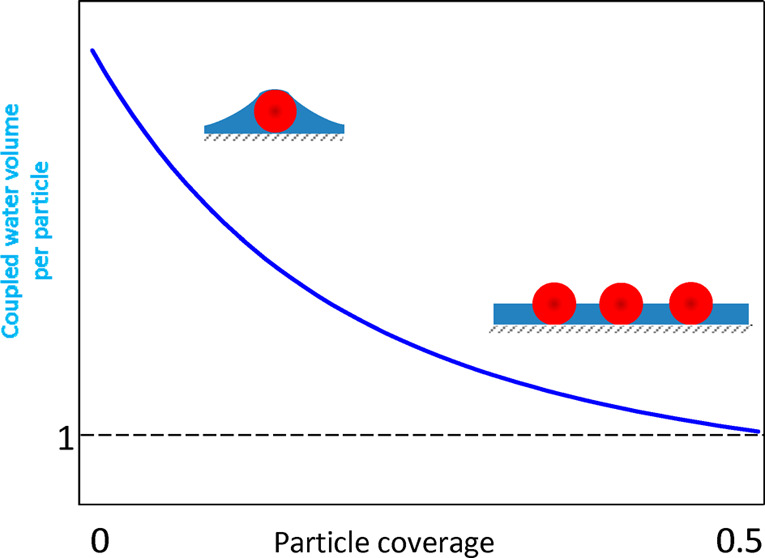
The dependence of the scaled solvent level in the monolayer on the particle coverage calculated from eq 8 is presented in Figure 5. One can observe that it abruptly increases with the particle size attaining unity for Θ = 0.20, which corresponds to the dimensional coupled solvent level equal to the particle radius. For this coverage, the average distance between the particle centers, assuming their random distribution pertinent to the RSA model, is equal to 3.8ap. Afterward, for Θ = 0.3 the water level attains a maximum value equal to 1.1, and then drops to unity.

Figure 5.

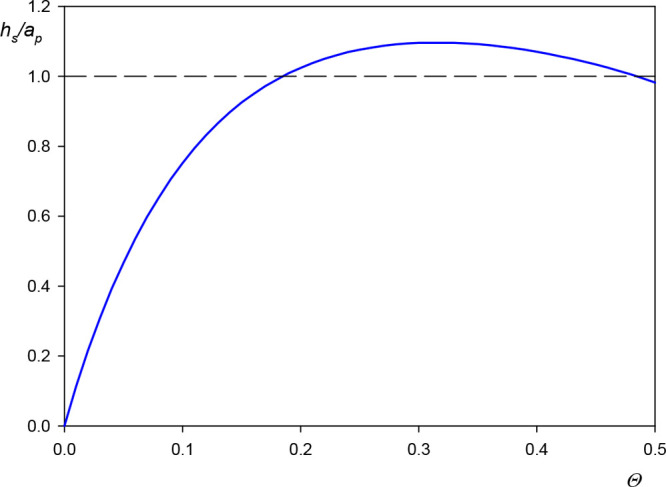
Figure 5

Open in a new tab

Dependence of the scaled water level in the monolayer h̅ = hs/ap on the particle dry coverage calculated from eq 8 in the limit of small particle size using the interpolation function given by eq 6.

One can expect that the results shown in Figure 5, which are independent of the particle density, can serve as useful reference data for predicting hydrodynamic coupling of solvents by rough surfaces. This becomes obvious if one considers that substrates covered by nanoparticles to a controlled degree can be treated as model ones with the characteristic roughness size equal to the particle diameter. For such surfaces, there appears hydrodynamically coupled solvent whose level is comparable with the particle (roughness) radius. For the A20 particles the solvent level is ca. 13 nm. This is expected to exert a significant influence on the adsorption of particles or protein molecules of the size below 10 nm because they will replace upon adsorption the stagnant solvent. Therefore, the mass change sensed by the QCM will be equal to the difference in the particle and the replaced solvent densities multiplied by the particle volume, which is much smaller than the bare particle mass. The appearance of such an effect was experimentally confirmed in ref (29) for human serum albumin adsorption on a gold sensor characterized by the rms factor of 2.5 nm corresponding to the peak-to-valley distance about 5 nm, which is comparable with the molecule dimension.29

Conclusion

Hydrodynamic coupling effects pertinent to QCM measurements of nanoparticle adsorption kinetics were evaluated using a combination of the theoretical modeling and AFM imaging.

It is confirmed that the particle adsorption was irreversible, which minimizes the probability of sliding or rolling motion; therefore, the specific effects leading to energy dissipation played a minor role. This agrees with the fact that the dissipation to frequency shift ratio was well below 10–8 Hz–1, for all particle suspensions, which validates the use of the Sauerbrey equation for calculating the particle coverage.

The QCM results were compared with the AFM measurements and the theoretical data derived from the hybrid RSA model yielding the amount of hydrodynamically coupled solvent as a function of the particle coverage. This allowed us to calculate the universal hydration function representing the ratio of the coupled solvent to the particle volumes and the coupled solvent level in particle monolayers. It is shown that the solvent level abruptly increases with the coverage attaining the maximum value comparable with the particle size for Θ > 0.2.

One can expect that these results are universally valid for nanometer-sized particles; therefore, they can serve as useful reference data for predicting hydrodynamic coupling of solvents by rough surfaces. This effect should exert a profound influence on the adsorption mechanism of protein molecules and bioparticles on such substrates because the coupled solvent is removed upon adsorption of these solutes; therefore, the coverage change sensed by QCM may become significantly lower than for smooth sensors.

Acknowledgments

This work was financially by the NCN Grant UMO-2015/19/B/ST5/00847 and the statutory activity of the J. Haber Institute of Catalysis and Surface Chemistry PAS (QCM and AFM measurements of deposition kinetics). The authors are deeply indebted to Mrs. Katarzyna Kusak for invaluable help in preparing the manuscript and the artwork.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.9b05397.

  • Basic characteristic of polymer particles, primary QCM adsorption runs, hydrodynamic boundary layer over an oscillating plate, estimation of the adhesion hydrodynamic and inertia forces, modeling adsorption kinetics of particles, and definition of solvation functions (PDF)

The authors declare no competing financial interest.

Supplementary Material

ac9b05397_si_001.pdf (463.5KB, pdf)

References

  1. Malmsten M. Ellipsometry studies of protein layers adsorbed at hydrophobic surfaces. J. Colloid Interface Sci. 1994, 166, 333–342. 10.1006/jcis.1994.1303. [DOI] [Google Scholar]
  2. Ortega-Vinuesa J. L.; Tengvall P.; Lundström I. Molecular packing of HSA, IgG, and fibrinogen adsorbed on silicon by AFM imaging. Thin Solid Films 1998, 324, 257–273. 10.1016/S0040-6090(98)00363-0. [DOI] [Google Scholar]
  3. Höök F.; Vörös J.; Rodahl M.; Kurrat R.; Böni P.; Ramsden J. J.; Textor M.; Spencer N. D.; Tengvall P.; Gold J.; Kasemo B. A comparative study of protein adsorption on titanium oxide surfaces using in situ ellipsometry, optical waveguide lightmode spectroscopy, and quartz crystal microbalance/dissipation. Colloids Surf., B 2002, 24, 155–170. 10.1016/S0927-7765(01)00236-3. [DOI] [Google Scholar]
  4. Carton I.; Brisson A. R.; Richter R. P. Label-free detection of clustering of membrane-bound proteins. Anal. Chem. 2010, 82, 9275–9281. 10.1021/ac102495q. [DOI] [PubMed] [Google Scholar]
  5. Bingen P.; Wang G.; Steinmetz N. F.; Rodahl M.; Richter R. P. Solvation effects in the quartz crystal microbalance with dissipation monitoring response to biomolecular adsorption. A phenomenological approach. Anal. Chem. 2008, 80, 8880–8890. 10.1021/ac8011686. [DOI] [PubMed] [Google Scholar]
  6. Sander M.; Madliger M.; Schwarzenbach R. P. Adsorption of transgenic insecticidal cry1ab protein to SiO2. 1. Forces driving adsorption. Environ. Sci. Technol. 2010, 44, 8870–8876. 10.1021/es103008s. [DOI] [PubMed] [Google Scholar]
  7. Vörös J.; Ramsden J. J.; Csucs G.; Szendro I.; De Paul S. M.; Textor M.; Spencer N. D. Optical grating coupler biosensors. Biomaterials 2002, 23, 3699–3710. 10.1016/S0142-9612(02)00103-5. [DOI] [PubMed] [Google Scholar]
  8. Kovacs N.; Patko D.; Orgovan N.; Kurunczi S.; Ramsden J. J.; Vonderviszt F.; Horváth R. Optical anisotropy of flagellin layers: in situ and label-free measurement of adsorbed protein orientation using OWLS. Anal. Chem. 2013, 85, 5382–5389. 10.1021/ac3034322. [DOI] [PubMed] [Google Scholar]
  9. Kovacs B.; Saftics A.; Biro A.; Kurunczi S.; Szalontai B.; Kakasi B.; Vonderviszt F.; Dér A.; Horváth R. Kinetics and structure of self-assembled flagellin monolayers on hydrophobic surfaces in the presence of hofmeister salts: experimental measurement of the protein interfacial tension at the nanometer scale. J. Phys. Chem. C 2018, 122, 21375–21386. 10.1021/acs.jpcc.8b05026. [DOI] [Google Scholar]
  10. Wasilewska M.; Adamczyk Z.; Sadowska M.; Boulmedais F.; Cieśla M. Mechanisms of fibrinogen adsorption on silica sensors at various pHs: experiments and theoretical modeling. Langmuir 2019, 35, 11275–11284. 10.1021/acs.langmuir.9b01341. [DOI] [PubMed] [Google Scholar]
  11. Santore M. M.; Wertz C. F. Protein spreading kinetics at liquid–solid interfaces via an adsorption probe method. Langmuir 2005, 21, 10172–10178. 10.1021/la051059s. [DOI] [PubMed] [Google Scholar]
  12. Kalasin S.; Santore M. M. Non-specific adhesion on biomaterial surfaces driven by small amounts of protein adsorption. Colloids Surf., B 2009, 73, 229–236. 10.1016/j.colsurfb.2009.05.028. [DOI] [PubMed] [Google Scholar]
  13. Reimhult E.; Larsson C.; Kasemo B.; Höök F. Simultaneous surface plasmon resonance and quartz crystal microbalance with dissipation monitoring measurements of biomolecular adsorption events involving structural transformations and variations in coupled water. Anal. Chem. 2004, 76, 7211–7220. 10.1021/ac0492970. [DOI] [PubMed] [Google Scholar]
  14. Tokarczyk K.; Jachimska B. Quantitative interpretation of PAMAM dendrimers adsorption on silica surface. J. Colloid Interface Sci. 2017, 503, 86–94. 10.1016/j.jcis.2017.05.002. [DOI] [PubMed] [Google Scholar]
  15. Wasilewska M.; Adamczyk Z. Fibrinogen adsorption on mica studied by AFM and in situ streaming potential measurements. Langmuir 2011, 27, 686–696. 10.1021/la102931a. [DOI] [PubMed] [Google Scholar]
  16. Adamczyk Z.; Nattich-Rak M.; Da̧bkowska M.; Kujda-Kruk M. Albumin adsorption at solid substrates: A quest for a unified approach. J. Colloid Interface Sci. 2018, 514, 769–790. 10.1016/j.jcis.2017.11.083. [DOI] [PubMed] [Google Scholar]
  17. Ramsden J. J. Experimental methods for investigating protein adsorption kinetics at surfaces. Q. Rev. Biophys. 1994, 27, 41–105. 10.1017/S0033583500002900. [DOI] [PubMed] [Google Scholar]
  18. Rabe M.; Verdes D.; Seeger S. Understanding protein adsorption phenomena at solid surfaces. Adv. Colloid Interface Sci. 2011, 162, 87–106. 10.1016/j.cis.2010.12.007. [DOI] [PubMed] [Google Scholar]
  19. Vogler E. A. Protein adsorption in three dimensions. Biomaterials 2012, 33, 1201–1237. 10.1016/j.biomaterials.2011.10.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Bhakta S. A.; Evans E.; Benavidez T. E.; Garcia C. D. Protein adsorption onto nanomaterials for the development of biosensors and analytical devices: A review. Anal. Chim. Acta 2015, 872, 7–25. 10.1016/j.aca.2014.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Richter R. P.; Brisson A. QCM-D on mica for parallel QCM-D -AFM studies. Langmuir 2004, 20, 4609–4613. 10.1021/la049827n. [DOI] [PubMed] [Google Scholar]
  22. Rechendorff K.; Hovgaard M. B.; Foss M.; Zhdanov V. P.; Besenbacher F. Enhancement of protein adsorption induced by surface roughness. Langmuir 2006, 22, 10885–10888. 10.1021/la0621923. [DOI] [PubMed] [Google Scholar]
  23. Johannsmann D.; Reviakine I.; Rojas E.; Gallego M. Effect of sample heterogeneity on the interpretation of QCM(-D) data: comparison of combined quartz crystal microbalance/atomic force microscopy measurements with finite element method modeling. Anal. Chem. 2008, 80, 8891–8899. 10.1021/ac8013115. [DOI] [PubMed] [Google Scholar]
  24. Johannsmann D.; Reviakine I.; Richter R. P. Dissipation in films of adsorbed nanospheres studied by quartz crystal microbalance (QCM). Anal. Chem. 2009, 81, 8167–8176. 10.1021/ac901381z. [DOI] [PubMed] [Google Scholar]
  25. Reviakine I.; Johannsmann D.; Richter R. P. Hearing what you cannot see and visualizing what you hear: interpreting quartz crystal microbalance data from solvated interfaces. Anal. Chem. 2011, 83, 8838–8848. 10.1021/ac201778h. [DOI] [PubMed] [Google Scholar]
  26. Kubiak K.; Adamczyk Z.; Wasilewska M. Mechanisms of fibrinogen adsorption at the silica substrate determined by QCM-D measurements. J. Colloid Interface Sci. 2015, 457, 378–387. 10.1016/j.jcis.2015.07.009. [DOI] [PubMed] [Google Scholar]
  27. Kubiak-Ossowska K.; Tokarczyk K.; Jachimska B.; Mulheran P. A. Bovine serum albumin adsorption at a silica surface explored by simulation and experiment. J. Phys. Chem. B 2017, 121, 3975–3986. 10.1021/acs.jpcb.7b01637. [DOI] [PubMed] [Google Scholar]
  28. Pomorska A.; Adamczyk Z.; Nattich-Rak M.; Sadowska M. Kinetics of human serum albumin adsorption at silica sensor: Unveiling dynamic hydration function. Colloids Surf., B 2018, 167, 377–384. 10.1016/j.colsurfb.2018.04.017. [DOI] [PubMed] [Google Scholar]
  29. Adamczyk Z.; Pomorska A.; Nattich-Rak M.; Wytrwal-Sarna M.; Bernasik A. Protein adsorption mechanisms at rough surfaces: serum albumin at a gold substrate. J. Colloid Interface Sci. 2018, 530, 631–641. 10.1016/j.jcis.2018.06.063. [DOI] [PubMed] [Google Scholar]
  30. Tellechea E.; Johannsmann D.; Steinmetz N. F.; Richter R. P.; Reviakine I. Model-independent analysis of QCM data on colloidal particle adsorption. Langmuir 2009, 25, 5177–5184. 10.1021/la803912p. [DOI] [PubMed] [Google Scholar]
  31. Olsson A. L. J.; Quevedo I. R.; He D.; Basnet M.; Tufenkji N. Using the quartz crystal microbalance with dissipation monitoring to evaluate the size of nanoparticles deposited on surfaces. ACS Nano 2013, 7, 7833–7843. 10.1021/nn402758w. [DOI] [PubMed] [Google Scholar]
  32. Zhang M.; Soto-Rodriguez J.; Chen I.-C.; Akbulut M. Adsorption and removal dynamics of polymeric micellar nanocarriers loaded with a therapeutic agent on silica surfaces. Soft Matter 2013, 9, 10155–10164. 10.1039/c3sm51692j. [DOI] [Google Scholar]
  33. Chen Q.; Xu S.; Liu Q.; Masliyah J.; Xu Z. QCM-D study of nanoparticle interactions. Adv. Colloid Interface Sci. 2016, 233, 94–114. 10.1016/j.cis.2015.10.004. [DOI] [PubMed] [Google Scholar]
  34. Gillissen J. J. J.; Tabaei S. R.; Jackman J. A.; Cho N.-J. A model derived from hydrodynamic simulations for extracting the size of spherical particles from the quartz crystal microbalance. Analyst 2017, 142, 3370–3379. 10.1039/C7AN00456G. [DOI] [PubMed] [Google Scholar]
  35. Gillissen J. J. J.; Jackman J. A.; Tabaei S. R.; Yoon B. K.; Cho N.-J. Quartz crystal microbalance model for quantitatively probing the deformation of adsorbed particles at low surface coverage. Anal. Chem. 2017, 89, 11711–11718. 10.1021/acs.analchem.7b03179. [DOI] [PubMed] [Google Scholar]
  36. Tarnapolsky A.; Freger V. Modeling QCM-D response to deposition and attachment of microparticles and living cells. Anal. Chem. 2018, 90, 13960–13968. 10.1021/acs.analchem.8b03411. [DOI] [PubMed] [Google Scholar]
  37. Martin S. J.; Frye G. C.; Ricco A. J.; Senturia S. D. Effect of surface roughness on the response of thickness-shear mode resonators in liquids. Anal. Chem. 1993, 65, 2910–2922. 10.1021/ac00068a033. [DOI] [Google Scholar]
  38. Johannsmann D. Viscoelastic, mechanical, and dielectric measurements on complex samples with the quartz crystal microbalance. Phys. Chem. Chem. Phys. 2008, 10, 4516–4534. 10.1039/b803960g. [DOI] [PubMed] [Google Scholar]
  39. Pomorska A.; Shchukin D.; Hammond R.; Cooper M. A.; Grundmeier G.; Johannsmann D. Positive frequency shifts observed upon adsorbing micron-sized solid objects to a quartz crystal microbalance from the liquid phase. Anal. Chem. 2010, 82, 2237–2242. 10.1021/ac902012e. [DOI] [PubMed] [Google Scholar]
  40. Macakova L.; Blomberg E.; Claesson P. M. Effect of adsorbed layer surface roughness on the QCM-D response: Focus on Trapped Water. Langmuir 2007, 23, 12436–12444. 10.1021/la7014308. [DOI] [PubMed] [Google Scholar]
  41. Kubiak K.; Adamczyk Z.; Oćwieja M. Kinetics of silver nanoparticle deposition at PAH monolayers: Reference QCM results. Langmuir 2015, 31, 2988–2996. 10.1021/la504975z. [DOI] [PubMed] [Google Scholar]
  42. Kubiak K.; Adamczyk Z.; Maciejewska J.; Oćwieja M. Gold nanoparticle monolayers of controlled coverage and structure. J. Phys. Chem. C 2016, 120, 11807–11819. 10.1021/acs.jpcc.6b02683. [DOI] [Google Scholar]
  43. Oćwieja M.; Maciejewska-Prończuk J.; Adamczyk Z.; Roman M. Formation of positively charged gold nanoparticle monolayers on silica sensors. J. Colloid Interface Sci. 2017, 501, 192–201. 10.1016/j.jcis.2017.04.038. [DOI] [PubMed] [Google Scholar]
  44. Sauerbrey G. Verwendung von Schwingquarzen zur Wägung Dünner Schichten und zur Mikrowägung. Eur. Phys. J. A 1959, 155, 206–222. 10.1007/BF01337937. [DOI] [Google Scholar]
  45. Adamczyk Z.Particles at Interfaces, Interactions, Deposition, Structure, 2nd ed.; Interface Science and Technology Series, Vol. 20; Academic Press: London, 2017. [Google Scholar]
  46. Adamczyk Z.; Sadlej K.; Wajnryb E.; Nattich M.; Ekiel-Jeżewska M. L.; Bławzdziewicz J. Streaming potential studies of colloid, polyelectrolyte and protein deposition. Adv. Colloid Interface Sci. 2010, 153, 1–29. 10.1016/j.cis.2009.09.004. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac9b05397_si_001.pdf (463.5KB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES