Abstract
We present a new coarse-grained Cα-based protein model with a nonradial multibody pseudo-improper-dihedral potential that is transferable, time-independent, and suitable for molecular dynamics. It captures the nature of backbone and side-chain interactions between amino acid residues by adapting a simple improper dihedral term for a one-bead-per-residue model. It is parameterized for intrinsically disordered proteins and applicable to simulations of such proteins and their assemblies on millisecond time scales.
1. Introduction
Molecular dynamics simulations provide insights into the properties of biomolecular systems. They make use of empirical potentials1−3 that depend on the length scale of the description. The atomic level descriptions4−9 are substantially distinct from the coarse-grained (CG) residue-level descriptions in which a residue is represented by a single bead. In between, there are CG models in which several atoms are grouped into beads with still different sets of potentials.10−14 The one-bead-per-residue CG protein models are especially useful when analyzing large systems at long time scales such as those occurring in the dynamics of virus capsids (assembly and indentation)15−17 or protein stretching at near-experimental speeds.18−20
The simplest versions of such a model are structure-based or Go-like,21−24 meaning that all parameters in the potentials are derived from the experimentally determined native structure25−28 and the solvent is implicit. There is no unique way to construct a Go-like model because its most important descriptor is the contact map, and there are various criteria to define it. In addition, various contact potentials and the backbone stiffness terms can be employed. Our benchmarking to the stretching experiments24 indicates that the Lennard-Jones (LJ) potential between the effective beads combined with the native contacts determined through an atomic overlap criterion29−31 can correctly recreate protein dynamics of stretching and, in addition, leads to proper folding. The criterion involves checking for an overlap between spherical spaces associated with heavy atoms in a pair of residues in the native state. Its presence introduces an attractive potential well, and its absence results in a soft repulsion between the beads.
The structure-based approach clearly cannot be applied to the intrinsically disordered proteins (IDP)32 because such proteins dynamically adopt significantly differing conformations and there is no dominant “native state”. Sampling their rich energy landscape may be challenging for all-atom models, especially in the case of simulating processes involving multiple chains, like aggregation.33 Short all-atom simulations may still be used to parameterize CG models built solely for the purpose of simulating one specific system (like in the multiscale approaches34−36); however, our goal is to construct a CG potential that is transferable to many systems.
We have argued37 that the contact-based CG description for IDPs is still possible provided that the contacts are determined dynamically from the instantaneous shape of the backbone, as described by the locations of the Cα atoms, and are thus allowed to form and disappear in an adiabatic fashion. The contacts can effectively arise either from the side-chain–side-chain, side-chain–backbone, or backbone–backbone interactions. This model also includes electrostatic interactions as described by a Debye–Hückel (D-H) potential,38 and it leads to a reasonable agreement with experimental and all-atom theoretical results pertaining to the average geometry of the conformations for a set of systems. It is also appealing computationally because it effectively involves only two-body interactions. We have already used this model to determine the phase diagram for aggregation of polyglutamines,39 which involved simulating 1800 residues for over 1 ms.
However, switching the contacts dynamically on and off violates the detailed balance and can lead to nonequilibrium stationary states, which have been studied, for example, in the context of active biomembranes.40−42 One may hope that sufficiently slow, adiabatic switches may mask such glitches, but it is nevertheless desirable to construct a model without any time-dependent potentials.
In our approach, we distinguish side-chain and backbone interactions using only the positions of the Cα atoms. Determining the type of interaction between two residues in the previous model required knowledge of the positions of six residues, but after the contact was quasi-adiabatically turned on, the forces were acting only between a pair of residues. Without this switching, we could either return to Monte Carlo sampling (where the idea was originally implemented43,44) or introduce a multibody term in the potential (such terms are crucial in reproducing the fine structure of residues that is lost in coarse-graining45,46). An example of such a term is the one used for dipole–dipole interactions that can describe hydrogen bonding in the protein backbone.47
Here, we propose a new and empirically motivated molecular dynamics model in which the short-range interactions are represented by time-independent four-body potentials. The point of departure is an observation that the backbone stiffness energy involves computation of a four-body dihedral potential48 that restricts the angle between two planes, each set by three residues. This potential can be used in an “improper” way to take into account the rigidity of the side chain in a two-bead-per-residue model. When two residues interact, this picture can be further simplified by removing the side-chain bead (in our one-bead-per-residue model, the beads are centered on the Cα atoms). We can still use the improper dihedral term by replacing the side-chain bead by the bead of the second residue that participates in the interaction and vice versa: the side-chain bead of the second residue in the interacting pair can be replaced by the bead representing the first residue. The planes defined by this procedure are shown in Figure 1. Thus, despite using the four-body terms, we still retain the pairwise nature of interactions. In our model, each contact between residues is described by two pseudo-improper-dihedral (PID) angles associated with each residue.
Figure 1.
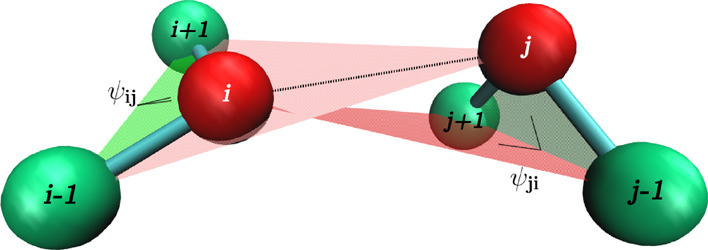
Idea of the PID angles. The interaction between residues i and j involves angles Ψij (defined by i – 1, i, i + 1, and j beads) and Ψji (defined by j – 1, j, j + 1, and i beads).
We made a survey of the structures from the Protein Data Bank, which showed specific patterns made by the PID angles. Those patterns are clearly different for the interactions made by the backbone and the side-chain groups, which proves that we can distinguish these two cases in our approach.
We show that our new model can successfully recreate the experimentally determined radii of gyration (Rg) for a set of 23 IDPs. Because replacing the quasi-adiabatic contacts with four-body PID potentials significantly changed the dynamics, we had to reparameterize all aspects of the model. In order to quantify which variant of the model after reparameterization agrees best with the experiment, we computed Pearson coefficients that show how close the simulation and experimental results are. The best variants surpass our previous model.
We also compared energy distributions of the models, which proved that adiabatic switching caused discrepancies from the Boltzmann distribution. Those discrepancies were not present in the new model with the PID potential. However, the new model turned out to require significantly more computational resources.
2. Methods
2.1. Results of the PDB Survey
Virtually all proteins are made from the same set of 20 amino acids, and the geometry of interactions between the residues should be similar for the case of IDPs and structured proteins even if the relative occurrence of those interactions may be different (since, e.g., the IDPs contain much fewer hydrophobic residues). Therefore, we made a survey of 21,090 structured proteins from the CATH database49 (the set of proteins with the sequence similarity not exceeding 40%: cath-dataset-nonredundant-S40.pdb) to determine which PID angles are favorable in the inter-residue interactions. We computed the values of PID angles for each pair of contacting residues from the database, where a contact between residues is defined through the overlap criterion. These heavy atoms may be a part of a backbone or a side chain. If a backbone atom from one residue overlaps with a side-chain atom from another residue, we call it a backbone–side-chain contact (bs). We analogously define side-chain–side-chain (ss) and backbone–backbone (bb) contacts. There may be many overlaps, so one residue pair can form more than one type of contact simultaneously.
In order to associate a characteristic set of PID angles and distances with a unique type of contact, we derive subdistributions corresponding to situations in which the overlaps arise only in one class of atoms (e.g., only ss). Table 1 shows how many overlap contacts of each type are in the database.
Table 1. Number of Overlap Contacts for All Proteins in the Used Database (7,974,804 in Total).
| type of contact | bb | bs | ss |
|---|---|---|---|
| number of residue pairs with only this type of contact | 624,699 | 953,782 | 1,870,746 |
| number of residue pairs that include this type of contact | 3,742,271 | 3,872,292 | 4,297,919 |
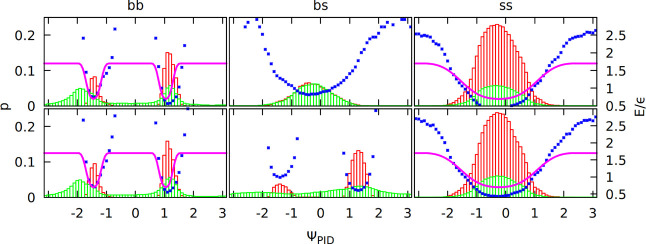
Figure 2 shows PID angle distributions for the ss, bs, and bb cases. The distinction between contact types is based on the overlap criterion described above (green histograms) or on a subset of these contacts that fulfill directional criteria introduced in the previous model37 (red histograms). Figure 2 shows distributions of contacts that are only one type (e.g., only bb overlaps). Figure S2 in the Supporting Information is the same as Figure 2, but contacts can be of more than one type (differences are minor and refer only to the bs case). The Boltzmann inversion potential VB = – kBT ln (p(ΨPID)) made from these distributions was fitted by an analytical function described in the next section. We observe that side-chain and backbone contacts are associated with different sets of the PID angles. The two minima for the bb case correspond to the parallel or antiparallel β sheet or to the right- or left-handed α helix (for the i, i +3 contacts, only one minimum is present, which reflects right-handedness, see Figure S3 in the Supporting Information).
Figure 2.
Distributions of the PID angles in the contacts from the PDB survey that are only of one type (green histograms). Local i, i + 3 and i, i + 4 contacts are excluded. Each contact has two angles. Distribution of the first (ΨPIDij) is on the top panels, and that of the second (ΨPID) is on the bottom panels. Subdistributions made from contacts that obey the directional criteria defined in ref (37) are shown as red histograms. The potential resulting from the Boltzmann inversion procedure (blue dots; unit of energy, ε ≈ 1.5 kcal/mol) was fitted to an analytical function (purple line).
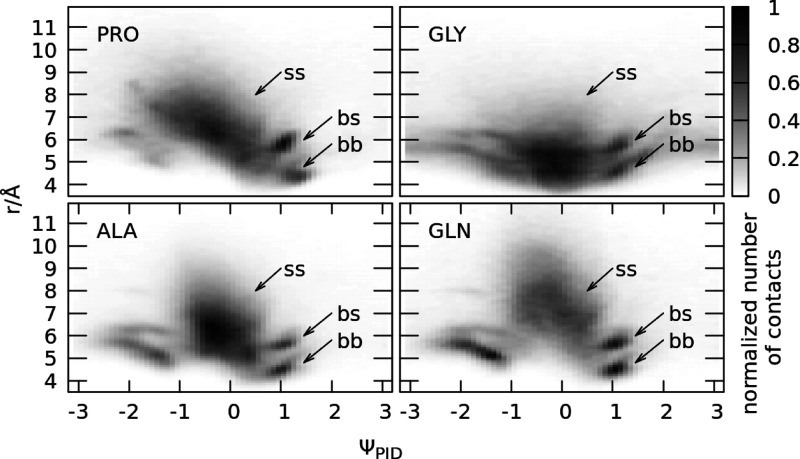
Figure 3 shows two-dimensional distributions, where the PID angle ΨPID is on one axis, and the Cα–Cα distance r is on the other axis. Different side chains result in different distance distributions, as shown for GLN or ALA residues, but the PID angle distributions stay mostly the same (with the exception of special cases, PRO and GLY). We find that the backbone contacts correspond to smaller and better defined distances than the side-chain contacts, which result in a diffuse cloud for ΨPID ≈ 0 rad and r > 6 Å (side chain) and sharp peaks for ΨPID ≈ ±1 rad and r < 6 Å (backbone). Two-dimensional distributions of the PID angle and distance for contacts made by all 20 types of residues are available in Figure S4 in the Supporting Information, and one-dimensional distance distributions used to determine the equilibrium distances for ss interactions (rminss) are available in our previous article;37 however, the values of rmin are reprinted in Table S1 in the Supporting Information.
Figure 3.
Two-dimensional distributions of contacts, where the PID angle ΨPID is on one axis, and the Cα–Cα distance r is on the other axis. The i, i + 3 and i, i + 4 contacts are excluded. The distributions include each contact obtained in the PDB survey where at least one residue in the pair was of the given amino acid type (PRO, GLY, ALA, and GLN). The PID angle ΨPID for each contact is the one associated with this residue (if both residues were the same amino acid, then it corresponds to two counts with two different PID angles).
2.2. Implementation of the PID Potential
In our model, the interaction between two residues
depends on their
distance and the two PID angles they make. Therefore, we chose our
PID potential to be a product of three terms: V(ψA, ψB, r) = λA(ψA)λB(ψB)ϕ(r), where ψA is the first PID angle in
a pair, ψB is the second angle in the pair, and r is the Cα–Cα distance.
As the first approximation, we decided to use the cosine function
for λ and the LJ potential for 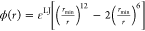 , where rmin is the minimum, and εLJ is the depth (discussed
later). Due to the broad character of the bs distribution (green histograms
in Figure 2), we take
only the bb and ss contacts into account (see section 2.3 in the Supporting Information). This feature is
distinct from our previous model in which the bs interactions were
included.37 For the bb and ss interactions,
we have clearly defined peaks that can be fitted to the potential
function (separately for PID angles and distances). Each peak has
a different width and center, so the detailed form of the λ
function is
, where rmin is the minimum, and εLJ is the depth (discussed
later). Due to the broad character of the bs distribution (green histograms
in Figure 2), we take
only the bb and ss contacts into account (see section 2.3 in the Supporting Information). This feature is
distinct from our previous model in which the bs interactions were
included.37 For the bb and ss interactions,
we have clearly defined peaks that can be fitted to the potential
function (separately for PID angles and distances). Each peak has
a different width and center, so the detailed form of the λ
function is
 |
Each pair of the ss contacts has rminss corresponding to the minimum identified in our previous work.37 Because for r < rmin the ϕ(r) potential becomes strongly repulsive, α parameters for ss and bb contacts must be chosen so that if λbb ≠ 0, then λss = 0 and vice versa.
Because the bb PID angle distribution has two peaks, the bb potential has two terms corresponding to both of them (ψ0bb+ and ψ0). Therefore
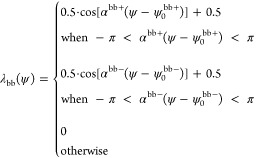 |
The repulsive part of the LJ potential should always be present for small distances to prevent the residues from passing through one another (excluded volume effect). This is why the bb terms have a more complicated form:
This formula ensures the presence of the excluded volume because, for r < rminbb, the LJ potential ϕbb is no longer multiplied by the λbb factors. For the ss contacts, Vss(ψA, ψB, r) = λss(ψA)λss(ψB)ϕss(r) and rmin depends on the types of amino acids in the pair in contact (see Section 2.4 about the details of the LJ potential). The total PID potential is V = Vss + Vbb.
Fitting the function to the Boltzmann inversion potential based on the contact distributions of only one type (bb, bs, or ss) that fulfill directional criteria defined in ref (37) (red histograms in Figure 2) resulted in the following parameters: αbb+ = 6.4, αbb– = 6.0, αss = 1.2, ψ0ss = – 0.23 rad, ψ0 = 1.05 rad, and ψ0bb– = – 1.44 rad. Fitting to the distributions that do not have to fulfill directional criteria (green histograms in Figure 2) resulted in a model that agreed poorly with the experiment (see section 3.2 of the Supporting Information). In order to improve numerical efficiency, the cosine function was replaced by its algebraic approximation, defined in section 1 of the Supporting Information.
Values of rmin are given in ref (37) and Table S1 in the Supporting Information. In Section 3, we denote the pseudo-improper-dihedral potential by letter P and the old, quasi-adiabatic model by letter A.
2.3. Backbone Stiffness and the Thermostat
Our model has an implicit solvent, represented
by the Langevin thermostat
with the damping term, so the equation of motion for the ith residue is 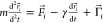 , where m is the average
amino acid mass, r⃗i is the position
of the residue, F⃗i is the force
resulting from the potential, γ = 2m/τ
is the damping coefficient, and Γ⃗i is the thermal white noise with the variance σ2 = 2γkBT. The time unit τ ≈ 1 ns was verified for a different
model with the same equations of motion,50 and even if for this new model τ is expected to be slightly
different, it should still correspond to an overdamped case with diffusional
(not ballistic) dynamics.
, where m is the average
amino acid mass, r⃗i is the position
of the residue, F⃗i is the force
resulting from the potential, γ = 2m/τ
is the damping coefficient, and Γ⃗i is the thermal white noise with the variance σ2 = 2γkBT. The time unit τ ≈ 1 ns was verified for a different
model with the same equations of motion,50 and even if for this new model τ is expected to be slightly
different, it should still correspond to an overdamped case with diffusional
(not ballistic) dynamics.
The residues in our model are connected harmonically with the spring constant k = 100 Å–2·ε and equilibrium distance 3.8 Å (ε ≈ 1.5 kcal/mol is the energy unit51). The backbone stiffness potential in our model consists of a bond angle and (proper) dihedral terms. Its depth and form were obtained from a Boltzmann inversion potential based on a random coil library.52 Its exact analytical form is described in ref (37). It is defined in kcal/mol, so it can be used to verify what is the effective room temperature. The results for polyproline, which cannot form side-chain–side-chain contacts (see the next section) and has high backbone stiffness, indicate37 that simulations for the room temperature 0.38 ε/kB give the best agreement with experimental values for the polyproline end-to-end distance, so we set the temperature to 0.38 in the reduced units.
Because the potential for backbone stiffness, as in the previous model, is based on a random coil library, it does not favor any secondary structure. In order to make structures like α helices or β turns possible, we allow attractive contacts between the ith and i + 3rd residues in the chains as these contacts correspond to hydrogen bonds between backbone atoms in an all-atom representation.53 However, the nature of i, i + 4 contacts is different (see section 2.1 in the Supporting Information), so in the results, we tried models with i, i + 4 contacts (+ in superscript) and without them (− in superscript).
2.4. Depth and Form of the Lennard-Jones Potential
The energy unit ε = 110 pN·Å ≈ 1.5 kcal/mol is taken from the earlier models,24,37 and although it corresponds to the strength of one contact in those models, it is not necessarily the case for the PID model. We keep εbb = ε because it is roughly equal to the energy of one hydrogen bond made by the protein backbone,54 but the varied nature of ss contacts required parameterization. We checked values between 0 and 1 ε for the uniform εss potential (we denote this case as ME) and tried two matrices where εss depends on the pair of residues: the classic Miyazawa–Jernigan matrix based on PDB statistics from 199655 (denoted MJ) and the MDCG matrix derived from all-atom simulations56 (denoted MD). We also tried scaling them by a factor from 0 to 1 (in the results, the factor is denoted in subscript). In all three cases (ME, MJ, and MD), εss = 0 for PRO and GLY residues.
The distance distributions for some pairs of residues are very broad.37 This is caused by the ability of longer side chains to deform and adapt different conformations. This ability is lost in any CG model in which each residue is represented by a spherical bead. To correct this, one may imagine a modified form of the LJ potential for ss contacts:
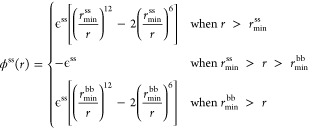 |
We tested both this modified form (denoted by letter F, for flat) and the traditional form (denoted by letter L) of the LJ potential.
2.5. Electrostatics
Our previous model
used a Debye–Hückel-screened electrostatic potential
with electric permittivity ϵ = 4 Å/r depending on the Cα– Cα distance r following the approach of Tozzini et al.38 (thus we denote this version of electrostatic interactions by letter
T). However, this approach was designed for structured proteins, where
the permittivity inside the hydrophobic core is significantly lower
than in water. IDPs lack this core and are more solvent-exposed, so
we tried a simpler term with ϵ = 80 (we denote this term by
letter C). In both cases, the form of the electrostatic potential
is 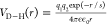 , where s is the screening
length that depends on the ionic strength. In our model, histidine
is considered to be uncharged.
, where s is the screening
length that depends on the ionic strength. In our model, histidine
is considered to be uncharged.
3. Results and Discussion
We tested our model on a benchmark of 23 IDPs whose radius of gyration was measured in SAXS (small-angle X-ray scattering) experiments57−67 (their sequences, screening lengths used, and a Pappu diagram68 are in section 3.1 of the Supporting Information). We considered over 200 variants of the model: with a pseudo-improper-dihedral potential (denoted by letter P) or the previous version with a quasi-adiabatic potential (letter A), with or without i, i + 4 attractive contacts (+ or – in superscript), with the standard (letter L) or flat (letter F) form of the LJ potential, different depths of this potential (we considered three residue–residue matrices: uniform, ME; Miyazawa–Jernigan, MJ; and all-atom based, MD; all scaled by a factor denoted in subscript), and with standard (letter C) or distance-dependent (letter T) electric permittivity. Thus, the name of each version is made from four symbols (the full legend is available in Table S4 in the Supporting Information), e.g., A+ L ME1 T is the model with quasi-adiabatic switching, attractive i, i + 4 contacts, LJ potential with uniform ε, and electrostatics used by Tozzini et al.38 P– F MD0.1 C means a model with the PID potential, no i, i + 4 contacts, LJ potential with a flat region and depth depending on the identity of residues according to the MDCG matrix rescaled by 0.1, and classic D-H electrostatics.
For each model, we computed its Pearson
coefficient24 defined as 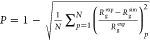 , where Rgexp is the radius of gyration from
the experiment, Rg is from the simulation, and the sum is over
each of N = 23 proteins. The full list of models
with their Pearson coefficients P and χ2 values is in section 2 of the
Supporting Information. Here, we show just the five most significant
ones, starting from the original model37 shown in panel (a) of Figure 4.
, where Rgexp is the radius of gyration from
the experiment, Rg is from the simulation, and the sum is over
each of N = 23 proteins. The full list of models
with their Pearson coefficients P and χ2 values is in section 2 of the
Supporting Information. Here, we show just the five most significant
ones, starting from the original model37 shown in panel (a) of Figure 4.
Figure 4.
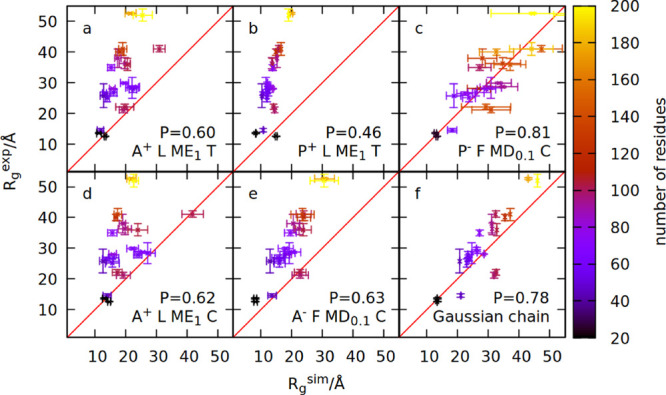
Comparison between the simulated and measured radius of gyration for 23 IDPs. Panels (a)–(f) show simulation results obtained within six different models. The model names are specified in the panels and defined in the text. The value of the Pearson coefficient is also indicated in each panel. Colors indicate the number of residues constituting a given IDP.
Applying a pseudo-improper-dihedral potential to this model results
in worse agreement with the experiment (panel (b)), so we reparameterized
the model by changing five features described above. The end result
(panel (c)) has much better agreement with the experiment. We checked
that this is indeed the result of using the new form of the potential
as applying the reparameterized features to the previous model (panels
(d) and (e)) improves it only slightly. Panel (f) shows the results
of the Gaussian chain model69 calculated
with the formula 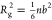 , where n is the number
of residues, and b is the effective Kuhn length that
may be treated as a fit parameter. By fitting with the least-squares
method to the set of 23 IDPs, we obtained b = 6.7
Å.
, where n is the number
of residues, and b is the effective Kuhn length that
may be treated as a fit parameter. By fitting with the least-squares
method to the set of 23 IDPs, we obtained b = 6.7
Å.
The Rg values for the set of 23 IDPs have been measured in SAXS experiments. We note that the direct result of a biomolecular SAXS experiment is a scattering profile that contains information not only about the value of Rg but also about the average shape and size of the IDP under study. It is possible to compute such a scattering profile from an ensemble of simulation structures and compare it with the experiment,70 but this task involves fitting parameters and requires raw experimental data, which are not available for many proteins used in the testing set. On the other hand, the value of Rg is a single number that can be easily compared to simulation results. For these reasons, we decided to compare our results only with the Rg values. An example of a comparison with a SAXS intensity profile for protein 6AAA is shown in Figure S12 in the Supporting Information.
Another way to validate our model is to perform a histogram test,71 where we can check if our simulation is consistent with the Boltzmann distribution of energy: the state with energy E should occur with the probability p(E) = Ω(E) exp ( – E/kBT)/Q, where Ω(E) is the state density, and Q is the normalization factor. If we perform simulations using two different temperatures T1 and T2, then we can compute the following quantity: log(p1(E)/p2(E)) = log (Q1/Q2) + E · (1/kBT2 – 1/kBT1). This quantity should depend on the energy linearly with the coefficient (1/kBT2 – 1/kBT1). We can plot this dependence (treating log(Q1/Q2) as a fit parameter) for the new version (P– F MD0.1 C) and previous version (A+ L ME1 T) of the model.37 Such a plot for proteins his5 (24 residues), NRG1 (75 residues), and p53 (93 residues) is shown in Figure 5. The data points obtained with the new model lie closer to the line with the coefficient (1/kBT2 – 1/kBT1).
Figure 5.
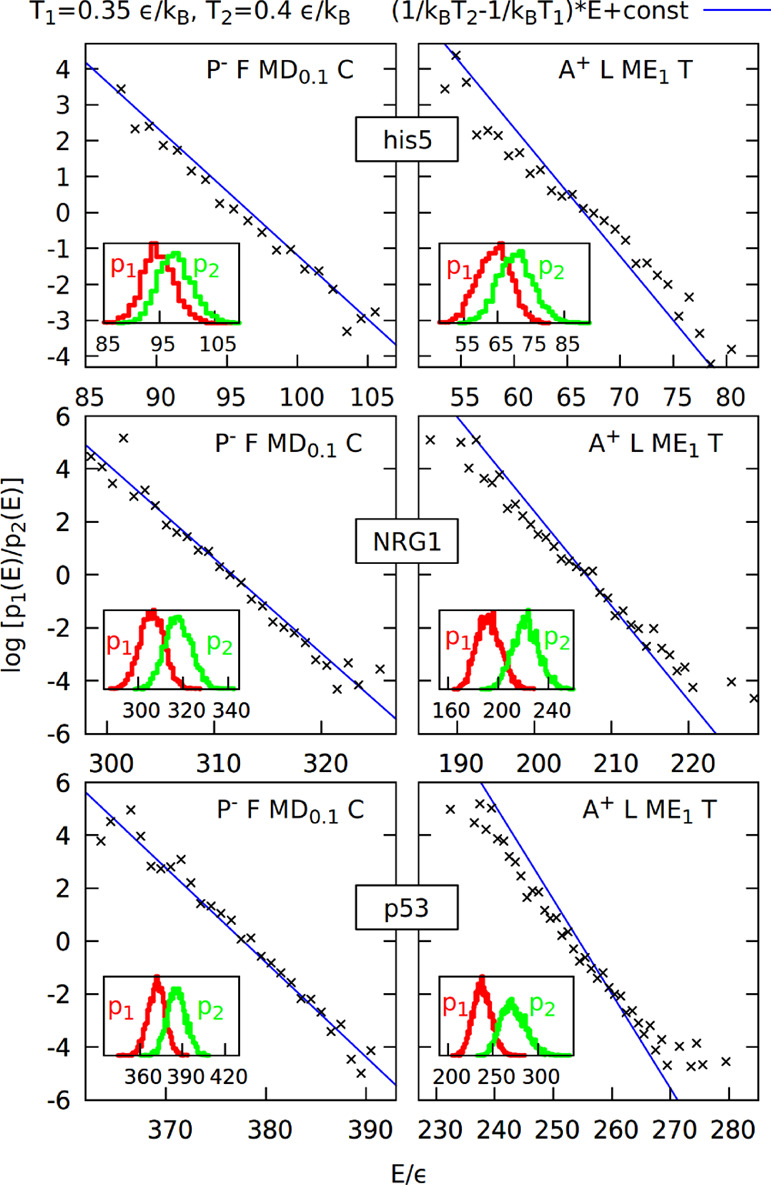
Histogram test71 for the new model (P– F MD0.1 C) and previous model (A+ L ME1 T) based on simulations of proteins his5, NRG1, and p53 at temperatures 0.35 and 0.4 ε/kB. Insets show the energy histograms binned every 1 ε and used to construct the quantity log(p1(E)/p2(E)) shown on the main plots as a function of energy.
The new version of the model has significant advantages over the previous one: it better agrees with the experimental data and the Boltzmann distribution. However, even though the computational speed of both models scales almost linearly with the system size, the new model is usually at least five times slower (see Figure 6).
Figure 6.
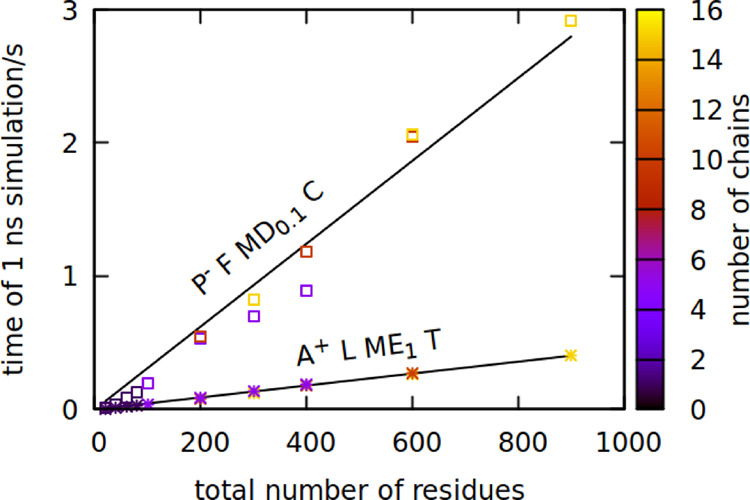
Physical time of 1 ns-simulation run on a single core for the new model (P– F MD0.1 C, squares) and previous model (A+ L ME1 T, stars) as a function of the system size. The number of protein chains in the simulation is indicated by color. The system density of multichain simulations was set to 1 residue/nm3. Fitted lines have coefficients of 0.003 and 0.0005 s/residue, respectively, with a fit error in the order of 0.0001 s/residue.
The new model is also harder to parallelize (due to multibody terms) and does not perform well for folded proteins: we tried folding small proteins (PDB access codes 1L2Y, 1UBQ, and 1ERY) with it but arrived with an RMSD of 6 Å or higher even for the smallest protein, 1L2Y (see section 4 of the Supporting Information). This is not surprising because IDPs have very weak inter-residue interactions: the top seven variants of our model considered in IDP parameterization had their residue–residue matrices multiplied by a factor smaller than 0.5 (see Figure 7). It is interesting to note that two out of our top seven variants multiply the matrix by 0, meaning that there are no interactions with the exception of excluded volume, backbone stiffness, and electrostatics. A simple Gaussian chain model also works quite well for IDPs (panel (f) in Figure 4). This proves that water is a good solvent for IDPs, and their inter-residue interactions affect chain dimensions in a minor way.32 This fact was also used in a recent hierarchical approach for studying IDPs, where only local fragments are modeled in detail, and the whole chain is constructed from those fragments.72
Figure 7.
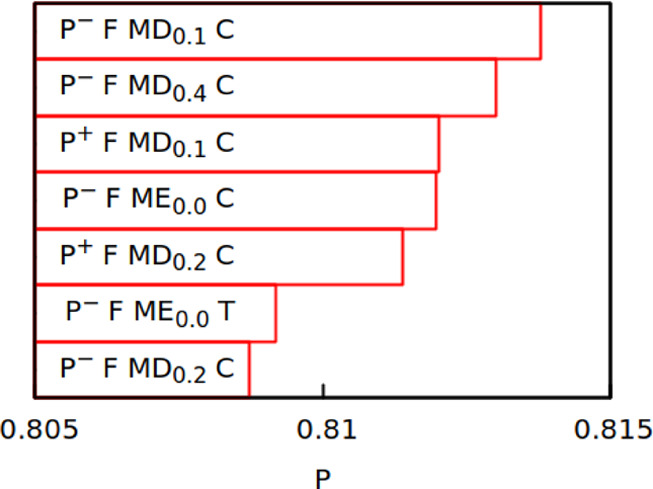
Top seven variants of the PID model ranked by their Pearson coefficient.
The top-ranked variants of the model may be further refined by fine-tuning the ss interactions. In future studies, our new CG model can be used to explore conformational dynamics of IDPs and their assemblies. It can also be adapted to study physical properties of flexible linkers in multidomain proteins.73,74 In this case, each of the structured domains can be kept stable by a Go-model potential,24 and each of the linkers (as well as their interactions with the domains) can be described by the PID potential.
Acknowledgments
This research has received support from the National Science Centre (NCN) under grant nos. 2018/31/B/NZ1/00047 (M.C. and Ł.M.) and 2016/21/B/NZ1/00006 (B.R. and M.C.). The computer resources were supported by the PL-GRID infrastructure.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00338.
Definition of the cosine function approximation, details of the distributions of distance and PID angle, information about all of the proteins used for the parameterization, full results of that parameterization, an exemplary comparison with an experimental SAXS profile, and preliminary results of structured protein simulations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bixon M.; Lifson S. Potential functions and conformations in cycloalkanes. Tetrahedron 1967, 23, 769–784. 10.1016/0040-4020(67)85023-3. [DOI] [Google Scholar]
- Lifson S.; Warshel A. Consistent force field for calculations of conformations, vibrational spectra, and enthalpies of cycloalkane and n-alkane molecules. J. Chem. Phys. 1968, 49, 5116–5129. 10.1063/1.1670007. [DOI] [Google Scholar]
- Levitt M.; Lifson S. Refinement of protein conformations using a macromolecular energy minimization procedure. J. Mol. Biol. 1969, 46, 269–279. 10.1016/0022-2836(69)90421-5. [DOI] [PubMed] [Google Scholar]
- McCammon J. A.; Gelin B. R.; Karplus M. Dynamics of folded proteins. Nature 1977, 267, 585. 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- Levitt M.; Warshel A. Computer simulation of protein folding. Nature 1975, 253, 694–698. 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- McCammon J. A.; Harvey S. C.. Dynamics of Proteins and Nucleic Acids; Cambridge University Press: Cambridge, 1988, 10.1017/CBO9781139167864. [DOI] [Google Scholar]
- Gao J.; Kuczera K.; Tidor B.; Karplus M. Hidden thermodynamics of mutant proteins: a molecular dynamics analysis. Science 1989, 244, 1069–1072. 10.1126/science.2727695. [DOI] [PubMed] [Google Scholar]
- Schlick T.Molecular Modeling and Simulations: An interdisciplinary guide; 2nd Edition; Springer Science & Business Media: New York, 2010. [Google Scholar]
- Duan Y.; Kollman P. A. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 1998, 282, 740–744. 10.1126/science.282.5389.740. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Baaden M.; Marrink S. J. Coarse-grain modelling of protein-protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 878–886. 10.1016/j.sbi.2013.09.004. [DOI] [PubMed] [Google Scholar]
- Bereau T.; Deserno M. Generic coarse-grained model for protein folding and aggregation. J. Chem. Phys. 2009, 130, 235106. 10.1063/1.3152842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poma A. B.; Cieplak M.; Theodorakis P. E. Combining the MARTINI and structure-based coarse-grained approaches for the molecular dynamics studies of conformational transitions in proteins. J. Chem. Theory Comput. 2017, 13, 1366–1374. 10.1021/acs.jctc.6b00986. [DOI] [PubMed] [Google Scholar]
- Wu H.; Wolynes P. G.; Papoian G. A. Awsem-idp: A coarse-grained force field for intrinsically disordered proteins. J. Phys. Chem. B 2018, 122, 11115–11125. 10.1021/acs.jpcb.8b05791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cieplak M.; Robbins M. O. Nanoindentation of 35 virus capsids in a molecular model: Relating mechanical properties to structure. PLoS One 2013, 8, e63640 10.1371/journal.pone.0063640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polles G.; Indelicato G.; Potestio R.; Cermelli P.; Twarock R.; Micheletti C. Mechanical and assembly units of viral capsids identified via quasi-rigid domain decomposition. PLOS Comput. Biol. 2013, 9, e1003331 10.1371/journal.pcbi.1003331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wołek K.; Cieplak M. Self-assembly of model proteins into virus capsids. J. Phys.: Condens. Matter 2017, 29, 474003. 10.1088/1361-648X/aa9351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sikora M.; Sułkowska J. I.; Cieplak M. Mechanical strength of 17 134 model proteins and cysteine slipknots. PLOS Comput. Biol. 2009, 5, e1000547 10.1371/journal.pcbi.1000547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valbuena A.; Oroz J.; Hervás R.; Vera A. M.; Rodríguez D.; Menéndez M.; Sulkowska J. I.; Cieplak M.; Carrión-Vázquez M. On the remarkable mechanostability of scaffoldins and the mechanical clamp motif. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 13791–13796. 10.1073/pnas.0813093106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Różycki B.; Mioduszewski Ł.; Cieplak M. Unbinding and unfolding of adhesion protein complexes through stretching: Interplay between shear and tensile mechanical clamps. Proteins: Struct., Funct., Bioinf. 2014, 82, 3144–3153. 10.1002/prot.24674. [DOI] [PubMed] [Google Scholar]
- Clementi C.; Nymeyer H.; Onuchic J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937–953. 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
- Hoang T. X.; Cieplak M. Molecular dynamics of folding of secondary structures in Go-type models of proteins. J. Chem. Phys. 2000, 112, 6851–6862. 10.1063/1.481261. [DOI] [Google Scholar]
- Karanicolas J.; Brooks C. L. III The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002, 11, 2351–2361. 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sułkowska J. I.; Cieplak M. Selection of optimal variants of Go̅-Like models of proteins through studies of stretching. Biophys. J. 2008, 95, 3174–3191. 10.1529/biophysj.107.127233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Go̅ N. Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng. 1983, 12, 183–210. 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
- Abe H.; Go̅ N. Noninteracting local-structure model of folding and unfolding transition in globular proteins. II. Application to two-dimensional lattice proteins. Biopolymers 1981, 20, 1013–1031. 10.1002/bip.1981.360200512. [DOI] [PubMed] [Google Scholar]
- Šali A.; Shakhnovich E.; Karplus M. How does a protein fold. Nature 1994, 369, 248–251. 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
- Shrivastava I.; Vishveshwara S.; Cieplak M.; Maritan A.; Banavar J. R. Lattice model for rapidly folding protein-like heteropolymers. Proc. Natl. Acad. Sci. U. S. A. 1995, 92, 9206–9209. 10.1073/pnas.92.20.9206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai J.; Taylor R.; Chothia C.; Gerstein M. The packing density in proteins: Standard radii and volumes. J. Mol. Biol. 1999, 290, 253–266. 10.1006/jmbi.1999.2829. [DOI] [PubMed] [Google Scholar]
- Settanni G.; Hoang T. X.; Micheletti C.; Maritan A. Folding pathways of prion and doppel. Biophys. J. 2002, 83, 3533–3541. 10.1016/S0006-3495(02)75353-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wołek K.; Gómez-Sicilia À.; Cieplak M. Determination of contact maps in proteins: A combination of structural and chemical approaches. J. Chem. Phys. 2015, 143, 243105. 10.1063/1.4929599. [DOI] [PubMed] [Google Scholar]
- Uversky V. N. Unusual biophysics of intrinsically disordered proteins. Biochim. Biophys. Acta 2013, 1834, 932–951. 10.1016/j.bbapap.2012.12.008. [DOI] [PubMed] [Google Scholar]
- Rauscher S.; Pomès R. Molecular simulations of protein disorder. Biochem. Cell Biol. 2010, 88, 269–290. 10.1139/O09-169. [DOI] [PubMed] [Google Scholar]
- Terakawa T.; Takada S. Multiscale ensemble modeling of intrinsically disordered proteins: p53 n-terminal domain. Biophys. J. 2011, 101, 1450–1458. 10.1016/j.bpj.2011.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X.; Chen J. Hyres: a coarse-grained model for multi-scale enhanced sampling of disordered protein conformations. Phys. Chem. Chem. Phys. 2017, 19, 32421–32432. 10.1039/C7CP06736D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Voth G. A. Molecular dynamics simulations of polyglutamine aggregation using solvent-free multiscale coarse-grained models. J. Phys. Chem. B 2010, 114, 8735–8743. 10.1021/jp1007768. [DOI] [PubMed] [Google Scholar]
- Mioduszewski Ł.; Cieplak M. Disordered peptide chains in an α-c-based coarse-grained model. Phys. Chem. Chem. Phys. 2018, 20, 19057–19070. 10.1039/C8CP03309A. [DOI] [PubMed] [Google Scholar]
- Tozzini V.; Trylska J.; Chang C.-e.; McCammon J. A. Flap opening dynamics in hiv-1 protease explored with a coarse-grained model. J. Struct. Biol. 2007, 157, 606–615. 10.1016/j.jsb.2006.08.005. [DOI] [PubMed] [Google Scholar]
- Mioduszewski Ł.; Cieplak M.. Protein droplets in systems of disordered homopeptides and the amyloid glass phase. Phys. Chem. Chem. Phys. 2020, accepted manuscript, 10.1039/D0CP01635G. [DOI] [PubMed] [Google Scholar]
- Różycki B.; Lipowsky R.; Weikl T. R. Adhesion of Membranes with Active Stickers. Phys. Rev. Lett. 2006, 96, 048101 10.1103/PhysRevLett.96.048101. [DOI] [PubMed] [Google Scholar]
- Różycki B.; Weikl T. R.; Lipowsky R. Adhesion of membranes via switchable molecules. Phys. Rev. E 2006, 73, 061908 10.1103/PhysRevE.73.061908. [DOI] [PubMed] [Google Scholar]
- Różycki B.; Weikl T. R.; Lipowsky R. Stochastic resonance for adhesion of membranes with active stickers. Eur. Phys. J. E: Soft Matter Biol. Phys. 2007, 22, 97–106. 10.1140/epje/i2006-10075-3. [DOI] [PubMed] [Google Scholar]
- Hung N. B.; Le D.-M.; Hoang T. X. Sequence dependent aggregation of peptides and fibril formation. J. Chem. Phys. 2017, 147, 105102. 10.1063/1.5001517. [DOI] [PubMed] [Google Scholar]
- Enciso M.; Rey A. A refined hydrogen bond potential for flexible protein models. J. Chem. Phys. 2010, 132, 235102. 10.1063/1.3436723. [DOI] [PubMed] [Google Scholar]
- Tozzini V. Minimalist models for proteins: a comparative analysis. Q. Rev. Biophys. 2010, 43, 333–371. 10.1017/S0033583510000132. [DOI] [PubMed] [Google Scholar]
- Liwo A.; Czaplewski C.; Pillardy J.; Scheraga H. A. Cumulant-based expressions for the multibody terms for the correlation between local and electrostatic interactions in the united-residue force field. J. Chem. Phys. 2001, 115, 2323–2347. 10.1063/1.1383989. [DOI] [Google Scholar]
- Alemani D.; Collu F.; Cascella M.; Dal Peraro M. A nonradial coarse-grained potential for proteins produces naturally stable secondary structure elements. J. Chem. Theory Comput. 2010, 6, 315–324. 10.1021/ct900457z. [DOI] [PubMed] [Google Scholar]
- Swope W. C.; Ferguson D. M. Alternative expressions for energies and forces due to angle bending and torsional energy. J. Comput. Chem. 1992, 13, 585–594. 10.1002/jcc.540130508. [DOI] [Google Scholar]
- Dawson N. L.; Lewis T. E.; Das S.; Lees J. G.; Lee D.; Ashford P.; Orengo C. A.; Sillitoe I. Cath: an expanded resource to predict protein function through structure and sequence. Nucleic Acids Res. 2017, 45, D289–D295. 10.1093/nar/gkw1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szymczak P.; Cieplak M. Stretching of proteins in a uniform flow. J. Chem. Phys. 2006, 125, 164903. 10.1063/1.2358346. [DOI] [PubMed] [Google Scholar]
- Poma A. B.; Chwastyk M.; Cieplak M. Polysaccharide-protein complexes in a coarse-grained model. J. Phys. Chem. B. 2015, 119, 12028–12041. 10.1021/acs.jpcb.5b06141. [DOI] [PubMed] [Google Scholar]
- Ghavami A.; van der Giessen E.; Onck P. R. Coarse-grained potentials for local interactions in unfolded proteins. J. Chem. Theory Comput. 2013, 9, 432–440. 10.1021/ct300684j. [DOI] [PubMed] [Google Scholar]
- Koliński A. Protein modeling and structure prediction with a reduced representation. Acta Biochim. Pol. 2004, 51, 349–371. 10.18388/abp.2004_3575. [DOI] [PubMed] [Google Scholar]
- Sheu S.-Y.; Yang D.-Y.; Selzle H. L.; Schlag E. W. Energetics of hydrogen bonds in peptides. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 12683–12687. 10.1073/pnas.2133366100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyazawa S.; Jernigan R. L. Residue – Residue Potentials with a Favorable Contact Pair Term and an Unfavorable High Packing Density Term, for Simulation and Threading. J. Mol. Biol. 1996, 256, 623–644. 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- Betancourt M. R.; Omovie S. J. Pairwise energies for polypeptide coarse-grained models derived from atomic force fields. J. Chem. Phys. 2009, 130, 195103. 10.1063/1.3137045. [DOI] [PubMed] [Google Scholar]
- Cragnell C.; Rieloff E.; Skepö M. Utilizing coarse-grained modeling and monte carlo simulations to evaluate the conformational ensemble of intrinsically disordered proteins and regions. J. Mol. Biol. 2018, 430, 2478–2492. 10.1016/j.jmb.2018.03.006. [DOI] [PubMed] [Google Scholar]
- Dignon G. L.; Zheng W.; Kim Y. C.; Best R. B.; Mittal J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018, 14, e1005941 10.1371/journal.pcbi.1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadi M.; Kosol S.; Lebrun P.; Valentini E.; Blackledge M.; Dunker A. K.; Felli I. C.; Forman-Kay J. D.; Kriwacki R. W.; Pierattelli R.; Sussman J.; Svergun D. I.; Uversky V. N.; Vendruscolo M.; Wishart D.; Wright P. E.; Tompa P. pE-DB: a database of structural ensembles of intrinsically disordered and of unfolded proteins. Nucl. Acids Res. 2014, 42, D326–D335. 10.1093/nar/gkt960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cragnell C.; Durand D.; Cabane B.; Skepö M. Coarse-grained modeling of the intrinsically disordered protein histatin 5 in solution: Monte carlo simulations in combination with SAXS. Proteins: Struct., Funct., Bioinf. 2016, 84, 777–791. 10.1002/prot.25025. [DOI] [PubMed] [Google Scholar]
- Rauscher S.; Gapsys V.; Gajda M. J.; Zweckstetter M.; de Groot B. L.; Grubmüller H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: A comparison to experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. 10.1021/acs.jctc.5b00736. [DOI] [PubMed] [Google Scholar]
- Mylonas E.; Hascher A.; Bernadó P.; Blackledge M.; Mandelkow E.; Svergun D. I. Domain conformation of tau protein studied by solution small-angle x-ray scattering. Biochemistry 2008, 47, 10345–10353. 10.1021/bi800900d. [DOI] [PubMed] [Google Scholar]
- Kung C. C.-H.; Naik M. T.; Wang S.-H.; Shih H.-M.; Chang C.-C.; Lin L.-Y.; Chen C.-L.; Ma C.; Chang C.-F.; Huang T.-H. Structural analysis of poly-sumo chain recognition by the rnf4-sims domain. Biochem. J. 2014, 462, 53–65. 10.1042/BJ20140521. [DOI] [PubMed] [Google Scholar]
- Chukhlieb M.; Raasakka A.; Ruskamo S.; Kursula P. The N-terminal cytoplasmic domain of neuregulin 1 type III is intrinsically disordered. Amino Acids 2015, 47, 1567–1577. 10.1007/s00726-015-1998-x. [DOI] [PubMed] [Google Scholar]
- Moncoq K.; Broutin I.; Larue V.; Perdereau D.; Cailliau K.; Browaeys-Poly E.; Burnol A.-F.; Ducruix A. The pir domain of grb14 is an intrinsically unstructured protein: implication in insulin signaling. FEBS Lett. 2003, 554, 240–246. 10.1016/S0014-5793(03)01095-0. [DOI] [PubMed] [Google Scholar]
- Wells M.; Tidow H.; Rutherford T. J.; Markwick P.; Jensen M. R.; Mylonas E.; Svergun D. I.; Blackledge M.; Fersht A. R. Structure of tumor suppressor p53 and its intrinsically disordered n-terminal transactivation domain. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 5762–5767. 10.1073/pnas.0801353105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordeiro T. N.; Herranz-Trillo F.; Urbanek A.; Estaña A.; Cortés J.; Sibille N.; Bernadó P.. Structural Characterization of Highly Flexible Proteins by Small-Angle Scattering. Biological Small Angle Scattering: Techniques, Strategies and Tips ;Springer: Singapore, 2017, 1009, 107–129, 10.1007/978-981-10-6038-0_7. [DOI] [PubMed] [Google Scholar]
- Holehouse A. S.; Das R. K.; Ahad J. N.; Richardson M. O. G.; Pappu R. V. CIDER: Resources to Analyze Sequence-Ensemble Relationships of Intrinsically Disordered Proteins. Biophys. J. 2017, 112, 16–21. 10.1016/j.bpj.2016.11.3200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teraoka I. Chapter 1. Models of Polymer Chains; John Wiley & Sons: 2002; 1–67, 10.1002/0471224510.ch1. [DOI] [Google Scholar]
- Różycki B.; Kim Y. C.; Hummer G. SAXS Ensemble Refinement of ESCRT-III CHMP3 Conformational Transitions. Structure 2011, 19, 109–116. 10.1016/j.str.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janke W.Monte Carlo Methods in Classical Statistical Physics. In Computational Many-Particle Physics ;Springer: Berlin Heidelberg, 2008, 79-140, 10.1007/978-3-540-74686-7_4. [DOI] [Google Scholar]
- Pietrek L. M.; Stelzl L. S.; Hummer G. Hierarchical ensembles of intrinsically disordered proteins at atomic resolution in molecular dynamics simulations. J. Chem. Theory Comput. 2020, 16, 725–737. 10.1021/acs.jctc.9b00809. [DOI] [PubMed] [Google Scholar]
- Różycki B.; Cazade P.-A.; O’Mahony S.; Thompson D.; Cieplak M. The length but not the sequence of peptide linker modules exerts the primary influence on the conformations of protein domains in cellulosome multi-enzyme complexes. Phys. Chem. Chem. Phys. 2017, 19, 21414–21425. 10.1039/C7CP04114D. [DOI] [PubMed] [Google Scholar]
- Różycki B.; Cieplak M. Stiffness of the C-terminal disordered linker affects the geometry of the active site in endoglucanase cel8a. Mol. BioSyst. 2016, 12, 3589–3599. 10.1039/C6MB00606J. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.