Abstract
Procathepsins are an inactive, immature form of cathepsins, predominantly cysteine proteases present in the extracellular matrix (ECM) and in lysosomes that play a key role in various biological processes such as bone resorption or intracellular proteolysis. The enzymatic activity of cathepsins can be mediated by glycosaminoglycans (GAGs), long unbranched periodic negatively charged polysaccharides found in ECM that take part in many biological processes such as anticoagulation, angiogenesis, and tissue regeneration. In addition to the known effects on mature cathepsins, GAGs can mediate the maturation process of procathepsins, in particular, procathepsin B. However, the detailed mechanism of this mediation at the molecular level is still unknown. In this study, for the first time, we aimed to unravel the role of GAGs in this process using computational approaches. We rigorously analyzed procathepsin B–GAG complexes in terms of their dynamics, energetics, and potential allosteric regulation. We revealed that GAGs can stabilize the conformation of the procathepsin B structure with the active site accessible for the substrate and concluded that GAGs most probably bind to procathepsin B once the zymogen adopts the enzymatically active conformation. Our data provided a novel mechanistic view of the maturation process of procathepsin B, while the approaches elaborated here might be useful to study other procathepsins. Furthermore, our data can serve as a rational guide for experimental work on procathepsin–GAG systems that are not characterized in vivo and in vitro yet.
1. Introduction
Majority of functions of living organisms are based on enzymatic reactions, in which various chemical compounds are processed by respective enzymes and, therefore, converted into other compounds with energy emission or consumption.1 Among a vast number of enzymes, there are cathepsins, which are predominantly cysteine proteases2 present in the extracellular matrix (ECM) and lysosomes, where they play a crucial role in various biologically relevant processes. These include bone resorption, intracellular proteolysis, regulation of programmed cell death, or degradation of antimicrobial peptides/proteins depending on the type of cathepsin.3−5 Cathepsins share a similar 3D fold regardless of differences in their amino acid sequence.6 Malfunction of different cathepsins’ activity, which might be potentially the result of misfolding,7 may lead to many serious diseases including pycnodysostosis, osteoporosis, rheumatoid arthritis, osteoarthritis, asthma psoriasis, atherosclerosis, cancer, obesity, autoimmune disorders, and viral infection.8,9 Therefore, to properly and effectively treat diseases caused by impaired cathepsin activity, it is important to understand these processes at a molecular level.
Cathepsins, an active form of enzymes, are products of the maturation process of procathepsins, their inactive precursors. In a procathepsin, a propeptide part occupies a cathepsin active site, rendering it inactive. This fragment can be removed in a specific reaction that requires a procathepsin with an active site accessible of either the same or a different type depending on the type of the processed procathepsin.10−14 Cathepsin activity might be mediated by glycosaminoglycans (GAGs).15 GAGs are long linear negatively charged polysaccharides that consist of recurring disaccharide units.16 With an exception of keratan sulfate, every GAG includes in its structure one hexosamine and one hexose or hexuronic acid. GAGs are present in ECM as well as in lysosomes,17 where they are involved in numerous processes like cell proliferation, angiogenesis, anticoagulation, adhesion, and signaling cascades.18 It is suggested that GAGs may play a vital role in the medical treatment of disorders associated with disruptions of the above-mentioned processes19−22 and represent one of the key targets for regenerative medicine.23 Binding GAGs by respective protein targets such as chemokines,24 growth factors,25 and collagen26 leads to the fundamental involvement of these polysaccharides in the aforementioned biological processes. Moreover, GAGs can mediate the activity of enzymes such as cathepsins by intermolecular interactions with them. Potentially, GAGs can inhibit cathepsin enzymatic activity, which might be fulfilled by several mechanisms: (i) a GAG can bind in an active site of the cathepsin, which makes it inaccessible for a substrate, (ii) a GAG can bind on the already formed complex between a protein and a substrate steoretically blocking the substrate, which makes dissociation of a substrate unfeasible, and (iii) a GAG can bind to the cathepsin in a way that causes an allosteric change in the active site.27,28 In addition, GAGs can also mediate the maturation process of procathepsin B, as proposed by Caglič et al.29 The results of this experimental work suggested that amino acid residues were crucial for GAG binding in the procathepsin B–GAG complex. The data obtained in the same study allowed the authors to propose a molecular mechanism in which binding of GAG on the procathepsin B surface leads to a conformational change of the proenzyme that exposes its active site, therefore allowing such an activated procathepsin to process another one. However, the detailed description of the maturation process mediated by GAGs at the atomic level that could explain the obtained experimental data is unavailable.
In the absence of experimentally available atomistic details of this process, computer modeling can be useful to opt for such details.30,31 However, applying the methodology of computational chemistry to study a GAG-containing system represents a substantial challenge. Features that make modeling GAG-containing systems challenging are (i) extensive conformational space of GAGs in terms of their glycosidic linkages and monosaccharide rings,32−35 (ii) GAGs’ highly charged nature,36 (iii) GAGs preference to bind at solvent-exposed and spatially closed but sequentially not necessarily successive positively charged amino acid patches37 made up of long and, therefore, flexible lysine or arginine residues, (iv) the multipose binding observed in several protein–GAG complexes,38,39 (v) highly variable sulfation pattern of GAGs known as “sulfation code”40 defining its structural properties, molecular recognition, and functional activity,41 and (vi) availability of two energetically similar antiparallel orientations of a GAG on the protein surface.42
In our study, we extensively analyzed the impact of GAGs on the procathepsin B maturation process by rigorous computational approaches. The calculation of the electrostatic potential map of (pro)cathepsin B allowed us to predict GAG binding sites on the enzyme and its immature zymogen and compare them. Using the molecular docking approach, we calculated various structures of (pro)cathepsin B–GAG complexes depending on the type and length of GAG addressing the aspect of putative specificity in these interactions. Application of coarse-grained molecular dynamics (CG MD) simulations yielded potentially probable procathepsin B structures, in which the active site was accessible for the substrate. All-atom molecular dynamics (AA MD) simulations allowed us to study the dynamics of various (pro)cathepsin B–GAG complexes and were complemented by free energy analysis to characterize the stability of these complexes in time. From the results obtained in this study, we could propose the role of GAGs in the maturation process of procathepsin. The computational procedures used in this work can be potentially applied to other procathepsin–GAG systems, therefore extending our knowledge about these highly biologically relevant complexes.
2. Materials and Methods
2.1. Structures of (Pro)cathepsin B and GAGs
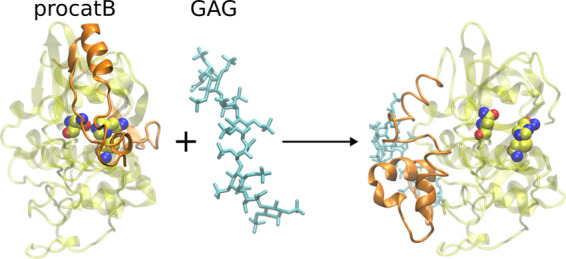
The structure of procathepsin B was obtained from the Protein Data Bank (PDB ID: 3PBH, 2.50 Å).43 Based on this structure, the cathepsin B structure was prepared by removing the propeptide from procathepsin (Figure 1).
Figure 1.
Crystallographic structures (PDB ID: 3PBH, 2.50 Å) of catB (A) and procatB (B).43 The enzyme is shown as white cartoon with the active site residues CYS92, HIS262, and ASN282 (C) and the propeptide shown as green sticks and gray cartoon.
The tetra- (dp4; dp stands for degree of polymerization) and hexasaccharides (dp6) of chondroitin-4-sulfate (C4-S: GalNAc(4S)-GlcA disaccharide unit), chondroitin-6-sulfate (C6-S: GalNAc(6S)-GlcA disaccharide unit), dermatan sulfate (DS: GalNAc(6S)-IdoA disaccharide unit), hyaluronic acid (HA: GlcNAc(6S)-GlcA disaccharide unit), heparin (HP: GlcNS(6S)-IdoA(2S) disaccharide unit), and heparan sulfate (HS: heterogenous structure; here, we modeled this molecule using its unsulfated form GlcNAc-IdoA) as well as octa- (dp8) and dodecasaccharides (dp12) of HP were built using tleap script of AMBER1644 from the building blocks of the sulfated GAG monomeric unit libraries.45 Their charges were taken from the GLYCAM06 force field46 and from the literature for sulfate groups.47
2.2. Electrostatic Potential Calculations
To calculate electrostatic potential isosurfaces for monomers of human cathepsin B and procathepsin B, a Poisson–Boltzmann surface area (PBSA) program from AmberTools44 was used with a grid spacing of 1 Å. The results of PBSA analysis allowed us to predict potential GAG-binding regions on the protein surface. Previously, we successfully applied this approach to predict GAG binding regions for X-ray protein–GAG structures.48 The obtained electrostatic potential maps were visualized with the use of VMD software.49
2.3. Molecular Docking
For docking simulations, Autodock 3 was used50 since it has proven to yield best results among different docking programs used in our previous study.51 A grid box with dimensions of 126 Å × 126 Å × 126 Å and a grid spacing of 0.475 Å containing the whole catB and procatB molecules was applied in GAG docking to catB and procatB, respectively. Independent runs (100) of the Lamarckian genetic algorithm with an initial population size of 300 and a termination condition of 105 generations and 9995 × 105 energy evaluations were carried out. The top 50 docking results were clustered using the DBSCAN algorithm52 with the parameters defined as follows: m, the minimal neighborhood size and ε, the neighborhood search radius. Three representative poses from each of the obtained clusters were selected for further MD calculations.
2.4. Molecular Dynamics
2.4.1. All-Atom Approach
(Pro)catB–GAG complexes were solvated in a TIP3P octahedral periodic box with a layer of water molecules of 6 Å from the border of the periodic box to the solute and neutralized with counterions (Na+). Energy minimization was carried out in two steps: first, 0.5 × 103 steepest descent cycles and 103 conjugate gradient cycles with harmonic force restraints of 100 kcal/(mol·Å2) on solute atoms and then, 3 × 103 steepest descent cycles and 3 × 103 conjugate gradient cycles without restraints. Afterward, the system was heated up to 300 K for 10 ps with harmonic force restraints of 100 kcal/(mol·Å2) on solute atoms and equilibrated for 100 ps at 300 K and 105 Pa in isothermal isobaric ensemble (NPT). Finally, a 50 ns productive MD run was carried out in an NTP ensemble. The SHAKE algorithm, 2 fs time integration step, 8 Å cutoff for nonbonded interactions, and the particle mesh Ewald method were used. The structures were written every 10 ps, which produced 104 in total per simulation used for further analysis. Additionally, the most stable structures of (pro)catB/HS dp4 selected based on free energy analysis results (see Section 2.5) were simulated using the same protocol as the one applied for the unbound (pro)catB structures with the production run of 1 μs. AA MD simulation was also used to obtain a structure of the procathepsin B dimer, in which one of the procathepsin B molecules had an uncovered active site. In this scenario, one procathepsin B is able to cut a propeptide part from another one. This MD simulation was performed with the same parameters as described above with the production run of 500 ns.
2.4.2. Coarse-Grained Approach
Multiplexed replica exchange molecular dynamics (MREMD) simulations in the UNRES force field53 were performed to obtain a procathepsin B structure with enzymatically active conformations, which is not feasible for the all-atom MD approach. In these simulations, restraints were set on cathepsin, which allowed us to predict probable conformations of propeptide keeping native the rest of the protein structure. The aforementioned restraints were used as was described in our previous work.54 In this study, we ran trajectories at 12 replica temperatures, 4 trajectories per temperature (48 trajectories per system total): 260, 262, 266, 271, 276, 282, 288, 296, 304, 315, 333, and 370 K. Such a range and spacing of temperatures covered the region of the folding–unfolding transition and provided an efficient exchange of replicas necessary to obtain convergence.54 Each trajectory consisted of 6 × 107 MD steps with a 4.89 fs step length. Replicas were exchanged and snapshots were saved every 104 MD steps. The temperature was controlled by the Berendsen thermostat55 with the coupling constant τ = 48.9 fs. Once an MREMD run was completed for a given target, the last 200 snapshots from each trajectory (a total of 14 400 conformations) were processed by the weighted histogram analysis method (WHAM),56 which was implemented in UNRES in the work of Liwo et al.57 WHAM enables the calculation of the probabilities of all conformations at a desired temperature and ensemble-averaged and thermodynamic quantities, in particular, the heat capacity. The temperature at which the conformational ensemble was analyzed (Tα) was determined to be 20 K below the major heat-capacity peak; usually it ranged from 260 to 300 K. The conformations were then sorted in the descending order of probabilities and those which constituted together 99% of the ensemble were dissected into five families by means of Ward’s minimum-variance clustering.58 After clustering was accomplished, the fractions of the families in the conformational ensemble at Tα, the selected temperature, were calculated using the procedure developed in the work of Liwo et al.57 The families were then ranked according to decreasing probabilities. A weighted-average conformation was calculated for each cluster (with weights determined by WHAM), and the conformation of the cluster closest to the average conformation was selected to represent the entire cluster.57,59 Each of the coarse-grained cluster representative structure was then converted to an all-atom model using the PULCHRA60 and SCWRL61 knowledge-based algorithms for all-atom backbone and side-chain reconstruction, respectively, and subjected to final refinement at the all-atom level with the AMBER14 force field.60 The refinement protocol used here has been explained in a different paper.54
2.4.3. UNRES Server MD Simulations
To study the impact of HIS173ALA mutation on the procathepsin B structure, molecular dynamics (MD) simulations were performed in UNRES server.62 The use of the coarse-grained approach was an appropriate choice because in this case, the all-atom approach would not be capable of revealing putative changes of the global structure of the protein upon a single residue mutation. The HIS173ALA mutant was prepared by replacing the HIS residue with ALA. For the experimental structure of both procathepsin B and its mutant, MD simulations were repeated 10 times. The simulations were performed under 300 K with a Langevin thermostat.63 Finally, a 40 ns productive MD run was carried out (5 × 104 steps). The structures were written every 200 ps (every 1000th step), which produced 5 × 102 in total per simulation used further for analysis.
2.5. Binding Free Energy Calculations
Energetic postprocessing of the trajectories, per-residue energy decomposition, and pairwise energy decomposition were carried out for all (pro)catB–GAG complexes in a continuous solvent model using molecular mechanics generalized Born surface area (MM–GBSA) and using a model with surface area and Borne radii default parameters as implemented in the igb = 2 model64 of AMBER16.44 For free energy calculation analysis, we used the frames of MD simulation before the first essential change of the GAG orientation in relation to the receptor (this applies to the scenario in which a GAG can potentially change its binding pose or even dissociate), which was reflected in RMSD. For calculation, we took those frames in which the GAG RMSD was lower than 10 Å and was bound to the protein surface. Otherwise, all frames from MD simulations were analyzed. The obtained free energy values accounted for the full enthalpy component of binding and partially for the solvent entropy and are indicated as ΔG throughout the article.
2.6. Allostery Analysis
The following properties of the (pro)catB–GAG complexes were analyzed to describe potential allostery regulation:
Distance distribution between the active site CYS92 and HIS262 residues of (pro)catB; the active site CYS92 and HIS262 residue distances were calculated for SG and ND1 atoms (ff14SB nomenclature65) of aforementioned residues. In this analysis, all MD simulation frames were taken into account.
Root-mean-square fluctuations (RMSFs) of a residue for unbound (pro)catB and in complex with HS; RMSF calculations were performed for all frames of MD simulation and for all atoms within the analyzed molecules. The output “byres” values were computed as average (mass-weighted) fluctuations for every residue of the analyzed protein.
Principal components describing the most important movements of the protein for unbound procatB and the procatB–HS dp4 complex; principal component analysis (PCA) was performed with the cpptraj module of AMBER16.44 Calculations of eigenvector and eigenvalues were performed only for Cα, C, N, and O atoms of the polypeptide chain. In our protocol, only the first 20 modes were used in calculations; these values corresponded to the normalized eigenvalues.
3. Results and Discussion
3.1. Analysis of the Impact of HIS173ALA Mutation on the procatB Structure
In the work of Caglič et al.,29 it was proposed that HIS173ALA mutation of procathepsin B leads to the lack of activity of the mutant due to inappropriate folding or autodegradation. To verify this theory, we performed MD simulations in a UNRES server with procathepsin B HIS173ALA mutant and the wild-type X-ray structure as a reference. These MD simulations were supposed to allow us to study the impact of HIS173ALA mutation on the fluctuations of procathepsin B residues. We observed that the proposed effect of this mutation was statistically insignificant, which was reflected in the similar fluctuations of procathepsin B and its mutant (Supporting Information, Figure S1). The fact that such a mutation might have an impact on the folding process of procathepsin B, therefore leading to a misfolded structure that is not able to process procathepsin B, cannot be, however, accounted for in our MD simulations starting from a natively folded structure.
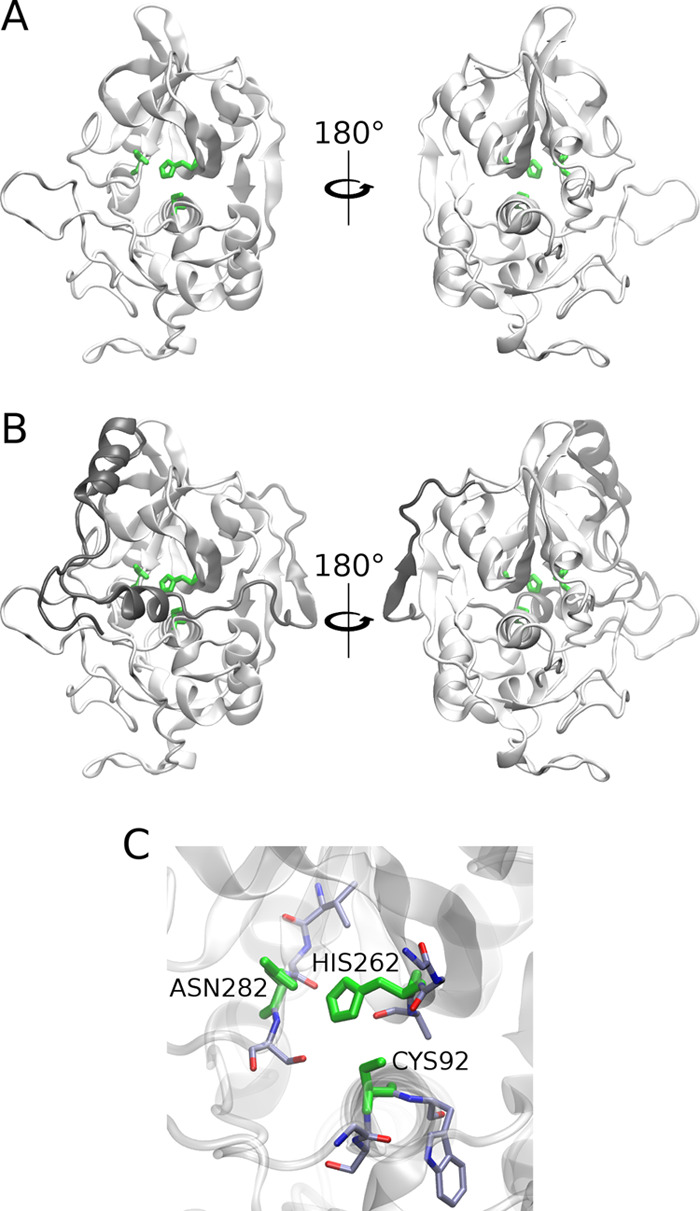
3.2. Predicting GAG-Binding Regions
To predict binding regions for GAG ligands on the (pro)catB surface, we employed the PBSA program from the AmberTools package, which allowed us to obtain electrostatic potential isosurfaces corresponding to the protein (Figure 2). This approach has previously been proven to be successful for the prediction of GAG-binding regions on the protein surface.48 The obtained results revealed that in procatB, the electrostatic potential in the region that is responsible for the inactivity of zymogen is slightly more positive than the one for catB. This could suggest that in the case of procatB, it might be possible that a GAG can bind to the surface of propeptide, while in the case of catB, GAG binding to the active site would be unfavorable due to more negative potential in that region.
Figure 2.
Electrostatic potential isosurfaces for catB (A) and procatB (B) in surface representation (red, −3 kcal/mol; blue, +3 kcal/mol, respectively).
3.3. Predicting procatB–GAG Complex Structures
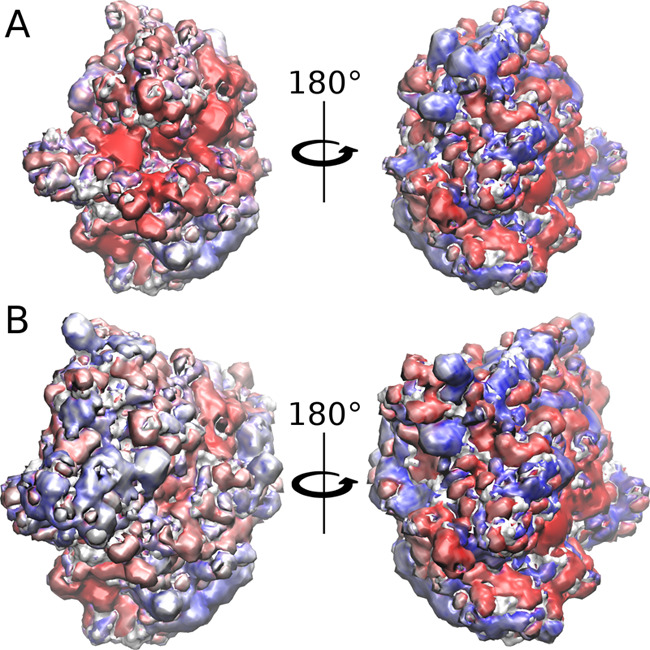
Molecular docking was performed to obtain representative structures of (pro)catB–GAG complexes that could be used for further MD and free energy analysis. In the case of (pro)catB–HS complexes, we could observe that one of the obtained clusters was conserved for catB and procatB (blue sticks in Figure 3A and green sticks in Figure 3B). Moreover, some clusters were conserved upon GAG elongation from dp4 to dp6 (green sticks in Figure 3A and red sticks in Figure 3B). Additionally, in the case of procatB–GAG dp6 complexes, GAGs bound to the propeptide part more often than in the case of procatB–GAG dp4 complexes. This could potentially mean that the longer GAG could stabilize the conformation adopted by the propeptide more efficiently. Last but not least, we could also observe that some clusters of GAG docking solutions were conserved in procatB complexes independent of the GAG type (for example, clusters represented in red sticks in both C4-S dp6 and HP dp6 solutions, Supporting Information, Figure S2).
Figure 3.
Docking poses obtained for catB–HS dp4 (A), catB–HS dp6 (C), procatB–HS dp4 (B), and procatB–HS dp6 (D) complexes. Cathepsin and propeptide are shown as white and gray cartoons, respectively; HS clusters are shown as blue, red, and green sticks. The colors of sticks stand for the size of clusters with blue, red, and green being the first, second, and third most populated clusters, respectively.
3.4. MD-Based Free Energy Analysis of procatB Complexes with Short GAGs
From the docking solutions described in Section 3.3, three random structures from each cluster were picked for MD simulations and furthermore for free energy analysis. Based on the obtained results, we could propose that the complexes of catB–GAG are likely stable as procatB–GAG ones (Figure 4A). Additionally, we could observe that, on average, complexes formed by dp4 GAGs were slightly more stable than those formed by dp6 GAGs. Among all calculated procatB–GAG complexes, the most stable ones were formed by HS dp4 (Figure 4C).
Figure 4.
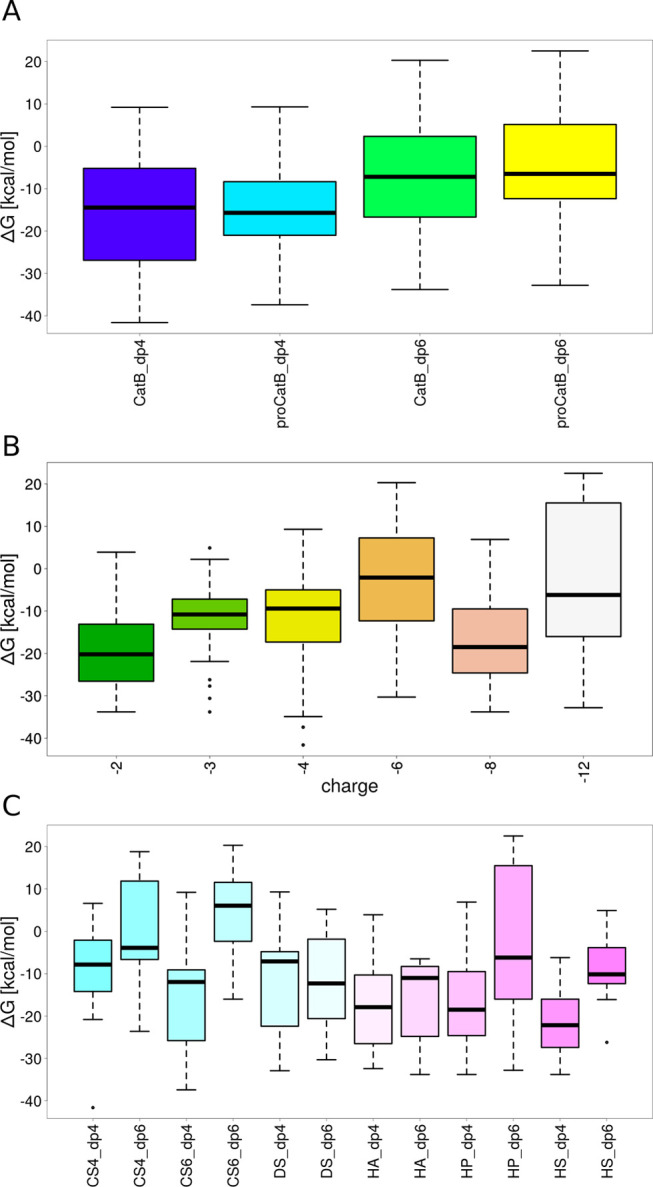
Binding free energy dependence on properties of (pro)catB–GAG complexes: (A) the maturation state and the length of a GAG, (B) the charge of a GAG, and (C) the type and length of a GAG.
The results also showed that with the increase of the GAG charge the complex stability decreased (Figure 4B). This trend we observed is statistically insignificant since the margin of the error is too large. To complement these data obtained for nanosecond-scale MD simulations, we performed 1 μs MD simulation for the (pro)catB–HS complexes since they were the most stable ones. For comparison, we also ran MD simulations for the unbound (pro)catB. From the results obtained from the 1 μs MD simulation of procathepsin B in the presence and absence of HS dp4, we aimed to study the potential impact of GAG binding on the active site geometry. The active site geometry was described in terms of the distance between the SG and ND1 atoms of the active site residues CYS92 and HIS262, respectively (Figure 5). Our results suggested that the active site pocket might adopt two different types of conformations, one of which is pronounced in procathepsin B with the enzymatically active conformation. In both simulations of unbound procathepsin B and in complex with HS dp4, the distance between active site residues slowly increased; however, in the case of the procathepsin B–HS dp4 complex, the changes occurred at a slower rate. When taking into consideration the results of the active site residues’ distance distribution over the time obtained from the MD simulation of the procathepsin B dimer, which corresponded to the scenario in which one procathepsin B is processed by another, we can propose that binding of GAG by the procathepsin B molecule stabilizes the conformation of the active site longer, which renders the enzymatic reaction potentially more feasible. In the next step, we performed RMSF analysis of (pro)catB residues for unbound (pro)catB and in complex with HS dp4 (Supporting Information, Figure S3) to study the impact of GAG on the dynamics of (pro)catB. In comparison to unbound procatB, the cathepsin B residues in the procatB–HS dp4 complex are potentially more flexible (residues 173–176 and 302–303). These results correspond to what we could observe in PCA for the loop consisted of 173–176 residues. PCA, which allows us to distinguish the most important movements appearing in the MD simulation in the molecular systems, was performed for unbound procatB and the procatB–HS dp4 complex. It showed that the presence of GAG changes significantly the distribution of principal components of protein movements. In particular, the highest normalized eigenvalues (which correspond to the most important movements in the system) for the first two components are 66.4 and 9.4% for procatB and 35.4 and 22.0% for procatB–HS (Figure 6). This might suggest that in the case of procatB, only the first principal movement is significant, while in the case of the procatB–HS complex, we should take into consideration the first two principal movements. The dominant component we observed in the case of unbound procatB was mainly involved in the movement of propeptide in a direction away from the active site. Such a conformational change could possibly lead to an increased accessibility of the enzymatic site for another procatB molecule. On the other hand, upon HS binding by procatB, we observed two principal movements, both of which are involved in the propeptide motion toward the active site, therefore maintaining the inactivity of the proenzyme.
Figure 5.
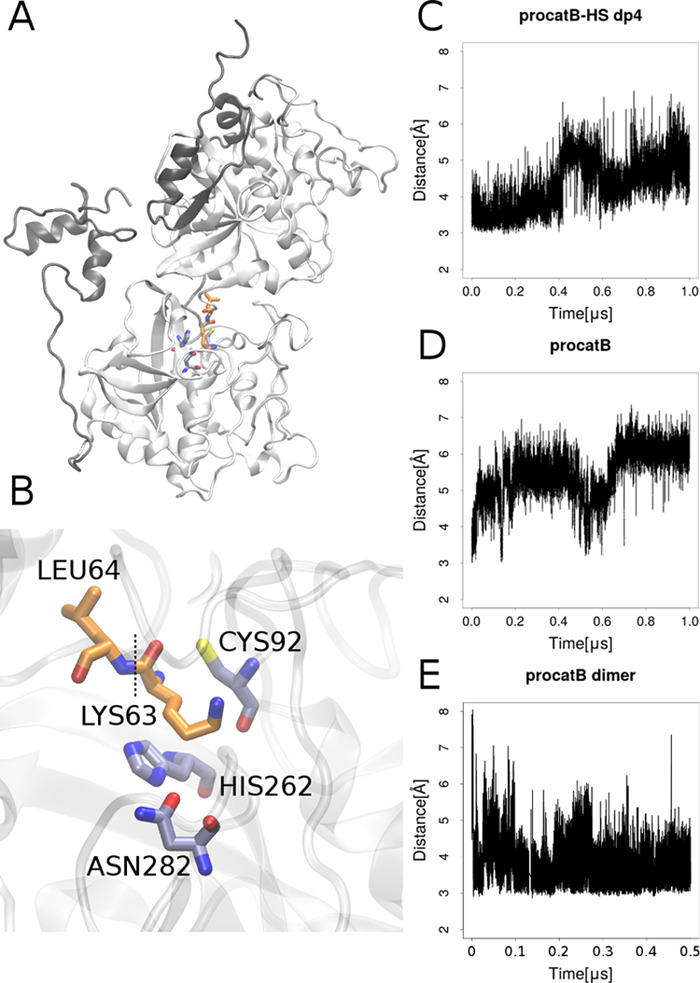
On the left: (A) model of the procathepsin B dimer representing the scenario in which one procathepsin B is processed by another. The propeptides and cathepsins are shown as gray and white cartoons, respectively. (B) Conformation of the active site. The active site residues CYS92 and HIS262 and residues of procathepsin B with native conformation, LYS63 and LEU64, between which the propeptide bond is cut (black dotted line) are in grayish-blue and orange sticks, respectively. On the right: the distance between SG and ND1 atoms of the active site residues CYS92 and HIS262, respectively, over MD simulation in (C) procathepsin B–HS dp4 complex, (D) unbound procathepsin B monomer, and (E) procathepsin B dimer in which one procathepsin molecule had the active site uncovered by the propeptide.
Figure 6.
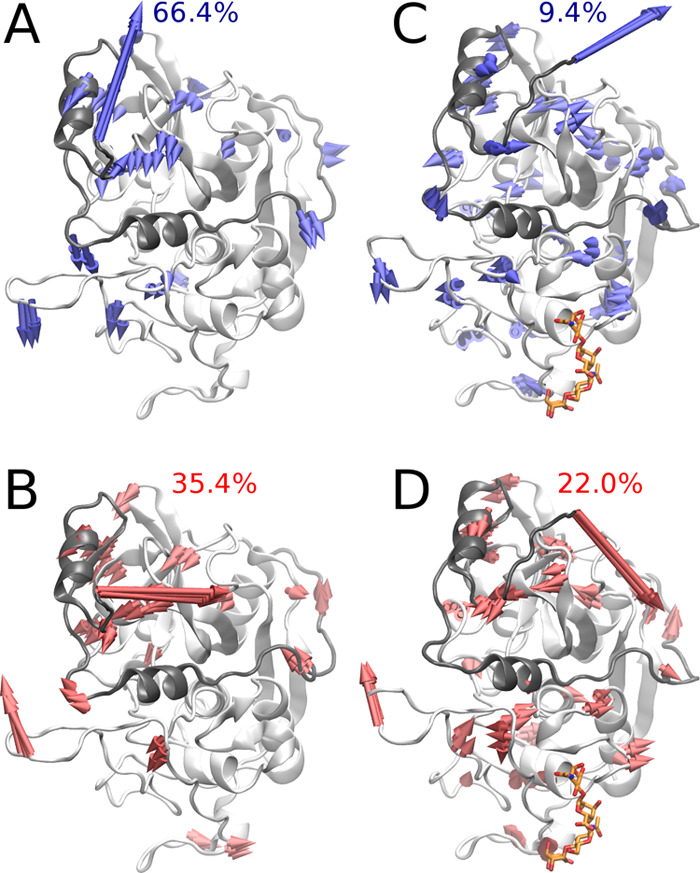
Principal component analysis of unbound procatB and the procatB–HP dp4 complex. The first (A) and the second (B) principal components of unbound procatB are shown by blue and red arrows, respectively. The first (C) and the second (D) principal components of procatB in complex with the HP dp4 complex are shown by blue and red arrows, respectively. The propeptide and the cathepsin are shown as gray and white cartoon, respectively. All arrows (A, B) were drawn if the amplitude of the corresponding movement observed in the MD simulation was greater than or equal to 0.5 Å.
3.5. MD-Based Study on the procatB Model with the Active Site Accessible and Its Complexes with HP and HS
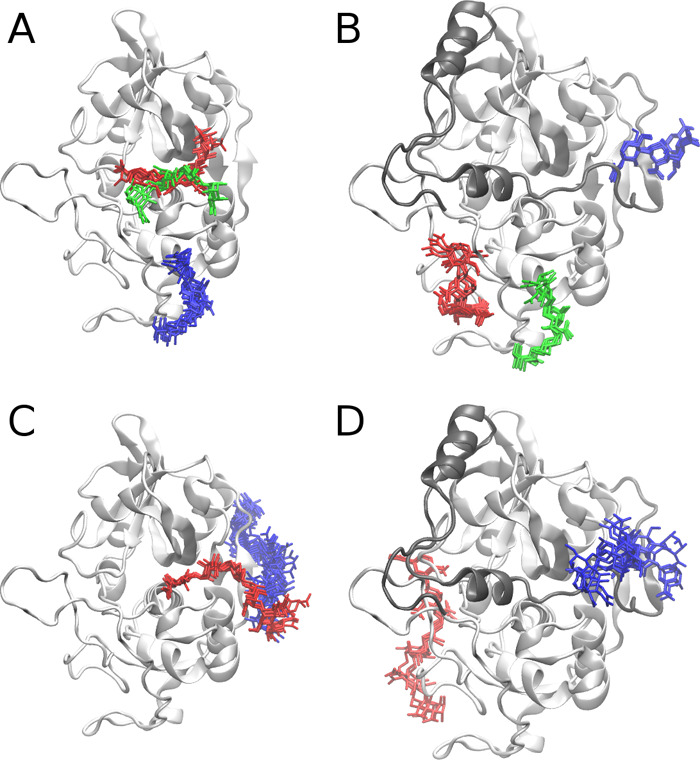
To study how GAG can bind to procathepsin B with the active site accessible, we modeled a structure of such procathepsin B. MREMD simulation with restraints on the cathepsin part of procathepsin B allowed us to obtain five different structures of the zymogen. Two of the five structures matched the model in which the active site was accessible. Therefore, for further analysis, we chose one of these structures with the highest probability (Supporting Information, Table S1). In the next step, we performed molecular docking of HP and HS dp4 to the calculated model as these GAGs are the most and the least charged representatives of the heterogeneous HP/HS chain, respectively. In both cases, one cluster of GAG structures was observed in a position in which it could be bound by the propeptide residues (Figure 7, red sticks in the HP dp4 structure and blue sticks in the HS dp4 structure). Additionally, in the case of the procatB–HS complex, a cluster in the active site was formed (Figure 7, red sticks in the HS dp4 structure) along with one cluster close to the occluding loop (Figure 7, green sticks in the HS dp4 structure). Free energy analysis performed in the next step showed that complexes obtained for HP structures within those clusters were unstable (Table 1). In most of the simulations taken for this analysis, we could also observe dissociation events during the MD simulation. In the case of HP docking solutions, two clusters (Figure 7, green and blue sticks in the HP dp4 structure) were found in the region relatively close to the propeptide and were described by energies that sufficiently favorized complex stability (−49.7 and −29.1 kcal/mol, Table 1). This could mean that a longer GAG could potentially bind in a way in which it would fix the conformation of propeptide making it unable to return to the original one. GAG bound in such a way could also stabilize the geometry of the active site. Such a bound GAG structure “links” docking solutions obtained for red and blue/green clusters in Figure 7. This hypothesis was additionally supported by the analysis of GAG docking solutions in terms of HS dp4/HP dp4 orientations (Table 1). These results revealed that GAGs most likely adopt the same orientation in each cluster and that the corresponding structures from the red and blue clusters (Figure 7) can be linked without the alteration of the GAG direction. This is a very important finding because a GAG orientation (or polarity) is very important for the specificity of GAG interactions with proteins as was observed in the study combining NMR experiments and molecular modeling.66 In the next step, we performed additional molecular docking and MD simulation with HP dp8 and dp12 to procathepsin B with the active site accessible to study a potential dependence of the length of a GAG on complex stability as well as on the location of a GAG binding site. From molecular docking results for the UNRES model of procathepsin B and HP dp8/dp12 ligands, we chose eight solutions in which GAG was bound by residues belonging to both the propeptide and the cathepsin (in particular, the solutions that overlapped blue and red clusters of HP dp4 structures in Figure 7). Free energy of binding analysis showed that in most MD simulations binding free energies were unfavorable, suggesting that these complexes might be unstable (Supporting Information, Table S2).
Figure 7.
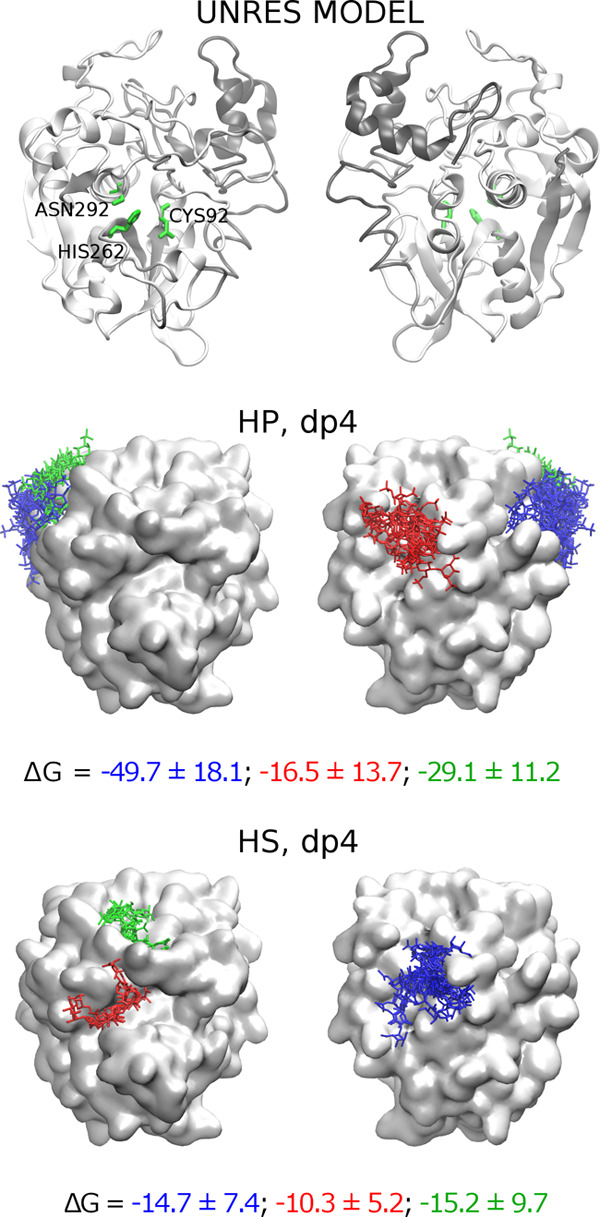
UNRES model of procathepsin B with the active site uncovered along with docking solutions of HP and HS dp4. Propeptide and cathepsin of procathepsin B are shown as gray and white cartoons, respectively, with the active site CYS92, HIS262, and ASN292 residues in green sticks and white surface, while docking solutions are shown as blue, red, and green sticks. The colors of sticks stand for the size of clusters with blue, red, and green being the first, second, and third most populated clusters, respectively.
Table 1. Molecular Docking MD-Based Analysis Summary for Procathepsin B UNRES Model/GAG Systems.
| GAG | m, εa | #b | sizec | ΔG [kcal/mol]d | topMM–GBSA 10 residues for GAG bindinge | polarityf |
|---|---|---|---|---|---|---|
| HP, dp4 | 3, 3.0 | 1 | 20 | –44.7 ± 12.5 | K167, K211, K222, R166, R333, K225, Y227, R182, K208, R22 | 14/6 |
| –49.7 ± 18.1 | ||||||
| –25.6 ± 12.3 | ||||||
| 2 | 9 | –2.8 ± 7.9 | R20, M19, K38, N34, N37, Q94, V33, R73, K99, R39 | 9/1 | ||
| –16.5 ± 13.7 | ||||||
| –2.4 ± 18.4 | ||||||
| 3 | 5 | –16.9 ± 7.1 | K211, K222, K167, K225, R166, K208, R333, R182, Y221, T220 | 5/0 | ||
| –29.1 ± 11.2 | ||||||
| –25.3 ± 10.7 | ||||||
| HS, dp4 | 3, 3.0 | 1 | 14 | –10.5 ± 6.1 | R20, R73, H26, S21, V33, K81, P27, L65, R22, N34 | 9/5 |
| –14.7 ± 7.4 | ||||||
| –7.7 ± 6.5 | ||||||
| 2 | 6 | –10.3 ± 5.2 | N153, G279, G108, G154, G278, S106, G202, W111, W302, H280 | 6/0 | ||
| 0.0 ± 5.0 | ||||||
| –7.8 ± 6.7 | ||||||
| 3 | 5 | –5.2 ± 4.4 | P187, C200, P207, C189, T201, S106, G204, R197, P198, G105 | 5/0 | ||
| –15.2 ± 9.7 | ||||||
| –2.7 ± 4.3 |
DBSCAN parameters: m, the minimal neighborhood size; ε, neighborhood search radius.52
Cluster number.
Cluster size.
Free energy of binding obtained by MM–GBSA.
Residues identified in the top 10 for binding according to MM–GBSA calculations per cluster.
The polarity of a GAG binding pose was defined as its preferred orientation in relation to the reducing and the nonreducing end (the first and second numbers correspond to the population sizes of different GAG orientations).
However, the analysis of the RMSD for HP showed that in most of these cases, the RMSD was lower than 10 Å (Figure 8), which corresponded to the altered binding mode but not to a dissociation. The dissociation of GAG from the procathepsin B surface occurred in four simulations. To further analyze the obtained data, we repeated MD simulations for procatB–HE dp8 and procatB–HE dp12 complexes. Again, free energy analysis results were unfavorable in terms of the complex stability (Supporting Information, Table S3), but the dissociation events were rare (Supporting Information, Figure S4). Such obtained results from free energy analysis could be explained by different systematic errors appearing in the calculations for GAGs of different lengths. In addition, such an error can be increased by the use of an implicit solvent model implemented in the MM–GBSA scheme, which is more pronounced for the bigger and therefore more charged GAGs than for the shorter and less charged ones.
Figure 8.
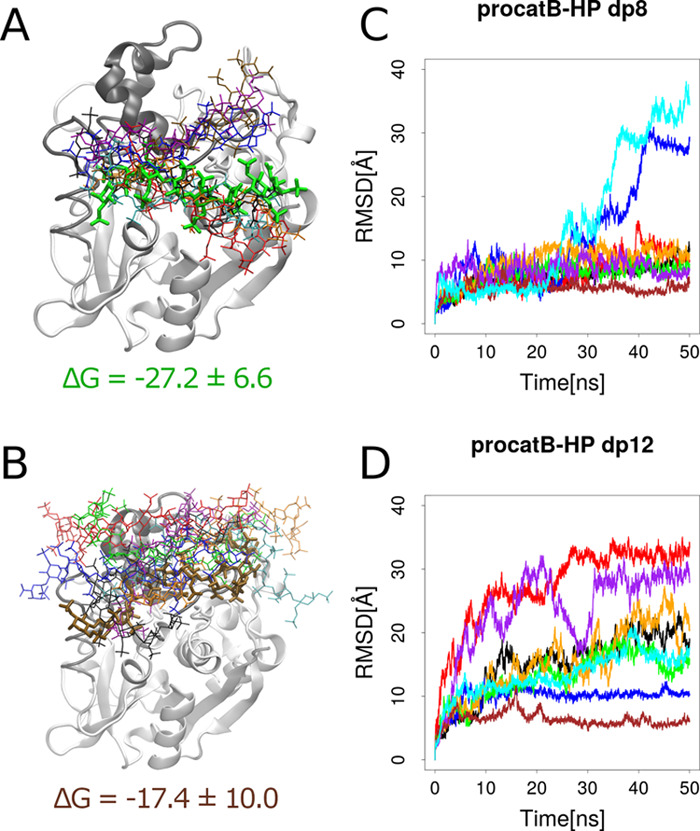
Complex structures of the UNRES model of procatB with the active site accessible with HP dp8 (A) and dp12 (B). The cathepsin and the propeptide are shown as white and gray cartoons, respectively. HP structures are shown as sticks, and the thick ones are the most stable structures. Colors of HP structures correspond to RMSD values shown in graphs (C, D) as well as to MM–GBSA results shown in the Supporting Information, Table S2.
4. Conclusions
In this study, for the first time, the impact of GAGs on the procathepsin B maturation process was analyzed computationally. When GAGs formed complexes with procathepsin B, they preferred to bind to the propeptide, which is in agreement with the experimental data proposed by Caglič et al.29 The docking solutions for different GAGs were potentially very similar, which means that the maturation process might be mediated by different GAGs in a similar way. In the course of MD simulation, these complexes proved to be potentially stable but no statistically significant correlation between complex stability and the maturation state of the cathepsin, charge, or type of GAG was observed. The 1 μs MD simulation performed to complement the results describing the (pro)catB–GAG interactions from nanosecond-scale simulations revealed that GAGs might not only play an important role in the process of the conformational change of the propeptide but also be crucial for preserving an appropriate conformation of the active site, which is required for the enzymatic reaction. The HP and HS dp4 docked to the UNRES model of procathepsin B, in which the active site was accessible, preferred to bind to the cathepsin part of zymogen, while the binding to the propeptide was less stable. From the results of MD simulations performed for HP dp8 and dp12 complexes with the UNRES model of procathepsin B obtained from docking (see Section 3.5), we concluded that GAGs in such complexes were able to preserve the overall conformation of the proposed UNRES model corresponding to the procathepsin B with the active site accessible.
To sum up, we propose that GAGs might bind rather to the procathepsin with the conformation in which the active site is accessible (Figure 9) in contrast to what was proposed by Caglič et al.,29 where formation of the procatB–GAG complex leads to a conformational change of the procatB structure, in turn making the active site accessible. Such binding could not only make procathepsin B unable to revert to its initial inactive conformation but also stabilize the conformation of the active site pocket, thus making the maturation process more feasible.
Figure 9.
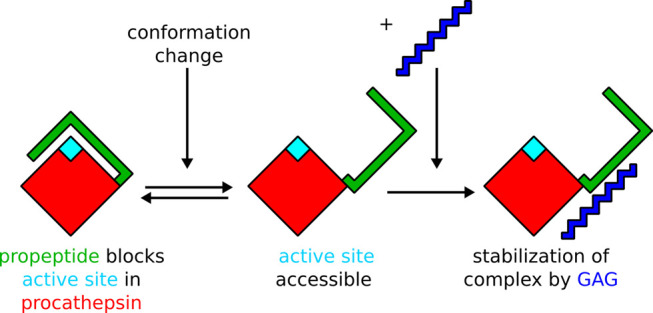
Proposed mechanism of procathepsin B maturation in the presence of a GAG.
Our findings presented in this study might have a significant impact on the understanding of the limitations of the computational methodologies applicable to protein–GAG systems and contribute to the general knowledge of the physicochemical basis underlying the interactions between proteins and GAGs as well as of their specificity. The data obtained in this study provided a detailed and systematic description of the interactions between procathepsin B and GAGs, which in turn allowed us to better understand the procathepsin maturation process. The results obtained in this study might have potential application in novel biomaterials’ development in the area of regenerative medicine.
Acknowledgments
This work was supported by the National Science Center of Poland (Narodowe Centrum Nauki, grant number: UMO-2018/31/N/ST4/01677, UMO-2017/26/M/ST4/00044, and UMO-2018/30/E/ST4/00037). The molecular docking calculations were performed on the ZIH cluster at TU Dresden (grant p_gag). The molecular dynamics simulations were performed on the PROMETHEUS cluster provided by Polish Grid Infrastructure (PL-GRID, grant kchtkat) as well as on the local “piasek” cluster.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c00023.
Free energies and corresponding probabilities of procathepsin B from UNRES MREMD simulations; MM–GBSA free energy analysis results for procatB–HS dp8/dp12 complexes; residue fluctuations of procatB and its HIS173ALA mutant; procatB–GAG dp4/dp6 structures obtained from molecular docking; GAG RMSD in complexes consisting of the UNRES model of procatB with the active site accessible and HP dp8/dp12 and the residue fluctuations of unbound (pro)catB and in HS dp4 complexes from 1 μs MD simulation (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Frey P. A.; Hegeman A. D.. Enzymatic Reaction Mechanisms; Oxford University Press, 2007. [Google Scholar]
- Kuester D.; Lippert H.; Roessner A.; Krueger S. The Cathepsin Family and Their Role in Colorectal Cancer. Pathol., Res. Pract. 2008, 204, 491–500. 10.1016/j.prp.2008.04.010. [DOI] [PubMed] [Google Scholar]
- Ebisui C.; Tsujinaka T.; Morimoto T.; Kan K.; Iijima S.; Yano M.; Kominami E.; Tanaka K.; Monden M. Interleukin-6 Induces Proteolysis by Activating Intracellular Proteases (Cathepsins B and L, Proteasome) in C2C12 Myotubes. Clin. Sci. 1995, 89, 431–439. 10.1042/cs0890431. [DOI] [PubMed] [Google Scholar]
- Teitelbaum S. L. Bone Resorption by Osteoclasts. Science 2000, 289, 1504–1508. 10.1126/science.289.5484.1504. [DOI] [PubMed] [Google Scholar]
- Repnik U.; Stoka V.; Turk V.; Turk B. Lysosomes and Lysosomal Cathepsins in Cell Death. Biochim. Biophys. Acta, Proteins Proteomics 2012, 1824, 22–33. 10.1016/j.bbapap.2011.08.016. [DOI] [PubMed] [Google Scholar]
- Turk D.; Gunčar G.; Podobnik M.; Turk B. Revised Definition of Substrate Binding Sites of Papain-Like Cysteine Proteases. Biol. Chem. 2009, 379, 137–148. 10.1515/bchm.1998.379.2.137. [DOI] [PubMed] [Google Scholar]
- Ketterer S.; Gomez-Auli A.; Hillebrand L. E.; Petrera A.; Ketscher A.; Reinheckel T. Inherited Diseases Caused by Mutations in Cathepsin Protease Genes. FEBS J. 2017, 284, 1437–1454. 10.1111/febs.13980. [DOI] [PubMed] [Google Scholar]
- Gelb B. D.; Shi G.-P.; Chapman H. A.; Desnick R. J. Pycnodysostosis, a Lysosomal Disease Caused by Cathepsin K Deficiency. Science 1996, 273, 1236–1238. 10.1126/science.273.5279.1236. [DOI] [PubMed] [Google Scholar]
- Vasiljeva O.; Reinheckel T.; Peters C.; Turk D.; Turk V.; Turk B. Emerging Roles of Cysteine Cathepsins in Disease and Their Potential as Drug Targets. Curr. Pharm. Des. 2007, 13, 387–403. 10.2174/138161207780162962. [DOI] [PubMed] [Google Scholar]
- Turk B.; Turk D.; Turk V. Lysosomal Cysteine Proteases: More than Scavengers. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 2000, 1477, 98–111. 10.1016/S0167-4838(99)00263-0. [DOI] [PubMed] [Google Scholar]
- Rowan A. D.; Mason P.; Mach L.; Mort J. S. Rat Procathepsin B. Proteolytic Processing to the Mature Form in Vitro. J. Biol. Chem. 1992, 267, 15993–15999. [PubMed] [Google Scholar]
- Brömme D.; Nallaseth F. S.; Turk B. Production and Activation of Recombinant Papain-like Cysteine Proteases. Methods 2004, 32, 199–206. 10.1016/S1046-2023(03)00212-3. [DOI] [PubMed] [Google Scholar]
- Dahl S. W.; Halkier T.; Lauritzen C.; Dolenc I.; Pedersen J.; Turk V.; Turk B. Human Recombinant Pro-Dipeptidyl Peptidase I (Cathepsin C) Can Be Activated by Cathepsins L and S but Not by Autocatalytic Processing. Biochemistry 2001, 40, 1671–1678. 10.1021/bi001693z. [DOI] [PubMed] [Google Scholar]
- Nägler D. K.; Zhang R.; Tam W.; Sulea T.; Purisima E. O.; Ménard R. Human Cathepsin X: A Cysteine Protease with Unique Carboxypeptidase Activity. Biochemistry 1999, 38, 12648–12654. 10.1021/bi991371z. [DOI] [PubMed] [Google Scholar]
- Li Z.; Yasuda Y.; Li W.; Bogyo M.; Katz N.; Gordon R. E.; Fields G. B.; Brömme D. Regulation of Collagenase Activities of Human Cathepsins by Glycosaminoglycans. J. Biol. Chem. 2004, 279, 5470–5479. 10.1074/jbc.M310349200. [DOI] [PubMed] [Google Scholar]
- Esko J. D.; Kimata K.; Lindahl U.. Proteoglycans and Sulfated Glycosaminoglycans. In Essentials of Glycobiology; Varki A.; Cummings R. D.; Esko J. D.; Freeze H. H.; Stanley P.; Bertozzi C. R.; Hart G. W.; Etzler M. E., Eds.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, 2009. [PubMed] [Google Scholar]
- Lamberg S. I.; Stoolmiller A. C. Glycosaminoglycans. A Biochemical and Clinical Review. J. Invest. Dermatol. 1974, 63, 433–449. 10.1111/1523-1747.ep12680346. [DOI] [PubMed] [Google Scholar]
- Bishop J. R.; Schuksz M.; Esko J. D. Heparan Sulphate Proteoglycans Fine-Tune Mammalian Physiology. Nature 2007, 446, 1030–1037. 10.1038/nature05817. [DOI] [PubMed] [Google Scholar]
- Snow A. D.; Willmer J.; Kisilevsky R. A Close Ultrastructural Relationship between Sulfated Proteoglycans and AA Amyloid Fibrils. Lab. Invest. 1987, 57, 687–698. [PubMed] [Google Scholar]
- Murch S. H.; MacDonald T. T.; Walker-Smith J. A.; Levin M.; Lionetti P.; Klein N. J. Disruption of Sulphated Glycosaminoglycans in Intestinal Inflammation. Lancet 1993, 341, 711–714. 10.1016/0140-6736(93)90485-Y. [DOI] [PubMed] [Google Scholar]
- Turk B. Targeting Proteases: Successes, Failures and Future Prospects. Nat. Rev. Drug Discovery 2006, 5, 785–799. 10.1038/nrd2092. [DOI] [PubMed] [Google Scholar]
- Yip G. W.; Smollich M.; Götte M. Therapeutic Value of Glycosaminoglycans in Cancer. Mol. Cancer Ther. 2006, 5, 2139–2148. 10.1158/1535-7163.MCT-06-0082. [DOI] [PubMed] [Google Scholar]
- Scharnweber D.; Hübner L.; Rother S.; Hempel U.; Anderegg U.; Samsonov S. A.; Pisabarro M. T.; Hofbauer L.; Schnabelrauch M.; Franz S.; Simon J.; Hintze V. Glycosaminoglycan Derivatives: Promising Candidates for the Design of Functional Biomaterials. J. Mater. Sci.: Mater. Med. 2015, 26, 232. 10.1007/s10856-015-5563-7. [DOI] [PubMed] [Google Scholar]
- Proudfoot A. E. I. Chemokines and Glycosaminoglycans. Front. Immunol. 2015, 6, 246 10.3389/fimmu.2015.00246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shute J.Glycosaminoglycan and Chemokine/Growth Factor Interactions. In Heparin - A Century of Progress; Handbook of Experimental Pharmacology; Springer: Berlin, Heidelberg, 2012; pp 307–324. [DOI] [PubMed] [Google Scholar]
- Delacoux F.; Fichard A.; Geourjon C.; Garrone R.; Ruggiero F. Molecular Features of the Collagen V Heparin Binding Site. J. Biol. Chem. 1998, 273, 15069–15076. 10.1074/jbc.273.24.15069. [DOI] [PubMed] [Google Scholar]
- Novinec M.; Lenarčič B.; Turk B. Cysteine Cathepsin Activity Regulation by Glycosaminoglycans. BioMed Res. Int. 2014, 2014, 309718 10.1155/2014/309718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sage J.; Mallèvre F.; Barbarin-Costes F.; Samsonov S. A.; Gehrcke J.-P.; Pisabarro M. T.; Perrier E.; Schnebert S.; Roget A.; Livache T.; Nizard C.; Lalmanach G.; Lecaille F. Binding of Chondroitin 4-Sulfate to Cathepsin S Regulates Its Enzymatic Activity. Biochemistry 2013, 52, 6487–6498. 10.1021/bi400925g. [DOI] [PubMed] [Google Scholar]
- Caglič D.; Pungercar J. R.; Pejler G.; Turk V.; Turk B. Glycosaminoglycans Facilitate Procathepsin B Activation through Disruption of Propeptide-Mature Enzyme Interactions. J. Biol. Chem. 2007, 282, 33076–33085. 10.1074/jbc.M705761200. [DOI] [PubMed] [Google Scholar]
- Almond A. Multiscale Modeling of Glycosaminoglycan Structure and Dynamics: Current Methods and Challenges. Curr. Opin. Struct. Biol. 2018, 50, 58–64. 10.1016/j.sbi.2017.11.008. [DOI] [PubMed] [Google Scholar]
- Sankaranarayanan N. V.; Nagarajan B.; Desai U. R. So You Think Computational Approaches to Understanding Glycosaminoglycan–Protein Interactions Are Too Dry and Too Rigid? Think Again!. Curr. Opin. Struct. Biol. 2018, 50, 91–100. 10.1016/j.sbi.2017.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casu B.; Petitou M.; Provasoli M.; Sinaÿ P. Conformational Flexibility: A New Concept for Explaining Binding and Biological Properties of Iduronic Acid-Containing Glycosaminoglycans. Trends Biochem. Sci. 1988, 13, 221–225. 10.1016/0968-0004(88)90088-6. [DOI] [PubMed] [Google Scholar]
- Sattelle B. M.; Shakeri J.; Almond A. Does Microsecond Sugar Ring Flexing Encode 3D-Shape and Bioactivity in the Heparanome?. Biomacromolecules 2013, 14, 1149–1159. 10.1021/bm400067g. [DOI] [PubMed] [Google Scholar]
- Bojarski K. K.; Sieradzan A. K.; Samsonov S. A. Molecular Dynamics Insights into Protein-Glycosaminoglycan Systems from Microsecond-Scale Simulations. Biopolymers 2019, 110, e23252 10.1002/bip.23252. [DOI] [PubMed] [Google Scholar]
- Samsonov S. A.; Pisabarro M. T. Importance of IdoA and IdoA(2S) Ring Conformations in Computational Studies of Glycosaminoglycan–Protein Interactions. Carbohydr. Res. 2013, 381, 133–137. 10.1016/j.carres.2013.09.005. [DOI] [PubMed] [Google Scholar]
- Samsonov S. A.; Teyra J.; Pisabarro M. T. Docking Glycosaminoglycans to Proteins: Analysis of Solvent Inclusion. J. Comput.-Aided Mol. Des. 2011, 25, 477–489. 10.1007/s10822-011-9433-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imberty A.; Lortat-Jacob H.; Pérez S. Structural View of Glycosaminoglycan–Protein Interactions. Carbohydr. Res. 2007, 342, 430–439. 10.1016/j.carres.2006.12.019. [DOI] [PubMed] [Google Scholar]
- Atkovska K.; Samsonov S. A.; Paszkowski-Rogacz M.; Pisabarro M. T. Multipose Binding in Molecular Docking. Int. J. Mol. Sci. 2014, 15, 2622–2645. 10.3390/ijms15022622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph P. R. B.; Mosier P. D.; Desai U. R.; Rajarathnam K. Solution NMR Characterization of Chemokine CXCL8/IL-8 Monomer and Dimer Binding to Glycosaminoglycans: Structural Plasticity Mediates Differential Binding Interactions. Biochem. J. 2015, 472, 121–133. 10.1042/BJ20150059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habuchi H.; Habuchi O.; Kimata K. Sulfation Pattern in Glycosaminoglycan: Does It Have a Code?. Glycoconjugate J. 2004, 21, 47–52. 10.1023/B:GLYC.0000043747.87325.5e. [DOI] [PubMed] [Google Scholar]
- Gama C. I.; Tully S. E.; Sotogaku N.; Clark P. M.; Rawat M.; Vaidehi N.; Goddard W. A.; Nishi A.; Hsieh-Wilson L. C. Sulfation Patterns of Glycosaminoglycans Encode Molecular Recognition and Activity. Nat. Chem. Biol. 2006, 2, 467–473. 10.1038/nchembio810. [DOI] [PubMed] [Google Scholar]
- Forster M.; Mulloy B. Computational Approaches to the Identification of Heparin-Binding Sites on the Surfaces of Proteins. Biochem. Soc. Trans. 2006, 34, 431–434. 10.1042/BST0340431. [DOI] [PubMed] [Google Scholar]
- Podobnik M.; Kuhelj R.; Turk V.; Turk D. Crystal Structure of the Wild-Type Human Procathepsin B at 2.5 Å Resolution Reveals the Native Active Site of a Papain-like Cysteine Protease Zymogen11Edited by R. Huber. J. Mol. Biol. 1997, 271, 774–788. 10.1006/jmbi.1997.1218. [DOI] [PubMed] [Google Scholar]
- Case D. A.; Cerutti D. S.; Cheatham T. E. III; Darden T. A.; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; Greene D.; Homeyer N.; Izadi S.; Kovalenko A.; Lee T. S.; LeGrand S.; Li P.; Lin C.; Liu J.; Luchko T.; Luo R.; Mermelstein D.; Merz K. M.; Monard G.; Nguyen H.; Omelyan I.; Onufriev A.; Pan F.; Qi R.; Roe D. R.; Roitberg A.; Sagui C.; Simmerling C. L.; Botello-Smith W. M.; Swails J.; Walker R. C.; Wang J.; Wolf R. M.; Wu X.; Xiao L.; York D. M.; Kollman P. A.. AMBER 2017; University of California: San Francisco, 2017. [Google Scholar]
- Pichert A.; Samsonov S. A.; Theisgen S.; Thomas L.; Baumann L.; Schiller J.; Beck-Sickinger A. G.; Huster D.; Pisabarro M. T. Characterization of the Interaction of Interleukin-8 with Hyaluronan, Chondroitin Sulfate, Dermatan Sulfate and Their Sulfated Derivatives by Spectroscopy and Molecular Modeling. Glycobiology 2012, 22, 134–145. 10.1093/glycob/cwr120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirschner K. N.; Yongye A. B.; Tschampel S. M.; González-Outeiriño J.; Daniels C. R.; Foley B. L.; Woods R. J. GLYCAM06: A Generalizable Biomolecular Force Field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. 10.1002/jcc.20820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huige C. J. M.; Altona C. Force Field Parameters for Sulfates and Sulfamates Based on Ab Initio Calculations: Extensions of AMBER and CHARMm Fields. J. Comput. Chem. 1995, 16, 56–79. 10.1002/jcc.540160106. [DOI] [Google Scholar]
- Samsonov S. A.; Pisabarro M. T. Computational analysis of interactions in structurally available protein-glycosaminoglycan complexes. Glycobiology 2016, 26, 850–861. 10.1093/glycob/cww055. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD - Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Morris G. M.; Goodsell D. S.; Halliday R. S.; Huey R.; Hart W. E.; Belew R. K.; Olson A. J. Automated Docking Using a Lamarckian Genetic Algorithm and an Empirical Binding Free Energy Function. J. Comput. Chem. 1998, 19, 1639–1662. . [DOI] [Google Scholar]
- Uciechowska-Kaczmarzyk U.; Chauvot de Beauchene I.; Samsonov S. A. Docking Software Performance in Protein-Glycosaminoglycan Systems. J. Mol. Graphics Modell. 2019, 90, 42–50. 10.1016/j.jmgm.2019.04.001. [DOI] [PubMed] [Google Scholar]
- Ester M.; Kriegel H.-P.; Sander J.; Xu X. A Density-Based Algorithm for Discovering Clustersin Large Spatial Databases with Noise. AAAI 1996, 226–231. [Google Scholar]
- Liwo A.; Ołdziej S.; Czaplewski C.; Kleinerman D. S.; Blood P.; Scheraga H. A. Implementation of Molecular Dynamics and Its Extensions with the Coarse-Grained UNRES Force Field on Massively Parallel Systems; towards Millisecond-Scale Simulations of Protein Structure, Dynamics, and Thermodynamics. J. Chem. Theory Comput. 2010, 6, 890–909. 10.1021/ct9004068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karczyńska A.; Mozolewska M. A.; Krupa P.; Giełdoń A.; Bojarski K. K.; Zaborowski B.; Liwo A.; Ślusarz R.; Ślusarz M.; Lee J.; Joo K.; Czaplewski C. Use of the UNRES Force Field in Template-Assisted Prediction of Protein Structures and the Refinement of Server Models: Test with CASP12 Targets. J. Mol. Graphics Modell. 2018, 83, 92–99. 10.1016/j.jmgm.2018.05.008. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. THE Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. 10.1002/jcc.540130812. [DOI] [Google Scholar]
- Liwo A.; Khalili M.; Czaplewski C.; Kalinowski S.; Ołdziej S.; Wachucik K.; Scheraga H. A. Modification and Optimization of the United-Residue (UNRES) Potential Energy Function for Canonical Simulations. I. Temperature Dependence of the Effective Energy Function and Tests of the Optimization Method with Single Training Proteins. J. Phys. Chem. B 2007, 111, 260–285. 10.1021/jp065380a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murtagh F.; Heck A.. Multivariate Data Analysis; Springer Science & Business Media, 2012. [Google Scholar]
- Krupa P.; Mozolewska M. A.; Wiśniewska M.; Yin Y.; He Y.; Sieradzan A. K.; Ganzynkowicz R.; Lipska A. G.; Karczyńska A.; Ślusarz M.; Ślusarz R.; Giełdoń A.; Czaplewski C.; Jagieła D.; Zaborowski B.; Scheraga H. A.; Liwo A. Performance of Protein-Structure Predictions with the Physics-Based UNRES Force Field in CASP11. Bioinformatics 2016, 32, 3270–3278. 10.1093/bioinformatics/btw404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotkiewicz P.; Skolnick J. Fast Procedure for Reconstruction of Full-Atom Protein Models from Reduced Representations. J. Comput. Chem. 2008, 29, 1460–1465. 10.1002/jcc.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q.; Canutescu A. A.; Dunbrack R. L. SCWRL and MolIDE: Computer Programs for Side-Chain Conformation Prediction and Homology Modeling. Nat. Protoc. 2008, 3, 1832–1847. 10.1038/nprot.2008.184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czaplewski C.; Karczynska A.; Sieradzan A. K.; Liwo A. UNRES Server for Physics-Based Coarse-Grained Simulations and Prediction of Protein Structure, Dynamics and Thermodynamics. Nucleic Acids Res. 2018, 46, W304–W309. 10.1093/nar/gky328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanden-Eijnden E.; Ciccotti G. Second-Order Integrators for Langevin Equations with Holonomic Constraints. Chem. Phys. Lett. 2006, 429, 310–316. 10.1016/j.cplett.2006.07.086. [DOI] [Google Scholar]
- Onufriev A.; Case D. A.; Bashford D. Effective Born Radii in the Generalized Born Approximation: The Importance of Being Perfect. J. Comput. Chem. 2002, 23, 1297–1304. 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penk A.; Baumann L.; Huster D.; Samsonov S. A. NMR and Molecular Modeling Reveal Specificity of the Interactions between CXCL14 and Glycosaminoglycans. Glycobiology 2019, 29, 715–725. 10.1093/glycob/cwz047. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


