Cancer: A turbulence problem

Highlights

• •Application of nonlinear dynamics to cancer ecosystems.
• •Chemical turbulence and strange attractor models in tumor growth, invasion and pattern formation are investigated.
• •Computational algorithms for detecting such structures are proposed.
• •Complex systems applications to cancer dynamics.

Abstract

Cancers are complex, adaptive ecosystems. They remain the leading cause of disease-related death among children in North America. As we approach computational oncology and Deep Learning Healthcare, our mathematical models of cancer dynamics must be revised. Recent findings support the perspective that cancer-microenvironment interactions may consist of chaotic gene expressions and turbulent protein flows during pattern formation. As such, cancer pattern formation, protein-folding and metastatic invasion are discussed herein as processes driven by chemical turbulence within the framework of complex systems theory. To conclude, cancer stem cells are presented as strange attractors of the Waddington landscape.

Introduction to complex systems

The Hanahan-Weinberg hallmarks demonstrate cancers are complex adaptive ecosystems [1], [2], [3]. A complex adaptive system is a dynamical system of many interacting agents which adaptively respond to the perturbations of their environment. Their nonlinear interactions result in emergent behaviors such as self-organization, dynamic multilevel structures, multiscale information flow, pattern formation, and unpredictability. The equations of motion pertaining to complex systems behaviors often do not have analytical solutions or remain computationally intractable. In simple terms, complex systems are whole systems in which the collective whole cannot be defined by the sum of its interacting parts [2,3].

One of the fundamental problems in systems science is the causal inference of gene expression patterns, which is at the root of distinguishing cancer dynamics from those of healthy cells. Gene expression is often termed a stochastic process, wherein signaling molecules are best-defined by stochastic differential equations characteristic of their Brownian motion [4], [5], [6]. For simplicity, let us not worry about the details of the Brownian motion itself (i.e., whether it exhibits multifractal behaviors, anomalous diffusion in a crowded space, etc.). Stochasticity of gene expression dynamics has become a central dogma of systems biology supported by repeated experimental confirmation. For instance, single-cell fluorescence studies show the binding/unbinding kinetics of a single transcription factor (TF) or protein complex to a gene promoter is best modeled as a random searching problem governed by diffusion equations (i.e., random walks) and kinetic rate laws [4]. There lies the problem, solving these differential equations often become intractable when the number of chemical species or control parameters surpasses three, reminiscent of Poincaré’s 3-body problem. This necessitates the use of exhaustive searching heuristics and data mining approaches to infer approximate solutions to such equations. The marriage between artificial intelligence (AI) and systems science may provide new alternatives to approaching the problem of gene expression causal inference, in time.

Cancer cells are open, nonequilibrium thermodynamic systems. Finding predictive patterns in their gene expression profiles is alike searching for a needle in a haystack, where one gets easily lost without a magnet. While it may be tempting to assume gene expression dynamics within cancer ecosystems are stochastic (random) processes, herein it is suggested they may be driven by chemical processes pertaining to deterministic chaos as opposed to statistical randomness. In argument, cancer cells are proposed to be strange attractors of the Waddington landscape, where the cancer cell fate can fluctuate back and forth between valleys and hills of the landscape in an “apparent random” motion. That is, by definition, they exhibit sensitive dependence to initial conditions and perturbations and their bounded trajectory in phase space has a (multi-) fractal-dimension. Unlike a random process, a strange attractor exhibits chaotic yet specific patterns that can be mapped in the analysis of its corresponding phase-space or frequency spectrum with attractor reconstruction methods such as time-delay coordinate embedding algorithms and Lyapunov exponents. However, these statistical methods have dimensionality limits and hence, complex systems approaches, such as the use of machine intelligence and computational algorithms are further required for strange attractor reconstruction in larger complex datasets.

Complex systems theory, or simply complexity science, is an emerging paradigm in systems science which branched off from dynamical systems theory. Complexity science attempts to provide a computational description of nature and its emergent phenomena through the lens of information [7]. Emergence is a characteristic signature of many nonequilibrium and nonlinear dynamical systems, the bread and butter of complexity science, which can be very difficult to characterize in terms of the current language in science. Emergent behaviors often do not have mathematical models nor equations to their description, it is alike quantifying the characteristics of turbulent flows observed in the swirls of Van Gogh's The Starry Night versus simply appreciating the raw complexity for its beauty. The latter is a sentiment shared by most complexity scientists in the study of complex emergent behaviors. A subset of complex systems pertains to the study of chaotic systems, i.e., systems exhibiting sensitive dependence to initial conditions and perturbations [8]. While keeping this vague but powerful definition in heart, keep in mind this is oddly a very unorthodox view of cancer systems- to think how changing small pieces of sections of a large-scale system can have unpredictable cascading or catastrophic effects in the time-course of the system's dynamics. Oddly, because most natural systems are indeed chaotic systems- a meteorologist, an ecologist or any whole systems scientist would greatly sympathize with this statement. As will be discussed in this brief communication, cancer pattern formation and cancer network dynamics are suggested here as chaotic systems.

Chaotic systems are often intractable. That is, in practical cases, the differential equations describing them do not have analytical solutions (i.e., nonintegrable); a property of most complex systems [8]. There is one chaotic system revered as the Holy Grail of mathematicians for centuries: the 3-dimensional, Navier-Stokes equations. Fluid turbulence is universal yet finding solutions to its equations of motion remains arguably the greatest unsolved problem in mathematical physics known as the Navier-Stokes smoothness, existence, and regularity problem. Although there are numerical methods in CFD (Computational Fluid Dynamics) to approximate solutions in turbulent flows, finding exact/analytical solutions remains intractable. Turbulence occurs in all scales from the very large to the very small; within the astrophysical, geological, ecological, biochemical, and quantum regimes. It is observed in the heat flow of coffee cups, the motion of galactic clusters, flickering solar flares, gusts of wind, the swirls of Van Gogh's The Starry Night, predator-prey dynamics, systemic blood flows, the dance of exosomes and airflow in the respiratory tract [9], [10], [11].

On the other hand, it remains debated whether only a subset or potentially any cell state of tumor ecosystems correspond to cancer stem cells (CSC; i.e., plastic cell fates with self-renewal and differentiation potency). CSCs account for the emergence of aggressive new phenotypes and therapy resistance in relapsed/refractory cancer patients. Mathematical models demonstrate stem cells are best represented as attractor states with high entropy (i.e., many possible molecular network configurations correspond to the cell fate structure) and hence, higher information flow. A fundamental question arises, whether such high entropy cell states are best defined as stable attractors under stochastic fluctuations, or chaotic attractors? In attempt to reconcile such problems in cancer systems biology, while the scales at which fluid turbulence occur is subjected to debate, herein, chemical turbulence will be discussed as a complex phenomenon responsible for many of the adaptive emergent behaviors in cancer ecosystems, such as their cancer stemness.

It would be a laborious attempt to not only interconnect the 2 problems, of cancer and chemical turbulence, but to further classify them under the fundamental roadblock of computer science: the P vs. NP problem. The P vs. NP problem asks, are problems to which solutions are quickly verifiable, easily solvable? In complexity theory, problems are classified by a complexity class, the time it takes an algorithm to efficiently solve them as a function of size. While P denotes the class of computational problems that are solvable in polynomial-time, NP (Nondeterministic Polynomial-time) problems are quickly checkable but are either intractable or solved by brute-force searching. That is, the exact solution of an NP problem grows exponentially (or factorially) with the size of the number of elements in the system. Reconstructing the gene-interaction networks of cancer ecosystems and reverse- engineering their attractor landscapes are NP-complete problems [12], [13], [14]. Finding the clique or master GRNs (Gene Regulatory Networks) controlling CSC fate transitions is a complex decision problem [15,16]. Attractors of Boolean gene networks then may represent key cellular phenotypes wherein even finding fixed-point attractors is an NP-hard problem [12]. Such complex optimization/decision problems are currently studied using methods from machine intelligence and a branch of computational complexity known as Algorithmic Information Dynamics (AID) [17]. While machine intelligence is useful for abstract pattern recognition from complex datasets, the notions of sense-making and meaning-making in machines remain relatively primitive hindering the investigation of chaotic dynamics in cancer systems. Perhaps the emerging field of Quantum Computing may shed further light on this matter.

If finding fixed-point attractors in the cancer network state-space is an NP-complete problem, then how complex might it be to find strange attractors? This will be precisely the motivation to this short perspective, to stimulate a shift in thinking in cancer research towards that of nonlinear dynamics, chemical turbulence, emergence, fractals, and chaos. These patterns of behaviors are prevalent in nature and denote the general characteristics of complex systems. In fact, the term strange attractor was first coined by Ruelle and Takens in the description of multi-fractal structures that emerged in the study of fluid turbulence [18]. In mathematical terms, the complex structures formed by fluid turbulence and cancer are suggested to share a common language: strange attractors.

Postulate

CSCs are strange attractors on the Waddington energy landscape governed by turbulence dynamics at the onset of pattern formation (i.e., stem cell division/differentiation).

An overview of gene expression

Throughout this review-perspective, the role of chaotic gene expression and chemical turbulence at the onset of CSC differentiation/division will be explored. Keep in mind these concepts are not widely-used in the current language of cancer biology, hence many of the findings surveyed here may only be indirectly related to the cancer problem and are discussed here to stimulate new research avenues in this direction. It remains debated whether CSCs conform a subset of the tumor hierarchy or whether all cancer cells are potentially stem cells (i.e., have the potency of phenotypic plasticity). In attempt to resolve such fundamental problems in the description of tumor complexity, precision oncology is transitioning towards the use of AI and Deep Learning neural networks in guiding clinical decision-making and cancer research [19]. CSCs form complex dynamic networks at many levels of interaction (i.e., GRNs, protein-protein interaction networks, metabolic networks, etc.) as do many complex systems. Our current statistical methods in modeling cancer networks mainly comprise of graph theoretic frameworks, information theory, and machine learning/data science algorithms [20], [21], [22]. These methods of network biology in current practice revolve around the central dogma of systems biology: gene expression stochasticity.

Classically, due to the unpredictable nature of molecules, the transitions between the attractors (i.e., low energy states of the state space) of a GRN are defined by random walks on the network [23]. The fluctuations around the epigenetic barriers of the attractor landscapes are then governed by diffusion and kinetic transport equations [24], [25], [26]. Current models adopt a probabilistic approach to cell state bifurcations on the Waddington landscape. The cell fate trajectories of CSCs (attractors) at a critical transition point are characterized by a bifurcation parameter μ. The dynamics of the system in attractor space in one dimension and in a general setting is given as ẋ(t) = F(x(t), μ) [26], wherein x is the gene expression state vector and F is the driving force (assumed to be the Langevin-equation). The observables of a system approaching a bifurcation can often be quantified as an increase in the amplitude and temporal autocorrelation of the stochastic fluctuations. The dynamics of the cell state is then mapped as a Fokker-Planck equation (i.e., time evolution of a Brownian particle's probability density function) with a fluctuation-dissipation term to account for the nonequilibrium statistical mechanics.

To illustrate the concept of an attractor in systems biology, consider a single motif with two TFs 1 and 2, where $x_1$and $x_2$corresponds to their expression levels. Let us assume these 2 TFs activate their own expression and mutually repress each others’ in an all-or-none fate decision-making, while ignoring other complexities such as multinested feedback loops with other genes, gene bursting, environmental cues, and information cascades. The following stochastic differential equations describe the motif's gene expression dynamics:

$$d{x}_1=\frac{{x_1}^2}{K_1+{x_1}^2+k_1{x}_2^2}-b_1{x}_1+{\sigma }_{1}dW$$

$$d{x}_2=\frac{k_2{x_2}^2}{K_2+k_3{x_1}^2+x_2^2}-b_2{x}_2+{\sigma }_{2}dW$$

Here, it is assumed for simplicity each TF cooperatively binds to its own promoter and to that of the other as a homodimer. The small k parameters correspond to the normalized rate constants at which the TFs bind to the promoters, the capitalized K parameters denote the normalized dissociation rate constants, b parameters denote the decay rate constants and the $\sigma$denotes the amplitude of noise in the system [92]. W denotes the Wiener process. The state space dynamics of these stochastic differential equations form a probability density ${\rho }_t\left(x_1,x_2\right)$which is defined as the attractor landscape. If the noise level $\sigma =0$, and time t is fixed, even this simple binary-TF system forms a stochastic multistable switch with many steady-state attractors in its phase-space (i.e., fixed point attractors and stable equilibria, visualized as energy minima on the landscape) [92]. However, with noise, unsteady attractors and aberrant structures emerge. Here lies the problem, (1) imagine the combinatorial complexity as the attractor space increases to hundreds and thousands of gene interactions, and (2) we are unable to distinguish stochastic noise from “chaotic fluctuations”in gene expression networks. Identifying the minimal set of TFs/motifs corresponding to cancer stemness remains an intractable problem in computational systems oncology.

The logical structure of gene networks and the above-defined attractor states corresponding to their gene expression dynamics are extensively modeled as Random Boolean Networks. For example, in the Kauffman NK model time is discrete and each network element computes a Boolean function based on the values of inputs to that element [27]. The on/off gene promoters can be represented as binary occupancies of 0 or 1. The length of attractors depends on the critical connectivity parameter K_c denoting phase-transitions in the network defined as:

$$K_C=\frac{1}{2p_c\left(1-p_c\right)}$$

where $p_c$denotes the critical probability [28]. A Boolean network can exhibit chaotic behavior when the critical value of the average number of connections of nodes $K=K_c$is reached. In the unstable regime, the Hamming distance between 2 initially close attractor states on average grows exponentially in time denoting chaotic phase-transition. Typically, values of $K>2$can result in chaotic network dynamics. Attractors, a concept derived from dynamical systems theory, formed by these networks may characterize the distinct cell types of the system. Attractors can be of many forms such as fixed-point attractors (stable equilibria), oscillatory and chaotic (strange attractors). While chaotic attractors are inherent to the mathematical fabric of these networks and emerge in computational simulations of gene expression dynamics, they lack evidence in experimental settings.

Given a first-order reaction rate k, let P_n be the probability that n proteins exist at time t. Then, the probability distribution of a single protein's production/degradation kinetics is given by the chemical master equation [29]:

$$\frac{\partial P_n}{\partial t}=k\left[P_{n-1}-P_n\right]-d\left[n{P}_n-\left(n+1\right)P_{n+1}\right].$$

For the cell fate decision of a simple gene-pair Boolean circuit, the minimal system of ordinary differential equations (ODE) is casted into the vector form: $\frac{dx}{dt}=F\left(x\right)=\left[F_1\left(x_1,x_2\right),F_2\left(x_1,x_2\right)\right],$where $x_1,x_2$represent the cellular expression or activation levels of the 2 lineage-determining TFs $x_1,x_2$. $F_1$and $F_2$are the driving forces of the system in a general 1D setting [30,31]. The above-defined stochastic differential equations are a good model system yet let us consider a slightly different model to illustrate how a different set of coupled differential equations can mimic new behaviors in the context of the same (simple) GRN motif. Here, $\frac{d{x}_1}{dt}=\frac{a_1{x}_1^n}{S^n+x_1^n}+\frac{b_1{S}^n}{S^n+x_2^n}-k_1{x}_1=F_1\left(x_1,x_2\right)$, and $\frac{d{x}_2}{dt}=\frac{a_2{x}_2^n}{S^n+x_2^n}+\frac{b_2{S}^n}{S^n+x_1^n}-k_2{x}_2=F_2\left(x_1,x_2\right)$, where in both expressions the first term denotes the self-activation (often assumed to be a sigmoidal transfer function of strength a_i, i = 1, 2, respectively), and the second term denotes the mutual inhibition given a basal expression of strength b_i, i = 1, 2, respectively; the last term in each of the two expressions is the first-order inactivation (degradation rates k_i, i = 1, 2, respectively). The aand bterms are the association/dissociation kinetic constants characterizing the binding/unbinding kinetics. The parameter S denotes the half-maximum of the Hill function (i.e., the activation function), while n denotes the Hill coefficient. Gene bursting and sudden abrupt changes in gene expression are ignored for simplicity of the model [30,31].

In general, these analytic methods of gene expression networks using differential equations become intractable once the number of chemical species in the system reaches more than 3 [29]. Again, it must be stressed differential equations are often without analytical solutions. Hence, rather than solving the master equation for the chemical kinetics, brute-force searching algorithms such as the Gillespie algorithm, Monte Carlo method or the piecewise deterministic Markov processes are often used to simulate the dynamics [29], [30], [31]. It is often assumed the mRNA transcription and its protein product synthesis-degradation dynamics settle to steady-state probability distributions (i.e., fixed-point attractors or stable equilibria). However, if GRNs exhibit chaotic gene expression dynamics, they are best defined as strange attractors - unsteady states exhibiting nonequilibrium fluctuations and chaotic behaviors. Although computational/mathematical models can exhibit strange attractors, their experimental verification in gene expression datasets remains limited primarily due to the lack of time-series datasets in systems biology, and adherence to the central dogma of systems biology (i.e., probabilistic interpretation of gene expression).

Symmetry-breaking

In this section, we will visualize how chemical turbulence could in principle emerge in cellular pattern formation systems. This section will cover some equations pertaining to pattern formation made available to all systems thinkers. Chemical systems form patterns as the various oscillatory modes of pertinent chemical species (e.g., protein complexes, receptors, protein fluids, etc.) combine in or out of phase. Only a subset of these oscillatory modes is periodic. Aperiodic chemical oscillations are then the root cause of chemical turbulence. Here, chemical turbulence will be used as a term to denote the spatiotemporal chaos observed in the reaction-diffusion systems of proteins during the onset of stem cell pattern formation (i.e., differentiation and division). Ruelle described nonperiodic cases of chemical oscillations in a reaction-diffusion system which may exhibit chaotic dynamics at critical phase-transitions [32]. Such nonperiodic oscillations may arguably be the problem underlying cancer pattern formation (e.g., onset of cell division, stem cell differentiation, etc.). That is the patterns of protein flows behave alike a fluid bath undergoing turbulent fluctuations at certain critical times or threshold of protein activities.

Turing in 1952 was the first to define morphogenesis using a set of nonlinear partial-differential equations characterizing the activator-inhibitor dynamics of morphogen gradients [33]. Tumorigenesis is merely a subset of morphogenesis (suggested here as that which exhibits chaotic pattern formation). The general reaction-diffusion equation for tissue patterning is given by:

$$\frac{\partial c}{\partial t}=F\left(c,x,y,z,t\right)+D\Delta c,$$

where D is the diagonal matrix of diffusion coefficients, $\left(x,y,z\right)$are the 3-dimensional Cartesian coordinates of space, tis time, F determines the local reactions of chemical species and c is the concentration density. The Turing pattern formation for 2 chemical species (u and v) is given by:

$$\frac{\partial u}{\partial t}=F\left(u,v\right)-du+D_u\Delta u$$

$$\frac{\partial v}{\partial t}=G\left(u,v\right)-dv+D_v\Delta v$$

The equations state that the rate of change of u and v is the result of Production - (degradation + diffusion) terms (i.e., F and G describe the production, d determines degradation, and D denotes the diffusion coefficients). These general equations are at the heart of pattern formation and are suggested as modeling tools for any systems scientists further willing to explore the complexity of cancer patterning.

Each tumor is analogous to an ecosystem. The fundamentals of ecology illustrate every ecosystem comprises of two essential role-players: predators and preys. The Lotka-Volterra equations, simple models to describe oscillatory behaviors in predator-prey interactions, are also well-known to produce chaotic behavior reminiscent of fluid turbulence [34,35]. The Lotka-Volterra dynamics are simple first order differential equations describing population density changes in time according to their growth rates given by:

$$\frac{dx}{dt}=ax-\beta xy$$

$$\frac{dy}{dt}=\delta xy-\gamma y$$

(x and y are coordinates of two species, t = time and the remainders are growth/decay parameters). Smale in 1976 showed that when the Lotka-Volterra model is applied to model the concentrations of N $\ge 5$chemical species at certain conditions, asymptotic behaviours occur resembling those seen in experimental fluid dynamics[36]. The Hopf-Turing bifurcations of such many-body chemical systems can form strange attractors. For cancer, being a complex, heterogeneous niche of dynamical phenotypes, the applicability of strange attractors must be self-evident – but science is a story built on repeated measurements and not intuition alone. Such is the motivation to this brief communication, to stimulate interest in investigating cancer pattern formation systems as dynamical systems.

Current mathematical models assume the chemical oscillations of morphogens behave as quasi-periodic oscillators. However, genetic oscillators and protein oscillations can exhibit nonlinearity/aperiodicity as just discussed and nonequilibrium behaviors when sudden outbursts of gene expression are encountered (i.e., intermittency). Such aperiodic flows of proteins and nonlinear oscillations in the gene expression networks regulating such morphogens/proteins are postulated to exhibit strange attractor dynamics in cancer ecosystems. In support of this argument, using the finite-elements method, Halatek and Frey recently showed that the mass-conserved reaction-diffusion system of an E. coli pattern formation complex––the Min system––must undergo an initial phase of turbulent flows characterized by a Kolmogorov-Richardson-like energy cascade [37], [38], [39]. Such dynamics govern in a highly coordinated process the biosystem's intracellular protein-mediated pattern formation, which plays a critical role in many cancer-related processes such as cell division and morphogenesis. If simple healthy cellular systems can exhibit chemical turbulence, then it is reasonable to assume chemical turbulence is observed at the onset of CSC pattern formation.

Simulations of the Min system showed that at the critical transition time (bifurcation), the propagating wavefront triggers an energy cascade of destabilized local equilibria entering a turbulent state whereby all state dynamics of the kymogram are spatially uncorrelated [39]. The Min protein complexes are key regulators of cell polarity and asymmetric stem cell division. The mammalian orthologue of these proteins is known as PAR complexes. The PAR 3/6-aPKC complexes are determinants of stem-cell fate choice. They interplay the self-renewal and cleavage of CSCs through feedback loops between the mitotic spindle network and cytoskeletal-ECM (Extracellular Matrix) remodeling pathways [40,41]. We must further investigate what other pathways pertaining to the CSC niche exhibit turbulent chemical oscillations at the onset of their pattern formation to potentially find reprogramming routes to their “chaotic” behaviors.

As mentioned, there are very little empirical findings in support of chaotic gene expression dynamics, since biosystems are very noisy systems. Distinguishing noise from chaos is currently an intractable problem. The following are few simple examples to demonstrate the few reported presence of chaotic gene expression dynamics in GRN. A recent modeling confirmed chaotic gene expression dynamics in the TF NF-κB, a well-described transcriptional regulator in cancer networks, can affect downstream protein production [42]. The TF NF-κB was modeled as a nonlinear oscillator, which when periodically driven by sufficiently large TNF (tumor necrosis factor) amplitudes, was shown to exhibit deterministic chaos. That is, small initial changes in a cell (e.g., mutation of a cancer driving gene) can lead to huge downstream cascading effects (i.e., the butterfly effect). In another study, the RNA-Seq data of the PI3K-mTOR axis was used as a toy-model to exhibit chaotic gene expression dynamics in breast cancer cells [43]. Chaotic motifs (subgraphs within a complex network) have been detected in few-node autonomous GRNs modeled by strongly coupled ODEs [44]. The study concluded that chaos can only appear in gene expression dynamics through competitions among different oscillatory modes and feedback loops of a GRN [44]. Although numerical/computational models of GRNs can exhibit chaotic behavior, the lack of time-series datasets remains a fundamental roadblock in experimentally detecting chaotic gene expression dynamics.

Fractals and chaos

Cancer is a chaotic patterning system with emergent, multi-fractal structures [45]. Fractal image analysis techniques show tumor vasculature is primarily determined by heterogeneity of the ECM (niche) rather than by gradients of diffusible angiogenic growth factors [46]. In hypoxic conditions, tumor vasculature responds by growing into an extended fractal network through a heterogeneous ECM (i.e., invasion percolation) [47,48]. The fractal dimension and multifractal analysis measures (e.g., Hurst indices, Hölder exponents, etc.) can detect subtle changes in images and could potentially provide clinically useful information relating to tumor type, stage, and response to therapy [49]. Numerical results show anomalous fluctuations in the fractal dimension at interfaces of tumor-host networks [49]. The increased fractal characteristics of chromatin structure have been proposed as a diagnostic indicator of tumor self-organization [50]. As mentioned, multifractality is also a characteristic signature of fluid turbulence [51].

Electric cell impedance recordings were performed in rat's prostate cancers. The time-series Fourier analysis of cancer micro-motions was assessed by Takens’ theorem (time-delay embedding) to detect patterns distinguishable from a random signal. The attractor reconstruction showed positive Lyapunov exponents in phase portraits (i.e., a signature of chaos) [52]. Posadas et al demonstrated the Verhulst logistic map is a simple chaotic oscillator that encapsulates the period-doubling bifurcations observed in the cancer cells [52]. Strange attractor solutions resembling the Lorenz attractor emerged in the reaction-diffusion-invasion model of melanoma with oxygen nutrient dependence.

A chaotic tumor growth model was shown by Itik and Banks adapted from an earlier model proposed by de Pillis and Radunskaya, describing the competitive interactions among three cell populations: host cells, effector immune cells, and tumor cells [53]. It only differed from the earlier model by a nonconstant influx of effector immune cells. Chaotic attractors emerged in the reaction-diffusion modeling of tumor growth depending on changes in the control bifurcation parameters, which vary amidst different phenotypes of a heterogeneous ecosystem (e.g., oxygen concentration, glucose level, tumor volume, diffusion from surface and growth parameters) [54]. Lyapunov exponents and fractal dimension were calculated for the tumor patterning. While the Lorenz attractor has a fractal dimension of $\approx$2.06 (assessed by the Box-counting algorithm), the cancer models showed a fractal dimension of $\approx$2.03 indicating a chaotic attractor with Shilnikov-like bifurcations [53,54]. Similar studies by Lettelier et al demonstrated the solutions to the competitive cancer growth model are topologically equivalent to the spiral Rössler attractor, a strange attractor [55].

Tumor growth rates are assumed to fit logistic equations or Gompertz functions, as deemed appropriate with experimental fitting. With a set of parameters defining the growth and death rates of each cell type chaotic attractors emerged along with fixed points (stable equilibria) in the bifurcation analysis [55]. The tumor-immune competitive networks described by a coupled set of three ODEs showed period-doubling bifurcations on the route to chaos with time-delay analysis, wherein oscillatory, strange attractor solutions emerged as indicators of tumor relapse. The results were recently reconfirmed for a time-delayed cancer model with time-delay as the bifurcation parameter. It exhibited periodic oscillations as well as chaotic behavior (strange attractors), which are indicators of long-term tumor relapse [56]. These findings collectively indicate cancer cells are unstable attractors of their network state-space forming chaotic structural patterns [57].

Chemical turbulence in pattern formation

As discussed, recent data suggests the role of chemical turbulence in the emergence of ordered structures during cellular pattern formation and protein folding. While the following discussion will not strictly speak of pattern formation in cancer cells, the implications are strongly connected. While conventionally cells are assumed to be highly viscous structures with laminar protein flows, phase-transition to chemical turbulences can occur in reaction-diffusion systems. Chemical turbulence at the onset of protein-mediated cellular pattern formation was recently confirmed experimentally [58]. Following turbulence transition, coherent patterns emerged through diffusively coupled local equilibria. The chemical turbulences were shown to occur in very rapid bursts followed by laminar-like flows (i.e., intermittency).

Cell division is orchestrated by intracellular protein patterning, mainly from EMT (epithelial-mesenchymal transition) pathways, cytoskeletal filaments and cell polarity complexes. Abnormal cell division is the primary signature of cancer. By convention, the dynamics corresponding to low concentrations of intracellular proteins are modeled as stochastic fluctuations. Classical theory states these chemical systems are close to equilibrium and inertial effects are negligible, given a highly crowded, viscous cytoplasm. However, the recent theory by Halatek and Frey challenged the dogma [39]. Using the finite elements method (FEM), a computational algorithm used to approximate complex fluid flows, simulations predicted chemical turbulence at the onset of the pattern-forming instabilities within cells. Chemical turbulence was qualitatively used to characterize the spatio-temporal chaos observed at the onset of pattern formation. Cytosolic diffusion constants $D_c$were in the order of 60 µm²s⁻¹, where the MinD-ATP/ADP in bulk were given by the Turing reaction-diffusion equations:

$${\partial }_t{u}_D\left(z,t\right)=D_c{\nabla }_z^2{u}_D-F_{u_D},$$

$${\partial }_t{u}_T\left(z,t\right)=D_c{\nabla }_z^2{u}_T+F_{u_D},$$

with $F_{u_D}$denoting the local-reaction term, and $u_D$and $u_T$defining the cytosolic densities of MinD- ATP/ADP conformations; the MinD-ATP was assumed to bind to the membrane via nonlinear coupling rate constants. The resultant kymograms demonstrated turbulent flow patterns at lowMinE/MinD ratios. As mentioned, low levels of gene expressions or protein fluctuations are filtered out in the single cell datasets in the pre-processing step for cell lineage tracking algorithms. Herein, low levels of the cell polarity complex MinE/MinD ratios were shown to produce the chemical turbulences. The theoretical predictions of Halatek and Frey have been confirmed experimentally [39,58].

The PAR cell polarity complex is the mammalian equivalence of the Min proteins complex which coordinate cancer cell division. According to these findings, chemical turbulence in pattern formation is used as a synonym for spatio-temporal chaos, i.e., a broad distribution in the power spectrum and a low spatial correlation length reminiscent of the Kolmogorov spectrum. The term was adapted from the work by Nobel laureate Gerhard Ertl on reactions of heterogeneous catalysis [59]. According to this work, during chemical turbulence, both the amplitude and the phase of local concentration oscillations are strongly fluctuating, creating spiral waves as seen in the findings of Denk et al concerning Min proteins pattern formation [58]. Turbulent chemical oscillations can give rise to both patchy multifractal structures and ordered patterns in cellular reaction-diffusion systems as seen in the multifractal self-organization of cancer cells [60,61].

Allow me to briefly mention a few other emerging data suggestive of the importance of turbulence in cancer stemness. In a recent study, Ito et al experimentally demonstrated turbulent flows in the environment can increase the level of iPSC production in hematopoietic stem cells [62]. Turbulent flow generating turbines and microPIV (particle imaging velocimetry) techniques were used to increase the production of platelet-forming stem cells [62]. Low levels of turbulence generated in turbines increased the levels of platelets produced by the iPSC-derived megakaryocytes significantly. Turbulence stimulated macrophage migration inhibitory factor (MIF), insulin growth factor binding protein 2 (IGFBP2) and nardilysin, accounting for the increased platelet generation [62]. In speculation, such mechanisms may be utilized by CSCs to undergo rapid clonal expansion and mass-production during metastatic flow. Such findings suggest CSCs of different tissues and molecular groups must be placed in turbulent flows as within this experiment, to observe what gene expression pathways are activated under systemic turbulence (Figure 1).

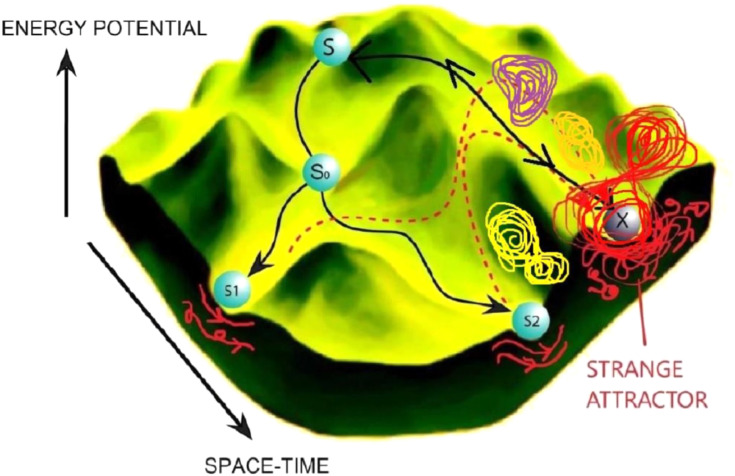
Figure 1.

Waddington landscape. The Waddington landscape shows a stem cell S bifurcating to various cell fates represented by the blue balls. As seen in red, the flows of gene expression underlying the differentiated cell states S1 and S2 seem more laminar. However, cell fates are reversible as indicated by the dotted line. Multiple bifurcation routes exist towards a local energy minimum X which shows highly turbulent protein flows and chaotic gene expression dynamics in its underlying gene regulatory networks. The attractor X is a chaotic cell fate (i.e., cancer stem cell). A cancer stem cell is shown as a strange attractor on the developmental landscape, with cell fate reprogramming towards the initial benign stem cell fate indicated by the two-way black arrow. Multiple other strange attractors (in different colors) are shown to occupy the attractor space.

Many of the attributes of cancer are associated to oncoproteins. As mentioned, we are currently adherent to the central dogma of systems biology, visualizing protein folding as a stochastic process. However, the simulated protein folding transitions of the SH3-domain (Src Homology 3) protein was shown to obey the vortex dynamics and hydrodynamical equations of Kolmogorov's statistical theory of turbulence [63,64]. The spatial flow distributions of the probability fluxes were determined to be self-similar (Kolmogorov-Richardson cascades) with a fractal dimension that decreases toward the native state, indicating that paradoxically the flow becomes more turbulent at more stable protein conformations [63,64]. To shed some context to fluid turbulence, the Kolmogorov-Richardson cascade observed in these protein folding simulations describes experimentally observed isotropic turbulence of an incompressible fluid, where large-scale flow structures (eddies and vortices) decay into smaller fractal structures. Most focal adhesion complexes and tyrosine receptor kinases mediating the initiation and progression of cancer metastasis (e.g., EMT transitions) depend on the structural conformation of SH3 domains (e.g., Src/FAK/Crk/Cas pathways; Figure 2). Likewise, the folding dynamics of the villin subdomain HP-35 protein in a FRET (Forster resonance energy transfer) experiment was shown to obey the $\beta$-model of turbulence with many orders (scales) of turbulent flow transitions for the eddies in the 3D conformational space [65].

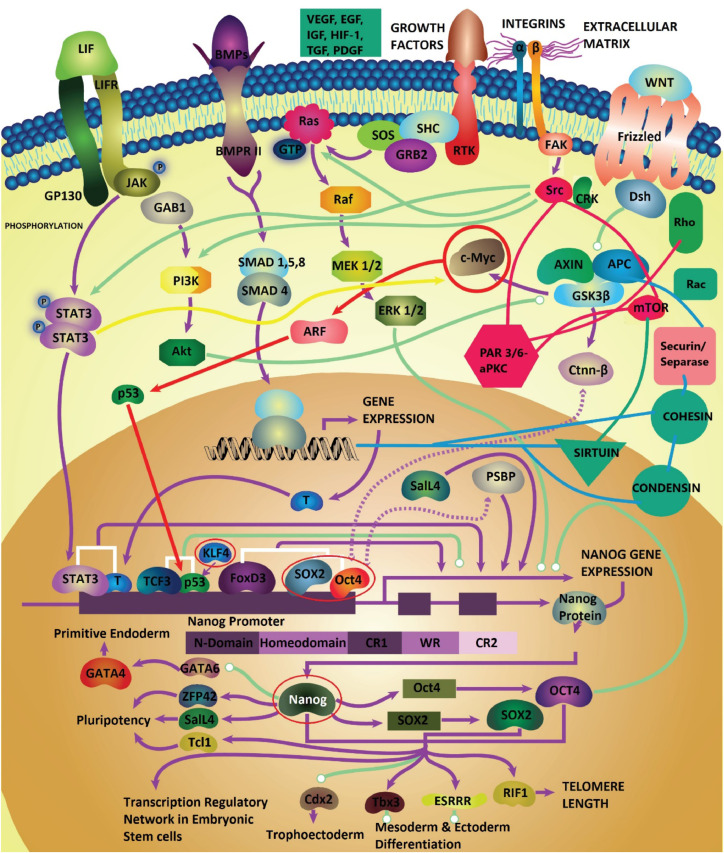
Figure 2.

Cancer Stem Cell Niche. A simplified representation of the cancer stem cells’ local microenvironment. Morphogens pertaining to the EMT program such as the Wnt/βcatenin pathway, Notch, VEGF, HIF-1, ECM (extracellular matrix)-remodeling pathways, etc. are shown to induce phenotypic plasticity and regulate the iPSC (induced pluripotency stem cell) network of Yamanaka factors (OCT4, SOX2, c-MYC, KLF4). They form multi-nested feedback loops with the ECM-stroma focal adhesion pathways and differentiation-cancer growth pathways such as the Src/mTOR pathway (note: these processes are not to be reduced to particular functions but seen as an undivided whole comprising of dynamic feedback loops/cybernetic systems).

On a final note with regards to turbulence, Ruelle treated turbulence as a heat flow problem using the nonequilibrium statistical mechanics of moving fluid particles in three-dimensional lattice boxes [66]. The macroscopic fluid transitions were characterized by Boltzmann-Gibbs distributions as would equally apply to the transitions in the metastable cell states of the Waddington attractor landscape. The critical Reynolds number was shown to be in the order of ∼60 to 100 for Taylor-Couette and Rayleigh-Benard convection systems, which is relatively feasible at biologically relevant scales [66,67]. Recall that the Reynolds number is an ill-defined parameter. For instance, whether one consider the diameter or radius of a pipe will alter the number by 2-fold. Thus, turbulence remains a scaling problem even in mathematical physics. Furthermore, the recent field of research deals with active turbulence in active matter such as cytoskeletal and bacterial suspensions [68,69]. The Reynolds number at which turbulence is observed is subject to debate, and within the field of active matter systems it is more ambiguous. Active matter systems suggest that turbulent energy cascades may help explain collective cell migration and pattern formation systems [70,71]. The cytoskeletal protein microtubules and actin are being recognized as candidates for these active turbulence models, wherein the swarming/flocking behaviors of proteins can phase-transition from Brownian motion to the turbulent regime of Navier-Stokes equations, at relatively low Reynolds numbers [72].

Prospects in stem cell reprogramming

With the brief survey of chemical turbulence in stem cell pattern formation, let us shift our thoughts to the posed problem of what is a CSC? In this section, we will briefly discuss how cancer stemness may be an emergent behavior in cancer ecosystems, wherein any differentiated cancer cell may potentially interconvert into a stem cell. Recent findings suggest current regiment therapies enhance cancer aggressiveness and stemness. Glioblastoma CSCs preferentially stimulated tumor angiogenesis in comparison to nonstem glioblastoma cells through VEGF secretion [73,74]. Bevacizumab, a standard-care chemotherapy for GBM patients, was shown to enhance the proangiogenic effects of CSCs, wherein hypoxia-associated pathways reprogrammed non-CSCs towards a stem cell phenotype. Hypoxia promotes the self-renewal capacity and asymmetric cell division of CSCs, as well as promoting a stem-like phenotype in the nonstem population. Furthermore, hypoxia upregulates stemness factors, such as OCT4, NANOG, and c-MYC through the hypoxia-inducible factor-2a (HIF-2a) [74].

Depending on the tumor microenvironment (stem cell niche), a cancer cell exhibits phenotypic plasticity/switching, i.e., it can transdifferentiate into another cell type, and terminally differentiated cancer cells can dedifferentiate and acquire stem cell properties [75]. It has been speculated that solid tumor cells exposed to chemotherapeutic agents can dedifferentiate to a plastic stem cell fate, and further transdifferentiate into other cancer cell types. The speculations were recently confirmed by Xiong et al, where cancer cells exposed to chemotherapy were shown to reprogram into plastic stem cell states leading to tumor relapse/recurrence as result of the increased cancer stemness [75]. Temozolomide, an oral chemotherapy drug, is often the first-line treatment for Glioblastoma. The findings showed that temozolomide not only increased the glioma stem cell population, but also reprogrammed CD133-negative glioma cell lines or patient-derived glioma cells into CD133-positive glioma stem cells, both in vitro and in vivo, in part by the activation of HIF and iPSC networks (Yamanaka factors) [75].

GBM stemness and recurrence was also seen in exposure of differentiated glioma cells to ionizing radiation therapy, causing the cells to acquire stem cell properties. Collectively, the findings suggest that despite the tremendous success rates in most pediatric cancer therapies with current regiments (ignoring the life-long side effects and quality of living), current treatments induce the cellular reprogramming of differentiated cancer cells to plastic stem cell fates, thereby causing resistance, disease progression and cancer recurrence [73,75]. The epigenetic landscape of GBMs (Glioblastoma Multiforme) shows tremendous spatiotemporal heterogeneity. Regardless, a core set of neurodevelopmental TFs (POU3F2, SOX2, SALL2, OLIG2) were identified to be essential drivers for GBM propagation and stemness [76]. These experiments must be repeated to further pave reprogramming CSCs to benignity (Figure 3).

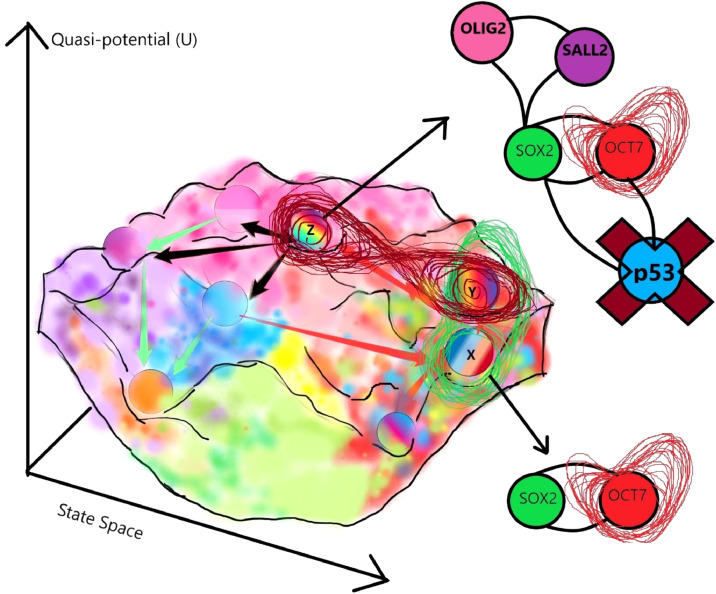
Figure 3.

GBM landscape. As discussed, the essential drivers of GBM stemness are shown on a Waddington landscape, based on the findings of reference [76]. The multicolored landscape demonstrates tumor heterogeneity. The attractor X represents a cancer stem cell expressing the SOX2 gene, while the attractor state Y represents a cell fate expressing the SOX2-OCT7 regulatory network. The cell fate Z represents the GBM stem cell expressing all of the identified essential drivers of cancer stemness (including OLIG2 and SALL2), and hence, at the highest peak of the mountain (i.e., highest stem cell potential). Note that the OCT7 gene is shown to exhibit a Rössler attractor-like dynamics, whereas the cell fate Z expressing all four factors displays a Lorenz-like strange attractor with chaotic gene expression dynamics as speculated by the flow cytometry/ FACS (fluorescence-activated cell sorting) data in reference [76]. The tumor suppressor p53 is shown as a cell cycle regulator in circuit with the stemness network. Cell cycle oscillations are the gateways to conferring cancer attractors. Epigenetic regulators are ignored for simplicity. These speculations are not experimentally supported due to the absence of dynamics (time-dependent information) in the datasets. Chaotic gene expression is predicted as a measure of cancer stemness.

Although only in speculation, it is proposed here that cancer stemness may be attributed to chaotic gene expression at the level of the stemness clique identified by Suva et al [76]. Furthermore, it is proposed here that these chaotic gene expressions are accompanied by chemical turbulence at the onset of CSC differentiation by certain proteins and morphogens. Identifying these complex networks remains an NP-hard problem. In proposition, algorithms which can detect strange attractor behaviors at the level of GRN dynamics, using time-series single cell datasets must be investigated to overcome this challenge in systems science and computational oncology. Therefore, I will bring this communication to an end with some suggested algorithms to explore the emergence of strange attractor dynamics in cancer gene expression and protein-mediated pattern formation.

Algorithms for strange attractors detection

As mentioned, there are no efficient algorithms for the detection of strange attractors in cancer datasets, whether it be the time lapse imaging of intracellular protein patterning or the attractor Waddington landscape reconstructed from time-series gene expression datasets. Athough various network science approaches currently exist, each pipeline consists of a distinct ensemble of machine learning algorithms specific to a target dataset wherein finding the optimal path and hyperparameter tuning are NP-complete optimization problems. The detection of strange attractors even in fluid turbulence is restricted to experimental mapping techniques such as power/frequency spectra analysis and phase portraits (Lyapunov spectra). However, the attractor reconstruction methods such as Takens’ time-delay coordinate embedding used to achieve these results are not well-suited for large complex datasets. Distinguishing noise from chaos remains a fundamental roadblock in cancer biology. The following are a few algorithmic prospects to overcome this challenge.

Takens mentioned entropy measures and multifractality as general techniques for strange attractor detection in turbulent systems [77]. Entropy and other information-theoretic measures remain amidst the most widely used algorithms used in the network visualization of gene expression datasets. Even simple machine learning algorithms such as decision trees and ensemble tree learners can help distinguish noise from chaos in biological signals [78].

AI is emerging as the most powerful statistical tool available in deciphering cancer networks. As such, 2 additional algorithms are proposed herein as heuristics (approximation tools) to map strange attractors in complex, chaotic datasets: ensemble Deep Learning Networks (DLN) and complexity measures from AID. Deep Learning architectures are the current state-of-the-art approaches in pattern recognition from complex datasets. Hopfield networks and Deep learning architectures can predict irregular patterns observed in complex fluid flows as well [79,80]. Strange attractors have been mapped in recurrent neural networks and gene networks [81]. Ling et al first-demonstrated the applicability of Deep Learning Networks (DLN) to predict the turbulent flows of the Reynolds-averaged Navier-Stokes equations [82], [83]. A Galilean-invariance embedded, DLN network architecture (Tensor Basis Neural Network) underwent training on various turbulent flow datasets followed by the Bayesian optimization for the neural network's hyper-parameters (i.e., the number of hidden layers, the number of nodes per hidden layer, and the gradient descent algorithm's learning rate). Therefore, Deep Learning architectures trained for mapping complex fluid flows can be optimized for detecting strange attractors within cancer networks.

Recurrent neural networks are subtypes of artificial neural networks that can accurately map the phase-space portraits of chaotic systems [84]. While time-delay coordinate embedding is effective for the attractor reconstruction of low-dimensional systems, Reservoir Computing (RC) is a machine-learning algorithm that trains recurrent neural networks to find the Lyapunov exponents of high-dimensional datasets. For example, RC has demonstrated applicability in the chaotic attractor reconstruction of complex fluid flows [85]. The RC well predicted the short-term time-series forecasting of the Kuramoto-Sivashinsky equation to several multiples of Lyapunov time. The KS equation is a chaotic system whose pattern formation closely resembles that of fluid turbulence [86,87]. Hence, this is another class of machine learning algorithm that can be utilized on time-series cancer datasets to test the presence of strange attractors.

Lastly, AID is an emerging frontier of complex systems science most pertinent to our discussion. AID treats cancer as a computer program with unresolved algorithmic complexity and studies dynamical systems with perturbation analysis in software space [17,88]. While currently employed machine learning algorithms in biological network reconstruction and pseudo-time ordering methods for gene expression datasets are based on statistical learning approaches, they do not inform us about cause and effect [88,89]. Current approaches perform pattern recognition on general statistical features of the datasets and are heavily dependent on dimensionality reduction techniques. As such, these fail to treat the cells and their interaction networks as dynamical systems. Therefore, AID is a vastly unexplored AI platform available for inferring causality in gene expression dynamics, CSC differentiation mapping and potentially map strange attractors in gene expression networks. According to AID, cancer is defined as a computer program in an infinite loop with no halting condition [17]. Cells are viewed as computing machines, nucleic acids as the operating system (software) and gene expressions as computer programs. Studies in AID have shown the high-dimensional phase space of the dynamical immune system to display healthy cells and unhealthy states as fixed and strange attractors, respectively [17]. Hence, AID is proposed as a promising tool to explore the emergence of strange attractors in cancer networks [89].

Conclusion

To conclude, tumor pattern formation is intrinsically a nonequilibrium, (nonlinear) dynamical system [90]. Reaction-diffusion systems can exhibit spatio-temporal chaos in the flows of their protein fluids at the onset of pattern formation, which is hereby defined as chemical turbulence [91]. Time-series single cell RNA-Seq in combination with machine intelligence and AID are suggested as tools for network reconstruction in CSCs, wherein strange attractor dynamics are suggested as the “missing tool” to map CSC fate choices and decision-making. Criticality in GRNs must be experimentally tested by perturbing gene expression networks and monitoring single-cell dynamics. Insights into chemical (fluid) turbulence within cells with the aid of algorithmic complexity measures and ensemble Deep Learning networks may pave the visualization of strange attractors in cancer datasets. The applications of quantum computing in solving these NP-hard problems can only be verified in time. In postulate, mapping strange attractors and chaotic gene expression dynamics at the level of gene-regulatory networks in CSCs with machine intelligence/algorithms may help identify the essential network structures that drive cancer stemness, and hence plausibly the phenotypic reprogramming of CSCs to benignity.