Local Phase Velocity Based Imaging (LPVI) of Viscoelastic Phantoms and Tissues

Abstract

Assessment of soft tissue elasticity and viscosity is of interest in several clinical applications. In this study we present feasibility of the local phase velocity based imaging (LPVI) method to create images of phase velocity and viscoelastic parameters in viscoelastic tissue-mimicking materials and soft tissues. In viscoelastic materials it is necessary to utilize wave mode isolation using a narrow bandpass filter combined with a directional filter in order to robustly reconstruct phase velocity images with LPVI in viscoelastic media over a wide range of frequencies. A pair of sequential focused acoustic radiation force push beams, focused once on the left side and once on the right side of the probe, was used to produce broadband propagating shear waves. The local shear wave phase velocity is then recovered in the frequency domain for multiple frequencies, for both acquired data sets. Then, a two-dimensional shear wave velocity map is reconstructed by combining maps from two separate acquisitions. By testing the method on simulated data sets and performing in vitro phantom and in vivo liver tissue experiments, we show the ability of the proposed technique to generate shear wave phase velocity maps at various frequencies in viscoelastic materials. Moreover, a nonlinear least-squares problem is solved in order to locally estimate elasticity and viscosity parameters. The LPVI method with added directional and wavenumber filters can produce phase velocity images, which can be used to characterize viscoelastic materials.

I. Introduction

Soft tissues exhibit viscoelastic behavior. As a result, over the last few decades many methods have been developed to measure mechanical properties of these soft tissues for evaluation of disease. One way to quantitatively evaluate viscoelastic materials is to measure the velocity dispersion, or variation with frequency, of propagating shear waves. Shear wave-based elastography utilizes different methods to introduce shear waves such as mechanical actuation, acoustic radiation force, or endogenous vibration [1]. After the shear waves are produced different means are used for the measurement of the shear wave motion such as ultrasound, magnetic resonance imaging (MRI), or optical coherence tomography (OCT) [1]–[4]. These methods have been used to investigate viscoelastic properties in healthy and pathologic conditions.

Liver fibrosis is a progressive disease that affects the liver stemming from multiple etiologies such as viral hepatitis, damage due to alcohol overuse, and fatty liver disease [5]. As hepatocytes are damaged due to inflammatory processes, collagen is deposited during the healing phase. The increase in collagen, or fibrosis, makes the liver stiffer. Liver fibrosis is a chronic condition and fibrotic infiltration can increase over time, which will progressively increase the liver stiffness further until cirrhosis occurs. This has been demonstrated in studies with biopsy comparison. Because of the intimate connection between liver fibrosis and liver mechanical properties [5], measurement of shear wave velocity and viscoelasticity has been used in clinical populations to evaluate diagnostic effectiveness. Changes in liver viscoelasticity with liver fibrosis have also been explored [6]–[11]. In addition to fibrosis in the liver, fat deposition can occur, a condition called steatosis, which can also have effects on the liver viscoelasticity [9], [12], [13]. Additionally, Nenadic, et al., has recently reported that acute cellular rejection involving inflammation processes in liver transplants can change viscoelastic parameters [14].

The kidney is also viscoelastic and its viscoelasticity can be modulated by blood flow alterations [15]. Additionally, the kidney is anisotropic and the viscoelastic properties can vary with the direction of measurement, along or across the natural orientations of the tubules and vessels in the kidney [16], [17]. Skeletal muscle also exhibits viscoelasticity and like the kidney is anisotropic [18], [19]. Shear waves propagating at different angles with respect to the muscle fibers will yield different results [20]–[22]. As many soft tissues exhibit viscoelastic behavior and those viscoelastic properties change with disease, it is important to develop robust methods for measurement of these properties, such as elasticity and viscosity. While one-dimensional or point-measurements of these parameters have been reported, images of these properties are an active area of research.

For developing and refinement of different methods to measure viscoelasticity, digital and physical tissue-mimicking phantoms have been created and tested. A good deal of work has been conducted to characterize these phantoms and conduct tests among different groups [23]–[28].

As mentioned above, one way to investigate the viscoelasticity of materials is to measure shear wave velocity dispersion, or change in the shear wave velocity with respect to frequency. Many clinical scanners measure the group velocity, or velocity with which the shear wave ”packet” travels with time-of-flight methods [29], [30]. Shear wave velocities at specific frequencies are denoted as phase velocities [31]. Two common methods to measure phase velocities include the phase gradient and two-dimensional Fourier transform $\left({\mathcal{F}}_{2D}\right)$ analysis [31], [32].

The phase gradient method utilizes the phase difference at specific frequencies evaluated at different spatial locations. This difference in phase values ϕ₁ and ϕ₂ can be computed between two specific locations r₁ and r₂ at a frequency ω

$$V_s(\omega )=\frac{\omega \left(r_2-r_1\right)}{{\varphi }_2-{\varphi }_1}$$ (1)

or computed using a linear regression of points from several locations [31], [33], [34]. The phase gradient is typically evaluated lateral to the shear wave source. V_s(ω) in Eq. (1) stands for phase velocity.

The ${\mathcal{F}}_{2D}$ methods use spatiotemporal data (x, t) and transform to a space that has coordinates of wavenumber and frequency (k, f) and have been used to measure the dispersion [32], [35]. The peaks in the magnitude distribution of the (k, f) space are used to measure the phase velocities using the relationship c = 2πf/k = 2πfλ/(2π) = fλ. The dispersion either from the phase gradient or ${\mathcal{F}}_{2D}$ can be fit to rheological models to quantify the viscoelastic parameters of the medium [9], [31], [33].

The phase gradient and ${\mathcal{F}}_{2D}$ approaches have been implemented in a one-dimensional sense using measurements lateral to the shear wave excitation. As a result, this can be regarded as a point measurement encompassing data from a certain limited region in the material or tissue. Recently, methods have been proposed to move past these point-based measurements, to make images of the phase velocities or viscoelastic parameters [36]–[40].

The method proposed by Budelli, et al. [36], uses the phase gradient method and calculates the phase velocity over a certain distance and performs this calculation at different axial locations to construct an image of the phase velocity. This method is considered free of assuming a rheological model for tissue characterization, but it only takes into account wave propagation in the lateral direction. The method proposed by Selzo, at al. [37], calculates a combined parameter which reflects elasticity and viscosity. This method does not give quantitative evaluation of the elasticity or viscosity independently. The method proposed by van Sloun, et al. [38], is based on fitting shear wave motion dynamics using a linear systems approach for estimating the local viscoelastic parameters assuming a Kelvin-Voigt (KV) rheological model. The method described by Bhatt, et al. [39], employs the frequency-shift method and calculates the shear wave attenuation over a certain distance. This method assumes that a shape parameter of a power spectrum amplitude is constant which may not hold for all viscoelastic materials.

Recently, we proposed an adaptation of a method called local wavenumber imaging to construct images of phase velocities called local phase velocity imaging (LPVI) [40]. In that work, we made measurements in elastic homogeneous and heterogeneous tissue mimicking phantoms to explore how the phase velocities in inclusions varied with frequency. In this paper we use the LPVI method to construct images of phase velocities and viscoelastic parameters in homogeneous viscoelastic tissue mimicking phantoms and in vivo healthy human livers. Directional and bandpass wavenumber filters are adopted in the LPVI approach. Two-dimensional (2D) shear wave phase velocity maps are reconstructed sequentially for two acquisition data, for a pair of sequential focused acoustic radiation force push beams and averaged at the end stage.

The rest of the article is organized as follows. First, we present the LPVI method as applied for the shear wave velocity mapping of viscoelastic materials. The effects of the filters are investigated in this manuscript, and advantages of the LPVI with these filters are shown. The LPVI method was tested on data from numerical simulations and experimental measurements. Then, the generated shear wave velocity maps were used to reconstruct elasticity and viscosity maps using a nonlinear least-squares fit applied to the KV rheological, viscoelastic model. In this paper, we use three homogeneous and three heterogeneous viscoelastic digital and two physical phantoms, as well as data from in vivo liver studies from five healthy subjects to test the methods. These testing platforms have viscoelastic properties that are relevant for applications in soft tissues. Results from these studies will be presented. The results will be followed with a discussion and conclusions.

II. Methods

In this section, the LPVI method is adapted for shear wave phase velocity estimation of viscoelastic materials. The LPVI method is tested with the local interaction simulation approach (LISA) numerical viscoelastic models, and experimentally using viscoelastic tissue-mimicking (TM) phantoms and data from in vivo healthy human livers. First, we provide a procedure for the LPVI method in Sec. II-A. The elasticity and viscosity mapping steps are described in Sec. II-B. A description of the numerical LISA viscoelastic phantom is provided in Sec. II-C. The experimental TM and in vivo human liver data used in our study are introduced in Secs. II-D and II-E, respectively. Appropriate examples are provided in order to show efficiency of LPVI in Sec. III.

A. Local-Phase-Velocity-based Imaging Approach

A new method called local phase velocity based imaging (LPVI), as an alternative technique to measure tissue elasticity, was previously proposed in [40]. The LPVI method recovers local shear wave velocity in the frequency domain for a single frequency or frequency band. In contrast to the work presented in [40] a bandpass filter in the wavenumber domain combined with a directional filter is added in this manuscript. The steps of the technique are presented in a flow chart in Fig. 1.

Fig. 1:

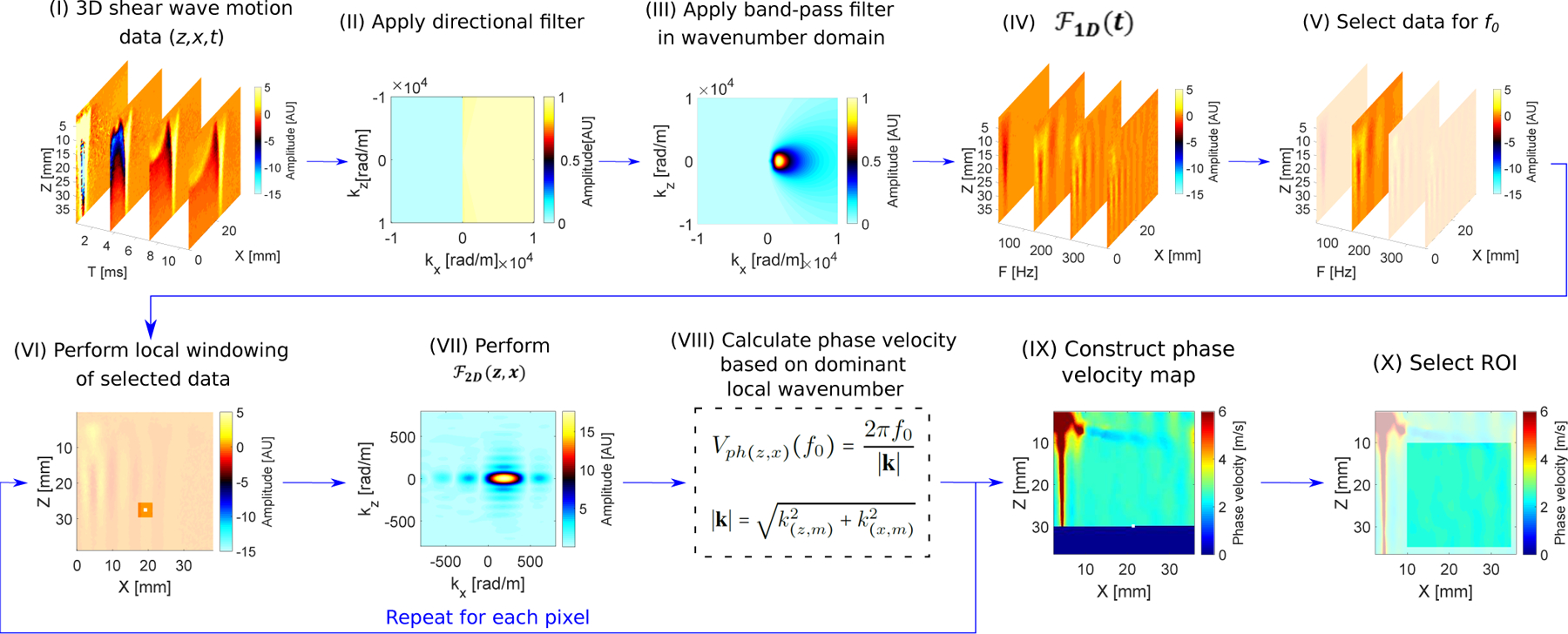
Flow chart of the proposed LPVI approach for one-sided push. Principal steps of the LPVI can be summarized as follows: (I) acquire a 3D shear wave velocity data; (II) apply directional filter to the data; (III) apply bandpass filter in a wavenumber domain; (IV) transform the spatio-temporal data into a frequency domain; (V) choose the spatial spectrum at a particular frequency f₀; (VI) execute a short space 2D Fourier transform in space domains; (VII) execute 2D Fourier transform on the windowed wavefield regions; (VIII) calculate spatial distribution of the phase velocity of the shear wave motion for the specified frequency and select ROI (IX–X). Repeat previous steps for shear wave velocity data for the second push. Average resulting LPVI data for ROI’s from two pushes.

First, the shear wave mode isolation of the spatio-temporal particle motion, particle velocity in this study, V (z, x, t) is performed using directional and bandpass filters in a 2D wavenumber (k_z − k_x) domain (marked as (II) and (III) in the flow chart in Fig. 1). A first order Butterworth bandpass filter is applied to each frame to remove spatial wavelengths representing shear wave speeds outside a predetermined range. The wavenumber bandwidth is centered about the nominal wavenumber k(f₀) of the shear wave mode. k(f₀) is a wavenumber of the shear wave mode estimated from the ${\mathcal{F}}_{2D}$ dispersion curve (as described in Sec. II-F). The wavenumber bandwidth is selected as

$${\Gamma }_{(k)}=\frac{2\pi f_0}{V_{{\mathcal{F}}_{2D}}\left(f_0\right)\pm V_k\left(f_0\right)},$$ (2)

where $V_{{\mathcal{F}}_{2D}}\left(f_0\right)$ is the phase velocity estimated from the ${\mathcal{F}}_{2D}$ dispersion curve, and V_k(f₀) was set to 0.5 m/s for homogeneous data. This value was determined empirically through preliminary processing of phantom data. Motion propagation in the axial direction is also reduced by filtering the corresponding spatial Fourier domain components using a rolled-off wedge filter [41]. Shear waves traveling in one lateral direction are taken into account through the use of a directional filter [42]. This can be expressed as the product between the spectrum in the frequency-wavenumber domain, Ṽ(k_z, k_x, f₀), of the particle motion and a filter function in the form

$${\tilde{V}}_w\left(k_z,k_x,f_0\right)=\tilde{V}\left(k_z,k_x,f_0\right)\cdot D\left(k_z,k_x,f_0\right)\cdot B_k\left(k_z,k_x\right),$$ (3)

where D(k_z, k_x, f₀) is the 3D directional filter in the k_z − k_x − f₀ domain, B_k(k_z, k_x) denotes the 2D bandpass filter in the k_z − k_x domain, and Ṽ_w(k_z, k_x, f₀) is the filtered spectrum. The 3D D filter can be multiplied with 2D B filter iteratively for each frequency f₀.

The filtered spectrum is then transformed back into the frequency-space domain (IV–V) by using the inverse ${\mathcal{F}}_{2D}\left({\mathcal{F}}_{2D}^{-1}\right)$

$${\tilde{V}}_w\left(z,x,f_0\right)={\mathcal{F}}_{2D}^{-1}\left[{\tilde{V}}_w\left(k_z,k_x,f_0\right)\right].$$ (4)

Then, a short space ${\mathcal{F}}_{2D}$ is applied in space domains z and x (VI). This step entails breaking down the Ṽ(z, x, f₀) wavefield into small segments over the spatial dimensions before Fourier transformation and retaining the spatial information. The Ṽ_w(z, x, f₀) wavefield is multiplied by a window function $W_{z,x}(\overline{z},\overline{x})$ which is non-zero for only a small region in space while constant over the entire frequency domain, which can be defined as follows

$${\tilde{V}}_w^{*}\left(\overline{z},\overline{x},f_0\right)={\tilde{V}}_w\left(z,x,f_0\right)\cdot W_{z,x}(\overline{z},\overline{x}),$$ (5)

where $W_{z,x}(\overline{z},\overline{x})$ is a 2D cosine-tapered window (i.e. Tukey window). $\overline{z}$ and $\overline{x}$ denote non-zero values in z and x directions, respectively. When the $W_{z,x}(\overline{z},\overline{x})$ window slides along the spatial dimensions, windowed wavefield regions, ${\tilde{V}}_w^{*}\left(\overline{z},\overline{x},f_0\right)$, are created. The ${\mathcal{F}}_{2D}$ is applied to the ${\tilde{V}}_w^{*}\left(\overline{z},\overline{x},f_0\right)$ region (VII), resulting in a set of 2D wavenumber (k_z, k_x) spectra for the frequency f₀, which mathematically is given as

$${\tilde{\tilde{V}}}_w\left(k_z,k_x,f_0\right)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\tilde{V}}_w^{*}\left(\overline{z},\overline{x},f_0\right)\cdot e^{-i\left(k_z\overline{z}+k_x\overline{x}\right)}\mathit{\text{dzdx}}.$$ (6)

The resulting spectra ${\tilde{\tilde{V}}}_w\left(k_z,k_x,f_0\right)$ are indexed by the locations of the window such that the spatial information is retained.

Next, the spatial distribution of the phase velocity is calculated (VIII). From the ${\tilde{\tilde{V}}}_w\left(k_z,k_x,f_0\right)$ spectra, for all spatial windows, the phase velocity is computed as

$$V_{ph(z,x)}\left(f_0\right)=\frac{2\pi f_0}{\left|k\right|},$$ (7)

where |k| is a wavenumber magnitude described as

$$\left|k\right|=\sqrt{k_{(z,m)}^2+k_{(x,m)}^2},$$ (8)

and k_(z,m) and k_(x,m) arguments are found using

$$\left[k_{(z,m)},k_{(x,m)}\right]=\underset{\left(k_z,k_x\right)}{\text{arg\hspace{0.17em}max}}\left\{{\tilde{\tilde{V}}}_w\left(k_z,k_x,f_0\right)\right\}.$$ (9)

Based on Eq. (7) the full field-of-view of the shear wave phase velocity image is reconstructed (IX–X).

The above procedure has been implemented in MATLAB (Mathworks, Natick, MA) to show and evaluate the principle and its basic performance. We examined tests using this method with LISA numerical phantom data, as well as the TM phantom and in vivo tissue experimental data.

B. Elasticity and Viscosity Mapping

Based on the local 2D shear wave velocity maps over a given frequency range, the elasticity and viscosity maps are deduced. In this work we assume the KV rheological viscoelastic model. We adopt this rheological model because it has been shown in literature, in multiple works, that the KV model does describe shear wave velocity dispersion over certain ranges of frequency such as 100 – 600 Hz [6], [15], [20]–[24], [34], [38], [43]. The values found in this manuscript can be compared against these previous publications.

The KV model requires only two parameters. It is composed of a dashpot and a spring placed in parallel. The stress-strain relationship of the KV model is represented in the form

$$\sigma =\left({\mu }_1-{\mu }_2\frac{\partial }{\partial t}\right)\epsilon ,$$ (10)

where, the stress, σ, is related to the strain, ε, by the shear elasticity μ₁, the shear viscosity μ₂ and the time derivative operator (∂/∂t). Inserting this relation into the equation of wave motion, one obtains the one-dimensional Helmholtz equation for the KV model. Then, from the complex wave vector, the shear wave velocity of the KV model can be computed as [43]

$$V_s(\omega )=\sqrt{\frac{2\left({\mu }_1^2+{\omega }^2{\mu }_2^2\right)}{\rho \left({\mu }_1+\sqrt{{\mu }_1^2+{\omega }^2{\mu }_2^2}\right)}},$$ (11)

where, ρ represents the density and ω is an angular frequency (ω = 2πf).

In order to locally estimate elasticity and viscosity parameters for each pixel, the curve of Eq. (11) over the frequency domain is estimated using a nonlinear least-squares problem (NLSQ). We formulate the following NLSQ in a form

$$\left[{\mu }_1,{\mu }_2\right]=\underset{{\mu }_1,{\mu }_2}{\text{min}}{\Vert V_s(z,x,f)-V_{ph}(z,x,f)\Vert }_2^2.$$ (12)

Equation (12) is numerically solved using a MATLAB solver, lsqcurvefit. Calculations are processed for each pixel of 2D shear wave velocity maps in z and x directions. Different ranges of frequency were used for viscoelastic material characterization, for various phantoms. However, they were selected to be the same for the LPVI and 2D-FT techniques, respectively, for a fair comparison.

C. Numerical LISA Phantoms Description

To produce digital phantoms of viscoelastic materials for which the mechanical properties are known, we used a 2D local interaction simulation approach (LISA) [44]–[46]. LISA has been used for SWE applications in our previous study [40]. One of the major advantages of the LISA algorithm when used for wave propagation is the local interaction nature of boundaries in the model. The sharp interface model was used to average physical properties at interface grid points which represent intersections of four elementary cells [47]. In other words, cells are considered as discontinuous (displacements and stresses are adjusted at interface grid points). The sharp interface model allows for a more physical and unequivocal treatment of interface discontinuities for different layers of material than standard finite difference schemes. Physical parameter smoothing across material interfaces is applied, leading to more precise results when treating wave propagation problems in complex media (e.g. layered structures).

The LISA technique for an elastic, isotropic, homogeneous, and nearly incompressible model for soft tissue is described by Navier’s equation

$$\left({\lambda }_1+2{\mu }_1\right)\nabla (\nabla \cdot u)+{\mu }_1\nabla \times (\nabla \times u)+F=\rho \frac{\partial }{\partial t}u,$$ (13)

where, λ₁ and μ₁ are the bulk and shear modulus, respectively, and ρ is the density. u is the local particle displacement, F is the induced body force, and t is the time. When the KV model for viscous loss is incorporated, Navier’s equation becomes [48]

$$\left({\lambda }_1+2{\mu }_1+\left({\lambda }_2+2{\mu }_2\right)\frac{\partial }{\partial t}\right)\nabla (\nabla \cdot u)+\left({\mu }_1+{\mu }_2\frac{\partial }{\partial t}\right)\nabla \times (\nabla \times u)+F=\rho \frac{\partial }{\partial t}u,$$ (14)

where, λ₂ and μ₂ denote the bulk viscosity and shear viscosity, respectively.

In the LISA implementation, similar to the standard finite difference scheme, the future time step is calculated as a combination of the same quantities taken in the already calculated time steps. As a result, the algorithm can be parallelized very efficiently. Therefore, we used parallel computation technology - offered by modern graphics processing units (GPUs) and compute unified device architecture (CUDA) used in low-cost graphical cards - for computation of the LISA equations. The entire process was implemented in MATLAB software.

The acoustic radiation force push beam, for the numerical models, was simulated using Field II [49], [50]. A linear array transducer (L7–4, Verasonics, Inc., Kirkland, WA, USA) was modeled. A linear array with 48 active elements, with element width of 0.283 mm, element height of 7 mm, element pitch of 0.308 mm, elevation focus of 25 mm was simulated with a center frequency of 5.0 MHz, and using a medium attenuation, α, of 0.5 dB/cm/MHz and sound velocity, c, of 1540 m/s. The intensity, I, was calculated by squaring the pressure to be used in the body force defined by F = 2αI/c. A focal depth of 21.6 mm was used for the push beams with a fixed f-number (F/N) of 1.46.

The domains were uniformly spatially sampled at 0.1 mm. The dimensions of the simulated domain are x = ±60 mm in the lateral direction and z = 60 mm in the axial dimension. We adopted a KV material model with three different material properties scenarios for homogeneous phantoms: μ₁ = 14.44 kPa and μ₂ = 3 Pa·s for Phantom 1, μ₁ = 3.34 kPa and μ₂ = 1.25 Pa·s for Phantom 2, and μ₁ = 1.48 kPa and μ₂ = 0.75 Pa·s for Phantom 3, respectively. ρ was equal to 1000 kg/m³ for both phantoms.

Three heterogeneous viscoelastic phantoms (Phantom I, II and III) were also simulated. The background shear modulus was set to 4.5 kPa and the circular inclusion shear modulus was set to 22 kPa for all models, respectively. The viscosity of the background was set to 0.3 Pa·s. The inclusion’s viscosity was set to 2 Pa·s for Phantom I, 4 Pa·s for Phantom II, and 6 Pa·s for Phantom III, respectively. In our study we investigated an inclusion with 10 mm diameter.

The data sets were then processed as described in Secs. II-A–II-B in order to obtain 2D estimates of shear wave velocity and viscoelasticity. The spatial window size, $W_{z,x}(\overline{z},\overline{x})$, used within the LPVI approach was set to 40 × 40 pixels, resulting in 4.0 × 4.0 mm. Two separate acquisitions with ultrasound push beams focused once on the left side (at x = 0 mm for Phantoms 1, 2, and 3) and once on the right side (at x = 30 mm for Phantom 1, x = 26 mm for Phantom 2, and x = 17 mm for Phantom 3, respectively) of the L7–4 probe were performed. From the push on the left of the ROI, we only used information for the wave traveling from left-to-right, and for the push on the right side of the ROI we only used information for the wave traveling right-to-left. A local shear wave velocity was then recovered in the frequency domain for a single frequency, for both acquired data sets. Then, a two-dimensional shear wave velocity map is reconstructed by averaging maps from two separate acquisitions.

D. Tissue-mimicking Viscoelastic Phantoms

Custom tissue-mimicking viscoelastic phantoms - similar to those used in a comparison study [25] - were used (CIRS Inc., Norfolk, VA, USA) in this work to test robustness of the LPVI approach for shear wave phase velocity and viscoelastic parameters mapping. The reference values of elasticity and viscosity of these phantoms are not known. A Verasonics ultrasound system equipped with a linear array transducer (L7–4, Verasonics, Inc., Kirkland, WA, USA) was used for data acquisition. The acoustic radiation force push beams were focused at 21.56 mm. The push duration was 400 μs and the push frequency was 4.09 MHz. The push beam was generated by 30 active elements. Push beams were placed on each side of the L7–4 probe (at x = 4.62 mm and x = 34.80 mm for Phantom A, and at x = 6.47 mm and x = 32.96 mm for Phantom B, respectively). A plane wave acquisition was used using 3 angularly directed plane waves (−4°, 0°, +4°) that were coherently compounded [51]. The effective frame rate after compounding was 4.1667 kHz. The ultrasound frequency for the tracking beam was 5 MHz. The motion (shear wave particle velocity) was calculated from the in-phase/quadrature data using an autocorrelation algorithm with an axial window of 3 pixels and temporal window of 2 frames [52]. For the 2D phase velocity maps reconstruction we used moving spatial window in a size of 4.0 × 4.0 mm. Similarly to the numerical phantoms (Sec. II-C), two acquisitions were used to construct final shear wave phase velocity maps.

E. In vivo Human Livers

SWE measurements were performed in the livers of five human subjects, with no history of liver, reported in [53], [54]. These data were used to test the efficacy of the LPVI approach in soft tissues. The experimental protocol was approved by the Mayo Clinic Institutional Review Board and written informed consent was obtained prior to scanning. Imaging and measurements were performed by an experienced sonographer with the ultrasound probe positioned at the eighth intercostal space during breath holds. A Vantage ultrasound system (Verasonics, Inc., Kirkland, WA, USA) equipped with a curved array transducer (C5–2v, Verasonics, Inc., Kirkland, WA, USA) was used. The acoustic radiation force push beams were focused in the middle of the probe (at x = 0 mm). The detection beams were wide beams with an f/9.9 focal configuration. The push duration was 600 μs, and the push frequency was 2 MHz. A plane wave imaging compounding method was used to improve the signal-to-noise of shear wave tracking [51]. Two frames at different steering angles (−1° and +1°) were used to obtain each imaging frame, giving an effective frame rate of 2.77 kHz. Because of different focal depths used in these studies, we characterized the MI, I_spta, and I_sppa for multiple possible push beams. The parameters for the push beams were hard-coded to make sure that we used parameters that provided acoustic output within FDA regulatory limits. Similar to the TM phantoms, the motion (shear wave particle velocity) was calculated from the in-phase/quadrature data using an autocorrelation algorithm with the same parameters as used for the TM phantoms [52]. The spatial window size used for the velocity maps reconstruction was the same as in the case of the numerical and TM phantoms. Final phase velocity maps were reconstructed from a single-sided acquisition only (no averaging was performed).

F. Dispersion Comparison

The following LPVI results are compared against the phase velocity estimates for ${\mathcal{F}}_{2D}$. First, the 2D particle velocity field was averaged along the depth dimension over 3 mm, centered at the focal depth. Then, the DC component was removed from the waveforms. It is well known that when data within a short distance from the focused push beam are considered, higher standard deviation of the phase velocity is observed. This is induced by a near-field effect. With this in mind the phase velocity estimates for ${\mathcal{F}}_{2D}$ were computed as a mean and standard deviation for various lengths of lateral segments of data. The starting measurement point varied from 0 to 4 mm away from the focused push beam location with a step size of Δ_x equal to 0.1 mm for the LISA numerical data, 0.154 mm for the TM experimental data, and 0.345 mm for the in vivo human liver data. The last measurement point was constant for all computations, equal to 30 mm for the LISA numerical and TM experimental data, respectively, and 20 mm for the in vivo human liver data. This means that the phase velocity curves were calculated for selected lateral segments equivalent to 0–30 mm, 0.1–30 mm, 0.2–30 mm, etc., for example, for the numerical data. Based on these computations multiple dispersion curves were evaluated and the standard deviation was calculated. Above procedure was repeated for both acquisitions coming from a pair of sequential focused acoustic radiation force push beams. The μ₁ and μ₂ parameters presented in Tables I, III, and IV were calculated based on the mean phase velocity fit to the KV model. In this case a standard deviation is not presented.

TABLE I:

Mean, standard deviation and uniformity coefficient (i.e. CV = SD/MEAN) of the phase velocity and viscoelastic parameters μ₁ and μ₂, calculated for the LISA numerical phantoms within the ROIs marked in Figs. 3 and 4. Results in triangular brackets, 〈·〉, present mean error calculated using the true values.

Parameter	Unit	Phantom 1		Phantom 2		Phantom 3
		Mean±SD	CV	Mean±SD	CV	Mean±SD	CV
Vph, filters Off	[m/s]	4.33±0.00 (150 Hz)	0.00	2.05±0.18 (200 Hz)	0.09	1.41±0.11 (150 Hz)	0.08
Vph, filters On	[m/s]	4.33±0.00 (150 Hz)	0.00	2.04±0.05 (200 Hz)	0.02	1.38±0.04 (150 Hz)	0.03
Vph, filters Off	[m/s]	4.74±0.01 (350 Hz)	0.00	2.04±0.27 (300 Hz)	0.13	1.60±0.24 (250 Hz)	0.15
Vph, filters On	[m/s]	4.72±0.03 (350 Hz)	0.01	2.11±0.02 (300 Hz)	0.01	1.45±0.04 (250 Hz)	0.03
Vph, filters Off	[m/s]	7.07±0.35 (550 Hz)	0.05	10.02±6.42 (400 Hz)	0.64	2.87±1.23 (350 Hz)	0.43
Vph, filters On	[m/s]	4.67±0.04 (550 Hz)	0.01	2.28±0.06 (400 Hz)	0.03	1.61±0.09 (350 Hz)	0.06
μ1, LPVI*	[kPa]	19.27±0.28 (4.83)	0.01	3.39±0.23 (0.05)	0.07	1.71±0.09 (0.23)	0.05
μ1, ${\mathcal{F}}_{2D}$	[kPa]	17.39 (2.93)	-	3.24 (0.10)		1.63 (0.15)	-
μ2, LPVI*	[Pa·s]	3.56±0.18 (0.56)	0.05	1.28±0.11 (0.03)	0.09	0.75±0.12 (0.00)	0.16
μ2, ${\mathcal{F}}_{2D}$	[Pa·s]	2.95 (0.05)	-	1.26 (0.01)	-	0.75 (0.00)	-

^*results for LPVI with adopted bandpass filters. LPVI without applying wavenumber and directional filters are not presented because, the nonlinear least-squares function was unable to solve this problem.

TABLE III:

Mean, standard deviation and uniformity coefficient (i.e. CV = SD/MEAN) of the phase velocity and viscoelastic parameters μ₁ and μ₂, calculated for the TM phantoms within the ROI marked in Figs. 9 and 10.

Parameter	Unit	Phantom A		Phantom B
		Mean±SD	CV	Mean±SD	CV
Vph, filters Off	[m/s]	2.44±0.13 (170 Hz)	0.05	1.43±0.13 (120 Hz)	0.09
Vph, filters On	[m/s]	2.55±0.10 (170 Hz)	0.04	1.48±0.03 (120 Hz)	0.02
Vph, filters Off	[m/s]	2.61±0.12 (350 Hz)	0.05	1.56±0.13 (260 Hz)	0.08
Vph, filters On	[m/s]	2.72±0.06 (350 Hz)	0.02	1.58±0.05 (260 Hz)	0.03
Vph, filters Off	[m/s]	5.22±4.92 (600 Hz)	0.94	3.83±4.87 (400 Hz)	1.27
Vph, filters On	[m/s]	2.85±0.07 (600 Hz)	0.02	1.64±0.05 (400 Hz)	0.03
μ1, LPVI*	[kPa]	6.62±0.27	0.04	2.28±0.06	0.03
μ1, ${\mathcal{F}}_{2D}$	[kPa]	5.96	-	2.08	-
μ2, LPVI*	[Pa·s]	1.23±0.11	0.09	0.52±0.08	0.15
μ2, ${\mathcal{F}}_{2D}$	[Pa·s]	1.21	-	0.58	-

^*results for LPVI with adopted bandpass filters. LPVI without applying wavenumber and directional filters are not presented because, the nonlinear least-squares function was unable to solve this problem.

TABLE IV:

Mean, standard deviation and uniformity coefficient (i.e. CV = SD/MEAN) of the phase velocity and viscoelastic parameters μ₁ and μ₂, calculated for the experimental in vivo liver studies within the ROIs marked in Figs. 12 and 13.

Parameter	Unit	Subject I		Subject II		Subject III		Subject IV		Subject V
		Mean±SD	CV	Mean±SD	CV	Mean±SD	CV	Mean±SD	CV	Mean±SD	CV
Vph, (80 Hz)	[m/s]	1.27±0.09	0.07	1.18±0.06	0.05	1.30±0.14	0.11	1.09±0.03	0.03	1.13±0.04	0.04
Vph, (140 Hz)	[m/s]	1.43±0.04	0.03	1.38±0.04	0.03	1.44±0.08	0.06	1.26±0.07	0.06	1.27±0.03	0.02
Vph, (200 Hz)	[m/s]	1.57±0.07	0.04	1.52±0.06	0.04	1.58±0.04	0.03	1.39±0.12	0.09	1.39±0.16	0.12
μ1, LPVI	[kPa]	1.37±0.08	0.06	1.40±0.15	0.11	1.81±0.25	0.14	1.04±0.18	0.17	1.13±0.11	0.10
μ1, ${\mathcal{F}}_{2D}$	[kPa]	1.23	-	1.14	-	1.94	-	1.07	-	1.01	-
μ2, LPVI	[Pa·s]	1.20±0.09	0.08	1.22±0.12	0.10	1.12±0.10	0.09	1.11±0.16	0.14	1.08±0.13	0.12
μ2, ${\mathcal{F}}_{2D}$	[Pa·s]	1.41	-	1.21	-	1.02	-	0.81	-	1.13	-

To have an objective measure of uniformity for reconstructed the 2D shear phase velocities, as well as viscoelastic parameters μ₁ and μ₂ we determined the unitless coefficient of variation using the following formula $CV=\frac{SD}{\mathit{\text{MEAN}}}$, where SD is the standard deviation. Results are presented in Tables I, III and IV, for the numerical LISA homogeneous and experimental TM phantoms data, and the in vivo human subjects, respectively.

III. Results

A. Shear Wave Elastography Using LPVI

Shear waves at higher frequencies typically undergo higher attenuation and therefore do not propagate as far leading to shorter lateral imaging lengths. Consequently, for higher frequencies smaller ROIs need to be selected. Hence, a trade off needs to be made between these two criteria. For a selected frequency range we reconstructed a full field of view of the shear wave phase velocity map. Then, we evaluated regions where the shear wave has been attenuated. This determination was made by examining the phase velocity images and determining when the reconstruction becomes inconsistent and noisy particularly at edges of the region-of-interest, which is indicative of insufficient motion information. Next, we selected the largest possible ROI for the highest frequency possible.

1). Numerical LISA Results:

Figure 2, top row, shows the wave motion of the simulated data described in Sec. II-C for three different viscoelastic digital phantoms, i.e. Phantoms 1, 2, and 3 respectively. The k-space spectra for these data sets are presented in the middle row of Fig. 2. The bottom row shows phase velocity curves for the numerical data superimposed with analytical results. The phase velocity estimates, based on a standard ${\mathcal{F}}_{2D}$ technique for the focused excitation push beam depth, as well as a mean phase velocity computed from LPVI for ROIs are presented, respectively. The ROIs for each phantom are marked in Fig. 3.

Fig. 2:

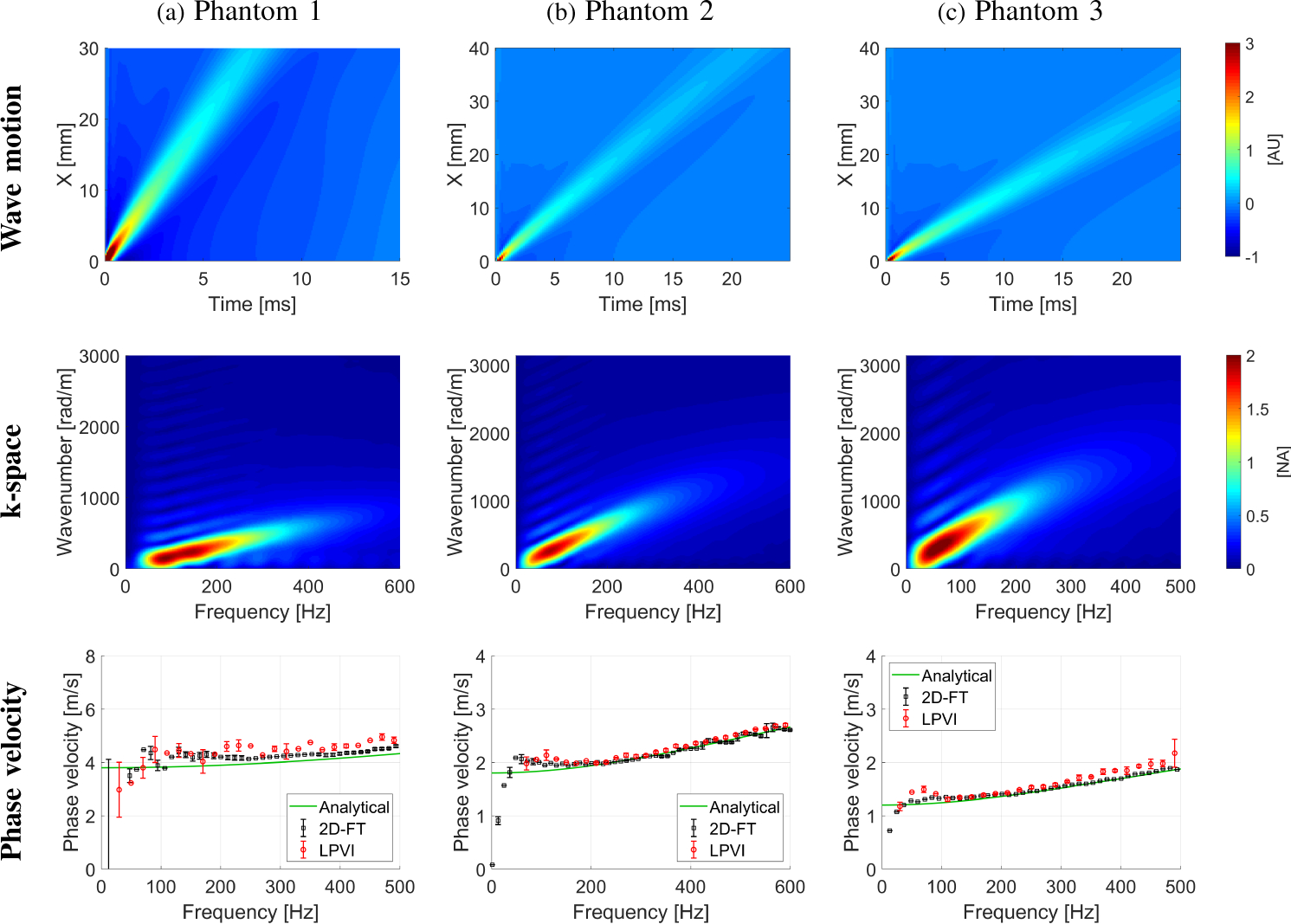
The wave motion (top row), the k-space spectrum (middle row) and the phase velocity (bottom row) calculated for the LISA homogeneous, viscoelastic phantoms numerical data. Phase velocity results (bottom row) for LPVI with active bandpass filters introduced in this manuscript are shown.

Fig. 3:

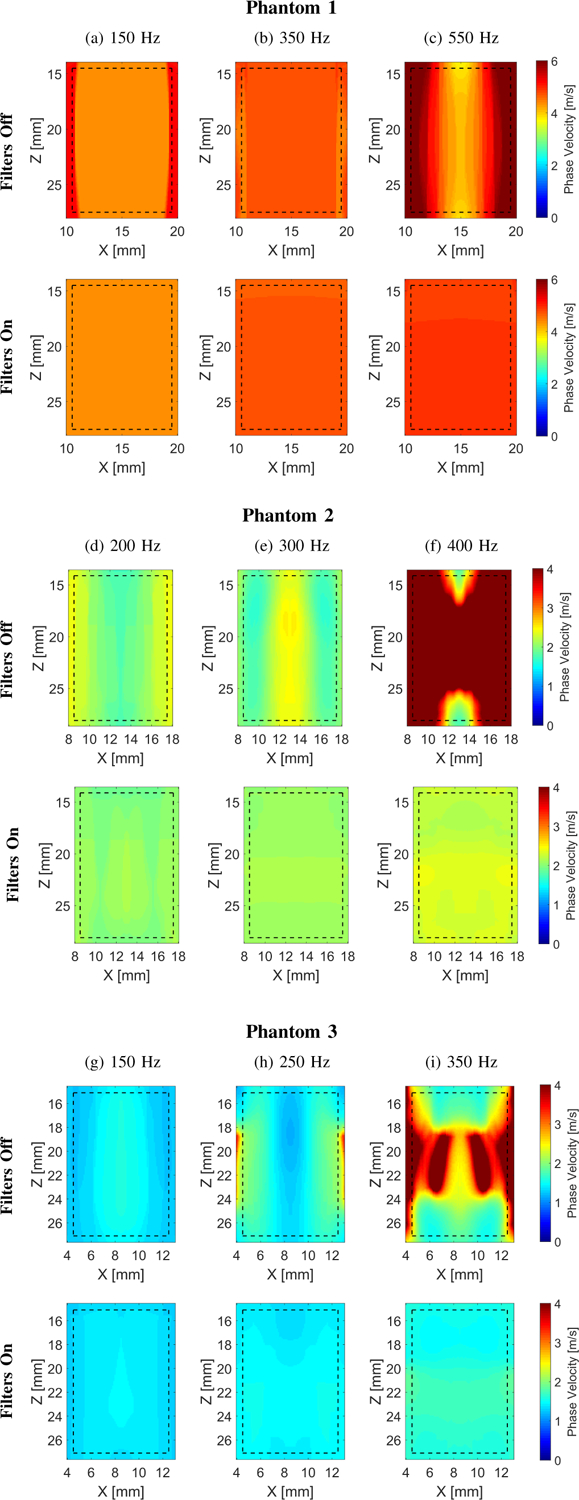
Two-dimensional shear wave phase velocity images for the LISA viscoelastic numerical data. The f₀ used for the calculations was equal to (a) 150, (b) 350, and (c) 550 for Phantom 1, (d) 200 Hz, (e) 300, and (f) 400 Hz for Phantom 2, and (g) 150, (h) 250, and (i) 350 Hz for Phantom 3, respectively. Results for LPVI without bandpass filters similar to the work described in [40] are shown in the top row (Filters Off). Results for LPVI with active filters introduced in this manuscript are shown in the bottom row (Filters On). The window size, W_z,x, was equal to 4.0 × 4.0 mm.

Figure 3 shows the 2D shear wave phase velocity maps reconstructed using the LPVI approach. Results presented in the top row, for each phantom, (Filters Off) were reconstructed using the approach described in [40], i.e. without applying bandpass wavenumber and directional filters. The bottom row (Filters On) however, shows results for the LPVI method described in Sec. II-A (i.e. with adopting wavenumber and directional filters). Three frequencies were selected in order to obtain estimates of the velocity maps for three numerical phantoms. Based on the reconstructed maps mean, standard deviation and CV of phase velocities were computed within the ROIs. Results are summarized in Table I (from Fig. 3) and superimposed in the bottom row of Fig. 2. One can appreciate that the mean phase velocity estimates using the LPVI approach with adopted bandpass filters (Table I) are very close to the true values. The reconstructed mean velocities for Phantom 1 are overestimated in comparison to the analytical solution. LPVI in its original form (without bandpass filters) gives higher mean phase velocity estimates with higher standard deviation. Similar phenomena are observed for Phantoms 2 and 3. It can be clearly seen that the shear wave mode isolation improves the quality of the reconstructed shear wave velocity maps (bottom row of Fig. 3). The shear wave mode isolation applied in LPVI also allows the retrieval of information over a wider frequency range (Figs. 3c, 3f and 3i).

The viscoelastic parameters were estimated considering the two-parameter KV model as described in Sec. II-B. The numerical phantom data were used and 2D elasticity (μ₁) and viscosity (μ₂) maps were evaluated (Fig. 4) based on the frequency-dependent 2D shear wave velocity maps reconstructed using LPVI, as described in Sec. III-A, for LPVI with adopted wavenumber and directional filters. The frequency ranges used for the 2D viscoelastic maps reconstructions were chosen as follow: Phantom 1: 150 – 550 Hz, Phantom 2: 160 – 600 Hz and Phantom 3: 130 – 500 Hz, corresponding to the main frequency content present in the k-space spectra (values corresponding to normalized magnitudes >0.2) in Fig. 2. We did not reconstruct similar μ₁ and μ₂ maps for the LPVI without applying wavenumber and directional filters because, the nonlinear least-squares function was unable to solve this problem.

Fig. 4:

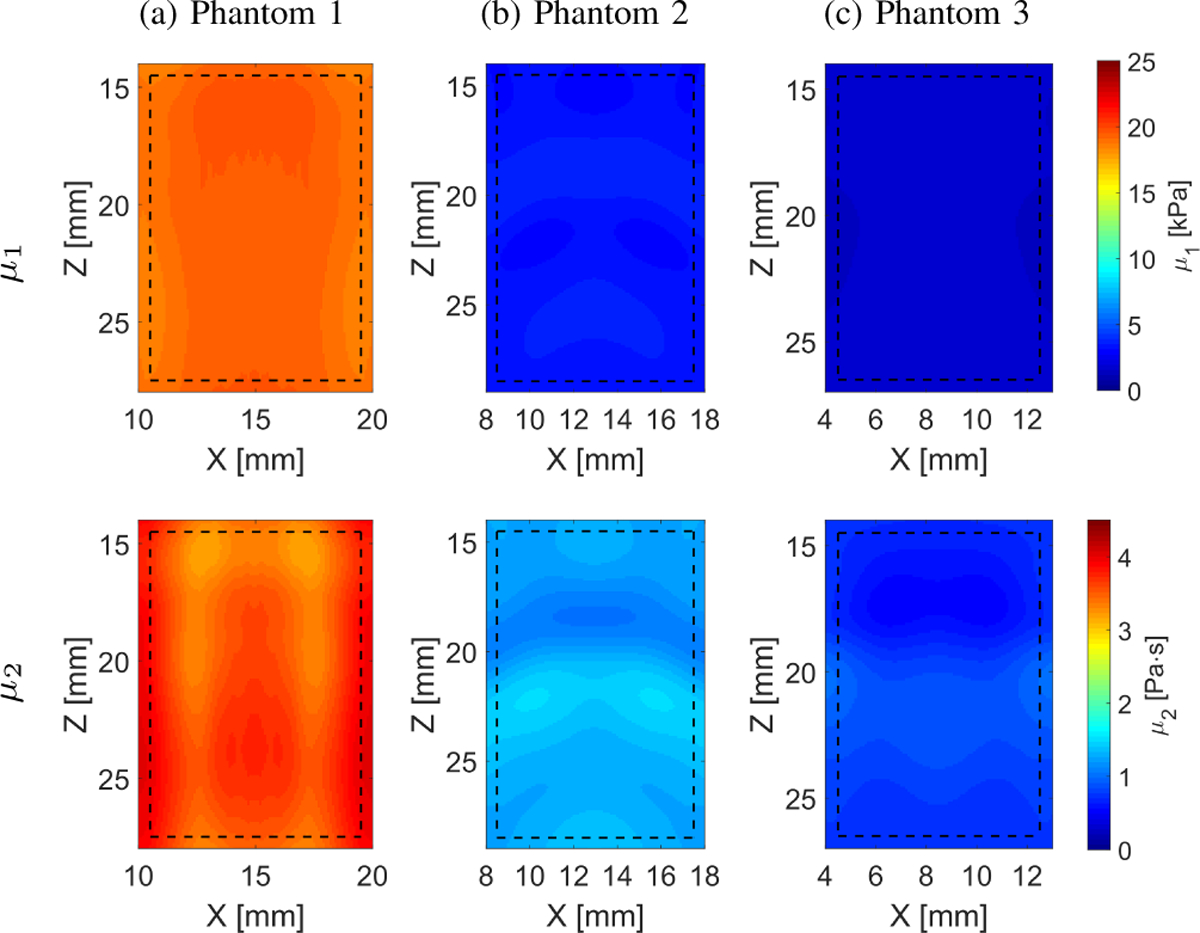
Two-dimensional image reconstructions of μ₁ and μ₂ calculated based on the Kelvin-Voigt rheological model for the LISA homogeneous, viscoelastic numerical data. Results for LPVI with active bandpass filters introduced in this manuscript are shown.

Relatively uniform elasticity and viscosity reconstructions were obtained for the numerical, homogeneous phantoms as can be seen in Fig. 4 and Table I. The estimated mean and standard deviation of elasticity and viscosity are tabulated in Table I. Bias is observed in comparison to the true values. The μ₁ has lower variation (CV ⩽ 0.07) than the viscosity, μ₂ (CV ⩽ 0.16).

Figure 5 shows 2D shear wave phase velocity images for the LISA heterogeneous, viscoelastic numerical Phantoms I, II, and III. The f₀ used for the calculations was equal to (Fig. 5a) 300, (Fig. 5b) 550, and (Fig. 5c) 800 Hz for Phantoms I–III, respectively. Results for LPVI with a constant bandpass filter set to 0.5–11 m/s are shown. The constant, wide range of the wavenumber filter was selected in order to cover a wide range of phase velocity present in the examined phantoms. As in Fig. 3, it is demonstrated in Fig. 5 that when the wavenumber filter is not used, the reconstructions have noticeable artifacts and higher variation.

Fig. 5:

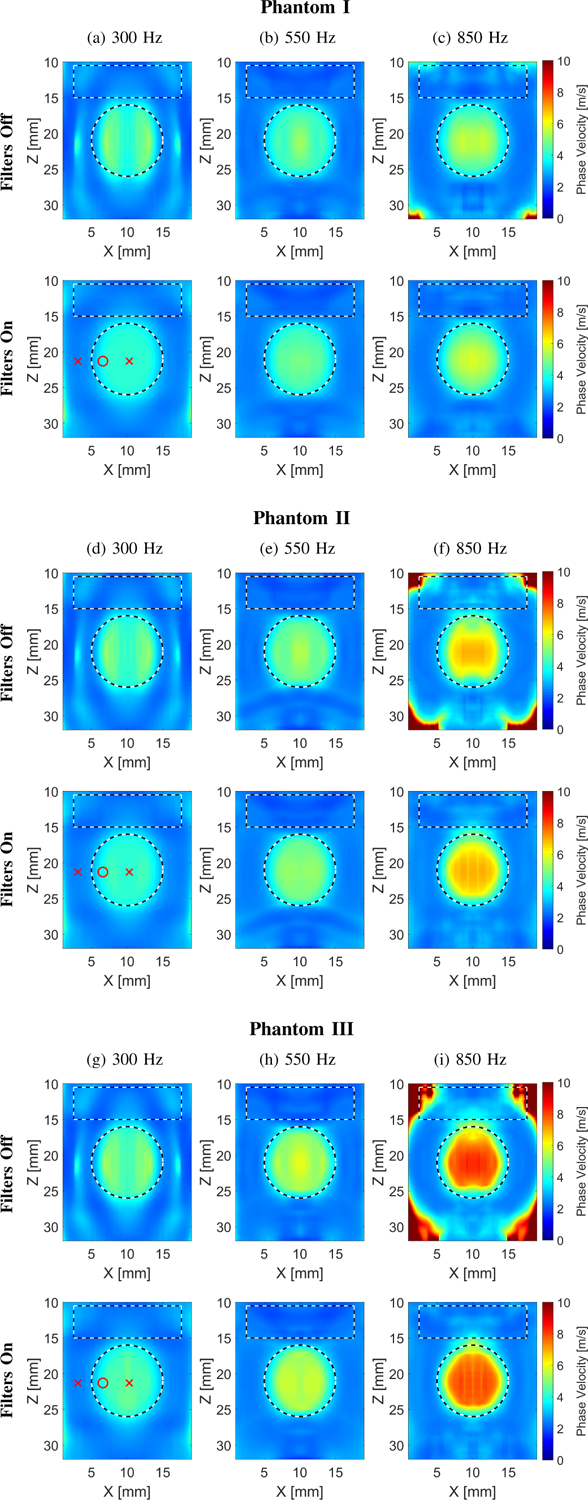
Two-dimensional shear wave phase velocity images for the LISA heterogeneous, viscoelastic numerical data. The f₀ used for the calculations was equal to (a), (d), (g) 300, (b), (e), (h) 550, and (c), (f), (i) 850 Hz for Phantoms I–III, respectively. Results for LPVI without bandpass filters similar to the work described in [40] are shown in the top row (Filters Off). Results for LPVI with active filters introduced in this manuscript (for a constant bandpass filter set to 0.5–11 m/s) are shown in the bottom row (Filters On). The window size, W_z,x, was equal to 4.0 × 4.0 mm. Red markers in (a), (d) and (g) in the bottom row correspond to positions, for the background and inclusion, for which phase velocity curves in Fig. 7 were plotted.

The viscoelastic parameters were estimated, similarly as for the numerical homogeneous phantoms. Results are summarized in Table II. The frequency ranges used for the 2D viscoelastic maps reconstruction shown in Fig. 6 were chosen to be constant and set from 200 to 900 Hz, for all heterogeneous phantoms investigated. The shape of the reconstructed viscoelastic inclusions are well preserved. However, bias in the reconstructed μ₁ and μ₂ values is observed. Figure 7 shows phase velocity dispersion curves calculated for the (Fig. 7a) background, and (Figs. 7b–7c) inclusion single locations marked in Fig. 5a. Blue dots correspond to LPVI data. Red, dashed lines represent NLSQ fit to the KV model for LPVI data. Black, continuous lines show theoretical dispersion curves computed using Eq. (11). Observed bias might be caused by a few phenomena which will be further discussed in Sec. IV.

TABLE II:

Mean, standard deviation and uniformity coefficient (i.e. CV = SD/MEAN) of the phase velocity and viscoelastic parameters μ₁ and μ₂, calculated for the LISA numerical phantoms within the ROIs marked in Fig. 5, for LPVI. Results in triangular brackets, 〈·〉, present mean error calculated using the true values. Results for ${\mathcal{F}}_{2D}$ are not presented because, the ${\mathcal{F}}_{2D}$ technique gives higher root-mean-sqaure-error (RMSE) when short lateral segment lenght is taken into account as it was discussed for example in [28].

Parameter	Unit	Phantom I		Phantom II		Phantom III
		Mean±SD	CV	Mean±SD	CV	Mean±SD	CV
Vph, Inclusion, filters On	[m/s]	3.93±0.30 (300 Hz)	0.08	3.98±0.33 (300 Hz)	0.08	4.16±0.44 (300 Hz)	0.10
Vph, Inclusion, filters Off	[m/s]	4.23±0.56 (300 Hz)	0.13	4.26±0.55 (300 Hz)	0.13	4.41±0.59 (300 Hz)	0.13
Vph, Background,, filters On	[m/s]	2.56±0.18 (300 Hz)	0.07	2.55±0.17 (300 Hz)	0.07	2.55±0.18 (300 Hz)	0.07
Vph, Background,, filters Off	[m/s]	2.59±0.21 (300 Hz)	0.08	2.58±0.23 (300 Hz)	0.09	2.59±0.27 (300 Hz)	0.11
Vph, Inclusion, filters On	[m/s]	4.25±0.46 (550 Hz)	0.11	4.54±0.57 (550 Hz)	0.13	4.90±0.75 (550 Hz)	0.15
Vph, Inclusion, filters Off	[m/s]	4.27±0.45 (550 Hz)	0.11	4.55±0.53 (550 Hz)	0.11	4.91±0.68 (550 Hz)	0.14
Vph, Background,, filters On	[m/s]	2.27±0.16 (550 Hz)	0.07	2.26±0.15 (550 Hz)	0.07	2.28±0.16 (550 Hz)	0.07
Vph, Background,, filters Off	[m/s]	2.27±0.14 (550 Hz)	0.06	2.25±0.14 (550 Hz)	0.06	2.23±0.15 (550 Hz)	0.07
Vph, Inclusion, filters On	[m/s]	4.66±0.73 (850 Hz)	0.16	5.53±1.20 (850 Hz)	0.22	6.42±1.44 (850 Hz)	0.22
Vph, Inclusion, filters Off	[m/s]	4.61±0.67 (850 Hz)	0.15	5.41±1.14 (850 Hz)	0.21	6.42±1.58 (850 Hz)	0.25
Vph, Background,, filters On	[m/s]	2.40±0.12 (850 Hz)	0.05	2.57±0.26 (850 Hz)	0.10	2.58±0.29 (850 Hz)	0.11
Vph, Background,, filters Off	[m/s]	2.58±0.32 (850 Hz)	0.12	3.16±1.17 (850 Hz)	0.37	4.18±2.44 (850 Hz)	0.58
μ1, Inclusion, filters On	[kPa]	15.43±2.19 (6.57)	0.14	13.85±1.72 (8.15)	0.12	11.0.4±1.72 (10.96)	0.15
μ1, Inclusion, filters Off	[kPa]	16.90±3.16 (5.10)	0.19	15.37±2.48 (6.63)	0.16	12.91±3.46 (9.09)	0.27
μ1, Background, filters On	[kPa]	5.42±0.66 (0.92)	0.12	5.33±0.61 (0.83)	0.11	5.80±0.27 (1.30)	0.05
μ1, Background, filters Off	[kPa]	5.43±0.61 (0.93)	0.11	5.30±0.70 (0.80)	0.13	4.67±0.93 (0.17)	0.20
μ2, Inclusion, filters On	[Pa·s]	2.16±1.04 (0.16)	0.48	3.83±1.55 (0.17)	0.46	4.64±1.84 (1.36)	0.40
μ2, Inclusion, filters Off	[Pa·s]	1.62±1.10 (0.38)	0.68	3.15±1.56 (0.85)	0.50	4.62±1.96 (1.38)	0.42
μ2, Background, filters On	[Pa·s]	0.30±0.19 (0.00)	0.64	0.34±0.20 (0.04)	0.61	0.35±0.21 (0.05)	0.59
μ2, Background, filters Off	[Pa·s]	0.29±0.19 (0.01)	0.66	0.43±0.28 (0.13)	0.65	1.35±0.94 (1.05)	0.70

Fig. 6:

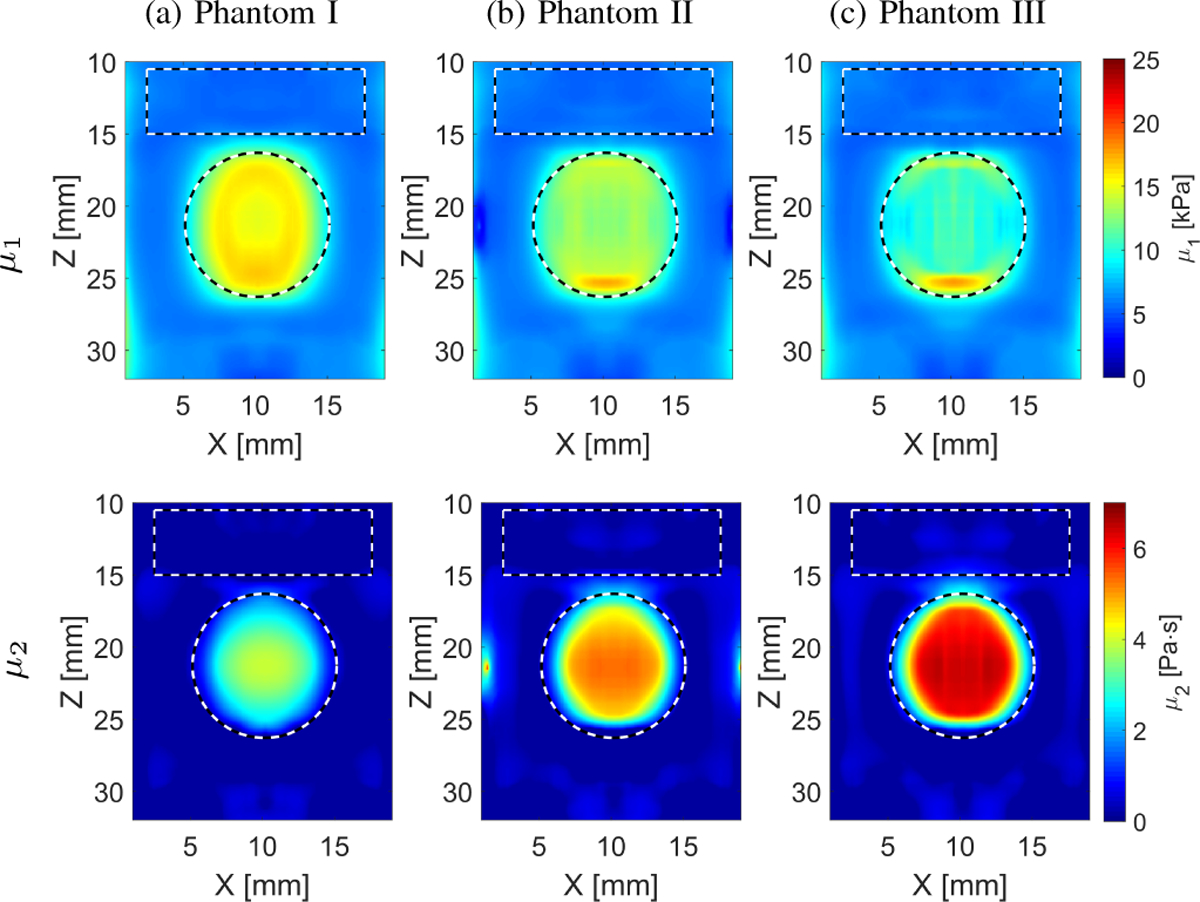
Two-dimensional image reconstructions of μ₁ and μ₂ calculated based on the Kelvin-Voigt rheological model for the LISA heterogeneous, viscoelastic numerical data. Results for LPVI with active bandpass filters introduced in this manuscript are shown. The theoretical background shear modulus was 4.5 kPa and the circular inclusion shear modulus was 22 kPa for all models, respectively. The viscosity of the background was 0.3 Pa·s. The inclusion’s viscosity was 2 Pa·s for Phantom I, 4 Pa·s for Phantom II, and 6 Pa·s for Phantom III, respectively.

Fig. 7:

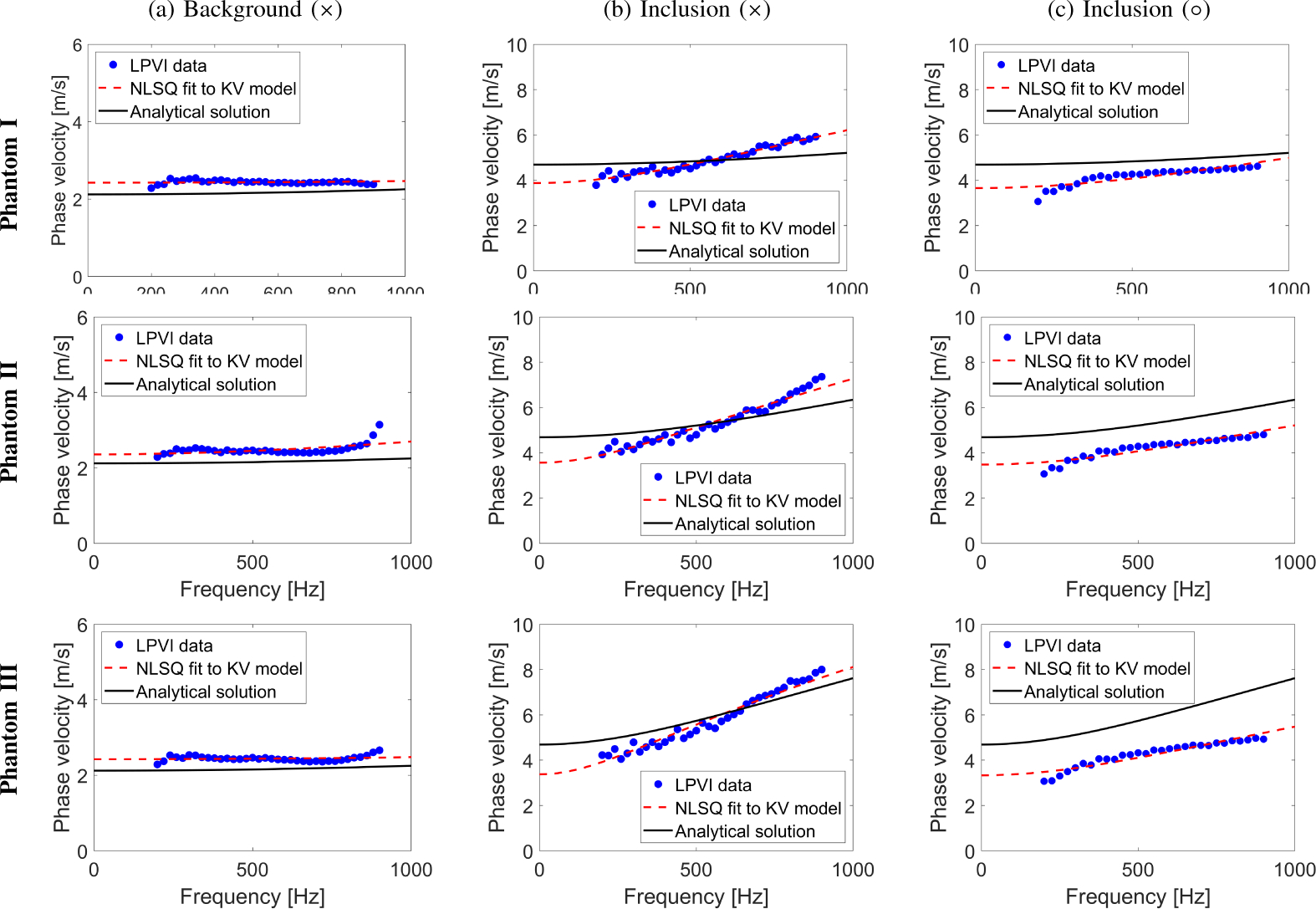
Phase velocity dispersion curves calculated for the (a) background, and inclusion locations marked as (b) ×, and (c) ○ in Fig. 5a using red markers. Blue dots correspond to LPVI data. Red, dashed lines represent NLSQ fit to the KV model for LPVI data. Black, continuous lines show theoretical dispersion curves computed using Eq. (11).

2). TM Phantoms Results:

The shear wave experiments were performed as described in Sec. II-D and processed according to Sec. II-A. Figure 8 shows the shear wave motion maps (top row), the k-space spectra (middle row) and phase velocity results (bottom row) for Phantom A (Fig. 8a), and Phantom B (Fig. 8b), respectively. The phase velocity results were calculated based on the standard ${\mathcal{F}}_{2D}$ technique for the focused excitation push beam depth, as well as using the LPVI approach (a mean, standard deviation and CV of phase velocity calculated for the ROIs marked in Fig. 9). Here, a similar estimate of the mean phase velocity based on the LPVI approach is observed. Results agree well with data calculated using standard ${\mathcal{F}}_{2D}$ as can be seen in Fig. 8, the bottom row.

Fig. 8:

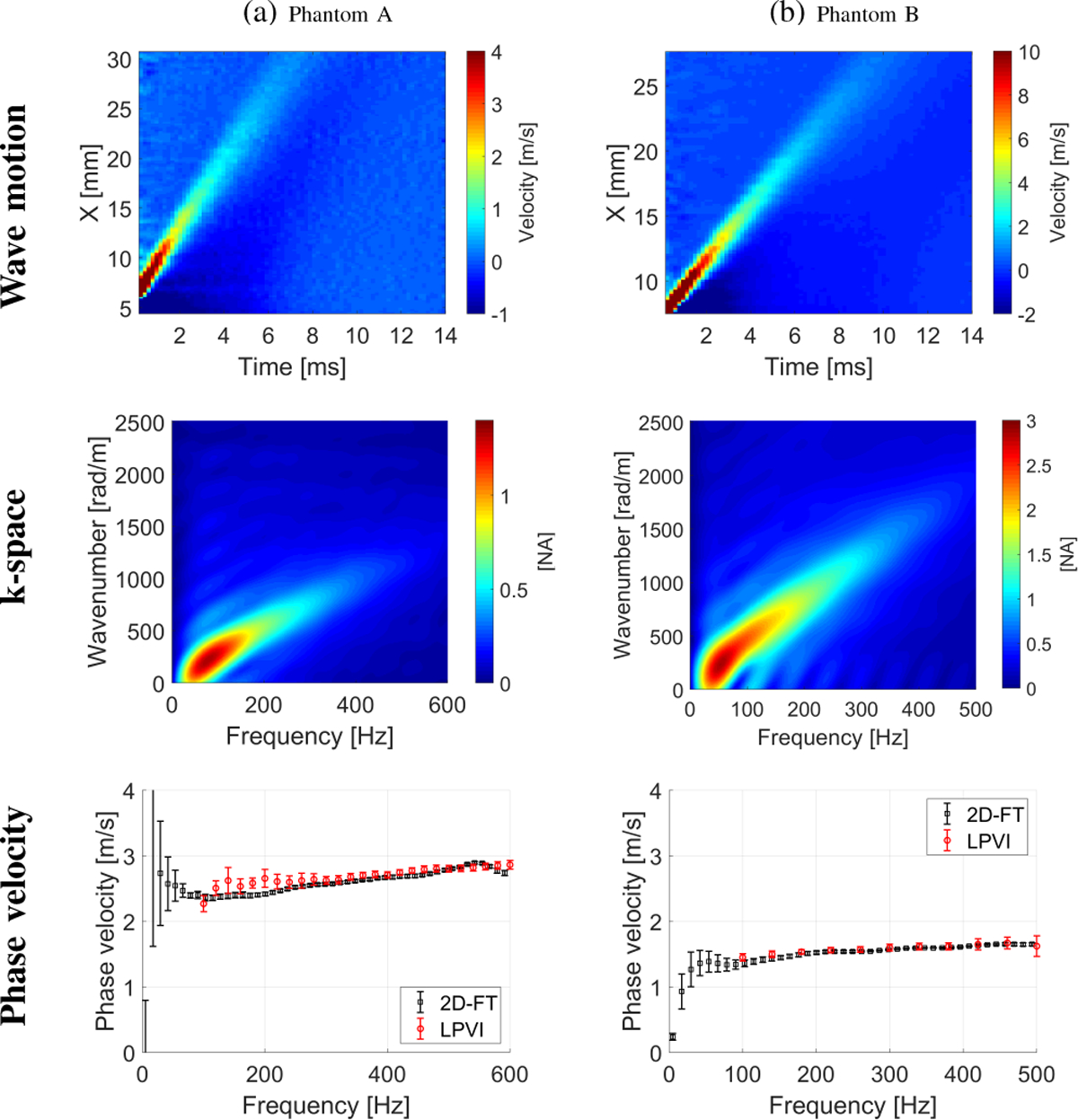
The shear wave motion (top row), the k-space spectrum (middle row) and phase velocity (bottom row) calculated for the TM viscoelastic phantom experimental data. Phase velocity results (bottom row) for LPVI with active bandpass filters introduced in this manuscript are shown.

Fig. 9:

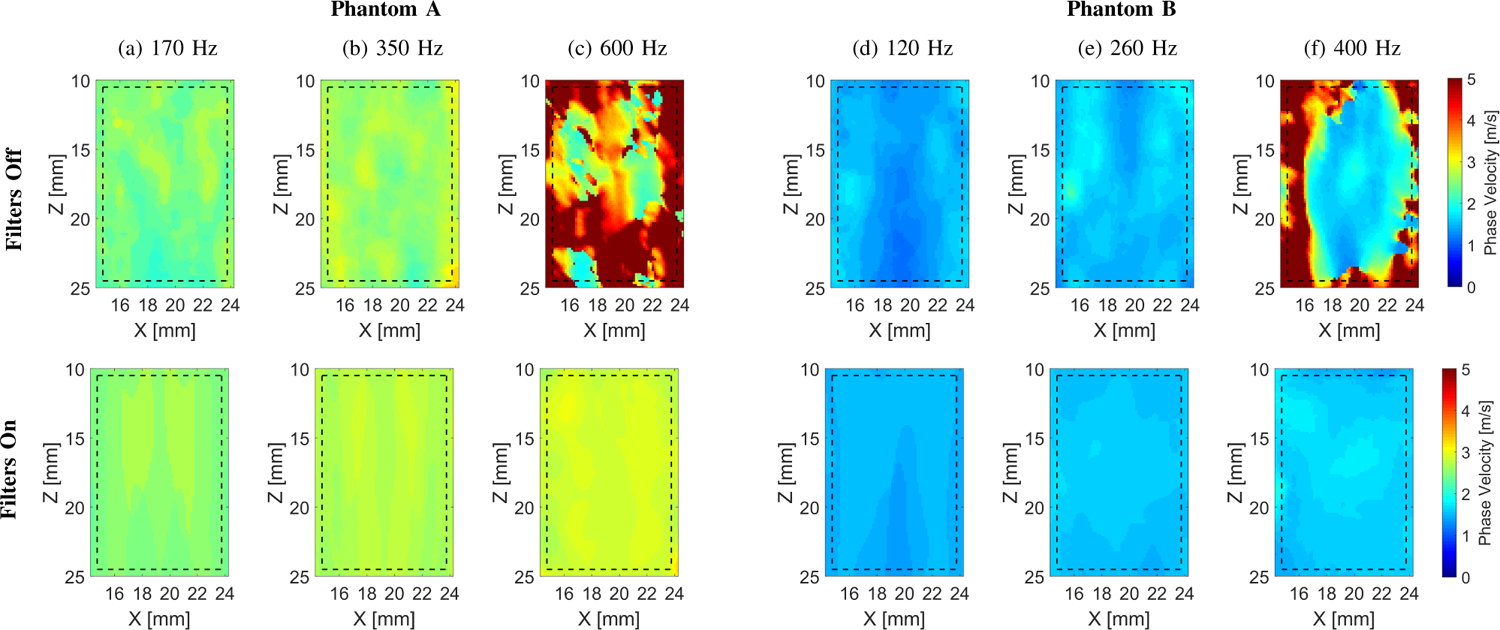
Two-dimensional shear wave phase velocity images for the experimental TM viscoelastic phantom data. The f₀ used for the calculations was equal to (a) 170, (b) 350, and (c) 600 for Phantom A, and (d) 120 Hz, (e) 260, and (f) 400 Hz for Phantom B, respectively. Results for LPVI without bandpass filters similar to the work described in [40] are shown in the top row (Filters Off). Results for LPVI with active filters introduced in this manuscript are shown in the bottom row (Filters On). The window size, W_z,x, was equal to 4.0 × 4.0 mm.

Figure 9 shows 2D shear wave phase velocity images for the experimental TM phantoms data. Results for LPVI without bandpass filters, similar to the work described in [40], are shown in the top row of Fig. 9. Similar results however, for LPVI with active filters described in Sec. II-A are presented in the bottom row of Fig. 9. The phantoms were imaged for three selected frequencies. Phase velocities from the images for active filters (Filters On) agreed well with the ${\mathcal{F}}_{2D}$ estimation. However, results for ‘Filters Off’ exhibited higher standard deviation. Moreover, 2D shear wave phase velocity images reconstructions failed for higher frequencies investigated in this work, i.e. 600 Hz for Phantom A (Fig. 9c), and 400 Hz for Phantom B (Fig. 9f). The measured mean shear wave phase velocity estimates along with standard deviation are also summarized in Table III for two TM phantoms.

The viscoelastic 2D maps, μ₁ and μ₂, were evaluated based on the frequency-dependent 2D shear wave velocity maps reconstructed using LPVI with adopted bandpass filters (bottom row of Fig. 9). The frequency ranges used for the 2D viscoelastic maps reconstructions were chosen as follow: Phantom A: 270 – 500 Hz and Phantom B: 100 – 400 Hz, respectively, corresponding to the main frequency content present in the k-space spectra (values corresponding to magnitudes >0.2) in Fig. 8. For the experimental CIRS phantom results presented in Fig. 10 some heterogeneity, especially for the viscosity map in Phantom B, is observed (CV = 0.15). This effect might be caused by sensitivity of the nonlinear least-squares function to data sets.

Fig. 10:

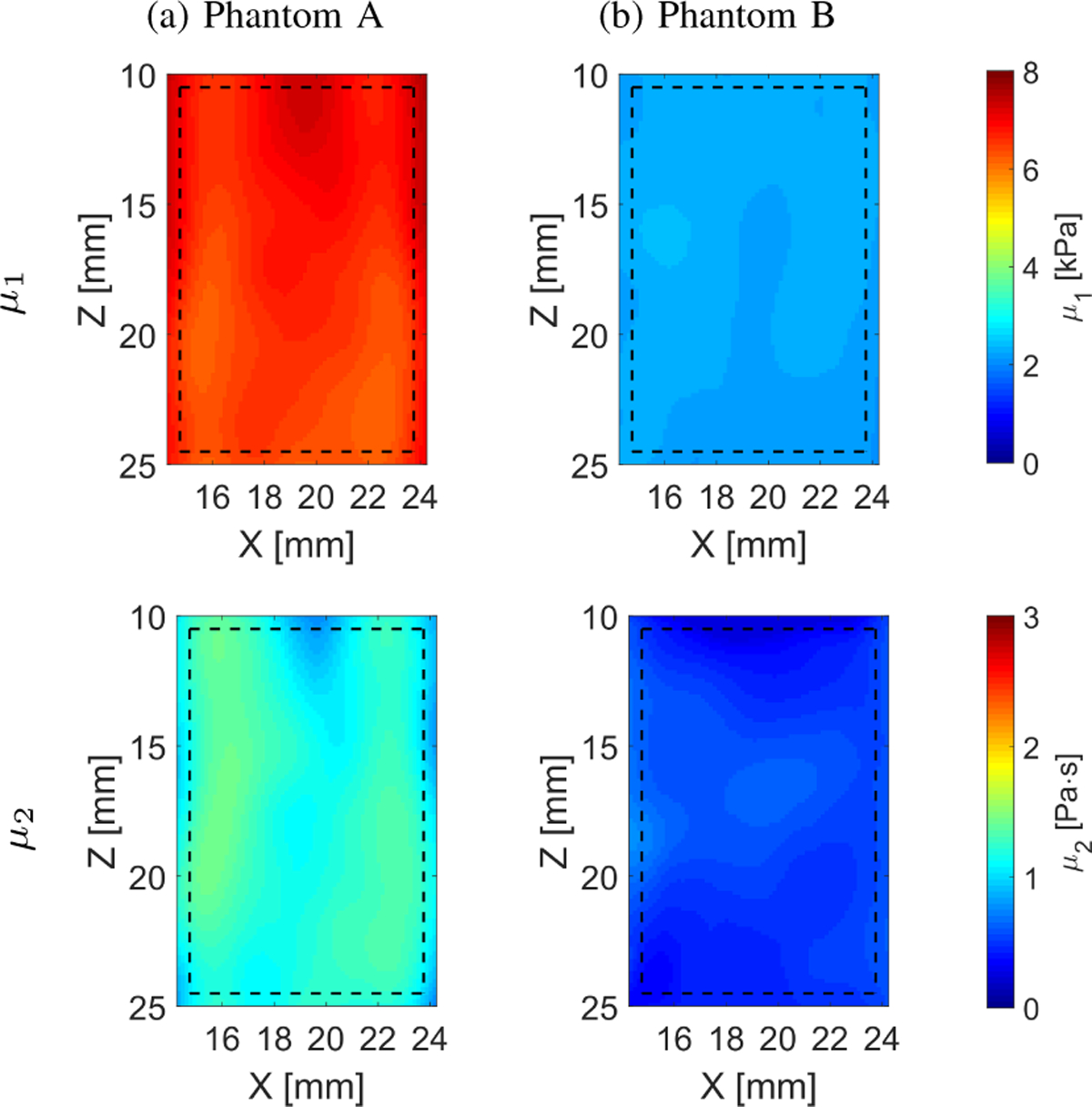
Two-dimensional image reconstructions of μ₁ and μ₂ calculated based on the Kelvin-Voigt rheological model for the TM viscoelastic phantoms experimental data. Results for LPVI with active bandpass filters introduced in this manuscript are shown.

3). In vivo Human Liver Results:

Figure 11 shows the wave motion (top row), the k-space (middle row) and phase velocity (bottom row) calculated for the in vivo human livers for five healthy volunteers. Figure 12 summarizes the 2D LPVI-based shear wave velocity distributions using the approach described in Sec. II-A. The shear wave velocity maps are presented for three frequencies (80, 140 and 200 Hz). Uniform phase velocity maps can be distinguished. An increase of the shear wave velocity with frequency is also visible in Fig. 12. This originates from liver’s viscoelastic nature. A summary of the measured mean, standard deviation and CV of shear wave phase velocity estimates for both locations are summarized in Table IV.

Fig. 11:

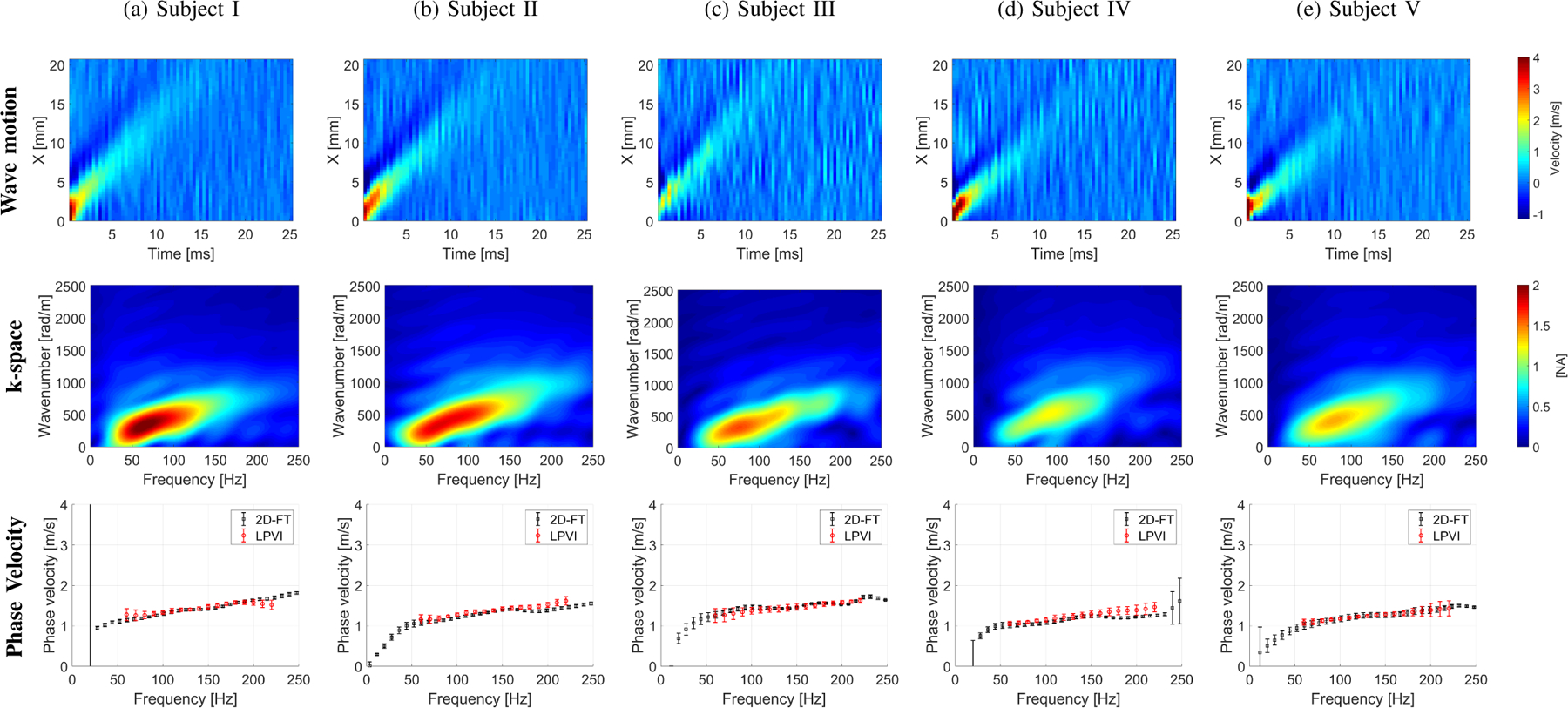
The shear wave motion (top row), the k-space spectrum (middle row) and phase velocity (bottom row) for the experimental in vivo human liver studies. Phase velocity results (bottom row) for LPVI with active bandpass filters introduced in this manuscript are shown.

Fig. 12:

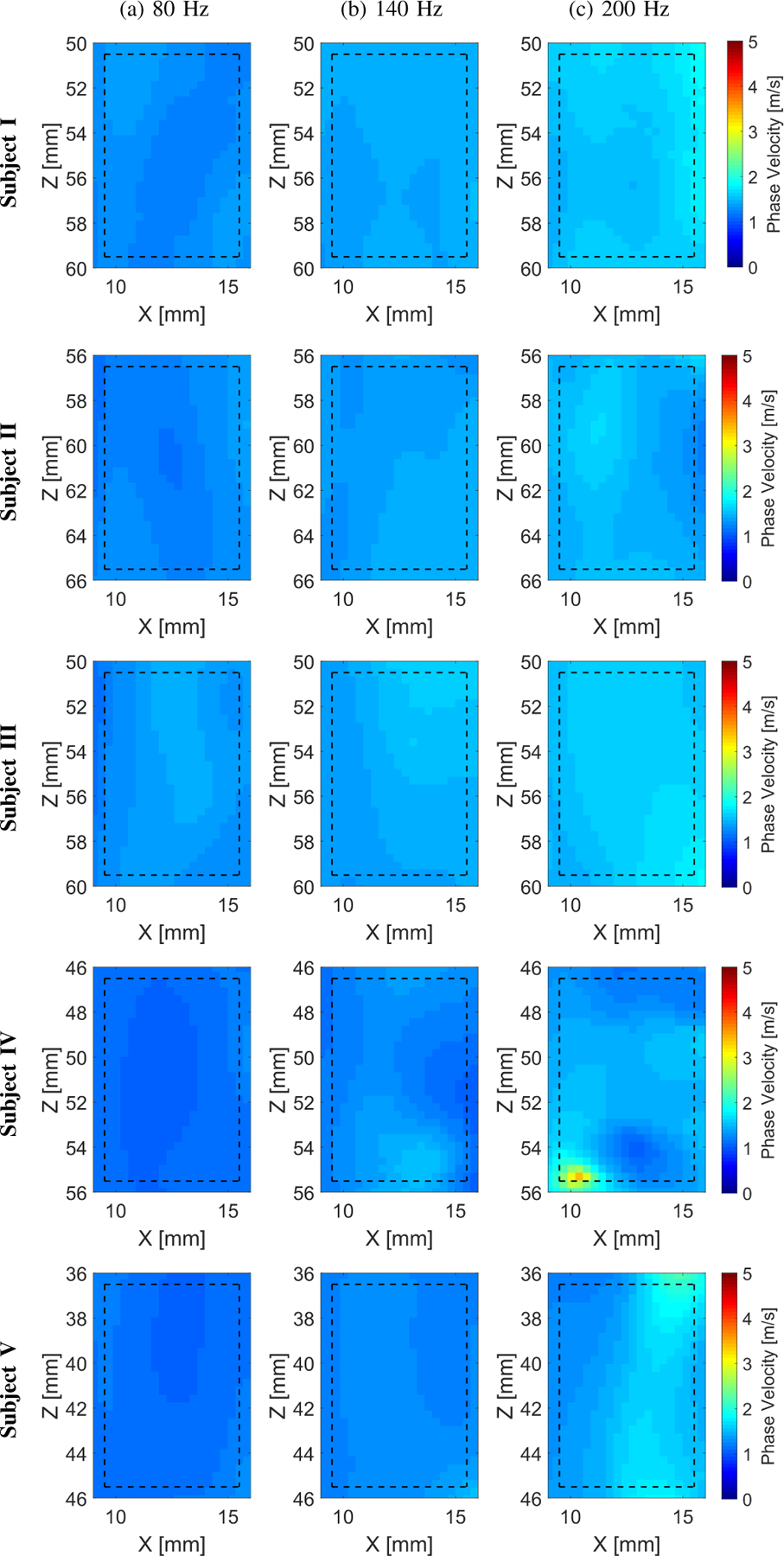
Two-dimensional shear wave phase velocity images for the experimental in vivo human liver studies. The f₀ used for the calculations was equal to (a) 80, (b) 140, and (c) 200 for all five subjects examined, respectively. Results for LPVI with active bandpass filters introduced in this manuscript are shown. The window size, W_z,x, was equal to 5.17 × 5.17 mm.

The viscoelastic 2D maps, μ₁ and μ₂, were evaluated based on the frequency-dependent 2D shear wave velocity maps. The frequency ranges used for the 2D viscoelastic maps reconstructions were chosen as follow: Subject I: 60 – 200 Hz; Subject II: 80 – 180 Hz; Subject III: 90 – 180 Hz; Subject IV: 80 – 190 Hz; and Subject V: 60 – 160 Hz, corresponding to the main frequency content present in the k-space spectra (values corresponding to magnitudes >0.2) in Fig. 11. More heterogeneity is observed for the in vivo liver on both elasticity and viscosity reconstruction maps (Fig. 13) for Subjects III (CV ⩽ 0.14) and IV (CV ⩽ 0.17), respectively.

Fig. 13:

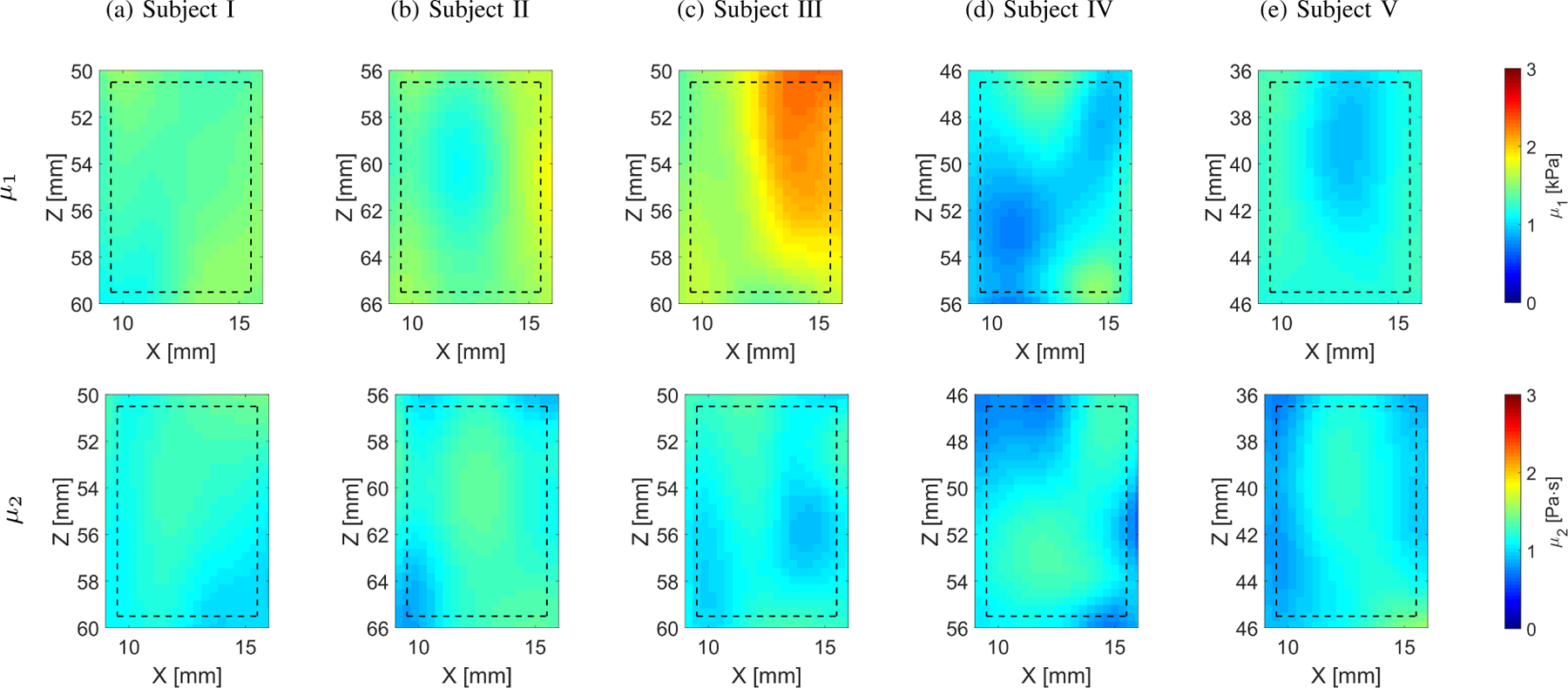
Two-dimensional image reconstructions of μ₁ and μ₂ calculated based on the Kelvin-Voigt rheological model for the in vivo human liver experimental data. Results for LPVI with active bandpass filters introduced in this manuscript are shown.

IV. Discussion

In this study, LPVI was used for shear wave velocity mapping in viscoelastic tissues. Results showed the proposed method is capable of measuring phase velocities accurately. Soft tissues are viscoelastic, which imposes higher attenuation of shear waves reducing the propagation distance in comparison to elastic phantoms [40]. The shear wave velocity is frequency dependent due to tissue viscosity. Therefore, an additional step to LPVI was added in contrast to the procedure and results presented in [40], that is, a bandpass filter in the wavenumber domain.

As examined numerical models and experimental data have shown, applying the bandpass filter in the wavenumber domain improves phase velocity maps reconstruction (Figs. 3 and 9, and Tables I and III). This overcomes issues shown in the top row of Figs. 3 and 9 with adequately estimating the shear wave phase velocity of viscoelastic materials. As a result, the reconstructed phase velocity maps are more accurate, as can be seen in bottom rows of Figs. 2 and 8, and results summarized in Tables I and III. Moreover, the estimation errors and their standard deviations are much smaller by using wave mode isolation. Shear wave mode isolation, due to suppressing noise, allows to retrieve an information over a wider frequency range (Figs. 3c, 3f and 3i, and Figs. 9c and 9f).

The bandpass filter is used in order to increase the frequency range for which 2D phase velocity maps could be reconstructed. The bandpass filter with narrower bandwidth is mostly beneficial for higher frequencies where the magnitude spectrum and SNR are reasonably low. For lower frequencies, with higher magnitude spectrum values and SNR, the bandpass filter could be omitted or the bandwidth could be set to be constant. This is confirmed for example in Figs. 9a–9c. Results for lower frequencies (170 and 350 Hz) are very similar for LPVI without (top row) and with (bottom row) the applied the bandpass filter. On the other hand, 2D phase velocity maps reconstructed for higher frequency, e.g. 600 Hz, were greatly improved when the bandpass filter was applied. Hence, one can conclude that the bandpass filter does not need to be applied for elastic or viscoelastic materials, for frequencies, where higher magnitude spectrum values and SNR are present. For these cases the bandpass filter might have limited impact (see as an example Figs. 9a and 9b).

If the bandpass filter is set to be too narrow, it could bias the results. In our work we performed multiple studies to determine the value of V_k(f₀) = 0.5 m/s for the homogeneous cases. For the heterogeneous phantoms the passband for the filter was widened substantially (0.5–11 m/s) to accommodate this situation. For clinical use, shear wave elastography is typically used for differentiation of tissues. A lesion would have likely been identified previously using mammography, ultrasound, magnetic resonance imaging, etc. and then if ultrasound imaging was used, the lesion would be located and shear wave elastography would be used. As a result, the wavenumber filter could be set wider knowing that two different classes of material are present (lesion and background). In the case of homogeneous liver, the wavenumber filter could be much narrower, but guided by the data as it is described in this paper (Eq. (2)).

Reconstructed μ₁ and μ₂ parameters for the heterogeneous numerical data investigated in this work exhibited some bias. The μ₁ values were underestimated, whereas the μ₂ values were overestimated for the circular inclusion, for Phantoms I–III (Fig. 6). The propagation velocity of shear waves within the inclusion may be physically modified by the boundary effects imposed by the background material. Therefore, the shear wave velocity within the inclusion may no longer be solely determined by the inclusion’s material properties. The bias is related to reconstructions of the phase velocity maps. First, the spatial resolution of LPVI is determined by the spatial shear wavelengths which are shorter at the higher frequencies. LPVI ideally requires one or more wavelengths to precisely estimate the shear wave velocity of inclusions as discussed in [40]. In our work, the 10 mm diameter inclusions have a shear wave speed of 4.69 m/s and this value is higher due to added viscosity. The investigated viscoelastic inclusions will have more than one wavelength at frequencies higher than 469 Hz. Second, the LPVI algorithm assumes local homogeneity by selecting a spatial window size. This is violated near boundaries between regions with different stiffness. The shear wave velocity gradually transitions between regions [40], leading to elevated shear wave velocities in the background (Fig. 7a) and diminished shear wave velocity inside the inclusion near the boundary (Fig. 7c). Third, the measured shear wave phase velocity in the inclusion varies with frequency even for purely elastic materials, as it was shown based on the numerical and experimental data in [40]. Due to the viscoelasticity there is a range of wavelengths at different frequencies that are possible. This further increases difficulties. Future work will be devoted to examining the sources of bias and estimating the shear elasticity and viscosity accurately.

The estimated mean phase velocities calculated within selected ROIs for the numerical phantoms, the bottom row of Fig. 3, showed good agreement with true values, as demonstrated comparing the values in the bottom row of Fig. 2. The results for frequencies below 100 Hz are slightly overestimated in comparison to the analytical solutions. However, they match with the values computed using the ${\mathcal{F}}_{2D}$ technique. There are two possible reasons for this behavior. First, the effect of the push beam excitation that has been used. The L7–4 probe with 48 active elements was modeled to generate the push beam excitation. Shear waves do not propagate in lateral locations close to the spatial extent of the pushing beam. The near-field effect, which is related to local effects of the acoustic radiation force push beam, is wider in the lateral direction in this region which may have influenced the reconstruction of phase velocity maps. This in turn introduces bias in computed mean phase velocities. Second, the shear wavelength increases for lower frequencies which can produce larger bias as was discussed in [40].

Results for the TM phantoms and in vivo human liver experimental acquisitions are also in good agreement with outcomes computed using the ${\mathcal{F}}_{2D}$. Data from the in vivo liver tests had significant levels of noise that were blurred by a spatial median filter in the spatial direction for different time points. It is worth noting that LPVI mean phase velocities were estimated within the selected ROIs, whereas ${\mathcal{F}}_{2D}$ results were computed for only one axial position as a result of averaging data from 3 mm in thickness at the push beam focus. Therefore, a bias in between the estimates is possible due to small phantom heterogeneity. For the in vivo data the coefficients of variation (CVs) are larger for the shear elasticity and viscosity compared to the numerical and physical phantom results. The viscosity CV values are relatively constant across the subjects, but there are large CV values for the shear elasticity. We cannot unambiguously state why more heterogeneity was observed for the in vivo data. The tissue-mimicking phantoms are very uniform due to control of the pouring conditions during manufacturing, where as there is more natural heterogeneity in the tissue that may be caused by presence of vessels and other anatomical variation. These subjects were different and were from healthy population.

A larger window size for the in vivo imaging was used because the pixel sizes for the in vivo experiments were roughly twice the size used in the numerical and TM experimental data. The in vivo data were acquired using a curved array transducer with a lower center frequency so higher spatial resolution could not be matched compared to the data acquired using a linear array transducer. We used a window size of 5.17 × 5.17 mm for the in vivo study which corresponds to 15 × 15 pixel segmented data. It was assumed in this study that this pixel size is a lower limit when used for the 2D-FT calculations. Reducing the 15 × 15 pixel segmented data will produce higher noise in reconstructed phase velocity maps.

The LPVI method is an alternative method used for 2D ultrasound SWE where local shear wave phase velocity results are recovered. The 2D-FT method instead, was used in order to reconstruct phase velocity at a focal depth and typically a long lateral segment length (>10 mm) is used for calculations. In this work an axial average of 3 mm was used in order to improve the SNR of the shear wave particle velocity signal for the 2D-FT. A larger lateral segment length for 2D-FT than for the LPVI method was used in order to retrieve the most robust dispersion results for the 2D-FT method. Taking into account a short lateral segment length (<5 mm) will provide higher standard deviation in the phase velocity measurement, as was discussed, for example in [28]. Due to this the 2D-FT method with sliding window may give higher root-mean-square error and standard deviation if used for 2D phase velocity maps reconstruction.

Different tissues have different levels of viscosity. Softer materials with higher viscosity impose higher attenuation of shear waves. Shear waves at higher frequencies typically undergo higher attenuation and therefore do not propagate as far leading to shorter lateral imaging lengths. This effect can be seen, for example, in a magnitude spectrum (k-space) map. Limited shear wave energy distribution, in the frequency domain, will be present for softer and more viscous tissues. In work [40], 2D phase velocity maps were reconstructed for wider frequency ranges because nearly elastic materials with a very limited viscosity content were examined. In those materials shear waves at higher frequencies, e.g. 1000 Hz, were not attenuated within ROIs considered as opposed to the models and phantoms described within this manuscript. In this study, cut-off frequencies were chosen based on the k-space spectra for each phantoms separately. Based on these frequencies the size of the ROIs were selected. It is expected that in practice, the frequency range can be increased and optimized for higher frequency content.

The ROI size in the lateral direction was limited to ~10 mm for the numerical homogeneous data and TM phantoms, and ~7 mm for the in vivo human liver experimental data. We determined these limits from the phase velocity images at different frequencies when the reconstruction was not consistent and started to contain mainly noise. This was an indication that shear wave motion has insufficient amplitude for use in the LPVI algorithm. The lateral distance is dependent on shear wave attenuation phenomena, as discussed above. In clinical applications, in order to cover a wider ROI, multiple simultaneous pushes as utilized in the comb-push ultrasound shear elastography (CUSE) method can be used [55], [56]. This, in turn, will eliminate the necessity of knowing how far shear wave propagates in examined tissue. For a specific application, if the range of viscoelastic properties is known, the positioning of acoustic radiation force pushes could be optimized.

Patient motion or sonographer hand motion may change the field-of-view between the left and right pushes. It should be noted that these measurements take on the order of 25 ms, so for two independent pushes it would take 50 ms, so depending on the situation motion may be limited. However, in this situation two simultaneous pushes can be used. A directional filter in LPVI is applied on the shear wave field to extract the left-to-right (LR) and right-to-left (RL) propagating shear waves. Then, a local shear wave phase velocity map will be recovered based on both LR and RL waves. Using multiple simultaneous pushes as utilized in the CUSE method will ensure a constant field-of-view.

We used the phase velocity, measured using the 2D-FT method, in order to estimate nominal wavenumbers in a frequency domain for propagating shear wave. The nominal wavenumbers correspond to the center of the bandpass filter of V_k(f₀) width. This procedure is mostly beneficial for higher frequencies where the power spectrum magnitude and a SNR are reasonable low. For lower frequencies, where the power spectrum magnitude and a SNR are higher, the bandpass filter could be set to be constant, e.g. from 0.5 to 4 m/s. At the same time a knowledge about the 2D-FT phase velocity would not be necessary. This could be determined for a given application, for instance, liver fibrosis staging. The threshold for the magnitude spectrum to select the lower frequency corresponds to magnitudes higher than approximately 40% of the maximum frequency content present in the k-space spectrum, for the data investigated in this work. The limiting threshold for SNR is 5 dB when shear wave particle velocity signals are used [56].

Equation 11 assumes plane wave propagation. Based on the numerical phantom data shown in Fig. 2 and Table I, the assumption of a plane wave does not introduce considerable error. For the estimation of phase velocity, the presence of a wave more similar to a cylindrical wave generated by the acoustic radiation force does not introduce considerable error.

Based on the 2D-FT measurements shown in Figs. 8 and 11, it can be reasonably stated that a Kelvin-Voigt model can describe the dispersion curves over a frequency range of 100 – 600 Hz. The accuracy of these characterizations can not be evaluated in a direct way. However, based on authors experience with this type of phantom data and liver data, as well as many literature studies, e.g. [6], [15], [20]–[24], [34], [38], [43], the model is considered to be reasonable for parameterization.

LPVI can be used for assessing 2D elasticity and viscosity from shear wave measurements. This approach enables the generation of shear wave phase velocity maps with a lateral and axial resolution that are primarily determined by the moving spatial window, W_z,x, and the spatial wavelengths which are shorter at the higher frequencies. Choosing an appropriate W_z,x leads to a trade-off. For lower frequencies a larger W_z,x window is preferred in order to capture enough information about the wavelength. It is preferred that the W_z,x window will capture at least one shear wavelength. However, for low frequencies, i.e. 100–200 Hz, and some soft materials this can be difficult. On the other hand, choosing a W_z,x that is too small (for high frequencies, i.e. 1000 Hz) provides a noisier image which was addressed in [40].

The elasticity and viscosity maps computed based on the reconstructed LPVI shear wave phase velocity images show deviation from the exact values for the LISA homogeneous, viscoelastic phantoms, Fig. 4. These are likely due to variations present in the LPVI velocity maps are transferred to the μ₁ and μ₂ mapping. The KV model dispersion relation has frequency ranges with upward and downward curvatures. Thus the KV model can yield variability in the fitted parameters as the fitting procedure attempts to identify these higher order variations. Moreover, the nonlinear least squares fit problem, for the KV model, is sensitive to the input data. Errors in reconstructed phase velocity will produce deviation in elasticity and viscosity results. Nevertheless, the idea of reconstructing the 2D images of mechanical properties is general hence, other rheological models can also be incorporated.

The computational time for the reconstruction of one 2D phase velocity map, for the TM phantom A, was ~9 seconds. Elasticity and viscosity images instead are reconstructed directly from a number of 2D phase velocity maps which takes a couple of seconds. In summary, a total computation time in order to get reconstructed elasticity and viscosity maps for Phantom A was ~3 minutes. The computation time will however depend on the ROI size which is to be reconstructed, as discussed in [56].

In this work particle motion for the numerical models was calculated by taking derivatives of displacements. The noise in the displacement estimation does not affect extensively phase velocity maps reconstruction. This was studied in a work presented by Kijanka and Urban in [56]. In this work the LPVI method’s performance with an addition of white Gaussian noise to the shear wave particle velocity and displacement motion data was examined.

The presented work has some limitations that should be addressed in future work. First, 2D simulation data were used in order to generate numerical phantom data. Ideally, 3D models would be preferred to account for all aspects of the acoustic radiation force and 3D wave propagation, even though a 2D image is produced. In data not shown, we compared a simulation of a material based on the fits to phase velocity measured in Phantom A, and we found that the frequency bandwidth was similar between the 3D experiment and 2D simulation. Second, we have not systematically evaluated how patient or sonographer motion would impact the LPVI measurements, and this would need to be evaluated for clinical applications. Third, the NLSQ fit is sensitive to a frequency range as was discussed, for example in [43]. In addition, reconstructed μ₁ and μ₂ maps for the heterogeneous materials need extra steps in order to reduce, or at least minimize observed bias. Fourth, the LPVI method needs to be tested in materials, either numerical or tissue-mimicking phantoms, with a wider range of viscoelastic properties. Additional rheological models could also be explored, to account for a larger range of biological tissues. Fifth, if different transducers, focal configurations, and focal depths were used, the results with a given value of V_k(f) could yield different results. We did not study this aspect which is also a limitation of the current work and will be investigated in the future work. Lastly, we did not apply simulated ultrasonic tracking for the numerical studies, which is a limitation of this work. However, the experimental results from tissue-mimicking phantoms and in vivo liver data demonstrate similar agreement with data acquired using the 2D-FT as a comparison point.

V. Conclusions

This paper introduces LPVI used for 2D viscoelastic material parameters imaging. This was accomplished by generating 2D phase velocity maps and fitting phase velocity dispersion to find viscoelastic parameters based on the KV rheological viscoelastic model. The LPVI method, in order to properly work for viscoelastic materials, requires applying bandpass filters to obtain maximal frequency range for the phase velocity. LPVI demonstrates good reconstructions of 2D shear wave phase phase velocity, μ₁, and μ₂ maps, respectively, in homogeneous, viscoelastic phantoms and soft tissues with lower stiffness. Homogeneous materials higher levels of stiffness, for which the motion SNR will be lower, will be improved in the future. Reconstructions of heterogeneous, viscoelastic materials require additional work in order to reduce observed bias in reconstructed viscoelastic parameters.