Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2020 Oct 27.
Published in final edited form as: Phys Med Biol. 2019 Aug 21;64(16):165010. doi: 10.1088/1361-6560/ab3238

Non-Invasive Determination of Blood Input Function to Compute Rate of Myocardial Glucose Uptake from Dynamic FDG PET Images of Rat Heart In Vivo: Comparative Study Between the Inferior Vena Cava and the Left Ventricular Blood Pool with Spill Over and Partial Volume Corrections

Qiao Huang 1,*, James C Massey 1,2,*, Krzysztof Mińczuk 1, Jie Li 1, Bijoy K Kundu 1,2,3
PMCID: PMC7590261  NIHMSID: NIHMS1637846  PMID: 31307015

Abstract

The purpose of this work was to compute blood input function from the inferior vena cava (IVC) with partial volume (PV) corrections and compare to that obtained from the left ventricular blood pool (LVBP) with spill-over (SP) and partial volume (PV) corrections. These were then used to compute and validate rates of myocardial 2-deoxy-2-[18F]fluoro-D-glucose (FDG) uptake (Ki) from dynamic positron emission tomography (PET) images of rat hearts in vivo in comparison to that obtained from invasive arterial blood sampling. Whole body 60 minute dynamic FDG PET/CT imaging of n=8 control Wistar Kyoto (WKY) rats were performed using Albira trimodal PET/CT/SPECT scanner. Image derived blood input function (IDIF) obtained from IVC corrected for PV averaging (IVC-PV) and IDIF from the left ventricular blood pool (LVBP) with SP and PV corrections (LVBP-SP-PV) were computed. Next, computed Ki (indirect comparison) in a 5-parameter (using IVC-PV) and a 15-parameter (using LVBP-SP-PV) 3-compartment models in WKY rat hearts in vivo were compared to that obtained using arterial blood sampling reported in literature in control Spraque Dawley (SD) rats. Using IVC-PV in a 3-compartment 5-parameter model resulted in a ~46% deviation in the mean computed Ki compared to that obtained with LVBP-SP-PV in a 3-compartment 15-parameter model with a ~57% deviation in the mean computed Ki. The mean computed Ki in WKY rat hearts using the above methods, however, did not differ significantly to that obtained from invasive arterial blood sampling in SD rat hearts (p=0.91 for IVC-PV and p=0.58 for LVBP-SP-PV). Hence, Ki obtained in WKY rat hearts with input curve from IVC (IVC-PV) in a dynamic FDG PET scan is comparatively more repetitive to that obtained from the LVBP (LVBP-SP-PV). Ki computed using both the methods, however, agree well with each other and that obtained using arterial blood sampling.

Keywords: Dynamic FDG PET, Blood input function, Inferior vena cava, Left ventricular blood pool, Spill over and Partial Volume corrections

1. Introduction

Determination of blood input function non-invasively from dynamic 2-[18F] fluoro-2-deoxy-D-glucose positron emission tomography (FDG PET) images of rodent hearts has been challenging due to small size of the left ventricle and the limited spatial resolution of small animal scanners. This results in incomplete radioactivity recovery or partial volume (PV) averaging for both the myocardium and the blood pool resulting in significant spill-out contamination from the blood to the tissue at the early time points and spill-in from the tissue to the blood at the late time points in a dynamic FDG PET scan. Non-invasive estimation of the blood input function thereby becomes challenging due to multi-parameter nature of the optimization problem in a 3-compartment model (Krivokapich J et al 1982). Prior work by others (Fang and Muzic 2008) and from our laboratory (Zhong and Kundu 2013) developed a 15-parameter model for simultaneous estimation of model corrected blood input function (MCIF) and compartment model parameters to determine rate of myocardial FDG uptake, Ki. This method, however, utilized a deterministic method (Interior Reflective Newton (IRN)) for optimization of the objective function, which determines only a local minimum. This optimization technique is sensitive to changes in the bounds and initial guess values of the kinetic parameters. Recent work from our laboratory (Li and Kundu 2018) developed a hybrid method combining stochastic (Artificial Immune System (AIS)) and deterministic methods (IRN) for non-invasive estimation of Ki. This method is more robust in that it determines a global minimum, thereby making it less sensitive to changes in the bounds and guess values of the kinetic parameters. However, both the above described methods developed in rodents involve optimization of 15 parameters, which may be challenging in a clinical setting.

The goal of this study was to obtain image derived blood input function and downstream Ki, from the inferior vena cava (IVC) and compare to that obtained from the left ventricular blood pool (LVBP) of dynamic FDG PET images of control Wistar Kyoto (WKY) rats in vivo with spill-over (SP) and PV corrections.

2. Materials and Methods

Eight (n=8) control male WKY rats, purchased from Charles River (Kingston, NY), were housed under controlled conditions (temperature 21±1°C, humidity 60±10%, 12-hours light/12-hours dark cycle, and free access to standard rat chow and water). Animal experiments were approved by the Institutional Animal Care & Use Committee of the University of Virginia.

2.1. Dynamic FDG PET Imaging:

Eight male WKY rats, 2 months of age, were imaged using a state-of-art Albira trimodal PET/SPECT/CT scanner (González et al 2016). The Albira PET imager is a 3-ring scanner with an axial field of view (FOV) of 150 mm and trans-axial FOV of 80 mm, thereby enabling whole body PET imaging of 2-month old rats weighing around 200 g. The homogenous intrinsic spatial resolution of the scanner was reported to be better than 1.2 mm in the whole FOV of 80 mm. Dynamic FDG PET imaging of the rats was performed using a similar protocol as described earlier in mice (Zhong and Kundu 2013, Zhong et al 2013) and more recently in rats (Li et al JAHA 2019). Briefly, a 60 minute list mode (LM) acquisition, under 2% isoflurane anesthesia with a respiratory pillow attached to the chest, was initiated followed by intravenous injection of ~200–300 uCi of FDG via a tail-vein catheter over a period of ~10–20 seconds. The rats were fasted for 5–6 hours prior to PET imaging. A 3-bed CT scan followed the emission scan for attenuation correction. A small-animal gating and monitoring system (Small Animal Instruments, Inc., model 1025L for PET) was used for continuously monitoring respiration and core body temperature (using a rectal probe). The LM data was then sorted into 23 time bins (frames, time (s): 11,8; 1,12; 2,60;1,180;8,400) and the sinograms reconstructed with attenuation correction using Maximum Likelihood Expectation Maximization (MLEM) algorithm with 6 iterations and 0.75 mm isotropic voxel resolution (Huang et al 2018).

2.2. Input curve from the Inferior Vena Cave (IVC) and Partial volume corrections (IVC-PV):

Regions of interest (ROI) were drawn in the early time frame in the region corresponding to the inferior vena cava (IVC) (median volume: 4.5 mm3) and time activity curve (TAC) generated (blood TAC).

2.3. Partial volume corrections:

Partial volume (PV) corrections was performed on the blood TAC using a recovery coefficient (RC) that was generated for each rat by performing a convolution of the finite size of the IVC with a Gaussian distribution representing the spatial resolution of the Albira PET system. Since PV averaging is a function of geometry and does not depend on time, the blood TAC for each rat was then boosted by its corresponding RC.

2.4. Kinetic modeling:

The blood TAC obtained from the IVC corrected for PV averaging was used in a 3-compartment model (Zhong and Kundu 2013) to compute rate of myocardial FDG uptake, Ki. The formalism for the 3-compartment model was written as follows:

Cm(t)=1(t2−t1)⋅[(1−TBV)ρ⋅∫t1t2CT(t)dt+TBV∫t1t2Cp(t)dt] (1)

where, Cm(t) is the activity concentration over time, obtained from the time-resolved images, for a ROI drawn in the region corresponding to the myocardium; t1 and t2 are the beginning and end times of an acquisition frame (time bin); TBV and (1-TBV) (Hutchins GD et al J Nucl Med 1992; Muzic O et al J Nucl Med 1993) accounts for the SP contamination from the LV blood pool to the myocardium at the early time points and PV recovery of the myocardium activity respectively, assuming that they add up to 1 and ρ is the myocardial tissue density (1.042 g of tissue/ml of tissue). Cp(t) is the computed blood input curve and CT(t) is the model tissue, obtained by solving the differential equations indicating the rate of change of FDG concentration in the tissue as it traverses from the vascular to the extravascular and then to the cellular spaces (Zhong and Kundu 2013), defined as follows:

CT(t)=K1a1−a2⋅[(k3+k4−a1)e−a1t+(a2−k3−k4)e−a2t]⊗Cp(t) (2),

where K1-k4 are the kinetic parameters of the 3-compartment model (Zhong and Kundu 2013), ⊗ is the convolution operator and

a2,1=(12)(k2+k3+k4±(k2+k3+k4)2−4k2k4) (3)

Substituting equation (2) in (1) and assuming k4=0, as FDG gets trapped as FDG-6-phosphate and does not de-phosphorylate, we obtain the following:

Cm(t)=1(t2−t1)∫t1t2{(1−TBV)ρ[K1k3k2+k3∫0TCp(u)du+K1k2k2+k3∫0TCp(u)⋅e−(k2+k3)(T−u)du]+TBV⋅Cp(T)}dT (4)

Equation (4) was numerically solved using non-linear regression analysis in MATLAB_r2018a (Mathworks Inc., Natick MA), to obtain K1-k3 and hence Ki, defined as:

Ki=K1k3(k2+k3) (5)

Input curve from the LV cavity and model corrected blood input function (LVBP-SP-PV):

In addition to the IVC, ROIs were drawn in the regions corresponding to the LV cavity (median volume: 8.4 mm3) and myocardium and time activity curves generated. Using the formalism developed in mice (Zhong and Kundu 2013) and recently validated in rats (Li et al JAHA 2019), wherein, the kinetic parameters and the model corrected blood input function (MCIF) with spill over and partial volume corrections are determined simultaneously by optimization of a 15-parameter objective function as described (Zhong and Kundu 2013), Ki was computed for WKY rat hearts.

2.5. Statistical Analysis:

All data were reported as mean ± SD. Computed and measured Ki were compared using paired Student’s t tests. A p value of less than 0.05 was considered statistically significant.

3. Results

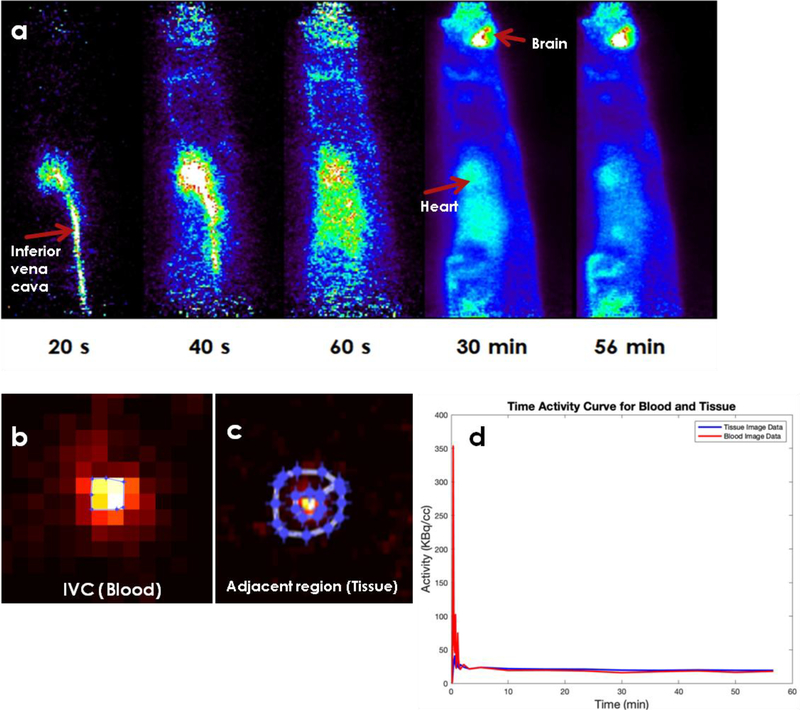
In Figure 1a, example time-resolved FDG PET images of IVC in control WKY rats are shown. Here we see that FDG in blood washes in and out of IVC very rapidly. This resulted in underestimation of image derived blood input function (IDIF) especially at late time points. The arrows in the image points toward the IVC, heart and the brain. Regions of interest are drawn on IVC (blood) (Figure 1b) and adjacent or surrounding regions (tissue) (Figure 1c) and time activity curves generated (Figure 1d). Using a dual output model (Zhong and Kundu 2013) the spill-in contribution from the tissue to blood was computed to be only 5.2% and hence not included in our computation of Ki.

Figure 1: Example time-resolved FDG PET images of IVC in control WKY rats.

Figure 1:

Open in a new tab

a) Time-resolved FDG PET images of the inferior vena cava (IVC) over a period of 60 minutes. The images indicate rapid wash-in and wash-out of FDG from IVC. The arrows point to the inferior vena cava, heart and brain. b) Regions of interest drawn on IVC (zoomed in), c) adjacent region and d) time activity curves for IVC and adjacent region. Computed adjacent region (tissue, t) to IVC (blood, b) spill-in (Stb) contamination using formalism developed earlier (Zhong and Kundu 2013) was negligible (~5%) and hence not included in the computation of Ki.

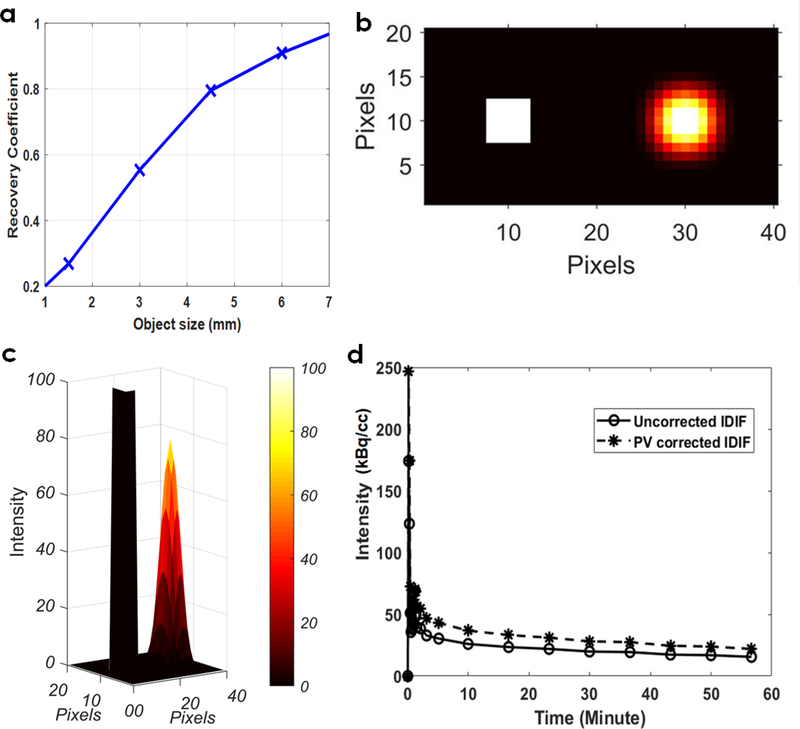
Partial volume correction was performed on IDIF obtained from IVC as shown in Figure 2 a–d. A RC plot was generated as a function of object size (1–7 mm) (Figure 2a) by performing a convolution of object size with a Gaussian distribution representing the spatial resolution of the Albira PET imaging system. Representative example 2D plot indicates original image of the simulated object (IVC) (left) (Seitz et al 2016) and that obtained after convolution (right) (Figure 2b). The 3D view of the intensity distributions are shown in Figure 2c, indicating a RC of ~70–80% for IVC after convolution considering detector blur. The average RC for eight control WKY rats were computed to be 75 ± 13%. In Figure 2d, example uncorrected IDIF and PV corrected IDIF for a control WKY rat are shown.

Figure 2: Partial volume corrections on IDIF obtained from IVC.

Figure 2:

Open in a new tab

(a) Recovery coefficient (RC) plot as a function of object size (1–7 mm) obtained by convolution of object size with a Gaussian distribution representing the spatial resolution of the Albira PET system. (b) Representative example 2D plot indicates image of the simulated object (IVC) (left) and that obtained after convolution (right). (c) 3D view of the intensities distributions are shown, indicating a RC of ~70–80% for IVC. (d) Example uncorrected IDIF and PV corrected IDIF for a control WKY rat.

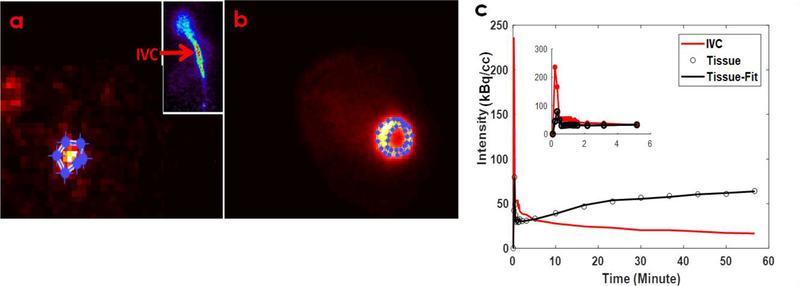
In Figure 3a–b, example transverse images of IVC and LV are shown with regions of interest (ROI) drawn and time activity curves (TAC) generated for the ROI’s. PV corrected IDIF from IVC (blood TAC) and model fit for tissue TAC correcting for the SP contamination from the LV blood pool to the myocardium at the early time points and the PV recovery of the myocardium in a 5-parameter 3-compartment kinetic model are shown in Figure 3c. The average Ki for control WKY rat hearts using input curve from IVC was computed to be 0.0409±0.019 (ml/min/g). Ratio of the standard deviation to the mean indicated a variation of 46.4% in the computed Ki.

Figure 3: FDG PET images of the IVC, LV and model fit.

Figure 3:

Open in a new tab

Example transverse images of IVC (a) and LV (b) are shown with regions of interest (ROI) drawn and time activity curves (TAC) generated for the ROI’s. (c) PV corrected IDIF from IVC (blood TAC; solid red line) and model fit (solid black line) for tissue TAC (open circles) correcting for SP contamination from the LV blood pool to the myocardium at the early time points and PV recovery of the myocardium in a 5-parameter 3-compartment kinetic model.

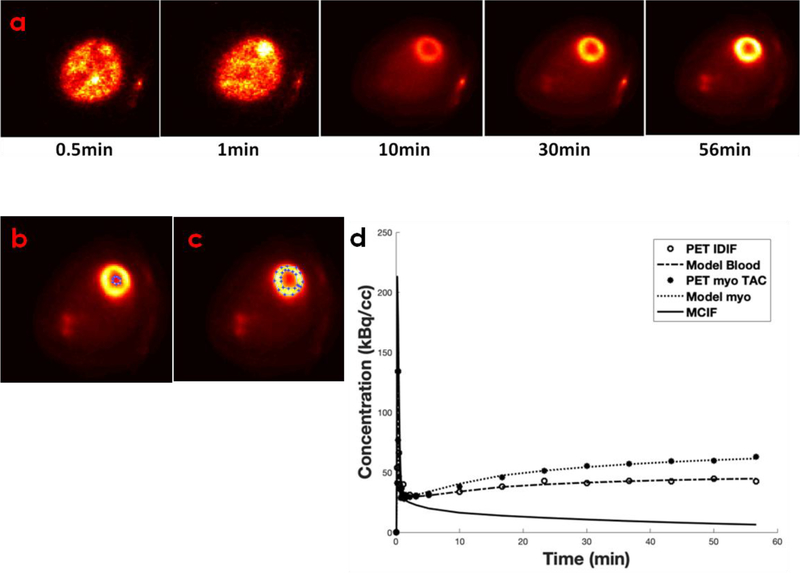
Representative time-resolved FDG PET images of the heart (Figure 4a) and regions of interest in the LV blood pool and the myocardium are shown in Figure 4b–c. Time activity curves obtained from the time-resolved images, computed model fits and model corrected blood input function (MCIF) are shown in Figure 4d. The average Ki for control KWY rat hearts using input curve from LV blood pool was computed to be 0.0479±0.026 ml/min/g. Ratio of the standard deviation to the mean indicated a variation of 55.7% in the computed Ki.

Figure 4: Time resolved FDG PET images of the heart and model corrected blood input function (MCIF).

Figure 4:

Open in a new tab

(a) Example dynamic FDG PET images of WKY rat heart in vivo over a period of 60 minutes. (b) Regions of interest drawn in the LV blood pool and (c) the myocardium. (d) Representative time activity curves for LV blood pools and myocardium, model fits, and model corrected blood input function (MCIF).

There is no significant difference between the computed Ki obtained from IVC and LVBP (p=0.56). The computed Ki using input curve from IVC (IVC-PV) and LVBP (LVBP-SP-PV) were then compared to that measured from arterial blood samples in control SD rats (0.042±0.022) (Fang and Muzic 2008). There was no significant difference observed between computed and measured Ki, using IVC-PV (p=0.91) and LVBP-SP-PV (p=0.76).

4. Discussion

The standard of care for obtaining blood input function in dynamic FDG PET imaging of rodents is arterial blood sampling (Laforest et al 2005, Pain et al 2004). This method is invasive (by catheterization of the carotid or femoral arteries) and requires significant blood sampling, more so at the early time points at a rapid rate (~10s intervals for a minute to catch the peak and coarser time intervals after that for 60 minutes to match the time bins obtained from imaging) due to quick changes in FDG metabolism at early time. Apart from the challenging nature of the surgical procedure for arterial blood sampling, due to limited blood volume of rodent hearts, significant blood sampling may compromise the physiological condition of the heart, there by affecting the resultant measured myocardial FDG uptake rates.

In order to minimize blood sampling, several methods have been developed over the years by us and others, which relies on image derived blood input function (IDIF), for computation of myocardial FDG uptake rates, Ki, in vivo. Hybrid methods (Shoghi and Welch 2007) rely on IDIF at the early time points and blood samples at the late time points to compute Ki. Due to the limited intrinsic spatial resolution of the rodent scanners, IDIF and tissue time activity curves are susceptible to PV averaging and SP contamination both at early and late time points in a dynamic PET scan. Prior methods by Fang et al (Fang and Muzic 2008) developed a parametric formulation of the output equation and optimized with the TACs derived from the FBP reconstructed dynamic PET images, which resulted in simultaneous estimation of model corrected input function (MCIF) and the kinetic parameters in vivo. Work performed in our lab concluded that high resolution reconstruction algorithm and cardiac gating can minimize SP contamination from the myocardium to the LV blood pool at the late time points, resulting in Ki not significantly different from that obtained using arterial blood sampling (Locke et al 2011). However, our results indicated that the above method did not completely eliminate SP contamination (~15%) at the late time points confounding its effect for smaller heart sizes. Therefore, a recent work from our lab combining high resolution reconstruction methods with parametric optimization and cardiac gating eliminated SP contamination (~5%) resulting in significant improvement in computed Ki when compared to that obtained from arterial blood sampling (Zhong and Kundu 2013). The optimization method here used “fmincon” in Matlab, which utilizes a deterministic algorithm based on Interior Reflective Newton (IRN) algorithm to search for a local minimum. Another recent work from our lab combined stochastic and deterministic methods to search for global minimum, resulting in improve estimation of the computed Ki in a 15-parameter 3-compartment model (Li and Kundu 2018). However, due to the multi-parameter nature of these methods, the computed Ki is sensitive to bounds of the model parameters and to initial guess values. Further work by others (Kim et al 2006, Fakhri et al 2005) and us (Huang et al 2018) used factor analysis techniques using principle component analysis (PCA) to segment out LV blood pool from the myocardium and the surrounding background to compute IDIF based on time-dependent pixels in dynamic FDG PET scans of WKY rat hearts. This method, although requires no human intervention in defining ROI’s, underestimates computed Ki by a factor of ~2 when compared to that obtained from arterial blood samples, due to significant SP-in contamination from the myocardium to the LV blood pool at the late time points.

Recent works utilized IVC as a source of the blood input function for computing Ki, as FDG washes in and out of IVC rapidly. Also since there is no tissue around IVC, SP contamination into blood is completely eliminated. However, due to the limited size of IVC, the IDIF is susceptible to incomplete radioactivity recovery or PV averaging. This results in underestimation of IDIF at the late time points and thereby overestimation of the computed Ki. One of the works (Lanz et al 2014) corrected for dispersion due to difference in sampling sites of the blood input curve (IVC opposed to LV blood pool) but had to rely on blood sampling for this correction to compute cerebral FDG uptake rates. Another work (Thackeray et al 2015) in mouse hearts did not perform PV or dispersion corrections and concluded IVC as a reliable source of obtaining Ki compared to LV blood pool in a graphical Patlak model (Patlak and Blasberg 1985).

Our work is different from the above in that we performed PV corrections to IDIF obtained from IVC non-invasively without correcting for dispersion effects in a 3-compartment kinetic model with SP corrections from the blood to the myocardium at the early time points and also correcting for PV averaging of the myocardium, for the first time, in WKY rat hearts in vivo. This resulted in ~46% deviation of the computed Ki from the mean and not significantly different from that measured using arterial blood sampling in control SD rat hearts. These computations however do not include SP contamination from adjacent regions (tissue) to the blood (IVC) at the late time points, which is negligible as shown in Figures 1b–d.

We used the metabolic tracer FDG to first validate our computation model in control WKY rat, which was then applied to sensitively detect failing versus non-failing experimental spontaneously hypertensive rat (SHR) hearts in vivo (Huang et al 2018). However, it should be noted that the computation model may be easily adapted to other tracers as the kinetics of FDG is very similar to 13N-ammonia or 82Rb.

Computations using input curve from the LVBP (LVBP-SP-PV), considered as the standard method (Zhong and Kundu 2013), in the same WKY rats in a 15-parameter model with SP and PV corrections resulted in a mean Ki not different from that using IVC with partial volume corrections (IVC-PV) and also not significantly different from that obtained using arterial blood sampling in SD rats (Fang and Muzic 2008). The multi-parameter nature of the optimization problem using LVBP-SP-PV, however, resulted in a higher deviation in the mean computed Ki compared to that obtained using the IVC (IVC-PV).

The method of deriving the input curve from the IVC and correcting for PV in a 5-parameter 3-compartment model maybe applicable for all dynamic FDG PET studies to compute Ki and maybe more robust compared to that obtained from LVBP in rats and mice. However, in case of applications with tracers wherein the IVC cannot be clearly discerned from the PET images and the input curve needs to be derived from the LVBP, the 15-parameter model is more appropriate especially in studies where we have smaller structure of the heart and SP contamination from the myocardium to the LVBP becomes significant.

Our study is not without limitations. We compare our downstream Ki to that obtained using arterial blood sampling in control SD rats. This is a limitation of the study as there is no study which has performed arterial sampling in control WKY rats. However, we expect the glucose metabolic rates to be similar in these strains of control rats. Studies in Zucker lean rats [control of Zucker Diabetic Fatty (ZDF) rats], which computed rates of myocardial glucose uptake and utilization, indicated a similar Ki range (Shogi et al 2008). Another study in healthy Fischer rats weighing around 200 g (Mabrouk et al 2013), based on their computed rates of myocardial glucose utilization, also indicated a similar Ki range. In a recent review article (Cicone et al 2017), the authors identified control WKY and SD rats as commonly used strains in both cardiac PET and SPECT imaging studies. In the future, we will perform dynamic FDG PET imaging and arterial blood sampling at the same time in control WKY rats for direct (IDIF) and indirect (Ki) comparison of the computed methods (from IVC and LVBP).

5. Conclusions

In conclusion, we find that the input curve obtained from the IVC corrected for PV averaging is comparatively more repetitive to that obtained from the LV cavity in that Ki obtained with the former exhibits 46% mean deviation in the computed values compared to 56% with the latter in control WKY rat hearts. The computed Ki using the input curve from IVC with PV corrections and LVBP with SP and PV corrections, however, compare well with each other and with measured Ki using arterial blood samples in control SD rats.

Table 1.

Abbreviations

PET Positron Emission Tomography
FDG 2-[18F] fluoro-2-deoxy-D-glucose
FOV Field of View
LM List-mode
MLEM Maximum Likelihood Expectation Maximization
IVC Inferior Vena Cava
LVBP Left Ventricular Blood Pool
PV Partial Volume
SP Spill-over
IVC-PV IVC corrected for PV
LVBP-SP-PV LVBP corrected for SP and PV
IDIF Image Derived Input Function
MCIF Model Corrected Input Function
ROI Regions of Interest
Ki Rate of myocardial FDG Uptake
WKY Wistar-Kyoto
SD Sprague Dawley
Open in a new tab

Acknowledgements

We thank Jeremy Gatesman in the center of comparative medicine for tail-vein catheterizations during PET imaging studies. We also thank the imaging core facility at UVA for access to PET pre-clinical imaging scanner obtained from NIH instrument grant S10OD21672 (Albira Trimodal PET/SPECT/CT scanner).

Grant support

The research in this study was supported by NIH grants R01 HL123627 and Radiology start-up funds at UVA (to BKK).

Footnotes

Conflict of Interest

The authors declare that they have no conflict of interest.

References

  1. Krivokapich J, Huang SC, Phelps ME, et al. (1982) Estimation of rabbit myocardial metabolic rate for glucose using fluorodeoxyglucose. Am J Physiol 243 H884–H895. [DOI] [PubMed] [Google Scholar]
  2. Fang YH, Muzic RF Jr. (2008) Spillover and Partial-Volume Correction for Image-Derived Input Functions for Small-Animal 18F-FDG PET Studies. J Nucl Med 49 606–614. [DOI] [PubMed] [Google Scholar]
  3. Zhong M, Kundu BK (2013) Optimization of a Model Corrected Blood Input Function From Dynamic FDG-PET Images of Small Animal Heart In Vivo. IEEE Trans Nucl Sci 60 3417–3422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Li Y, Kundu BK (2018) An improved optimization algorithm of the three-compartment model with spillover and partial volume corrections for dynamic FDG PET images of small animal hearts in vivo. Phys Med Biol 63 055003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. González AJ, Aguilar A, Conde P et al. (2016) A PET Design Based on SiPM and Monolithic LYSO Crystals: Performance Evaluation. IEEE Trans Nucl Sci 63 2471–2477. [Google Scholar]
  6. Zhong M, Alonso CE, Taegtmeyer H, Kundu BK (2013) Quantitative PET Imaging Detects Early Metabolic Remodeling in a Mouse Model of Pressure-Overload Left Ventricular Hypertrophy In Vivo. J Nucl Med 54 609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Li J, Kemp B, Howell N et al. (2019) Metabolic Changes in Spontaneously Hypertensive Rat Hearts Precede Cardiac Dysfunction, and Left Ventricular Hypertrophy. J Am Heart Assoc 8 e010926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Huang Q, Li J, Neumann K et al. (2018) Total body dynamic FDG PET imaging of spontaneously hypertensive rats. Abstract EJNMMI Phys. 5 A7. [Google Scholar]
  9. Hutchins GD, Caraher JM, Raylman RR (1992). A region of interest strategy for minimizing resolution distortions in quantitative myocardial PET studies. J Nucl Med 33 1243–1250. [PubMed] [Google Scholar]
  10. Muzik O, Beanlands RS, Hutchins GD et al. (1993). Validation of nitrogen-13-ammonia tracer kinetic model for quantification of myocardial blood flow using PET. J Nucl Med 34 83–91. [PubMed] [Google Scholar]
  11. Seitz BM, Krieger-Burke T, Fink GD, Watts SW (2016). Serial Measurements of Splanchnic Vein Diameters in Rats Using High-Frequency Ultrasound. Front Pharmacol 7, Article 116 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Laforest R, Sharp TL, Engelbach JA, et al. (2005) Measurement of input functions in rodents: challenges and solutions. Nucl Med Biol 32 679–685. [DOI] [PubMed] [Google Scholar]
  13. Pain F, Laniece PL, Mastrippolito R, et al. (2004) Arterial input function measurement without blood sampling using a beta-microprobe in rats. J Nucl Med 45 1577–1582. [PubMed] [Google Scholar]
  14. Shoghi KI, Welch MJ (2007) Hybrid image and blood sampling input function for quantification of small animal dynamic PET data. Nucl Med Biol 34 989–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Locke LW, Berr SS, Kundu BK (2011) Image-Derived Input Function from Cardiac Gated Maximum a Posteriori Reconstructed PET Images in Mice. Mol Imaging Biol 13 342–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kim J, Herrero P, Sharp T, et al. (2006) Minimally invasive method of determining blood input function from PET images in rodents. J Nucl Med 47 330–336. [PubMed] [Google Scholar]
  17. Fakhri GE, Sitek A, Guerin B, et al. (2005) Quantitative dynamic cardiac 82Rb PET using generalized factor and compartment analyses. J Nucl Med 46 1264–1271. [PubMed] [Google Scholar]
  18. Huang Q, Li J, Taegtmeyer H, Kundu BK (2018) Blood input function from dynamic FDG PET images of Wistar Kyoto rat heart to compute rate of myocardial glucose utilization in vivo: comparison between region of interest and factor analysis methods. J Nucl Med Abstract 59 367. [Google Scholar]
  19. Lanz B, Poitry-Yamate C, Gruetter R (2014) Image-derived input function from the vena cava for 18F-FDG PET studies in rats and mice. J Nucl Med 55 1380–1388. [DOI] [PubMed] [Google Scholar]
  20. Thackeray JT, Bankstahl JP, Bengel FM (2015) Impact of Image-Derived Input Function and Fit Time Intervals on Patlak Quantification of Myocardial Glucose Uptake in Mice. J Nucl Med 56 1615–1621. [DOI] [PubMed] [Google Scholar]
  21. Patlak CS, Blasberg RG (1985) Graphical Evaluation of Blood-To-Brain Transfer Constants from Multiple-Time Uptake Data - Generalizations. J Cereb Blood Flow Metab 5 584–590. [DOI] [PubMed] [Google Scholar]
  22. Shogi KI, Gropler RJ, Sharp T, et al. (2008) Time Course of Alterations in Myocardial Glucose Utilization in the Zucker Diabetic Fatty Rat with Gene Expression of Glucose Transporters: A Small-Animal PET Investigation. J Nucl Med 49 1320–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mabrouk R, Dubeau F, Bentabet L.(2013) Cardiac PET imaging of 18F-FDG metabolism: study of healthy and infarcted hearts of rats. Conf Proc IEEE Eng Med Biol Soc. 2013 2481–2484. [DOI] [PubMed] [Google Scholar]
  24. Cicone F, Viertl D, Quintela Pousa AM, et al. (2017) Cardiac Radionuclide Imaging in Rodents: A Review of Methods, Results and Factors at Play. Front Med 4 35. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES