Abstract
Microsecond-long all-atom molecular dynamics (MD) simulations, circular dichroism, laser Doppler velocimetry, and dynamic light-scattering techniques have been used to investigate pH-induced changes in the secondary structure, charge, and conformation of poly l-lysine (PLL) and poly l-glutamic acid (PGA). The employed combination of the experimental methods reveals for both PLL and PGA a narrow pH range at which they are charged enough to form stable colloidal suspensions, maintaining their α-helix content above 60%; an elevated charge state of the peptides required for colloidal stability promotes the peptide solvation as a random coil. To obtain a more microscopic view on the conformations and to verify the modeling performance, peptide secondary structure and conformations rising in MD simulations are also examined using three different force fields, i.e., OPLS-AA, CHARMM27, and AMBER99SB*-ILDNP. Ramachandran plots reveal that in the examined setup the α-helix content is systematically overestimated in CHARMM27, while OPLS-AA overestimates the β-sheet fraction at lower ionization degrees. At high ionization degrees, the OPLS-AA force-field-predicted secondary structure fractions match the experimentally measured distribution most closely. However, the pH-induced changes in PLL and PGA secondary structure are reasonably captured only by the AMBER99SB*-ILDNP force field, with the exception of the fully charged PGA in which the α-helix content is overestimated. The comparison to simulations results shows that the examined force fields involve significant deviations in their predictions for charged homopolypeptides. The detailed mapping of secondary structure dependency on pH for the polypeptides, especially finding the stable colloidal α-helical regime for both examined peptides, has significant potential for practical applications of the charged homopolypeptides. The findings raise attention especially to the pH fine tuning as an underappreciated control factor in surface modification and self-assembly.
Introduction
Poly l-lysine (PLL), and poly l-glutamic acid (PGA) often serve as a model pair of pH-tunable polypeptides (PPs). Their biodegradability and biocompatibility make them perfect candidates for the design and assembly of advanced materials for biomedical applications,1 such as drug-delivery vehicles,2−5 antimicrobial surfaces,6 or implantable device coatings.7
Due to the wide range of applications, extensive research to understand the pH-induced changes of the PLL and PGA structure by a variety of experimental methods including turbidimetry, dynamic light-scattering, and zeta-potential analysis exists.8 The peptide conformational changes have been investigated using circular dichroism (CD),9−13 UV resonance Raman spectroscopy,14,15 Fourier-transform infrared spectroscopy,11 and low-angle laser light measurements.10 It should be mentioned that besides the pH, the structure and conformation of PPs can also be controlled by the ionic strength,16 temperature,17 or their chirality.18 The existing works show that both PGA and PLL change their secondary structure from random coil to α-helix when the pH shifts from neutral to lower (for PGA) or higher (for PLL). Even though the pH dependency has received significant attention, studies connecting directly the peptide protonation state and secondary structure remain lacking.
The properties of PP assemblies are dictated by their properties, such as the secondary structure and charge state, in the bulk solution. For example, PLL has been reported to maintain its secondary structure upon adsorption on a quartz surface,19 and the PLL peptide self-assembly morphology is sensitive to pH fine tuning in solution.20 PLL adsorption has been investigated over a wide pH range with the findings revealing significant changes in the adsorption kinetics and maximal coverage of the adsorbed layer21 as well as the surface morphology and roughness22 as a function of solution pH. Possible secondary structure changes at different pH values were not discussed in ref (22). Furthermore, polypeptide multilayer films assembled by the layer by layer (LbL) technique show a significant pH dependency of the morphology and the thickness of the films resulting from the polycation/polyanion binding.23 Also, the pH dependency of the structure of PLL/PGA LbL films24 as well as their application as pH-responsive coatings25 have been investigated.
In addition, changes in the secondary structure of the peptides have been shown to have a significant effect on the mechanical properties of the LbL films. For example, PLL/PGA multilayers composed of chains with a random coiled structure result in rather soft coatings, while similar films containing a high degree of intermolecular β pleated sheets reveal an increased Young’s modulus.26 The assembly of PPs into biodegradable LbL capsules has also been investigated as a function of pH and salt concentration.27 Furthermore, the pH is crucial for the phase behavior of the PLL and PGA solutions mixture: depending on the solution pH, the mixture either forms a coacervate or precipitates.18,28,29 The findings above indicate clearly the strong pH dependency of PLL and PGA assemblies but in addition to the pH change-induced charge state difference also point toward secondary structure changes being an important factor in driving the changes. Furthermore, bulk solution characteristics of the peptides appear to translate strongly to assembly differences. However, direct mapping of the pH–structure relation of charged homopolypeptides both in bulk solutions and in assemblies remains largely lacking.
Molecular simulations are clearly a useful tool for studying molecular level structure dependencies as they have the potential to yield information about the structural and dynamic properties of macromolecules and their functions at high spatiotemporal resolution.30 Specifically, the molecular dynamics (MD) method in atomistic detail has been frequently used for modeling polyelectrolytes31−34 and charged polypeptides8,16,31,35,36 in bulk solution as well as polyelectrolyte complexes37−42 and multilayers.43−45 Most importantly, these studies have charted intermolecular interactions, complexation, and solution characteristics. To our knowledge, charge state dependency of PP secondary structure has not been studied computationally.
However, any modeling and simulation predictions are subject to the underlying model. In the case of classical MD simulations, the employed empirical force field models the interactions and typically a fixed molecular charge distribution is assumed despite the dynamic nature of, e.g., proton transfer or charge polarization. Significant recent development of constant-pH methods exists, see for example refs (46−51). However, their usage is limited by computational cost and system simplifications. It has been demonstrated numerous times that empirical force fields verified for some biomolecular systems and conditions, may lead to less than precise predictions under different conditions or test systems, see, e.g., refs (52−56). In particular, protein folding is challenging to capture due to a delicate balance between the solute–solvent dispersion interactions.56,57 An extensive validation (up to 250 ns) of several commonly used atomistic force fields (OPLS-AA, CHARMM22, GROMOS96-43a1, GROMOS96-53a6, AMBER99sb, and AMBER03) against nuclear magnetic resonance data for globular proteins points toward the AMBER99sb as being the most reliable.58 Detailed comparisons between the performance of different Amber force-field variants exist.57,59
However, homopolypeptides are composed of repeating units of the same amino acid, so in principle, their response should be simpler to capture via a model accurately. Typical choices for PGA MD modeling in recent years have been the different variants of the AMBER force field13,35,36,60 and the OPLS-AA force field.31,61 For PLL, the most frequent force-field choice in recent years has been AMBER,8,16,60,62−68 but also OPLS-AA,31,61,69,70 CHARMM,71 and GROMOS72 have been used. Also, coarse-grained MD approaches using the MARTINI force field73 exist for PLL.72 The existing PLL and PGA studies employ dominantly a single force field. An exception is a recent 1 ns long MD simulation of l and d enantiomers of neutral poly(lysine) and poly(glutamic acid) with 5 and 10 repeat units.74 In the study, comparison of the OPLS-AA, CHARMM27, and AMBER force fields led to promoting CHARMM27 and AMBER.74
Here, we determine experimentally via circular dichroism (CD), laser Doppler velocimetry (LDV), and dynamic light scattering (DLS) the secondary structure, electrophoretic mobility, and colloidal stability of PLL and PGA solutions at various pH values and compare the predictions of three different force fields, OPLS-AA,75 CHARMM27,76,77 and AMBER99SB*-ILDNP78 at the protonation states corresponding to the measured peptide charge. The force fields are chosen as a commonly used limited selection of force fields for peptide simulations to check for consistency between the force fields. To our knowledge, this is the first time that the secondary structure and electrophoretic mobility have been determined for the same PLL and PGA solution samples as a function of pH. The findings enable resolving pH-dependent fine tuning of the polypeptide solution characteristics in terms of the secondary structure, peptide charge state, chain extension, and ensuing colloidal stability. Comparison of our simulation results against the experimental data shows that the modeling descriptions of the charged homopolypeptides in terms of the structure may deviate significantly from the experimental data.
Materials and Methods
Experimental Methods
Pure crystalline poly-l-lysine hydrobromide with a molar mass of 150–300 kg mol–1, determined by the manufacturer and approximately one HBr per lysine residue, and pure crystalline poly-l-glutamic acid sodium salt with a molar mass of 50–100 kg mol–1, determined by the manufacturer, were purchased from Sigma-Aldrich-Merck KGaA. These polypeptides are hereafter referred to as PLL and PGA. The stock solutions of PLL and PGA were prepared by dissolving a proper amount of the amino acids in NaCl solution. The NaCl solution of a desired ionic strength was prepared using deionized water obtained from Milli-Q Elix and a Simplicity 185 purification system from Millipore SAS Molsheim, France. All reagents used during the studies (analytical-grade sodium chloride, sodium hydroxide, and hydrochloric acid) were also purchased from Sigma-Aldrich as powders and used during the course of studies without further purification.
The electrophoretic mobility and diffusion coefficients of PLL and PGA were examined by the DLS and LDV techniques using a Malvern Zetasizer Nano ZS apparatus. These measurements are based on time-dependent fluctuations in the intensity of scattered light. All experiments were carried out under a constant temperature of 298 K. For each experimental data point from DLS, 10 measurements with 20 runs per single measurement cycle were performed. In the case of LDV, for each single experimental point, 15 measurements with 15 runs per single measurement were performed. The measurements were carried out simultaneously for the same samples using both techniques.
The samples were prepared according to the following procedure.
-
(1)
The appropriate amount of crystalline PLL (0.07029 g) and PGA (0.07079 g) was weighted using an analytical balance with a precision of 0.00001g.
-
(2)
Afterward, the weighted amount of the polypeptide was transferred quantitatively to a volumetric flask (200 mL) and dissolved with the 10–2 M NaCl electrolyte.
-
(3)
Then the freshly prepared solution was left for 24 h on a magnetic stirrer to ensure complete dispersion of the polypeptide suspensions.
-
(4)
The diffusion coefficient and the electrophoretic mobility of PLL and PGA in the freshly prepared suspensions were investigated within a broad pH range (3.5–12).
-
(5)
In addition, the stability of the suspensions was investigated by repeating the measurements for the same solutions (left in room temperature) after 3 weeks from preparation.
The electrophoretic mobility of the PLL and PGA molecules (350 mg L–1) in the samples was directly measured by applying the LDV technique. The diffusion coefficient of PLL and PGA molecules for I = 10–2 M NaCl and different pH values was determined by DLS. The diffusion coefficient D enables determining the hydrodynamic diameter dH of the molecules using the Stokes–Einstein relationship
| 1 |
where dH is the hydrodynamic diameter, k the Boltzmann constant, T the absolute temperature, and η the dynamic viscosity.
The hydrodynamic diameter dH corresponds to the radius of a spherical particle having the same hydrodynamic friction coefficient as the arbitrary-shaped particle under investigation. As this quantity is independent of the temperature and liquid viscosity, using it instead of the diffusion coefficient is advantageous and it provides an appropriate parameter for analyzing aggregation phenomena.79−81
In addition, with the electrophoretic mobility μ and the diffusion coefficient D known, the electrokinetic (uncompensated) charge q of the PLL and PGA molecules can be obtained from the Lorentz–Stokes relationship82
| 2 |
Consequently, the number of elementary charges Nc per one polypeptide molecule can be calculated from the formula
| 3 |
where e is the elementary charge, D is expressed in m2 s–1, kT is in units of J (kg m2 s–2), and μ is in units of μm cm (V s)−1.
The same solutions as for the LDV and DLS were used for the CD measurements. The CD spectra were recorded at 293 K on a JASCO J-710 spectropolarimeter. A quartz cuvette with a 200 μm path length was used. Due to the polydispersity of the PPs, the spectra were normalized by the peptide bonds concentration: 2.1 mM for PGA and 1.7 mM for PLL. Three scanning acquisitions were collected and averaged to yield the final spectrum, which was then corrected by the solution baseline. The conversion of ellipticity to the extinction coefficients difference as well as the secondary structure composition were estimated using the BeStSel web server.83,84 Unless otherwise stated, error estimates are based on the standard deviation of the data.
Molecular Dynamics Simulations
All-atom-detailed MD simulations were carried out using the GROMACS software, version 2018.3.85 Two homopolymers, i.e., PLL and PGA, were generated using Tinker.86 The N- and C-termini of the polypeptides were capped with acetyl (ACE) and N-methyl amide (NME) groups, respectively. For both PPs, four different ionization degrees (ID) were modeled, i.e, 1 (fully charged), 0.66, 0.33, and 0 (neutral). For this, the appropriate protonation state (see Table 1) of the amino acids was selected using the pdb2gmx tool provided by GROMACS. The protonated and deprotonated individual amino acids of the PLL and PGA chains are referred to as Glu and Glu– (PGA) and Lys+ and Lys (PLL), respectively. At a particular pH, realization of the charge distribution can be different. However, at low ionic strength the electrostatic repulsions remain strong, which promotes separation of the charges, and the configuration in which the charges are most separated are the most favorable. Therefore, we do not consider the charge distribution fluctuations but instead assume a constant charge and an evenly spaced, uniform distribution for it in the simulations. All of the PP chains consisted of 15 repeat units. This chain length was chosen as it is sufficiently long to show secondary structure behavior while still allowing a microsecond time scale needed for equilibration. The finite-size effects rising from the peptide chain length should be negligible for the highly charged polypeptides at low ionic strength, because the electrostatic repulsions make the peptide end-to-end distance then linearly dependent on the molar mass.16 On the other hand, for the low ionization degrees, it is very likely that longer peptides would fold onto themselves more than these short segments. However, examining this would need a significantly longer equilibration and larger box size, which makes such simulations computationally very demanding. The chemical structure of the protonated and deprotonated amino acids as well as the corresponding snapshots with their hydration shells are presented in Figure 1. The single PP molecules were solvated in a 7 × 7 × 7 nm3 cubic box with periodic boundary conditions applied. To neutralize the system, a sufficient number of Na+ or Cl– ions was added. To make the comparison between the experiments and the modeling feasible, we focused on dilute solution conditions. At higher salt concentration, the chloride ion’s absorbance hinders the CD measurements and, due to the electrode reactions, the electrophoretic mobility measurements are less reliable. Notably, at higher polyelectrolyte concentrations, deviations from the here reported findings can be expected, in particular, in terms of secondary structure weights but also in the pH response.
Table 1. Polypeptides Used in Simulations.
| no. | sequence | ionization degree | force field |
|---|---|---|---|
| 1 | ACE-(Glu–)15-NME | 1 | AMBER99SB*-ILDNP |
| 2 | CHARMM27 | ||
| 3 | OPLS-AA | ||
| 4 | ACE-Glu–-Glu-(Glu–)2-Glu-(Glu–)2-Glu-(Glu–)2-Glu-(Glu–)2-Glu-Glu–-NME | 0.66 | AMBER99SB*-ILDNP |
| 5 | CHARMM27 | ||
| 6 | OPLS-AA | ||
| 7 | ACE-Glu-Glu–-(Glu)2-Glu–-(Glu)2-Glu–-(Glu)2- Glu–-(Glu)2-Glu–-Glu-NME | 0.33 | AMBER99SB*-ILDNP |
| 8 | CHARMM27 | ||
| 9 | OPLS-AA | ||
| 10 | ACE-(Glu)15-NME | 0 | AMBER99SB*-ILDNP |
| 11 | CHARMM27 | ||
| 12 | OPLS-AA | ||
| 13 | ACE-(Lys+)15-NME | 1 | AMBER99SB*-ILDNP |
| 14 | CHARMM27 | ||
| 15 | OPLS-AA | ||
| 16 | ACE-Lys+-Lys-(Lys+)2-Lys-(Lys+)2-Lys-(Lys+)2-Lys-(Lys+)2-Lys-Lys+-NME | 0.66 | AMBER99SB*-ILDNP |
| 17 | CHARMM27 | ||
| 18 | OPLS-AA | ||
| 19 | ACE-Lys-Lys+-(Lys)2-Lys+-(Lys)2-Lys+-(Lys)2-Lys+-(Lys)2-Lys+-Lys-NME | 0.33 | AMBER99SB*-ILDNP |
| 20 | CHARMM27 | ||
| 21 | OPLS-AA | ||
| 22 | ACE-(Lys)15-NME | 0 | AMBER99SB*-ILDNP |
| 23 | CHARMM27 | ||
| 24 | OPLS-AA |
Figure 1.
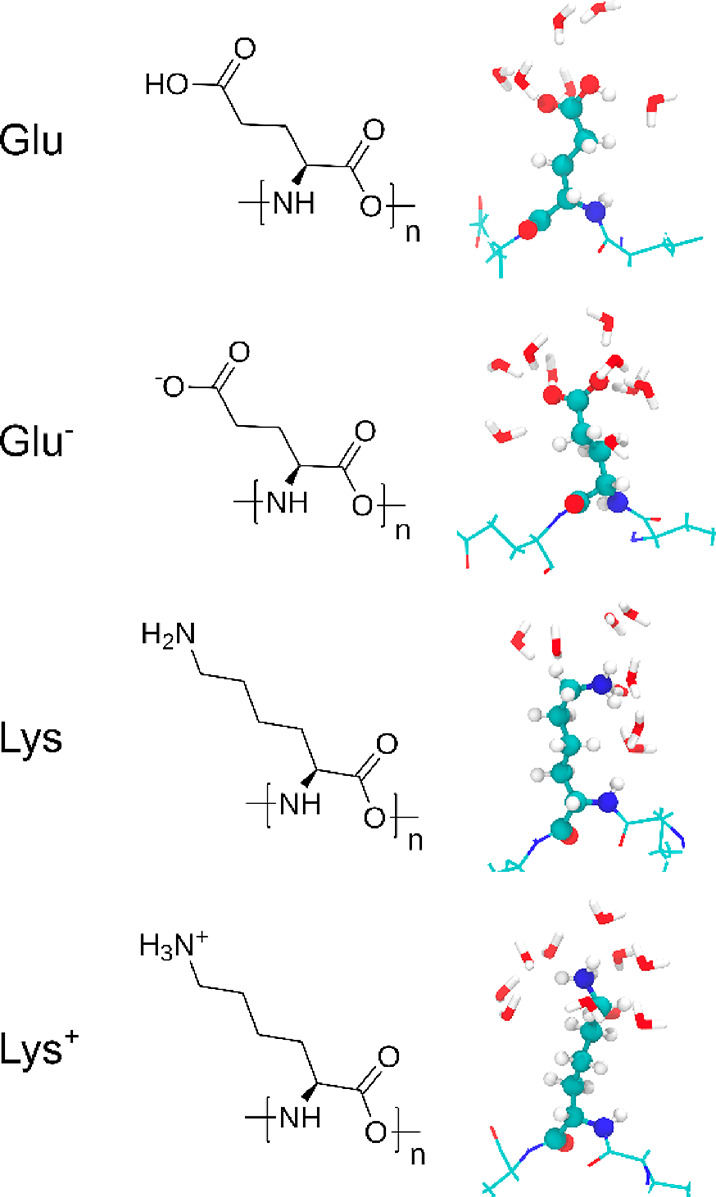
Chemical structures and MD simulation snapshots of the examined amino acids in the charged and neutral states. Snapshots show also the surrounding water molecules.
Three different force fields were used for the simulations of the PPs, i.e., OPLS-AA,75 CHARMM27,76 and AMBER99SB*-ILDNP.78 Detailed information about their functional forms and parametrization protocols is presented in ref (87), which provides a comparative review of the models. For water, the TIP3P water model was employed.88 For the CHARMM27 simulations, also the standard variant of the TIP3P was used.89 However, it should be noted that the PP’s properties might be sensitive to the water model choice.90
The van der Waals interactions between atoms were described using the Lennard–Jones potential with a 1.0 nm cutoff. The long-range dispersion corrections for energy and pressure were applied. The long-range electrostatics interactions were calculated by applying the particle mesh Ewald method with the Fourier grid spacing set to 0.16 nm and using a fourth-order smoothing spline.91 The temperature at 298 K was controlled for the PPs and solvent separately using the V-rescale thermostat92 with a coupling constant 0.1 ps. The Parrinello–Rahman barostat93 with a coupling constant of 2 ps was used to maintain the pressure at 1 bar.
In order to use a 2 fs time step, all of the bonds in PPs and water molecules were constrained using the LINCS94 and SETTLE95 algorithms, respectively. The trajectory frames were saved every 10 ps. Prior to the 1 μs long NPT production run, the system was energy minimized using the steepest descent algorithm for 5000 steps. The minimization was followed by an NVT ensemble initial equilibration for 40 ps. The first 500 ns of the production run has been disregarded in the analysis as the relaxation time. The sufficiency of this time period was verified by monitoring the equilibration of the PP secondary structure features and their fluctuations. All of the visualizations were done using the VMD software.96
Results and Discussion
The electrophoretic mobility, diffusion coefficient, hydrodynamic radius, and zeta potential of the PLL and PGA molecules in I = 10–2 M NaCl solution were determined using the LDV technique and DLS. A summary of the bulk physicochemical characteristics of PLL and PGA molecules measured in the LDV and DLS measurements is gathered in Table 2.
Table 2. Experimental Characteristics of PLL and PGA Solutions at Different pH Values for I = 10–2 M NaCl (Debye length ≈ 3 nm) Solutions at 298 Ka.
| pH | D [cm2 s–1] | dH [nm] | μ [μm cm (V s)−1] | ζ [mV] | Nc |
|---|---|---|---|---|---|
| PLL | |||||
| 5.7 | 2.2 × 10–7 ± 0.3 | 22 ± 3 | 3.3 ± 0.1 | 63 ± 3 | 38 |
| 8.6 | 2.0 × 10–7 ± 0.5 | 24 ± 5 | 3.2 ± 0.2 | 61 ± 4 | 40 |
| 9.1 | 2.2 × 10–7 ± 0.2 | 22 ± 2 | 2.5 ± 0.2 | 46 ± 4 | 29 |
| 9.7 | 1.8 × 10–7 ± 0.5 | 27 ± 6 | 2.1 ± 0.2 | 40 ± 3 | 29 |
| 9.9 | 2.4 × 10–7 ± 0.3 | 20 ± 3 | 1.8 ± 0.2 | 35 ± 2 | 19 |
| 10.4 | 2.6 × 10–7 ± 0.4 | 19 ± 4 | 1.7 ± 0.2 | 33 ± 2 | 17 |
| 11.2b | 0.1 ± 0.1 | 11 ± 1 | |||
| PGA | |||||
| 3.6b | 0.78 ± 0.09 | –15 ± 8 | |||
| 4.3 | 4.1 × 10–7 ± 0.8 | 12 ± 3 | –1.8 ± 0.2 | –34 ± 5 | 11 |
| 5.1 | 4.4 × 10–7 ± 0.8 | 11 ± 5 | –1.9 ± 0.4 | –36 ± 8 | 11 |
| 5.4 | 4.9 × 10–7 ± 0.8 | 10 ± 2 | –2.0 ± 0.3 | –39 ± 7 | 10 |
| 5.9 | 4.9 × 10–7 ± 0.8 | 10 ± 2 | –2.7 ± 0.2 | –52 ± 4 | 14 |
| 7.2 | 4.1 × 10–7 ± 0.8 | 12 ± 3 | –2.5 ± 0.8 | –50 ± 8 | 16 |
| 10.4 | 3.1 × 10–7 ± 0.9 | 16 ± 4 | –3.4 ± 1 | –65 ± 10 | 28 |
The zeta potential (ζ) was calculated from Henry’s model.
Aggregation occurs.
Figure 2 presents the pH dependence of the electrophoretic mobility μ as a function of pH as measured by the LDV. The results indicate that the electrophoretic mobility of PGA molecules increased with pH, attaining the highest value of −3.5 μm cm (V s)−1 in the pH range 8–11.5. Contrary to PGA, the mobility of PLL molecules decreased with increasing pH, attaining the highest value of 3.5 μm cm (V s)−1 for the pH range 3.5–7.5. The isoelectric point of PLL molecules was defined to be between pH 10.5 and 11, which agrees well with the literature data.97,98
Figure 2.
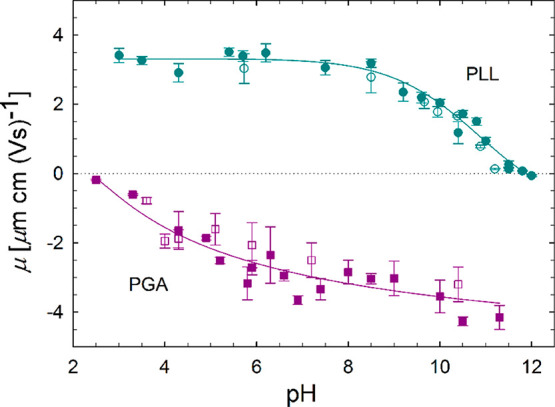
pH dependence of the electrophoretic mobility μ at I = 10–2 M NaCl solution for PLL and PGA molecules. Filled symbols correspond to data obtained from measurements of freshly prepared solutions, and hollow points correspond to data obtained from measurements performed for 3-week old dispersions. Solid lines provide a guide to the eye. Dashed line indicates the level of isoelectric point (zero charge level).
The electrokinetic charge is physically interpreted as the charge moving with the molecule, i.e., located below the shear plane.99 Therefore, the electrokinetic charge is usually smaller (in absolute terms) than the condensed (specifically adsorbed) charge. This deduction is supported by a previous MD modeling work that predicted the condensed charge on PLL is 26% of the nominal charge of the molecule.31 This is ca. three times larger than the electrokinetic charge.16
The average diffusion coefficient of PLL and PGA molecules at their highly charged states was equal to DPLL= 2.0 × 10–7 ± 0.3 cm2 s–1 and DPGA = 4.1 × 10–7 ± 0.3 m2 s–1, respectively. The pH-mediated differences in D, visible in Table 2, are comparable with the standard deviations, which makes it impossible to speculate about the trend. However, it should be mentioned that very accurate determination of the diffusion coefficient, e.g., by using the laser-induced transient-grating method with a photoreactive probe molecule, would enable investigating, for example, the PGA conformational changes.12
The dependence of the hydrodynamic diameter on pH for PLL and PGA molecules is illustrated in the SI in Figure S2. For PGA molecules, the hydrodynamic diameter dH = 12 ± 3 nm in the pH range 4.5–11 remains constant in the range. Changes in the PGA hydrodynamic diameter are observed at pH ≤ 4.5 and associated with the instability of the PGA suspension, which leads to aggregation of the molecules. On the other hand, for PLL molecules in the pH 3.5–10.8 range, the hydrodynamic diameter remains constant with an average value of dH = 22 ± 5 nm. An increase in the hydrodynamic diameter is observed at pH ≈ 11 and analogous to PGA indicates instability of the suspension and onset of aggregation. These DLS results correlate well with the electrophoretic data, see Figure 2. The observed onset of aggregation occurs near the isoelectric points of the examined molecules at pH = 10.5 and 4.0 for PLL and PGA, respectively, see Figure 2. This indicates that the colloidal suspension stability is mainly governed by the electrostatic repulsion between the charged PPs.
The electrophoresis and dynamic light-scattering data of Table 2 enables calculating, based on eq 3, the number of uncompensated charges per molecule Nc. While at low pH values, the PLL Nc value is approximately constant, reaching Nc = 40 at pH = 5.7, the PLL charge decreases with increasing pH and is only Nc = 10 close to pH = 11. For PGA molecules, the Nc increases with pH: The PGA charge at pH 10.4 is Nc = 28 and at pH 4.5 the charge Nc = 11. The inverse response to pH changes in the number of uncompensated charges for these two amino acids results directly from their chemical structure, see Figure 1.
Besides the pH, the PP structure and behavior in solution are affected by the chain length and polydispersity,13 temperature,17 and salt type and concentration.16,101 The purity of used reagents, due to a different batch or manufacturer, might also affect the PP behavior. All of these hinder the direct comparison between the results reported by different groups. Therefore, the corresponding changes in PGA and PLL secondary structure as a function of pH were investigated experimentally via CD measurements for the same samples to connect the PP charge and their secondary structure. Figure 3 presents the overall summary of these results together with the electrophoretic mobility data that indicates the peptide charge state. Molecular visualizations of representative peptide conformations corresponding to the AMBER99SB*-ILDNP force-field simulations at charge states corresponding to the electrophoretic mobility data are presented. The original CD spectra and fittings to them are presented in the SI (Figure S1), and the more detailed resulting secondary structure compositions of the peptides at the different pH values are summarized in Table 3 for PGA and Table 4 for PLL. For the CD data, it is worth noting that even though the fittings are reasonable for both PPs and at every measurement pH, the highest fitting RMSDs are for the data of PGA at pH > 7.2 and PLL at pH < 8.6. These pH ranges both correspond to extended molecule conformations due to the strong electrostatic repulsions.16 This may cause structural alignments to be less pronounced, which complicates CD analysis for the highly charged peptides.
Figure 3.
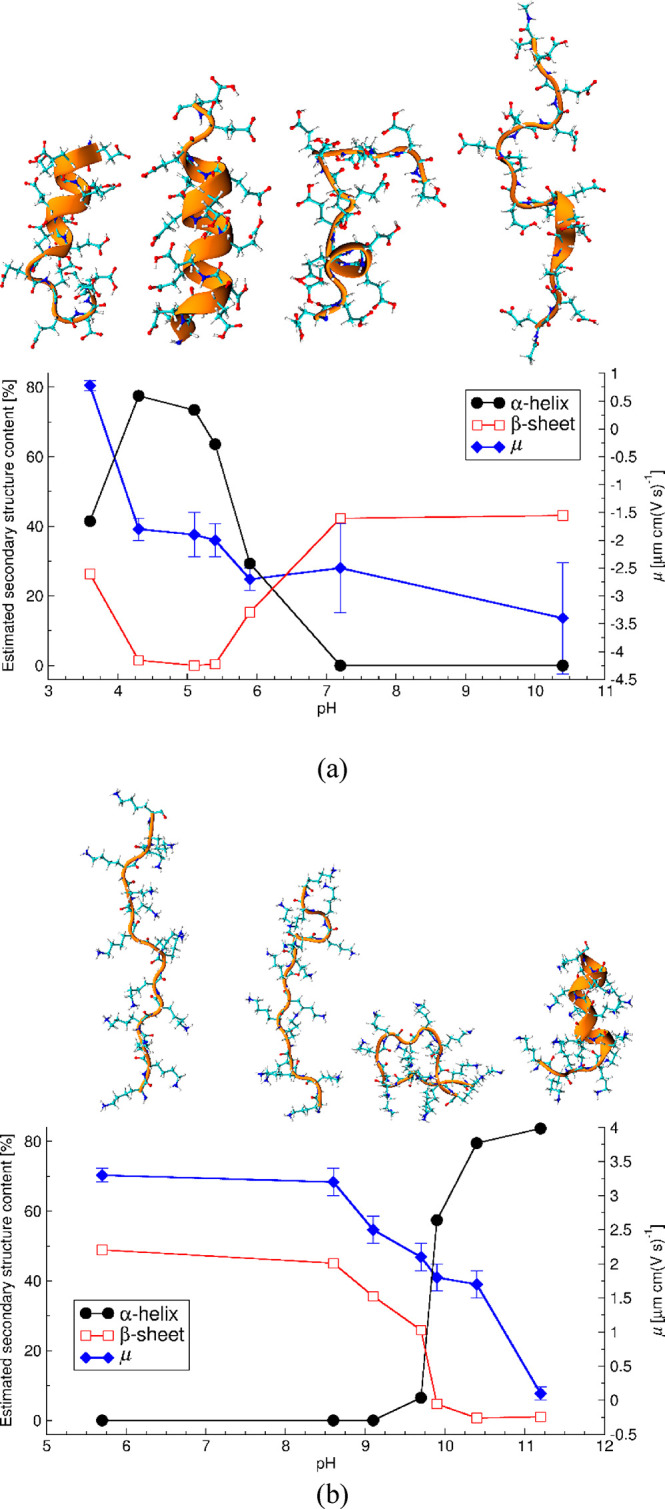
Experimentally determined electrophoretic mobility (μ) and PP secondary structure content as a function of the solution pH for (a) PGA and (b) PLL. Simulation snapshots present the AMBER99SB*-ILDNP force-field-predicted configurations for the corresponding pH range.
Table 3. Estimated Secondary Structure Content (%) of PGA Determined from Fitting to the CD Spectraa.
| secondary structure |
pH |
|||||||
|---|---|---|---|---|---|---|---|---|
| 3.6 | 4.3 | 5.1 | 5.4 | 5.9 | 7.2 | 10.4 | ||
| helix | helix1 (regular) | 30.9 | 58.4 | 56.8 | 48.5 | 20.1 | 0.0 | 0.0 |
| helix2 (distorted) | 10.6 | 19.2 | 16.7 | 15.1 | 9.2 | 0.0 | 0.0 | |
| antiparallel | anti1 (left-twisted) | 2.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| anti2 (relaxed) | 8.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| anti3 (right-twisted) | 0.0 | 0.0 | 0.0 | 0.4 | 15.3 | 42.3 | 43.1 | |
| parallel | 15.7 | 1.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| turn | 16.5 | 9.5 | 7.4 | 10.1 | 13.1 | 14.0 | 13.3 | |
| others | 15.7 | 11.4 | 19.1 | 26.0 | 42.4 | 43.8 | 43.6 | |
| RMSD | 0.1114 | 0.1902 | 0.1442 | 0.0636 | 0.1435 | 0.728 | 0.89 | |
| NRMSD | 0.00561 | 0.00589 | 0.0048 | 0.0026 | 0.01422 | 0.06347 | 0.07192 | |
The fitting has been completed by dividing the spectrum into eight secondary structure elements following ref (83).
Table 4. Estimated Secondary Structure Content (%) of PLL Determined from Fitting to the CD Spectraa.
| secondary structure |
pH |
|||||||
|---|---|---|---|---|---|---|---|---|
| 5.7 | 8.6 | 9.1 | 9.7 | 9.9 | 10.4 | 11.2 | ||
| helix | helix1 (regular) | 0.0 | 0.0 | 0.0 | 3.7 | 44.2 | 63.6 | 65.1 |
| helix2 (distorted) | 0.0 | 0.0 | 0.0 | 2.7 | 13.2 | 15.8 | 18.6 | |
| antiparallel | anti1 (left-twisted) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| anti2 (relaxed) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| anti3 (right-twisted) | 48.9 | 45.1 | 35.6 | 25.9 | 4.7 | 0.0 | 0.0 | |
| parallel | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.7 | 1.0 | |
| turn | 10.7 | 12.4 | 15.9 | 14.1 | 7.1 | 6.8 | 5.4 | |
| others | 40.5 | 42.5 | 48.5 | 53.5 | 30.8 | 13.0 | 10.0 | |
| RMSD | 1.0151 | 0.7881 | 0.3211 | 0.2795 | 0.1752 | 0.2869 | 0.2472 | |
| NRMSD | 0.06953 | 0.06017 | 0.0367 | 0.03294 | 0.00728 | 0.00803 | 0.00706 | |
The fitting has been completed by dividing the spectrum into eight secondary structure elements following ref (83).
Changes in PGA structure can be divided into four regions. (1) At pH above 7, PGA is highly charged and the CD spectra indicate only a β-sheet structure. (2) In the pH range between 5.5 and 7, a significant decrease in β-sheet, increase in α-helix content, and decrease in absolute value of electrophoretic mobility (|μ|) occurs. (3) In the pH range between 4.2 and 5.5 a further decrease of |μ| occurs, accompanied by a maximum of α-helix content and no β structure. Finally, (4) at pH below 4.2, a decrease in α-helix content and partial recuperance of the β-sheet structure is observed. However, at the higher pH, antiparallel β-sheets dominate, while the β-sheets structure contributions at low pH are parallel at low pH, see Table 3. The parallel β-sheets have somewhat more distorted and consequently weaker hydrogen bonding, according to the Pauling–Corey models.
Changes in PLL structure can be divided into three regions. (1) At pH below 8.6, PLL is a highly charged, elongated molecule with β-sheet structure. (2) At pH range between 8.6 and 10.4, the β-sheet structure and |μ| decrease while the α-helix content increases. (3) At pH above 10.4, the α-helical structure is dominant and the very low value of |μ| suggests that the molecule is almost charge neutral. For PLL, significant changes in the secondary structure and electrophoretic mobility occur around pH 9.8. This corresponds to the pKa for poly l-lysine (9.85).102 However, in the pH range from 9.8 to 10.4, the electrophoretic mobility remains significantly positive. This indicates that PLL carries charge. Furthermore, the PLL solution remains colloidally stable at pH 10.4, and aggregation occurs only above pH 11, see Figure S2.
The results suggest that in a narrow pH range, pH 9.8–10.4 for the PLL and pH 5.0–5.5 for PGA, both PPs remain sufficiently charged so that their solutions form a stable colloidal suspension (see Figure S2). However, a sufficient decrease in charge has occurred, so that their α-helix content is already above 60%. As the secondary structure change influences strongly the response of these peptides, e.g., as adsorbed films or PEMs, this might have very important implications for further use of these PPs. This narrow range typically remains overlooked, as PLL and PGA are the most commonly used at pH around 7, where both are highly charged. However, at this pH the dominant structural composition, in addition to random coils, is beta sheet. On the other hand, the secondary structure has a significant influence on the materials properties resulting from PP adsorption of PEMs or PPs.26 This suggests that fine tuning using the pH has a significant potential for providing more control on the properties of materials composed of the PLL and PGA.
Interestingly, the β-sheet content seems to be strongly correlated with |μ| for both PPs. The experiments show that for both PPs at their fully charged states, at pH above 8 for PGA and at pH below 8 for PLL, the β-sheet secondary structure covers ∼40–50% of the PP chain. This is related with strong electrostatic repulsion between neighboring charge groups that forces elongation of the PP. Recently, viscosity measurements have showed that the PLL has an extremely extended conformation at pH 5.6.16
Let us next move to simulations-based characterization of the corresponding polypeptides. The pKa of the side chain group depends on the neighboring groups. It might differ significantly between amino acids in the protein, typically surrounded by neutral amino acids, and in charged homopolypeptide molecules. Assuming the PLL and PGA pKa to be 9.85102 and 6.5,103 respectively, the charge states of PLL and PGA in MD simulations can be set to correspond to the mean charge state in a given pH using the Henderson–Hasselbalch equation. The ionization degree of the polypeptides, i.e., 1, 0.66, 0.33, and 0, in the MD simulations has been chosen so that the charge states cover pH regions on both sides around the pKa and cover also the fully charged and neutral states, see Figure 3.
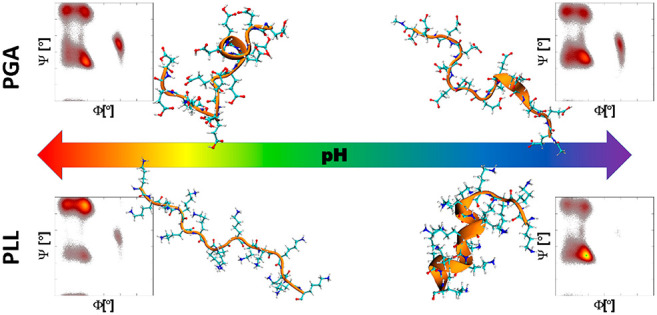
In Figure 4, Ramachandran plots calculated based on the MD simulation trajectories show the secondary structure distribution of PLL and PGA simulated using the three examined force fields, AMBER99SB*-ILDNP, CHARMM27, and OPLS-aa. Notably, in the Ramachandran plots, the top-left spots correspond to backbone configurations characteristic of beta sheets, the center-left spots to right-handed α-helical structure, and the center-right spots characteristic to backbone angles of left-handed α-helices. The three examined force fields differ significantly in their prediction both within a given charge state but also in response to charge state changing.
Figure 4.
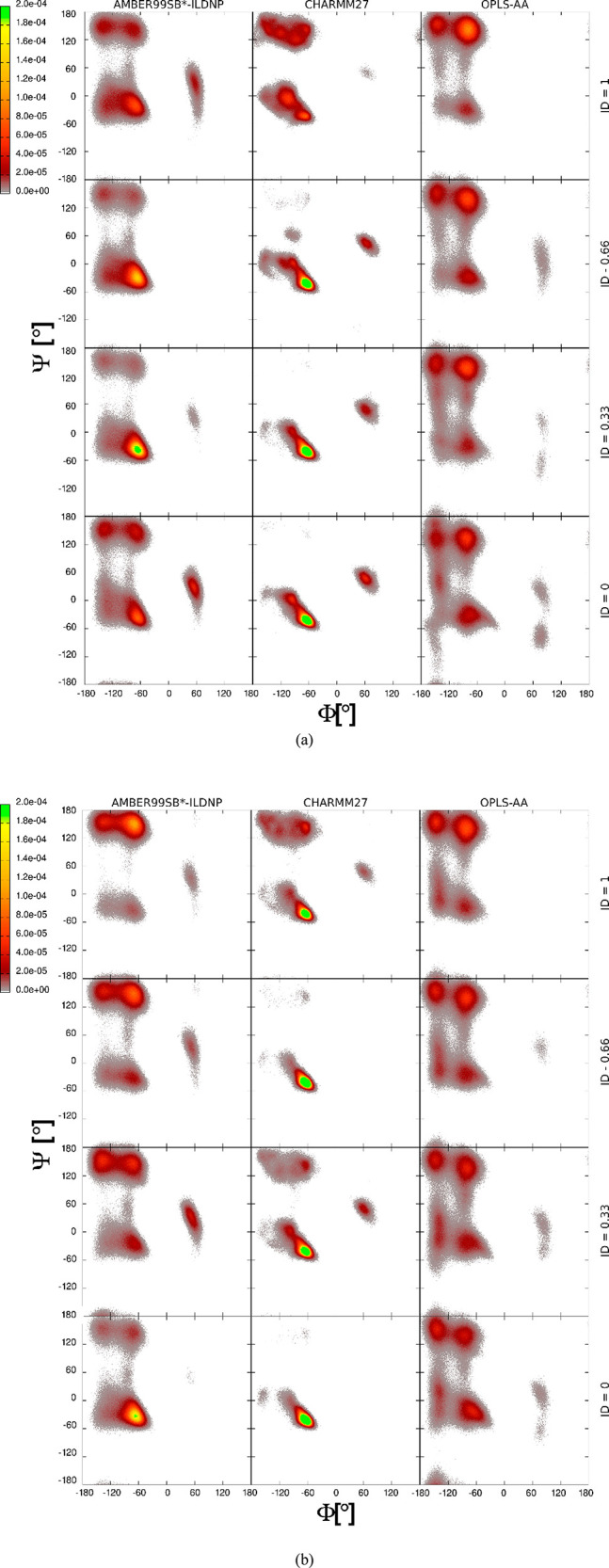
Ramachandran plots for the (a) PGA and (b) PLL calculated from the molecular dynamics simulations trajectories. Subplots show the distribution of the Ψ and Φ angles of the peptide backbone for the different ionization degrees (ID) with the three examined force fields.
Comparison with the experimental secondary structure data in Figure 3 and the MD simulations predicted conformations distribution in Figure 4 shows that the AMBER99SB*-ILDNP force field reproduces the changes in the secondary structure due to changing ionization degree. In particular, the conformation distributions shown by the Ramachandran plots follow for PGA the experimentally observed increase in α-helix content when the ionization degree decreases from 1 to 0.33 and also the decrease in α-helix content at ID 0. Likewise, the inverse response for backbone configurations corresponding to β-sheet content as a function of pH (charge ID) is reproduced with the exception that at high ionization degree the AMBER99SB*-ILDNP force field predicts that the α-helical conformation dominates, while experiments clearly indicate preference for β-sheet. As with PGA, for PLL, the simulation data shows a preference of the conformations adopting backbone angles corresponding to the β-sheet structure at high ID of the peptide (corresponding to elevated pH) and a sudden increase in the α-helix content at very low ID. Notably, the examined peptides are so short (15 amino acids) that full formation of beta sheets is not visible in the simulations even though the backbone configurations of the peptides may correspond to the extended configurations typical to beta sheets. This result is in line with experimental data.
The AMBER99SB*-ILDNP force field is optimized for the correct description of the helix–coil equilibrium.104 An accurate balance between α and β structures in protein folding via the force field has been tested against NMR and Förster resonance energy transfer measurements.105 For the AMBER force field, we also investigated the effect of the chain length on the conformation distribution, see Figure S3. The differences in the exhibited secondary structure fractions between 5 and 15 repeat units are relatively small. The visible differences mostly result from much better sampling of the 15 amino acids long peptide (more dihedrals) than the 5 amino acid long chain. It might be expected, however, that for much longer chains the β-sheet content might increase as several β-strands can assemble into proper β-sheets. Therefore, the much shorter PPs in the simulations than in the experiments hinder quantitative comparison of the exact α- and β-structure fractions. Also, analysis of the populated regions of the Ramachandran plot determined from MD simulation trajectory is crudely simplified with no further subdivision of the individual structures as specified in the recent nomenclature.106
The Ramachandran plots corresponding to both CHARMM27 and OPLS-AA force fields, Figure 4, are much less sensitive to the changes in the PPs protonation state than the AMBER99SB*-ILDNP force field. The OPLS-AA prediction shows the same structural features as with AMBER99SB*-ILDNP but with very little sensitivity to a change of the PP charge state. However, the CHARMM27 force-field prediction looks quite different from the other two examined force fields. In comparison to the experimental results, it significantly overestimates the α-helix content at every charge ID for both PPs. This means a qualitative match with the secondary structure content observed experimentally is obtained only for PLL at ID 0 or PGA at ID 0.33. Similar overestimation of the α-helix fraction for the same force field has been previously reported for polyalanine.107 On the other hand, CHARMM27 seems to work for PGA and PLL in their neutral state.74 In comparison to CHARMM27, the more recent CHARMM36 version might result in significantly better results as the backbone CMAP potentials have been refined and the side-chain dihedrals have been reparametrized.108,109
The OPLS-AA force field shows the best agreement with the experiments for both PLL and PGA at their highly charged protonation states. This corresponds to the pH above 8 for PGA and below 8 for PLL. However, for the lower IDs, this force field does not properly map the changes in the secondary structure. At the lower IDs, the β-sheet conformations are overestimated, contrary to the CHARMM27, which promoted α-helical structure. Notably, in temporal analysis of the secondary structure evolution in the simulations, the OPLS-AA force field shows more pronouncedly the bridge regions between the α-helix and the β-sheet, see Table S1 in the SI. This suggests that the transition between these α-helix and β-sheet structures occurs within the simulation time. The comparison of the evolution of the secondary structure for different force fields can be found in Table S1. For example, the OPLS-AA force field predicts that PLL with ID 0 has α- and β-structures that are stable for more than 200 ns in duration of the 1 μs total simulation time here. This suggests that simulations concerning the changes in the secondary structure should be sufficiently long or employ an enhanced sampling method, like TREMD110 or HREMD.111
A further characterization of the differences between the peptide structures predicted by the force fields is provided by the radius of gyration Rg, Figure S4. On the basis of the experimental data, an increase of Rg with ID can be expected due to the stronger repulsion between the charged side chain groups. Indeed, for the AMBER99SB*-ILDNP and OPLS-AA, the Rg increases significantly with ID, while only a small increase is visible for CHARMM.
As the secondary structure is dictated by hydrogen-bond formation, we analyzed the number of PP internal and PP–water hydrogen bonds as a function of the ID and force field, see Figure S5. The data shows that the AMBER99SB*-ILDNP and OPLS-AA force fields lead to similar data sets in terms of hydrogen-bond formation. For both force fields the number of internal hydrogen bonds in PPs decrease with increasing ID, while the number of PP–water hydrogen bonds increases. For PLL, the number of internal hydrogen bonds at ID 1 is close to zero, which corresponds with the highly extended conformation. On the other hand, for PGA, even at ID 1, on average 0.3 internal hydrogen bonds per amino acid form. Moreover, the number of PP–water hydrogen bonds increases more for PGA for all of the studied force fields. However, for the CHARMM27 force field, the hydrogen bonding seems to be less sensitive to the changes in the protonation state. Only at ID 1, the decrease in PP internal hydrogen bonding shows.
Only small differences in the simulation performance were observed. The simulations employing the OPLS-AA force field were ∼5% faster than AMBER99SB*-ILDNP and CHARMM for ionization degrees 1, 0.66, and 0.33 and ∼5% slower for ID 0.
Conclusions
The ability to accurately reproduce pH-induced changes in PLL and PGA homopolypeptide secondary structure and conformation by different atomistic resolution molecular modeling force fields was investigated via the MD method. The simulation results were validated against experimental CD, LDV, and DLS measurements data that also provided a full characterization of the secondary structure and charge state pH dependency of these homopolypeptides. The simulation results show that the studied force fields, i.e., OPLS-AA, CHARMM27, and AMBER99SB*-ILDNP, have significant differences in their predictions, and only the AMBER99SB*-ILDNP properly captured the secondary structure response versus pH. However, for the fully charged PLL and PGA, i.e., the most important state for practical applications of these PPs, the OPLS-AA has the best quantitative match with the experimental data. On the other hand, the CHARMM27 force field, which systematically overestimates the α-helix content of the charged PPs in this work, has been previously shown to work well for neutral PLL and PGA.74
We emphasize that the results in this work should not be considered as indications of the best available force field. Rather, the results demonstrate how force field sensitive the results can be and that the force field choice should be done with great care and tested against the experimental data whenever possible.
The experiments indicate that both PGA and PLL adopt a partial, ∼40–50% β-sheet secondary structure when highly charged (at high pH for PGA and low for PLL). Close to the pKa, peptides experience a gradual loss of the partial β-sheet structure and rise to up to 80% α-helical structure as their charge decreases. Furthermore, at very low charge (very low pH), PGA loses partially the α-helical structure. In addition, the presented experimental results suggest that pH fine tuning with the aim of high-precision control of the secondary structure of the PPs can provide access to a very interesting tuning option for the properties of the molecules. The experimental data shows that both PLL and PGA have a narrow pH range in which they are charged enough to form a stable colloidal suspension but having at the same time α-helix content above 60%; the dominant charged state secondary structure of the peptides is β-sheet. Such pH sensitivity in secondary structure has major implications for the practical application of these PPs, e.g., in adsorption or multilayer film formation. Direct implications of this pH sensitivity in secondary structure is that the experimental protocols should be carefully investigated and connected with the properties of the molecules in the bulk solution. This could help understand, improve, and control the properties of the assemblies built from oppositely charged polypeptides.
Acknowledgments
This study was financed by the National Science Centre Research Grant Sonata, UMO 2018/31/D/ST5/01866, and Academy of Finland Grant No. 309324. M.S. is grateful for the support by the FinnCERES Materials Bioeconomy Ecosystem. We thank Jukka Määttä for useful discussions. Computational resources by the CSC IT Centre for Science, Finland, and RAMI–RawMatTERS Finland Infrastructure are also gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c01475.
CD spectra measured at 293 K for PGA and PLL at different pH values; dependence of the hydrodynamic diameter of PLL molecules and PGA molecules on pH at I = 10–2 M NaCl; Ramachandran plots for PGA chains with 5 and 15 amino acids and PLL chains with 5 and 15 amino acids; radius of gyration as a function of ionisation degree and force field type; number of internal (NI) and polypeptide–water (NH) hydrogen bonds per single amino acid as a function of the ionisation degree and the force field type; evolution of secondary structure of PGA and PLL with different ionisation degrees (ID) and force fields (FF) in the MD simulations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Chow D.; Nunalee M. L.; Lim D. W.; Simnick A. J.; Chilkoti A. Peptide-Based Biopolymers in Biomedicine and Biotechnology. Mater. Sci. Eng., R 2008, 62, 125–155. 10.1016/j.mser.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepanowicz K.; Bazylińska U.; Pietkiewicz J.; Szyk-Warszyńska L.; Wilk K. A.; Warszyński P. Biocompatible Long-Sustained Release Oil-Core Polyelectrolyte Nanocarriers: From Controlling Physical State and Stability to Biological Impact. Adv. Colloid Interface Sci. 2015, 222, 678–691. 10.1016/j.cis.2014.10.005. [DOI] [PubMed] [Google Scholar]
- Łukasiewicz S.; Szczepanowicz K.; Podgórna K.; Błasiak E.; Majeed N.; Ogren S. O. Ö.; Nowak W.; Warszyński P.; Dziedzicka-Wasylewska M. Encapsulation of Clozapine in Polymeric Nanocapsules and Its Biological Effects. Colloids Surf., B 2016, 140, 342–352. 10.1016/j.colsurfb.2015.12.044. [DOI] [PubMed] [Google Scholar]
- Piotrowski M.; Szczepanowicz K.; Jantas D.; Leśkiewicz M.; Lasoń W.; Warszyński P. Emulsion-Core and Polyelectrolyte-Shell Nanocapsules: Biocompatibility and Neuroprotection against SH-SY5Y Cells. J. Nanopart. Res. 2013, 15 (11), 2035. 10.1007/s11051-013-2035-1. [DOI] [Google Scholar]
- Podgórna K.; Szczepanowicz K. Synthesis of Polyelectrolyte Nanocapsules with Iron Oxide (Fe3O4) Nanoparticles for Magnetic Targeting. Colloids Surf., A 2016, 505, 132–137. 10.1016/j.colsurfa.2016.02.017. [DOI] [Google Scholar]
- Boulmedais F.; Frisch B.; Etienne O.; Lavalle P.; Picart C.; Ogier J.; Voegel J. C.; Schaaf P.; Egles C. Polyelectrolyte Multilayer Films with Pegylated Polypeptides as a New Type of Anti-Microbial Protection for Biomaterials. Biomaterials 2004, 25 (11), 2003–2011. 10.1016/j.biomaterials.2003.08.039. [DOI] [PubMed] [Google Scholar]
- Borges J.; Mano J. F. Molecular Interactions Driving the Layer-by-Layer Assembly of Multilayers. Chem. Rev. 2014, 114, 8883–8942. 10.1021/cr400531v. [DOI] [PubMed] [Google Scholar]
- Naassaoui I.; Aschi A. Evaluation of Properties and Structural Transitions of Poly-L-Lysine: Effects of pH and Temperature. J. Macromol. Sci., Part B: Phys. 2019, 58, 673. 10.1080/00222348.2019.1638593. [DOI] [Google Scholar]
- Myer Y. P. The pH-Induced Helix-Coil Transition of Poly-L-Lysine and Poly-L-Glutamic Acid and the 238-Mn Dichroic Band. Macromolecules 1969, 2 (6), 624–628. 10.1021/ma60012a012. [DOI] [Google Scholar]
- Grigsby J. J.; Blanch H. W.; Prausnitz J. M. Effect of Secondary Structure on the Potential of Mean Force for Poly-L-Lysine in the α-Helix and β-Sheet Conformations. Biophys. Chem. 2002, 99 (2), 107–116. 10.1016/S0301-4622(02)00138-2. [DOI] [PubMed] [Google Scholar]
- Kimura T.; Takahashi S.; Akiyama S.; Uzawa T.; Ishimori K.; Morishima I. Direct Observation of the Multistep Helix Formation of Poly-L-Glutamic Acids. J. Am. Chem. Soc. 2002, 124 (39), 11596–11597. 10.1021/ja026639f. [DOI] [PubMed] [Google Scholar]
- Inoue K.; Baden N.; Terazima M. Diffusion Coefficient and the Secondary Structure of Poly-L-Glutamic Acid in Aqueous Solution. J. Phys. Chem. B 2005, 109 (47), 22623–22628. 10.1021/jp052897y. [DOI] [PubMed] [Google Scholar]
- Hernik-Magoń A.; Puławski W.; Fedorczyk B.; Tymecka D.; Misicka A.; Szymczak P.; Dzwolak W. Beware of Cocktails: Chain-Length Bidispersity Triggers Explosive Self-Assembly of Poly-l-Glutamic Acid B2-Fibrils. Biomacromolecules 2016, 17 (4), 1376–1382. 10.1021/acs.biomac.5b01770. [DOI] [PubMed] [Google Scholar]
- Ma L.; Ahmed Z.; Asher S. A. Ultraviolet Resonance Raman Study of Side Chain Electrostatic Control of Poly-l-Lysine Conformation. J. Phys. Chem. B 2011, 115 (14), 4251–4258. 10.1021/jp2005343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S.; Asher S. A. UV Resonance Raman Studies of Peptide Conformation in Poly(L-Lysine), Poly(L-Glutamic Acid), and Model Complexes: The Basis for Protein Secondary Structure Determinations. J. Am. Chem. Soc. 1989, 111 (12), 4295–4305. 10.1021/ja00194a022. [DOI] [Google Scholar]
- Adamczyk Z.; Morga M.; Kosior D.; Batys P. Conformations of Poly-l-Lysine Molecules in Electrolyte Solutions: Modeling and Experimental Measurements. J. Phys. Chem. C 2018, 122 (40), 23180–23190. 10.1021/acs.jpcc.8b07606. [DOI] [Google Scholar]
- Chiou J. S.; Tatara T.; Sawamura S.; Kaminoh Y.; Kamaya H.; Shibata A.; Ueda I. The α-Helix to β-Sheet Transition in Poly(l-Lysine): Effects of Anesthetics and High Pressure. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 1992, 1119 (2), 211–217. 10.1016/0167-4838(92)90394-S. [DOI] [PubMed] [Google Scholar]
- Perry S. L.; Leon L.; Hoffmann K. Q.; Kade M. J.; Priftis D.; Black K. A.; Wong D.; Klein R. A.; Pierce C. F.; Margossian K. O.; et al. Chirality-Selected Phase Behaviour in Ionic Polypeptide Complexes. Nat. Commun. 2015, 6 (1), 6052. 10.1038/ncomms7052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binazadeh M.; Faghihnejad A.; Unsworth L. D.; Zeng H. Understanding the Effect of Secondary Structure on Molecular Interactions of Poly-l-Lysine with Different Substrates by SFA. Biomacromolecules 2013, 14 (10), 3498–3508. 10.1021/bm400837t. [DOI] [PubMed] [Google Scholar]
- Ghosh A.; Haverick M.; Stump K.; Yang X.; Tweedle M. F.; Goldberger J. E. Fine-Tuning the pH Trigger of Self-Assembly. J. Am. Chem. Soc. 2012, 134 (8), 3647–3650. 10.1021/ja211113n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morga M.; Adamczyk Z.; Kosior D.; Kujda-Kruk M. Kinetics of Poly- l -Lysine Adsorption on Mica and Stability of Formed Monolayers: Theoretical and Experimental Studies. Langmuir 2019, 35 (37), 12042–12052. 10.1021/acs.langmuir.9b02149. [DOI] [PubMed] [Google Scholar]
- Choi J. H.; Kim S. O.; Linardy E.; Dreaden E. C.; Zhdanov V. P.; Hammond P. T.; Cho N. J. Influence of pH and Surface Chemistry on Poly(l -Lysine) Adsorption onto Solid Supports Investigated by Quartz Crystal Microbalance with Dissipation Monitoring. J. Phys. Chem. B 2015, 119 (33), 10554–10565. 10.1021/acs.jpcb.5b01553. [DOI] [PubMed] [Google Scholar]
- Burke S. E.; Barrett C. J. pH-Responsive Properties of Multilayered Poly(L-Lysine)/Hyaluronic Acid Surfaces. Biomacromolecules 2003, 4 (6), 1773–1783. 10.1021/bm034184w. [DOI] [PubMed] [Google Scholar]
- Lavalle P.; Gergely C.; Cuisinier F. J. G.; Decher G.; Schaaf P.; Voegel J. C.; Picart C. Comparison of the Structure of Polyelectrolyte Multilayer Films Exhibiting a Linear and an Exponential Growth Regime: An in Situ Atomic Force Microscopy Study. Macromolecules 2002, 35 (11), 4458–4465. 10.1021/ma0119833. [DOI] [Google Scholar]
- Garza J. M.; Jessel N.; Ladam G.; Dupray V.; Muller S.; Stoltz J. F.; Schaaf P.; Voegel J. C.; Lavalle P. Polyelectrolyte Multilayers and Degradable Polymer Layers as Multicompartment Films. Langmuir 2005, 21 (26), 12372–12377. 10.1021/la051465b. [DOI] [PubMed] [Google Scholar]
- Grohmann S.; Rothe H.; Liefeith K. Investigations on the Secondary Structure of Polypeptide Chains in Polyelectrolyte Multilayers and Their Effect on the Adhesion and Spreading of Osteoblasts. Biointerphases 2012, 7 (1), 62. 10.1007/s13758-012-0062-6. [DOI] [PubMed] [Google Scholar]
- Ochs C. J.; Such G. K.; Städler B.; Caruso F. Low-Fouling, Biofunctionalized, and Biodegradable Click Capsules. Biomacromolecules 2008, 9 (12), 3389–3396. 10.1021/bm800794w. [DOI] [PubMed] [Google Scholar]
- Priftis D.; Tirrell M. Phase Behaviour and Complex Coacervation of Aqueous Polypeptide Solutions. Soft Matter 2012, 8 (36), 9396–9405. 10.1039/C2SM25604E. [DOI] [Google Scholar]
- Li L.; Srivastava S.; Andreev M.; Marciel A. B.; De Pablo J. J.; Tirrell M. V. Phase Behavior and Salt Partitioning in Polyelectrolyte Complex Coacervates. Macromolecules 2018, 51 (8), 2988–2995. 10.1021/acs.macromol.8b00238. [DOI] [Google Scholar]
- Zerze G. H.; Zheng W.; Best R. B.; Mittal J. Evolution of All-Atom Protein Force Fields to Improve Local and Global Properties. J. Phys. Chem. Lett. 2019, 10 (9), 2227–2234. 10.1021/acs.jpclett.9b00850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batys P.; Luukkonen S.; Sammalkorpi M. Ability of the Poisson-Boltzmann Equation to Capture Molecular Dynamics Predicted Ion Distribution around Polyelectrolytes. Phys. Chem. Chem. Phys. 2017, 19 (36), 24583–24593. 10.1039/C7CP02547E. [DOI] [PubMed] [Google Scholar]
- Michna A.; Batys P.; Morga M.; Pomorska A.; Wytrwal-Sarna M.; Kepczynski M.; Adamczyk Z. Formation of Strong Polycation (Poly[(3-Allylamino-2-Hydroxypropyl)Trimethylammonium Chloride]) Monolayers on Mica, Silica, and Gold Substrates: Modeling and Experimental Studies. J. Phys. Chem. C 2019, 123 (31), 19022–19032. 10.1021/acs.jpcc.9b04533. [DOI] [Google Scholar]
- Carrillo J. M. Y.; Dobrynin A. V. Polyelectrolytes in Salt Solutions: Molecular Dynamics Simulations. Macromolecules 2011, 44 (14), 5798–5816. 10.1021/ma2007943. [DOI] [Google Scholar]
- Bodnarchuk M. S.; Doncom K. E. B.; Wright D. B.; Heyes D. M.; Dini D.; O’Reilly R. K. Polyelectrolyte PKa from Experiment and Molecular Dynamics Simulation. RSC Adv. 2017, 7 (32), 20007–20014. 10.1039/C6RA27785C. [DOI] [Google Scholar]
- Ogasawara N.; Kasahara K.; Iwai R.; Takahashi T. Unfolding of α-Helical 20-Residue Polyglutamic Acid Analyzed by Multiple Runs of Canonical Molecular Dynamics Simulations. PeerJ 2018, 6, e4769. 10.7717/peerj.4769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyda J.; Dzubiella J. Ion-Specific Counterion Condensation on Charged Peptides: Poisson-Boltzmann vs. Atomistic Simulations. Soft Matter 2012, 8 (36), 9338–9344. 10.1039/c2sm25599e. [DOI] [Google Scholar]
- Batys P.; Zhang Y.; Lutkenhaus J. L.; Sammalkorpi M. Hydration and Temperature Response of Water Mobility in Poly(Diallyldimethylammonium)-Poly(Sodium 4-Styrenesulfonate) Complexes. Macromolecules 2018, 51 (20), 8268–8277. 10.1021/acs.macromol.8b01441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Batys P.; O’Neal J. T.; Li F.; Sammalkorpi M.; Lutkenhaus J. L. Molecular Origin of the Glass Transition in Polyelectrolyte Assemblies. ACS Cent. Sci. 2018, 4 (5), 638–644. 10.1021/acscentsci.8b00137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao B.; Cerdà J. J.; Holm C. Poly(Styrenesulfonate)–Poly(Diallyldimethylammonium) Mixtures: Toward the Understanding of Polyelectrolyte Complexes and Multilayers via Atomistic Simulations. Macromolecules 2010, 43 (18), 7828–7838. 10.1021/ma101091k. [DOI] [Google Scholar]
- Batys P.; Kivistö S.; Lalwani S. M.; Lutkenhaus J. L.; Sammalkorpi M. Comparing Water-Mediated Hydrogen-Bonding in Different Polyelectrolyte Complexes. Soft Matter 2019, 15, 7823–7831. 10.1039/C9SM01193E. [DOI] [PubMed] [Google Scholar]
- Yildirim E.; Zhang Y.; Lutkenhaus J. L.; Sammalkorpi M. Thermal Transitions in Polyelectrolyte Assemblies Occur via a Dehydration Mechanism. ACS Macro Lett. 2015, 4 (9), 1017–1021. 10.1021/acsmacrolett.5b00351. [DOI] [PubMed] [Google Scholar]
- Zhang R.; Zhang Y.; Antila H. S.; Lutkenhaus J. L.; Sammalkorpi M. Role of Salt and Water in the Plasticization of PDAC/PSS Polyelectrolyte Assemblies. J. Phys. Chem. B 2017, 121 (1), 322–333. 10.1021/acs.jpcb.6b12315. [DOI] [PubMed] [Google Scholar]
- Patel P. A.; Jeon J.; Mather P. T.; Dobrynin A. V. Molecular Dynamics Simulations of Multilayer Polyelectrolyte Films: Effect of Electrostatic and Short-Range Interactions. Langmuir 2006, 22 (24), 9994–10002. 10.1021/la061658e. [DOI] [PubMed] [Google Scholar]
- Cerdà J. J.; Qiao B.; Holm C. Understanding Polyelectrolyte Multilayers: An Open Challenge for Simulations. Soft Matter 2009, 5 (22), 4412. 10.1039/b912800j. [DOI] [Google Scholar]
- Sánchez P. A.; Vögele M.; Smiatek J.; Qiao B.; Sega M.; Holm C. Atomistic Simulation of PDADMAC/PSS Oligoelectrolyte Multilayers: Overall Comparison of Tri- and Tetra-Layer System. Soft Matter 2019, 15, 9437. 10.1039/C9SM02010A. [DOI] [PubMed] [Google Scholar]
- Landsgesell J.; Holm C.; Smiatek J. Wang–Landau Reaction Ensemble Method: Simulation of Weak Polyelectrolytes and General Acid–Base Reactions. J. Chem. Theory Comput. 2017, 13 (2), 852–862. 10.1021/acs.jctc.6b00791. [DOI] [PubMed] [Google Scholar]
- Landsgesell J.; Holm C.; Smiatek J. Simulation of Weak Polyelectrolytes: A Comparison between the Constant pH and the Reaction Ensemble Method. Eur. Phys. J.: Spec. Top. 2017, 226 (4), 725–736. 10.1140/epjst/e2016-60324-3. [DOI] [Google Scholar]
- Baptista A. M.; Teixeira V. H.; Soares C. M. Constant-pH Molecular Dynamics Using Stochastic Titration. J. Chem. Phys. 2002, 117 (9), 4184–4200. 10.1063/1.1497164. [DOI] [Google Scholar]
- Machuqueiro M.; Baptista A. M. Constant-pH Molecular Dynamics with Ionic Strength Effects: Protonation-Conformation Coupling in Decalysine. J. Phys. Chem. B 2006, 110 (6), 2927–2933. 10.1021/jp056456q. [DOI] [PubMed] [Google Scholar]
- Donnini S.; Ullmann R. T.; Groenhof G.; Grubmüller H. Charge-Neutral Constant pH Molecular Dynamics Simulations Using a Parsimonious Proton Buffer. J. Chem. Theory Comput. 2016, 12 (3), 1040–1051. 10.1021/acs.jctc.5b01160. [DOI] [PubMed] [Google Scholar]
- Donnini S.; Tegeler F.; Groenhof G.; Grubmüller H. Constant pH Molecular Dynamics in Explicit Solvent with λ-Dynamics. J. Chem. Theory Comput. 2011, 7 (6), 1962–1978. 10.1021/ct200061r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fluitt A. M.; De Pablo J. J. An Analysis of Biomolecular Force Fields for Simulations of Polyglutamine in Solution. Biophys. J. 2015, 109 (5), 1009–1018. 10.1016/j.bpj.2015.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews C. T.; Elcock A. H. Molecular Dynamics Simulations of Highly Crowded Amino Acid Solutions: Comparisons of Eight Different Force Field Combinations with Experiment and with Each Other. J. Chem. Theory Comput. 2013, 9 (10), 4585–4602. 10.1021/ct400371h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cino E. A.; Choy W. Y.; Karttunen M. Comparison of Secondary Structure Formation Using 10 Different Force Fields in Microsecond Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8 (8), 2725–2740. 10.1021/ct300323g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vierros S.; Sammalkorpi M. Phosphatidylcholine Reverse Micelles on the Wrong Track in Molecular Dynamics Simulations of Phospholipids in an Organic Solvent. J. Chem. Phys. 2015, 142 (9), 094902. 10.1063/1.4914022. [DOI] [PubMed] [Google Scholar]
- Robustelli P.; Piana S.; Shaw D. E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (21), E4758–E4766. 10.1073/pnas.1800690115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serafeim A. P.; Salamanos G.; Patapati K. K.; Glykos N. M. Sensitivity of Folding Molecular Dynamics Simulations to Even Minor Force Field Changes. J. Chem. Inf. Model. 2016, 56 (10), 2035–2041. 10.1021/acs.jcim.6b00493. [DOI] [PubMed] [Google Scholar]
- Lange O. F.; Van Der Spoel D.; De Groot B. L. Scrutinizing Molecular Mechanics Force Fields on the Submicrosecond Timescale with NMR Data. Biophys. J. 2010, 99 (2), 647–655. 10.1016/j.bpj.2010.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins: Struct., Funct., Genet. 2006, 65, 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W.; Zheng B.; Haynie D. T. A Molecular Dynamics Study of the Physical Basis of Stability of Polypeptide Multilayer Nanofilms. Langmuir 2006, 22 (15), 6668–6675. 10.1021/la060527a. [DOI] [PubMed] [Google Scholar]
- Pandey P. R.; Roy S. Distinctions in Early Stage Unwinding Mechanisms of Zwitterionic, Capped, and Neutral Forms of Different α-Helical Homopolymeric Peptides. J. Phys. Chem. B 2012, 116 (16), 4731–4740. 10.1021/jp301556x. [DOI] [PubMed] [Google Scholar]
- Szyk-Warszyńska L.; Raszka K.; Warszyński P. Interactions of Casein and Polypeptides in Multilayer Films Studied by FTIR and Molecular Dynamics. Polymers (Basel, Switz.) 2019, 11 (5), 920. 10.3390/polym11050920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasiliu T.; Cojocaru C.; Rotaru A.; Pricope G.; Pinteala M.; Clima L. Optimization of Polyplex Formation between DNA Oligonucleotide and Poly(L-Lysine): Experimental Study and Modeling Approach. Int. J. Mol. Sci. 2017, 18 (6), 1291. 10.3390/ijms18061291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francoia J. P.; Rossi J. C.; Monard G.; Vial L. Digitizing Poly-L-Lysine Dendrigrafts: From Experimental Data to Molecular Dynamics Simulations. J. Chem. Inf. Model. 2017, 57 (9), 2173–2180. 10.1021/acs.jcim.7b00258. [DOI] [PubMed] [Google Scholar]
- Kostritskii A. Y.; Kondinskaia D. A.; Nesterenko A. M.; Gurtovenko A. A. Adsorption of Synthetic Cationic Polymers on Model Phospholipid Membranes: Insight from Atomic-Scale Molecular Dynamics Simulations. Langmuir 2016, 32 (40), 10402–10414. 10.1021/acs.langmuir.6b02593. [DOI] [PubMed] [Google Scholar]
- Elder R. M.; Emrick T.; Jayaraman A. Understanding the Effect of Polylysine Architecture on DNA Binding Using Molecular Dynamics Simulations. Biomacromolecules 2011, 12 (11), 3870–3879. 10.1021/bm201113y. [DOI] [PubMed] [Google Scholar]
- Antila H. S.; Härkönen M.; Sammalkorpi M. Chemistry Specificity of DNA–polycation Complex Salt Response: A Simulation Study of DNA, Polylysine and Polyethyleneimine. Phys. Chem. Chem. Phys. 2015, 17 (7), 5279–5289. 10.1039/C4CP04967E. [DOI] [PubMed] [Google Scholar]
- Antila H. S.; Sammalkorpi M. Polyelectrolyte Decomplexation via Addition of Salt: Charge Correlation Driven Zipper. J. Phys. Chem. B 2014, 118 (11), 3226–3234. 10.1021/jp4124293. [DOI] [PubMed] [Google Scholar]
- Roberts B. P.; Scanlon M. J.; Krippner G. Y.; Chalmers D. K. Molecular Dynamics of Poly(L-Lysine) Dendrimers with Naphthalene Disulfonate Caps. Macromolecules 2009, 42 (7), 2775–2783. 10.1021/ma802154e. [DOI] [Google Scholar]
- Pandey P. R.; Roy S. Early Stages of Unwinding of Zwitterionic α-Helical Homopolymeric Peptides. Chem. Phys. Lett. 2011, 514 (4–6), 330–335. 10.1016/j.cplett.2011.08.050. [DOI] [Google Scholar]
- Paradossi G.; Chiessi E.; Malovikova A. Conformational Study of the Diastereomeric Pairs in Poly(Lysine)-Pectate Complexes. Macromolecules 2001, 34 (23), 8179–8186. 10.1021/ma010418x. [DOI] [Google Scholar]
- Rahimi A.; Amjad-Iranagh S.; Modarress H. Molecular Dynamics Simulation of Coarse-Grained Poly(L-Lysine) Dendrimers. J. Mol. Model. 2016, 22 (3), 59. 10.1007/s00894-016-2925-0. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Tieleman D. P. Perspective on the Martini Model. Chem. Soc. Rev. 2013, 42 (16), 6801. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
- Biswas S.; Sarkar S.; Pandey P. R.; Roy S. Transferability of Different Classical Force Fields for Right and Left Handed α-Helices Constructed from Enantiomeric Amino Acids. Phys. Chem. Chem. Phys. 2016, 18 (7), 5550–5563. 10.1039/C5CP06715D. [DOI] [PubMed] [Google Scholar]
- Robertson M. J.; Tirado-Rives J.; Jorgensen W. L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11 (7), 3499–3509. 10.1021/acs.jctc.5b00356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102 (18), 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- Lindahl E.; Bjelkmar P.; Larsson P.; Cuendet M. A.; Hess B. Implementation of the Charmm Force Field in GROMACS: Analysis of Protein Stability Effects from Correction Maps, Virtual Interaction Sites, and Water Models. J. Chem. Theory Comput. 2010, 6 (2), 459–466. 10.1021/ct900549r. [DOI] [PubMed] [Google Scholar]
- Aliev A. E.; Kulke M.; Khaneja H. S.; Chudasama V.; Sheppard T. D.; Lanigan R. M. Motional Timescale Predictions by Molecular Dynamics Simulations: Case Study Using Proline and Hydroxyproline Sidechain Dynamics. Proteins: Struct., Funct., Genet. 2014, 82 (2), 195–215. 10.1002/prot.24350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K. L.; Mylon S. E.; Elimelech M. Aggregation Kinetics of Alginate-Coated Hematite Nanoparticles in Monovalent and Divalent Electrolytes. Environ. Sci. Technol. 2006, 40 (5), 1516–1523. 10.1021/es0518068. [DOI] [PubMed] [Google Scholar]
- Kobayashi M.; Juillerat F.; Galletto P.; Bowen P.; Borkovec M. Aggregation and Charging of Colloidal Silica Particles: Effect of Particle Size. Langmuir 2005, 21 (13), 5761–5769. 10.1021/la046829z. [DOI] [PubMed] [Google Scholar]
- Mylon S. E.; Chen K. L.; Elimelech M. Influence of Natural Organic Matter and Ionic Composition on the Kinetics and Structure of Hematite Colloid Aggregation: Implications to Iron Depletion in Estuaries. Langmuir 2004, 20 (21), 9000–9006. 10.1021/la049153g. [DOI] [PubMed] [Google Scholar]
- Adamczyk Z.; Zembala M.; Warszyński P.; Jachimska B. Characterization of Polyelectrolyte Multilayers by the Streaming Potential Method. Langmuir 2004, 20 (24), 10517–10525. 10.1021/la040064d. [DOI] [PubMed] [Google Scholar]
- Micsonai A.; Wien F.; Bulyáki É.; Kun J.; Moussong É.; Lee Y. H.; Goto Y.; Réfrégiers M.; Kardos J. BeStSel: A Web Server for Accurate Protein Secondary Structure Prediction and Fold Recognition from the Circular Dichroism Spectra. Nucleic Acids Res. 2018, 46 (W1), W315–W322. 10.1093/nar/gky497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micsonai A.; Wien F.; Kernya L.; Lee Y. H.; Goto Y.; Réfrégiers M.; Kardos J. Accurate Secondary Structure Prediction and Fold Recognition for Circular Dichroism Spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (24), E3095–E3103. 10.1073/pnas.1500851112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Pall S.; Smith J. C.; Hess B.; Lindahl E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Rackers J. A.; Wang Z.; Lu C.; Laury M. L.; Lagardère L.; Schnieders M. J.; Piquemal J. P.; Ren P.; Ponder J. W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14 (10), 5273–5289. 10.1021/acs.jctc.8b00529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guvench O.; MacKerell A. D. Comparison of Protein Force Fields for Molecular Dynamics Simulations. Methods Mol. Biol. 2008, 443, 63–88. 10.1007/978-1-59745-177-2_4. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Boonstra S.; Onck P. R.; van der Giessen E. CHARMM TIP3P Water Model Suppresses Peptide Folding by Solvating the Unfolded State. J. Phys. Chem. B 2016, 120 (15), 3692–3698. 10.1021/acs.jpcb.6b01316. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Mittal J. Protein Simulations with an Optimized Water Model: Cooperative Helix Formation and Temperature-Induced Unfolded State Collapse. J. Phys. Chem. B 2010, 114 (46), 14916–14923. 10.1021/jp108618d. [DOI] [PubMed] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126 (1), 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52 (12), 7182. 10.1063/1.328693. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18 (12), 1463–1472. . [DOI] [Google Scholar]
- Miyamoto S.; Kollman P. A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13 (8), 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14 (1), 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Dos A.; Schimming V.; Tosoni S.; Limbach H.-H. Acid–Base Interactions and Secondary Structures of Poly-l-Lysine Probed by 15N and 13C Solid State NMR and Ab Initio Model Calculations. J. Phys. Chem. B 2008, 112 (49), 15604–15615. 10.1021/jp806551u. [DOI] [PubMed] [Google Scholar]
- Fändrich M.; Dobson C. M. The Behaviour of Polyamino Acids Reveals an Inverse Side Chain Effect in Amyloid Structure Formation. EMBO J. 2002, 21 (21), 5682–5690. 10.1093/emboj/cdf573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter R. J.Zeta Potential in Colloid Science: Principles and Applications; Colloid Sciences Series; Academic Press: London, 1981. [Google Scholar]
- Jin X.; Leclercq L.; Sisavath N.; Cottet H. Investigating the Influence of Phosphate Ions on Poly(L-Lysine) Conformations by Taylor Dispersion Analysis. Macromolecules 2014, 47 (15), 5320–5327. 10.1021/ma501058v. [DOI] [Google Scholar]
- Dos A.; Schimming V.; Tosoni S.; Limbach H. H. Acid-Base Interactions and Secondary Structures of Poly-l-Lysine Probed By15N And13C Solid State NMR and Ab Initio Model Calculations. J. Phys. Chem. B 2008, 112 (49), 15604–15615. 10.1021/jp806551u. [DOI] [PubMed] [Google Scholar]
- Donten M. L.; Hamm P. pH-Jump Induced α-Helix Folding of Poly-L-Glutamic Acid. Chem. Phys. 2013, 422, 124–130. 10.1016/j.chemphys.2012.11.023. [DOI] [Google Scholar]
- Best R. B.; Hummer G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J. Phys. Chem. B 2009, 113 (26), 9004–9015. 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Mittal J. Balance between α and β Structures in Ab Initio Protein Folding. J. Phys. Chem. B 2010, 114 (26), 8790–8798. 10.1021/jp102575b. [DOI] [PubMed] [Google Scholar]
- Hollingsworth S. A.; Karplus P. A. A Fresh Look at the Ramachandran Plot and the Occurrence of Standard Structures in Proteins. Biomol. Concepts 2010, 1 (3–4), 271–283. 10.1515/bmc.2010.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Buchete N. V.; Hummer G. Are Current Molecular Dynamics Force Fields Too Helical?. Biophys. J. 2008, 95 (1), L07. 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone φ, ψ and Side-Chain X1 and X2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8 (9), 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J.; Mackerell A. D. CHARMM36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data. J. Comput. Chem. 2013, 34 (25), 2135–2145. 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grasso G.; Deriu M. A.; Patrulea V.; Borchard G.; Möller M.; Danani A. Free Energy Landscape of SiRNA-Polycation Complexation: Elucidating the Effect of Molecular Geometry, Polymer Flexibility, and Charge Neutralization. PLoS One 2017, 12 (10), e0186816. 10.1371/journal.pone.0186816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostermeir K.; Zacharias M. Hamiltonian Replica-Exchange Simulations with Adaptive Biasing of Peptide Backbone and Side Chain Dihedral Angles. J. Comput. Chem. 2014, 35 (2), 150–158. 10.1002/jcc.23476. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


