Abstract
Accurate determination of the binding affinity of the ligand to the receptor remains a difficult problem in computer-aided drug design. Here, we study and compare the efficiency of Jarzynski’s equality (JE) combined with steered molecular dynamics and the linear interaction energy (LIE) method by assessing the binding affinity of 23 small compounds to six receptors, including β-lactamase, thrombin, factor Xa, HIV-1 protease (HIV), myeloid cell leukemia-1, and cyclin-dependent kinase 2 proteins. It was shown that Jarzynski’s nonequilibrium binding free energy ΔGneqJar correlates with the available experimental data with the correlation levels R = 0.89, 0.86, 0.83, 0.80, 0.83, and 0.81 for six data sets, while for the binding free energy ΔGLIE obtained by the LIE method, we have R = 0.73, 0.80, 0.42, 0.23, 0.85, and 0.01. Therefore, JE is recommended to be used for ranking binding affinities as it provides accurate and robust results. In contrast, LIE is not as reliable as JE, and it should be used with caution, especially when it comes to new systems.
Introduction
In computer-aided drug design, the binding affinity between the receptor and the ligand can be classified according to several quantities, but the most important one is the binding free energy (ΔGbind) because it is directly related to the inhibition constant that can be measured experimentally. Many methods have been developed to compute the free energy difference between bound and unbound states. Among them, molecular docking1 is the fastest but not sufficiently accurate. However, because of its high speed, it is commonly used in computer-aided drug design to select potential compounds from large databases.
Molecular dynamics (MD)-based methods such as molecular mechanics Poisson–Boltzmann or generalized Born surface area (MM/PB(GB)SA),2 linear interaction energy (LIE),3 thermodynamics integration (TI),4 and free energy perturbation (FEP)5 are more accurate than the docking method. Different from other MD methods, FEP and TI are exact and, as expected, the most accurate6 but much more time consuming. The underlying phenomenological description of FEP and TI is based on the equilibrium mechanics, and in the case of the system with more than 105 atoms, an equilibrium transition from the bound state to the unbound state is practically impossible.
A less computationally demanding method is the LIE method,3,7 in which it is assumed that the ligand–protein binding affinity linearly depends on the polar and nonpolar binding energies. LIE does not consume a lot of computational time because it takes into account only bound and unbound states, while the others mentioned above require knowledge of the transformation process, including transition/intermediate states.7−9 The contribution from the electrostatic and van der Waals (vdW) interaction energy is obtained through the thermodynamic cycle.10 In the past few decades, several groups have successfully applied the LIE method to predict new inhibitors of human dihydrofolate reductases10 and to obtain the binding affinity of inhibitors of neuraminidase,11 BACE-1,12 cytochrome P450,13,14 farnesoid X receptor,15 and others.16 Several improved versions of LIE were proposed.17−19
After the appearance of the atomic force microscopy (AFM) technique in 1985, the steered MD (SMD) method20−23 was used to study unbinding of the ligand from the protein pocket. Several groups24−29 showed that SMD is accurate and still fast enough to deal with a large number of compounds. In comparison to MM/PBSA, the SMD method is not only similar in accuracy25 but also requires less computational time. In the context of SMD-based drug design, it is important to notice that Colizzi et al.30 and Mai et al.24 reported that the rupture force (Fmax in the force–displacement/time profile) correlates with the experimental inhibition constant IC50 in such a way that the greater the rupture force, the higher the binding affinity. In addition, it has been shown31 that the nonequilibrium work Wpull has a better correlation with experiment than the rupture force because it is a function of the entire process, while Fmax is computed only in a single state. Thus, both rupture force and nonequilibrium work can be used as a score function for ranking the binding affinity. Recently, it has been shown32 that the rupture time and unbinding and binding barriers are also reliable measures for binding affinity. The SMD method becomes a promising tool in Computer-aided drug design25 as it has been successfully applied to access the binding affinity for a large number of protein–ligand complexes, such as influenza virus, cancer target LSD1, and so forth.33−37
Combining Jarzynski’s equality (JE)38 and the Hummer–Szabo formalism,39 we showed that32 the nonequilibrium binding free energy ΔGneqJar is a good descriptor for binding affinity. Because this conclusion was obtained only for one data set, which includes 23 ligands in complex with β-lactamase protein, it remains unclear if it is valid for other systems. Therefore, one of our main goals is to check the validity of ΔGneq for ranking binding affinity for other complexes. It would be ideal to compare JE with exact methods such as FEP and TI. However, these methods are very laborious if we want to study a large number of protein–ligand complexes. Among MD-based methods, LIE is not only well tested for a number of systems11−13,15,18,40−42 but also the fastest and, in terms of computational time, comparable to JE. Therefore, our second goal is to choose LIE and compare its effectiveness with JE.
We conducted simulations for six sets of complexes that include 23 ligands bound to six different targets: β-lactamase, thrombin, factor Xa, HIV-1 protease (HIV), myeloid cell leukemia-1 (MCL-1), and cyclin dependent kinase 2 (CDK-2) proteins. The correlation level of ΔGneqJar with experimental data exceeds 0.80 for the six data sets, while the LIE method gives lower correlations of 0.73, 0.80, 0.42, 0.23, 0.85, and 0.01. Thus, ΔGneq is reliable for ranking binding affinities of all the studied systems and one can expect that this is true in all cases. However, ΔGLIEis less robust and the LIE method should be used with caution.
Materials and Methods
Materials
The atomic structures of all the studied complexes were collected from Research Collaboratory for Structural Bioinformatics Protein Data Bank (RCSB PDB) (https://www.rcsb.org/). The PDB identifiers of 23 ligands in complex with thrombin, factor Xa, HIV-1, MCL-1, CDK-2, proteins are shown in Tables S1–S5 in the Supporting Information. Their inhibition constant was experimentally measured using kinetic enzyme assay (see, e.g., Baum et al.43 and references in the Supporting Information). Similar information on β-lactamase complexes is available in our previous work.32
Note that thrombin (or factor IIa) is a serine protease that plays an important role in thrombosis and hemostasis because it converts the fibrinogen into fibril in blood clotting.44 This enzyme occurs in the coagulation process by cleaving two peptide bonds of prothrombin (factor II)45−48 which is synthesized in the liver.49 The conversion of prothrombin to thrombin takes place at the penultimate stage in the cascade model of coagulation with the association of factor Xa protein.44,46 At this stage, the platelet acts as a binding site for coagulation of the combined complexes.50,51 The structure of thrombin includes two polypeptide chains, a light chain (A) and a heavy one (B). In humans, chains A and B have 36 and 259 residues, respectively.52
According to the coagulation cascade, factor Xa protein is involved not only in extrinsic but also in intrinsic coagulation.44,46 When interacting with factor Va protein, factor Xa activates the cleavage of prothrombin to thrombin; thus, thrombin will catalyze the conversion of fibrinogen to fibril. Thrombin inhibitors block the activity of thrombin, whereas factor Xa inhibitors decrease the thrombin production. The conformation of factor Xa includes two chains: a heavy chain with 303 amino acids and a light chain with 139 amino acids. Because of the structural similarities between factor Xa and thrombin protein, factor Xa inhibitors can also bind to thrombin, but this has not yet been confirmed by experiment and simulation. In addition, one factor Xa molecule is responsible for generating more than 1000 molecules of thrombins,53,54 which makes factor Xa protein a more attractive target for the development of antithrombotic drugs than thrombin.
HIV-1 protease has been known as the dimeric aspartic protease which cleaves the nascent polyproteins of HIV and plays a key role in viral replication.55−57 HIV-1 protease inhibitors are a good example of the success of structure-based drug design in the AIDS treatment.58,59 However, besides the high ratio of side effects, more and more HIV-1 mutants are found and linked toward HIV viral replication.60,61 The development of new efficient HIV-1 protease inhibitors remains a challenge.
MCL-1 protein, a member of the Bcl-2 family, is an important target in the treatment of human cancer.62 Previous studies have shown that overexpression of MCL-1 can help cancerous cells escape death.63,64 Amplification of MCL-1 has been observed not only in the lung, breast, pancreatic, and ovarian cancers but also in melanoma and leukemia.65−71 In addition, overexpression of MCL-1 has triggered a resistance mechanism that is against a number of anticancer drugs including paclitaxel, vincristine, and gemcitabine.72,73 The silencing of MCL-1 also potently induced the disappearance of subgroups of non-small-cell lung cancer cell lines.74 However, no MCL-1 inhibitor has been passed into clinical trial. This problem prompts us to consider MCL-1 as a promising target for various types of cancers.
CDK-2 protein is a member of 20 serine kinase proteins and plays a crucial role in cell division, transcription, and post-transcriptional modification.75,76 CDK-2 is especially important as it can prevent cell cycle dysfunction.77 In association with cyclin E and cyclin A, CDK-2 protein was observed in the regulation of the G1-S phase of the cell cycle. The idea of using CDK-2 inhibitors to influence cancer progression has been supported with much evidence.78 Thus, CDK-2 is a potential drug target for anticancer therapy.
Experimental Binding Free Energy
Experimental binding free energy is related to the inhibition constant Ki by the following equation
| 1 |
where Ki is measured in M.
The Ki values, obtained in various experimental studies, are given in Tables S1–S5 for thrombin, factor Xa, HIV-1, MCL-1, and CDK-2 complexes, respectively. Ki of 23 β-lactamase complexes is available in our previous work.32
Steered MD Simulation
In SMD, an external force with a constant pulling speed v is applied to the ligand through a spring with a spring constant k. Then, the force acts on the ligand, F = k(Δx – vt), where Δx is the displacement of a pulled atom from its initial position. As in the typical AFM experiment, we chose k = 600 kJ/mol nm2. Similar to our previous studies,24,32 we used the pulling speed v = 5 m/s because the rupture force79 and work31 depend on v, but the correlation between the experimental and simulation data on the binding affinity is not sensitive to it.
SMD simulations were conducted using the GROMACS package.80 It is well known that the rupture force is sensitive to the pulling direction,24,81 which prompted us to determine which pulling path should be chosen. For this purpose, we followed the approach proposed earlier24,81 that Caver software82 was first employed to search for all possible pulling paths. Then, for each target, we selected a representative ligand to pull along these directions using SMD simulation and chose a path that corresponds to the lowest rupture force. The chosen direction was used for SMD simulation for the remaining compounds and was adapted along the z-axis for six targets, including thrombin, factor Xa, HIV-1, MCL-1, CDK-2, and β-lactamase (Figure 1).
Figure 1.
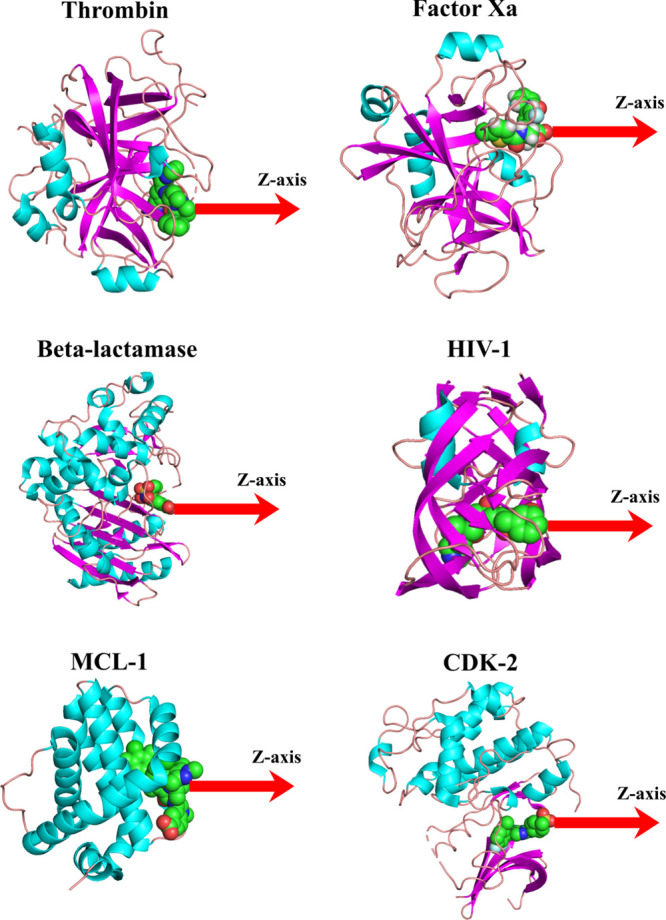
3D structure of typical complexes of thrombin, factor Xa, β-lactamase, HIV-1, MLC-1, and CDK-2 protein. The pulling direction along the z-axis in SMD simulation is shown. Plots were made using PyMol.
A receptor–ligand complex was simulated with the CHARMM27 force field83 and TIP3P water model.84 A solvated box was set to ensure that the smallest distance between the protein and the boundary was large enough to prevent protein–protein self-interaction. The ligand conformation and the SwissParam server (http://www.swissparam.ch)85 were used to create its topology. The system including the receptor–ligand complex, solvents, and counter ions was equilibrated through three steps. First, energy minimization was carried out using the steepest descent method and the criterion that convergence is achieved when the maximum force becomes less than 100 kJ/mol/nm. Then, position-restrained MD simulation was performed for 500 ps in the NVT ensemble with a velocity rescaling thermostat86 followed by 500 ps in the NPT ensemble with a Parrinello–Rahman barostat87 to make sure that the system was stable. Temperature and pressure, in our simulation, were set at 300 K and 1 atm, respectively. Twenty independent SMD trajectories of 600 ps were performed for each complex. We also restrained all Cα atoms of the receptor to avoid the drift of the protein under the external force. From the force–time/position profile, we collected the rupture force Fmax, a force needed for the protein–ligand dissociation. We can compute the pulling work as
| 2 |
Equation for Jarzynski’s Nonequilibrium Binding Free Energy ΔGneqJar
According to JE,38 for an irreversible process, the difference between the equilibrium free energies of the two states can be calculated from the distribution of work performed for transformation between them. Extending JE to the case when the external force with a constant pulling speed is applied, Hummer and Szabo88 showed that the time-dependent binding free energy is given by the following equation
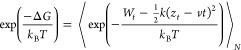 |
3 |
where ⟨...⟩ is the average over N trajectories, zt is the time-dependent displacement, and Wt is the nonequilibrium or pulling work at time t, that is, Wt = Wpull(t), where Wpull is defined by eq 2. Equation 3 means that we can truly extract an equilibrium quantity by assembling the external work of an infinite number of nonequilibrium processes. In this study, when the transformation is not slow enough and the number of SMD runs is finite, we can obtain only Jarzynski’s nonequilibrium binding free energy ΔGneqJar.32 Therefore ΔGneq is defined by eq 3, but for the nonequilibrium case.
LIE Method
In LIE, the binding free energy of a ligand ΔGLIE can be expressed with two terms: polar and nonpolar contributions, ΔGLIE = ΔGpolar + ΔGnonpolar. The entropy is implicitly taken into account. In MD simulation, the polar and nonpolar energy are the electrostatic and vdW interaction energies, respectively. To express free energy in terms of potential energy, Åqvist et al.3 adopted the linear approximation89,90 for the electrostatic interaction, where ΔGpolar = ΔGelec ∼1/2Δ⟨Velec⟩. The exact scale factor 1/2 was subsequently changed to improve the accuracy.40,41 The studies of Pratt–Chandler91 and Ben-Naim–Marcus92 also showed that we can replace ΔGnonpolar with a part of the difference in the vdW interaction energy. Therefore, an estimation of the binding free energy through a thermodynamic cycle in the LIE method is given by the following equation
| 4 |
where Vl–sel and Vl–s denote the electrostatic and vdW interaction between the ligand and surrounding (protein, water, and counter ions), respectively.
The interaction energy in the bound and free states is the energy at the time t = 0 and at the end of simulation, when the ligand is completely released from the binding site. In the bound state, the ligand is the most stable in the protein active site, whereas in the unbound state, the ligand is far from the active site and practically does not interact with the receptor. The radius of polar/nonpolar interaction is infinite, but using the cutoff parameters, protein–ligand’s association will be broken down if the pulling time is long enough for us to drive the ligand far away from the protein’s pocket than 1.4 nm. As shown below, the initial and final snapshots, obtained in SMD simulations, are sufficient for estimation of the LIE binding free energy, which is given in eq 4. However, to enhance structural sampling, for each SMD trajectory, initial and final snapshots were selected as initial conformations for performing short molecular dynamic simulation with 250 ps and 500 conformations were recorded for evaluating ΔGLIE.
Parameters for Estimation of ΔGLIE
To obtain ΔGLIE, in the original model9 scale factor β = 1/2, γ = 0 and the value of α is found by fitting to experimental data or by the so-called semi-empirical method. However, one can expect that41,42 electrostatic effects are different in aqueous and protein environments. Then, the polar scale coefficient β is different for these conditions and is denoted as βprotein and βwater. The same is true for the vdW interaction with the scale factors αprotein and αwater. Later, it was realized that the use of parameters separately for protein and water is not necessary. Instead, one can use four values of parameter β ranking from 0.35 to 0.5, which is linked with the number of charged groups of the ligand. Further studies13,40,42,93 allowed the parametrization of α, β, and γ which are used to compute the absolute binding free energy. In this scheme, scale factors β of all complexes, which depend on the chemical structure of the ligand, are presented in Tables S6–S11. A compound that contains a charged group has β = 1/2, while for the dipolar compound without any hydroxyl groups, β = 0.43. The dipolar compound that has one hydroxyl group has β = 0.37 and β = 0.33 for the dipolar compounds with two or more hydroxyl groups. Following Ljungberg et al.,94 we set γ = 0 (kcal/mol) and tried to find the best value of the α parameter that would provide the best correlation between modeling and experiment.
Results and Discussion
Rupture Force and Time
When the pulling spring began to move away from the anchored molecule, the force exerted on the ligand increased rapidly, as evident from the force–time and force–displacement profiles (Figures 2 and S1). At this stage, the ligand can be considered as being restrained in a harmonic potential as the force almost linearly depends on the displacement. The appearance of the maximum force Fmax at time tmax demonstrated the rupture event after which the ligand–protein association is broken down. It was shown that the higher the rupture force Fmax, the stronger the binding affinity,24,30,32 and this conclusion was obtained for many systems.
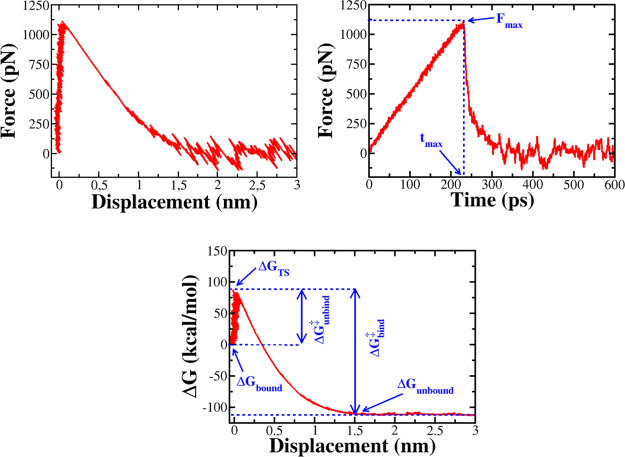
Figure 2.
Top panel: Dependence of the force acting on the ligand on displacement (left) and time (right). Rupture force Fmax occurs at time tmax. Bottom panel: Displacement dependence of Jarzynski’s binding free energy, showing that the ligand binding/unbinding is a barrier crossing event with the unbinding barrier ΔGunbind‡ and the binding barrier ΔGbind.
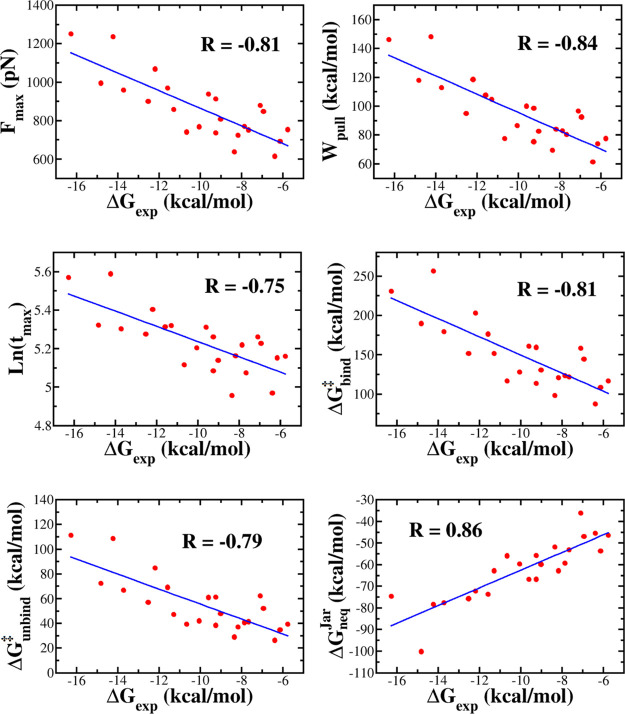
Over 23 thrombin complexes, 1SL3 has the highest Fmax of 1250.9 pN, while 3SV2 has the lowest Fmax of 754 pN (Table 1). From the force–time profiles of 23 ligands complexed with factor Xa and MCL-1, we found that the rupture force ranked from 695.3 to 1199.2 pN and from 536.8 to 1408.4 pN, respectively (Tables S12 and S14). The correlation between rupture force and experimental binding free energies is R = 0.81, 0.78, and 0.80 for thrombin (Figure 3), factor Xa (Figure S2), and MCL-1 (Figure S4), respectively. These correlation levels are close to R = 0.82 for the β-lactamase complexes.32 As evident from Figures S3 and S5, a lower correlation was obtained for HIV-1 (R = 0.64) and CDK2 (R = 0.66), but, as will be shown below, the JE method remains reliable for these sets because Jarzynski’s nonequilibrium free energy highly correlates with experiment (Table 2).
Table 1. SMD Results Obtained for 23 Thrombin Complexesa.
| no. | ligand PDB ID | complex PDB ID | ΔGexp (kcal/mol) | Fmax (pN) | Wpull (kcal/mol) | ΔGneqJar (kcal/mol) | tmax (ps) | ΔGunbind‡ (kcal/mol) | ΔGbind‡ (kcal/mol) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 170 | 1SL3 | –16.3 | 1250.9 ± 135.5 | 146.3 ± 22.2 | –74.7 ± 1.9 | 226.7 ± 35.5 | 111.2 ± 24.3 | 230.9 ± 40.0 |
| 2 | IH2 | 1C4V | –14.8 | 996.1 ± 109.2 | 118.0 ± 12.6 | –100.0 ± 1.8 | 205.0 ± 22.7 | 72.4 ± 15.8 | 190.0 ± 28.1 |
| 3 | IH1 | 1C4U | –14.2 | 1235.8 ± 217.4 | 148.2 ± 35.3 | –78.4 ± 1.9 | 267.8 ± 39.5 | 108.6 ± 37.0 | 256.3 ± 71.1 |
| 4 | 33U | 2ZO3 | –13.7 | 959.6 ± 136.5 | 113.0 ± 18.3 | –77.6 ± 1.9 | 200.9 ± 27.6 | 66.9 ± 18.8 | 179.5 ± 35.8 |
| 5 | 177 | 1TA6 | –12.5 | 901.0 ± 128.0 | 94.9 ± 15.8 | –75.6 ± 1.8 | 195.5 ± 23.4 | 57.0 ± 17.3 | 151.6 ± 33.0 |
| 6 | T76 | 1NT1 | –12.2 | 1069.8 ± 189.7 | 118.6 ± 22.6 | –72.2 ± 1.9 | 222.5 ± 41.6 | 84.8 ± 27.2 | 203.0 ± 49.7 |
| 7 | BM9 | 1BMN | –11.6 | 969.4 ± 136.6 | 107.7 ± 18.0 | –73.7 ± 1.9 | 203.1 ± 25.4 | 69.3 ± 19.2 | 176.7 ± 36.7 |
| 8 | MID | 1ETS | –11.3 | 859.2 ± 131.0 | 104.8 ± 17.2 | –62.8 ± 1.9 | 204.3 ± 29.7 | 47.3 ± 15.0 | 151.8 ± 30.7 |
| 9 | 894 | 2JH6 | –10.7 | 741.8 ± 108.1 | 77.6 ± 9.5 | –55.7 ± 1.8 | 166.8 ± 19.1 | 39.4 ± 12.6 | 116.8 ± 20.2 |
| 10 | 23U | 3DHK | –10.0 | 769.0 ± 148.2 | 86.5 ± 13.2 | –59.7 ± 1.9 | 182.1 ± 21.0 | 42.2 ± 17.2 | 128.1 ± 29.9 |
| 11 | 64U | 3DUX | –9.6 | 938.3 ± 119.0 | 100.2 ± 15.1 | –66.8 ± 1.9 | 202.9 ± 28.8 | 61.2 ± 15.1 | 160.9 ± 28.5 |
| 12 | 22U | 2ZC9 | –9.2 | 736.8 ± 112.8 | 75.5 ± 9.0 | –55.7 ± 1.9 | 161.5 ± 23.4 | 38.6 ± 13.0 | 113.7 ± 20.8 |
| 13 | 29U | 2ZGX | –9.2 | 913.4 ± 143.9 | 98.6 ± 16.0 | –66.7 ± 1.9 | 192.7 ± 30.2 | 61.2 ± 19.8 | 159.6 ± 35.0 |
| 14 | 895 | 2JH5 | –9.0 | 808.7 ± 111.8 | 82.8 ± 8.9 | –59.8 ± 1.9 | 170.6 ± 21.8 | 47.9 ± 12.4 | 130.5 ± 19.9 |
| 15 | GR3 | 1AWH | –8.3 | 638.4 ± 88.3 | 69.5 ± 9.4 | –51.6 ± 1.8 | 142.2 ± 21.8 | 29.1 ± 9.4 | 98.4 ± 17.0 |
| 16 | 00R | 1D6W | –8.2 | 723.3 ± 158.0 | 84.0 ± 16.8 | –62.5 ± 1.8 | 174.6 ± 36.5 | 37.2 ± 17.2 | 121.0 ± 31.5 |
| 17 | B01 | 3SHC | –7.8 | 769.8 ± 130.1 | 83.0 ± 13.6 | –59.3 ± 1.9 | 185.0 ± 24.8 | 40.8 ± 16.0 | 123.5 ± 28.0 |
| 18 | P97 | 3SHA | –7.7 | 752.5 ± 126.0 | 80.5 ± 12.1 | –53.1 ± 1.9 | 159.9 ± 26.3 | 41.6 ± 13.8 | 121.9 ± 24.6 |
| 19 | 19U | 2ZFP | –7.1 | 879.3 ± 257.6 | 96.6 ± 42.6 | –36.1 ± 1.9 | 192.9 ± 54.1 | 62.3 ± 40.0 | 158.5 ± 82.5 |
| 20 | 91U | 3F68 | –6.9 | 847.8 ± 164.1 | 92.6 ± 17.4 | –47.0 ± 1.9 | 186.3 ± 34.4 | 52.1 ± 23.4 | 144.5 ± 39.8 |
| 21 | M18 | 3EGK | –6.4 | 616.0 ± 86.3 | 61.3 ± 8.7 | –45.4 ± 1.9 | 144.0 ± 13.4 | 26.5 ± 8.7 | 87.3 ± 17.1 |
| 22 | 99P | 3P17 | –6.1 | 692.7 ± 166.0 | 74.1 ± 18.1 | –53.3 ± 1.6 | 173.0 ± 31.6 | 34.9 ± 18.7 | 108.5 ± 34.3 |
| 23 | P05 | 3SV2 | –5.8 | 754.4 ± 110.7 | 77.8 ± 12.3 | –46.3 ± 1.9 | 174.1 ± 26.6 | 39.4 ± 12.6 | 117.0 ± 23.6 |
ΔGneqJar, ΔGunbind, and ΔGbind‡ were obtained using JE.
Figure 3.
Correlation between the experimental binding free energy ΔGexp and the rupture force Fmax, pulling work Wpull, rupture time tmax, binding ΔGbind‡ and unbinding ΔGunbind barriers, and Jarzynski’s binding free energy ΔGneqJar, obtained in the SMD simulation for the thrombin complexes. The correlation coefficient R is also shown.
Table 2. Correlation between the Experimental Binding Free Energy ΔGexp with the Rupture Force Fmax, Pulling Work Wpull, Rupture Time tmax, Binding ΔGbind‡ and Unbinding ΔGunbind Barriers, and Jarzynski’s Binding Free Energy ΔGneqJar, Obtained in the SMD Simulation for Six Complexesa.
| thrombin | factor Xa | β-lactamase | HIV-1 | MCL-1 | CDK-2 | |
|---|---|---|---|---|---|---|
| Fmax | 0.81 | 0.78 | 0.82 | 0.64 | 0.80 | 0.66 |
| Wpull | 0.84 | 0.74 | 0.84 | 0.68 | 0.79 | 0.73 |
| ln(tmax) | 0.75 | 0.75 | 0.84 | 0.70 | 0.83 | 0.61 |
| ΔGunbind‡ | 0.79 | 0.76 | 0.80 | 0.58 | 0.78 | 0.69 |
| ΔGbind‡ | 0.81 | 0.77 | 0.83 | 0.63 | 0.77 | 0.68 |
| ΔGneqJar | 0.86 | 0.83 | 0.89 | 0.80 | 0.83 | 0.81 |
Results for β-lactamase were taken from Truong et al and Li.32
Recently, based on the data set of 23 β-lactamase complexes, it has been found that32 the rupture time tmax also correlates with binding affinity in such a way that the larger the tmax, the higher the binding affinity. An interesting question arises: does this conclusion remain true for other complexes? In order to answer this question, we estimated the rupture time for another five sets (Tables 1 and S12–S15). For example, tmax varies between 144 and 267.8 ps for thrombin complexes (Table 1), while for factor Xa, this range is narrower, from 168 to 249.7 ps (Table S12). The correlation level between simulation and experiment is R = 0.75 for both these data sets (Figures 3 and S2). MCL-1 has a higher value of R = 0.81, while for CDK-2 and HIV-1, we obtained R = 0.62 and 0.69. Recall that the correlation between ln(tmax) and the experimental binding free energy is better for the β-lactamase complexes32 with R = 0.84. Thus, for all the systems studied, the rupture time correlated with the binding affinity, and this result is reasonable because the stronger the binding, the longer it takes to extract the ligand from the binding site. More importantly, the rupture time can be used as a measure for binding affinity.
Correlation between Pulling Work and Binding Affinity
Pulling work was calculated using eq 2, and its time dependence is shown in Figure S1 for several systems. At the beginning, the work is almost zero because the ligand cannot move from the binding point. As the time increases, the work increases, reaching a stable value, which is called the nonequilibrium pulling work Wpull, necessary to drive the complex from a bound state to an unbound state.
In the thrombin set, 1C4U has the greatest work of 148.2 kcal/mol, although its inhibition constant is ranked third (Table 1). 1SL3, which holds the record for the inhibition constant, has slightly lower Wpull (146 kcal/mol), while Wpull of the second complex 1C1U is significantly lower (118 kcal/mol).
In the case of factor Xa, the three strongest inhibitors, including 2P3T, 1MQ6, and 3CS7, have nonequilibrium work values of 115.4, 139.5, and 114.8 kcal/mol, respectively (Table S12). For the whole set, Wpull ranges from 73 to 139.5 kcal/mol. The nonequilibrium pulling work of HIV-1, MCL-1, and CDK-2 complexes is shown in Tables S13–S15.
The correlation level between Wpull and ΔGexp is R = 0.84, 0.74, 0.68, 0.79, and 0.73 for thrombin, factor Xa, HIV-1, MCL-1, and CDK-2, respectively (Figures 3 and S2–S5, Table 2). For a set of 23 β-lactamase complexes, the corresponding correlation is 0.84.32 The worst correlation was observed for HIV-1 (R = 0.68), but overall, for all data sets, the correlation between Wpull and ΔGexp is good. Thus, along with Fmax and tmax, Wpull can be used to rank binding affinity. In most of the cases, Wpull is a better indicator than Fmax because it has a higher correlation with experiment (Table 2).
Nonequilibrium Binding and Unbinding Free Energy Barriers
The escape of a ligand from the protein binding site is the crossing over a free energy barrier. In the presence of the external force, using Hummer–Szabo eq 3, we can obtain the time-dependent free energy profiles (Figures 2 and S1). The bound state at small times is separated from the unbound state at large times by the transition state (TS). The binding free energy barrier is defined as ΔGbind‡ = ΔGTS – ΔGunbound, while the unbinding barrier ΔGunbind = ΔGTS – Gbound. The values of ΔGbind‡ and ΔGunbind obtained in SMD simulation are shown in Tables 1 and S12–S15 for the thrombin, factor Xa, HIV-1, MCL-1, and CDK-2, respectively. Over 23 thrombin complexes, 1SL3 has the highest ΔGunbind‡ (111.2 kcal/mol), while the lowest unbinding barrier (26.5 kcal/mol) belongs to 3EGK. For factor Xa complexes, it runs from 27.3 kcal/mol (2J94) to 101.4 kcal/mol (1MQ6). The correlation of ΔGunbind with ΔGexp is pretty good with R = 0.79, 0.76, 0.58, 0.78, and 0.69 for thrombin (Figure 3), factor Xa (Figure S2), HIV-1 (Figure S3), MCL-1 (Figure S4), and CDK-2 (Figure S5), respectively (see also Table 2). These values are lower than R = 0.80 of β-lactamase.32
Under nonequilibrium conditions, the binding process always passes through a barrier approximately two times higher than the unbinding barrier. This is consistent with the experimental fact that the process of ligand unbinding from a protein pocket is much faster than the binding process.95 As expected, the nonequilibrium ΔGbind‡ also correlates well with ΔGexp with R = 0.81, 0.77, 0.63, 0.77, and 0.68 for thrombin (Figure 3), factor Xa (Figure S2), HIV-1 (Figure S3), MCL-1 (Figure S4), and CDK-2 (Figure S5), respectively. Again, as in the unbinding case, the best correlation was obtained for β-lactamase32 (R = 0.83). Although the correlation level of the nonequilibrium unbinding and binding barrier data with experiment is not as high as Jarzynski’s binding free energy (see below), we expect that a combination of these three quantities is useful for studying ligand binding.
Jarzynski’s Nonequilibrium Binding Free Energy
Using SMD simulation and eq 3, we obtained the time dependence of the binding free energy from each trajectory, as shown in Figure S1, for several systems. The binding free energy between the bound and unbound states is defined as ΔG at large time scales (Figure 2). Averaging over all SMD trajectories, we obtained ΔGneqJar which characterizes the binding/unbinding process out of equilibrium because the pulling speed is not small and the number of trajectories is not large enough. ΔGneq of 23 β-lactamase complexes was obtained in the previous work,32 showing that the correlation between ΔGneqJar and the experimental binding free energy is high (R = 0.89). This implies that the nonequilibrium binding free energy can be used to discern the relative binding affinities. Here, we want to further verify this conclusion for five more data sets.
For thrombin, as shown in the experiment, 1SL3 has the highest binding affinity (Table 1) but its ΔGneqJar (−74.7 kcal/mol) takes the fifth place. According to the ΔGexp rating, 1C4V is the second but has the lowest ΔGneq of −100 kcal/mol. 2ZFP has the highest Jarzynski’s nonequilibrium binding free energy of −36 kcal/mol. Twenty-three factor Xa complexes had the ΔGneqJar values that ranked between −96 (3CS7) and −62.1 kcal/mol (2J38) (Table S12). ΔGneq of HIV-, MCL-1, and CDK-2 complexes is given in Tables S13–S15. Because ΔGneqJar was obtained out of equilibrium, it is much lower that ΔGexp in all studied systems including the β-lactamase set.32 As the pulling speed decreases, the rupture force and work decrease,31,79 and therefore, the nonequilibrium binding free energy becomes smaller. Thus, in order to narrow the gap between simulation and experiment, we must reduce v, but this problem is left for further study.
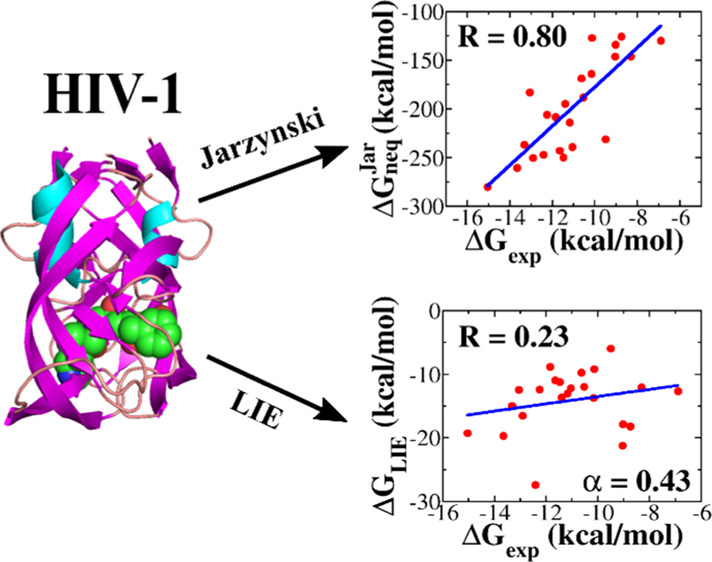
As can be seen from Figures 3 and S2–S5, ΔGneqJar correlates with ΔGexp to a greater extent for the thrombin set (R = 0.86) compared with factor Xa (R = 0.83), HIV (R = 0.80), CDK-2 (R = 0.81), and MCL-1 (R = 0.83). However, these correlation levels are slightly lower than R = 0.89 of the β-lactamase set.32 Interestingly, for all complexes, ΔGneq agrees with experiment better than other quantities (Table 2).
Binding Free Energy Estimated by the LIE Method and Correlation with Experiment
A typical time dependence of the electrostatic and vdW interaction energy between the ligand and the protein is shown in Figure S6, where, for clarity, the interaction with the solvent was excluded. Obviously, the simulation time was long enough to turn off the ligand–protein interaction. To calculate ΔGLIE, we used eq 3 with γ = 0, β given in Tables S6–S11 for the six sets and α ranged from 0 to 1. The average values of the polar and nonpolar interaction energies in the bound and unbound states for the six sets are shown in Tables 3 and S16–S20 in the Supporting Information.
Table 3. Average Polar and Nonpolar Interaction Energy in the Bound and Free States for 23 β-Lactamase Complexesa.
| no. | AmpC PDB ID | ΔGexp | ⟨Velec⟩bound | ⟨Velec⟩free | ⟨VvdW⟩bound | ⟨VvdW⟩free | ΔGLIE α = 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1XGJ | –8.2 | –29.8 ± 4.9 | –33.4 ± 2.5 | –48 ± 5.8 | –16.8 ± 3 | –30 ± 11.2 |
| 2 | 2R9W | –7.0 | –32.3 ± 5.9 | –33.2 ± 2.7 | –58 ± 7.3 | –22.2 ± 3.1 | –35.5 ± 13.2 |
| 3 | 1XGI | –6.7 | –25.4 ± 5.3 | –26.3 ± 2.7 | –51.9 ± 5.4 | –19.3 ± 2.6 | –32.2 ± 11 |
| 4 | 2R9X | –6.7 | –31.2 ± 4.8 | –34.1 ± 2.8 | –64.4 ± 4.9 | –23 ± 3.2 | –40.5 ± 10.6 |
| 5 | 4JXS | –6.5 | –34 ± 5.9 | –31.2 ± 3.1 | –60.7 ± 5.4 | –17.8 ± 3.3 | –43.8 ± 11.7 |
| 6 | 4JXW | –6.5 | –33.6 ± 6.9 | –32.8 ± 2.9 | –54.7 ± 6 | –20.5 ± 3 | –34.4 ± 12.2 |
| 7 | 1L2S | –6.3 | –22.4 ± 2.7 | –20.1 ± 2.1 | –54.8 ± 3.4 | –18 ± 2.4 | –37.7 ± 7.5 |
| 8 | 4JXV | –6.2 | –29.1 ± 5.4 | –34.4 ± 3.1 | –63.8 ± 6.9 | –18.6 ± 3.4 | –43.4 ± 13.1 |
| 9 | 2PU2 | –6.1 | –45.1 ± 7.3 | –36.3 ± 3.2 | –50.6 ± 5.7 | –17.8 ± 3.4 | –35.7 ± 12.6 |
| 10 | 4KZ4 | –5.7 | –25.4 ± 7 | –21.6 ± 2.8 | –47.1 ± 4.1 | –15 ± 2.8 | –33.5 ± 10.5 |
| 11 | 4KZA | –5.1 | –32.5 ± 5.2 | –24.4 ± 3 | –51.1 ± 5.3 | –13.2 ± 2.7 | –40.9 ± 11.1 |
| 12 | 4KZ6 | –4.3 | –11.9 ± 2.8 | –16 ± 2.2 | –45.7 ± 4.1 | –16.4 ± 2.4 | –27.8 ± 8.3 |
| 13 | 3GRJ | –4.1 | –16.1 ± 3.9 | –21 ± 2.1 | –33.2 ± 3.5 | –10.5 ± 2.5 | –21 ± 8.2 |
| 14 | 4KZ8 | –3.8 | –9.6 ± 1.9 | –12.2 ± 1.6 | –45.4 ± 3.6 | –15.7 ± 1.9 | –28.6 ± 6.9 |
| 15 | 4KZ3 | –3.8 | –25.9 ± 4.6 | –25.3 ± 3 | –39.2 ± 5.1 | –10.3 ± 3 | –29.1 ± 10.9 |
| 16 | 3GSG | –3.7 | –14.5 ± 3 | –20.4 ± 1.9 | –43.5 ± 4.1 | –15.4 ± 2.4 | –25.9 ± 8.3 |
| 17 | 3GVB | –3.5 | –23 ± 4.4 | –18.3 ± 2.1 | –41.9 ± 4.9 | –14.2 ± 2.3 | –29.3 ± 9.4 |
| 18 | 3GR2 | –3.5 | –16.6 ± 3 | –21.7 ± 2.3 | –40.9 ± 4.7 | –14.9 ± 2.2 | –24.1 ± 8.9 |
| 19 | 4KZ7 | –3.4 | –16.6 ± 4.2 | –14.9 ± 2 | –33.8 ± 3.5 | –12.7 ± 2.3 | –21.6 ± 8 |
| 20 | 2HDU | –3.2 | –14.3 ± 3.5 | –16.7 ± 2.1 | –29.4 ± 4.4 | –11.3 ± 2.1 | –17.2 ± 8.6 |
| 21 | 3GV9 | –2.9 | –18.5 ± 4.7 | –14.9 ± 2 | –33.9 ± 3.9 | –11.8 ± 2.3 | –23.5 ± 8.8 |
| 22 | 4KZ5 | –2.7 | –15.9 ± 3.4 | –18.3 ± 2.7 | –48.1 ± 5.3 | –18.2 ± 2.7 | –29 ± 10.2 |
| 23 | 2HDR | –2.4 | –18.7 ± 3.4 | –21.5 ± 2.7 | –25.5 ± 3.8 | –6.2 ± 2.7 | –18.3 ± 8.5 |
Absolute binding free energy ΔGLIE was obtained at an optimal value of α = 1.
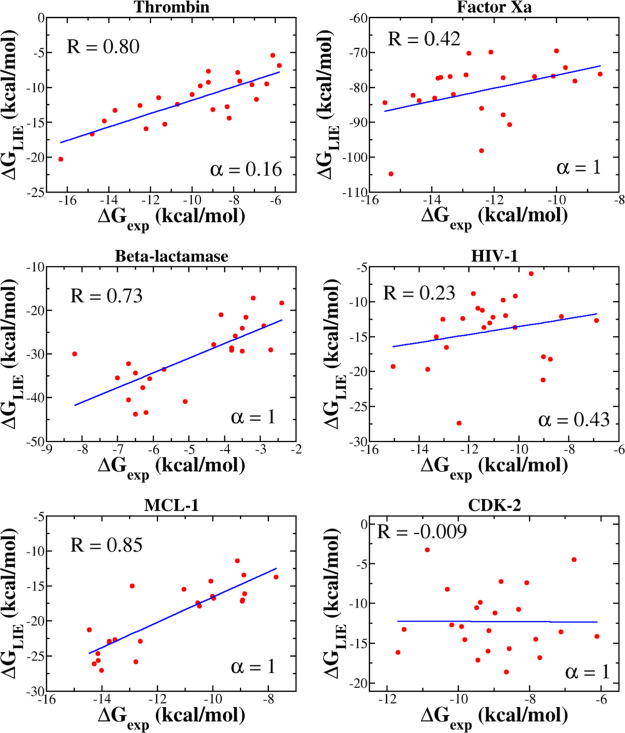
The correlation between ΔGLIE and ΔGexp depends on α (Figure 4). For MCL-1, β-lactamase, factor Xa, and CDK-2, the best correlations R = 0.85, 0.73, 0.42, and 0.01, respectively, were obtained at α = 1, while for thrombin and HIV-1, R = 0.80 at α = 0.16 and R = 0.23 at α = 0.43, respectively (Figure 5). Thus, for all six data sets, the correlation, provided by the LIE method, is lower than JE (Table 4), with the exception of MCL-1 for which the two methods gave almost the same R. In particular, R, obtained by LIE, is even lower than 0.5 for factor Xa, HIV, and CDK-2. The JE method provides a better fit with experiment than LIE because the former is based on the exact JE, while the latter accepts an approximation in which the binding free energy is a linear combination of the electrostatic and vdW interaction energies. In such an approximation, the entropy contribution was not estimated explicitly.
Figure 4.
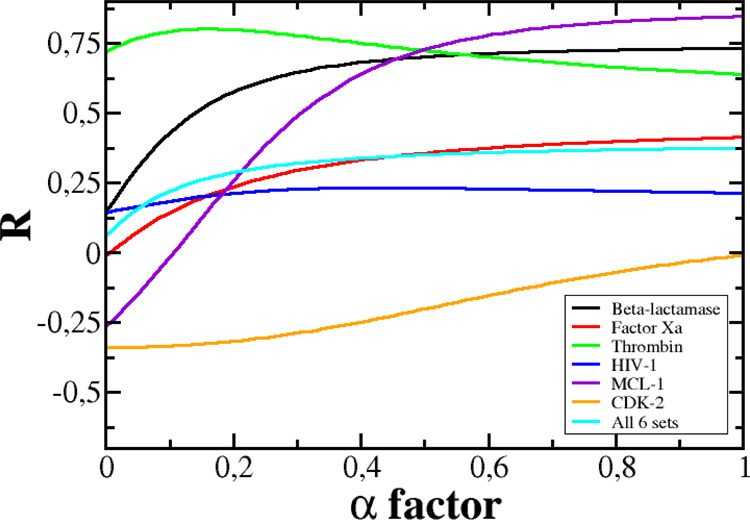
Dependence of R on parameter α for six data sets and the combined set.
Figure 5.
Correlation between ΔGexp and ΔGLIE. The LIE binding free energy was computed at the α factor, shown in the figure. In all cases, we used γ = 0 and β, given in Tables S6–S11.
Table 4. Correlation Coefficient R between Experimental and Theoretical Binding Free Energies Obtained by JE and LIE Methods.
| data set | JE | LIE |
|---|---|---|
| β-lactamase | 0.89 | 0.73 |
| thrombin | 0.86 | 0.80 |
| factor Xa | 0.83 | 0.42 |
| HIV-1 | 0.80 | 0.23 |
| MCL-1 | 0.83 | 0.85 |
| CDK-2 | 0.81 | 0.01 |
| all six sets | 0.45 | 0.37 |
| combined set of thrombin, factor Xa, β-lactamase, and MCL-1 | 0.88 | 0.43 |
| combined set of HIV-1 and CDK-2 | 0.84 | 0.52 |
| combined set of β-lactamase, thrombin, and factor Xa | 0.93 | 0.85 |
Another disadvantage of LIE is that at α = 1, where the best correlation was achieved for β-lactamase, factor Xa, CDK-2, and MCL-1, the difference between ΔGLIE and ΔGexp is significant (Tables 3 and S16, S19, and S20). This drawback becomes less pronounced for thrombin, where the best fit was obtained at α = 0.16 with ΔGLIE close to ΔGexp (Table S17) (a similar value of α was also chosen by other research groups9,10).
To monitor the dependence of the difference between ΔGLIE and ΔGexp on α, we introduced the root mean square of the energy distance (RMSED) as follows
| 5 |
where N is the number of complexes in the data set. RMSED reaches a maximum at α = 1 and a minimum at αmin = 0.16, 0.12, 0.13, 0.35, 0.61, and 0.00 for β-lactamase, factor Xa, thrombin, HIV-1, MCL-1, and CDK-2, respectively (Figure S7 and Table S21). At αmin, we obtained R = 0.53, 0.17, 0.80, 0.23, 0.78, and 0.0 for β-lactamase, factor Xa, thrombin, HIV-1, MCL-1, and CDK-2, respectively. Therefore, the best agreement with the experiment was achieved for thrombin and MCL-1 not only in terms of high value of R but also from the point of view of the proximity of ΔGLIE to ΔGexp.
Correlation between Theory and Experiment for Combined Data Sets
As can be seen above, for the six data sets, JE gives better agreement with the experiment compared to the LIE method, in particular, for factor Xa. Combining six sets into one set of 138 complexes, we can show that the correlation level between ΔGneqJar and ΔGexp fell sharply to R = 0.45 (Figure 6), which is well below the level of individual sets (Table 4). For this large set, the best correlation between ΔGLIE and ΔGexp is achieved at α = 1 (Figure 4) with R = 0.37 (Figure 6), which is lower than that in JE case. However, in both cases, the correlation is poor, with R below 0.5.
Figure 6.
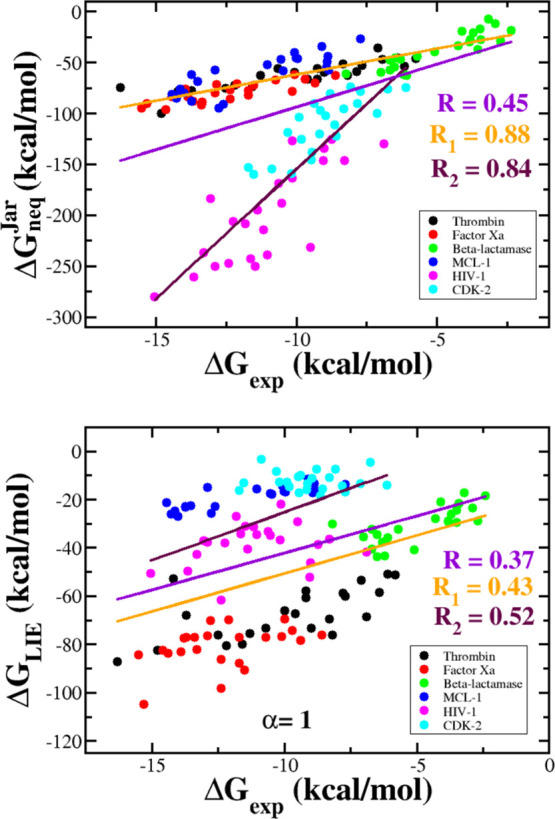
Correlation between the ΔGneqJar (upper panel) and ΔGLIE (lower panel) with the experimental binding free energy for combined data sets. Straight lines refer to the linear fit for all six data sets (violet, correlation R), the combined set of thrombin, factor Xa, β-lactamase, and MCL-1 (orange, correlation R1), and the combined set of HIV-1 and CDK-2 (maroon, correlation R2). For JE, we obtained R = 0.45, R1 = 0.88, and R2 = 0.84, whereas for LIE, we obtained R = 0.37, R1 = 0.43, and R2 = 0.52.
If we combined four data sets involving β-lactamase, thrombin, factor Xa, and MCL-1, then the correlation between ΔGneqJar and ΔGexp will become high (R = 0.88, Figure 6), but ΔGLIE remains poorly correlated with experiment (R = 0.43). Similarly, for a kit that consists of the two remaining HIV and CDK-2 kits, the correlation with experiment is R = 0.84 and 0.52 for JE and LIE, respectively (Figure 6).
The best agreement between ΔGLIE and ΔGexp was obtained for a set that comprises β-lactamase, thrombin, and factor Xa complexes (R = 0.85, Figure S8). However, for this combined set, the JE method remains better than LIE, having R = 0.93 (Figure S8 and Table 4). Therefore, for all four combined sets, JE gives much better agreement with experimental data than LIE (Table 4). The main difference between the two methods is that ΔGneqJar is less sensitive to the size of the data set than ΔGLIE.
The minimum root-mean-square deviation and correlation at αmin are shown in Table S21 for all four combinations. The largest deviation from the experiment was obtained for the set of 138 compounds (7.5 kcal/mol), while the best agreement was obtained for the set of thrombin, factor Xa, and β-lactamase (4.4 kcal/mol). The latter has the highest R = 0.85, which was achieved at αmin = 0.13 (Table S21). The remaining three combinations do not agree well with the experiment. Therefore, we advocate by comparing simulation with experiment for a given target but not for a set of several targets.
Conclusions
We studied nonequilibrium thermodynamics of small molecules in association with thrombin, factor Xa, HIV-1, MCL-1, and CDK-2 using JE and SMD. Similar to the β-lactamase case,32 rating of ligand–protein binding affinities can be accessed by several quantities, among which Jarzynski’s nonequilibrium binding free energy is the most reliable.
Because MD-based methods are the best tool for evaluating the equilibrium binding free energy, it is highly desirable to compare their ability in ranking binding affinity with the nonequilibrium JE approach. To start research in this direction, we have chosen the LIE method because it is computationally not expensive but still reliable in many cases.11−13,15,18,40−42 Thus, the binding affinity of small molecules to six different proteins was studied using LIE. We found that in all cases, the correlation between the experimental and the simulation results is lower than that of JE, with the exception of MCL-1, where LIE (R = 0.85) is slightly better than JE (R = 0.83) (Table 4). In particular, for HIV-1 and CDK-2, the LIE method gives R = 0.23 and 0.01, which are much lower than 0.80 and 0.81 obtained using JE (Table 2).
Because both ΔGLIE and ΔGneqJar were calculated using the data generated by the SMD simulation, the two methods consume approximately the same amount of computational time. Therefore, in terms of computation time, the two methods are equivalent, but JE has a clear advantage over LIE because it gives better agreement with experiment. From this point of view, JE in combination with SMD is a valuable tool for the computer-aided drug design. In addition, to rate the binding affinities, it is not necessary to carry out a time consuming equilibrium simulation because the nonequilibrium ΔGneq, which can be quickly calculated, is a good indicator for this purpose. It would be interesting to compare the effectiveness of JE in assessing binding affinity with other methods such as FEP, TI, MM-PBSA, MM-GBSA, and umbrella sampling. Our work in this direction is in progress.
Acknowledgments
This work was supported by the Department of Science and Technology at Ho Chi Minh city, Vietnam (grant 07/2019/HĐ-KHCNTT), and the Polish NCN grant 2015/19/B/ST4/02721, Poland.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c02009.
Inhibition constant, molecular weight, chemical formula, and 2D structure of the ligands in complex with thrombin, factor Xa, HIV-1, MCL-1, and CDK-2; scale factor β for thrombin, factor Xa, β-lactamase, HIV-1, MCL-1, and CDK-2 complexes; results obtained by SMD simulations for factor Xa, HIV-1, MCL-1, and CDK-2; average polar and nonpolar interaction energy in the bound and free states for factor Xa, thrombin, HIV-1, MCL-1, and CDK-2 complexes; minimum value of RMSED and αmin for all studied data sets; time dependence of the force, pulling work, and Jarzynski’s binding free energy for six reference ligands of thrombin; correlation between the experimental binding free energy ΔGexp and Fmax, Wpull, tmax, ΔGbind‡, ΔGunbind, and ΔGneqJar for factor Xa, HIV-1, MCL-1, and CDK-2; time dependence of polar and nonpolar interaction energy between the ligand and protein in the absence of water for the 1SL3 complex from the thrombin set; dependence of RMSED on α for six data sets and the combination of all six sets; and correlation between the binding free energies of Jarzynski and LIE with the experimental binding free energy for three combined data sets including β-lactamase, thrombin, and factor Xa (PDF)
Author Contributions
K.H. and D.T.T. contributed equally. D.T.T. and M.S.L. conceived in silico experiments. K.H. and D.T.T. conducted the experiment. D.T.T., K.H., and M.S.L. analyzed the results. D.T.T., K.H., and M.S.L. wrote the paper. All authors reviewed the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Trott O.; Olson A. J. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genheden S.; Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Åqvist J.; Medina C.; Samuelsson J.-E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng., Des. Sel. 1994, 7, 385–391. 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- Bhati A. P.; Wan S.; Wright D. W.; Coveney P. V. Rapid, Accurate, Precise, and Reliable Relative Free Energy Prediction Using Ensemble Based Thermodynamic Integration. J. Chem. Theory Comput. 2017, 13, 210–222. 10.1021/acs.jctc.6b00979. [DOI] [PubMed] [Google Scholar]
- Miyata T.; Ikuta Y.; Hirata F. Free energy calculation using molecular dynamics simulation combined with the three dimensional reference interaction site model theory. I. Free energy perturbation and thermodynamic integration along a coupling parameter. J. Chem. Phys. 2010, 133, 044114. 10.1063/1.3462276. [DOI] [PubMed] [Google Scholar]
- Wang L.; Wu Y.; Deng Y.; Kim B.; Pierce L.; Krilov G.; Lupyan D.; Robinson S.; Dahlgren M. K.; Greenwood J.; et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015, 137, 2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- Aqvist J.; Mowbray S. L. Sugar recognition by a glucose/galactose receptor. Evaluation of binding energetics from molecular dynamics simulations. J. Biol. Chem. 1995, 270, 9978–9981. 10.1074/jbc.270.17.9978. [DOI] [PubMed] [Google Scholar]
- Hultén J.; Bonham N. M.; Nillroth U.; Hansson T.; Zuccarello G.; Bouzide A.; Åqvist J.; Classon B.; Danielson U. H.; Karlén A.; Kvarnström I.; Samuelsson B.; Hallberg A. Cyclic HIV-1 protease inhibitors derived from mannitol: synthesis, inhibitory potencies, and computational predictions of binding affinities. J. Med. Chem. 1997, 40, 885–897. 10.1021/jm960728j. [DOI] [PubMed] [Google Scholar]
- Hansson T.; Åqvist J. Estimation of binding free energies for HIV proteinase inhibitors by molecular dynamics simulations. Protein Eng., Des. Sel. 1995, 8, 1137–1144. 10.1093/protein/8.11.1137. [DOI] [PubMed] [Google Scholar]
- Marelius J.; Graffner-Nordberg M.; Hansson T.; Hallberg A.; Åqvist J. Computation of affinity and selectivity: binding of 2,4-diaminopteridine and 2,4-diaminoquinazoline inhibitors to dihydrofolate reductases. J. Comput.-Aided Mol. Des. 1998, 12, 119–131. 10.1023/a:1007929626986. [DOI] [PubMed] [Google Scholar]
- Wall I. D.; Leach A. R.; Salt D. W.; Ford M. G.; Essex J. W. Binding constants of neuraminidase inhibitors: An investigation of the linear interaction energy method. J. Med. Chem. 1999, 42, 5142–5152. 10.1021/jm990105g. [DOI] [PubMed] [Google Scholar]
- Tounge B. A.; Reynolds C. H. Calculation of the binding affinity of beta-secretase inhibitors using the linear interaction energy method. J. Med. Chem. 2003, 46, 2074–2082. 10.1021/jm020513b. [DOI] [PubMed] [Google Scholar]
- Capoferri L.; Verkade-Vreeker M. C. A.; Buitenhuis D.; Commandeur J. N. M.; Pastor M.; Vermeulen N. P. E.; Geerke D. P. Linear interaction energy based prediction of cytochrome P450 1A2 binding affinities with reliability estimation. PLoS One 2015, 10, e0142232 10.1371/journal.pone.0142232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dijk M.; Ter Laak A. M.; Wichard J. D.; Capoferri L.; Vermeulen N. P. E.; Geerke D. P. Comprehensive and automated linear interaction energy based binding-affinity prediction for multifarious cytochrome P450 aromatase inhibitors. J. Chem. Inf. Model. 2017, 57, 2294–2308. 10.1021/acs.jcim.7b00222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rifai E. A.; van Dijk M.; Vermeulen N. P. E.; Geerke D. P. Binding free energy predictions of Farnesoid X receptor (FXR) agonists using a linear interaction energy (LIE) approach with reliability estimation: application to the D3R grand challenge 2. J. Comput.-Aided Mol. Des. 2018, 32, 239–249. 10.1007/s10822-017-0055-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vosmeer C. R.; Pool R.; Van Stee M.; Perić-Hassler L.; Vermeulen N.; Geerke D. Towards automated binding affinity prediction using an iterative linear interaction energy approach. Int. J. Mol. 2014, 15, 798–816. 10.3390/ijms15010798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunes-Alves A.; Arantes G. M. Ligand–Receptor Affinities Computed by an Adapted Linear Interaction Model for Continuum Electrostatics and by Protein Conformational Averaging. J. Chem. Inf. Model. 2014, 54, 2309–2319. 10.1021/ci500301s. [DOI] [PubMed] [Google Scholar]
- Miranda W. E.; Noskov S. Y.; Valiente P. A. Improving the LIE Method for Binding Free Energy Calculations of Protein–Ligand Complexes. J. Chem. Inf. Model. 2015, 55, 1867–1877. 10.1021/acs.jcim.5b00012. [DOI] [PubMed] [Google Scholar]
- He X.; Man V. H.; Ji B.; Xie X.-Q.; Wang J. Calculate protein–ligand binding affinities with the extended linear interaction energy method: application on the Cathepsin S set in the D3R Grand Challenge 3. J. Comput.-Aided Mol. Des. 2019, 33, 105–117. 10.1007/s10822-018-0162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubmüller H.; Heymann B.; Tavan P. Ligand binding: Molecular mechanics calculation of the streptavidin biotin rupture force. Science 1996, 271, 997. 10.1126/science.271.5251.997. [DOI] [PubMed] [Google Scholar]
- Isralewitz B.; Izrailev S.; Schulten K. Binding pathway of retinal to bacterio-opsin: a prediction by molecular dynamics simulations. Biophys. J. 1997, 73, 2972–2979. 10.1016/s0006-3495(97)78326-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izrailev S.; Stepaniants S.; Balsera M.; Oono Y.; Schulten K. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 1997, 72, 1568–1581. 10.1016/s0006-3495(97)78804-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izrailev S.; Stepaniants S.; Isralewitz B.; Kosztin D.; Lu H.; Molnar F.; Wriggers W.; Schulten K.. Steered molecular dynamics. Computational Molecular Dynamics: Challenges, Methods, Ideas; Springer, 1999; pp 39–65. [Google Scholar]
- Mai B. K.; Viet M. H.; Li M. S. Top leads for swine influenza A/H1N1 virus revealed by steered molecular dynamics approach. J. Chem. Inf. Model. 2010, 50, 2236–2247. 10.1021/ci100346s. [DOI] [PubMed] [Google Scholar]
- Li M. S.; Mai B. K. Steered molecular dynamics - A promising tool for drug design. Curr. Bioinf. 2012, 7, 342–351. 10.2174/157489312803901009. [DOI] [Google Scholar]
- Do P.-C.; Lee E. H.; Le L. Steered Molecular Dynamics Simulation in Rational Drug Design. J. Chem. Inf. Model. 2018, 58, 1473–1482. 10.1021/acs.jcim.8b00261. [DOI] [PubMed] [Google Scholar]
- Villarreal O. D.; Yu L.; Rodriguez R. A.; Chen L. Y. Computing the binding affinity of a ligand buried deep inside a protein with the hybrid steered molecular dynamics. Biochem. Biophys. Res. Commun. 2017, 483, 203–208. 10.1016/j.bbrc.2016.12.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L. Y. Hybrid Steered Molecular Dynamics Approach to Computing Absolute Binding Free Energy of Ligand-Protein Complexes: A Brute Force Approach That Is Fast and Accurate. J. Chem. Theory Comput. 2015, 11, 1928–1938. 10.1021/ct501162f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ytreberg F. M. Absolute FKBP binding affinities obtained via nonequilibrium unbinding simulations. J. Chem. Phys. 2009, 130, 164906. 10.1063/1.3119261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colizzi F.; Perozzo R.; Scapozza L.; Recanatini M.; Cavalli A. Single-molecule pulling simulations can discern active from inactive enzyme inhibitors. J. Am. Chem. Soc. 2010, 132, 7361–7371. 10.1021/ja100259r. [DOI] [PubMed] [Google Scholar]
- Vuong Q. V.; Nguyen T. T.; Li M. S. A new method for navigating optimal direction for pulling ligand from binding pocket: application to ranking binding affinity by steered molecular dynamics. J. Chem. Inf. Model. 2015, 55, 2731–2738. 10.1021/acs.jcim.5b00386. [DOI] [PubMed] [Google Scholar]
- Truong D. T.; Li M. S. Probing the Binding Affinity by Jarzynski’s Nonequilibrium Binding Free Energy and Rupture Time. J. Phys. Chem. B 2018, 122, 4693–4699. 10.1021/acs.jpcb.8b02137. [DOI] [PubMed] [Google Scholar]
- Nguyen T. T.; Mai B. K.; Li M. S. Study of Tamiflu sensitivity to variants of A/H5N1 virus using different force fields. J. Chem. Inf. Model. 2011, 51, 2266–2276. 10.1021/ci2000743. [DOI] [PubMed] [Google Scholar]
- Nguyen T. T.; Tran D. P.; Pham Dinh Quoc H.; Hoang Z.; Carloni P.; Van Pham P.; Nguyen C.; Li M. S. Ligand binding to anti-cancer target CD44 investigated by molecular simulations. J. Mol. Model. 2016, 22, 165. 10.1007/s00894-016-3029-6. [DOI] [PubMed] [Google Scholar]
- Thai N. Q.; Nguyen H. L.; Linh H. Q.; Li M. S. Protocol for fast screening of multi-target drug candidates: Application to Alzheimer’s disease. J. Mol. Graphics Modell. 2017, 77, 121–129. 10.1016/j.jmgm.2017.08.002. [DOI] [PubMed] [Google Scholar]
- Nguyen T. T.; Viet M. H.; Li M. S. Effects of water models on binding affinity: evidence from all-atom simulation of binding of tamiflu to A/H5N1 neuraminidase. Sci. World J. 2014, 2014, 536084. 10.1155/2014/536084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truong D. T.; Nguyen M. T.; Vu V. V.; Ngo S. T. Fast pulling of ligand approach for the design of β-secretase 1 inhibitors. Chem. Phys. Lett. 2017, 671, 142–146. 10.1016/j.cplett.2017.01.032. [DOI] [Google Scholar]
- Jarzynski C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. 10.1103/physrevlett.78.2690. [DOI] [Google Scholar]
- Hummer G.; Szabo A. Kinetics from nonequilibrium single-molecule pulling experiments. Biophys. J. 2003, 85, 5–15. 10.1016/s0006-3495(03)74449-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almlöf M.; Carlsson J.; Åqvist J. Improving the accuracy of the linear interaction energy method for solvation free energies. J. Chem. Theory Comput. 2007, 3, 2162–2175. 10.1021/ct700106b. [DOI] [PubMed] [Google Scholar]
- Åqvist J.; Hansson T. On the validity of electrostatic linear response in polar solvents. J. Phys. Chem. 1996, 100, 9512–9521. 10.1021/jp953640a. [DOI] [Google Scholar]
- Hansson T.; Marelius J.; Åqvist J. Ligand binding affinity prediction by linear interaction energy methods. J. Comput.-Aided Mol. Des. 1998, 12, 27–35. 10.1023/a:1007930623000. [DOI] [PubMed] [Google Scholar]
- Baum B.; Mohamed M.; Zayed M.; Gerlach C.; Heine A.; Hangauer D.; Klebe G. More than a Simple Lipophilic Contact: A Detailed Thermodynamic Analysis of Nonbasic Residues in the S1 Pocket of Thrombin. J. Mol. Biol. 2009, 390, 56–69. 10.1016/j.jmb.2009.04.051. [DOI] [PubMed] [Google Scholar]
- Thiagarajan P.; Narayanan A. S.. Thrombin. eLS; John Wiley & Sons, Ltd: Chichester, 2014. [Google Scholar]
- Coughlin S. R. Thrombin signalling and protease-activated receptors. Nature 2000, 407, 258–264. 10.1038/35025229. [DOI] [PubMed] [Google Scholar]
- Davie E. W.; Fujikawa K.; Kisiel W. The coagulation cascade: initiation, maintenance, and regulation. Biochemistry 1991, 30, 10363–10370. 10.1021/bi00107a001. [DOI] [PubMed] [Google Scholar]
- Davie E.; Kulman J. An overview of the structure and function of thrombin. Semin. Thromb. Hemostasis 2006, 32, 003–015. 10.1055/s-2006-939550. [DOI] [PubMed] [Google Scholar]
- Davie E. W.; Ratnoff O. D. Waterfall Sequence for Intrinsic Blood Clotting. Science 1964, 145, 1310–1312. 10.1126/science.145.3638.1310. [DOI] [PubMed] [Google Scholar]
- Robert A.; Chazouilleres O. Prothrombin time in liver failure: time, ratio, activity percentage, or international normalized ratio?. Hepatology 1996, 24, 1392–1394. 10.1002/hep.510240613. [DOI] [PubMed] [Google Scholar]
- Monroe D. M.; Hoffman M. What does it take to make the perfect clot?. Arterioscler., Thromb., Vasc. Biol. 2006, 26, 41–48. 10.1161/01.atv.0000193624.28251.83. [DOI] [PubMed] [Google Scholar]
- Monroe D. M.; Hoffman M.; Roberts H. R. Platelets and thrombin generation. Arterioscler., Thromb., Vasc. Biol. 2002, 22, 1381–1389. 10.1161/01.atv.0000031340.68494.34. [DOI] [PubMed] [Google Scholar]
- Stubbs M. T.; Bode W. A player of many parts: the spotlight falls on thrombin’s structure. Thromb. Res. 1993, 69, 1–58. 10.1016/0049-3848(93)90002-6. [DOI] [PubMed] [Google Scholar]
- Mann K. G.; Brummel K.; Butenas S. What is all that thrombin for?. J. Thromb. Haemostasis 2003, 1, 1504–1514. 10.1046/j.1538-7836.2003.00298.x. [DOI] [PubMed] [Google Scholar]
- Norgard N. B.; Dinicolantonio J. J.; Topping T. J.; Wee B. Novel anticoagulants in atrial fibrillation stroke prevention. Ther. Adv. Chronic Dis. 2012, 3, 123–136. 10.1177/2040622312438934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves M. C.; Lim J. J.; Heimer E. P.; Kramer R. A. An 11-kDa form of human immunodeficiency virus protease expressed in Escherichia coli is sufficient for enzymatic activity. Proc. Natl. Acad. Sci. U.S.A. 1988, 85, 2449–2453. 10.1073/pnas.85.8.2449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohl N. E.; Emini E. A.; Schleif W. A.; Davis L. J.; Heimbach J. C.; Dixon R. A.; Scolnick E. M.; Sigal I. S. Active human immunodeficiency virus protease is required for viral infectivity. Proc. Natl. Acad. Sci. U.S.A. 1988, 85, 4686–4690. 10.1073/pnas.85.13.4686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debouck C.; Gorniak J. G.; Strickler J. E.; Meek T. D.; Metcalf B. W.; Rosenberg M. Human immunodeficiency virus protease expressed in Escherichia coli exhibits autoprocessing and specific maturation of the gag precursor. Proc. Natl. Acad. Sci. U.S.A. 1987, 84, 8903–8906. 10.1073/pnas.84.24.8903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sepkowitz K. A. AIDS—the first 20 years. N. Engl. J. Med. 2001, 344, 1764–1772. 10.1056/nejm200106073442306. [DOI] [PubMed] [Google Scholar]
- Wlodawer A.; Vondrasek J. Inhibitors of HIV-1 protease: a major success of structure-assisted drug design. Annu. Rev. Biophys. Biomol. Struct. 1998, 27, 249–284. 10.1146/annurev.biophys.27.1.249. [DOI] [PubMed] [Google Scholar]
- Wei X.; Ghosh S. K.; Taylor M. E.; Johnson V. A.; Emini E. A.; Deutsch P.; Lifson J. D.; Bonhoeffer S.; Nowak M. A.; Hahn B. H.; Saag M. S.; Shaw G. M. Viral dynamics in human immunodeficiency virus type 1 infection. Nature 1995, 373, 117–122. 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- Williams K.; Loeb L.. Retroviral reverse transcriptases: error frequencies and mutagenesis. Genetic Diversity of RNA Viruses; Springer, 1992; pp 165–180. [DOI] [PubMed] [Google Scholar]
- Danial N. N.; Korsmeyer S. J. Cell death: critical control points. Cell 2004, 116, 205–219. 10.1016/s0092-8674(04)00046-7. [DOI] [PubMed] [Google Scholar]
- Willis S. N.; Fletcher J. I.; Kaufmann T.; van Delft M. F.; Chen L.; Czabotar P. E.; Ierino H.; Lee E. F.; Fairlie W. D.; Bouillet P.; Strasser A.; Kluck R. M.; Adams J. M.; Huang D. C. S. Apoptosis initiated when BH3 ligands engage multiple Bcl-2 homologs, not Bax or Bak. Science 2007, 315, 856–859. 10.1126/science.1133289. [DOI] [PubMed] [Google Scholar]
- Adams J. M.; Cory S. The Bcl-2 apoptotic switch in cancer development and therapy. Oncogene 2007, 26, 1324–1337. 10.1038/sj.onc.1210220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brotin E.; Meryet-Figuière M.; Simonin K.; Duval R. E.; Villedieu M.; Leroy-Dudal J.; Saison-Behmoaras E.; Gauduchon P.; Denoyelle C.; Poulain L. Bcl-XL and MCL-1 constitute pertinent targets in ovarian carcinoma and their concomitant inhibition is sufficient to induce apoptosis. Int. J. Cancer 2010, 126, 885–895. 10.1002/ijc.24787. [DOI] [PubMed] [Google Scholar]
- Ding Q.; He X.; Xia W.; Hsu J.-M.; Chen C.-T.; Li L.-Y.; Lee D.-F.; Yang J.-Y.; Xie X.; Liu J.-C.; Hung M.-C. Myeloid cell leukemia-1 inversely correlates with glycogen synthase kinase-3β activity and associates with poor prognosis in human breast cancer. Cancer Res. 2007, 67, 4564–4571. 10.1158/0008-5472.can-06-1788. [DOI] [PubMed] [Google Scholar]
- Song L.; Coppola D.; Livingston S.; Cress W. D.; Haura E. B. Mcl-1 regulates survival and sensitivity to diverse apoptotic stimuli in human non-small cell lung cancer cells. Cancer Biol. Ther. 2005, 4, 267–276. 10.4161/cbt.4.3.1496. [DOI] [PubMed] [Google Scholar]
- Andersen M. H.; Becker J. C.; Thor Straten P. The antiapoptotic member of the Bcl-2 family Mcl-1 is a CTL target in cancer patients. Leukemia 2005, 19, 484–485. 10.1038/sj.leu.2403621. [DOI] [PubMed] [Google Scholar]
- Derenne S.; Monia B.; Dean N. M.; Taylor J. K.; Rapp M.-J.; Harousseau J.-L.; Bataille R.; Amiot M. Antisense strategy shows that Mcl-1 rather than Bcl-2 or Bcl-xL is an essential survival protein of human myeloma cells. Blood 2002, 100, 194–199. 10.1182/blood.v100.1.194. [DOI] [PubMed] [Google Scholar]
- Miyamoto Y.; Hosotani R.; Wada M.; Lee J.-U.; Koshiba T.; Fujimoto K.; Tsuji S.; Nakajima S.; Doi R.; Kato M.; Shimada Y.; Imamura M. Immunohistochemical analysis of Bcl-2, Bax, Bcl-X, and Mcl-1 expression in pancreatic cancers. Oncology 1999, 56, 73–82. 10.1159/000011933. [DOI] [PubMed] [Google Scholar]
- Krajewska M.; Krajewski S.; Epstein J. I.; Shabaik A.; Sauvageot J.; Song K.; Kitada S.; Reed J. C. Immunohistochemical analysis of bcl-2, bax, bcl-X, and mcl-1 expression in prostate cancers. Am. J. Pathol. 1996, 148, 1567. [PMC free article] [PubMed] [Google Scholar]
- Wertz I. E.; Kusam S.; Lam C.; Okamoto T.; Sandoval W.; Anderson D. J.; Helgason E.; Ernst J. A.; Eby M.; Liu J.; Belmont L. D.; Kaminker J. S.; O’Rourke K. M.; Pujara K.; Kohli P. B.; Johnson A. R.; Chiu M. L.; Lill J. R.; Jackson P. K.; Fairbrother W. J.; Seshagiri S.; Ludlam M. J. C.; Leong K. G.; Dueber E. C.; Maecker H.; Huang D. C. S.; Dixit V. M. Sensitivity to antitubulin chemotherapeutics is regulated by MCL1 and FBW7. Nature 2011, 471, 110–114. 10.1038/nature09779. [DOI] [PubMed] [Google Scholar]
- Wei S.-H.; Dong K.; Lin F.; Wang X.; Li B.; Shen J.-j.; Zhang Q.; Wang R.; Zhang H.-Z. Inducing apoptosis and enhancing chemosensitivity to gemcitabine via RNA interference targeting Mcl-1 gene in pancreatic carcinoma cell. Cancer Chemother. Pharmacol. 2008, 62, 1055–1064. 10.1007/s00280-008-0697-7. [DOI] [PubMed] [Google Scholar]
- Zhang H.; Guttikonda S.; Roberts L.; Uziel T.; Semizarov D.; Elmore S. W.; Leverson J. D.; Lam L. T. Mcl-1 is critical for survival in a subgroup of non-small-cell lung cancer cell lines. Oncogene 2011, 30, 1963–1968. 10.1038/onc.2010.559. [DOI] [PubMed] [Google Scholar]
- Gu Y.; Rosenblatt J.; Morgan D. O. Cell cycle regulation of CDK2 activity by phosphorylation of Thr160 and Tyr15. EMBO J. 1992, 11, 3995–4005. 10.1002/j.1460-2075.1992.tb05493.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane M. E.; Yu B.; Rice A.; Lipson K. E.; Liang C.; Sun L.; Tang C.; McMahon G.; Pestell R. G.; Wadler S. A novel cdk2-selective inhibitor, SU9516, induces apoptosis in colon carcinoma cells. Cancer Res. 2001, 61, 6170–6177. [PubMed] [Google Scholar]
- Harbour J. W.; Luo R. X.; Santi A. D.; Postigo A. A.; Dean D. C. Cdk phosphorylation triggers sequential intramolecular interactions that progressively block Rb functions as cells move through G1. Cell 1999, 98, 859–869. 10.1016/s0092-8674(00)81519-6. [DOI] [PubMed] [Google Scholar]
- Chohan T. A.; Qian H.; Pan Y.; Chen J.-Z. Cyclin-dependent kinase-2 as a target for cancer therapy: progress in the development of CDK2 inhibitors as anti-cancer agents. Curr. Med. Chem. 2015, 22, 237–263. 10.2174/0929867321666141106113633. [DOI] [PubMed] [Google Scholar]
- Heymann B.; Grubmüller H. AN02/DNP-hapten unbinding forces studied by molecular dynamics atomic force microscopy simulations. Chem. Phys. Lett. 1999, 303, 1–9. 10.1016/s0009-2614(99)00183-9. [DOI] [Google Scholar]
- Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B.; Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mai B. K.; Li M. S. Neuraminidase inhibitor R-125489–a promising drug for treating influenza virus: steered molecular dynamics approach. Biochem. Biophys. Res. Commun. 2011, 410, 688–691. 10.1016/j.bbrc.2011.06.057. [DOI] [PubMed] [Google Scholar]
- Chovancova E.; Pavelka A.; Benes P.; Strnad O.; Brezovsky J.; Kozlikova B.; Gora A.; Sustr V.; Klvana M.; Medek P.; Biedermannova L.; Sochor J.; Damborsky J. CAVER 3.0: a tool for the analysis of transport pathways in dynamic protein structures. PLoS Comput. Biol. 2012, 8, e1002708 10.1371/journal.pcbi.1002708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A. D. Jr. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark P.; Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. 10.1021/jp003020w. [DOI] [Google Scholar]
- Zoete V.; Cuendet M. A.; Grosdidier A.; Michielin O. SwissParam: a fast force field generation tool for small organic molecules. J. Comput. Chem. 2011, 32, 2359–2368. 10.1002/jcc.21816. [DOI] [PubMed] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Hummer G.; Szabo A. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 3658–3661. 10.1073/pnas.071034098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus R. A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. 10.1146/annurev.pc.15.100164.001103. [DOI] [Google Scholar]
- Lee F. S.; Chu Z.-T.; Bolger M. B.; Warshel A. Calculations of antibody-antigen interactions: microscopic and semi-microscopic evaluation of the free energies of binding of phosphorylcholine analogs to McPC603. Protein Eng. 1992, 5, 215–228. 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
- Pratt L. R.; Chandler D. Theory o the hydrophobic effect. Chem. Phys. 1977, 67, 3683–3704. 10.1063/1.435308. [DOI] [Google Scholar]
- Ben-Naim A.; Marcus Y. Solvation thermodynamics of nonionic solutes. J. Chem. Phys. 1984, 81, 2016–2027. 10.1063/1.447824. [DOI] [Google Scholar]
- Wang W.; Wang J.; Kollman P. A. What determines the van der Waals coefficient β in the LIE (linear interaction energy) method to estimate binding free energies using molecular dynamics simulations?. Proteins: Struct., Funct., Bioinf. 1999, 34, 395–402. . [DOI] [PubMed] [Google Scholar]
- Ljungberg K. B.; Marelius J.; Musil D.; Svensson P.; Norden B.; Åqvist J. Computational modelling of inhibitor binding to human thrombin. Eur. J. Pharm. Sci. 2001, 12, 441–446. 10.1016/s0928-0987(00)00185-8. [DOI] [PubMed] [Google Scholar]
- Bruce N. J.; Ganotra G. K.; Kokh D. B.; Sadiq S. K.; Wade R. C. New approaches for computing ligand–receptor binding kinetics. Curr. Opin. Struct. Biol. 2018, 49, 1–10. 10.1016/j.sbi.2017.10.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.