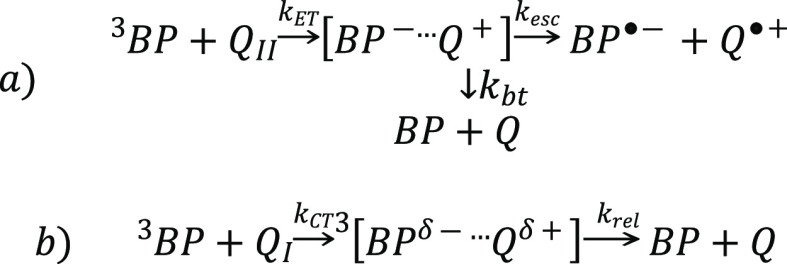Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 10;124(27):5654–5664. doi: 10.1021/acs.jpcb.0c02635

Water-Triggered Photoinduced Electron Transfer in Acetonitrile–Water Binary Solvent. Solvent Microstructure-Tuned Reactivity of Hydrophobic Solutes

Anna Lewandowska-Andralojc †,‡,*, Gordon L Hug §, Bronislaw Marciniak †,‡, Gerald Hörner ∥, Dorota Swiatla-Wojcik ⊥,*
PMCID: PMC7590979  PMID: 32520554

Abstract

graphic file with name jp0c02635_0011.jpg

The solvent-composition dependence of quenching triplet states of benzophenone (3BP) by anisole in acetonitrile–water (ACN–H2O) mixtures was investigated by laser flash photolysis over the water mole fraction (xw) increasing from 0 to 0.92. Single exponential decay of 3BP was observed over the whole composition range. The quenching rate constant consistently increased with the water content but increased far more rapidly with xw > 0.7. The water-triggered electron-transfer (ET) mechanism was confirmed by a steeply growing quantum yield of the benzophenone ketyl radical anion, escaping back-ET when the partial water volume exceeded the acetonitrile one. The water-content influence on the 3BP quenching rate was described by a kinetic model accounting for the microheterogeneous structure of the ACN–H2O mixtures and the very different solubility of the reactants in the solvent components. According to the model, the ET mechanism occurs at a rate constant of 1.46 × 109 M–1 s–1 and is presumably assisted by the ACN–H2O hydrogen-bonding interaction.

Introduction

Modern spectroscopic techniques and advanced theoretical approaches have provided ample insights into the structure and bonding of molecular liquids.1−4 The results left no doubt that the assumption of a “dielectric continuum”, though useful and common, underestimates the complexity of even the simplest liquids in many respects. Associative phenomena dominate the microscopic dynamics of a solvent while, in many cases, solvent molecules have been identified to play active roles in the mechanism of chemical reactions far beyond “walk-on” parts of a passive electrostatic background. Optimization of macroscopic chemical processes with respect to reaction rates and selectivity thus subsumes the continuous tuning of sub-microscopic solvent–solute interactions. Hydrogen bonding among solvent molecules provides a prominent source of association (solvent–solvent interaction) and often is the strongest among the non-covalent bonding interactions with solutes.5,6

In this context, we have provided experimental and theoretical evidence for expressed specific solvent-composition effects on the excited-state chemistry of ketones.7 A qualitative change from charge transfer (CT) to electron transfer (ET) has been found for quenching of triplet excited ketones by weak electron donors. This mechanistic branching was correlated with the state of solvation of the excited ketone that greatly differs in nonprotic media such as neat acetonitrile (ACN) or dichloromethane on the one hand or trifluoroethanol on the other. In qualitative terms, two quenching mechanisms (CT and ET) have been operating in two-component solvent mixtures of a nonprotic (ACN) and a protic constituent (hexafluoro-2-propanol).8 Competition between full ET and polarization (CT) of the reaction partners is omnipresent in photochemistry. It is discussed in some detail both for singlet-born9 and triplet-born10 quenching reactions. In quantitative terms, both the variation of the reaction rates and the mechanistic selectivity with the solvent composition revealed a very steep increase at high loads of the protic component.

These observations have instructive parallels with the effects of protic cosolvents on a number of thermal organic multicomponent reactions. Massive accelerating effects on the reaction rates have been observed when water was co-added to an organic solvent.11−15 The idea of reactions “on water” assumes an enhanced reactivity/hydrogen bond (HB)-donating ability of individual water molecules at the phase boundary between bulk water and bulk organic phases.16 It emphasizes the high HB-donating ability of water as a source of rate acceleration; HB stabilization of, in particular, polar transition states necessarily implies decreasing reaction barriers. In an alternative view, Breslow associated the accelerating effects of water as a (co) solvent on Diels–Alder reactions with a ‘hydrophobic effect’. In this picture, the high polarity of bulk water interferes with efficient solvation of nonpolar reactants.14 The “hydrophobic effect” on bimolecular reaction rates “in water” essentially reflects the high cohesive pressure in the highly associated water network.

The obvious parallels between the solvent effects on thermally induced organic reactions and those driven by photonic energy clearly justify a broader inquiry into the fundamental sources of their similarity.

To this end, we have studied the quenching dynamics and the mechanism of the reaction of triplet excited benzophenone (BP) and anisole in ACN–water mixtures in some detail. Our previous results in neat ACN were compatible with unproductive quenching via a CT state, whereas the generally fast quenching in ACN–H2O (1:4 v/v) was accompanied by efficient formation of free-radical products.7 The observed solvent dependence was analyzed in terms of the Marcus theory,17,18 which revealed that the ET pathways cannot be referred to unspecific solvation effects in terms of a dielectric continuum model but must be attributed to specific solvent–solute interactions. Here, we are focusing our attention on a more systematic study of the solvent-composition dependence on the kinetics of the BP triplet quenching by anisole. As we will show in the current study, the specific solvent–solute interactions are insufficient to properly describe a steep rate increase with the load of the protic component in the case of water–ACN mixtures. Our quenching experiments in mixtures of ACN with water provide the experimental backbone to further underpin a kinetic model that takes root in the submicroscopic structure of the solvent mixture as well as the very different solubility of the reactants in the solvent components. The role of the submicroscopic structure of ACN–water mixtures on the reaction rates has been discussed previously in a qualitative manner for catalytic water oxidation by iridium oxide nanoparticles19 or in the quenching of triplet BPs by sulfur-containing amino acids.20

In this paper, we demonstrate quantitatively, for the first time, the effect of microscopic structures in binary-mixed solvents on the kinetic competition among quenching mechanisms: CT and ET. The predominance of one path versus another, with regard to the reaction rates, is intimately correlated with the microscopic structure of the ACN–H2O binary solvents together with the solvation status of the reactants in mixtures of ACN with water.

The present study shows, exemplarily, for photoinduced triplet-state quenching that reaction kinetics and reaction mechanisms are sensitive to molecular interactions in ACN–H2O mixtures and can be used to probe microheterogeneous structures of these binary solvents.

Experimental Section

Materials

Anisole and BP were purchased from Aldrich. ACN was purchased from Merck and was of the highest available analytical grade. These chemicals were used without further purification. Deionized water, used throughout this study, was obtained from a Millipore (Simplicity) purification system.

Laser Flash Photolysis

The setup for the nanosecond laser flash photolysis (LFP) experiments, and its data acquisition system have been previously described in detail.21 The LFP experiments employed a pulsed Nd:YAG laser (355 nm, 5 mJ, 7–9 ns) for excitation. Transient decays were recorded at individual wavelengths by the step-scan method with a step distance of 10 nm in the range of 320–700 nm as the mean of 10 pulses. Samples for LFP were deoxygenated with high-purity argon for 15 min prior to the measurements. Experiments were performed in rectangular quartz cells (1 cm × 1 cm). All experiments were performed with freshly prepared solutions at room temperature (295 ± 1 K). The concentrations of BP were set in the millimolar range, corresponding to optical densities at 355 nm of 0.3–0.6. The concentrations of the quencher ranged from 1 × 10–3 to 7.0 × 10–2 M. The quantum yields of free-radical formation were derived by relative actinometry with optically matched solutions of BP in ACN. The absorbances at the respective spectral maxima of the transient photoproducts were measured and compared with the end-of-pulse absorbance at 520 nm because of the BP triplet. The concentration of anisole was sufficiently high to quench the triplet almost totally (>90%). The quantum yields ΦP were calculated according to the formula

graphic file with name jp0c02635_m001.jpg 1

Therein Aλ denotes the observed absorbance of the transient under study at λ, with the molar absorption coefficient ελP; A520 denotes the transient absorbance of the BP triplet at 520 nm in the actinometer solution (ε520 = 6500 M–1 cm–1 in ACN),22 measured under conditions of no quenching. For the transient intermediates relevant to this study, namely the BP ketyl radical, radical anion BP•–, and the anisole radical cation, we have used molar absorption coefficients of ε (BPH•; 540 nm) = 3400 M–1 cm–1, ε (BP•–; 590 nm) = 7600 M–1 cm–1, and ε (anisole•+; 430 nm) = 3800 M–1 cm–1 from pulse radiolysis or flash photolysis in aqueous solutions.22,23 A multi-regression analysis has to be done on the optical transient spectra resulting from LFP to extract the individual transient concentrations ci. Within any time window, following the excitation pulse, the absorbance of the signal is related to the concentrations and molar absorption coefficients of the transients through Beer’s law

graphic file with name jp0c02635_m002.jpg 2

In the regression analysis of the experimental spectra by the above equation, the concentrations of the individual transients times the optical path-length, l × ci(t), are the regression parameters to be fit.24 The sets of εi(λj) are the reference spectra of the underlying transients enumerated by the i-th subscript. Reference spectra for the BP triplet state and the BP radical anion were obtained by bimolecular quenching of the triplet state of BP with 2-propanol (1 M) in the absence and in the presence of KOH, respectively. The spectra were scaled with the known molar absorption coefficients.22,25 The reference spectra for the anisole radical cation were taken from the literature.26

Results and Discussion

Laser Flash Photolysis

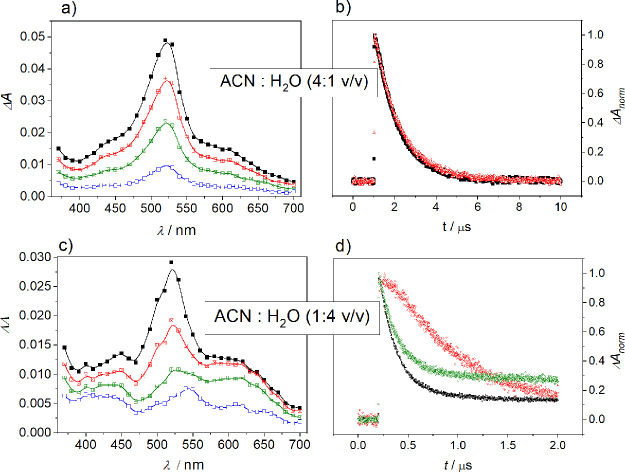
The initial step in the quenching of triplet-excited BP by anisole in nonprotic solvents has CT character and is fairly slow. This conclusion had been drawn earlier by us and by a number of workers.7,27−29 Accordingly, quenching of BP triplets by anisole in ACN was not connected with any formation of free radical-ion products that would signify the occurrence of a full ET. This type of CT-induced quenching was observed even in ACN–H2O mixtures with water content up to 20%.27 Thus, transient spectra, recorded upon 355 nm excitation of BP in ACN or in an ACN–H2O (4:1 v/v) mixture in the presence of anisole, were dominated by strong absorptions at 325 nm (not shown) and 525 nm (Figure 1a) that matched those previously reported for the BP triplet state.30 The spectra exhibited no spectral evolution during the decay; that is, the decay profiles coincided, irrespective of the wavelengths (Figure 1b). The spectral and kinetic data presented in Figure 1a,c agree quite well with the data reported under similar conditions in ref (7).

Figure 1.

Figure 1

Open in a new tab

Transient absorption spectra obtained during LFP at 355 nm of deoxygenated solutions of BP (2.5 × 10–3 M) and anisole in ACN–H2O (4:1 v/v), (0.027 M anisole) (a,b) and ACN–H2O (1:4 v/v), (4.6 × 10–3 M anisole) at neutral pH (c,d); (a) time delays after flash (from top to bottom): 90, 200, 400, and 2000 ns; (b) normalized decay profiles of the transient absorption for the quenching of BP (2.5 × 10–3 M) by anisole (0.027 M) in ACN–H2O (4:1 v/v) monitored at 520 nm (black) and 600 nm (red); (c) time delays after flash (from top to bottom): 100, 200, 400, and 1000 ns; and (d) normalized decay profiles of the transient absorption for the quenching of BP (2.5 × 10–3 M) by anisole (4.6 × 10–3 M) in ACN–H2O (1:4 v/v) monitored at 520 nm (black), 600 nm (red), and 540 (green).

Products of Triplet Quenching in ACN–Water Mixtures

The ET quenching mechanism is exemplified within the following discussion of the transient spectra that were recorded during triplet quenching of BP by anisole in the ACN–H2O mixture of high water content. In mixtures of ACN with neutral water ACN–H2O (1:4 v/v), transient absorptions were observed with maxima at 430 nm, around 540, and 600 nm (Figure 1c). The residual absorption of the intermediate at 430 nm was identified as the anisole radical cation, an oxidized product of ET. The inertness toward oxygen and the high sensitivity of this transient toward the presence of added nucleophiles (here, NaOH) (Figure 2a) strongly suggest this transient to be the cation radical of anisole. In particular, the low oxygen sensitivity of the oxidized anisole intermediates rules out the presence of carbon-centered radicals formed via H-abstraction from the methoxy group. Taking also into account the small rate constants for H-abstraction in the order of 106 M–1 s–131 in comparison to the fast rate constants measured for the BP triplet quenching by anisole for high water content (vide infra), it is justified to assume that ET is the initial quenching process. This is in agreement with the presence of the BP radical anion identified by the absorption peak with a maximum at 600 nm. The third species with the absorption at 540 nm was attributed to the BP ketyl radical formed from an additional proton transfer step, presumably from the solvent to the BP anion radical as the initial reduction product (Figure 1d). This finding in regard to the presence of BP ketyl radicals, interpreted as resulting from a fast, secondary protonation of the radical anion has been observed before during BP triplet quenching in the acidic media trifluoroethanol and hexafluoro-2-propanol. In our previous work, the stepwise nature of the BP ketyl formation was corroborated by experiments at high anisole concentrations (1.2 M), where the dynamics of the primary reaction intermediates were studied without interference of residual triplet excited BP. These experiments revealed contributions of very short-lived intermediates with absorptions at λ > 580 nm, which were assignable to ketyl radical anions.7

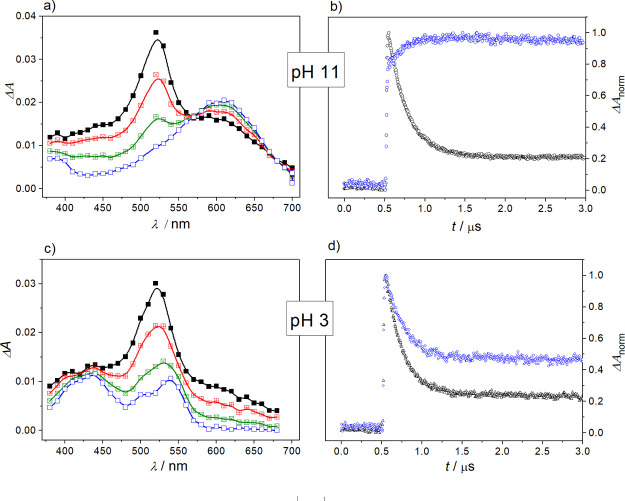
Figure 2.

Figure 2

Open in a new tab

Transient absorption spectra obtained during LFP at 355 nm of deoxygenated solutions of BP (2.6 × 10–3 M) and anisole (4.8 × 10–3 M) in ACN–H2O (1:4 v/v) at (a) pH 11 and (c) pH 3; time delays after flash (from top to bottom): 100, 200, 400, and 1000 ns; (b,d) normalized decay profiles of the transient absorption for the quenching of BP by anisole in ACN–H2O (1:4 v/v) monitored at (b) 520 nm (black) and 600 nm (blue) for pH 11; (d) 520 nm (black) and 540 nm (blue) for pH 3.

As can be seen in Figure 1d, decay profiles obtained for neutral water ACN–H2O (1:4 v/v), are quite complex due to the overlapping of absorptions related to the BP triplet state, the BP ketyl radical, and the BP radical anion. In order to simplify the kinetic data analyses and the determination of the quantum yields of radical formation, the solution pH was adjusted such that the diagnostic products (BP radical anion or BP ketyl radical) could be spectroscopically isolated (see below). It is instructive to note that variation of the pH did not affect the quenching kinetics, the stoichiometry, and the nature of the primary quenching products. Working under basic solvent conditions shifted the equilibrium between the BP radical anion and the BP ketyl radical (pKa = 9.2)32 to the radical anion side and allowed for the triplet absorption to be monitored at 520 nm without interference from the ketyl radical’s absorption.

Accordingly, when the LFP for BP and anisole in ACN–H2O (1:4 v/v) was performed in a basic solution (pH 11), the observed rapid triplet-state quenching was actually accompanied by an efficient formation of ET product, BP•– (Figure 2a,b). This can be seen from the characteristic absorption of the respective ketyl-radical anions at λmax = 600 nm (Figure 2a). The rapid and efficient thermal decay of the anisole radical cation’s absorption at 430 nm under these conditions via reaction with the nucleophile OH– interferes with kinetic analysis (for spectral deconvolution and quantification of transient species, see below).26 Complementary experiments at lower pH (Figure 2c) revealed the presence of this radical cation as the stoichiometric oxidation product of the quenching reaction together with the ketyl radical.

Under acidic conditions the first-order decay of the triplet–triplet absorption spectrum due to 3BP resulted in significant residual absorption bands with maxima at 540 and 430 nm after 1 μs (Figure 2c,d). The transients can be assigned to the anisole cation radical (λmax = 430 nm)23 and the BP ketyl radical (λmax = 540 nm).33 The predominance of the BP ketyl radicals and anisole radical cations in the transient spectra points to an ET reaction from anisole to the BP triplet which is followed by rapid protonation of the BP•– by the added acid in the bulk solvent.

Figure 3 summarizes the transient absorption spectra obtained for BP and anisole in various ACN–H2O mixtures at pH 11. Although the initial transient absorption spectra recorded just after the laser pulse reflects the spectra of 3BP and is independent of the solvent composition (red spectra in Figure 3), the transient spectra recorded after the complete decay of 3BP correspond to the transient photoproducts, that is BP•–. From Figure 3, it is clear that the quantum yield of BP•– formation increases with the increase of the water content. The importance of the ET mechanism is found to scale in a monotonic but nonlinear fashion with the water content. This becomes most evident from the water-content driven increase of the amount of free-radical ions that is present after complete triplet decay.

Figure 3.

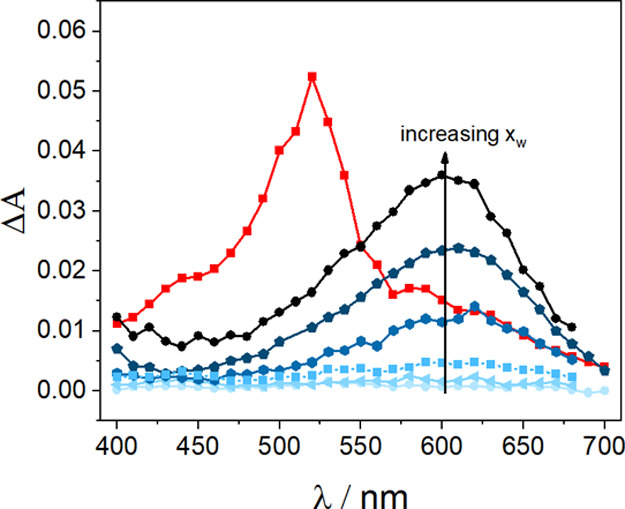
Figure 3

Open in a new tab

Transient absorption spectra obtained during LFP at 355 nm of deoxygenated solutions of BP (2.6 × 10–3 M) and anisole in various ACN–H2O mixtures at pH 11; red symbols are the transient absorption measured just after the laser pulse (the same for all solvent compositions) and blue symbols represent transient absorption spectra measured after complete decay of the BP triplet state for various ACN–H2O mixtures (xw from 0.55 to 0.92).

Interestingly, the quantum yields for the formation of the transient photoproducts (the sum of the ketyl radical BPH• and BP•–) were found to be independent of the pH, which was expected for those two species being in equilibrium (Figure 4). For example, when the LFP for BP and anisole in ACN–H2O (1:4 v/v) was performed at pH 11, the quantum yield for BP•– formation was found to be 0.4. The quantum yield for BPH• formation, in turn, was also found to be 0.4 for the solution with the same concentration of the components but at pH 3. The same quantum yield of the transient reductive photoproducts obtained at basic and acidic conditions confirms the correct determination of this value. Detection of the anisole radical cation, the oxidative product of the quenching, together with BP•– and (or) BPH• provides evidence that the significant mechanism of quenching is provided via full ET in binary ACN–H2O, when a sufficiently large fraction of water is present.

Figure 4.

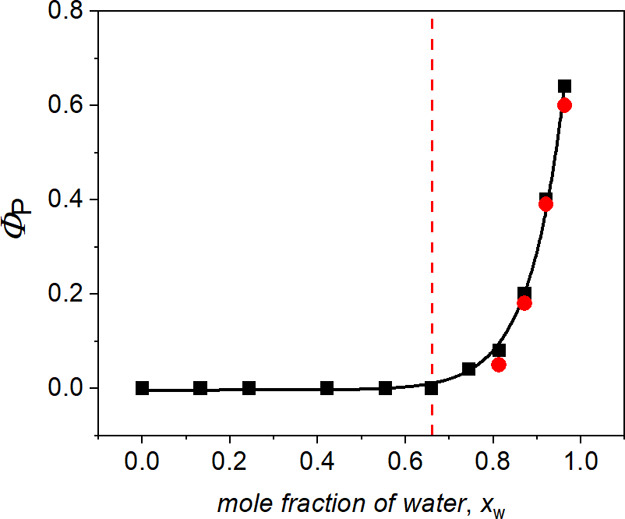
Figure 4

Open in a new tab

Solvent-composition dependence for quantum yields of free-radical-ion formation in the system BP–anisole in ACN–H2O mixture at pH 11 (black symbols). Quantum yield of ketyl radical BP formation in the system BP–anisole in ACN–H2O mixtures at pH 3 (red symbols). The concentration of anisole was sufficiently high to quench the triplet almost totally (>90%). The solid line represents a fit of the experimental points to an exponential function A0·exp(A1·xw), where A0 = (3.8 ± 1.7) × 10–6 and A1 = 12.5 ± 0.5. The red vertical line marks where VACN ≈ Vw.

The respective solvent dependences of the free-radical ion quantum yields measured at pH 11 are summarized in Figure 4 (details of the determination of the free-radical quantum yields are in the Experimental Section). Additionally, the quantum yields of the BP ketyl radical obtained at pH 3 and high water content are included in Figure 4. It is clear that the quantum yield of the transient photoproducts is independent of pH.

No free radicals were detected in pure ACN and binary ACN–H2O solutions containing less than 70 mol % of water, but at the higher H2O load, the quantum yield Φp increased rapidly with increasing mole fraction xw. Using nonlinear regression, we approximated the observed solvent-composition dependence by an exponential function A0·exp(A1·xw) (the solid line in Figure 4). The high value of the upward slope (A1 = 12.5 ± 0.5) shows that the free-radical-ion formation was triggered by the added water. Taking the fitted parameters A0 and A1, one obtains Φp ≈ 1 in the aqueous solvent.

Kinetics of Triplet Quenching in ACN–Water Mixtures

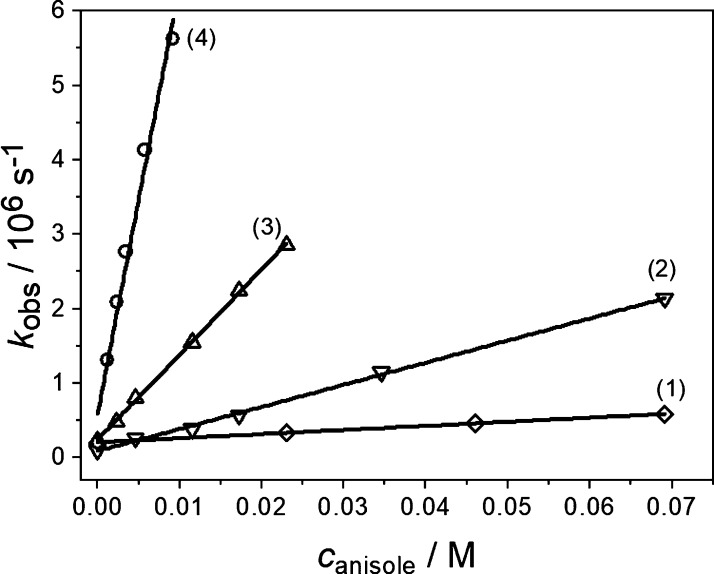
An extended study was undertaken on bimolecular quenching of the triplet state of BP by anisole in order to trace the reported changes in the mechanism (vide supra) to the changes in the dynamics of the quenching process in ACN–H2O mixtures (vide infra). In our studied system, the decay of the triplet state of BP is monitored at various anisole concentrations. In order to determine the bimolecular quenching rate constants kq for the triplet quenching of BP by anisole, the formal kinetics for data analysis were used where the relevant chemical and physical processes were considered as independent events with the quenching process itself being considered pseudo-first order. Alternative approaches such as distance- and time-dependent quenching were found to be irrelevant in the studied system (see the Supporting Information).34 The pseudo-first order rate constants kobs for the solvent composition up to xw = 0.66 (no detectable transient photoproducts) were extracted from the experimental absorption decay profiles at 630 and 520 nm. Under these experimental conditions (absence of the BP radical anion and the ketyl radical), decay profiles at 630 and 520 nm are attributed solely to the absorption of the BP triplet state. For higher water content where the formation of photoproducts (BP radical anion, BP ketyl radical and anisole radical cation) was detected, the quenching rate constants were obtained from the fits of the decay profiles at 480 and 520 nm. Detection at λobs = 480 nm was chosen because the triplet–triplet extinction coefficient greatly exceeds those of the quenching products. Decay profiles were adequately fitted to first-order exponential decay functions (Figure S1). Plots of these derived pseudo-first order constants against the anisole concentration were linear in all cases. Some illustrative examples are given in Figure 5. The values obtained at 630 or 480 nm have been cross-checked by fits to the profiles at 520 nm. Good agreement was obtained in all cases.

Figure 5.

Figure 5

Open in a new tab

Concentration dependence of the triplet-decay rate constants kobs for BP quenched by anisole in differently composed ACN–H2O mixtures; mole fraction of water xw: (1) 0, (2) 0.66, (3) 0.81, and (4) 0.92.

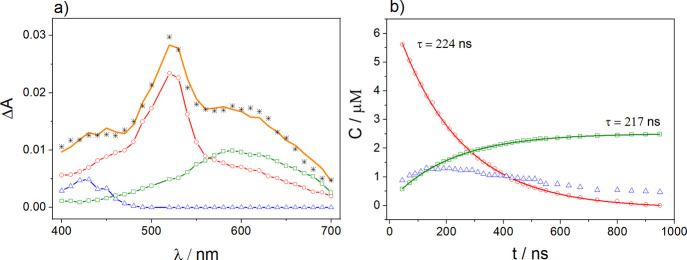
Exemplary validation of the such-derived quenching rate constants and quantum yields of free radicals was performed by applying spectral resolution techniques. Deconvolution procedures (vide supra in the Experimental Section) allowed us to obtain concentrations of the intermediates present in the BP triplet quenching by anisole in ACN–H2O (1:4 v/v) at pH 11. To simulate the experimental data quantitatively, three components were needed: the triplet state 3BP, anisole radical cation, and the BP radical anion BP•–. Exemplary resolutions and the resulting concentration profiles constructed from these spectral resolutions for the 3BP triplet quenching by anisole in ACN–H2O (1:4 v/v) at pH 11 are depicted in Figure 6.

Figure 6.

Figure 6

Open in a new tab

(a) Resolutions of transient absorption spectra taken 150 ns after the 355 nm laser pulsing of a deoxygenated solution of BP (2.5 × 10–3 M) and anisole (4.6 × 10–3 M) in ACN–H2O (1:4 v/v), pH 11; (b) concentration profiles for the BP triplet state, BP radical anion, and anisole radical cation obtained from resolutions of the transient absorption spectra. The symbols represent: ○ triplet state 3BP; Δ anisole radical cation; □ BP radical anion; and * experimental data; solid curves in (a,b) are the resulting fits from the regression analyses, the number represents the value obtained from the fit to the triplet concentration profile.

The initial triplet concentration, actinometrically determined, was 6.4 ± 0.3 μM. The maximum concentration of the BP radical anion determined from the concentration profile was found to be 2.5 ± 0.3 μM. Based on that concentration, the quantum yield of the free-radical-ion formation was calculated to be 0.39 ± 0.05, which is in good agreement with the quantum yield obtained from the analysis of the kinetic profiles (Figure S3). The triplet lifetime of BP in the presence of 4.6 × 10–3 M anisole in ACN–H2O (1:4 v/v) at pH 11 obtained from the monoexponential fit to the concentration profile (Figure 6b) was determined to be 224 ± 2 ns, which is also in good agreement with the analogous value measured from the kinetic profile at 480 nm (Figure S4). In addition, the rate of formation of the BP radical anion, within experimental error, is identical to the triplet-decay rate.

The good agreement of the values of triplet state 3BP lifetime and quantum yield of BP•– derived from concentration profiles constructed from spectral decomposition methods compared to the respective values obtained from kinetic profiles’ analyses confirms that extracting quenching rate constants and quantum yield of radical formation from the kinetic profiles yields the correct results in this system.

A comparison of the kinetic data in Figure 5 shows that triplet quenching by anisole is dramatically dependent on the composition of the ACN–H2O mixture. The bimolecular rate constants kq cover a range of two orders of magnitude between 4.4 × 106 and 5.4 × 108 M–1 s–1, with the highest being found for the water mole fraction xw of 0.92 (Figure 5). Similarly, big differences were observed by us for the triplet-quenching rate constants in nonprotic and protic solvents and in particular for the intramolecular H-atom transfer between phenols and BP in its triplet excited state.35 The same observation was also reported by Hörner et al. for a related BP–tyrosine dyad.36 In the cited work, the solvent effect was attributed to a change in the reaction mechanism to an ET-initiated process in protic solvents.36 Actually, H-bonding of one or both of the reacting partners to the solvent had been invoked by us in the past as a dominant control of the quenching dynamics. Stabilization of charged products of ET through H-bonding to the solvent has been increasingly identified in other electrochemical37 and photochemical38 studies and certainly also plays some activating role in the present study. However, as we have found in our initial treatments, the effect cannot be accounted for quantitatively in simple terms of homogeneous kinetics, implicitly assuming an ideally mixed medium.

Initially, we spent time attempting to explain quantitatively the kinetics and yield data described above by using a continuous solvent model.20 It included diffusion and radical escape processes with the solvent parameters of viscosity, dielectric constant, and refractive index that were associated with competitive triplet-quenching processes, ET, and CT.7 Clearly, all of these bulk solvent parameters are prone to significant change upon moving from neat ACN to (almost) neat water. Dielectric constant, for instance, is increasing by a factor of two in this direction. It is clear also that these changes must be expected to affect the energetics of ET to some extent, as has been discussed in much detail in the past.39,40 We found, however, that variations in these solvent parameters were way too small to account for the large differences in the chemical processes observed without considering the heterogeneity of the mixed solvents (see details in the Supporting Information).

As will be shown below, the solvent-composition dependence of kq can be quantitatively described in terms of a kinetic model if microscopic properties of the ACN–H2O binary solvent are considered. In particular, the “late rise” of reactivity at very high water content gives strong indication of nonideal behavior.

Microheterogeneity

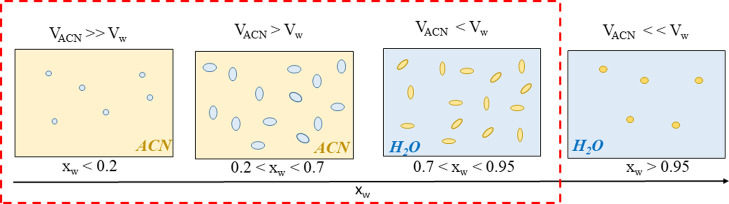
ACN–H2O mixtures are known for the temperature- and composition-dependent microheterogeneity, occurring in the form of coexisting aqueous and organic microscopic domains, without a visible phase separation.5,41 An incomplete mixing at the molecular level was observed in various experiments,42−46 including X-ray scattering, neutron diffraction, nuclear magnetic resonance (NMR) measurements, and vibrational spectroscopy. It has also been reported from numerous computer simulations and theoretical studies.6,42,47 The structural transformations in the binary solvent, described by Marcus,41 are schematically illustrated in Figure 7.

Figure 7.

Figure 7

Open in a new tab

Schematic picture of the microheterogeneity of ACN–H2O mixtures. The red line indicates the region for which experimental data were collected. Blue color represents water, and yellow color represents ACN.

In ACN-rich mixtures (xw < 0.2), H2O molecules form small aggregates, embedded in the bulk ACN solvent. With increasing H2O content, these aggregates expand to aqueous microdomains coexisting with the organic ones. Within their domains, water molecules form HB networks, whereas ACN molecules keep an antiparallel dipole–dipole arrangement. The H2O–ACN interactions, mostly by hydrogen bonding, are limited to the interfaces between the microdomains. The most pronounced volume contraction upon mixing occurs (the minimum of the excess volume) at xw ≅ 0.7. At this composition, the partial volumes of the solvent components are similar (VACN ≈ Vw). With increasing the water content above 0.7, the excess molar volume becomes less negative indicating better mixing at the molecular level, that is gradual diminishment of microheterogeneity. Simulations of H2O-rich mixtures showed that 5 mol % is the smallest ACN fraction needed for permanent ACN clustering.41,47 At xw > 0.95, individual ACN molecules are hydrated.

The specificity of the BP–anisole–ACN–water systems investigated in this work results not only from the microheterogenic structure of the binary solvent, but also from the very different solubility of the reactants in water and ACN. Both, BP and anisole, are well soluble in ACN but poorly in water. At ambient conditions, the solubility of BP in water is only 7.5 × 10–4 mol·kg–1 compared to 1.4 × 10–2 mol·kg–1 of anisole.48,49 The solubilities of both solutes in ACN are orders of magnitude larger.

The microheterogeneity of the system and, in addition, the extreme difference in solubility of the reactants in the solvent components make description of the reaction challenging. Below, we propose a simple kinetic model that is indeed able to describe this behavior, both in qualitative and quantitative terms.

Kinetic Model

Assumption 1

The reaction volume is restricted to the partial volume of ACN (VACN), and both reactants are only there. We based this assumption on the extremely different solubility of BP in the solvent components.

Assumption 2

3BP is present in one solvated form (by ACN), and anisole exists in two different forms: QI—exclusively solvated by ACN and QII—partially solvated by water molecules. We formed this assumption considering that anisole solubility in water is about 2 orders of magnitude higher compared to that of BP.

Assumption 3

Concentrations of QI and QII in the reaction volume VACN, [QI] = nQI/VACN and [QII] = nQII/VACN, depend on the molar numbers of QI (nQI) and QII (nQII), and the molar number ratio is directly proportional to the partial volume ratio of ACN (VACN) and water (Vw)

graphic file with name jp0c02635_m003.jpg 3

where the partition coefficient PQ is independent of the solvent composition. In other words, we assume that the ratio of the quencher molecules in the reaction volume, that is, those which are exclusively solvated by ACN versus those which are partially solvated by water, is determined by VACN/Vw. The partition coefficient PQ is treated here as a fitting parameter. An intuitive rationalization of eq 3 can be based on the Nernst’s distribution law if one decomposes solvation shells of the quencher molecules into organic and aqueous parts.

Assumption 4

3BP quenching by QI occurs via a CT mechanism with the rate constant kCT.

Assumption 5

3BP quenching by QII occurs via an ET mechanism with the rate constant kET.

Using the above assumptions, one can write eq 4 describing the dynamic quenching of 3BP by anisole in ACN–H2O mixtures

graphic file with name jp0c02635_m004.jpg 4

where [3BP] denotes the molar concentration of the excited BP triplets in the reaction volume.

The partial volume of ACN can be expressed by the partial molar volume ratio of the solvent components (V̅w/V̅ACN) and the system volume (V) as follows

graphic file with name jp0c02635_m005.jpg 5

From the material balance, the sum of nQI and nQII is approximately equal to the molar number of the added anisole nQ = nQI + nQII because the number of anisole in the water compartments is negligibly small due to the limited solubility of anisole in water compared to that in ACN. Thus, we have

graphic file with name jp0c02635_m006.jpg 6

Using eqs 3, 5, and 6, one can relate [QI] and [QII] with the molar concentration of the added anisole canisole = nQ/V, which when substituted into eq 4 gives

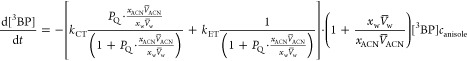graphic file with name jp0c02635_m007.jpg 7

Thus, the solvent-composition dependence for the second-order quenching rate constant kq is

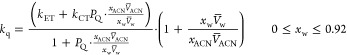graphic file with name jp0c02635_m008.jpg 8

From the present measurements, kCT = (4.42 ± 0.09) × 106 M–1 s–1 for 3BP quenching in the nonprotic ACN solvent. In ACN-rich media, the contribution from the ET mechanism is damped by the partition coefficient PQ that accounts for the different solubility of anisole in the solvent components. The last factor in eq 8 can be interpreted in terms of the compartment-volume effect. Equation 8 holds for xw ≤ 0.92. The region of higher water content is not accessible experimentally because the solubility of BP is too low. It is obvious to expect no contribution from the CT process as xw → 1. Using empirical data for the density of ACN–H2O mixtures50 and following the definition of the partial molar volume, we calculated V̅ACN and V̅w as a function of water mole fraction xw. Taking kET and PQ as parameters, we obtained a good fit to the experimental points with PQ = 53 ± 1 and kET = (1.46 ± 0.01) × 109 M–1 s–1 (see solid line and black circles in Figure 8). The value of kET seems reasonable. Our previous study showed that ET quenching rate constants of triplet BPs are of the order of 109 M–1 s–1.7,8,20,35 The value of the partition coefficient PQ can be estimated from molecular simulation or, alternatively, using experimental techniques enabling insight into the composition of the nearest molecular surrounding of the solute, for example NMR, neutron scattering. However, such data are not available at present.

Figure 8.

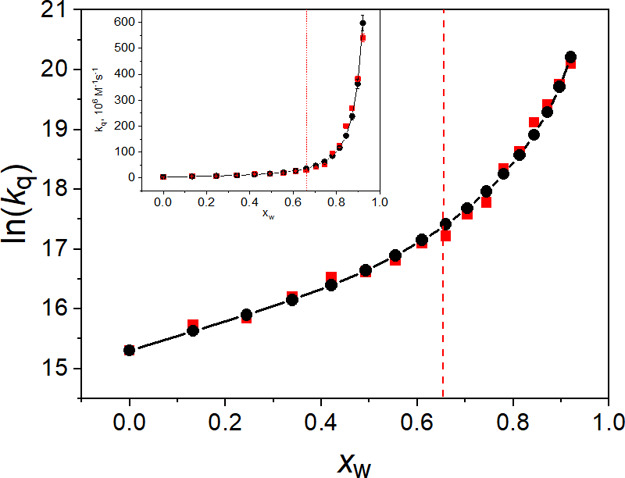
Figure 8

Open in a new tab

Solvent-composition dependence of the quenching rate constant kq in the system BP–anisole in the ACN–H2O solvent: experimental (red squares); calculated from eq 8 using kET = (1.46 ± 0.01) × 109 M–1 s–1; PQ = 53 ± 1 (black solid line + circles). The experimental data uncertainty is 3%. The inset shows the data in the non-logarithmic form.

According to our picture, all of the BP triplets are solvated only by ACN, and all of the ET quenching occurs inside ACN microdomains. The solvent-composition dependence of kq reflects a competition between reactive and nonreactive encounters of 3BP with the two different anisole species, that is partially solvated by water and exclusively solvated by ACN, the former being reactive ET and the latter nonreactive CT (Scheme 1).

Scheme 1. Schematic Illustration of BP Triplet Quenching via the ET Mechanism (a) and the Charge Transfer One (b).

Scheme 1

Open in a new tab

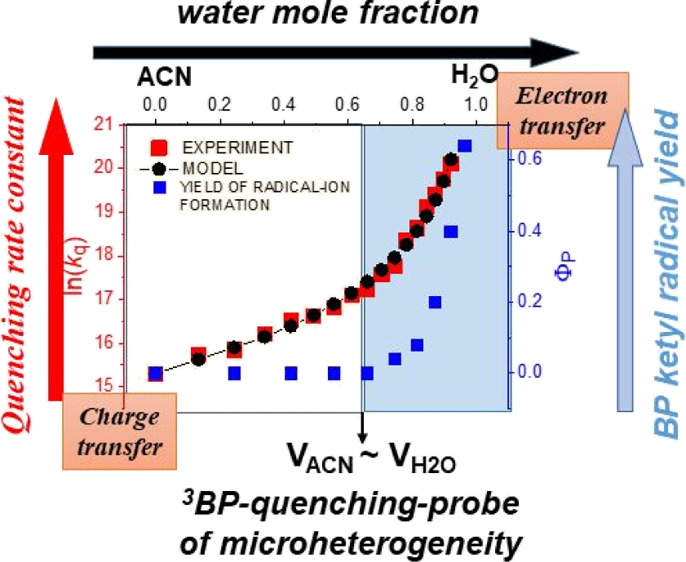
The impact of the solute–solvent-specific interaction on the ET driving force and the quenching kinetics was indicated in our earlier studies of 3BP quenching in a series of protic and nonprotic solvents.7,8 In that previous work, the driving force was ascribed to one or both of the ET reactants, 3BP (predominantly) and anisole (secondarily), being H-bonded to the solvent. Good accordance with the experiment, obtained here, shows that in a highly nonideal solution such as the BP–anisole–ACN–H2O system, a similar basis for the quenching dynamics is operative. In the current system, the possibility of forming BP-water H-bonds (being the dominant ET driving force) within the ACN microregions is controlled by encounters with the particular quenchers that are already partially solvated by water. From Figure 8, it can be seen that there is an inflection in the curve representing the solvent-composition dependence of kq. The inflection occurs in the composition range 0.5 < xw < 0.7, where the excess volume of the mixed solvent reaches a flat minimum and the solvent-component partial volumes are similar. The red vertical line in Figure 8 marks where VACN ≈ Vw. At higher water content (xw > 0.7 and VACN < Vw), there is a diminishment of the structural microheterogeneity and changes in the nature of the solvent (Figure 7). These features of the changing solvent medium effectively force the potential ET reactants together into smaller spaces, increasing the number of reactive encounters per unit of time, resulting in the observed faster quenching kinetics. The inset in Figure 8, presenting the kinetic data in a non-logarithmic form, may suggest that the solvent-composition dependence can be described by a single exponential function, like the quantum yield of free-radical-ion formation ΦP in Figure 4, but the dependence of ln(kq) on xw shows that it is not true. The inflection in the logarithmic curve coincides with detection of the transient photoproducts. As can be seen in Figure 4, irrespective of the pH, the quantum yield ΦP becomes nonzero at xw ≈ 0.7, and its rapid increase is associated with diminishment of the structural microheterogeneity.

At the same time, the quantum yield of free-radical-ion formation ΦP in Figure 4 becomes non-zero and rapidly increases when Vw exceeds VACN (xw > 0.7). Quenching of 3BP via the ET mechanism results in the formation of radical-ion pairs [BP–···Q+] which may decay by diffusional separation into free ions (kesc) or may undergo stepwise back-ET (kbt) (Scheme 1a).

According to Scheme 1, the solvent-composition dependence for the quantum yield of BP•– can be expressed by eq 9, where Φ[BP–···Q+] represents quantum yield of the radical-ion pairs [BP–···Q+] formed via the ET mechanism, and Pesc is the fraction escaping into free ions. In eq 9, the unimolecular decay rate was neglected because the yields of the radical-ion formation were obtained for high anisole concentrations that were sufficient to quench over 90% of the BP triplets.

graphic file with name jp0c02635_m009.jpg 9

Following Assumption 3 to express [QI] and [QII] and using the fitted values of kET and PQ, we calculated Φ[BP–···Q+] as a function of the water mole fraction (solid line in Figure 9). It can be seen in Figure 9 that Φ[BP–···Q+] increases monotonically from 0.244 at xw = 0.13 to 0.96 at xw = 0.92.

Figure 9.

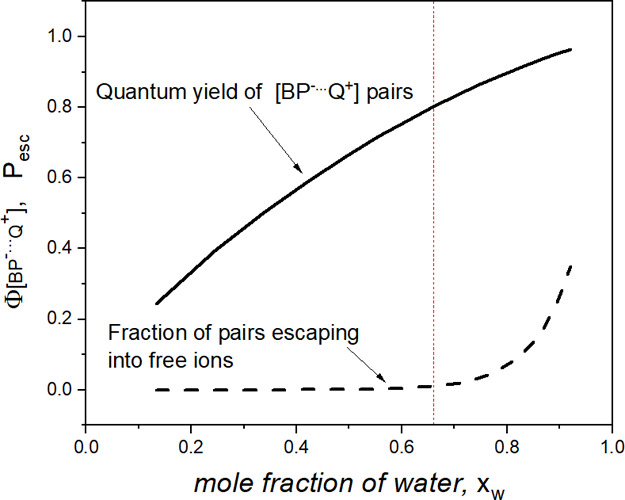
Figure 9

Open in a new tab

Water-content influence on the quantum yield of the radical-pair [BP–···Q+] formed via the ET mechanism of 3BP quenching by anisole in microheterogeneous ACN–H2O (solid line) and the fraction Pesc of pairs escaping into free ions (dashed line), anticipated from the experimental free-radical-ion quantum yield ΦP presented in Figure 4 (see text). The vertical line delimits two regions: VACN > Vw (left) and Vw > VACN (right).

The dashed curve in Figure 9 shows the solvent-composition dependence of Pesc, which is to be anticipated based on the observed free-radical-ion quantum yield ΦP presented in Figure 4. This behavior suggests that back-ET prevails (kbt ≫ kesc) when the ACN reaction volume exceeds the partial volume of water. The experimentally observed increase in the free-radical-ion quantum yield at xw > 0.7 suggests that the separation into free-radical ions begins to be competitive when the partial volume relation is the opposite (Vw > VACN), and the ACN reaction volume shrinks to islands surrounded by water (see Figure 7). A decreasing volume of ACN microregions seems to promote the escape of radical ions into aqueous regions, where BP•– and Q•+ are much more soluble than are the neutral species, and the diffusional re-encounter of the radical ions is slowed down due to the 2.6 times higher viscosity and twice weaker electrostatic attraction.

Summary and Conclusions

The observed dramatic solvent dependence of 3BP quenching by anisole in ACN–H2O binary mixtures exhibits strong parallels to a number of synthetically relevant multicomponent coupling reactions that have been previously reported.7 A “late rise” of reactivity was and is observed at high water content consistently, irrespective of the reaction being initiated thermally or photochemically. The photoinduced chemistry studied herein allowed more direct insights into the reaction pathways. Time-resolved transient spectroscopy clearly associates the massive gain in reactivity with a switch of the reaction mechanism from unproductive, CT-like to productive, ET-like.

Although the causal connection of the mechanistic switch to the water content had been drawn by us earlier,1−6 we lacked a quantitative description of the solvent dependence. Herein, a model is established that rationalizes the occurrence of single exponential decay of 3BP, both qualitatively and quantitatively, by accounting for the microheterogeneous structure of ACN–H2O mixtures and the very different solubility of the reactants in the solvent components. Restriction of the reaction volume to the ACN partial volume and a bimodal dependence of the 3BP reactivity on the solvation of the quencher as the basic assumptions suffice to reproduce the strongly nonlinear solvent dependence of the reaction rates. Reaction with anisole exclusively solvated by ACN occurs via a CT mechanism with the rate constant of 4.42 × 106 M–1 s–1. The dynamics of intermolecular encounters with the solvated quencher molecules is affected by the enrichment of the reaction partners within solution compartments, rendering this view compatible with Breslow’s hydrophobic effect.51 The compartment-volume effect, however, is only partially responsible for the increase of the quenching rate constant (kq) and a more direct impact of water has to be accounted for as well. The observed rapid increase in kq is driven by the growing concentration of anisole partially solvated by water molecules. The presence of water in the anisole solvation shell triggers an ET mechanism that occurs at the rate constant of 1.46 × 109 M–1 s–1 and is presumably assisted by the ACN–water hydrogen-bonding interaction. This latter point, which implies a direct action of water, is highly reminiscent of the “on-water” hypothesis. As a matter of fact, our results give indication that both the hydrophobic effect and the more specific “on-water” effect act in concert here. The present study shows that quenching kinetics measurements are sensitive to molecular interactions in ACN–H2O mixtures and can be used to probe microheterogeneous structures of these binary solvents.

Acknowledgments

This is Document no. NDRL-5263 from the Notre Dame Radiation Laboratory which is supported by the Office of Basic Energy Sciences at the United States Department of Energy through grant number DE-FC02-04ER15533.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c02635.

  • Decay profiles at 520 and 600 and 480 nm of the solutions of BP and anisole in different ACN–H2O mixtures, Collins–Kimball solution to diffusion quenching in free space, description of the viscosity effect on the quenching rate constants, and description of the ET rate constant in continuous solvent model in the Marcus theory (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp0c02635_si_001.pdf (891.1KB, pdf)

References

  1. Bertie J. E.; Lan Z. Liquid Water–Acetonitrile Mixtures at 25 °C: The Hydrogen-Bonded Structure Studied through Infrared Absolute Integrated Absorption Intensities. J. Phys. Chem. B 1997, 101, 4111–4119. 10.1021/jp9639511. [DOI] [Google Scholar]
  2. Venables D. S.; Schmuttenmaer C. A. Spectroscopy and Dynamics of Mixtures of Water with Acetone, Acetonitrile, and Methanol. J. Chem. Phys. 2000, 113, 11222–11236. 10.1063/1.1328072. [DOI] [Google Scholar]
  3. Mountain R. D. Molecular Dynamics Study of Water–Acetonitrile Mixtures. J. Phys. Chem. A 1999, 103, 10744–10748. 10.1021/jp992305+. [DOI] [Google Scholar]
  4. Kovacs H.; Laaksonen A. Molecular Dynamics Simulation and NMR Study of Water-Acetonitrile Mixtures. J. Am. Chem. Soc. 1991, 113, 5596–5605. 10.1021/ja00015a013. [DOI] [Google Scholar]
  5. Marcus Y.; Migron Y. Polarity, Hydrogen Bonding, and Structure of Mixtures of Water and Cyanomethane. J. Phys. Chem. 1991, 95, 400–406. 10.1021/j100154a070. [DOI] [Google Scholar]
  6. Mountain R. D. Microstructure and Hydrogen Bonding in Water–Acetonitrile Mixtures. J. Phys. Chem. B 2010, 114, 16460–16464. 10.1021/jp105272q. [DOI] [PubMed] [Google Scholar]
  7. Lewandowska A.; Hug G. L.; Hörner G.; Pedzinski T.; Filipiak P.; Marciniak B. Efficient Photochemical Oxidation of Anisole in Protic Solvents. Electron Transfer Driven by Specific Solvent-Solute Interactions. ChemPhysChem 2010, 11, 2108–2117. 10.1002/cphc.201000196. [DOI] [PubMed] [Google Scholar]
  8. Lewandowska-Andralojc A.; Hug G. L.; Hörner G.; Pedzinski T.; Marciniak B. Unusual Photobehavior of Benzophenone Triplets in Hexafluoroisopropanol. Inversion of the Triplet Character of Benzophenone. J. Photochem. Photobiol., A 2012, 244, 1–8. 10.1016/j.jphotochem.2012.06.010. [DOI] [Google Scholar]
  9. Richert S.; Rosspeintner A.; Landgraf S.; Grampp G.; Vauthey E.; Kattnig D. R. Time-Resolved Magnetic Field Effects Distinguish Loose Ion Pairs from Exciplexes. J. Am. Chem. Soc. 2013, 135, 15144–15152. 10.1021/ja407052t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Shizuka H.; Yamaji M. Triplet Energy Transfer and Triplet Exciplex Formation of Benzophenone. Bull. Chem. Soc. Jpn. 2000, 73, 267–280. 10.1246/bcsj.73.267. [DOI] [Google Scholar]
  11. Gajewski J. J. The Claisen Rearrangement. Response to Solvents and Substituents: The Case for Both Hydrophobic and Hydrogen Bond Acceleration in Water and for a Variable Transition State. Acc. Chem. Res. 1997, 30, 219–225. 10.1021/ar9600493. [DOI] [Google Scholar]
  12. Pirrung M. C. Acceleration of Organic Reactions through Aqueous Solvent Effects. Chem.—Eur. J. 2006, 12, 1312–1317. 10.1002/chem.200500959. [DOI] [PubMed] [Google Scholar]
  13. Pirrung M. C.; Sarma K. D. Multicomponent Reactions Are Accelerated in Water. J. Am. Chem. Soc. 2004, 126, 444–445. 10.1021/ja038583a. [DOI] [PubMed] [Google Scholar]
  14. Pirrung M. C.; Sarma K. D.; Wang J. Hydrophobicity and Mixing Effects on Select Heterogeneous, Water-Accelerated Synthetic Reactions. J. Org. Chem. 2008, 73, 8723–8730. 10.1021/jo801134r. [DOI] [PubMed] [Google Scholar]
  15. Butler R. N.; Cunningham W. J.; Coyne A. G.; Burke L. A. The Influence of Water on the Rates of 1,3-Dipolar Cycloaddition Reactions: Trigger Points for Exponential Rate Increases in Water–Organic Solvent Mixtures. Water-Super Versus Water-Normal Dipolarophiles. J. Am. Chem. Soc. 2004, 126, 11923–11929. 10.1021/ja040119y. [DOI] [PubMed] [Google Scholar]
  16. Jung Y.; Marcus R. A. On the Theory of Organic Catalysis “on Water”. J. Am. Chem. Soc. 2007, 129, 5492–5502. 10.1021/ja068120f. [DOI] [PubMed] [Google Scholar]
  17. Marcus R. A. On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. III. Applications to Data on the Rates of Organic Redox Reactions. J. Chem. Phys. 1957, 26, 872–877. 10.1063/1.1743424. [DOI] [Google Scholar]
  18. Marcus R. A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. 10.1146/annurev.pc.15.100164.001103. [DOI] [Google Scholar]
  19. Hidalgo-Acosta J. C.; Méndez M. A.; Scanlon M. D.; Vrubel H.; Amstutz V.; Adamiak W.; Opallo M.; Girault H. H. Catalysis of Water Oxidation in Acetonitrile by Iridium Oxide Nanoparticles. Chem. Sci. 2015, 6, 1761–1769. 10.1039/c4sc02196g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Marciniak B.; Bobrowski K.; Hug G. L. Quenching of Triplet States of Aromatic Ketones by Sulfur-Containing Amino Acids in Solution. Evidence for Electron Transfer. J. Phys. Chem. 1993, 97, 11937–11943. 10.1021/j100148a015. [DOI] [Google Scholar]
  21. Pedzinski T.; Markiewicz A.; Marciniak B. Photosensitized Oxidation of Methionine Derivatives. Laser Flash Photolysis Studies. Res. Chem. Intermed. 2009, 35, 497–506. 10.1007/s11164-009-0046-4. [DOI] [Google Scholar]
  22. Baral-Tosh S.; Chattopadhyay S. K.; Das P. K. A Laser Flash Photolysis Study of Paraquat Reduction by Photogenerated Aromatic Ketyl Radicals and Carbonyl Triplets. J. Phys. Chem. 1984, 88, 1404–1408. 10.1021/j150651a035. [DOI] [Google Scholar]
  23. O’Neill P.; Steenken S.; Schulte-Frohlinde D. Formation of Radical Cations of Methoxylated Benzenes by Reaction with Hydroxyl Radicals, Thallium(2+), Silver(2+), and Peroxysulfate (SO4-) in Aqueous Solution. Optical and Conductometric Pulse Radiolysis and in Situ Radiolysis Electron Spin Resonance Study. J. Phys. Chem. 1975, 79, 2773–2779. 10.1021/j100592a013. [DOI] [Google Scholar]
  24. Wisniowski P.; Hug G. L.; Mirkowski J.. Decom2006, Warsaw, 2006.
  25. Hayon E.; Ibata T.; Lichtin N. N.; Simic M. Electron and Hydrogen Atom Attachment to Aromatic Carbonyl Compounds in Aqueous Solution. Absorption Spectra and Dissociation Constants of Ketyl Radicals. J. Phys. Chem. 1972, 76, 2072–2078. 10.1021/j100659a003. [DOI] [Google Scholar]
  26. Grabner G.; Rauscher W.; Zechner J.; Getoff N. Photogeneration of Radical Cations from Aqueous Methoxylated Benzenes. J. Chem. Soc., Chem. Commun. 1980, 222–223. 10.1039/c39800000222. [DOI] [Google Scholar]
  27. Okada K.; Yamaji M.; Shizuka H. Laser Photolysis Investigation of Induced Quenching in Photoreduction of Benzophenone by Alkylbenzenes and Anisoles. J. Chem. Soc., Faraday Trans. 1998, 94, 861–866. 10.1039/a707900a. [DOI] [Google Scholar]
  28. Das P. K.; Bobrowski K. Charge-Transfer Reactions of Methoxybenzenes with Aromatic Carbonyl Triplets. J. Chem. Soc., Faraday Trans. 2 1981, 77, 1009–1027. 10.1039/f29817701009. [DOI] [Google Scholar]
  29. Wolf M. W.; Brown R. E.; Singer L. A. Deactivation of Benzophenone Triplets Via Exciplex Formation. Evidence for Dual Reaction Pathways. J. Am. Chem. Soc. 1977, 99, 526–531. 10.1021/ja00444a036. [DOI] [Google Scholar]
  30. Leigh W. J.; Lathioor E. C.; St Pierre M. J. Photoinduced Hydrogen Abstraction from Phenols by Aromatic Ketones. A New Mechanism for Hydrogen Abstraction by Carbonyl n,π* and π,π* Triplets. J. Am. Chem. Soc. 1996, 118, 12339–12348. 10.1021/ja961973v. [DOI] [Google Scholar]
  31. Lakowicz J. R.Principles of Fluorescence Spectroscopy; Springer US, 2006. [Google Scholar]
  32. Porter G.; Wilkinson F. Primary Photochemical Processes in Aromatic Molecules. Part 5—Flash Photolysis of Benzophenone in Solution. Trans. Faraday Soc. 1961, 57, 1686–1691. 10.1039/tf9615701686. [DOI] [Google Scholar]
  33. Bensasson R. V.; Gramain J.-C. Benzophenone Triplet Properties in Acetonitrile and Water. Reduction by Lactams. J. Chem. Soc., Faraday Trans. 1 1980, 76, 1801–1810. 10.1039/f19807601801. [DOI] [Google Scholar]
  34. Angulo G.; Rosspeintner A.; Lang B.; Vauthey E. Optical Transient Absorption Experiments Reveal the Failure of Formal Kinetics in Diffusion Assisted Electron Transfer Reactions. Phys. Chem. Chem. Phys. 2018, 20, 25531–25546. 10.1039/c8cp05153d. [DOI] [PubMed] [Google Scholar]
  35. Lewandowska A.; Hug G. L.; Hörner G.; Pogocki D.; Kazmierczak F.; Marciniak B. Intramolecular H-Atom Transfer Reactions in Rigid Peptides. Correlated Solvent and Structural Effects. Can. J. Chem. 2011, 89, 266–279. 10.1139/v10-110. [DOI] [Google Scholar]
  36. Hörner G.; Lewandowska A.; Hug G. L.; Marciniak B. Solvent Effects on the Intramolecular Hydrogen-Atom Transfer between Tyrosine and Benzophenone. Diverting Reaction Mechanisms in Protic and Nonprotic Media. J. Phys. Chem. C 2009, 113, 11695–11703. 10.1021/jp901740z. [DOI] [Google Scholar]
  37. Savéant J.-M.; Tard C. Proton-Coupled Electron Transfer in Azobenzene/Hydrazobenzene Couples with Pendant Acid–Base Functions. Hydrogen-Bonding and Structural Effects. J. Am. Chem. Soc. 2014, 136, 8907–8910. 10.1021/ja504484a. [DOI] [PubMed] [Google Scholar]
  38. Sjödin M.; Irebo T.; Utas J. E.; Lind J.; Merényi G.; Åkermark B.; Hammarström L. Kinetic Effects of Hydrogen Bonds on Proton-Coupled Electron Transfer from Phenols. J. Am. Chem. Soc. 2006, 128, 13076–13083. 10.1021/ja063264f. [DOI] [PubMed] [Google Scholar]
  39. Heitele H.; Finckh P.; Weeren S.; Poellinger F.; Michel-Beyerle M. E. Solvent Polarity Effects on Intramolecular Electron Transfer. 1. Energetic Aspects. J. Phys. Chem. 1989, 93, 5173–5179. 10.1021/j100350a030. [DOI] [Google Scholar]
  40. Heitele H. Dynamic Solvent Effects on Electron-Transfer Reactions. Angew. Chem., Int. Ed. 1993, 32, 359–377. 10.1002/anie.199303591. [DOI] [Google Scholar]
  41. Marcus Y. The Structure of and Interactions in Binary Acetonitrile + Water Mixtures. J. Phys. Org. Chem. 2012, 25, 1072–1085. 10.1002/poc.3056. [DOI] [Google Scholar]
  42. Bakó I.; Megyes T.; Grósz T.; Pálinkás G.; Dore J. Structural Investigation of Water–Acetonitrile Mixtures: Small-Angle and Wide-Angle Neutron Diffraction Study Compared to Molecular Dynamics Simulation. J. Mol. Liq. 2006, 125, 174–180. 10.1016/j.molliq.2005.11.022. [DOI] [Google Scholar]
  43. Lange K. M.; Könnecke R.; Soldatov M.; Golnak R.; Rubensson J.-E.; Soldatov A.; Aziz E. F. On the Origin of the Hydrogen-Bond-Network Nature of Water: X-Ray Absorption and Emission Spectra of Water–Acetonitrile Mixtures. Angew. Chem., Int. Ed. 2011, 50, 10621–10625. 10.1002/anie.201104161. [DOI] [PubMed] [Google Scholar]
  44. Takamuku T.; Noguchi Y.; Matsugami M.; Iwase H.; Otomo T.; Nagao M. Heterogeneity of Acetonitrile–Water Mixtures in the Temperature Range 279–307 K Studied by Small-Angle Neutron Scattering Technique. J. Mol. Liq. 2007, 136, 147–155. 10.1016/j.molliq.2007.02.009. [DOI] [Google Scholar]
  45. Takamuku T.; Noguchi Y.; Nakano M.; Matsugami M.; Iwase H.; Otomo T. Microinhomogeneity for Aqueous Mixtures of Water-Miscible Organic Solvents. J. Ceram. Soc. Jpn. 2007, 115, 861–866. 10.2109/jcersj2.115.861. [DOI] [Google Scholar]
  46. Takamuku T.; Noguchi Y.; Yoshikawa E.; Kawaguchi T.; Matsugami M.; Otomo T. Alkali Chlorides-Induced Phase Separation of Acetonitrile–Water Mixtures Studied by Small-Angle Neutron Scattering. J. Mol. Liq. 2007, 131–132, 131–138. 10.1016/j.molliq.2006.08.048. [DOI] [Google Scholar]
  47. Oldiges C.; Wittler K.; Tönsing T.; Alijah A. MD Calculated Structural Properties of Clusters in Liquid Acetonitrile/Water Mixtures with Various Contents of Acetonitrile. J. Phys. Chem. A 2002, 106, 7147–7154. 10.1021/jp025506d. [DOI] [Google Scholar]
  48. Yalkowsky S. H.; He Y.; Jain P.. Handbook of Aqueous Solubility Data, 2nd ed.; CRC Press: New York, 2010; p 939. [Google Scholar]
  49. Chiou C. T.; Porter P. E.; Schmedding D. W. Partition Equilibria of Nonionic Organic Compounds between Soil Organic Matter and Water. Environ. Sci. Technol. 1983, 17, 227–231. 10.1021/es00110a009. [DOI] [PubMed] [Google Scholar]
  50. del Carmen Grande M.; Juliá J. A.; Barrero C. R.; Marschoff C. M.; Bianchi H. L. The (Water+Acetonitrile) Mixture Revisited: A New Approach for Calculating Partial Molar Volumes. J. Chem. Thermodyn. 2006, 38, 760–768. 10.1016/j.jct.2005.08.009. [DOI] [Google Scholar]
  51. Breslow R. Hydrophobic Effects on Simple Organic Reactions in Water. Acc. Chem. Res. 1991, 24, 159–164. 10.1021/ar00006a001. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c02635_si_001.pdf (891.1KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES