Unveiling the Physics Behind Hybrid Functionals

Abstract

We show that accurate exchange–correlation hybrid functionals give very physically optimized effective-correlation potentials, capable of correctly describing the quantum oscillations of atoms and molecules. Based on this analysis and on understanding the error cancellation between semilocal exchange and correlation functionals, we propose a very simple, semilocal correlation potential model compatible with the exact exchange of density functional theory, which performs remarkably well for charge densities and orbital energies.

1. Introduction

The ground-state Kohn–Sham (KS)¹ self-consistent, orbital formulation of density functional theory (DFT)² is the most used method for electronic structure calculations. In KS–DFT, the noninteracting kinetic energy functional, representing usually a dominant/important part of the total energy,³⁻⁵ is treated exactly with KS one-particle orbitals, and only the exchange–correlation (XC) energy E_xc[ρ] must be approximated as a functional of the electronic density ρ(r). Even if the XC energy is just a small fraction of the total energy, it contains all the many-body effects beyond the Hartree method, having crucial theoretical and computational importance.

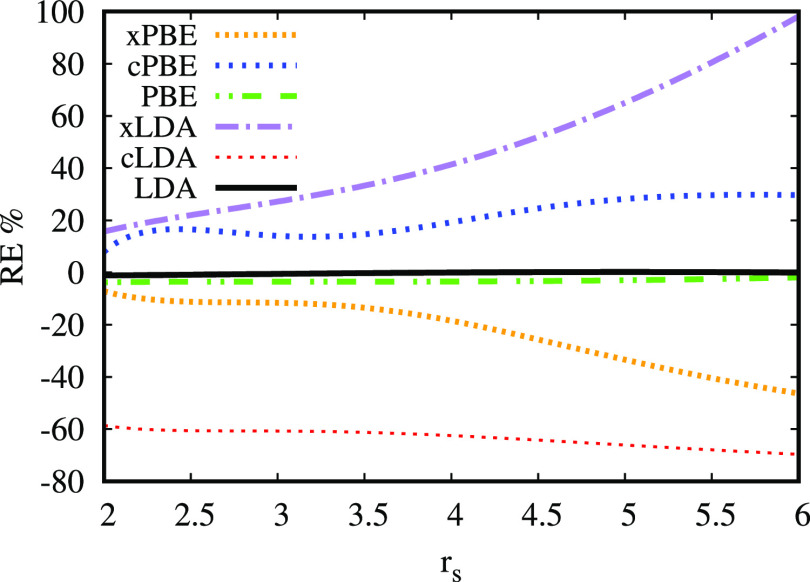
Starting from the local density approximation (LDA),¹ many useful semilocal density functional approximations (DFA) such as generalized gradient approximations (GGAs)⁶ and meta-GGAs⁷ have been developed. Most of the standard semilocal XC functionals work by mutual error cancellation effects between the exchange and correlation parts.^8,9 The error cancellation is significantly diminished for the sophisticated meta-GGA functionals (in comparison with the LDA), but this problem is still important especially in the low-density regime, where the correlation energy starts to behave as the exchange energy under the uniform density scaling of the density.¹⁰ Noting that in most of the non-covalent molecular bonds, the density is small,¹¹ we may conclude that the error cancellation issue plays important role in semilocal DFT calculations of material science. To exemplify this problem, we show in Figure 1 the relative errors (RE) in % of jellium surface exchange, correlation, and XC energies. Even if the LDA is one of the most accurate functionals for jellium and metal surface energies,^12,13 its outstanding performance is based on a huge error cancellation between exchange and correlation. The popular PBE GGA¹⁴ improves the exchange and correlation parts, as reported in the figure, but the total XC results are not as accurate as the LDA ones. Another class of DFAs widely applied in quantum chemistry calculation are the hybrid functionals.¹⁷ They are mixture of a fraction of the Hartree–Fock (HF) exchange energy with fractions of given semilocal exchange and correlation functionals. Similar in popularity are the functionals based on range-separation^18,19 of Coulomb electron–electron interaction w_ee(r₁₂) = 1/r₁₂ into the short-range and long-range contributions (w_ee(r₁₂) = w_ee^sr(r₁₂) + w_ee(r₁₂)). The former interaction is described by specially developed short-range semilocal DFAs,²⁰⁻²³ whereas the later one, in general, takes the form of long-range HF exchange energy which captures the right −1/r dependence in the tail of XC potential. From here on, we will refer to these two types of functionals as hybrid functionals.

Figure 1.

RE (in %) of the LDA and PBE jellium surface exchange, correlation, and XC energies, vs the bulk parameter r_s. The correlation and exchange-only reference values are the diffusion Monte Carlo¹⁵ and the exact exchange (EXX)¹⁶ ones, respectively.

Because the HF optimum potential is non-local, the calculations for both types of functionals (and meta-GGAs as well) are typically done within the generalized KS framework.^24,25 However, in order to remain in the true KS self-consistent scheme, the HF should be replaced with the KS EXX that gives a local-multiplicative exchange potential through the optimized effective potential (OEP) approach.²⁶⁻²⁹ The HF- and OEP-based hybrids give practically the same accuracy for ground-state properties³⁰⁻³² (see also Figure S4 of ref (33)), differing only for quantities involving excited states, electron affinities, and band gaps.³⁴ Moreover, EXX satisfies the uniform scaling relation (E_x[ρ_λ] = λE_x[ρ], with ρ_λ(r) = λ³ρ(λr) being the uniformly scaled density and λ ≥ 0), in contrast to HF that (slightly) violates this condition.³⁵

In the following, we show that XC hybrid functionals give very physically optimized effective correlation potentials, capable of correctly describing the quantum oscillations of atoms and molecules. Moreover, based on the analysis of error cancellation between semilocal exchange and correlation functionals, we propose a very simple, semilocal correlation potential model compatible with the EXX potential supported by analysis of charge densities and orbital energies.

2. Theory

In general, for a given KS orbital-(ϕ_pσ) and/or eigenvalue-(ε_pσ) dependent XC energy functional, the OEP equation for the XC potential reads^{26,27,29,36−40}

1

which is an integral equation (Fredholm of the first kind) with the inhomogeneity given by

2

where X_σ^–1 is the inverse of the static KS linear response function

3

The KS orbitals and eigenvalues are determined by solutions of standard KS equations

4

with v_ext(r) and v_J(r) being the external (nuclear) and the Coulomb/Hartree potentials, respectively. In all equations, we use the convention that i, j, ... label occupied KS orbitals, a, b, ... label virtual ones; the indexes p, q, ... are used otherwise, while σ, τ denotes the spin degrees of freedom. In particular, the corresponding OEP potential of EXX energy expression

5

labeled as OEPx is defined by the

6

with (p_σq_σ|r_σs_σ) being a two-electron integral (in the Mulliken notation) computed using KS orbitals. Let us now consider the OEP-versions of several most popular hybrid functionals, namely, the global hybrid B3LYP⁴² and PBE0⁴³ XC functionals, and one example of range-separated XC functional, that is, ωPBE,^44,45 where only exchange-part of functional is divided into the short- and long-range part and correlation is kept in the original PBE¹⁴ form.

Now, using the OEP formalism, we are able to calculate the correlation potential v_c(r) = δE_c[ρ]/δρ(r), where the correlation energy functional is by definition

7

Keeping eq 7 in mind, the corresponding correlation energy functionals (for all aforementioned XC functionals) have the following expressions

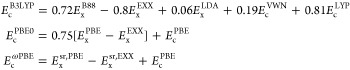8

which, as one can note, depend explicitly on EXX energy.

3. Computational Details

All calculation have been carried out with locally modified version of ACES II⁴⁶ program. As in our previous studies^{8,31,32,47−49} in order to solve OEP equation (eq 1), we have employed the finite-basis set procedure of refs (50) and (51). To calculate pseudo-inverse of density–density response matrix, we have utilized a truncated singular-value decomposition (TSVD). This step is essential for determining stable and physically meaningful OEP solutions.^48,52,53 The cutoff criteria in the TSVD procedure was set to 10^–6. For more technical details on this type of calculations, we refer the reader to refs (8) and (48).

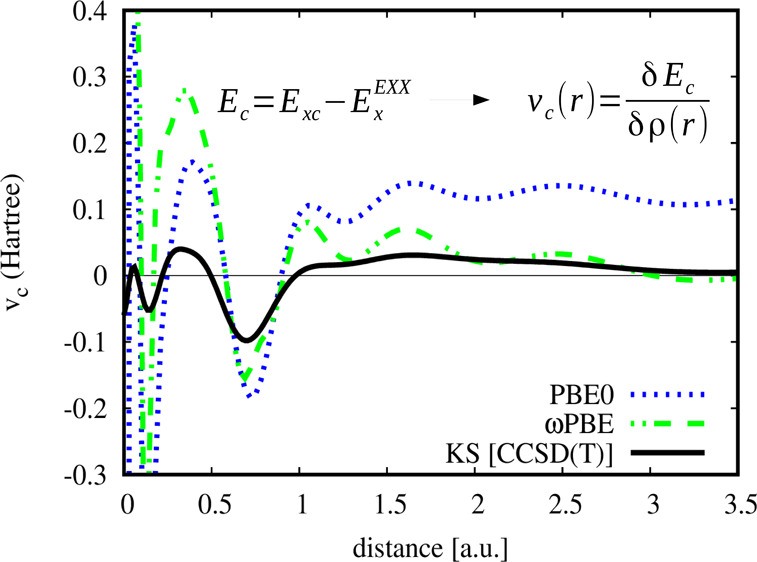
In all calculations, we employed uncontracted triple zeta quality basis sets as in refs (9) and (48), namely, an even tempered 20s10p2d basis set⁸ for He and He₂, an uncontracted ROOS-ATZP basis set⁵⁴ for Ne atom and Ne₂, and for Ar atom, we used a modified basis set which combines s and p type basis functions from the uncontracted ROOS-ATZP⁵⁴ with d and f functions coming from the uncontracted aug-cc-pwCVQZ basis set.⁵⁵ Remaining systems were treated in uncontracted cc-pVTZ basis set of dunning.⁵⁶ For all molecular systems, we considered their equilibrium geometries from refs (57−59) also used in our previous studies.^8,48 To assess the results, we considered the reference data from the Ab Initio DFT OEP2-sc method^60,61 and CCSD(T)⁶² calculations. The reference KS[CCSD(T)] correlation potentials (depicted on Figures 2 and 4) and CCSD(T) KS orbital energies (used to calculated error statistics in Table 1) have been obtained using inverse KS method from ref (41) taking as a starting point the relaxed densities⁶³⁻⁶⁶ constructed using the Lagrangian approach.⁶⁷⁻⁷⁰ For more technical details, we refer the reader to refs (8, 41, 71).

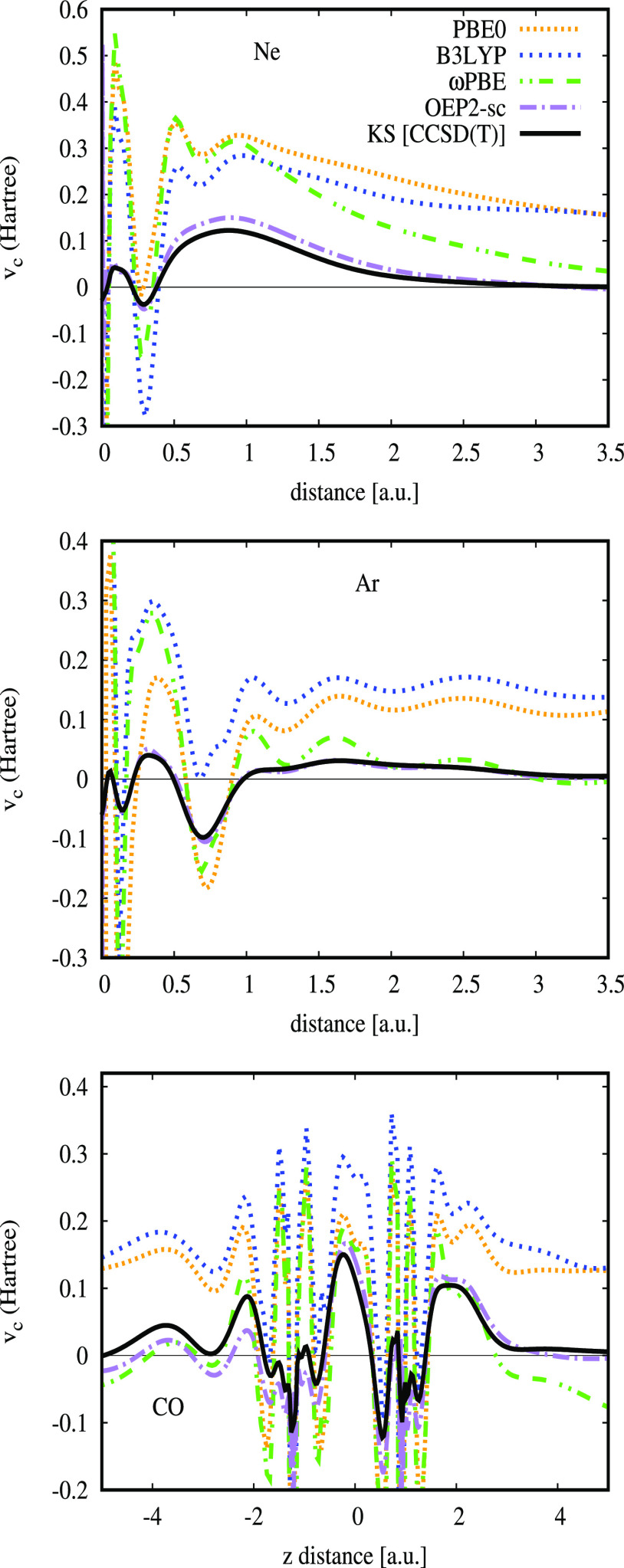
Figure 2.

Correlation potentials of the Ne (upper panel), Ar (middle panel) atoms, and CO molecule (lower panel) for various methods. The reference KS[CCSD(T)] have been obtained using the method from ref (41).

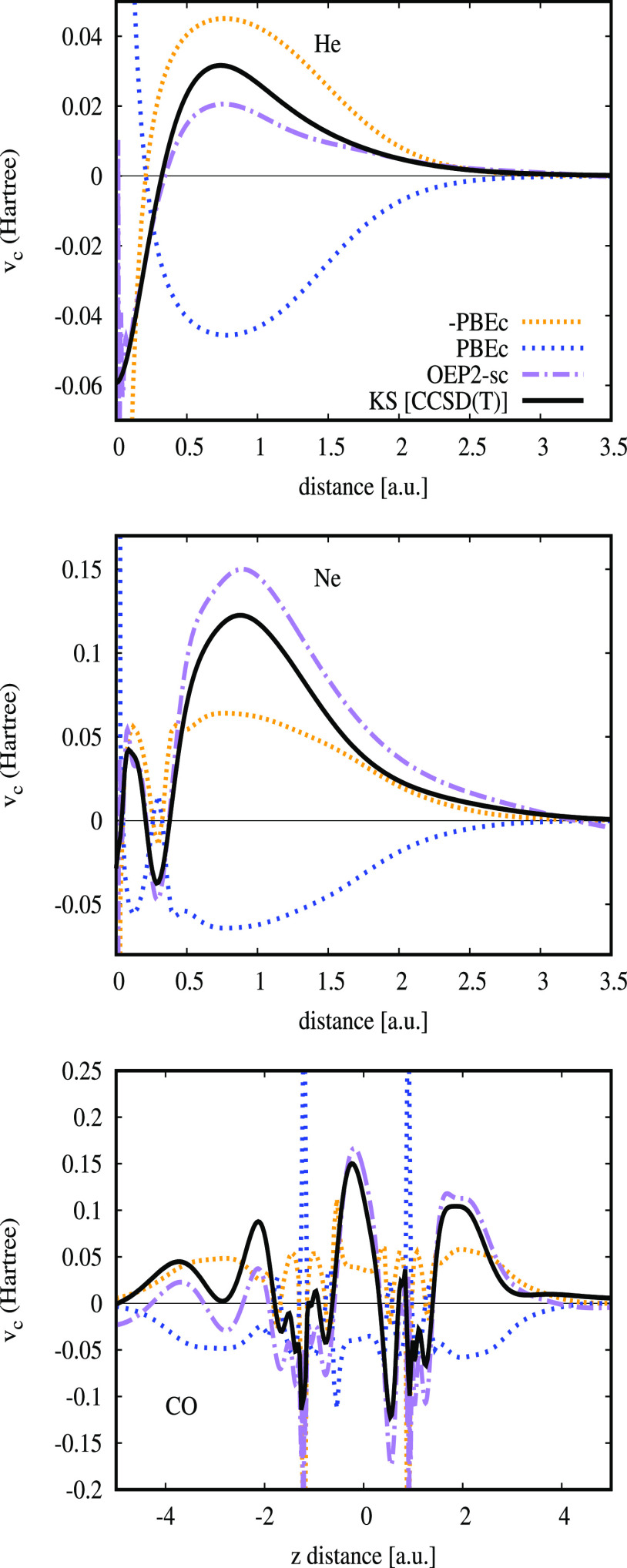
Figure 4.

Correlation potentials for the He and Ne atoms and CO molecule. The reference KS[CCSD(T)] have been obtained using method from ref (41).

Table 1. Error Statistics of Several Properties [∑_i^MICDD_i/(N_e)_i))]/M^a.

		OEPx-
	PBE	+ACSC	–ACSC	+PBEc	–PBEc	OEPx	OEP2-sc
ICDD
MAE	19.31	21.37	13.95	18.64	13.45	-	3.43
MAE/Ne	1.58	1.71	1.07	1.53	1.03	-	0.29
HOMO (IP)
MAE [eV]	6.17	1.78	0.51	1.81	0.50	0.90	0.66
MARE [%]	38.03	11.54	3.26	11.68	3.17	5.67	4.43
LUMO
MAE [eV]	4.04	1.66	0.91	1.65	0.85	1.30	0.64
MARE [%]	111.49	45.01	27.94	44.57	26.07	36.70	19.77
HOMO–LUMO Energy Gap
MAE [eV]	1.11	1.14	0.39	1.13	0.39	0.64	0.22
MARE [%]	8.38	10.96	4.50	10.76	4.46	6.56	1.91

^aFor the ICDD of eq 10, we report the mean absolute error (MAE) in units of 10^–2, and the MAE weighted with the number of electrons (MAE/N_e = [∑_i^MICDD_i/(N_e)_i))]/M, where (N_e)_i is the number of electrons of the i-th system and M = 14 is the total number of systems). In case of HOMO, LUMO and HOMO–LUMO gaps results, we report additionally the mean absolute RE (MARE) calculated with respect to the reference data.^47,94

4. Results

The correlation potentials corresponding to eq 8 are shown on Figure 2 for three representative cases of Ne and Ar atoms and CO molecule. Inspection of Figure 2 reveals that:

• (i)The B3LYP, PBE0, and ωPBE correlation potentials are very physical, being in phase with and having the shape of the reference (coupled cluster singles–doubles with perturbative triples⁶² - CCSD(T)) and Ab Initio DFT OEP2-sc^60,61) curves in all the cases. Note that the correlation potentials of, E_c^LYP, and E_c fail badly to describe such a feature.^8,9 Consequently, even if the semilocal exchange is very accurate, as are E_x^B88(72) and E_x,¹⁴ they still contain correlation effects that are crucial for the shape of the correlation potential.
• (ii)Figure 2 additionally reveals the physics behind the hybrid functionals and can be considered an elegant proof on the hybrid functional construction. Until now, the widely accepted rationale for mixing EXX with semilocal functionals was based on the adiabatic connection formula with a heuristic model for the hybrid coupling-constant dependence given in eq 6 of ref (73). We also note that the correlation potential v_c is well defined, entering the KS scheme, as shown in eq 4, in sharp contrast to the correlation energy per particle ϵ_c (defined by E_c = ∫dr ρ(r)ϵ_c(r)) which is not unique, being defined up to a gauge transformation.⁷⁴ Thus, this finding shows that inspection of OEP correlation potentials should be seen as a powerful criterion in the construction of new hybrid functionals, whose parameters can be found such that to give the optimal correlation potential.
• (iii)In the tail of the density, the EXX potential behaves as −1/r, while the semilocal exchange potentials are usually vanishing much faster (e.g., B88⁷² and xPBE¹⁴ behave as −1/r² and e^–r, respectively). This issue gives significant errors of v_c in the asymptotic region (see Figure 2) directly transferring on the quality of ionization and excited state energies. On the other hand, this region is energetically evanescent, being not relevant for most of ground state properties. Additionally, Figure 2 shows that in the case of range-separated ωPBE functional, the v_c decays much faster in the tail, being similar to the reference OEP2-sc and CCSD(T) potentials, thus explaining the dramatically improvement upon global hybrids XC functionals in the calculation of many properties.⁷⁵⁻⁷⁷

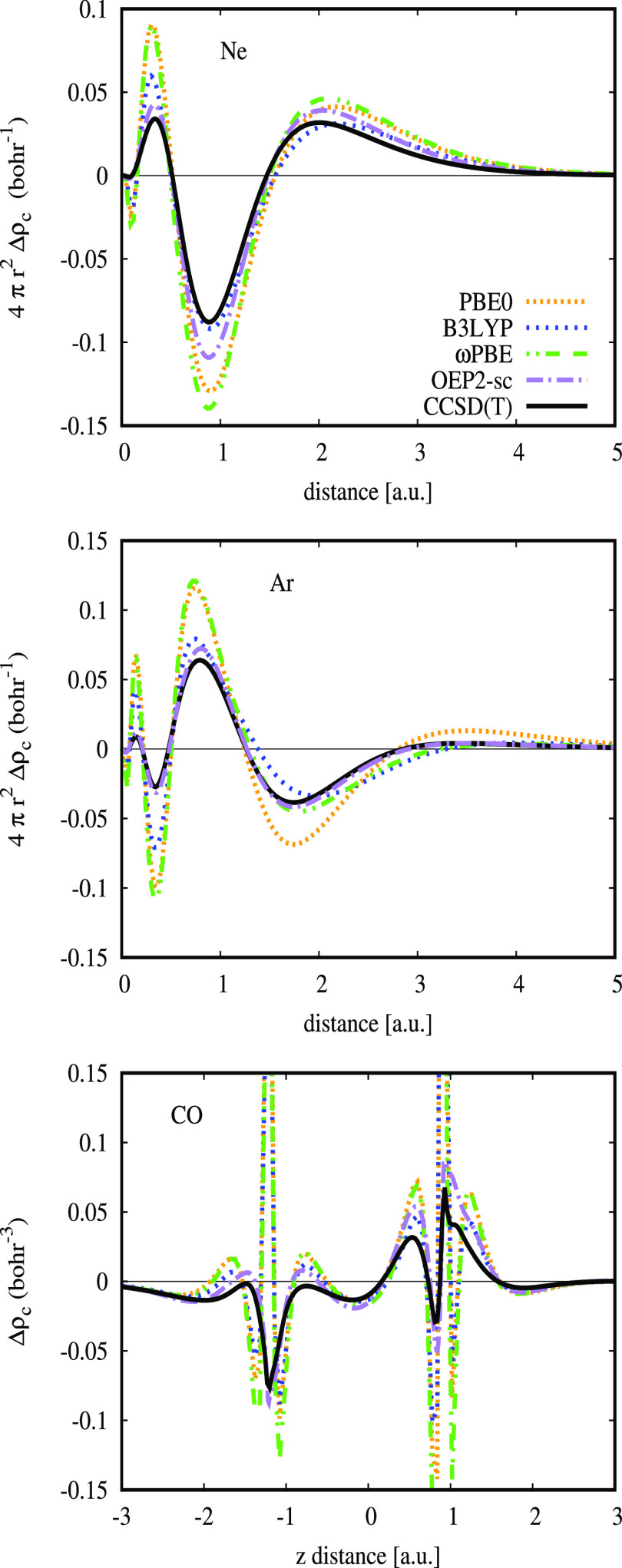
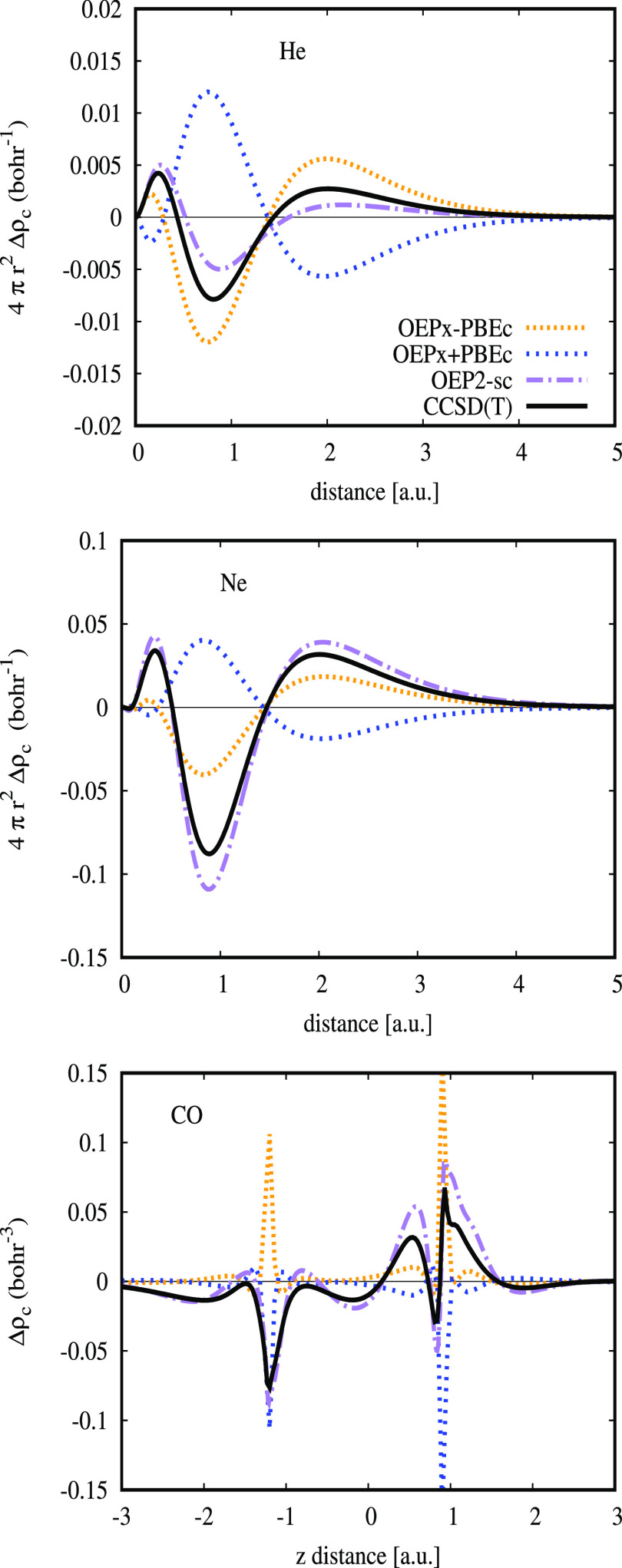
In Figure 3 we report the correlation densities^8,9,48 Δρ_c = ρ^method – ρ^EXX obtained for same systems. All hybrid densities are reasonably accurate everywhere, including the tail region. Overall, B3LYP slightly outperforms PBE0 and ωPBE for these systems being much more similar to reference CCSD(T) results.

Figure 3.

Correlation densities Δρ_c = ρ^method – ρ^EXX, of the Ne and Ar atoms and CO molecule for various methods. The reference CCSD(T) correlation density was calculated with respect to HF density as Δρ_c = ρ^CCSD(T) – ρ^HF.

As shown above for the case of PBE0 and ωPBE hybrids, the exchange potential difference 0.75(v_x^PBE – v_x) and v_x^sr,PBE – v_x, respectively, give the right phase of the correlation potential, almost inverting the v_c^PBE. Therefore, they can be seen as EXX compatible functionals in some sense.

In several works,^11,78−80 it has been observed that v_c^PBE is out of phase in comparison with the exact correlation potential. On the other hand, the −v_c exhibits similar features as shown in Figure 2. Thus, in the following, we combine v_x^OEPx with v_c, where we chose very simple test cases

9

with v_c^ACSC being the adiabatic connection semilocal correlation (ACSC) GGA potential of ref (78) which gives a correlation potential close to but smoother than the v_c one, as shown in Figure S5 of ref (33). We recall that the ACSC GGA correlation functional has been constructed from the modified interaction strength interpolation method.⁷⁸ Note that the GGA–OEPx correlation potential of eq 9 is a stray potential (is not a functional derivative of any correctly defined correlation energy functional), failing the line-integral test proposed in ref (81). This fact gives severe limitations, such as for electronic excitation calculations.⁸² However, most of model XC potentials that are very useful in DFT calculations (e.g., Becke–Johnson potential and its modifications⁸³⁻⁸⁵) are not functional derivatives.⁸¹

In Figure 4, we compare the correlation potentials of v_c^PBE and −v_c with high-level Ab Initio OEP2-sc method and the CCSD(T) reference curve. Indeed, v_c^GGA–OEPx can remarkably reproduce the features of the exact correlation potential, with the exception of the inherent GGA divergence at the nucleus. Nevertheless, comparing to the hybrid functionals behavior of Figure 2, we observe a less prominent description of the quantum oscillations, especially for the CO molecule, but with a better performance in the density tail region (the decay is similar to the one of ωPBE hybrid potential).

Next, in Figure 5, we show the correlation density Δρ_c(r) obtained from the self-consistent OEPx method combined with v_c^GGA–OEPx correlation potential (denoted as OEPx–PBEc/ACSC) and also (for comparison) with standard PBEc/ACSC potentials (denoted as OEPx + PBEc/ACSC). The OEPx–PBEc and OEPx–ACSC methods give the right shapes of the correlation densities (reported for ACSC in ref (33)) with exception of nucleus region, while both OEPx + PBEc and OEPx + ACSC fail badly. The compatibility between semilocal correlation functionals and the EXX is one of the most difficult DFT challenges.^{50,51,86−88} Even the sophisticated meta-GGA non-empirical correlation functionals, developed to satisfy many constraints of the exact correlation energy, do not perform better than simple GGAs for various molecular properties,^89,90 and the reason behind that seems to be intimately related to the shape of their OEP-based correlation potentials which basically is GGA quality.⁹¹ (In Figure S1 of ref (33), we show for Ne atom that the v_xc(92) of PBE GGA, TPSS meta-GGA, and SCAN meta-GGA agree closely. All these semilocal functionals give accurate densities,⁹³ see also Figure S2 of ref (33), because of a large error cancellation between exchange and correlation parts, as proved in Figure S3 of ref (33).). In this respect, we recall that very complex, non-local, and orbital-dependent hyper-GGA correlation functionals have been developed,^87,88 with the aim to be compatible with full EXX, but still they do not achieve good overall accuracy.

Figure 5.

Correlation densities for the He and Ne atoms and CO molecule. The reference CCSD(T) correlation density was calculated with respect to HF density as Δρ_c = ρ^CCSD(T) – ρ^HF.

To quantify the method accuracy, we consider several small atoms and molecules (He, Ne, Ar, H₂, He₂, HF, CO, Cl₂, N₂, Ne₂, HCl, H₂O, NH₃, and C₂H₆) used in our previous studies,^9,48 and we calculate

• the integrated correlation density differences (ICDDs) defined as

10

where δρ_c^method(r) = ρ^method(r) – ρ^xref(r), and xref denotes the corresponding exchange method. ICDDs provide a direct test of the quality of the correlation potential.^9,48 Note that δρ_c is a generalization of Δρ_c;

• the energy of the highest occupied molecular orbital (HOMO), and we compare it with the results from ref (47)

• the energy of the lowest unoccupied molecular orbital (LUMO), and we use the CCSD(T) results as reference values.⁹⁴

• the HOMO–LUMO gap energies, considering the CCSD(T) results as refs (94) and (95)

The full results are reported in ref (33), while in Table 1, we summarize them showing the error statistics. The v_x^OEP + v_c method gives a significant and systematic improvement over the v_x^OEP, v_x + v_c^GGA and PBE, for all the properties, but it is not as accurate as the high-level Ab Initio OEP2-sc method, with exception of the HOMO energies where it gives the best performance. The ACSC results are in line with the PBEc ones. Somehow, this was expected because the ACSC construction is based on PBE functional.⁷⁸ Similar trends can also be observed for HOMO and HOMO–LUMO gap energies (see Tables S5 and S6 of ref (33)) obtained with Becke–Johnson potential⁸³ combined with PBEc and v_c correlation potentials. This can be important from the standpoint of further application of the potential model in solid-state calculations.

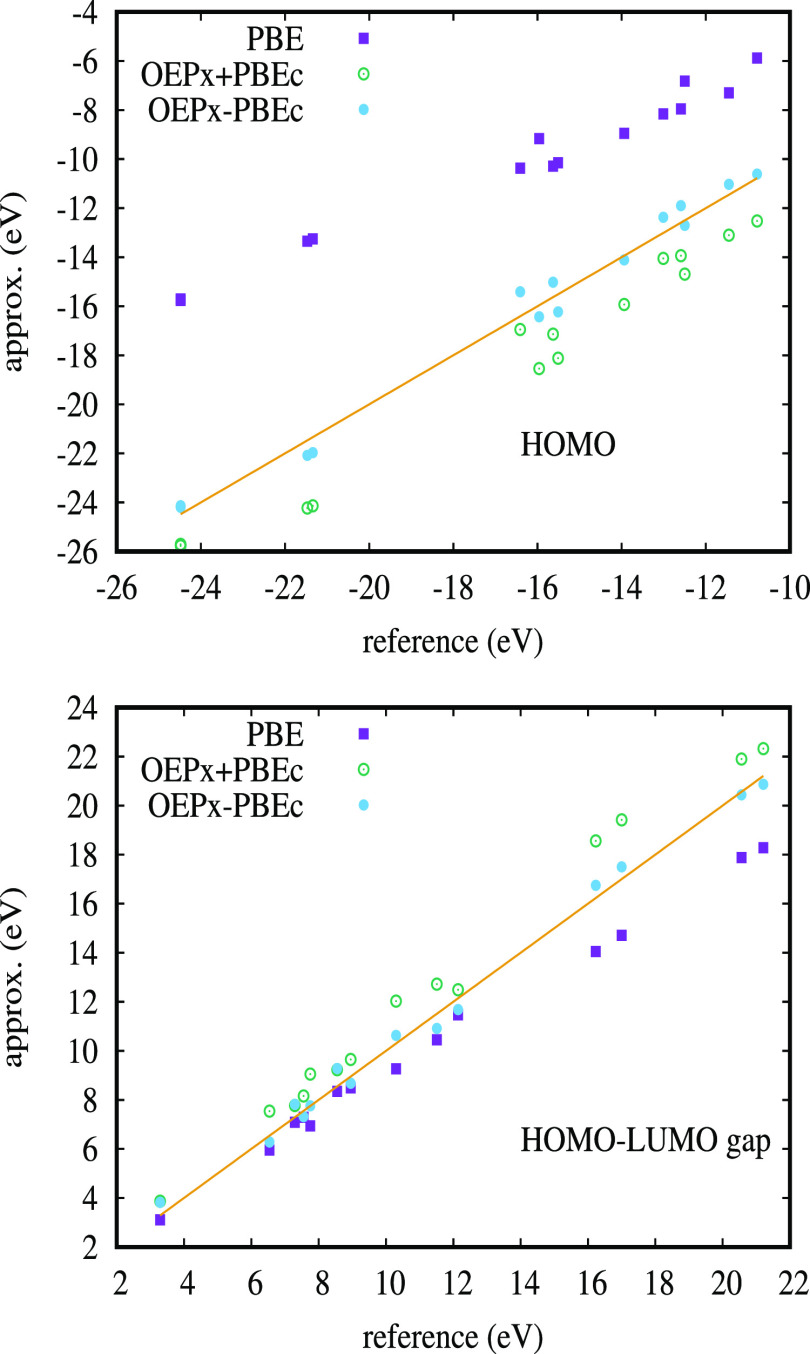
To assess in detail the performance of these functionals, we show in Figure 6 the correlation plots for HOMO and HOMO–LUMO gap energies, respectively, calculated with respect to reference data. For all the benchmark systems, OEPx–PBEc is remarkably accurate despite its simplicity.

Figure 6.

Correlation plots for HOMO energies (upper panel) and HOMO–LUMO gap energies (lower panel).

We note that even for the exact HOMO–LUMO gap energy, one needs to add the uniform shift Δ because of derivative discontinuity of the KS potential when the particle number changes, in order to obtain the band gap energy E_g.⁹⁶ The derivative discontinuity can be rigorously taken into account by perturbation theory methods⁹⁷ but can also be modeled by non-local potentials of the generalized KS, in both hybrid^98,99 and meta-GGA calculations,^84,85,100 and, to some extent, even by the semilocal GGA potentials.¹⁰¹

5. Conclusions

We have shown that the correlation potential/densities of the OEP-based hybrid functionals can reproduce the quantum shell oscillations of the high-level reference CCSD(T) correlation potential/densities, providing an alternative but very physical explanation on the success of this type of functionals. The presented analysis might shed some light on how to overcome some current DFT limitations and face challenges, as described in ref (102). Thus, for example, using the reverse engineering method, one can build more accurate hybrid XC functionals by fixing the functional parameters (e.g., the mixing fraction of EXX), eventually using the machine learning techniques,¹⁰³ to give the optimum OEP correlation potential.

We have also explained the error cancellation between the semilocal exchange and correlation functionals. Thus, as in the case of popular PBE GGA,¹⁴ even if both exchange (E_x) and correlation (E_c) energies are very accurate for a given system, still only the XC potential is realistic, while the correlation potential is out of phase. Based on these considerations, we have shown that the OEPx–PBEc potential method gives an outstanding performance in spite of its simplicity, showing accurate correlation densities and orbital energies.

Semilocal correlation potential models compatible with OEPx are of utmost theoretical and computational importance, having the ability to become the next generation method in electronic structure calculations.¹⁰⁴ The simplicity of the semilocal correlation potential combined with the almost-exact description of the many-electron self-interaction given by OEP EXX can be of high interest for solid-state applications.

In this sense, the here developed v_c^GGA–OEPx may open such a path, but more accurate potential models can be built considering exact conditions on correlation potentials (including derivative discontinuity problem^96,101), and right semilocal ingredients, such as the Laplacian of the density (∇²ρ), which is crucial for describing various quantum oscillations¹⁰⁵ and to impose exact properties in the bond and core regions.^106,107

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c04156.

• Data of all calculations and accompanying statistical analysis and additional figures and tables (PDF)

The authors declare no competing financial interest.