Advancing methodologies for applying machine learning and evaluating spatiotemporal models of fine particulate matter (PM_2.5) using satellite data over large regions

Abstract

Reconstructing the distribution of fine particulate matter (PM_2.5) in space and time, even far from ground monitoring sites, is an important exposure science contribution to epidemiologic analyses of PM_2.5 health impacts. Flexible statistical methods for prediction have demonstrated the integration of satellite observations with other predictors, yet these algorithms are susceptible to overfitting the spatiotemporal structure of the training datasets. We present a new approach for predicting PM_2.5 using machine-learning methods and evaluating prediction models for the goal of making predictions where they were not previously available. We apply extreme gradient boosting (XGBoost) modeling to predict daily PM_2.5 on a 1×1 km² resolution for a 13 state region in the Northeastern USA for the years 2000–2015 using satellite-derived aerosol optical depth and implement a recursive feature selection to develop a parsimonious model. We demonstrate excellent predictions of withheld observations but also contrast an RMSE of 3.11 μg/m³ in our spatial cross-validation withholding nearby sites versus an overfit RMSE of 2.10 μg/m³ using a more conventional random ten-fold splitting of the dataset. As the field of exposure science moves forward with the use of advanced machine-learning approaches for spatiotemporal modeling of air pollutants, our results show the importance of addressing data leakage in training, overfitting to spatiotemporal structure, and the impact of the predominance of ground monitoring sites in dense urban sub-networks on model evaluation. The strengths of our resultant modeling approach for exposure in epidemiologic studies of PM_2.5 include improved efficiency, parsimony, and interpretability with robust validation while still accommodating complex spatiotemporal relationships.

Introduction

The spatial distribution of ground-level fine particulate air pollution, including particulate matter with an average diameter less than 2.5 microns (PM_2.5), is complex due to the interactions of sources, topography, and atmospheric conditions. Statistical prediction approaches often combine data capturing putative sources and proxy exposure metrics, including satellite remote sensing retrievals of aerosol optical depth (AOD), in reconstructing concentrations of PM_2.5 (Bernardo S Beckerman et al., 2013; Di et al., 2016; Hu et al., 2017; Just et al., 2015; Kloog et al., 2014; Sampson et al., 2013; van Donkelaar et al., 2015). Our group has developed multiple models including statistical models integrating remote sensing with land use regression predictors using random effects and interpolation approaches (Just et al., 2015; Kloog et al., 2014; Sarafian et al., 2019). Additional approaches have included partial least squares (Sampson et al., 2013), geographically weighted regression (Hu et al., 2013), and use of chemical transport models (van Donkelaar et al., 2015). Increasingly, exposure scientists have been utilizing more flexible machine-learning approaches such as tree-based random forests (Hu et al., 2017), gradient boosting (Just et al., 2018; Reid et al., 2015), support vector machines (Stafoggia et al., 2017), and neural networks (Di et al., 2016). The adoption of prediction algorithms from the field of machine learning has been driven by apparent increases in predictive performance attributed to the ability to accommodate broader sets of covariates and complex relationships in space-time (Di et al., 2016; Hu et al., 2017; Reid et al., 2015). However, without adequate care for the structure of the data, these methods are prone to overfitting in areas with denser monitoring coverage (adopting values from nearby monitoring sites with limited use of covariates) and data leakage (inadvertent use of testing data in model fitting), which can lead to an overly optimistic assessment of model performance. Importantly, flexible models that are fit without considering the spatial structure of the underlying phenomenon will appear to have substantially lower prediction errors than the same approaches fit with consideration of underlying dependence, and this difference is evidence of overfitting.

Our review of the current literature on algorithmic prediction of air pollution led to a concern that some of the gains in the reported performance of these recent studies are overly optimistic. Just as new machine-learning tools have advanced the complexity of our models, new approaches and refinement are needed in the evaluation of model performance. Performance of prediction models is evaluated on data that have been withheld from training. Evaluating models on random subsets of the data (e.g. cross-validation in which the dataset is randomly divided into folds without regards to which monitor or region they come from) may give inappropriate estimates of model performance due to spatiotemporal autocorrelation. Algorithmic models such as gradient boosted trees and neural networks have so many parameters that they can memorize the structure of exposed training data rather than encoding physical relationships with predictors that generalize to new contexts (e.g. locations of participants in health studies).

In our view, the value of a model that predicts ground observations of PM_2.5 using satellite data is that it can make predictions for locations that are far away from monitoring sites. The Northeast USA has many such remote locations in rural regions, far from the denser network of monitors found in some urban areas. But when random cross-validation folds are chosen such that two observations from the same monitor, or two monitors that are close together, can appear in different folds, the accuracy of such predictions is not well tested. For most observations, the model will have a close nearby monitor in its training data. In extreme cases, it can “predict” the held-out observation by just copying another observation from across the street on the same day without reliance on the other predictors in the model. That is, the model evaluation would reward overfitting in which the flexible model memorizes the spatiotemporal non-independence in the dataset rather than learning more complex yet generalizable relationships encoded in the features. One of the aims of the current study was to develop and compare the impact of evaluation metrics that account for this structure in applying flexible machine-learning approaches.

Another tradeoff in building statistical models for air pollution predictions is in the number and diversity of predictor variables, particularly given the limited number of unique monitoring sites with which to build these models. Previous approaches have varied widely in model building strategies. Some leading prediction models that utilize algorithms that can incorporate many weak predictors can include >100 covariates with varying spatial and temporal resolution (Di et al., 2016; Sampson et al., 2013). Others have used feature selection including the step-wise deletion-substitution-addition algorithm (Bernardo S. Beckerman et al., 2013), or have used feature importance measures (Di et al., 2019). While predictive performance may not suffer from the inclusion of largely redundant features, advantages of constructing a more parsimonious model include improved interpretability and scalability for updating and iteratively improving these models in the future.

We present a parsimonious 1×1 km daily model for PM_2.5, constructed via a hybrid satellite gradient boosting machine-learning model. We employ new machine-learning tools such as tree dropout with DART (Vinayak and Gilad-Bachrach, 2015) to avoid overfitting. Our model evaluation strategy carefully reflects the spatial structure of the ground monitoring network and compares traditional approaches (random cross-validation) with our novel spatial cross-validation. Finally, we utilize Shapley Additive Explanations (SHAP) (Lundberg et al., 2018) for feature selection and interpretation of our resulting PM_2.5 predictions, offering a versatile variable importance metric. The methods and results we present here may help future air pollutant modeling efforts to simultaneously take advantage of the strengths of machine-learning approaches while avoiding the dangers of flexible learning.

Methods

Study domain

The study area included all mid-Atlantic and New England states to cover the Northeastern region of the USA (Figure 1).

Figure 1.

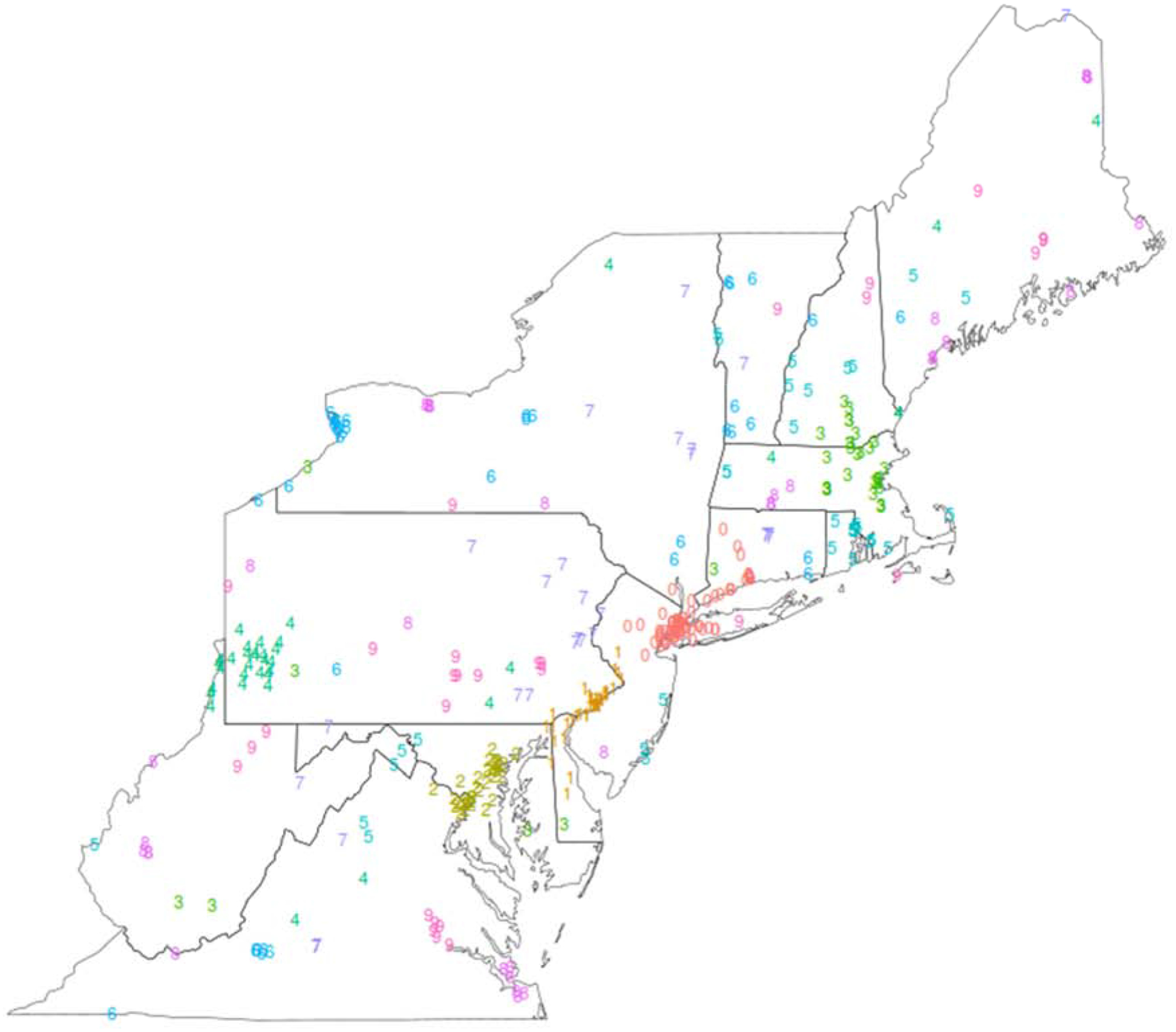
Study area in the Northeastern USA. PM_2.5 monitoring sites are clustered spatially and assigned to 10 separate folds shown with distinct numeral labels and colors.

We included the District of Columbia and the 13 states of Connecticut, Delaware, Maine, Maryland, Massachusetts, New Hampshire, New Jersey, New York, Pennsylvania, Rhode Island, Vermont, Virginia, and West Virginia. The study period spanned 15 years from 2000-02-24 (when AOD data from the Terra satellite are first available) to 2015-12-31. The study area included 627,255 1×1 km grid cells.

Satellite AOD data

We used our reprocessed version of the MAIAC retrieval algorithm (Lyapustin et al., 2018, 2011) which provides a 1×1 km resolution AOD estimate from MODIS instruments on both Aqua and Terra satellites. The MAIAC data from MODIS Terra and Aqua represent a late morning and early afternoon measurement, respectively. We previously used an XGBoost model with 52 predictor variables, including MAIAC quality assurance, retrieval geometry, AOD spatial patterns, and land use, to reduce measurement error in MAIAC AOD (Just et al., 2018). This algorithmic correction versus overservations from the Aerosol Robotic Network (AERONET) of sun photometers, which does not utilize any ground measurements of particulate matter, decreased the root mean squared prediction error 43% for Aqua and 44% for Terra on withheld AERONET observations. The resulting corrected-MAIAC dataset included at least one satellite AOD observation for 30% of all possible site-days with PM_2.5 observations, which is consistent with our previous work in the New England region (Kloog et al., 2014).

PM_2.5 monitoring data

Data for daily PM_2.5 mass concentrations across the Northeast region (see Figure 1) for the years 2000–2015 were obtained from the U.S. Environmental Protection Agency (EPA) Air Quality System (AQS) precomputed daily summary files. Because each monitoring site may contain multiple instruments reporting measurements for PM_2.5, the best available value was selected by prioritizing the designated primary monitor, or if not available, prioritizing Federal Reference Method (FRM) or Federal Equivalent Method (FEM) values; prioritizing filter-based measures over continuous monitors; and finally selecting the lowest available parameter occurrence code (POC; an index on instrument). To maximize the spatial and temporal coverage of the monitoring dataset, we used daily measures from non-FRM/FEM devices (parameter code 88502) if no FRM/FEM data were available, substantially increasing the number of unique locations and days with ground monitoring data.

While PM_2.5 data were retained regardless of exceptional event flags or the length of time that an instrument had reported data, one outlying value was dropped from a non-FRM collection on an atypical monitor that far exceeded all regional values (209.9 μg/m³). In addition, one site proximal to a large point source (the Clairton Coke Works in western Pennsylvania) was dropped as our previous work has shown that the monitor values are highly atypical (Just et al., 2018). When more than one monitoring site in the same 1×1 km grid cell reported PM_2.5 on the same day (and thus would share all covariate values), we retained only the measure from the site with the most available daily measures (dropping n=4,533 site-days between 2000–2015). There were 388 monitoring sites in the resulting Northeast US dataset during the study period, for which EPA designated 41% as urban and city center, 39% as suburban, and 19% as rural (n=2 sites not reporting). In total the cleaned daily PM_2.5 dataset included 692,306 observations, of which 76% were FRM/FEM (parameter code 88101), and 68% were from filter-based integrated 24-hour measurements versus 24-hour block averages reported from continuous monitors.

Selected Predictors

Inverse Distance Weighted (IDW) PM monitoring surface:

To create a daily surface of the PM_2.5 data coming from the monitors, we used inverse-distance weighting (IDW), either unmodified or as a feature provided to another model. To make an IDW prediction of PM_2.5 for a given point, we computed the mean of the observations available on the same day, weighted by the reciprocal of the squared distance to the point in question. To avoid overfitting from proximal monitoring sites and to avoid leakage (where data from the test set are used in training), observations were excluded from the IDW calculation if they were in the same cross-validation fold as the given point, or if they were in the currently held-out (testing) fold. Thus, for each day a total of 9*10=90 IDW surfaces were calculated.

Percentage of Developed Area:

We used the United States Geological Survey (USGS) National Land Cover Dataset (NLCD) from 2011 (Homer et al., 2015), available as raster files with a 30 m spatial resolution. We calculated the percentages of all categories of developed area in each 1×1 km grid cell across the study area.

Planetary Boundary Layer Height:

We used publicly available 3-hour estimates on the height of the planetary boundary layer (PBL) obtained from the North America Regional Reanalysis (Mesinger et al., 2006). The spatial scale of the data was 32 × 32 km. Estimates were averaged to each 24 hour period and assigned to the study grid without interpolation. The height of the boundary layer may vary with wind speed, influencing the concentration and vertical profile of pollutants (Oke, 2002). The boundary layer not only controls transport and location of pollutants and aerosols but also their concentrations would be different in variable boundary layer structures (Angevine et al., 2013).

Other spatial/temporal predictors:

Because a feature selection approach (described below) found that a parsimonious model with 8 covariates was able to predict PM_2.5 as well as a model with many more covariates, we present detailed methods for the full set of spatial/temporal predictors in the Supplemental Materials. Additional derived 1×1 km resolution predictors were included in the initial model but ultimately not selected for the final model: elevation, local topography, road density, percentages of land use according to 11 other NLCD land use categories, meteorological estimates, normalized difference vegetation index, point emissions for PM_2.5, and characteristics of the PM_2.5 monitor measurement (FRM/FEM 88101 versus non-FRM/FEM 88502 data, and 24-hour integrated versus block-averaged measures from continuous sensors).

Statistical Methods

Predictive model fits were evaluated primarily with the root mean square error (RMSE) to aid in the comparability of performance metrics across subsets of the data (e.g. by year) and in comparison with other models in other regions. The improvement afforded by each model can be seen by comparing the RMSE with the standard deviation (SD) of the relevant set of AQS ground station observations which represents the relevant variability in PM_2.5 air pollution that our model seeks to explain. We also computed the R², calculated as 1 minus the mean square error divided by the variance (rather than the square of the correlation coefficient between predictions and observations).

XGBoost modeling

Most of our models are based on extreme gradient boosting (Chen and Guestrin, 2016). XGBoost works by building an ensemble of regression trees, like a random forest. Unlike random forests, which fit all trees independently, XGBoost uses the residuals of the first n trees to build the (n + 1)st tree. It also uses several types of regularization, each controlled by its own tuning parameter, and it chooses split directions for missing values of predictors (such as AOD observations missing due to clouds or snow) as part of its training. We trained our XGBoost models with DART (Vinayak and Gilad-Bachrach, 2015), a method of temporarily dropping randomly selected trees, which has been shown to increase the contributions of later trees and decrease overfitting in order to obtain good accuracy with fewer trees.

For each XGBoost ensemble, we used 100 trees with mean square error as the objective function, and we enabled the one_drop option to DART (so that at least one tree is dropped in each round of training). We allowed six tuning hyperparameters to vary: η, γ, λ, α, the maximum tree depth, and DART’s dropout rate. Each time we trained an XGBoost model, we ran 50 rounds of an inner cross-validation to evaluate 50 different vectors of hyperparameters, and chose the one with the lowest RMSE. Our hyperparameter tuning strategy incorporates a stochastic random search (rather than a grid search), but ensures an efficient exploration of the hyperparameter space by generating combinations of hyperparameters that are far apart from each other in the six-dimensional hyperparameter space using Latin hypercube sampling. This inner cross-validation used 2 folds, which were constructed as aggregates of the 9 training folds available at the current stage of the outer cross-validation scheme. When there was no outer cross-validation to fit the full model, we constructed the 2 folds from all 10 folds of the spatial cross-validation scheme that is described below.

Comparing model evaluation strategies

To appropriately assess model accuracy, even in areas far from denser, urban groups of monitors, we developed a rigorous spatial cross-validation scheme, such that any two monitors sufficiently close together were assigned to the same fold (Figure 1). First, we grouped monitors into spatial clusters, such that any two monitors within a prespecified threshold distance were placed in the same cluster. We set the threshold at 31 km, the median distance from all 1-km grid centroids to the nearest monitor; thus, the minimum distance between clusters is representative of the distance from the nearest monitor in out-of-sample prediction. We defined the clusters by applying single-link hierarchical clustering and cutting the tree at a height equal to the threshold distance. Note that this approach does not require prespecifying cluster centers or the number of clusters. Then, we assigned these clusters to 10 folds with a greedy algorithm that considered clusters in order of decreasing size (in terms of number of total daily observations) and put each cluster in the fold that was so far the smallest, breaking ties randomly. The resulting cross-validation structure (“Spatial CV”) emulates the need to evaluate model performance for populations that do not live directly next to a monitor by excluding from training all proximal monitor-level information for each location.

We evaluated the spatial cross-validation strategy and the potential for overfitting by comparing it with other cross-validation strategies. In the 2009 data, we compared the accuracy of our full XGBoost model as estimated by Spatial CV to its accuracy as estimated by two simpler and commonly used strategies. For “Site-wise CV”, we kept all observations from a given monitoring site in the same fold, but we randomly assigned monitoring sites to folds without regard for distance to other sites. For “Random CV”, we assigned observations to ten folds randomly and independently, regardless of monitoring site. We hypothesized that the less strict cross-validation strategies would show evidence of overfitting with apparently improved accuracy.

Because the layout of monitors is uneven, with many more observations coming from dense urban networks than remote areas, estimates of overall accuracy (like RMSE) will predominantly reflect performance in more densely monitored areas rather than sparsely monitored (rural and suburban) areas. To offset this, we constructed a spatially weighted evaluation, in which each observation’s error was divided by the number of observations in the same day and spatial cluster, making each cluster of equal weight regardless of density of monitors.

Comparing models

To evaluate the predictive value of a model with the complexity of XGBoost, we compared our model to two simpler models and evaluated them with the same cross-validation schemes. On the 2009 data, we compared our XGBoost model with an IDW of PM_2.5 sites alone and a linear regression model using the same predictors as the XGBoost model. To handle missing AOD, we augmented the linear-regression model with dummy variables for AOD missingness, and set the missing values themselves to 0.

The contributions of each feature to cross-validated predictions were quantified with Shapley Additive Explanations (SHAP) values (Lundberg et al., 2018). These SHAPs are an additive feature attribution measure to interpret complex machine-learning models. Each SHAP is the contribution of each feature to a specific individual prediction; for PM_2.5, the contributions are in units of μg/m³. Specifically, the SHAP for a given predictor and a given observation is the difference in the output, i.e. a predicted PM_2.5 concentration, if the model is fit with or without the predictor. For each observation, the sum of all SHAPs, plus the bias term (which is the overall mean PM_2.5 concentration in the training data), equals the prediction from the XGBoost model. The resulting matrix of SHAPs can be summarized to understand how a predictor contributes to the predictions. The mean absolute SHAP across all observations summarizes the overall contribution of each feature, and more local model interpretation is possible through exploratory data visualization, such as scatterplots of individual predictors versus their SHAPs.

Feature selection

As with many other complex machine-learning methods, XGBoost’s performance is not impaired very much by the inclusion of uninformative features, so long as it is tuned appropriately. Still, removing features that do not appreciably improve predictions makes a model easier to interpret and easier to use. There were six predictors that were included in all multi-variable models based on the data structure and a priori knowledge from our previous research: longitude, latitude, and date to reduce spatial and temporal autocorrelation in prediction errors, height of the PBL, and Aqua and Terra AOD satellite measures. We examined the contribution of each of 38 additional features (including meteorological and land use terms commonly used in land use regression) with a backwards stepwise scheme. After a model with all features was fit with spatial CV on the 2009 data, and its spatially weighted RMSE was computed, we removed the feature with the least mean absolute SHAP. Then we refit the model with the remaining features and continued the process.

Predictions across the whole study area

For making predictions out to arbitrary days and grid cells, we trained the final model with all observations of PM_2.5. For consistency and to avoid overfitting with the IDW predictor, for grid cells whose distance to the nearest monitoring site was less than or equal to the clustering threshold, we computed the IDW predictor holding out all observations in that nearest site’s spatial fold. For all other grid cells, we did not hold out any observations. We used R 3.6.0 (R Core, 2019) with data.table 1.12.2 (Dowle and Srinivasan, 2019) and xgboost [commit f2277e7 Dec 3, 2019] (Chen et al., 2019) for analysis.

Results

The mean of all available PM_2.5 measurements in the Northeast during the study period was 10.54 μg/m3 with a SD of 7.07 μg/m³ and an interquartile range of 8.00 μg/m³.

Comparing cross-validation strategies

We clustered the 387 PM_2.5 monitoring sites using the previously mentioned 31-km threshold. The result was 91 clusters, 52 of which include only 1 site, and the three largest having 75, 40, and 36 sites, corresponding to New York City, Philadelphia, and the greater Baltimore-Washington D.C area. Finally, these clusters were assigned to ten spatial folds. For the year 2009, the resulting spatial folds had 3,591 to 11,743 observations; for the full 2000–2015 period, the spatial folds had 60,301 to 130,200 observations. In the study-area map (Figure 1), each monitoring site is numbered with its fold in the latter set of folds.

In the 2009 data, we examined the accuracy achieved by XGBoost models under different cross-validation approaches. Random CV appeared to have the best performance (suggesting substantial overfitting when the model training includes observations from other dates at testing sites), followed by Site-wise CV, in which the model training includes data from nearby monitoring sites, and then Spatial CV, in which the model training mimics a lack of nearby monitoring sites. The unweighted RMSEs are 2.10 μg/m³ for Random CV, 2.63 μg/m³ for Site-wise CV, and 3.12 μg/m³ for Spatial CV. With spatially weighted evaluation (such that denser subnetworks are not more important than rural subnetworks), error further increases, but the performance gap between cross-validation strategies shrinks, with RMSEs of 2.45 μg/m³ for Random CV, 2.94 μg/m³ for Site-wise CV, and 3.22 μg/m³ for Spatial CV. Importantly, even in the case of Spatial CV with spatial weighting, the RMSE represents a substantial improvement over the SD of PM_2.5, which is 5.74 μg/m³, or 5.69 μg/m³ with spatial weighting. Values of R² are 0.87 for Random CV, 0.79 for Site-wise CV, and 0.70 for Spatial CV.

We also examined weighted training, in which observations were weighted during training with the same scheme as for weighted evaluation. This change had little effect on model performance (results not shown).

Figure 2 shows how per-monitor RMSEs appear lower under Site-wise CV than Spatial CV especially when the monitor in question is close to another monitor.

Figure 2.

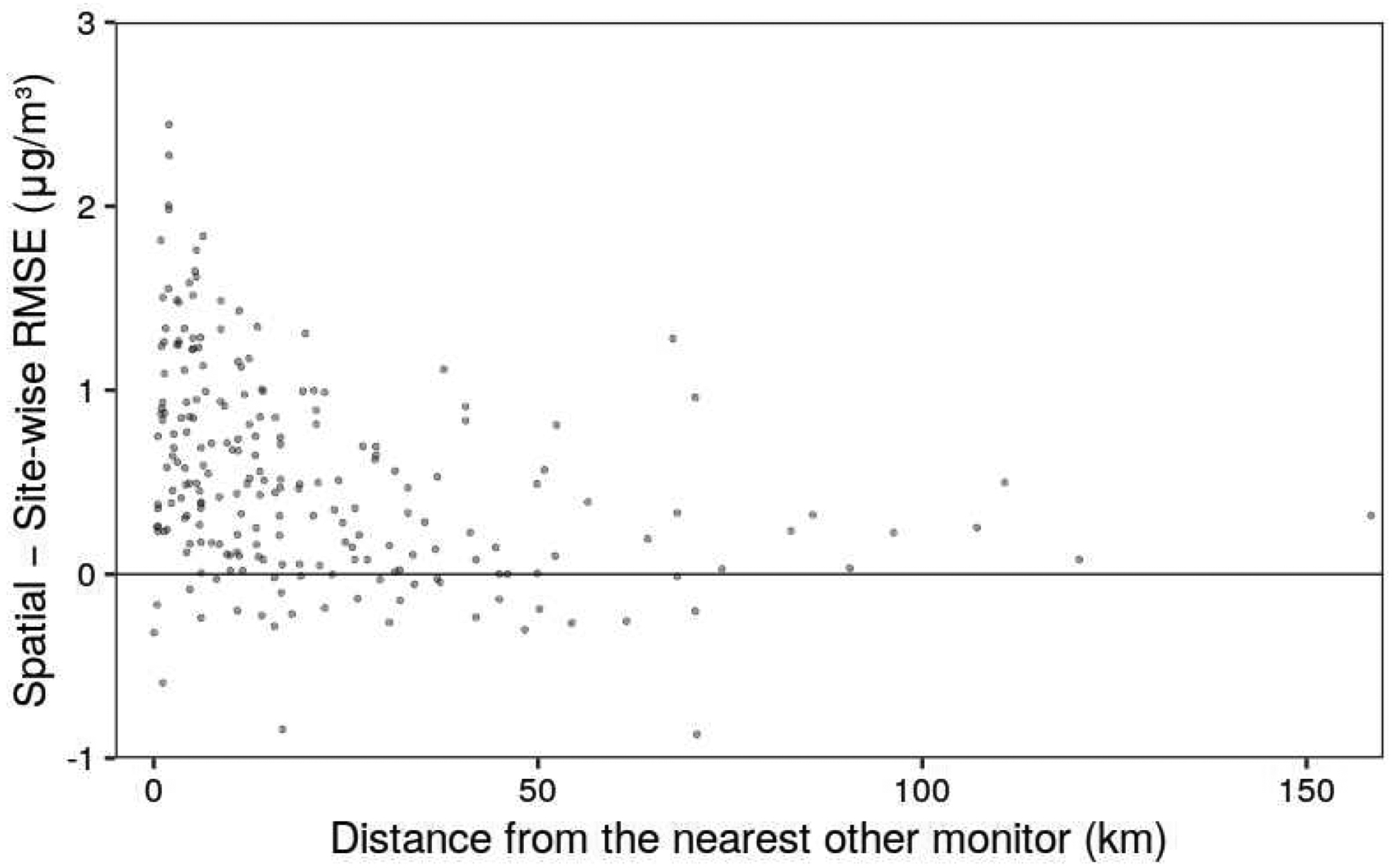
The difference in RMSE for 2009 observations, grouped by monitor, between predictions under Site-wise CV and Spatial CV strategies. Greater positive values mean greater accuracy under Site-wise CV. Monitors with less than 50 observations in 2009, and an outlier at (0.53 km, −3.51 μg/m³), are not shown.

XGBoost versus other modeling approaches

We also compared our model with simpler modeling approaches. Using spatial cross-validation with weighted evaluation, a daily IDW surface achieved a RMSE of 3.57 μg/m³ and a linear regression model with the same covariates achieved a RMSE of 3.35 μg/m³, compared to the XGBoost RMSE of 3.22 μg/m³ and the weighted SD of 5.69 μg/m³.

Feature selection

To develop a more parsimonious and interpretable model, we implemented a recursive feature selection in the dataset for the year 2009 (Figure 3)

Figure 3.

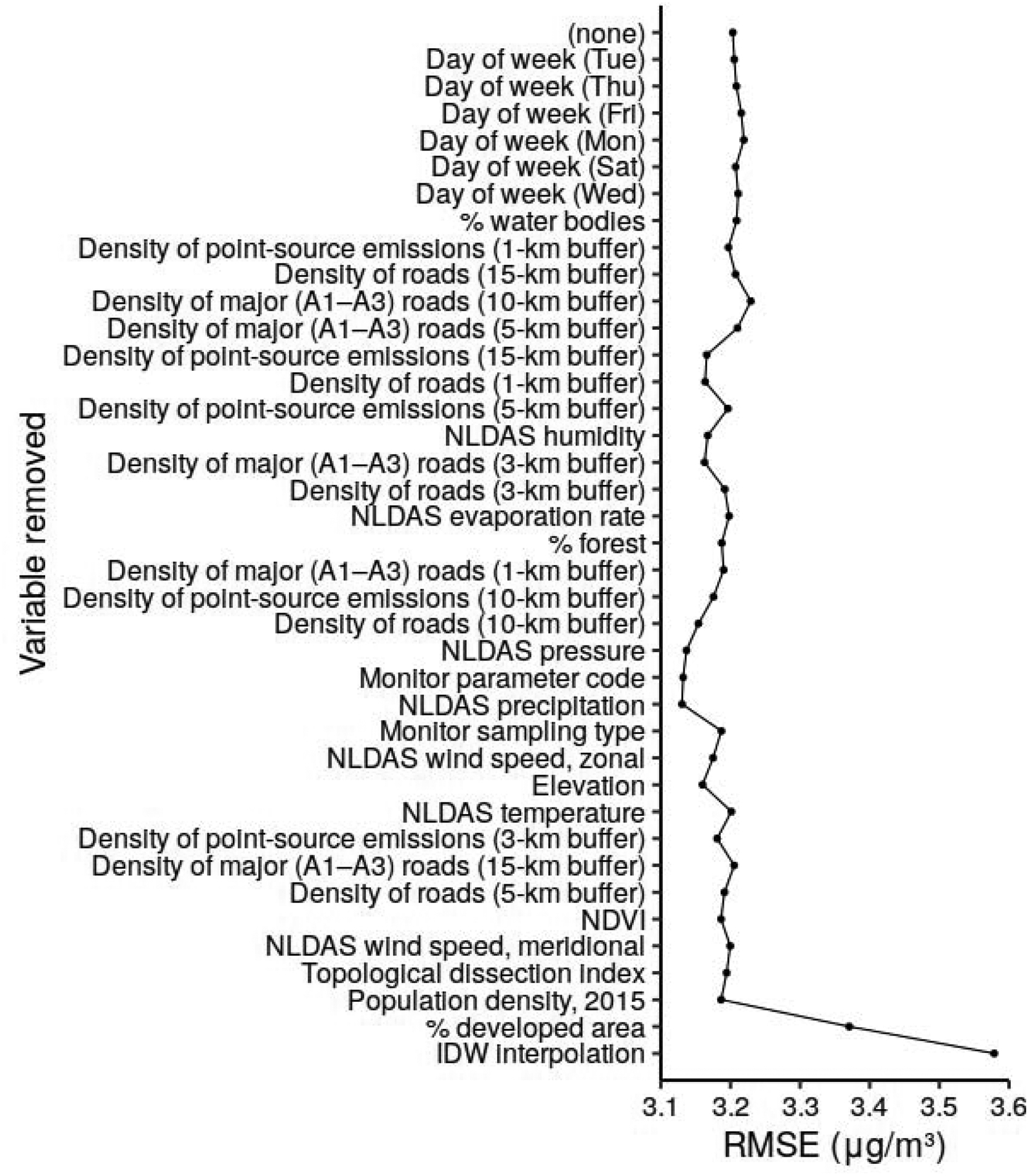
Cross-validation RMSE in the year 2009 model using recursive feature selection. Labels show the variable dropped at each step (top to bottom) based on the smallest mean absolute SHAP.

As shown in Figure 3, few features beyond the base six were needed to achieve the performance of the model with all features. The proportion of developed area and daily IDW interpolation (the last two features to be dropped) are clearly helpful; each reduces the RMSE by about 0.2 μg/m³. The other features have noisy effects that bring the RMSE from 3.19 μg/m³ with daily IDW and proportion developed area to a minimum of 3.13 μg/m³ with larger sets of variables. On the basis of these results, we chose to retain only the daily IDW and the proportion developed area, in addition to the preselected features of longitude, latitude, date, height of the PBL, and the corrected MAIAC AOD for Aqua and Terra, for a total of eight predictors.

Multi-year results

Using the parsimonious model, we cross-validated our XGBoost model on the full multi-year dataset (2000–2015). Supplemental Table S1 shows the hyperparameters that were selected in each fold. The 688,724 observations had a weighted SD of 6.93 μg/m³. We obtained a weighted RMSE of 3.56 μ g/m³, and an R² of 0.76 under our rigorous spatial cross-validation. Table 1 shows model performance when stratifying predictions by year. We emphasize the importance of the RMSE to describe model performance across datasets - our model improves (lower RMSE) in more recent years, but the R² worsens as the SD decreases faster than RMSE in more recent years. Figure 4 shows how the RMSE in 2015 varies over space.

Table 1.

An assessment of cross-validated predictions of the final model using Spatial CV, stratified by year.

Year	R2	SD	RMSE	R2, spatial	RMSE, spatial	R2, temporal	RMSE, temporal
2000	0.72	8.16	4.36	0.67	1.58	0.72	4.05
2001	0.76	8.75	4.27	0.70	1.50	0.77	4.03
2002	0.78	9.41	4.42	0.72	1.39	0.79	4.21
2003	0.78	8.51	4.00	0.72	1.42	0.79	3.75
2004	0.77	7.81	3.76	0.74	1.35	0.78	3.49
2005	0.76	8.37	4.14	0.74	1.51	0.76	3.89
2006	0.80	7.90	3.52	0.66	1.52	0.81	3.23
2007	0.76	7.84	3.87	0.68	1.56	0.77	3.59
2008	0.73	6.51	3.39	0.68	1.31	0.74	3.15
2009	0.70	5.74	3.12	0.62	1.27	0.72	2.85
2010	0.76	6.32	3.08	0.69	1.25	0.77	2.84
2011	0.70	5.98	3.25	0.67	1.31	0.72	2.96
2012	0.68	5.13	2.91	0.63	1.13	0.69	2.67
2013	0.71	5.27	2.85	0.58	1.14	0.73	2.57
2014	0.64	4.95	2.97	0.50	1.50	0.66	2.64
2015	0.68	5.20	2.93	0.58	1.24	0.70	2.66

Figure 4.

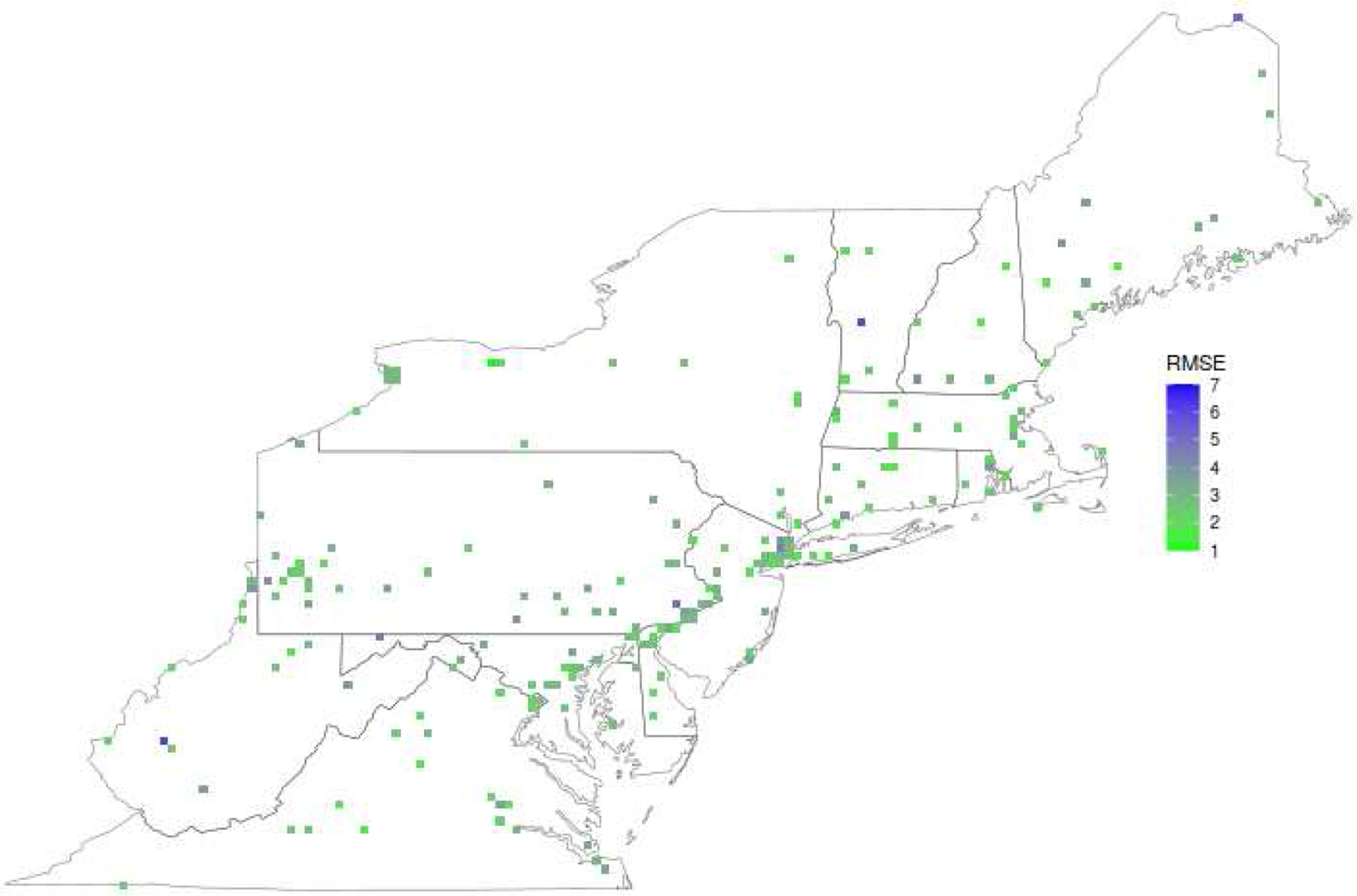
Unweighted RMSE across the study area in 2015, aggregated into 0.1° × 0.1° squares for data visualization.

Our model included EPA AQS non-regulatory observations (parameter code 88502) in the dependent variable at monitoring site-days without regulatory PM_2.5 observations (parameter code 88101), making up 24% of all cases. To evaluate if our model performance was worse when using this expanded set of observations, we stratified our cross-validated predictions by parameter code. Among regulatory observations, the weighted SD was 7.09 μg/m³ whereas the RMSE was 3.58 μg/m³. Among non-regulatory observations, the SD was 5.96 μg/m³ whereas the RMSE was 3.46 μg/m³. Thus, performance was slightly better among non-regulatory observations, likely due to a lower SD.

Predictions across the whole study area

Finally, we refit our XGBoost model to the entire dataset in order to make daily predictions across the whole study area for use in health study applications. Figure 5 shows the mean annual predicted PM_2.5 value at each grid square throughout 2015.

Figure 5.

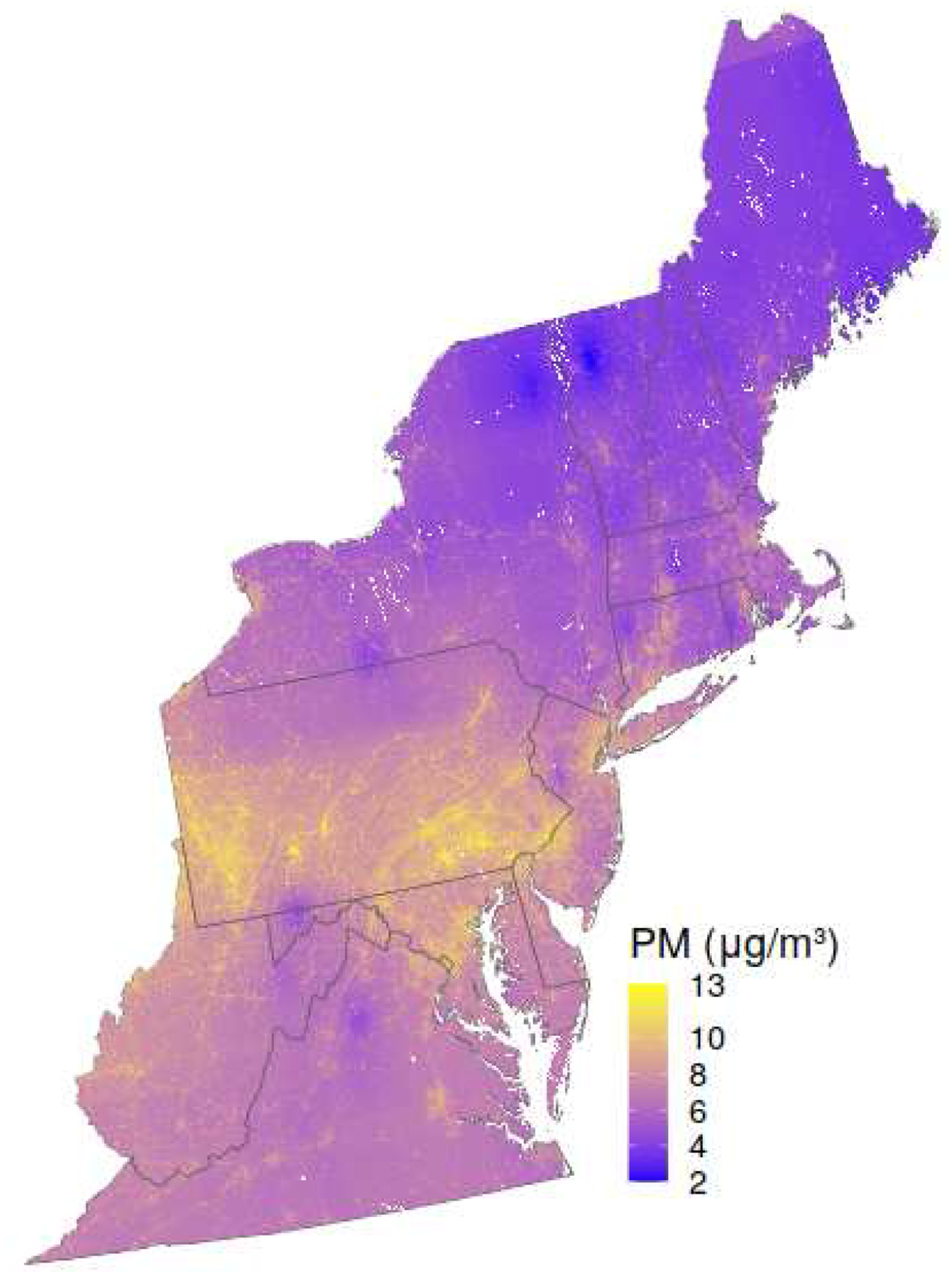
Annual average PM_2.5 for the year 2015 across the full Northeastern USA study area.

Figure 6 zooms in on New Jersey and compares the 2015 means to the 2005 means and shows the well-documented regional decrease in PM_2.5 seen across this period of time (Chan et al., 2017).

Figure 6.

Annual average PM_2.5 estimates over the New Jersey region in 2005 and 2015.

Interpreting model fits

We calculated SHAPs for the contribution of each feature to each prediction in order to generate exploratory visualizations. In the Northeastern US, a low AOD more consistently contributes to a lower PM_2.5 prediction (SHAP < 0), while higher AOD values (>0.25) correspond to higher SHAPs but with a substantially more diffuse point cloud (Figure 7). We also examined whether the relationships between predictors and their SHAPs (the contributions to the predictions) varied by site. Using a subset of 59 monitoring sites with at least 100 days of collocated PM2.5 and Terra AOD, we plotted a histogram of the Pearson correlation coefficient of the AOD and the SHAPs which were strongly positive but also varied substantially from site to site (Figure 8).

Figure 7.

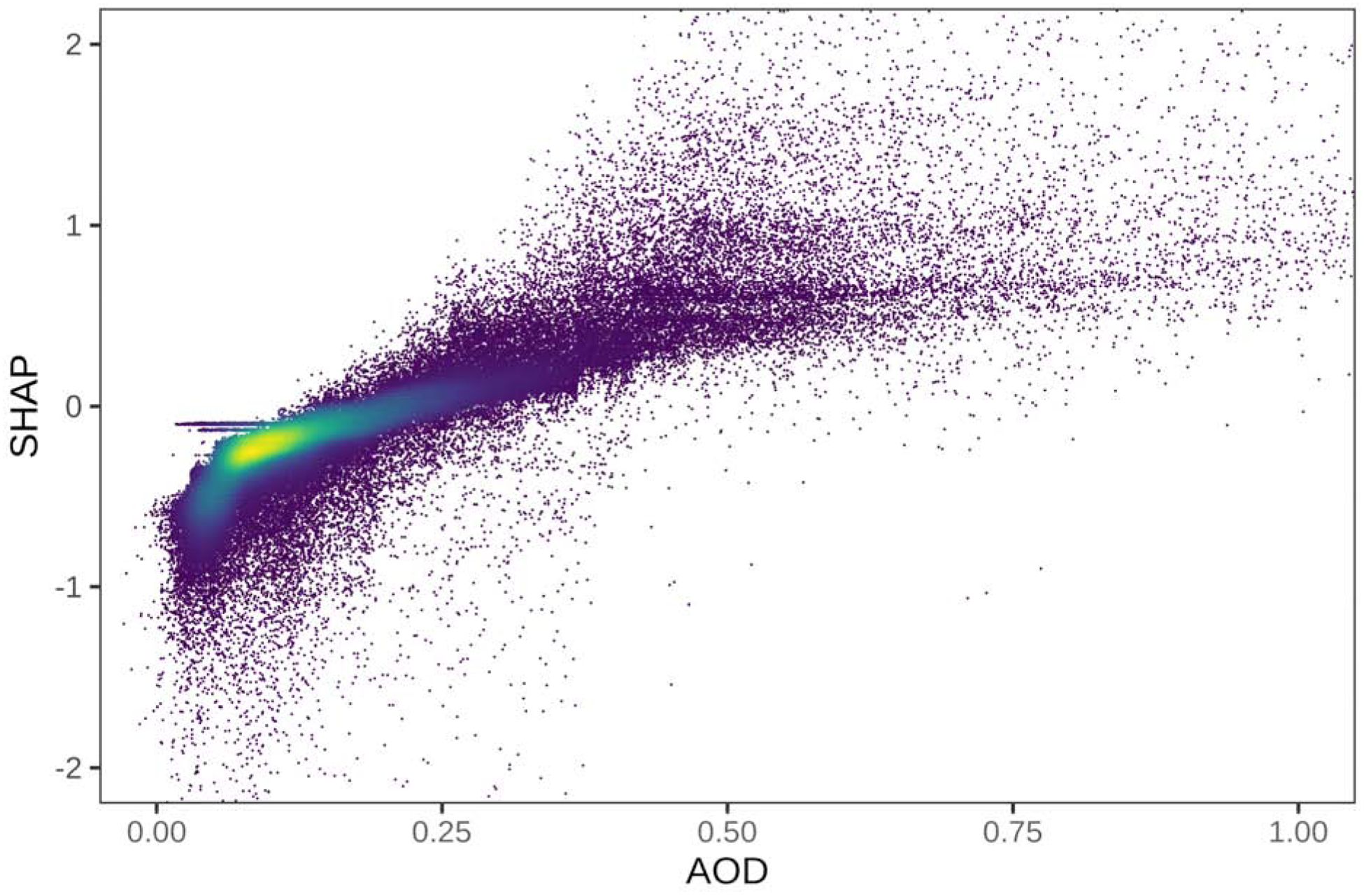
Scatterplot of the non-missing MAIAC AOD from Terra versus the SHAP contribution to the XGBoost prediction model for all sites for all days. The density of points is indicated by color.

Figure 8.

Histogram of the per-site Pearson correlations between non-missing Terra AOD values and corresponding SHAPs for 59 sites with at least 100 non-missing values in 2015.

Discussion

Prediction models such as those estimating air pollution exposures need to be evaluated with care to avoid overfitting in order to provide accurate and unbiased exposure predictions for health studies. Similarly, the use of large numbers of minimally informative covariates within highly parameterized algorithms leads to complex and inefficient models that are computationally expensive and hard to interpret. With the increasing use of flexible and highly parameterized machine-learning methods, issues of overfitting are amplified because learning algorithms will incorporate any form of data leakage in evaluating model fit, while training data for spatio-temporal phenomena like PM_2.5, that are strongly associated with time and space.

Advancing the field of air pollution prediction modeling requires reevaluating our approaches - not just looking for the highest reported R². For environmental epidemiology studies using these types of prediction models to assign exposures, the error in the prediction is more relevant to estimating health impacts rather than the overall fit of the exposure model (where R² can increase just by modeling a larger space-time region with more overall variation). In addition, the main purpose for air pollution prediction models is to estimate concentrations in areas lacking monitors. Because most PM_2.5 monitors are in dense and largely urban sub-networks, other models missing an explicitly spatial approach to cross-validation are overstating their overall performance and may not be evaluating their performance in more sparsely monitored areas. A novel contribution of this study is the consideration of the impact of uncritical cross-validation within our model. This includes a random cross-validation that ignores the structure of the data entirely and leads to overly optimistic assessment of model performance after learning site-specific biases, a site-wise cross-validation that emulates prediction at new locations but ignores the tendency of models to copy nearby values, and a spatial cross-validation that stringently evaluates performance in new areas that are not near other monitors. We show in Figure 2 that the apparent greater performance (lower RMSE) due to overfitting of the site-wise versus spatial cross-validation is greater at sites that are closer to their respective nearest other site. Furthermore, we adopt a weighted evaluation to compensate for the larger proportion of data coming from denser subnetworks of monitoring sites. We demonstrate a large impact of these approaches on model performance measures (RMSE and R²) as evidence of overfitting when using flexible machine-learning approaches like XGBoost. The adoption of spatial cross-validation and careful consideration of the structure of the training data may lead to less overly optimistic measures of model performance.

To advance the field of air pollution prediction modeling, we focused on constructing a flexible yet parsimonious model for computational efficiency and interpretability of the resulting fits. While many machine-learning algorithms handle additional predictors, there are still important benefits to more parsimonious models for scalability of generating and organizing the predictor datasets and interpretability of the contributions of the component predictors. We incorporate several specific methods to constrain our modeling in order to preserve parsimony. First, because XGBoost iteratively refits on residual error, we incorporate random tree dropout with DART (Vinayak and Gilad-Bachrach, 2015) which has been shown to decrease over-specialization and results in similar performance of models with many fewer rounds (100 versus 10,000+ without DART). Secondly, we avoid overfitting in model tuning by conducting our hyperparameter tuning within a nested cross-validation (without exposing testing data). Finally, we apply feature selection using a recently developed measure of variable importance (mean absolute SHAP) to select a top-performing feature subset for our final model.

Compared with previous regional PM_2.5 models, we include a substantially larger set of monitoring data for PM_2.5 24-hour concentration from the EPA AQS which are used both as predictors (in our inverse distance weighted surfaces) and outcome measures that are predicted by the model. Specifically, we included regulatory (parameter code 88101) measures and also used non-regulatory (parameter code 88502) observations for site-days without available regulatory measures, with the latter making up 24% of our training data. In a sensitivity analysis, we demonstrate that cross-validated predictions were similar for these non-regulatory measures, supporting their inclusion to expand monitoring coverage. The use of a larger set of ground monitoring data, alongside our robust cleaning of other covariates, including MAIAC AOD (Just et al., 2018), contributes to our confidence in these results. Because we propose a more stringent and spatially explicit evaluation of prediction model fits, our summaries are not easily compared with previously published PM_2.5 models.

In spite of their impressive predictive performance, machine-learning algorithms including XGBoost are often criticized as “black box” models that lack interpretability. We use SHAP values to quantify and visualize complex relations captured in our model (Lundberg et al., 2018). For example, our SHAP plots provide new context on the contribution of satellite AOD (a measure that integrates the entire atmospheric column) when an IDW of surface PM_2.5 is also available approximating local conditions. Our scatterplot of AOD values versus their SHAP contribution to PM_2.5 predictions shows that a low AOD more consistently contributes to a lower predicted surface PM_2.5 concentration (as there are lower concentrations of aerosols anywhere in the atmospheric column), while higher AOD (>0.2) makes a diffuse contribution to predictions of ground-level concentrations that is more dependent on complex interactions (such as with PBL). When summarizing the SHAPs by site, we saw strong positive correlations between non-missing AOD and the SHAP contribution to the prediction that varied substantially from site to site. Although we constructed our SHAP values from the spatial cross-validation using withheld data, the variation from site to site is further support for the idea that the XGBoost model incorporates sufficient complexity to approximate site-specific associations. This may lead to overly optimistic assessments of model fit without careful cross-validation. Concurrent with the decrease in average PM_2.5 concentrations across the Northeast during the 16-year study time period, we also compared the fits of our annual models to each other. While the RMSE has been decreasing, indicating an improvement with lower prediction error in more recent years, the proportion of the total variance explained (R²), which is commonly reported to summarize overall fits of exposure models, is also going down (getting worse). As average PM_2.5 concentrations decreased over the study period (2000–2015) in response to air quality regulations, the proportion of the PM_2.5 distribution that is explained by less predictable stochastic variation has increased with dampening of the seasonality and the contribution of larger regional pollutant trends.

Like all prediction models for environmental pollutant concentrations, our model has some limitations. The highly performant predictive modeling algorithm (XGBoost) that we employed requires more expertise with model training versus parametric and semi-parametric models or even related but simpler predictive algorithms, such as random forests, that have many fewer tuning parameters. In addition, we have not yet evaluated how well our modeling approach that explicitly divides up training data based on their spatial pattern would apply in different regions that may have a very different spatial structure in their distribution of ground monitors (e.g. more uniformly distributed or far more sparse). Finally, we use information about time and space as predictors in our model which means that while our approach is an important advance on completing spatio-temporal exposure matrices for a given time-space domain, it is not appropriate for hindcasting/forecasting outside of the time period used in training nor can we directly apply this model to new regions that are outside the training area.

Our model joins a growing set of daily PM_2.5 prediction models for the United States that utilize satellite AOD and machine-learning approaches to advance exposure assessment for health applications. For example, Hu et al. applied a Random Forest (Hu et al., 2017), and Di et al. used artificial neural networks (Di et al., 2016) and ensembles of multiple machine-learning models (Di et al., 2019). These machine-learning hybrid models join a larger body of literature combining chemical transport models or land use regression approaches to estimating PM_2.5 over large regions of the USA (van Donkelaar et al., 2015; Wang et al., 2018).

Our daily 1×1 km resolution PM_2.5 model has excellent performance, although we demonstrate that good metrics are harder to achieve when carefully considering the goals of evaluating predictions from satellite-based hybrid models in areas that are not near existing monitors. Strengths of our model include improved efficiency, parsimony, and interpretability while still accommodating complexity and robust validation without overfitting.

Highlights:

• Flexible machine-learning models can estimate fine particulate PM_2.5 concentrations

• Models require spatial cross-validation or else are assessed overly optimistically

• Gradient boosting with a small number of predictors creates excellent predictions

• New daily 1 km model for health studies in Northeastern USA 2000–2015