Updated Software for Automated Assessment of Glucose Variability and Quality of Glycemic Control in Diabetes

Abstract

Background: Glycemic variability is an important factor to consider in diabetes management. It can be assessed with multiple glycemic variability metrics and quality of control indices based on continuous glucose monitoring (CGM) recordings. For this, a robust repeatable calculation is important. A widely used tool for automated assessment is the EasyGV software. The aim of this work is to implement new methods of glycemic variability assessment in EasyGV and to validate implementation of each glucose metric in EasyGV against a reference implementation of the calculations.

Methods: Validation data used came from the JDRF CGM study. Validation of the implementation of metrics that are available in EasyGV software v9 was carried out and the following new methods were added and validated: personal glycemic state, index of glycemic control, times in ranges, and glycemic variability percentage. Reference values considered gold standard calculations were derived from MATLAB implementation of each metric.

Results: The Pearson correlation coefficient was above 0.98 for all metrics, except for mean amplitude of glycemic excursion (r = 0.87) as EasyGV implements a fuzzy logic approach to assessment of variability. Bland–Altman plots demonstrated validation of the new software.

Conclusions: The new freely available EasyGV software v10 (www.phc.ox.ac.uk/research/technology-outputs/easygv) is a validated robust tool for analyzing different glycemic variabilities and control metrics.

Introduction

People with type 1 diabetes (T1D) face a lifelong challenge to effectively manage glucose and minimize pre- and postprandial hyperglycemia while avoiding hypoglycemia.¹ Glucose profiles in T1D can greatly differ even among people with HbA1c values approaching target, suggesting that glucose variability is an important component of dysglycemia.² Reduction of glucose variability by addressing the risk of hypo- and hyperglycemia is a target in diabetes treatment, while variability has been associated with endothelial insult leading to macro- and microvascular complications,^3–6 neuropathy,⁷ retinopathy,³ atherosclerosis,⁸ kidney disease,⁹ cardiovascular disease,¹⁰ and impairment of cognitive function.¹¹

Continuous glucose monitoring (CGM) provides immediate feedback on the glucose concentration, and on the magnitude, direction, and rate of change of glucose in real time.¹² These measurements enable direct assessment of the dynamics of glycemic fluctuations, and calculation of variability metrics can give an objective reflection of homeostasis.

Numerous indices for the evaluation of glycemic variability are currently available, including coefficient of variation (CV), mean amplitude of glycemic excursions (MAGE), continuous overlapping net glycemic action (CONGA), mean absolute glucose (MAG), and the mean of daily differences (MODD). Likewise, quality of glycemic control indices such as the M-value, Glycemic Risk Assessment in Diabetes Equation (GRADE), and the J-index; and the glycemic risk metrics such as low blood glucose index (LBGI), high blood glucose index (HBGI), and the average daily risk range (ADRR) have also been described, although the J-index is a more robust measure of hyperglycemia by virtue of its tight correlations with HBGI, GRADE%_hyper, and the hyperglycemia index.¹³ Assessment of these measures has been implemented and made freely available in the EasyGV tool.^14,15

Newer metrics for the assessment of glycemic control based on CGM data have been defined for use in clinical practice and in the research setting. The personal glycemic state (PGS) is a composite index that assesses four domains of glycemic control: mean glucose, glycemic variability, time in range, and frequency and severity of hypoglycemia¹⁶; the Index Glucose Control (IGC) transforms glucose values into a “score” with an adjustable weight assigned to hypoglycemic values relative to hyperglycemic values¹⁷; and the glucose variability percentage (GVP) has been defined.¹⁸

All of these indices have been used in clinical research, but are not easy to derive, and a validated platform is needed to make their calculation simpler and to ensure homogeneity of calculation and reporting.

EasyGV¹⁵ is a user-friendly software application developed in visual basic and enabled in an Excel (Microsoft) workbook, which calculates glycemic variability metrics and quality of glucose control indicators from CGM data. This software platform was chosen as clinicians and researchers are familiar with it and it is intuitive, simple, and available across multiple platforms. EasyGV has 195 citations and 1719 downloads to date (correct in 2019).

Previously, EasyGV derived values for the followings metrics: mean, standard deviation (SD), CONGA, Lability Index (LI), J-index, LBGI, HBGI, GRADE, %GRADE-hypo, %GRADE-hyper, %GRADE-Eu, MODD, MAGE, ADRR, M-VALUE, and MAG, but had not been cross-validated against a reference method. Moreover, the previous versions of EasyGV do not include the implementation of the newest abovementioned metrics.

Several other glucose variability calculators are available—GlyCulator,¹⁹ The MAGE computer program,²⁰ The Glycemic Variability Analyzer Program (GVAP),²¹ and CGManalysis²²—that facilitate calculation of some, but not all, of the existing glycemic variability metrics. Table 1 summarizes their main features. EasyGV provides the most comprehensive and accessible assessment; we have therefore implemented the newer methods of glycemic variability assessment in EasyGV and have sought to validate implementation of each EasyGV metric against a reference implementation of the calculations.

Table 1.

Features of the Main Glycemic Variability Calculation Tools That Are Available in Literature

Glycemic variability calculation tools	Features
	Metrics available	Environment	Open source
EasyGV	Mean, standard deviation, CONGA, Lability Index, J-index, LBGI, HBGI, GRADE, %GRADE-hypo, %GRADE-hyper, %GRADE-Eu, MODD, MAGE, ADRR, M-value, and MAG.	User-friendly software application developed in visual basic and enabled in an Excel (Microsoft).	Yes
	Times in ranges, PGS, IGC, GVP, have been included in the last version (EasyGV v10).
GlyCulator19	Standard deviation, %CV, MAGE, weighted average of glucose values, J-index, MODD, CONGA, fractal dimension.	There are two available versions: Web-based application and installable application.	Yes
The MAGE computer program20	MAGE	Software program	Yes
GVAP21	Average area above/below target range, percentage spent above/below target range, CONGA, MODD, MAGE, excursion frequency, MAGE.	Software application developed with MATLAB	Yes
CGManalysis22	Sensor use, eA1c, GMI, median, quartiles, SD, CV, minimum/maximum, excursions above and below threshold, times in ranges, area under curve, MAGE, J-index, CONGAn, MODD, LBGI, HBGI.	Implemented in R	Yes

ADRR, average daily risk range; CGM, continuous glucose monitoring; CONGA, continuous overlapping net glycemic action; CV, coefficient of variation; GIC, Index Glucose Control; GMI, Glucose Management Indicator; GRADE, Glycemic Risk Assessment in Diabetes Equation; GVAP, Glycemic Variability Analyzer Program; GVP, glycemic variability percentage; HBGI, high blood glucose index; LBGI, low blood glucose index; MAG, mean absolute glucose; MAGE, mean amplitude of glycemic excursions; MODD, mean of daily differences; PGS, personal glycemic state.

Methods

EasyGV feature expansion

Three novel variability and quality of glucose control metrics—IGC,¹⁷ PGS,¹⁶ and GVP¹⁸—were included in the new version of EasyGV software v10. The mathematical formulae were taken from their original publications for inclusion in the updated version of the software. The following times in ranges have also been added: percentage of time below 50 mg/dL, 54 mg/dL, 70 mg/dL, and Th mg/dL; percentage of time in range 70—140 mg/dL, 70–180 mg/dL, and Th1–Th2 mg/dL; and percentage of time above 180 mg/dL and Th, where Th, Th1, and Th2 are customizable thresholds. A summary of the improvements carried out in EasyGV software v10 is included in Supplementary Figure S1.

MAGE calculation

The original description of the derivation of MAGE²³ has led to various interpretations of how to translate this into a computed algorithm. Indeed, there are several algorithms with small differences in their implementations.^24,25 The MAGE calculation in EasyGV software v10 was carried out according to the original description as follows. Glycemic excursions exceeding 1 SD were included and the direction of calculation was established by the direction of the first excursion (peak-to-nadir or nadir to-peak). Then, MAGE was implemented as this formula describes:

$$MAGE\left(mg∕dL\right)=\frac{\sum AGE}{n}$$

where AGE is the amplitude of glycemic excursions and n is the number of glycemic excursions greater than 1 SD.

The MAGE calculation procedure is summarized in the following main steps:

• 1.Determination of all local maximum and minimum values across the glucose recordings.
• 2.Evaluation of the maximum/minimum pair values with the 1 SD criterion.
• 3.If the difference between the maximum/minimum pairs is greater than 1 SD, the value is included in the global summation. If it is not, the pair difference value is disregarded.

Validation and data analysis

CGM data from 30 participants (10 adults, 10 adolescents, and 10 children) in the JDRF CGM study (http://diabetes.jaeb.org/Dataset.aspx) were selected at random to validate each variability and quality glucose control index in EasyGV v10. This sample size allows differences of 10 mg/dL in the MAGE calculations to be identified between the reference standard and EasyGV v10 outcomes with 95% confidence and with 80% power.

Validation was carried out by comparison between the outcomes from MATLAB implementation and the outputs of EasyGV v10. MATLAB implementation of each metric was based on the original publications; hence, the results obtained with this algorithm were considered the reference values for the EasyGV v10 validation.

The reference standard for MAGE calculation remains the manual “pencil and ruler” approach. Therefore, validation was performed comparing MAGE manually calculated by an expert clinician (M.G.) with the outcomes of the MAGE-MATLAB code. In this case, CGM data from 10 participants only were used, with the duration of data for each participant at least 60 days.

The considered metrics in the updated EasyGV software v10 are as follows: mean; SD; CV; CONGA²⁶; LI²⁷; J-index²⁸; LBGI and HBGI²⁹; GRADE³⁰ and the risk attributable to hypoglycemia and hyperglycemia from GRADE values (%GRADE-hypo, %GRADE-hyper); MODD³¹; MAGE²³; ADRR²⁹; M-value³²; MAG³³; IGC¹⁷; PGS¹⁶; GVP¹⁸; percentage of time between 70 and 140 mg/dL, and between 70 and 180 mg/dL; percentage of time below 50, 54, and 70 mg/dL; and percentage of time above 180 mg/dL.

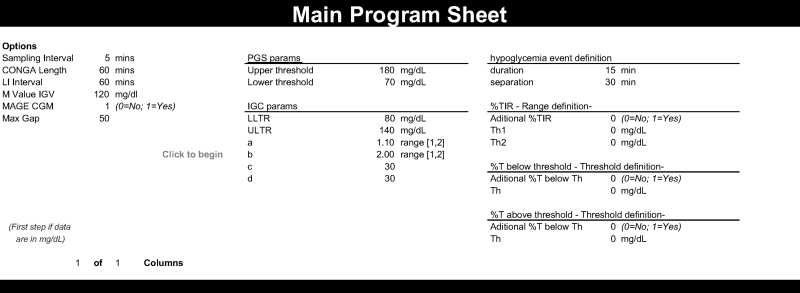
In EasyGV software v10, the user can change the interval used for CONGA; the default is 60 min or CONGA1, and this was used for the analysis. The LI period can also be changed; the default is 60 min, and this was used in this analysis. For M-value calculations, the ideal glucose value can be set. The default of 120 mg/dL was used here. In the IGC, the upper and lower limits of target range (ULTR and LLTR, respectively), the exponents (a, b), and the scaling factors (c, d) are customizable. The default values were used in this analysis (ULTR = 80 mg/dL; LLTR = 140 mg/dL; a = 1.10; b = 2; c = 30; d = 30). In PGS, the upper and lower thresholds are configurable. For this analysis, 180 and 70 mg/dL were used for the upper and lower thresholds, respectively. Finally, the user can calculate additional times above, below, and within ranges.

Where there are missing CGM data, periods without glucose values that are longer than the defined “Max Gap” are considered gaps. Linear glucose interpolation can be included when the duration of missing data is less than the predefined Max Gap. This point is important when the CGM recordings are large since calibration periods or sensor changes could add error to the calculations.

Statistical analysis

Results were analyzed using Pearson correlation to assess the consistency of the measurements made by both implementations (MATLAB software and EasyGV v10). Furthermore, Bland–Altman plots for each metric were obtained to show the error of EasyGV v10 against the MATLAB reference values. A P-value of <0.05 was considered to indicate statistical significance.

Results

Addition of new metrics

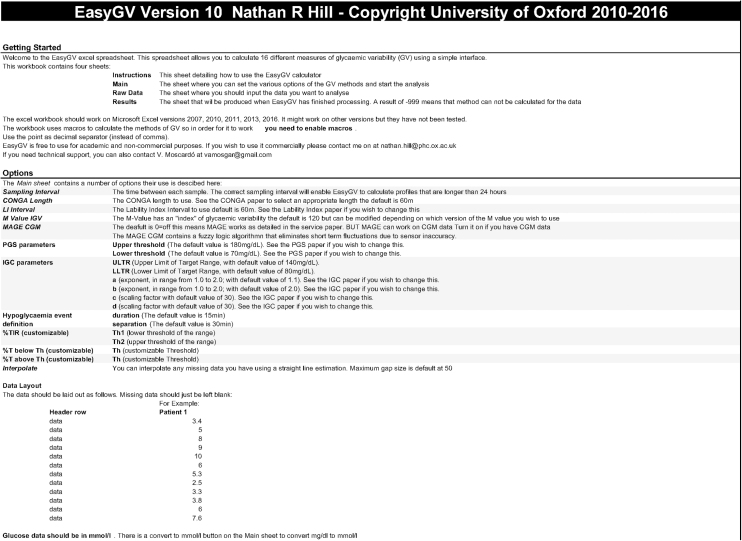
The implementation of PGS, IGC, and GVP in addition to times in ranges and the hypoglycemia event detection function, needed for PGS calculations, was successfully undertaken. Figure 1 shows the instruction page (a) and main interface (b). The default values of the tuning parameters for each metric are seen. It is important to note that parameters a and b in IGC can only have values between 1 and 2.

FIG. 1.

Appearance of the Instructions sheet (top) and the Main sheet (bottom).

To use EasyGV v10, CGM data are copied into the Raw Data sheet. If glucose values are in mg/dL, the mg/dL >mmol/L from the “main” sheet has to be pressed before commencing the analysis. The Max Gap has to be defined. Depending on the defined max gap, the program will interpolate the data for each missing sample time, or it will analyze the raw data when the period without data is longer than the defined max gap time. The results are displayed in the “Results” sheet.

Validation

Manual MAGE versus MAGE-MATLAB

The analysis shows that there is consistency in the measurements made by both methodologies (MATLAB and manually) measuring the same metrics (r = 0.9856 with a 95% confident interval 0.9423–0.9967, P < 0.0001). The mean difference is −0.0616 mmol/L, and the Bland–Altman plot for the mean differences shows randomness of the mean difference distribution.

Based on these results, the MAGE-MATLAB implementation and the MAGE manual are equivalent. Therefore, the subsequent validation of EasyGV v10 with the MATLAB implementation is feasible.

EasyGV validation

All the correlations calculated for each metrics were 0.98 or better, except for MAGE where the Pearson correlation coefficient was 0.87. The statistical analysis is shown in Supplementary Tables S1 and S2 with correlation plots between the reference and EasyGV metrics for all assessed glucose outcomes. The value of r approaching 1.0 across all evaluated metrics demonstrates that the implementation of EasyGV corresponds with the original and referenced definition of each one implemented in MATLAB.

Discussion

The new metrics (PGS, IGC, GVP, and times in ranges) were successfully incorporated into EasyGV v10 and robust validation against reference, and in the case of MAGE, manual analysis.

The small discrepancies in the correlation analyses were not significant and may reflect the differing methods that each software uses to round the number of decimals considered to complete the calculations. For example, the discrepancies in GRADE may result from the decimal differences in the value of the double logarithmic function by both implementations. This error is then carried forward in the calculation of the several risk GRADE percentages. The same occurs with the PGS since this metric is obtained by means of the sum of four functions, and these functions have several further functions within their definition.

Of particular interest is the MAGE validation since, to date, the gold standard technique for this metric's estimation has been the manual pencil and ruler approach. Our software has been validated and has been shown to be comparable with the manual method. The small variance seen is due to the preprocessing of the temporal signal. The EasyGV v10 and MATLAB software implementations follow slightly different techniques to filter the noise, further explaining the differences seen, but the nadir and peak detection were equivalent.

In addition, validation results for our MAGE implementation are similar to the results showed by other software in the literature (Fritzsche,²⁰ GlyCulator,¹⁹ and GVAP),²¹ which have been implemented to calculate MAGE. A comparative study²⁵ showed varying agreement among the available computer programs developed and validated to calculate MAGE. MAGE derived with EasyGV may differ from the values obtained with other calculators and it would therefore be interesting to compare the results that EasyGV v10 provides with the results obtained with other software, along with the manual method, quantifying and identifying the sources of such differences where feasible. Of special interest is the comparison with Baghurst's algorithm,²⁴ which has previously been assessed in a small data set with short CGM periods and implemented in R resulting in a complete R package,^22,24 but has not been validated against the pencil and ruler method.

Other calculators for a variety of variability metrics have been described. In addition to the variety of metrics considered, the main difference between the GlyCulator and our approach is the consideration of the missing data. EasyGV v10 considers a gap when there is lack of data during at least the minutes defined as a max gap by the user (50 min is considered the default). However, the other software applies a linear interpolation. This approach may add some small errors in large CGM data sets. Fritzsche's MAGE computer program has been assessed with short CGM recordings (72 h) from a predominantly type 2 diabetes cohort only. Finally, both GlyCulator and GVAP consider fewer parameters and fewer that are customizable by the user than in EasyGV (e.g., the n value for CONGA).

For optimal use of EasyGV, it is important to carefully check the data and correctly configure glucose units and the sampling frequency, as incorrect settings may give erroneous results. This is a weakness of the spreadsheet format and would be improved by implementing EasyGV 10 in solutions with direct access to raw glucose data, such as the Tidepool platform.

In addition, sampling times without glucose values should be entered in the spreadsheet as an empty cell to ensure robust results. The maximum duration of missing data for interpolation can be defined in the main spreadsheet of EasyGV (by default, it is defined as 50 min). If gaps are greater than this threshold, data are considered internally as a new fragment of data, and interpolation is not carried out. Not including time stamps in the spreadsheet is a further limitation of the EasyGV design but would increase complexity.

Another important point to consider is the upper and lower limit of CGM data, which are different depending on the different manufacturers. If glucose values are outside of the limit of detection, the sensor gives the saturation value (e.g., <2.2 mmol/L). In these cases, values are considered constant at the saturated value (e.g., 2.2 mmol/L) until the glucose values return to the working region of the sensor. Different limits of detection may bias some reported values in EasyGV. There are several approaches to this issue. The simplest approach is to leave the data at the saturated value and report only those metrics unaffected by the potential differences, such as times above and below ranges, which sit wholly within the continuous reporting range of the sensor. A second approach would be to replace values out of range with empty cells and report as missing data, which will avoid biasing metrics of variability but may sacrifice the accuracy of times in ranges. Finally, a third approach would be to undertake a sensitivity analysis when analyzing such data to assess the effect of either truncating the data or using the saturation point value.

Glucose variability assessment in T1D patients has become more relevant with the advent of continuous data and literature supporting its role in the pathogenesis of diabetes complications. The reduction of glucose variability is a potential therapeutic target, and therefore, robust reproducible measurement is critical. The calculation of GV metrics is time-consuming, has not been standardized, and is resource-intensive. EasyGV v10 facilitates calculation to support glucose control evaluation and treatment. In the present work, a successful EasyGV v10 validation has been carried out as well as the incorporation of new indices and times in ranges. EasyGV v10 is, therefore, an appropriate tool to use for glycemic assessment in clinical practice and in clinical research. To our knowledge, it is the only comprehensive, customizable, and validated tool for glucose variability and continuous glucose data outcomes.

For MAGE, manual calculation is susceptible to human factor errors because the quality of calculations may be subject to the capacity and concentration of the person undertaking it. Thus, having an analysis tool that is able to undertake the operation with traceability to reference standard is critical.

EasyGV v10 computes all of the most important variability metrics and quality control indices in the current literature and can be customized, allowing the user to change the value of the tuning parameters.

One limitation of the EasyGV v10 is the fact that it needs a spreadsheet application or program to be used. However, this is unlikely to be an important limitation since most research groups and clinical teams have access to an office software package. Future work might include implementation of the EasyGV software in a web platform with the addition of graphical representations of reported metrics.

In summary, EasyGV v10 has been successfully validated to be a robust tool to use for glucose variability and control quality assessment. Moreover, the incorporation of novel metrics and the times in ranges in a simple interface makes this tool useful, practical, and comprehensive in glycemic evaluation.

Authors' Contributions

V.M., N.R.H., and N.O. directed the statistical analysis, interpreted the data, and wrote the article. V.M. also carried out the validation process and the statistical analysis. M.G. contributed to the validation process and interpreting the results and reviewing the article. V.M and N.O. are the guarantors of this work and, as such, had full access to all of the data in the study and take the responsibility for the integrity of the data and the accuracy of the data analysis.

Disclaimer

The views expressed are those of the authors and not necessarily those of the NHS, the NIHR, or the Department of Health.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

This research was supported by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Imperial College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR, or the Department of Health. Vanessa Moscardó was a recipient of an FPU grant, FPU13/04253, from the Spanish Ministry.

Supplementary Material

Supplementary Table S1

Supplementary Table S2

Supplementary Figure S1