Machine learning analysis of whole mouse brain vasculature

SUMMARY

Tissue clearing methods enable the imaging of biological specimens without sectioning. However, reliable and scalable analysis of large imaging data in 3D remains a challenge. Here, we developed a deep learning-based framework to quantify and analyze the brain vasculature, named Vessel Segmentation & Analysis Pipeline (VesSAP). Our pipeline uses a convolutional neural network (CNN) with a transfer learning approach for segmentation and achieves human-level accuracy. Using VesSAP we analyzed vascular features of whole C57BL/6J, CD1 and BALB/c mouse brains at the micrometer scale after registering them to the Allen mouse brain atlas. We reported evidence of secondary intracranial collateral vascularization in CD1 mice and found reduced vascularization of the brainstem compared to the cerebrum. Thus, VesSAP enables unbiased and scalable quantifications of the angioarchitecture of cleared mouse brains and yields biological insights into the vascular function of the brain.

INTRODUCTION

Changes in cerebrovascular structures are key indicators for a large number of diseases affecting the brain. Primary angiopathies, vascular risk factors (e.g., diabetes), traumatic brain injury, vascular occlusion and stroke all affect the function of the brain’s vascular network^1–3. The hallmarks of Alzheimer’s disease including tauopathy and amyloidopathy can also lead to aberrant remodeling of blood vessels^1,4, allowing capillary rarefaction to be used as a marker for vascular damages⁵. Therefore, quantitative analysis of the entire brain vasculature is pivotal to developing a better understanding of brain function in physiological and pathological states. However, quantifying micrometer scale changes in the cerebrovascular network of brains has been difficult for two main reasons.

First, labeling and imaging of the complete mouse brain vasculature down to the smallest blood vessels has not yet been achieved. Neither magnetic resonance imaging (MRI), micro-computed tomography (MicroCT), nor optical coherence tomography have sufficient resolution to capture capillaries in bulk tissue^6–8. Fluorescent microscopy provides a higher resolution, but can typically only be applied to tissue sections up to 200 μm thickness⁹. Recent advances in tissue clearing could overcome this problem¹⁰, but so far there has been no systematic description of all vessels of all sizes in an entire brain in three dimensions (3D).

The second challenge relates to the automated analysis of large 3D imaging data with substantial variance in signal intensity and signal-to-noise ratio at different depths. Simple intensity and shape-based filtering approaches such as Frangi’s vesselness filters, or more advanced image processing methods with local spatial adaptation cannot reliably differentiate vessels from a background in whole brain scans^11,12. Finally, imaging of a whole brain vascular network at capillary resolution results in datasets of terabyte size. Established image processing methods do not scale well to terabyte-sized image volumes as they don’t generalize well to large images and they require intensive manual fine-tuning^13–15.

Here, we present VesSAP (Vessel Segmentation & Analysis Pipeline), a deep learning-based method for the automated analysis of the entire mouse brain vasculature, overcoming the above limitations. VesSAP encompasses 3 major steps: 1) staining, clearing and imaging of the mouse brain vasculature down to the capillary level by two different dyes: wheat germ agglutinin (WGA) and Evans blue (EB), 2) automatically segmenting and tracing the whole brain vasculature data via convolutional neural networks (CNN) and 3) extracting vascular features for hundreds of brain regions after registering the data to the Allen brain atlas (Fig. 1). Our deep learning-based approach for network extraction in cleared tissue is robust, despite variations in signal intensities and structures, outperforms previous filter-based methods and reaches the quality of segmentation achieved by human annotators. We applied VesSAP to the three commonly used mouse strains C57BL/6J, CD1 and BALB/c.

Figure 1 |. Summary of the VesSAP pipeline.

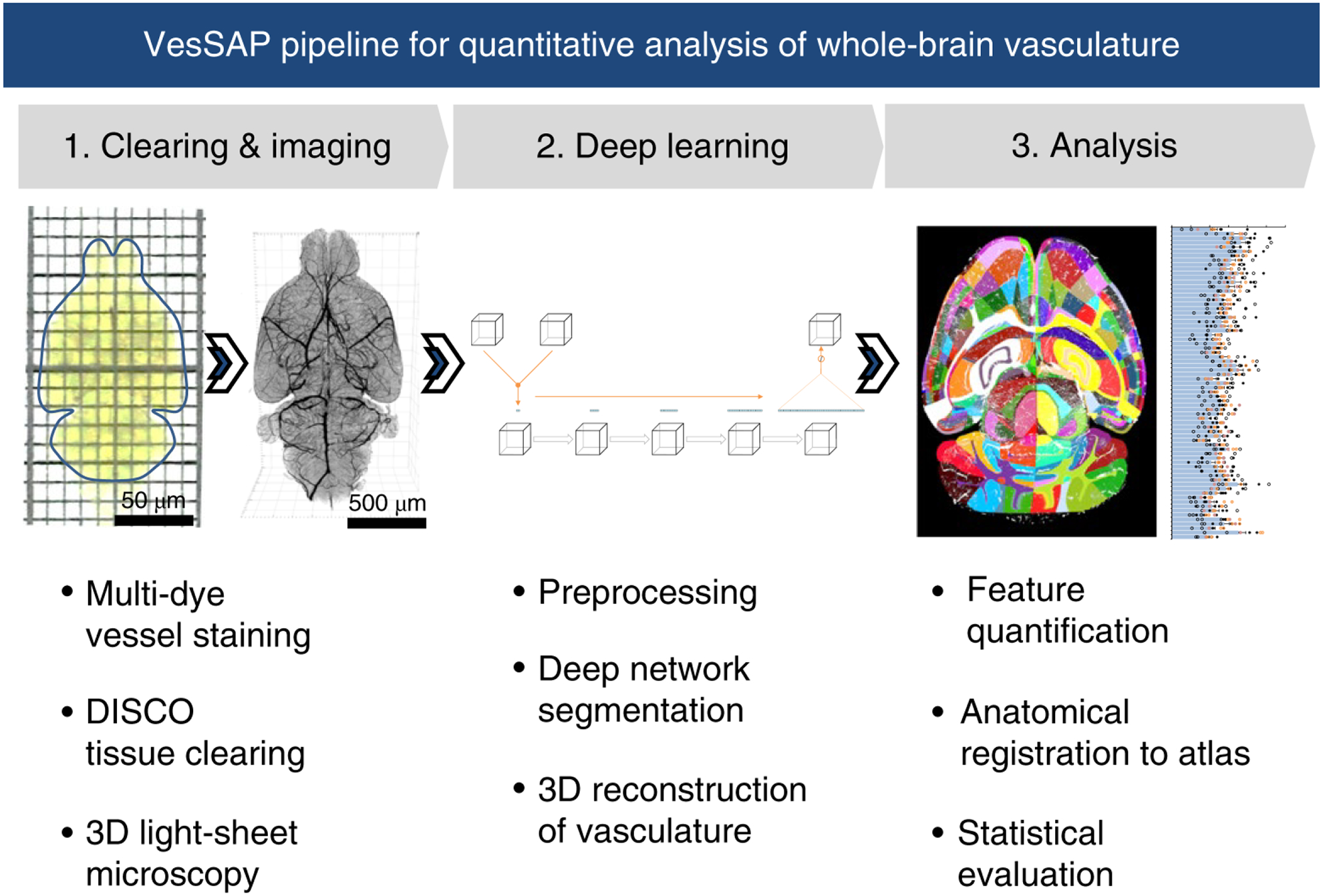
The method consists of three modular steps: 1, multi dye vessel staining and DISCO tissue clearing for high imaging quality using 3D light-sheet microscopy; 2, dep-learning based segmentation of blood vessels with 3D reconstruction and 3, anatomical feature extraction and mapping of the entire vasculature to the Allen adult mouse brain atlas for statistical analysis.

RESULTS

Vascular staining, DISCO clearing, and imaging

To reliably stain the entire vasculature, we used dyes WGA and EB dyes, which can be visualized in different fluorescence channels. We injected the EB dye into the living mice 12 hours before WGA perfusion, allowing its long-term circulation to mark vessels under physiological conditions¹⁶, while we perfused the WGA dye during fixation. We then performed 3DISCO clearing¹⁷ and light-sheet microscopy imaging of whole mouse brains (Fig. 2a–c, Supplementary Fig. 1, 2). WGA highlights microvessels, and EB predominantly stains major blood vessels, such as the middle cerebral artery and the circle of Willis (Fig. 2d–i, Supplementary Fig. 3). Merging the signals from both dyes yields a more complete staining of the vasculature than relying on individual dyes only (Fig. 2c,f, Supplementary Video 1). Staining from both dyes is congruent in mid-sized vessels, with signals originating from the vessel wall layer (Fig. 2j–l, Supplementary Fig. 3a–c). Using WGA, we reached a higher signal-to-noise ratio (SNR) for microvessels than bigger vessels. With EB, the SNR for small capillaries was lower but larger vessels reached a high SNR (Supplementary Fig. 4). Integrating the information from both channels allows acquisition of the entire vasculature, and results in an optimized SNR. We also compared fluorescence signal quality of the WGA staining (targeting the complete endothelial glycocalyx lining¹⁸) with a conventional vessel antibody (anti-CD31, targeting endothelial cell-cell adhesion¹⁹) and found that WGA produced a higher SNR for the blood vessels in general (Supplementary Fig. 5).

Figure 2 |. Enhancement of vascular staining using two complementary dyes.

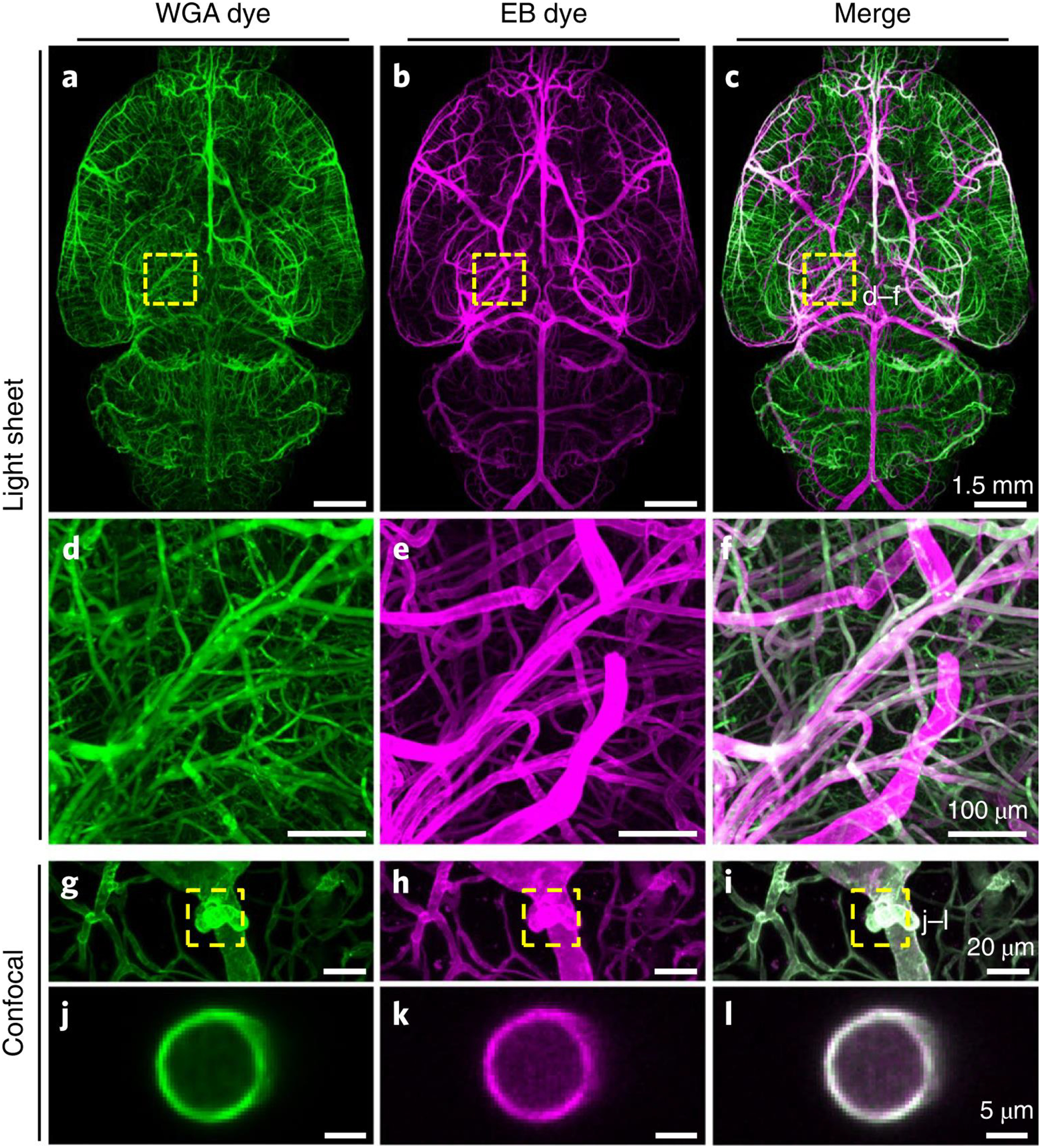
a-c, Maximum intensity projections of the automatically reconstructed tiling scans of WGA (a) and Evans blue (b) signals in the same sample and the merged view (c). d-f: Close-up of marked region in (c). g–l, Confocal images of WGA- and EB-stained vessels and vascular wall (g–i, maximum intensity projections of 112 μm and j–l, single slice of 1 μm). The experiment was performed on 9 different mice with similar results.

Segmentation of the volumetric images

To enable the extraction of quantitative features of the vascular structure, vessels in the acquired brain scans need to be segmented in 3D. Motivated by deep learning-based approaches in biomedical image data analysis^20–28, we used a five layer CNN (Fig. 3a) to exploit the complementary signals of both dyes to derive a complete segmentation of the entire brain vasculature.

Figure 3 |. Deep learning architecture of VesSAP and performance on vessel segmentation.

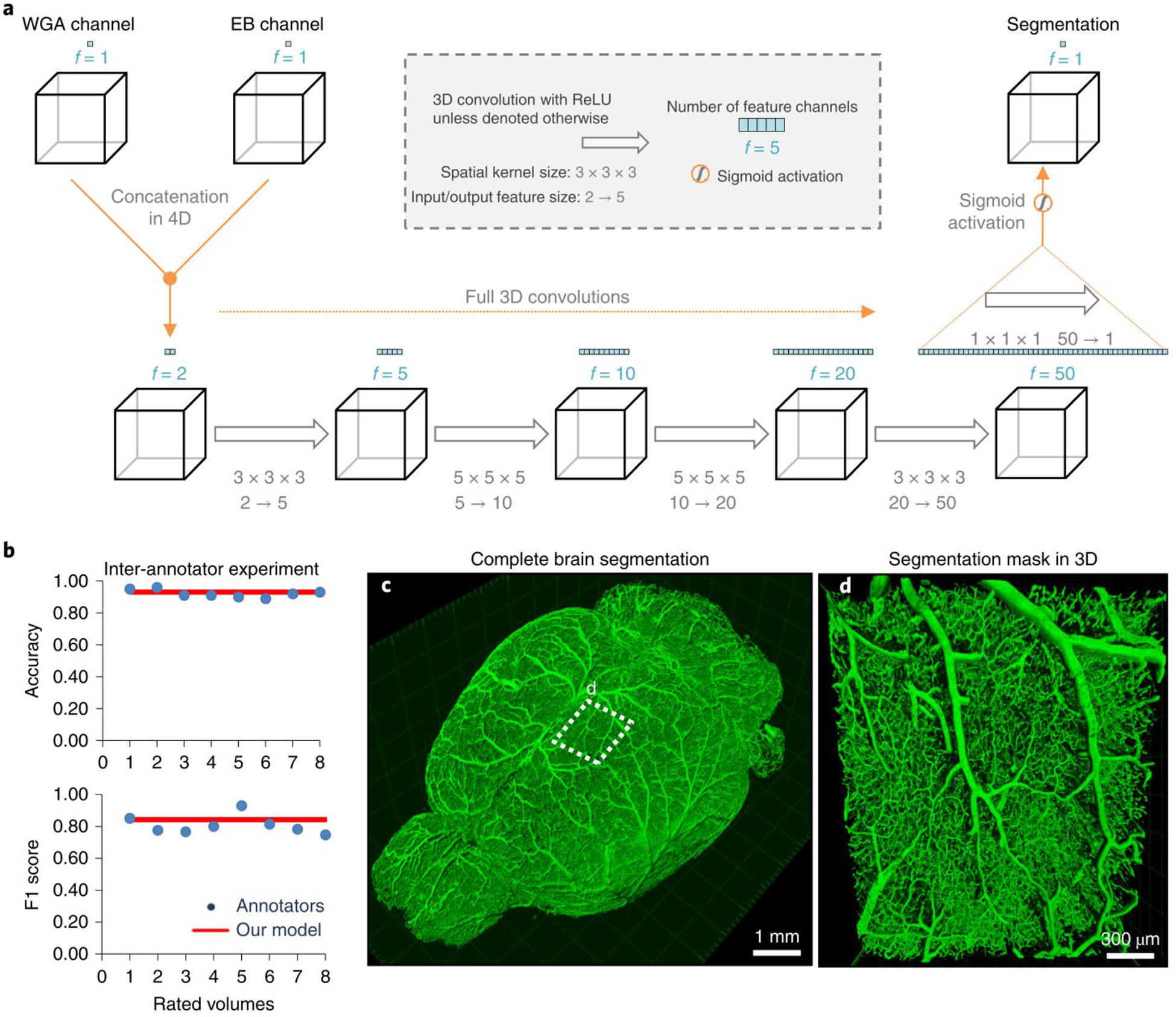
a, The 3D VesSAP network architecture consisting of five convolutional layers and a sigmoid activation for the last layer including the kernel sizes and input/output of the feature size. b, The F1-score for inter-annotator experiments (blue) compared to VeSAP (red). c, 3D rendering of full brain segmentation from a CD1-E mouse. d, 3D rendering of a small volume marked in (c). The experiment was performed on 9 different mice with similar results.

In the first step, the two input channels (WGA and EB) are concatenated. This yields a matrix in which each voxel is characterized by two features. Then, each convolutional step integrates the information from a voxel’s 3D neighborhood. We use full 3D convolutions²⁰ without further down or up sampling and fewer trainable parameters in comparison to e.g., the 3D U-Net and V-Net^29,30 in order to achieve high inference speeds. After the fourth convolution, the information from 50 features per voxel is combined with a convolutional layer with kernel size one and a sigmoidal activation to estimate the likelihood that a given voxel represents a vessel. Subsequent binarization yields the final segmentation. In both training and testing, the images are processed in sub-volumes of 50 × 100 × 100 pixels.

Deep neural networks often require large amounts of annotated data or many iterations of training. Here, we circumvented this requirement with a transfer learning approach³¹. In short, we first pre-trained the network on a large, synthetically generated vessel-like data set (Supplementary Fig. 6)³² and then refined on a small amount of manually annotated parts of the real brain vessel scans. This approach reduced the training iterations on manually annotated training data.

To assess the quality of the segmentation, we compared the VesSAP CNN prediction with manually labeled ground truth and alternative computational approaches (Table 1). We report voxel-wise segmentation metrics, namely accuracy, the F1-score³³, Jaccard coefficient, and cl-F1, which weight the centerlines and volumes of the vessels (detailed in Methods). Compared to the ground truth, our network achieved an accuracy of 0.94 ± 0.01 and an F1-score of 0.84 ± 0.05 (for additional scores see Table 1, all values are mean ± SD). As controls, we implemented alternative state-of-the-art deep learning and classical methods. Our network outperforms classical Frangi filters¹¹ (accuracy: 0.85 ± 0.03; F1-Score: 0.47 ± 0.18), as well as recent methods based on local spatial context via Markov random fields^13,34 (accuracy: 0.85 ± 0.03; F1-score: 0.48 ± 0.04). VesSAP achieved similar performance compared to 3D U-Net and V-Net architectures, which require substantially more trainable parameters (3D U-Net: accuracy: 0.95 ± 0.01; F1-score: 0.85 ± 0.03 and V-Net: accuracy: 0.95 ± 0.02; F1-score: 0.86 ± 0.07, no statistical difference compared to VesSAP CNN, two sided t-test all, p-values > 0.3). However, VesSAP CNN outperformed the other architectures substantially in terms of speed, being ~20 and ~50 times faster in the feedforward path than V-Net and 3D U-Net, respectively. This is particularly important for our large datasets (hundreds of gigabytes). For example, VesSAP CNN segments a single brain in 4 hours, while V-Net and 3D U-Net require 3.3 days and 8 days, respectively. The superior speed of the VesSAP CNN is due to the substantially fewer trainable parameters in its architecture (e.g., our implementation of the 3D U-Net has ~178 million parameters, VesSAP CNN has ~0.059 million parameters) (Table 1). Next, we compared the segmentation accuracy of our network with human annotations. A total of 4 human experts independently annotated two volumes. We found that inter-annotator accuracy and F1-score of experts were comparable to the predicted segmentation of our network (human annotators: accuracy: 0.92 ± 0.02 and F1-score: 0.81 ± 0.06, Fig. 3b). Importantly, we extrapolate that human annotators would need more than a year to process a whole brain instead of the 4 hours required by our approach. Moreover, we observed differences in the human segmentations due to annotator bias. Thus, VesSAP CNN can segment the whole brain vasculature consistently at human-level accuracy with a substantially higher speed than currently available methods, enabling high throughput for large-scale analysis.

Table 1:

Evaluation metrics of the different segmentation approaches for 75 volumes of 100 × 100 × 50 pixels (s: seconds). All values are given as mean ± SD. Best performing algorithms in bold and underlined; algorithms whose performance does not differ more than 2% from the best performing one in bold. Number of trainable parameters for deep learning architectures in millions (m).

Segmentation model	CI-F1	Accuracy	F1-Score	Jaccard	Parameters	Speed
VesSAP CNN	0.93 ± 0.02	0.94 ± 0.01	0.84 ± 0.05	0.84 ± 0.04	0.0587 m	1.19 s
VesSAP CNN, trained from scratch	0.93 ± 0.02	0.94 ± 0.01	0.85 ± 0.04	0.85 ± 0.04	0.0587 m	1.19 s
VesSAP CNN, synthetic training data	0.87 ± 0.02	0.90 ± 0.05	0.72 ± 0.07	0.70 ± 0.05	0.0587 m	1.19 s
3D U-Net	0.93 ± 0.02	0.95 ± 0.01	0.85 ± 0.03	0.85 ± 0.03	178.4537 m	61.22 s
V-Net	0.94 ± 0.02	0.95 ± 0.02	0.86 ± 0.07	0.86 ± 0.07	88.8556 m	26.87 s
Frangi Vesselness	0.84 ± 0.03	0.85 ± 0.03	0.47 ± 0.19	-	-	117.00 s
Markov Random Field	0.86 ± 0.02	0.85 ± 0.03	0.48 ± 0.04	-	-	24.31 s

We show an example of a brain vasculature that was segmented by VesSAP in 3D (Fig. 3c and Supplementary Video 2, 3). Zooming into a smaller patch reveals that the connectivity of the vascular network was fully maintained (Fig. 3d, Supplementary Video 2). Comparing single slices of the imaging data with the predicted segmentation shows that vessels are accurately segmented regardless of absolute illumination or vessel diameter (Supplementary Fig. 7).

Feature extraction and atlas registration

Vessel lengths, radii and the number of bifurcation points are commonly used to describe the angioarchitecture². Hence, we used our segmentation to quantify these features as distinct parameters to characterize the mouse brain vasculature (Fig. 4a, Supplementary Video 4). We evaluated local vessel length (length normalized to the size of the brain region of interest), local bifurcation density (sum of occurrences normalized to the size of the brain region of interest) and local vessel radius (average radius along the full length) of the blood vessels in different brain regions.

Figure 4 |. Pipeline showing feature extraction and registration process.

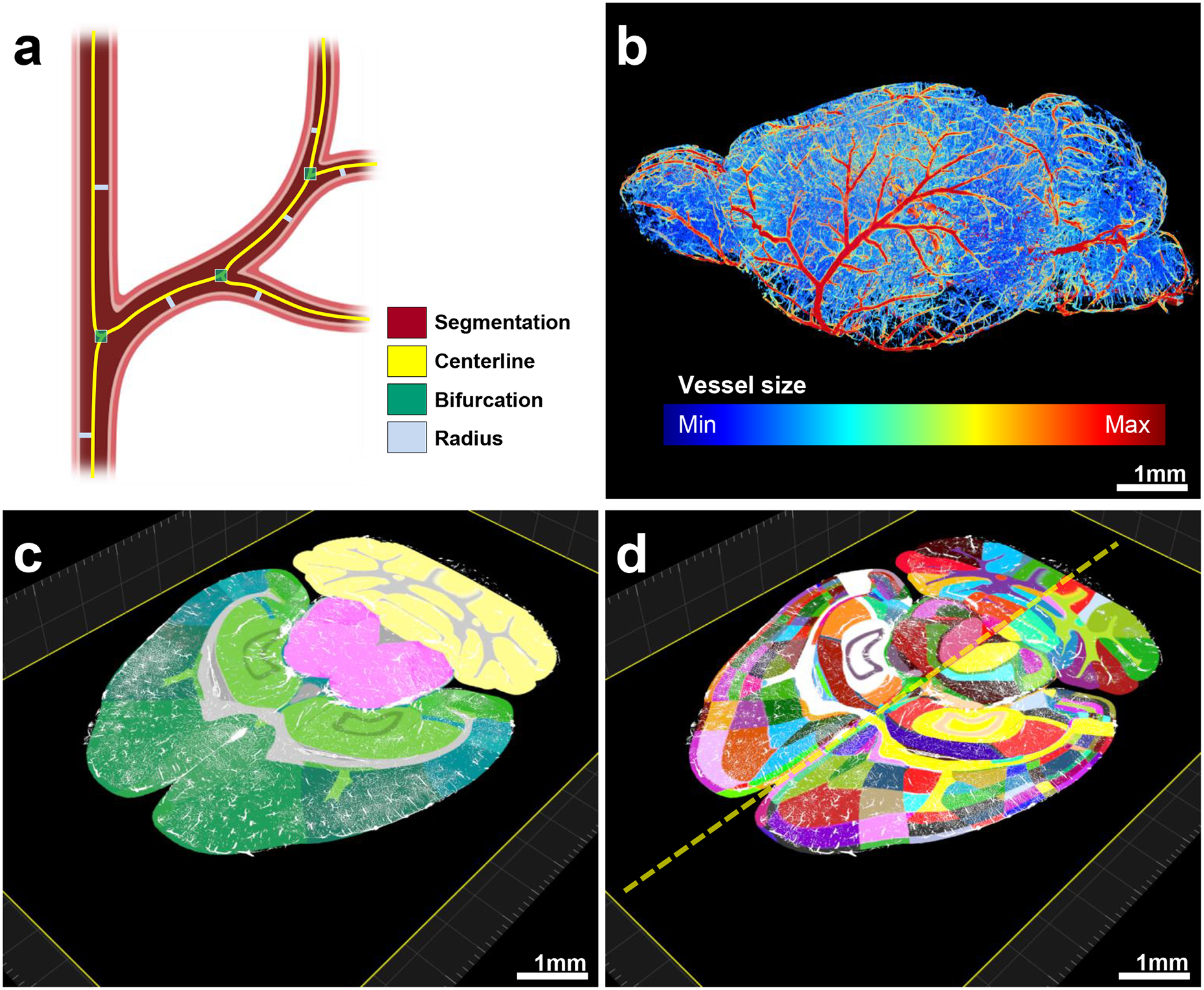
a, Representation of the features extracted from vessels. b, Radius illustration of the vasculature in a CD1 mouse brain. C–d, Vascular segmentation results overlaid on the hierarchically (c) and randomly color-coded atlas to reveal all annotated regions (d) available including hemispheric difference (dashed-line in d). The experiment was performed on 9 different mice with similar results.

We reported the vascular features in three ways to enable a comparison with various previous studies that differed in the measures used (Supplementary Fig. 8). More specifically, first, we provided a count of segmented voxels as compared to total voxels within a specific brain region (voxel space). Second, we provided the measurements by calculating the voxel size of our imaging system and accounted for the Euclidean length (microscopic space). Third, we corrected the microscopic measurements to account for the tissue shrinkage caused by the clearing process (anatomical space) (Supplementary Tables 2–10). We calculated this shrinkage rate by measuring the same mouse brain volume using MRI prior to clearing.

Here, we use the anatomical space to report our specific biological findings as it is closest to the physiological state. For the average blood vessel length of the whole brain, we found a value of 545.74 ± 94 mm/mm³ (mean ± SD). Because our method quantifies brain regions separately, we could compare our results to the literature, which mostly reported the quantifications for either specific brain regions or extrapolations to the whole brain from regional quantifications. For example a vascular length of 922 ± 176 mm/mm³ (mean ± SD) was previously reported for cortical regions (size of 508 × 508 × 1500 μm)¹⁰. We found a similar vessel length for the same region in the mouse cortex (C57BL/6J) (913 ± 110 mm/mm³), substantiating the accuracy of our method. We performed additional comparisons to other reports (Supplementary Table 11). Moreover, we compared the measurements acquired with our algorithms to manually labeled ground truth data and found a deviation of 8.21% for the centerlines, 13.18% for the number of bifurcation points and 16.33% for the average radius. These deviations are substantially lower than the average deviation among human annotators (Methods).

We quantified and visualized the vessel radius along the entire vascular network (Fig. 4b). After extracting vascular features of the whole brain with VesSAP, we registered the volume to the Allen brain atlas (Supplementary Video 5, 6). This allowed us to map the segmented vasculature and corresponding features topographically to distinct anatomical brain regions (Fig. 4c). Each anatomical region can be further divided into sub-regions, yielding a total of 1238 anatomical structures (619 per hemisphere) for the entire mouse brain (Fig. 4d). This allows the analysis of each denoted brain region and grouping regions into clusters such as left vs. right hemisphere, gray vs. white matter or any hierarchical clusters of the Allen brain atlas ontology. For our subsequent statistical feature analysis, we grouped the labeled structures according to the 71 main anatomical clusters of the current Allen brain atlas ontology. We thus provide the whole mouse brain vascular map with extracted vessel lengths, bifurcation points and radii down to the capillary level.

VesSAP provides a reference map of the whole brain vasculature in mice

Studying the whole brain vasculature in C57BL/6J, CD1 and BALB/c strains (n = 3 mice for each strain), we found that the local vessel length and local bifurcation density differ in the same brain over different regions, while they correlate highly among different mice for the same regions (Fig. 5a,b). Furthermore, the local bifurcation density correlates highly with the local vessel length in most brain regions (Supplementary Fig. 9), and the average vessel radius is evenly distributed in different regions of the same brain (Fig. 5c). In addition, the extracted features show no statistical difference (Cohen’s d, Supplementary Table 12) between the same anatomical cluster among the strains (Supplementary Fig. 9). Finally, microvessels make up the overwhelming proportion of the total vascular composition in all brain regions (Fig. 5d). We visually inspected exemplary brain regions to validate the output of VesSAP. Both VesSAP and visual inspection revealed that the gustatory areas had a higher vascular length per volume compared to the anterodorsal nucleus (Fig. 6a–c). Visual inspection also suggested that the number of capillaries was the primary reason for regional feature variations within the same brain.

Figure 5 |. Anatomical properties of the neurovasculature in the adult mouse brain mapped to the Allen brain atlas clusters.

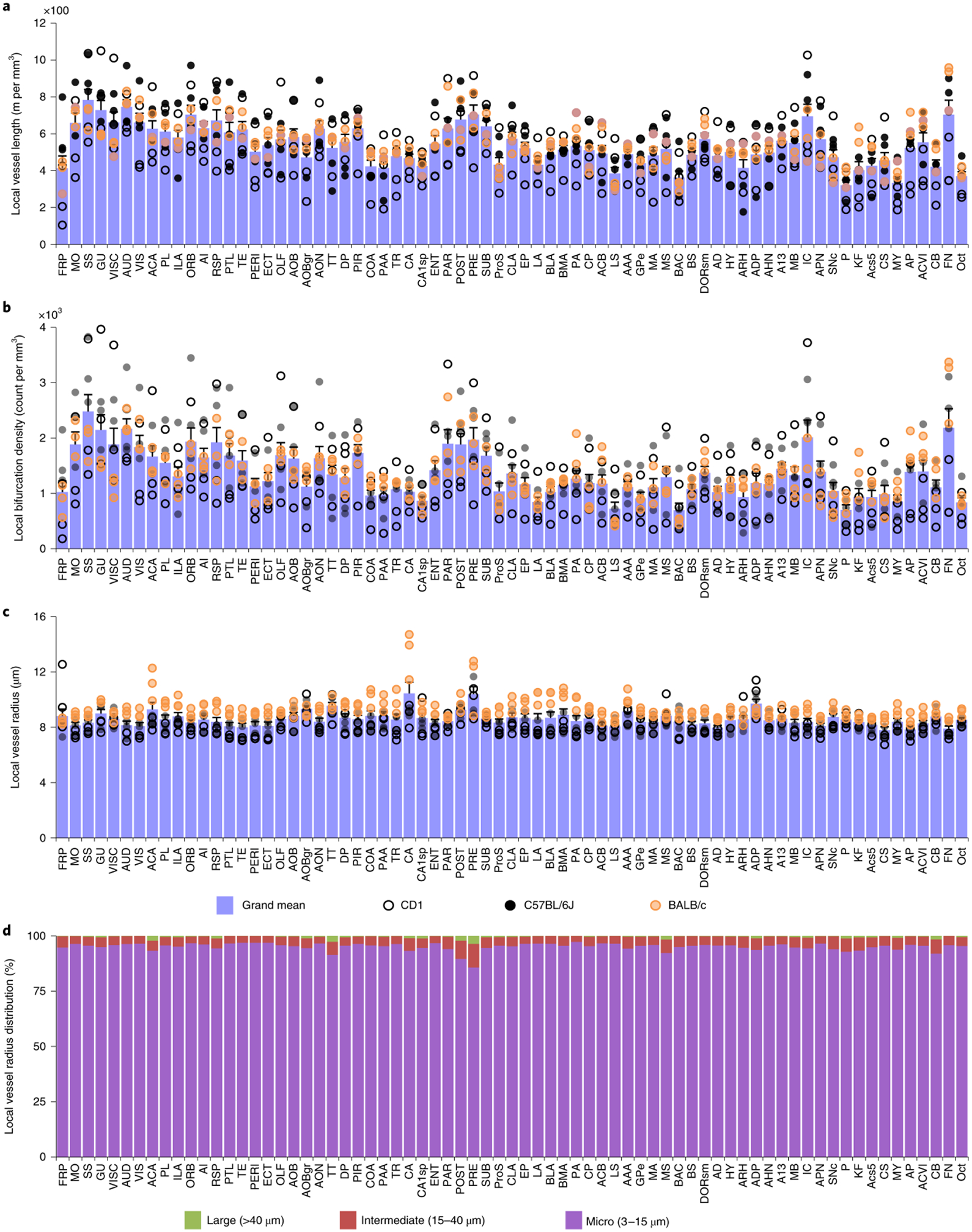
a–c, Representation of the local vessel length (a), the density of bifurcations (b) and the average radius (c) in each of the 71 main anatomical clusters of the Allen brain atlas. Open, black and orange circles denote measurements in CD1, C57BL/6J and BALB/c strains respectively; each circle represents a single mouse (a–c). d, Local distribution of the large, middle and micro vessels in the same anatomical clusters. All abbreviations are listed in the Supplementary table 1. All data values are given as mean ± SEM and n=3 mice per strain (a–c).

Figure 6 |. Exemplary quantitative analysis enabled by VesSAP.

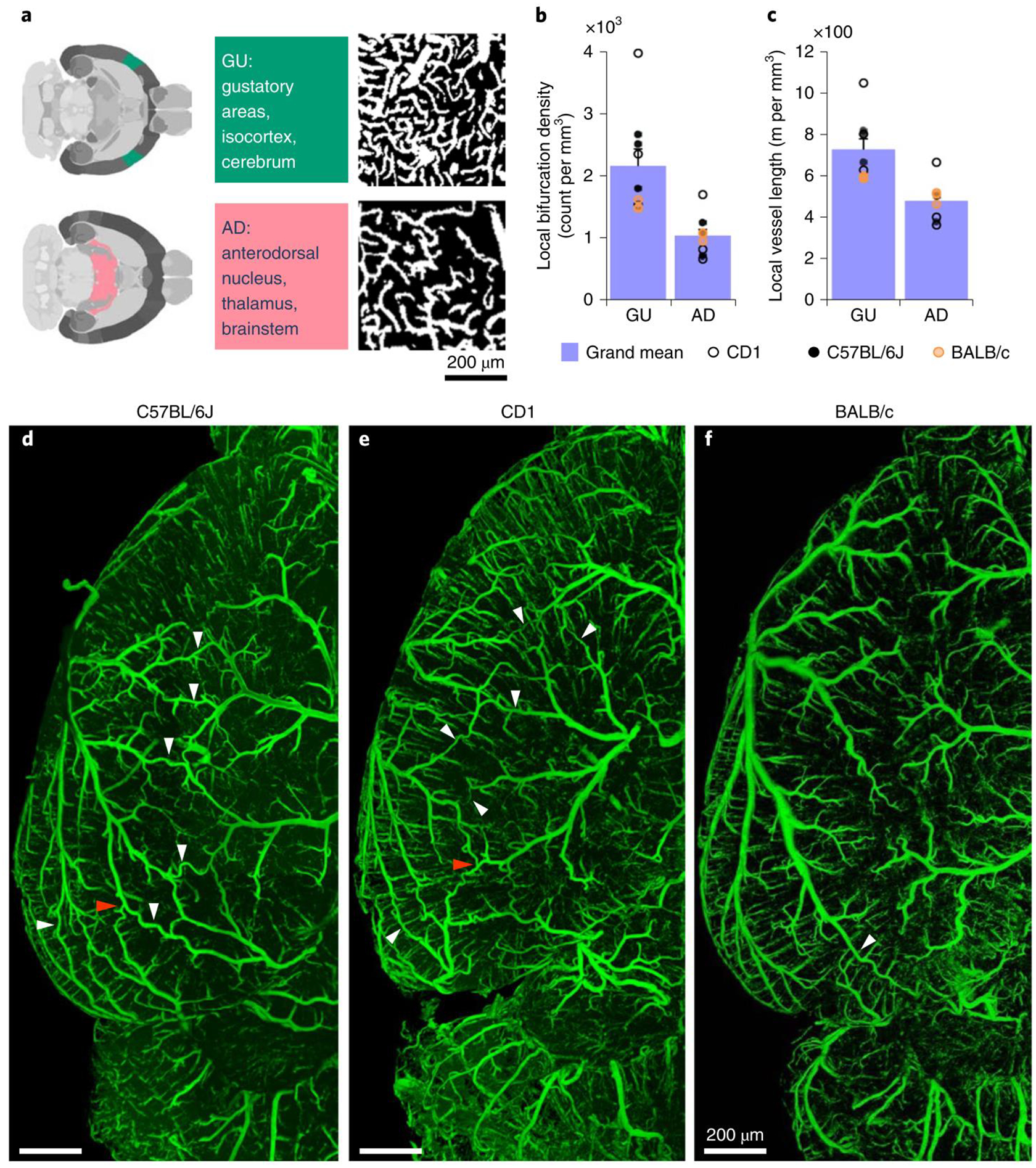
a, The respective location of AD and GU areas in the mouse brain (left panels), maximum intensity projections of representative volumes from the gustatory areas (GU) and anterodorsal nucleus (AD) segmentation (600 × 600 × 33 μm) (right panels). b, c, Quantification of the bifurcation density and local vessel length for the AD and GU clusters. CD1 mice shown by open circles, BALB/C by orange circles, and C57BL/6J by black circles. Values are mean ± SEM, n=3 mice per strain. D–f, Images of the vasculature in a representative C57BL/6J (d), CD1 (e) and BALB/c mouse (f) where the white arrowheads indicate anastomoses between the major arteries. Direct vascular connections between the medial cerebral artery (MCA), the anterior cerebral artery (ACA) and the posterior cerebral artery (PCER) are indicated by red arrowheads. The experiment was performed 3 times with similar results.

Finally, VesSAP offered insights into the neurovascular structure of the different mouse strains in our study. There are direct intracranial vascular anastomoses in the C57BL/6J, CD1 and BALB/c strains (white arrowheads, Fig. 6d–f). The anterior cerebral artery, middle cerebral artery and the posterior cerebral artery are connected at the dorsal visual cortex in CD1 (red arrowheads, Fig. 6d,e) unlike in the BALB/c strains³³ (Fig. 6f).

DISCUSSION

VesSAP can generate a reference map of the adult mouse brain vasculature. These maps can potentially be used to model synthetic cerebrovascular networks³⁵. In addition to the metrics we obtain to describe the vasculature, advanced metrics e.g., Strahler values, network connectivity, and bifurcation angles can be extracted using the data generated by VesSAP. Furthermore, the centerlines and bifurcation points can be interpreted as the edges and nodes for building a full vascular network graph, offering a means for studying local and global properties of the cerebrovascular network in the future.

The VeSAP workflow relies on staining of the blood by two different dyes. WGA binds to the glycocalyx of the endothelial lining of the blood vessels³⁶ but may miss some segments of the large vessels¹⁸. EB is a dye with a high affinity to serum albumin³⁷, thus, it remains in the large vessels after a short perfusion protocol. In addition, EB labeling is not affected by subsequent DISCO clearing.

Vessels have long and thin tubular shapes. In our images, the radii of capillaries (about 3 μm) are in the range of our voxel size. Therefore, a segmentation, which yields the correct diameter down to a single-pixel resolution poses a challenge as we observed a 16% deviation for the radius. This sub-pixel deviation did not pose a problem for segmenting the whole vasculature network and extracting features, because the vascular network can be defined by its centerlines and bifurcations.

The described segmentation concept is based on a transfer learning approach, where we pretrained the CNN and refined it on a small labeled dataset of 11% of the synthetic dataset and only 0.02% of one cleared brain. We consider this a major advantage compared to training from scratch. Thus, our CNN might generalize well to different types of imaging data (such as microCT angiography) or other curvilinear structures (e.g., neurons), as only a small labeled dataset is needed to adjust our pre-trained network.

Based on our vascular reference map, unknown vascular properties can be discovered and biological models can be confirmed. VesSAP showed a high number of collaterals in albino CD1 mice. Such collaterals between large vessels can substantially alter the outcome of ischemic stroke lesions: the blood deprived brain regions from the occlusion of a large vessel can be compensated by a blood supply from the collateral extensions of other large vessels^33,40. Therefore, our VesSAP method can lead to the discovery of previously unknown anatomical details that could be functionally relevant.

In conclusion, VesSAP is a scalable, modular and automated machine learning-based method to analyze complex imaging data from cleared mouse brains. We foresee that our method will accelerate the applications of tissue clearing in particular for studies assessing the brain vasculature.

METHODS

Tissue preparation

Animal experiments were conducted according to institutional guidelines (Klinikum der Universität München/Ludwig Maximilian University of Munich), after approval of the ethical review board of the government of Upper Bavaria (Regierung von Oberbayern, Munich, Germany), and in accordance with the European directive 2010/63/EU for animal research. The animals were housed under a 12/12 hr light/dark cycle. For this study we injected 150 μl (2% V/V% in saline) of Evans blue dye (Sigma-Aldrich, E2129) intraperitoneally into three C57BL/6J, CD1 and BALB/c (Charles River, Strain Codes 027; 482 and 028 respectively) male, 3 months old mice (n=3 per group). After 12 hrs of postinjection time, we anaesthetized the animals with a triple combination of midazolam + medetomidine + fentanyl (i.p.; 1 ml per 100 g body mass for mice; 5 mg, 0.5 mg and 0.05 mg per kg body mass) and opened their chest for transcardial perfusion. The following media was supplied by a peristaltic pump set to deliver 8 ml/min volume: 0.25 mg wheat germ agglutinin conjugated to Alexa 594 dye (ThermoFisher Scientific, W11262) in 150 μl PBS (pH 7.2) and 15 ml PBS 1x and 15 ml 4% PFA. This short perfusion protocol was established based on preliminary experiments, where both WGA and EB staining partially washed out (data not shown) and with the goal to deliver fixative to the brain tissue using the vessels to achieve a homogenous preservation effect⁴¹.

After perfusion, the brains were extracted from the neurocranium while severing some of the segments of the circle of Willis, which is an inevitable component of most retrieval processes besides corrosion cast techniques. Next, the samples were incubated into 3DISCO clearing solutions as described¹⁷. Briefly, we immersed them in a gradient of tetrahydrofuran (Sigma-Aldrich, 186562): 50 vol%, 70 vol%, 80 vol%, 90 vol%, 100 vol% (in distilled water), and 100 vol% at 25 °C for 12 h at each concentration. At this point we modified the protocol by incubating the samples in tert-Butanol incubation for 12 hrs at 35 °C followed by immersion in dichloromethane (Sigma-Aldrich, 270997) for 12 hrs at room temperature and finally incubation with the refractive index matching solution BABB (benzyl alcohol + benzyl benzoate 1:2; Sigma-Aldrich, 24122 and W213802), for at least 24 hrs at room temperature until transparency was achieved. Each incubation step was carried out on a laboratory shaker.

Imaging of the cleared samples with light-sheet microscopy

We used a 4× objective lens (Olympus XLFLUOR 340) equipped with an immersion corrected dipping cap mounted on a LaVision UltraII microscope coupled to a white light laser module (NKT SuperK Extreme EXW-12) for imaging. The images were taken in 16 bit depth and at a nominal resolution of 1.625 μm / voxel on the XY axes. For 12× imaging we used a LaVision objective (12x NA 0.53 MI PLAN with an immersion corrected dipping cap). The brain structures were visualized by the Alexa 594 (using a 580/25 excitation and a 625/30 emission filter) and Evans blue fluorescent dyes (using a 640/40 excitation and a 690/50 emission filter) in a sequential order. We maximized the signal to noise ratio (SNR) for each dye independently to avoid saturation of differently sized vessels when only a single channel is used. We achieved this by independently optimizing the excitation power so that the strongest signal in the major vessels does not exceed the dynamic range of the camera. In z-dimension we took the sectional images in 3 μm steps using left and right sided illumination. Our measured resolution was 2.83 μm × 2.83 μm × 4.99 μm for X, Y and Z, respectively (Supplementary Fig. 2). To reduce defocus, which derives from the Gaussian shape of the beam, we used a 12 step sequential shifting of the focal position of the light-sheet per plane and side. The thinnest point of the light-sheet was 5 μm.

Imaging of the cleared samples with confocal microscopy

Additionally, the cleared specimens were imaged with an inverted laser-scanning confocal microscope (Zeiss, LSM 880) for further analysis. Before imaging, samples were mounted by placing them onto the glass surface of a 35 mm glass-bottom petri dish (MatTek, P35G-0–14-C) immersed in BABB. A 40x oil-immersion objective lens was used (Zeiss, ECPlan-NeoFluar 40x/1.30 Oil DIC M27, 1.3 NA, WD = 0.21 mm). The images were acquired by the settings for Alexa 594 (using a 561 excitation and a 585–733 emission range) and Evans blue fluorescent dyes (using a 633 excitation and a 638–755 emission range) in a sequential order.

Magnetic resonance imaging

We used a nanoScan PET/MR device (3 Tesla, Mediso Medical Imaging Systems) equipped with a head coil for murine heads to acquire anatomical scans in the T1 modality.

Reconstruction of the datasets from the tiling volumes

We stitched the acquired volumes using TeraStitcher’s automatic global optimization function (v1.10.3). We produced volumetric intensity images of the whole brain considering each channel separately. To improve the alignment to the Allen brain atlas we downscaled our dataset in the XY plane to achieve pseudo-uniform voxel spacing matching the Z plane.

Deep learning network architecture

We rely on a deep 3D convolutional neural network (CNN) for segmentation of our blood vessel dataset. The networks general architecture consists of 5 convolutional layers, 4 with ReLu (rectified linear unit) followed by one convolutional layer with a sigmoid activation (Fig. 3a). The input layer is designed to take n images as an input. In the implemented case, the input to the first layer of the network are n=2 images of the same brain, which have been stained differently (Fig. 3a). To specifically account for the general class imbalance (much more tissue background than vessel signals) in our dataset, and the potential of high false positive rates associated with the class imbalance, we chose the generalized soft-Dice as the loss function to our network. At all levels we used full 3D convolutional kernels (Fig. 3a).

The networks training is driven by an Adam optimizer with a learning rate of 1e⁻⁵ and exponential decay rate of 0.9 for the 1^st moment and 0.99 for the 2^nd moment⁴². A prediction or segmentation with a trained model takes volumetric images of arbitrary size as input and outputs a probabilistic segmentation map of identical size. To deal with volumes of arbitrary size and extension, we processed them in smaller sub-volumes of 100 ×100 × 50 pixels size. The algorithms have been implemented using the Tensorflow framework and KERAS⁴³. They are trained and tested on two NVIDIA Quadro P5000 GPUs and on machines with 64GB and 512GB RAM respectively.

Transfer learning

Typically, supervised learning tasks in biomedical imaging are aggravated by a scarce availability of labeled training data. Our transfer learning approach aims to circumvent this problem by pre-training our models on synthetically generated data and refining them on a small set of real images⁴⁴. Specifically, our approach pre-trains the VesSAP CNN on 3D volumes of vascular image data, synthetically generated together with the corresponding training labels, using the approach by Schneider and colleagues⁴⁵. The pre-training is carried out on a dataset of 20 volumes of a size of 325 × 304 × 600 pixels for 38 epochs. During pre-training we applied a learning rate of 1e⁻⁴. Afterwards, the pre-trained model was fine-tuned by retraining on a real microscopic dataset consisting of eleven volumes with a size of 500 × 500 × 50 pixels. The image volumes were manually annotated by a commission including the expert who had previously prepared the samples and operated the microscope. The labels were verified and further refined in consensus by two additional human raters. The data we used in this fine-tuning step amounts to 11 % of the volume of the synthetic datasets and only a fraction of 0.02% of the voxel volume of a single whole brain. For the fine-tuning step, we used a learning rate of 1e⁻⁵. The final model was obtained after training on the real dataset for 6 epochs. This is a substantially shorter training compared to training from scratch, where we train the same VesSAP CNN architecture for 72 epochs until we reach the best F1-Score on the validation set. The labeled dataset consists of 17 volumes of 500 × 500 × 50 pixels from 5 mice brains. Three of those brains are from the CD1 and two from the C57BL/6J strain. The volumes are chosen from regions throughout the whole brain, to represent the variability in the vascular dataset, both in terms of vessel shapes and illumination. To ensure independence, volumes of the training set and test/validation set are chosen from independent brains. All datasets include brains from the two strains. Our training dataset consists of eleven volumes, the validation dataset of three volumes and the test dataset of three volumes, too. We cross-test on our test and validation dataset by rotating these. The volumes are processed during training and inference in 25 small sub-volumes of 100 × 100 × 50 pixels.

We observed an average F1-Score of 0.84 ± 0.02 (mean ± SD), an average accuracy of 0.94 ± 0.01 (mean ± SD), and an average Jaccard coefficient of 0.84 ± 0.04 (mean ± SD) on our test datasets (Fig. 3b). We tested for statistical significance among the top three learning methods (VesSAP CNN, V-Net and 3D U-Net) using a paired t-test. We found that the differences in F1-Scores are not statistically significant (all p-values > 0.3, rejecting the hypothesis of different distributions).

Since the F1-Score, accuracy and Jaccard coefficient are all voxel wise volumetric scores and can fall short in evaluating connectedness of components we developed the cl-F1 score. cl-F1 is calculated on the intersection of centerlines and vessel volumes and not on volumes only, like the traditional F1-score is⁴⁶. To determine this score we first calculate the intersection of the centerline of our prediction with the labeled volume and then calculated the intersection of the labeled volume’s centerline with the predicted volume. Next, we treat the first intersection as recall, as it is susceptible to false negatives, and the second as precision, as it is susceptible to false positives, and input this into the traditional F1-score formulation below:

$$F1=2\times \frac{\mathit{\text{precision\hspace{0.17em}}}\times \mathit{\text{\hspace{0.17em}recall}}}{\mathit{\text{precision\hspace{0.17em}}}+\mathit{\text{\hspace{0.17em}recall}}}$$ (I.)

We report an average cl-F1 score of 0.93 ± 0.02 (mean ± SD) on the test set.

All scores are given as mean and standard deviation. Our model reached the best model selection point on the validation dataset after 6 epochs of training.

Comparison to 3D U-Net and V-Net

To compare our proposed architecture to different segmentation architectures, we implemented the V-Net and 3D U-Net, both more complex CNNs with substantially more trainable parameters, which further include down- and up-sampling. While experiments show that 3D U-Net and V-Net reach marginally higher performance scores, the differences are not statistically significant (two sided t-test, p > 0.3). Their amount of parameters make them a factor of 51 and 23 slower during the inference stage. For the segmentation of one of our large whole brain datasets this translates to a time of 4 hours versus 8 days for 3D U-Net and 3.8 days for V-Net. This difference is also prevalent in the number of trainable parameters. VesSAP CNN has 0.058 million parameters, whereas 3D U-Net consists of more than 178 million and V-Net of more than 88 million. Furthermore, the light VesSAP CNN already reaches human-level performance. We therefore consider the problem of vessel segmentation as solved by the VesSAP CNN for our data. It should be mentioned that the segmentation network is a modular building block of the overall VesSAP pipeline, and can be chosen by each user according to his or her own preferences and, importantly, according to the computational power available.

Pre-processing of segmentation

The pre-processing factors into the overall success of the training and segmentation. The intensity distribution among the brains and among brain regions differs substantially. To account for the intensity distributions, two preprocessing strategies have been applied successively.

1. High-cut filter: In this step the intensities x above a certain threshold c, which is defined by a global percentile, where each volume was set to that threshold. Next, they were normalized by f(x).

   $$g(x)=\{\begin{array}{l}c,x>c\hfill \\ x,x\le c\hfill \end{array}$$ (II.)
2. Normalization of intensities: The original intensities were normalized to the range of 0 to 1, where x is the pixel intensity and X are all intensities of the volume.

   $$f(x)=\frac{x-\text{min}(X)}{\text{max}(X)-\text{min}(X)}$$ (III.)

Inter-annotator experiment for the segmentation

To compare VesSAP’s segmentation to a human level annotation we implemented an inter-annotator experiment. For this experiment we determined a gold standard label (ground truth) for two volumes of 500 × 500 × 50 pixels from a commission of three experts, including the expert who imaged our data and is therefore most familiar with the images. Next, we gave the two volumes to 4 other experts to label the complete vasculature. The experts spend multiple hours to label each patch within the ImageJ and ITK-snap environment and were allowed to use their favored approaches to generate what they considered to be the most accurate labeling. Finally, we calculated the accuracy and dice scores for the different annotators, compared to the gold standard and compared them to the scores of our model (Table 1).

Feature extraction

In order to quantify the anatomy of the mouse brain vasculature we extracted descriptive features based on our segmentation. First, we calculate the features in voxel space. Later we registered them to the Allen brain atlas.

As features we extracted the centerlines, the bifurcation points and the radius of the segmented blood vessels. We consider those features to be independent to the elongation of the light-sheet scans and the connectedness of the vessels due to staining, imaging and/or segmentation artefacts.

Our centerline extraction is based on a 3D thinning algorithm⁴⁷. Before extracting the centerlines we applied two cycles of binary erosion and dilation to remove false negative pixels within the volume of segmented vessels as those would induce false centerlines. Based on the centerlines we extracted bifurcation points. A bifurcation is the branching point on a centerline where a larger vessel splits into two or more small vessels (Fig. 4a). In a network analysis context they are significant as they represent the nodes of a vascular network⁴⁸. Furthermore, bifurcation points have significance in a biological context. In neurodegenerative diseases, capillaries are known to degenerate⁴⁹, thereby substantially reducing the number of bifurcation points in an affected brain region compared to a healthy brain. We implemented an algorithm to detect the bifurcation points by taking the centerlines as an input and calculating the surrounding centerline pixels for every point on that centerline to determine whether a point is a centerline. The radius of a blood vessel is a key feature to describe vascular networks. The radius yields information about the flow and hierarchy of the vessel network. The proposed algorithm calculates the Euclidean distance transform for every segmented pixel v to the closest background pixel b_closest. Next, the distance transform matrix was multiplied with the 3D centerline mask equaling the minimum radius of the vessel around the centerline.

$$d\left(v,b_{\mathit{\text{closest}}}\right)=\sqrt{\sum _1^3{\left(v_i-b_{\mathit{\text{closest}},i}\right)}^2}$$ (IV.)

Feature quantification

Here we describe in detail how we calculated the features between the three different spaces:

Voxel space to microscopic space

To quantify our vessel length in SI units instead of voxels we calculated their Euclidean length, which depends on the direction of the connection of skeleton pixels (Supplementary Fig. 9). To calculate the Euclidean length of our centerlines, we carried out a connected component analysis, which transformed each pixel of the skeleton into an element of an undirected weighted graph, where zero weight means no connection and non-zero weights denote the Euclidean distance between two voxels (considering 26 connectivity). Thus, we obtain a large and sparse adjacency matrix. An element-wise summation of such a matrix provides the total Euclidean length of the vascular network along the extracted skeleton.

As measuring connected components is computationally very expensive, we calculated this Euclidean length of the centerlines for twelve representative volumes of 500 × 500 × 50 pixels, and divided by the number of skeleton pixels. We calculate an average Euclidean length ε_Cl of 1.3234 ± 0.0063 (mean ± SD) voxels per centerline element. This corresponds to a length of 3.9701±0.0188 (mean ± SD) μm in cleared tissue. Since the standard deviation of this measurement is low at less than 0.5% of the length, we apply this correction factor to the whole brain centerline measurements. This correction does not apply to the bifurcation points and our radius statistics, as bifurcations are independent of length and the radius extraction returns a Euclidean distance by default. Euclidean length, depending on the direction of the connection of skeleton pixels, the length of a skeleton pixel is different (Supplementary Fig. 9).

Microscopic space to anatomical space

To account for the tissue shrinkage (Supplementary Fig. 9), which is inherent to DISCO clearing, we carried out an experiment to measure the degree of shrinkage. Before clearing, we imaged three live BALB/c mice brains with magnetic resonance imaging and calculated their brain’s average volumes, through precise manual segmentation by an expert. Next, we cleared three BALB/c brains, processed them using VesSAP and measured the total brain volumes using the atlas alignment. We report an average volume of 423.84 ± 2.04 mm³ for the live mice and 255.62 ± 6.57 mm³ for the cleared tissue. This accumulates to a total volume shrinkage of 39.69 %. We applied this as a correction factor for the volumetric information (e.g. brain regions).

Similar to previous studies, the shrinkage is uniform in all three dimensions. This is important, when considering shrinkage in one dimension as needed to account for the shrinkage in the centerlines and the radius. The one dimensional correction factor К_L then corresponds to the cube root of the volumetric correction factor К_V.

Accounting for those factors we calculate the vessel length per volume (Z) in cleared (Z_cleared) and real tissue (Z_real) in Equation V., where N_V,vox is the number of total voxels in the reference Volume and N_Cl,vox is the number of centerline voxels in the image Volume:

$$Z_{\mathit{\text{cleared}}}=\frac{N_{Cl,vox}}{N_{V,vox}}\times {\epsilon }_{Cl}{Z}_{\mathit{\text{real}}}=\frac{N_{Cl,vox}}{N_{V,vox}}\times {\epsilon }_{Cl}\times \frac{{\kappa }_L}{{\kappa }_V}$$ (V.)

Similarly, we calculate the bifurcation density (B) in cleared and real tissue in Equation VI., where N_Bif,vox is the number of bifurcations in the reference Volume:

$$B_{\mathit{\text{cleared}}}=\frac{N_{Bif,vox}}{N_{V,vox}}{B}_{\mathit{\text{real}}}=\frac{N_{Bif,vox}}{N_{V,vox}}\times \frac{1}{{\kappa }_V}$$ (VI.)

Please note, the voxel spacing of 3 μm has to be considered when reporting the features in SI-units.

Inter-annotator experiment for the features

To estimate the error in VesSAP’s feature quantification, we extracted the features on a labeled test set of 5 volumes of 500 × 500 × 50 pixels. When comparing to the gold standard label, we calculate errors (disagreements) of 8.21% for the centerlines, 13.18% for the number of bifurcation points and 16.33% for the average radius. To compare VesSAP’s extracted features to a human level annotation we implemented an inter-annotator experiment. For this experiment we had 4 annotators, who labeled the vessels and radius in 2 volumes of 500 × 500 × 50 pixels using the ImageJ and ITK-snap. Finally, we calculated the agreement of the extracted features between all annotators and compared to the gold standard label.

We calculated this for each of the volumes and find an average error (disagreement) of 34.62% for the radius, 25.20% for the bifurcation count and 12.55% for the centerline length.

The agreement between the VesSAP output and the gold standard is higher than the average agreement between the annotators and the gold standard. This difference underlines the quality and reproducibility of VesSAP’s feature extraction.

Registration to the reference atlas

We used the average template, the annotation file and the latest ontology file (Ontology ID: 1) of the current Allen mouse brain atlas CCFv3 201710. Then we scaled the template and the annotation file up from 10 to 3 μm³ to match our reconstructed brain scans and multiplied the left side of the (still symmetrical) annotation file with −1 so that the labels could be later assigned to the corresponding hemispheres. Next, the average template and the 3D vascular datasets were downsampled to 10% of their original size in each dimension to achieve a reasonably fast alignment with the elastix toolbox⁵⁰ (v4.9.0). For the sake of the integrity of the extracted features, we aligned the template to each of the brain scans individually using a two-step rigid and deformable (B-Spline, optimizer: AdaptiveStochasticGradientDescent, metric: AdvancedMattesMutualInformation, grid spacing in physical units: 90, in the VesSAP repository we host the log and parameter files for each brain scan) registration and applied the transformation parameters to the full resolution annotation volume (3 μm resolution). Subsequently, we created masks for the anatomical clusters based on the current Allen brain atlas ontology.

Statistical analysis of features

Data collection and analysis were not performed blind to the strains. Data distribution was assumed to be normal, though this was not formally tested. All data values of the descriptive statistics are given as mean ± SEM unless stated otherwise. Data were analyzed with standardized effect size indices (Cohen’s d)⁵¹ to investigate differences of vessel length, number of bifurcation points and radii between brain areas across the three mouse strains (n=3 per strain). Descriptive statistics were evaluated across brain regions in the pooled (n=9) dataset.

Data visualization

All volumetric datasets were rendered using Imaris, Vision4D and ITK Snap.

CODE AND DATA AVAILABILITY

VesSAP codes and data are publicly hosted at http://DISCOtechnologies.org/VesSAP, and include the imaging protocol, data (original scans, registered atlas data), trained algorithms, training data and a reference set of features describing the vascular network in all brain regions. Additionally, the source code is hosted on GitHub (https://github.com/vessap/vessap) and on the executable platform CodeOcean (https://doi.org/10.24433/CO.1402016.v1). Implementation of external libraries is available on request.