Quantifying the impact of public health protection measures on the spread of SARS-CoV-2

Abstract

The new virus, SARS-CoV-2, has probably affected millions of people world-wide since December 2019 and killed thousand. We have designed a model and used it to quantify the effect of local protective measures on the SARS-CoV-2 epidemic, assess their effectiveness and adapt health service strategies in Toulouse, France.

Dear Editor,

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emerged in Wuhan, China in December 2019 and spread, mainly by sustained human-to-human transmission, so rapidly that it threatened to saturate health services¹. This led the governments of several countries to employ strict lockdown to slow the progression of the pandemic at the start of 2020^{2 , 3}. The SARS-CoV-2 epidemic has resumed in European countries, including France, since the end of the summer. As a result, several large cities have taken measures to limit the transmission of the virus⁴. A recent study published in this journal assessed the impact of different strategies including lockdown to contain the spread of the SARS-CoV-2 in the London population during the first phase of epidemic in March 2020⁵. In a complementary way, we evaluated here the effectiveness of each individual public health measure chosen as alternatives to a new strict lockdown, on the basis of the real SARS-CoV-2 dynamics. modeling the global evolution of the epidemic in France has become very complicated since the strategies used differ between regions and cities⁴. But their effectiveness could be assessed by quantifying the local impact of protective measures against SARS-CoV-2. These could then be adapted for use in other contexts.

Our statistical model is based on a diffusion and transmission coefficient that varies with an individual's age, the likelihood of contagion, and a reduction coefficient that accounts for the impact of public health measures on virus transmission in the French city of Toulouse. We have used models to measure how the dynamics of the SARS-CoV-2 infection is influenced by each individual public health measure.

Consider the variables $\left(S_n,P_n,I_n,\widehat{S_n},\widehat{P_n},\widehat{I_n}\right)$. $A$ is defined as the age class variable:

$$A\in \{<18y.o,18-64,65-74,\ge 75y.o\}.$$

On day $n,$ for a given age class $A,S_{n,A}$ is the real number of healthy people and$\widehat{S_{n,A}}$ is the estimated number. $P_{n,A}^i$ and $\widehat{P_{n,A}^i}$ are the real and the estimated numbers of contagious carriers infected for $i$ days $\left(1\le i\le N_T\right)$. $I_{n,A}$ and $\widehat{I_{n,A}}$ are the real and estimated numbers of people in a given age class $A$ who are immunized or have died. We assume that the risk of reinfection by SARS-CoV-2 after a first infection is negligible.

$N_T$ is defined as the number of days a person is contagious. $R_0$ is the number of healthy people who a contagious person contacts and infects. We assume that the contagion coefficient varies over time and peaks when the virus load is maximal: 7 days after the start of infection⁶. $N$ is the total population at the start of the epidemic phase, $c$ is the real multiplier for the rate at which the epidemic spreads according to the protective measures applied $\left(0\le c\le 1\right)$, $\widehat{c}$ is the estimated coefficient. $c$ and $\widehat{c}$ are equal to 1 when no protective measures are in use.

$$P_n=\sum _A\sum _{i=1}^{N_T}{P}_{n,A}^i$$

$N$ is given by:

$$N=\sum _A{N}_A=\sum _A{S}_{n,A}+P_{n,A}+I_{n,A}$$

On the transition from day $n$ to day $n+1$, we have:

$$\forall 1\le i\le N_T-1,P_{n+1,A}^{i+1}=P_{n,A}^i$$ (1)

$$P_{n+1,A}^1=\frac{S_{n,A}}{N_A}.\left[\sum _i{P}_{n,A}^i.R_0^i.c\right]$$ (2)

$$I_{n+1,A}=I_{n,A}+P_{n,A}^{N_T}$$ (3)

The model is a discretized version of a Susceptible Infectious and Recovered (SIR)-type model⁷

We have set $R_0=1.17$ based on current data in our area.⁸

We estimated the initial model settings using data collected by the Toulouse Virology Laboratory. $\forall n\in \left[[d+1,+\infty ]\right]\widehat{c}$ is corrected by fitting the predicted data ${\widehat{P}}_n$ to the real data $P_n$ as:

$$\widehat{c}=\underset{c}{\text{argmin}}{\left|{\widehat{P}}_n-P_n\left(c\right)\right|}_{n\in \left[\right[1,d\left]\right]}$$

The data obtained by the Toulouse Virology Laboratory using serological tests showed that the real seroprevalence in the Toulouse urban area was around 1.5% at the end of lockdown (May 11, 2020). The population of the Toulouse urban area is around 1 million, which implies a number of immune individuals $I_0$ close to 15,000 in mid-May. The number of SARS-CoV-2 cases gradually increased from July 21, 2020. Date $d$ corresponds to October 6, 2020.

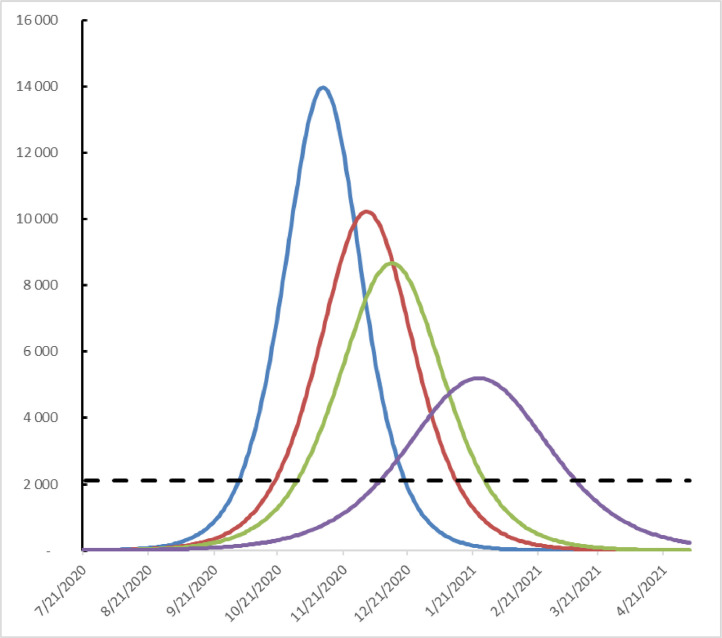
We estimated $\widehat{c}$ to be 82% at the end of July 2020, with no specific local protective measures in place. The epidemic is evolving as shown by the blue curve, with a peak of nearly 14,000 new cases on November 11 (Fig. 1 ). But the local authorities decided to make the wearing of masks compulsory in certain areas of the city on August 5. This reduced the virus coefficient of transmission ($\widehat{c}=$75%). The epidemic then evolved as shown by the red curve with a maximum of new cases approaching the 10,000 expected on December 2 (Fig. 1). Mask wearing was made compulsory throughout Toulouse on August 21, and the estimated value of $\widehat{c}$ became 72%. The epidemic therefore evolved as shown by the green curve with a peak around 8500 new cases on December 13 (Fig. 1). Finally, some public spaces, such as bars, were placed under curfew and certain sports structures were added to the measures already in force on September 26. This resulted in a $\widehat{c}$ value of 65% and the epidemic evolved as indicated by the purple curve with a peak approaching 5000 new cases on January 22, 2021 (Fig. 1). Making compulsory the mask wearing and restricting access to some spaces open to the public reduced the maximum number of new infected cases per day by more than 75% and delayed the infected peak by approximately 2 months (from blue curve to purple curve). But these measures did not make it possible to avoid the saturation of the intensive care units in Toulouse (2100 new cases per day: black dotted line), which led the government authorities to add a global curfew on October 16. Its impact on the spread of the SARS-CoV-2 remains to be assessed.

Fig. 1.

Dynamics of SARS-CoV-2 infection per day from July 21, 2020 to May 5, 2021 according to the decisions on the protective measures .blue: no specific local measure red: masks are mandatory in some urban areas, green: masks are mandatory in the all Toulouse urban area, purple: closure of some public spaces and compulsory masks. The black dotted line corresponds to the new infections threshold at which the intensive care units could be saturated.

We believe that this provides a basis for estimating the effect of specific restrictions on the dynamics of the SARS-CoV-2 epidemic. Its application could well indicate how local strategies can be tailored to avoid saturation of health services.