Measurement error correction and sensitivity analysis in longitudinal dietary intervention studies using an external validation study

Summary:

In lifestyle intervention trials, where the goal is to change a participant’s weight or modify their eating behavior, self-reported diet is a longitudinal outcome variable that is subject to measurement error. We propose a statistical framework for correcting for measurement error in longitudinal self-reported dietary data by combining intervention data with auxiliary data from an external biomarker validation study where both self-reported and recovery biomarkers of dietary intake are available. In this setting, dietary intake measured without error in the intervention trial is missing data and multiple imputation is used to fill in the missing measurements. Since most validation studies are cross-sectional, they do not contain information on whether the nature of the measurement error changes over time or differs between treatment and control groups. We use sensitivity analyses to address the influence of these unverifiable assumptions involving the measurement error process and how they affect inferences regarding the effect of treatment. We apply our methods to self-reported sodium intake from the PREMIER study, a multi-component lifestyle intervention trial.

1. Introduction

Lifestyle intervention studies—which aim to change a participant’s weight or eating behavior—often use self-reported measures of diet, but obtaining accurate measurement of diet and its change over time is a major challenge due to measurement error. Measurement error in intervention studies can result in biased estimates of the treatment effect as well as reduced power to detect treatment effects (Forster et al. 1990). Little attention has been paid to correcting for measurement error when an outcome is measured with error, partly due to the fact that when outcomes measured with error are unbiased, parameters for means can still be estimated without error, although with less power (Carroll et al. 2006). In this paper we focus on intervention studies where longitudinal trends in an outcome are of interest. In these settings—particularly in lifestyle interventions—outcomes measured with error are not unbiased and the process that gives rise to measurement error may change—resulting in more or less bias—as a function of time and as a result of the intervention.

Dietary intake in lifestyle interventions is often measured using a 24-hour dietary recall in which the previous day’s intake is reported. Estimates from 24-hour recalls are subject to measurement error, primarily due to memory limitations and poor quantification of portion sizes, as well as the fact that the selected days of intake may not be representative of a participant’s usual intake (Willet 2013, Chapter 4).

Longitudinal dietary intervention studies involve repeated dietary assessments over time and produce measurement error issues in addition to those encountered in descriptive studies. Participants may modify their reporting behavior to appear compliant with the dietary recommendations of the intervention (Espeland et al. 2001), or they may attempt to reduce reporting time and reporting difficulty by omitting items or by erroneously reporting foods that are easier to measure or describe (Buzzard et al. 1996). Alternatively, their accuracy may improve due to training in portion size assessment and a more general awareness of their dietary intake (Natarajan et al. 2010, Espeland et al. 2001).

Dietary validation studies measure—on the same set of participants—both self-reported diet as well as unbiased estimates of dietary intake using urinary biomarkers, which require a participant to collect their urine for 24 hours. Currently, urinary biomarkers exist for protein, potassium, and sodium intake.

With a validation study, one can model the relationship between the self-reported variable measured with error and true intake. Then, true intake in the intervention study can be imputed so that dietary intake estimands of interest can be based on measurement error-corrected values. This approach of using external validation samples and treating variables measured without error as missing data has been used in a number of applications, see for example, Shardell et al. (2010), Schenker et al. (2010) and Guo et al. (2012).

In this paper, we extend missing data approaches for measurement error correction to intervention studies with longitudinal outcomes. External dietary validation studies are almost always cross-sectional, meaning that information on changes in measurement error over time and in response to treatment is not available. As a result, identification of parameters in our measurement error correction model requires parameter restrictions based on unverifiable assumptions regarding the measurement error process and its change over time and in response to treatment. We describe the use of sensitivity analyses to address the influence of these unverifiable assumptions on inferences.

2. Scientific background and data sources

The PREMIER Study (Appel et al. 2003), a randomized trial designed to determine the effects of lifestyle interventions on blood pressure among free-living individuals, enrolled 810 adults with above-optimal blood pressure who were not taking antihypertensive medications. Participants were randomly assigned to one of three intervention groups: Established, Established Plus DASH, and an Advice-Only comparison group. Participants in the Established group received instruction and counseling over 6 months to modify their diet—including calorie and sodium consumption—and increase their physical activity. Those in the Established Plus DASH group had the same intervention as the Established group, and were also taught to follow a diet rich in fruits, vegetables, and low fat dairy products. Participants in both active intervention conditions received 18 face-to-face intervention contacts during the initial 6 months of the study and were counseled to reduce sodium intake to less than 2300 mg/day. Participants in the Advice-Only condition received lifestyle advice during two 30-minute individual sessions, one at baseline and one at 6-months.

Self-reported dietary intake in PREMIER—including sodium intake, our outcome of interest—was measured using two unannounced, non-consecutive, 24-hour recalls conducted by telephone on one weekday and one weekend day at baseline and at 6- and 18-months. We combine the Established and the Established Plus DASH groups into a single treatment condition since changes in sodium intake were similar in the two groups (Appel et al. 2003). We compare this single treatment condition to the Advice-Only condition.

PREMIER was the rare lifestyle intervention that collected 24-hour urine samples on all participants at each time point. We will revisit these biomarker data in Section 7 when we compare the results of our measurement error correction methods to an analysis that uses PREMIER 24-hour urinary sodium. For now, we will ignore the PREMIER 24-hour urine samples and treat the PREMIER study as a “typical” lifestyle intervention where only self-reported dietary data are collected.

To correct for measurement error in PREMIER self-reported sodium intake, we use data from the Observing Protein and Energy Nutrition (OPEN) validation study (Subar et al. 2003). OPEN participants were 484 men and women aged 40-69 years. In addition to two 24-hour recalls, participants were assessed for sodium, potassium, and nitrogen intake via two 24-hour urine collections. As only 86% of sodium intake appears in urine, urinary sodium values were divided by 0.86 to convert them to dietary sodium values (Willet 2013, Chapter 8).

Table 1 presents demographic characteristics and sodium intake in PREMIER at baseline and in OPEN. Participant ages in the two studies are similar, although PREMIER participants have higher BMI, slightly lower self-reported sodium intake, and a smaller percentage of men. A small proportion of outliers were removed from both samples using criteria detailed in Web Appendix A.

Table 1:

Demographic characteristics and baseline sodium intake in PREMIER and OPEN by gender. Values are mean (SD) unless otherwise noted. Three PREMIER participants were missing self-reported sodium intake at all three time points and were not included in our analysis. Ten PREMIER and 25 OPEN participants were excluded due to extreme self-reported total energy intake values.

Variable	PREMIER (n=797)	OPEN (n=459)
Male, n (%)	303 (38)	244 (53)
Age	50.0 (8.9)	53.7 (8.3)
BMI	33.0 (5.7)	27.7 (5.1)
(Log) Self-reported sodium	8.0 (0.41)	8.2 (0.43)
(Log) Urinary sodium	8.4 (0.44)	8.4 (0.45)

Note. PREMIER age values are from (Svetkey et al. 2003) and include the entire sample

We estimate the treatment effect in PREMIER by comparing the change in (log-transformed) sodium intake from baseline to the end of the intervention phase (6-months) between the Treatment and Advice-Only conditions. Let Z_j be the true value of the outcome we wish to measure at time j, j = 0, … , m where baseline is j = 0. Let Y_j be Z_j measured with error and D an indicator as to whether a participant has been randomized to the intervention group (D = 1) or the control group (D = 0). The treatment effect is,

$$\psi =\{E(Z_1\mid D=1)-E(Z_0\mid D=1)\}-\{E(Z_1\mid D=0)-E(Z_0\mid D=0)\}.$$ (1)

When ψ < 0, reduction in mean log sodium intake is greater in the treatment group than the control group (or less commonly, increase in intake is less in the treatment group than the control group). Significance of the treatment effect is based on a two-sample t-test of the difference in change scores between treatment and control groups. We report the effect size: the estimate of the treatment effect in (1) divided by the pooled standard deviation of the change scores.

An analysis of the self-reported PREMIER data produced a significant treatment effect where the effect size at 6-months was −0.49 (p<.0001). Our goal is to estimate the treatment effect in (1) using measurement error corrected sodium intake.

3. Definitions

We define how measurement error correction models can change over time and with respect to treatment. Our measurement error correction models condition on the variable measured with error so we refer to them as calibration models to highlight connections with regression calibration (Carroll et al. 2006) in which a similar approach is used. Let X represent background covariates measured at baseline.

Definition 1: The calibration model is treatment invariant if f(Z_j | Y_j, X, D = 1) = f(Z_j | Y_j, X, D = 0), for j ⩾ 0. That is, the parameters of the calibration model do not change in response to treatment and are the same in both treatment and control groups. We assume calibration model invariance with respect to treatment holds at baseline (j = 0) because treatment has not started yet.

Definition 2: The calibration model is time invariant if f(Z_j | Y_j, X, D = d) = f(Z_k | Y_k, X, D = d), for all j ≠ k, where j and k are two different time points. Here, within a treatment condition, the parameters of the calibration model will be the same across all time points.

Definition 3: The calibration model is treatment and time invariant if f(Z_j | Y_j, X, D = 1) = f(Z_k | Y_k, X, D = 0), for all j, k.

Definition 4: If the parameters of the calibration model in the intervention data at time j for treatment group d are the same as the parameters of the calibration model using external validation data, then the parameters from the calibration model using external validation data are transportable to the calibration model for that treatment-by-time combination. Let S denote whether a participant is in the lifestyle intervention (S = ℓ) or validation study (S = v). Under calibration model transportability, the following holds: f(Z_j | Y_j, X, D = d, S = ℓ) = f(Z₀ | Y₀, X, S = v).

Our definition of calibration model transportability assumes the external validation study is cross-sectional (corresponding to the baseline time point in the intervention study) and observational (no treatment conditions) and that transportability can apply at some treatment-by-time combinations but not others. When the calibration model is treatment and time invariant, transportability at any treatment-by-time combination implies transportability at all treatment-by-time combinations. In Web Appendix B, we show that our definition of calibration model transportability implies that selection into the trial or validation study does not depend on unobserved Z after conditioning on observed characteristics Y and X, which is a plausible selection mechanism our setting where study inclusion criteria are based on observed characteristics.

4. Methods

The top half of Table 2 represents data from PREMIER where the outcomes Y₀ and Y₁ represent self-reported sodium intake via 24-hour recall measured at baseline and 6-months, respectively.

Table 2:

Patterns of missing data in the PREMIER and OPEN studies. The variables Y₀ and Y₁ represent self-reported sodium intake via 24-hour recall measured at baseline, and 6-months, respectively. The variables Z₀ and Z₁ are versions of Y measured without error. The variables W₀₁ and W₀₂ are replicate urinary sodium values taken at baseline in OPEN and are considered unbiased measures of Z₀. The variables X and D represents background covariates and treatment condition, respectively. OPEN participants are assumed to all belong to the control condition. Grey cells indicate observed values, white cells indicate missing values. Note that all values are missing for Z₀ and Z₁ in both studies.

Data Source	Y0	W01	W02	Z0	Y1	Z1	X	D
PREMIER Intervention Study
OPEN External Validation Study

The bottom half of Table 2 represents data from OPEN which contains Y₀, self-reported sodium, but also contains the variables W₀₁ and W₀₂ which are the two replicate urinary sodium samples taken at baseline in OPEN. The shaded cells in Table 2 represent values that are observed, the white cells are values that are missing. Urinary sodium is an unbiased measure of true sodium intake but is also subject to error. In Section 4.1 we describe use of W₀₁ and W₀₂ in OPEN to correct for measurement error in urinary sodium intake in order to obtain true sodium intake at baseline Z₀. The column labeled X in Table 2 represents background covariates available on all participants in both studies. Here we condition on sex and (log) BMI in all our models as there is some evidence that these variables are associated with measurement error (Willet 2013, Chapter 4).

Since OPEN—like most external validation studies—is cross-sectional, we assume that its data correspond to baseline values Y₀ and Z₀ and that all OPEN participants belong to the control condition. Values of Z₁ in Table 2 are completely unobserved for all participants, both those in the intervention study and those in the validation study. We thus have no information on the relationship between Y₁ and Z₁.

The joint distribution of Y and Z, conditional on X and D in PREMIER, can be written as f(Z₁, Z₀, Y₁, Y₀ | X, D, θ), where θ is a finite-dimensional parameter vector. While the focus of our inference is on Z, it is necessary to also model Y due to missing values in Y which we assume are ignorable.

The joint distribution can be further decomposed into observed and missing components. Suppressing D and the parameters θ we have:

$$f(Z_1,Y_1,Z_0,Y_0\mid \mathbf{X})=f(Z_1\mid Y_1,Z_0,Y_0,\mathbf{X})f(Z_0\mid Y_1,Y_0,\mathbf{X})f(Y_1,Y_0\mid \mathbf{X}).$$ (2)

We assume multivariate normality on a log sodium scale. Most of the parameters in (2) are not identified due to the fact that Z₁ is completely unobserved. To help identify the conditional distributions in (2), we make the first-order Markov assumption that f(Z₁|Y₁, Z₀, Y₀, X) = f(Z₁ | Y₁, Z₀, X) such that the conditional distribution of Z at time 1 (6-months) depends only on its version measured with error and its previous (baseline) measurement. For f(Z₀ | Y₁, Y₀, X) we make the similar assumption that f(Z₀ | Y₁, Y₀, X) = f(Z₀ | Y₀, X). These conditional independence assumptions cannot be checked in our data. Equation (2) reduces to:

$$f(Z_1,Z_0,Y_1,Y_0\mid \mathbf{X})=f(Z_1\mid Y_1,Z_0,\mathbf{X})f(Z_0\mid Y_0,\mathbf{X})f(Y_1,Y_0\mid \mathbf{X}),$$ (3)

where, under our multivariate normality assumption, the conditional distributions in (3) are a sequence of linear regression models. Only the parameters associated with f(Y₁, Y₀ | X) on the right-hand-side of (3) are identified. The parameters from the conditional distributions of Z₁ and Z₀ are not identified.

In the following subsections, we describe our strategies for identification of the unidentified parameters in f(Z₁ | Y₁, Z₀, X) and f(Z₀ | Y₀, X) on the right-hand side of (3).

4.1. Identification of f(Z₀ | Y₀, X)

Identification of the conditional distribution of Z given Y and X at baseline in PREMIER is based on the transportability assumption that f(Z₀ | Y₀, X, S = ℓ) = f(Z₀ | Y₀, X, S = v). However, urinary sodium, while considered unbiased, is subject to classical measurement error (Prentice et al. 2002). Therefore, to estimate f(Z₀|Y₀, X, S = v) in OPEN, we must first correct for measurement error in urinary sodium intake in order to estimate the distribution of “true” sodium intake conditional on self-reported sodium intake. We do this using the replicate measures of urinary sodium in OPEN to partition the conditional variance of urinary sodium into its between-subject and within-subject components. The within-subject variance is considered measurement error and is removed (Willet 2013, chap. 12), resulting in error-corrected urinary sodium intake.

Let W_0r, r = 1, 2 represent the two replicate values of urinary sodium that were obtained from OPEN participants around the time of the 24-hour recall (Y₀). We assume W_0r = Z₀+e_r where the e_r are independent with mean 0 and common variance and independent of X and Y₀. Then E(W_0r | Y₀, X) = E(Z₀ | Y₀, X) and Cov(W₀₁, W₀₂ | Y₀, X) = Var(Z₀ | Y₀, X). We fit the following random-intercept regression model for OPEN participant i.

$$W_{0\mathit{ir}}={\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(v)}+{\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(v)}{Y}_{0i}+{\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(v)}{\mathbf{X}}_{\mathbf{i}}+b_{0i}+{\epsilon }_{\mathit{ir}}$$ (4)

where $b_{0i}\sim N(0,{\sigma }_{Z_0\cdot Y_0\mathbf{X}}^{2(v)})$ and ${\epsilon }_{\mathit{ir}}\sim N(0,{\sigma }_w^2)$.

The distribution f(Z₀ | Y₀, X) in OPEN is

$$Z_0\mid Y_0,\mathbf{X},S=v\sim N({\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(v)}+{\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(v)}{Y}_0+{\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(v)}\mathbf{X},{\sigma }_{Z_0\cdot Y_0\mathbf{X}}^{2(v)})$$ (5)

where the parameters in (5) are obtained from fitting model (4).

The distribution of f(Z₀|Y₀, X, S = ℓ) in the intervention study is specified as the following linear regression model:

$$Z_0\mid Y_0,\mathbf{X},S=\ell \sim N({\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}+{\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}{Y}_0+{\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}\mathbf{X},{\sigma }_{Z_0\cdot Y_0\mathbf{X}}^{2(\ell )}).$$ (6)

To identify the parameters in (6), we make the transportability assumption that the parameters in (6) are equal to those in (5). That is,

$${\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}={\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(v)};{\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}={\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(v)};{\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(\ell )}={\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(v)};{\sigma }_{Z_0\cdot Y_0\mathbf{X}}^{2(\ell )}={\sigma }_{Z_0\cdot Y_0\mathbf{X}}^{2(v)}.$$ (7)

In Section 4.2 we use the parameters in (7) to help identify the conditional distribution of Z₁ in (3). For the rest of this manuscript we omit the superscript ℓ on all parameters and assume they are associated with PREMIER.

4.2. Identification of f(Z₁ | Y₁, Z₀, X)

Identification of the parameters in f(Z₁ | Y₁, Z₀, X) is problematic because Z₁ is completely unobserved in both PREMIER and OPEN. Thus, we need to make several assumptions regarding the joint relationship of Z₁, Y₁, and Z₀ conditional on X. The first assumption is that the calibration model is time and treatment invariant (Definition 3), that is, f(Z₁|Y₁, X, S = ℓ) = f(Z₀|Y₀, X, S = ℓ). This assumption results in the following parameter restrictions:

$${\beta }_{0,Z_1\cdot Y_1\mathbf{X}}={\beta }_{0,Z_0\cdot Y_0\mathbf{X}};{\beta }_{1,Z_1\cdot Y_1\mathbf{X}}={\beta }_{1,Z_0\cdot Y_0\mathbf{X}};{\beta }_{2,Z_1\cdot Y_1\mathbf{X}}={\beta }_{2,Z_0\cdot Y_0\mathbf{X}};{\sigma }_{Z_1\cdot Y_1\mathbf{X}}^2={\sigma }_{Z_0\cdot Y_0\mathbf{X}}^2.$$ (8)

For f(Z₁ | Y₁, Z₀, X); there are two sets of unidentified parameters: the partial correlation between Y₁ and Z₀ given X and the partial correlation between Z₁ and Z₀ given Y₁ and X. Both of these parameters are unrestricted and independently range from −1 to 1 (Daniels and Pourahmadi 2009). To identify these parameters we make assumptions which we incorporate into our model using informative prior distributions. First, we assume 0 < corr(Y₁, Z₀ | X) < corr(Y₀, Z₀ | X) such that the partial correlation between self-reported sodium at time 1 and true sodium intake at baseline is positive and less than the partial correlation of these two variables at baseline. The correlation of Y₀ and Z₀ given X is given in Web Appendix C. Based on this assumption, a non-degenerate prior distribution for corr(Y₁, Z₀|X) is corr(Y₁, Z₀|X) ~ Uniform{0, corr(Y₀, Z₀ | X)}.

The second unidentified parameter in f(Z₁ | Y₁, Z₀, X) is the partial correlation of Z₁ and Z₀ given Y₁ and X. Positing this quantity directly is difficult, so we instead posit the partial correlation of Z₁ and Z₀ given X while taking into account that this correlation is bounded by ${\rho }_{Z_1{Y}_1\cdot \mathbf{X}}{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}\pm \sqrt{(1-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}^2)(1-{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}^2)}$. We assume corr(Z₁, Z₀ | X) = corr(Y₁, Y₀ | X) + Δ_Zρ such that the partial correlation between two adjacent measurement error corrected variables is centered around the partial correlation between two adjacent self-reported measurements. The parameter Δ_Zρ can be viewed as an error term and has the prior distribution Δ_Zρ ~ Uniform(−δ, δ).

Combining our assumption regarding the partial correlation of Z₁ and Z₀ with its boundary constraints gives the following prior for corr(Z₁, Z₀ | X):

$${\rho }_{Z_1{Z}_0\cdot \mathbf{X}}\sim \text{Uniform}\left\{\mathit{max}\left({\rho }_{Y_1{Y}_0\cdot \mathbf{X}}-\delta ,{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}-\sqrt{(1-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}^2)(1-{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}^2)},0\right),\mathit{min}\left({\rho }_{Y_1{Y}_0\cdot \mathbf{X}}+\delta ,{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}+\sqrt{(1-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}^2)(1-{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}^2)},1\right)\right\}.$$ (9)

and the partial correlation of Z₁ and Z₀ conditional on Y₁ and X is

$${\rho }_{Z_1{Z}_0\cdot Y_1\mathbf{X}}=\frac{{\rho }_{Z_1{Z}_0\cdot \mathbf{X}}-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}{\rho }_{Z_0{Y}_1\cdot \mathbf{X}}}{\sqrt{1-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}}\sqrt{1-{\rho }_{Z_1{Y}_1\cdot \mathbf{X}}}}.$$

After obtaining corr(Y₁, Z₀ | X) and corr(Z₁, Z₀ | Y₁, X), we obtain f(Z₁ | Y₁, Z₀, X) using

$$f(Z_1\mid Y_1,Z_0,\mathbf{X})=\frac{f(Z_1,Z_0\mid Y_1,\mathbf{X})}{f(Z_0\mid Y_1,\mathbf{X})}.$$

Parameter estimators for the regression of Z₀ on Y₁ and X are given in Web Appendix C. The regression of Z₁ on Y₁, Z₀, and X can be written as

$$Z_1\sim N({\beta }_{0,Z_1\cdot Y_1{Z}_0\mathbf{X}}+{\beta }_{1,Z_1\cdot Y_1{Z}_0\mathbf{X}}{Y}_1+{\beta }_{2,Z_1\cdot Y_1{Z}_0\mathbf{X}}{Z}_0+{\beta }_{3,Z_1\cdot Y_1{Z}_0\mathbf{X}}\mathbf{X},{\sigma }_{Z_1\cdot Y_1{Z}_0\mathbf{X}}^2).$$ (10)

Estimators for the parameters of this regression are also given in Web Appendix C.

4.3. Estimation

Parameter draws from the posterior distribution of f(Y₁, Y₀ | X)—as well as imputations of missing values of Y₁ and Y₀ were obtained using Markov Chain Monte Carlo (MCMC) via a Bayesian multivariate normal model implemented in the R package norm2 (Schafer 2016). We used an improper Jeffreys’ prior for the covariance matrix and the mean parameters.

Estimation of the model parameters in (4) also used MCMC based on the Bayesian linear mixed-effects approach implemented in the R package pan (Zhao and Schafer 2016). We used an improper uniform density for the regression coefficients ${\beta }_{0,Z_0\cdot Y_0\mathbf{X}}^{(v)}$, ${\beta }_{1,Z_0\cdot Y_0\mathbf{X}}^{(v)}$ and ${\beta }_{2,Z_0\cdot Y_0\mathbf{X}}^{(v)}$ and gamma priors with shape and scale parameters equal to 0.5 for the random effects and error precision parameters.

In both models, after a 10,000 iteration burn-in period, we performed an additional 50,000 iterations and obtained 100 imputations for each missing value of Y₁ and Y₀ and 100 parameter values by selecting every 500th iteration. We assessed convergence of our Markov chains by visual inspection of trace plots and autocorrelation plots.

5. Sensitivity Analyses

We investigate how sensitive the effects of the PREMIER intervention are to changes in measurement error over time and between treatment conditions. A longitudinal study may 1) result in more accurate/precise reports of diet due to improved self-monitoring; 2) encourage participants to misreport their diet in order to appear compliant with the intervention; and/or 3) result in no change in the measurement error seen at baseline.

Sensitivity analyses are anchored at calibration model invariance with respect to treatment and time (Definition 3 in Section 3) which is represented by the parameter constraints in (8). Our sensitivity analyses are based on exploring departures from these constraints and their results on our inferences. For interpretability, we consider sensitivity to the assumption that the intercept of the regression of Z on Y and X at baseline is the same at follow-up (β_0,Z1·Y1X = β_0,Z0·Y0X). We also consider sensitivity to the assumption that the slope between Z and Y is the same at baseline as at follow-up (β_1,Z1·Y1X = β_1,Z0·Y0X).

5.1. Intercept sensitivity parameter

Departures from calibration model invariance with respect to treatment and time in terms of the intercept parameters in (8) are based on the following reparameterization: ${\beta }_{0,Z_1\cdot Y_1\mathbf{X}}^{(d)}={\beta }_{0,Z_0\cdot Y_0\mathbf{X}}+{\Delta }_{{\beta }_0}^{(d)}$; where the sensitivity parameter ${\Delta }_{{\beta }_0}^{(d)}$ measures the additional under or over reporting at month 6 (t = 1) as compared to baseline for a given level of self-report. The superscripts correspond to the treatment group (d=1) or control group (d=0).

We scale Δ_β0 in terms of a percent increase or decrease in the residual standard deviation σ_Z0·Y0X in (7). For example, when Δ_β0 = 1.2 × σ_Z0·Y0X, the intercept of the regression of Z₁ on Y₁ and X is 20% of a residual standard deviation greater than the intercept of Z₀ on Y₀ and X. This sensitivity parameter can be both greater and less than 1 so that the amount of underreporting can both increase or decrease.

5.2. Slope sensitivity parameter

In PREMIER, participants in both the Established and the Established Plus DASH conditions were counseled to reduce sodium intake to less than 2300 mg/day. We center the regression line at baseline around this intervention target value of sodium intake and then multiply the baseline slope by the sensitivity parameter ${\Delta }_{{\beta }_1}^d$ so that we have the following reparameterizations:

$$\begin{gathered} {\beta }_{0,Z_1\cdot Y_1\mathbf{X}}^{(d)}={\beta }_{0,Z_0\cdot Y_0\mathbf{X}}+(1-{\Delta }_{{\beta }_1}^{(d)})\times {\beta }_{1,Z_0\cdot Y_0\mathbf{X}}\times \log (2300) \\ {\beta }_{1,Z_1\cdot Y_1\mathbf{X}}^{(d)}={\Delta }_{{\beta }_1}^{(d)}\times {\beta }_{1,Z_0\cdot Y_0\mathbf{X}}. \end{gathered}$$

The idea here is that whether or not a participant has met the target influences their reporting behavior. When ${\Delta }_{{\beta }_1}^{(d)}>1$, participants who fail to meet (i.e . exceed) the target value self-report less—for a given level of true intake—than they did at baseline. And participants who did achieve the target value self-report more—for a given level of true intake—than they did at baseline. The degree of deviation from baseline is based on how far the participant deviates from the target value. When the mean of Y₁ is greater than the target value, values of ${\Delta }_{{\beta }_1}^{(d)}>1$ have the effect of increasing the mean of Z₁ and values of ${\Delta }_{{\beta }_1}^{(d)}<1$ decrease the mean of Z₁ as compared to a time-invariant calibration model (${\Delta }_{{\beta }_1}^{(d)}=1$). See Web Appendix D for details.

6. Application to the PREMIER study

6.1. Imputation and analyses

We used the nested imputation approach and associated combining rules of Reiter (2008) for settings where data are used for imputation but not analysis. Specifically, we obtain 100 parameter draws and generate 20 imputations for each parameter draw resulting in 2000 imputations for each value of Z.

Using imputed values of sodium intake measured without error drawn from Models (6) and (10) where X represents log BMI and sex, we estimated the difference in reduction of sodium intake between treatment conditions as in (1). We report the effect size of the intervention (the treatment difference scaled by its pooled standard deviation) and the p-value from a two-sample t-test. For each treatment group, we have an intercept sensitivity parameter (${\Delta }_{{\beta }_0}^{(1)}$, ${\Delta }_{{\beta }_0}^{(0)}$) and a slope sensitivity parameter (${\Delta }_{{\beta }_1}^{(1)}$, ${\Delta }_{{\beta }_1}^{(0)}$). We examine the effect of the PREMIER intervention across a range of values for these parameters. We scale ${\Delta }_{{\beta }_0}^{(1)}$ and ${\Delta }_{{\beta }_0}^{(0)}$ as a percent of the residual standard deviation parameter σ_Z0·Y0 in (7) and allow both ${\Delta }_{{\beta }_0}^{(1)}$ and ${\Delta }_{{\beta }_0}^{(0)}$ to range in 10% increments from −50% to 50% of the residual standard deviation. Both slope sensitivity parameters ${\Delta }_{{\beta }_1}^{(1)}$ and ${\Delta }_{{\beta }_1}^{(0)}$ range from 1/3 to 3. Finally, we set the δ parameter in (9) equal to 0.2 throughout all our analyses so that corr(Z₁, Z₀ | X) ranges uniformly between corr(Y₁, Y₀|X)±0.2 (subject to the positive definiteness restriction in (9)).

6.2. Results

Figures 1(a) and 1(b) are contour plots of the results of our sensitivity analyses of the effect of the PREMIER intervention at month 6 based on varying the intercept sensitivity parameters described in Section 5.1. Slope sensitivity parameters in Figures 1(a) and 1(b) are fixed across all scenarios and equal to 1. The x-axis displays values for the residual standard deviation multiplier of ${\Delta }_{{\beta }_0}^{(1)}$, the sensitivity parameter for the treatment group intercept term. The y-axis displays values for the multiplier of ${\Delta }_{{\beta }_0}^{(0)}$, the sensitivity parameter for the control group intercept term. The solid dot represents calibration model invariance with respect to treatment and time (${\Delta }_{{\beta }_0}^{(1)}={\Delta }_{{\beta }_0}^{(0)}=0$). Departures from time invariance occur when ${\Delta }_{{\beta }_0}^{(d)}\ne 0$. The top panel (Figure 1(a)) displays effect sizes and the bottom panel (Figure 1(b)) their associated p-values.

Figure 1:

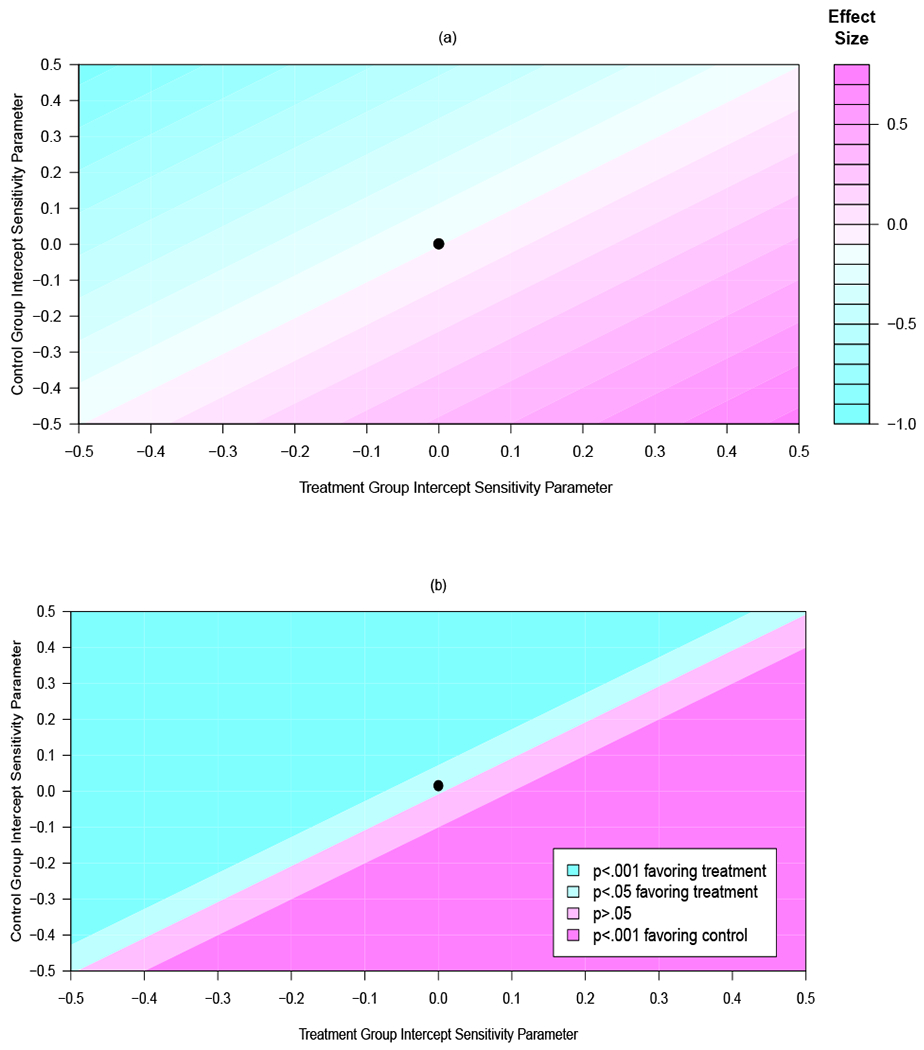
Contour plot for (a) effect sizes at 6-months and (b) their associated p-values from an analysis of the PREMIER data across a range of sensitivity parameters for the intercept of the measurement error model at follow-up as compared to baseline. The x-axis displays values for the sensitivity parameter for the treatment group, the y-axis displays values for the sensitivity parameter for the control group. The point plotted at (0, 0) corresponds to an assumption of calibration model invariance with respect to treatment and time. A color version of this Figure can be found in the electronic version of this article.

Under calibration model invariance with respect to treatment and time, the effect size (ES) is −0.11, a small effect favoring the treatment condition (p=.004). This effect size remains constant under calibration model invariance with respect to treatment (i.e. ${\Delta }_{\beta }^{(1)}={\Delta }_{\beta }^{(0)}$). Further, as illustrated by the diagonal bands in Figure 1(a), effect sizes are constant across values of ${\Delta }_{{\beta }_0}^{(1)}-{\Delta }_{{\beta }_0}^{(0)}$. It is the difference in ${\Delta }_{\beta }^{(1)}$ and ${\Delta }_{\beta }^{(0)}$ that drives the treatment effect, not the individual values themselves (see Web Appendix D for details). However, inferences are very sensitive to departures from calibration model invariance with respect to treatment. The top left quadrant of Figures 1(a) and 1(b) is the scenario where participants in the treatment condition under-report less at follow-up than they did at baseline while those in the control condition under-report more at follow-up. Here, effect sizes are very large (ES=−1.0), and significant (p<.001). The opposite scenario—treatment participants under-report more, control participants under-report less—is displayed in the bottom right portion of Figures 1(a) and 1(b). Here, the intervention now favors the control group. More modest assumptions are reflected in between these two extremes.

Figures 2(a) and 2(b) are contour plots of effect sizes and p-values based on varying the slope sensitivity parameters described in Section 5.2. Intercept sensitivity parameters in Figures 2(a) and 2(b) are fixed across all scenarios and equal to 0. The x-axis displays values for ${\Delta }_{{\beta }_1}^{(1)}$, the sensitivity parameter for the treatment group intercept term. The y-axis displays values for ${\Delta }_{{\beta }_1}^{(0)}$, the sensitivity parameter for the control group intercept term. The solid dot represents calibration model invariance with respect to treatment and time (${\Delta }_{{\beta }_1}^{(1)}={\Delta }_{{\beta }_1}^{(0)}=1$). Departures from time invariance occur when ${\Delta }_{{\beta }_1}^{(d)}\ne 1$. As mentioned in Section 5.2, when the mean of Y₁ is greater than the target value (as is true in the control condition), values of ${\Delta }_{{\beta }_1}^{(d)}>1$ have the effect of increasing the mean of Z₁ and values of ${\Delta }_{{\beta }_1}^{(d)}<1$ decrease the mean of Z₁. In the treatment condition, where the 6-month sodium value is less than the target value, values of ${\Delta }_{{\beta }_1}^{(d)}$ have the opposite effect. As a result, effect sizes in Figure 2(a) are largest and smallest in the upper right and lower left quadrants, respectively (see Web Appendix D for details). In general, the slope sensitivity parameters have less of an impact on the treatment effect as compared to the intercept sensitivity parameters. The p-values of the treatment effects displayed in Figure 2(b) are significant across all values of the slope sensitivity parameters. Tabulations of point estimates, treatment differences, 95% confidence intervals, as well as effect sizes and p-values from the sensitivity analyses in Figures 1 and 2 are reported in Web Appendix E.

Figure 2:

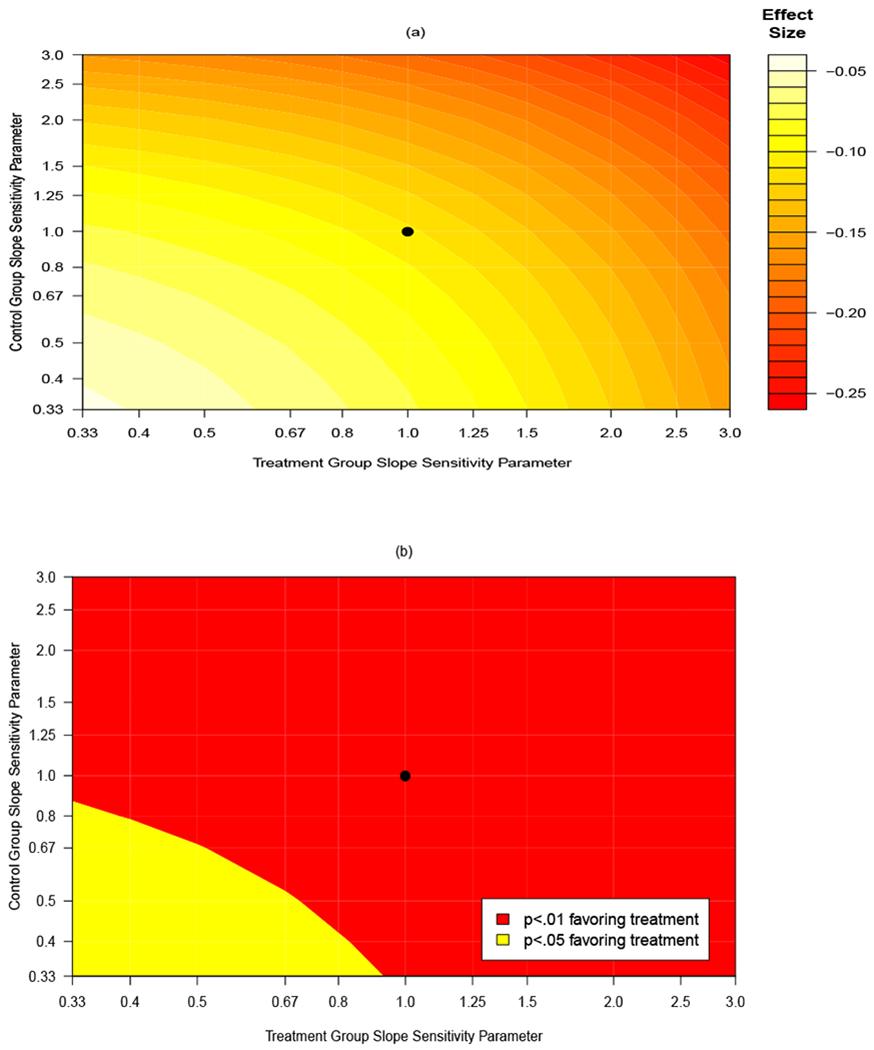
Contour plot for (a) effect sizes at 6-months and (b) their associated p-values from an analysis of the PREMIER data across a range of sensitivity parameters for the slope of the measurement error model at follow-up as compared to baseline. The x-axis displays values for the sensitivity parameter for the treatment group, the y-axis displays values for the sensitivity parameter for the control group. The point plotted at (1, 1) corresponds to an assumption of calibration model invariance with respect to treatment and time. A color version of this Figure can be found in the electronic version of this article.

7. Evaluation using internal biomarker data

A unique aspect to the PREMIER study was that 24-hour urine samples were obtained on all participants both at baseline and at follow-up. Figure 3 displays a forest plot of effect sizes and their associated 95% confidence intervals for observed 24-hour urinary sodium (top row), self-reported sodium, and a range of measurement error-corrected analyses based on different sensitivity parameters. Analyses have been sorted based on how far they deviate from the 24-hour urine results (vertical dotted line).

Figure 3:

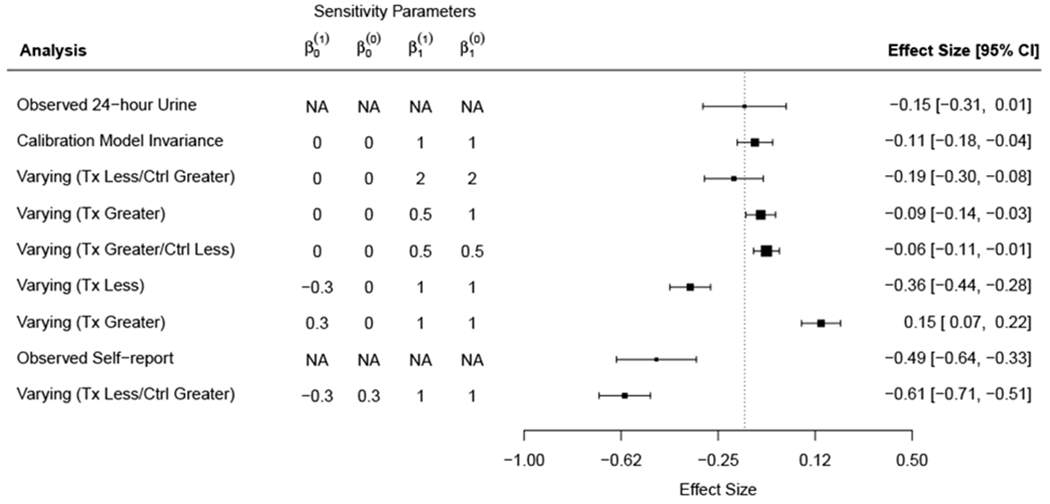
Forest plot of effect sizes and their associated 95% confidence intervals for observed 24-hour urinary sodium (top row), self-reported sodium, and a range of measurement error-corrected analyses based on different sensitivity parameters. The terms “Greater” and “Less” refer to whether—for a given value of self-report—true intake at follow-up is greater or less than true intake at baseline, respectively. Analyses have been sorted based on how far they deviate from the 24-hour urine results (vertical dotted line). Measurement error corrections that are based on calibration model invariance with respect to treatment and time (or mild departures from it) provide results similar to the 24-hour urine analysis. Sensitivity analyses that assume treatment group participants under-report less at follow-up as compared to baseline provide results in line with self-reported sodium values. Note that measurement error corrected analyses are more precise than analyses based on observed values due to the fact that the measurement error corrected analyses are based on “true” sodium intake after removing within-subject variability.

Measurement error corrections that are based on calibration model invariance with respect to treatment and time (or mild departures from it) provide results similar to the 24-hour urine analysis. Sensitivity analyses that assume treatment group participants under-report less at follow-up as compared to baseline provide results in line with self-reported sodium values. Note that measurement error corrected analyses are more precise than those analyses based on observed urinary sodium values due to the fact that the measurement error corrected analyses are based on “true” sodium intake after removing within-subject variability as described in Section 4.1.

8. Discussion

After correcting for measurement error, effect sizes in PREMIER were smaller than effect sizes based on using self-reported sodium but still significant. Treatment effects were sensitive to modest assumptions regarding shifts in the intercept of the calibration model. An assumption that treatment participants underreported 20% more of a standard deviation at follow-up as compared to baseline—and control participants had no change in underreporting—resulted in an effect size close to 0 that was no longer significant. This sensitivity is partly due to the fact that the measurement error corrected effect size (under calibration model invariance with respect to treatment and time) was small initially. Thus modest assumptions that result in a shrinking of this already small treatment effect can result in a non-significant finding. In other applications with larger effect sizes, the treatment effect may be more robust to these assumptions.

Our sensitivity analyses also included more extreme assumptions which resulted in inferences favoring the control group. As in any sensitivity analysis, the analyst must consider which assumptions are plausible based on evidence from previous studies and which are not. For example, in some settings one might consider it unrealistic that control participants would under-report more at follow-up than at baseline. This assumption would restrict the sensitivity analyses to the bottom halves of the plots in Figures 1(a) and 1(b), thus narrowing the range of inferences. Alternatively, the analyst could draw treatment and control sensitivity parameters from a joint prior where the two sensitivity parameters are correlated (Linero and Daniels 2015).

We only dealt with two time points and as the number of time points increases, so does the number of unidentified parameters. This is a also a concern in longitudinal studies with nonignorable drop-out (Daniels and Hogan 2008) and an area of future work is to build on approaches from the longitudinal missing data literature for reducing the dimension of nonidentifed parameters and adapt them to measurement error correction.

The fact that our measurement-error corrected inferences were similar to inferences that used urinary sodium values in PREMIER suggests that our methods are appropriately reducing measurement error. However, a more thorough evaluation is necessary to further validate our approach. In Web Appendix F we give the results of a simulation study that examines the performance of our method under a range of invariant and varying calibration model scenarios using both fixed values (point-mass priors) and proper priors for the sensitivity parameters in order to propagate the uncertainty of the sensitivity parameters. We obtained low bias and good coverage when the calibration model was correctly specified and the use of non-degenerate priors improved coverage when the true calibration model was misspecified.

Throughout the paper we assumed transportability of the calibration model. This is a critical assumption and analysts should think carefully before transporting the results from an external validation study. Our model conditions on baseline demographics which may make the transportability assumption more feasible but the transportability assumption deserves a sensitivity analysis of its own and the methods described in Section 5 could be used to assess the sensitivity of inferences to violations of the transportability assumption.

We take a missing data approach to measurement error correction where the unknown true quantities are treated as unobserved. To do this, we model the joint distribution of Y and Z in the trial as f(Z, Y) = f(Z | Y)f(Y). Here, the identified and unidentified parameters of the joint distribution are transparent and easy to posit. Many measurement error methods begin by specifying the measurement error model as f(Y | Z). Modeling the joint distribution as f(Z, Y) = f(Y | Z)f(Z) is more difficult because the unidentified parameters of these distributions are both unidentified and restricted by the observed marginal distribution of Y. In addition, the validation study provides us with no information regarding the marginal distribution of Z in the trial.

A limitation of our work is that recovery biomarkers do not exist for many relevant outcomes in dietary intervention studies. Work is ongoing to widen the class of unbiased biomarkers (Hedrick et al. 2012). Further, we are interested in extending our current work using concentration biomarkers which are biomarkers that are correlated with dietary intake (many of which are targets of interventions) but, unlike recovery biomarkers, are not unbiased. Here, feeding studies that measure both true intake and concentration biomarkers could be used as external validation studies for measurement error correction.

We made other assumptions regarding conditional independence and associations between unobserved variables that were not subject to sensitivity analysis. In order to make the results from our sensitivity analyses manageable and interpretable, it was necessary to focus on those assumptions in our analyses which we felt were the least plausible and at the same time would have the most influence on our inferences. This is true of any sensitivity analysis and an advantage of the Bayesian approach investigated here is that sensitivity analyses for other parameters can easily be incorporated into our imputation models through the use of informative priors.