Abstract
This paper reviews and advances a data science framework for capturing and communicating critical information regarding the evolution of material structure in spatiotemporal multiscale simulations. This approach is called the MKS (Materials Knowledge Systems) framework, and was previously applied successfully for capturing mainly the microstructure-property linkages in spatial multiscale simulations. This paper generalizes this framework by allowing the introduction of different basis functions, and explores their potential benefits in establishing the desired process-structure-property (PSP) linkages. These new developments are demonstrated using a Cahn-Hilliard simulation as an example case study, where structure evolution was predicted three orders of magnitude faster than an optimized numerical integration algorithm. This study suggests that the MKS localization framework provides an alternate method to learn the underlying embedded physics in a numerical model expressed through Green’s function based influence kernels rather than differential equations, and potentially offers significant computational advantages in problems where numerical integration schemes are challenging to optimize. With this extension, we have now established a comprehensive framework for capturing PSP linkages for multiscale materials modeling and simulations in both space and time.
Keywords: Materials Knowledge Systems, Spectral representations, Cahn-Hilliard model, Phase field, Structure evolution, Multiscale modeling, Homogenization, Localization
1. Introduction
Customized materials design (including the design of a manufacturing process route) resulting in the combination of properties desired for a specific application is a highly challenging inverse problem, owing mainly to the extremely large parameter space involved in defining the hierarchical internal structure of the material. However, this endeavor has great potential for impacting virtually all emerging technologies [1–11], with significant economic consequences. The central impediment comes from the need to consider the relevant details of the hierarchical internal structure (spanning a multitude of length scales) that control the properties of interest to a specific application. Additionally, a diverse range of coupled physical phenomena occur at different timescales at each of the different length scales. Therefore, one is generally daunted by the enormous difficulty involved in tailoring the material structure to yield desired combinations of properties or performance characteristics.
Historically, and mainly because of the difficulties mentioned above, materials development efforts have relied largely on experimentation. Consequently, many of the efforts aimed at designing and developing new/improved materials have incurred significant cost and time. Recent advances in physics-based modeling of multiscale materials phenomena [12–21] have raised the exciting possibility that the vast design space for experimentation can be constrained to a significant degree by embracing in silico simulations and explorations. In other words, there is a tremendous potential for significant reductions in cost and time incurred in materials development effort if one could judiciously utilize multiscale materials modeling and simulation tools in combination with a reduced number of experiments.
The central impediments associated with the effective utilization of physics-based multiscale materials models in the materials development include: path dependent microstructure evolutions that depend on initial conditions, non-unique parameter selection for coupling multiscale models, approximations in microstructure representation, material property dependence on extreme values of microstructure distributions, large optimization space, metastablity of microstructure during use, and uncertainty in data, models and model parameters [18,22]. An important strategy in addressing these impediments involves the formulation and utilization of robust surrogate models (also called metamodels or emulators) for computationally efficient communication of critical information between well separated structure/length/time scales. Such low-dimensional, but sufficiently accurate, models present a computationally viable approach for exploring efficiently the extremely large materials design space.
In the context of hierarchical materials (with details of the material structure spanning multiple well-separated scales) surrogate models are needed to exchange high value information in both directions between the scales. Depending on the direction of information flow, the models can be classified as homogenization (information flowing from lower scales to higher scales) or localization (information flowing from higher scales to lower scales) relationships. It should be noted that localization linkages are significantly more difficult to establish compared to the homogenization linkages; indeed the latter are implicitly embedded within the former and can be recovered from them when needed.
2. Review of homogenization and localization approaches
Theories for predicting the properties of composite materials go as far back as 1873, with Maxwell predicting an effective conductivity for a region of a material with dilute inhomogeneities through a mean-field approximation [23–25]. The simplest, and most commonly used, homogenization methods for mechanical properties were developed by Voigt and Reuss [26,27], and provide “elementary” bounds for the estimates of the effective properties. These calculations typically involve simple volume-averaging of the properties at the microscale. The bounds obtained in this approach also correspond to the correct effective values for highly specialized microstructures. For example, the upper bounds obtained in these approaches typically correspond to microstructures where the microscale constituents have uniform shape, and are continuous and perfectly aligned along the loading direction (e.g., unidirectional, straight, and continuous fibers).
Hill and Hashin introduced the concept of a Representative Volume Element (RVE) [28,29] which can be defined as a statistically homogeneous subvolume where the length scale associated with the local perturbation in material properties is sufficiently small compared to the length scale of the subvolume (typically referred as “well-separated” length scales). With this definition, a mean-field approximation can be used to assign an effective property to a RVE. It can be shown that good estimates for a broad class of effective properties associated with an RVE can be expressed in the following generalized form [28]:
| (1) |
where Peff denotes the effective property, 〈〉 denotes ensemble average (also equal to volume average by virtue of the ergodic assumption), and A(x) is a suitably defined tensor operator. The central challenge of this theory lies in the computation of the tensor operator.
While the theory described above emerged in the context of mechanical properties, it has also been successfully applied to material properties such as thermoelectric, piezoelectric, diffusion, and conductivity for composite materials [30]. A large variety of approaches have been built on this foundational framework, and have been employed successfully in addressing practical problems of interest in composite material systems. Hill developed the self-consistent method which employs Eshelby’s solution to ellipsoidal inclusions in an infinite medium to find an approximate estimate of the effective properties [31,32]. An improved generalized self-consistent method emerged from the work of Hashin, Shtrikman, Christensen and Lo [29,33–36], which allows for more complex geometric shapes of the reinforcement phase. A good overall treatment of such approaches for homogenization theory or estimates can be found in the textbook by Qu and Cherkaoui [37] as well as the report by Bohm [24]. Further advanced theories of homogenization were established by Willis [38], and subsequently by Ponte-Castanada [39].
In a completely different approach, advanced composite theories were developed to specifically take into account the rich details of the material microstructure. These approaches utilized the formalism of n-point spatial correlations to quantify the details of the material microstructure together with the concept of Green’s function to estimate the effective property of interest [40–46]. An overview of this more sophisticated approach for composite theories can be found in the book by Milton [30]. One of the earliest demonstration of this approach comes from Brown, who used a series expansions of a localization tensor to predict the electrical conductivity of a 2-phase material [47]. More rigorous applications of this approach can be found in the work of Torquato and co-workers [48,49].
The main limitation of the approach described above is that the Green’s functions needed to implement the method are only available for cases involving highly idealized and simplified physics (i.e., material constitutive laws). The recently formulated Materials Knowledge Systems framework (MKS) addresses this critical gap by advancing a data-driven approach [20,50–53].
3. Homogenization and localization with MKS
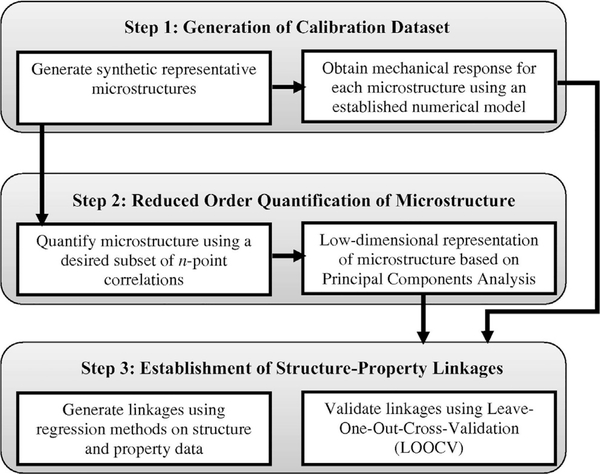
MKS homogenization and localization linkages are created by merging concepts from the physics-based statistical continuum theories developed by Kroner [54,55], machine learning [56–58] and digital signal processing [59]. A generalized workflow for establishing the homogenization linkage (e.g., structure-property linkage) is shown in Fig. 1. Broadly, this workflow includes a calibration step and a validation step. More specifically, this data-driven approach captures the pertinent microstructure features through n-point spatial correlations and employs dimensionality reduction techniques to create low-dimensional microstructure descriptors [60–62]. Linkages between effective properties and these low dimensional descriptors are then created using regression techniques [63–65].
Fig. 1.
Generalized MKS homogenization workflow for structure-property linkages [64].
The MKS localization linkages are expressed as a series, where each term involves convolutions of physics-capturing kernels (based on Green’s functions) with hierarchical microstructure descriptors. These kernels (referred to as influence functions) capture and organize the governing physics as convolution operators that are independent of the spatial arrangements of the local states in the material microstructure. Therefore, in the MKS localization approach, these kernels are calibrated with results produced using numerical tools (e.g., finite element models).
It is emphasized here that once the influence kernels in the MKS linkages are calibrated and validated, they can be used to predict the local responses for new microstructures at very minimal computational expense. Therefore, this approach is of particular value when one needs to explore a very large number of potential microstructures. It should be noted that the design of multiscale material systems for optimized performance is expected to require a consideration of a very large number of potential microstructures. As a simple illustration, let us assume that the specification of an RVE at any selected material structure scale would require a minimum of 8000 (i.e. 20 × 20 × 20) spatial cells or voxels. Further assume that the specific material system being explored allows for placement of only ten distinct potential local states (could be based on differences in thermodynamic phases and/or chemical composition and/or defect densities and/or local orientation attributes such as the crystal lattice orientation). Even with such highly conservative estimates, the number of different RVEs that one can imagine producing in a comprehensive materials design exploration is 108000. While an exhaustive search of the structure space is impractical, the subspaces explored during optimization are also extremely large. An efficient exploration of such large design spaces demands innovative new approaches.
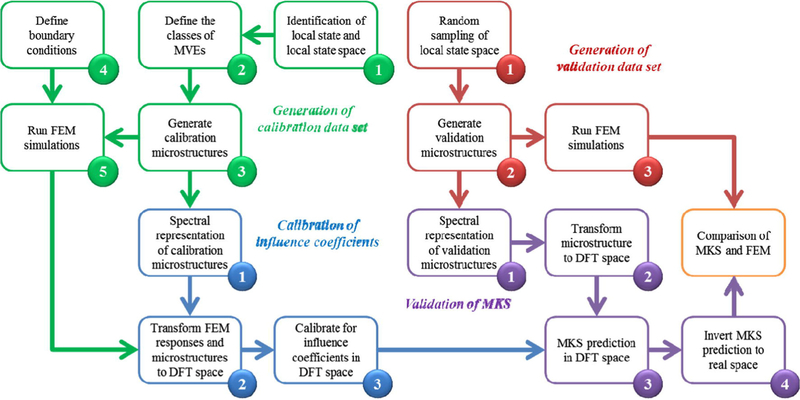
Prior effort in MKS localization was largely focused on steady state structure-property localization linkages [20,50–52], with the exception of one prior study exploring the time evolution of the microstructure field [66]. Previous studies have shown that if the local states are discrete, influence coefficients can be calibrated with a small number of simulations and then used to predict the local response of microstructures with any new spatial configuration of the local states [50,51]. Similar to Green’s functions, the MKS localization kernels depend on the boundary conditions and physical constants that govern the constitutive behavior of the local states present in the material system. It has been shown that the influence kernels can be suitably parametrized to include such dependencies (i.e., interpolation between sets of kernels can provide remarkably accurate predictions for new conditions [53]). A generalized MKS localization workflow, including both calibration and validation steps, can be found in Fig. 2. It is noted here that the workflows presented in Figs. 1 and 2 are highly generalized, and can be applied broadly to a range of material systems experiencing a range of multiscale materials phenomenon.
Fig. 2.
Generalized MKS Localization workflow for structure-property linkage at the meso-scale [53].
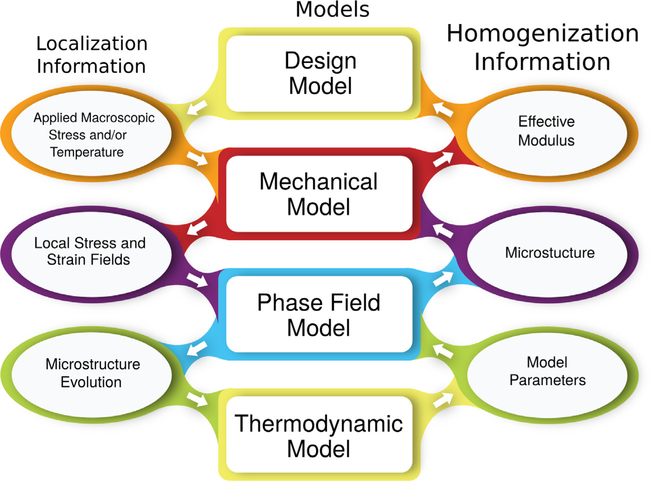
A schematic illustration of a multiscale simulation using the MKS framework is shown in Fig. 3. This chain of models passes homogenization information from the lower length scales to higher lengths. The thermodynamic model computes thermodynamic quantities that define the phase field model parameters. In turn the phase field model predicts the microstructure as a result of processing conditions. The effective modulus of the microstructure is found using the mechanical model (e.g. finite element method), which is used in the design model for a component. In the model chain, localization information is also passed from the higher length scales to the lower length scales. Using a microstructure and the applied stress and/or temperature provided by the design model, the mechanical model computes local stress and strain fields. These local fields provide information about the free energy density to the phase field model for microstructure evolution which in turn refines the thermodynamic calculations from the thermodynamic model. The current approaches for multiscale simulations based on numerical approaches such as finite element method or the phase-field method are not ideally suited for such bi-directional explorations due to their high computation costs. In the MKS framework, computationally cheap and sufficiently accurate surrogate models will serve as surrogates, and can greatly expedite this process.
Fig. 3.
One instance of a multiscale simulation covering multiple length and time scales. The homogenization information is passed to models at higher length scales, while the localization information is passed to models at lower length scales. Sufficiently accurate and computationally cheap surrogate models created using the MKS framework serve as replacements for the models which use the microstructure (i.e., mechanical and phase field models) to speed up exploration for a new material.
Although most of the previous work in the MKS framework has focused on the mesoscale [20,50–52,63–65], the approach can indeed be extended to other length and time scales involved in multiscale materials phenomenon as long as the phenomena involved are well separated and the heterogeneity at each scale is statistically homogeneous or weakly stationary [67]. Although some preliminary work with MD simulations has been reported [68,69], much additional work is still needed to further refine and demonstrate the details of such implementations.
The current effort is aimed at the extension and application of the MKS approach to include transient process-structure evolution localization linkages. In general, the process-structure evolution linkages are significantly harder to establish compared to the structure-property linkages, because of the need to explicitly account for the time evolution of the important field quantities (in addition to their spatial distributions), many of which demand continuous descriptions. Consequently, there currently exist only a few reports in literature describing efforts aimed at capturing the salient process-structure evolution metamodels for multiscale materials phenomena. One area that has received a lot of attention in prior literature is the evolution of crystallographic texture in deformation processing of polycrystalline metals [70–82]. However, in this set of applications, all the attention is generally focused on capturing the salient details of the time evolution, while ignoring or grossly simplifying the spatial distribution of the important field variables involved. More recently, there have been a limited number of efforts aimed at mining low-dimensional process-structure evolution linkages from results accumulated in phase-field simulations [21,83–85]. In these prior applications, gross simplifications were made by limiting the set of initial microstructures, the microstructure descriptors or the local states allowed in the microstructure.
In this paper, we extend the MKS localization framework to allow efficient capture of the process-structure evolution localization linkages. Indeed, this extension when suitably combined with the existing MKS framework has the potential to facilitate a common, consistent, broadly applicable, framework for casting all of the relevant process-structure-property (PSP) linkages in a selected class of materials. A second major thrust of this paper is the derivation of the MKS framework using spectral representations for some of the main functions (kernels) involved in these linkages. The novel protocols described above are demonstrated in this paper through a specific case study involving the extraction of process-structure evolution linkages embedded in the simulation results produced by a selected phase-field model.
4. Generalized MKS framework for process-structure linkages
The development of the generalized MKS framework for process-structure linkages will be presented here using the Cahn-Hilliard model as an example. However, the generalized final expression formulated here is broadly applicable to various other microstructure evolution models. The Cahn-Hilliard description of microstructure evolution can be expressed as [86]
| (2) |
In Eq. (2), ϕ(x, t) is an order parameter used to represent the concentration field at location x and time t, represents the interface width, and D is the diffusivity. Note also that a double well potential with minima at −1 and 1 has been used in Eq. (2) for the free energy term [87,88].
The theoretical framework of MKS is built on perturbation expansions. For the present case, we therefore start by expressing the concentration field ϕ(x, t) in terms of a reference quantity (constant in both space and time) and a local perturbation from that reference as
| (3) |
Introducing Eq. (3) into Eq. (2) results in the following differential equation.
| (4) |
where
| (5) |
We can use a Green’s function approach to find the solution to Eq. (4) where
| (6) |
and with a suitable change of variables we have
| (7) |
In Eq. (7), is the initial value of the perturbed concentration. Assuming periodic boundary conditions, the operators ∇r can be moved from concentration terms to the Green’s functions.
| (8) |
Recursive substitution of into Eq. (8) produces a series (called the weak contrast expansion) that can be used to compute the perturbed concentration field [49,54,55,67].
| (9) |
with
| (10) |
The higher order terms in Eq. (9) (i.e., the terms denoted by …) will be discussed later (see the description near Eq. (15)).
Simplified analytical solutions for Eqs. (9) and (10) are very difficult and demand highly sophisticated approaches to handle the convergence of the terms in the series [43,89]. There have also been numerous approaches utilizing numerical iterative schemes to solve the same equations [90–95]. The numerical approaches generally demand significant computational resources because of the highly nonlinear expressions embedded in Eqs. (9) and (10). More importantly, most conventional numerical approaches do not facilitate learning. In other words, when the equations are solved for one specific set of inputs there is no established formalism for transferring the knowledge gained in the process to the next application of the same set of equations for a different set of inputs. This is precisely where data science approaches, such as the MKS approach, bring many potential benefits. In the data science approach, we recognize that each term in the series is essentially a convolution, where the kernel is completely independent of the topological details of the material microstructure. Suitable algorithms are then designed and employed to efficiently learn these kernels from previously accumulated results. In many ways, the calibrated MKS localization linkages take full advantage of the known physics of the phenomena, and supplement only the mathematically intractable components with data science approaches, where they exhibit a clear advantage.
The MKS kernels facilitate learning and transfer of knowledge to a new set of microstructure inputs. In order to accomplish this, Eqs. (9) and (10) need to be reformulated using the concepts of microstructure function and local states [96,97]. The local state captures all the attributes (thermodynamic state variables) needed to identify the physical properties to be assigned to the spatiotemporal location of interest in the material internal structure. In the problem described here, either the concentration value or the perturbed concentration value (after selecting a reference concentration value) can serve as local state variables. The local state will be denoted as h. The set of all values that h can take is denoted as the local state space, H. The main distinction between h and ϕ′ (or ϕ) is that the later is a specific value assigned to a specific spatiotemporal location, while the former denotes any value that could have been assigned to the later.
The introduction of the concept of the local state now allows us to describe a microstructure function m(h, x, t) as the probability density associated with finding the local state h at spatial position x at time t. The expectation value obtained using this probability density distribution (on the local state space) should be taken as the specific value assigned in the fully deterministic framework described earlier. In other words, for the fully deterministic case, one could write . For the more general case, the definitions introduced above lead to the following mathematical statements
| (11) |
| (12) |
The introduction of the microstructure function as a probability density function brings the added benefit that it maps complex descriptions of local state (potentially could be a combination of several scalar and tensor thermodynamic state variables) into a continuous scalar-valued function that lends itself naturally to spectral representations [98–101]. Extending the treatment above to the term containing the Green’s function in Eq. (9) allows us to define an influence function or localization kernel as
| (13) |
Recasting Eq. (9) with the terms defined in Eqs. (12) and (13) takes the following form.
| (14) |
The derivation of Eq. (14) is a key step in the formulation of the MKS approach for the process-structure evolution localization linkages sought in this work. The main benefit of the form of Eq. (14) lies in the fact that α(h, x, t) serves as a convolution kernel capturing all of the relevant physics in the problem, and operates on the initial microstructure function m(h, x, 0). Even more importantly, when the series is expanded properly, the localization kernel is completely independent of the microstructure function m(h, x, 0). Furthermore, Eq. (14) is the exact analog of the structure-property localization linkages established previously in the MKS framework [20,50–53]. Therefore, the extension presented here now makes it possible to explore the complete set of process-structure-property linkages in a consistent MKS framework in both space and time.
Because of the specific way in which Eq. (14) was derived, it is relatively easy to write the additional terms in the series expansion. For example, the second term in this expansion would be expressed as
| (15) |
Therefore, another way to interpret the series expansion in Eq. (14) is to recognize that each term in the series captures the contribution arising from a specific arrangement of the local microstructure in the neighborhood of the spatial voxel of interest as a function of time.
The next step in the practical implementation of the MKS framework is to transform Eq. (14) into a discrete representation. In other words, the functions ϕ′(x, t), α(h, x, t) and m(h, x, t) need to be discretized. Following notations and conventions employed in signal processing [102,103], we will use round brackets to represent variables with continuous domains and square brackets to represent variables with discrete domains.
The discrete version of ϕ′(x, t) is denoted as p[s, n] these are formally related to each other as
| (16) |
In Eq. (16), s and n enumerate uniformly partitioned intervals that fully span the continuous domains of space V and time T, respectively, and Δx and Δt denote appropriate measures of the intervals. Therefore, the discrete version of ϕ′(x, t) essentially captures the averaged values within the uniformly subdivided intervals in space within the time step n.
Two different discretization methods for the local state space variable h can be used. Both methods result in the same discretized equation. The details for both methods can be found in Appendix A, and the discretized version of Eq. (14) has the following form.
| (17) |
In the remainder of this paper, we first demonstrate the viability of the extended MKS framework presented above for capturing process-structure evolution linkages. Furthermore, in conducting this case study, we will explore two approaches for the discretization of the functions on the local state space for multiscaling in time by extending the length of time step n to match the time domain of the simulation T through a specific case study.
5. Cahn-Hilliard simulations and MKS linkage calibrations
5.1. Simulation and MKS linkage details
The simulation data as well as the MKS localization linkages used in this case study were generated using the Python library PyMKS [104]. A Cahn-Hilliard simulation is used to generated data for the calibration of the MKS linkages and serves as a reference to compare and validate their performance. The Cahn-Hilliard equation presented earlier in Eq. (2) was solved using the optimized semiimplicit spectral scheme with periodic boundary conditions described by Cheng and Rutenberg [105]. The parameter γ was set equal to 0.2, and the time step for the calibration dataset was set equal to 10−2 s. Two spatial domains with sizes of 100 × 100 and 300 × 300 were used to examine how the different methods scale for larger simulations. The simulations and the MKS linkages were computed on a machine with eight 1.0 GHz processors and 8 GB of memory.
In the present study, we focus on capturing processmicrostructure localization linkage in one large time step using the MKS framework. Note that this differs from the approach used in the earlier study [66] where the time derivative of the concentration was used as the output response field (the LHS of Eq. (17)) and it was shown that once this linkage is established for one time step, it can be recursively applied to march forward in time. In the present study, we have used the concentration at the end of 500 time steps (or one large time step) as the output response field.
In this study, we explore two discretization approaches described Appendix A for the functions on the local state space. The approaches result in two different MKS localization linkages that look alike in their mathematical forms. The linkage referred to as Legendre MKS linkage throughout the remainder of the paper uses the discretization method outlined in Eqs. (A.9) and (A.10) with Legendre polynomials as the basis functions. The other linkage uses the discretization method outlined in Eqs. (A.4) and (A.5) and is referred to as the Primitive MKS linkage throughout the remainder of this paper. Both models restrict the local state space domain to h ∈ [−1, 1]
5.2. First order influence coefficients and discrete fourier transforms
Only the first term in Eq. (17) is used in this work. In prior work [20,50–53], it was shown that the first term is dominant for problems with low to moderate contrast, which in turn controls the degree of heterogeneity of the response field. In the present problem, this criterion is met within the 500 time steps of the simulation. This results in significant computational advantages as the calibration of the first-order MKS localization kernels can be done efficiently by taking advantage of discrete Fourier transforms and the convolution theorem [106,107]. This transformation leads to
| (18) |
In Eq. (18) P[k, n], β[l, k, n] and M[l, k, 0] are the discrete Fourier transforms of P[s, n], α[l, s, n] and m[l, s, n] for Eq. (17) respectively.
With the uncoupled spatial frequency representation shown in Eq. (18), the β terms can be calibrated easily using multiple linear regression techniques using the known values for P and M. The discretization used for the Primitive MKS linkage (Eqs. (A.4) and (A.5)) is subject to the constraint that the discretized microstructure function sums to one at any instance in space and time,
| (19) |
therefore multiple linear regression with categorical variables as outlined in previous studies is used [20,50–52]. The discretized microstructure function in the Legendre MKS linkage is not subject to the constraint shown in Eq. (19) and therefore standard multiple linear regression is used.
5.3. Calibration data
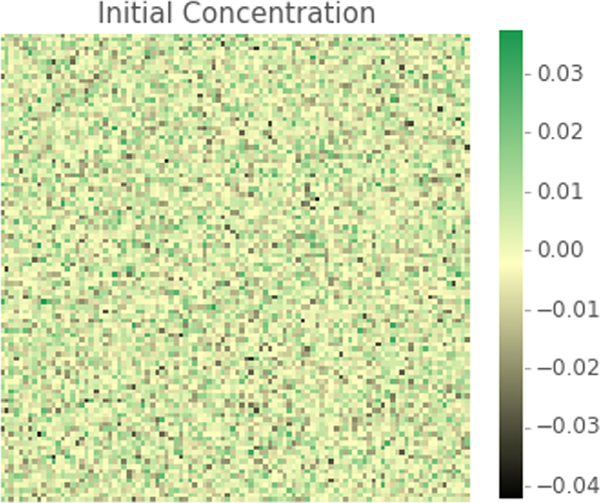
The first step in the calibration of MKS localization kernels is the generation of a calibration dataset. For this purpose, Eq. (2) was numerically solved for 500 time steps for 500 randomly generated initial concentration fields with values sampled from a normal distributions. The mean values of the normal distribution were randomly selected between [−0.5,0.5] and standard deviations of 102. The concentration fields at the beginning and the end of the 500 small time steps constitute the input and output, respectively for the calibration of the MKS localization linkages. An example of these fields is shown in Fig. 4.
Fig. 4.
One instance of an initial microstructure (100 × 100) and its corresponding microstructure after 500 small time steps, which were used to calibrate the influence coefficients for MKS localization linkages using both the Legendre and the Primitive basis functions.
5.4. Selection of local states and calibration of influence coefficients
One of the main MKS parameters for either of the discretization methods is the selection of the of total number of local states (or number of basis functions) L used to describe the local state space. In the previous study it was shown that an increase the in variable L can potentially lead to increased accuracy for small time steps at the cost of making the MKS linkage computationally more expensive [66]. Therefore, the minimum value of L that provides a sufficient level of accuracy is desired.
In order to explore the selection of L for both discretization methods with one large step, the calibration ensemble of data was randomly split into two sets. One set which will be referred to as the linkage selection dataset contains 320 (or 80%) of the microstructures and remaining 80 (or 20%) of the microstructures will be referred to as the linkage validation dataset. In the present work, the two MKS localization linkages were calibrated using the linkage selection dataset while varying L between 2 and 15. In order to avoid over fitting the linkage for a given value of L, 10-fold cross-validation was used. This method randomly partitions the linkage selection dataset into ten equally sized sub-datasets and calibrates the linkage ten times while systematically leaving out each of the sub-datasets once. This method results in 10 calibrations for each value of L amounting to a total of 280 calibrations between the two MKS localization linkages.
| (20) |
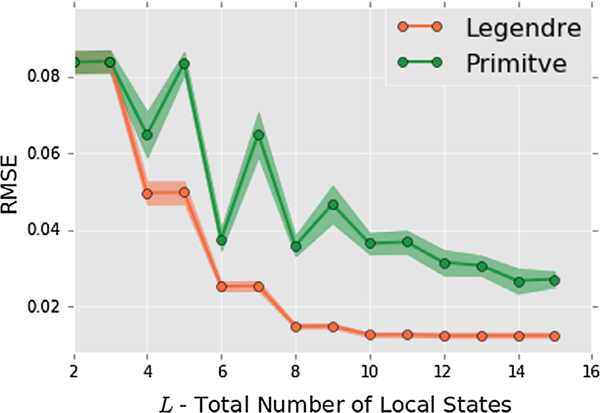
In order to evaluate the accuracy of the linkages while varying L, the root mean squared error (RMSE) value was computed over every voxel in the sub-datasets used for each of the calibrations with reference to the Cahn-Hilliard simulation (as shown in Eq. (20)) and was averaged over the ten cross-validation scores. The averaged RMSE values and their standard deviations are shown in Fig. 5.
Fig. 5.
Root mean squared error (points) and standard deviation (line widths) values of the predicted concentration fields found using 10-fold cross-validation of MKS localization evolution-linkages using the Legendre and Primitive basis functions to represent the microstructure function and influence function.
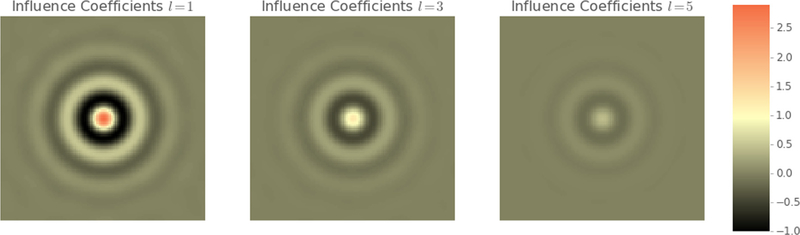
The two MKS linkages exhibit a downward overall trend with increasing L. Large and small oscillations were seen in the case of Primitive and Legendre MKS linkages respectively. In the Legendre MKS, it was also observed that the coefficients of the even polynomials in the series were all orders of magnitude smaller than the coefficients of odd polynomials. These observations suggest that the influence functions for the Cahn-Hilliard in Eq. (13) are odd functions. For L greater than 3, the Legendre MKS linkage consistently produced a lower RMSE values compared to the corresponding Primitive MKS linkage. It should also be noted that with the Primitive basis, the dominant kernels are the ones associated with the important regions in the local state space. With the Legendre basis, we get a more organized descriptions of the kernels with the higher-order terms representing the less important contributions, in general, as one would expect for smooth decaying functions such as the influence functions. Fig. 5 shows that L = 6 provides sufficiently accurate low-cost linkages that can be used to predict processing-structure evolution for the present case study.
The Primitive and Legendre MKS linkages were both calibrated using the entire calibration dataset with the value of L set equal to 6. These two linkages are used for the remainder of the case study. The discretized influence functions (referred to as influence coefficients) for both linkages can be found in Figs. 6 and 7.
Fig. 6.
Significant influence coefficients for the Primitive basis with L equal to 6. All other influence coefficients were less than 10−5.
Fig. 7.
Significant influence coefficients for the Legendre basis with L equal to 6. All other fields had maximum values of less than 10−2.
6. Microstructure evolution linkages for Cahn-Hilliard simulation
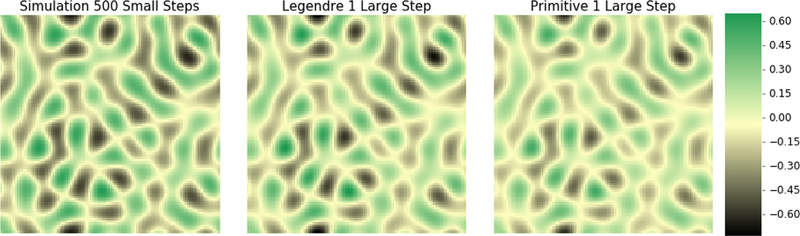
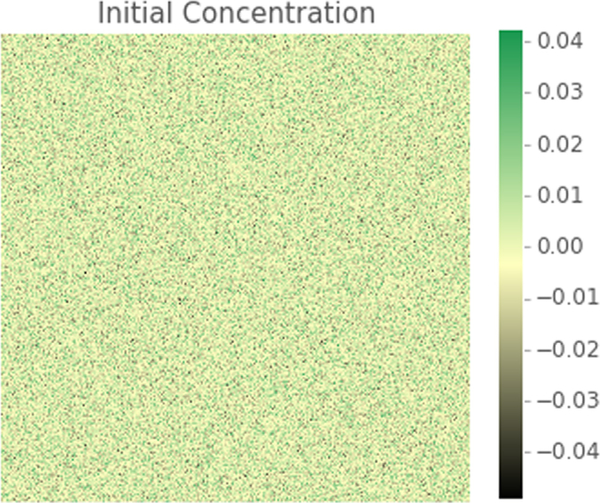
Both MKS linkages calibrated in this study were used to predict the microstructure evolution of the same set of 250 initial concentration fields. The initial microstructures, one instance shown in Fig. 8, generated from normal distributions with mean values randomly selected between [−0.1, 0.1] and standard deviations of 10−2 were used as inputs into the Cahn-Hilliard simulation and the two MKS linkages. The simulation numerically predicted each of the microstructures after 500 small time steps with an average run time of 1.33 s. The MKS linkages used the same initial inputs and the predicted microstructures equivalent to running the simulation for 500 small time steps, but with one large step. The average run time of the Primitive and Legendre MKS linkages were 3.82 × 10−3 s and 4.94 × 10−3 s with RMSE values of 5.68 × 10−2 and 3.36 × 10−2 respectively. An instance of the final predicted microstructures for the MKS linkages and the simulation are compared in Fig. 9.
Fig. 8.
Initial microstructure (100 × 100) used as a common input for the Cahn-Hilliard simulations as well as the MKS localization linkages with Primitive and Legendre basis functions.
Fig. 9.
Predicted concentration fields by simulations using 500 small time steps (left) as well as the concentration fields predicted by the two MKS localization linkages using one large time step.
One of the major advantages of using the MKS localization linkage is that the learning in the form of the MKS influence coefficients (discretized kernels) can be transferred to other initial microstructures that may be defined on larger spatial domains. In other words, the same influence coefficients that are calibrated on a small dataset can be used to predict the structure evolution for a much larger microstructures. This allows for the influence coefficients to be calibrated once and used to represent the processing-microstructure evolution for simulations with equal or larger domains sizes. Because of the decaying nature of the discretized influence functions in real space as shown in Figs. 6 and 7, the edges can be zero padded to expand their domain size to match the domain of new initial microstructure. The influence coefficients for both of the Primitive and the Legendre MKS linkages were scaled up from a domain of size 100 by 100 to 300 by 300 using the method outlined by Landi et al. [51].
A set of 250 initial microstructures were created using the same method as described above, but on a larger spatial domain of 300 × 300, is shown in Fig. 10. These microstructures were used as inputs to the same the Cahn-Hilliard simulations and the MKS localization linkages and the final microstructures were predicted. The average run time for the simulation using 500 time steps was 1.13 × 10−2 s. Primitive and Legendre MKS linkages had run times of 3.54 × 10−2 s and 7.00 × 10−2 s, with RMSE values 7.10 × 10−2 and 4.00 × 10−2 respectively. The predicted concentration fields are compared in Fig. 11.
Fig. 10.
Initial large microstructure (300 × 300) used as a common input for the Cahn-Hilliard simulations and the MKS localization linkages.
Fig. 11.
The concentration fields predicted by the numerical simulation with a 500 small time steps (left) as well as the concentration fields predicted by the MKS localization linkages with one large time step using scaled up influence coefficients from a domain size of 100 by 100 to 300 by 300 with Primitive and Legendre bases.
As one should expect, the accuracy of the MKS linkages generally improves when a larger number of terms in the series are retained (see Fig. 5). In practice, the level of desired accuracy would be controlled by the application. However, it is important to note that the MKS approach allows the user to establish the desired accuracy level and make the necessary trade-offs between the accuracy and the effort involved.
7. Conclusion
A new generalized MKS localization framework with two different discretization methods for the local state variables has been developed for formulating computationally low-cost process-structure linkages which allow for temporal multiscaling. This framework is quite general and allows compact representation of the influence functions (or kernels) on the local state spaces. The overall framework was presented and demonstrated using a Cahn-Hilliard microstructure evolution as a prime example.
Although the computational cost of the Primitive MKS linkage was slightly lower than the Legendre MKS linkage, and the Legendre MKS linkage was more accurate and showed more smooth decay of error with increasing number of terms in the series. Both MKS localization linkages predicted the process-structure evolution for the concentration fields three orders of magnitude faster than the simulation with a small time step.
This case study suggests that MKS localization framework provides an alternate method to learn the underlying embedded physics in a numerical model. This form of expression of the underlying physics as Green’s function based influence kernels (as opposed to expression in the form of differential equations) may provide certain computational advantages in rapid exploration of large spaces in process design to attain desired or specified microstructures. This is especially the case for problems where traditional numerical integration schemes have been difficult to optimize.
Overall, it was demonstrated that the MKS kernels extracted for the example studied were indeed insensitive to the details of the initial microstructure (in other words the same kernel can be applied to any initial microstructure in the selected material system) and could be trivially expanded for applications to larger domain sizes with comparable accuracy. The method described here has laid a strong foundation for future developments addressing a broad range of materials systems with richer microstructures and more complex governing physics.
Acknowledgments
DBB and SRK acknowledge support from NSF-IGERT Award 1258425 and NIST 70NANB14H191.
Appendix A. Discretization methods for local state space
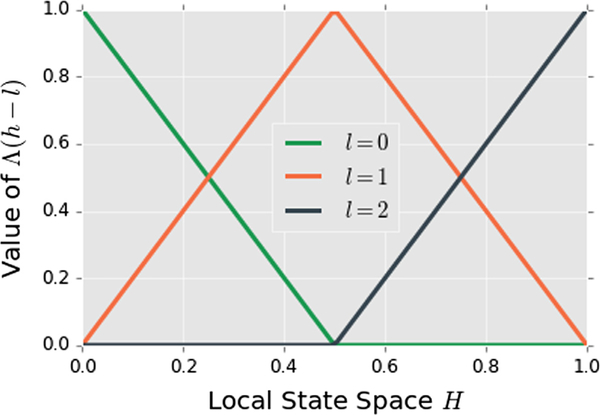
Functions α(h, x, t) and m(h, x, t) exhibit a dependence on the local state variable, in addition to the spatial and temporal variables. The spatial and temporal variables are discretized using the same method outlined in Eq. (16), but there are two potential strategies to deal with the discretization of these functions with respect to the local state variable. The simplest approach is to discretize the local state space H using triangle or hat basis functions Λ(h-l) to divide the local state space into intervals. The hat basis functions are defined in Eq. (A.1).
| (A.1) |
In Eq. (A.1), h and H maintain their definitions as the local state variable and a measure of the local state space, respectively, L is the total number of hat basis functions used to span the local state space and l enumerates the hat functions. The hat functions are placed along the local state space such that the maximum and minimum values of the local state space domain fall on the peak values of the hat functions associated with the largest and smallest values of l. An example of these hat functions with L = 3 and h ∈ [0, 1] is found in Fig. A.12]. Using this method to position the hat functions in the local state space ensures the sum of all hat functions contained within the local state space sum to 1, and that a summation of the hat functions times the microstructure function returns the original microstructure function.
| (A.2) |
| (A.3) |
Fig. A.12.
Three hat basis functions Λ used to discretize the local state space H. This method is referred to as Primitive basis functions.
In previous work [66], this approach has been referred to as primitive binning using the Primitive basis functions [20,50–53] leading to
| (A.4) |
| (A.5) |
where l now enumerates the number of basis functions used to represent the local state variable h. This primitive binning approach results in the MKS formulation that is consistent with most of the prior studies [20,50–53], where it is expressed as
| (A.6) |
Alternatively, the functions on the local state space can be represented to adequate accuracy using highly efficient orthogonal basis functions. For example, it is well known that orthogonal functions developed through classical Sturm-Liouville theory can be used as basis functions in many applications. Using such basis orthogonal functions, one can establish representations such as the ones shown below for an arbitrary function [108–111]:
| (A.7) |
| (A.8) |
In Eq. (A.8) ξl is the lth order orthogonal basis function, w(h) is the weighting function, is the Kronecker delta and Nl is a normalization constant that depends on the order and type of the basis functions. The most important feature of Eq. (A.7) is that the set of coefficients cl now provide a discrete representation of the function f(h). This approach is particularly attractive when only a small number of cl dominate the representation, but requires that the local state domain H is mapped into the interval over which the basis function is orthogonal and orthogonality relationship has a weighting function equal to one, i.e., w(h) = 1. Two potential orthogonal bases that meet these criteria are Legendre polynomials and Fourier series [112–114].
Applying this discretization approach to capture the h dependence in functions m(h, x, t) and α(h, x, t) in Eq. (14), by selecting orthogonal basis functions with w(h) = 1 and mapping the local state space to the orthogonal domain leads to the following discretized versions:
| (A.9) |
| (A.10) |
The introduction of these discretized representations into Eq. (14)) produces the exact same MKS formulation as shown previously in Eq. (17), but with a new interpretation of the index l.
References
- [1].Ward C, Materials genome initiative for global competitiveness, in: 23rd Advanced Aerospace Materials and Processes (AeroMat) Conference and Exposition, ASM, 2012. [Google Scholar]
- [2].Allison J, Backman D, Christodoulou L, Integrated computational materials engineering: a new paradigm for the global materials profession, JOM 58 (11) (2006) 25–27. [Google Scholar]
- [3].National Science and Technology Council Executive Office of the President, Materials Genome Initiative for Global Competitiveness, 2011. http://www.whitehouse.gov/sites/default/files/microsites/ostp/materials_genome_initiative-final.pdf.
- [4].Materials Genome Initiative National Science and Technology Council Committee on Technology Subcommittee on the Materials Genome Initiative, Materials Genome Initiative Strategic Plan, 2014. <mailto:http://www.whitehouse.gov/sites/default/files/microsites/ostp/NSTC/mgi_strategic_plan_-_dec_2014.pdf>.
- [5].Allison J, Integrated computational materials engineering: a perspective on progress and future steps, JOM Journal of the Minerals, Metals and Materials Society 63 (4) (2011) 15–18. [Google Scholar]
- [6].Olson GB, Designing a new material world, Science 288 (5468) (2000) 993–998. [Google Scholar]
- [7].N.R.C.U.C. on Integrated Computational Materials Engineering, Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security, National Academies Press, 2008. [Google Scholar]
- [8].Schmitz GJ, Prahl U, Integrative Computational Materials Engineering: Concepts and Applications of a Modular Simulation Platform, John Wiley & Sons, 2012. [Google Scholar]
- [9].Robinson L, TMS study charts a course to successful ICME implementation, JOM 65 (9) (2013) 1087. [Google Scholar]
- [10].Allison JE, Integrated Computational Materials Engineering (ICME): A Transformational Discipline for the Global Materials Profession, Allied Publishers, New Delhi, 2009. [Google Scholar]
- [11].Spanos G, Allison J, Cowles B, Deloach J, Pollock T, Integrated computational materials engineering (icme): Implementing icme in the aerospace, automotive, and maritime industries, miner, Met. Mater. Soc. (TMS) (2013). [Google Scholar]
- [12].Buehler MJ, Hartmaier A, Gao H, Hierarchical multi-scale modelling of plasticity of submicron thin metal films, Model. Simul. Mater. Sci. Eng. 12 (4) (2004) S391. [Google Scholar]
- [13].Groh S, Marin E, Horstemeyer M, Zbib H, Multiscale modeling of the plasticity in an aluminum single crystal, Int. J. Plast. 25 (8) (2009) 1456–1473. [Google Scholar]
- [14].Luscher DJ, McDowell DL, Bronkhorst CA, A second gradient theoretical framework for hierarchical multiscale modeling of materials, Int. J. Plast. 26 (8) (2010) 1248–1275. [Google Scholar]
- [15].Oden JT, Vemaganti K, Moës N, Hierarchical modeling of heterogeneous solids, Comp. Meth. Appl. Mech. Eng. 172 (1) (1999) 3–25. [Google Scholar]
- [16].McDowell DL, A perspective on trends in multiscale plasticity, Int. J. Plast. 26 (9) (2010) 1280–1309. [Google Scholar]
- [17].Olson GB, Computational design of hierarchically structured materials, Science 277 (5330) (1997) 1237–1242. [Google Scholar]
- [18].Panchal JH, Kalidindi SR, McDowell DL, Key computational modeling issues in integrated computational materials engineering, Comp.-Aided Des. 45 (1) (2013) 4–25. [Google Scholar]
- [19].Shenoy M, Tjiptowidjojo Y, McDowell D, Microstructure-sensitive modeling of polycrystalline in 100, Int. J. Plast. 24 (10) (2008) 1694–1730. [Google Scholar]
- [20].Al-Harbi HF, Landi G, Kalidindi SR, Multi-scale modeling of the elastic response of a structural component made from a composite material using the materials knowledge system, Model. Simul. Mater. Sci. Eng. 20 (5) (2012) 055001. [Google Scholar]
- [21].The Minerals Metals & Materials Society (TMS), Modeling Across Scales: A Roadmapping Study for Connecting Materials Models and Simulations Across Length and Time Scales, TMS, Warrendale, PA, 2015. doi: [Google Scholar]
- [22].Kalidindi SR, Data science and cyberinfrastructure: critical enablers for accelerated development of hierarchical materials, Int. Mater. Rev. 60 (3) (2015) 150–168. [Google Scholar]
- [23].Maxwell J et al. , A Treatise on Electricity and Magnetism, Oxford at the Clarendon press, 1873. [Google Scholar]
- [24].Böhm HJ, A Short Introduction to Basic Aspects of Continuum Micromechanics, Tech. Rep., CDLFMD Report, Technical Report 020624, 31998, 1998. [Google Scholar]
- [25].Sevostianov I, Giraud A, Generalization of maxwell homogenization scheme for elastic material containing inhomogeneities of diverse shape, Int. J. Eng. Sci. 64 (2013) 23–36. [Google Scholar]
- [26].Voigt W, Lehrbuch der kristallphysik:(mit ausschluss der kristalloptik), vol. 34, BG Teubner, 1910. [Google Scholar]
- [27].Reuss A, Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle, ZAMM-J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 9 (1) (1929) 49–58. [Google Scholar]
- [28].Hill R, Elastic properties of reinforced solids: some theoretical principles, J. Mech. Phys. Solids 11 (5) (1963) 357–372. [Google Scholar]
- [29].Hashin Z, Analysis of composite materials—a survey, J. Appl. Mech. 50 (3) (1983) 481–505. [Google Scholar]
- [30].Milton GW, The Theory of Composites, vol. 6, Cambridge University Press, 2002. [Google Scholar]
- [31].Hill R, A self-consistent mechanics of composite materials, J. Mech. Phys. Solids 13 (4) (1965) 213–222. [Google Scholar]
- [32].Eshelby JD, The determination of the elastic field of an ellipsoidal inclusion, and related problems, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 241, The Royal Society, 1957, pp. 376–396. [Google Scholar]
- [33].Hashin Z, Shtrikman S, Note on a variational approach to the theory of composite elastic materials, J. Frank. Inst 271 (4) (1961) 336–341. [Google Scholar]
- [34].Bornert M, Bretheau T, Gilormini P, Homogénéisation en mécanique des matériaux: comportements non linéaires et problèmes ouverts, Hermes Science Publications, 2001. [Google Scholar]
- [35].Christensen R, Lo K, Solutions for effective shear properties in three phase sphere and cylinder models, J. Mech. Phys. Solids 27 (4) (1979) 315–330. [Google Scholar]
- [36].Herve E, Zaoui A, N-layered inclusion-based micromechanical modelling, Int. J. Eng. Sci. 31 (1) (1993) 1–10. [Google Scholar]
- [37].Qu J, Cherkaoui M, Frontmatter, Wiley Online Library, 2006. [Google Scholar]
- [38].Willis J, Properties of composites, Adv. Appl. Mech. 21 (1982) 1. [Google Scholar]
- [39].Castañeda PP, Willis JR, The effect of spatial distribution on the effective behavior of composite materials and cracked media, J. Mech. Phys. Solids 43 (12) (1995) 1919–1951. [Google Scholar]
- [40].Kröner E, Statistical Continuum Mechanics, Springer, 1972. [Google Scholar]
- [41].Etingof P, Adams BL, Representations of polycrystalline microstructure by n-point correlation tensors, Text., Stress, Microstruct. 21 (1) (1993) 17–37. [Google Scholar]
- [42].Adams BL, Olson T, The mesostructureproperties linkage in polycrystals, Prog. Mater. Sci. 43 (1) (1998) 1–87. [Google Scholar]
- [43].Fullwood DT, Adams BL, Kalidindi SR, A strong contrast homogenization formulation for multi-phase anisotropic materials, J. Mech. Phys. Solids 56 (6) (2008) 2287–2297. [Google Scholar]
- [44].Torquato S, Random Heterogeneous Materials: Microstructure and Macroscopic Properties, vol. 16, Springer Science & Business Media, 2013. [Google Scholar]
- [45].Li D, Saheli G, Khaleel M, Garmestani H, Quantitative prediction of effective conductivity in anisotropic heterogeneous media using two-point correlation functions, Comput. Mater. Sci. 38 (1) (2006) 45–50. [Google Scholar]
- [46].Milhans J, Li D, Khaleel M, Sun X, Garmestani H, Prediction of the effective coefficient of thermal expansion of heterogeneous media using two-point correlation functions, J. Power Sour. 196 (8) (2011) 3846–3850. [Google Scholar]
- [47].Brown WF Jr, Solid mixture permittivities J Chem. Phys. 23 (8) (1955) 1514–1517. [Google Scholar]
- [48].Torquato S, Effective electrical conductivity of two-phase disordered composite media, J. Appl. Phys. 58 (10) (1985) 3790–3797. [Google Scholar]
- [49].Torquato S, Effective stiffness tensor of composite media—i. Exact series expansions, J. Mech. Phys. Solids 45 (9) (1997) 1421–1448. [Google Scholar]
- [50].Kalidindi SR, Niezgoda SR, Landi G, Vachhani S, Fast T, A novel framework for building materials knowledge systems, Comp., Mater., Cont. 17 (2) (2010) 103–125. [Google Scholar]
- [51].Landi G, Niezgoda SR, Kalidindi SR, Multi-scale modeling of elastic response of three-dimensional voxel-based microstructure datasets using novel DFT-based knowledge systems, Acta Mater. 58 (7) (2010) 2716–2725. [Google Scholar]
- [52].Yabansu YC, Patel DK, Kalidindi SR, Calibrated localization relationships for elastic response of polycrystalline aggregates, Acta Mater. 81 (2014) 151–160. [Google Scholar]
- [53].Yabansu YC, Kalidindi SR, Representation and calibration of elastic localization kernels for a broad class of cubic polycrystals, Acta Mater. 94 (2015) 26–35. [Google Scholar]
- [54].Kröner E, Statistical modelling, in: Modelling Small Deformations of Polycrystals, Springer, 1986, pp. 229–291. [Google Scholar]
- [55].Kröner E, Bounds for effective elastic moduli of disordered materials, J. Mech. Phys. Solids 25 (2) (1977) 137–155. [Google Scholar]
- [56].Suits DB, Use of dummy variables in regression equations, J. Am. Statist. Assoc. 52 (280) (1957) 548–551. [Google Scholar]
- [57].Galton F, Regression towards mediocrity in hereditary stature, J. Anthropol. Inst. Great Brit. Irel (1886) 246–263. [Google Scholar]
- [58].Cooley JW, Tukey JW, An algorithm for the machine calculation of complex fourier series, Math. Comput 19 (90) (1965) 297–301. [Google Scholar]
- [59].Volterra V, Theory of Functionals and of Integral and Integro-Differential Equations, Courier Corporation, 2005. [Google Scholar]
- [60].Niezgoda SR, Kanjarla AK, Kalidindi SR, Novel microstructure quantification framework for databasing, visualization, and analysis of microstructure data, Integ. Mater. Manuf. Innov 2 (1) (2013) 1–27. [Google Scholar]
- [61].Niezgoda SR, Yabansu YC, Kalidindi SR, Understanding and visualizing microstructure and microstructure variance as a stochastic process, Acta Mater. 59 (16) (2011) 6387–6400. [Google Scholar]
- [62].Cecen A, Fast T, Kalidindi SR, Versatile algorithms for the computation of 2point spatial correlations in quantifying material structure, Integ. Mater. Manuf. Innov 5 (1) (2016) 1–15. [Google Scholar]
- [63].Kalidindi SR, Niezgoda SR, Salem AA, Microstructure informatics using higher-order statistics and efficient data-mining protocols, JOM 63 (4) (2011) 34–41. [Google Scholar]
- [64].Gupta A, Cecen A, Goyal S, Singh AK, Kalidindi SR, Structure-property linkages using a data science approach: application to a non-metallic inclusion/steel composite system, Acta Mater. 91 (2015) 239–254. [Google Scholar]
- [65].Çeçen A, Fast T, Kumbur E, Kalidindi S, A data-driven approach to establishing microstructure-property relationships in porous transport layers of polymer electrolyte fuel cells, J. Power Sour. 245 (2014) 144–153. [Google Scholar]
- [66].Fast T, Niezgoda SR, Kalidindi SR, A new framework for computationally efficient structure-structure evolution linkages to facilitate high-fidelity scale bridging in multi-scale materials models, Acta Mater. 59 (2) (2011) 699–707. [Google Scholar]
- [67].Adams BL, Kalidindi S, Fullwood DT, Microstructure-Sensitive Design for Performance Optimization, Butterworth-Heinemann, 2013. [Google Scholar]
- [68].Kalidindi SR, Gomberg JA, Trautt ZT, Becker CA, Application of data science tools to quantify and distinguish between structures and models in molecular dynamics datasets, Nanotechnology 26 (34) (2015) 344006. [DOI] [PubMed] [Google Scholar]
- [69].Dong X, McDowell DL, Kalidindi SR, Jacob KI, Dependence of mechanical properties on crystal orientation of semi-crystalline polyethylene structures, Polymer 55 (16) (2014) 4248–4257. [Google Scholar]
- [70].Bunge H, Esling C, Texture development by plastic deformation, Scripta Metall. 18 (3) (1984) 191–195. [Google Scholar]
- [71].Kalidindi SR, Duvvuru HK, Knezevic M, Spectral calibration of crystal plasticity models, Acta Mater. 54 (7) (2006) 1795–1804. [Google Scholar]
- [72].Shaffer JB, Knezevic M, Kalidindi SR, Building texture evolution networks for deformation processing of polycrystalline fcc metals using spectral approaches: applications to process design for targeted performance, Int. J. Plast. 26 (8) (2010) 1183–1194. [Google Scholar]
- [73].Knezevic M, Levinson A, Harris R, Mishra RK, Doherty RD, Kalidindi SR, Deformation twinning in az31: influence on strain hardening and texture evolution, Acta Mater. 58 (19) (2010) 6230–6242. [Google Scholar]
- [74].Al-Harbi HF, Knezevic M, Kalidindi SR, Spectral approaches for the fast computation of yield surfaces and first-order plastic property closures for polycrystalline materials with cubic-triclinic textures, Comp., Mater., Cont 15 (2) (2010) 153–172. [Google Scholar]
- [75].Duvvuru HK, Knezevic M, Mishra RK, Kalidindi SR, Application of microstructure sensitive design to fcc polycrystals, Materials Science Forum, vol. 546, Trans Tech Publ, 2007, pp. 675–680. [Google Scholar]
- [76].Li D, Garmestani H, Schoenfeld S, Evolution of crystal orientation distribution coefficients during plastic deformation, Scripta Mater. 49 (9) (2003) 867–872. [Google Scholar]
- [77].Li D, Garmestani H, Adams B, A texture evolution model in cubicorthotropic polycrystalline system, Int. J. Plast. 21 (8) (2005) 1591–1617. [Google Scholar]
- [78].Li D, Garmestani H, Ahzi S, Processing path optimization to achieve desired texture in polycrystalline materials, Acta Mater. 55 (2) (2007) 647–654. [Google Scholar]
- [79].Li DS, Bouhattate J, Garmestani H, Processing path model to describe texture evolution during mechanical processing, Materials Science Forum, vol. 495, Trans Tech Publ, 2005, pp. 977–982. [Google Scholar]
- [80].Creuziger A, Hu L, Gnäupel-Herold T, Rollett AD, Crystallographic texture evolution in 1008 steel sheet during multi-axial tensile strain paths, Integ. Mater. Manuf. Innov 3 (1) (2014) 1. [Google Scholar]
- [81].Sundararaghavan V, Zabaras N, A multi-length scale sensitivity analysis for the control of texture-dependent properties in deformation processing, Int. J. Plast. 24 (9) (2008) 1581–1605. [Google Scholar]
- [82].Sundararaghavan V, Zabaras N, Linear analysis of texture–property relationships using process-based representations of Rodrigues space, Acta Mater. 55 (5) (2007) 1573–1587. [Google Scholar]
- [83].Sekimoto K, Evolution of the domain structure during the nucleation-andgrowth process with non-conserved order parameter, Phys. A: Statist. Mech. Appl 135 (2) (1986) 328–346. [Google Scholar]
- [84].Samudrala SK, Zola J, Aluru S, Ganapathysubramanian B, Parallel framework for dimensionality reduction of large-scale datasets, Sci. Program. 2015 (2015) 1. [Google Scholar]
- [85].Chang K, Krill III CE, Du Q, Chen L-Q, Evaluating microstructural parameters of three-dimensional grains generated by phase-field simulation or other voxel-based techniques, Model. Simul. Mater. Sci. Eng. 20 (7) (2012) 075009. [Google Scholar]
- [86].Cheng M, Warren JA, Controlling the accuracy of unconditionally stable algorithms in the Cahn-Hilliard equation, Phys. Rev. E 75 (1) (2007) 017702. [DOI] [PubMed] [Google Scholar]
- [87].Chen L-Q , Phase-field models for microstructure evolution, Ann. Rev. Mater. Res 32 (1) (2002) 113–140. [Google Scholar]
- [88].Bi Z, Sekerka RF, Phase-field model of solidification of a binary alloy, Phys. A: Statist. Mech. Appl 261 (1) (1998) 95–106. [Google Scholar]
- [89].Kalidindi SR, Binci M, Fullwood D, Adams BL, Elastic properties closures using second-order homogenization theories: case studies in composites of two isotropic constituents, Acta Mater. 54 (11) (2006) 3117–3126. [Google Scholar]
- [90].Pellegrini Y-P, Self-consistent effective-medium approximation for strongly nonlinear media, Phys. Rev. B 64 (13) (2001) 134211. [Google Scholar]
- [91].Pellegrini Y-P, Barthélémy M, Self-consistent effective-medium approximations with path integrals, Phys. Rev. E 61 (4) (2000) 3547. [DOI] [PubMed] [Google Scholar]
- [92].Monchiet V, Bonnet G, A polarization-based fft iterative scheme for computing the effective properties of elastic composites with arbitrary contrast, Int. J. Numer. Meth. Eng 89 (11) (2012) 1419–1436. [Google Scholar]
- [93].Monchiet V, Bonnet G, Numerical homogenization of nonlinear composites with a polarization-based fft iterative scheme, Comput. Mater. Sci. 79 (2013) 276–283. [Google Scholar]
- [94].Moulinec H, Silva F, Comparison of three accelerated fft-based schemes for computing the mechanical response of composite materials, Int. J. Numer. Meth. Eng 97 (13) (2014) 960–985. [Google Scholar]
- [95].Willot F, Abdallah B, Pellegrini Y-P, Fourier-based schemes with modified green operator for computing the electrical response of heterogeneous media with accurate local fields, Int. J. Numer. Meth. Eng 98 (7) (2014) 518–533. [Google Scholar]
- [96].Adams BL, Gao XC, Kalidindi SR, Finite approximations to the second-order properties closure in single phase polycrystals, Acta Mater. 53 (13) (2005) 3563–3577. [Google Scholar]
- [97].Fullwood D, Adams B, Kalidindi S, Generalized pareto front methods applied to second-order material property closures, Comput. Mater. Sci. 38 (4) (2007) 788–799. [Google Scholar]
- [98].Young N, An Introduction to Hilbert Space, Cambridge university press, 1988. [Google Scholar]
- [99].Halmos PR, Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea Pub Co, New York, 1957. [Google Scholar]
- [100].Rudin W, Real and Complex Analysis, Tata McGraw-Hill Education, 1987. [Google Scholar]
- [101].Folland GB, Fourier Analysis and Its Applications, vol. 4, American Mathematical Soc., 1992. [Google Scholar]
- [102].Oppenheim AV, Schafer RW, Buck JR, et al. , Discrete-Time Signal Processing, vol. 2, Prentice-hall Englewood Cliffs, 1989. [Google Scholar]
- [103].Mitra SK, Kuo Y, Digital Signal Processing: A Computer-Based Approach, vol. 2, McGraw-Hill; New York, 2006. [Google Scholar]
- [104].Wheeler D, Brough D, Fast T, Kalidindi S, Reid A, PyMKS: Materials Knowledge System in Python <mailto: 10.7449/multiscale_1>. [DOI] [Google Scholar]
- [105].Cheng M, Rutenberg AD, Maximally fast coarsening algorithms, Phys. Rev. E 72 (2005) 055701, 10.1103/PhysRevE.72.055701. http://link.aps.org/doi/10.1103/PhysRevE.72.055701. [DOI] [PubMed] [Google Scholar]
- [106].Bracewell R, The Fourier Transform and it’s Applications, McGrawHill, New York, 1965. [Google Scholar]
- [107].Brigham EO, Brigham E, The Fast Fourier Transform and Its Applications, vol. 1, Prentice Hall Englewood Cliffs, NJ, 1988. [Google Scholar]
- [108].Arfken GB, Weber HJ, Spector D, Mathematical methods for physicists, Am. J. Phys 67 (2) (1999) 165–169. [Google Scholar]
- [109].Zettl A, Sturm-Liouville Theory, vol. 121, American Mathematical Soc., 2010. [Google Scholar]
- [110].Weidmann J, Spectral Theory of Ordinary Differential Operators, Springer, 1987. [Google Scholar]
- [111].Al-Gwaiz M, Sturm-Liouville Theory and Its Applications, Springer, 2007. [Google Scholar]
- [112].Redheffer RM, Young RM, Completeness and basis properties of complex exponentials, Trans. Am. Math. Soc. 277 (1) (1983) 93–111. [Google Scholar]
- [113].Rainville ED, Special Functions, Macmillan, New York, 1960. [Google Scholar]
- [114].Arfken GB, Mathematical Methods for Physicists, Academic Press, 2013. [Google Scholar]