Super Charge Separation and High Voltage Phase in Na_xMnO₂

Abstract

Na_xMnO₂ shows Mn³⁺ and Mn⁴⁺ charge separation with the charge stripe ordering upon Na deintercalation at x = 5/8. In this paper it is shown that, surprisingly, at lower Na compositions of 5/8 > x ≥ 1/18 the phase evolution pathway of Na_xMnO₂ upon Na deintercalation shows a unique phenomenon of super charge separation, where the Mn³⁺ and Mn⁴⁺ ions fully charge-separate into charge superplanes formed by succession of charge stripes in the third dimension. The Mn³⁺ superplanes attract Na ions electronically, and dominate the antiferromagnetic interactions in NaMnO₂. Na ions in Mn³⁺ superplanes also naturally pillar the MnO₂ layers to form the unusual O1 phases with large interlayer distances at x < 1/3, which dominates the unique electrochemical behavior of NaMnO₂.

1. Introduction

NaTMO₂ (TM = 3d transition metal) layered compounds have attracted strong interests in the fields of Na ion battery as well as solid-state chemistry and condensed matter physics. For a single type of TM, Na orderings form at various Na compositions and couple with the spin, charge, and orbital orderings of the transition metal ions.^[1–10] Specifically, it was found that the magnetic stripe ordering is coupled with Mn charge and Na stripe orderings in Na_5/8MnO₂.^[2] When NaTMO₂ are studied as battery materials,^[11–23] these superstructure Na orderings also control the Na diffusion and the overall structure evolution. Among single TM layered NaTMO₂ compounds, NaMnO₂ phases were found to be electrochemically active,^[24,25] and O3-NaMnO₂ shows some unique electrochemical properties. For example, although there are multiple obvious ordering phase transitions in charge, the discharge seems largely absent from such phase transitions from the shape of voltage profiles.^[16] Moreover, it is featured by a surprisingly high initial discharge capacity of over 190 mAh g⁻¹,^[16] which is at least 40 mAh g⁻¹ larger than O3-NaTMO₂ with all other types of single TM element.^{[11–15,17–23]} The asymmetry between charge and discharge accompanied by the high capacity in the prototype cathode material of NaMnO₂ is a fundamental puzzle in the field of Na ion batteries, understanding of which may form the first step to further unlock the electrochemical potential of layered NaTMO₂. In this article, we try to elucidate the critical electronic and magnetic interactions among Na, Mn, and O that dictate the lattice–orbital–charge–spin coupled structural evolution in Na_xMnO₂ at different Na compositions, which dominates the unique electrochemical behavior. Three strong orderings at x ≈ 5/8 (as reported previously^[2]), x ≈ 1/2 and x ≈ 1/3 in charge are solved by analyzing in situ synchrotron X-ray diffraction (SXRD) patterns. The characteristic “superplanes” in all these superstructure orderings are identified, which are formed by a succession of Mn and Na stripes that cut through the parallel MnO₂ layers in the 3rd dimension periodically. The superplanes are Jahn–Teller (JT) active Mn³⁺ rich and also Na rich, while the non-JT active Mn⁴⁺ rich and Na deficient blocks are divided by these Mn³⁺ superplanes periodically. This phenomenon of “super charge separation” is further investigated by density functional theory (DFT) simulations, neutron diffraction and magnetic susceptibility measurements to understand the underlying mechanism, including the unique electronic attraction to the Na ions in the Mn³⁺ superplane that competes with the Columbic repulsion and the antiferromagnetic superexchange-like interaction^[26,27] along the JT active long axis. SXRD, high-resolution transmission electron microscopy (HRTEM), and Cs-corrected scanning transmission electron microscopy (STEM) further show the appearance of the O1 phase below 1/3 Na composition in charge. The O1 phase with empty Li layer was known in Li transition metal oxide layered compounds upon charge,^[28–30] however; here we report its coupling with the Na ions through the superplanes in Na-ion batteries down to extremely low Na composition of 1/18. The spontaneously formed pillaring effect provided by the Na ions in Mn³⁺ superplanes supports the unusually high interlayer distances of the O1 phases, which helps the sodium ion diffusion and creates an asymmetric phase evolution with strong-ordering-free discharge of high capacity. The cycling performance with higher voltage cutoff to the O1 phase region beyond 3.6 V is hence surprisingly better than the one with lower voltage cutoff.

2. Results and Discussion

2.1. General Structure Evolution of Na_xMnO₂

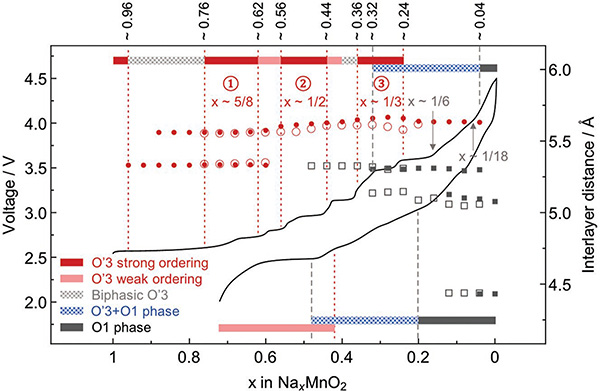
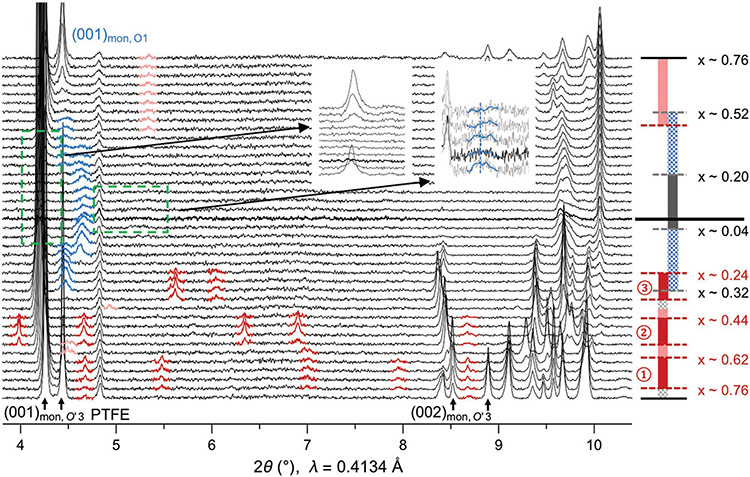
We first show the general structure and superstructure evolution from an in situ SXRD test of Na_xMnO₂ in the first cycle. The electrochemical profile and the corresponding in situ SXRD data are shown in Figures 1 and 2, respectively. At low charge voltage <3.6 V (Na composition x > 1/3), the material stays in the O′3 phase with the oxygen stacking notation introduced by Delmas^[18] (The prime on O represents extra monoclinic distortion^[16]). Notably, below the voltage of 3.5 V, there are several voltage plateaus in the charge, corresponding to the phase transitions between the three strong ordering phases of 5/8, 1/2, and 1/3 Na compositions with a series of characteristic superstructure peaks (highlighted by dark red) on SXRD patterns (Figure 2). Note that we show the SXRD patterns starting from the end of the first voltage plateau with x < 0.76 in both charge and discharge for better visualization, as the two-phase evolution in this particular plateau in charge was well understood.^[2]

Figure 1.

Electrochemical profile and phase evolution of O′3-NaMnO₂. The voltage profile of NaMnO₂ in the first cycle between 2.0 and 4.5 V at C/50 rate as a function of Na composition measured from an in situ synchrotron XRD battery cell (XRD is shown in Figure 2), from which the phase evolution for charge (top bar) and discharge (bottom bar) is obtained. The corresponding interlayer distance at each Na composition for charge or discharge is shown by filled or empty symbols, respectively. The symbols for interlayer distance of O′3 phase are in red circles (filled or empty) and O1 phase in gray squares (filled or empty).

Figure 2.

In situ synchrotron XRD showing the superstructure evolution of NaMnO₂ in the first electrochemical cycle. The phase evolution is the same as in Figure 1, and the thick black line in the middle region separates charge and discharge. The (001) and (002) peaks of O′3 phase, along with the static peak of the PTFE (polytetrafluoroethylene) binder, are marked at the bottom. The superstructure peaks are highlighted with dark red for the three strong ordering phases and lighter red for the weak ordering phases. The (001) O1 peaks in the high voltage O′3+O1 phase and O1 phase are highlighted by blue. The insets magnify the (001) peak regions at high voltage for O′3 phases (left inset) and O1 phases with lowest interlayer distance of 4.5 Å (right inset).

At high voltage (>3.6 V) below the Na composition of 1/3, there is the O′3 to O1 phase transition. SXRD shows that the O′3 phase gradually evolves into a region with a mixture of O′3 phase and multiple other high voltage phases with broadened (001) peaks highlighted in blue in Figure 2. The SXRD result is also consistent with our in situ lab XRD result (Figure S1a, Supporting Information). XRD analysis shows that these high voltage phases are more consistent with O1 rather than O3 stacking, which will be confirmed directly by HRTEM later. Note that the angle dependence of peak broadening in the high voltage SXRD patterns agree well with the size broadening rather than strain broadening model (Figure S1b, Supporting Information), which suggests that the multiple phase coexistence at high voltage is with relatively small domains in each phase. We can identify three different high voltage phases with interlayer distances at around 4.5, 5.1, and 5.3 Å, respectively, in both charge and discharge, from the positions of (001) peaks in Figure 2. All these three phases are also directly observed by our HRTEM along the b-direction of samples charged to high voltage (Figure S2, Supporting Information), which confirms both the O1 stackings and the small domain size indicated by in situ SXRD. First, the interlayer stackings are typical O1 type with the transition metal ions aligned along the c direction perpendicular to the ab plane. Second, the O1 phases with multiple corresponding interlayer distances to the XRD (001) peaks are in relatively small domains in the HRTEM (Figure S2, Supporting Information). The reduced domain size supports the size broadening conclusion from the analysis of the high voltage XRD peaks (Figure S1b, Supporting Information).

DFT simulation with Van der Waals correction suggests that the 4.5 Å O1 phase, which is a very minor phase based on the weak in situ XRD peak intensity, has to be Na-empty, as any Na occupancy will increase the interlayer distance far above 4.5 Å. This is similar to the Li-empty O1 phases previously found in the lithium electrode materials.^[28–30] The abnormal 5.1 Å O1 phase, which is the major phase toward the end of charge based on the XRD peak intensity, shows a highly unusual Na ordering solved from the Cs-corrected STEM images (discussed later) with the Na composition determined to be 1/18 (labeled in Figure 1). The 5.3 Å O1 phase labeled in Figure 1, which is between the 1/3 Na composition 5.7 Å O′3 phase and the 1/18 Na composition 5.1 Å O1 phase, most probably has a Na composition of 1/6, corresponding to the last voltage plateau at 3.6 V in charge, which starts in the region of 1/3 Na O′3 phase, ends at the 1/6 Na composition.

Remarkably, the structural evolution and the corresponding features in the voltage curve in discharge vary significantly from the ones in charge, giving an asymmetric charge and discharge evolution. All the three strong orderings and the corresponding voltage plateaus and steps disappear in discharge, while a weak ordering exists starting at around the Na composition of 0.56 (light red peaks in Figure 2), corresponding to the last discharge plateau. In addition, two weak superstructure peaks around the Na compositions of 0.58 and 0.4 in charge are also observed, corresponding to the two short voltage plateaus in charge. The strong and weak orderings together provide a close match to the step and plateau features of the electrochemical voltage curve throughout the entire in situ battery charge and discharge.

Furthermore, upon discharge when the Na composition is larger than 40%, the structure goes back to the O′3 phase with the (001) peak being significantly resharpened again (Figure 2). In addition, the general crystal structure after one cycle goes reversibly back to the pristine O′3 phase based on both in situ synchrotron and lab XRD (Figure S3a, Supporting Information), although some structural defects like stacking faults or dislocations generated at high voltage may still exist after discharge, as the (001) peak full-width-half-maximum (FWHM) is increased slightly after one cycle (Figure S3c, Supporting Information), which may contribute to the known capacity fading effect.^[16] However, upon the 2nd charge all the plateau and step features in the voltage curve can largely repeat the 1st charge (Figure S3e (Supporting Information) and previous literature^[16]), suggesting that the structure evolution is largely reversible from cycle to cycle, albeit with asymmetric charge and discharge profiles within each cycle. In comparison, NaCrO₂ shows a strong irreversible layered-to-rocksalt structural change due to the Cr migration, leading to a significantly reduced discharge capacity together with the irreversible XRD pattern and peak broadening after one cycle (Figure S3b,d,f (Supporting Information) and previous literatures^[31,32]). Therefore, the significantly resharpened XRD peaks and reversible pristine phase after one cycle of NaMnO₂ suggest that the irreversible structural defects are not the major factor for the high voltage peak broadening here, which is fundamentally different from NaCrO₂.

2.2. Super Charge Separation Coupled with Na Orderings

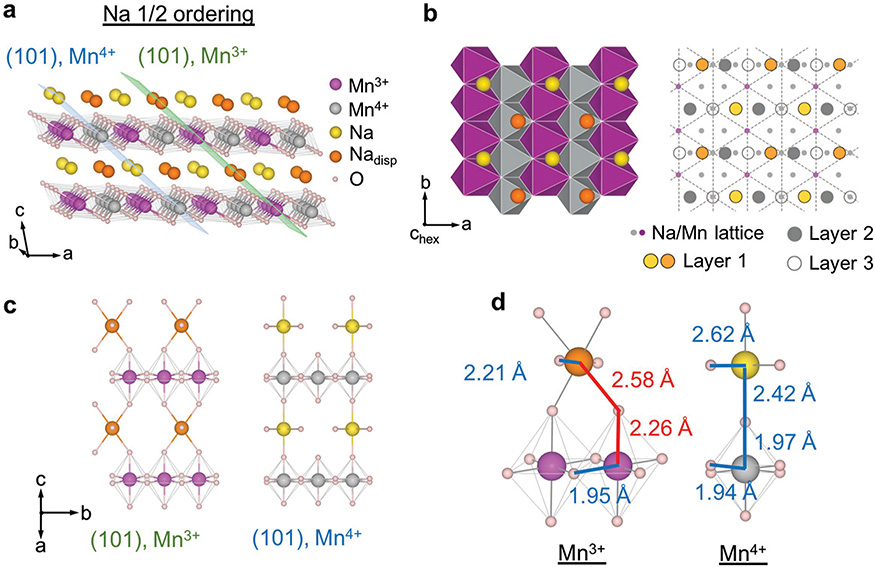
We refined the SXRD curve corresponding to the Na-5/8, Na-1/2, and Na-1/3 orderings and solved the superstructures (See Figures S4 and S5 and Tables S1–S4 in the Supporting Information for details of the Rietveld refinements). The refined structure of 5/8 ordering here agrees well with the reported structure.^[2] The comparison of Na-5/8 and Na-1/2 orderings shows that the Na-1/2 ordering (Figure 3a,b) evolves from the Na-5/8 ordering by deintercalating 1/8 Na out of the only full Na stripe to form the fourth half-full stripe, in addition to the original three half-full ones in the Na-5/8 ordering. The newly formed half-full Na stripe also experienced the same Na displacement as one of the original half-full stripes in Na-5/8 ordering^[2] (See Figure S6 in the Supporting Information).

Figure 3.

Na—1/2 ordering and the corresponding Mn charge ordering. a) 3D view of the Na—1/2 superstructure solved by SXRD and relaxed by DFT. The corresponding Mn charge orderings relaxed from DFT are labeled by purple (3+) and grey (4+). The Mn³⁺ and Mn⁴⁺ superplanes are labeled by green and blue planes, respectively. Na_disp refers to the Na ions that are displaced away from the octahedral sites. b) Projective view of inset (a) in the direction perpendicular to the MnO₂ plane (the hexagonal c direction). The left figure shows the basal structure of one Na layer and one MnO₆ layer and the right figure illustrates the interlayer stacking in detail. Points at the intersections of dashed triangular pattern corresponds to Mn lattice from layer 1, with the Mn³⁺ and Mn⁴⁺ marked in purple and grey, respectively, showing the Mn charge stripe along the b direction, as also can be seen in inset (a). The Na triangular lattice is a projection of three neighboring layers, labeled in small grey dots, with the actual Na occupation in the three layers labeled by big circles in different colors. c) Section of the two types of (101) superplanes with Na and Mn³⁺ or Mn⁴⁺. d) Elementary Na–O–Mn units of Mn³⁺ and Mn⁴⁺ superplanes for Na-1/2 ordering. Representative bonds are marked by colors, with the corresponding bond length from DFT simulation.

There are some new features in the Na-1/2 ordering compared with the Na-5/8 one, which are critical to the understanding of the fundamental interactions in NaMnO₂. Starting from the Na-1/2 ordering during Na deintercalation, the Mn⁴⁺ ions form the complete Mn⁴⁺ planes, which separates the Mn³⁺ and Mn⁴⁺ ions into two different sets of (101) parallel “superplanes” alternating each other, labeled by green and blue planes, respectively, in Figure 3a. We will see later that such charge separation into different superplanes, or “super charge separation,” is universal in Na_xMnO₂ with low Na compositions (x ≤ 0.5). The Mn³⁺ superplane at x = 0.5 contains all the JT elongated Mn–O bonds, or JT long axis bonds, and displaced Na ions (Na_disp in Figure 3), while the Mn⁴⁺ superplane only contains the non-JT Mn–O bonds and nondisplaced Na ions in the normal octahedral Na sites (Figure 3c). The general definition of a Mn³⁺ superplane in Na_xMnO₂ at any given Na composition follows the above description that all the JT long axis bonds have to be included in the superplane, while the Mn⁴⁺ superplanes are naturally defined in parallel. Such a definition will be justified when we discuss the formation mechanism of superplanes. Note that the Na composition is 50% in both Mn³⁺ and Mn⁴⁺ superplanes in Na_1/2MnO₂ (Figure 3c), suggesting that the Mn³⁺ ions have to localize the electrons provided by the Na ions in both the Mn³⁺ and Mn⁴⁺ superplanes. It is worth mentioning that the structure from SXRD refinement in Figure 3 is slightly different from the previous DFT prediction of the ground state structure^[33] (See also Figure S4 in the Supporting Information). Contrary to the Na-5/8 structure, the Na displacement in the Na-1/2 structure here increases the DFT energy slightly above the ground state structure without the Na displacement. However, the superstructure (112) peak we observed in SXRD (Figure S4a, Supporting Information) will be extinguished without such Na displacement, as the (112) lattice plane (Figure S4c, Supporting Information) cuts exactly through the displaced Na sites. Any other structures with perturbation of Na ions away from the displaced site in our Na-1/2 structure, including the DFT ground state structure, will also extinguish the (112) peak, leading to worse XRD refinement. It is possible that Na ions are relaxed to the metastable displaced sites, which are forced kinetically by the structural evolution pathway from Na-5/8 to Na-1/2 structures.

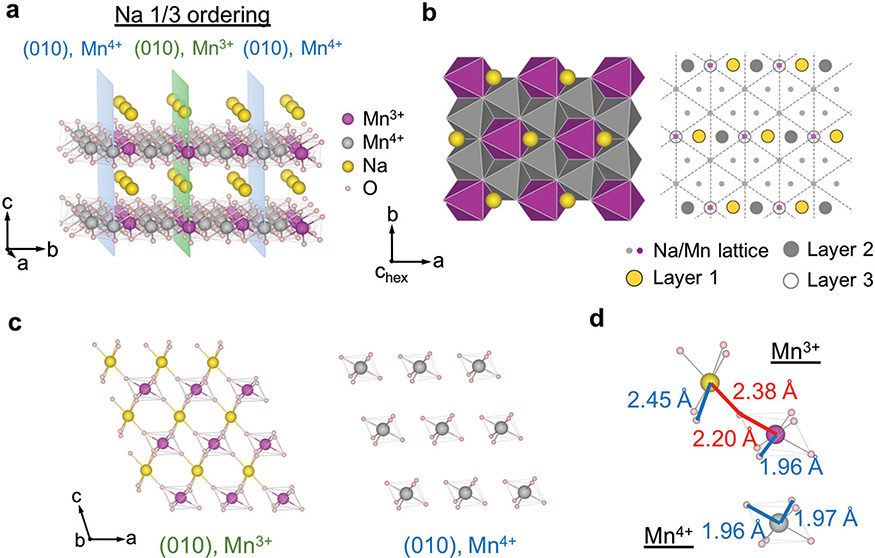
In the solved Na-1/3 ordering, although the Mn charge ordering or Na ordering in each ab plane is threefold symmetric, their relative positions in the ab plane and stackings along c make the a direction special, which preserves the monoclinic distortion (Figure 4a,b). The solved Na-1/3 ordering is consistent with the previous prediction by DFT simulations.^[33] The (010) superplanes that completely separate Mn³⁺ from Mn⁴⁺ ions in Na-1/3 ordering contain the Mn charge stripes along the a direction that are rotated by 90° from the b direction in Na-1/2 ordering (Figures 3a and 4a). Note that in the Na-1/3 ordering the Na composition is 100% in Mn³⁺ superplanes while the Mn⁴⁺ superplanes are Na empty (Figure 4c). The basic units of the superplanes in Na-1/2 and Na-1/3 orderings are shown in Figures 3d and 4d. From the calculated bond lengths, which are also consistent with the refined ones from SXRD, we can see the significant JT elongation of the Mn³⁺–O bond beyond 2.20 Å is only along the directions where Na or displaced Na ions are located near the bond extension. Note that at x ≤ 1/3 for Na_xMnO₂ no Na ions are found in the Mn⁴⁺ superplanes, suggesting that both Na ions and electrons are more strongly bound to the Mn³⁺ superplane in this system. Moreover, in the Na-1/3 ordering the Mn³⁺ superplanes are now separated at 4.2 Å apart by two consecutive Mn⁴⁺ superplanes (Figure 4a) rather than 3.2 Å apart by one Mn⁴⁺ superplane in the Na-1/2 case (Figure 3a). This trend will become clearer in the O1 phase at lower Na composition of 1/18, where Mn³⁺ and Na ions still tend to accumulate together in the superplanes. Also note that the Mn charge ordering here is obtained from DFT relaxation of the experimentally solved Na ordering. The validity of such a procedure to determine the charge ordering in NaMnO₂ is well supported by the agreement of XRD refined and DFT relaxed bond lengths with Jahn–Teller distortions (Figures 3d and 4d; Tables S1–S4, Supporting Information) and the fact that in Na_5/8MnO₂ the DFT predicted charge ordering matches exactly with the direct STEM-EELS measurement and the neutron diffraction analysis of coupled magnetic ordering at low temperatures.^[2]

Figure 4.

Na—1/3 ordering and the corresponding Mn charge ordering. Each subfigure shows the same type of information as in the corresponding subfigure of Figure 3. a,b) 3D and projective view of Na-1/3 ordering. c) Section of the (010) Mn³⁺ superplane with Na and Mn⁴⁺ superplane without Na. d) Elementary Na–O–Mn units of Mn³⁺ and Mn⁴⁺ superplanes for Na-1/3 ordering.

2.3. Magnetic Ordering in Na_1/3MnO₂

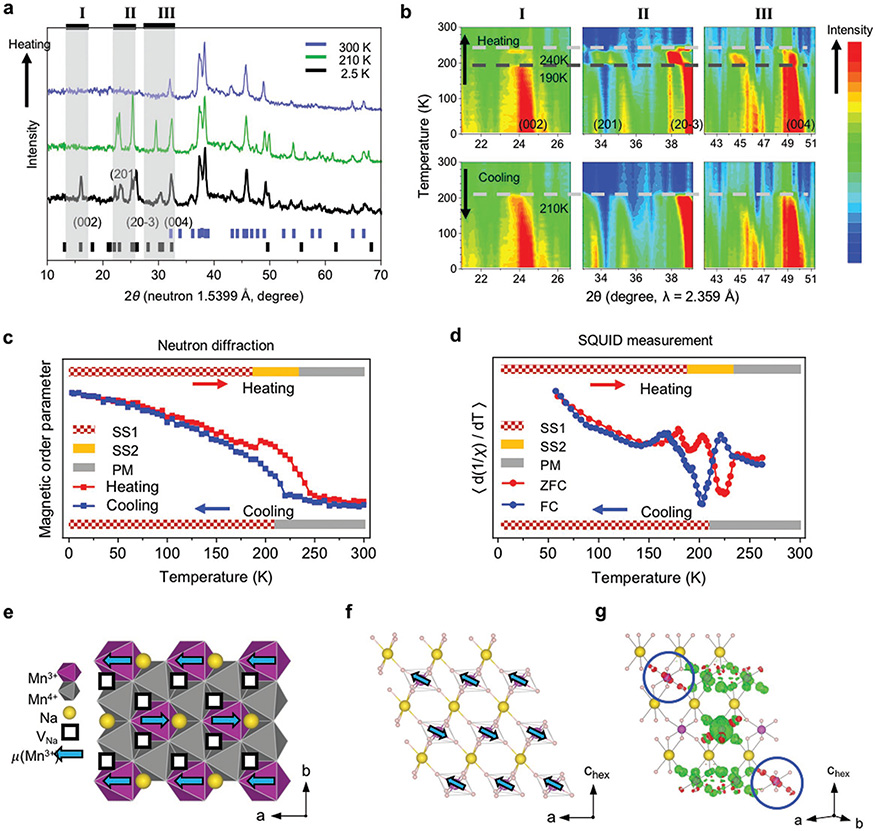
To further provide a more direct experimental confirmation of the Mn charge ordering in Na_xMnO₂ and understand the magnetic property of the superplanes, we performed magnetic neutron diffraction measurements on the chemically desodiated powder of Na_1/3MnO₂. The neutron diffraction pattern at room temperature confirms the Na-1/3 crystal structure solved by SXRD (Figure S7, Supporting Information), while the comparison with the pattern taken at 2.5 and 210 K shows clearly the appearance of magnetic diffraction peaks (Figure 5a). Interestingly, the temperature evolution of these magnetic peaks shows an abnormal discontinuity in heating at around 190 K and a paramagnetic (PM) transition beyond 240 K, while no such discontinuity is observed in cooling with the magnetic phase developed below 210 K (Figure 5b). Correspondingly, the magnetic order parameter upon warming also shows a discontinuity at 190 K, well before the paramagnetic phase transition at 240 K, while the order parameter in cooling is continuous (Figure 5c). These trends and transition temperatures in both neutron diffraction and order parameter analysis agree well with the magnetic susceptibility analysis (Figure 5d), where the two peaks in the curve for the slope of the inverse magnetic susceptibility from zero field cooling (ZFC) measurement correspond well with the discontinuity and PM transition temperatures from neutron diffraction measurement upon heating, while the single peak from field cooling (FC) measurement agrees well with the magnetic transition temperature from neutron diffraction upon cooling.

Figure 5.

Magnetic ordering and transition in Na_1/3MnO₂. a) High resolution neutron diffraction patterns of chemically desodiated Na_1/3MnO₂ sample upon heating up. Blue bars mark the crystallographic peaks corresponding to the blue pattern recorded at 300 K, while black bars mark all the magnetic peaks below 35° and the major magnetic peaks at high angle corresponding to the black pattern recorded at 2.5 K. b) Heat diagram showing the evolution of several magnetic peaks upon heating (top) and cooling (bottom) between 2.5 and 300 K. The three ranges (I, II, III) of the diffraction angles from left to right are labeled in inset (a) correspondingly. c) The intensity integral of the peak from 33° to 39° in inset (b) versus temperature for both heating (red) and cooling (blue). The bar on top shows the transition from magnetic superstructure 1 (SS1) to magnetic superstructure 2 (SS2) to paramagnetic (PM) phase in heating, while the bar on bottom shows the PM-SS1 transition in cooling. d) The slope of the inverse magnetic susceptibility 1/χ versus temperature from 2 to 300 K in ZFC (red) and FC (blue) SQUID measurement. e,f) The simplest magnetic ordering model that describes the observed neutron diffraction, showing antiferromagnetic (AFM) coupling of ferromagnetic (FM) stripes in each e) MnO2 ab layer and f) interlayer AFM ordering in the Mn3+ superplane. g) Spin polarized charge density difference of one Mn3+ superplane calculated by DFT, where the spin of one Mn3+ ion in the middle Mn row was flipped from “spin up” to “spin down” in the three-layer supercell. The induced changes to the dz2 orbital of the JT long axis Mn3+ ions (circled) are up (red), while to other Mn3+ ions are down (green).

The simplest magnetic model with smallest magnetic supercell that contains all the magnetic peaks is shown in Figure 5e,f, where the ferromagnetic (FM) Mn³⁺ stripes along the a direction are coupled antiferromagnetically (AFM) along b in the MnO₂ ab plane (Figure 5e), while the interlayer coupling is AFM in the Mn³⁺ superplane (Figure 5f). The magnetic orderings in the Mn⁴⁺ superplanes have to be not exactly the same as the Mn³⁺ superplanes at 2.5 K to give the (002) peak of a two-layer supercell, corresponding to the ground state magnetic superstructure (SS1), while the anomalous transition at 190 K corresponds to a phase transition toward higher symmetry that may also align the magnetic moments in the Mn⁴⁺ superplanes to follow exactly the neighboring Mn³⁺ ones, which extinguishes the (002) peak and also decreases the magnetic peak splitting (SS2). It is worth noting that our DFT simulation suggests that the interlayer AFM ordering in the Mn³⁺ superplane is dominated by the Mn³⁺ interaction along the JT long axis. The magnetic moments of Mn³⁺ and Mn⁴⁺ in DFT simulations are 3.8 and 3.2 μ_B, respectively. Figure 4g shows that flipping down the spin of one Mn³⁺ ion in the middle layer induces the “spin up” component on the two Mn³⁺ ions in the neighboring layers along its JT long axis, suggesting AFM coupling among them, while the couplings to other in-superplane nonlong-axis Mn³⁺ ions and out-of-superplane Mn⁴⁺ and Mn³⁺ ions are all FM. The spin charge density difference simulation also suggests that the interlayer magnetic couplings in the Mn⁴⁺ superplanes are all FM. Interestingly, this long axis AFM interaction is similar to the superexchange interaction in colossal magnetoresistive materials,^[26,27] where the oxygen bridge is replaced by the –O–Na–O– bridge here to mediate the same AFM coupling at longer range. The magnetic structures revealed by neutron diffraction measurements emphasize the importance of the Mn³⁺ superplane, especially the JT long axis interactions, in determining the magnetic superstructure evolution. The general magnetic structures disclosed by neutron diffraction also confirm the charge ordering predicted by our DFT relaxation of the experimentally solved Na-1/3 ordering.

2.4. Superplane Pillared O1 Phase with Large Interlayer Distances

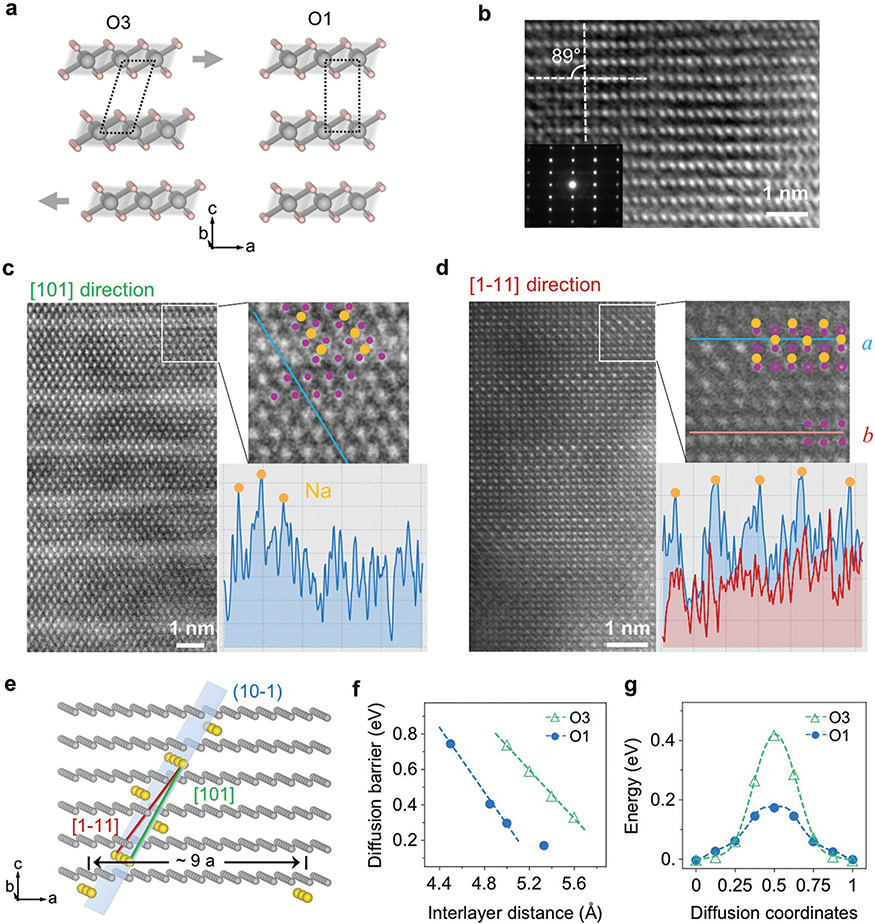
With the formation of the O1 phases when charging below the 1/3 Na composition, the phenomenon of super charge separation surprisingly continues to exist down to a very low Na composition around 5%–6%. A structural model in Figure 6a shows a possible gliding transition from O′3 (C2/m) to O1 (P-3m). The high voltage phase was directly confirmed by HRTEM and electron diffraction as O1 (Figure 6b) with the characteristic rectangular TM stacking, which agrees with the in situ SXRD analysis. The atomic resolution STEM images (Figure 6c,d) provide the direct evidence of a special Na superstructure ordering in the O1 phase, with the model shown in Figure 6e. In the sample charged to 4.0 V, corresponding to a Na composition of around 6% based on the electrochemical capacity, bright stripes are observed in the STEM images with wide separations (Figure 6c,d), suggesting the condensation of Na ions in the bright regions to give the additional Z contrast on the Mn background. The low magnification STEM image (Figure S8, Supporting Information) taken in the same [101] direction as Figure 6c shows that the stripe distance is 9 atomic rows or around 20 Å apart in each block, with some imperfections between the blocks, which is understandable for such super long ranged ordering. This superstructure in the O1 phase is solved using the two STEM images taken along the two crystallographic axes of [101] and [1–11] (Figure 6c,d). The solved superstructure gives a Na composition of 1/18 that agrees well with the electrochemically determined composition of 6%. The intensity line scans of the STEM images match well with the structural details of the Na locations in the solved superstructure model (Figure 6c,d). Note that the superstructure cannot be solved if assuming the O3 stacking instead.

Figure 6.

High voltage O1 phase with Na condensation into widely separated superplanes at extremely dilute Na composition in Na_0.06MnO₂. a) Illustration of O3 (left) to O1(right) transition by gliding of the MnO₂ planes. Gray arrows show the gliding direction. b) HRTEM image and inset electron diffraction taken in the b direction of the NaMnO₂ sample charged to 4.0 V, showing the rectangle O1 stacking. c,d) STEM images taken along [101] and [1–11] directions, respectively, of the O1 phase Na_0.06MnO₂. The projected view of the solved superstructure model is superimposed on the magnified STEM images. An intensity line scan in inset (c) shows three peaks corresponding to the Na ion positions in our model. In inset (d), line scan of a (blue) shows much stronger peaks corresponding to the Na ions than the line scan of b (red) without expected Na ions in our model. e) Solved superstructure Na ordering in the O1 phase with zigzagged superplanes near the (10–1) plane (indexed with a 1 × 1 × 1 O1 unit cell). f) DFT calculated diffusion barrier of the O3 and O1 phases with changing interlayer distance. g) Comparison of diffusion energy profile of O3 and O1 phases.

The zigzagged superplane of Na ions in Figure 6e consists of a three-layer basis largely along the (10–1) plane, which might result from the gliding of TMO₂ layers in the O′3–O1 phase transition. Our DFT simulation shows that, in contrast to the Na-1/2 and Na-1/3 orderings with the superplanes fully filled by either Mn³⁺ or Mn⁴⁺ ions, in the Na-1/18 ordering the Mn³⁺ ions now have to mix with equal composition of Mn⁴⁺ ions in each zigzagged Na rich superplane due to the extremely low Na composition. These Na rich superplanes serve as the naturally formed pillars for the novel O1 phase with high interlayer distances of 5.1 or 5.3 Å. Importantly, the Na diffusion barrier in the O1 phase is much lower than in the O3 phase at a given interlayer distance (Figure 6f,g). In the entire range of phase evolution in Na_xMnO₂, the interlayer distance varies between 5.1 and 5.6 Å considering both O1 and O′3 phases (Figure 1). Within this range the Na diffusion barrier in the O1 phase is always lower than in the O3 phase (Figure 6f), suggesting that the O1 phase, once formed upon charging to high voltage, is at least kinetically preferred over the O3 phase. It is worth noting that once the O1 phase is developed in charge at x < 1/3, it tends to stay in a wider Na composition range during discharge until x > 0.5, driving the system to bypass the O′3 Na-1/3 and Na-1/2 orderings through an asymmetric structural evolution pathway in discharge to the charge one (Figures 1 and 2).

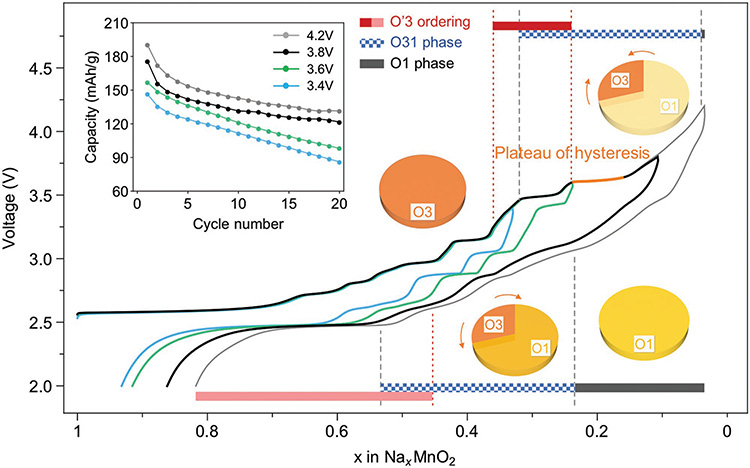
Note that as mentioned earlier, toward the end of discharge XRD shows that NaMnO₂ goes back to the pristine phase with just very slight peak broadening compared with pristine one (Figure S3, Supporting Information), which explains that the 2nd charge curve can largely repeat the voltage plateaus and steps of the 1st charge one,^[16] indicating that the asymmetric charge–discharge evolution in each cycle is largely reversible from cycle to cycle, i.e., a novel reversible asymmetrical evolution. However, if the charge process does not go beyond the 3.6 V plateau to avoid the full development of the O1 phase, the discharge will largely follow the voltage plateaus and steps in charge (Figure 7), indicating a much more symmetric O′3 phase evolution between charge and discharge. Therefore, the activation of the high voltage pillared O1 phase with superior Na diffusivity is strongly correlated with the suppression of the strong ordering phases in discharge, which can also explain the abnormal phenomenon of significantly improved cyclability by cycling to higher voltage beyond 3.6 V (Figure 7 inset). Note that such reversible asymmetric evolution of NaMnO₂ when charged beyond 3.6 V is fundamentally different from the irreversible asymmetric evolution found in NaTiO₂ charged beyond 1.6 V,^[11,34] NaVO₂ charged beyond 3.0 V,^[12] NaCrO₂ charged beyond 3.8 V,^[31,32] and NaFeO₂ charged beyond 3.4 V,^[17,35] where the structures are destroyed at high voltage with significantly reduced discharge capacities and cyclabilities, as shown earlier for NaCrO₂ in Figure S3 in the Supporting Information.

Figure 7.

Relationship between structural evolution and electrochemical performance of NaMnO₂. Hysteresis between charge and discharge appears after passing the “Plateau of hysteresis.” Blue, green, black, and dotted curves are the first cycle of cells at C/10 rate charged to 3.4, 3.6, 3.8, and 4.2 V high voltage cutoff, respectively. The phase evolution in charge (top bar) and discharge (bottom bar) for 4.2 V cell is predicted by matching the same features of the voltage curve with the in situ SXRD one. The structural evolution of a cycle beyond the plateau of hysteresis is illustrated by four pie charts, where qualitatively darker (more red) corresponds to higher Na composition in that phase. Arrows show the evolution direction of phases. Inset shows the comparison of cyclability for different high cutoff voltages with the same low voltage cutoff of 2.0 V.

2.5. Origin of Super Charge Separation

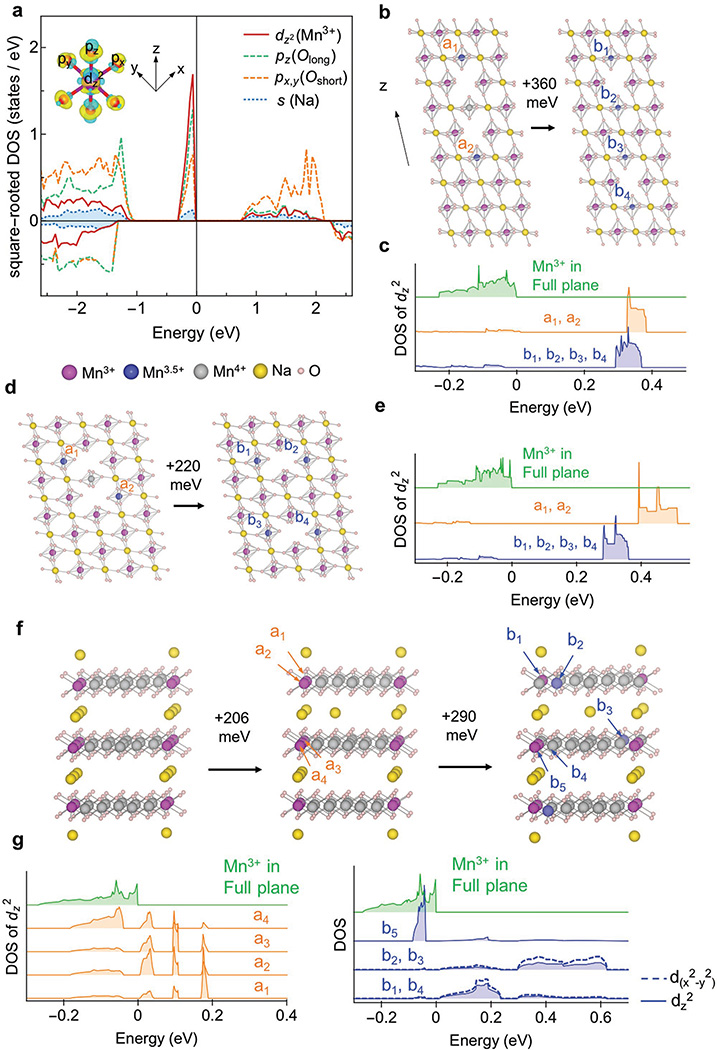
The calculated density of states (DOS) show the evidence of pd hybridization along both the long and “double-short” axis of the JT distortion of the Mn³⁺ in the superplane, where all p_x, p_y, p_z, and d_z2 orbitals participate in the hybridization below the Fermi level (Figure 8a). The JT long axis is along the z direction, while the double-short axis is along the 45° direction between the two JT short axes in the x and y directions (called double-short axis hereafter). The 3d_z2 electron participating in the hybridization is provided by the Na 3s orbital, because when the Na ions are removed the hybridization peak below the Fermi level disappears, leading to the oxidation to Mn⁴⁺ without the JT distortion (Figure S9a, Supporting Information). Note that there is no Na-s orbital involvement in the pd-hybridization due to the highly ionic nature of Na–O bonds. As we can see from Figure 8a, the peak for Na is still an order of magnitude lower than the peak for Mn³⁺ in this square-rooted plot. The Mn³⁺ superplane for the Na-1/2 ordering shows similar hybridization (Figure S9b, Supporting Information), while the Na occupied non-JT Mn⁴⁺ superplane shows no such hybridization DOS peak (Figure S9c, Supporting Information), indicating that the stronger binding force of Na ions in the Mn³⁺ superplane is originated from pd hybridization and associated JT distortion.

Figure 8.

Mechanism of superplane formation in Na_xMnO₂. a) DOS of the d_z2 orbital of Mn³⁺ (red), the p_z orbital of JT long axis O(green), the p_x and p_y orbitals of two double-short axes O (orange) and the s orbital of Na(blue) in Na_1/3MnO₂. The two branches of positive and negative DOS correspond to two spin directions. The magnitude of the DOS in this figure is square root of the calculated actual value for better visualization. Inset shows charge density for a Mn³⁺ and surrounding oxygen. d and p orbitals are marked. b–e) Binding energy and DOS of Na or Na vacancy moving along b,c) JT long and d,e) double-short axes inside a Mn³⁺ superplane in Na_1/3MnO₂. DOS figure shows the hybridization peak positions of any Mn³⁺ in the original full Na superplane (green), two Mn^3.5+ marked by a₁ and a₂ in the left structure with vacancy distance 1 (orange), and four Mn^3.5+ marked by b₁ to b₄ in the right structure with vacancy distance 2 (blue). a₁ and a₂ show the same DOS while b₁ to b₄ show the same DOS. f) Binding energy of one Na moving 1 or 2 sites away from the Mn³⁺ superplane in a hypothetical Na_1/6MnO₂ structure. The Na rich Mn³⁺ planes are separated by three lattice constants, twice the distance in the Na_1/3MnO₂ ordering. g) DOS figure for inset (f) shows the hybridization peak positions of any Mn³⁺ in the original full Na superplane (green), four Mn³⁺ in the structure with the Na moving 1 site away (orange) marked by a₁ to a₄, and 3 Mn³⁺ (b₁, b₄, b₅) and 2 Mn^3.5+ (b₂, b₃) with the Na 2 sites away (blue). Note that the JT distortion of b₁–b₄ in inset (f) are changed from z direction to x direction (See inset (a) for definition of axes). For all other cases in this figure the JT distortion is always in the z direction. The energy reference in the DOS calculations in each model is the Fermi energy of the corresponding full-plane structure.

To estimate the strength of such binding force, we move a pair of Na vacancies away from each other in the Mn³⁺ superplane of Na-1/3 ordering, which generates around 360 meV (Figure 8b) and 220 meV (Figure 8d) energy penalties, respectively, along the long and double-short axes of JT distortion according to our DFT simulations. In Figure 8b, when the Na vacancy pairs are neighboring each other along the JT long axis, there is no isolated Na along this direction in the superplane. When they move apart by one step, the two Na along the JT long axis become isolated between the Na vacancies, corresponding to the increased energy. The same phenomenon is observed when the Na vacancy pairs are moved apart along the double-short axis in Figure 8d. It is clear that the property of the Mn³⁺ superplane to hold the Na vacancy pairs close together is equivalent to the tendency of the plane to eliminate the isolated Na by making all the Na ions connected through the Mn³⁺O₆ octahedra along both the long and double-short axes.

Our calculations also show that the energy penalty to move one Na ion one step away from the complete Mn³⁺ superplane, leaving a Na vacancy in the superplane, is 206 meV, while the energy penalty of moving that Na ion one further step away from the superplane is another 290 meV (Figure 8f). Therefore, we observed the very interesting property of the Mn³⁺ superplane to bind more Na ions into the plane and to attract the Na ions close together inside the plane by pushing the Na vacancies together. Equivalently speaking, the NaMnO₂ system shows a strong tendency to form the complete 2D Na–Mn³⁺ superplanes, as observed in O3 Na-5/8, Na-1/2, and N-1/3 orderings. The O1 Na-1/18 ordering shows a mixture of Mn³⁺ and Mn⁴⁺ in the Na rich superplane due to insufficient Na ions at the extremely low Na composition. Therefore, the Na-s electron induced pd hybridization and associated JT distortion not only provides the binding force to form the Na–O–Mn–O–Na JT long axis unit, as argued previously,^[36,37] but also generates the double-short axis Na–O=Mn=O–Na attraction, driving the super charge separation of Mn³⁺ superplanes rather than stripes in Na_xMnO₂.

Further analysis of DOS and band structure shows that when two neighboring Na vacancies are created in the Mn³⁺ superplane, one Mn⁴⁺ ion and two Mn^3.5+ ions (a₁, a₂) are generated nearby (Figure 8b–e). Note that we use the magnetization value to determine the valence of Mn ion. No hybridization DOS peak is seen for the Mn⁴⁺ due to the lack of e_g electrons, while the energies of hybridized orbitals related to the two Mn^3.5+ ions are increased significantly (orange a₁, a₂ DOS) compared with the d_z2 e_g electron of Mn³⁺ ions in the Na full superplane (green DOS). When the two Na vacancies are moved one step away along the JT long or double-short axes, four Mn^3.5+ ions (b₁ to b₄) are generated at the expense of the original Mn⁴⁺ ion, which doubles the high energy d_z2 orbital electrons (blue b₁–b₄ DOS), accounting for the energy penalty of moving apart the two Na vacancies. Therefore, the property of the Mn³⁺ superplane to squeeze the Na vacancies together is accompanied by pushing the high valence Mn ions together to generate more fully oxidized Mn⁴⁺ without the high energy e_g orbital electrons.

When the Na ion is moved out of the superplane one step away (Figure 8f,g), the e_g electron DOS of four Mn³⁺ ions (a₁–a₄) inside the plane is shifted toward higher energy (orange DOS), accounting for the energy penalty. When the Na ion is moved one step further away from the superplane, two out-of-plane Mn^3.5+ ions (b₂, b₃) are generated, in addition to three Mn³⁺ ions (b₁, b₄, b₅) in the superplane, among which the e_g electron energies of Mn b₁–b₄ are further increased. The distribution of electrons in the d_x2–y2 orbital here is due to the change of JT distortion direction of b₁ to b₄ from the z to x direction. The property of the Mn³⁺ superplane to attract the out of plane Na ion is hence accompanied by the tendency to lock more electrons into the superplane to reduce the high energy electron population. Note that our analysis of the Mn³⁺ superplane in the Na-1/2 ordering shows very similar properties as the Na-1/3 case discussed here.

3. Conclusion

Our results provide new critical insights into the structural evolution of the O′3-NaMnO₂. As a result of the pd hybridization coupled Jahn–Teller distortion and collective condensation, the superplanes and associated super charge separation dominate the electrochemical phase evolution of O′3-NaMnO₂. The Na-5/8, Na-1/2, and Na-1/3 orderings in the O′3 phase together with the Na-1/18 ordering in the O1 phase with unusually high interlayer distance are solved, which strongly influence the electrochemical charge–discharge behavior of NaMnO₂. The Mn³⁺ superplane shows strong electronic attraction to both the Na ions and electrons, as well as the dominating JT-long axis superexchange-like magnetic interactions. The coupling of electrochemical, electronic, and magnetic properties of the novel superplanes from super charge separation can be of great interest to the broad fields of electrochemistry, solid state chemistry, and condensed matter physics.

4. Experimental Section

Synthesis and Electrochemical Test

The pristine NaMnO₂ powder was synthesized by solid-state reaction, and the electrochemical cells were configured on the basis of previous publication.^[2,16] The Na_1/3MnO₂ powder for the neutron diffraction was obtained by chemical deintercalation of pristine NaMnO₂ powder in an iodine acetonitrile solution.^[2] Electrochemical tests were performed on Solartron 1470E.

In Situ Synchrotron/Lab XRD

In situ SXRD experiments were performed at the powder diffraction beamline, 11-BM, at the Advanced Photon Source at Argonne National Laboratory. High angular resolution X-ray diffraction data were collected using a 12 channel analyzer detector array (λ = 0.413609 Å, beam size 1.5 × 0.5 mm). Data spanning a 0°–26° 2θ range were collected using a step size of 0.002°. Measurements were taken at C/50 rate on every 2 h interval with 30 min scanning time for each pattern, corresponding to 4% Na composition interval between patterns and 1% Na composition resolution per pattern. The in situ lab XRD was taken on a Bruker D8 X-ray diffractometer equipped with a Mo source from a homemade in situ electrochemical cell with Be window. The in situ cell was charged galvanostatically at C/50 rate between 2.0 and 4.5 V with each XRD pattern scanned from 6.5° to 30.5° 2θ (equivalent to 14.1° to 69.7° on Cu source) for 1 h, corresponding to 2% Na composition resolution per pattern and 2% composition interval among patterns. Rietveld refinements were performed within the Topas software.^[38]

TEM

TEM samples were made by sonication of the charged cathode films in anhydrous dimethyl carbonate inside a glove box, and sealed in airtight bottles before immediate transfer into the TEM column. The HRTEM and electron diffraction were taken on the JEOL 2010F at MIT. STEM images were recorded with a probe-corrected FEI Titan G2 60–300 kV operated at 200 kV with a beam current of ≈80 pA, a probe semiconvergence angle of either 13.5 or 19.6 mrad, and an HAADF detector inner semiangle of 77 mrad. STEM images were acquired and processed with the RevSTEM technique including 20–40 1024 × 1024 pixel frames with a 2 μs per pixel dwell time and a 90° rotation between each successive frame.^[39]

Neutron Diffraction and Magnetic Susceptibility

Neutron diffraction measurements were performed on 5 g of chemically deintercalated Na_1/3MnO₂ powder using the high-resolution BT-1 instrument and the triple-axis spectrometer BT-7 at the NIST Center for Neutron Research.^[40] Relatively coarse resolution measurements were taken in two-axis mode with a fixed initial neutron energy of 14.7 meV (λ = 2.359 Å), collimator configuration (FWHM) open-25′-sample-40′ radial and position sensitive detector, to determine the detailed temperature dependence of the scattering. For BT-1 we employed the Cu (311) monochromator (λ = 1.540 Å), 60′–20′-sample-7′ collimation and angular steps of 0.05°. A closed cycle He refrigerator with a base temperature of 2.5 K was employed. The magnetic susceptibility measurements were obtained using a Quantum Design MPMS-3 SQUID at 20 Oe. The magnetic refinement of room temperature data was done by GSAS software with the background estimated by a shifted Chebyschev function. The structure used for refinement is the same Na-1/3 ordering solved from SXRD.

DFT

All DFT calculations in this work were performed using the Vienna ab initio Simulation Package (VASP) within the projector augmentedwave approach using the Perdew–Burke–Ernzerhof GGA functional and the GGA+U extension to it. The U value for Mn is 3.9 eV, in line with previous literature.^[41] A 520 eV plane-wave energy cutoff was used for all calculations. For calculating the Na–Na attraction in the (010) superplane of Na-1/3 ordering, large supercells with 48 formula units were used, with two axes of the supercell along the two Na–O–Mn Jahn–Teller long and short axis direction in (010) plane and the third axis perpendicular to (010) plane (See Figure 8). The calculation in Figure 8f,g used 24 formula units and 1/6 Na composition. The NEB method was employed to calculate the Na-ion diffusion barrier in O3 and O1 phases.^[42,43] The supercell size for both O3 and O1 was 4 × 4 × 3 and the a, b lattice parameters were 2.82 Å according to the experimental value. To model compounds at high voltage with dilute Na concentrations, only one Na atom was kept in the supercell. In other calculations except NEB the lattice parameters were fully relaxed and the DFT-D3BJ van der Waals correction is employed.^[44,45] The charge density of spin in Figure 5g was obtained by flipping the spin direction of one Mn³⁺ in a spin-polarized calculation to determine the induced charge density difference.