Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Oct 19;36(42):12745–12754. doi: 10.1021/acs.langmuir.0c02535

Nanoscale Work Function Contrast Induced by Decanethiol Self-Assembled Monolayers on Au(111)

Martina Tsvetanova †,*, Valent J S Oldenkotte †,*, M Candelaria Bertolino ‡, Yuqiang Gao §, Martin H Siekman †, Jurriaan Huskens ‡, Harold J W Zandvliet †, Kai Sotthewes †,*
PMCID: PMC7594278  PMID: 33074008

Abstract

graphic file with name la0c02535_0006.jpg

In this paper, we obtain maps of the spatial tunnel barrier variations in self-assembled monolayers of organosulfurs on Au(111). Maps down to the sub-nanometer scale are obtained by combining topographic scanning tunneling microscopy images with dI/dz spectroscopy. The square root of the tunnel barrier height is directly proportional to the local work function and the dI/dz signal. We use ratios of the tunnel barriers to study the work function contrast in various decanethiol phases: the lying-down striped β phase, the dense standing-up φ phase, and the oxidized decanesulfonate λ phase. We compare the induced work function variations too: the work function contrast induced by a lying-down striped phase in comparison to the modulation induced by the standing-up φ phase, as well as the oxidized λ phase. By performing these comparisons, we can account for the similarities and differences in the effects of the mechanisms acting on the surface and extract valuable insights into molecular binding to the substrate. The pillow effect, governing the lowering of the work function due to lying-down molecular tails in the striped low density phases, seems to have quite a similar contribution as the surface dipole effect emerging in the dense standing-up decanethiol phases. The dI/dz spectroscopy map of the nonoxidized β phase compared to the map of the oxidized λ phase indicates that the strong binding of molecules to the substrate is no longer present in the latter.

1. Introduction

Self-assembled monolayers (SAMs) of alkanethiols on metal surfaces have drawn attention across many fields over the past decades due to their wide array of potential applications, such as work function engineering, corrosion inhibition, and biosensing.1−6 Many of these applications rely on the incorporation of foreign atoms or molecules in the SAM or the deployment of functionalized end groups. However, many urgent questions related to the self-assembly process itself remain, such as the stability of the monolayers, the variety of the electronic properties between and within the different molecular phases, and the exact bonding mechanism between the molecules and the substrate. A proper fundamental understanding of self-assembly and its consequences for the properties of SAM-covered surfaces is paramount to continue improving the capabilities of SAMs.

A popular model system to study the self-assembly process is decanethiol SAMs on Au(111). Scanning tunneling microscopy (STM) studies by Poirier et al. have revealed that the ordering of these SAMs depends strongly on the coverage.7 In particular, they reported a multitude of molecular formations establishing when depositing gas-phase decanethiol onto Au(111) substrates in ultra-high vacuum (UHV): coexisting disordered and ordered phases. It was shown that the molecules chemisorb onto the surface by deprotonation of the sulfur heads and the subsequent formation of S–Au–S complexes,8,9 in which Au adatoms participate. The decanethiol phases can be characterized through different orientations of the molecular tails. The various tail orientations can be categorized into two broad groups: standing-up (at a slight angle with respect to the surface normal) and lying-down (on the substrate or on top of other tails). 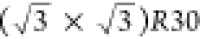The most abundant stable phases representative for these categories are the Inline graphic lying-down β phase and the Inline graphic structure with a c(4 × 2) superlattice, the standing-up φ phase.10,11

Hydrocarbon molecular SAMs oxidize readily in ambient conditions, causing the thiolate SAM to rearrange. It has been shown that this rearrangement is due to the breaking of the Au–S bond, bonding of sulfur to oxygen, and the ensuing transition from a chemisorbed thiolate SAM to a physisorbed sulfonate one, where the molecules form a low-density lying-down λ phase, whose adsorbant structure is reminiscent of that of the β phase. The molecules adopt a similar lamellar structure in which they are packed side-by-side. 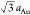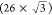The unit distance along the molecular rows is again 0.5 nm (Inline graphic) and the width of the rows is about 3.5 nm or approximately twice the length of a decanethiol molecule. Sotthewes et al. have shown that this molecular phase adopts the Inline graphic structure and the so-formed SAM is stable at ambient conditions.12,13

An important property of SAMs for surface engineering is their ability to tune the work function. The effect of organic phases on the work function has been studied in great detail.14−17 The standing-up phases induce surface dipoles which alter the work function, as it is immediately clear from the definition of the work function, ϕ = μ + D, where μ is the chemical potential in the bulk and D is the energy gained by/needed to pass the total surface dipole.18

The induced change in the work function for standing-up phase alkanethiols on various metals can be attributed to three mechanisms: surface reconstruction of the substrate, charge transfer in a chemical bond between the S atom and a metal atom, and the molecular dipole of the tail. In the case of thiols on Au(111), the charge transfer in the Au–S bond is relatively small (the bond is nearly apolar19), followed by the contribution due to the formation of adatoms and vacancies to accommodate the SAM.20 Finally, the work function modulation is primarily determined by the dipole of the standing-up molecules.19−21

However, in lying-down phases, the tails are oriented in-plane with respect to the surface. In case that the molecular dipole is aligned along the backbone of the molecule, it will no longer contribute to the total surface dipole. Nevertheless, hydrocarbon molecular SAMs induce a drop in the work function when physisorbed to a metal substrate22,23 through the pillow effect: a surface dipole which arises due to Pauli repulsion between electrons in the molecular orbitals of the physisorbed molecules and electrons inside the metal.24

We have formerly studied the remarkable room temperature dynamics of decanethiol SAMs and also showed the signatures of various decanethiol phases in current–time I(t) spectra.25,26 In this paper, we show that the decanethiol SAMs also lead to local work function variations, emerging in the separate molecular phases, governed by the different mechanisms discussed above. We focus on several decanethiol phases and provide a detailed description of the observed work function variations. These include the lying-down β phase, the standing-up φ phase, and the oxidized decanesulfonate λ phase. Comparisons between some of the phases are provided too: a standing-up phase in comparison to a lying-down phase and an oxidized phase in comparison to a nonoxidized phase. To perform this study, a scanning tunneling microscope equipped with a lock-in amplifier (LIA) was used to perform dI/dz spectroscopy while imaging the topography, creating a spatially resolved apparent tunnel barrier map. The measured tunnel barrier is directly linked to the local work function,27 allowing this method to map the work function on a sub-nanometer scale, whereas most studies on the effect of SAMs on the work function utilize techniques which are limited to a much lower resolution.28−32

2. Methods

Decanethiolate SAMs were prepared via the solution-based method. As a substrate, flame-annealed Au(111) with a thickness of 200 nm and size of 4 × 4 mm2 on top of mica was used, purchased from Phasis, Geneva, Switzerland. The substrates were cleaned by dipping around 1 min in a fresh piranha solution (with volume ratio H2SO4/H2O2 of 3:1), after which they were rinsed with a copious amount of Milli-Q water and ethanol. Finally, the samples were submerged in an ethanolic 1-decanethiol (99% purity, purchased from Sigma-Aldrich Chemie NV, Netherlands) solution for variable amounts of time. After being taken out of the solution, the samples were rinsed with ethanol and dried with nitrogen. The sample discussed in “Section 4” was prepared by submerging the substrate in 1 mM decanethiol solution for 1 h (sample 1). The sample discussed in “Section 5” was prepared by submerging the substrate in 2 mM decanethiol solution for 16 h (sample 2). The sample discussed in “Section 6” was prepared by submerging the substrate in 1 mM decanethiol solution for 30 min (sample 3). We note that the same submersion time in the decanethiol solution did not always lead to a reproducible SAM density. We accept this variation as inherent to solution-based deposition. Alternative explanation points to the fact that not all substrates belong to the same purchased batch.

For the presence of a SAM, each time, the static water contact angle of a control sample was measured, showing values above 90°, consistent with the report of Li et al.(33) STM images were obtained with an RHK Technology system at UHV conditions and at room temperature. Pt–Ir STM tips were prepared via electrochemical etching. The freshly prepared decanethiolate samples were loaded in the system as soon as possible to avoid oxidation of the SAM. Some of the samples were intentionally oxidized. The sample discussed in “Section 8” was prepared by leaving an originally prepared decanethiolate SAM (sample 2) in vacuum over 6 weeks, followed by a 2 h exposure to air. While under UHV conditions, the samples go through considerable dilution (molecules desorbing in the vacuum), which is strongly accelerated by the exposure to air, followed by oxidation. The dilution of a dense alkanethiol SAM in UHV conditions was previously observed but, without oxidation, was shown to lead to lower coverage reordering or a disordered layer.34 By introducing an air exposure step, we also let this layer to interact with oxygen, which finally results in the formation of the lamellae-like structures of the λ phase.12

To achieve nanoscale mapping of the variation in the work function induced by decanethiol phases, the dI/dz spectroscopic technique was deployed, combining with simultaneous topographic imaging. In this paper, we comment on work function modulation induced by different SAM regions with the use of the measured tunnel barrier height ratios, which we extract from the dI/dz maps: the tunnel barrier height is proportional to the square of the dI/dz signal and is mainly determined by the averaged work functions of the tip and substrate. To perform the dI/dz measurement, an external LIA was deployed. The tip z-piezo was oscillated by an internally generated voltage signal, resulting in a small oscillation in the tip–sample distance (a few Å). The frequency of that oscillation (2.577 kHz) was above the cut-off frequency of the feedback loop; thus, the constant-current topography images could still be recorded simultaneously. The time constant τ of the LIA was set to 1–2 ms. In our experiments, a bias was applied to the sample, while the tip was grounded. We used bias voltages of magnitude around 1 V which fall within the intermediate voltage regime for tunneling. However, the 1/I(dI/dz) signal still remains proportional to the square root of the tunnel barrier. Details regarding this approximation are presented in “Section 3” and in the Supporting Information of this paper. Additional remarks regarding the extracted ratios are provided in “Section 7” as well. The effect of the simultaneous dI/dz measurement on the topographic resolution is also discussed in the Supporting Information.

3. dI/dz Measurement in the Intermediate Bias Voltage Regime

We use the dI/dz measurements of decanethiol phases to obtain an approximation for the local tunnel barrier heights ϕ for different regions within the dI/dz map. If a low scan voltage magnitude was used (≪ 1 V), the dI/dz signal would be directly proportional to the square root of the tunnel barrier or Inline graphic.35 However, to scan decanethiolate SAMs, we deploy a scan voltage with a magnitude around 1 V. Therefore, we need to obtain the correct approximation which holds for the intermediate bias regime (∼1 V).

Simmons derived expressions for the tunneling current in a few voltage regimes36 (low, intermediate, and high voltage biases). We deal here with the expression for the intermediate bias voltage

3. 1

where A and D are constants, ϕ is the average tunnel barrier (average between the tip and surface), z is the tunnel barrier width, and V is the voltage bias. In the Supporting Information for this paper, we have shown the full derivation of the derivative dI/dz. Finally, the normalized derivative reads

3. 2

For the dI/dz signal to be directly proportional to the square root of the tunnel barrier ϕ, the last two terms in eq 2 must nearly cancel each other and have negligible contribution. In the Supporting Information of this paper, we provide analysis (Figures S4–S6) demonstrating that for realistic for our study values of ϕ (2–6 eV) and z (0.5–1.5 nm) in eq 2, as well as for V ∼ 1 V, 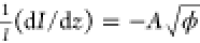Inline graphic, with only a few percent inaccuracy. Thus, the dI/dz signal remains proportional to the square root of the tunnel barrier (or the work function). In the main text, we always discuss in terms of dI/dz ratios performed at the same current set point I; therefore, 1/I normalization is not needed. To obtain work function ratios, we calculate the dI/dz signal ratios and square the results.

4. Work Function Contrast Induced by the β Phase

Figure 1A shows a topographic image that was recorded while mapping the tunnel barrier of a decanethiol SAM on Au(111). Two phases are found: a striped ordered phase and a disordered phase. The striped phase has an interstripe distance of 3.3 nm, which corresponds to the 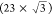Inline graphic β phase.10 Other features showcase the surface reconstruction that is induced by the chemically bound SAM: several vacancy islands have formed. These vacancy islands result from Au adatoms being lifted out of the surface and incorporated into the SAM.37 Lastly, in the middle of the image, a Au island is located. The step from this center island to the surrounding SAM covered area is roughly 0.2 Å smaller than a Au(111) step (2.5 Å). This suggests that the island is a step in the Au substrate but does not contain a SAM [see the Supporting Information for a comparison to a clean Au(111) step].

Figure 1.

Figure 1

Open in a new tab

(A) 50 × 50 nm2 topography image of a decanethiol SAM (sample 1) on Au(111) (set-points: −1 V, −80 pA, scale bar: 15 nm). Two phases have formed: the ordered β phase and a disordered phase (indicated with a “*”). Vacancy islands have formed, one of which is indicated with an arrow, showing that the Au(111) surface underwent a reconstruction. A nanometer-sized Au island sits near the center of the image. (B) dI/dz map that was captured simultaneously to the topography in (A) by a LIA, using a z modulation of 1 Å at a frequency of 2577 Hz. (C) KDE of the combined dI/dz signal in five dI/dz maps corresponding to different parts of the scan image. The exact region segmentation can be found in the Supporting Information. On the y axis the normalized density (ρ̅) is shown in arbitrary units; on the x axis the magnitude of the dI/dz signal (R) is shown in volts.

Figure 1B shows the dI/dz map captured simultaneously to the topography in Figure 1A. It reveals a strong contrast between the sulfur rows (bright) and the tails rows (dark) of the molecules. The sulfur rows consist of S–Au–S complexes,8,9 where the S head makes a covalent bond with a Au adatom. The tails of the molecules are hydrocarbon backbones, 10 carbon atoms long, lying close to the substrate surface. While the signal is very similar on the sulfur rows, disordered phase, and even on the top of the Au island, it drops significantly over the tails. A similarity between the sulfur rows and Au is expected due to the relatively small size of the dipole induced by charge transfer in the Au–S bond.19 Therefore, it can be concluded that the variation of the dI/dz signal observed between the sulfur rows and the tails originates from a work function reduction over the tails.

To estimate the magnitude of the local work function reduction, dI/dz data of five consecutive images over the same area was combined into histograms corresponding to different regions. These are shown in Figure 1C. After filtering out points that are separated more than 4σ from the means, the resulting histograms were fitted using kernel density estimations (KDEs) and normalized for easier comparison. The location of the maxima of these fits is listed in Table 1. Here, σ’s from Gaussian fits are also included as an indicator of the histogram widths. We would like to point out that these σ’s should not be interpreted as large uncertainties in the position of the peaks, as they also include the physical smoothing of the apparent tunnel barrier between the regions separated by the drawn boundaries. The difference in the apparent tunnel barrier height can be addressed by examining the proportionality between the peak positions squared for the KDEs in Figure 1C, resulting in 40% higher apparent tunnel barrier over the sulfur rows compared to over the tail rows.

Table 1. dI/dz KDE Maxima and Standard Deviations σ from Normal Distribution Fits for the Data Shown in Figures 1C, 2E, 3D, and 4Da.

figure/region KDE maximum (V) σ (V) R
Figure 1C
S heads 0.58 0.16 1.4
tails 0.49 0.12 1.0
disordered 0.52 0.13 1.1
Au island 0.54 0.15 1.2
Figure 2E
φ domains 1.37 0.1  
Figure 3D
S heads 1.41 0.21 1.5
tails 1.154 0.14 1.0
φ domains 1.151 0.1 0.99
Figure 4D
S heads 0.51 0.03 1.08
tails 0.49 0.03 1.0
Open in a new tab
a

The exact region segmentation can be found in the Supporting Information. The last column includes the calculated barrier height ratios (R) with respect to the tail regions (when applicable). R should not be mistaken with the magnitude of the dI/dz signal in Figures 1–4.

Overall, the biggest difference in the apparent barrier height is observed when we compare the S heads and the carbon tails. Next, from the ratios of the barrier heights listed in Table 1, we see that the second big difference is observed when comparing the Au island region to the carbon tails. This is not strange, considering the discussion above: the S heads themselves lead only to a slight barrier height increase as compared to bare Au. Note that the big difference in the heads and the tails regions hints to a large difference in interaction with the substrate: at the strong S–Au bond sites, the work function might not drop as in the weakly bound tail regions, but there is a clear transition between the two types of binding. This is very different for the oxidized decanethiol phase, discussed in Section 8.

Finally, in the disordered phase, no separation is observed between the head and tail regions. Additionally, the tails can be randomly oriented with respect to each other or with respect to the S heads. This is consistent with the obtained ratio in the barrier heights between the disordered phase and tail regions of the striped phase: the drop in the work function induced by the disordered phase cannot be larger than the drop induced by the ordered tail regions in the β phase because the randomly distributed S heads will lead to a slight increase too.

5. Standing-Up φ Phase

Figure 2 presents the STM measurements performed on the high-density standing-up φ phase. The currently discussed sample (sample 2) featured the upright phase exclusively and typical for the decanethiol SAM pits of a single Au layer depth. In Figure 2A,B, a zoomed topography and a dI/dz map of only few φ patches are shown. In Figure 2C, a typical Fourier transform (2D FFT) of a φ phase patch can be found. It corresponds to a hexagonal lattice with the 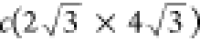Inline graphic overlayer superstructure, observed formerly by helium diffraction38 and STM.11 The maps presented in (A) and (B) feature satisfactory resolution; the molecular resolution is preserved on the dI/dz map, and the periodicity at the bottom of the Au vacancy can be seen too. We can also resolve a change in the potential across the steps of the pits (more visible in Figure 2D), which is expected for the Au substrate.27 Further on, four separate patches of the standing-up phase are isolated from the map in (D) (see Figure S.1B from the Supporting Information), and a normalized KDE for the measured dI/dz values in these regions is plotted in Figure 2E.

Figure 2.

Figure 2

Open in a new tab

(A) 20 × 20 nm2 STM topographic image of a φ region on sample 2 (set-points: −1 V, −80 pA, scale bar: 7 nm). (B) dI/dz spectroscopic map (1 Å tip oscillation amplitude, oscillation frequency 2.577 kHz, τ = 1 ms) that corresponds to the area in (A). (C) Typical FFT pattern of a single φ phase domain. A hexagonal polygon and small circles are provided to guide the eye, marking the c(4 × 2) superstructure. The pattern was obtained from one of the standing-up phase domains from (D). (D) 50 × 50 nm2 dI/dz spectroscopic map (2 Å tip oscillation amplitude, oscillation frequency: 2.577 kHz, τ = 2 ms, set-points: −1.2 V, −80 pA, scale bar: 15 nm) that contains several φ domains (topography not shown). (E) KDE of the dI/dz data, selected from a few φ phase domains from (D). The exact region segmentation can be found in the Supporting Information. On the y axis, the normalized density (ρ̅) is shown in arbitrary units; on the x axis, the magnitude of the dI/dz signal (R) is shown in volts.

Although the separate KDE plots of the patches taken from the map in Figure 2D have slightly different maxima (not shown), from the combined KDE in (E), it is clear that the distribution of the dI/dz values for the φ phase domains is very close to each other. We obtain a KDE with a nicely defined maximum and without additional shoulders. There may always be reasons for slight variations in the measured signal. For instance, variation can be induced by the patch edge effects, where the ordering will deviate from the ideal 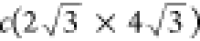Inline graphic structure and, of course, the dI/dz signal will be affected. Additionally, due to the different orientations of the standing-up molecular tails, the molecules would interact differently with the STM tip in different patches. Thus, the reasons for the spread in the data are partly due to work function variations and partly due to geometry-related effects. Note that although we obtain contrast (molecular resolution) within the φ patches, for this phase, we restrict ourselves from separating the head and the tail regions. We explain this contrast as a result from the altered tunneling path for the tip on top of different locations of the SAM. In the dense φ phase, the molecular tails are standing-up at small angles to the surface normal. When the tip is positioned on the top of a carbon backbone end group, the electrons will tunnel to the molecular tail. However, when the tip is positioned between the neighboring end groups (when it does small excursions downward in-between molecular tails), the tunneling path cannot be resolved well any longer, and thus, the resulting resolution does not reflect a true change in the tunneling barrier, as a cosine relation exists between the true tunneling path and the tip modulation direction dẑ.39 The current discussion does not hold for the rest of the phases measured in this paper. The molecular resolution in their dI/dz maps is related directly to a change in the tunneling barrier and not to a geometric nonuniformity.

Even though another phase is not present in the measurement in Figure 2 and we cannot obtain a ratio with respect to the work function modification induced by the φ phase, we obtained a further insight into the standing-up domains. In Kelvin probe force microscopy or spectroscopic studies of SAMs, for instance, a single value is reported for the surface potential of a whole monolayer or a region of a patterned sample due to limitations in the spatial resolution.28,40−42 We showed that via dI/dz mapping, we can go a step further. The measurements in Figure 2 demonstrate that the surface potential modulation induced by the standing-up molecules features local variations which, when combined, lead to an overall surface potential drop, suggested by the well-centered KDE. This implies further that the slightest variations in molecular ordering in a standing-up phase SAM can lead to different macroscopic surface potentials. For instance, the average domain size, the domain boundaries, the size and density of Au pits with their step edge potential variations, and, of course, the spatial sample homogeneity will be important.

6. Comparison between a Lying-Down Phase and a Standing-Up Phase

Here, we compare dI/dz maps of a striped low-density phase and the standing-up high-density phase. Note that the comparison of these phases is essentially a comparison of different mechanisms via which the work function of Au(111) can be modulated. In the latter case, the leading mechanism is the surface dipole effect due to the tails in the φ phase, which stand upright (at a small angle ∼30° to the surface normal). In the former case, the mechanism is dominated by lying-down molecules (the pillow effect).

Figure 3 presents STM data of a region on a sample where both striped and standing-up phase patches are present. Mostly, φ phase domains were observed on this sample too (sample 3). However, sometimes, in a region as the one presented in Figure 3, several stripes would form, featuring a highly dynamic phase: for instance, shifting, partially transforming into a disordered region, and reforming. Such switching phenomena are typical for as-deposited and for annealed decanethiol films.25,26,43,44 We captured a moment in which these stripes lay close enough to the ordered φ patches.

Figure 3.

Figure 3

Open in a new tab

(A) 50 × 50 nm2 STM topographic image (set-points: −1 V, −80 pA, scale bar: 15 nm) of sample 3. A profile (red) is taken across a striped phase region. The profile is shown in (B). (B) Profile that corresponds to the red line in (A). At each minimum in the periodical landscape, the distance from the first minimum is indicated (in nm), showing that the stripe periodicity changes. (C) dI/dz spectroscopic map (1 Å tip oscillation amplitude, oscillation frequency: 2.577 kHz, τ = 1 ms) that corresponds to the area in (A). (D) KDEs of the dI/dz data for three different regions of the map: S heads, tails, and φ phase domains. The exact region segmentation can be found in the Supporting Information. On the y axis, the normalized density (ρ̅) is shown in arbitrary units; on the x axis, the magnitude of the dI/dz signal (R) is shown in volts.

It is not straightforward to label the exact striped phase that is observed. As shown in the profile taken in Figure 3B, the interstripe distance varies. This is also clear from Figure 3C, where the bright line segments correspond to the S heads of the molecules. As the SAM shows considerable dynamics, the molecular rows shift in time. Equilibrium is not achieved, and there is no particular striped phase that forms and stabilizes for a long period of time. Nonetheless, it is known that in the striped region of the measurement, the density of decanethiol molecules is lower as compared to the standing-up patches in the surroundings, and a considerable portion of the region between the stripes is occupied by the carbon tails of the molecules which are lying down on the Au surface. Qian et al.(45) reported the existence of several striped decanethiol phases in which half of the molecular tails between the stripes lay down on the substrate and the other half is standing up. The stripe periodicities in these phases are well within the range of the periodicities for the β phase and for the measurement here. It is well possible that we deal with such a configuration. Thus, to remain accurate, we consider the interstripe mechanism for work function modulation to be a mixed effect, with both contributions of the pillow effect due to lying-down carbon chains (with larger areal fraction) and the dipoles over the tails of standing-up molecules.

Having established the landscape, we move on to the dI/dz map in Figure 3C. Again, the image is segmented into regions that correspond to either the striped phase or some of the dense patches (see Figure S.1C from the Supporting Information). The striped phase is further divided into regions, corresponding to the sulfur heads and the carbon tails. The KDE curves corresponding to all regions are plotted in Figure 3D. The dI/dz KDE maximum, as well as the spreads for the regions, is shown in Table 1.

First, we comment on the visibly largest spread of values which corresponds to the molecular heads (the discussion is also applicable to the results of the β phase presented earlier). This result is expected, given the fact that the S heads are the only locations where strong binding to the substrate exists (the S–Au complex). It is easily visible that in the dI/dz map, the head region is not perfectly localized, either due to the fact that the observed phase is very dynamic, distorted because of the presence of standing-up tails, or simply because the effect of the heads spreads over a wide area around the Au–S bond. Therefore, here, we expect the largest spread in dI/dz values, as from the center of the head stripes to the periphery of the stripes, the dI/dz signal will drastically change.

Next, we focus specifically on the striped region. The head-to-tail ratio of the measured barrier heights, obtained from squaring the ratio of the KDE maxima for these two segments of the map, is approximately 1.5. The earlier reported head-to-tail work function ratio for the β phase is slightly lower, approximately 1.4. However, the values are quite close, considering the spread in the data sets. We are able to obtain very similar ratios, even when considering that the striped phases discussed here are structurally different. This result is exciting, as it suggests that a narrow range of modulation across the head-to-tail step is expected for striped phases. Thus, a large pool of phases for potential future applications is available, when, for instance, simply the molecular chain length is varied.

It is clear that the distributions of the tails and the dense patches overlap quite well. Therefore, we can expect that the mixed mechanism acting (lying-down molecules and a potential fraction of standing-up molecules) in the tail region of the striped phase has quite a similar impact as the surface dipole mechanism acting at the standing-up φ phase patches. This finding demonstrates that when a macroscopic measurement of a molecular SAM is made, there is no straightforward route to separate easily the contribution of dense standing-up molecular phases from the contribution of more diluted striped ones, as the head stripes do not have a large areal fraction and cannot be resolved. The practical implications are even more exciting: working with less dense SAMs might be beneficial compared to always having to prepare dense monolayers. Striped phases also present higher diversity in the periodicities possible which on their own suggests a wider range of applicable SAM geometries for various surface engineering purposes, where not only the surface potential shift but also the local monolayer ordering is important.

Although the ratios speak for themselves, we can only expect that the different effects discussed here are comparable; it is not possible to claim with certainty that the pillow mechanism at lying-down tails tunes the work function equally as the dipole layer mechanism emerging due to standing-up tails. This is because we cannot exclude the possibility that at the different decanethiol phases there is also different tip–molecule interaction. Although called as lying-down phases, the carbon tails of molecules do not lie flat on the substrate; there is distance between the Au surface and the chains. If, for instance, the tip pushes down the tails additionally, then the pillow effect can be enlarged only by the act of measurement. Similarly, the tip can have quite complex interaction with the standing-up molecules. We also already discussed the geometric nonuniformities that the standing-up molecules induce for the tunneling electrons. Apart from that the dynamics of the monolayer can always add further variation in the measurements via the movement of molecules. Nevertheless, we kept the current set-point as low as possible in this study. The maximum I set-point was only about 100 pA, meaning the tip is kept as far away as possible from the surface. To really study the tip-induced work function variation, a separate variable set-point study would be required in the future.

7. Variations in the Measured dI/dz Signal

Now that several data sets were presented, it is important to provide an account on the difference in dI/dz value ranges, especially for measurements that are taken at the same settings (see for instance Figures 1C and 3D). The explanation is that the LIA cannot provide absolute data. The LIA output is proportional to the local slope of I(z) dependence. That is why, in this paper, we comment on the work function modulation induced by the SAMs in terms of ratios which correspond to separate molecular regions. Of course, the ratios would still contain the contribution of the tip too as the apparent barrier height measured at any location is an average of the tip and the local sample barrier height (ϕ = ϕT + ϕs). However, in all cases, the same material for the tip was used (Pt–Ir), and all variation in the tip’s barrier height is expected to be due to its shape, which is not expected to give a large effect when the ratios are considered. Other small uncertainties in the ratios can be due to any small LIA offset, but still this offset, just as the contribution of the tip, will be taken with the same load in a ratio. Thus, the ratio is mostly affected by the barrier heights that belong to the regions that are being compared. Note that exactly because of that reason, it is possible to comment on ratios from different data sets but not compare data from different images in terms of absolute values taken from the KDEs.

8. Oxidized Decanethiol λ Phase

In this section, the investigation of the oxidized decanethiol phase is presented. STM data is available in Figure 4. Note that after oxidation, disordered regions are visible, and in these disordered phases, the former triangular symmetry of the standing-up φ phase is frequently preserved (see Figure 4A). In between the disordered regions, the lamellae-like structures of the λ phase are observed (see Figure 4B).12,13 During oxidation, oxygen attaches to the S heads, which breaks the S–Au–S complex present in the nonoxidized layer, leading to a reduced interaction with the surface. Now, the typical herringbone reconstruction for Au(111) is visible underneath the molecules. This is normally possible only for the most diluted lattice gas α phase and rarely for the striped β phase.7 The presence of the herringbone for this system in particular is strong evidence for a small decanesulfonate–gold interaction, and thus, the λ phase can be considered a physisorbed phase.

Figure 4.

Figure 4

Open in a new tab

(A) 50 × 50 nm2 STM topographic image (set-points: −1 V, −80 pA, scale bar: 15 nm) of the oxidized SAM (sample 2). With a triangle, the disordered leftover region of the former upright φ phase is marked. In the remaining areas, the λ phase extends. (B) 15 × 15 nm2 zoom to the λ phase is provided (set-points: −0.2 V, −55 pA, scale bar: 4 nm). The ridges of the characteristic herringbone reconstruction of Au(111) are marked with gray dashed lines. (C) 25 × 25 nm2 dI/dz spectroscopic map (set-points: −1 V, −80 pA, scale bar: 8 nm, 1 Å tip oscillation amplitude, oscillation frequency: 2.577 kHz, τ = 1 ms) of a region covered only with the λ phase. (D) KDEs of the dI/dz data for the molecular heads and for the tails areas. The exact region segmentation can be found in the Supporting Information. On the y axis, the normalized density (ρ̅) is shown in arbitrary units; on the x axis, the magnitude of the dI/dz signal (R) is shown in volts.

Based on the current discussion, in the λ phase, we no longer expect a large difference in bonding between the molecular S head region (now S bonded to oxygen) and the carbon chains, arranged similarly to the nonoxidized β phase but now farther from the surface. To support this claim, we performed dI/dz spectroscopy on this phase too. The data is presented in Figure 4C,D. In Figure S.1D in the Supporting Information, we segmented the dI/dz map presented here, by excluding the defect and disordered regions. Again, we distinguish between the areas where the S heads are expected and the carbon tails. Now, the ratio of the head-to-tail tunnel barriers is considerably smaller (only 1.08) compared to the ratio for the nonoxidized striped phases discussed earlier (1.4, 1.5). Additionally, now the spread of the KDEs in Figure 4D is also quite comparable. This is not strange; there is no large gradient in the values around the S head regions, further supporting the claim that there is no location where a strong bond to the substrate is formed.

We do observe the signature of the herringbone on the dI/dz map too. A slight variation is expected for the potential at the ridges, separating the fcc and the hcp regions of the Au reconstruction. However, these variations amount to less than 100 meV in the electron potential landscape.27,46 The fact that we can distinguish the ridges leaves the discussion regarding the binding of the molecules self-explanatory: although small variations are present on the dI/dz map of the oxidized phase, these are most likely well in the range of tens of meV only; there is no strong bond between S and Au.

Additional experiments are needed to establish the work function modulation induced by the air-oxidized phase versus the bare Au(111) substrate, as for this phase there are no surface potential measurements reported. To perform a comparison with our method, regions of other ordered phases close by are needed. These are, however, absent here. Furthermore, more theoretical effort would be required to establish the correct mechanisms which play a role, as now there is no bond to the substrate that forms at the S heads, while the tails of the molecules lie at larger distance from the substrate. However, although the exact mechanisms to the work function modulation in the λ phase are less clear, there is no strong spatial modulation variation present. In addition to the superior stability of the decanesulfonate phase in ambient conditions,13 the λ phase may be a good route toward work function engineering of more stable devices that operate in air and around room temperature.

9. Discussion

We performed simultaneously topographic and dI/dz spectroscopic measurements on various decanethiol phases on Au(111), the lying-down striped β phase, the dense standing-up φ phase, and the oxidized decanesulfonate λ phase, using scanning tunneling microscopy. Combining these STM techniques, we were able to learn more about the work function modulation signatures of the decanethiol phases. Different from the techniques that lack spatial resolution, we obtained maps down to the sub-nanometer scale of the spatial variation of the tunnel barrier, directly available from the dI/dz images. Within the same molecular SAM, regions could be distinguished and a ratio of the tunnel barriers (the work function) were directly obtainable.

For the β striped phase, the work function is lowered at the lying-down molecular carbon tails via the pillow effect. Our measurements are consistent with this view. At the locations of the S heads, the tunnel barrier is closest to the tunnel barrier at a clean Au region, while the tunnel barrier is lowered considerably at the C-backbone tails. For the standing-up phase, the effect responsible for the work function change on a substrate is the formation of a surface dipole layer due to upright molecular tails. We were able to obtain resolution in the dI/dz images with periodicity corresponding to the superstructure of the φ phase and assigned this effect to the geometrical nonuniformity of the electron tunneling path. Apart from that, the variations in the work function of the φ phase domains can be explained by local variations in the SAM ordering and homogeneity. The work function signature of a low density lying-down molecular phase was also compared to the measurements of the dense φ phase, showing that similarity exists in the work function at the regions of lying-down molecular tails and standing-up molecules, indicating that although the pillow and the surface dipole effects are different mechanisms, they lead to a similar surface potential lowering. Unfortunately, here, we reach the limitations in our technique. Although the ratios in the tunnel barriers speak for themselves, it is not possible to judge if the tip–molecule interactions are the same at the lying-down and the standing-up molecular tails. It is possible, for instance, that the tip pushes the lying-down molecules downward and brings them even closer to the substrate in the striped phase, thus enlarging the pillow effect, while in the standing-up phase, the tip–molecule interactions are even more complex. This can be evaluated in future studies by performing current set-point variation measurements in order to estimate how large such an effect can be. Nevertheless, the very low current set-points used in our study should already bring us to a regime where such a tip effect is of the lowest possible strength.

Of course, the tip work function contribution in the measurement of the tunnel barrier could never be removed; that is why we approached the problem of studying the work function modulation of decanethiol SAMs by referring to the obtained ratios. Our approach cannot provide absolute work function measurements. There is also no well-established mechanism for comparing our findings to the results of techniques which lack spatial resolution but provide work function measurements on a large scale. At this stage, we can only claim that, overall, the work function of a substrate surface is an average result of the local work function modulations which an organic SAM induces.

The dI/dz spectroscopic technique also allows us to deduce information regarding the binding of molecules to the substrate. Comparing dI/dz maps of the nonoxidized β phase and the oxidized decanesulfonate phase shows that in the oxidized state, molecules lose their strong binding to the Au(111) surface because there is an absence of strong work function modulation difference at the molecular sulfur heads and the carbon tails, a clear signature present for the nonoxidized phase. More theoretical and experimental investigation is needed in order to fully understand the work function variation in the λ phase SAMs.

10. Conclusions

We have measured and compared the spatial work function variations of various ordered decanethiol phases on the Au(111) surface using scanning tunneling spectroscopy. We have considered the standing-up phase, the striped lying-down phase, and the oxidized phase. Since the molecular phases in our study are imaged at a sample bias magnitude ∼1 V, we have to use the Simmons model for moderate voltages. We have shown that for intermediate voltages, the derivative of the tunneling current to the tip-substrate displacement, dI/dz, is still proportional to the square root of the tunnel barrier (derivation is provided in the Supporting Information). The variations between the different phases can be explained by variations of the surface dipole and the pillow effects. Our results demonstrate that the dI/dz spectroscopy technique is suitable for studying the work function contrast in SAMs at the sub-nanometer scale. Even though a large scale estimation of the work function cannot be obtained, our approach raises relevant questions in the field of surface potential engineering, as clearly the overall surface work function will strongly depend on the density and homogeneity of a SAM.

Acknowledgments

M.T., Y.G., and H.J.W.Z. acknowledge the Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO) for the provided financial support. The Netherlands Organization for Scientific Research (NWO, TOP project 715.015.001) is also acknowledged by M.C.B. and J.H. for the provided financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.0c02535.

  • dI/dz map segmentations into regions; additional measurements and analysis; dI/dz measurement effect on the resolution; 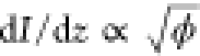Inline graphic approximation; and additional discussion on the obtained tunnel barrier ratios (PDF)

Author Contributions

∥ M.T. and V.J.S.O. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

la0c02535_si_001.pdf (6.5MB, pdf)

References

  1. Love J. C.; Estroff L. A.; Kriebel J. K.; Nuzzo R. G.; Whitesides G. M. Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem. Rev. 2005, 105, 1103–1170. 10.1021/cr0300789. [DOI] [PubMed] [Google Scholar]
  2. Ellis L. D.; Trottier R. M.; Musgrave C. B.; Schwartz D. K.; Medlin J. W. Controlling the surface reactivity of titania via electronic tuning of self-assembled monolayers. ACS Catal. 2017, 7, 8351–8357. 10.1021/acscatal.7b02789. [DOI] [Google Scholar]
  3. Wang Q.; Chueh C.-C.; Zhao T.; Cheng J.; Eslamian M.; Choy W. C. H.; Jen A. K.-Y. Effects of self-assembled monolayer modification of nickel oxide nanoparticles layer on the performance and application of inverted perovskite solar cells. ChemSusChem 2017, 10, 3794–3803. 10.1002/cssc.201701262. [DOI] [PubMed] [Google Scholar]
  4. Casalini S.; Bortolotti C. A.; Leonardi F.; Biscarini F. Self-assembled monolayers in organic electronics. Chem. Soc. Rev. 2017, 46, 40–71. 10.1039/c6cs00509h. [DOI] [PubMed] [Google Scholar]
  5. Narasimha K. T.; Ge C.; Fabbri J. D.; Clay W.; Tkachenko B. A.; Fokin A. A.; Schreiner P. R.; Dahl J. E.; Carlson R. M. K.; Shen Z. X.; et al. Ultralow effective work function surfaces using diamondoid monolayers. Nat. Nanotechnol. 2016, 11, 267. 10.1038/nnano.2015.277. [DOI] [PubMed] [Google Scholar]
  6. Kim G.-H.; García de Arquer F. P.; Yoon Y. J.; Lan X.; Liu M.; Voznyy O.; Yang Z.; Fan F.; Ip A. H.; Kanjanaboos P.; et al. High-efficiency colloidal quantum dot photovoltaics via robust self-assembled monolayers. Nano Lett. 2015, 15, 7691–7696. 10.1021/acs.nanolett.5b03677. [DOI] [PubMed] [Google Scholar]
  7. Poirier G. E.; Fitts W. P.; White J. M. Two-dimensional phase diagram of decanethiol on Au (111). Langmuir 2001, 17, 1176–1183. 10.1021/la0012788. [DOI] [Google Scholar]
  8. Maksymovych P.; Voznyy O.; Dougherty D. B.; Sorescu D. C.; Yates J. T. Gold adatom as a key structural component in self-assembled monolayers of organosulfur molecules on Au(111). Prog. Surf. Sci. 2010, 85, 206–240. 10.1016/j.progsurf.2010.05.001. [DOI] [Google Scholar]
  9. Gao J.; Li F.; Zhu G.; Yang Z.; Lu H.; Lin H.; Li Q.; Li Y.; Pan M.; Guo Q. Spontaneous breaking and remaking of the RS–Au–SR staple in self-assembled ethylthiolate/Au(111) interface. J. Phys. Chem. C 2018, 122, 19473–19480. 10.1021/acs.jpcc.8b04157. [DOI] [Google Scholar]
  10. Poirier G. E. Coverage-dependent phases and phase stability of decanethiol on Au (111). Langmuir 1999, 15, 1167–1175. 10.1021/la981374x. [DOI] [Google Scholar]
  11. Poirier G. E.; Tarlov M. J. The c(4x2) superlattice of n-alkanethiol monolayers self-assembled on Au(111). Langmuir 1994, 10, 2853–2856. 10.1021/la00021a001. [DOI] [Google Scholar]
  12. Sotthewes K.; Kap Ö.; Wu H.; Thompson D.; Huskens J.; Zandvliet H. J. W. Ordering of air-oxidized decanethiols on Au(111). J. Phys. Chem. C 2018, 122, 8430–8436. 10.1021/acs.jpcc.8b01389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kap Ö.; Kabanov N.; Tsvetanova M.; Varlikli C.; Klavsyuk A. L.; Zandvliet H. J. W.; Sotthewes K. Structural stability of physisorbed air-oxidized decanethiols on Au(111). J. Phys. Chem. C 2020, 124, 11977–11984. 10.1021/acs.jpcc.0c02806. [DOI] [Google Scholar]
  14. Zangmeister C. D.; Picraux L. B.; van Zee R. D.; Yao Y.; Tour J. M. Energy-level alignment and work function shifts for thiol-bound monolayers of conjugated molecules self-assembled on Ag, Cu, Au, and Pt. Chem. Phys. Lett. 2007, 442, 390–393. 10.1016/j.cplett.2007.06.012. [DOI] [Google Scholar]
  15. Marmont P.; Battaglini N.; Lang P.; Horowitz G.; Hwang J.; Kahn A.; Amato C.; Calas P. Improving charge injection in organic thin-film transistors with thiol-based self-assembled monolayers. Org. Electron. 2008, 9, 419–424. 10.1016/j.orgel.2008.01.004. [DOI] [Google Scholar]
  16. Rusu P. C.; Giovannetti G.; Weijtens C.; Coehoorn R.; Brocks G. First-principles study of the dipole layer formation at metal-organic interfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 125403. 10.1103/physrevb.81.125403. [DOI] [Google Scholar]
  17. Szwajca A.; Wei J.; Schukfeh M. I.; Tornow M. Self-assembled monolayers of alkyl-thiols on InAs: A Kelvin probe force microscopy study. Surf. Sci. 2015, 633, 53–59. 10.1016/j.susc.2014.11.023. [DOI] [Google Scholar]
  18. Bardeen J. Theory of the work function. II. The surface double layer. Phys. Rev. 1936, 49, 653. 10.1103/physrev.49.653. [DOI] [Google Scholar]
  19. Rusu P. C.; Brocks G. Surface dipoles and work functions of alkylthiolates and fluorinated alkylthiolates on Au (111). J. Phys. Chem. B 2006, 110, 22628–22634. 10.1021/jp0642847. [DOI] [PubMed] [Google Scholar]
  20. Otálvaro D.; Veening T.; Brocks G. Self-assembled monolayer induced Au (111) and Ag (111) reconstructions: Work functions and interface dipole formation. J. Phys. Chem. C 2012, 116, 7826–7837. 10.1021/jp300512k. [DOI] [Google Scholar]
  21. Rusu P. C.; Brocks G. Work functions of self-assembled monolayers on metal surfaces by first-principles calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 073414. 10.1103/physrevb.74.073414. [DOI] [Google Scholar]
  22. Ito E.; Oji H.; Ishii H.; Oichi K.; Ouchi Y.; Seki K. Interfacial electronic structure of long-chain alkane/metal systems studied by UV-photoelectron and metastable atom electron spectroscopies. Chem. Phys. Lett. 1998, 287, 137–142. 10.1016/s0009-2614(98)00153-5. [DOI] [Google Scholar]
  23. Hill I. G.; Rajagopal A.; Kahn A.; Hu Y. Molecular level alignment at organic semiconductor-metal interfaces. Appl. Phys. Lett. 1998, 73, 662–664. 10.1063/1.121940. [DOI] [Google Scholar]
  24. Bagus P. S.; Staemmler V.; Wöll C. Exchangelike effects for closed-shell adsorbates: Interface dipole and work function. Phys. Rev. Lett. 2002, 89, 096104. 10.1103/physrevlett.89.096104. [DOI] [PubMed] [Google Scholar]
  25. Sotthewes K.; Wu H.; Kumar A.; Vancso G. J.; Schön P. M.; Zandvliet H. J. W. Molecular dynamics and energy landscape of decanethiolates in self-assembled monolayers on Au(111) studied by scanning tunneling microscopy. Langmuir 2013, 29, 3662–3667. 10.1021/la400082z. [DOI] [PubMed] [Google Scholar]
  26. Wu H.; Sotthewes K.; Kumar A.; Vancso G. J.; Schön P. M.; Zandvliet H. J. W. Dynamics of decanethiol self-assembled monolayers on Au(111) studied by time-resolved scanning tunneling microscopy. Langmuir 2013, 29, 2250–2257. 10.1021/la304902y. [DOI] [PubMed] [Google Scholar]
  27. Aoki T.; Yokoyama T. Mapping the surface electrostatic potentials of Au (111) by using barrier-height measurements. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 155423. 10.1103/physrevb.89.155423. [DOI] [Google Scholar]
  28. de Boer B.; Hadipour A.; Mandoc M. M.; van Woudenbergh T.; Blom P. W. M. Tuning of metal work functions with self-assembled monolayers. Adv. Mater. 2005, 17, 621–625. 10.1002/adma.200401216. [DOI] [Google Scholar]
  29. Hong J.-P.; Park A.-Y.; Lee S.; Kang J.; Shin N.; Yoon D. Y. Tuning of Ag work functions by self-assembled monolayers of aromatic thiols for an efficient hole injection for solution processed triisopropylsilylethynyl pentacene organic thin film transistors. Appl. Phys. Lett. 2008, 92, 143311. 10.1063/1.2907691. [DOI] [Google Scholar]
  30. Alloway D. M.; Graham A. L.; Yang X.; Mudalige A.; Colorado R. Jr.; Wysocki V. H.; Pemberton J. E.; Lee T. R.; Wysocki R. J.; Armstrong N. R. Tuning the effective work function of gold and silver using ω-functionalized alkanethiols: varying surface composition through dilution and choice of terminal groups. J. Phys. Chem. C 2009, 113, 20328–20334. 10.1021/jp909494r. [DOI] [Google Scholar]
  31. Qi Y.; Yaffe O.; Tirosh E.; Vilan A.; Cahen D.; Kahn A. Filled and empty states of alkanethiol monolayer on Au (111): fermi level asymmetry and implications for electron transport. Chem. Phys. Lett. 2011, 511, 344–347. 10.1016/j.cplett.2011.06.050. [DOI] [Google Scholar]
  32. Tseng C.-T.; Cheng Y.-H.; Lee M.-C. M.; Han C.-C.; Cheng C.-H.; Tao Y.-T. Study of anode work function modified by self-assembled monolayers on pentacene/fullerene organic solar cells. Appl. Phys. Lett. 2007, 91, 233510. 10.1063/1.2823579. [DOI] [Google Scholar]
  33. Li S.-S.; Xu L.-P.; Wan L.-J.; Wang S.-T.; Jiang L. Time-dependent organization and wettability of decanethiol self-assembled monolayer on Au (111) investigated with STM. J. Phys. Chem. B 2006, 110, 1794–1799. 10.1021/jp055616v. [DOI] [PubMed] [Google Scholar]
  34. Ito E.; Kang H.; Lee D.; Park J. B.; Hara M.; Noh J. Spontaneous desorption and phase transitions of self-assembled alkanethiol and alicyclic thiol monolayers chemisorbed on Au(111) in ultrahigh vacuum at room temperature. J. Colloid Interface Sci. 2013, 394, 522–529. 10.1016/j.jcis.2012.12.035. [DOI] [PubMed] [Google Scholar]
  35. de Vries R. J.; Saedi A.; Kockmann D.; Van Houselt A.; Poelsema B.; Zandvliet H. J. Spatial mapping of the inverse decay length using scanning tunneling microscopy. Appl. Phys. Lett. 2008, 92, 174101. 10.1063/1.2917716. [DOI] [Google Scholar]
  36. Simmons J. G. Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 1963, 34, 1793. 10.1063/1.1702682. [DOI] [Google Scholar]
  37. Poirier G. E. Mechanism of formation of Au vacancy islands in alkanethiol monolayers on Au (111). Langmuir 1997, 13, 2019–2026. 10.1021/la960777z. [DOI] [Google Scholar]
  38. Camillone N.; Leung T. Y. B.; Scoles G. A low energy helium atom diffraction study of decanethiol self-assembled on Au(111). Surf. Sci. 1997, 373, 333–349. 10.1016/s0039-6028(96)01167-3. [DOI] [Google Scholar]
  39. Gómez-Rodríguez J. M.; Gómez-Herrero J.; Baró A. M. Imaging cos(s,z): A method to separate the geometric and compositional contributions on STM barrier height profiles. Surf. Sci. 1989, 220, 152–164. 10.1016/0039-6028(89)90469-x. [DOI] [Google Scholar]
  40. Lü J.; Delamarche E.; Eng L.; Bennewitz R.; Meyer E.; Güntherodt H.-J. Kelvin probe force microscopy on surfaces: Investigation of the surface potential of self-assembled monolayers on gold. Langmuir 1999, 15, 8184. 10.1021/la9904861. [DOI] [Google Scholar]
  41. Tantitarntong P.; Zalar P.; Matsuhisa N.; Nakano K.; Lee S.; Yokota T.; Tajima K.; Someya T. High sensitivity tuning of work function of self-assembled monolayers modified electrodes using vacuum ultraviolet treatment. ACS Appl. Mater. Interfaces 2017, 9, 28151–28156. 10.1021/acsami.7b09756. [DOI] [PubMed] [Google Scholar]
  42. Venkataraman N. V.; Zurcher S.; Rossi A.; Lee S.; Naujoks N.; Spencer N. D. Spatial tuning of the metal work function by means of alkanethiol and fluorinated alkanethiol gradients. J. Phys. Chem. C 2009, 113, 5620–5628. 10.1021/jp809156a. [DOI] [Google Scholar]
  43. Seo S.; Lee H. Thermal-processing-induced structural dynamics of thiol self-assembly in solution. J. Phys. Chem. C 2011, 115, 15480–15486. 10.1021/jp203919w. [DOI] [Google Scholar]
  44. Toerker M.; Staub R.; Fritz T.; Schmitz-Hübsch T.; Sellam F.; Leo K. Annealed decanethiol monolayers on Au(111)- intermediate phases between structures with high and low molecular surface density. Surf. Sci. 2000, 445, 100–108. 10.1016/s0039-6028(99)01056-0. [DOI] [Google Scholar]
  45. Qian Y.; Yang G.; Yu J.; Jung T. A.; Liu G.-Y. Structures of annealed decanethiol self-assembled monolayers on Au (111): an ultrahigh vacuum scanning tunneling microscopy study. Langmuir 2003, 19, 6056–6065. 10.1021/la0267701. [DOI] [Google Scholar]
  46. Bürgi L.; Brune H.; Kern K. Imaging of electron potential landscapes on Au(111). Phys. Rev. Lett. 2002, 89, 176801. 10.1103/physrevlett.89.176801. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la0c02535_si_001.pdf (6.5MB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES