Using a Natural Ratio to Compare DC and AC Resistances

Abstract

The simulation and construction of a direct current (DC) and alternating current (AC) resistor, based on a silicon wafer, has been described and demonstrated. By applying the van der Pauw method and the Thompson-Lampard theorem, to within approximations accommodating the conditions of the resistor’s construction, a constant resistance ratio, (π/ln2)², was derived that is independent of the sample resistivity and thickness. The constant ratio, valued at approximately 20.5, can theoretically be used as a basis of comparison between two distinct calibration chains, one based on the traceability from a calculable capacitor and the other based on the quantum Hall effect. To support the calculated ratio, several sets of simulations were performed for both DC and AC cases. The DC simulation results agreed with the ratio value to within 0.035 % when using a wafer thickness of 0.53 mm. Additionally, the experimental DC and AC (1 kHz) results agreed with the calculated ratio value to within 0.23 %, with at most a 0.06 % standard uncertainty before point contact errors from device fabrication.

I. INTRODUCTION

A LTERNATING current (AC) resistors play an important role in linking capacitances to DC resistances. Since the revision of the SI, the very concept of using a calculable capacitor (CC) as the basis for impedance has been under reassessment as efforts in pursuing graphene-based AC quantum Hall standards have been underway [1–3]. Though the linking of the two calibration chains is not necessarily required for fields like metrology, linking the two chains by using a naturally occurring ratio to compare quantities is a mathematical inquiry that warrants some investigation.

In this work, a mathematical technique is presented to provide a proof of principle for comparing AC and DC resistors traceable to the CC and the QHE. This technique depends on the Thompson-Lampard theorem, which stipulates that a geometry-independent capacitance ratio naturally emerges from preceding mathematical descriptions of a physical capacitor or resistor. The ratio is expressed as the constant value ${\left(\frac{\pi }{\ln 2}\right)}^2\cong 20.5423$. Furthermore, by combining measurements of resistance with this technique with those from the van der Pauw method [4], other physical quantities about the resistor may be neglected.

Because this ratio is a mathematical constant, one need only generate the ratio of the resistances obtained from both methods. One should note that the conditions upon which the use of this constant is appropriate are limited due to the inherent constraints of the two theorems. Using both theorems is only truly valid for two identical copies of the material being measured, with one copy having four corner point contacts for van der Pauw measurements, and the other having four side contacts for Thompson-Lampard measurements. Furthermore, samples are required to be homogenous in all three spatial dimensions for the theorems to be applicable. Though the experimental device has all eight contacts to demonstrate convenient fabrication, the simulations and results suggest that some of the error in the obtained ratios arises from the breakdown of the two theorems when a single device has all the contacts, even when four of them are not being used in a particular measurement.

II. NUMERICAL CONSIDERATIONS

A. The van der Pauw Method

One of the methods needed to derive this constant resistance ratio is the van der Pauw (vdP) method, which has been extensively used in a variety of modern experiments for thin materials as well as some error analysis [5–8]. For van der Pauw equations found in the literature pertaining to a sample with four infinitesimally small point contacts [9], one finds the material resistivity $\rho =\frac{\mathrm{\pi }t}{\mathit{ln}2}{R}_{vdP}f\left(\frac{R_{\alpha }}{R_{\beta }}\right)$, where t and ρ are the wafer thickness and specific sheet resistance, respectively. Here, R_α and R_β are two separate vdP measurements using different sets of contacts (for instance, by rotating a square sample with only four corner point contacts by 90°). In the case where the difference between R_α and R_β is less than 1 %, the correction function $f\left(\frac{R_{\alpha }}{R_{\beta }}\right)$ approaches unity to within 5 × 10⁻⁶ and the resistivity is instead given by $\rho \approx \frac{\pi t}{\mathit{ln}2}{R}_{vdP}$.

B. The Thompson-Lampard Theorem

Applications of the Thompson-Lampard (TL) theorem include CC development [10–14]. For our case, we consider the side walls of a second, hypothetical device that is identical to the one supposed for vdP measurements. If C₁ and C₂ represent the mean capacitance per unit thickness between the two pairs of opposing sides, then by the Thompson-Lampard (TL) theorem [15, 16]:

$$e^{\frac{-\mathrm{\pi }{C}_1}{{\epsilon }_0}}+e^{\frac{-\mathrm{\pi }{C}_2}{{\epsilon }_0}}=1$$ (1)

Next, consider a medium of known electrical conductivity σ instead of the dielectric constant ε. Then one may establish the simple relation $\frac{G}{\sigma }=\frac{C}{\epsilon }$, where G is the conductance (inverse of R). Applying this relation to the resistivity yields a result derived in the literature [17, 18]:

$$\begin{gathered} e^{\frac{-\pi \rho G_1}{t}}+e^{\frac{-\pi \rho G_2}{t}}=1 \\ \rho =\frac{t\cdot \mathit{ln}2}{\mathrm{\pi }{G}_{\text{TL}}}=\frac{\mathit{ln}2}{\mathrm{\pi }}{R}_{\text{TL}}t \end{gathered}$$ (2)

R_TL is typically the average of two sheet resistance measurements, R₁ and R₂. With the resistivity defined in both the vdP method and the TL theorem, one can equate the two to obtain an expression that is independent of resistivity and thickness, and the remaining terms yield a numerical ratio ${\overline{R}}_{\pi }$ (the square of the van der Pauw constant) as shown in equation (3) [19]:

$${\overline{R}}_{\pi }=\frac{R_{\text{TL}}}{R_{\text{vdP}}}={\left(\frac{\pi }{\ln 2}\right)}^2\approx 20.54228$$ (3)

One of the more significant consequences of equation (3) is that ${\overline{R}}_{\pi }$ is not dependent on geometry or properties of the selected medium. To reiterate, the use of this ratio is only fully valid for experimental data when two identical devices are prepared such that one has four point contacts (vdP) and the other has the four side contacts (TL). The use of the actual device shown in Fig. 1 may not yield this exact ratio despite its ease of fabrication. However, as will be explained in the next sections, such a device can provide a reasonable estimation of the ratio.

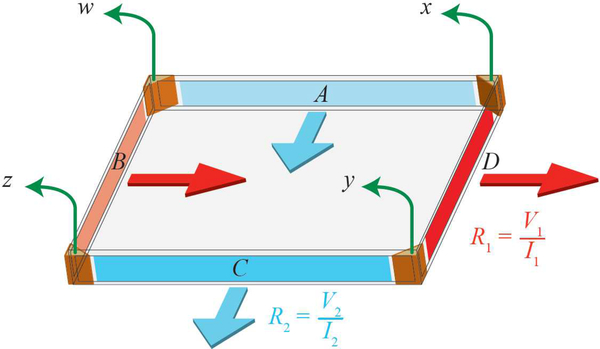
Fig. 1.

An illustration of the wireframe drawing of the square silicon wafer used for device fabrication is shown. There are eight electrical contacts made for two separate measurement methods. The four contacts labelled w, x, y, and z extend along the corners of the wafer (orange) and are used for van der Pauw measurements. A, B, C, and D represent four side contacts colored in alternating light blue and red for Thompson-Lampard measurements. The use of the two theorems for this device is only truly valid if we simulate two identical devices – one with four corner point contacts and the other with four large side contacts.

In addition to not being geometry-dependent, ${\overline{R}}_{\pi }$ can be used to determine either R_TL or R_vdP when the other is known or measured. It should be noted that the use of equations (1) and (2) for AC resistances is only approximate and, in this case, appropriate for a silicon wafer with silver contacts. It has been shown that the vdP method can be used for frequency-dependent quantities [20], as has the TL theorem [21]. Especially with the latter, care must be taken as the TL theorem has not been generalized for electrodynamics and thus may introduce an error if appropriate approximations are not made. Though measurements on silicon have been previously reported [22], the conditions of our system (i.e. having eight contacts on the same device) render the use of the TL theorem in its true form inappropriate. For this reason, simulations must be performed for the ideal case scenarios in addition to those performed for this hybridized device, shown in Fig. 1.

III. DC SIMULATIONS

The simulations to obtain an approximate ${\overline{R}}_{\pi }$, reflecting the actual hybridized device, were carried out using ANSYS Maxwell electromagnetic software [see notes]. The same holds true for simulating the two ideal case scenarios – that is, two identical square wafers having the same specifications as our real device, with one of the two having four corner point contacts for vdP measurements and the other having four side wall contacts for TL measurements. An example model of the hybridized device and its corresponding mesh structure are shown in Fig. 2 (a). The device used for the simulation had dimensions 65 mm by 65 mm in lateral size and a 0.53 mm thickness. The relative permittivity was input as 2.23 and the resistivity was 580 Ω∙cm. The vdP contacts are shown in red and are insulated from the TL contacts that go across the sides of the device (in blue).

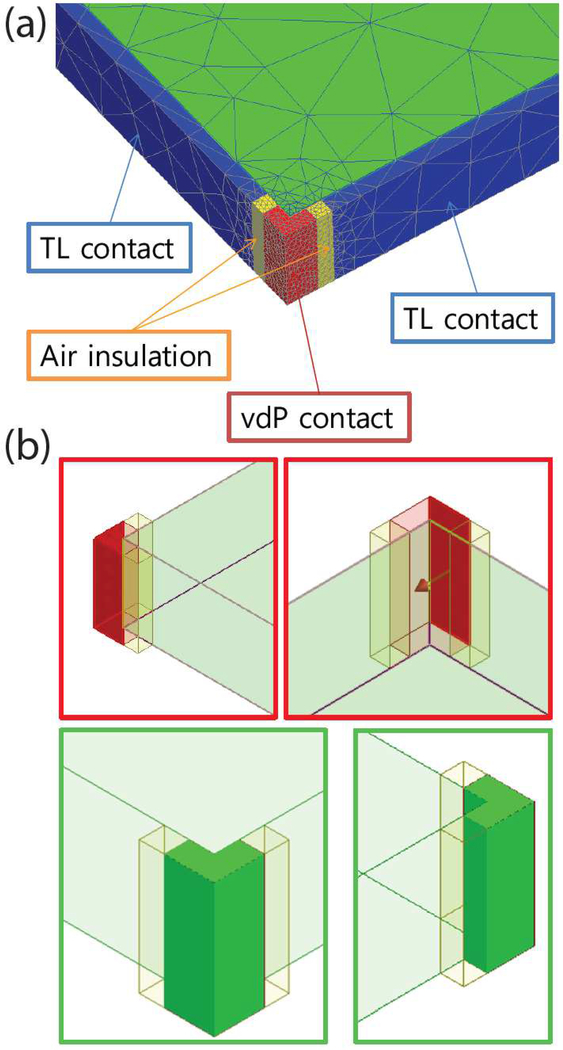
Fig. 2.

(a) The simulation model is shown above reflecting the hybridized square silicon wafer, as well as its corresponding meshes. The red corners are designated as the four vdP contacts, whereas the blue contacts on the side are designated for TL measurements, with a well-defined pocket of air insulating the two sets of contacts. (b) For comparison, a set of simulations was performed to fully understand the possible improvements in achieving the calculated ratio ${\overline{R}}_{\pi }$. The vdP simulations involved having only four corner point contacts (with examples marked in red for current injection and green for voltage measurements). The TL simulations, not shown, were straightforward, as only the four side wall contacts were used.

Table I shows the simulation results for approximate forms of R_TL, R_vdP and the obtained ${\overline{R}}_{\pi }$ as a function of thickness. The results suggest that there is no significant difference in the error between the simulated and actual ${\overline{R}}_{\pi }$ for thicknesses above approximately 0.1 mm. This higher error for small thicknesses may be a result of insufficient or inadequate meshing parameters.

TABLE I.

DC Simulation Results for a Hybridized Square Silicon Wafer

Thickness (mm)	RTL (kΩ)	RvdP (kΩ)	${\overline{\mathit{R}}}_{\mathit{\pi }}$	Rel. Deviation from ${\left(\frac{\mathit{\pi }}{\mathbf{ln}\mathbf{2}}\right)}^{\mathbf{2}}$ (%)
0.001	26264.375	1678.37186	15.64872	23.8
0.01	2628.7286	128.14555	20.51362	0.139
0.1	262.87545	12.80122	20.53519	0.034
0.5	52.57529	2.56007	20.53668	0.027
0.53	49.59932	2.41535	20.53507	0.035
1	26.2877	1.28012	20.53527	0.034
5	5.25754	0.25601	20.53632	0.029

Table II, on the other hand, shows the simulation results for approximate forms of R_TL, R_vdP and the obtained ${\overline{R}}_{\pi }$ as a function of thickness. These simulations were based on two modeled cases. In the first case (for TL), the silicon wafer was modeled having only four side wall contacts. In the second case, the wafer was modeled having only four corner point contacts (see Fig. 2 (b)). Though the results suggest that having two identical devices would yield a better ratio, the comparison of Tables I and II indicate that the hybridized device simulations do not provide an unreasonable estimate of the calculated ratio for thicknesses greater than 0.01 mm. More specifically, the relative deviations from the ratio are larger by slightly more than one order of magnitude. Though the TL simulations from Tables I and II appear to be identical, differences did emerge between the two sets of simulations, but were concealed by the significant digits reported.

TABLE II.

DC Simulation Results for Two Identical Square Silicon Wafers (Ideal Cases)

Thickness (mm)	RTL (kΩ)	RvdP (kΩ)	${\overline{\mathit{R}}}_{\mathit{\pi }}$	Rel. Deviation from ${\left(\frac{\mathit{\pi }}{\mathbf{ln}\mathbf{2}}\right)}^{\mathbf{2}}$ (%)
0.001	26264.375	1118.82839	23.47489	14.27598
0.01	2628.7286	127.96636	20.54234	0.000296
0.1	262.87545	12.79655	20.54267	0.00192
0.5	52.57529	2.55934	20.54252	0.00119
0.53	49.59932	2.41446	20.54260	0.00157
1	26.2877	1.27966	20.54267	0.00188
5	5.25754	0.25593	20.54256	0.00137

IV. RESISTANCE MEASUREMENTS

A. Sample Selection, Electrical Contacts, and Assembly Unit

The material used for the wafer was float zone silicon that was neutron transmutation doped (NTD), as provided by Topsil [see notes]. It had resistivity of about 580 Ω∙cm, 100 mm diameter, 0.53 mm thickness, lateral dimensions of 65 mm by 65 mm, and a crystal orientation of (111).

Ag paste and 99.9999 % purity Al were used as the electrical contact material. The Al contacts were thermally evaporated at 450 °C until a thickness of 600 nm was obtained, at which point a 15 min anneal was performed in a molecular beam epitaxy loading chamber. The Ag paste contacts were made by coating the four sides of a silicon wafer using a soft brush. The assembled unit of the silicon wafer with TL and vdP contacts, coaxial cables, and Bayonet Neill–Concelman (BNC) connectors is shown in Fig. 3. Lead resistances were on the order of 6 mΩ.

Fig. 3.

The assembled unit of a square silicon wafer with eight electrical contacts is shown in an Al case. The leads bonded to the corners of the wafers for R_vdP measurements are connected to the black outer terminals of the box. The red outer terminals are connected to wires bonded to the wafer walls for R_TL measurements.

B. Measurements of R_vdP and R_TL

Once the unit was assembled, both DC and AC R_vdP measurements were performed, using the simplified circuit diagram shown in Fig. 4 (a). With the four metal electrodes w, x, y, and z, current was injected (I_vdP) between w and z with a voltage (V_vdP) being measured between x and y with a digital multimeter (DMM). A complementary measurement was also made by reconfiguring the leads such that current was injected (I_vdP) between w and x and the voltage (V_vdP) was measured between y and z. The measurements, along with their counterparts made by reversing the leads, were averaged to determine an approximate R_vdP.

Fig. 4.

The measurement circuits to determine approximate values of both R_vdP and R_TL, and by extension an approximate ${\overline{R}}_{\pi }$, are illustrated here, with the silicon wafer depicted as a wireframe drawing. (a) In the R_vdP measurements, a current is injected through two adjacent corners while the voltage is measured across the other two corners using a digital multimeter (DMM). Another combination of pairs is then measured to obtain an average value for R_vdP. (b) A similar set of resistance measurements (R_TL) is performed, with a key difference being that the two measured contacts are opposite one another and the two idle contacts are placed at the same (zero) potential, as shown by a blue wire shorting contacts A and C.

For measurements (DC and 1 kHz) of an approximate R_TL, refer to the example in Fig. 4 (b), which shows an example. There were four metal electrodes, labelled A, B, C, D, that were bonded to the walls of the wafer. A voltage was applied on one opposite pair of wafer contacts (B and D in Fig. 4 (b)), allowing the current to be measured (at D) using a DMM. In this configuration, sides A and C were held at zero potential. Determining an approximate R_TL from these measurements (and again, their reversals) can be done by averaging the resistances from the two TL measurements.

V. MEASUREMENT RESULTS AND DISCUSSION

The DC and 1 kHz measurement results for both R_TL and R_vdP (approximate form) are shown in Table III. The simulation results for ${\overline{R}}_{\pi }$ differences were on the order of 10⁻⁴ (in the case of the hybridized device) and experimental results suggested ${\overline{R}}_{\pi }$ differences on the order of 10^-3. These relatively higher errors are primarily attributed to the construction of the wafer samples since the procedure for preparing them did not implement more precise methods and practices. For instance, ensuring the equality of the lateral dimensions by metrological means may contribute a reduction in the error. Furthermore, the application of a more evenly-coated contact on the walls of the wafer would inhibit stray capacitances or inhomogeneous electric fields. Most importantly, the implementation of point contacts for vdP measurements would reduce the error, as seen by the high uncertainties approximated for this factor. For the scope of this manuscript, however, such processes were not required for proof of concept. Simulations were performed with thicknesses in the neighborhood of the commercially-obtained silicon wafer in order to verify the behavior of the differences in ${\overline{R}}_{\pi }$, namely as a realistic representation of the thickness variation.

TABLE III.

Measurement Results for a Square Si Wafer

	Measured value (A)			Theory (B)	(A – B)/B (%)	Standard Uncertainty (Excluding Point Contact Errors) (%)
	RTL (kΩ)	RvdP (kΩ)	${\overline{\mathit{R}}}_{\mathit{\pi }}$	${\overline{\mathit{R}}}_{\mathit{\pi }}$
DC	54.2953	2.6492	20.4954	20.5423	−0.228	0.010
1 kHz	48.3405	2.3505	20.5661	20.5423	0.116	0.055

The sources of uncertainty were analyzed and are summarized in Table IV. One of these sources includes the position of the contacts and the effects of their sizes, more relevantly in regard to vdP measurements [23]. By comparing the approximate size of the point contacts (in this case, 100 μm) with the length of the silicon wafer (6.5 cm), we can include an uncertainty in the vdP measurement of the order of 0.1 %. Based on the manufacturer, thickness variations of this family of wafers have an upper bound of 10 μm. Since both resistance measurements would contain the same error, such errors would drop out. Another source comes from assuming that the resistivity is uniform throughout the wafer. One major source of uncertainty to consider is the measurement repeatability, and this is determined approximately by the measurement differences between R_α and R_β in the vdP configuration and R₁ and R₂ in the TL configuration. Other uncertainties come from DC and AC voltage and current sources in the calibrator, the DC and AC current measurements of the DMM to measure R_TL, and the DC and AC voltage measurements of the DMM to determine R_vdP. Overall, before the addition of point contact errors, standard uncertainties summed to about 0.01 % for the DC case and 0.055 % for the AC case, both of which indicate a possible limitation to other systematic errors. The point contact sources of error contribute an order of magnitude more error and should be of heavy consideration when fabricating devices. Furthermore, these results suggest that the uncertainties are dependent on frequency. A future inquiry of interest would be to determine if constructing two nearly identical devices would yield better ratios, or if the methods of construction would hinder the attempts of improving the ratio.

TABLE IV.

The Uncertainty for vdP and TL Resistance Measurements

Uncertainty factor	Uncertainty (%)
	DC	1 kHz
vdP Point Contacts	0.15	0.15
Repeatability	0.01	0.05
Assumption of Constant ρ	<0.001	<0.001
10 V Source for RTL	0.00025	0.01
Current Measurements for RTL (< 2 mA)	0.0005	0.015
10 μA Source for RvdP	0.002	0.015
Voltage Measurements for RvdP (< 200 mV)	0.0001	0.005
Combined Standard Uncertainty	0.160	0.205
Expanded Uncertainty (k=2)	0.320	0.41

VI. CONCLUSION

This work presents a mathematical approach to comparing AC and DC resistances by using a silicon wafer. We provide simulations for the experimental case where a hybridized device is used for both vdP and TL measurements as well as for the hypothetical case where two identical devices are constructed so that both the vdP and TL theorems are properly implemented. The simulation results for the hybridized device agreed with those of the hypothetical cases to within a tenth of a percent, indicating that a single wafer could provide a reasonable estimate of the natural ratio ${\overline{R}}_{\pi }$. An experiment was also designed, which included the fabrication of a single silicon wafer with all eight contacts. The resulting standard uncertainties from all sources except for point contact errors (about 0.15 %) were found to be 0.01 % and 0.055 % for the DC and AC cases, respectively.

Biography

Kwang Min Yu was born in Busan, South Korea, in 1960. He received the B.S. and M.S. degrees in physics from Pusan National University, Busan, South Korea in 1983 and 1985, respectively, and the Ph.D. degree in solid-state physics from Chungnam National University, Daejeon, South Korea, in 2012. In 1986, he joined the Korea Research Institute of Standards and Science (KRISS), Daejeon, South Korea, where he has been involved in electrical resistance standards. He is currently a Senior Researcher with the Center for Electricity and Magnetism, KRISS.

Dean G. Jarrett (S’88–M’90–SM’99) was born in Baltimore, MD, in 1967. He received the B.S. degree in electrical engineering from the University of Maryland, College Park, in 1990 and the M.S. degrees in electrical engineering and applied biomedical engineering from Johns Hopkins University, Baltimore, in 1995 and 2008, respectively.

Since 1986, he has been with the National Institute of Standards and Technology (NIST), in Gaithersburg, MD, where he was a Cooperative Education Student from the University of Maryland. During this time, he worked in the DC resistance area on the automation of resistance calibration systems. In 1991 he joined NIST full time as an electrical engineer working on the development of an automated AC resistance calibration system and the development of new resistance standards. Since 1994, he has worked in the high resistance laboratory developing automated measurement systems and improved standard resistors to support high resistance calibration services and key comparisons. In recent years, he has worked on sensor technologies for the detection of biological molecules and low-current source and measure techniques. Since 2014, he has led the Metrology of the Ohm Project at NIST.

Andrew D. Koffman (S’86–M’90– SM’08) received the B.S. degree in electrical engineering from the University of Maryland, College Park, MD, USA, in 1988, and the M.S. degree in electrical engineering from Vanderbilt University, Nashville, TN, USA, in 1990. He joined the Electricity Division, National Institute of Standards and Technology, in 1990. He is currently with the NIST Quantum Measurement Division in the area of AC impedance measurements.

Albert F. Rigosi (M’17–18) was born in New York, NY, USA in 1989. He received the B.A., M.A., M.Phil., and Ph.D. degrees in physics from Columbia University, New York, NY, in 2011, 2013, 2014, and 2016, respectively.

From 2008 to 2015, he was a Research Assistant with the Columbia Nano Initiative. From 2015 to 2016, he was a Joint Visiting Research Scholar with the Department of Applied Physics of Stanford University in Stanford, CA, and the PULSE Institute of SLAC National Accelerator Laboratory in Menlo Park, CA. Since 2016, he has been a Physicist at the National Institute of Standards and Technology in Gaithersburg, MD. His research interests include two-dimensional electron systems and applications of those systems’ behaviors for electrical metrology.

Dr. Rigosi is a member of the American Physical Society and the Mellon-Mays Initiative of The Andrew W. Mellon Foundation. He was awarded associateships and fellowships from the National Research Council (USA), the Optical Society of America, the Ford Foundation, and the National Science Foundation (Graduate Research Fellowship Program).

Shamith U. Payagala received the B.S. degree in electrical engineering from the University of Maryland, College Park, MD, in 2015.

He joined the National Institute of Standards and Technology (NIST), Gaithersburg, MD, in 2014, and he serves as an Electrical Engineer for the Metrology of the Ohm project.

Kwon Sang Ryu was born in the Republic of Korea in 1956. He received the B.S. and M.S. degrees in physics from Pusan National University, Busan, Republic of Korea, in 1983 and 1985, respectively, and the Ph.D. degree in physics from Hannam University, Daejeon, Republic of Korea, in 2000. He joined the Korea Institute of Standards and Science (KRISS), Daejeon, Republic of Korea in 1988, where he has been involved in measurements of magnetic properties. He is currently a senior Researcher with the Center for Materials and Energy Measurement.

Jeon Hong Kang received his B.S. and M.S. degrees in electrical engineering from Hanbat National University, Daejeon, Republic of Korea in 1998 and the Ph.D. degree in electrical engineering from Chungnam National University, Daejeon, Republic of Korea in 2008. Since 1987, he has been working as a Senior Engineer at the Center for Electricity and Magnetism at Korea Research Institute of Standards and Science (KRISS). His area of research interest is the evaluation of resistivity characteristics for metals, semiconductors and insulators.

Sang Hwa Lee was born in 1967 in the Republic of Korea. He received the B.S. degree in electronics from Hanbat National University, Daejeon, Republic of Korea, and the M.E. degree in electrical engineering from Chungnam National University, Daejeon, Republic of Korea. He is currently working toward the Ph.D. degree. In 1985, he joined the Korea Research Institute of Standards and Science (KRISS), Deajeon, Republic of Korea, where he has been working with ratio standards for direct and alternating-current (AC) high voltage and heavy AC applications. He is responsible for performing calibration services in those areas. Currently, he is a Principal Technician with the Center for Electricity and Magnetism, KRISS.