Inequality-Constrained and Robust 3D Face Model Fitting

Abstract

Fitting 3D morphable models (3DMMs) on faces is a well-studied problem, motivated by various industrial and research applications. 3DMMs express a 3D facial shape as a linear sum of basis functions. The resulting shape, however, is a plausible face only when the basis coefficients take values within limited intervals. Methods based on unconstrained optimization address this issue with a weighted ℓ₂ penalty on coefficients; however, determining the weight of this penalty is difficult, and the existence of a single weight that works universally is questionable. We propose a new formulation that does not require the tuning of any weight parameter. Specifically, we formulate 3DMM fitting as an inequality-constrained optimization problem, where the primary constraint is that basis coefficients should not exceed the interval that is learned when the 3DMM is constructed. We employ additional constraints to exploit sparse landmark detectors, by forcing the facial shape to be within the error bounds of a reliable detector. To enable operation “in-the-wild”, we use a robust objective function, namely Gradient Correlation. Our approach performs comparably with deep learning (DL) methods on “in-the-wild” data that have inexact ground truth, and better than DL methods on more controlled data with exact ground truth. Since our formulation does not require any learning, it enjoys a versatility that allows it to operate with multiple frames of arbitrary sizes. This study’s results encourage further research on 3DMM fitting with inequality-constrained optimization methods, which have been unexplored compared to unconstrained methods.

1. Introduction

Estimation of 3D facial shape from 2D data via 3D morphable models (3DMMs), a.k.a. face reconstruction, is a fundamental computer vision problem that attracts great interest due to its various applications [10], such as facial expression synthesis or analysis [18], gaze estimation [38] and facial landmark detection [45].

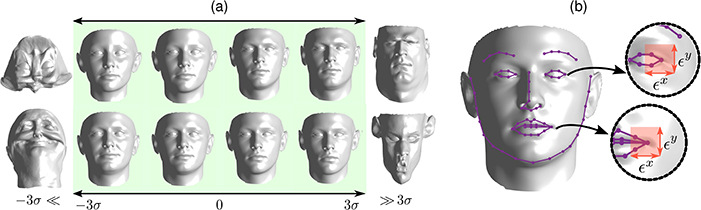
Most 3DMMs reconstruct facial shape as a linear sum of basis functions that are typically learned via a variant of principal component analysis (PCA) [3,5,7] or other models [14,10]. Then, 3D facial shape reconstruction from 2D data is performed by inferring the basis coefficients in this sum, often using unconstrained pseudo-second-order (PSO) optimization. The magnitude of basis coefficients must not be too large; otherwise, the resulting shape may hardly look like a face (Fig. 1a). More specifically, the coefficients should be within the bounds of their distributions, which are learned when the 3DMM is constructed. For example, if the 3DMM is learned with PCA (e.g., [21]), the coefficients should very rarely exceed ±3 standard deviations (Section 2.2). A similar interval can be found for 3DMMs learned with other stochastic approaches (e.g.,[14]).

Fig.1.

Illustration of why inequality constraints are useful. (a) Morphable model constraints. Each row shows the effect of a basis function of the Basel’09 model [21] when generating facial shapes. The shapes may become implausible when the basis coefficient is outside a certain interval (in this case, ±3 standard deviations, [−3σ, 3σ]); thus, the optimization algorithm is constrained to this interval. (b) Sparse landmark constraints. The purple dots show the output of a landmark detector, and the red rectangles depict the maximal error for two landmarks (i.e., eye and mouth corner), learned on a large dataset (Section 2.2). When a dense facial mesh is fit to this image, the mouth and eye corner of the mesh should remain inside the red rectangles

Many methods address the above-mentioned issue by adding a weighted ℓ₂ penalty on the coefficients (Section 1.1). Unfortunately, the weights of those penalties are not easy to tune, and such ℓ₂ regularization can lead to overly smooth faces that miss personal characteristics, or images that exaggerate those characteristics to minimize reconstruction error (Fig. 2). Using deep learning (DL) is another alternative to 3DMM fitting. However, the DL methods that achieve the best performance “in-the-wild” also tend to produce overly-smooth faces (Fig. 2). Moreover, DL methods may lack versatility, as they rely on a fixed architecture that may not be suitable for working with images of arbitrary size, or with multiple frames of a person when available (Section 1.1).

Fig.2.

Illustration of the output of two state-of-the-art deep learning-based methods, PRNet [11] and 3DDFA [45], in comparison to our method (3DI; used with Basel 2009 model [21]), two optimization-based methods with ℓ₂ regularization (3DMM edges [1] and ITW [7]) and ground truth. Deep learning methods are remarkably robust, but tend to produce over-smooth faces, whereas our method is better capable of applying the right amount of detail. More illustrations are provided in Supplementary Material

This paper introduces a novel and theoretically compelling alternative to unconstrained PSO optimization, which achieves a robustness on par with DL methods, without sacrificing the versatility of 3DMMs. Specifically, we formulate 3DMM fitting as an inequality-constrained optimization problem, where the primary constraint is that no basis function coefficient should be outside the coefficient interval that is learned while the 3DMM is constructed (Fig. 1a). Thus, we prevent coefficients from taking prohibitively large values, but unlike ℓ₂ regularization, do not require the tuning of any application-specific parameter. Additional inequality constraints are used to exploit (sparse) facial landmark detectors (Fig. 1b). To enable our approach to operate “in-the-wild”, we use Gradient Correlation (GC) [34] as the objective function, since GC is robust against illumination variations and occlusion. Finally, our approach can fit a 3DMM to multiple frames of a person. We refer to our formulation as 3DI (3D estimation via Inequality constraints).

This paper has two technical contributions. First, we propose a novel formulation for 3DMM fitting as an inequality-constrained optimization problem. Second, we show how to use GC as a robust objective function for fitting 3DMMs. Our results on a widely-used “in-the-wild” dataset, AFLW2000–3D [44], are comparable to those of DL methods, even though our method does not require any training at all, and the 3DMM that we use is learned under controlled conditions [14]. Moreover, we demonstrate that our method actually outperforms the state-of-the-art methods on data where exact ground truth is known (improvement between 21% and 39% on the BU-4DFE dataset [41] and a synthesized dataset). The performance improves significantly with multiple frames, highlighting the benefits of a versatile method that can use multiple images.

1.1. Related Work

Many 3DMM fitting methods use unconstrained PSO optimization [10], such as stochastic gradient [24,3], Levenberg-Marquardt [27,23] or Gauss-Newton [46,30,17,6,7,15,40]. These methods usually use various weighted ℓ₂ regularization terms in the cost function [27,2,3,1,6,7,15,12,46,24,39,30,4,17]. Unfortunately, the determination of the weight of these terms can be ad hoc [3]. Moreover, it is highly unlikely that there are specific optimal weights that can work on all images under all circumstances. For example, the optimal weight for the ℓ₂ penalty on deviation from landmarks should ideally depend on the error of the landmark detector, which is different for each image. A key novelty of our approach is to replace ℓ₂ regularization strategies with inequality constraints. Our formulation requires only determination of the bounds of the inequalities, which is learned for each 3DMM only once, without tuning w.r.t. a problem-specific metric (Section 2.2). Some recent methods can operate “in-the-wild” by using robust representations [1,6,7]. We also use a robust approach to fit morphable models, namely GC, which is robust against illumination variation and has a built-in outlier elimination, rendering it robust against occlusions [34].

Deep learning (DL) techniques are increasingly popular for 3D shape estimation [43,11,13,28,20,22,26,29,31]. Herein, we focus on DL methods that prioritize 3D shape reconstruction, which is the purpose of our study (but, see a recent survey on using DL for other tasks; e.g., texture reconstruction [10]). Two DL methods are particularly robust, namely 3DDFA [45] and PRNet [11]. To our knowledge, PRNet achieves the best performance on one of the most popular “in-the-wild” datasets, AFLW2000–3D [45], as also shown in a recent independent study [43]. Like most DL methods, PRNet and 3DDFA work with a single frame, and cannot be trivially extended to use multiple frames of a person without creating a new architecture (e.g. [22]). In contrast, multi-frame operation is a rather straightforward extension for PSO approaches [7] and for our formulation. Also, the faces reconstructed by those DL methods tend to be too smooth (Fig. 2), missing person-specific details, and possibly limiting their performance when working with simpler images from relatively controlled conditions (Section 3.2). This is unfortunate, as in many applications the conditions are not “in-the-wild”, such as Skype interviews or video recordings for clinical research [36].

2. Inequality-Constrained 3D Model Fitting

We first give background for fitting a 3D model to 2D frames and introduce our notation (Section 2.1). We then explain why it is natural to formulate 3DMM fitting as an inequality-constrained optimization problem (Section 2.2). Finally, we describe the robust objective function that we use (Section 2.3) and how to optimize it subject to inequality constraints (Section 2.4).

2.1. Background and Notation

Fitting a 3DMM to a set of 2D frames, I₁, …, I_T, amounts to finding the facial shape, texture, camera view, and illumination coefficients that best reconstruct the frames.

3D facial shape

The 3D facial shape is represented with a dense mesh of N points at each frame. Let p_t be the mesh at frame t, ${\mathbf{p}}_t:={\left({\mathbf{p}}_{t1}^T,{\mathbf{p}}_{t2}^T,\dots ,{\mathbf{p}}_{tN}^T\right)}^T\in {ℝ}^{3N}$, where p_ti is a single point, i.e., ${\mathbf{p}}_{ti}={\left(p_{ti}^x,p_{ti}^y,p_{ti}^z\right)}^T$. Then, morphable models represent the facial shape as a linear sum,

$${\mathbf{p}}_t=\overline{\mathbf{p}}+\mathbf{A}\alpha +\mathbf{E}{\epsilon }_t,$$ (1)

where $\overline{\mathbf{p}}$ is the mean face shape, $\mathbf{A}\in {ℝ}^{3N\times K_{\alpha }}$ is the (shape) identity basis of the morphable model, $\alpha \in {ℝ}^{K_{\alpha }}$ is the vector of shape parameters, $\mathbf{E}\in {ℝ}^{3N\times K_{\epsilon }}$ is the facial expression basis and ${\epsilon }_t\in {ℝ}^{K_{\epsilon }}$ is the vector of expression coefficients. Note that α does not depend on t as facial identity does not change over time, but the expression ε_t can. The points undergo a camera view transformation; that is, a rotation by a matrix R_t ∈ SO(3) and translation by a vector τ_t = (τ_tx, τ_ty, τ_tz)^T. The view-transformed points are represented as v_t1, v_t2, …, v_tN, where

$${\mathbf{v}}_{ti}:={\left(v_{ti}^x,v_{ti}^y,v_{ti}^z\right)}^T:={\mathbf{R}}_t{\mathbf{p}}_{ti}+{\mathit{\tau }}_t.$$ (2)

The rotation matrix can be represented via quaternion parameters $q_0^t,q_1^t,q_2^t$ and $q_3^t$ [7]. The camera view transformation is represented concisely as a 6-vector ${\mathbf{c}}_t:={\left(c_{t1},\dots ,c_{t6}\right)}^T:={\left(q_1^t,q_2^t,q_3^t,{\mathit{\tau }}_t^T\right)}^T;q_0^t$ is ignored, as it can be determined when $q_1^t,q_2^t,q_3^t$ are known due to the unit-norm constraint of quaternions [7].

3D-to-2D mapping

The next step towards reconstructing the face image is to project each 3D point v_ti onto the image plane. For a CCD camera, this process is carried out with a perspective transformation [16], and the 2N-vector containing image points, ${\mathbf{x}}_t:=\left(x_1^t,y_1^t,\dots ,x_N^t,y_N^t\right)$, is obtained as:

$$x_i^t={\varphi }_x{v}_{ti}^x/v_{ti}^z+c_x,y_i^t={\varphi }_y{v}_{ti}^y/v_{ti}^z+c_y$$ (3)

where ϕ_x and ϕ_y are the parameters of the perspective transformation, and c_x and c_y are the coordinates of the image center.

Texture

To obtain the reconstructed face image, ${\widehat{\mathbf{I}}}_t$, one needs to determine the texture (i.e., the pixel intensity) that will be assigned to each image point. This essentially depends on two factors: the facial texture of the person (e.g., color of skin) and the illumination. A morphable model represents the facial texture of a person, ${\widehat{\mathbf{I}}}_t^f$, as a linear sum, ${\widehat{\mathbf{I}}}_t^f:=\overline{\mathbf{t}}+\mathbf{B}\mathit{\beta }$, where $\overline{\mathbf{t}}$ is the mean texture and $\overline{\mathbf{t}}\in {ℝ}^N$ for a grayscale image; $\mathbf{B}\in {ℝ}^{N\times K_{\beta }}$ is the texture basis of the morphable model; and $\mathit{\beta }\in {ℝ}^{K_{\beta }}$ is the vector of texture coefficients. Using a simplified version of the Phong illumination model (i.e., we ignore specular reflection [3]), the pixel intensities of the reconstructed image can finally be computed as

$${\widehat{\mathbf{I}}}_t={\widehat{\mathbf{I}}}_t^f+\Lambda {\widehat{\mathbf{I}}}_t^f\odot {\widehat{\mathbf{I}}}_t^d,$$ (4)

where ⊙ is element-wise vector production, ${\widehat{\mathbf{I}}}_t^d$ is the diffuse reflection component of the Phong model and Λ is a scalar—the diffuse reflection coefficient. The ith element of ${\widehat{\mathbf{I}}}_t^d$ is ${\widehat{\mathbf{I}}}_t^d[i]:=\langle {\mathbf{n}}_{ti},{\mathit{\lambda }}_t-{\mathbf{v}}_{ti}\rangle$, where n_ti is the unit-norm the surface normal vector of the facial mesh at the ith point, ⟨·,·⟩ is the standard inner product on ℓ₂, and λ_t:=(λ_tx, λ_ty, λ_tz)^T is the 3D location of the illumination source. Eq. (4) can be extended to use multiple illumination sources [3].

Image formation

Rendering of reconstructed face image is carried out by filling the pixels whose location is specified in x_t with the intensity values specified in ${\widehat{\mathbf{I}}}_t$. The true rendering process is slightly more complicated, as it requires rasterization to identify the pixels that will be rendered and Z-buffering to discard occluded pixels. However, for notational simplicity, we will suppose that ${\widehat{\mathbf{I}}}_t$ is the (vectorized) rendered image—that the ith value of ${\widehat{\mathbf{I}}}_t$ contains the pixel intensity at image location (x_i, y_i).

2.2. Inequality Constraints

The facial shape and texture bases of morphable models are learned from a large number of 3D facial scans [3]. Often, a statistical learning approach that underlies the assumption of Normal distribution (e.g., PCA [2,7]) is used, in which case basis coefficients should very rarely exceed ±3 standard distribution [35]. Thus, the distributions learned while constructing the 3DMM can be used to determine hard upper and lower bounds for basis coefficients. Importantly, one can set those bounds a priori, in an application-independent manner. Nevertheless, since the basis coefficients are empirical distributions, it is worth visually confirming that the hard bounds generated using the statistics of those distributions do indeed generate plausible-looking faces, as the aim is to have universally-valid bounds.

Let us define h^α, h^β and ${\mathbf{h}}_t^{\epsilon }$ as the constraint functions h^α := α, h^β := β, and ${\mathbf{h}}_t^{\epsilon }:={\epsilon }_t$. Then, the morphable model constraints are

$${\alpha }^{-}⪯{\mathbf{h}}^{\alpha }⪯{\alpha }^{+},{\epsilon }^{-}⪯{\mathbf{h}}_t^{\epsilon }⪯{\epsilon }^{+},{\mathit{\beta }}^{-}⪯{\mathbf{h}}^{\beta }⪯{\mathit{\beta }}^{+},$$ (5)

where ${\alpha }^{-}\in {ℝ}^{K_{\alpha }}$, ${\alpha }^{+}\in {ℝ}^{K_{\alpha }}$, ${\epsilon }^{-}\in {ℝ}^{K_{\epsilon }}$, ${\epsilon }^{+}\in {ℝ}^{K_{\epsilon }}$, ${\beta }^{-}\in {ℝ}^{K_{\beta }}$ and ${\beta }^{+}\in {ℝ}^{K_{\beta }}$ are vectors containing the bounds for the morphable model’s facial shape, expression and texture coefficients. The symbol $⪯$ is componentwise inequality [8].

Additional inequality constraints can be used to further improve the fitting via (sparse) 2D landmark detectors, as in Fig. 1b. Suppose that we have a detector that estimates the locations of L landmark points. Let those landmark points on the facial mesh be ${\mathbf{x}}_t^{\prime }:=\left(x_{i_1}^t,y_{i_1}^t,\dots ,x_{i_L}^t,y_{i_L}^t\right)$, and let ${\widehat{\mathbf{x}}}_t^{\prime }:=\left({\widehat{x}}_{i_1}^t,{\widehat{y}}_{i_1}^t,\dots ,{\widehat{x}}_{i_L}^t,{\widehat{y}}_{i_L}^t\right)$ be the location of the same landmarks as estimated by the detector. Let us suppose that the maximal error of the landmark detector is measured for each landmark on a very large dataset and encoded in a vector ϵ as $ϵ:=\left({ϵ}_1^x,{ϵ}_1^y,\dots ,{ϵ}_L^x,{ϵ}_L^y\right)$ (Fig. 1b). Here, the maximal error of a landmark, ${ϵ}_j^x$, ${ϵ}_j^y$, can be defined in the strict sense (i.e., the error on the ith landmark does not exceed ${ϵ}_i^x$, ${ϵ}_i^y$ for any image in the dataset) or in a slightly loose sense, such as the error that is valid for 99% of the images. Then, the discrepancy between ${\widehat{\mathbf{x}}}_t^{\prime }$ and the image location of the same landmarks under the morphable model, ${\mathbf{x}}_t^{\prime }:=\left(x_{i_1}^t,y_{i_1}^t,\dots ,x_{i_L}^t,y_{i_L}^t\right)$ [see (3)], should not exceed ϵ. Thus, the sparse landmark constraint can be represented as

$$-s_b^tϵ⪯{\mathbf{h}}_t^L⪯s_b^tϵ,$$ (6)

where ${\mathbf{h}}_t^L:={\mathbf{x}}_t^{\prime }-{\widehat{\mathbf{x}}}_t^{\prime }$, and s_b is the bounding box size $s_b^t:=\sqrt{w_{bbox}^t\times h_{bbox}^t}$, which is used for normalizing the error [9]. The width and height of the box, $w_{bbox}^t$ and $h_{bbox}^t$, are computed from the landmarks.

2.3. Objective Function

Fitting a 3DMM to an input image I_t requires a cost function to measure the quality of fit. One may simply use the squared pixel-wise difference between the input and reconstructed image [3], but this would hardly be robust (e.g., against occlusions). We use GC, as it is a robust function due to its outlier elimination property [34]. GC has been used for rigid [32,34] and non-rigid 2D registration [33]; however, to our knowledge, it has not been used for 3DMM fitting. We derive the mathematical expressions needed for the latter in Section 2.4.

To compute GC, we need to compute the magnitude-normalized gradient of the input image I_t and the fitted image ${\widehat{\mathbf{I}}}_t$ [34]. Let us denote the magnitude-normalized gradients of I_t along the x and y axes with the N-dimensional vectors g_tx and g_ty. If we approximate the ideal gradient operator with centered difference, then the kth entry of those vectors can be computed as

$${\mathbf{g}}_{tx}[k]:=\left({\mathbf{I}}_t\left[k_r\right]-{\mathbf{I}}_t\left[k_l\right]\right)/h,{\mathbf{g}}_{ty}[k]:=\left({\mathbf{I}}_t\left[k_b\right]-{\mathbf{I}}_t\left[k_a\right]\right)/h,$$ (7)

where k_a, k_b, k_l, and k_r are the pixels above, below, to the left, and right of the kth pixel, and $h:=\sqrt{{\left({\mathbf{I}}_t\left[k_r\right]-{\mathbf{I}}_t\left[k_l\right]\right)}^2+{\left({\mathbf{I}}_t\left[k_b\right]-{\mathbf{I}}_t\left[k_a\right]\right)}^2}$ is the magnitude. The magnitude-normalized gradients of ${\widehat{\mathbf{I}}}_t$, ${\widehat{\mathbf{g}}}_{tx}$ and ${\widehat{\mathbf{g}}}_{ty}$, are computed similarly. For notational simplicity, we concatenate those gradients and represent them as ${\mathbf{g}}_t:={({\mathbf{g}}_{tx}^T,{\mathbf{g}}_{ty}^T)}^T$ and ${\widehat{\mathbf{g}}}_t:={({\widehat{\mathbf{g}}}_{tx}^T,{\widehat{\mathbf{g}}}_{ty}^T)}^T$. The objective function f that we aim to maximize, namely the GC between the input and the fitted frames, is

$$f=\sum _{t=1}^T{\mathbf{g}}_t^T{\widehat{\mathbf{g}}}_t.$$ (8)

2.4. Optimization

Inequality-constrained optimization problems are more difficult to solve than unconstrained problems [8]. Algorithms that are standard for 3DMM fitting, such as Gauss-Newton, cannot be used with inequality constraints. Fortunately, there are high-quality solvers for inequality-constrained problems, such as IPOPT [37], that require only the derivative of the objective function f and the Jacobian of inequality constraints. We derive these terms below.

Derivative of objective function

The derivative of f in (8) w.r.t. any parameter y that affects the rendered image ${\widehat{\mathbf{I}}}_t$ is

$$\frac{\partial f}{\partial \mathbf{y}}=\sum _{t=1}^T{\mathbf{g}}_t^T\frac{\partial {\widehat{\mathbf{g}}}_t}{\partial \mathbf{y}}=\sum _{t=1}^T{\mathbf{g}}_t^T\frac{\partial {\widehat{\mathbf{g}}}_t}{\partial {\widehat{\mathbf{I}}}_t}\frac{\partial {\widehat{\mathbf{I}}}_t}{\partial \mathbf{y}}.$$ (9)

Since the normalized gradient depends only on neighboring values of the input image [see (7)], $\partial {\widehat{\mathbf{g}}}_t/\partial {\widehat{\mathbf{I}}}_t$ is a sparse 2N × N matrix. This matrix is obtained by horizontally concatenating $\partial {\widehat{\mathbf{g}}}_{tx}/\partial {\widehat{\mathbf{I}}}_t$ and $\partial {\widehat{\mathbf{g}}}_{ty}/\partial {\widehat{\mathbf{I}}}_t$. The entries of the latter matrices are provided in Supplementary Material. To compute the partial derivatives of f for all needed variables, we must compute $\partial {\widehat{\mathbf{I}}}_t/\partial \mathit{\alpha }$, $\partial {\widehat{\mathbf{I}}}_t/\partial \mathit{\beta }$, $\partial {\widehat{\mathbf{I}}}_t/\partial {\epsilon }_t$, $\partial {\widehat{\mathbf{I}}}_t/\partial {\mathbf{c}}_t$ and $\partial {\widehat{\mathbf{I}}}_t/\partial {\mathit{\lambda }}_t$ and then replace them in turn with $\partial {\widehat{\mathbf{I}}}_t/\partial \mathbf{y}$ in (9). $\partial {\widehat{\mathbf{I}}}_t/\partial \mathit{\beta }$ is rather simple as β affects only the ${\widehat{\mathbf{I}}}_t^f$ in (4):

$$\frac{\partial {\widehat{\mathbf{I}}}_t}{\partial \mathit{\beta }}=\frac{\partial {\widehat{\mathbf{I}}}_t^f}{\partial \mathit{\beta }}+\frac{\partial {\widehat{\mathbf{I}}}_t^f}{\partial \mathit{\beta }}\odot ({\mathbf{1}}_{K_{\mathit{\beta }}}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^d)=\mathbf{B}+\mathbf{B}\odot ({\mathbf{1}}_{K_{\mathit{\beta }}}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^d),$$ (10)

where ${\mathbf{1}}_{K_{\mathit{\beta }}}^T$ is the transpose of the K_β-dimensional column vector whose all entries are 1, and ⊗ is the Kronecker product; therefore, $({\mathbf{1}}_{K_{\mathit{\beta }}}^T\otimes {\widehat{\mathbf{I}}}_t^d)$ is an N ×K_β matrix whose every column is $\Lambda {\widehat{\mathbf{I}}}_t^d$. The derivative w.r.t. illumination source λ is also simple as λ has no effect on ${\widehat{\mathbf{I}}}_t^f$:

$$\frac{\partial {\widehat{\mathbf{I}}}_t}{\partial \mathit{\lambda }}=({\mathbf{1}}_3^T\otimes {\widehat{\mathbf{I}}}_t^f)\odot \frac{\partial {\widehat{\mathbf{I}}}_t^d}{\partial \mathit{\lambda }}=({\mathbf{1}}_3^T\otimes {\widehat{\mathbf{I}}}_t^f)\odot {\left({\mathbf{n}}_{t1},{\mathbf{n}}_{t2},\dots ,{\mathbf{n}}_{tN}\right)}^T.$$ (11)

The derivatives w.r.t. remaining parameters are obtained as follows:

$$\begin{gathered} \frac{\partial {\widehat{\mathbf{I}}}_t}{\partial \alpha }=\frac{\partial {\widehat{\mathbf{I}}}_t^f}{\partial {\mathbf{x}}_t}\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial \alpha }\odot \left({\mathbf{1}}_{N{K}_{\mathit{\alpha }}}+{\mathbf{1}}_{K_{\mathit{\alpha }}}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^d\right)+\left({\mathbf{1}}_{K_{\alpha }}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^f\right)\odot \frac{\partial {\widehat{\mathbf{I}}}_t^d}{\partial {\mathbf{x}}_t}\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial \alpha }, \\ \frac{\partial {\widehat{\mathbf{I}}}_t}{\partial {\epsilon }_t}=\frac{\partial {\widehat{\mathbf{I}}}_t^f}{\partial {\mathbf{x}}_t}\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial {\epsilon }_t}\odot \left({\mathbf{1}}_{N{K}_{\epsilon }}+{\mathbf{1}}_{K_{\epsilon }}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^d\right)+\left({\mathbf{1}}_{K_{\epsilon }}^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^f\right)\odot \frac{\partial {\widehat{\mathbf{I}}}_t^d}{\partial {\mathbf{x}}_t}\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial {\epsilon }_t}, \\ \frac{\partial {\widehat{\mathbf{I}}}_t}{\partial {\mathbf{c}}_t}=\frac{\partial {\widehat{\mathbf{I}}}_t^f}{\partial {\mathbf{x}}_t}\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{c}}_t}\odot \left({\mathbf{1}}_{N6}+{\mathbf{1}}_6^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^d\right)+\left({\mathbf{1}}_6^T\otimes \Lambda {\widehat{\mathbf{I}}}_t^f\right)\odot \frac{\partial {\widehat{\mathbf{I}}}_t^d}{\partial {\mathbf{c}}_t} \end{gathered}$$ (12)

where 1_N is an N-dimensional vector of ones. $\partial {\widehat{\mathbf{I}}}_t^f/\partial {\mathbf{x}}_t$ is an N × 2N block-diagonal matrix that contains the (un-normalized) gradient of the image ${\widehat{\mathbf{I}}}_t^f$; specifically, the nth block on its diagonal is a 1 × 2 matrix comprising the horizontal and vertical gradient of the nth pixel of ${\widehat{\mathbf{I}}}_t^f$. ∂p/∂α and ∂p/∂ε_t are respectively A and E. ∂x_t/∂p_t is a block-diagonal matrix whose nth block is a 2 × 3 matrix containing the derivative of the nth image point w.r.t. p_n. The remaining terms that are needed to complete the computation of derivatives, namely ∂x_t/∂c_t and $\partial {\widehat{\mathbf{I}}}_t^d/\partial {\mathbf{c}}_t$, are provided in Supplemental Material.

Jacobian of constraints

Our problem has 2 + 2T constraint functions h^α, h^β, ${\mathbf{h}}_1^{\epsilon },\dots ,{\mathbf{h}}_T^{\epsilon }$, ${\mathbf{h}}_1^L,\dots ,{\mathbf{h}}_T^L$ and 2+3T sets of variables α, β, ε₁,…, ε_T, c₁, …, c_T, λ₁, …, λ_T. The Jacobian of the constraints is therefore a matrix partitioned into a grid of (2+2T)×(2+3T) blocks, where each partition is the partial derivative of one of the afore-listed constraint functions w.r.t. one of the sets of variables. J is a sparse matrix, as each constraint depends only on a small set of variables. We list all of the non-zero derivatives in this partitioning below. The derivatives for the morphable model constraints are

$$\frac{\partial {\mathbf{h}}^{\alpha }}{\partial \mathit{\alpha }}=I_{K_{\alpha }},\frac{\partial {\mathbf{h}}_t^{\epsilon }}{\partial {\epsilon }_t}=I_{K_{\epsilon }}\frac{\partial {\mathbf{h}}^{\mathit{\beta }}}{\partial \mathit{\beta }}=I_{K_{\beta }},$$ (13)

where $I_{K_{\alpha }}$, $I_{K_{\epsilon }}$ and $I_{K_{\beta }}$ are identity matrices of size K_α, K_ε and K_β, respectively. The derivatives for the landmark constraints are

$$\frac{\partial {\mathbf{h}}_t^L}{\partial {\epsilon }_t}=\frac{\partial {\mathbf{x}}_t^{\prime }}{\partial {\mathbf{p}}_t^{\prime }}\frac{\partial {\mathbf{p}}_t^{\prime }}{\partial {\epsilon }_t},\frac{\partial {\mathbf{h}}_t^L}{\partial {\mathbf{c}}_t}=\frac{\partial {\mathbf{x}}_t^{\prime }}{\partial {\mathbf{c}}_t},$$ (14)

where ${\mathbf{p}}_t^{\prime }$ is the 3L-vector obtained by concatenating the 3D points corresponding to landmarks, ${\mathbf{p}}_t^{\prime }:={\left({\mathbf{p}}_{t{i}_1}^T,\dots ,{\mathbf{p}}_{t{i}_L}^T\right)}^T$. The matrix $\partial {\mathbf{x}}_t^{\prime }/\partial {\mathbf{p}}_t^{\prime }$ is a block-diagonal matrix obtained similarly to the ∂x_t/∂p_t described for (12); the only difference is that it comprises L blocks –corresponding to L landmarks– and not N blocks. The derivative $\partial {\mathbf{p}}_t^{\prime }/\partial \alpha$ is a 3L×K_α matrix containing the rows of A corresponding to the L landmarks. Similarly, $\partial {\mathbf{p}}_t^{\prime }/\partial {\epsilon }_t$ contains the rows of E corresponding to landmarks. The partial derivative $\frac{\partial {\mathbf{x}}_t^{\prime }}{\partial {\mathbf{c}}_t}$ is also similar to the $\frac{\partial {\mathbf{x}}_t}{\partial {\mathbf{c}}_t}$ in (12), with the difference that it is computed from L landmark points.

3. Experimental Validation

We validate our method experimentally on three tasks, namely (sparse) 2D facial landmark estimation (a.k.a. face alignment), 3D landmark estimation, and dense (3D) facial shape estimation. We show the robustness of the method, as well as its ability to attain high precision, through experiments conducted with “in-the-wild” data in addition to controlled data.

3.1. Experimental Setup

Evaluation metric and datasets

We evaluate performance with the commonly used Normalized Mean Error (NME) for all tasks [9,11,45]. For 2D landmark estimation, the NME of one image is computed by calculating the estimation error for each landmark via ℓ2 norm, then computing the average of those errors, and finally normalizing this average by dividing it by the bounding box size computed as $\sqrt{w_{bbox}\times h_{bbox}}$, where the bounding box width w_bbox and height h_bbox are computed from the labeled landmarks. We report performance on the commonly employed L = 68 landmark points (Fig. 1b) as well as the L = 51 (inner-face) points [25]. When computing NME for 3D landmark estimation, the point-wise error is computed in terms of 3D points, and Z-normalization is applied to all points to resolve the ambiguity along the depth axis. For NME for dense facial shape estimation, the average error is computed from all the points on the dense facial mesh, and normalization is performed by dividing by outer interocular distance [11]. Similarly to previous studies, we use Iterative Closest Point (ICP) prior to computing the dense NME, but only to establish the point correspondence between the ground truth mesh shape and the estimated facial mesh [42,19] (i.e., rigid alignment is not used).

We use three datasets. First, AFLW2000–3D [45]— a widely used dataset [45,9,43,19] that contains 2D and 3D landmark annotations. Second, a Synthesized dataset that we generated using the Basel’09 3DMM [21]. This dataset has two advantages: It enables us to compute exact ground truth for 2D and 3D landmarks, and to run multi-frame experiments, as the images of the same face from different angles can be generated trivially (examples of images for the Synthesized dataset are in Supplementary Material). We use the Basel’09 model, as its facial mesh is used by many previous methods [1,45,6,7] and the ground truth location of the L = 68 landmarks on this mesh are established. Thus, an exact comparison between the estimated and true location of 3D points becomes possible. We synthesize 900 images from 100 subjects in 9 poses as in previous works [19,45]; that is, we apply 9 yaw rotations of, −80, −60, …, 80 degrees, and a pitch rotation randomly selected from −15, 20 and 25 degrees. We also apply a random illumination variation. Finally, we use the BU-4DFE [41] dataset for dense facial shape estimation. BU-4DFE contains 3D facial data collected from 101 subjects, and allows us to evaluate our method on faces of real subjects from various ethnic and racial backgrounds. This is important for our study as the Basel models that we use for fitting are constructed from European participants; therefore, our methods’s ability to generalize to non-European populations must be explicitly tested. Similarly to the Synthesized dataset, we generate 9 images per subject, but also add one of the six basic facial expressions, namely happiness, sadness, anger, surprise, fear and disgust.

Compared methods and implementation of 3DI

To validate different aspects of our method, we compare with five very recent state-of-the-art methods. First, we compare with PRNet [11], which, to our knowledge, attains the best performance on AFLW2000–3D, even in an independent study [43]. Second, we compare with 3DDFA [45]. While 3DFFA was outperformed by some recent studies [11,43,19], it now has an updated code³ that is considerably improved. Third, we compare with one of the most popular landmark estimation methods, 3D-FAN [9]. Fourth, we compare with two robust optimization-based methods that use ℓ₂ regularization, namely 3DMM Edges [1] and ITW [7]. Finally, we compare with a video-based variant of the latter, ITW-V [7].

We implemented our method, 3DI, in MATLAB. We used IPOPT [37] for inequality-constrained optimization, and 3D-FAN [9] for landmark estimation. To learn the maximal landmark detection error (ϵ) as discussed in Section 2.2, we synthesized a large face dataset with the Basel’09 model, and computed the error of 3D-FAN for each landmark. We ignored the outliers by not taking into account the 1% of the images with the highest errors. However, we expanded the error bounds by 15% to account for the difficulties associated with “in-the-wild” images. We resized each image to 100×100, and applied Gaussian smoothing as suggested for GC [34]. We used the Basel’17 3DMM[14], except for the experiments on the Synthesized dataset, where we used Basel’09 for landmark estimation experiments with the aim of providing exact comparison using the common keypoints with other methods (see Datasets above). We applied the coefficient constraints of ±3 standard deviations for the Basel’09 model. For the Basel’17 model, we used a reduced interval of ±1.5 standard deviations as the interval of ±3 generates implausible looking faces with this model (see Supplementary Material). Note that these intervals were determined only through evaluating Basel 3DMMs, and fixed for all experiments. The source code of our method is available on https://github.com/sariyanidi/3DI for research purposes.

3.2. Results

2D and 3D landmark estimation

Our method’s qualitative 2D landmark estimation and dense 3DMM fitting results are shown in Fig. 3. Overall, Fig. 3 demonstrates that our method operates well “in-the-wild”, producing compelling results even in the presence of large illumination or expression variations, or occlusions (more qualitative results are provided in Supplementary Material). This is a remarkable outcome that validates the theoretical appeal of our formulation in practice; to our knowledge, we propose the first method that can generalize to “in-the-wild” data, without requiring a morphable model constructed from uncontrolled images (e.g., [7]) or a deep architecture trained with large amounts of “in-the-wild” data. Fig. 4 shows the 2D and 3D landmark estimation performance of all methods via cumulative error distribution (CED) on the AFLW2000–3D dataset, and Table 1 shows the mean NME. The 2D landmark estimation performance of our method on 51 or 68 landmarks (Fig. 4 and Table 1) is very similar to that of PRNet, which, to our knowledge, is the best-performing method on this dataset. Our method’s error is slightly higher than other methods on 3D landmark estimation, but one must take those results with a pinch of salt, because the annotations of AFLW2000–3D are controversial [11]. 3D landmark annotations on AFLW are obtained from single frames. Such annotations can hardly be called ground truth, as inferring 3D points from 2D data is an ill-posed problem. We next investigate the performance of the same methods on BU-4DFE and the Synthesized dataset, where true ground truth is available.

Fig.3.

Qualitative illustration of our method’s performance on the AFLW2000–3D dataset. Top row: input images; middle row: 2D landmarks estimated by our method; bottom row: dense 3D shape estimated by our method. It is notable that our method can successfully operate in such uncontrolled conditions, even though we use a 3DMM collected from controlled data, namely Basel 2017 [14]

Fig.4.

Cumulative error distribution (CED) of compared methods on the AFLW2000-3D dataset for the tasks of 2D and 3D (sparse) landmark estimation. Performance is reported separately for L=68 and L=51 landmarks

Table 1.

Mean NME of compared methods on the AFLW2000-3D and Synthesized datasets for the tasks of 2D and 3D landmark estimation for L = 51 and L=68 landmarks. Bold and underline indicate best and second best performance, respectively

	AFLW2000-3D dataset				Synthesized dataset
	2D landmarks		3D landmarks		2D landmarks		3D landmarks
	L=51	L=68	L=51	L=68	L=51	L=68	L=51	L=68
PRNet	0.041	0.035	0.048	0.044	0.041	0.038	0.045	0.045
3DDFA	0.049	0.040	0.050	0.046	0.048	0.042	0.048	0.048
3D-FAN	0.041	0.038	0.060	0.053	0.041	0.041	0.050	0.052
ITW	0.047	0.042	0.066	0.060	0.041	0.034	0.048	0.041
ITW-V (multi-frame)	N/A	N/A	N/A	N/A	0.060	0.045	0.043	0.038
3DI Single-frame (our)	0.042	0.038	0.057	0.056	0.025	0.027	0.034	0.036
3DI Multi-frame (our)	N/A	N/A	N/A	N/A	0.026	0.027	0.026	0.032

Fig. 5 shows the 2D and 3D landmark estimation results on the Synthesized dataset. Results for multiframe methods are computed by using 5 randomly selected frames simultaneously; additional results with 3 and 9 frames are reported in Supplementary Material. Our method outperforms all other methods when the performance metric is reliable (i.e., a true ground truth is available). Of note, using our method with multiple frames significantly improves 3D landmark estimation even though it does not improve 2D landmark estimation. This is because 3DMM fitting is an ill-posed problem; even though single-frame estimation is generally capable of finding a good fit for 2D landmarks, the 3D location of the same landmarks is not necessarily as accurate. In particular, the 2D landmark estimation of our method on 51 landmarks is ∼39% better than the next best method. The 3D estimation is ∼21% better than the next best method for single-frame and ∼39% better for multi-frame. Note that the morphable model that we used for fitting in the experiments on the Synthesized dataset (i.e., Basel’09) is also the model that was used to generate the images of the dataset. This may be seen as a possible explanation of our method’s superiority in this experiment. To alleviate this concern, we re-run experiments using our method with the Basel’17 model and results (see Supplementary material) show that our method attains similar results even when we use a different morphable model.

Fig.5.

Cumulative error distribution (CED) of compared methods on the Synthesized dataset for the tasks of 2D and 3D (sparse) landmark estimation. Performance is reported separately for L=68 and L=51 landmarks

Dense shape estimation

Fig. 6 and Fig. 7 show the dense shape estimation performance of the compared methods on the Synthesized and BU-4DFE datasets, respectively. Dense estimation is performed on a facial shape mesh with ∼23,000 points that cover the facial region and ignore the ear, neck etc. Results show that our method outperforms existing methods; in particular, our method’s mean NME is ∼34% (∼21%) lower compared to the next best method on the BU-4DFE (Synthesized) dataset, when we use multiple frames.

Fig.6.

Normalized mean error (NME) of compared methods on the Synthesized dataset for dense face reconstruction, reported in terms of Cumulative Error Distribution (CED) and NME against pose. Numbers in legend indicate mean NME

Fig.7.

Normalized mean error (NME) of compared methods on the BU-4DFE dataset for dense face reconstruction, reported in terms of Cumulative Error Distribution (CED) and NME against pose. Numbers in legend indicate mean NME

Ablation study

We performed an ablation study to show the effect of our formulation’s two critical components, namely the two inequality constraints. Our ablation study is conducted on 2D/3D landmark detection (L=68). When we omit the first constraint, mean NME increases by 17.4% for 2D points and 45% for 3D points on the AFLW2000–3D dataset; and by 16.7% for 2D points and 11.1% for 3D points on the Synthesized dataset. When we omit the second constraint, mean NME increases by 9.5% for 2D points and 12.5% for 3D points on the AFLW2000–3D dataset; and by 19.3% for 2D points and 8.6% for 3D points on the Synthesized dataset. Another component that can be subjected to ablation is GC—it can be replaced by a simpler objective function such as squared pixel-wise difference. However, the latter proved inadequate in uncontrolled conditions with illumination variations and occlusions as was shown in studies of 3DMM fitting [7] or the closely related problem of image alignment [34].

4. Conclusions and Future Work

This paper proposes a new and theoretically compelling formulation to a well-established computer vision problem, namely 3D morphable model (3DMM) fitting. We show that when 3DMM fitting is formulated as an inequality-constrained optimization problem with a robust objective function, the resulting approach performs on par with top-performing deep learning (DL) methods on “in-the-wild” data where ground truth is not exact, and outperforms those methods on more controlled data with exact ground truth. Moreover, this approach enjoys the versatility of standard optimization approaches, as it is capable of working with multiple frames of arbitrary sizes. The results of this paper strongly encourage future research to evaluate the efficiency of existing inequality-constrained minimization algorithms (e.g., the log-barrier method, primal-dual interior-point methods [8]), which, unlike unconstrained methods, remain unexplored in the context of 3DMM fitting and similar problems.