Abstract
Flow of fluids within biological tissues often meets with resistance that causes a rate- and size-dependent material behavior known as poroelasticity. Characterizing poroelasticity can provide insight into a broad range of physiological functions, and is done qualitatively in the clinic by palpation. Indentation has been widely used for characterizing poroelasticity of soft materials, where quantitative interpretation of indentation requires a model of the underlying physics, and such existing models are well established for cases of small strain and modest force relaxation. We showed here that existing models are inadequate for large relaxation, where the force on the indenter at a prescribed depth at long-time scale drops to below half of the initially peak force (i.e., F(0)/F(∞) > 2). We developed an indentation theory for such cases of large relaxation, based on Biot theory and a generalized Hertz contact model. We demonstrated that our proposed theory is suitable for biological tissues (e.g., spleen, kidney, skin and human cirrhosis liver) with both small and large relaxations. The proposed method would be a powerful tool to characterize poroelastic properties of biological materials for various applications such as pathological study and disease diagnosis.
Keywords: Mechanical characterization, porous biomaterials, shear modulus, Poisson ratio, diffusion coefficient
1. Introduction
Many biological tissues show time-dependent, poroelastic properties arising from resistance to the fluid flow by a porous scaffold, which play important roles in their physiological functions [1–4]. Analogous to the Biot theory of soil compaction, the poroelastic properties of biological tissues arise from a combination of the mechanical properties of the scaffold and the transport properties of the fluid within the scaffold [5]. The most typical example of poroelastic tissue is cartilage, where the scaffold is predominantly collagen and charged proteoglycans, and the fluid phase is predominantly water [1], which plays an important role in energy dissipation and nutriment transport [6, 7]. Many other tissues (e.g., liver, cornea, arterial endothelium and the intervertebral disc) exhibit poroelasticity as well [8–11]. Disruption of poroelastic properties is a hallmark of a range of pathologies. For instance, liver fibrosis results in the change of poroelastic properties of liver tissue, where upregulation of perisinusoidal collagen (in the space of Disse) stiffens matrix and decreases blood perfusion and tissue permeability [12]. Similar changes to poroelasticity also occur in renal [13] and pulmonary fibrosis [14], attenuating bio-mass transfer and exacerbating pathology. Therefore, understanding the poroelastic properties (i.e., interplay between scaffold mechanics and fluid permeability) of biological tissues is of great importance for the diagnosis and treatment of these pathologies [15–17].
Palpation is the clinical standard for qualitative mechanical characterization of biological tissues [18]. Inferring quantitative mechanical properties and permeability from palpation requires performing a calibrated indentation through fitting a theoretical poroelastic model with a displacement-controlled load relaxation test or force-controlled creep test [7, 19, 20]. The first theoretical poroelastic solution designed for interpretation of indentation experiments was derived for the biphasic theory by Mak et al. [21], who obtained the solution for stress-relaxation and creep behavior of articular cartilage. More recently, Oyen and co-workers developed a set of a computational algorithm and master curves for interpretation of experiments involving a sphere indenter indented a gel with a linear force ramp [22, 23]. To further simplify the approach, Hu et al. [20, 24] and Lin et al. [25, 26] obtained semi-analytical solutions by finite element method between the initial pressed load and completely relaxed (infinite time) load of rigid indenters in different shapes (i.e., flat circular, rectangular, conical and spherical). The analysis has been successfully used to obtain poroelastic properties of various soft materials including biological tissues [27–30]. However, the theoretical models used in fitting are typically derived by neglecting the liquid transport as induced by deformation over the timescale of the indentation, which may be not applicable when force relaxation is substantial. For example, recent studies have reported negative Poisson ratios in hydrogels [31, 32] and liver tissues [33] when force relaxes to below half of the peak indentation force. These measurements are unreasonable because uniaxial tests reveal positive Poisson ratios for both liver (0.04–0.33 [34]) and PVA gels (0.34–0.5 [35]).
To meet this need for a more accurate theory of poroelastic indentation, it is more reasonable by considering the fluid-flow-induced deformation during the indentation process. We modeled fluid flow during both the indentation and isometric holding in an indentation test by combining Biot theory with Hertz contact theory. Using this improved model, we characterized several poroelastic properties of biological tissues, including shear modulus, Poisson ratio and diffusion coefficient. Our theory approached prior small-relaxation theory asymptotically for small relaxation, showing prospects for characterizing a broad range of biological materials and tissues and also for detecting changes to poroelasticity associated with diseases.
2. Materials and methods
2.1. Large relaxation indentation theory
We developed an indentation theory that included fluid flow during both the indentation and the isometric holding of an indentation test by combining Biot theory with Hertz contact theory. Following the work of Biot and other soft hydrated tissue models [5, 36], we treated the indented tissue as linear, isotropic, and poroelastic, and fully saturated with solvent throughout the indentation process. We considered the asymmetrical, small strain, large displacement problem of indentation in a semi-infinite space (Fig. 1B).
Figure 1. Indentation schematic diagram.
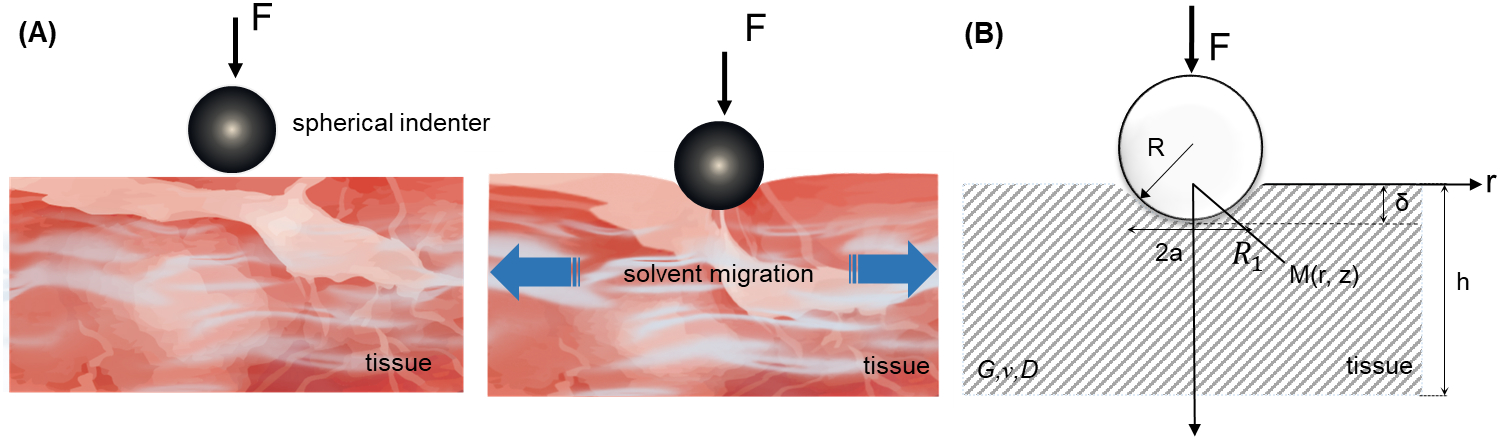
(A) Indentation test of poroelastic properties of biological tissues. (B) Asymmetrical problem of indentation in a semi-infinite space and cylindrical coordinates. The parameters G, v and D are the Poisson’s ratio, shear modulus and diffusion coefficient of the biological tissue, respectively; a is the contact radius between the indenter and the tissue.
2.1.1. Governing equations
Kinematics.
The linearized, axisymmetric, strain fields within the tissue at each time t can be written in terms of a radial displacement field, u(r, z, t), and a vertical displacement field, w(r, z, t), in a cylindrical (r, θ, z) coordinate system:
| (1) |
Where ϵr, ϵθ, and ϵz are the diagonal terms of the strain tensor ϵ; ϵzr is the only non-zero shear term. For a tissue fully saturated with solvent, the volumetric dilatation (volume change per unit volume) e = trace(ϵ) represents the change in solvent volume per unit tissue volume. In the following, unless otherwise noted, all variables are functions of r, z, and t.
Constitutive equations.
A linear poroelastic material consists of a linearly elastic, porous scaffold, permeated by a fluid phase [37]. Most homogenizations of these phases, including the MAK biphasic model of cartilage [36], arise from a treatment analogous to that of Biot theory [5]. For isotopically poroelastic materials, the constitutive model is [37]:
| (2) |
Where σ is the linearized stress tensor; I is the identity tensor; G and v are the shear modulus and Poisson ratio of the scaffold in the absence of fluid, respectively; p is the pore fluid pressure. This constitutive law is purely elastic, but is made to vary with time by considering a pressure-gradient driven volumetric rate of flow, q. According to Darcy’s law:
| (3) |
Where K is constant of proportionality in Darcy’s law between the fluid flux vector (volumetric fluid discharge per unit time and per unit area) and the pressure gradient. K, which is often referred to as the hydraulic permeability [38], has units of m2/(Pa s) and is the ratio of the intrinsic permeability of the tissue and the dynamic viscosity of the solvent.
Equilibrium equations.
For cases such as indentation in which body forces are negligible compared to other forces, and for cases in which inertial terms are small, the stress fields satisfy the equilibrium conditions:
| (4) |
Boundary and initial conditions.
Analogous to the Boussinesq solution for an elastic half-space subjected to a vertical concentrated force [39], traction free boundary conditions were applied to the surface of the tissue outside of the indenter, and stresses approached zero infinitely far from it. For intermediate tissue in a region beneath the indenter, with a radius ρ greater the contact radius of indenter, the applied force F is balanced by the normal stress at each depth z:
| (5) |
The initial displacement fields are u = w = 0 at time t = 0.
2.1.2. Solution
Based on the Boussinesq solution and Hertz contact theory, we deduced the relationship between the time-dependent applied force and the indentation depth by considering poroelasticity during both loading and holding. Substituting Eqs. (1–2) into Eq. (4), we rewrote the equilibrium equations as:
| (6) |
| (7) |
where the axisymmetric Laplace operator is . The problem was solved by separation of variables, with p = f1(t) f2(r, z), so that the general solution of Eqs. (6–7) is given by:
| (8) |
Eq. (8) reveals that the total displacement can be decomposed into the displacements due to fluid transport and the elastic deformation of solid.
The mass conservation of pore fluid can be stated as the continuity equation div q = −∂e/∂t [5], namely:
| (9) |
Due to the independence of the variables, we obtain:
| (10) |
Substituting Eq. (10) into Eq. (3) and observing the separated variable form of p, we obtain:
| (11) |
so that the general solution of Eq. (8) is:
| (12) |
Comparing Eq. (8) and Eq. (12) reveals that f1(t) should have an exponential form:
| (13) |
Where τp is the poroelastic relaxation time-scale, which can be written:
| (14) |
in which a is the radius of the spherical contact and D is the diffusion coefficient [9, 25]. Here, the diffusion coefficient represents the constant of proportionality, in the absence of pressure gradients, of the gradient of the solvent volume fraction within the porous tissue matrix and the flux of solvent per unit time and per unit area through that matrix [40]. Based on the Boussinesq solution, U0 and W0 (displacement duo to elastic deformation) in Eq. (8) are given by [41]:
| (15) |
Where C1 and C2 are constants, . Combining Eq. (15) with the initial conditions and the boundary conditions in Eq. (8), the displacement equation is given by:
| (16) |
We assume that the spherical indenter is rigid, and that the substrate is elastic and semi-infinite. According to the Hertz solution [42, 43] for contact between elastic bodies and combining with Eq. (16), we obtain the relationship between the time-dependent applied force F and the indentation depth δ:
| (17) |
Where , the FHertz(δ, R) is initial force of the elastic basement from the Hertz solution, G is the shear modulus of the scaffold, and v is Poisson’s ratio, and R is the radius of the spherical indenter. This satisfies the initial condition that u = F = 0 at t = 0. Setting t0 as the time needed for the indenter to be pushed from u(t = −t0) = 0 to u(t = 0) = δmax, in which δmax is the maximum displacement, at which the indenter is held, and applying the time coordinate transform, Eq. (17) can be rewritten as:
| (18) |
where A ≈ exp(−t0/τp) is a coefficient that quantifies the effect of solvent diffusion during indentation (−t0 ≤ t ≤ 0) on subsequent force relaxation (t > 0), and FHertz is the force for a displacement δmax predicted for linear elasticity by the Hertz contact model. The coefficient A thus represents a correction factor that accounts for fluid flow during indentation. For fast loading, in which the loading timescale t0 is much smaller the poroelastic timescale τp (that is, the Deborah number t0/τp is very small), A approaches unity. However, the poroelastic material properties (i.e., shear modulus, Poisson ratio and diffusion coefficient) are not affected by the loading speed.
2.2. Sample preparation
Fresh samples of porcine liver, kidney, spleen and skin were obtained from a local abattoir in Xi’an, Shaanxi, China. An apple of the species Malus pumila was obtained from a local farm. All specimens were preserved at 4 °C and tested within a few hours of acquisition. Cirrhotic human liver tissues were obtained a local hospital, and the experiments were performed within 24 hours of resection (Fig. S3). This study was approved by ethic committee of the first affiliated hospital of Xi’an Jiaotong university. Porcine organs, apple, and human tissues were cut into 3 cm × 3 cm rectangular specimens that were 2.5 cm thick. Glisson’s capsule was removed from the liver. All tissues were allowed to swell to equilibrium in 4 °C saline for 3 hours. Porcine skin tissue was cut to 3 cm × 3 cm rectangular specimens that were 0.5 mm thick and allowed to swell to equilibrium in 4 °C colza oil for 5 hours.
2.3. Indentation testing
Indentation by metal spheres of four different diameters (2R = 10 mm, 5 mm, 4 mm and 3 mm) was used to characterize the biological tissues poroelastic properties. The indenter consisted of a stainless steel ball bonded to a hollow stainless steel tube (Fig. S1). Following standard protocols to ensure that the substratum did not affect the indentation [20, 44, 45], we ensured in all cases that the sample thickness h was large enough compared to the radius of the indenter contact area, in which δ is the depth of indentation:
| (19) |
For the spherical indenters of diameter 10 mm, 5 mm, 4 mm and 3 mm, we set δ to 3 mm, 2.5 mm, 2 mm and 1.5 mm, respectively. For porcine skin tissue, we applied δ = 1 mm due to its limited thickness.
Experiments were performed on a Bose ElectroForce 3220 (Bose Corporation, Framingham, MA) using a load sensor with a force resolution of 0.001 N and a displacement resolution of 0.01 μm (Fig. S1). Before performing displacement control tests, the indenter tip was adjusted to a position slightly above the surface, and proceeded with indentation to a fixed depth δ at a speed of 0.5 mm/s. The indenter was held isometrically for a time interval sufficient to enable relaxation. This time interval was based upon the characteristic poroelastic relaxation time τp. This time interval is size-dependent, and scales as τp ≈ a2/D = Rδ/D, in which D is the diffusion constant of the solvent in the tissue. We chosed the data collection time during relaxation based upon the maximum value of Rδ and upon results of initial tests. For liver, spleen, and apple, Rδ=30 mm2, and . For kidney, diffusion was slower and . Rδ was substantially smaller for skin, so that . To ensure adequate data for curve-fitting, the indenter was thus held at the fixed depth δ for 350 s of relaxation for liver and spleen specimens, and for 900 s for the other tissues; this time was substantially longer than needed for the apple tissue. For load control tests, the indenter touched with a preload of approximately 1 μN.
In each of the displacement-controlled relaxation tests, the solvent in the tissues migrated, affecting the force on the indenter both in the rising period during indentation and the relaxation period during the isometric hold (Fig. 1&5A). We repeated indentation tests at least three times at different locations for each of the four spherical indenters and their associated indentation depths.
Figure 5. Displacement and force curves, and comparison of methods.

(A) Force response of a poroelastic tissue to a ramp-and-hold indentation test. The green line represents the indentation process and the red line represents the relaxation process. (B) The loading curve and subsequent relaxation are better fit by the proposed method than by the method of Hu, et al. [20].
2.4. Protocol for extracting poroelastic properties from indentation tests
Through fitting the indentation relaxation curve with the theoretical model, we characterized the poroelastic properties of several biological tissues, specifically the shear modulus, Poisson ratio, and diffusion coefficient. The protocol began with estimating the parameters A and τp by fitting Eq. (18) to an experimentally measured stress relaxation curve using ordinary least squares (Fig. S2). The diffusion coefficient D could then be estimated from τp using Eq. (14). Following this, the Poisson ratio v and shear modulus G were estimated by comparing the short-time and long-time response. At short times, the poroelasticity of tissue cannot be reflected, hence v ≈ 0.5 is adopted when t = 0. However, due to the influence of pressing process on poroelastic relaxation curve, the relaxation force when t = 0 is distinguished from traditional indentation theory as shown in Eq. (20) (noted 1 − A is applied to modify F(0) in Eq. (21)):
| (20) |
| (21) |
At long time-scales, after the fluid within the specimen equilibrates with external fluid, the tissue behaves like a compressible elastic solid and:
| (22) |
The two limits are related as:
| (23) |
Where F(0)/F(∞) is the ratio between the peak force and steady force on the indenter (Fig. 5A & Fig. S2). For biological tissues, the synergy between the relaxation amount F(0)/F(∞) and the correction factor A ensures that the Poisson ratio stays positive when approriate.
3. Results and discussion
3.1. The model fits poroelastic indentation force-displacement curves
The force required to indent a poroelastic material increases with indentation depth, but decreases with solvent flow away from the compressed region. Thereafter, as the indenter is held isometrically, the force needed to hold the indenter at a fixed depth relaxes over time with continued solvent flow (Fig. 1), which can be well predicted by our model (Fig. 2). The three parameters governing the response (i.e., force v.s. time) are the steady applied force, FHertz(δmax, R), which comes from the Hertz solution, and two free fitting parameters, i.e., the poroelastic time-scale, τp, and the fluid flow correction factor, A. To assess the effect of these three parameters, we performed parameter analysis by changing values of each parameter (e.g. FHertz(δmax, R), τp and A) in turn and controlling two parameters invariant (Fig. 2). We observed that FHertz(δmax, R), associated with the elastic properties of the material, influences the peak value of the force-time curve, but not the rate of relaxation or the amplitude (Fig. 2A). Increasing the poroelastic relaxation time-scale, τp, slows the asymptotic approach to steady state (Fig. 2B). The correction factor A ≈ exp(−t0/τp) quantifies the effect of solvent diffusion during indentation. This factor affects both the peak force and the relaxation rate as shown in Fig. 2C. The peak force scales as 1/(1 − A), and therefore increases with increasing A. The degree of relaxation, F(∞)/F(0) = (1 − A), also increases with increasing A. The poroelastic relaxation timescale τp is independent of A; however, for a given indentation ramp time t0 A will increase with decreasing τp because more liquid will flow away during the indentation process.
Figure 2. The force-relaxation curves for indentation of a poroelastic solid.
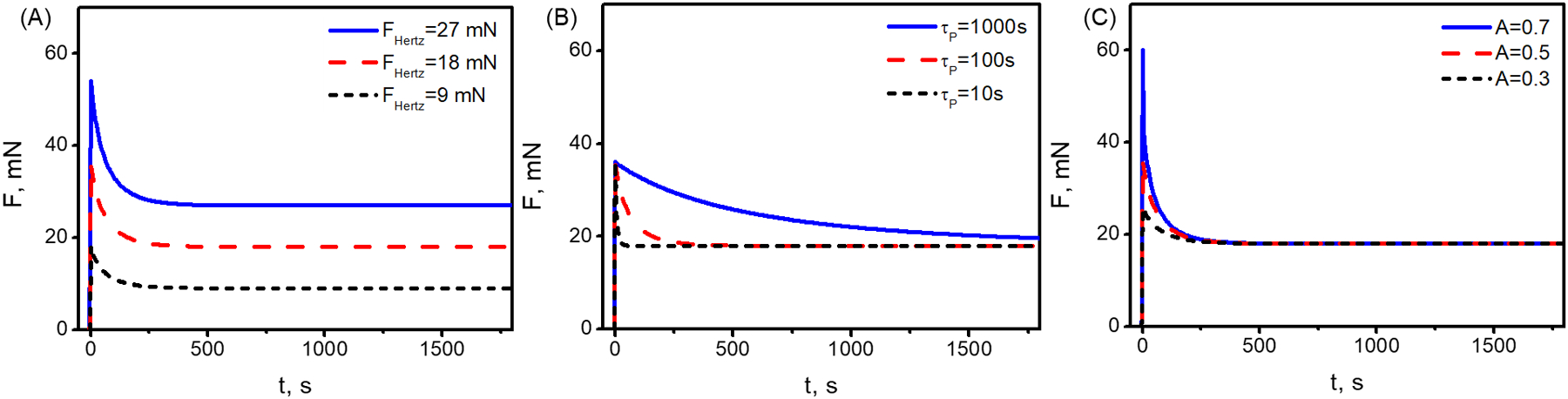
(A) The force required to indent a poroelastic material increases with indentation depth, but decreases as the indenter is held isometrically. The plateau is affected by the elastic properties of the material, represented by FHertz(δmax, R). For all curves, the poroelastic time-scale is τp = 100 s, and the fluid flow correction factor is A = 0.5. (B) The relaxation rate but not the peak or plateau was affected by τp. Here, FHertz(δmax, R) = 18 mN, and A = 0.5. (C) The peak force but not the plateau force or relaxation rate were affected by A. Here, FHertz(δmax, R) = 18 mN and τp = 100 s.
3.2. Poroelastic properties could be extracted from indentation tests
Both viscoelasticity and poroelasticity contribute to force relaxation in most biological tissues, and distinguishing the contributions of these two factors is important. In biological tissues, viscoelasticity typically arises from conformational changes and breakage of transient bonds amongst macromolecules, processes for which the viscoelastic relaxation timescale (τv) is independent of lengthscales [32]. Poroelasticity arises from resistance to fluid flow by a tissue’s porous protein scaffold, so that the poroelastic relaxation timescale (τp = a2/D) increases with increasing lengthscale [31, 46]. To first order, viscoelastic timescales are material properties [47, 48], as is the diffusion constant for specific combinations of solvent and protein structure at a defined temperature, over a broad range of concentrations [49–51]. Both viscoelastic and poroelastic responses can be observed and quantified from the results of indentation tests.As an example, we considered the case of a biomaterial whose viscoelastic and poroelastic properties are unknown. The material was indented by indenters of four different sizes that were pressed to fixed depth and held isometrically. The relaxation of force during this sustained isometric loading were recorded. The key to dissecting the poroelastic and viscoelastic responses is the normalization of these force versus time data (Fig. 4).
Figure 4. Analysis of isometric force versus time curves during indentation of liver tissue with indenters of four different diameters.

(a) Following a ramped indentation (data not shown), the peak force for indentation increased with increasing indenter size. The isometric force subsequently relaxed over time. These results showed that the material is not elastic. (b) The first normalization used is that appropriate for linear viscoelasticity, in which the isometric force curves should converge into one curve when normalized as F/aδ. However, a clear size dependence was evident, indicating that the material was either nonlinear viscoelastic or poroelastic. (c) When time is additionally renormalized as appropriate for poroelasticity, the curves collapse onto a master curve for longer timscales, indicating a transition from some combination of viscoelasticity and poroelasticity to pure poroelasticity. (d) Normalized relaxation function [F(t) − F(∞)]/[F(0) − F(∞)], assuming that the end point of each experiment represents a fully relaxed state, versus renormalized time t/a2.
The un-normalized force versus time curves show the same general trends, with a peak force following indentation decaying to an asymptote over time intervals of 10–300 s (Fig. 4a). The peak force and long-relaxation asymptotes increases with increasing indenter size.
Insight into the underlying physical processes can be found be renormalizing the force and time to account for potential underlying physics. The first model to check is elasticity. Consistent with linear elasticity and the Hertz solution, the peak indentation force in Fig. 4a increased with indentation depth, but the force decay evident in that figure rules out an elastic response for the material. The next model to check is linear viscoelasticity. At the initial peak and at the asymptote, force, displacement, and indenter size should be related by the Hertz solution. When the isometric force is renormalized by 3aδ/4, the Hertz solution predicts that the quantity 3F(0)aδ/4 should be a constant that, for a relatively rigid indenter, equals E(0)/(1 – v(0)2); for infinite time in a linear viscoelastic material, the asymptote should be 3F(∞)aδ/4 = E(∞)/(1 – v(∞)2). However, neither the peaks nor the asymptotes in Fig. 4b meet at a single point, indicating that linear viscoelasticity is not the correct model for the material.
The next model to evaluate is poroelasticity. For this, the renormalization arises from the diffusion timescale, which scales as τp~a2/D. According to Equation (18), renormalizing the time as t/a2 should thus make the curves collapse to a single master curve. The curves do indeed collapse onto a master curve for t/a2 > 10 s/m2 but diverge over shorter times (Fig. 4c). This indicates that the tissues are poroelastic at long times, but exhibit both poroelastic and viscoelastic behavior at shorter times. Therefore, we can decouple the viscoelastic effect through fitting the long-term poroelastic relaxation.
Another way to view this is in the context of a normalized relaxation function, g(τ) = [F(t) − F(∞)]/[F(0) − F(∞)] (Fig. 4d). When plotted against renormalized time t/a2, and when approximating the experimental endpoint as the fully relaxed state of the material, the curves further collapse into a single master curve, once more suggesting that poroelastic effects contribute throughout the relaxation process.
For the liver tissue studied in Figure 4, the viscoelastic time scale is ~10 seconds and the poroelastic time scale is ~100 seconds. This separation of scales is evident in a number of other tissues as well in millimeter scale experiments. In kidney the dominant viscoelastic time scale of 50 s [52] is much faster than the poroelastic timescale of 440 s; in hydrogels the dominant viscoelastic time scale of 100 s [31] is much faster than the poroelastic time scale of 105 s; in PDMS, the dominant viscoelastic timescale of 10 s [44] is much faster than the poroelastic time scale of 104 s. Although most viscoelastic materials exhibit a spectrum of such responses [53, 54] especially when nonlinearity is considered [55–57], the separation of scales for the dominant time constants enables a poroelastic interpretation of data at slower timescales in these materials. Furthermore, remodeling of tissue by cells can alter these viscoelastic response spectra, the timescales for this are typically slow compared to the poroelastic responses [58]; remodeling of cells themselves can occur, especially in response to mechanical force, but these occur over time intervals of 10s of seconds [59–61]. Taken together, these factors enable the application of the present model to the poroelastic characterization of a range of biological tissues.
Through fitting our model to indentation relaxation curves, we characterized the poroelastic properties of several biological tissues and quantified their shear modulus, Poisson ratio, and diffusion coefficient. The protocol for interpreting experimental relaxation curves began with choosing A and τp in Eq. (18) to fit the data using ordinary least squares (Fig. S2). If the peak and steady state values of the force are known with sufficient reliability, this can be achieved directly from Eqs. (22) and (23).
The first tissue studied was porcine liver tissue in normal saline. Based on Eq. (23), the Poisson ratio was obtained as v = 0.39 ± 0.026, which is on the order of published values for porcine liver (v = 0.04 – 0.33) from uniaxial stretching [34]. Based on Eq. (22) and the steady state force F(∞), the shear modulus was estimated as G =0.31 ± 0.070 kPa, which falls into the range of previously reported rheological test results (G = 0.3 − 1 kPa) [12, 62].
Because the time τp = a2/D = Rδmax/D is related to the diffusion coefficient D [63], D could be estimated from the data as well. The diffusion coefficient was obtained, D = (1.6 ± 0.91) × 10−7 m2/s, which is within the reported range for various mammalian liver tissues [64]. We also observed that estimates of Poisson ratio, shear modulus, and diffusion coefficient were relatively insensitive to the size of the spherical indenters, indentation depth (Table S1) and loading speed (Table S2).
3.3. The indentation and isometric portions of the force relaxation curve
We compared our predictions to those of the model of Hu, et al., in two ways, again using the data for porcine liver (Fig. 5B). Our predictions account for fluid flow during both the indentation and isometric relaxation, and, as expected, provide a vastly superior fit of the indentation force versus time curve. Our predictions have a better fit for the overall force versus time trend in the relaxation portion. The model of Hu, et al., has a superior fit of the initial force peak, but then predicts that relaxation occurs quickly. Our model misses the initial peak, suggesting that multiple timescales of poroelasticity and/or viscoelasticity are at work in the porcine liver specimen. Because the poroelastic relaxation model is a linear model, multiple poroelastic timescales can be added through superposition, in much the same way that Maxwell elements are combined in the Generalized Maxwell model [47]. As mentioned above, both viscoelasticity and poroelasticity contribute to force relaxation in most biological tissues, with the viscoelastic relaxation timescale (τv) is independent of lengthscales [32] and the poroelastic relaxation timescale (τp = a2/D) increasing with increasing lengthscale [31, 46]. At the millimeter scale, the poroelastic timescale (~100 s) is longer than viscoelastic time scale (~10 s) for liver tissue. Thus, relaxation in liver under our testing conditions is dominated is viscoelasticity-dominated over the short term and poroelasticity-dominated over the long term. Therefore, we could decouple the viscoelastic effect by fitting only the long-term poroelastic relaxation, with the correction factor A reflecting the effect of solvent diffusion only.
Next, we compared predictions of normalized force () versus the normalized time (τ = Dt/a2) for a material with small relaxation (e.g., PDMS) (Fig. S4). We observed that both models are able to predict the relaxation with the normalized force asymptoting to zero over time, demonstrating that our proposed theory is applicable for the full range of small-to-large relaxation
3.4. Validation against and application to a broad range of biological tissues
To extend the applicability of the proposed theory for biological tissues, we characterized several poroelastic properties of biological tissues (e.g., spleen, kidney, skin and human cirrhosis liver), including shear modulus, Poisson ratio and diffusion coefficient (Fig. 6 and Table S3). From the perspective of experimental analysis, the fundamental shortcoming of the model of Hu, et al., is that it predicts negative Poisson ratios for tissues that undergo large relaxation (Fig. 6A). These include the porcine liver described above, and cirrhotic human liver (F(0)/F(∞) > ~3.6), porcine kidney (F(0)/F(∞) > ~1.7), porcine spleen (F(0)/F(∞) > ~1.6), and porcine skin (F(0)/F(∞) > ~3.9).
Figure 6. The proposed poroelastic indentation theory improves upon prior models by correctly predicting positive Poisson ratios.
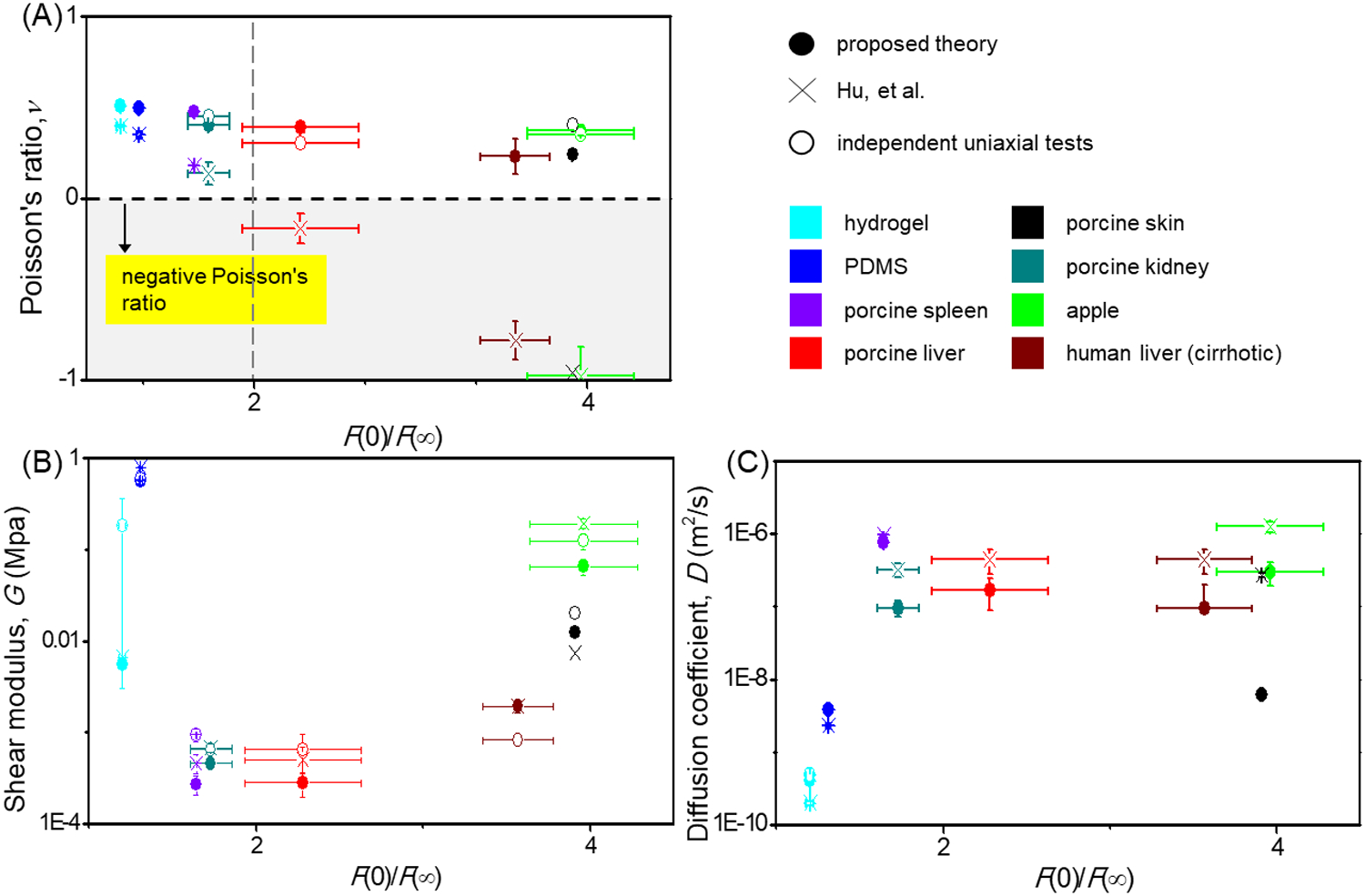
(A) Poisson’s ratio v, (B) shear modulus G and (C) Diffusivity D predicted for indentation tests using the proposed theory and the model of Hu, et al. Data shown are from the following sources: (Poisson’s ratio ν: liver [34], kidney [72], apple [78], skin [79], hydrogel [35]; shear modulus, G: PDMS [80], liver [62], kidney [65], spleen [81], skin [82], apple [78], human liver [83]; diffusion constant: hydrogel [73]).
Our method outperforms that of Hu, et al., in that it predicts positive Poisson ratios that are consistent with results obtained from tensile and compressive tests in literature (Fig. 6A). We observe that the deviation from experimental data of predictions using the method of Hu, et al., increases with the degree of relaxation, F(0)/F(∞). Predictions of Poisson ratio using that method become negative for large relaxation, F(0)/F(∞) > 2, despite experimental data from other methods to the contrary. Predictions obtained using our method are consistent with those obtained using other methods for tissues with both large and small relaxations.
The diffusivity D and shear modulus G estimated from experimental data using our proposed theory are relaxation-independent. These estimates agree with those obtained using the method of Hu, et al., and are likewise on the order of other experimental results (Fig. 6B&C). For instance, for porcine kidney, our estimate of G = 0.46 ± 0.052 kPa is on the order of that using the method of Hu, et al. (G = 0.68 ± 0.080 kPa), and neither estimate has a statistically significant difference from previously published (G = 0.32 ± 0.41 kPa) [65]. Combining the Biot theory of poroelastic medium, the Darcy’s law and continue equation, the relationship between diffusion coefficient and permeability can be written as [28]: D = (2G (1 − v))/((1 − 2v)) K, where G and v are the shear modulus and the Poisson ratio of the drained network respectively, K is hydraulic permeability, and D is the poroelastic diffusion coefficient. According to this relationship, the hydraulic permeability of biological tissues can be obtained from diffusion coefficient. Our estimates of transport properties result in slightly lower hydraulic permeabilities than found elsewhere in the literature, as is expected due to the accounting for fluid flow during indentation: models that do not account for this must force predictions of fluid flow “catch up” to with the fluid flow that is ignored during indentation, and must do so by predicting a greater hydraulic permeability. The hydraulic permeability of porcine liver tissue estimated using the proposed theory 1.8 m2/GPa s, whereas those reported by others range from 8.6–110 m2/GPa s [66]. The hydraulic permeability of a hydrogel estimated using the proposed theory is 0.12 × 10−5 m2/GPa s, whereas that reported using a swelling test is 5.1±0.9 × 10−5 m2/GPa s [32]. Our results show that, using the proposed method, we can characterize a broad range of biological tissues and biomaterials with shear modulus ranging from ~0.1 kPa for brain [67] to ~GPa of bone [68, 69].
To demonstrate potential diagnostic value for the proposed method, we performed an indentation test and cirrhotic human liver tissues (Fig. S3). Cirrhosis, a stage in the progression of liver fibrosis, is characterized by extracellular matrix protein (e.g., collagen) accumulation in Disse gap’s (Fig. 3B), which stiffens the tissue [12, 70]. Cirrhosis further attenuates transport in liver tissue as resistance and pressure in portal tracts increases, along with that in associated collateral circulation through shunts [71]. Our estimate for the Poisson ratio of that tissue is v = 0.23 ± 0.099, which is significantly different from the values associated with healthy liver tissues of v = 0.4 – 0.5 [72], suggesting a possible metric for diagnosis. These indentations also show elevated shear modulus of G = 0.83 ± 0.032 kPa, compared to that of healthy human liver tissue with a shear modulus of 0.3 kPa [62]. The theory of Hu, et al., provides a higher estimate of shear modulus based upon our measurements, with G = 1.9 ± 0.32 kPa. The diffusion coefficient we obtained is D = 0.94 × 10−7 m2/s, on the same order of magnitude as the estimate using the theory of Hu, et al., D = 4.4 × 10−7 m2/s.
Figure 3. SEM images of biological tissues (porcine liver, cirrhotic human liver, porcine spleen and porcine kidney) show obvious porosity of the microstructure of different biological tissues.

(A) Dehydrated, fractured liver specimens showed the polyhedral, multifaceted hepatocytes which form one-cell-thick muralia separated by sinusoids. (B) Cirrhotic human liver showed fibrosis between hepatocytes. (C) Porcine spleen and (D) Porcine kidney showed similar porosity. Scale bars: 10 μm. (HITACHI TM-1000 scanning electron microscope).
For materials with smaller relaxation, the predictions of both approaches are similar. For PDMS, we obtained G = 5.54 ± 0.183 kPa and D = 4.0 × 10−10 m2/s, while the method of Hu, et al., gave G = 6.70 ± 0.050 kPa and D = 1.97 × 10−10 m2/s. The diffusion constant is is comparable to the values reported in the literature [73].
4. Conclusions
By modifying a spherical indentation model to characterize the poroelastic properties of biological tissues, we were able to improve estimation of poroelastic material properties in three ways. The first is the elimination of internal inconsistencies in the interpretive model that lead to predictions of negative Poisson ratios when these are not expected. We note that, despite this internal inconsistency, previous models are capable of fitting and replicating force relaxation data. This is a well-known problem in viscoelastic fitting, and has been explored extensively in the context of other models. A commonly cited example of this is Fung’s quasilinear viscoelastic (QLV) theory, which can often replicate relaxation data without having the capacity to predict the response of the material without being able to predict material behavior under different loading conditions [74–76]. However, these inadequacies of underlying viscoelastic models are well known to introduce substantial error into extrapolations of fittings to new loading scenarios [55, 74, 75, 77]. In the context of the current model, the prediction of negative Poisson ratios for many tissues will lead to such error.
Second, in addition to being free of unfortunate internal inconsistencies such as a negative Poisson ratio, our proposed theory can predict the entire indentation and isometric force relaxation experiment. This provides a vastly superior fit of the indentation force versus time curve, as was shown in Figure 4B.
Finally, we also emphasize that, although prior theories can handle the limiting case of smallscale relaxation (Figure S4), it cannot handle large scale relaxation without incorrectly predicting a negative Poisson ration. The modifications in our proposed theory are required to accommodate large relaxation; we validated this for .
Supplementary Material
Acknowledgement
This work was financially supported by the National Natural Science Foundation of China (11522219, 11532009), by the New Faculty Foundation of NUAA (1001-YAH19016), by the National Science Foundation through the Science and Technology Center for Engineering Mechanobiology (CMMI 1548571), and by the NIH through grant U01EB016422.
References
- 1.Mow VC, Holmes MH, and Lai WM, Fluid transport and mechanical properties of articular cartilage: a review. Journal of Biomechanics, 1984. 17(5): p. 377–394. [DOI] [PubMed] [Google Scholar]
- 2.Simon BR, Multiphase Poroelastic Finite Element Models for Soft Tissue Structures. Applied Mechanics Reviews, 1992. 45(6): p. 191–218. [Google Scholar]
- 3.Cowin SC, Bone poroelasticity. Journal of Biomechanics, 1999. 32(3): p. 217–238. [DOI] [PubMed] [Google Scholar]
- 4.Mow VC and Hayes WC, Basic orthopaedic biomechanics. 1991: Raven Pr. [Google Scholar]
- 5.Biot MA, General Theory of Three‐Dimensional Consolidation. Journal of Applied Physics, 1941. 12(2): p. 155–164. [Google Scholar]
- 6.Nia HT, et al. , Poroelasticity of cartilage at the nanoscale. Biophys J, 2011. 101(9): p. 2304–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mow VC, et al. , Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. Journal of Biomechanical Engineering, 1980. 102(1): p. 73. [DOI] [PubMed] [Google Scholar]
- 8.Malandrino A, et al. , Poroelastic modeling of the intervertebral disc: A path toward integrated studies of tissue biophysics and organ degeneration. MRS Bulletin, 2015. 40(4): p. 324–332. [Google Scholar]
- 9.Chan EP, et al. , Spherical indentation testing of poroelastic relaxations in thin hydrogel layers. Soft Matter, 2012. 8(5): p. 1492–1498. [Google Scholar]
- 10.Ricken T, Dahmen U, and Dirsch O, A biphasic model for sinusoidal liver perfusion remodeling after outflow obstruction. Biomech Model Mechanobiol, 2010. 9(4): p. 435–50. [DOI] [PubMed] [Google Scholar]
- 11.Louf JF, et al. , Universal poroelastic mechanism for hydraulic signals in biomimetic and natural branches. Proceedings of the National Academy of Sciences of the United States of America, 2017. 114(42): p. 11034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wells RG, Tissue mechanics and fibrosis. Biochim Biophys Acta, 2013. 1832(7): p. 884–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Youhua L, Renal fibrosis: new insights into the pathogenesis and therapeutics. Kidney International, 2006. 69(2): p. 213–217. [DOI] [PubMed] [Google Scholar]
- 14.Strieter RM and Mehrad B, New Mechanisms of Pulmonary Fibrosis. Chest, 2009. 136(5): p. 1364–1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Levental KR, et al. , Matrix Crosslinking Forces Tumor Progression by Enhancing Integrin signaling. Cell, 2009. 139(5): p. 891–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Frantz C, Stewart KM, and Weaver VM, The extracellular matrix at a glance. Journal of Cell Science, 2010. 123(24): p. 4195–4200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Butcher DT, Alliston T, and Weaver VM, A tense situation: forcing tumour progression. Nature Reviews Cancer, 2009. 9(2): p. 108–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ezzat S, ., et al. , Thyroid incidentalomas. Prevalence by palpation and ultrasonography. Archives of Internal Medicine, 1994. 154(16): p. 1838–1840. [DOI] [PubMed] [Google Scholar]
- 19.Lin WC, et al. , Contact measurement of internal fluid flow within poly(n-isopropylacrylamide) gels. J Chem Phys, 2007. 127(9): p. 094906. [DOI] [PubMed] [Google Scholar]
- 20.Hu Y, et al. , Using indentation to characterize the poroelasticity of gels. Applied Physics Letters, 2010. 96(12): p. 121904. [Google Scholar]
- 21.Mak AF, Lai WM, and Mow VC, Biphasic indentation of articular cartilage--I. Theoretical analysis. Journal of Biomechanics, 1987. 20(7): p. 703–714. [DOI] [PubMed] [Google Scholar]
- 22.Oyen ML, Poroelastic nanoindentation responses of hydrated bone. Journal of Materials Research, 2011. 23(05): p. 1307–1314. [Google Scholar]
- 23.Oyen ML, Nanoindentation of Biological and Biomimetic Materials. Experimental Techniques, 2013. 37(1): p. 73–87. [Google Scholar]
- 24.Hu Y, et al. , Indentation of polydimethylsiloxane submerged in organic solvents. Journal of Materials Research, 2011. 26(6): p. 785–795. [Google Scholar]
- 25.LIN, et al. , Load relaxation of a flat rigid circular indenter on a gel half space. Journal of Non-Crystalline Solids, 2006. 352(38): p. 4034–4040. [Google Scholar]
- 26.Hui CY, et al. , A contact mechanics method for characterizing the elastic properties and permeability of gels. Journal of Polymer Science Part B Polymer Physics, 2010. 44(2): p. 359–370. [Google Scholar]
- 27.Hu Y, et al. , Indentation: A simple, nondestructive method for characterizing the mechanical and transport properties of pH-sensitive hydrogels. Journal of Materials Research, 2011. 27(01): p. 152–160. [Google Scholar]
- 28.Moeendarbary E, et al. , The cytoplasm of living cells behaves as a poroelastic material. Nat Mater, 2013. 12(3): p. 253–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oyen ML, Nanoindentation of hydrated materials and tissues. Current Opinion in Solid State & Materials Science, 2015. 19(6): p. 317–323. [Google Scholar]
- 30.Mauck RL, Hung CT, and Ateshian GA, Modeling of Neutral Solute Transport in a Dynamically Loaded Porous Permeable Gel: Implications for Articular Cartilage Biosynthesis and Tissue Engineering. J Biomech Eng, 2003. 125(5): p. 602–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang Q-M, et al. , Separating viscoelasticity and poroelasticity of gels with different length and time scales. Acta Mechanica Sinica, 2014. 30(1): p. 20–27. [Google Scholar]
- 32.Strange DGT, et al. , Separating poroviscoelastic deformation mechanisms in hydrogels. Applied Physics Letters, 2013. 102(3): p. 031913. [Google Scholar]
- 33.Ahn B and Kim J, Measurement and characterization of soft tissue behavior with surface deformation and force response under large deformations. Medical Image Analysis, 2010. 14(2): p. 138–148. [DOI] [PubMed] [Google Scholar]
- 34.Chen X, et al. Identification of physical properties of swine liver for surgical simulation using a dynamic deformation model. in Ieee/sice International Symposium on System Integration. 2011. [Google Scholar]
- 35.Urayama K, Takigawa T, and Masuda T, Poisson’s ratio of poly(vinyl alcohol) gels. Macromolecules, 1993. 26(12): p. 3092–3096. [Google Scholar]
- 36.Mow VC, et al. , Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. Journal of Biomechanical Engineering, 1980. 102(1): p. 73–84. [DOI] [PubMed] [Google Scholar]
- 37.Rudnicki JW, Linear Poroelasticity. Handbook of Materials Behavior Models, 2001: p. 1118–1125. [Google Scholar]
- 38.Childs E, The measurement of the hydraulic permeability of saturated soil in situ I. Principles of a proposed method. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1952. 215(1123): p. 525–535. [Google Scholar]
- 39.Green AE and Zerna W, Theoretical elasticity. 1992: Courier Corporation. [Google Scholar]
- 40.Detournay E, Comprehensive rock engineering: principles, practice and projects. Fundamentals of poroelasticity, 1993. 2: p. 113–171. [Google Scholar]
- 41.Sneddon IN, The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. International Journal of Engineering Science, 1965. 3(1): p. 47–57. [Google Scholar]
- 42.Hertz H, Über die berührung fester elastischer Körper (On the contact of rigid elastic solids). In: Miscellaneous Papers Jones and Schott, Editors, J. reine und angewandte Mathematik 92, Macmillan, London: (1896), 1896: p. 156. [Google Scholar]
- 43.Hertz HR, Ueber die Beruehrung elastischer Koerper (On Contact Between Elastic Bodies) in Gesammelte Werke (Collected Works), 1882. 1(Leipzig, Germany, 1895). [Google Scholar]
- 44.Hu Y, et al. , Indentation of polydimethylsiloxane submerged in organic solvents. Journal of Materials Research, 2011. 26(06): p. 785–795. [Google Scholar]
- 45.Zhu X, et al. , Investigation of fullerenol-induced changes in poroelasticity of human hepatocellular carcinoma by AFM-based creep tests. Biomechanics & Modeling in Mechanobiology, 2017(1): p. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hu Y and Suo Z, Viscoelasticity and poroelasticity in elastomeric gels. Acta Mechanica Solida Sinica, 2012. 25(5): p. 441–458. [Google Scholar]
- 47.Bird RB, Armstrong RC, and Hassager O, Dynamics of polymeric liquids. Vol. 1: Fluid mechanics. 1987. [Google Scholar]
- 48.Rowe RA, et al. , Stable fitting of noisy stress relaxation data. Mechanics of Soft Materials, 2019. 1(1): p. 9. [Google Scholar]
- 49.Elson EL and Magde D, Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers: Original Research on Biomolecules, 1974. 13(1): p. 1–27. [DOI] [PubMed] [Google Scholar]
- 50.Magde D, Elson EL, and Webb WW, Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers: Original Research on Biomolecules, 1974. 13(1): p. 29–61. [DOI] [PubMed] [Google Scholar]
- 51.Koppel D, et al. , Dynamics of fluorescence marker concentration as a probe of mobility. Biophysical Journal, 1976. 16(11): p. 1315–1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mattice JM, et al. , Spherical indentation load-relaxation of soft biological tissues. Journal of Materials Research, 2011. 21(08): p. 2003–2010. [Google Scholar]
- 53.Xu B, Li H, and Zhang Y, Understanding the viscoelastic behavior of collagen matrices through relaxation time distribution spectrum. Biomatter, 2013. 3(3): p. e24651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Babaei B, et al. , Efficient and optimized identification of generalized Maxwell viscoelastic relaxation spectra. Journal of the mechanical behavior of biomedical materials, 2016. 55: p. 32–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Babaei B, et al. , Discrete quasi-linear viscoelastic damping analysis of connective tissues, and the biomechanics of stretching. Journal of the mechanical behavior of biomedical materials, 2017. 69: p. 193–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Provenzano P, et al. , Application of nonlinear viscoelastic models to describe ligament behavior. Biomechanics and modeling in mechanobiology, 2002. 1(1): p. 45–57. [DOI] [PubMed] [Google Scholar]
- 57.Fung Y. c., Biomechanics: mechanical properties of living tissues. 2013: Springer Science & Business Media. [Google Scholar]
- 58.Babaei B, et al. , Remodeling by fibroblasts alters the rate-dependent mechanical properties of collagen. Acta biomaterialia, 2016. 37: p. 28–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Nekouzadeh A, et al. , Stretch-activated force shedding, force recovery, and cytoskeletal remodeling in contractile fibroblasts. Journal of biomechanics, 2008. 41(14): p. 2964–2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Krishnan R, et al. , Reinforcement versus fluidization in cytoskeletal mechanoresponsiveness. PloS one, 2009. 4(5): p. e5486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lee S-L, et al. , Physically-induced cytoskeleton remodeling of cells in three-dimensional culture. PloS one, 2012. 7(12): p. e45512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Marchesseau S, et al. , Fast porous visco-hyperelastic soft tissue model for surgery simulation: application to liver surgery. Prog Biophys Mol Biol, 2010. 103(2–3): p. 185–96. [DOI] [PubMed] [Google Scholar]
- 63.Detournay E, Cheng, Fundamentals of poroelasticity. Comprehensive Rock Engineering: Principles, Practice and Projects. 2. [Google Scholar]
- 64.Stock RJ, Cilento EV, and Mccuskey RS, A quantitative study of fluorescein isothiocyanate-dextran transport in the microcirculation of the isolated perfused rat liver. Hepatology, 2010. 9(1): p. 75–82. [DOI] [PubMed] [Google Scholar]
- 65.Umale S, et al. , Experimental mechanical characterization of abdominal organs: liver, kidney & spleen. J Mech Behav Biomed Mater, 2013. 17: p. 22–33. [DOI] [PubMed] [Google Scholar]
- 66.Kerdok A, Characterizing the Nonlinear Mechanical Response of Liver to Surgical Manipulation. 2006.
- 67.Bayly PV, Clayton EH, and Genin GM, Quantitative imaging methods for the development and validation of brain biomechanics models. Annual review of biomedical engineering, 2012. 14: p. 369–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hinz and Boris, Matrix mechanics and regulation of the fibroblast phenotype. Periodontology. 63(1): p. 14–28. [DOI] [PubMed] [Google Scholar]
- 69.Osterhoff G, et al. , Bone mechanical properties and changes with osteoporosis. Injury, 2016. 47: p. S11–S20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Schuppan D and Afdhal NH, Liver Cirrhosis. Lancet, 2008. 371(9615): p. 838–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Malay S and Rameshbabu CS, Collateral pathways in portal hypertension. Journal of Clinical & Experimental Hepatology, 2012. 2(4): p. 338–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hostettler A, et al. , Bulk Modulus and Volume Variation Measurement of the Liver and Kidneys in vivo using Abdominal Kinetics during free Breathing. Computer Methods & Programs in Biomedicine, 2010. 99(2): p. 149–157. [DOI] [PubMed] [Google Scholar]
- 73.Ju H, et al. , Characterization of sodium chloride and water transport in crosslinked poly(ethylene oxide) hydrogels. Journal of Membrane Science, 2010. 358(1): p. 131–141. [Google Scholar]
- 74.Lakes R and Vanderby R, Interrelation of creep and relaxation: a modeling approach for ligaments. 1999. [DOI] [PubMed]
- 75.Provenzano P, Lakes R, and Keenan T, Nonlinear ligament viscoelasticity. Annals of biomedical engineering, 2001. 29(10): p. 908–914. [DOI] [PubMed] [Google Scholar]
- 76.Babaei B, et al. , A discrete spectral analysis for determining quasi-linear viscoelastic properties of biological materials. Journal of The Royal Society Interface, 2015. 12(113): p. 20150707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Babaei B, et al. , Energy dissipation in quasi-linear viscoelastic tissues, cells, and extracellular matrix. Journal of the mechanical behavior of biomedical materials, 2018. 84: p. 198–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Dintwa E, et al. , Finite element analysis of the dynamic collision of apple fruit. Postharvest Biology & Technology, 2008. 49(2): p. 260–276. [Google Scholar]
- 79.Choi AP and Zheng YP, Estimation of Young’s modulus and Poisson’s ratio of soft tissue from indentation using two different-sized indentors: finite element analysis of the finite deformation effect. Medical & Biological Engineering & Computing, 2005. 43(2): p. 258–64. [DOI] [PubMed] [Google Scholar]
- 80.Xiang H, et al. , Development of a micro-indentation device for measuring the mechanical properties of soft materials. Theoretical & Applied Mechanics Letters, 2013. 3(5): p. 054004. [Google Scholar]
- 81.Nicolle S, Noguer L, and Palierne JF, Shear mechanical properties of the spleen: experiment and analytical modelling. J Mech Behav Biomed Mater, 2012. 9(3): p. 130–136. [DOI] [PubMed] [Google Scholar]
- 82.Kirkpatrick SJ, Duncan DD, and Fang L, Low-frequency surface wave propagation and the viscoelastic behavior of porcine skin. Journal of Biomedical Optics, 2004. 5474(9): p. 1311–1319. [DOI] [PubMed] [Google Scholar]
- 83.Palmeri ML, et al. , Quantifying hepatic shear modulus in vivo using acoustic radiation force. Ultrasound in Medicine & Biology, 2008. 34(4): p. 546–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


