Data mining in Raman imaging in a cellular biological system

Graphical abstract

Highlights

• •Working flow of data mining in Raman imaging of cell system described.
• •Pre-processing, pattern recognition and validation discussed.
• •Machine learning methods applied at each step discussed.
• •Single-cell visualization, cell type classification and quantification applications.

Abstract

The distribution and dynamics of biomolecules in the cell is of critical interest in biological research. Raman imaging techniques have expanded our knowledge of cellular biological systems significantly. The technological developments that have led to the optimization of Raman instrumentation have helped to improve the speed of the measurement and the sensitivity. As well as instrumental developments, data mining plays a significant role in revealing the complicated chemical information contained within the spectral data. A number of data mining methods have been applied to extract the spectral information and translate them into biological information. Single-cell visualization, cell classification and biomolecular/drug quantification have all been achieved by the application of data mining to Raman imaging data. Herein we summarize the framework for Raman imaging data analysis, which involves preprocessing, pattern recognition and validation. There are multiple methods developed for each stage of analysis. The characteristics of these methods are described in relation to their application in Raman imaging of the cell. Furthermore, we summarize the software that can facilitate the implementation of these methods. Through its careful selection and application, data mining can act as an essential tool in the exploration of information-rich Raman spectral data.

1. Introduction

Understanding the mechanics of cellular systems is essential to elucidate the inner workings of a living system. Areas of interest include the transcriptomic information of the cell [1], [2], [3], [4], the pharmacology of medicinal therapeutics [5], [6], [7], [8], the expansion of tumor cells [9], [10], [11], [12], [13], [14], and the structure of the cell [15], [16], [17], [18], [19], [20]. Raman spectroscopy can serve as a non-destructive imaging tool for biomolecules by accessing the vibrational spectra of its molecular interior. Since Raman imaging is label-free, the native cellular function is not affected, and no potentially toxic materials are introduced into the living system of interest. This is in contrast to fluorescence imaging, where fluorescent labels are widely used for the study of living cells and tissues. Also, it captures the chemical information of the cell as a whole rather than simply probing the region of the cell where the fluorescence label is situated. Furthermore, it might not be possible to label the region of the cell of interest. Raman spectroscopy is an excellent technique for biomolecular analysis since it has rich information of biomolecular specificity. Generally, it is common to observe characteristic biomolecular peaks in the Raman region between 200 and 3,000 cm⁻¹ (wavenumbers). More specifically, the vibrational modes of proteins lead to the Raman peaks between 1,500 and 1,700 cm⁻¹. Materials in the nucleus have Raman peaks at 980, 1,080, and 1,240 cm⁻¹. The symmetric stretching of –CH, –NH, and –OH in lipids and proteins produce the Raman band at 2,700–3,500 cm⁻¹, known as the fingerprint region [21]. These characteristic bands allow Raman imaging to yield a wealth of information about the biomolecules present [21], [22], [23], [24], [25], [26] making it a compelling alternative to fluorescence.

However, the Raman bands of these biomolecules are generally overlapped with each other and with the signal that results from the biofluid. Thus, the information-rich Raman imaging dataset is comprised of many covariate features of multiple biomolecules and other materials in the cellular system. Furthermore, a dynamic living system is a spatial and temporal structure rather than simply a group of randomly distributed biomolecules, which adds to the inherent heterogeneity of the cellular system. The heterogeneity and the abundance/variety of biomolecules present results in highly complex data.

Data mining techniques are used in Raman imaging to uncover the patterns in the Raman imaging dataset that would, otherwise, go undetected [27]. When data mining is included as an analytical tool, the most popular applications of Raman imaging of the cellular system include the visualization of the cell at the biomolecular level [4], [21], [26], [28], the classification of different types of cells [2], [11], [29], [30] and the quantification of the biomolecules/drugs in the cell [5], [6], [16], [31]. There are three main stages of data mining involved in Raman imaging for cellular systems, namely pre-processing, pattern recognition and validation. There is a wide variety of methods available for each stage. Note that we only discuss data analysis methods for spontaneous Raman spectral data. This is because there are significant differences between the data analysis procedure for spontaneous Raman spectroscopy and other Raman spectroscopy methods, such as signal enhancing approaches (resonance Raman scattering and surface-enhanced Raman scattering) and non-linear Raman imaging (coherent anti-Stokes Raman scattering and stimulated Raman scattering).

This review paper summarizes the various data mining methods particular to Raman imaging data analysis. As well as describing these methods, we also introduce the characteristics of each method and the software available for their implementation. The first step in the data analysis workflow is the pre-processing of the data, which results in “clean spectra” that are ready for further analysis. Following pre-processing, the critical stage of data mining is pattern recognition. This is based on machine learning methods that employ statistical strategies to extract the rich chemical/biochemical information hidden within the complex Raman spectra.

Machine learning methods allow for successful pattern recognition in Raman imaging datasets of the cellular system. Those methods can be supervised or unsupervised depending on whether there is a training set with known information. One of the most popular unsupervised methods is principal component analysis (PCA) [32] and a common supervised method is partial least squares (PLS) [33] but there are many more machine learning methods in both categories. Validating the results based on machine learning methods is the last step in the workflow but it is far from the least important, because the machine learning analysis might provide an over-optimistic result. Multiple validation methods are introduced in this review paper. As well as data mining, we also introduce the application of machine learning in sample size planning (sampling), which estimates the minimal number of measurements for cell characterization or quantification. Sampling can make Raman measurements much more efficient since large numbers of Raman measurements of a cellular sample are required.

2. Data mining in Raman imaging of the biological cellular system

2.1. Basic terms

The acquisition of high volumes of data can lead to a veritable 'Data Tsunami' in numerous disciplines such as biology, chemistry, and medical science, etc. The identification of common elements within these vast datasets is known as pattern recognition, especially when they are partly hidden in a large dataset [34]. Data mining is a broad term which describes the process of extracting patterns and useful information from 'big data' using statistics [35]. Machine learning, on the other hand, is a term which describes the use of algorithms to learn from data and make predictions [36]. They are two sides of the same coin since data mining informs the machine learning algorithm and machine learning allows for improved data mining. Multivariate analysis is defined as the analysis of data where each sample has numerous corresponding variables [37]. Generally, multivariate analysis includes three different types of method:

• (1)explorative methods, including principal component analysis (PCA) [32], independent component analysis (ICA) [38], and vertex component analysis (VCA) [39];
• (2)classification methods, both unsupervised cluster methods (hierarchical cluster analysis (HCA) and k-means) [40] and supervised methods, e.g. linear discriminant analysis (LDA) [41];
• (3)quantification methods such as partial least squares (PLS) [33], multivariate curve resolution (MCR) [42], etc.

Machine learning includes multivariate analysis and some other statistical methods, and it can be classified into two types, supervised and unsupervised machine learning. Supervised/unsupervised signifies whether or not the data is associated with a sample set, known as a training set, of known values. The unsupervised machine learning methods (no training set) include all the explorative methods (e.g. PCA) and all the cluster methods (e.g. HCA); the supervised machine learning methods include supervised classification methods, such as LDA, support vector machine (SVM) [43], artificial neural network (ANN) [44], k-nearest neighbor (KNN) [45], t-distributed stochastic neighbor embedding (t-SNE) [46] and all the quantification methods. Note that while MCR is generally classified as a supervised method, it can be performed in an unsupervised capacity, without using concentration/spectral constraints. In this review, pattern recognition is discussed in reference to cell characterization and quantification using machine learning methods.

2.2. Workflow

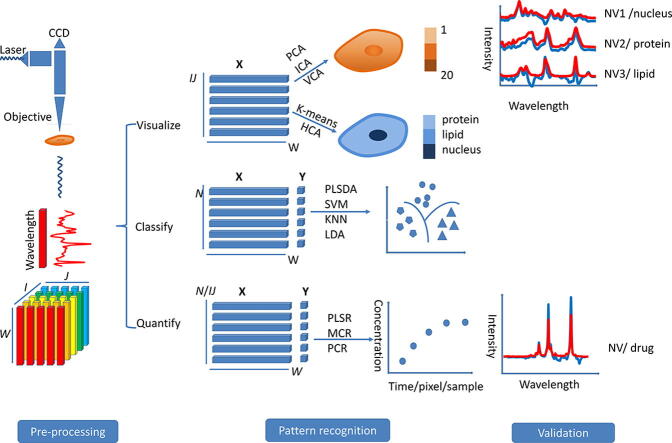
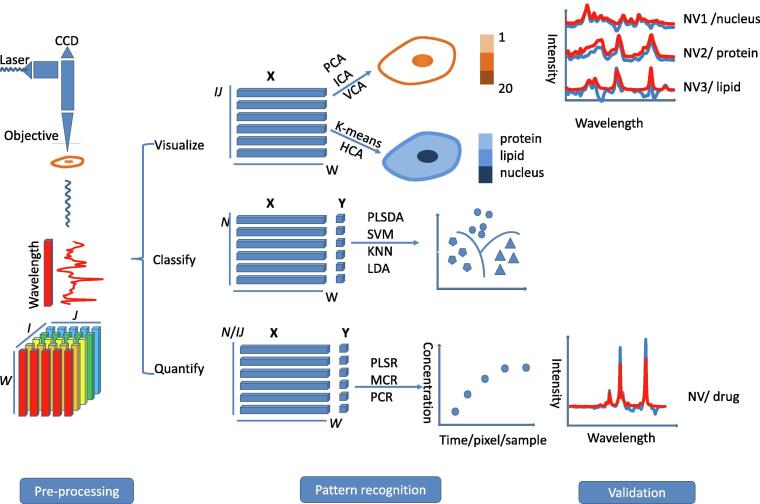
In order to analyze the spectral data successfully a particular protocol or workflow should be followed. First, an understanding of how the data is structured is essential. A 3-D dataset of a cell sample, which includes a geographic dimension (I and J), and a Raman spectral dimension (W) can be obtained from a Raman imaging measurement (Fig. 1). The I and J values represent the number of pixels in a Raman imaging area, and W is the number of wavenumbers in the dataset. There are three ways to unfold the 3-D dataset depending on the goal of the analysis:

• 1.If cell visualization is desired, the pixels along both the I- and J-axes are unfolded onto a single axis so that all pixels are arranged back-to-back. The unfolded matrix is sized IJ and W.
• 2.If many cells are analyzed and the micro-information of the individual cell is not of interest the entire spectral dataset of the cell is considered as a whole and an averaged spectrum is obtained. The unfolded matrix is sized N (the number of cells) and W.
• 3.Sometimes, a number of cells are being analyzed and the micro information is required. In this case, the pixels along the I- and J-axes and the samples are unfolded. The unfolded matrix is sized IJN and W. This method is similar to the first way of unfolding the data. It is not shown in Fig. 1.

Fig. 1.

Stages of Raman imaging data collection and analysis. A Raman spectrum is acquired for each I, J-coordinate and this spectrum is translated to the form of a pixel in the final image. The I- and J-axes (lower left corner) represent the plane over which the sample is analysed. I and J are the number of pixels or the number of the measurements along the I and J-coordinates. The total number of data points/pixels in the final dataset is equal to IJ. W is equal to the number of wavenumbers collected for the Raman spectrum along the w-coordinate in the 3-D cube. Matrix X represents the spectral data for analysis, and matrix Y represents the concentration/classification information in the training data. Note the difference between the vertical axis for the three modes of analysis (IJ/N). Visualization involves the analysis of a single cell whereas classification and quantification may involve the analysis of multiple cell types (the number of cells: N). An average spectrum generally is obtained from the full data set of a single cell and this is used for further analysis of a dataset of N cells.

The unfolded spectral data is then represented by X and the classification/concentration information are put in Y. Y is a matrix if there is more than one source of information (e.g. concentration for two compounds); otherwise it is a vector. The spectral data is then pre-processed. Numerous methods (Table 1) are available for spectral preprocessing and a suitable method can help us obtain the “clean spectra” (Fig. 2). Following pre-processing, spectral data are analyzed for the purpose of visualizing the cell biomolecules, classifying different types of cells, or quantifying cell biomolecules /drugs in the cell (Fig. 1). We can choose the appropriate machine learning method for pattern recognition based on the purpose of bioanalysis. Numerous machine learning methods have been applied to Raman imaging data analysis for the cell system. These methods are briefly introduced in Table 2 and their characteristics are listed. We generally use the unsupervised methods such as, explorative analysis (e.g. PCA) and cluster analysis (e.g. HCA) to visualize the cell biomolecules. Supervised classification, such as SVM, is used to classify different types of cells. As well as characterization, quantification of the biomolecules or the drug in the cell is another popular application of Raman imaging, which is usually achieved based on multivariate regression methods such as PLS. The result of pattern recognition modelling generally needs to be validated to ensure the reliability of the data analysis. This can be achieved using cross-validation, permutation or a confusion matrix/ receiver operator characteristic (ROC) curve (Fig. 3).

Table 1.

Short description and characteristics of the methods for pre- processing.

	Method	Description	Characteristic
Denoise	Kernel smoothing	Smooths the spectra based on a normal kernel function	Parameter free
	Savitzky-Golay differentiation	Estimates the derivative by consecutively fitting window-wised sub-sets of adjoining data points with a degree (custom designed) polynomial using linear least squares	Parameter-free; can be used for both baseline correction and smoothing/noise reduction.
Baseline removal	MPLS	Finds a rough background based on a penalized least squares function	Relatively time-consuming; competitive results; insensitive to the parameters.
	SNV	Transposes and then auto-scales the data.	Parameter free; scales the data
	MSC	Each input spectrum is regressed against a reference (e.g. the mean spectrum) and the results are used to correct the input spectrum.	Reference dependent; scales the data.
Cosmic ray removal	Sharp spike detection	Detects spikes which are significantly narrower than the peaks in the spectrum.	Insensitive to the relatively wide spikes; threshold dependent.
	Abnormal spike detection	A series of replicate spectra are compared. A spike is detected and removed since the probability of a spike occurring at the same point in multiple spectra is considered low.	Time-consuming since multiple spectra must be compared.
	Image curvature correction	Optimizes optical systems by comparing spectra from different rows of pixels on the detector.	User intervention needed for implementation; parameter based; time-consuming.
	Mapping based technique	The abnormal spikes are detected by comparing the neighboring spectra from the map.	A relatively large number of pixels needed for the accuracy of the detection.
Scaling method	Normalization by a peak (e.g. maximal peak).	Divides every row (spectrum) by the value at the selected peak of that row (e.g. maximal peak). ${\mathbf{X}}_{\left(n,:\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(n,:)}}{{\mathbf{X}}_{(n,peak)}}$	Emphasizes the variation of the Raman bands against the selected peak
	Auto-scaling	Subtracts the mean and then divides the standard deviation of that row. ${\mathbf{X}}_{\left(n,:\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(n,:)}-\stackrel{-}{{\mathbf{X}}_{(n,:)}}}{\mathit{std}({\mathbf{X}}_{\left(n,peak\right)})}\pi r^2$	The shape of the spectra may be lost; reduces the variation in the objects and gathers the objects towards the center.
	Row normalization (length/area)	Divides every row/ object by the length (Manhattan distance)/area (Euclidean distance) of that row.${\mathbf{X}}_{\left(n,:\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(n,:)}}{\mathit{sum}(\left|{\mathbf{X}}_{(n,:)}\right|)}$(length)${\mathbf{X}}_{\left(n,:\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(n,:)}}{\sqrt{\mathit{sum}({{\mathbf{X}}_{(n,:)}}^2)}}$(area)	The variation of objects is reduced.
	Column normalization (length/area)	Divides every column/variable by the length (Manhattan distance)/area (Euclidean distance) of that column. ${\mathbf{X}}_{\left(:,w\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(:,w)}}{\mathit{sum}(\left|{\mathbf{X}}_{(:,w)}\right|)}$(length) ${\mathbf{X}}_{\left(:,w\right)}^{\mathit{scaled}}=\frac{{\mathbf{X}}_{(:,w)}}{\sqrt{\mathit{sum}({{\mathbf{X}}_{(:,w)}}^2)}}$(area)	The shape of the spectra may be lost; Reduces the variation from variables
	Mean-center	Subtracts the mean of each row for all the elements${\mathbf{X}}_{\left(n,:\right)}^{\mathit{scaled}}={\mathbf{X}}_{(n,:)}-\stackrel{-}{{\mathbf{X}}_{(n,:)}}$	Reduces the deviation of the data from its center; gathers the objects towards the center.

n/w represents the n^th/w^th row /column of the spectral matrix X for scaling. All the X blocks in the paper are arranged in a way that objects are stored in different rows and variables are stored in different columns.

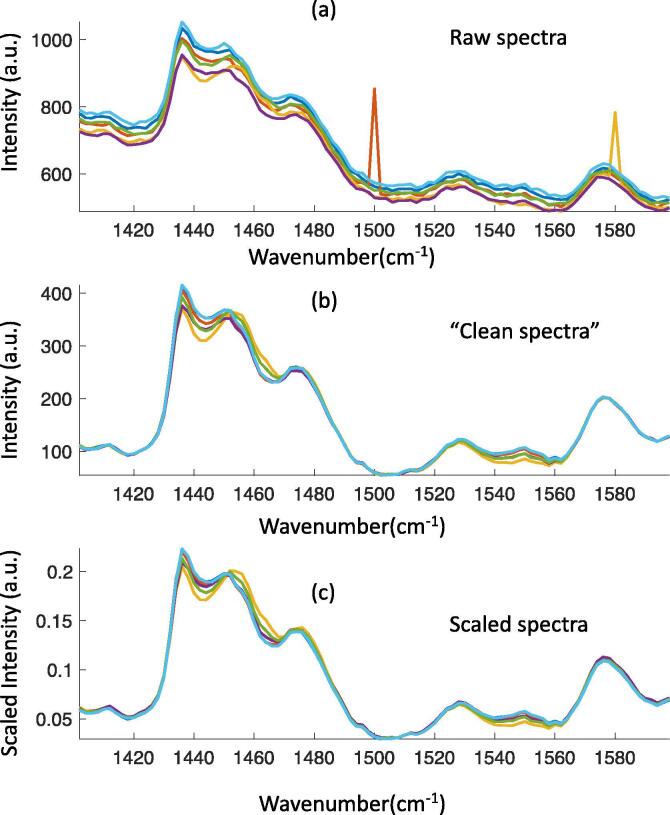
Fig. 2.

Pre-processing of Raman spectra including spike removal, denoise, baseline correction and scaling. (a) Raw spectra with noise, cosmic spikes and baseline; (b) “Clean spectra” after spike removal, denoise, baseline correction; (c) Scaled “clean spectra”

Table 2.

Short description and characteristics of some machine learning methods.

	Method	Description	Characteristics
Explorative analysis (unsupervised method): Decomposing the original data into two matrices including weight and new variable (NV) matrix	PCA	Explains the systematic structure of the variability within a multivariate dataset through the expression of this structure in a relatively low number of new variables (PCs)	PCs are orthogonal to each other; The first principle component explains the most variance, the second explains the second most variance etc.; PCs are uncorrelated variables
	ICA	Finds a linear representation of the new variables, statistically independent, or as independent as possible from non-Gaussian data	The new variables minimize the mutual information that exists between them.
	VCA	Decomposes the original matrix into two matrices (pure spectral matrix and concentration matrix) based on the following two assumptions 1) there are pure spectra of the components in the data and 2) the affine transformation of a simplex is also a simplex	The new variables are expected to be the pure spectra: effective in the hyperspectral decomposition
	MCR	Iteratively decomposes the matrix into the product of the concentration and the pure spectra of the compounds based on the singular vector decomposition (SVD) product.	Multiple constraints such as concentration and pure spectrum can be used. The results depend on the constraints.
Cluster analysis (unsupervised method): Grouping the samples which are more similar (in some sense) to each other than to those in other groups (clusters)	HCA	Recursively partitions a dataset into clusters having an increasingly finer granularity.	Excellent performance for small datasets.
	k-means	partitions samples into k clusters with the principle that the sample belongs to the cluster with the nearest mean value	Excellent performance for large datasets.
Classification methods (supervised method): Classifying the samples based on the training data	PLS-DA	Reduces the variable dimension by maximizing the covariance matrix between X and Y, where X indicates the spectral response and Y consists of the quality variables, which is classification information.	Easy to explain the result. It might provide an over-optimistic result.
	LDA	Aims to find a linear combination of variables that separates the classes of samples	Excellent performance with a limited number of training observations.
	KNN	Classifies the samples according to its k-nearest neighbour.	k-dependent
	SVM	Finds the hyperplane that maximizes the margins between both classes.	Memory efficient; parameter-free
	ANN	Learns to separate samples into different classes by finding common features between samples of the known classes.	Parametric classifier; relatively slow; the result is not easy to explain; good performance with noisy (non-linear) data; good performance with a large volume data.
	t-SNE	Illustrates high-dimensional data in a two or three-dimensional map and clusters similar objects based on a t-distribution test	Suitable for a large-scale dataset; the result is dependent on the parameter, e.g. number of close neighbors; may produce an over-optimistic result
Quantification (supervised method): Quantifying the samples based on the known concentrations of the training data.	MCR	Explained in the explorative section in this table; Uses a concentration constraint for quantification.	Multiple constraints can be used; Results are dependent on constraints.
	PLS-R	Explained in the explorative section in this table; Y consists of concentration information.	The result can be over-optimistic.

PLS-DA:Partial least squares discriminant analysis; PLS-R: Partial least squares regression.

Fig. 3.

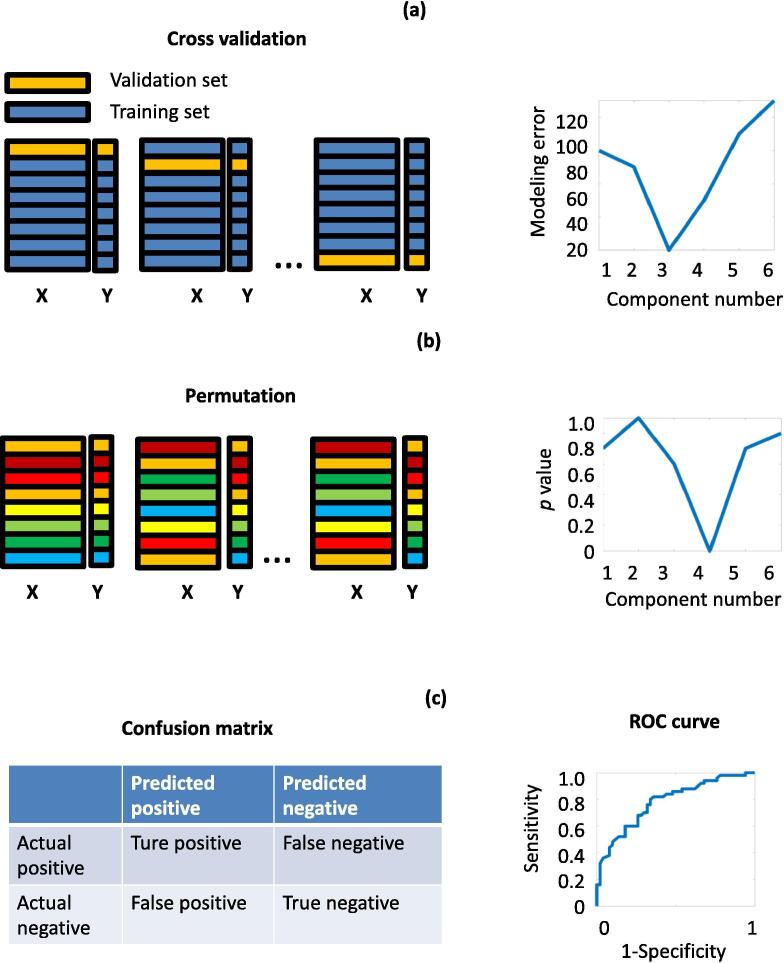
Validation methods for machine learning results, including cross-validation, permutation, confusion matrix and receiver operator characteristic (ROC) curve. Matrix X represents the spectral dataset and Y represents the classification/concentration information (a) Cross-validation illustration using the Leave-One-Out (LOO) strategy as an example. Each time a single sample is left out and the remaining samples are used as a training set to build the multivariate model. This step is repeated for all the samples. The modelling error is calculated for each multivariate model with different numbers of components (the plot on the right side). (b) The permutation test shuffles the samples in the X block. The samples in the Y block remain in the same order as the original data. Pseudo machine learning models are built and statistical tests are applied to compare the original model with the pseudo machine learning models. The permutation test can be applied with different parameters (e.g. the number of components), and only the models with p-values lower than 0.05 are considered statistically reliable (the plot on the right side). (c) Confusion matrix indicating the number of true positive, false positive, false negative and true negative samples predicted by the machine learning method. Specificity and sensitivity are related to the number of samples that fall into each category (Equation (1), (2)). The ROC curve shows the relationship between specificity and sensitivity of the models where the threshold of the classifier is varied.

2.3. Pre-processing

Since ideal conditions for data collection are next to impossible to achieve it is generally not possible to use the raw, unaltered data for analysis; data must first be processed before pattern recognition analysis. Pre-processing techniques are expected to improve the linear relationship between spectral signals and analyte concentration by correcting irregularities, removing artefacts and generally “cleaning-up” the data. Pre-processing may include some or all of the following: denoising, baseline correction, cosmic spike removal, and scaling (Fig. 2). There are numerous methods developed for these pre-processing steps. The description and characteristics of those methods are summarized in Table 1.

Heteroscedastic and homoscedastic noise are two types of noise associated with Raman spectroscopy. Shot noise is homoscedastic, which is caused by the instrument. Most commercial instruments have spectral pre-processing software embedded that can reduce this type of noise automatically. Kernel smoothing and the Savitzky-Golay method can be applied for additional denoising after the measurement if necessary. The baseline signal, which is the broad underlying spectral background, is often observed in Raman spectra of biological samples. It is considered as heteroscedastic noise and is caused by the fluorescent contaminants. The Savitzky-Golay method can reduce baseline shift as well as the homoscedastic noise [47]. As well as the Savitzky-Golay method, there are a number of other methods for baseline removal, such as morphological weighted penalized least squares (MPLS) [48], standard normal variate (SNV) [49], and multiplicative scatter correction (MSC) [49]. As well as noise, cosmic ray artefact (CRA) spikes can interfere with the real Raman signals. The sharp CRA spikes occasionally occur in a small number of adjacent pixels in the charge-coupled device (CCD) of Raman spectroscopy. They vary significantly in width and intensity and can distort spectra considerably. Also, a CRA spike can increase the variance of the spectra when it is overlapped with the signal of interest. This would influence the accuracy of the multivariate modelling and complicate signal interpretation. The spike removal methods are classified into four types, and each of them has different characteristics [50]. After obtaining the “clean spectra” via denoising, spike removal and baseline correction methods, scaling is generally needed to better understand the data, reduce the unwanted variance, and emphasize the variance which reveals the information [51], [52], [53]. Table 1 shows the equations pertaining to the various scaling methods. It is essential to choose the appropriate pre-processing methods based on both the spectral data and the characteristics of the pre-processing method (Table 1), and to estimate the influence of the selected pre-processing methods on the results of the data analysis. For the purposes of illustrating the pre-processing procedure, we semi-simulated the spectral data based on the measurements of 6 samples of piracetam (various concentrations) mixed with proline, microcrystalline cellulose, and CaCO₃. Spectra of biological material (protein, nucleus, and lipid) and homoscedastic noise were introduced artificially to better replicate Raman spectral data of a cell system. The raw spectra clearly exhibit the presence of a baseline shift and cosmic rays (Fig. 2). Pre-processing of the raw dataset included noise removal using Kernel smoothing, baseline calibration based on MPLS and cosmic ray removal based on the abnormal spike detection method. Fig. 2 (b), which shows the “clean spectra”, possesses much clearer Raman bands. Scaling (row normalization) is conducted based on the “clean spectra”. The scaling step is expected to reduce the variance between measurements that results due to noise. Pre-processing methods, including scaling methods, should be carefully chosen and the analyst should be particularly wary of introducing spectral distortion. Gerretzen et al, developed a strategy, Design of Experiments (DOE), to aid in the selection of the optimal pre-processing methods for a particular dataset, which would ideally result in a subsequent boost in model performance [53], [54].

2.4. Application of machine learning methods to Raman imaging data of a cellular system

2.4.1. Pattern recognition

Following pre-processing, the “clean spectra” should have a better linear relationship with the concentration of the biochemical compounds. However, it is common to find Raman spectral overlap between different biochemical compounds such as proteins, lipids and the nucleus. This makes pattern recognition the critical step in Raman imaging analysis in the cellular system. The methods of machine learning help to reveal the biochemical information hidden within the complex spectral data. The three main applications of Raman imaging in the cellular system include visualization of the cell at the biomolecular level, classification of different types of cells, and quantification of biomolecules / drugs in the cell (Fig. 1). Table 2 provides a short description and lists the characteristics of the machine learning methods that are often implemented when using Raman imaging to analyze the cellular system. The machine learning method should be carefully chosen based on the purpose of the analysis and the character of the machine learning method.

2.4.2. Visualization of cell biomolecules

Single-cell visualization at the biomolecular level, is one of the most popular applications of Raman imaging in the cellular system. One reason for its suitability is the scale of the measurement; a spot size of ~㎛, or even lower, can be obtained with Raman imaging instrumentation [4], [21], [26], [28]. Furthermore, cellular components such as proteins, nuclei, and lipids have a spontaneous Raman signal, which gives rise to their spectral “fingerprint”, revealing the biomolecular distribution in the cell. Those “fingerprints” can be extracted and better explained using machine learning methods to show the cell’s spatial structure (Fig. 1). One of the most common strategies for single-cell visualization involves reducing the dimension of the spectral matrix by creating new variables (new coordinates). Examples include PCA, ICA, VCA and MCR. They decompose the data matrix into two matrices, loadings and scores. The loading matrix contains the new variables, which are expected to contain the relevant spectral information from the biomolecules (Fig. 1). The score matrix provides the corresponding weights of the samples in the new coordinate system. The scores represent the relative concentrations of the new variables. Semi-quantification can be achieved, as well as visualization of the cell, because of this relative concentration information. Gaifulina et al. obtained the chemical information from a formalin-fixed, paraffin-embedded rat colon tissue section by making use of this form of analysis. The new variables in the PCA model contained the spectral information that explained most of the variance. Those new variables were related to the spectral information of the paraffin and the biochemicals (muscle, mucin and nuclei).The scores showed the relative concentration scatter of those biochemicals, which provided a superior image in terms of contrast and sharpness compared to conventional haematoxylin and eosin (H&E) staining [28]. Similarly, Kallepitis et al. used VCA modelling for the semi-quantification and visualization of cells at different stages of macrophage differentiation. They succeeded in visualizing the scatter of the nucleus, cholesterol and cytoplasm of the cells in 3-D cell culture [4]. For a VCA model, in contrast to that of a PCA, the new variables in the loading and score matrices are expected to contain the spectral information of the pure components. This is why the loadings of the new variables in the VCA model are more representative of the true biochemical spectral profiles, compared with the loadings of an equivalent PCA model. As well as the dimension reduction method (e.g. PCA), cluster analysis (HCA and k-means) is another type of method that is commonly implemented to visualize cell structure (Fig. 1). Instead of extracting the Raman spectral information of the biochemicals via new variables, cluster analysis directly groups the objects/pixels in the Raman imaging dataset based on common spectral features. Cluster analysis doesn’t provide concentration information. Therefore, it is commonly applied when the relative concentration of the cellular components is not the purpose of analysis. For instance, Kochan et al. characterized the biochemicals in live liver sinusoidal endothelial cells isolated from the murine liver based on HCA and k-means cluster analysis [55]. The cluster analysis of the Raman imaging dataset illustrated the areas of the cell occupied by the different biochemicals, e.g. nucleus and lipid droplets, and clearly revealed the locations of the biochemical components in the two types of cell (hepatocytes and Hepatic Stellate Cells).

2.4.3. Classification of different types of cells

As well as visualizing the biomolecules within the cell, another popular application of Raman imaging is to classify cells according to various factors including different stages of tumour development [9], [10], [11], [12], [13], [14], different species of cells [30], and cell differentiation [2], [29] (Fig. 1). It is generally achieved by supervised machine learning methods (SVM, PLS-DA, KNN, ANN, t-SNE and LDA (Table 2)) that relate the mean Raman spectrum of each sample (X block) to the classification reference (Y block) of that sample. Note that PCA is generally used for explorative analysis or variable reduction prior to the supervised machine learning application. A recent example of how a classification analysis might be carried out can be found in a study by Kobayashi-Kirschvink et al., in which a discriminant analysis (PCA and LDA) resulted in the identification of distinct cellular states under different cell culture conditions. They related the averaged Raman spectra of each cell (X block) to cells from different cell cultures (Y block) using a 5-D PCA-LDA model. t-SNE was subsequently used to visualize this relatively high dimension data in a 2-D coordinate plot where cells from different cell cultures were classified appropriately [2]. As well as identifying cells by cell culture, classifying different stages of tumour cell growth is another popular application of Raman imaging in cell systems [9], [10], [11], [12], [13], [14]. For example, Tolstik et al. successfully classified the liver cancer cell at different stages of tumour growth using SVM to model the dimensionally reduced Raman imaging data [14]. The SVM model related the averaged Raman spectrum of each cell to different cancer cell types and different stages of tumour growth. Furthermore, the classification model was improved by using the averaged spectra of different cell compartments (nucleus, cytoplasm and lipid) instead of the averaged spectrum of the whole cell. This machine learning method coupled with Raman imaging helped to improve the diagnosis accuracy of liver cancer compared with the traditional method (examined de novo lipogenesis), which makes Raman imaging a potential alternative detection method for liver cancer.

2.4.4. Quantification in the cell system

Raman imaging can be used for quantification analysis as well as for characterization purposes (single-cell visualization and cell type classification) in cell systems. The quantification analysis based on Raman imaging can be applied to biomolecules or to a specific drug introduced into a cell system [5], [6], [16], [31]. Both macro- and micro- concentration levels can be interrogated by Raman imaging quantification analysis. When a single concentration level is determined for the analyte of interest this is referred to as the macro-concentration. However, when the concentration of the analyte of interest within each individual pixel across the cell is required this is referred to as the micro-concentration. For both types of quantification, a calibration model is built by relating the known concentration of the analyte to the averaged Raman spectrum of each cell. The known concentration is generally obtained using chromatography-based methods. Based on the calibration model, these compounds can be quantified at the macro-level by using the averaged spectrum for a single cell in the prediction set. The micro-concentration can also be determined based on the Raman spectra collected from different locations within the cell (Fig. 1). He et al. carried out both micro- and macro- quantification of starch, protein, and triacylglycerol in microalgal cells using PLSR modelling [16]. The calibration curve was built by relating the concentration of the components of interest (starch, protein, and triacylglycerol) within the cell to the averaged Raman spectrum of that cell. The concentrations of these components were estimated by thin-layer chromatography/gas chromatography-mass spectrometry. Based on the calibration model, the macro quantification result was obtained by using the averaged Raman spectrum of each cell in the prediction set. Furthermore, the micro concentrations of all the components were also determined from the Raman spectra collected from different locations in the cells. A histogram of the micro concentrations shows how the distribution of those biomolecules in the microalgal cell is changing dynamically in the cell culture at different time points. It should be noted that the quantification results using a PLS model developed from the complete Raman spectra has significantly higher precision than results based on single peak models.

2.5. Software

There are a number of software packages available for the full data analysis procedure, including preprocessing, multivariate analysis and validation. These software packages can be classified into two categories based on whether or not they require prior programming knowledge (Table 3). Software-based on computer languages such as Matlab, R, and Python require the analyst to have some programming skills in order to carry out the data analysis. Data analysis implemented with these software packages is more flexible, since most of the methods can be implemented. Programming is not needed for the other types of software such as The Unscrambler X, SIMCA, CytoSpec, Origin for Spectroscopy, ImageLab and PeakFit. Some graphical user interfaces (GUI) based on Matlab have been developed that can be implemented without programming, such as Biodata, EMSC, MIA, MCR-ALS, PLS, Raman processing program, HYPER-Tools, HIA. Only the methods installed in the software can be applied for data analysis. The choice of data analysis software should be based on the goal of the analysis.

Table 3.

Short description and characteristics of the software including Raman imaging data analysis function.

Software	Functions	Programming
PeakFit	Spectral pre-processing; visualization tool	No
ImageLab	Spectral pre-processing; univariate analysis for images	No
Origin for Spectroscopy	Spectral processing and visualization tool; rich resource for pre-processing methods; multivariate analysis for spectral analysis	No
CytoSpec	Hyperspectral imaging processing tool; spectral pre-processing; image segmentation (uni- and multivariate)	No
The Unscrambler X	Multi/uni-variate methods for quantification/qualification	No
SIMCA	Pre-processing; multi/uni-variate methods for quantification/qualification	No
Matlab	Computer language with a number of toolboxes/GUIs, such as Biodata, EMSC, MIA, MCR-ALS, PLS, Raman processing program, HYPER-Tools, HIA developed for spectral pre-processing and multivariate analysis.	Yes (no for GUI)
R	ChemoSpec, HyperSpec	Yes (no for GUI)
Python	Pychem, Pyvib2	Yes (no for GUI)

2.6. Validation of the pattern recognition model

2.6.1. Methods of pattern recognition model validation

Once the spectral data has been pre-processed and a pattern recognition model has been developed, one further step is required to check the reliability of the model. This is because pattern recognition models, especially the ones based on supervised machine learning methods, might provide over-optimistic results. Thus, no matter for classification or quantification, it is critical to validate the results from a pattern recognition model, especially for those that have low sample numbers and many variables. There are a few methods developed for validating machine learning results, including, cross-validation [56], permutation tests [56], confusion matrices and ROC curves [57] (Fig. 3). Validation methods can be chosen based on the machine learning method used for modelling. For example, a result based on PLS modelling is usually validated by cross-validation and/or a permutation test. Confusion matrix validation is commonly used to validate classification modelling. ROC curves are also used to validate classification modelling but they can only be used for binary classification models.

2.6.2. Cross-validation

Cross-validation estimates the performance of a predicted model. It creates a series of validation models through sampling, which involves removing a subset of samples from the full dataset (validation samples), constructing a model using the remaining samples (training samples), and estimating the model error by applying the training model to the validation samples. The modelling error can be estimated using the sum of the squares of all the resulting prediction errors (PRESS). The Leave-One-Out (LOO) strategy is a typical cross-validation method, which leaves one sample out each time before building the validation model (Fig. 3). As well as LOO, there are a number of cross-validation methods, such as Venetian Blinds, Contiguous Blocks, and Random Subsets, or the sampling method can be customized. We can choose the sampling method based on a few factors including, the ordering of the samples, the number of samples, the number of replicate samples, the modelling purpose, the costs of modelling error, as well as the time available for the cross-validation analysis. Cross-validation is commonly used to estimate the correct number of new variables in the variable reduction method, e.g. the number of PCs in a PCA model. The number of components related to the model with the lowest cross-validation error should be chosen. Meksiarun et al. used cross-validation to estimate the number of ICA components to extract from a Raman imaging spectral dataset of paraffin-embedded cancer tissue [58]. Cross-validation performs better in predicting component numbers compared with some other commonly used methods such as scree plots where a high level of noise and nonlinearity is often present [59]. As well as predicting the number of components, cross-validation is one of the most widely used methods to estimate the performance of classification models. Furthermore, it can be applied to most machine learning methods. For example, Tolstik et al. employed cross-validation to estimate the performance of a predictive classification model that was developed using SVM. The low value of the relative error from the cross-validation model indicated satisfactory discrimination and classification of different liver cancer cells and their proliferation states by Raman spectroscopic imaging [14].

2.6.3. Permutation

As well as cross-validation, the permutation test is another validation method that helps us identify an over-optimized model. It is based on a different sampling strategy. It builds a number (100 s or 1000 s) of pseudo pattern recognition models based on spectral data (X block) where the samples have been placed in a random order (samples in the X block are shuffled) while the Y block is left in the original order (Fig. 3). Those pseudo pattern recognition models are then compared with the original pattern recognition model using probability tests, such as a randomization t-test. The p-value indicates the significance of the difference between the original and pseudo pattern recognition model. Generally, a p-value higher than 5% indicates an unreliable model. Permutation tests can also be used to choose the optimized parameter for the pattern recognition model, e.g. the number of components in multivariate analysis modelling. Generally, we should choose the model with the lowest p-value, and only models with a p-value lower than 0.05 should be considered. A permutation test can be applied to most machine learning methods, both quantification and classification. Kobayashi-Kirschvink et al. used a permutation plot to validate the performance of a classification model for identifying cells from different environments. A total of 10,000 permutations were carried out to assess the exceptional performance of the LDA classification model. A low p-value supported the results of the model [2].

2.6.4. Confusion matrix and ROC

The confusion matrix is a useful tool to estimate the performance of a supervised classification model. A binary classification confusion matrix (Fig. 3) consists of a 2 × 2 matrix that lists the number of False Positives, False Negatives, True Positives and True Negatives that have resulted from the validation test. The confusion matrix can also be expanded for models with more than two classifiers. The True Positive (sensitivity) rate and False Positive (1 - specificity) rate are used to estimate the performance of classification, which are estimated using Equation (1), (2):

$$\mathit{Sensitivity}=\frac{\mathit{True}positive}{\mathit{True}positive+Falsenegative}$$ (1)

$$1-Specificity=\frac{\mathit{False}positive}{\mathit{False}positive+Truenegative}$$ (2)

A sensitivity value close to 1, and a (1 - specificity) value close to 0 indicate a highly accurate classifier. Both sensitivity and (1 - specificity) vary depending on the selected threshold of the classifier in the model. The receiver operator characteristic (ROC) curve is a graphical plot of (1 - specificity) versus sensitivity where the threshold value is varied. If the classifier, for example, is concentration, the analyst must decide on a threshold value for high concentration. If all concentration values are considered high, of course every result will be a true positive and no result will be a false positive. The opposite is true if no concentration values are considered high. The ROC curve shows the variation in between these two extremes. In short it illustrates the quality of the two classifier model (Fig. 3). The closer the curve is to the diagonal, the less accurate the model. To measure the quality of the model, we use the area under the ROC curve (AUROC), which varies from 0 to 1. The higher the value of the AUROC the better the separation between classes. A value close to 0.5 indicates no separation between classes. Hsu et al. used the sensitivity and specificity values to highlight the accuracy of their classification model, which was based on the machine learning method of t-SNE. The high values of sensitivity and specificity (larger than 95%) indicate successful classification of human pluripotent stem cell-derived neurons at different developmental stages [60].

2.7. Sampling

A relatively long integration time is generally needed to obtain a sufficient signal-to-noise ratio for spontaneous Raman Imaging. This limits the applications of Raman imaging, as the long measurement time is a problem for both experiments with numerous samples, and dynamic analysis. Sample-size planning, which is also known simply as sampling, should estimate the minimal number of measurements required to achieve robust and significant results. Note, “sample” here indicates the pixels in the Raman measurement rather than the cell sample. The appropriate sampling should reduce the measurement time and improve the efficiency of cell imaging. There are a number of sampling methods available, the selection of which depends on the purpose of the Raman imaging analysis [61], [62], [63], [64]. Schie et al. estimated the number of samples required based on whether the mean spectrum can detect the drug-induced changes of the chemotherapy agent, doxorubicin, in the cell [63]. Also, a number of sampling methods were developed for the purpose of achieving a reasonable classification result using the minimal number of measurements. They built multivariate classification models for different cell types based on spectral data having different numbers of measurements. Following this, a statistical test such as the effect size is applied. The effect size may be determined, for example, from a plot of the error from multivariate classification modelling versus the number of measurements taken [61], [62]. As well as estimating the minimal number of measurements, Zhang et al. developed a dynamic sparse sampling strategy. This strategy involves choosing the location of the measurement dynamically, based on the multivariate classification result within a cell [64].

3. Summary and outlook

Raman imaging allows label-free, non-destructive biomolecular analysis at the cellular level by generating detailed biochemical images. Currently, there is a strong drive to improve the Raman imaging instrumentation in order to better apply Raman imaging in the cellular system. As well as optimizing the instrumentation, the application of the appropriate data mining methods plays a critical role in deciphering the Raman imaging information. There are a number of methods developed for the three main stages of data mining in Raman spectral analysis, including pre-processing, pattern recognition and validation. These methods can be implemented by various software packages, which are introduced in the review paper. The first step of pre-processing should help us obtain the “clean spectra” by denoising, spike removal, baseline correction and scaling. Following pre-processing, machine learning methods facilitate pattern recognition in Raman imaging data of the cellular system. This makes certain modes of analysis possible, including single-cell visualization, cell type classification and quantification analysis. Biomolecular visualization can be achieved using cluster methods such as HCA and k-means, and dimension reduction methods such as PCA, ICA, VCA and MCR. As well as visualizing the cell biomolecules, classifying different types of cells is another popular application that can be achieved based on supervised classification methods such as SVM, PLS-DA, KNN, ANN and LDA. Methods such as PLSR and MCR can be used to quantify, as well as characterize, the biomolecules or drugs in a cellular system. After the pattern recognition step it is critical to validate the result using validation methods such as cross-validation, permutation tests and confusion matrices/ROC curves. The validation method is selected based on the machine learning method used. Sample size planning is another important aspect of Raman imaging data analysis. This involves estimating the minimal number of measurements required for meaningful Raman imaging data analysis. It reduces measurement time and allows for a more efficient experimental procedure in general.

Currently it is common to apply data mining, based on machine learning methods, to Raman imaging datasets of the cellular system instead of using traditional univariate analysis. This is due to the efficiency of machine learning methods compared to univariate analysis. However, those machine learning methods should be carefully applied, validated and explained based on the relationship between the mathematical result and the physical/biochemical meaning. For example, Westerhuis et al. pointed out that a classification result based on PLS can be over-optimistic and even random samples can be classified perfectly using a score plot from PLS modelling [56]. Data mining in Raman imaging of cellular systems can be better applied if those machine learning methods are better understood. Also, in order to better implement data mining, more and more biologists are beginning to learn how to program based on R, Matlab or Python, which is another reason for the growing popularity of machine learning methods in the life sciences. Data mining can be implemented in a flexible way based on programming. Furthermore, the development of intuitive software has helped to promote the implementation of data mining methods in Raman imaging of cellular systems to some extent. However, not many software packages are specialized in data mining of Raman imaging datasets of cellular systems. Biologists must explore the methods and workflow independently in order to obtain the bioinformation from the spectral data. Also, spectral databases of common biomolecules are not available yet. Due to the development of Raman imaging of cell systems, it is likely that more and more software packages and databases, pertinent to data mining of Raman imaging of cellular systems, will be released. This will surely accelerate developments in data mining of Raman imaging datasets of the cellular system.

CRediT authorship contribution statement

Ya-Juan Liu: Conceptualization, Writing - original draft. Michelle Kyne: Writing - review & editing. Cheng Wang: Conceptualization, Supervision. Xi-Yong Yu: Supervision, Conceptualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.