Abstract
Introduction
The biological and mechanical properties of circulating tumor cells (CTCs) in combination with the hemodynamics affect the preference of metastatic sites in the vasculature. Despite the extensive literature on the effects of biological properties on cell adhesion, the effects of hydrodynamic forces on primary attachment remains an active area of research. Using simulations in conjunction with experimentation, we provide new insight into the interplay of CTCs dynamics and local hydrodynamics.
Methods
A flow experiment of CTC attachment was performed within a bioprinted, double branching endothelialized vessel. Simulations of fluid flow and CTC transport in the reconstructed and idealized bifurcated vessel were respectively performed by HARVEY, our in-house massively parallel computational fluid dynamics solver. HARVEY is based on the lattice Boltzmann and finite element methods to model the fluid and cells dynamics. The immersed boundary method is employed for resolving the fluid–structure interaction.
Results
CTC attachment was quantified experimentally at all regions of the complex vessel. The results demonstrate a clear preference for CTCs to attach at the branch points. To elucidate the effect of the vessel topology on the location of attachment, a fluid-only simulation was performed assessing the differences in the hydrodynamics along the vessel. CTC transport in idealized bifurcated vessels was subsequently studied to examine the effects of cell deformability on the local hydrodynamics patterns and, thus, the preference of attachment sites.
Conclusions
The current work provides evidence on the correlation of the hydrodynamics forces arising from the vessel topology and CTC properties on the attachment regions.
Keywords: Hemodynamics, Circulating tumor cell, Wall shear stress, Cell deformability, Residence time
Introduction
Local hemodynamics play an important role in influencing the location of metastatic sites.22,52 Particular attention has been given to the study of local shear stress due to its relation with the residence time of a CTC at the vessel wall. Given a sufficiently long residence time, a chain of interactions between the CTC and endothelium occurs leading to the formation of adhesive bonds and subsequent extravasation.8,9,49,52 Therefore, knowledge of the hemodynamic factors, in particular the wall shear stress (WSS) distribution along the vasculature, is of crucial importance in predicting potential sites of metastatic colonization.
It is evident that the vessel anatomy is instrumental in the distribution profile of hemodynamic features along the vessel. Most of the previous experimental and computational works focused on the effect of WSS on cell adhesion in planar surfaces10,11,24,26,30,31 or a straight vessel.8 Reference 27 investigated by means of experiments and computational modelling the effects of CTC cluster size and shape on its trajectory and rolling velocity in a straight microvessel. Various CTC aggregate shapes were also computationally considered to explore the effects on the trajectory and contact time during the collisions between the CTC aggregate and a planar surface.1 However, from a physiological perspective, the vast majority of the vasculature is either curved or bifurcated. To this end, works in the literature have begun to explore the effects of curved or bifurcated microvessels on the local hemodynamics and, consequently, cell adhesion.17,39,58,59
Reference 59 studied the effect of microvessel curvature on the adhesion of CTCs to the endothelium by means of two-dimensional numerical simulations. A higher cell adhesion probability was found for the curved microvessel when compared to a straight one. In a later study, the previous observation was experimentally validated, and elevated WSS and its gradient were reported at the preferred locations where cell adhesion occurred.58 Reference 17 investigated experimentally the mechanical mechanisms behind the arrest and adhesion of human breast carcinoma cells in the microvasculature of rat mesentery. To elucidate the effect of hemodynamic factors on the locations of tumor cell arrest and adhesion, three-dimensional numerical simulations considering only the presence of fluid were performed to obtain the velocity, strain rate and vorticity profiles across the microvasculature. Enhanced shear rates and its gradients as well as vorticity were found at the side branching intersections where increased tumor cell adhesion was observed. Reference 39 performed two-dimensional numerical simulations of singlet, doublet, and aggregate circulating tumor microemboli (CTM) transport in a branching arteriole. It was found that the CTM clusters can result in vascular plugging, while the singlet and doublet CTM experience multiple interactions with the vessel wall.
It is worth noting that there is an extensive literature on the motion of elastic capsules and cells in bifurcated channels. For example, the effects of flow-rate ratio, suspending viscosity and cell rigidity on the motion of isolated red blood cells (RBCs) have been studied in symmetric and asymmetric bifurcations of Y and T shape.3,56,57 Suspensions of red blood cells in bifurcating microvessels have been investigated both experimentally and computationally.2,23,25,32,45,61 These works have been primarily focused on the effects of the bifurcation geometry, flow-rate ratio, hematocrit, and RBCs’ deformability and initial position on the cellular partitioning phenomenon. Similarly, the motion and deformation of elastic capsules in vessels with a side branch53 or Y/T-bifurcation12,19,50,51,60 have been explored for varying flow rates and capsule deformabilities. In the aforementioned studies, the main focus has been on the changes in the elastic capsules/cells trajectory.
In the present work, we are interested in investigating WSS variations caused by the interplay between CTCs behaviour and local hemodynamics. Quantifying changes in WSS is of particular importance as it is believed that there is a threshold/optimal range resulting in CTC residence time sufficient for cell adhesion to occur.52 We focus on bifurcated vessels, as they are physiologically relevant, by incorporating flow characteristics of both the arterial and venous system encountered by CTCs moving in a complex vasculature. Table 1 summarizes the different components of the current work. A flow experiment of CTC attachment has been performed within a bioprinted, double branching vessel lined with endothelial cells. In our work, we leverage bioprinting technology as it offers a method for printing a controllable geometry for comparison with computational models. Similarly to Reference 17, we have simulated fluid flow in the reconstructed, double branching vessel model to elucidate the effect of local hydrodynamics on the preferred locations of CTC attachment. We have subsequently studied the dynamic interactions between CTCs and local hydrodynamics by performing simulations of a CTC suspension with varying cell stiffness in an idealized bifurcated vessel matching the flow features of the engineered vessel used in the experiment. Finally, we have computationally considered the case of a single CTC flowing in a microvessel to focus on near-wall behavior and impact on wall shear stress for circumstances with strong cell–wall interactions. Thus, using both experiment and simulations, this study provides new insight into the connections between local hemodynamics, near-wall CTC behavior, and WSS trends.
Table 1.
Summary of the studies performed in the present work.
| Case | Experiment | Computational modelling |
|---|---|---|
| CTC attachment in double bifurcation vessel | (Fluid-only) | |
| CTC suspension in an idealized bifurcated vessel | – | |
| Single CTC in a bifurcated microvessel | – |
Methods
In the current section, the procedure for the endothelial cell culture and labelling of the CTCs is briefly discussed. The hydrogel materials used in the bioreactor fabrication process are presented along with a demonstration of the latter. The evaluation process of the CTC attachment and image processing analysis are also reviewed. Finally, the numerical framework employed in the present work is discussed in detail.
Experimental Methods
Cell Culture
Immortalized human cerebral microvascular endothelial cells (hCMEC/D3, Cedarlane) were cultured between passage 30 and 31 in collagen-coated culture flasks containing EndoGRO-MV (EMD-Millipore) media supplemented with 1 ng/mL bFGF (Sigma) and 100 U/mL penicillin/streptomycin (Gibco). Murine mammary gland carcinoma cells (4T1, ATCC) were maintained in RPMI-1640 supplemented with 10% FBS (ATCC) and 100 U/mL penicillin/streptomycin at passage 19–21. For both cell types, culturing and sub-culturing methods followed the vendors’ protocol and incubated in a humidified 5% CO incubator maintained at 37 C .
To visualize CTCs introduced into the in vitro vascular model, 4T1 cells were labeled with Vybrant Dil lipophilic dye (Invitrogen) at a concentration of 0.01 mM for 30 min. Cells were spun down to remove exogenous lipophilic dye and then resuspended in EndoGRO-MV media. The labeled cell suspension was gently strained to remove cell aggregates with a 40 nylon cell strainer (VWR) before further diluting to a final cell density of 100,000 cells/mL.
The cell lines were employed here so as to ensure high probability of metastatic attachment. For this reason, we selected the rapidly metastatic mammary gland carcinoma cell line, which has been extensively used in the literature.40 Indeed, a large number of attached CTCs was found after 1 h of CTC circulation.
Hydrogel Materials
Stock solutions for bioreactor gels included 150 mg/mL gelatin (Type A, 300 Bloom, Sigma), 50 mg/mL fibrinogen (Type I-S, Sigma), 120 mg/mL transglutaminase (TG, Type TI, Modern Pantry), 250 mM CaCl (Sigma), and 200 U/mL thrombin (sigma), with phosphate buffered saline (PBS, Gibco) as the solvent for all solutions. Gelatin solution was prepared by heating the mixture at 70 C for 16 h with gentle stirring until completely dissolved followed by adjustment to pH 7.5, filter sterilization, and storage at 4 C. Sacrificial ink was prepared using a 35% (w/w) solution of Pluronic F-127 (Sigma) in sterile filtered deionized water (diHO) followed by mixing with sterile thrombin solution at 4000 U/mL in diHO to a final concentration of 100 U/mL.
Bioreactor Fabrication
Bioreactor fabrication process was modified and adapted from Reference 28. Briefly, bioreactor walls were fabricated using custom injection stainless steel molds for (PDMS), Sylgard 184 (Dow Corning) prepared with a 10:1 elastomer to catalyst ratio and cured at 65 C for at least 8 h. PDMS walls were then bonded to glass slides using a printed layer of SE1700 (Dow Corning) and cured at 65 C for at least 2 h to complete bonding.
To assemble the in vitro devices, base layer gel was cast within the bioreactor sidewalls, prior to sacrificial ink printing of vasculature design. Base layer protein solution (final composition of 75 mg/mL gelatin, 10 mg/mL fibrinogen, 2 mg/mL TG, and 2.5 mM CaCl) was incubated at 37 C for 20 min before mixing in thrombin (final concentration of 1 U/mL). After casting, air drying for 25 min, and printing of the vascular channel geometry perfusion pins (Scanivalve) were pushed into contact with the ink to permit connection to fluidic tubing. The print was then encapsulated using another layer of fibrin–gelatin hydrogel and sealed with a glass slide followed by clamping within a custom designed reactor housing. The device was then incubated at 37 C for 1 h prior to transferring to 4 C for 20 min to liquifying the sacrificial ink. The ink was then evacuated using gentle suction and rinsed with chilled EndoGRO-MV media through the resulting channel. The devices were then connected with fluidic tubing at the pins equipped with an in-line MFS3 flow rate sensor (Elveflow) and reservoirs pressure driven by a connected OB1 microfluidic flow controller (Elveflow). Entry and exit reservoirs were filled with 85 and 15 mL of media equilibrated with 5% CO respectively and the devices were maintained under a 10 L/min flow rate with EndoGRO-MV media for the duration of their culture, with media exchanged between the exit and entry reservoir on day 4. After perfusion for 12 h reactors were taken offline and seeded with hCMECs at a density of 1 cells/mL at six 15 min intervals at 37 C with the device being inverted between each interval. Following the inversion steps, the devices were cultured for 7 days under flow conditions.
CTC Attachment Evaluation
Lipophilically dyed cell suspensions were loaded into the fluidic line of the device and flow was resumed. For these studies, the bioreactors were perfused by a peristaltic pump (MRC Scientific Instruments) with an average flow rate of 1690 L/min, as measured by an MFS5 flow sensor (Elveflow), for a total of 1 h. Following perfusion, the bioreactors were rinsed with 3 mL of warm EndoGRO-MV media to remove any unattached cells, fixed for 30 min in 4% paraformaldehyde (Alfa Aesar), and rinsed thrice in PBS prior to storing at 4 C. For cytoskeleton stain actin, samples were permeabilized in 0.5% (v/v) Tween-20 (Millipore-Sigma) in PBS for 15–30 min, followed by incubation with 1:40 Alexafluor-488 phalloidin (A12379, ThermoFisher) and Hoechst-33342 (62249, ThermoFisher, at 10 g/ml) in PBS for 1 h at room temperature. Samples were washed in PBS+ 0.1% and imaged with an LSM700 confocal microscope (Carl Zeiss) using a objective. For whole gel imaging, z-stacks were tile-stitched to capture the entire vascular geometry. CTC positional analysis upon the resulting tile-stitched 3D images was performed using MATLAB as detailed below in “Image Processing”.
Image Processing
For analyzing CTC attachment, the vessel walls were identified from confocal stacks of the endothelium. CTCs were identified by filtering and thresholding each frame in a confocal stack. Next, morphological operations were performed to determine the volume of each CTC cluster and its position relative to the vessel.
Computational Modelling
Lattice Boltzmann Method
The in-house massively parallel computational fluid dynamics solver, HARVEY, is used to perform simulations.42 HARVEY employs the lattice Boltzmann method (LBM) to solve the fluid flow governing equations. In the LBM framework, distribution functions denoting the density of particles at position and time t with velocity along the ith lattice direction are tracked. The evolution of the distribution functions is governed by the lattice Boltzmann equation:
| 1 |
HARVEY makes use of the standard Bhatnagar–Gross–Krook (BGK) collision operator,4. The distribution functions relax towards the equilibrium distribution function (EDF) at a rate determined by the relaxation time The latter is linked to the kinematic viscosity by where is the speed of sound with being respectively the lattice spacing and time step. The EDF is given by the second-order expansion of the Maxwell–Boltzmann distribution:
| 2 |
where are weight coefficients depending on the chosen lattice arrangement for the velocity discretization, and denotes the identity tensor. Following Reference 18, the discrete forcing scheme takes the form:
| 3 |
with the force term accounting for the interaction between the CTCs and ambient fluid. The fluid density and velocity are given by the 0th and 1st moments of the distribution function:
| 4 |
| 5 |
In HARVEY, the D3Q19 lattice arrangement41 is implemented. The no-slip condition is realized at the vessel walls by the half-way bounce-back boundary scheme,20 while the Zou–He and finite difference boundary schemes adapted to the D3Q19 lattice arrangement13,21 are used to enforce known velocity and pressure profiles at the vessels inlet and outlet. Finally, the WSS is given by the norm of whose vector components are computed by:
| 6 |
denotes the outward unit normal vector, and represent the viscous stress tensor components.
CTC Model and Finite Element Method
CTCs are modelled as fluid-filled capsules of initially spherical shape surrounded by an infinitely thin membrane.7,15,47 The CTCs’ cytoskeleton components, i.e. the actin and intermediate filaments and the microtubules, are treated as cytoplasm, while the presence of nucleus is neglected. For simplicity, the cytoplasm is considered to be an incompressible and Newtonian fluid with the same kinematic viscosity as the ambient fluid. The cell membrane is composed of an isotropic and hyperelastic material whose shear and dilational elastic responses to strain are modelled by the Skalak constitutive law46:
| 7 |
denotes the shear elastic modulus, and C is a dimensionless parameter representing area incompressibility. and are the strain invariants of the Green–Lagrange strain tensor, and further details can be found at Reference 16.
The cell membrane surface is discretized using Loop subdivision elements,5,35 composed of linear triangles refined by a subdivision process. Successive refinements of an icosahedron are considered here, resulting in a triangular mesh of high homogeneity and isotropy.29 The mesh is then projected onto the initially spherical shape.
Immersed Boundary Method
To account for the interaction between the ambient fluid and CTCs, we employ the immersed boundary method, IBM.38 The effect of the cell membrane force density acting on the lth vertex located at is reproduced on the fluid flow using the following spreading operation:
| 8 |
where is a discretized Dirac delta function, and denotes the initial distance between two neighbouring vertices. Once the force is known, Eq. (1) can be solved to obtain the flow field at the next time step The updated velocity field is then interpolated at the membrane vertices as:
| 9 |
with d being the domain dimensionality. Here, Finally, the following formulation of 38 is used to perform the convolution in Eqs. (8) and (9):
| 10 |
The multidimensional is given by .
Modelling Parameters
As mentioned earlier, simulations are performed for three different scenarios:
Considering only the presence of fluid in the re-constructed, double branching vessel model, whose dimensions are mm.
A cluster of CTCs flowing in an idealized bifurcated vessel of diameter which is comparable to that of the vessel used in experiments.
A single CTC in an idealized microvessel bifurcation of diameter
In all simulations, the fluid kinematic viscosity and density are set equal to those of the 3.57% bead solution in HBSS used in experiments, that is m/s and kg/m A relaxation time of is considered here. To ensure accuracy of the numerical solutions, the spacing is taken equal to in case 1, and in cases 2 and 3. CTCs are modelled as initially spherical capsules of diameter where 3 successive refinements of an icosahedron were considered here for the cell surface discretization. The shear elastic modulus varies between and N/m,8,24,47,58 while the dimensionless parameter C is kept constant to for all simulations.
Results and Discussion
Experiment and Simulation in the Double Branching Vessel
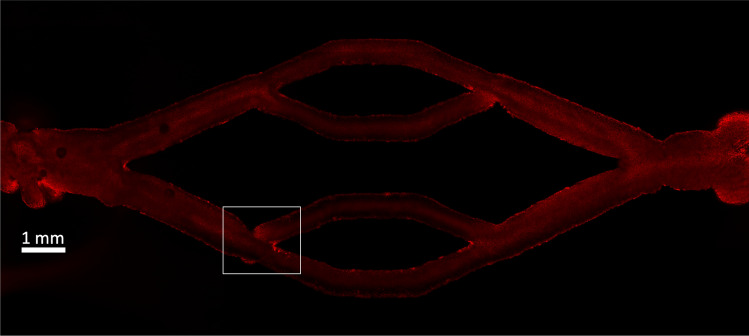
Qualitative visualization found that CTCs have a clear preference to adhere at the bifurcation points of the endothelium-lined vessel, presented in Fig. 1. Greater CTC attachment was observed at the in-flow, or arterial, side of the vessel compared to the out-flow, or venous, side. Higher numbers of attached CTCs were also measured at the second bifurcations on the arterial side, compared to the first bifurcation. Figure 2a shows the fluorescently labelled CTCs attached to the lower-most of the secondary arterial bifurcations—denoted as the region enclosed by the white boundary in Fig. 1, where the highest CTC attachment was experimentally observed. Using morphological operations, the foci and volume of CTCs or contiguous CTC clusters were identified. Figure 2b presents the measured volume in denoted by the numbers in white color, of each identified CTC attachment, where each is depicted by different color. It can clearly be seen that many CTC attachments are multi-cellular, located close to the bifurcation apex rather than the straight portions of the vessel. As mentioned in “Experimental Methods” section, the CTCs suspension was strained with a filter prior to perfusion. Hence, clusters consisting of 2 up to 4 CTCs, or possessing diameters smaller than may have been present in the solution during perfusion. However, it is improbable that the potential presence of these clusters would account for the multi-cellular CTC attachment observed at the bifurcation points, as the volumes of the latter suggest that they are comprised of greater than 4 CTCs. We also acknowledge that the species mismatch between the human endothelial cells and mouse CTCs may have had unknown effects on attachment patterns.
Figure 1.
Cross-section image of the endothelium-lined vessel. The region enclosed by the white boundary corresponds to the site of highest CTC attachment.
Figure 2.

(a) Maximum intensity projection of fluorescently labelled CTCs (red) attached to the wall of the bioprinted vessel (white) shows preferential attachment at the in-flow, lower-most daughter bifurcation. (b) Volume measured in (depicted in white color) of each identified cell attachment (represented by different colors) demonstrates that many attachments are multi-cellular.
To isolate the effect of local hydrodynamics on the location of attachment, a simulation was conducted considering only the presence of fluid in the three-dimensional (3D) vessel model. The 3D vessel model was reconstructed by segmenting axial images of the vessel, as obtained by confocal imaging, using the commercial image processing software “Materialize Mimics”. A steady flow rate of L/min was applied at the vessel inlet to match the flow rate from the experiments. Figure 3a presents the WSS distribution across the 3D vessel model. The colormap was capped at a maximum value of 150.0 dyne/cm for better visual distinction purposes to highlight the local WSS gradient while still visualizing the peak at the lower bifurcation. Higher levels of WSS can be seen at all the bifurcation points except the out-flow, parent one, where no CTC attachment was experimentally observed. At the first and upper-most secondary bifurcations on the arterial side, the WSS increases up to 75.0 dyne/cm A similar observation can be made for the venous, lower-most secondary bifurcation. The WSS elevates to values higher than 150.0 dyne/cm with the maximum WSS being 300.0 dyne/cm at the lower-most secondary bifurcation on the arterial side and upper-most secondary bifurcation on the venous side. It is worth noting that these positions of elevated WSS coincide with the portions of the vessel geometry which were printed with sacrificial ink material connecting back to an existing ink filament.
Figure 3.
(a) Distribution of WSS in the reconstructed, double bifurcation geometry. Higher values of WSS can be seen at the in-flow and out-flow bifurcation points. (b) Velocity streamlines in the double bifurcation geometry recapitulated from experiments. Streamlines indicate areas of higher volumetric flow where cells are more likely to congregate, such as the zoomed-in secondary bifurcation. The flow direction is from left to right.
The velocity streamlines, highlighting areas of higher volumetric flow, are depicted in Fig. 3b. It is known that elastic particles flow closely along the streamlines of the underlying flow when their dimensions are relatively small compared to the flow field.3 Thus, a higher number of CTCs are expected to move towards the arterial, lower-most secondary bifurcation which experiences higher velocities with respect to the arterial, upper-most one. It can clearly be seen at the zoomed-in region of Fig. 3b that the highest velocity magnitudes occur close to the lower-most secondary bifurcation on the arterial side. This observation in conjunction with the elevated WSS of that region clearly demonstrate that the local hydrodynamics significantly affect the preferred CTC attachment sites.
While these results highlight the impact of hydrodynamics on CTC attachment behavior, it should be noted that both the experimental and computational modeling were performed using perfusion solutions that deviate from that of whole blood. Here, a simplified perfusion solution of endothelial cell media containing suspended tumor cells with a known viscosity was used to evaluate the effects of hydrodynamics in a tractable manner. The presence of red blood cells within the flow stream could lead to thrombi formation at the high shear rates of the present experiment, blocking the impingement of CTCs upon the vessel walls. The presence of the blood protein milieu could also affect the probability of CTCs tethering to the endothelium and, thus, their observed cluster formation behaviors.
CTCs Flowing in a Bifurcated Vessel
To further examine the hydrodynamics of the arterial, lower daughter bifurcation, we created an idealized geometry with matched fluid dynamics characteristics to the experimental geometry. This idealized geometry consisted of a 200 diameter parent vessel with a symmetric bifurcation, considering a maximum inlet velocity of 20 mm/s. 45 Cells were randomly placed within a domain in the x and y dimensions centered upstream of the bifurcation. We quantify cell deformability using the capillary number, defined as where U is the undisturbed fluid velocity, is the dynamic viscosity, and is the membrane shear elastic modulus. The capillary numbers examined here are: 0.2, and 2.0, with corresponding to the stiffer CTCs and the most deformable ones. It should be noted that associating certain cancer cell types with the aforementioned capillary numbers is not straightforward. The deformability of cancer cells may vary orders of magnitude among different cell lines and cells of differing metastatic potential.6,33,34 The measured elastic modulus of cancer cells depends also significantly on the employed measurement technique.54
Figure 4 shows a zoomed-in trace of the general path of the centroids of the 45 cells advecting through the bifurcation geometry for a representative case of This trace describes the location of all cell centroids over the course of the entire simulation time of 40 ms and represents a residence time across all cells. We simulated the idealized bifurcation until all of the cells had passed the apex of the bifurcation. As the cells were initially placed near the center of the vessel, they linger and spend more time near the apex of the bifurcation. This result for a suspension of deformable cells matches the streamlines results for the fluid-only simulation presented in Fig. 3b, showing more flow focusing around the secondary bifurcation and, in particular, near the apex of the bifurcation.
Figure 4.

Trace of the 45 cells’ centroid with representing the residence time of all cells for the entire simulation duration. The longer the residence time of a centroid in a given space, the larger the bin count.
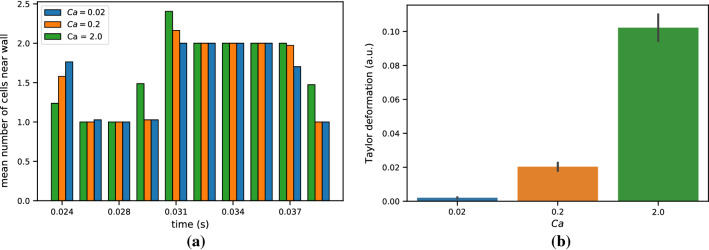
As most of the cells spent the majority of their time near the apex of the bifurcation, we quantified the distribution of WSS in this spatial region centered on the apex of the bifurcation, as highlighted in the upper part of Fig. 5. To elucidate the effect of cell mechanical properties on the fluid dynamics of flow in the bifurcation, we examined the aforementioned WSS characteristics as they vary by 0.2, and 2.0. While the mean WSS in the apex region was similar between the three cell type deformabilities, the maximum WSS in the region showed differences between the three capillary numbers as seen in Fig. 5. This difference in maximum WSS coincided with the time when the majority of the cells have already passed by the primary portion of the bifurcation, but cells near the rear of the group lingered closer to the apex of the bifurcation than the others.
Figure 5.

Maximum WSS in the spatial region near the apex of bifurcation, as indicated by the red box above. The simulation snapshots shown above correspond to the () case. The maximum instantaneous WSS occurs when most of the cells have passed the bifurcation, with the last few approaching closest to the wall.
We further explored the effects of cell deformability on the trajectory of a bolus of cells in the idealized bifurcation. This was followed by quantification of how many cells closely approached the walls, as this convergent motion may affect the local WSS and provide insight on the causes leading to differences in maximum WSS between the varying cell deformabilities. We show that the more deformable cells stray nearer to the wall than their less deformable counterparts, as exhibited by the average count of cells near the wall in Fig. 6a. Cells were characterized as near the wall by determining whether their centroid was within a set threshold distance from the nearest endothelial wall point. This threshold was set to be 1.25 times the cell diameter (12.5 ). As expected, the cells with greater deformability possessed a greater average Taylor deformation than those with lower Skalak moduli when in close proximity to the wall, as exhibited in Fig. 6b. The Taylor deformation was averaged over all the cells considered to be near the wall and averaged over the span of simulation time.
Figure 6.
(a) The average number of cells within 12.5 of the bifurcation wall, as measured by the distance to the cell centroid. The cell count has been averaged over a time window for presentation purposes. (b) The average Taylor deformation over the span of simulated time for cells near the wall, as defined in (a). The error bars denote standard deviation.
Single CTC in a Microvessel Bifurcation
Lastly, we investigate CTC behavior in a microvessel bifurcation. While the hydrodynamics are different in microscale vessels, as compared to the larger vessels considered in the previous sections, we use these simulations to provide further insight into wall shear stress trends for cases with strong near-wall cell behavior.
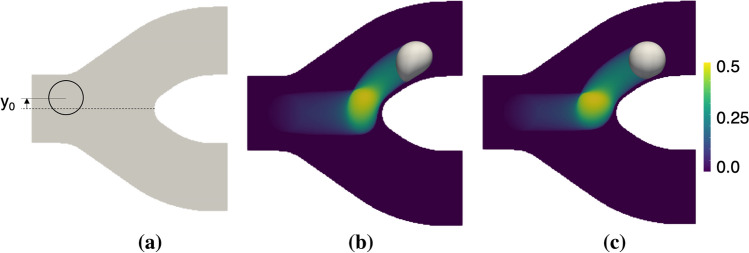
Figure 7a provides a schematic depicting the simulated bifurcation. Cells are initially placed in the feeding vessel, offset from the centerline by a distance The bifurcation geometry is symmetric, consisting of parent and daughter vessels with diameters of and we consider an inlet velocity of 5 mm/s. In the present study, we consider three different capillary numbers spanning the same order of magnitude as that used in the previous section, and for simplicity we consider Ca = 0.01, 0.1 and 1.0. As mentioned before, the higher the capillary number, the more deformable the cell is. For each of these, we investigate cell behavior and impact on the WSS at four different initial cell positions, namely 0.5, 1.0 and 1.5 Figures 7b and 7c depict behavior we generally observe as a CTC flows through the bifurcation, whereby the cell rapidly approaches the apex, it lingers on the apex for some time, and then eventually flows into the daughter branch. In these figures, the contours depict an occupational probability function (OPF), which here gives the relative magnitude of residence time at locations in space as the cell traverses the bifurcation. Figures 7b and 7c are for Ca = 1.0 and 0.01 cells, respectively. For each scenario, the bright contours around the bifurcation apex depict this lingering behavior, and differences in deformability between the two can be seen in the width of the OPF field as well as the instantaneous cell shapes.
Figure 7.
Simulation setup and observed cell behavior. (a) Schematic depicting the simulated bifurcation. Cells are initially placed in the feeding vessel, offset from the centerline by a distance (b and c) OPF contours giving the relative magnitude of residence time at a location in space as the cell traverses the bifurcation, for cells with Ca = 1.0 and 0.01, respectively.
We subsequently investigate the impact of cell deformability and initial cell location on the time-averaged wall shear stress (TAWSS), calculated at all Eulerian wall points and then spatially averaged over a region encapsulating the bifurcation apex. We utilize TAWSS here in lieu of WSS in order to better facilitate a parametric analysis of the behavior. In this study, we seek to provide insight into the differences in the general TAWSS trends owing primarily to variations in the cell deformability. Cells of varying deformability will experience differing near-wall interactions during their transport through the bifurcated microvessel, manifesting through differences in the resulting cell shapes. The latter will cause, in turn, changes in the observed TAWSS trends.
Contours of the TAWSS are provided in Fig. 8 for two representative cases, along with snapshots of the CTC superimposed at four successive instants in time. Figures 8a and 8b are for a Ca = 1.0 cell with initial offset The region of enhanced TAWSS along the upper side of the bifurcation apex is apparent in Fig. 8a, and occurs due to the trajectory and near-wall behavior of the cell for this case. In Fig. 8b the cell trajectory and evolving shape are depicted at successive time-instants denoted as The cell lingers for a short time around the bifurcation apex, before quickly moving towards the upper daughter microvessel. In contrast, Figs. 8c and 8d are for a cell with the same stiffness but with an initial offset Due to the initial placement and cell deformability, the cell spends a much longer time moving around the bifurcation apex compared with that in Fig. 8b. This finding is illustrated in Fig. 8d, where snapshots of the cell are given at the same time instants as in Fig. 8b. This near-wall behavior results in the lower TAWSS values shown in Fig. 8c, an observation discussed below in more detail.
Figure 8.
TAWSS contours and cell behavior. (a) Contours of TAWSS for a Ca = 1.0 cell with initial placement which are also shown in (b) behind snapshots of the cell at four successive instants in time (). (c) Contours of TAWSS for a Ca = 1.0 cell with initial placement along with (d) snapshots of the cell at the same four time instances as in (b).
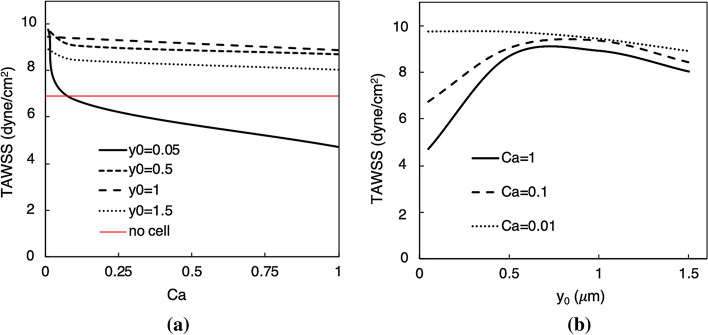
Figure 9a provides results for TAWSS vs. Ca, at each of the four initial positions. First, it can be generally seen that for a given the average TAWSS decreases with increasing capillary number. This is most pronounced for the case, which represents the case where the cell is initially placed very close to the bifurcation centerline. For this case we observe that as the cell deformability increases (i.e. increasing Ca), the cell tends to spend a relatively long time lingering around the apex before slowly flowing into the daughter branch. Due to the slow near-wall cell velocity during this process, the near-wall velocity gradient is reduced which results in a sharply decreasing TAWSS relative to the other cases in Fig. 9a. Interestingly, this slow near-wall behavior causes the TAWSS to become lower than that observed in the absence of a cell (red line in Fig. 9a). With increasing distance from the wall, Fig. 9a shows that the TAWSS is higher than that observed without cells. The curve for the case is below that for the which reveals that as the cell is initially displaced progressively off of the centerline, when it flows through the bifurcation the near-wall cell velocity and thus TAWSS increases. However, we observe that at the TAWSS curve falls below these curves. This occurs because at this initial location the corresponding trajectory of the cell through the bifurcation is relatively farther from the inner wall.
Figure 9.
Time-averaged TAWSS trends for the region around the bifurcation apex. (a) TAWSS vs. capillary number (Ca), for different values of initial cell placement ( in ). Here, the red line gives the TAWSS value in the absence of any CTC. (b) TAWSS vs. initial placement, for different values of capillary number
Figure 9b further depicts the observed relationship between and TAWSS, except that here curves correspond to different Ca values. As it can be seen, for the more deformable cells (i.e. Ca = 1.0 and 0.1) the trend is non-monotonic. For small values of with these cells the TAWSS is relatively small, which we observe due to increased cell residence time around the apex and reduced near-wall velocity. With increasing the TAWSS increases to a maximum between and due to increasing near-wall velocity. At distances farther than this, the TAWSS begins to decrease again as the cells generally begin to flow farther from the wall. For the stiffest cell (Ca = 0.01), the picture in Fig 9b is different as the trend is monotonic. We observe that because the cell does not appreciably deform for this case, the residence time is not enhanced by motion and interaction around the apex as occurs with the more deformable cells. As such, the cell more quickly flows around the apex resulting in the observed TAWSS behavior.
Conclusions
In the current study, a series of examinations have been pursued to further explore the relationship between local hydrodynamics, in particular WSS, and residence time of CTCs with varying deformability at vessels of different characteristic length scales. We have conducted a bioreactor-based flow experiment examining murine mammary gland carcinoma cells attachment within a bioprinted, endothelium-lined vessel with a double bifurcation. This double branching vessel encompasses both arterial (in-flow) and venous (out-flow) flow characteristics, that are crucial for the understanding of CTC transport in complex vasculature. Experimentally, CTCs demonstrated a clear preference to adhere at the bifurcation points, in particular the arterial, daughter ones. We have next performed a fluid-only simulation in the reconstructed, 3D vessel model of the bioprinted device to explore the effect of local hydrodynamics on the CTC attachment sites using HARVEY, our in-house massively parallel computational fluid dynamics solver. Increased values of velocity magnitude (3-fold) and WSS (up to 7-fold) were observed at the regions of high CTC attachment observed in experiments. This indicates the significant impact that vessel topology has upon the preferred CTC attachment locations.
To further investigate the interactions between the local hydrodynamics and CTC motion around a branching point, we have conducted simulations in an idealized, cylindrical bifurcation vessel, providing a more controlled environment while allowing for matched flow characteristics. We have examined CTCs with three different cell deformabilities. Higher values of maximum WSS were observed in the apex region of the bifurcation for the stiffer CTCs ( N/m). The relative difference in the maximum WSS when the CTCs reside or not close to the apex wall was measured to be about for the most deformable cell ( N/m) and for the stiffer CTCs. This demonstrates that the vessel topology affects primarily the local hydrodynamics, with the presence of CTCs having a secondary role.
This secondary role is amplified in the case of a single CTC flowing in a bifurcated microvessel, as shown by simulations. Depending on the initial position and deformability of the CTC, different behaviors are observed in the WSS patterns. Additionally, we find that there is an optimal position displaced from the centerline that results in the highest WSS. Locations farther away cause the WSS to decrease, which is also observed at locations closer to the centerline. For more deformable cells initially placed very close to the centerline we find a significant reduction in near-wall velocity on account of the interaction with the geometry that can reduce the WSS to below that which is experienced without cells. As the cells become less deformable they tend to flow relatively more easily around the apex which results in a monotonic trend between WSS and initial position.
In the present work, we have focused computationally on the early stage of the metastatic process involving the circulation of tumor cells in the vasculature and their initial collision with the vessel walls. This stage, preceding the CTC arrest mediated by the formation of adhesive bonds and ensuing extravasation, is of crucial importance in anticipating prospective extravasation sites in the vasculature. Local hemodynamics variations in this stage are, however, primarily owing to the vessel anatomy. Taking into account the insights gained from the current study, we aim in the future to extend our understanding on the correlation between CTC arrest sites and local hemodynamics by taking into consideration a ligand–receptor interaction model, recently incorporated in HARVEY.7 CTC adhesion to the endothelium requires a fine balance of hydrodynamic shear and adhesion forces. It is known that reduced fluid shear forces promote CTC attachment.14,31,43 During CTC arrest, increases in the wall shear stress at the attachment site have been observed, which depend on the flow rate and cell deformability.10,11,24,26 Quantifying the optimal values of fluid shear rate, CTC deformability, adhesion forces and WSS leading to firm CTC adhesion and extravasation in complex vasculatures remains still an open question. In vivo, CTCs interact with flowing red blood cells (RBCs) too, where the presence of the latter enhances the CTCs collisions with the vascular wall and, thus, the probability of CTC adhesion to occur.36,37,55 Having recently incorporated a RBC model in our numerical framework44 will enable us in the future to explore more physiologically relevant situations in conjunction with experiments performed with whole blood, thus accounting for the effect of hematocrit in the interplay of CTC attachment and hemodynamics.
Acknowledgments
Research reported in this publication was supported by the Office of the Director of the National Institutes of Health under Award Number DP5OD019876. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This work was funded by LDRD 17ERD054 and LDRD 18ERD062 and performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 (LLNL-JRNL-805606). Computing support for this work came from the LLNL Institutional Computing Grand Challenge Program. This work also used the Extreme Science and Engineering Discovery Environment (XSEDE) resource, Stampede2, at the Texas Advanced Computing Center through Allocation TG-IBN190011.48 The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper.
Conflict of interest
Marianna Pepona, Peter Balogh, Daniel F. Puleri, William F. Hynes, Claire Robertson, Karen Dubbin, Javier Alvarado, Monica L. Moya, and Amanda Randles declare that they have no conflict of interest.
Ethical Approval
No human studies were carried out by the authors for this article. No animal studies were carried out by the authors for this article.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Anderson KJ, de Guillebon A, Hughes AD, Wang W, King MR. Effect of circulating tumor cell aggregate configuration on hemodynamic transport and wall contact. Math. Biosci. 2017;294:181–194. doi: 10.1016/j.mbs.2017.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Balogh P, Bagchi P. Analysis of red blood cell partitioning at bifurcations in simulated microvascular networks. Phys. Fluids. 2018;30:051902. [Google Scholar]
- 3.Barber JO, Alberding JP, Restrepo JM, Secomb TW. Simulated two-dimensional red blood cell motion, deformation and partitioning in microvessel bifurcations. Ann. Biomed. Eng. 2008;36:1690–1698. doi: 10.1007/s10439-008-9546-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bhatnagar PL, Gross EP, Krook M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954;94:511–525. [Google Scholar]
- 5.Cirak F, Ortiz M, Schröder P. Subdivision surfaces: a new paradigm for thin-shell finite-element analysis. Int. J. Numer. Methods Eng. 2000;47:2039–2072. [Google Scholar]
- 6.Correia Faria E, Ma N, Gazi E, Gardner P, Brown M, Clarke NW, Snook RD. Measurement of elastic properties of prostate cancer cells using AFM. Analyst. 2008;133:1498–1500. doi: 10.1039/b803355b. [DOI] [PubMed] [Google Scholar]
- 7.Dabagh M, Gounley J, Randles A. Localization of rolling and firm–adhesive interactions between circulating tumor cells and the microvasculature wall. Cell. Mol. Bioeng. 2020;13:141–154. doi: 10.1007/s12195-020-00610-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dabagh M, Randles A. Role of deformable cancer cells on wall shear stress-associated-VEGF secretion by endothelium in microvasculature. PLoS ONE. 2019;14:e0211418. doi: 10.1371/journal.pone.0211418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.dela Paz NG, Walshe TE, Leach LL, Saint-Geniez M, D’Amore PA. Role of shear-stress-induced VEGF expression in endothelial cell survival. J. Cell Sci. 2012;125:831–843. doi: 10.1242/jcs.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dong C, Cao J, Struble EJ, Lipowsky HH. Mechanics of leukocyte deformation and adhesion to endothelium in shear flow. Ann. Biomed. Eng. 1999;27:298–312. doi: 10.1114/1.143. [DOI] [PubMed] [Google Scholar]
- 11.Dong C, Lei XX. Biomechanics of cell rolling: shear flow, cell–surface adhesion, and cell deformability. J. Biomech. 2000;33:35–43. doi: 10.1016/s0021-9290(99)00174-8. [DOI] [PubMed] [Google Scholar]
- 12.Doyeux V, Podgorski T, Peponas S, Ismail M, Coupier G. Spheres in the vicinity of a bifurcation: elucidating the Zweifach–Fung effect. J. Fluid Mech. 2011;674:359–388. [Google Scholar]
- 13.Feiger B, Vardhan M, Gounley J, Mortensen M, Nair P, Chaudhury R, Frakes D, Randles A. Suitability of lattice Boltzmann inlet and outlet boundary conditions for simulating flow in image-derived vasculature. Int. J. Numer. Methods Biomed. Eng. 2019;35:e3198. doi: 10.1002/cnm.3198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Follain G, Osmani N, Azevedo AS, Allio G, Mercier L, Karreman MA, Solecki G, GarciaLèon MJ, Lefebvre O, Fekonja N, Hille C, Chabannes V, Dollé G, Metivet T, DerHovsepian F, Prudhomme C, Pichot A, Paul N, Carapito R, Bahram S, Ruthensteiner B, Kemmling A, Siemonsen S, Schneider T, Fiehler J, Glatzel M, Winkler F, Schwab Y, Pantel K, Harlepp S, Goetz JG. Hemodynamic forces tune the arrest, adhesion and extravasation of circulating tumor cells. Dev. Cell. 2018;45:33–52. doi: 10.1016/j.devcel.2018.02.015. [DOI] [PubMed] [Google Scholar]
- 15.Gounley, J., E. W. Draeger, and A. Randles. Numerical simulation of a compound capsule in a constricted microchannel. Procedia Comput. Sci. 108, 175–184 (2017). In: International Conference on Computational Science, ICCS 2017, 12–14 June 2017, Zurich, Switzerland. [DOI] [PMC free article] [PubMed]
- 16.Green AE, Adkins JE. Large Elastic Deformations. Oxford: Oxford University Press; 1960. [Google Scholar]
- 17.Guo P, Cai B, Lei M, Liu Y, Fu BM. Differential arrest and adhesion of tumor cells and microbeads in the microvasculature. Biomech. Model. Mechanobiol. 2014;13:537–550. doi: 10.1007/s10237-013-0515-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Guo Z, Zheng C, Shi B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E. 2002;65:046308. doi: 10.1103/PhysRevE.65.046308. [DOI] [PubMed] [Google Scholar]
- 19.Häner E, Heil M, Juel A. Deformation and sorting of capsules in a T-junction. J. Fluid Mech. 2020;885:A4. [Google Scholar]
- 20.He X, Zou Q, Luo LS, Dembo M. Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model. J. Stat. Phys. 1997;87:115–136. [Google Scholar]
- 21.Hecht M, Harting J. Implementation of on-site velocity boundary conditions for D3Q19 lattice Boltzmann simulations. J. Stat. Mech. 2010;2010:P01018. [Google Scholar]
- 22.Huang Q, Hu X, He W, Zhao Y, Hao S, Wu Q, Li S, Zhang S, Shi M. Fluid shear stress and tumor metastasis. Am. J. Cancer Res. 2018;8:763–777. [PMC free article] [PubMed] [Google Scholar]
- 23.Hyakutake T, Nagai S. Numerical simulation of red blood cell distributions in three-dimensional microvascular bifurcations. Microvasc. Res. 2015;97:115–123. doi: 10.1016/j.mvr.2014.10.001. [DOI] [PubMed] [Google Scholar]
- 24.Jadhav S, Eggleton CD, Konstantopoulos K. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 2005;88:96–104. doi: 10.1529/biophysj.104.051029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kaliviotis E, Sherwood JM, Balabani S. Partitioning of red blood cell aggregates in bifurcating microscale flows. Sci. Rep. 2017;7:44563. doi: 10.1038/srep44563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Khismatullin DB, Truskey GA. A 3D numerical study of the effect of channel height on leukocyte deformation and adhesion in parallel-plate flow chambers. Microvasc. Res. 2004;68:188–202. doi: 10.1016/j.mvr.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 27.King MR, Phillips KG, Mitrugno A, Lee TR, de Guillebon AME, Chandrasekaran S, McGuire MJ, Carr RT, Baker-Groberg SM, Rigg RA, Kolatkar A, Luttgen M, Bethel K, Kuhn P, Decuzzi P, McCarty OJT. A physical sciences network characterization of circulating tumor cell aggregate transport. Am. J. Physiol. Cell Physiol. 2015;308:C792–C802. doi: 10.1152/ajpcell.00346.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kolesky DB, Homan KA, Skylar-Scott MA, Lewis JA. Three-dimensional bioprinting of thick vascularized tissues. Proc. Natl Acad. Sci. USA. 2016;113:3179–3184. doi: 10.1073/pnas.1521342113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Krüger T, Varnik F, Raabe D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 2011;61:3485–3505. [Google Scholar]
- 30.Lawrence MB, McIntire LV, Eskin SG. Effect of flow on polymorphonuclear leukocyte/endothelial cell adhesion. Blood. 1987;70:1284–1290. [PubMed] [Google Scholar]
- 31.Lawrence MB, Smith CW, Eskin SG, McIntire LV. Effect of venous shear stress on CD18-mediated neutrophil adhesion to cultured endothelium. Blood. 1990;75:227–237. [PubMed] [Google Scholar]
- 32.Leble V, Lima R, Dias R, Fernandes C, Ishikawa T, Imai Y, Yamaguchi T. Asymmetry of red blood cell motions in a microchannel with a diverging and converging bifurcation. Biomicrofluidics. 2011;5:044120. doi: 10.1063/1.3672689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lekka M, Pogoda K, Gostek J, Klymenko O, Prauzner-Bechcicki S, Wiltowska-Zuber J, Jaczewska J, Lekki J, Stachura Z. Cancer cell recognition—mechanical phenotype. Micron. 2012;43:1259–1266. doi: 10.1016/j.micron.2012.01.019. [DOI] [PubMed] [Google Scholar]
- 34.Li QS, Lee GYH, Ong CN, Lim CT. AFM indentation study of breast cancer cells. Biochem. Biophys. Res. Commun. 2008;374:609–613. doi: 10.1016/j.bbrc.2008.07.078. [DOI] [PubMed] [Google Scholar]
- 35.Loop, C. Smooth Subdivision Surfaces Based on Triangles. Master’s Thesis, The University of Utah, 1987.
- 36.Melder RJ, Munn LL, Yamada S, Ohkubo C, Jain RK. Selectin- and integrin-mediated T-lymphocyte rolling and arrest on TNF--activated endothelium: augmentation by erythrocytes. Biophys. J. 1995;69:2131–2138. doi: 10.1016/S0006-3495(95)80087-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Munn LL, Melder RJ, Jain RK. Role of erythrocytes in leukocyte–endothelial interactions: mathematical model and experimental validation. Biophys. J. 1996;71:466–478. doi: 10.1016/S0006-3495(96)79248-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 39.Phillips KG, Lee AM, Tormoen GW, Rigg RA, Kolatkar A, Luttgen M, Bethel K, Bazhenova L, Kuhn P, Newton P, McCarty OJT. The thrombotic potential of circulating tumor microemboli: computational modelling of circulating tumor cell-induced coagulation. Am. J. Physiol. Cell Physiol. 2015;308:C229–C236. doi: 10.1152/ajpcell.00315.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pulaski BA, Ostrand-Rosenberg S. Mouse 4T1 breast tumor model. Curr. Protoc. Immunol. 2000;39:20.2.1–20.2.16. doi: 10.1002/0471142735.im2002s39. [DOI] [PubMed] [Google Scholar]
- 41.Qian YH, D’Humières D, Lallemand P. Lattice BGK models for Navier–Stokes equation. EPL. 1992;17:479–484. [Google Scholar]
- 42.Randles, A. P., V. Kale, J. Hammond, W. Gropp, and E. Kaxiras. Performance analysis of the lattice Boltzmann model beyond Navier–Stokes. In: 2013 IEEE 27th International Symposium on Parallel and Distributed Processing (IPDPS). IEEE, 2013, pp. 1063–1074.
- 43.Regmi S, Fu A, Luo KQ. High shear stresses under exercise condition destroy circulating tumor cells in a microfluidic system. Sci. Rep. 2017;7:39975. doi: 10.1038/srep39975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roychowdhury, S., J. Gounley, and A. Randles. Evaluating the influence of hemorheological parameters on circulating tumor cell trajectory and simulation time. In: The Platform for Advanced Scientific Computing (PASC) Conference. ACM, 2020.
- 45.Secomb TW, Styp-Rekowska B, Pries AR. Two-dimensional simulation of red blood cell deformation and lateral migration in microvessels. Ann. Biomed. Eng. 2007;35:755–765. doi: 10.1007/s10439-007-9275-0. [DOI] [PubMed] [Google Scholar]
- 46.Skalak R, Tozeren A, Zarda RP, Chien S. Strain energy function of red blood cell membranes. Biophys. J. 1973;13:245–264. doi: 10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Takeishi N, Imai Y, Yamaguchi T, Ishikawa T. Flow of a circulating tumor cell and red blood cells in microvessels. Phys. Rev. E. 2015;92:063011. doi: 10.1103/PhysRevE.92.063011. [DOI] [PubMed] [Google Scholar]
- 48.Towns J, Cockerill T, Dahan M, Foster I, Gaither K, Grimshaw A, Hazlewood V, Lathrop S, Lifka D, Peterson GD, et al. Xsede: accelerating scientific discovery. Comput. Sci. Eng. 2014;16(5):62–74. [Google Scholar]
- 49.Urbich C, Stein M, Reisinger K, Kaufmann R, Dimmeler S, Gille J. Fluid shear stress-induced transcriptional activation of the vascular endothelial growth factor receptor-2 gene requires Sp1-dependent DNA binding. FEBS Lett. 2003;535:87–93. doi: 10.1016/s0014-5793(02)03879-6. [DOI] [PubMed] [Google Scholar]
- 50.Wang Z, Sui Y, Salsac AV, Barthès-Biesel D, Wang W. Motion of a spherical capsule in branched tube flow with finite inertia. J. Fluid Mech. 2016;806:603–626. [Google Scholar]
- 51.Wang Z, Sui Y, Salsac AV, Barthès-Biesel D, Wang W. Path selection of a spherical capsule in a microfluidic branched channel: towards the design of an enrichment device. J. Fluid Mech. 2018;849:136–162. [Google Scholar]
- 52.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 2011;11:512–522. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Woolfenden HC, Blyth MG. Motion of a two-dimensional elastic capsule in a branching channel flow. J. Fluid Mech. 2011;669:3–31. [Google Scholar]
- 54.Wu PH, Raz-Ben Aroush D, Asnacios A, Chen WC, Dokukin ME, Doss BL, Durand-Smet P, Ekpenyong A, Guck J, Guz NV, Janmey PA, Lee JSH, Moore NM, Ott A, Poh YC, Ros R, Sander M, Sokolov I, Staunton JR, Wang N, Whyte G, Wirtz D. A comparison of methods to assess cell mechanical properties. Nat. Methods. 2018;15:491–498. doi: 10.1038/s41592-018-0015-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Xiao LL, Liu Y, Chen S, Fu BM. Effects of flowing RBCs on adhesion of a circulating tumor cell in microvessels. Biomech. Model. Mechanobiol. 2017;16:597–610. doi: 10.1007/s10237-016-0839-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Xiong W, Zhang J. Two-dimensional lattice Boltzmann study of red blood cell motion through microvascular bifurcation: cell deformability and suspending viscosity effects. Biomech. Model. Mechanobiol. 2012;11:575–583. doi: 10.1007/s10237-011-0334-y. [DOI] [PubMed] [Google Scholar]
- 57.Xu Y, Tian F, Li H, Deng Y. Red blood cell partitioning and blood flux redistribution in microvascular bifurcation. Theor. Appl. Mech. Lett. 2012;2:024001. [Google Scholar]
- 58.Yan WW, Cai B, Liu Y, Fu BM. Effects of wall shear stress and its gradient on tumor cell adhesion in curved microvessels. Biomech. Model. Mechanobiol. 2012;11:641–653. doi: 10.1007/s10237-011-0339-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yan WW, Liu Y, Fu BM. Effects of curvature and cell–cell interaction on cell adhesion in microvessels. Biomech. Model. Mechanobiol. 2010;9:629–640. doi: 10.1007/s10237-010-0202-1. [DOI] [PubMed] [Google Scholar]
- 60.Ye H, Huang H, Lu X. Numerical study on dynamic sorting of a compliant capsule with a thin shell. Comput. Fluids. 2015;114:110–120. [Google Scholar]
- 61.Yin X, Thomas T, Zhang J. Multiple red blood cell flows through microvascular bifurcations: cell free layer, cell trajectory, and hematocrit separation. Microvasc. Res. 2013;89:47–56. doi: 10.1016/j.mvr.2013.05.002. [DOI] [PubMed] [Google Scholar]