Abstract
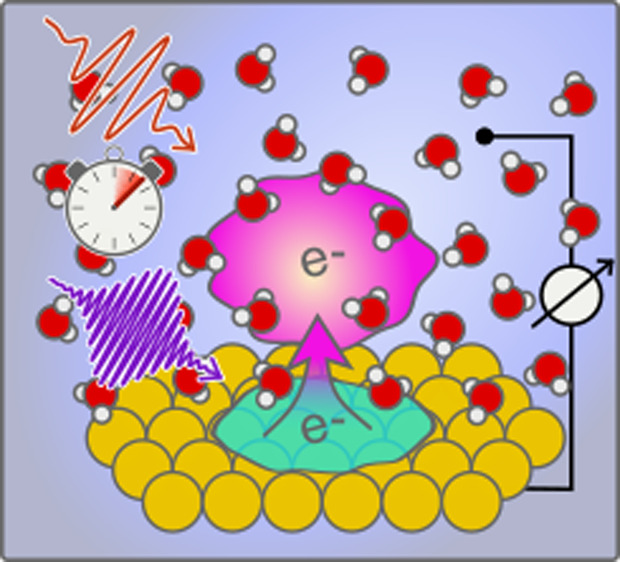
The hydrated electron has fundamental and practical significance in radiation and radical chemistry, catalysis, and radiobiology. While its bulk properties have been extensively studied, its behavior at solid/liquid interfaces is still unclear due to the lack of effective tools to characterize this short-lived species in between two condensed matter layers. In this study, we develop a novel optoelectronic technique for the characterization of the birth and structural evolution of solvated electrons at the metal/liquid interface with a femtosecond time resolution. Using this tool, we record for the first time the transient spectra (in a photon energy range from 0.31 to 1.85 eV) in situ with a time resolution of 50 fs revealing several novel aspects of their properties at the interface. Especially the transient species show state-dependent optical transition behaviors from being isotropic in the hot state to perpendicular to the surface in the trapped and solvated states. The technique will enable a better understanding of hot electron driven reactions at electrochemical interfaces.
Introduction
The hydrated electron is the most fundamental ion in aqueous solution,1 a metastable structure of water molecules interacting with a free electron. In bulk water, the hydrated electron’s lifetime is relatively long, reaching up to microseconds,2 but its strong reducing potential renders it highly reactive, and thus short-lived, in the presence of electron acceptors. Consequently, hydrated electrons can damage DNA, create radicals, and induce a plethora of reductive reactions. Electrons in solution have been extensively studied from the standpoint of radiobiology, radical and radiation chemistry, and charge transfer systems for their importance in radiotherapy, physiology, catalysis, and atmospheric reactions.3−6
The hydrated electron structure and dynamics from inception to solvation are well-known from experimental work in the bulk,7−11 in clusters,12−14 and at the metal/thin amorphous ice interface.15−17 Numerous theoretical and computational contributions have been instrumental to the understanding of the hydrated electron and its precursor states.18,19 Work is also underway to better understand its behavior at the air/water interface.20−25 In bulk water, the generally accepted model proposes that a four-to-six-molecule solvation shell hosts the electron in a cavity18,26 with a radius of gyration (rg) of ∼2.45 Å.1 Schwartz et al. proposed an alternative noncavity model where the bulk hydrated electron would reside in a volume of increased water density,27,28 but the noncavity model still lacks extensive support from experimental and computational evidence and is contested in the literature.19 The hydrated electron is, however, much less well understood at the metal/liquid water interface than in the bulk, presumably because of the lack of suitable experimental characterization tools for such an environment.
Assuredly, the electrified metal/electrolyte interface29,30 is highly relevant to technological systems—e.g., batteries, fuel cells, Grätzel’s cells—that rely on heterogeneous electron transfer31,32 to store and convert energy or to carry out electrochemical reactions. Improving such devices requires understanding the mechanism by which the electron moves across the solid/liquid interface. However, such a task is extremely challenging as the charge transfer dynamics are exceedingly short, on the femto- to picosecond time scale.
Conventional electrochemical methods, such as those based on potential sweep or impedance measurements, may access the time scale of tens of nanoseconds at best,33,34 which may be sufficient to address the mass diffusion physics. They are, however, unfit to provide the desired dynamical information on ultrafast time scales (≪picoseconds), on which hot electron relaxation, solvent reorganization, and photoexcited isomerization take place. To study these processes, an integration of ultrashort laser pulses and electrochemical control has the potential to grant access to the relevant time scales, provided that several significant obstacles can be resolved.
From an experimental perspective, elucidating the mechanism of electron transfer under steady-state nonequilibrium conditions is generally not possible: a perturbation experiment is required, in which the electron transfer is triggered at a well-defined time and the electrochemical interface is characterized with a high time resolution as the system returns to steady state.35 However, as mentioned above, performing such an experiment with a conventional electrical detection scheme also has a limited time resolution, which is set by the RC value of the system, i.e., ≫nanoseconds, regardless of the electrical or optical trigger length.36−41
To investigate with higher time resolution the ejection of an electron from a metal and the formation of a solvated electron, several groups have characterized model systems in UHV, i.e., solids with a few monolayers of ice, using femtosecond optical pulses to initiate the electron transfer and femtosecond-resolved photoemission measurements as a probe.42,43 While this approach to model systems yielded important and interesting developments, we need to perform measurements with a similar time resolution under operando conditions to appropriately characterize the reactions at the electrified electrochemical interface. Unfortunately, the thick liquid layer covering the buried interface precludes direct application of UHV surface science techniques in which electrons or atoms are probes. Moreover, purely optical techniques often suffer from interfering signals from the metal surface charge dynamics: the pump pulse both perturbs the metal surface electronic structure and causes an electron transfer, making the deconvolution from the sought-after signal difficult. In part because of those challenges, there are no reports of the spectral observables that offer insight into the structure of the hydrated electron at electrochemical interfaces.
We have developed a surface-sensitive optoelectronic technique for the synthesis and detection of hydrated electrons at the electrode/electrolyte interface that gives access to the interfacial dynamics from birth to the solvation of the electron species. This method reveals not only the transient spectra of different interfacial hydrated electron states, from the terahertz/mid-infrared (THz/MIR) to the near-infrared (NIR) spectral region, but also the polarization properties of the transient species. Because the method demonstrated here is quite general, we expect it to find wide applicability in the study of the structure and dynamics of short-lived ionic species at electrochemical interfaces.
Experimental Section
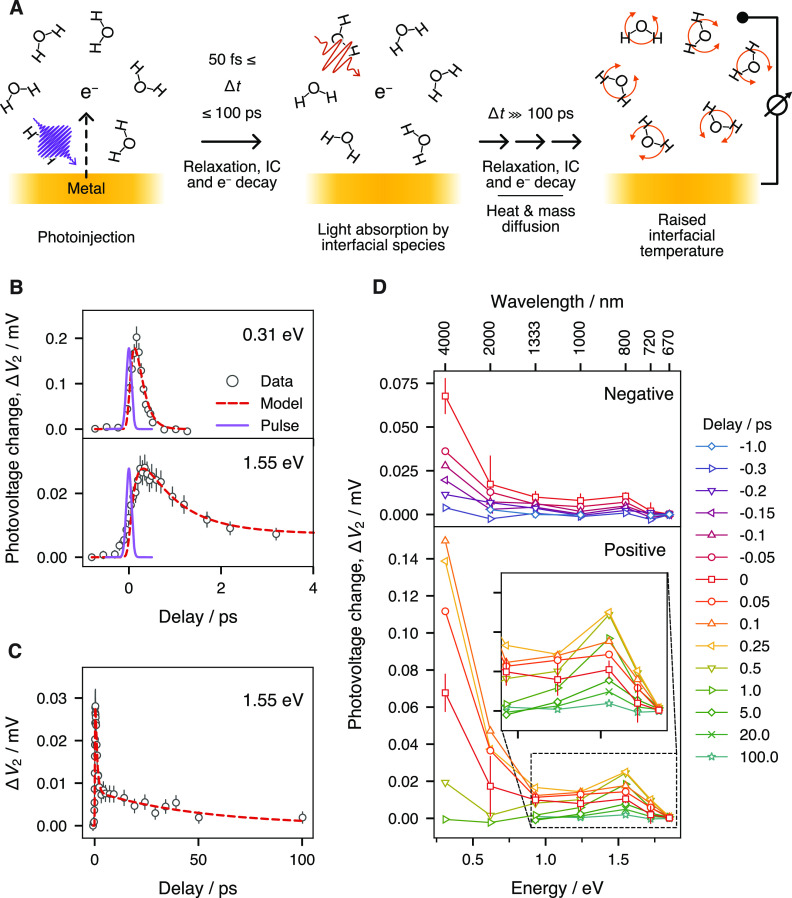
Schematics of the principles of the method are depicted in Figure 1A, and the idealized photovoltage profile at various stages of the measurement is shown in Figure S1. In brief, through excitation by an ultrashort UV pulse (1 kHz, 267 nm) with a fluence of ≈0.6 mJ/cm2, electrons are ejected from the electrode into the solution using the photoelectric process. This creates a photovoltage ΔV1, which can be measured using a conventional potentiostat, that reaches a stationary value after 20–30 min as governed by mass transport and the cell geometry. A second pulse of lower photon energy (same repetition rate) is used to perturb the stabilized system at a variable ultrashort time delay. A photovoltage change ΔV2 is induced that depends strongly on the photon energy of the second pulse and the delay between the two pulses. Measuring and extracting ΔV2 for a series of delay values yields a trace reflecting the ultrafast hydrated electron dynamics at the electrode interface. It is noteworthy that, while the electrochemical equilibrium is slow, an ultrafast time resolution can still be achieved because it is controlled by the cross-correlation of the two pump pulses. A detailed explanation of how these laser-related factors and ultrafast dynamics of the excess electrons are decoupled from the slow electrochemical kinetics at the metal/solution interface is given in the Supporting Information.
Figure 1.
(A) Schematic of the method. (B, C) Photovoltage change ΔV2 versus delay time. (B) At delay times smaller than 4 ps. (C) At longer delay times, up to 100 ps. Red dashed traces show the best fit of the three-level hydrated electron model, while the thin blue lines show the position and width of the UV pump pulse. (D) Photovoltage change ΔV2 sliced at different delay times, presented against the second pump energy. (top panel) At negative delay times. (bottom panel) Positive delay times. (inset) Zoom of the region around the shoulder at 1.55 eV. Error bars were estimated from the potentiostat readout noise and laser beam power fluctuations. For the sake of clarity, representative error bars are given only for the data at a delay of 0 ps in (D).
The UV pulse at 267 nm (4.64 eV) is generated by tripling a 800 nm (1.55 eV) pulse in two β-barium borate (BBO) crystals in series. The Gaussian full width at half-maximum (fwhm) of the UV pulse is ≈110 fs after transmission through the lens, window, and water layer overlying the sample (see the Supporting Information). Various combinations of an optical parametric amplifier (OPA) and a noncollinear difference frequency generation accessory (nDFG) were used to obtain pulses of different photon energies for the second pump (see the Supporting Information for details). The second pump pulses had an estimated Gaussian fwhm of ∼80 fs. The second laser pulse is delayed with respect to the first pulse by times ranging from −4 to 100 ps, such that a full delay trace is created at every photon energy. The UV-induced bleaching of the nonresonant sum-frequency-generation (SFG) signal of the gold surface, generated by mixing a 1.55 eV beam with the second pump beam, is used to define the position of time zero.
Three electrodes (auxiliary, pseudoreference, and working electrodes; see Figure S2 for details) were patterned on a quartz plate of 45 mm diameter by electron beam evaporation resulting in a 5 nm chromium adhesion layer overlain by 200 nm of gold. Copper foil strips electrically connected the gold pads to the potentiostat. The cell is capped with a CaF2 window of 25 mm in diameter that has been drilled with two holes to allow for the flow of electrolyte (∼6 μL/s, maintained by a peristaltic pump). A spacer of polytetrafluoroethylene (PTFE; 50 μm thick) sets the height of the cell’s inner chamber for a volume of approximately 6 μL, such that absorption of light by the liquid phase is minimized. For the electrolyte, we used a solution of 0.5 M Na2SO4 in deionized water (18.2 MΩ·cm, Millipore), degassed by bubbling N2 for at least 30 min prior to the experiment. The photoinduced electrode potential was measured in open circuit mode (open circuit potential, OCP) and corrected for the pulse energy of the first and second pulses and water absorption coefficient at the second pulse wavelength (see the Supporting Information).
Results and Discussion
Figure 1B presents the photovoltage change ΔV2 (induced by the second laser beam) as a function of the time delay between the two pulses for a range of <4 ps. At a second pulse photon energy of 0.31 eV (4 μm in wavelength, upper panel of Figure 1B), we observe a rapid rise, but the signal decays almost as fast reaching a null intensity in about 500 fs. As we tune to higher second pulse photon energies, e.g., 1.55 eV (800 nm in wavelength, lower panel of Figure 1A), the rise is delayed by 50–100 fs, the signal decays much more slowly, and it persists for tens of picoseconds (Figure 1C). The dynamics traces for all second pulse photon energies used are shown in the Supporting Information (Figure S6).
Figure 1D shows the transient, coarse spectral profile of the response of the electrode/electrolyte interface excitation from its inception to its stabilization with the change in photovoltage ΔV2 plotted as a function of the energy of the second pump. Figure 1D is created by slicing the dynamics data for a set of representative delays, with negative delays in the upper panel and positive delays in the lower panel. Before the arrival of the first pump pulse (e.g., at −1 ps), we observe a null response (blue diamonds). The onset of the UV-induced excitation is marked by the rapid rise of a component in the mid-infrared region that culminates at ∼ +0.1 ps (upward facing triangles, orange, Figure 1D, lower panel). The rise is followed by a signal decay that is almost as fast, reaching a null intensity in less than 1 ps. This component is a broad feature whose maximum intensity clearly lies at photon energies below our measurement window. Similar spectra in the far- to mid-infrared were observed previously in bulk water experiments7,11,44 and were attributed to photon absorption of delocalized excess electrons prior to localization.
The broad feature also shows a shoulder that concomitantly appears at ∼1.55 eV (800 nm) (inset of Figure 1D), continues to grow until approximately +0.25 ps, and then starts to slowly decay. A small residual of the shoulder is still observable even after 100 ps, while ΔV2 for the other energies has already returned to 0. The feature appears at energies close to, but slightly lower than, the reported p ← s transition of the solvated electron at 1.72 eV (720 nm) in bulk liquid water,7 and much lower than gold’s interband transitions (2.38 eV).45
In a simplified portrait, the delocalized hot electron population in the water conduction band would yield a Drude-like optical response in the THz/MIR region of the electromagnetic spectrum, and hydrogen-like localized electrons in a spherical cavity would behave as particles-in-a-box, with the p ← s transition resonant in the near-infrared region. The low and high energy features in our experimental spectra (Figure 1D) thus closely coincide with the optical transitions of the bulk localized solvated electron and its precursor states.7,8,11,46−48 Thereby, here we propose that the resonant species at the electrode/electrolyte interface is the hot electron synthesized by the UV pulse, and that we follow the localization and relaxation to the solvated state.
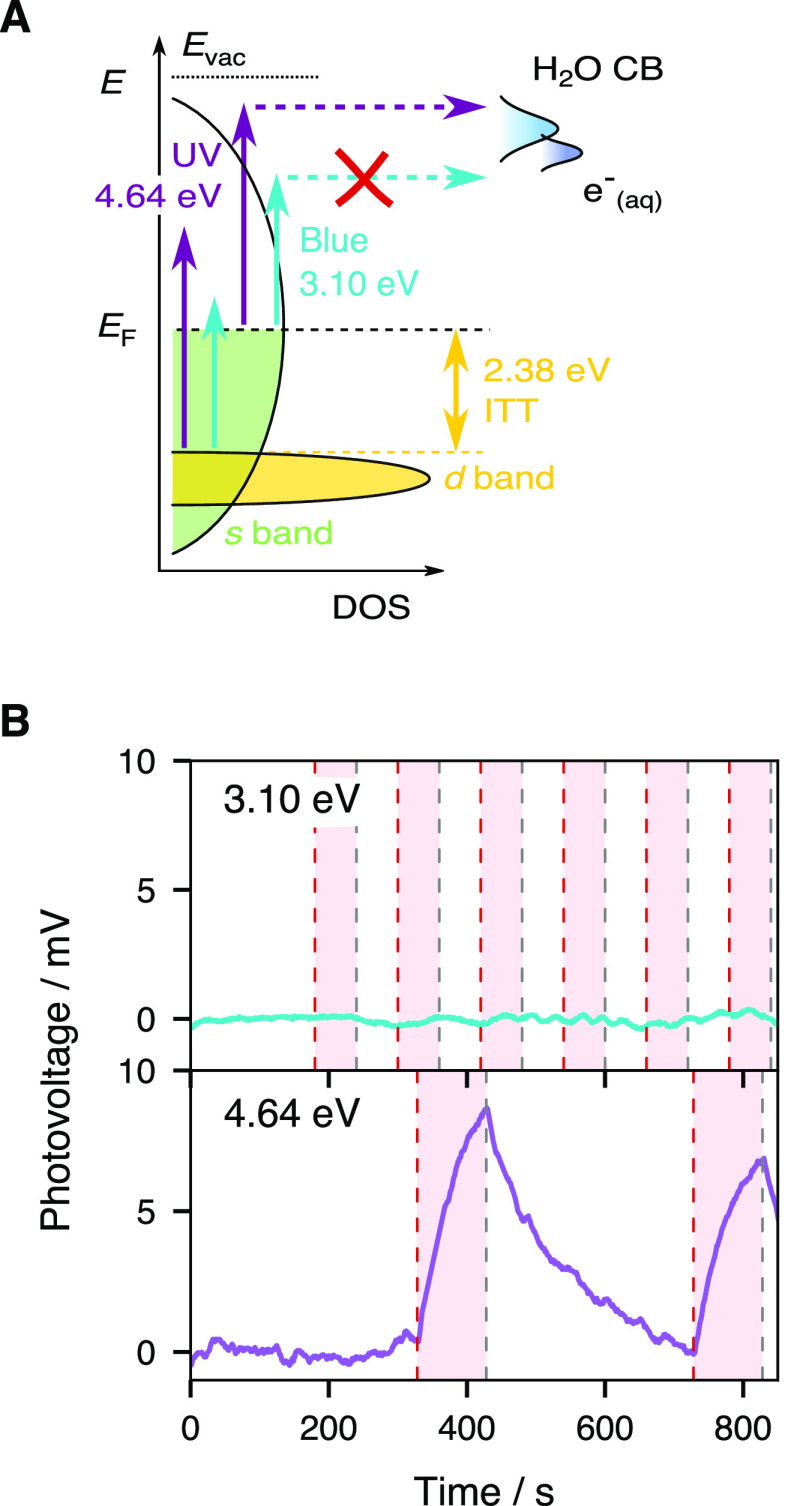
In our experimental configuration, we envision two ways in which incident UV photons can be transduced into a photovoltage: by heating the metal and creating a temperature gradient at the metal/solution boundary (such as in temperature jump measurements49−51), or by injecting uncompensated charges in the electrical double layer (EDL), which acts as a capacitor.36 In order to prove that the observed photovoltage ΔV2 is related to photoinjection and not to the metal film heating, we conducted an experiment where the UV (4.64 eV, 267 nm) first pump was replaced by a blue (3.10 eV, 400 nm) pump beam of equal power such that photoinjection would be attenuated, while a hot nonequilibrium electron population would still be generated in the metal (Figure 2A).45 In the metal film heating scenario, the effects of the two colors on the system should not differ dramatically. The 267 nm pumped signal is displayed in the lower panel of Figure 2B, where a photovoltage increase of 7–9 mV is observed when the shutter of the second pump beam (0.31 eV) is open. In stark contrast, the 400 nm pumped signal (upper panel) is barely modulated by the second pump. As sketched in Figure 2A, we deduce that metal electrons excited by 3.10 eV photons are unable to efficiently reach the water conduction band, or any other solution-side acceptor states, while UV pumped electrons do so and thus the measured photovoltage arising from the spatial and temporal overlap of two pulsed beams is the result of photoinjected charges in solution.
Figure 2.
(A) Schematics of gold’s density of states (DOS) and water’s conduction band (CB) with optical transitions enabled by UV (4.64 eV) and blue (3.10 eV) photons. (B) Comparison of the photovoltage when the first excitation pulse is changed from UV (bottom) to blue (top). The second pulse’s photon energy is 0.31 eV in both cases. A polynomial baseline has been removed from the traces to facilitate comparison. The red stripes show the times during which the shutter is open and the second pulse impinges on the electrode.
Elucidating the physical origin of the photovoltage ΔV2 (Figure 1) caused by the second pump beam presents a challenge. The following contributions could be ruled out on the basis of control experiment results, the second pump photon energy dependent dynamics, the relative signs of the signal, and the power- and polarization-dependent results (see the Supporting Information for details): further photoinjection from the electrode, photoejection of charge carriers from the aqueous interface to the electrode, and also the metal’s optical properties thermomodulation. We deduce that the second pulse photons are absorbed by species located at the interface with a cross section that is proportional to the transition probability. The relaxation back to ground state then releases the extra energy to the solvent and thus locally raises the temperature, inducing a photovoltage from the temperature gradient at the metal/solution boundary. Namely, the ΔV2 is caused by a resonant excitation subsequent to the photoinjection.
Our results suggest that we measure for the first time the transient spectra of the hydrated electron and its precursors at the gold/water interface using the two-photon excitation–photovoltage detection scheme. Because the structure, structural dynamics, and relative permittivity of electrolyte solutions at an electrode boundary differ dramatically from those of the bulk solution, one might expect that the solvated electron’s dynamics and structure should differ as well. Indeed, as shown below, our optoelectronic technique reveals one such difference with the bulk properties: different states of the hydrated electron actually display distinct properties with respect to light polarization.
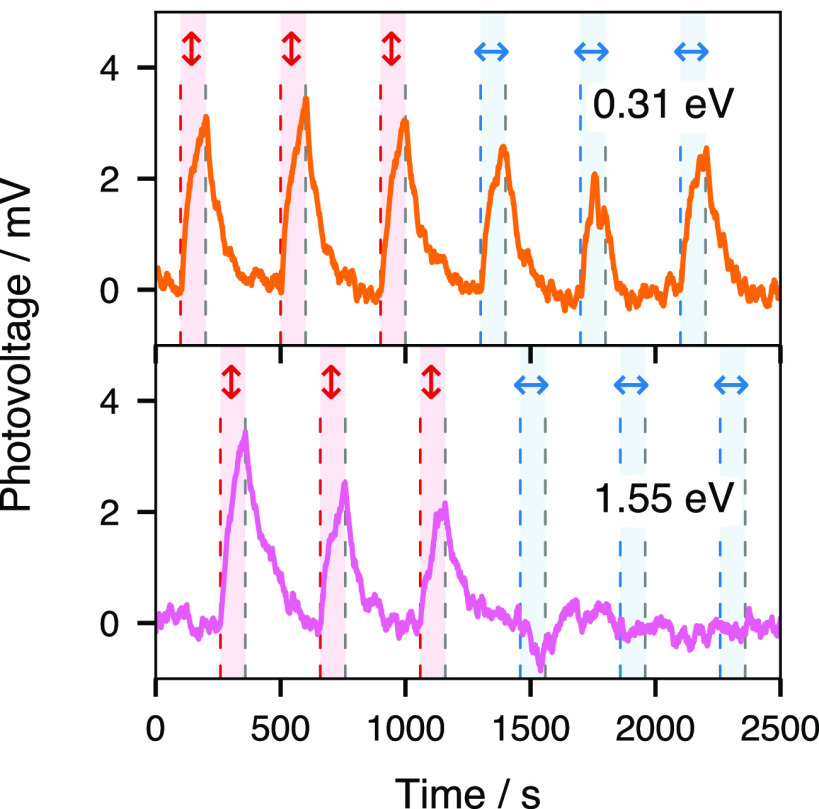
To elucidate the interaction of different states of the hydrated electron with the substrate, we conducted polarization dependence measurements of the photovoltage induced by the second pump beam at 0.31 and 1.55 eV photon energies. The delay condition was set independently in order to maximize the signal for each second pump beam photon energy (∼0 at 0.31 eV, ∼ +0.25 ps at 1.55 eV). As shown in Figure 3, a small change (≈1 mV) of ΔV2 is observed for the 0.31 eV laser upon the polarization change from p (red vertical arrows) to s (blue horizontal arrows). In comparison, ΔV2 measured in the same conditions, but for a second pump beam at 1.55 eV (lower panel), is almost entirely attenuated in the s polarization state, with a possible small negative component appearing upon the change of polarization. The presence of an anisotropic response contrasts strongly with the isotropic feature observed for equilibrated hydrated electrons in the bulk (a response typically attributed to the sphericity of the cavity52,53). An anisotropic second harmonic generation (SHG) response was previously reported at the air–water interface for a charge transfer to solvent (CTTS) state, prior to the proper photodetachment of the electron from the iodide center.54 The anisotropy in a CTTS system at the air–water interface thus appears early and switches to an isotropic response with the electron photodetachment while, in comparison, the electron at the metal/water interface starts with an isotropic signal in the hot state and later displays anisotropy. Conversion from an isotropic to an anisotropic response at different stages of the relaxation dynamics can be rationalized as the consequence of the nature of the optical transitions taking place at the metal interface for different states of the hydrated electron, as will be discussed in detail below.
Figure 3.
Comparison of the photovoltage with respect to incident polarization of the second pulse for two energies (0.31 and 1.55 eV) at a time delay close to 0 with a first excitation pulse energy of 4.64 eV and p polarization. A baseline has been removed from the traces to facilitate comparison. Vertical double arrows indicate that the second pulse incident polarization is p, and horizontal double arrows indicate that the second pulse incident polarization is s. The red and blue stripes show the times during which the shutter is open and the second pulse impinges on the electrode.
The hydrated electron properties at electrochemical interfaces have been discussed early on55 after the report of the solvated electron’s bulk spectrum,46 but limited by the available tools, conclusions were largely speculative. Various models such as the “electron cloud”, the “charge transfer layer”, and the “hot electrode” were proposed to describe the behavior of photoinjected electrons.55 Here, combining femtosecond laser pulses and photovoltage measurement, we measured the transient spectra of interfacial hydrated electrons and their polarization dependence, hence providing essential information to establish a molecular picture of the hydrated electron’s evolution from synthesis to decay. The similarities in the spectra of hydrated electrons at the electrochemical interface and those in the bulk and at the metal/ice interface in UHV support a relaxation process similar to the ones in those systems, with intriguing differences described below. In brief, at the metal/ice interface the first step in the photoinjection of electrons from the metal is the creation of hot electrons, right after the transfer, while a small proportion may directly reach preexisting traps.15 From that hot electron population, a large portion will rapidly return to the electrode (∼85%56), but the remaining fraction (∼15%) is now in a delocalized state in the aqueous medium. In bulk liquid water, the hot electron will first localize in an excited p state and subsequently relax via an internal conversion (IC) step to a modified s state in a nonadiabatic manner.14 Reorganization of the surrounding solvent molecules completes the relaxation.
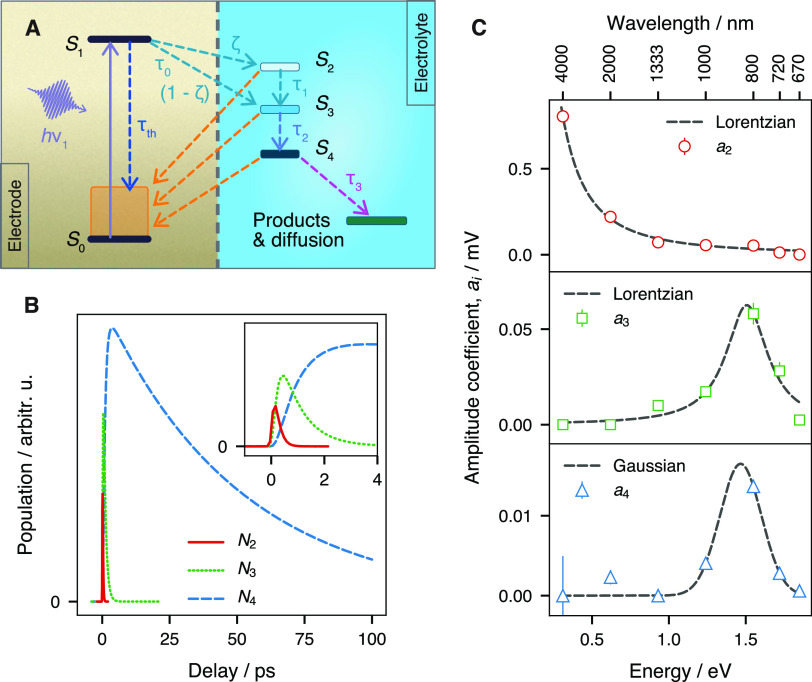
Following these works, here we also adopt a three-level hydrated electron model to fit our results that is depicted in Figure 4A and is fully described in the Supporting Information. We tried other models, including a two-level model, but they provided unsatisfactory fits with a single set of relaxation times (see the Supporting Information). Tentatively, the state S0 is assigned to gold’s ground state “Au”, S1 is assigned to gold’s nonequilibrium athermal state “Au*”, S2 is assigned indiscriminately to hot electrons in the water conduction band “CB” and to localized electrons in the excited state, S3 is assigned to hydrated electrons in the trapped state “e–trap”, and S4 is assigned to the solvated state “e–aq”. Electrons are injected from the Au* state into the electrolyte with a time constant τ0. The great majority of these electrons reach the CB state. A minor fraction (1 – ζ) is directly injected to the e–trap state;15,17 we estimate ζ to be approximately 0.98. Although there is currently no report of preexisting trap states in liquid water at the metal interface, the appearance from time zero of the shoulder at 1.55 eV in Figure 1D suggests that a similar process happens as in amorphous ice15,17 or in the bulk liquid phase.19 This is plausible since it is known that the hydrogen bond lifetime in bulk liquid water is ∼2.5 ps.57 While interfacial water molecules may perform libration motions during the 250 fs initial period in which the peak intensity at 1.55 eV continuously grows, it is unlikely that significant changes would occur in the water network structure. Finally, the hot, trapped, and solvated electron populations are related to the measured signal ΔV2 through absorption coefficients, ai, with i = 2, 3, and 4.
Figure 4.
(A) Schematics of the proposed molecular kinetics model. (B) Evolution of hot, trapped, and solvated electron populations. (inset) Zoom near origin. (C) Absorption coefficient for the three electron populations in solution. The error bars correspond to 3σ from the fit results.
The results of the fits are shown in Figure 1B,C as the red dashed lines and in the Supporting Information (Figure S6). The model describes well the experimental data at all energies for a common set of parameters. The sharp initial transient is mainly caused by the hot and trapped electron populations in the electrolyte (red and green traces, respectively, Figure 4B), while the persisting, slowly decreasing signal is due to the decaying solvated electron population (blue trace, Figure 4B). The corresponding lifetimes are determined to be τ1 ∼ 140 fs, τ2 ∼ 820 fs, and τ3 ∼ 51 ps for IC, solvent reorganization, and slow population decay, respectively. As depicted in Figure 4A, the solvated electron population (S4) has two possible loss channels lumped into τ3: recapture by the electrode or oxidized species from the solution and transport outside of the EDL into the bulk. In the bulk, the solvated electron diffuses ∼0.3 nm in 10 ps (diffusion constant ∼4.75 × 10–5 cm2 s–1).58 This distance being comparable to the solvated electron radius and the average hydrogen bond length, the transport channel’s contribution is likely negligible. Interestingly, the e–trap, i.e., S3, state lifetime (820 fs) matches the reorientation dynamics of the free (non H-bonded) water −OH at the air–water interface.59 Such free −OH species have also been detected at the gold/water interface,60 but their dynamics remain to be determined. Further studies along this line may provide insight into the interface-specific mechanisms of electron localization.
From the fits, we also obtained the effective spectra of the hydrated electron at different states (Figure 4C) (see the Supporting Information for a discussion of the center energy and fwhm of the spectra). The spectrum a2 (top panel), which belongs to the state S2, can be understood as a Drude-like optical transition, while the spectra a3 (middle) and a4 (bottom), assigned to the states S3 and S4, respectively, are consistent with p ← s optical transitions. These physical models explain well the polarization behavior in Figure 3, where the photovoltage is mostly independent of polarization at a 0.31 eV photon energy, but displays a significant dependence at 1.55 eV. This is because Drude-like transitions involving a population uncoupled to the substrate are mostly isotropic, and the p ← s transitions of populations in proximity with the electrodes display anisotropy due to image dipoles in the metal (dipole cancellation rule).
It is noteworthy that the center energy of the spectral response of the e–trap and e–aq species, i.e., the S3 and S4 states (∼1.5 eV), appears at a significantly lower photon energy than reported in the bulk (1.7 eV), despite the large uncertainty on the exact value due to the low signal-to-noise ratio and coarse spectral resolution. The center energy of the absorption peak in the bulk shifts under the influence of a number of factors such as the electrolyte composition (nature of cations, concentration, and the ion pair formation),61−63 the temperature,64,65 and the isotopic effect.63−65 A temperature increase causes a red shift of ∼0.3 eV per 100 K in the bulk, but the limited lattice temperature rise in our system upon laser irradiation (∼15 K, as calculated using a two-temperature model, see Supporting Information for details) fails to fully explain the observed shift and cannot account alone for the spectral shape and the dynamics. Moreover, the hydrated electron resides at a heterogeneous interface, where the EDL structure makes a direct comparison between the observed spectra and previous reports difficult. According to the well-accepted Gouy–Chapman–Stern model, and depending on the nature of the anion, the gold surface might be covered by either specifically adsorbed anions or water molecules (the inner Helmholtz layer, IHL); the outer Helmholtz layer (OHL) contains solvated anions/cations on top of the IHL; farther from the surface, the ions form the diffuse layer. Given the low kinetic energy of the electrons excited by the 267 nm laser, only the IHL and OHL components need to be considered in this discussion. Specific adsorption of SO42– anions does not take place on the gold surface at the potential of current study;66 hence the IHL plane is fully occupied by a layer of water, while solvated ions are restricted to the OHL. An estimate of the cation concentration (the relevant ions) within the OHL gives a value of ∼6 M (see the Supporting Information for details), which causes a maximum blue shift of 0.15 eV,62 which is opposite to the observed shift. In addition to the temperature effect, the experimental red shift may be due to the displacement of the absolute energy of either or both the ground and excited states of the solvated electron by the proximity of the highly polarizable gold electrode and a low density water network in the presence of the electron or to the extremely strong electric field in the Helmholtz layers. Furthermore, as pointed out above, the dipole cancellation rule at the metal surface allows only the pz suborbital as optically active. The observed lower energy maximum may thus be due to the splitting of the p suborbitals,53,67,68 by solvent polarization and an incomplete solvation shell.
Upon close inspection of the spectra in Figure 1D, an isosbestic point at ∼1.24 eV (1 μm) can be found between 0 and +0.25 ps. This points to the transformation from the state S2 to states S3 and/or S4. Does the hydrated electron evolve smoothly from the hot to the solvated states, adopting a continuum of in-between states, or does it jump from one state to another at the gold/liquid water interface? In bulk solution, work by Migus et al.,7 followed by measurements by Eisenthal et al.,69,70 seemed to support the latter scenario, because an isosbestic point was observed in the transient absorption of the hydrated electron species. Later, a time-dependent shift of the spectral weight from low to high energy was confirmed first in the NIR8,9 and then in the terahertz.11 No studies ever showed the evolution of the spectrum in one set of experiments. Our measurements, which give access to a large breadth of the spectrum, suggest that the discrete states model seems also valid at the metal/liquid water interface. Further comparison with bulk data will require better spectral resolution and testing against purely optical sampling.
Further work will address open questions regarding, notably, the actual molecular level changes in the EDL during relaxation, the influence of the electrolyte flow, and the tracking of the electron as it induces chemistry using a mixture of nonlinear optical and optoelectronic approaches.
Conclusion
A novel, double optical pump, photovoltage detection method enables the unprecedented observation of a wavelength-dependent time-resolved response after excitation by an ultrafast UV pulse of a polycrystalline gold electrode immersed in an aqueous electrolyte. The original spectra provide a window on the interfacial solvated electron and its precursor states, and their analysis reveals several unreported aspects of the hydrated electron at the metal/electrolyte interface. Notably, the solvated species absorption displays a marked red shift in contrast to the bulk that possibly originates from the high electric field in the EDL. A kinetic model with three electrolyte-side levels, i.e., hot, trapped, and solvated electron states, produces a satisfactory fit of the dynamics. Fitting the model to the data yields lifetimes (convoluted with the oxidation by the electrode) of the hot electron of τ1 ∼ 140 fs, the trapped electron of τ2 ∼ 820 fs, and the solvated electron (at the electrode) of τ3 ∼ 51 ps. The results provide the first evidence of preexisting trap states at the gold/liquid water interface. An isosbestic point near 1.24 eV is observable at short time delays, consistent with the transformation of electrons from a localized state to a trap state. The hot and trapped states exhibit significantly different dipole properties: the hot electron state is isotropic and the trapped electron state is anisotropic with a transition dipole perpendicular to the surface. In contrast to conventional electrical methods, the optoelectronic technique thus provides the means for the study of hot electron-driven processes at the electrified metal/electrolyte interface, and it gives access to unique energy- and time-resolved information about charge transfer mechanisms and interfacial chemistry. Granting access to the hydrated electron’s birth and stabilization, our approach offers a promising pathway—observing its structure and dynamics evolution with respect to the substrate material and geometry, and the electrolyte nature—to advance the fundamental physics and chemistry of photoelectrocatalysis.
Acknowledgments
We gratefully acknowledge the technical support from S. Wasle, W. Krauß, and S. Kubala. F.L. thanks the Fonds de recherche du Québec—Nature et technologies (FRQNT) for a postdoctoral scholarship. This study was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No.772286, to R.K.C.). This work was supported by RESOLV, funded by the Deutsche Forschungsgemeinschaft (DFG) within the framework of Exzellenzstrategie des Bundes und der Länder (EXC2033), Project No. 390677874.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c08289.
Description of the experimental principles; detailed methodology with description of the spectroelectrochemical cell, electrochemical measurements, laser setup, optoelectronic measurements, data processing, and calculated ultrafast pulse dispersion; considerations regarding heating of the interface; models and fitting (three-state and two-state models); detailed results and simulations; discussion of the nature of the photovoltage ΔV2, effective spectra, local concentration in Helmholtz layers, and comparison of the technique with CTTS and two-photon photoelectron spectroscopy measurements (PDF)
Author Present Address
§ F.L.: National Research Council Canada, 1200 Montreal Road, Ottawa, ON K1A 0R6, Canada.
The authors declare no competing financial interest.
Supplementary Material
References
- Herbert J. M.; Coons M. P. The Hydrated Electron. Annu. Rev. Phys. Chem. 2017, 68, 447–472. 10.1146/annurev-physchem-052516-050816. [DOI] [PubMed] [Google Scholar]
- Abel B.; Buck U.; Sobolewski A. L.; Domcke W. On the Nature and Signatures of the Solvated Electron in Water. Phys. Chem. Chem. Phys. 2012, 14, 22–34. 10.1039/C1CP21803D. [DOI] [PubMed] [Google Scholar]
- Boudaïffa B.; Cloutier P.; Hunting D.; Huels M. A.; Sanche L. Resonant Formation of DNA Strand Breaks by Low-Energy (3 to 20 eV) Electrons. Science 2000, 287, 1658–1660. 10.1126/science.287.5458.1658. [DOI] [PubMed] [Google Scholar]
- Garrett B. C.; Dixon D. A.; Camaioni D. M.; Chipman D. M.; Johnson M. A.; Jonah C. D.; Kimmel G. A.; Miller J. H.; Rescigno T. N.; Rossky P. J.; Xantheas S. S.; Colson S. D.; Laufer A. H.; Ray D.; Barbara P. F.; Bartels D. M.; Becker K. H.; Bowen K. H.; Bradforth S. E.; Carmichael I.; Coe J. V.; Corrales L. R.; Cowin J. P.; Dupuis M.; Eisenthal K. B.; Franz J. A.; Gutowski M. S.; Jordan K. D.; Kay B. D.; LaVerne J. A.; Lymar S. V.; Madey T. E.; McCurdy C. W.; Meisel D.; Mukamel S.; Nilsson A. R.; Orlando T. M.; Petrik N. G.; Pimblott S. M.; Rustad J. R.; Schenter G. K.; Singer S. J.; Tokmakoff A.; Wang L.-S.; Zwier T. S. Role of Water in Electron-Initiated Processes and Radical Chemistry: Issues and Scientific Advances. Chem. Rev. 2005, 105, 355–390. 10.1021/cr030453x. [DOI] [PubMed] [Google Scholar]
- Siefermann K. R.; Abel B. The Hydrated Electron: A Seemingly Familiar Chemical and Biological Transient. Angew. Chem., Int. Ed. 2011, 50, 5264–5272. 10.1002/anie.201006521. [DOI] [PubMed] [Google Scholar]
- Alizadeh E.; Sanche L. Precursors of Solvated Electrons in Radiobiological Physics and Chemistry. Chem. Rev. 2012, 112, 5578–5602. 10.1021/cr300063r. [DOI] [PubMed] [Google Scholar]
- Migus A.; Gauduel Y.; Martin J. L.; Antonetti A. Excess Electrons in Liquid Water: First Evidence of a Prehydrated State with Femtosecond Lifetime. Phys. Rev. Lett. 1987, 58, 1559–1562. 10.1103/PhysRevLett.58.1559. [DOI] [PubMed] [Google Scholar]
- Pépin C.; Goulet T.; Houde D.; Jay-Gerin J.-P. Observation of a Continuous Spectral Shift in the Solvation Kinetics of Electrons in Neat Liquid Deuterated Water. J. Phys. Chem. A 1997, 101, 4351–4360. 10.1021/jp970354l. [DOI] [Google Scholar]
- Vilchiz V. H.; Kloepfer J. A.; Germaine A. C.; Lenchenkov V. A.; Bradforth S. E. Map for the Relaxation Dynamics of Hot Photoelectrons Injected into Liquid Water Via Anion Threshold Photodetachment and Above Threshold Solvent Ionization. J. Phys. Chem. A 2001, 105, 1711–1723. 10.1021/jp003974m. [DOI] [Google Scholar]
- Kambhampati P.; Son D. H.; Kee T. W.; Barbara P. F. Solvation Dynamics of the Hydrated Electron Depends on Its Initial Degree of Electron Delocalization. J. Phys. Chem. A 2002, 106, 2374–2378. 10.1021/jp014291p. [DOI] [Google Scholar]
- Savolainen J.; Uhlig F.; Ahmed S.; Hamm P.; Jungwirth P. Direct Observation of the Collapse of the Delocalized Excess Electron in Water. Nat. Chem. 2014, 6, 697–701. 10.1038/nchem.1995. [DOI] [PubMed] [Google Scholar]
- Ayotte P.; Johnson M. A. Electronic Absorption Spectra of Size-Selected Hydrated Electron Clusters: (H2O)n–, n = 6–50. J. Chem. Phys. 1997, 106, 811–814. 10.1063/1.473167. [DOI] [Google Scholar]
- Bragg A. E.; Verlet J. R. R.; Kammrath A.; Cheshnovsky O.; Neumark D. M. Hydrated Electron Dynamics: From Clusters to Bulk. Science 2004, 306, 669–671. 10.1126/science.1103527. [DOI] [PubMed] [Google Scholar]
- Elkins M. H.; Williams H. L.; Shreve A. T.; Neumark D. M. Relaxation Mechanism of the Hydrated Electron. Science 2013, 342, 1496–1499. 10.1126/science.1246291. [DOI] [PubMed] [Google Scholar]
- Gahl C.; Bovensiepen U.; Frischkorn C.; Wolf M. Ultrafast Dynamics of Electron Localization and Solvation in Ice Layers on Cu (111). Phys. Rev. Lett. 2002, 89, 107402. 10.1103/PhysRevLett.89.107402. [DOI] [PubMed] [Google Scholar]
- Stähler J.; Gahl C.; Bovensiepen U.; Wolf M. Ultrafast Electron Dynamics at Ice-Metal Interfaces: Competition Between Heterogeneous Electron Transfer and Solvation. J. Phys. Chem. B 2006, 110, 9637–9644. 10.1021/jp060538c. [DOI] [PubMed] [Google Scholar]
- Stähler J.; Deinert J.-C.; Wegkamp D.; Hagen S.; Wolf M. Real-Time Measurement of the Vertical Binding Energy During the Birth of a Solvated Electron. J. Am. Chem. Soc. 2015, 137, 3520–3524. 10.1021/ja511571y. [DOI] [PubMed] [Google Scholar]
- Turi L.; Rossky P. Theoretical Studies of Spectroscopy and Dynamics of Hydrated Electrons. Chem. Rev. 2012, 112, 5641–5674. 10.1021/cr300144z. [DOI] [PubMed] [Google Scholar]
- Herbert J. M. Structure of the Aqueous Electron. Phys. Chem. Chem. Phys. 2019, 21, 20538–20565. 10.1039/C9CP04222A. [DOI] [PubMed] [Google Scholar]
- Sagar D. M.; Bain C. D.; Verlet J. R. R. Hydrated Electrons at the Water/Air Interface. J. Am. Chem. Soc. 2010, 132, 6917–6919. 10.1021/ja101176r. [DOI] [PubMed] [Google Scholar]
- Buchner F.; Schultz T.; Lübcke A. Solvated Electrons at the Water–air Interface: Surface Versus Bulk Signal in Low Kinetic Energy Photoelectron Spectroscopy. Phys. Chem. Chem. Phys. 2012, 14, 5837–5842. 10.1039/c2cp23305c. [DOI] [PubMed] [Google Scholar]
- Matsuzaki K.; Kusaka R.; Nihonyanagi S.; Yamaguchi S.; Nagata T.; Tahara T. Partially Hydrated Electrons at the Air/Water Interface Observed by UV-Excited Time-Resolved Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy. J. Am. Chem. Soc. 2016, 138, 7551–7557. 10.1021/jacs.6b02171. [DOI] [PubMed] [Google Scholar]
- Uhlig F.; Jungwirth P.; Marsalek O. Electrons at the Surface of Water: Dehydrated or Not?. J. Phys. Chem. Lett. 2013, 4, 338–343. 10.1021/jz3020953. [DOI] [PubMed] [Google Scholar]
- Uhlig F.; Herbert J. M.; Coons M. P.; Jungwirth P. Optical Spectroscopy of the Bulk and Interfacial Hydrated Electron from Ab Initio Calculations. J. Phys. Chem. A 2014, 118, 7507–7515. 10.1021/jp5004243. [DOI] [PubMed] [Google Scholar]
- Coons M. P.; You Z. Q.; Herbert J. M. the Hydrated Electron at the Surface of Neat Liquid Water Appears to Be Indistinguishable from the Bulk Species. J. Am. Chem. Soc. 2016, 138, 10879–10886. 10.1021/jacs.6b06715. [DOI] [PubMed] [Google Scholar]
- Kevan L. Solvated Electron Structure in Glassy Matrices. Acc. Chem. Res. 1981, 14, 138–145. 10.1021/ar00065a002. [DOI] [Google Scholar]
- Larsen R. E.; Glover W. J.; Schwartz B. J. Does the Hydrated Electron Occupy a Cavity?. Science 2010, 329, 65–69. 10.1126/science.1189588. [DOI] [PubMed] [Google Scholar]
- Casey J. R.; Kahros A.; Schwartz B. J. To Be or Not to Be in a Cavity: The Hydrated Electron Dilemma. J. Phys. Chem. B 2013, 117, 14173–14182. 10.1021/jp407912k. [DOI] [PubMed] [Google Scholar]
- Bockris J. O.; Conway B. E.; White R. E.. Modern Aspects of Electrochemistry; Springer Science & Business Media: New York, 1992; Vol. 22. [Google Scholar]
- Magnussen O. M.; Groß A. Toward an Atomic-Scale Understanding of Electrochemical Interface Structure and Dynamics. J. Am. Chem. Soc. 2019, 141, 4777–4790. 10.1021/jacs.8b13188. [DOI] [PubMed] [Google Scholar]
- Marcus R. A. On the Theory of Electron-Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions. J. Chem. Phys. 1965, 43, 679–701. 10.1063/1.1696792. [DOI] [Google Scholar]
- Adams D. M.; Brus L.; Chidsey C. E. D.; Creager S.; Creutz C.; Kagan C. R.; Kamat P. V.; Lieberman M.; Lindsay S.; Marcus R. A.; Metzger R. M.; Michel-Beyerle M. E.; Miller J. R.; Newton M. D.; Rolison D. R.; Sankey O.; Schanze K. S.; Yardley J.; Zhu X. Charge Transfer on the Nanoscale: Current Status. J. Phys. Chem. B 2003, 107, 6668–6697. 10.1021/jp0268462. [DOI] [Google Scholar]
- Bard A. J.; Faulkner L. R.. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons, Inc.: New York, 2000. [Google Scholar]
- Bradbury C. R.; Zhao J.; Fermin D. J. Distance-Independent Charge-Transfer Resistance at Gold Electrodes Modified by Thiol Monolayers and Metal Nanoparticles. J. Phys. Chem. C 2008, 112, 10153–10160. 10.1021/jp710165d. [DOI] [Google Scholar]
- Zwaschka G.; Tong Y.; Wolf M.; Campen R. K. Probing the Hydrogen Evolution Reaction and Charge Transfer on Platinum Electrodes on Femtosecond Timescales. ChemElectroChem 2019, 6, 2675–2682. 10.1002/celc.201900336. [DOI] [Google Scholar]
- Gurevich Y. Y.; Pleskov Y. V.; Rotenberg Z. A.. Photoelectrochemistry; Springer US: Boston, MA, 1980. [Google Scholar]
- Felske A.; Plieth W. J. Photoelectrochemical Investigation of Electrode-Electrolyte Interfaces Using Ultraviolet, Pulsed Laser Irradiation. J. Opt. Soc. Am. B 1986, 3, 815–820. 10.1364/JOSAB.3.000815. [DOI] [Google Scholar]
- Baldwin R. P.; Perone S. P. Chronoamperometric Studies of Flash Photoemission at a Mercury Electrode. J. Electrochem. Soc. 1976, 123, 1647–1653. 10.1149/1.2132661. [DOI] [Google Scholar]
- Richardson J. H.; Deutscher S. B.; Maddux A. S.; Harrar J. E.; Johnson D. C.; Schmelzinger W. L.; Perone S. P. Laser-Induced Photoelectrochemistry: Coulostatic Measurements of Photoemission in Aqueous and Non-Aqueous Solutions. J. Electroanal. Chem. Interfacial Electrochem. 1980, 109, 95–114. 10.1016/S0022-0728(80)80109-4. [DOI] [Google Scholar]
- Harata A.; Shen Q.; Sawada T. Photothermal Applications of Lasers: Study of Fast and Ultrafast Photothermal Phenomena at Metal-Liquid Interfaces. Annu. Rev. Phys. Chem. 1999, 50, 193–219. 10.1146/annurev.physchem.50.1.193. [DOI] [PubMed] [Google Scholar]
- Krivenko A. G.; Krüger J.; Kautek W.; Benderskii V. A. Subpicosecond-Pulse-Laser-Induced Electron Emission from Mercury and Silver into Aqueous Electrolytes. Berich. Bunsen. Gesell. 1995, 99, 1489–1494. 10.1002/bbpc.199500113. [DOI] [Google Scholar]
- Ge N.-H.; Wong C.; Lingle R.; McNeill J.; Gaffney K.; Harris C. B. Femtosecond Dynamics of Electron Localization at Interfaces. Science 1998, 279, 202–205. 10.1126/science.279.5348.202. [DOI] [PubMed] [Google Scholar]
- Onda K.; Li B.; Zhao J.; Jordan K. D.; Yang J.; Petek H. Wet Electrons at the H2O/TiO2(110) Surface. Science 2005, 308, 1154–1158. 10.1126/science.1109366. [DOI] [PubMed] [Google Scholar]
- Anderson N. A.; Hang K.; Asbury J. B.; Lian T. Ultrafast Mid-IR Detection of the Direct Precursor to the Presolvated Electron Following Electron Ejection from Ferrocyanide. Chem. Phys. Lett. 2000, 329, 386–392. 10.1016/S0009-2614(00)01046-0. [DOI] [Google Scholar]
- Schoenlein R. W.; Lin W. Z.; Fujimoto J. G.; Eesley G. L. Femtosecond Studies of Nonequilibrium Electronic Processes in Metals. Phys. Rev. Lett. 1987, 58, 1680–1683. 10.1103/PhysRevLett.58.1680. [DOI] [PubMed] [Google Scholar]
- Hart E. J.; Boag J. W. Absorption Spectrum of the Hydrated Electron in Water and in Aqueous Solutions. J. Am. Chem. Soc. 1962, 84, 4090–4095. 10.1021/ja00880a025. [DOI] [Google Scholar]
- Jacobson L. D.; Herbert J. M. Polarization-Bound Quasi-Continuum States Are Responsible for the “Blue Tail” in the Optical Absorption Spectrum of the Aqueous Electron. J. Am. Chem. Soc. 2010, 132, 10000–10002. 10.1021/ja1042484. [DOI] [PubMed] [Google Scholar]
- Ambrosio F.; Miceli G.; Pasquarello A. Electronic Levels of Excess Electrons in Liquid Water. J. Phys. Chem. Lett. 2017, 8, 2055–2059. 10.1021/acs.jpclett.7b00699. [DOI] [PubMed] [Google Scholar]
- Benderskii V. A.; Velichko G. I. Temperature Jump in Electric Double-Layer Study. Part I. Method of Measurements. J. Electroanal. Chem. Interfacial Electrochem. 1982, 140, 1–22. 10.1016/0368-1874(82)85295-7. [DOI] [Google Scholar]
- Smalley J. F.; Geng L.; Feldberg S. W.; Rogers L. C.; Leddy J. Evidence for Adsorption of Fe(CN)63–/4– on Gold Using the Indirect Laser-Induced Temperature-Jump Method. J. Electroanal. Chem. 1993, 356, 181–200. 10.1016/0022-0728(93)80520-R. [DOI] [Google Scholar]
- Climent V.; Coles B. A.; Compton R. G. Laser Induced Current Transients Applied to a Au(111) Single Crystal Electrode. A General Method for the Measurement of Potentials of Zero Charge of Solid Electrodes. J. Phys. Chem. B 2001, 105, 10669–10673. 10.1021/jp012402e. [DOI] [Google Scholar]
- Rossky P. J.; Schnitker J. The Hydrated Electron: Quantum Simulation of Structure, Spectroscopy, and Dynamics. J. Phys. Chem. 1988, 92, 4277–4285. 10.1021/j100326a009. [DOI] [Google Scholar]
- Assel M.; Laenen R.; Laubereau A. Dynamics of Excited Solvated Electrons in Aqueous Solution Monitored with Femtosecond-Time and Polarization Resolution. J. Phys. Chem. A 1998, 102, 2256–2262. 10.1021/jp972499y. [DOI] [Google Scholar]
- Nowakowski P. J.; Woods D. A.; Verlet J. R. R. Charge Transfer to Solvent Dynamics at the Ambient Water/Air Interface. J. Phys. Chem. Lett. 2016, 7, 4079–4085. 10.1021/acs.jpclett.6b01985. [DOI] [PubMed] [Google Scholar]
- Berg H. On Three Hypotheses in Photo-Polarography. Electrochim. Acta 1968, 13, 1249–1252. 10.1016/0013-4686(68)80051-9. [DOI] [Google Scholar]
- Konovalov V. V.; Raitsimring A. M.; Tsvetkov Y. D. Thermalization Lengths of “Subexcitation Electrons” in Water Determined by Photoinjection from Metals into Electrolyte Solutions. Int. J. Radiat. Appl. Instrumentation. Part C. Radiat. Phys. Chem. 1988, 32, 623–632. 10.1016/1359-0197(88)90076-8. [DOI] [Google Scholar]
- Bakker H. J.; Skinner J. L. Vibrational Spectroscopy As a Probe of Structure and Dynamics in Liquid Water. Chem. Rev. 2010, 110, 1498–1517. 10.1021/cr9001879. [DOI] [PubMed] [Google Scholar]
- Schmidt K. H.; Buck W. L. Mobility of the Hydrated Electron. Science 1966, 151, 70–71. 10.1126/science.151.3706.70. [DOI] [PubMed] [Google Scholar]
- Hsieh C.-S.; Campen R. K.; Vila Verde A. C.; Bolhuis P.; Nienhuys H.-K.; Bonn M. Ultrafast Reorientation of Dangling OH Groups at the Air-Water Interface Using Femtosecond Vibrational Spectroscopy. Phys. Rev. Lett. 2011, 107, 116102. 10.1103/PhysRevLett.107.116102. [DOI] [PubMed] [Google Scholar]
- Tong Y.; Lapointe F.; Thämer M.; Wolf M.; Campen R. K. Hydrophobic Water Probed Experimentally at the Gold Electrode/Aqueous Interface. Angew. Chem., Int. Ed. 2017, 56, 4211–4214. 10.1002/anie.201612183. [DOI] [PubMed] [Google Scholar]
- Spezia R.; Nicolas C.; Archirel P.; Boutin A. Molecular Dynamics Simulations of the Ag+ or Na+ Cation with an Excess Electron in Bulk Water. J. Chem. Phys. 2004, 120, 5261–5268. 10.1063/1.1648631. [DOI] [PubMed] [Google Scholar]
- Bonin J.; Lampre I.; Soroushian B.; Mostafavi M. First Observation of Electron Paired with Divalent and Trivalent Nonreactive Metal Cations in Water. J. Phys. Chem. A 2004, 108, 6817–6819. 10.1021/jp047492c. [DOI] [Google Scholar]
- Asaad A. N.; Chandrasekhar N.; Nashed A. W.; Krebs P. Is There Any Effect of Solution Microstructure on the Solvated Electron Absorption Spectrum in LiCl/H2O Solutions?. J. Phys. Chem. A 1999, 103, 6339–6343. 10.1021/jp990863i. [DOI] [Google Scholar]
- Jou F.-Y.; Freeman G. R. Temperature and Isotope Effects on the Shape of the Optical Absorption Spectrum of Solvated Electrons in Water. J. Phys. Chem. 1979, 83, 2383–2387. 10.1021/j100481a016. [DOI] [Google Scholar]
- Lin M.; Kumagai Y.; Lampre I.; Coudert F.-X.; Muroya Y.; Boutin A.; Mostafavi M.; Katsumura Y. Temperature Effect on the Absorption Spectrum of the Hydrated Electron Paired with a Lithium Cation in Deuterated Water. J. Phys. Chem. A 2007, 111, 3548–3553. 10.1021/jp070615j. [DOI] [PubMed] [Google Scholar]
- Ataka K.-i.; Osawa M. In Situ Infrared Study of Water-Sulfate Coadsorption on Gold(111) in Sulfuric Acid Solutions. Langmuir 1998, 14, 951–959. 10.1021/la971110v. [DOI] [Google Scholar]
- Borgis D.; Staib A. Excited States of a Hydrated Electron and Aqueous Chloride by Computer Simulation. Chem. Phys. Lett. 1994, 230, 405–413. 10.1016/0009-2614(94)01185-0. [DOI] [Google Scholar]
- Turi L.; Borgis D. Analytical Investigations of an Electron-Water Molecule Pseudopotential. II. Development of a New Pair Potential and Molecular Dynamics Simulations. J. Chem. Phys. 2002, 117, 6186–6195. 10.1063/1.1503308. [DOI] [Google Scholar]
- Long F. H.; Lu H.; Eisenthal K. B. Femtosecond Studies of the Presolvated Electron: An Excited State of the Solvated Electron?. Phys. Rev. Lett. 1990, 64, 1469–1472. 10.1103/PhysRevLett.64.1469. [DOI] [PubMed] [Google Scholar]
- Shi X.; Long F. H.; Lu H.; Eisenthal K. B. Femtosecond Electron Solvation Kinetics in Water. J. Phys. Chem. 1996, 100, 11903–11906. 10.1021/jp961261r. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.