Abstract
Using data from the Panel Study of Income Dynamics (PSID) and the Medical Expenditure Panel Survey (MEPS), we analyze the health gap between married and unmarried individuals of working-age. Controlling for observables, we find a gap that peaks at 10 percentage points at ages 55–59 years. The marriage health gap is similar for men and women. If we allow for unobserved heterogeneity in innate health (permanent and age-dependent), potentially correlated with timing and likelihood of marriage, we find that the effect of marriage on health disappears below age 40 years, while about 5 percentage points difference between married and unmarried individuals remains at older ages (55–59 years). This indicates that the observed gap is mainly driven by selection into marriage at younger ages, but there might be a protective effect of marriage at older ages. Exploring the mechanisms behind this result, we find that better innate health is associated with a higher probability of marriage and a lower probability of divorce, and there is strong assortative mating among couples by innate health. We also find that married individuals are more likely to have a healthier behavior compared to unmarried ones. Finally, we find that health insurance is critical for the beneficial effect of marriage.
Keywords: Health, Marriage, Innate Health, Protective Effect of Marriage, Assortative Mating, Panel Data, Grouped-Fixed-Effects Estimator, I10, I12, J10
I. Introduction
Married individuals are healthier and live longer than unmarried ones. This fact was first documented by British epidemiologist William Farr more than 150 years ago, and has been established by many studies since then.1 The question is, of course, why? Does the association between marriage and health indicate a protective effect of marriage, or is it simply an artifact of selection, as healthier people are more likely to get married in the first place? The answer to this question is critical as it has important implications for public policy.2 Studies on the link between public policy and health suggest that “upstream social and economic determinants of health are of major health importance, and hence that social and economic policy and practice may be the major route to improving population health.” (House, Schoeni, Kaplan and Pollack, 2008, p.22). The alarming increase in morbidity and mortality among white males in recent years in the U.S. highlighted once again the importance of socio-economic determinants of health (Case and Deaton, 2015). Marriage is often portrayed as a solution for many social problems in the U.S. (see Waite and Gallagher, 2000), and the effectiveness of pro-marriage policies depends on whether marriage indeed makes individuals healthier, wealthier and happier.
In this paper we study the relationship between health and marriage using the U.S. data from the Panel Study of Income Dynamics (PSID) and the Medical Expenditure Panel Survey (MEPS). In both data sets married individuals report to be healthier than unmarried ones, and they do so in remarkably similar levels. The gap in self-reported health persists after we control for observable characteristics such as education, income, race, gender and the presence of children; starting at about 3 percentage points at younger ages (20 to 39 years), and increasing continuously for older ages, reaching a peak of 10 percentage points around ages 55 to 59 years. A similar picture emerges when we consider objective instead of self-reported measures of health, or when we use the occurrence of chronic conditions as an indicator of poor health.
We define the marriage health gap as the difference between age-dependent health curves for married and single individuals, which we specify nonparametrically. Different studies in evolutionary biology suggest that several physical and personality traits that define a person as attractive for mating are associated with youth and health, and as a result, with reproductive capacity.3 Hence, individuals with better innate health tend to be more attractive in the marriage market. If individuals with better innate health are more attractive marriage partners, and, as a result, more likely to get married in the first place and stay married afterwards, least squares estimation of these curves would provide biased estimates of the effect of marriage on health.
Using the panel structure of the PSID, we try to overcome this selection bias by accounting for individual heterogeneity in (unobserved) innate health, potentially correlated with the timing and likelihood of marriage. We consider three models. We first consider a standard fixed-effects specification, which allows for unobserved differences in permanent innate health. This is, however, a restrictive approach, since it assumes that the innate health is constant over time, while it is reasonable to expect that differences in innate health become more important at older ages. To allow for age-dependent effects of innate health, our second model follows a grouped-fixed-effects approach, developed by Bonhomme and Manresa (2015). The grouped-fixed-effects estimator that we implement allows for age-dependent patterns of unobserved heterogeneity that are common for individuals that belong to the same group but potentially differ across groups (e.g. groups formed by individuals with high and low innate health). The two approaches give very similar results: the observed effect of marriage on health disappears for younger ages (20–39 years), while about a 5 percentage point gap between married and unmarried individuals remains for older ages (55–59 years). This is half of the total difference for this age group (10 percentage points). These results suggest that the association between marriage and health at younger ages is likely to be driven by selection of healthier individuals into marriage, while there might be a protective effect of marriage that shows up at older ages. Finally, since health shocks might affect the probability of getting or staying married in subsequent periods, we control for previous health shocks by using a dynamic panel data model with fixed effects. We estimate this model by the system-GMM approach in Arellano and Bover (1995). This approach delivers a larger marriage health gap (about 10 percentage points by for ages 50–59 years), and suggests that our fixed-effects and grouped-fixed-effects estimates might be on the conservative side. We also find that three alternative estimation strategies produce similar marriage health gaps for males and females.
Next we provide evidence that is indicative of how selection and protection might show up in the data. On the selection side, we first document that individuals who are ever married by age 30 (or 40) years have better average innate permanent health than those individuals who are never married by that age. The variance of permanent health, on the other hand, is larger for those who are never married. These facts are consistent with a world in which individuals look for healthy partners in the marriage market. In such a world, healthy singles have an incentive to wait for a healthy partner, healthy individuals are more likely to marry and less likely to divorce. As a result, innate health should be a good predictor of marriage and divorce probabilities and individuals would mate assortatively in terms of innate health. We then corroborate that data supports both predictions. Having better innate health is associated with higher probability of marriage and lower probability of divorce. Likewise, the correlation between husbands’ and wives’ uncovered measures of innate health is about 37%, and remains large and significant (about 32%) even after controlling for college, race, and a measure of permanent income.
On positive effects of marriage on health that are not captured by selection, we find that married individuals are more likely to engage in preventive medical care than singles are, even after controlling for observable characteristics (including health expenditures, health insurance, and socio-economic variables). Married individuals around ages 50 to 54 years, for example, are about 6% more likely to check their cholesterol or have a prostate or breast examination. Marriage also promotes healthy habits. We focus on smoking, a major health risk. Our results show that a single individual is about 23 percentage points more likely to quit smoking if he/she gets married than if he/she stays single. Furthermore, a majority (about 74%) of singles who get married and quit smoking do so while they are married. The importance of healthy behavior also shows up in health expenditure patterns. While married individuals spend more on their health when they are young and healthy, singles end up spending more than married individuals when they are older and less healthy.
A possible important factor behind these differences in healthy behavior is health insurance: while about 10% of married individuals do not have any public or private insurance, this share amounts to 20% for unmarried females and 25% for unmarried males. Indeed, if we focus on individuals without health insurance, we do not find a significant marriage health gap. These findings suggest that the availability of health insurance is an important facilitator for positive effects of marriage on health.
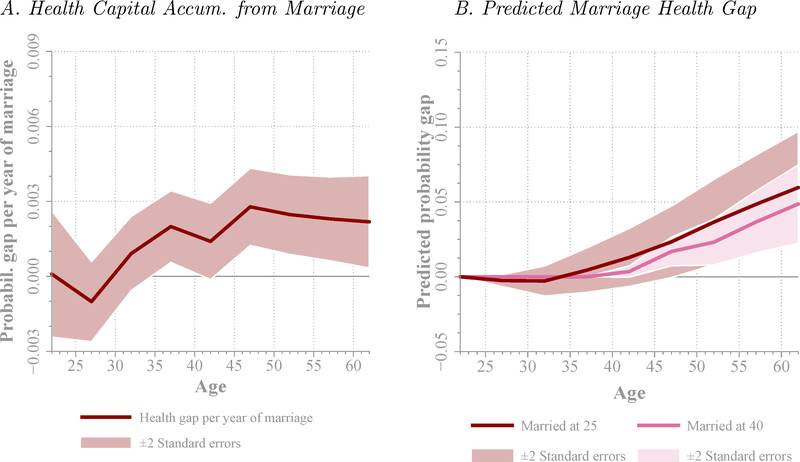
We finally show that the effect of marriage on health is cumulative. In particular, we estimate the effect of the total number of years an individual has been married (marriage capital) and find a positive and significant effect on health, especially at older ages. These results are consistent with our baseline estimates.
This paper is related to the large literature on the relation between socioeconomic status and health (Stowasser, Heiss, McFadden and Winter, 2012). It is well documented that marriage is associated with positive health outcomes. Wood, Avellar and Goesling (2009) and Wilson and Oswald (2005) provide reviews of existing evidence. Pijoan-Mas and Ríos-Rull (2014) estimate, using the Health and Retirement Study (HRS), age-specific survival probabilities conditional upon socio-economic characteristics and show that married females (males) are expected to live 1.2 (2.2) years longer than their single counterparts. The existing literature also documents that health outcomes and healthy behavior are correlated between spouses, see e.g. Clark and Etilé (2006), Oreffice and Quintana-Domenque (2010), Chiappori, Oreffice and Quintana-Domenque (2012, 2018) and Banks, Kelly and Smith (2014). There is also a large and positive effect of education on health (e.g. Lleras-Muney, 2005; Cutler and Lleras-Muney, 2010), which goes beyond the higher financial resources that it brings (Gardner and Oswald, 2004; Smith, 2007). Finally, there is a growing literature in labor economics and macroeconomics that introduce health shocks and expenditures into life-cycle models with heterogeneous agents. French (2005), De Nardi, French and Jones (2010), Prados (2013), Ozkan (2014), Cole, Kim and Krueger (2014), Kopecky and Koreshkova (2014), Jung and Tran (2016), Jung, Tran and Chambers (2017), and Braun, Kopecky and Koreshkova (2017) are recent examples.
In the existing literature, one approach to estimate the effect of marital status on health (mortality or self-reported health) is to regress health outcomes on marital status (or history) with controls for health in early ages. This approach is used to mitigate the effects of the selection of healthier individuals into marriage. Murray (2000), who follows a sample of male graduates from Amherst College in Massachusetts, finds evidence both of selection of healthy individuals into marriage as well as of a protective effect of marriage on health outcomes. Another approach to control for selection is to estimate fixed-effects regressions. Using this approach on Canadian data, Averett, Argys and Sorkin (2013) find that while marriage has a positive effect on health in the form of better mental health and lower alcohol consumption, it is also associated with weight gain and less frequent exercising. Using a duration analysis and exploiting a timing-of-events approach for identification, van den Berg and Gupta (2015) correct the potential selection into marriage by accounting for fixed permanent unobserved heterogeneity. Using Dutch registry data for individuals born between 1812 and 1902, they study the age-dependent effect of marriage on mortality and how this effect is influenced by the early childhood conditions. Finally, an alternative approach is to find valid instruments that generate exogenous variation in health or marriage outcomes. Finding such instruments in not an easy task (Adams, Hurd, McFadden, Merrill and Ribeiro, 2003). Lillard and Panis (1996), using data on males from the PSID, take a simultaneous equations (instrumental variables) approach and find that there might be negative selection into marriage as less healthy men have more to gain from marriage.
In this paper, we make three contributions to the existing literature. First, we study self-reported health status for working age (20 to 64 years) individuals and identify nonparametrically the marriage health gap as a function of age. Second, we allow for unobserved heterogeneity in innate health (permanent and age- dependent), potentially correlated with timing and likelihood of marriage. Our approach to deal with potentially correlated age-dependent unobserved heterogeneity is novel in this literature. In particular, we estimate the effect of marriage on health using a grouped-fixed-effects estimator, which allows for a flexible and yet parsimonious specification of age-dependent unobserved heterogeneity. Finally, our exploration of the potential channels through which selection and protection may show up in the data is also a contribution. We find that our uncovered measures of innate health are associated with higher probabilities of marriage and lower probabilities of divorce; there is also strong assortative mating among couples by innate health; and we highlight preventive health care and health insurance as possible factors behind the protective effects of marriage on health.
The paper is organized as follows. In Section II, we describe data sources and provide descriptive statistics. We discuss our empirical strategy in Section III. Section IV presents main results. In Section V, we document suggestive evidence on selection and protection. Section VI concludes.
II. Data and Descriptive Statistics
We use two data sources to document the relationship between marriage and health. The first data source is the Panel Study of Income Dynamics (PSID). The PSID began in 1968 with a nationally representative sample of over 18,000 individuals living in 5,000 families in the United States. Extensive demographic and economic data on these individuals and their descendants have been collected continuously since then. Starting in 1984, the PSID has been collecting data on self-reported health of individuals. We use data from 1984 to 2013. The data are annual until 1997 and biannual afterwards. Sample selection and variable definitions are explained in Appendix A. Appendix B shows descriptive statistics.
The main health variable we use in this analysis is self-rated health.4 Each household head is asked to rate his/her as well as his/her spouse’s health as excellent, very good, good, fair, or poor.5 We consider those with excellent, very good or good health as healthy and others as unhealthy. As Table B1 in Appendix B shows, throughout the sample period, about 88% of individuals are healthy according to this definition. Likewise, about 66% of individuals are married. We consider those who declare themselves married in the surveys as married and others (never married, divorced or widowed, separated, as well as cohabitants) as unmarried. In the sample, about 32% of individuals have a college degree. Per-adult household income is about 38,000 in 2005 U.S. dollars.
The second data source is the Medical Expenditure Panel Survey (MEPS). The MEPS is a set of surveys of families and individuals, their medical providers, and employers across the U.S. and is the most complete source of data on the cost and use of health care and health insurance coverage. The MEPS has two major components: the Household Component and the Insurance Component. The Household Component, which is used here, provides data from individual households and their members, which is supplemented by data from their medical providers. The Household Component contains detailed information for each person in the household on demographic characteristics, health conditions, health status, usage of medical services, charges and source of payments, access to care, satisfaction with care, health insurance coverage, income, and employment. The MEPS is a rotating panel where panel members are interviewed 5 times over a 2-year interval. In the analysis below we use pooled data from panels from 1996 to 2009.
Table B2 in Appendix B shows descriptive statistics for the MEPS sample. The MEPS and the PSID samples are quite similar in terms of education and household income. A smaller fraction of the MEPS sample is married, which reflects the facts that it covers relatively more recent years than the PSID does. About 16% of individuals in the MEPS sample do not have any, public or private, insurance. Individuals on average spend about 3,000 per year on health in 2005 U.S. dollars, which is about 9% of their total income.
Table 1 documents the marital status of the population in the PSID and MEPS samples (Panel A) and marital transitions in the PSID (Panel B). In both samples, almost all individuals eventually marry. Less than 5% of individuals remain never-married by ages 60–64 years. The fractions of individuals who are married, divorced or widowed increase monotonically by age. The fraction of people who are married in younger ages is larger in the PSID, which, as we commented above, reflects the fact that the MEPS covers more recent years than the PSID. For younger ages, there is significant turnover in marital status (Panel B). About 5% of married individuals between ages 25 to 29 years become unmarried each year (mainly divorced), and about 11% of singles in the same age group get married. The size of marital transitions declines as individuals age.
Table 1—
Marriage Ratios and Transitions In and Out of Marriage by Age
| A. Marriage Ratios |
B. Marriage Transitions |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Married |
Divorced/Sep. |
Widowed |
Never Married |
Marr. | Single | |||||
| Age: | PSID | MEPS | PSID | MEPS | PSID | MEPS | PSID | MEPS | Single | Marr. |
| 20–24 | 36.9 | 16.4 | 7.1 | 2.5 | 0.1 | 0.0 | 55.8 | 81.1 | 8.1 | 11.6 |
| 25–29 | 52.1 | 43.4 | 10.8 | 7.3 | 0.3 | 0.2 | 36.9 | 49.1 | 5.3 | 11.3 |
| 30–34 | 63.5 | 60.3 | 14.7 | 10.8 | 0.5 | 0.2 | 21.2 | 28.7 | 3.9 | 10.1 |
| 35–39 | 69.3 | 65.2 | 17.2 | 14.9 | 0.8 | 0.6 | 12.7 | 19.4 | 3.1 | 7.2 |
| 40–44 | 70.8 | 66.2 | 19.1 | 18.4 | 1.0 | 1.1 | 9.1 | 14.4 | 2.7 | 7.0 |
| 45–49 | 71.5 | 68.0 | 19.8 | 19.8 | 1.6 | 1.8 | 7.1 | 10.5 | 2.1 | 4.4 |
| 50–54 | 73.0 | 68.8 | 18.1 | 20.2 | 3.3 | 2.8 | 5.7 | 8.2 | 1.9 | 4.5 |
| 55–59 | 74.1 | 69.1 | 16.3 | 19.3 | 5.5 | 5.0 | 4.0 | 6.5 | 1.4 | 2.2 |
| 60–64 | 73.7 | 68.2 | 14.2 | 17.1 | 9.0 | 9.7 | 3.1 | 4.9 | 1.8 | 2.2 |
Note: Panel A presents the weighted proportion of individual-year observations in each of four marital situations, and Panel B presents the proportion of married individuals getting unmarried in the following year (left column) and of unmarried individuals transiting into marriage (right column), within five-year age groups. Panel A is computed using the PSID and the MEPS as indicated; in Panel B, the PSID is used. PSID sample covers 1984–2013, annually until 1997, biannually since then; MEPS sample covers 1996–2009 annually. One-year transitions in Panel B are computed for 1984–1997, when yearly observations are available.
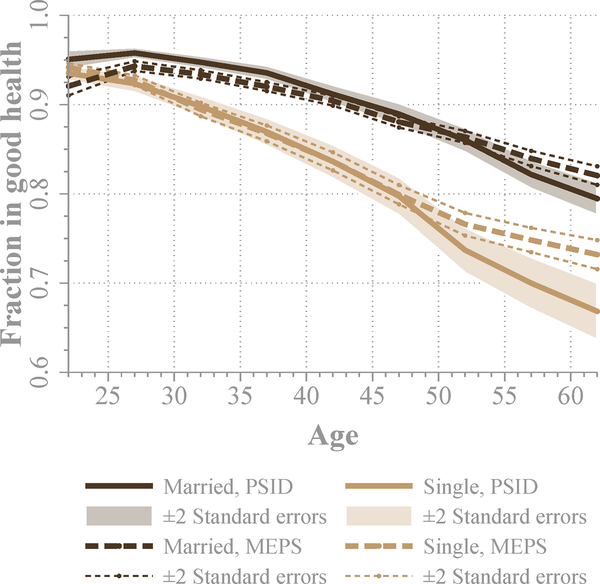
Figure 1 shows differences between married (dark brown lines) and unmarried (light brown lines) individuals in self-reported health from the PSID (dashed lines) and the MEPS (solid lines) for ages between 20 and 64 years. Age patterns of self-reported health as well as the health gap between married and unmarried individuals are remarkably similar in the two data sets. On average for all ages considered (20–64 years), 90% of married individuals indicate that they are healthy, while only 85% of unmarried ones do so. Not surprisingly, in very early ages most individuals (more than 90%) are in good health and the marriage health gap is small. For older ages the marriage health gap widens, and among those who are 40 to 64 years old, 86% of married individuals are healthy in contrast to 76% of unmarried.
Figure 1. Health and Marital Status (PSID and MEPS).
Note: Plotted lines represent the weighted fraction of married and unmarried individuals that report being healthy, computed using the PSID and the MEPS. The horizontal axis indicates age, which is grouped in five-year categories (20–24 through 60–64). Confidence bands of ± two standard errors are computed according to the corresponding survey design: sample weights are used for the PSID, and Taylor linearized standard errors are computed for the MEPS. PSID standard errors are clustered at the household level.
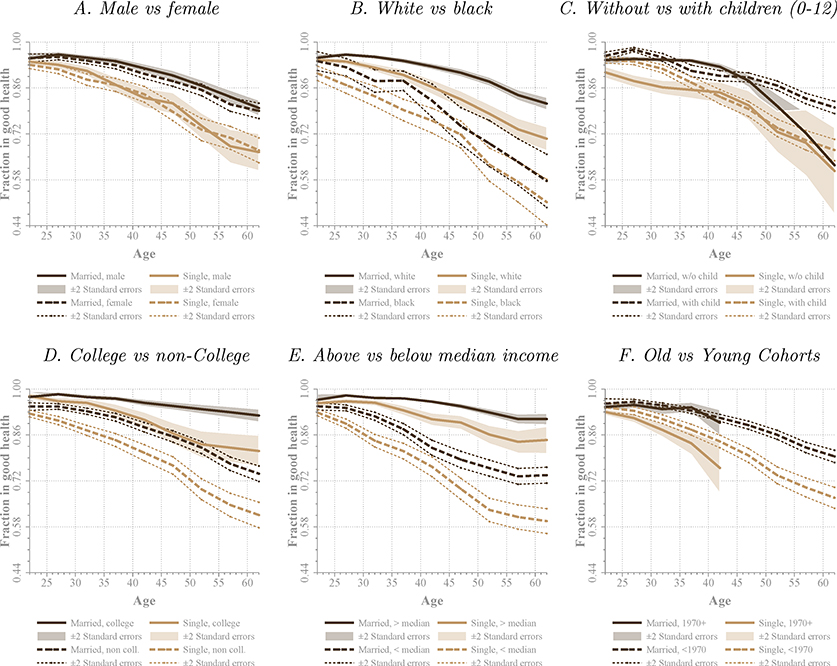
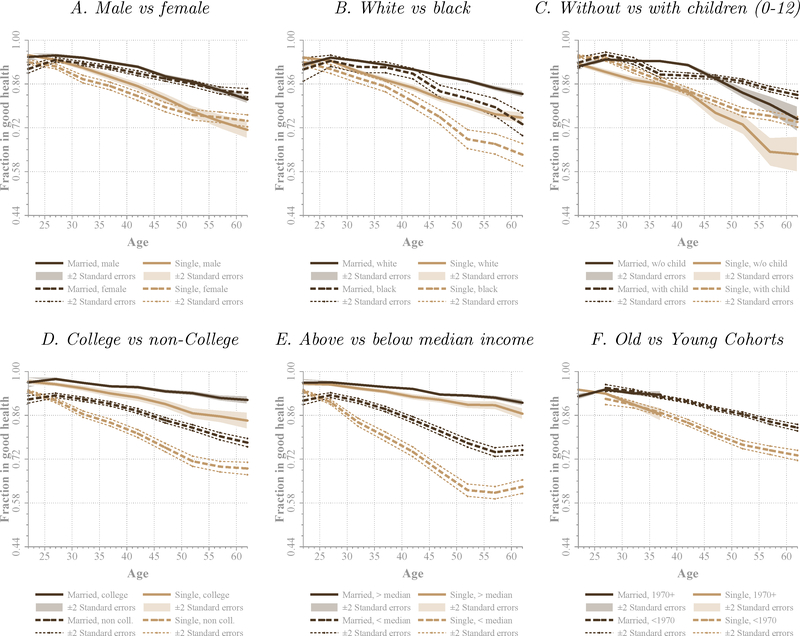
The fact that married individuals are healthier than single ones could be due to a host of factors. Figure 2 reproduces Figure 1 for different sub-populations based on a few observable characteristics for the PSID sample.6 In each sub-panel, dark brown lines indicate married individuals while light brown lines are for unmarried ones, and solid and dashed lines indicate the different sub-populations. As Panel A shows, males and females report very similar levels of health both when they are married and when they are single. According to Panel B, blacks have on average worse health than whites and the marriage health gap vanishes for blacks at older ages. In Panel C, the marriage health gap is visible and comparable whether or not one conditions on the presence of young children (ages 0 to 12 years) — estimates become imprecise at older ages, because few of those individuals have young children). Consistent with findings from the previous literature, individuals with better education and income have much better health. While the marriage health gap is similar conditional on college education (Panel D, the gap is larger for poorer individuals (Panel E). Finally, while younger cohorts report slightly lower levels of good health when unmarried, the marriage health gap is similar for individuals born before and after 1970 (Panel F).
Figure 2. Health and Marital Status for Different Socioeconomic Groups.
Note: Plotted lines represent the weighted fraction of married and unmarried individuals that report being healthy, obtained from the PSID. Fractions are reported, as indicated, for male and female, white and black, without and with children aged 0–12 living in the household, college graduates and non-college, above and below median income, and born after and before 1970. The horizontal axis indicates age, which is grouped in five-year categories (20–24 through 60–64). Confidence bands of ± two standard errors are computed using sample weights. Standard errors are clustered a the household level.
III. Model Specification and Identification
In this section we describe our empirical strategy and discuss briefly how we aim to identify the effect of marriage on health. Our objective is to estimate how being married affects an individual’s health at each point along his/her life cycle. Thus we are interested in heterogeneous treatment effect along the life cycle. The main challenge in identifying the effects of marriage on health is that married individuals might differ from unmarried ones along several observed and more importantly unobserved characteristics. As a result, if healthy individuals select themselves into marriage in the first place, simple correlations between marriage and health will capture a combination of selection and protection effects.
We estimate three different models that take unobserved heterogeneity and selection into account. First, we consider a fixed effects model that allows for individual-specific permanent innate health to be correlated with the treatment (i.e. with being married). Second, we study a less restrictive model that allows the individual-specific innate component of health to differ by age. Finally, since health shocks might also affect probabilities of getting or staying married later on in life, we consider a dynamic panel data model that controls for the lagged health status together with permanent innate health.
We start from the following model:
| (1) |
for i ∈ {1, …, N} and t ∈ {1, …, T}, where hit is the health status of individual i in year t, ait is his/her age, mit is an indicator variable that equals one if the individual is married in period t, xit is a vector of individual characteristics, including gender, race, education, income, children, and year of birth dummies, and (ηi + εit) is the error term, unobserved by the econometrician. The function α(ait) is the health curve for single individuals as a function of age, and α(ait) + β(ait) is the one for married individuals. These functions are non-parametrically specified. Our main interest is in the marriage health gap, which is given by β(a).
The residual ηi + εit is unobservable to the econometrician. The term εit captures health innovations, which are assumed to be uncorrelated with observables, contemporaneously and also in all leads and lags, but potentially autocorrelated over time (and across individuals within a household). If εit is correlated across individuals and/or over time, but not correlated with regressors, the consistency results discussed below still hold, but standard errors need to be corrected appropriately. In estimation, we allow for correlation across individuals within a given household and over time, by clustering the standard errors at the household level.
The unobserved error term also includes an individual-specific permanent component ηi. This type of unobserved heterogeneity generates parallel health curves for different types of individuals, shifted by a different intercept. We interpret this as a permanent innate health component, which shifts health curves vertically, making them parallel across individuals. If certain types of individuals are more likely to get married in the first place (or, more generally, there are systematic differences in the timing and likelihood of marriage for different types), the error term (ηi + εit) will be correlated with the regressors, and Ordinary Least Squares (OLS) estimates will be biased, as we discuss below. Studies in evolutionary biology, for example, suggest that individuals with better innate health are more attractive mates in the marriage market, as better health is a clear indication of reproductive success. This is summarized in Buss (1994) as follows: “Our ancestors had access to two types of observable evidence of a woman’s health and youth: features of physical appearance, such as full lips, clear skin, smooth skin, clear eyes, lustrous hair and good muscle tone, and features of behavior, such as bouncy, youthful gait, and animated facial expression, and a high energy level. These physical cues to youth and health, and hence reproductive capacity, constitute the ingredients of male standards of female beauty” (p.53).7
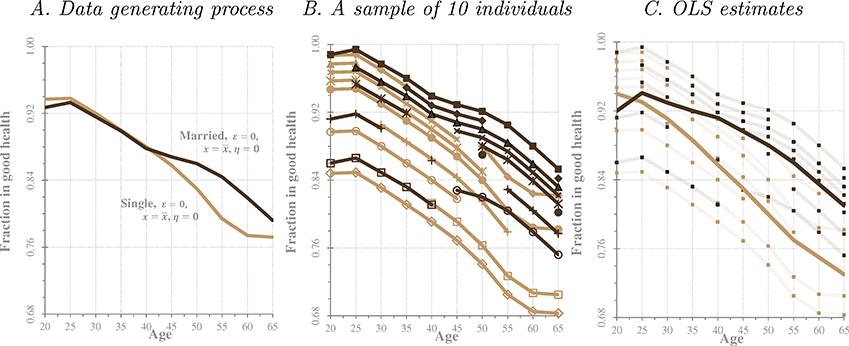
This pattern of self-selection would lead OLS to overestimate the marriage health gap in Equation (1). Furthermore, the size of the bias would differ at different ages. Since a majority of individuals eventually gets married at some point, the bias is likely to be larger at younger ages. We illustrate this bias in Figure 3. Consider the data generating process described in Figure 3A, which shows health curves for married (dark brown line) and single (light brown line) individuals. The curves are drawn with η = 0, and ε = 0. As Figure 3A shows, this process does not generate a marriage health gap at younger ages, while it generates a marriage gap in later years. Our choice for particular health curves in Figure 3A is not random; they approximately reproduce the marriage health gap we obtain from a fixed effects estimation of Equation (1) on the PSID sample. As noted above, since innate health η enters as an additive shifter for given xit and εit, individuals with different η values are represented by health curves that are parallel to those in Figure 3A and shifted by the corresponding ηi.
Figure 3. Unobserved Heterogeneity and the Self-Selection Bias: An Example.
Note: This figure illustrates the bias from omitting unobserved heterogeneity in the estimation of the health curves. Panel A presents the data generating process. Married health curves are dark and single health curves are light. Panel B plots a hypothetical sample of 10 individuals simulated from the data generating process, all of them with and ε = 0. Types of markers identify individuals. Panel C shows OLS estimates of the married and single curves on the simulated sample.
Figure 3B shows a simulated sample of 10 individuals generated by the process just described. Each individual is indicated by a different marker. There is, for example, an individual with the highest value of η who is always married (marked by dark brown squares at the top), and another individual with the lowest value of η who is always single (marked by empty light brown diamonds at the bottom). In between, there are individuals with different marital histories. The individual, who is indicated by empty circles, for example, is single before age 45 years and then he/she gets married. In the generated sample, there is positive self-selection as individuals with higher η are more likely to get married and do so earlier.
If we average observed health of married and of singles (or, equivalently, we fit Equation (1) to those data by OLS), we obtain the health curves depicted in Figure 3C. Given the selection into early marriage by high η individuals, OLS overestimates the underlying marriage health gap. The health curves obtained in Figure 3C intentionally replicate the (unconditional) average health curves by marital status obtained from the PSID, depicted in Figure 1 in Section II.
A fixed-effects estimation of Equation (1) provides consistent estimates of the health curves, as long as our assumption of additive separability of η is satisfied. It is important to note that since α(a) and β(a) are time-varying for a given individual, as he/she is observed over different ages, identification does not rely exclusively on individuals who change their marital status. Individuals contribute to the identification of the shape of married health curves (up to their intercept) whenever they are married, even if they never switch marital status. Likewise, whenever they are single, individuals contribute to the identification of the singles health curve up to the intercept. Changes in marital status thus identify the gap between single and married intercepts.8 Consequently, identification of the marriage health gap at a given age, say 60 to 64 years, is not identified exclusively by individuals who switch marital status within that age range.
As Figure 3C makes clear, we estimate Equation (1) under the assumption that innate health shifts health curves in a parallel way. It is, however, very likely that good or bad innate health maps into small differences in observed health early in the life cycle, while these differences might get magnified as one ages. In order to allow for age-dependent effects of innate health, we next consider the following model:
| (2) |
for i ∈ {1, …, N} and t ∈ {1, …, T}, where now α(a, ηg) is the unmarried health curve for type-g ∈ {1, …, G} individuals, with G < N, and α(a, ηg) + β(a) is the curve for married ones. Thus, Equation (2) allows for age-dependent unobserved heterogeneity that shapes the entire health curves through α(a, ηg).
Bonhomme and Manresa (2015) develop an estimator, to which they refer as grouped fixed effects, for models with grouped patterns of unobserved heterogeneity like the one specified in Equation (2). The estimator optimally groups the N cross-sectional units into types using a least squares criterion. In particular, it is based on an iterative routine that starts from an initial guess of parameters, classifies each individual into the type that provides the smallest mean squared error based on the parameter guess, and updates the parameters reestimating the model conditioning on the resulting classification.9
The intuition for self-selection and identification arguments is analogous to the one illustrated in Figure 3. The main difference is that now the entire health curve is allowed to differ by type in a flexible way (over and above the different intercept). In order to identify such models, however, one needs to set a relatively small number of types. For example, in line with the results below, high types could have a higher intercept and a flatter decrease in their health status by age, while low types could have a lower intercept as well as a more steep health deterioration. The estimator is described in further detail in Appendix C.
The models described in Equations (1) and (2) both assume that there is no feedback from health shocks to marriage probabilities, and that all self-selection occurs through innate unobserved heterogeneity. Health shocks, however, could affect the probability of getting or staying married in subsequent periods.10 To account for this type of self-selection, we consider the following transformation of the model in Equation (1):
| (3) |
for i ∈ {1, …, N} and t ∈ {1, …, T}. By controlling for lagged health, hit−1, Equation (3) analyzes the effect of marriage on health innovations. In this case, a fixed-effects estimation does not deliver consistent estimates, e.g. see Arellano and Bond (1991). Therefore, we use a generalized method of moments approach, in the way described in Arellano and Bover (1995), often known as System-GMM. This procedure delivers consistent estimates if health shocks only affect marriage probabilities with some lag (so that they are captured by ht−1), but health innovations εit are not correlated with contemporaneous marriage probabilities. This assumption is plausible, since we focus on yearly data and, in reality, marriage formation and dissolution decisions take some time to execute.
IV. Estimation Results: the Marriage Health Gap
In this section we present OLS and fixed-effects estimates of Equation (1), grouped-fixed-effects estimates of Equation (2), and system-GMM estimates of Equation (3). We also show that the main results are robust to different definitions of two key variables, health and marriage.
A. Main Results
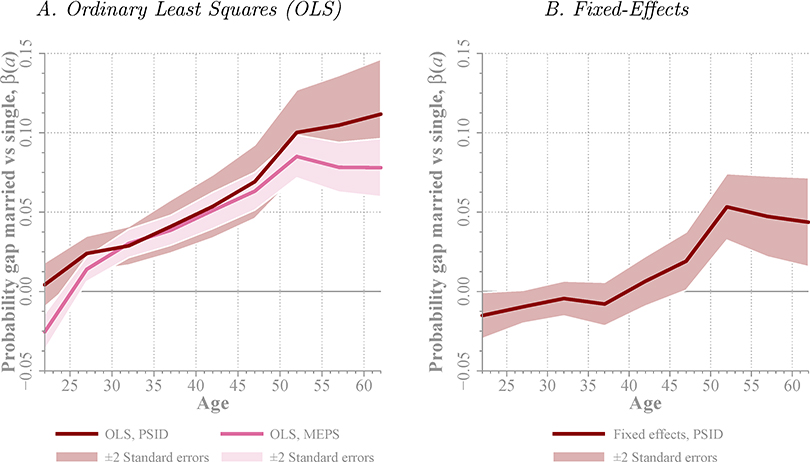
Panel A of Figure 4 presents OLS estimates of β(a) from the PSID (dark blue) and the MEPS (light blue) samples.11 In estimation, we use five-year age bins, from 20–24 to 60–64.12 Health, h, is an indicator variable that takes a value of one whenever the individual is healthy. Control variables, x, include income, gender (female dummy), race (black dummy), education (college dummy), children (dummies for presence of children in the household of ages 0–3, 4–12, and 13–18 years), and cohort (year of birth dummies).
Figure 4. Marriage Health Gap: OLS and Fixed-Effects Estimation Results.
Note: Solid lines show estimated marriage health gaps β(a) from Equation (1). The regression is fitted to the PSID and the MEPS. Left figure presents estimates from OLS regressions, and right figure presents fixed-effects estimates. The dependent variable is an indicator variable that takes a value of one if the individual is healthy. Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate α(a). The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Weights are used in estimation. Confidence bands of ± two standard errors around point estimates are computed following the survey design of each database. Standard errors are clustered at the household level in the PSID.
The results show that after controlling for observable characteristics, there is a positive and significant difference between the reported health of married and unmarried individuals. The gap starts at about 3 percentage points at younger ages (20 to 39 years), and increases continuously for older ages, reaching a peak of 10 percentage points at age 55 to 59 years in the PSID sample. Similar results are obtained from the MEPS sample when we estimate the model with the same controls. The gap is initially small and grows to about 8 percentage points for 55-to-59-years age group. Panel B of Figure 4 shows fixed-effects estimates for the PSID sample. Fixed-effects estimation reduces the size of the marriage health gap substantially. Indeed for ages up to 40 years the marriage health gap disappears completely. After age 40 years, however, the positive effect of marriage on health starts to show up. At the peak of the gap (between ages 50–59 years), married individuals are about 5 percentage points more likely to be healthy than unmarried ones. This is about half of the OLS gap.13
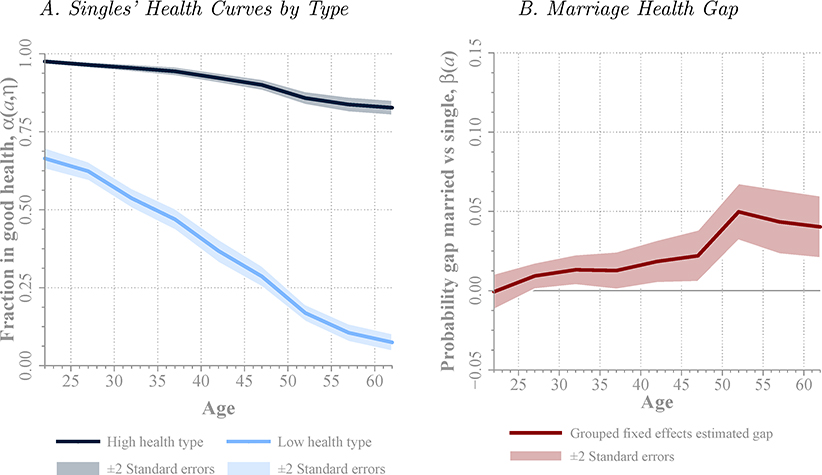
Next, we estimate Equation (2) that allows for age-dependent unobserved heterogeneity. We assume that unobserved heterogeneity is summarized by two (high and low innate health) types. Panel A of Figure 5 shows the health curves for single individuals of each type. It is apparent that two types are clearly separated with respect to their health curves. High types, who are about 81.3% of the sample, have consistently better health at all ages. On the other hand, low-type individuals, 18.7% of the sample, are less healthy to begin with and their health deteriorate faster. These results provide evidence of age-dependent patterns of unobserved heterogeneity in (innate) health.
Figure 5. Marriage Health Gap: Grouped-Fixed-Effects Estimation Results.
Note: Left plot shows α(a, ηg), the estimated health curves for unmarried individuals of high and low health types, and the right plot shows β(a), the estimated marriage health gap, both of them from Equation (2). The model is fitted to the PSID, implementing the algorithm described in Bonhomme and Manresa (2015) for two types. The algorithm was started from 1,000 different random points, and it generally converged to the same minimum. It identified 81.3% healthy-type individuals (12,660), and 18.7% of unhealthy-type (2,909). The dependent variable is an indicator variable that takes the value of one if the individual is healthy. Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies. The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Weights are used in estimation. Confidence bands of ± two standard errors are computed clustering standard errors at the household level.
Panel B of Figure 5 shows the resulting marriage health gap. Marriage health gap is negligible at younger age (below 40–45 years) and then grows to about 5% at around ages 50–55 years. This is again about half of the gap estimated by OLS for these ages. These results are almost identical to those in Panel B of Figure 4. This is remarkable as they are obtained from two models that are quite different. In particular, while the fixed-effects model assumes permanent unobserved heterogeneity, the grouped-fixed-effects one allows for unobserved heterogeneity that is age-dependent. Additionally, estimates are obtained from very different techniques. While the first model is estimated using standard fixed-effects panel data tools, in the second one we allow for two unobserved types, and we use an estimation algorithm that classifies individuals into these types to minimize the predicted squared error for each individual (see Bonhomme and Manresa, 2015).
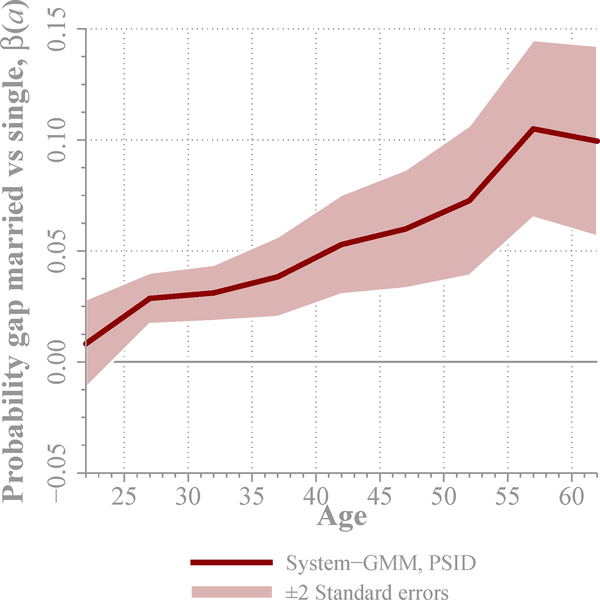
Finally, Figure 6 presents estimates for Equation (3). While the overall pattern of the marriage health gap is similar to what we obtain from fixed-effects and grouped-fixed-effects estimates, the marriage health gap is now larger. This suggests that health innovations are negatively correlated with future marriage prospects (a negative health shock increases the probability of getting or staying married in later periods). As a result, by not including lagged health in Equation (1), we underestimate the effect of marriage on health. Once this bias is corrected, the effect of marriage on health is estimated to be larger. In Figure 6, marriage health gap is already 5% for ages 40 to 49 years and increases up to 10% for later years.14 These results suggest that the results in Figures 4 and 5, are, if anything, conservative estimates of the effect of marriage on health.15
Figure 6. Marriage Health Gap: System-GMM Estimation Results.
Note: The solid line shows the estimated marriage health gap β(a) from the dynamic model in Equation (3). The regression is estimated by System-GMM (Arellano and Bover, 1995) from the PSID for the subperiod 1985–1997. The dependent variable is an indicator variable that takes a value of one if the individual is healthy. Control variables include the lagged dependent variable and a vector of controls that includes female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate α(a). The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Weights are used in estimation. Confidence bands of ± two standard errors are computed clustering at the household level.
The results from these three specifications tell a similar story: there is an role for self-selection in explaining the observed marriage health gap, especially at earlier ages, while some protective effects of marriage on health remain at older ages. We next show that this result is robust to different definitions of the two key variables, health and marriage. In Section V, we then explore both self-selection patterns and the potential remaining protective effects of marriage on health in further detail.
B. Males versus Female
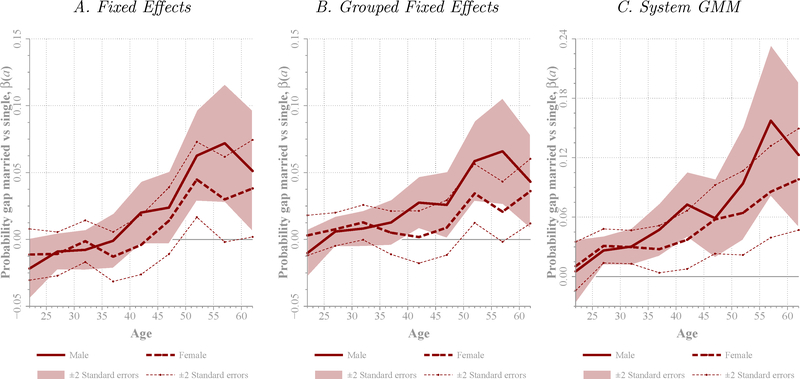
We next study whether the marriage health gap is different for males and females. There is a long-held position in the literature that health benefits of marriage are larger for men than they are for women (see, e.g., the review by Coombs, 1991). This position seems to be established by empirical studies from 1970s when labor market disparities between men and women were much larger, and it was conjectured that marriage produced greater stress for women by making them economically dependent on their husbands (Williams, 2003). Recent medical studies, however, report that men and women benefit equally from marriage (see, e.g., Williams, 2003 and Strohschein, 2016). Figure 7 shows our results for the marriage health gap for males and females. In all specifications, marriage heath gap is slightly larger for males but the difference is never statistically significant. For both genders, there is an important role for self-selection at earlier ages, while protective effects show up later on.
Figure 7. Marriage Health Gap: Results by Gender.
Note: Solid lines show estimated marriage health gaps β(a) from Equations (1), (2), and (3) respectively, estimated separately on the samples of males and females. The regression is fitted to the PSID. The dependent variable is an indicator variable that takes a value of one if the individual is healthy. Control variables include black and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies. The regressions also estimate α(a), α(a, ηgi), and φhit−1 + α(a) respectively. The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Weights are used in estimation. Confidence bands of ± two standard errors around point estimates are computed following the survey design of each database. Standard errors are clustered at the household level in the PSID.
C. Robustness
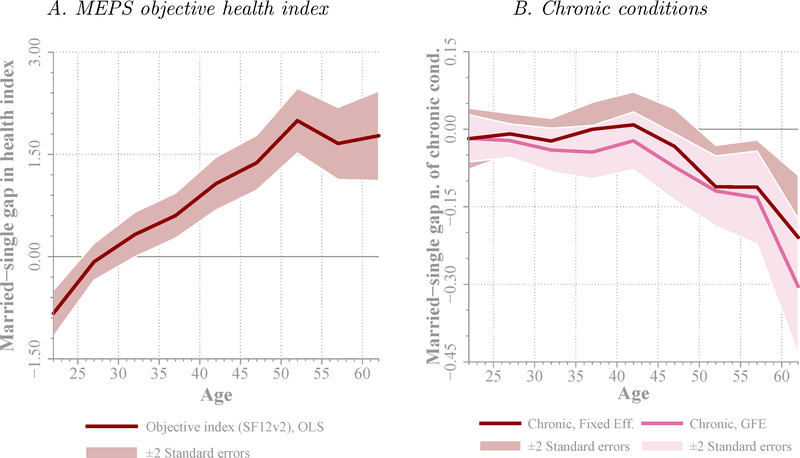
The results in Figure 4 are based on self-reported measures of health. The MEPS contains another measure, SF12v2 (short form 12 version 2), that is constructed as an index from answers that respondents give to a set of health-related objective questions. The left panel of Figure 8 replicates the OLS estimates from the MEPS sample with this measure of health, and show that the basic qualitative picture remains the same. Another objective measure of health is the presence of chronic conditions (such as cancer, hypertension, diabetes, stroke, hearth attack, etc.), which is provided in the PSID. The right panel of Figure 8 shows the fixed-effects and grouped-fixed-effects and estimates of the marriage gap obtained from this health measure.16 The dependent variable is the number of different chronic conditions an individual ever had by any given age. Consistent with the self-reported and SF12v2 measures of health, the difference between married and single individuals is very small for younger ages, but as individuals age, the model predicts that married individuals have a much smaller number of chronic conditions than singles do. Around ages 50 to 54 years, for example, a married individual is expected to have, all else equal, 0.15 fewer chronic conditions than if he/she was unmarried. As we summarize in Table B1 in Appendix B, on average individuals have about 0.73 chronic conditions. Hence, the marriage gap is about 20,5% of the mean. Again the results from the two estimation strategies give similar results.
Figure 8. Alternative Health Measures.
Note: Plotted lines show the estimated marriage health gaps β(a) for two alternative measures of health: SF12v2 objective index of health (left), estimated by OLS from the MEPS, and the cumulative number of different chronic conditions suffered by the individual (right), which includes fixed-effects estimates and group fixed effects estimates as indicated, both obtained from the PSID for the subperiod 1999–2013. The following chronic conditions are considered: stroke, heart attack, hypertension, diabetes, cancer, lung disease, arthritis, asthma, memory loss, and learning disorder, as defined in the PSID. Group fixed effects estimates from the right plot are obtained implementing the algorithm described in Bonhomme and Manresa (2015) for two types. The algorithm was started from 1,000 different random points, and in general converged to the same global minimum. The algorithm identified 63% hightype individuals (9,804), and 37% of low-type (5,765). Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate α(a) or α(a, ηg). The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Confidence bands of ± two standard errors around point estimates are computed following the survey design of each database. Standard errors are clustered at the household level in the PSID.
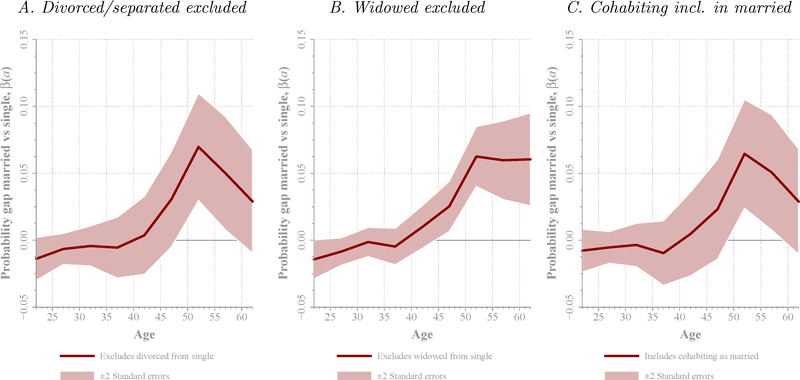
We also check whether the way we define married and unmarried individuals affect the results. In our first check, we would like to understand whether divorce (in contrast to being never married) has a particularly adverse effect on health. To this end, we drop divorced agents from the pool of unmarried, and compare married individuals with those who are never married or widowed. Results in Panel A of Figure 9, are very much in line with our basic results. Indeed, the marriage health gap is now slightly larger, which suggests that divorced individuals have better, not worse, health than those who are never married or widowed. This could possibly reflects a positive effect of marriage capital (measured as the total number of years one is married) on health, which we explore further below. Next, we exclude widows from the pool of single agents (Panel B). In this case, results are similar to our baseline results. Finally, we consider all cohabitants as married (Panel C). As documented in Table B1 in Appendix B, this increases the fraction of married in the PSID from 66% to 72%. Point estimates of the marriage health gap are now slightly smaller, but not statistically different from baseline results.17
Figure 9. Alternative Definitions of Married and Single.
Note: Solid lines show within-groups estimated marriage health gaps β(a) from Equation (1) for different definitions of married and unmarried populations: excluding divorced/separated or widowed from the sample, and including cohabitants in the married group, as indicated. The regression is fitted to the PSID. Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate α(a). The horizontal axis indicates age. In estimation, five-year age bins (20–24, through 60–64) are considered. The center point of the bin is represented in the figure. Weights are used in estimation. Confidence intervals of ± two standard errors are computed clustering at the household level.
V. Exploring Selection and Protection Mechanisms
Results in previous section suggest that both selection of healthy individuals into marriage at early ages as well as protection and improvement of health within marriage at later ages play a role in generating the marriage health gap observed in the data. This section explores how selection and protection may show up in the data.
A. Self-Selection into Marriage and Divorce
We start by documenting the relation between permanent innate health and observed individual characteristics. The left panel of Table 2 shows the coefficients of a regression of when we regress innate health on several individual characteristics. In the first and second columns, the dependent variable is ηi, the estimated fixed effects from Equation (1) and Equation (3), while in the third column, it is a binary variable indicating whether an individual belongs to the healthy type in Equation (2). All specifications give very similar results. In general, more height, less weight, college education, being white, and higher income are associated with higher levels of permanent innate health. There are, however, no significant differences by gender, i.e. females do not have higher innate health than males. Focusing on the first column, additional 10,000$ of income (roughly one third of a standard reviation) is associated with about 0.03 higher value of ηi, about one-eigth of standard deviation of ηi (which is about 0.24). Similarly, being black is associated with 0.063 lower value of ηi, about one-fourth of a standard deviation, and being college graduated is associated with 0.053 additional points, about one fifth of a standard deviation. In panel B of Table 2, we repeat the same exercise for chronic conditions. Individuals experiencing a chronic condition at one point along the life cycle are also much less likely to have higher levels of innate health. Having a stroke, for example, is associated with 18.4 percentage points lower probability of belonging to the healthy type.
Table 2—
Correlation between Innate Health and Observable Characteristics
| A. Demographic characteristics | B. Chronic conditions | ||||||
|---|---|---|---|---|---|---|---|
| Innate permanent health (ηi) |
Probabil. healthy type (ηg(i)) | Innate permanent health (ηi) |
Probabil. healthy type (ηg(i)) | ||||
| Fixed effects | System-GMM | Fixed effects | System-GMM | ||||
| Height (inches) | 0.009 | 0.004 | 0.013 | Stroke | −0.135 | −0.082 | −0.184 |
| (0.001) | (0.001) | (0.002) | (0.027) | (0.026) | (0.042) | ||
| Weight (pounds) | −0.001 | −0.000 | −0.001 | Hypertension | −0.034 | −0.006 | −0.053 |
| (0.000) | (0.000) | (0.000) | (0.006) | (0.005) | (0.009) | ||
| Female | 0.008 | 0.006 | 0.007 | Diabetes | −0.101 | −0.041 | −0.143 |
| (0.008) | (0.009) | (0.014) | (0.011) | (0.011) | (0.019) | ||
| College | 0.053 | −0.028 | 0.080 | Cancer | 0.002 | −0.002 | −0.018 |
| (0.005) | (0.005) | (0.009) | (0.011) | (0.009) | (0.020) | ||
| Black | −0.063 | −0.046 | −0.056 | Lung disease | −0.123 | −0.094 | −0.173 |
| (0.011) | (0.010) | (0.017) | (0.013) | (0.015) | (0.021) | ||
| Income | 0.003 | 0.001 | 0.004 | Heart attack | −0.057 | −0.048 | −0.084 |
| (0.001) | (0.000) | (0.001) | (0.016) | (0.017) | (0.029) | ||
| Constant | −0.508 | −0.182 | 0.171 | Arthritis | −0.074 | −0.039 | −0.115 |
| (0.073) | (0.081) | (0.129) | (0.008) | (0.007) | (0.013) | ||
| Asthma | −0.049 | −0.032 | −0.059 | ||||
| (0.010) | (0.009) | (0.014) | |||||
| Memory loss | −0.206 | −0.131 | −0.320 | ||||
| (0.031) | (0.027) | (0.041) | |||||
| Learning disord. | −0.116 | −0.095 | −0.183 | ||||
| (0.017) | (0.022) | (0.030) | |||||
| Constant | 0.042 | 0.031 | 0.937 | ||||
| (0.002) | (0.002) | (0.004) | |||||
Note: The table presents the coefficients of a regression of innate health on the listed characteristics. Innate permanent health (ηi) refers to the estimated fixed effect from Equations (1) and (3) as indicated. Probability healthy type (ηg(i)) refers to a dependent variable that is a dummy variable that takes the value of one if the individual is of the healthy type as defined in the estimation of Equation (2). The standard deviation of is 0.244 for fixed effects, and 0.209 for System-GMM. Regressions are fitted to the PSID. Standard errors, clustered at the household level, are reported in parentheses.
We next document how innate permanent health is distributed among married and unmarried individuals. The upper panel of Table 3 shows innate health differences between individuals who are never and ever married by ages 30 and 40 years, measured by recovered individual fixed effects from Equations (1) and (3). For both ages, the average innate health of ever-married individuals is higher than never-married ones, but the variance is higher among never married. In the lower panel of Table 3, we report the mean and the standard deviiation of the fraction of individuals who belong to the healthy group by their marital status. Consistent with the results in the upper panel, a smaller fraction of individuals belong to the high health type and innate health is more unequally distributed among never married individuals.
Table 3—
Empirical Distribution of Innate Health
| Individuals that at age […] are […]: |
||||||||
| Age 30 |
Age 40 |
|||||||
| Never married |
Ever married |
Never married |
Ever married |
|||||
| Fixed effects | System-GMM | Fixed effects | System-GMM | Fixed effects | System-GMM | Fixed effects | System-GMM | |
| Innate permanent health (ηi): | ||||||||
| Mean | −0.027 | −0.005 | 0.008 | 0.002 | −0.039 | −0.008 | 0.008 | −0.000 |
| Standard dev. | 0.204 | 0.159 | 0.163 | 0.134 | 0.227 | 0.185 | 0.193 | 0.154 |
| Num. of indiv. | 2,207 | 1,159 | 4,827 | 3,330 | 810 | 670 | 4,963 | 4,353 |
| Age30 |
Age 40 |
|||||||
| Never married | Ever married | Never married | Ever married | |||||
| Innate health type (ηg(i)): | ||||||||
| Fraction of high type | 0.845 | 0.895 | 0.824 | 0.884 | ||||
| Standard deviation | 0.131 | 0.094 | 0.145 | 0.102 | ||||
| Number of individuals | 1,806 | 4,249 | 642 | 4,264 | ||||
Note: The table reports statistics that summarize the empirical distribution of recovered fixed effects ηi in Equations (1), and (3), and of innate health types ηg(i) in Equation (2) for different groups of individuals. Each block includes individuals that, at the listed age, are never married and ever married as indicated. Statistics are computed from the PSID. Weights are used in the estimation. Three year windows are constructed around the indicated age to increase the number of observations.
These patterns are consistent with selection of healthy individuals into marriage. Consider a world in which innate health is observable and singles look for healthy partners. In such a world, given large variance of health among never married individuals, those with good health wait until they find a suitable partner with better health. As a result, the average innate health among married will be higher, while the dispersion of health will be smaller (as in our data). Those with bad health are unattractive partners in the marriage market and those with better health are more selective. Hence, in such a world, health is a good predictor of entry into marriage and there will be positive assortative mating by health among married individuals.18 As we discuss next, the data supports both of these predictions.
We first explore whether health is a good predictor of entry into marriage in the PSID. We focus on individuals who are never married by age 25 years and analyze how innate permanent health (either the estimated fixed effect from Equation (1) or Equation (3), or the health type in Equation (2)) affect their probability of getting married between ages 30 and 40 years. To this end, we first categorize each individual as a high or low innate health type. The estimation of Equation (2) indicates that 81.3% of all individuals in our sample are high health types. As a result, for the fixed-effect and system-GMM estimates, we also label the top 81.3% and bottom 18.7% of individuals in the innate health distribution as high and low health types, respectively. Next, for individuals who are never married by age 25 years, we calculate the difference between high and low types in their probability of getting married between ages 30 and 40 years. The results are shown in the first three columns of Table 4. The first column shows that an individual who is unmarried by age 25 years has about 41% chance of getting married by ages 30 and 40 years if she belongs to the low health type. The probability of getting married, however, is increased by about 19 percentage points if she was a high health type. The results with system-GMM and grouped-fixed-effect estimates of innate health tell a similar story: healthy individual have higher chances of getting married. We implement an analogous analysis for divorce, i.e. we look at individuals who are married at age 25 years and analyze how their innate health correlates with the probability of getting a divorce by ages 30–40 years. We follow a similar strategy to split individuals between high and low health types. The columns fourth to sixth of Table 4 shows the results. A 25-year old married low health type individual has about 33 to 38% chances of getting a divorce by ages 30 to 40 years. This probability declines by 10 to 15% points, i.e. by about a third, if the individual is a high health type.
Table 4—
Health and Marriage/Divorce Probabilities
| Probability that never married by age 25 are married at age 30–40 |
Probability that married at age 25 are divorced at age 30–40 |
|||||
|---|---|---|---|---|---|---|
| Types defined from: | Fixed effects | System GMM | Grouped Fixed Eff. | Fixed effects | System GMM | Grouped Fixed Eff. |
| Low-type probability | 0.413 | 0.540 | 0.429 | 0.333 | 0.388 | 0.331 |
| (0.041) | (0.062) | (0.042) | (0.017) | (0.022) | (0.018) | |
| High-type/Low-type prob. gap | 0.194 | 0.046 | 0.175 | −0.105 | −0.159 | −0.101 |
| (0.044) | (0.064) | (0.044) | (0.018) | (0.023) | (0.019) | |
Note: The left panel presents the coefficients of three regressions of a dummy variable that takes the value of one if the individual is married at some point between ages 30 and 40 on a constant and a dummy variable that equals one if the individual is of high type based on the fixed effects recovered from the estimation of Equations (1), (3), and (2) —for the first two, a high type is defined as an individual at a percentile above the fraction of high types recovered in the third— fitted on the sub-sample of individuals who had never been married by age 25. The right panels present analogous coefficients for a dependent variable that equals one if the individual gets divorced at some point between ages 30 and 40 and it is estimated on the sub-sample of individuals that are married by age 25. These regressions are fitted to the PSID. Robust standard errors in parenthesis.
B. Assortative Mating by Health
The results in the previous section indicate that healthy individuals are more likely to get and stay married. The marriage market outlined above would also predict assortative mating in health. To explore this possibility, the top left panel of Table 5 shows the contingency table for marriages formed by husbands and wives from different quintiles of the innate health distribution, together with marginal distributions of innate health for husbands and wives. Marriages in which both husbands and wives are from the bottom (top) health quintiles, for example, are about 8.1% (8.4%) of all marriages. By construction, the sum of all entries is 100% in a contingency table and due to positive assortative mating, almost half, 47.2%, of all the entries are along the diagonal. How would the contingency table look like if the matching was completely random by innate health? This is shown in the top right panel of Table 5. Entries in the random contingency table are obtained as a product of husbands’ and wives’ marginal distributions. The contin-gency table with random matching looks very different than the actual one. With random matching, there would be only 3.2% (in contrast to 8.1%) of marriages between husbands and wives from the bottom quintile. The fraction of marriages between husbands and wives from the top quintile would decline even more, from 8.4% to 2.5%. Overall, if the matching was random, the sum of diagonal elements in the contingency table would be 21.2%, a 26 percentage points decline from the observed 47.2%. The middle panel presents the same results using innate health measured estimates from Equation Equation (3), while the lower panels of Table 5 repeats the same exercise using the two types (high and low) from Equation (2). Again individuals are more likely to marry someone from their own health type.19
Table 5—
Contingency Tables: Assortative Mating by Innate Health
| Innate permanent health — Fixed effects (ηi) | ||||||||||||
| Observed marital sorting % |
Random matching % |
|||||||||||
| Wife | Wife | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | Marginal | ||
| Husband | 1 | 8.1 | 3.0 | 2.4 | 2.4 | 2.1 | 3.2 | 2.5 | 4.5 | 4.8 | 3.0 | 18.0 |
| 2 | 2.6 | 3.2 | 3.1 | 3.4 | 1.7 | 2.5 | 1.9 | 3.5 | 3.8 | 2.3 | 14.1 | |
| 3 | 2.5 | 2.5 | 14.7 | 5.5 | 0.7 | 4.7 | 3.5 | 6.5 | 7.0 | 4.3 | 26.0 | |
| 4 | 2.6 | 3.3 | 4.2 | 12.8 | 3.6 | 4.8 | 3.6 | 6.6 | 7.1 | 4.4 | 26.5 | |
| 5 | 2.1 | 1.7 | 0.5 | 2.7 | 8.4 | 2.8 | 2.1 | 3.9 | 4.1 | 2.5 | 15.4 | |
| Marginal | 18.0 | 13.6 | 25.0 | 26.8 | 16.5 | 18.0 | 13.6 | 25.0 | 26.8 | 16.5 | 100.0 | |
| Innate permanent health — System-GMM (ηi) | ||||||||||||
| Observed marital sorting % |
Random matching % |
|||||||||||
| Wife | Wife | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | Marginal | ||
| Husband | 1 | 8.9 | 2.7 | 2.3 | 2.6 | 2.7 | 3.7 | 4.2 | 4.5 | 4.3 | 2.5 | 19.2 |
| 2 | 2.6 | 9.8 | 4.6 | 3.3 | 0.8 | 4.1 | 4.6 | 4.9 | 4.7 | 2.7 | 21.0 | |
| 3 | 2.4 | 4.9 | 10.0 | 4.1 | 0.7 | 4.3 | 4.8 | 5.2 | 5.0 | 2.9 | 22.2 | |
| 4 | 2.9 | 3.6 | 5.4 | 10.2 | 2.4 | 4.8 | 5.3 | 5.8 | 5.5 | 3.2 | 24.6 | |
| 5 | 2.7 | 0.7 | 1.2 | 2.1 | 6.3 | 2.5 | 2.8 | 3.1 | 2.9 | 1.7 | 13.1 | |
| Marginal | 19.5 | 21.8 | 23.5 | 22.3 | 12.9 | 19.5 | 21.8 | 23.5 | 22.3 | 12.9 | 100.0 | |
| Innate health type (ηg(i)) | ||||||||||||
| Observed sorting % |
Random matching % |
|||||||||||
| Wife | Wife | |||||||||||
| Husband | Low | High | Low | High | Marginal | |||||||
| Low | 5.7 | 8.2 | 2.0 | 11.9 | 13.9 | |||||||
| High | 8.6 | 77.5 | 12.3 | 73.8 | 86.1 | |||||||
| Marginal | 14.3 | 85.7 | 14.3 | 85.7 | 100.0 | |||||||
Note: In the left columns of the two top panels, each cell gives the observed percentage of married households in which husbands and wifes lie in each indicated quintile of innate permanent health estimated from Equations (1) and (3) respectively). In the right columns of each panel, each cell gives the predicted percentage from multiplying marginal distributions of husbands and wives, which are reported, respectively, at the last column and row. The bottom panel provides similar statistics computed for the innate health types obtained from the estimation of Equation (2).
Table 6 shows that the simple correlation coefficient between innate permanent health of husbands and wives is about 0.30 to 0.37 (as a comparison, the one for years of education among husbands and wives is about 0.5).20 When we control for education and race (by regressing recovered innate health, on these controls and looking at the correlations between residuals), the correlation remains almost unchanged. Even when we add a measure of permanent income (predicted fixed effects from a regression of taxable individual income on education, age, age squared, marriage and year dummies) as a further control, innate permanent health is still highly correlated between husbands and wives (about 0.28 to 0.32).
Table 6—
Correlation of Husband’s and Wife’s Innate Permanent Health
| (1) |
(2) |
(3) |
||||
|---|---|---|---|---|---|---|
| Permanent health (ηi) from: | Fixed Effects | System-GMM | Fixed Effects | System-GMM | Fixed Effects | System-GMM |
| Self-reported health | 0.374 | 0.302 | 0.347 | 0.295 | 0.318 | 0.279 |
| (0.019) | (0.025) | (0.020) | (0.025) | (0.019) | (0.025) | |
| Chronic conditions | 0.221 | 0.206 | 0.191 | |||
| (0.022) | (0.022) | (0.022) | ||||
| College and race | No | Yes | Yes | |||
| Permanent income | No | No | Yes | |||
Note: The table reports conditional correlation coefficients between husband and wife’s estimated innate permanent health (ηi from Equations (1) and (3)). The first row corresponds to the baseline regression,in which the self-reported measure of health is used in the regression. The second row is computed using the number of chronic conditions as a dependent variable, as in Figure 8. To control for college and race, we introduce dummies for individuals and spouses having a college degree and being black, as well as the corresponding interactions. For the permanent income, we include husband’s, wife’s, and interacted individual fixed effects obtained from a regression of taxable individual income on years of education, age, age squared, marriage, and year dummies. All correlations are estimated from the PSID. Weights are used in the estimation. Bootstrapped standard errors in parenthesis.
Since health status in the PSID is reported by the household head for both himself/herself and his/her spouse, one might wonder whether these correlations simply reflect this particular feature of the data collection.21 In order to address this potential concern, we repeat our exercise with innate health estimates obtained using the presence of chronic conditions as a measure of health in Equation (1) (second row of Table 6). Even if reported by the household head, chronic conditions, unlike a subjective measure of health, are much less likely to result in spurious correlations. We find that the correlation between innate healths of husbands and wives is again significant (estimated value is 0.22 in this case, which is while still large, somewhat smaller than 0.37 above). Moreover, the correlation remains significant when we control for education, race and permanent income.
C. Healthy Behavior
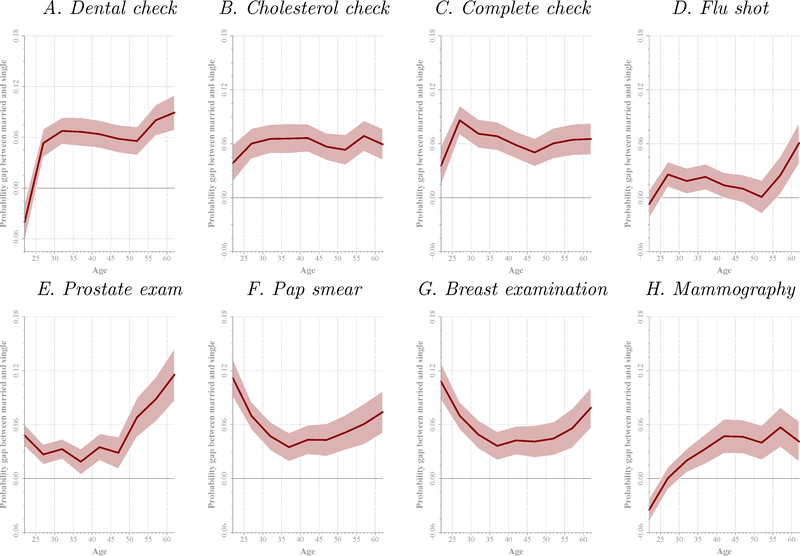
What factors can explain the protective effect of marriage on health? This section documents that married individuals are more likely to engage in healthy behavior than unmarried ones. Figure 10 shows differences between the probabilities that married and unmarried individuals do preventive health checks. The figure shows coefficients form regressions similar to Equation (1), where the dependent variable is an indicator variable that equals one if the individual undertakes a particular check at a given age. This regression is fitted to the MEPS.
Figure 10. Preventive Health Checks and Marital Status.
Note: Plotted lines show OLS estimates of the marriage gap in the probability of doing preventive checks. These differential curves are obtained from a regression that is similar to (1) but where the dependent variable is an indicator variable that takes the value of one if the individual did the indicated preventive check in previous years. The following preventive checks are considered: dental check at least once every year; cholesterol check, general physical examination, flu shot, prostate examination, Pap smear, breast examination, and mammography at least once in the last two years. The equation is fitted to data from the MEPS. Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies, as well as current health, health insurance (public and private insurance dummies) and total health expenditures; regressions also estimate probability curve for singles. Weights are used in the estimation. The horizontal axis indicates age. In estimation, five-year age bins (20–24 through 60–64) are considered. The center point of the bin is represented in the figure. Dotted lines indicate ± two standard errors confidence bands around point estimates, which are Taylor linearized using survey stratification design in the MEPS.
The results show that there are significant differences between married and single individuals for all categories of preventive care. Married individuals around ages 50 to 54 years, for example, are about 6 percentage points more likely to check their cholesterol or have a prostate or breast examination. Note that these differences come from regressions that control for education and income. Hence, the effect of marriage on healthy behavior goes beyond the well documented effect (see e.g. Cutler and Lleras-Muney, 2010) of education on healthy behavior.
Why would married individuals be more likely to do preventive care? One possible factor, which is well documented in the medical literature, is that having a partner encourages individuals to follow up on medical appointments, check-ups, etc.22 Another factor, which we focus on in the next subsection, is the fact that married individuals are more likely to have health insurance than unmarried are.
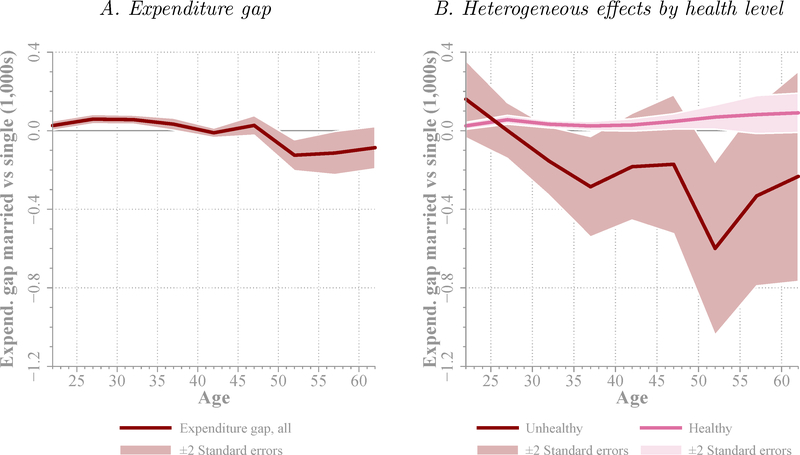
Differences between married and unmarried individuals in healthy behavior are also reflected in their medical expenditures. To analyze differences in medical expenditures, we specify the conditional median of the total medical expenditure to be given by a similar expression to the right hand side of Equation (1).23 Panel A of Figure 11 shows our estimates of the marriage gap in median health expenditure estimated from the MEPS. Results suggest that median health expenditure of married individuals aged below 40 years is around 40–60$ larger per year than that of unmarried individuals at the same age range. This gap is quite significant and represents about 12% of the median medical expenditure by individuals below age 40 years (about 420$). At older ages, though, unmarried individuals spend more than married ones; at ages 50–59 years, median expenditure of unmarried individuals is around 100–110$ larger. This is about 6.5% of the median medical expenditure for this age group (about 1,600$).
Figure 11. Median Health Expenditures and Marital Status.
Note: Solid line in the left plot shows the marriage gap in median health expenditures obtained from a regression to Equation (1), but with total health expenditures as the dependent variable. Solid lines in the right plot shows estimated heterogeneous marriage gaps in median expenditures by health level (healthy, dark blue, and unhealthy, light blue). Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies, as well as health insurance (public and private insurance dummies); regressions also estimate median expenditure curves for singles in each health level. The regressions are estimated from the MEPS. The horizontal axis indicates age. In estimation, five-year age bins (20–24 through 60–64) are considered. The center point of the bin is represented in the figure. Dotted lines represent ± two bootstrapped standard error confidence bands.
This higher expenditure by married individuals at earlier ages may be due to preventive motives, while the higher expenditure by unmarried at older ages may be due to curative motives, as a result of worse health. To further explore this hypothesis, we estimate marriage expenditure gaps for different health statuses. In particular, we extend the median expenditure model to account for heterogeneous expenditure curves for different health levels. Panel B of Figure 11 presents median regression estimates of the marriage health expenditure gap for healthy and unhealthy individuals. Married individuals consistently spend more when they are healthy, which is in line with the fact that they are more likely to do preventive checks. In contrast, unmarried individuals spend substantially more than married ones when they are unhealthy, which suggests that when the unmarried are unhealthy, they are more likely to face serious (and expensive) conditions.24
Finally, we check whether marriage is associated with healthy habits. We focus on smoking, a key health factor. In particular, we look at all individuals who were smokers in 1999 and document how many of them quit smoking between 1999 and 2013 conditional on their marital transitions.25 As Table 7 shows, a single individual is about 23 percentage points points more likely to quit smoking if he/she gets married than if he/she stays single (53% versus 30%); additionally, a majority (about 74%) of singles who get married and quit smoking do so while they are married. Likewise, a married individual is more likely to quit smoking if he/she stays married than if he/she becomes single (41% versus 31%).
Table 7—
Probability of Quitting Smoking and Marital Transitions
| Probability of quitting smoking | Probability of quitting smoking… |
||
|---|---|---|---|
| while married | while single | ||
| Single → Single | 0.298 | 0.005 | 0.293 |
| (0.024) | (0.003) | (0.024) | |
| Single → Married | 0.526 | 0.390 | 0.135 |
| (0.050) | (0.049) | (0.034) | |
| Married → Single | 0.312 | 0.084 | 0.228 |
| (0.045) | (0.027) | (0.041) | |
| Married → Married | 0.414 | 0.407 | 0.007 |
| (0.025) | (0.025) | (0.004) | |
Note: The table presents the probability that an individual quits smoking between 1999 and 2013 conditional on smoking in 1999, by marital transition. These probabilities are calculated from the PSID. Weights are used in the estimation. In the left column, the numerator is the number of individuals in a given marital transition that were nonsmokers either in 2013 or in the last year for which smoking information is available, and were smokers in 1999. The denominator is the number of individuals in the indicated marital transition who were smokers in 1999. In the right panel, the numerator is restricted to individuals that were married/single in the first year they are observed as nonsmokers after their last smoking spell. The total number of observations is 1,373. Standard errors are in parenthesis.
Overall, these results suggest that marriage goes together with healthy behavior. Even after controlling for observables (most importantly income, education and health insurance) preventive health care, measured both by frequency of preventive medical checks and by health expenditure while healthy, is more prevalent among married individuals than it is among singles. Marriage is also associated with a higher probability of quitting smoking.26
D. Health Insurance
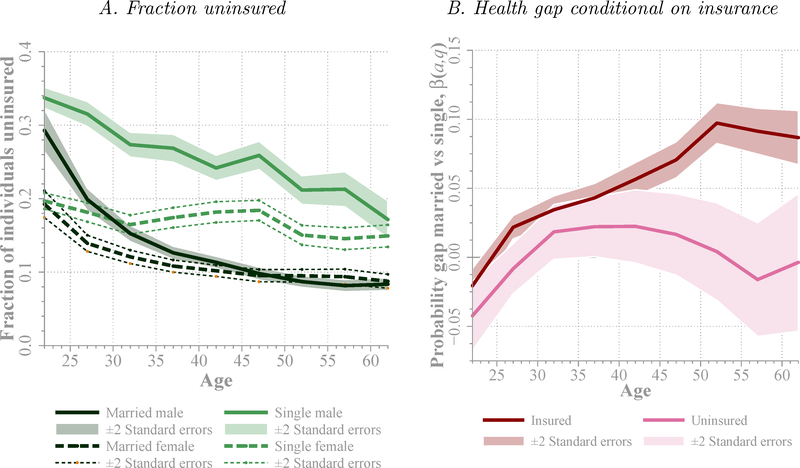
Health insurance status is a key determinant of health care utilization in the United States.27 In the MEPS sample, about 16% of individuals, who are between 20 and 64 years old, do not have any public or private health insurance. Panel A in Figure 12 shows how health insurance status differ by marital status for males and females. For both genders, unmarried individuals are more likely to be uninsured than married ones. The gap is, however, larger for males. At ages 45 to 49 years, for example, about 10% of married individuals, male or female, do not have any health insurance. The fraction of uninsured among the unmarried of the same age is less than 20% for females, while it is higher than 25% for males.28 The smaller gap for females reflects the effect of Medicaid that provides health insurance for children and their parents, in particular single mothers, in low-income families. In the MEPS sample, 9.0% and 17.6% of unmarried males and females have public health insurance, respectively.
Figure 12. Health Insurance, Health, and Marital Status.
Note: Thick lines in the left plot show the weighted fraction of married and unmarried males and females that are not covered by any health insurance (public or private). Solid lines in the right plot are OLS estimates of the marriage health gap for insured and uninsured individuals. Results are obtained from the MEPS. In the right figure, control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate health curves for singles with and without insurance. The horizontal axis indicates age. In estimation, age is grouped in five-year bins (20–24 through 60–64) and the center point of the bin is graphed. Dotted lines indicate ± two standard errors confidence bands around point estimates, which are Taylor linearized computed following the survey stratification design.
Panel B in Figure 12 documents how medical insurance affects the marriage health gap. We report OLS estimates of heterogeneous health curves for individuals with (dark blue) and without (light blue) health insurance. For individuals with health insurance, the results are similar to what we document in Panel A of Figure 4 for the MEPS sample. Married individuals are healthier and the estimated health gap grows by age. For uninsured individuals, however, we do not find any significant health gap between married and unmarried. These results suggest that the availability of health insurance is an important facilitator for positive effects of health on marriage.
E. Health Accumulation Through Marriage
Finally, we investigate whether the benefits of marriage on health are cumulative, i.e. whether the duration of marriage matters. In Panel A of Figure 13, we show results from a regression that is very similar to Equation (1) except that mit is replaced by a measure of marriage capital, defined as the total number of years an individual has been married by year t.29 Hence β(a) now measures the effect of one extra year of being married at a given age a on the probability of being healthy. The effect of an extra year of marriage is positive and significant and roughly constant after ages 35–39 years: having accumulated 10 extra years of marriage increases the probability of being healthy by about 3 percentage points. At earlier ages, the estimated effects are negligible.
Figure 13. Health Accumulation Through Marriage.
Note: The left figure shows fixed-effect estimates of the health capital accumulated from marriage from a modified version of equation (1) in which the married dummy m is replaced by the number of years an individual have been married (zero if never married). Estimates are done with the PSID. The right figure plots the predicted marriage health gap for individuals married at age 25 and at age 40. Control variables include female, black, and college dummies, income, dummies for 0–3, 4–12, and 13–18 year-old children at home, and year of birth dummies; regressions also estimate the health curve for singles. The horizontal axis indicates age. In estimation, five-year age bins (20–24 through 60–64) are considered and the center point of the bin is graphed. Dotted lines are ± two standard errors confidence bands around point estimates, clustered at the household level.
Based on estimates from Panel A, in Panel B we show predictions for two possible marital histories for an average person and their cumulative effects on health. The red (dark) line shows the predicted marriage health gap for a person who gets married at age 25 years and stay married afterwards compared to someone who never gets married. Hence, the simulated line is simply the cumulative sum of the estimates in Panel A. Consistent with our estimates in Section IV, marriage does not contribute to better health in early ages, but a health gap starts to emerge after around age 40 years. By ages 55–60 years, this individual is about 5 percentage points more likely to be healthy compared to someone who has never been married. Furthermore, since the effect of marriage on health appear only after around age 40 years, an individual who gets married at age 40 years, the pink (light) line, enjoys almost the same benefits from marriage compared to the individual who marries at age 25 years. This is very reassuring, since although they rely on a different estimation strategy, these simulations produce almost identical results to our estimates from Figures 4 and 5. Hence, it provides interesting insight for the interpretation of our main results in Section IV.
VI. Conclusions
We use data from the Panel Study of Income Dynamics (PSID) and the Medical Expenditure Panel Survey (MEPS) to document differences in health between married and unmarried individuals. After controlling for observables (education, income, race and gender), there exists a marriage health gap of about 10 percentage points in both data sets. We estimate the marriage health gap as the difference between health curves for married and single individuals, nonparametrically specified as a function of age. Allowing for heterogeneity in innate health (both permanent and age-dependent), our results suggest that the marriage health gap disappears for younger ages (20–39 years), while a positive gap of 5 percentage points remains for older ages (50–59 years). We interpret these results as evidence that self-selection into marriage drives the observed marriage health gap at younger ages, while, at older ages, an important fraction of the observed gap is explained by protective effects of marriage on health.
We provide detailed evidence of self-selection patterns in the data, and on different mechanisms through which marriage exerts a beneficial effect on health. We observe that the distribution of innate permanent health of married individuals has a higher mean and lower variance than that of unmarried individuals. This would be consistent with a marriage search model in which innate health is observable. Such model implies positive assortative mating by innate health, and innate health is a good predictor of early entry into marriage. The data supports both of these predictions. On the other hand, we document that married individuals are much more likely to engage in preventive care and that the total years of being married (not just current marital status) has a positive effect on health. We interpret these results as indicators of better health production within marriage. We find that health insurance plays an important role in this difference.
We close the paper by two comments for future research. First, the current paper focuses on the U.S. where the effect of marriage on different socioeconomic outcomes, including heath, received attention both in academic research and popular press. The results in this paper suggest that the availability of health insurance is an important factor for the positive effects of health on marriage. As a result, it will be interesting to extend the analysis to countries where public health insurance systems differ significantly from the U.S. The British Household Panel Survey or the German Socioeconomic Panel, which contain health data comparable to the PSID, can be used to this end. Second, a growing literature highlights how household and family structure might be critical to understand key questions in macroeconomics and public finance —Doepke and Tertilt (2016) and Greenwood, Guner and Vandenbroucke (2017) provide recent reviews. Models with two-earner households are used in this literature to understand the key life-cycle decisions, such as consumption, savings, and labor supply, as well as to assess how households reacts to changes in public policy. Our results in this paper show that household structure (who is married, who is single and who is married with whom) might also be critical to understand health profiles along the life-cycle. Thus, incorporating health production with an explicit model of household formation can be critical to evaluate health policies.
Acknowledgments
We would like to thank the Editor, Robert Sauer, and two anonymous referees for their comments. We also thank Matt Delventhal, Giacomo De Giorgi, Francesco Fasani, Ada Ferrer-i-Carbonell, Eric French, Elena Manresa, Francesc Obiols, Andrew Shephard, and workshop and conference participants at the European Meeting of the Econometric Society in Toulouse, the Annual Meetings of the Spanish Economic Association in Santander, Barcelona GSE Winter Workshop, CINCH Summer Academy at the University of Duisburg-Essen, Koç University, and Universitat Autònoma de Barcelona. Financial support from European Research Council (ERC) through Starting Grant n.263600, from the Spanish Ministry of Economy and Competitiveness (ECO2013–49357-EXP, ECO2014–59056-JIN, ECO2014–54401-P, and Severo Ochoa Programme for Centers of Excellence in R&D, SEV-2011–0075 and SEV-2015–0563), and from the Generalitat de Catalunya (2017-SGR-1765) is gratefylly acknowledged. A previous version of this paper was circulated under the title ”Does Marriage Make You Healthier?”.
Appendix A: Data Description and Variable Definitions
A1. Sample Selection
Panel Survey of Income Dynamics (PSID)
The Panel Study of Income Dynamics (PSID) is administered by the Survey Research Center in the Institute for Social Research at the University of Michigan (University of Michigan, 2015). The study began in 1968 with a nationally representative sample of over 18,000 individuals living in 5,000 families in the United States. Extensive demographic and economic data on these individuals and their descendants have been collected continuously since then, yearly until 1997 and biannually after that. The PSID started to collect data on health in 1984. We use data from 1984 to 2013 (the latest year of the survey). The analysis is based on the core PSID sample. While the PSID has extensive data on heads and spouses, available data for other household members is limited. Our analysis focuses on heads and spouses based on “sequence number” 1 (head) or 2 (wife).
Medical Expenditure Panel Survey (MEPS)
The Medical Expenditure Panel Survey (Agency of Healthcare Research and Quality, 2011) began in 1996 and it is the most complete source of data on the cost and use of health care and health insurance coverage in the United States. The survey has two major components: the Household Component and the Insurance Component. We use the Household Component, which contains extensive information on demographic characteristics, health conditions, health status, usage of medical services, access to care, satisfaction with care, health insurance coverage, income, and employment, at both individual and household levels, supplemented by information from their medical providers. The survey has a rotating panel structure in which each individual is interviewed 5 times during a 2-year period and then replaced. The sample includes about 31,000 individuals per year, with some variation across years, and it is representative of the U.S. population. As we do not exploit the short panel dimension of the data set, for each year we consider the cross-section of available individuals. Some of the variables are only available at a yearly basis. Others are available at each of the five interviews over the two-year period. In the latter case, for each individual, we consider his/her first interview of the year. We use survey years 1996 to 2009.
Both in the PSID and in the MEPS, we clean our samples by dropping observations that have no compete information on self-reported health, marital status, gender, race, or income. We focus on working-age individuals, so we consider individuals aged 20 to 64.
A2. Variable Definitions
Self-Reported Health
Our main health variable is constructed from the reported self-rated health. Individuals rate their health as “excellent”, “very good”, “good”, “fair” or “poor”. We create a health dummy where 1 (healthy) corresponds to the first three grades, and 0 (unhealthy) to the other two.
Marital Status
Marital status is defined as one of four possible status as reported by individuals: “married”, “divorced/separated”, “widowed”, “separated” and “never married”. In the PSID, if a respondent reported to be widowed, divorced or separated in a previous period, but reports to be never married in current one, he/she is assigned his/her previously-reported marital status. The MEPS contains two questions on marital status: “what is your current marital status?” and “what was your marital status in previous round” (which means after the previous interview, but before the current one). Whenever available, marital status is determined based on the first question; the second question is used otherwise.
Age
We create five-year age bins: 20–24, 25–29, 30–34, etc.
Gender
Gender is self-reported.
Race
Based on self-reported race, we create a “black” dummy, which we use as a control in most of the regressions. Additionally, we also create a “white” dummy that is used when we compute heterogeneous health gaps by race (Figures 2 and B1).
Education
Our main education variable is a dummy that takes the value of one if the individual received a college degree, based on the responses to “did you receive a college degree?” or “did your wife receive a college degree?” in the PSID or “highest degree attained” in the MEPS (in which case, college degree is defined as bachelor’s degree or more). In the PSID, if a person reported that he/she has a college degree in a previous year, but the answer to this question is missing in a later year, we use previous answer to fill the missing observation. In the last column of Table 6, we use the number of years of education of the individual to compute our measure of permanent income. This information is based on the response to the question “what is the highest grade or year of school that you have completed?”. For that particular exercise, observations with DK/NA codes are dropped. Whenever possible, missing or zero observations are imputed from valid answers to this questions from preceding or following interviews. If a respondent reports a lower completed grade in an interview after he/she reports a higher one in a previous interview, we consider the higher value.
Children
Presence of children in the household is identified from the question “children under 18 in the family unit”. From the record of each child in the household, we identify their age and create dummy variables for the presence of children of the ages 0 to 3, 4 to 12, and 13 to 18.
Income
Our definition of income is “taxable income” in the PSID or “total person’s income” in the MEPS. For couples (married or cohabiting), we calculate household taxable income by summing the total taxable incomes of the head and the spouse and then divide the total taxable income by 2. This variable is deflated using 2005 Consumer Price Index (CPI), obtained from the Bureau of Labor Statistics.
Marital capital (PSID)
Marital capital is defined as the sum of the durations of all (past and present) marriages. Duration of a given marriage is calculated as the difference between either the year of divorce/separation/widowhood or the current year (depending on whether the marriage ended or is ongoing), and the starting year of the marriage. This information is obtained from the Marriage History Supplement of the PSID.
Chronic conditions (PSID)
We consider the following chronic conditions: stroke, hypertension, diabetes, cancer, lung disease, heart attack, heart disease, arthritis, asthma, memory loss, and learning disorder. For each of them, we create a dummy that equals one if you ever suffered that condition. Our chronic conditions variable is defined as the sum of these dummies across all conditions. Hence, it measures the number of different conditions the individual ever suffered.
Smoking (PSID)
An individual is classified as a smoker if he answered the question “do you smoke cigarettes?” affirmatively or the household head did so for the question “does your wife smoke cigarettes?”. Smoking transitions conditional on marital transitions are then computed as described in the main text.
Cohabitation (PSID)
Cohabitants are identified from the variable “relationship to head”. This variable takes the following values: 10 (head), 20 (legal wife), 90 (legal husband of head, if in rare cases the head is a female), 22 (female cohabitant who has lived with the head for 12 months or more), 88 (first-year cohabitant, boyfriend or girlfriend, of head). To identify cohabitants we use codes 22 and 88.
Objective Health Index (MEPS)
We use the Physical Summary Component of the Short Form 12 version 2 (SF-12v2) as an objective index of health. In 2000, 2001, and 2002, MEPS used Version 1 of the SF-12. Therefore for these years, Version 1 scores are converted to Version 2 scores by adding 1.07897. Further details are available at http://meps.ahrq.gov/data_stats/download_data/pufs/h147/h147doc.pdf.
Preventive checks (MEPS)
For each preventive check (dental, cholesterol, general, flu shot, prostate check, pap smear, breast examination and mammography), we create a dummy variable that is equal to 1 if a person did the corresponding check within the preceding two years and zero otherwise.
Medical expenditure (MEPS)
We use total medical (health care) expenditures. Expenditures are defined as the sum of direct payments for care provided during the year, including out-of-pocket payments and payments by private insurance, Medicaid, Medicare, and other sources. Payments for over the counter drugs and for alternative care services are not. Indirect payments not related to specific medical events, such as Medicaid Disproportionate Share and Medicare Direct Medical Education subsidies, are not included either. Whenever medical expenditure is used, we drop observations with unavailable medical expenditure. Expenditures are deflated by 2005 medical CPI, available at http://data.bls.gov/cgi-bin/surveymost?cu.
Insurance (MEPS)
We use the insurance coverage variable and distinguish between “any private insurance”, “any public insurance” and “no insurance”. Whenever indicated, we create two dummies, public or private, which take the value of one if the individual holds the corresponding insurance (public and private insurance are not mutually exclusive). Otherwise, we create an indicator variable that equals one if the individual holds any insurance, public or private. Whenever insurance information is used, observations with unavailable insurance are dropped.
Appendix B: Descriptive Statistics
Table B1—
Descriptive Statistics: Panel Study of Income Dynamics (PSID)
| Mean | St. dev. | Min | Max | N.obs. | |
|---|---|---|---|---|---|
| i. Baseline | |||||
| Healthy | 0.88 | 0.33 | 0.0 | 1.0 | 150,062 |
| Married | 0.66 | 0.47 | 0.0 | 1.0 | 150,062 |
| Age | 41.63 | 11.82 | 20.0 | 64.0 | 150,062 |
| Female | 0.53 | 0.50 | 0.0 | 1.0 | 150,062 |
| Black | 0.12 | 0.33 | 0.0 | 1.0 | 150,062 |
| College | 0.32 | 0.47 | 0.0 | 1.0 | 150,062 |
| Children 0–3 years | 0.16 | 0.36 | 0.0 | 1.0 | 150,062 |
| Children 4–12 years | 0.28 | 0.45 | 0.0 | 1.0 | 150,062 |
| Children 13–18 years | 0.21 | 0.41 | 0.0 | 1.0 | 150,062 |
| Taxable income (in 1000$) | 37.76 | 50.03 | −590.2 | 5,500.0 | 150,062 |
| ii. Robustness and further explorations | |||||
| Married+cohabiting | 0.72 | 0.45 | 0.0 | 1.0 | 150,062 |
| Divorced/separated | 0.16 | 0.36 | 0.0 | 1.0 | 150,062 |
| Widowed | 0.02 | 0.15 | 0.0 | 1.0 | 150,062 |
| Never Married | 0.16 | 0.37 | 0.0 | 1.0 | 150,062 |
| Marriage capital | 18.65 | 11.97 | 0.0 | 52.0 | 114,627 |
| Height (inches) | 67.21 | 3.86 | 51.0 | 82.0 | 111,397 |
| Weight (pounds) | 175.11 | 42.77 | 75.0 | 400.0 | 42,975 |
| Smoke | 0.22 | 0.42 | 0.0 | 1.0 | 61,360 |
| Num. of chronic conditions | 0.73 | 1.09 | 0.0 | 10.0 | 54,466 |
| Chronic conditions: | |||||
| Stroke | 0.02 | 0.13 | 0.0 | 1.0 | 54,443 |
| Hypertension | 0.22 | 0.41 | 0.0 | 1.0 | 54,430 |
| Diabetes | 0.07 | 0.26 | 0.0 | 1.0 | 54,432 |
| Cancer | 0.04 | 0.20 | 0.0 | 1.0 | 54,430 |
| Lung disease | 0.04 | 0.20 | 0.0 | 1.0 | 54,432 |
| Heart attack | 0.02 | 0.14 | 0.0 | 1.0 | 54,444 |
| Arthritis | 0.14 | 0.35 | 0.0 | 1.0 | 54,435 |
| Asthma | 0.10 | 0.30 | 0.0 | 1.0 | 54,437 |
| Memory loss | 0.01 | 0.11 | 0.0 | 1.0 | 54,433 |
| Learning disord. | 0.03 | 0.16 | 0.0 | 1.0 | 54,433 |
Note: Means and standard deviations are computed using weights. The sample covers 1984–2013, annually until 1997, bianually since then. Chronic conditions and smoking data is only available starting in 1999. Taxable income is deflated by 2005 CPI.
Table B2—
Descriptive Statistics: Medical Expenditure Panel Survey (MEPS)
| Mean | St. dev. | Min | Max | N.obs. | |
|---|---|---|---|---|---|
| i. Baseline | |||||
| Healthy | 0.88 | 0.31 | 0.0 | 1.0 | 235,094 |
| Married | 0.58 | 0.47 | 0.0 | 1.0 | 235,094 |
| Age | 40.66 | 11.70 | 20.0 | 64.0 | 235,094 |
| Female | 0.51 | 0.48 | 0.0 | 1.0 | 235,094 |
| Black | 0.12 | 0.31 | 0.0 | 1.0 | 235,094 |
| College | 0.35 | 0.46 | 0.0 | 1.0 | 235,094 |
| Children 0–3 years | 0.15 | 0.34 | 0.0 | 1.0 | 235,094 |
| Children 4–12 years | 0.26 | 0.42 | 0.0 | 1.0 | 235,094 |
| Children 13–18 years | 0.38 | 0.46 | 0.0 | 1.0 | 235,094 |
| Taxable income (in 1000$) | 34.61 | 30.70 | 0.0 | 658.6 | 235,094 |
| ii. Robustness and further explorations | |||||
| Objective health index | 51.15 | 9.26 | 4.6 | 76.1 | 160,057 |
| Total health expenditure | 3.04 | 9.47 | 0.0 | 1,051.5 | 235,094 |
| Uninsured | 0.16 | 0.35 | 0.0 | 1.0 | 235,094 |
| Preventive checks: | |||||
| Dental | 0.50 | 0.48 | 0.0 | 1.0 | 231,873 |
| Cholesterol | 0.51 | 0.48 | 0.0 | 1.0 | 221,942 |
| Complete | 0.57 | 0.47 | 0.0 | 1.0 | 227,623 |
| Flu shot | 0.26 | 0.42 | 0.0 | 1.0 | 229,296 |
| Prostate | 0.22 | 0.38 | 0.0 | 1.0 | 90,412 |
| Pap smear | 0.54 | 0.48 | 0.0 | 1.0 | 140,965 |
| Breast | 0.55 | 0.48 | 0.0 | 1.0 | 136,720 |
| Mammography | 0.36 | 0.46 | 0.0 | 1.0 | 119,403 |
Note: Means and standard deviations are computed exploiting sampling stratification design. The sample covers 1996–2009 annually. Taxable income is deflated by 2005 CPI.
Figure B1. Health and Marital Status, Different Socioeconomic Groups (MEPS).
Note: This figure reproduces the results in Figure 2 using the MEPS sample. Plotted lines represent the weighted fraction of married and unmarried individuals that report being healthy. Fractions are reported, as indicated, for male and female, white and black, without and with children aged 0–12 living in the household, college graduates and non-college, above and below median income, and born after and before 1970. The horizontal axis indicates age, which is grouped in five-year categories (20–24 through 60–64). Confidence bands of ± two standard errors are computed using sample stratification design.
Appendix C: Further Description of the GFE Estimator
This description borrows heavily on Bonhomme and Manresa (2015). A more detailed description and discussion about the estimator’s properties can be found at the original source. The GFE estimator is defined as the solution of the following minimization problem:
| (C1) |
where the minimum is taken over the functions α and β, the parameter vector γ, and over all possible groupings ϱ = {g1, …, gN} of the N individuals into G groups (i.e., gi ∈ {1, …, G} for i = 1, …, N). Thus, for given values of α, β, and γ, the optimal assignment of an individual i to a group gi is given by:
| (C2) |
which allows writing the GFE estimator of α, β, and γ as:
| (C3) |
The estimation algorithm proposed by Bonhomme and Manresa (2015) follows from an iterative implementation of Equations (C2) and (C3). Starting from an initial guess of (α, β, γ), individuals are assigned to types based on Equation (C2). Given the assigned types, estimation of Equation C3 follows from standard least squares. This allows reassigning types using Equation (C2), and iterate again.
Unlike standard finite mixture modeling, this approach does not specify group probabilities as parametric or semi-parametric functions of observed covariates. Bonhomme and Manresa (2015) provide the conditions for consistency. Given the application that we do in this paper, we can additionally assume that the G population groups (2 in our case) have a large number of observations and are well separated.30 In this case, identification comes from the comparison of health levels of married and single individuals in each group and at each age. Once again, individuals who do not change marital status still contribute to the identification of the single (or married) health curves.
Appendix D: Detailed Baseline Results
Table D1—
Estimated Coefficients from Baseline Regressions
| PSID |
MEPS |
|||||
|---|---|---|---|---|---|---|
| Fixed-Effects | Grouped F.E. |
System-GMM | ||||
| OLS | Type I | Type II | OLS | |||
| Marriage gap β(a): | ||||||
| 20–24 | 0.004 | −0.015 | −0.001 | 0.008 | −0.025 | |
| (0.007) | (0.007) | (0.006) | (0.010) | (0.006) | ||
| 25–29 | 0.024 | −0.010 | 0.009 | 0.029 | 0.014 | |
| (0.005) | (0.005) | (0.004) | (0.006) | (0.004) | ||
| 30–34 | 0.029 | −0.004 | 0.013 | 0.031 | 0.030 | |
| (0.006) | (0.006) | (0.005) | (0.006) | (0.004) | ||
| 35–39 | 0.041 | −0.008 | 0.013 | 0.038 | 0.039 | |
| (0.008) | (0.007) | (0.006) | (0.009) | (0.005) | ||
| 40–44 | 0.054 | 0.006 | 0.018 | 0.053 | 0.051 | |
| (0.010) | (0.008) | (0.007) | (0.011) | (0.006) | ||
| 45–49 | 0.069 | 0.019 | 0.022 | 0.060 | 0.063 | |
| (0.012) | (0.009) | (0.008) | (0.013) | (0.006) | ||
| 50–54 | 0.100 | 0.053 | 0.050 | 0.073 | 0.085 | |
| (0.013) | (0.010) | (0.009) | (0.017) | (0.007) | ||
| 55–59 | 0.105 | 0.047 | 0.043 | 0.105 | 0.078 | |
| (0.016) | (0.013) | (0.010) | (0.020) | (0.008) | ||
| 60–64 | 0.112 | 0.044 | 0.040 | 0.099 | 0.078 | |
| (0.017) | (0.014) | (0.010) | (0.021) | (0.009) | ||
| Singles health curve α(a): | ||||||
| 20–24 | 0.914 | 0.948 | 0.975 | 0.664 | 0.747 | 0.914 |
| (0.008) | (0.006) | (0.004) | (0.017) | (0.014) | (0.004) | |
| 25–29 | 0.883 | 0.936 | 0.964 | 0.624 | 0.736 | 0.873 |
| (0.009) | (0.005) | (0.005) | (0.015) | (0.014) | (0.005) | |
| 30–34 | 0.859 | 0.918 | 0.955 | 0.537 | 0.727 | 0.836 |
| (0.010) | (0.005) | (0.006) | (0.016) | (0.014) | (0.007) | |
| 35–39 | 0.828 | 0.904 | 0.944 | 0.469 | 0.711 | 0.804 |
| (0.012) | (0.007) | (0.008) | (0.017) | (0.015) | (0.008) | |
| 40–44 | 0.785 | 0.868 | 0.922 | 0.368 | 0.687 | 0.771 |
| (0.014) | (0.008) | (0.008) | (0.019) | (0.015) | (0.008) | |
| 45–49 | 0.743 | 0.834 | 0.900 | 0.286 | 0.656 | 0.729 |
| (0.015) | (0.009) | (0.009) | (0.017) | (0.017) | (0.009) | |
| 50–54 | 0.687 | 0.779 | 0.858 | 0.169 | 0.617 | 0.687 |
| (0.016) | (0.010) | (0.011) | (0.014) | (0.019) | (0.010) | |
| 55–59 | 0.656 | 0.752 | 0.837 | 0.106 | 0.549 | 0.670 |
| (0.018) | (0.012) | (0.012) | (0.014) | (0.020) | (0.011) | |
| 60–64 | 0.646 | 0.736 | 0.827 | 0.075 | 0.531 | 0.660 |
| (0.019) | (0.013) | (0.012) | (0.014) | (0.021) | (0.013) | |
| Lagged health | 0.150 | |||||
| (0.013) | ||||||
| College | 0.069 | 0.002 | 0.020 | 0.060 | 0.055 | |
| (0.006) | (0.008) | (0.002) | (0.005) | (0.002) | ||
| Female | −0.004 | −0.001 | 0.000 | |||
| (0.005) | (0.002) | (0.002) | ||||
| Black | −0.087 | −0.038 | −0.020 | |||
| (0.011) | (0.005) | (0.003) | ||||
| Children 0–3 years | 0.001 | 0.000 | 0.000 | 0.001 | 0.001 | |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | ||
| Children 4–12 years | −0.004 | 0.006 | 0.000 | −0.003 | 0.001 | |
| (0.003) | (0.003) | (0.002) | (0.004) | (0.002) | ||
| Children 13–18 years | −0.000 | 0.006 | −0.001 | −0.002 | 0.001 | |
| (0.004) | (0.003) | (0.002) | (0.004) | (0.003) | ||
| Taxable income (in 1000$) | −0.012 | 0.006 | −0.003 | −0.015 | 0.001 | |
| (0.004) | (0.003) | (0.003) | (0.005) | (0.003) | ||
| Birth year dummies: | Yes | Yes | Yes | Yes | Yes | |
Appendix E: Assortative Mating: Additional Results
Table E1—
Contingency Tables: Assortative Mating from Chronic Conditions
| Innate permanent health (ηi) | ||||||||||||
| Observed marital sorting % |
Random matching % |
|||||||||||
| Wife | Wife | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | Marginal | ||
| Husband | 1 | 8.6 | 3.6 | 1.3 | 3.5 | 2.4 | 3.9 | 4.7 | 3.7 | 3.8 | 3.2 | 19.3 |
| 2 | 3.6 | 8.6 | 3.5 | 4.4 | 3.0 | 4.7 | 5.7 | 4.4 | 4.6 | 3.8 | 23.2 | |
| 3 | 1.6 | 4.0 | 7.4 | 3.6 | 3.0 | 4.0 | 4.8 | 3.7 | 3.9 | 3.2 | 19.7 | |
| 4 | 3.7 | 5.2 | 3.8 | 4.4 | 3.6 | 4.2 | 5.1 | 3.9 | 4.1 | 3.4 | 20.7 | |
| 5 | 2.6 | 3.2 | 3.0 | 3.9 | 4.5 | 3.5 | 4.2 | 3.3 | 3.4 | 2.8 | 17.2 | |
| Marginal | 20.1 | 24.6 | 19.0 | 19.8 | 16.4 | 20.1 | 24.6 | 19.0 | 19.8 | 16.4 | 100.0 | |
| Innate health type (ηg(i)) | ||||||||||||
| Observed sorting % |
Random matching % |
|||||||||||
| Wife | Wife | |||||||||||
| Husband | Low | High | Low | High | Marginal | |||||||
| Low | 20.0 | 17.4 | 17.3 | 20.1 | 37.4 | |||||||
| High | 26.2 | 36.4 | 28.9 | 33.7 | 62.6 | |||||||
| Marginal | 46.2 | 53.8 | 46.2 | 53.8 | 100.0 | |||||||
Footnotes
On Farr’s study, see Parker-Pope (2010).
“Between 1950 and 2011, real GDP per capita grew at an average of 2.0% per year, while real national health care expenditures per capita grew at 4.4% per year. The gap between the two rates of growth —2.4% per year— resulted in the share of the GDP related to health care spending increasing from 4.4% in 1950 to 17.9% in 2011.” (Fuchs, 2013, p.108).
For instance, see Buss (1994) and Dawkins (1989).
Bound (1991) discusses the implications of using subjective and objective health measures.
The fact that head is reporting the health status of himself/herself and his/her spouse could be of potential importance for our analysis of assortative mating. This issue is discussed in Section V.B.
The results for the MEPS sample are in Figure B1 in Appendix B.
Pointing in the same direction: “From the point of view of a female trying to pick good genes with which to ally her own, what is she looking for? One thing she wants is evidence of ability to survive” (Dawkins, 1989, p.157).
Therefore, individuals who are, for example, always married (like the individual with the highest η in Figure 3B) contribute to the identification of the shape of the married health curve, despite not contributing to the identification of the gap between married and single intercepts.
While the algorithm often reaches the same global minimum, if initial conditions are very much off, the algorithm can stop at a local minimum. In our application, we run the algorithm repeatedly for a 1,000 times starting from random initial guesses for the parameters of the health curves by type, and 95% of the times we reach the global minimum (up to the fourth decimal).
Medical literature documents that health shocks such as cancer, or unhealthy habits such as heavy drinking and smoking, are associated with divorce. See, for example, Kirchhoff, Yi, Wright, Warner and Smith (2012) and Torvik, Gustavson, Roysamb and Tambs (2015).
The full set of regression coefficients are shown in Table D1 in Appendix D.
Results are robust to different bin widths. Figures plot the mid point of the interval.
We also checked whether health curves differ by several socioeconomic characteristics, such as gender, race, education, the presence of children, and income, as well as by different cohorts. Our results, which are available upon request, do not show significantly different patterns across any of these dimensions.
OLS and System-GMM deliver similar results. On the one hand, when we compare the fixed-effects estimation with OLS, we see that not controlling for innate health leads to an overestimation of the effect of marriage on health. On the other hand, when we compare the results from the dynamic model with ones obtained from the fixed-effect regression, we see that not controlling for lagged health results in an underestimation of the effect. These two biases seem to be of a similar size (and opposite sign), and they cancel each other.
There is another reason why these estimates might be conservative. If individuals make pre-marital investment in health to make themselves more attractive in the marriage market, the estimated effect of marriage on health will be small as singles health will also be higher due to these premarital investment. In other words, marriage has an indirect effect on untreated individuals which makes them look healthier. Lafortune (2013) shows that worse marriage conditions indeed lead individuals to make higher pre-marital investment in education.
The data on chronic conditions in the PSID are available since 1999 and only biannually. This renders the estimation of a system-GMM with chronic conditions unfeasible.
The slightly lower effect could be the result of cohabitants being more similar to unmarried individuals than to married ones. This would be consistent with Schoenborn (2004), who document that “health limitations, conditions, and unhealthy behaviors among adults living with a partner resembled or exceeded prevalence among adults who are divorced or separated.
There is evidence that husbands and wives sort by smoking behavior as well as by body-mass index. See Clark and Etilé (2006), Oreffice and Quintana-Domenque (2010) and Chiappori, Oreffice and Quintana-Domenque (2012, 2018). Domingue, Fletcher, Conley and Boardman (2014) compare genetic similarities between married and non-couple (random) pairs in the population and find genetic assortative mating.
Table E1 in Appendix E repeats the same exercises with innate health measures obtained from the regressions that use the number of chronic as a dependent variable with similar results.
For the evidence on assortative mating by education and the related literature in economics, see Greenwood, Guner, Kocharkov and Santos (2014). Schwartz (2013) provides a review of the literature in sociology.
Banks, Kelly and Smith (2014) highlight this point. Using health data from the English Longitudinal Survey of Aging (ELSA) and the American Health and Retirement Survey (HRS), where health is reported by each individual, they still find that couples have similar health status and healthy behavior along several dimensions.
There is a large medical literature that documents the link between marriage and specific health outcomes. In an interview to CNN, Dr. Paul L. Nguyen, summarizing his research published in Aizer, Chen, McCarthy, Mendu, Koo, Wilhite, Graham, Choueiri, Hoffman, Martin, Hu and Nguyen (2013), states that “You are going to nag your wife to go get her mammograms. You are going to nag your husband to go get his colonoscopy.... If you are on your own, nobody is going to nag you.” Interview available at http://thechart.blogs.cnn.com/2013/09/23/marriage-may-improve-cancer-survival-odds/?hpt=he_c2, accessed on December 6, 2013. See Waite and Gallagher (2000) for further evidence on what they call “the virtues of nagging”.
Similarly, we consider regressions for mean expenditures as opposed to median, which deliver very similar results, with a different scale.
Ozkan (2014) documents similar life-cycle patterns for medical expenditure among poor and rich individuals
Note that Table 7 shows a small but positive probability of quitting smoking while married in single to single transitions (0.005). This is so because in the 1999–2013 period individuals can transit into marriage and back to single, and quit smoking during the period they are married. The same logic applies to quitting smoking while single in married to married transitions (0.007).
Cole, Kim and Krueger (2014) evaluate the short and long-run effects of the Affordable Heath Care Act. In their model, individuals’ incentives to have a healthy life style, which are affected by the availability health insurance, play a key role.
See e.g. Anderson, Dobkin and Gross (2012) and Finkelstein, Taubman, Wright, Bernstein, Gruber, Newhouse, Allen, Baicker and the Oregon Health Study Group (2012). Both papers document that changes in health insurance status has a large effect on health care utilization.
Bernstein, Cohen, Brett and Bush (2008), using, National Health Interview Survey, report that 13% of married women between ages 25 and 64 years were uninsured in contrast to 21% of unmarried women of the same age in 2007. For characteristics of uninsured population in the U.S., see Kaiser Family Foundation (2012).
Independent of whether the person is married to the same partner.
Bonhomme and Manresa (2015) derive the asymptotic distribution for this case.
Contributor Information
Nezih Guner, CEMFI.
Yuliya Kulikova, Banco de España.
Joan Llull, Universitat Autònoma de Barcelona, MOVE and Barcelona GSE.
REFERENCES
- Adams Peter, Hurd Michael D., McFadden Daniel, Merrill Angela, and Ribeiro Tiago, “Healthy, wealthy, and wise? Tests for direct causal paths between health and socioeconomic status,” Journal of Econometrics, January 2003, 112 (1), 356. [Google Scholar]
- Agency of Healthcare Research and Quality, “Medical Expenditure Panel Survey,” household component, public use data set. Produced and Distributed by The Agency for Healthcare Research and Quality 2011. [Google Scholar]
- Aizer Ayal A., Chen Ming-Hui, McCarthy Ellen P., Mendu Mallika L., Koo Sophia, Wilhite Tyler J., Graham Powell L., Choueiri Toni K., Hoffman Karen E., Martin Neil E., Hu Jim C., and Nguyen Paul L., “Marital Status and Survival in Patients With Cancer,” Journal of Clinical Oncology, November 2013, 31 (31), 3869–3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson Michael, Dobkin Carlos, and Gross Tal, “The Effect of Health Insurance Coverage on the Use of Medical Services,” American Economic Journal: Economic Policy, February 2012, 4 (1), 1–27. [Google Scholar]
- Arellano Manuel and Bover Olympia, “Another Look at the Instrumental Variable Estimation of Error-Components Models,” Journal of Econometrics, July 1995, 68 (1), 29–51. [Google Scholar]
- Arellano Manuel and Bond Stephen, “Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations,” Review of Economic Studies, April 1991, 58 (2), 277–297. [Google Scholar]
- Averett Susan L., Argys Laura M., and Sorkin Julia, “In Sickness and in Health: An examination of Relationship Status and Health using Data from the Canadian National Public Health Survey,” Review of Economics of the Household, December 2013, 11 (4), 599–633. [Google Scholar]
- Banks James, Kelly Elaine, and Smith James P, “Spousal Health Effects: the Role of Selection,” in Wise David A., ed., Discoveries in the Economics of Aging, University of Chicago Press, 2014, chapter 7, pp. 255–279. [Google Scholar]
- Bernstein Amy B., Cohen Robin A., Brett Kate M., and Bush Mary Ann, “Marital Status is Associated With Health Insurance Coverage for Working-age Women at all Income Levels, 2007,” National Center for Health Statistics Data Brief 11, U.S. Department of Health and Human Services, Center for Disease Control and Prevention; December 2008. [PubMed] [Google Scholar]
- Bonhomme Stephane and Manresa Elena, “Grouped Patterns of Heterogeneity in Panel Data,” Econometrica, May 2015, 83 (3), 1147–1184. [Google Scholar]
- Bound John, “Self-Reported Versus Objective Measures of Health in Retirement Models,” Journal of Human Resources, Winter 1991, 26 (1), 106–138. [Google Scholar]
- Braun R. Anton, Kopecky Karen A., and Koreshkova Tatyana, “Old, Sick, Alone, and Poor: A Welfare Analysis of Old-Age Social Insurance Programs,” Review of Economic Studies, April 2017, 84 (2), 580–612. [Google Scholar]
- Buss David M., The Evolution of Desire: Strategies of Human Mating, New York: Basic Books, 1994. [Google Scholar]
- Case Anne and Deaton Angus, “Rising Morbidity and Mortality in Midlife Among White Non-Hispanic Americans in the 21St Century,” Proceedings of the National Academy of Sciences, December 2015, 112 (49), 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiappori Pierre-Andre, Oreffice Sonia, and Quintana-Domenque Climent, “Fatter Attraction: Anthropometric and Socioeconomic Matching on the Marriage Market,” Journal of Political Economy, August 2012, 120 (4), 659–695. [Google Scholar]
- Chiappori Pierre-Andre, Oreffice Sonia, and Quintana-Domenque Climent, “Bidimensional Matching with Heterogeneous Preferences: Smoking in the Marriage Market,” Journal of the European Economic Association, February 2018, 16 (1), 161–198. [Google Scholar]
- Clark Andrew E. and Etilé Fabrice, “Don’t Give up on Me Baby: Spousal Correlation in Smoking behaviour,” Journal of Health Economics, September 2006, 25 (5), 958–978. [DOI] [PubMed] [Google Scholar]
- Cole Harold L., Kim Soojin, and Krueger Dirk, “Analyzing the Effect of Insuring Health Risks: On the Trade-off between Short Run Insurance Benefits vs. Long Run Incentive Costs,” NBER Working Paper n. 18572, April 2014. [Google Scholar]
- Coombs Robert H., “Maritat Status and Personal Well-Being: A Literature Review,” Family Relations, January 1991, 40 (1), 97–102. [Google Scholar]
- Cutler David M. and Lleras-Muney Adriana, “Understanding Differences in Health Behaviors by Education,” Journal of Health Economics, January 2010, 29 (1), 1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawkins Richard, The Selfish Gene, second ed., New York City: Oxford University Press, 1989. [Google Scholar]
- De Nardi Mariacristina, French Eric, and Jones John Bailey, “Why Do the Elderly Save? The Role of Medical Expenses,” Journal of Political Economy, February 2010, 118 (1), 39–75. [Google Scholar]
- Doepke Matthias and Tertilt Michèle, “Families in Macroeconomics,” in Taylor John B. and Uhlig Harald, eds., Handbook of Macroeconomics, Vol. 2B, Amsterdam: Elsevier Science, 2016, chapter 23, pp. 1789–1891. [Google Scholar]
- Domingue Benjamin W., Fletcher Jason, Conley Dalton, and Boardman Jason D., “Genetics and Educational Assortative Mating Among US Adults,” Proceedings of the National Academy of Sciences of the United States of America, June 2014, 111 (22), 7996–8000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein Amy, Taubman Sarah, Wright Bill, Bernstein Mira, Gruber Jonathan, Newhouse Joseph P., Allen Heidi, Baicker Katherine, and the Oregon Health Study Group, “The Oregon Health Insurance Experiment: Evidence from the First Year,” Quarterly Journal of Economics, August 2012, 127 (3), 1057–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French Eric, “The Effects of Health, Wealth and Wages on Labor Supply and Retirement Behavior,” Review of Economic Studies, April 2005, 72 (2), 395–427. [Google Scholar]
- Fuchs Victor R., “The Gross Domestic Product and Health Care Spending,” The New England Journal of Medicine, July 2013, 369 (2), 107–109. [DOI] [PubMed] [Google Scholar]
- Gardner Jonathan and Oswald Andrew J., “How is mortality affected by money, marriage, and stress?,” Journal of Health Economics, November 2004, 23 (6), 1181–1207. [DOI] [PubMed] [Google Scholar]
- Greenwood Jeremy, Guner Nezih, and Vandenbroucke Guillaume, “Family Economics Writ Large,” Journal of Economic Literature, December 2017, 55 (4), 1346–1434. [Google Scholar]
- Greenwood Jeremy, Guner Nezih, Kocharkov Georgi, and Santos Cezar, “Marry Your Like: Assortative Mating and Income Inequality,” American Economic Review: Papers and Proceedings, May 2014, 104 (5), 348353. [Google Scholar]
- House James S., Schoeni Robert F., Kaplan George A., and Pollack Harold, “The Health Effects of Social and Economic Policy: The Promise and Challenge for Research and Policy,” in House James S., Schoeni Robert F., Kaplan George A., and Pollack Harold, eds., Making Americans Healthier: Social and Economic Policy as Health Policy, Russell Sage Foundation, 2008. [Google Scholar]
- Jung Juergen and Tran Chung, “Market Inefficiency, Insurance Mandate and Welfare: U.S. Health Care Reform 2010,” Review of Economic Dynamics, April 2016, 20 (2), 132–159,. [Google Scholar]
- Jung Juergen, Tran Chung, and Chambers Matthew, “Aging and Health Financing in the US: A General Equilibrium Approach,” European Economic Review, November 2017, 100, 428–462. [Google Scholar]
- Kaiser Family Foundation, “The Uninsured: A Primer. Key Facts About Americans Without Health Insurance,” Technical Report, October 2012. [Google Scholar]
- Kirchhoff Anne C., Yi Jaehee, Wright Jennifer, Warner Echo L., and Smith Ken R., “Marriage and Divorce among Young Adult Cancer Survivors,” Journal of Cancer Survivorship, December 2012, 6 (4), 441–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopecky Karen A. and Koreshkova Tatyana, “The Impact of Medical and Nursing Home Expenses on Savings,” American Economic Journal: Macroeconomics, July 2014, 6 (3), 29–72. [Google Scholar]
- Lafortune Jeanne, “Making Yourself Attractive: Pre-marital Investments and the Returns to Education in the Marriage Market,” American Economic Journal: Applied Economics, April 2013, 5 (2), 151–78. [Google Scholar]
- Lillard Lee A. and Panis Constantijn W. A., “Marital Status and Mortality: The Role of Health,” Demography, August 1996, 33 (3), 313–327. [PubMed] [Google Scholar]
- Lleras-Muney Adriana, “The Relationship Between Education and Adult Mortality in the United States,” Review of Economic Studies, January 2005, 72 (1), 189–221. [Google Scholar]
- Murray John E., “Marital Protection and Marital Selection: Evidence from a Historical-Prospective Sample of American Men,” Demography, November 2000, 37 (4), 511–521. [DOI] [PubMed] [Google Scholar]
- Oreffice Sonia and Quintana-Domenque Climent, “Anthropometry and Socioeconomics among Couples: Evidence in the United States,” Economics and Human Biology, December 2010, 8 (3), 373–384. [DOI] [PubMed] [Google Scholar]
- Ozkan Serdar, “Preventive vs. Curative Medicine: A Macroeconomic Analysis of Health Care over the Life Cycle,” mimeo, University of Toronto, December 2014. [Google Scholar]
- Parker-Pope Tara, “Is Marriage Good for Your Health,” The New York Times Magazine, April 14 2010. [Google Scholar]
- Pijoan-Mas Josep and Ríos-Rull José-Víctor, “Heterogeneity in Expected Longevities,” Demography, December 2014, 51 (6), 2075–2102. [DOI] [PubMed] [Google Scholar]
- Prados María José, “Health and Earnings Inequality Over the Life Cycle: The Redistributive Potential Of Health Policies,” mimeo, University of Southern California, July 2013. [Google Scholar]
- Schoenborn Charlotte A., “Marital Status and Health: United States, 1999–2002,” Advance Data from Vital and Health Statistics 351, U.S. Department of Health and Human Services, Center for Disease Control and Prevention; December 2004. [PubMed] [Google Scholar]
- Schwartz Christine R., “Trends and Variation in Assortative Mating: Causes and Consequences,” The Annual Review of Sociology, July 2013, 39 (1), 451–70. [Google Scholar]
- Smith James P., “The Impact of Socioeconomic Status on Health over the Life-Course,” Journal of Human Resources, Fall 2007, XLII (4), 739–764. [Google Scholar]
- Stowasser Till, Heiss Florian, McFadden Daniel, and Winter Joachim, “Healthy, Wealthy and Wise? Revisited: An Analysis of the Causal Pathways from Socioeconomic Status to Health,” in Wise David A., ed., Investigations in the Economics of Aging, Chicago: University of Chicago Press, 2012. [Google Scholar]
- Strohschein Lisa, “Do Men Really Benefit More From Marriage than Women?,” American Journal of Public Health, September 2016, 106 (9), e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torvik Fartein Ask, Gustavson Kristin, Roysamb Espen, and Tambs Kristian, “Health, Health Behaviors, and Health Dissimilarities Predict Divorce: Results from the HUNT Study,” BMC Psychology, May 2015, 3 (13), 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- University of Michigan, “Panel Study of Income Dynamics,” public use dataset Produced and distributed by the Survey Research Center, Institute for Social Research, University of Michigan, Ann Arbor, MI: 2015. [Google Scholar]
- van den Berg Gerard J. and Gupta Sumedha, “The Role of Marriage in the Causal Pathway from Economic Conditions Early in Life to Mortality,” Journal of Health Economics, March 2015, 40 (1), 141–158. [DOI] [PubMed] [Google Scholar]
- Waite Linda J. and Gallagher Maggie, The Case for Marriage: Why Married People are Happier, Healthier and Better Off Financially, New York: Doubleday, 2000. [Google Scholar]
- Williams Kristi, “Has the Future of Marriage Arrived? A Contemporary Examination of Gender, Marriage, and Psychological Well-Being,” Journal of Health and Social Behavior, December 2003, 44 (4), 470–487. [PMC free article] [PubMed] [Google Scholar]
- Wilson Chris M. and Oswald Andrew J., “How Does Marriage Affect Physical and Psychological Health? A Survey of the Longitudinal Evidence,” IZA Discussion Paper n. 1619, May 2005. [Google Scholar]
- Wood Robert G., Avellar Sarah, and Goesling Brian, The Effects of Marriage on Health: A Synthesis of Recent Research Evidence, New York: Nova Science Publishers Inc., 2009. [Google Scholar]