Abstract
Objective:
To investigate the clinical utility of deep convolutional neural network (DCNN) tract classification as a new imaging tool in the preoperative evaluation of children with focal epilepsy (FE).
Methods:
A DCNN tract classification deeply learned spatial trajectories of DWI white matter pathways linking electrical stimulation mapping (ESM) findings from 89 children with FE, and then automatically identified white matter pathways associated with eloquent functions (i.e., primary motor, language, and vision). Clinical utility was examined by 1) measuring the nearest distance between DCNN-determined pathways and ESM, 2) evaluating the effectiveness of DCNN-determined pathways to optimize surgical margins via Kalman filter analysis, and 3) evaluating how accurately changes in DCNN-determined language pathway volume can predict changes in language ability via canonical correlation analysis.
Results:
DCNN tract classification outperformed other existing methods, achieving an excellent accuracy of 98% while non-invasively detecting eloquent areas within the spatial resolution of ESM (i.e., 1cm). The Kalman filter analysis found that the preservation of brain areas within a surgical margin determined by DCNN tract classification predicted lack of postoperative deficit with a high accuracy of 92%. Postoperative change of DCNN-determined language pathway volume showed a significant correlation with postoperative changes in language ability (R=0.7, p<0.001).
Conclusion:
Our findings demonstrate that postoperative functional deficits substantially differ according to the extent of resected white matter, and that DCNN tract classification may offer key translational information by identifying these pathways in pediatric epilepsy surgery.
Significance:
DCNN tract classification may be an effective tool to improve surgical outcome of children with FE.
Index Terms—: Deep Convolutional Neural Network, Diffusion Tractography, Eloquent Function, Electrical Stimulation Mapping, Epilepsy
I. Introduction
To treat children with disabling focal epilepsy, surgical resection of epileptogenic brain tissue including the seizure onset zone (SOZ) is considered an evidence-based option for seizure control when pharmaceutical therapy is not effective. Such procedures necessarily disturb brain tissue, and therefore strive to avoid or strictly minimize disturbance of brain areas supporting eloquent functions (e.g., primary motor, language, and vision processing) [1]. Prior to surgical resection, preoperative evaluation of these patients should localize eloquent areas as accurately as possible in order to optimize a resection margin (i.e., the boundary between SOZ and eloquent areas) which maximizes the chance of postoperative preservation of individual eloquent functions [2], [3], [4]. Approximately 30–40% of children with focal epilepsy have drug-resistant seizures that cannot be controlled with antiepileptic medications, and are therefore considered candidates for surgery who must carefully undergo this critical preoperative evaluation.
The gold standard for delineating eloquent cortex in clinical epilepsy populations is electrical stimulation mapping (ESM), a surgically invasive methodology that outperforms state-of-the-art noninvasive function-localizing techniques such as fMRI. ESM localizes the areas essential for performing a given task, whereas fMRI can localize those involved in a task. ESM is not dependent on ill-posed neurovascular coupling mechanisms, which often provide insufficient sensitivity for fMRI to localize independent regional activation during relevant functional tasks [5]. For example, fMRI is useful for localizing entire areas involved in a given language task, but fMRI-based cortical activation per se does not specify the underlying function like ESM can [6]. However, the disadvantages of ESM are not negligible, since this invasive approach inherently carries a risk of stimulation-induced seizures [7]. Moreover, ESM often lacks sufficient sensitivity to identify eloquent areas in more complicated cases, like developing children [8]. Importantly, current ESM procedures cannot provide any quantitative information to predict the degree of functionality in individual eloquent areas. Thus, there is altogether a great need for other complementary assessment modalities to improve the preoperative evaluation of pediatric epilepsy. The present study presumes that functional maps systematically incorporating DWI tractography and ESM data using deep learning processes can provide effective and comprehensive information to localize eloquent areas, even in children where ESM and fMRI may not have an optimal diagnostic capability [9], [10], [11].
Recent developments in deep learning methodology facilitate solutions to complex neuroimaging pattern recognition problems, even when data sets are greatly diverse in shape and spatial trajectory. For instance, deep learning networks have been utilized to classify DWI tracts of interest and remove superficial tracts from whole brain tractography [8], [12], [13], [14]. Lam et al.[12] trained a network to distinguish 53 language tract classes in children under 2 years of age using two layers with geometric features such as tract curvature, torsion, and distance from landmark points, achieving a high classification accuracy up to 98.8%. However, their ground truth (i.e., true class membership for individual tracts) was manually segmented by an expert without considering specific functionality, and consequently the accuracy of their model might be limited when applied to patient populations, whose eloquent areas may be variably displaced by different disease etiologies and compensatory neural plasticity. Wasserthal et al. [13] also applied deep learning techniques to classify DWI tractography, and proposed a novel 2D encoder-decoder fully convolutional neural network that directly segments white matter tracts in fields of fiber orientation distribution function peaks. They had trained a network to distinguish 72 anatomically well-described tracts and verified that their model showed a significant improvement of tract classification compared with other conventional methods. Yet, their performance has not been validated by comparing their ground truth data at the level of individual subjects (e.g., ESM and clinical outcome). In contrast, our previous studies using Bayesian tract classification methods to automatically identify eloquent white matter pathways [15] achieved clinically promising accuracy to detect ESM-determined eloquent areas, predicted postoperative outcomes in eloquent functions, and optimized surgical margins balancing maximal benefit (seizure freedom) and minimal risk (functional deficit) [16]. However, it was also found that the classification of streamline tracts from DWI collected under clinical time constraints, having incomplete intravoxel information to resolve the crossing fiber problem, became highly susceptible to spurious tracts (i.e., false positive tracts including wiggly tracked or broken fibers). This type I error inevitably increases cases of ambiguous mismatch between white matter pathway terminals and ESM-determined eloquent areas, especially near the cortical mantle. To reduce this false positive classification, our recent studies have proposed a deep convolutional neural network (DCNN) to classify only true positive DWI tracts into functionally important white matter pathways connecting ESM-determined eloquent areas [8], [17]. Our working hypothesis is that, rather than first building a tract atlas based on priori information and then feeding the input into a statistical model, we can instead utilize DCNN to provide an end-to-end learning framework which integrates ESM-driven DWI tractography (i.e., electro-physiologically validated tract classes associated with individual eloquent functions) with an artificial intelligence approach (i.e., directly mining the heterogeneous trajectories of white matter tract classes associated with individual eloquent functions).
Via intensive in-vivo comparisons with current gold standard ESM data, the goal of this study is to investigate whether the DCNN tract classification [8] can further improve current preoperative evaluation for children with focal epilepsy by 1) providing accurate localization of ESM-determined eloquent areas at a large cohort (n=89), 2) providing an optimal resection margin achieving minimal functional deficits and maximal seizure freedom via Kalman filter analysis, and 3) predicting expressive and receptive language ability via canonical correlation analysis (CCA).
Our primary hypothesis is that DCNN tract classification is capable of non-invasively identifying the spatial trajectories of eloquent white matter pathways in preoperative DWI. We will specifically test the hypothesis that 1) the preservation of individual DCNN tract class within the resection margin determined by Kalman filter is associated with avoidance of unnecessary resection of functionally important tissues. We will also test the hypothesis that 2) postoperative volumetric change in DCNN-determined language pathway is a valuable biomarker for predicting postoperative change in specific language function. These hypotheses will be systematically assessed in a large cohort of children with varied epilepsy etiologies to demonstrate the utility of the proposed DCNN tract classification in preoperative surgical planning.
To our knowledge, we are the first to translate the advanced DCNN technique to clinical DWI tractography, where currently available approaches are suboptimal for controlling false positives, by systematically demonstrating that DCNN tract classification can detect both categorical and quantitative ground truth data (i.e., ESM-determined eloquent areas and neuropsychology-determined language scores) in children with focal epilepsy. Ultimately, such an analysis could help candidates for epilepsy surgery achieve seizure control while minimizing the risk of postoperative functional deficits.
II. Methods
A. Study Subjects
The present study recruited 128 children with focal epilepsy (age: 10.57±5.13 years, 66 boys). Inclusion criteria required that patients: (1) underwent two-stage epilepsy surgery involving extraoperative intracranial EEG recording and ESM via subdural grid and strip electrodes at Children’s Hospital of Michigan (Detroit, Michigan) between 2007 and 2018; (2) had no massive brain malformations (such as large perisylvian polymicrogyria or hemimegalencephaly), and (3) exhibited no hemiplegia, aphasia, or hemianopsia on examination prior to surgery.
Among 128 children, 89 children (age: 9.95±5.41 years, 45 boys) had DWI scans available, obtained as part of their preoperative evaluation. To investigate whether the proposed DCNN tract classification can accurately detect ESM-determined eloquent areas and optimize resection margins via Kalman filter, all preoperative scans (n = 89) were randomly assigned into one of three cohorts: a training set (n = 40) to implement the DCNN tract classification via deep learning of ESM-driven DWI tractography, a testing set (n = 16) to confirm the convergence of the DCNN tract classification implemented in the training set, and a validation set (n = 33) to reproduce the accuracy of the DCNN tract classification in an independent cohort.
To investigate how effectively and comprehensively the proposed DCNN tract classification predicts the likelihood of seizure freedom (benefit) or functional deficit (risk) after surgery, we studied 40 children (age: 9.0±4.9 years, 18 boys) who underwent both pre- and post-operative DWI scans. The presence or absence of subacute and newly developed postoperative functional deficits was determined clinically by a pediatric neurologist, as well as by physical, occupational, and speech therapists, between two to three weeks following resective surgery. All clinical team members were blinded to the results of the imaging data analysis. Postoperative deficits were categorized as (1) face motor deficit, (2) hand motor deficit, (3) foot motor deficit, (4) dysphasia, and/or (5) visual-field deficits. Postoperative seizure outcome was evaluated using International League Against Epilepsy (ILAE) classification every 6 months, either at clinical visit or by phone interview [18], and was ultimately determined at least 1 year after surgery. The following clinical outcomes were observed after surgery: seizure freedom (n = 24, 60%), recurrent seizures (n = 16, 40%), face motor deficit (n = 7, 17.5%), hand motor deficit (n = 6, 15%), foot motor deficit (n = 6, 15%), dysphasia (n = 6, 15%), and visual field deficit (n = 13, 33%).
Finally, to investigate whether the proposed DCNN tract classification can predict language abilities of individual children from pre- and postoperative DWI data, we studied 21 children (age: 12.42±3.41 years, 10 boys) who underwent both pre- and postoperative DWI scans as well as neuropsychological language assessments measuring expressive and receptive language functions with either the CELF-Preschool (CELF-P) for children aged 2–5 years or the CELF-4 for children aged six years and above [19]. CELF assessments yielded expressive and receptive language subscores that, in a healthy population, standardize to a mean of 100 and standard deviation of 15. Subscores in our population varied from 84±24/80±24 and 84±26/78±22 in preoperative expressive/receptive and post-operative expressive/receptive language ability, respectively.
The study was approved by the University Institutional Review Board, and written informed consent was obtained from the patients or guardians of patients.
B. Data Acquisition
All subjects underwent extraoperative intracranial EEG monitoring as well as ESM as part of clinical management [1], [2], [20]. Subdural electrode pairs were stimulated with a pulse-train of 5 s maximum duration, a pulse width of 0.3 ms, a frequency of 50 Hz, and an intensity ranging from 3 to 9 mA. Electrode sites where stimulation consistently induced contralateral body movement of face, hand, and foot, expressive aphasia during auditory naming task, expressive aphasia during visual naming task, receptive aphasia during auditory naming task, speech arrest, visual phosphene (lower-order visual areas), and visual distortion (higher-order visual areas) were defined as eloquent functions of interest. The procedure of ESM recording is described in detail in our previous study [21].
DWI data were acquired using a GE Signa 3T scanner (GE Healthcare, Milwaukee, WI) equipped with an 8-channel head coil at TR = 12500 ms, TE = 88.7 ms, FOV = 24 cm, 128 × 128 acquisition matrix, contiguous 3 mm slice thickness, 55 isotropic gradient directions with b = 1000 s/mm2, and single b = 0 acquisition. T1-weighted structural images were also acquired using a 3D fast spoiled gradient echo sequence (FSPGR) at TR = 9.12 ms, TE = 3.66 ms, TI = 400 ms, slice thickness = 1.2 mm, and planar resolution = 0.94 × 0.94 mm2.
C. Data Preprocessing for ESM-driven DWI Tractography
For each subject, a brain pial surface was reconstructed from a preoperative T1-weighted MRI image using FreeSurfer software ([22], http://surfer.nmr.mgh.harvard.edu). The locations of subdural electrodes were mapped onto this brain surface by referring to intraoperative photographs and post-implantation x-ray or CT scan [21], [23], [24]. Each electrode was spatially normalized to an averaged FreeSurfer pial template [25] using the symmetric diffeomorphic image normalization algorithm provided through the Advanced Normalization Tools (ANTs) package [26].
We generated 14 probabilistic maps of eloquent functions in the template space by overlapping ESM-determined eloquent areas across 95 subjects (excluding 33 subjects in validation, Fig. 1). Each probability map was smoothed at 3mm full width at half maximum and thresholded at a 97% confidence interval. These thresholded maps were used to define binary seed masks of the subsequent DWI tractography in template space, generating 14 ESM-driven DWI tract classes, Ci=1–14: C1,2 = left, right face motor area–internal capsule, C3,4 = left, right hand motor area–internal capsule, C5,6 = left, right foot motor area–internal capsule, C7 = expressive-aphasia (auditory naming) in left hemisphere, C8 = expressive-aphasia (visual naming) in left hemisphere, C9 = receptive aphasia in left hemisphere, C10 = speech arrest in left hemisphere, C11,12 = left, right visual phosphene, and C13,14 = left, right visual distortion. In addition, we defined C15 as an ”other” class which includes all tracts from whole-brain tractography not belonging to any of C1−14. All 15 classes were trained together in the DCNN classification in order to discriminate 14 ESM-driven DWI tract classes of interest from any given whole brain tractography.
Fig. 1.
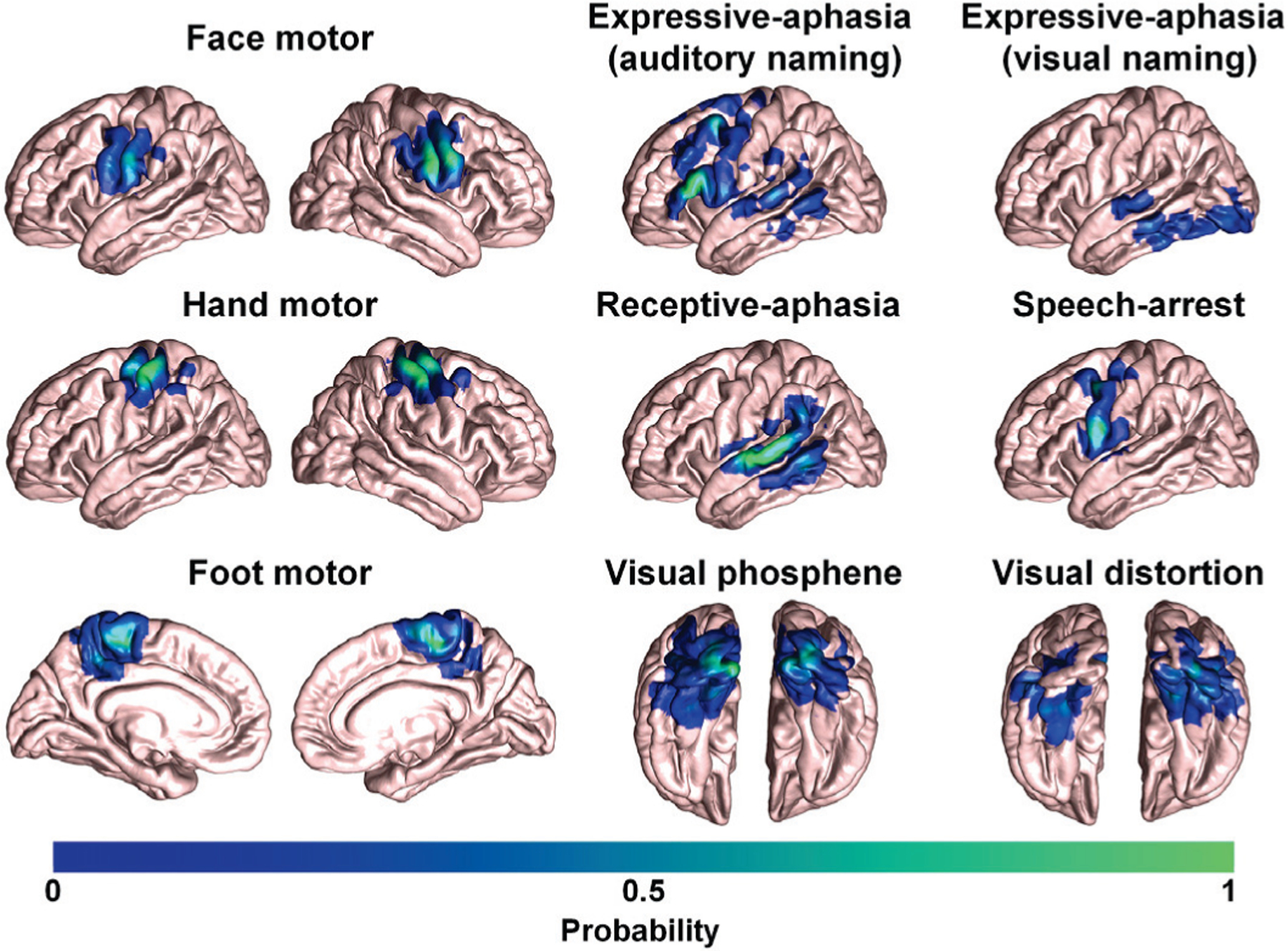
3D probabilistic maps of 14 ESM-determined eloquent areas associated with primary motor, language, and visual functions in an averaged FreeSurfer pial template.
To correct motion, noise, physiological artifacts, susceptibility-induced distortion, B1 field inhomogeneity, and eddy current-induced distortion in DWI data, the FSL eddy tool [27], [28], [29], [30] was used. All tractography analyses were performed using the MRtrix3 package (http://www.mrtrix.org/). Briefly, to generate C1−14 from each subject of the training set, probabilistic streamline tractography was reconstructed using 2nd order integration over fiber orientation distributions (iFOD2) [31] incorporating anatomically constrained tractography (ACT) [32] with 1000 dynamically randomized seeding points within the seed mask of each Ci which was inversely normalized from the template space to native space for each individual subject. The reconstructed streamlines of Ci were then spatially normalized to the template space using the ANTs package [26], followed by an exemplar-based clustering approach using the QuickBundles package [33] to remove noisy tracts from each Ci: any tract of Ci was considered a noisy false positive tract if its average direct-flip distance (ADFD) to its group exemplar (defined by Ci of 40 subjects in the training set) was greater than 5 mm. Finally, each tract of Ci was resampled into 100 equidistant segments, and the 3D coordinates of each segment were used as an input to the DCNN tract classification.
D. DCNN Tract Classification using ESM-driven DWI Tractography
Fig. 2 shows the architecture of the proposed DCNN, a residual network (i.e., ResNet) with 18 layers [8]. In conventional ResNet, skip connections are introduced by skipping one or more layers, which makes it possible to train much deeper networks without adding extra parameters or computational complexity. ResNet has been widely used in medical imaging applications such as image segmentation [34] and image synthesis [35], and it has achieved superior performance over other deep learning models, winning the 2015 ILSVRC competition with a 152-layer deep architecture [36]. Thus, the present study adopted ResNet as our backbone deep learning architecture. There are several common choices for the number of layers in ResNet: 18, 34, 50, or 101 [8]. Our previous study [8] tested three ResNets with 18, 34 and 50 layers. No significant difference was found on the classification accuracy. Thus, the present study chose an 18-layer ResNet for trading-off computational complexity. This DCNN was implemented by our group using PyTorch 0.2, and is now available for downloading at https://github.com/HaotianMXu/Brain-fiberclassification-using-CNNs.
Fig. 2.
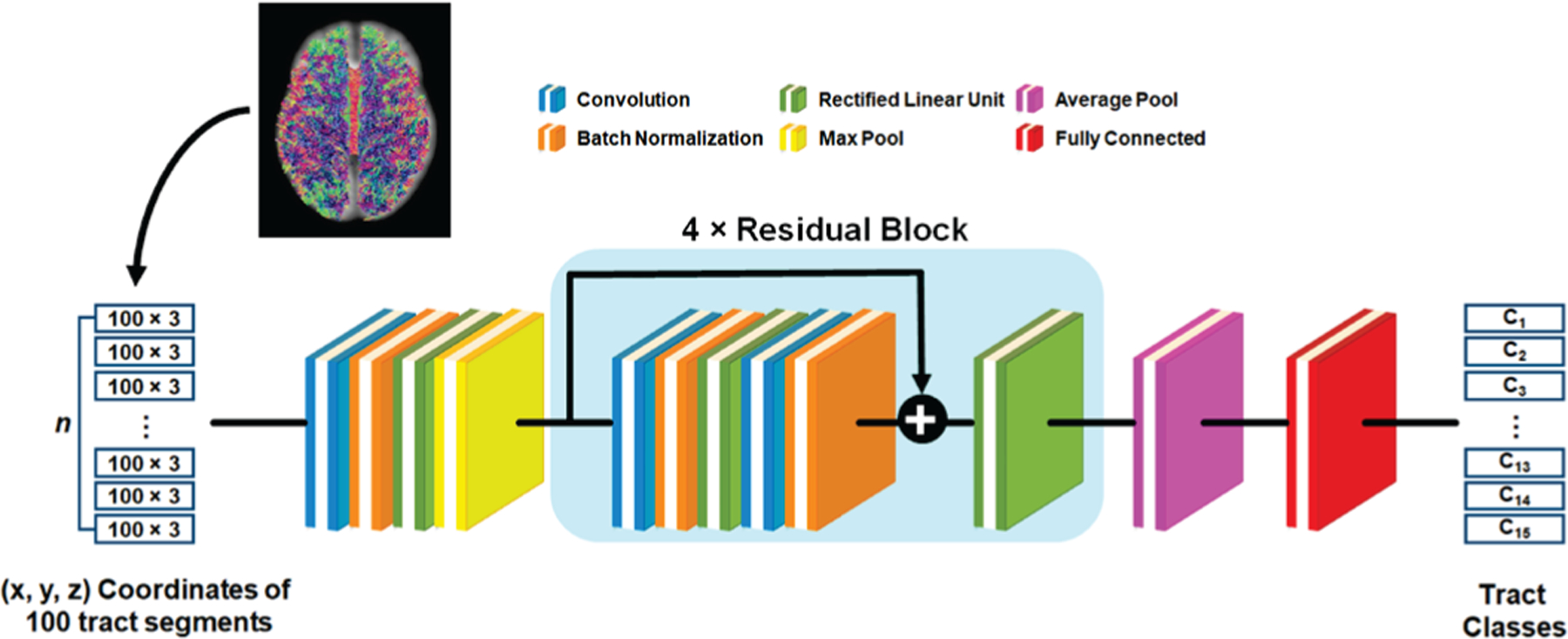
Schematic architecture of the deep convolutional neural network (DCNN), where each colored square represents a specific network layer.
Briefly, each tract is converted to a 100 × 3 matrix consisting of the 3D coordinates of 100 equidistant segments and input to our DCNN. Given the jth tract, the total loss between the prediction and its true membership, Ci, is defined as,
| (1) |
where and are the focal loss and center loss, respectively (defined below). The loss Lj is minimized through iterative optimization via sequential feed-forward/backward propagation.
Here, focal loss [37] adds a modulating term () to the cross-entropy loss :
| (2) |
where γ is the focusing parameter, and is predicted probability of the jth tract belonging to the class Ci. We empirically choose γ = 2, as recommended in [37], in order to focus on fitting data points with low prediction probability. The modulating term diminished loss for well/easily classified samples (i.e., high ) and increased importance of misclassified samples.
Cluster-based loss, center loss [38], is also adopted in our model to learn more discriminative features:
| (3) |
where denotes the deep feature vector of the jth tract in class Ci, and denotes the center of class Ci in the deep feature space. updates itself during the mini-batch training of our model.
Adam [39], an adaptive learning rate approach for stochastic gradient descent, was utilized to minimize total loss at the learning rate of 0.0001. Drop-out rate of the initial learning rate and total number of epochs were 0.01 and 100, respectively. After training, the fully connected layer produced the output probability vector,
| (4) |
where is the predicted probability of the input jth tract belonging to the class Ci, w is the convolution filter, G(fj) is the output of max pooling layer, ∘ is the element-wise multiplication operator, r is the dropout mask vector of Bernoulli variables with probability 0.5 of being set as 0, and b is the bias term. The class with the highest probability, , is taken as the final prediction of the jth tract. F1 score was calculated to evaluate overall prediction performance.
To evaluate the accuracy of our tract classification model in an independent cohort (i.e., not included in either training or test sets), DWI data of a validation set (n = 33) underwent whole brain tractography using MRtrix3 package (http://www.mrtrix.org/) iFOD2 [31] and ACT [32] with 2000 dynamically randomized seeding points on the gray-matter/white-matter interface. Each tract from whole brain tractography was spatially normalized to the template space using the ANTs package [26], resampled into 100 equidistant segments, and the 3D coordinates of these segments were classified by the trained DCNN into one of Ci=1–15. This study applied an experimental threshold, β of , to control the confidence level of the prediction. That is, the tracts whose values of were greater than β = 0.9 were included in final class, Ci.
E. Comparison with Other Existing Methods
Computational experiments using the same data set were carried out to compare the performance of the DCNN tract classification with those of the following methods: 1) DWI-MAP [15], [40], 2) DWI-MAP+ADFD [16], [41], and 3) RecoBundles [42].
1). DWI-MAP:
Based on fMRI-driven stereotactic probability maps and Bayesian interference, the DWI-MAP classifier identified 9 functionally-important white matter pathways in each hemisphere: = face motor area to internal capsule, = hand motor area to internal capsule, = leg motor area to internal capsule, = Broca’s area (BA 44/45) to Wernicke’s area (BA 22), = premotor area (BA 6) to Broca’s area, = premotor area to Wernicke’s area, = parietal area (BA 39) to Wernicke’s area, = premotor area to parietal area, and = occipital lobe to lateral geniculate nucleus. The DWI-MAP classifier utilizes stereotactic probability maps of obtained from healthy children. To classify a given tract into , the a posteriori probability of belonging to a class was calculated by averaging the probability values of over the entire fiber trajectory, assuming an equal class prior of Bayesian inference. A given tract was assigned to having the maximum a posteriori probability.
2). DWI-MAP+ADFD:
To reduce false positive tracts in our original DWI-MAP analysis, an additional tract clustering procedure based on ADFD using the QuickBundles algorithm was adopted. Briefly, the tracts in under the original DWI-MAP classification were reclassified by referring their minimum ADFDs to the class exemplars, which are mathematically centroid streamlines of in healthy controls.
3). RecoBundles:
Exemplars of 14 ESM-driven DWI tract pathways, Ci=1–14 were created using QuickBundles at the threshold of inter-tract ADFD = 30 mm. Tract classification of Ci was then performed using RecoBundles at the threshold of tract-examplar ADFD = 10 mm.
To avoid any potential biases of tract pruning, final tract classes for each methodology were adjusted at the same confidence level (i.e., 90%), where cumulative distribution function of ADFD between an individual tract and the class example was evaluated, and any tract of each class was included as a true positive tract only if the ADFD to its class exemplar does not exceed 10% of the cumulative ADFD distribution.
F. Benefit and Risk Analysis using DCNN Tract Classification
To understand how the retrospective surgical margins suggested by our tract classification model relate to the actual outcomes of surgical resection, we need to determine the surface distance di between resected brain tissue and DCNN-determined white matter pathways Ci, and also determine the volumetric postoperative change ri of our DWI-generated ”eloquent” pathways. Since determining ri requires a postoperative DWI b0 image, this is impossible at the preoperative stage. To overcome this limitation, we employed Kalman filter prediction with Rauch-Tung-Striebel smoothing [43], which can reveal hidden relationships between the preoperatively unmeasurable ri and measurable di. To accomplish this we first focused on patients with both pre- and post-operative DWI, calculating ri as (volume of preoperative Ci ∩ volume of resected tissue) / volume of preoperative Ci, and we then determined resection margin di by calculating the minimal Euclidean distance between voxels of Ci and the actual surgical resection boundary. In cases where Ci was resected, di was assumed to be negative and calculated as (−1) × the average Euclidean distance between every voxel inside the resected Ci.
In pre- and postoperative data, high-resolution T1-weighted images were co-registered to b0 images using the ANTs package [26]. The same co-registration package was also utilized to obtain an affine transformation spatially matching postoperative T1-weighted images to preoperative T1-weighted images. The obtained transformation was then applied to co-register a given patient’s post-operative b0 image to their preoperative b0 image. The difference image of two co-registered b0 images was thresholded to define a binary mask of the surgically resected brain volume. A series of morphological filtering was applied to the binary mask until all holes and islands greater than a single voxel were removed. Finally, the outer surface contour of the filtered mask was spatially transformed to the postoperative T1-weighted image and manually corrected by two raters (M.H. and J.J.), ensuring that the final resection boundary included the entire surgical cavity of an individual patient.
To identify the hidden relationship between two variables, we employed a modified Kalman filter [15], [16] which works as follows:
| (5) |
where the system matrix (Sx, Sr, Sd) is iteratively updated to determine the hidden stochastic process between dynamics and observation [44]. Σs and Σd represent system covariance and observation covariance, respectively. N(μ, Σ) indicates white Gaussian noise with mean μ and covariance Σ. For a given jth patient, is assumed as a dynamic variable to control the unknown state variable associated with the actual surgical margin . The state variable of the (j + 1)th patient is then formulated as a function of the state variable and the measured of the (j + 1)th patient. Finally, we defined a preservation zone of Ci satisfying the Kalman-defined margin , balancing postoperative seizure freedom and functional deficits at di(ri) satisfying P(deficit|di(ri)) = P(seizurefreedom|di(ri)), where P(deficit|di(ri)) and P(seizurefreedom|di(ri)) represent cumulative probability density functions of seizure freedom and functional deficit at d ≤ di(ri), respectively.
G. Prediction of Language Ability using DCNN Tract Classification
Postoperative tract volume change for language pathway, Δi=7–10 was first defined as (volume of preoperative Ci - volume of postoperative Ci) / volume of preoperative Ci. The change of postoperative language ability, Δreceptive | expressive was defined as (preoperative CELF score - postoperative CELF score)/preoperative CELF score. To identify the relationship between Δi=7–10 and Δreceptive|expressive, canonical correlation analysis (CCA) [45] was performed. CCA is a method to investigate regressions between two multivariate random variables (X and Y), finding a linear combination of variables that maximally correlate. The canonical variables (u, v) are defined by the pair of linear combination vectors {a, b} that maximize the canonical correlation coefficient:
| (6) |
where Σ is the covariance. The present study constructed data matrices X and Y by concatenating the different Δi=7–10 and Δreceptive|expressive column vectors of subjects.
III. Results
A. DCNN Tract Classification
Fig. 3 shows the convergence of DCNN tract classification. In both training and test sets, total loss converged to 0.002 after 34 epochs and F1 scores converged to 0.98 after 28 epochs. As marked by white arrows in Fig. 4, the proposed DCNN tract classification occasionally yielded low prediction probability values, (Eq. 4), for a given tract. These false-positive tracts deviated from cortical centroids linking ESM-determined areas, and could be appropriately deleted from their pathways by thresholding their prediction probability values at β = 0.90. It is clear that false-positive predictions localized outside the ESM electrodes were significantly reduced at without reducing true positives, suggesting that the 90% confidence interval for true positive classification (i.e., β = 0.90) provided sufficient specificity to delineate true positive white matter pathways.
Fig. 3.
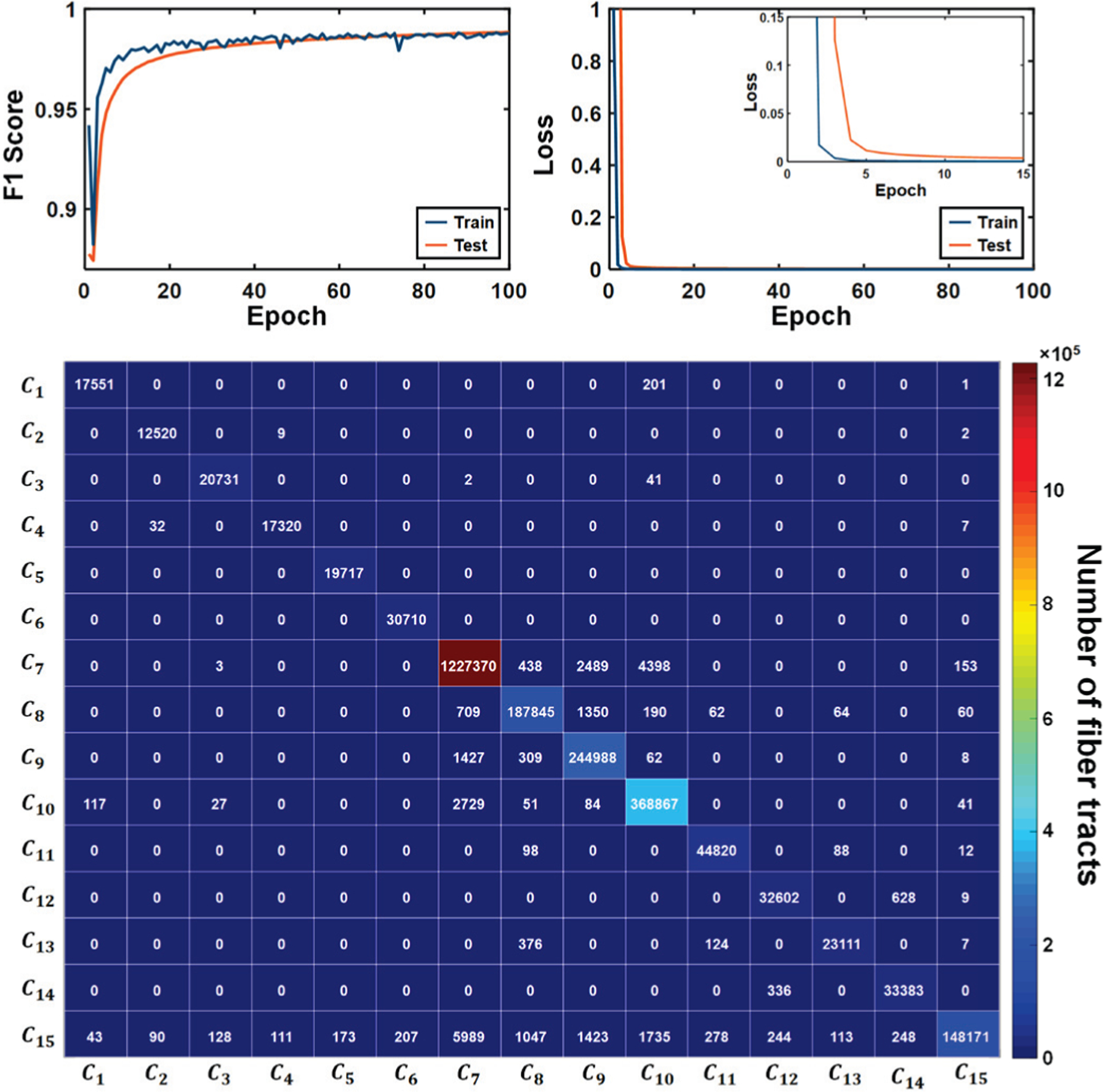
Convergence curve of DCNN for training (blue colored curve) and test (orange colored curve) data sets in the top figure. The bottom figure shows the confusion matrix computed on the test set at 96 epochs which showed maximal F1 score (0.9880). The diagonal components of the matrix represent true positives. The sum of column and row for each Ci denote the false positives and false negatives, respectively.
Fig. 4.
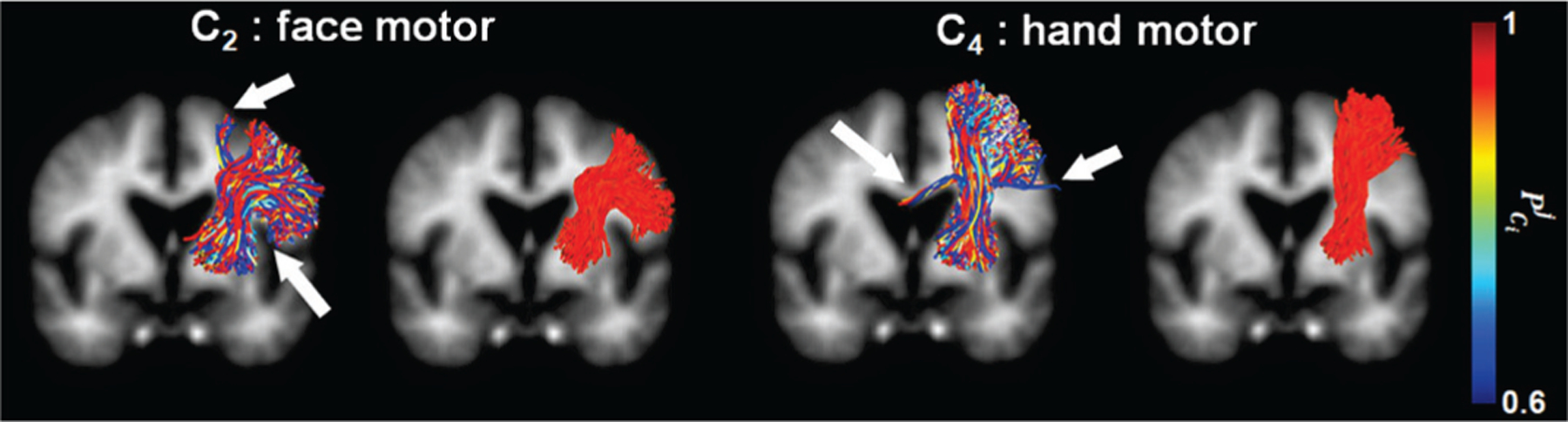
Examples of prediction probability, estimated by the proposed DCNN tract classification. White arrows indicate false positives with low .
Fig. 5 shows representative examples of the proposed DCNN tract classification Ci=1–14 spatially well-matched to ESM-determined eloquent areas. To assess the performance of the our DCNN tract classification in localizing eloquent areas defined by ESM recordings, we calculated the Euclidean distance from cortical terminal of DCNN-defined tracts to ESM electrode. Our DCNN tract classification model achieved high average accuracy for the tracts terminating in the proximity of eloquent areas determined by ESM recordings (see Fig. 6): motor area (98.5% for learning set, 95.5% for validation set), language area (100%, 96%) and visual field (98.5%, 99.5%) within range of 10 mm distance from cortical terminal of DCNN-tract class to ESM electrode.
Fig. 5.
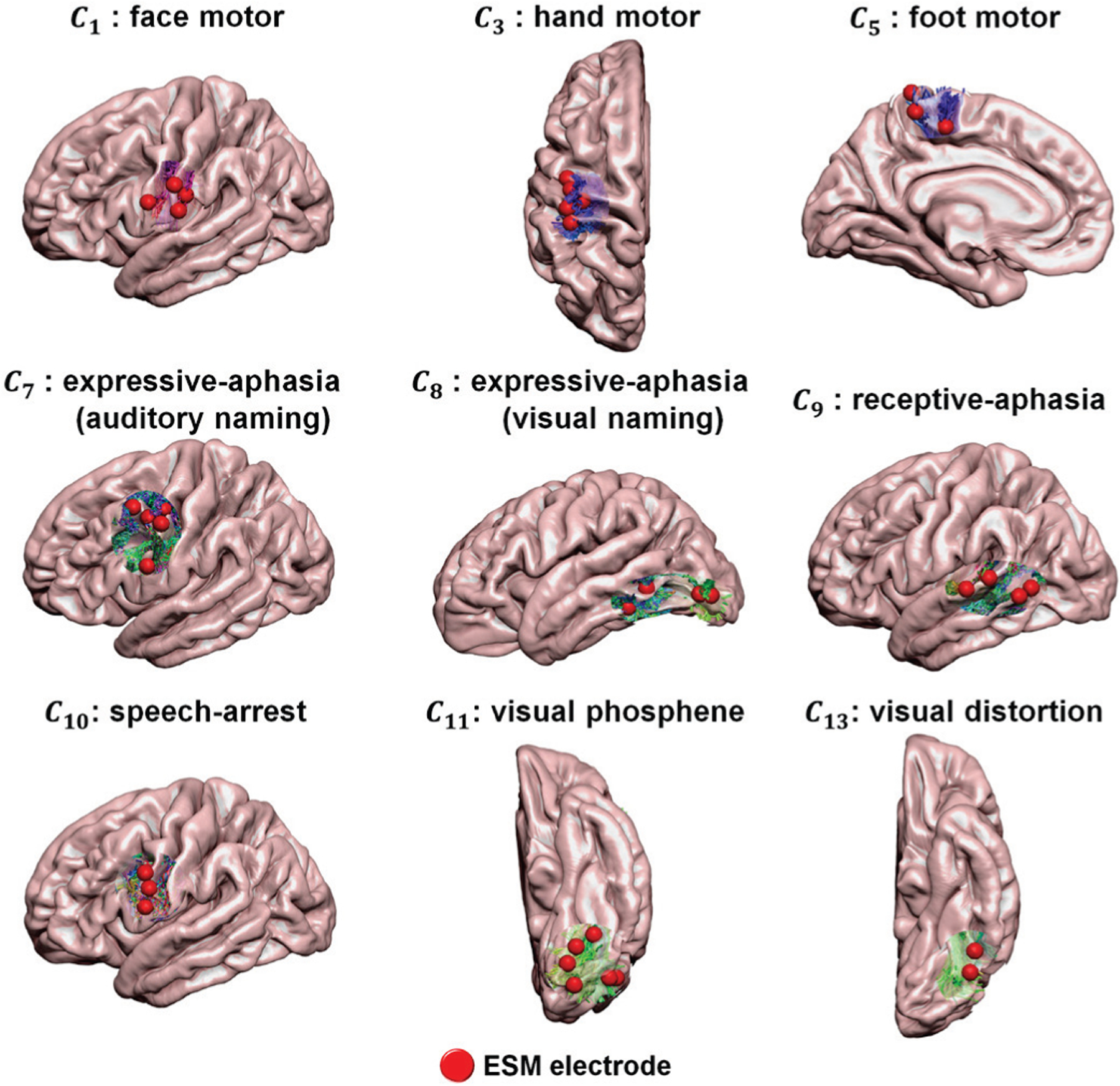
Examples of DCNN-determined tract classes, Ci=1–14 spatially well-matched with ESM-determined eloquent areas. Whole brain tractography data in validation set were classified by the proposed DCNN tract classification and the cortical terminals of the resulting Ci (i.e., streamline tracts presented by red-green-blue color coding) were compared with their ground truth, ESM-determined eloquent areas (ESM electrodes marked by red spheres).
Fig. 6.
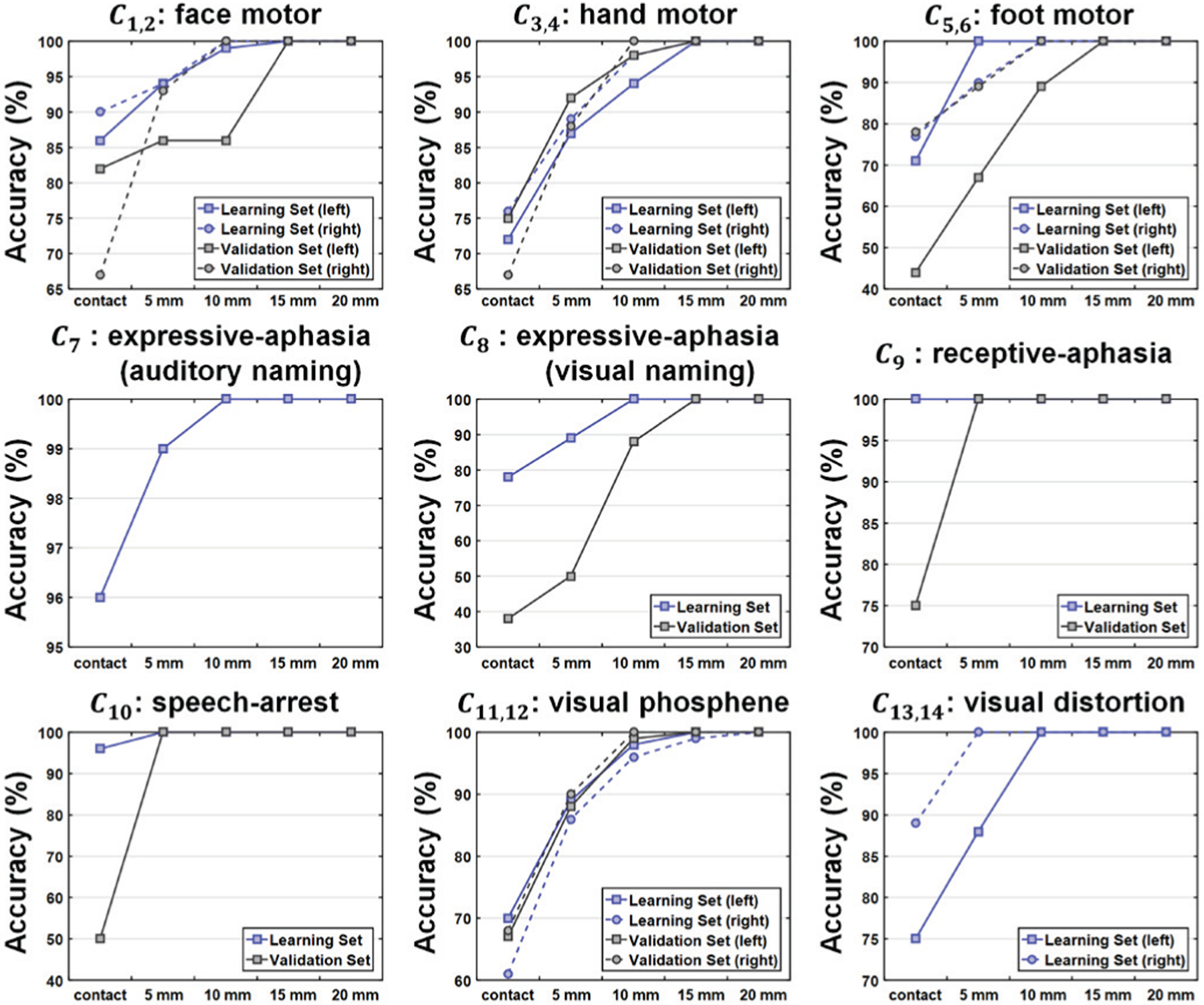
Localization accuracy provided by the proposed DCNN tract classification model for individual eloquent functions. The accuracy was assessed for learning (i.e., training and testing) and validation sets at five different levels of Euclidean distance between the cortical terminal of individual tracts and ESM electrodes.
Fig. 7 presents representative examples supporting the advantage of our DCNN tract classification, compared to more conventional cortical localization, to detect true ESM-determined eloquent cortex: the group average atlas of individual function (e.g., 3D probabilistic maps of ESM-determined eloquent areas shown in Fig. 1) spatially normalized from template space to native brain space can mischaracterize eloquent cortex at the individual level. Deep learning of coordinates over the entire tract trajectory helps overcome this cohort heterogeneity, detecting eloquent cortices in clinical cases where functional areas are often deviated from group average areas.
Fig. 7.
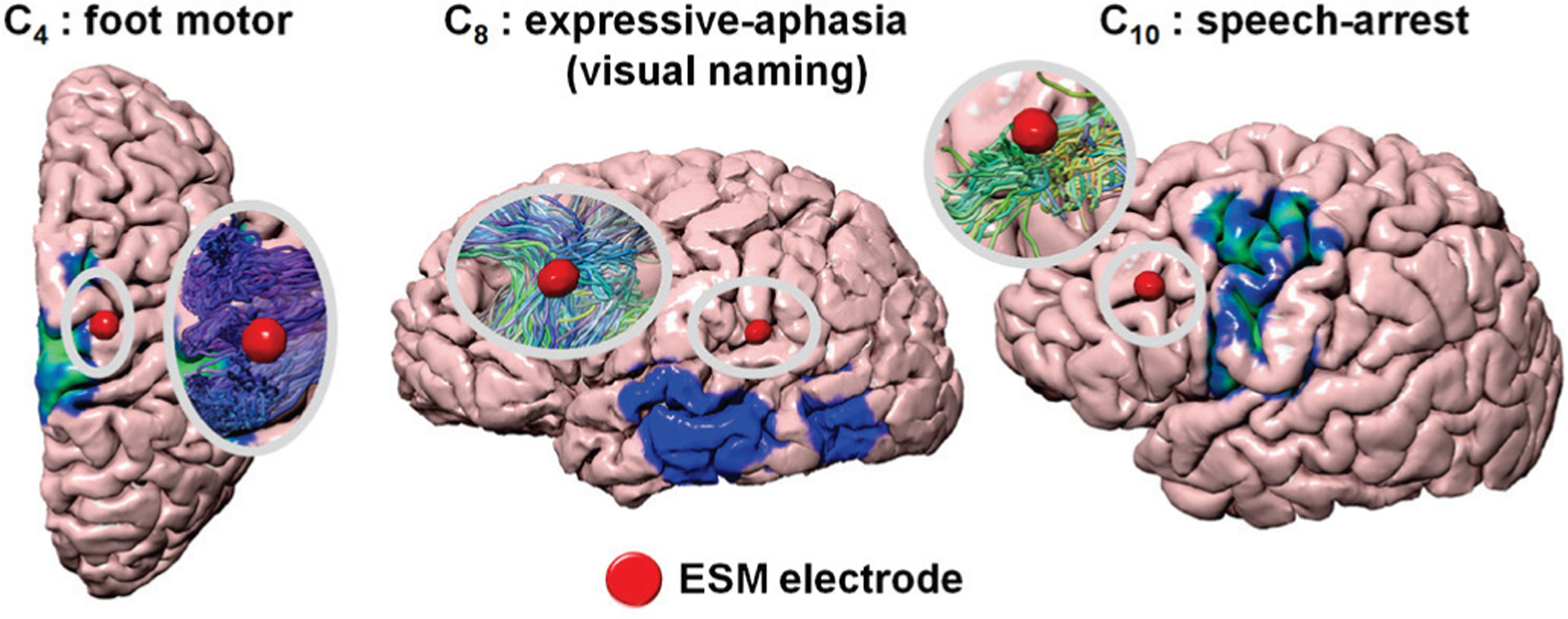
Representative cases in which the proposed DCNN tract classification could accurately detect ESM-determined eloquent areas that direct cortical mapping of 3D probability maps (Fig. 1) failed to detect.
Fig. 8 presents representative examples of pre- and postoperative DCNN tract pathways Ci in two patients with tumor (A) and cortical dysplasia (B). This figure effectively demonstrates the performance of our DCNN tract classification in patients with structural lesions. It should be noted that even in cases with structural lesions, the proposed DCNN tract classification provided accurate detection of eloquent white matter pathways whose cortical terminals were well-matched with the corresponding ESM localizations. Furthermore, the proposed DCNN tract classification provided consistent localization of eloquent white matter pathways without depending on the size of a resected lesion. To finalize the classification, our DCNN method considered the entire trajectory of an individual tract (i.e., not spatially limited to the vicinity of a structural lesion). This process effectively improves classification accuracy of true positives whose trajectories were completely or partially interrupted by the lesions (e.g., the portion in closest proximity to lesion). This rationale is supported by the absence of a noteworthy decline in the overall classification accuracy across different subgroups, including epilepsy type, the presence of structural lesion visible in MRI, pathology, and volume of resected tissue (Table I). This outstanding reproducibility directly demonstrates that the proposed DCNN tract classification can be an alternative imaging tool potentially reducing the use of invasive ESM procedure by providing the accurate locations of intact brain pathways, also saving substantial time, effort, and cost of presurgical evaluation.
Fig. 8.
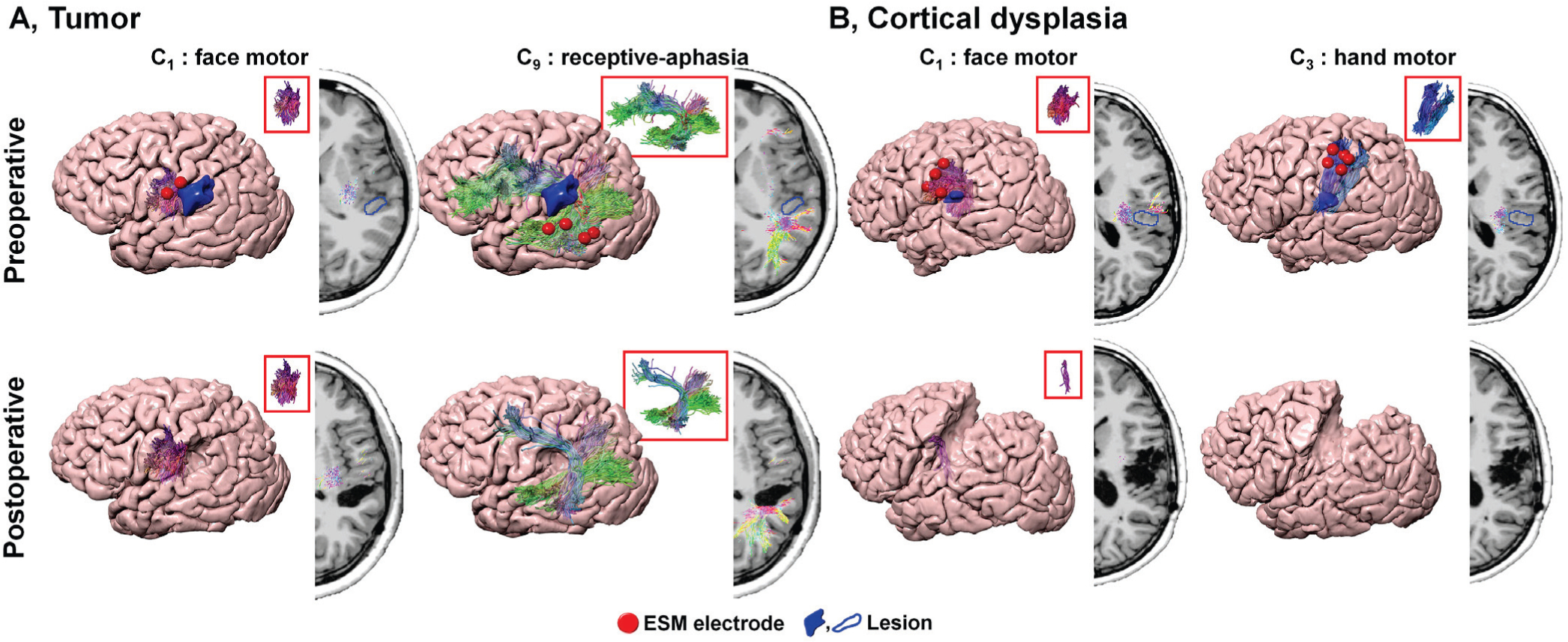
Pre- and postoperative DCNN tract classification in patients with structural lesions, A. tumor and B. cortical dysplasia. While postoperative DCNN tracts of A showed no volume change in C1 and slight volume change in C9 causing normal face motor and mild language deficit after surgery, postoperative DCNN classes, C1,3 of B indicated significantly reduced or removed volumes following resection. This resection resulted in severe postoperative motor deficits on right face and hand motor functions.
Table I.
Reproducibility of the proposed DCNN tract classification to detect ESM-determined eloquent areas in different subgroups constructed from total study cohort (n=89). Euclidean distance was measured between the cortical terminal of DCNN-determined tract and ESM electrode.
| Motor | Language | Vision | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sub-group | contact | 5mm | 10mm | contact | 5mm | 10mm | contact | 5mm | 10mm |
| Left temporal epilepsy (n= 15) | 0.75 | 0.99 | 0.96 | 0.94 | 0.99 | 1.00 | 0.72 | 0.87 | 0.99 |
| Right temporal epilepsy (n= 11) | 0.79 | 0.98 | 1.00 | N.A. | N.A. | N.A. | 0.78 | 0.96 | 1.00 |
| Left extra-temporal epilepsy (n= 17) | 0.73 | 0.84 | 0.980 | 0.82 | 0.9 | 0.98 | 0.82 | 0.94 | 0.99 |
| Right extra-temporal epilepsy (n= 28) | 0.83 | 0.92 | 1.00 | N.A. | N.A. | N.A. | 0.67 | 0.88 | 0.97 |
| MR positive lesion (n= 53) | 0.80 | 0.92 | 0.98 | 0.85 | 0.92 | 1.00 | 0.49 | 0.79 | 0.98 |
| MR negative lesion (n= 36) | 0.69 | 0.87 | 0.94 | 0.94 | 0.96 | 0.98 | 0.80 | 0.94 | 0.99 |
| Non-lesional (n= 36) | 0.69 | 0.87 | 0.94 | 0.94 | 0.96 | 0.98 | 0.80 | 0.94 | 0.99 |
| Cortical dysplasia (n= 21) | 0.74 | 0.88 | 0.720 | 0.93 | 0.720 | 0.720 | 0.72 | 0.90 | 0.99 |
| Tumor (n= 21) | 0.79 | 0.91 | 0.99 | 0.85 | 0.92 | 1.00 | 0.40 | 0.75 | 1.00 |
| Resected volume < 50000 mm3 (n= 15) | 0.73 | 0.88 | 0.97 | 0.96 | 0.99 | 1.00 | 0.71 | 0.94 | 1.00 |
| 50000 ≤ Resected volume < 150000 mm3 (n= 10) | 0.77 | 0.86 | 1.00 | 1.0 | 1.00 | 1.00 | 0.74 | 0.93 | 1.00 |
| Resected volume ≥ 150000 mm3 (n= 12) | 0.86 | 0.93 | 1.00 | 1.00 | 1.00 | 1.00 | 0.71 | 0.89 | 1.00 |
B. Benefit and Risk Analysis
The hidden relationships defined by Kalman filter analysis between r1−14 and d1−14 yielded , 6.12, 1.10, −0.18, −2.72, −1.91, 4.47, −3.53, and −3.66 mm, which ultimately balanced the values of P (deficit|di(ri)) and P(seizurefreedom|di(ri)) for DCNN tract classification as plotted on Fig. 9. To demonstrate the clinical reliability of Kalman-analysis-defined preservation zones, we investigated cases in which the preoperative preservation zones were ultimately not resected, to determine whether the DCNN tract classification method outperforms other methods (i.e., DWI-MAP, DWI-MAP+ADFD and RecoBundles) in predicting the lack of a functional deficit. The actual resection margin di, when the DCNN tract classification proposed preservation zone of Ci is preserved or minimally resected within , achieved high average accuracy for predicting the pathway’s corresponding functional outcomes: 0.98 for motor deficits, 0.89 for language deficits, and 0.91 for visual deficits. Furthermore, our proposed method achieved higher average accuracy than alternative methods: compared to 0.95/0.96/0.96 for motor deficit prediction, 0.89/0.88/0.83 for language deficit prediction, and 0.78/0.85/0.81 for visual deficit prediction, for DWI-MAP/DWI-MAP+ADFD/RecoBundles accuracy, respectively (see Table II). These results suggest that our proposed method could possibly help guide surgery by identifying eloquent pathways that may be most important to preserve and effectively assessing the risk of postoperative deficit. In addition, the preservation zones defined by DCNN tract classification with Kalman filter analysis are more reliable than those of other methods.
Fig. 9.
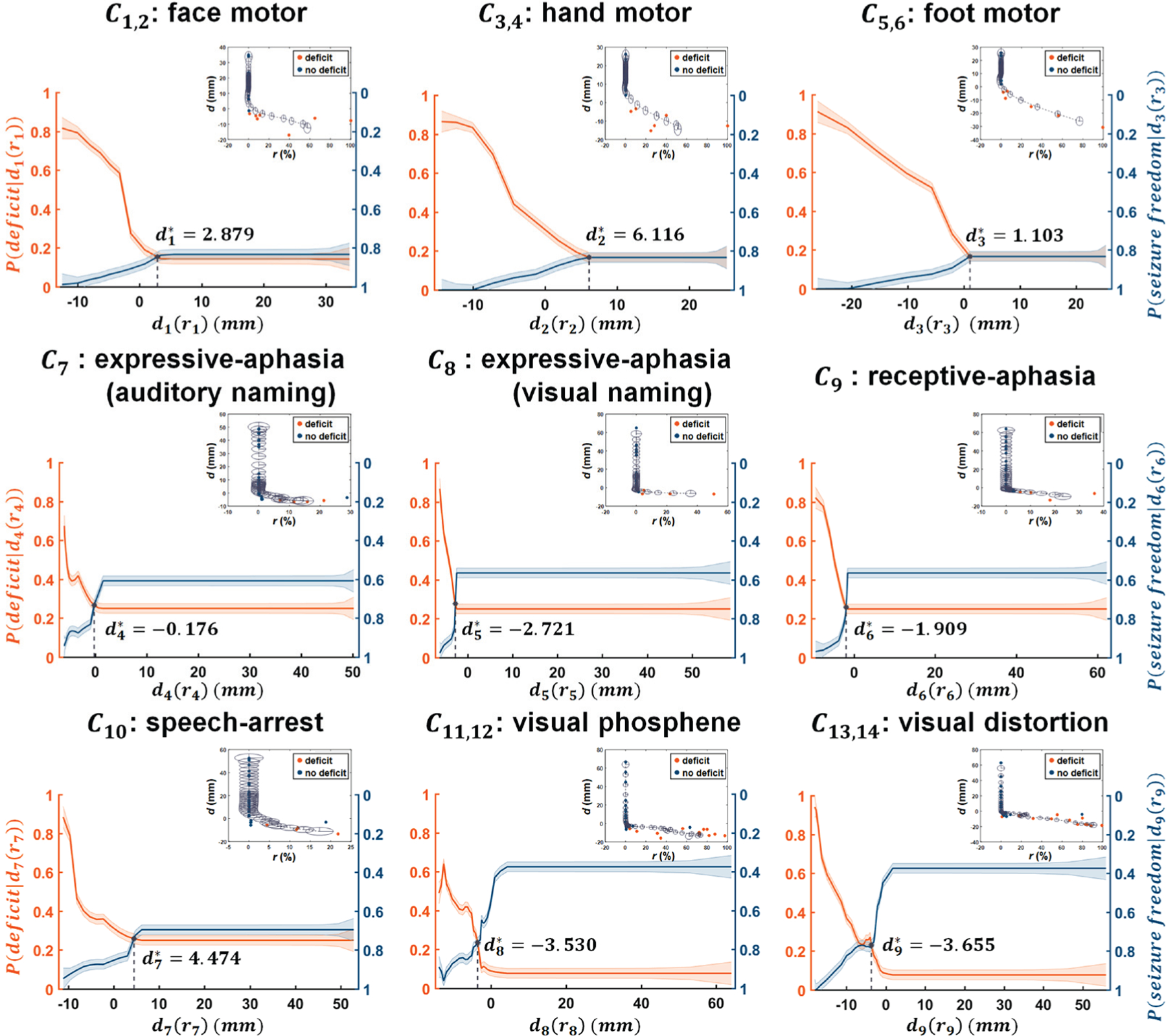
Modeling the hidden relationship between resection margin, di, and the portion of Ci that is resected, ri. In the top right portion of each plot, orange/blue circles indicate patients with/without postoperative deficit, respectively. Kalman filter prediction was applied to fit di as a function of a dynamic variable ri, resulting in di(ri) (gray dotted line). The radius of gray colored ellipsis indicates the covariance of the state variable x(ri), approximating the 95% confidence interval of di(ri). Solid orange and blue lines indicate the values of the predicted P(deficit|di(ri)) and P(seizurefreedom|di(ri)), where the width of the strips indicates ± 1 × covariance of the predicted P(deficit|di(ri)) and P(seizurefreedom|di(ri)), estimated from covariance of the state variable x(ri) of Kalman filter analysis.
Table II.
Performance comparison of individual classification methods to predict the occurrence of postoperative deficit.
| Function | DWI-MAP | DWI-MAP+ADFD | RecoBundles | DCNN tract classification | ||
|---|---|---|---|---|---|---|
| Motor deficit | Face motor | 0.88 | 0.90 | Face motor | 0.95 | 0.98 |
| Hand motor | 1.00 | 0.98 | Hand motor | 0.93 | 0.98 | |
| Leg motor | 0.98 | 1.00 | Foot motor | 1.00 | 1.00 | |
| Language deficit | Broca’s-Wernicke’s | 0.88 | 0.83 | Expressive-aphasia (auditory naming) | 0.83 | 0.83 |
| Broca’s-Premotor | 0.93 | 0.95 | Expressive-aphasia (visual naming) | 0.90 | 0.98 | |
| Wernicke’s-Premotor | 0.90 | 0.90 | Receptive-aphasia | 0.75 | 0.88 | |
| Wernicke’s-Parietal | 0.93 | 0.88 | Speech-arrest | 0.85 | 0.85 | |
| Premotor-Parietal | 0.83 | 0.85 | ||||
| Visual deficit | Primary visual pathway | 0.78 | 0.85 | Phosphene | 0.88 | 0.93 |
| Distortion | 0.80 | 0.88 |
The maximized canonical coefficient R between the canonical variables (u, v) was associated with the linear combination of the following: postoperative tract volume change, x1−4 language function pathways, Ci=7–10 and the change of neuropsychological language score, yreceptive and yexpressive with combination vectors {a, b},
| (7) |
C. Prediction of Language Ability
Our CCA model achieved high Rreceptive = 0.773 (p < 0.001) and Rexpressive = 0.627 (p = 0.002). In addition, our CCA model accounted for more variance than our DWI-MAP model (Rreceptive = 0.438, p = 0.047 and Rexpressive = 0.648, p = 0.002), DWI-MAP+ADFD model (Rreceptive = 0.626, p = 0.002 and Rexpressive = 0.145, p = 0.530), and RecoBundles model (Rreceptive = 0.277, p = 0.225 and Rexpressive = 0.470, p = 0.032) (Fig. 10). These findings suggest that CCA based on DCNN-determined tracts may provide the most accurate prediction of language ability using non-invasive diffusion MRI tractography, and may prove especially useful for cases when neuropsychological language assessments are unreliable due to developmental or behavioral difficulties.
Fig. 10.
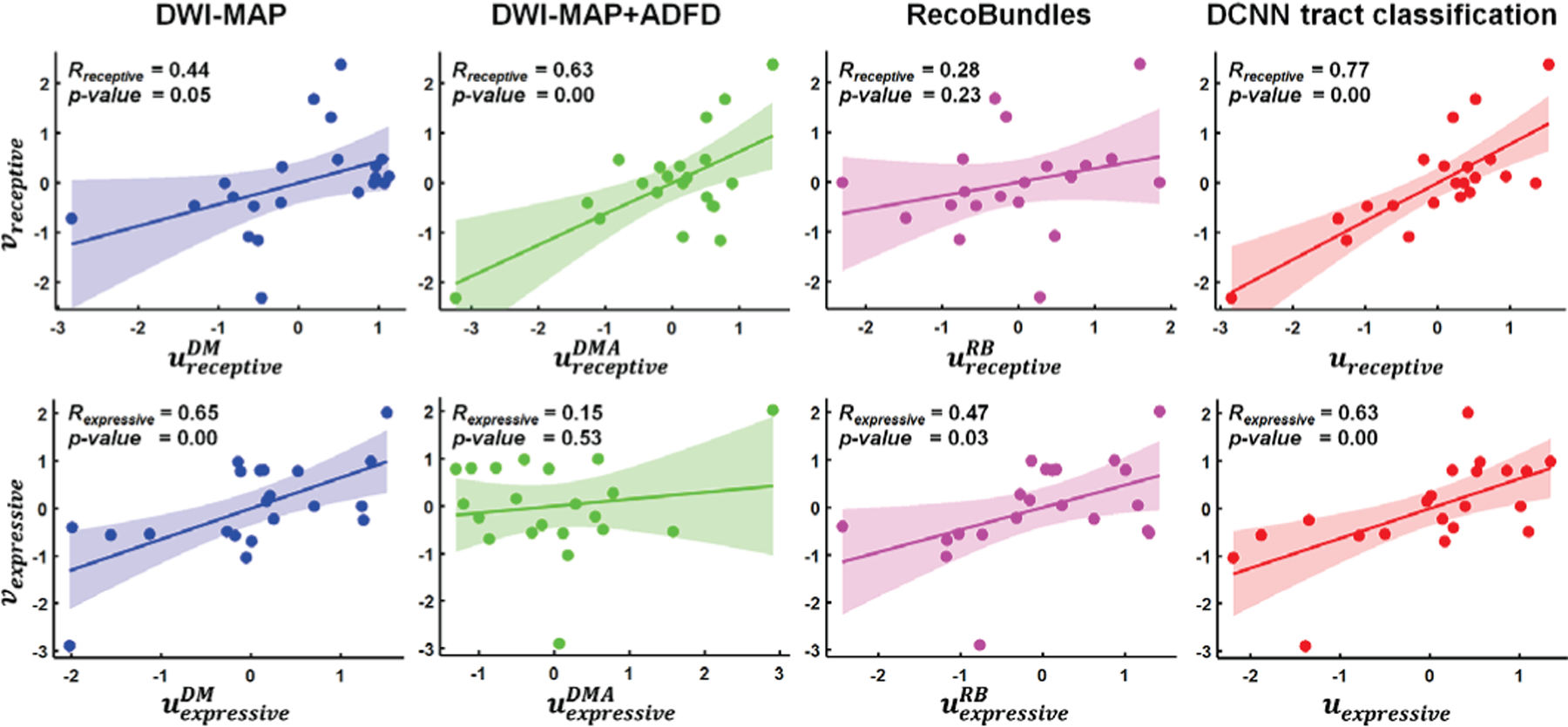
Canonical correlation coefficients, Rexpressive and Rreceptive between the change of postoperative language ability, Δexpressive|receptive, and postoperative tract volume change, Δi obtained from DWI-MAP, DWI-MAP+ADFD, RecoBundles, and DCNN tract classification, which were determined by CCA. u and v are the linear combination of the postoperative tract volume change normalized by preoperative tract volume and the change of postoperative neuropsychological language score.
IV. Discussion
The present study provides three major findings supporting DCNN tract classification performance over other existing methods (DWI-MAP, DWI-MAP+ADFD and RecoBundles) to detect ESM-determined eloquent areas, optimize surgical margin balancing maximal benefit (seizure freedom) with minimal risk (functional deficit), and predict neuropsychological language ability based on the clinical DWI data. First, our DCNN tract classification model could accurately discriminate 14 functionally important white matter pathways (i.e., C1−14) at an average F1 score of 0.993, yielding DCNN-determined cortical terminals that are spatially well-matched to their ground truth data (i.e., eloquent areas determined by ESM) in both the learning set and validation set (overlap accuracy ranging 86% to 100% within the 10 mm spatial resolution of ESM). Second, DCNN-determined pathways can optimize surgical margins via Kalman filter analysis, which models a state variable of interest (i.e., surgical margin) as a dynamic function of the postoperative volume change in DCNN-determined pathways, and in this way may help avoid postoperative functional deficits. The preservation of surgical margin determined by DCNN tract classification predicted the lack of postoperative deficits at the highest prediction accuracy of 92%, compared with DWI-MAP (90%), DWI-MAP+ADFD (90%), and RecoBundles (87%). Third, DCNN-determined pathways can be used to accurately predict post-surgical changes in language ability via CCA, where an imaging variable is defined by a linear combination of DCNN-determined language pathways and correlated with neuropsychological language variables. Postoperative change in DCNN-determined tract volume showed the most significant correlation with postoperative change in language ability (R= 0.70), compared with DWI-MAP (R= 0.54), DWI-MAP+ADFD (R= 0.39), and RecoBundles (R= 0.37).
Over the last decades, there have been a few DWI studies reporting systematic comparisons of tract classifications with clinically validated ground truth data from ESM. For example, Berman et al. [46] reported that their manual demarcations of primary motor tracts could localize eloquent motor pathways within 10 mm, with an accuracy of 63% as confirmed by subcortical stimulation. Also, our previous study using DWI-MAP [15] reported a localization accuracy of 82% within 10 mm as confirmed by ESM. Compared with the above studies, the present study demonstrated superior performance of the DCNN tract classification, with improved non-invasive localization of ESM-determined eloquent function at an excellent accuracy of 97% for motor pathways, 98% for language pathways and 99% for visual pathways, within 10 mm distance. This finding suggests a high translational value of our DCNN tract classification model, which may save effort and time by guiding current ESM procedures and/or providing functional localization information in future cases where ESM fails to localize.
Determination of a surgical margin to preserve eloquent function varies across centers, ranging from 0 to 2 cm [11]. The lack of standardization when determining surgical margins may contribute to persistent postoperative language deficits, as seen in approximately 40% of 56 centers despite preservation of all ESM-identified positive sites [11]. Improvements towards refining surgical margins are critical but must also be considered cautiously, as overestimating the extent of eloquent areas or incorrectly classifying eloquent areas may lead to poor surgical outcomes including recurrent seizures and functional deficits after surgery [11]. To standardize an optimal margin across patients our previous study first proposed a novel DWI tractography method (DWI-MAP+ADFD) which can optimize resection margin via Kalman filter analysis. We reported that resections remaining within the analysis-generated optimized margin achieved seizure-freedom and avoided functional deficit with a promising accuracy of 90% [16]. However, the DWI-MAP+ADFD approach was inherently limited by the many false positive tracts often seen in clinically acquired DWI data, significantly increasing type I error near cortical mantle [16]. To overcome this limitation, the present study proposed DCNN tract classification which can effectively control false positive tracts via deep learning classification of true positive tracts confirmed by their ground truth data. This configuration indeed improved analysis of the same data and further optimized a resection margin that minimizes functional deficit and maximizes the likelihood of seizure freedom.
Language dysfunction may cause long-term social, professional, and psychological problems [47]. Thus, accurate prediction of language areas using non-invasive imaging such as DWI tractography [48] becomes essential. Although ESM has been regarded as the gold standard for identifying eloquent language areas in epilepsy surgery, it cannot reveal subcortical structures of the language pathway. Our previous study reported that the extent of preoperative white matter language pathway resection is important to estimate the likelihood of postoperative language deficits [41]. However, this previous study could not estimate changes in language ability based on the extent of resected language-associated white matter pathways. The finding of our CCA analysis demonstrated that the resected volume of language white matter pathway determined by the DCNN tract classification may be an effective marker of postoperative language impairment.
Our working hypothesis is that spatial coordinates of ESM-determined true positive tracts from a given subject should be identical to group-level true positive tracts in the same template space. Under this hypothesis, the detection of true positives becomes a classification task, and can be accomplished by deeply learning spatial coordinates of true positive tracts belonging to a set of tract classes (i.e., sets of true positive tracts well-defined by their ground truths at group level). Our previous study [8] supported this hypothesis by showing that actual streamline coordinates outperformed tractography shape features such as curvature and torsion in training the DCNN model, providing better anatomical characteristics of individual tract classes in most white matter trajectories. The present study also found that the tractography based on group-level ESM can be feasibly learned using the DCNN model to demarcate ESM-determined eloquent areas at the individual level. This information may not be reliably detected by other methods, including DWI-MAP, DWI-MAP+ADFD, Recobundles, or the group-level ESM probability maps themselves (see examples reported in Fig 7).
The higher reliability of streamline coordinates makes some intuitive sense, considering that malformation of cortical development (MCD) is by far the most common epileptogenic pathology in pediatric epilepsy surgery cohorts, accounting for up to 50% of the cases. A diagnosis of MCD includes a variety of pathologies, most commonly focal cortical dysplasia types I/II, in which MRI can detect cortical thinning/thickening, hypointense/hyperintense signals, abnormal gyrification, and enlargement of the lateral ventricles, which limits the registration accuracy of cortico-cortical mapping between patients and healthy controls. An additional level of complexity in MCD-related epilepsy is that about 2/3 of the cases show more than a single epileptogenic structure; Each of these foci can influence abnormal reorganization, and this significantly increases type I/II errors during atlas-based classification. Epileptogenic brain tumors can also affect the development of the cortical mantle associated with peritumoral cortical dysplasia. Thus, the proposed DCNN method utilizing spatial coordinates of entire white matter trajectories (beyond the vicinity of MCD-related cortical lesions or tumors) may minimize the effect of cortical malformations on tract classification, where cortical-atlas-based tract clustering would likely be limited by malformed gyrification, especially near the cortical mantle. In contrast to parametric Gaussian approaches such as DWI-MAP, the proposed DCNN method makes no assumption regarding a priori probabilistic distribution of individual streamlines.
In addition, it should be noted that our fiber targets of interest (i.e., classes) are not major white matter fasciculi but functionally-specific white matter pathways of primary motor areas associated with different body parts (face/hand/leg), language areas responsible for different aphasias (expressive/receptive/speech arrest), and visual areas (phosphorene/spatial distortion), where individual pathways share similar tract shapes but differ in location. For instance, fiber trajectories associated with each category of somatosensory functions are very similar in pattern and geometry, causing current clustering methods to erroneously conflate them. This study was initially motivated to overcome these limitations by proposing a new tract classification paradigm which can effectively discriminate subtle difference in tract location, with minimal feature design and selection effort, independent of cortical abnormality severity.
There are at least two limitations that need to be considered in the present study. First, DWI scans were acquired for the purpose of clinical diagnosis. Thus, our data were limited in scan time, the number of diffusion encoding directions, and may be measured at a relatively low diffusion weight (i.e., b = 1000 s/mm2). Under these conditions, we can not fully resolve tractography in voxels with predominant crossing, kissing, fanning, and curving fiber configurations, and this may ultimately lead to incorrect and ambiguous estimates of fiber orientation [49], [50], [51], [52], [53]. Considering these inherent challenges of DWI tractography, we focused on motor pathways and major pathways of language and vision, which are functionally confirmed by ESM and also anatomically consistent with postmortem human brain studies [54], [55]. Second, the present study is observational in nature, and all data were obtained for the routine clinical management of epilepsy surgery. Therefore, these are retrospective and observational results with inherent limitations to the sample size, availability of postoperative information, and time available for detailed functional testing measures. Additional prospective studies are needed to confirm the present results, studying larger numbers of children and a more detailed accounts of postoperative deficits, especially in young children.
In summary, the present study demonstrated that the DCNN tract classification method can be an effective tool to non-invasively localize functionally important white matter pathways needed to be preserved in pediatric epilepsy surgery. Clinical utility of the DCNN-determined tract pathway was systematically validated by electrophysiologically acquired ground truth data. Although preliminary, our findings suggest that the DCNN-determined tract pathways may be used to help standardize and improve preoperative planning of pediatric epilepsy without relying on additional, functional data (e.g., ESM and fMRI).
Supplementary Material
Acknowledgments
This work was supported by grants from the National Institutes of Health (R01 NS089659 to J.J. and R01 NS064033 to E.A.).
Contributor Information
Min-Hee Lee, Department of Pediatrics, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Masaki Sonoda, Department of Pediatrics, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Naoto Kuroda, Department of Pediatrics, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Nolan O’Hara, Translational Neuroscience Program, Wayne State University School of Medicine and Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Ming Dong, Department of Computer Science, Wayne State University, Detroit, MI 48202 USA..
Csaba Juhasz, Departments of Pediatrics, Neurology, and Translational Neuroscience Program, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Eishi Asano, Departments of Pediatrics, Neurology, and Translational Neuroscience Program, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
Jeong-Won Jeong, Departments of Pediatrics, Neurology, and the Translational Neuroscience Program, Wayne State University School of Medicine, and the Translational Imaging Laboratory, Children’s Hospital of Michigan, Detroit, MI 48201 USA..
References
- [1].Hader WJ et al. , “Complications of epilepsy surgery: a systematic review of focal surgical resections and invasive eeg monitoring,” Epilepsia, vol. 54, no. 5, pp. 840–847, 2013. [DOI] [PubMed] [Google Scholar]
- [2].Lesser RP et al. , “Subdural electrodes,” Clin. Neurophysiol, vol. 121, no. 9, pp. 1376–1392, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Santiago Medina BBL et al. , “Seizure disorders: Functional mr imaging for diagnostic evaluation and surgical treatment-prospective study,” Radiology, vol. 236, no. 1, pp. 247–253, 2005. [DOI] [PubMed] [Google Scholar]
- [4].de Ribaupierre S et al. , “Presurgical language mapping in children with epilepsy: Clinical usefulness of functional magnetic resonance imaging for the planning of cortical stimulation,” Epilepsia, vol. 53, no. 1, pp. 67–78, 2012. [DOI] [PubMed] [Google Scholar]
- [5].Austermuehle A et al. , “Language functional mri and direct cortical stimulation in epilepsy preoperative planning,” Ann. Neurol, vol. 81, no. 4, pp. 526–537, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Spena G et al. , “Preoperative and intraoperative brain mapping for the resection of eloquent-area tumors. a prospective analysis of methodology, correlation, and usefulness based on clinical outcomes,” Acta Neurochir, vol. 152, no. 11, pp. 1835–1846, 2010. [DOI] [PubMed] [Google Scholar]
- [7].So EL and Alwaki A, “A guide for cortical electrical stimulation mapping,” J. Clin. Neurophysiol, vol. 35, no. 2, pp. 98–105, 2018. [DOI] [PubMed] [Google Scholar]
- [8].Xu H et al. , “Objective detection of eloquent axonal pathways to minimize postoperative deficits in pediatric epilepsy surgery using diffusion tractography and convolutional neural networks,” IEEE Trans. Med. Imaging, vol. 38, pp. 1910–1922, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Haseeb A et al. , “Young patients with focal seizures may have the primary motor area for the hand in the postcentral gyrus,” Epilepsy Res, vol. 76, no. 2–3, pp. 131–139, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Yerys BE et al. , “The fmri success rate of children and adolescents: typical development, epilepsy, attention deficit/hyperactivity disorder, and autism spectrum disorders,” Hum. Brain Mapp, vol. 30, no. 10, pp. 3426–3435, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hamberger MJ et al. , “Extraoperative neurostimulation mapping: results from an international survey of epilepsy surgery programs,” Epilepsia, vol. 55, no. 6, pp. 933–939, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Lam PDN et al. , “Trafic: Fiber tract classification using deep learning,” in Proc. SPIE Int. Soc. Opt. Eng, vol. 10574, 2018, p. 1057412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wasserthal J et al. , “Tractseg - fast and accurate white matter tract segmentation,” Neuroimage, vol. 183, pp. 239–253, 2018. [DOI] [PubMed] [Google Scholar]
- [14].Zhang F et al. , “Deep white matter analysis: Fast, consistent tractography segmentation across populations and dmri acquisitions,” in MICCAI, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Jeong J-W et al. , “Localization of specific language pathways using diffusion-weighted imaging tractography for presurgical planning of children with intractable epilepsy,” Epilepsia, vol. 56, no. 1, pp. 49–57, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Lee M-H et al. , “Novel diffusion tractography methodology using kalman filter prediction to improve preoperative benefit-risk analysis in pediatric epilepsy surgery,” J. Neurosurg.-Pediatr, vol. 24, no. 3, pp. 293–305, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Xu H et al. , “Automatic detection of eloquent axonal pathways in diffusion tractography using intracanial electrical stimulation mapping and convolutional neural networks,” in Proc. IEEE 15th Int. Symp. Biomed. Imag. (ISBI 2018), 2018, pp. 1034–1037. [Google Scholar]
- [18].Wieser HG et al. , “Ilae commission report. proposal for a new classification of outcome with respect to epileptic seizures following epilepsy surgery,” Epilepsia, vol. 42, no. 2, pp. 282–286, 2001. [PubMed] [Google Scholar]
- [19].Semel E et al. , Clinical evaluation of language fundamentals, fourth edition. San Antonio: TX, 2003. [Google Scholar]
- [20].Asano E et al. , “Role of subdural electrocorticography in prediction of long-term seizure outcome in epilepsy surgery,” Brain, vol. 132, pp. 1038–1047, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Nakai Y et al. , “Three- and four-dimensional mapping of speech and language in patients with epilepsy,” Brain, vol. 140, pp. 1351–1370, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Fischl B et al. , “Highresolution intersubject averaging and a coordinate system for the cortical surface,” Hum. Brain Mapp, vol. 8, no. 4, pp. 272–284, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Wellmer J et al. , “Digital photography and 3d mribased multimodal imaging for individualized planning of resective neocortical epilepsy surgery,” Epilepsia, vol. 43, no. 12, pp. 1543–1550, 2002. [DOI] [PubMed] [Google Scholar]
- [24].Dalal SS et al. , “Localization of neurosurgically implanted electrodes via photograph-mri-radiograph coregistration,” J. Neurosci. Methods, vol. 174, no. 1, pp. 106–115, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Desikan RS et al. , “An automated labeling system for subdividing the human cerebral cortex on mri scans into gyral based regions of interest,” Neuroimage, vol. 31, no. 3, pp. 968–980, 2006. [DOI] [PubMed] [Google Scholar]
- [26].Avants B and Gee JC, “Geodesic estimation for large deformation anatomical shape averaging and interpolation,” Neuroimage, vol. 23, pp. S139–S150, 2004. [DOI] [PubMed] [Google Scholar]
- [27].Andersson JLR and Sotiropoulos SN, “An integrated approach to correction for off-resonance effects and subject movement in diffusion mr imaging,” Neuroimage, vol. 125, pp. 1063–1078, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Andersson JLR et al. , “Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion mr images,” Neuroimage, vol. 141, pp. 556–572, 2016. [DOI] [PubMed] [Google Scholar]
- [29].Andersson JL et al. , “Towards a comprehensive framework for movement and distortion correction of diffusion mr images: Within volume movement,” Neuroimage, vol. 152, pp. 450–466, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Zhang Y et al. , “Segmentation of brain mr images through a hidden markov random field model and the expectation-maximization algorithm,” IEEE Trans. Med. Imaging, vol. 20, no. 1, pp. 45–57, 2001. [DOI] [PubMed] [Google Scholar]
- [31].Tournier J-D et al. , “Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions,” in Proc. Int. Soc. Magn. Reson. Med, 2010, p. 1670. [Google Scholar]
- [32].Smith RE et al. , “Anatomically-constrained tractography: Improved diffusion mri streamlines tractography through effective use of anatomical information,” Neuroimage, vol. 62, no. 3, pp. 1924–1938, 2012. [DOI] [PubMed] [Google Scholar]
- [33].Garyfallidis E et al. , “Quickbundles, a method for tractography simplification,” Front. Neurosci, vol. 6, p. 175, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Morris ED et al. , “Cardiac substructure segmentation with deep learning for improved cardiac sparing,” Med. Phys, vol. to be published, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Emami H et al. , “Generating synthetic cts from magnetic resonance images using generative adversarial networks,” Med. Phys, vol. 45, pp. 3627–3636, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].He K et al. , “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit, 2016, pp. 770–778. [Google Scholar]
- [37].Lin T-Y et al. , “Focal loss for dense object detection,” in Proc. IEEE Int. Conf. Vis. (ICCV), 2017, pp. 2980–2988. [Google Scholar]
- [38].Wen Y et al. , “A discriminative feature learning approach for deep face recognition,” in Proc. Eur. Conf. Comput. Vis. Cham, 2016, pp. 499–515. [Google Scholar]
- [39].Kingma DP and Ba J. (2017) Adam: A method for stochastic optimization. [Online]. Available: http://arxiv.org/abs/1412.6980v9
- [40].Jeong J-W et al. , “Automatic detection of primary motor areas using diffusion mri tractography: Comparison with functional mri and electrical stimulation mapping,” Epilepsia, vol. 54, no. 8, pp. 1381–1390, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Lee M-H et al. , “Prediction of postoperative deficits using an improved diffusion-weighted imaging maximum a posteriori probability analysis in pediatric epilepsy surgery,” J. Neurosurg.-Pediatr, vol. 23, no. 5, pp. 648–659, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Garyfallidis E et al. , “Recognition of white matter bundles using local and global streamline-based registration and clustering,” Neuroimage, vol. 170, pp. 283–295, 2018. [DOI] [PubMed] [Google Scholar]
- [43].Rauch HE et al. , “Maximum likelihood estimates of linear dynamic systems,” AIAA J, vol. 3, no. 8, pp. 1445–1450, 1965. [Google Scholar]
- [44].Hamilton JD, “State-space models,” Handbook of econometrics, vol. 4, pp. 3039–3080, 1994. [Google Scholar]
- [45].Hotelling H, “Relations between two sets of variates,” Biometrika, vol. 23, pp. 321–377, 1936. [Google Scholar]
- [46].Berman JI et al. , “Accuracy of diffusion tensor magnetic resonance imaging tractography assessed using intraoperative subcortical stimulation mapping and magnetic source imaging,” J. Neurosurg, vol. 107, pp. 488–494, 2007. [DOI] [PubMed] [Google Scholar]
- [47].Overvliet GM et al. , “Nocturnal epileptiform eeg discharges, nocturnal epileptic seizures, and language impairments in children: review of the literature,” Epilepsy Behav, vol. 19, no. 4, pp. 550–558, 2010. [DOI] [PubMed] [Google Scholar]
- [48].Walton M et al. , “Brain white matter structure and language ability in preschool-aged children,” Brain Lang, vol. 176, pp. 19–25, 2018. [DOI] [PubMed] [Google Scholar]
- [49].Leergaard TB et al. , “Quantitative histological validation of diffusion mri fiber orientation distributions in the rat brain,” PLoS One, vol. 5, no. 1, p. e8595, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Tournier JD, The Biophysics of Crossing Fibers. New York: Oxford University Press, 2010. [Google Scholar]
- [51].Daducci A et al. , “Quantitative comparison of reconstruction methods for intra-voxel fiber recovery from diffusion mri,” IEEE Trans. Med. Imaging, vol. 33, no. 2, pp. 384–399, 2014. [DOI] [PubMed] [Google Scholar]
- [52].Schilling KG et al. , “Histological validation of diffusion mri fiber orientation distributions and dispersion,” Neuroimage, vol. 165, pp. 200–221, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Thomas C et al. , “Anatomical accuracy of brain connections derived from diffusion mri tractography is inherently limited,” Proc. Natl. Acad. Sci. U. S. A, vol. 111, no. 46, pp. 16 574–16 579, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Fernndez-Miranda JC et al. , “Subcomponents and connectivity of the superior longitudinal fasciculus in the human brain,” Brain Struct. Funct, vol. 220, no. 3, pp. 1665–1680, 2015. [DOI] [PubMed] [Google Scholar]
- [55].Wang X et al. , “Subcomponents and connectivity of the superior longitudinal fasciculus in the human brain,” Brain Struct. Funct, vol. 221, no. 4, pp. 2075–2092, 2016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


