Abstract
Noise has a negative impact on our environment and human health. For this reason, it is necessary to eliminate excessive noise levels. This paper is focused on the study of the sound absorption properties of materials with open-porous structures, which were made of acrylonitrile butadiene styrene (ABS) material using additive technology. Four types of structures (Cartesian, Octagonal, Rhomboid, and Starlit) were evaluated in this work, and every structure was prepared in three different volume ratios of the porosity and three different thicknesses. The sound absorption properties of the investigated ABS specimens were examined utilizing the normal incidence sound absorption and noise reduction coefficients, which were experimentally determined by the transfer function method using a two-microphone acoustic impedance tube. This work deals with various factors that influence the sound absorption performance of four different types of investigated ABS material’s structures. It was found, in this study, that the sound absorption performance of the investigated ABS specimens is strongly affected by different factors, specifically by the structure geometry, material volume ratio, excitation frequency of an acoustic wave, material’s thickness, and air space size behind the tested sound-absorbing materials.
Keywords: acrylonitrile butadiene styrene, 3D printing technique, acoustic impedance tube, sound absorption coefficient, volume ratio, excitation frequency of acoustic wave, air space size, material thickness
1. Introduction
Sound absorption can be defined as a decrement of sound energy upon contact of sound waves with sound absorbing material, such as, e.g., walls, ceilings, floors, or other subjects, which causes the sound to not be reflected back into space [1,2]. Sound absorption can be a particularly important factor not only for spaces such as concert venues, cinemas, and theatres but also, e.g., for schools, lecture aulas, and for many other materials of daily applications. This also became important for various fields of industrial practice, e.g., for the correction of noise that may arise from machines, railroad cars, or computer server array cooling fans in search engines or cloud computing, or for the components belonging to the automotive industry [3,4,5,6].
Sound absorption efficiency is mostly connected with the thickness of the bulk material [7,8]. On the other hand, to improve the effectivity of sound absorbent materials at lower frequencies, this can be compensated by the air space behind the acoustic board [1]. However, the homogeneous fully infilled materials are not sufficient for good sound absorption, but better sound absorption characteristics are usually shown for porous materials such as foams and fibers [9,10,11,12]. When sound waves propagate inside a porous material, they pass through the fibers (thin walls) connecting the pores and, as a result of viscous losses, the acoustic energy is converted into heat. To dissipate acoustic energy, air movement inside the porous material is required, which causes the material located near the fixed boundary (where the particle velocity is zero) to become ineffective [13,14]. The optimum sound absorption coefficient related to an optimum viscous boundary layer thickness of a micro lattice metamaterial has been analyzed by Cai et al. [15].
Deshmukh et al. [16] compared the sound properties of the bulk samples with the samples of lattice sandwich structures. It was found that the lattice structures exhibit excellent insulating sound properties compared to the bulk samples. The different geometries of porous structures produced by 3D printing technique have been studied from the aspect of acoustic absorption. Excellent mechanical properties are ensured by the face-centered cubic (FCC) core within the additively produced structures. Wang et al. [17] and Jiménez et al. [18] investigated highly porous materials supported by rigid supports of multiple layers with a solid frame and theoretically analyzed various configurations of porous materials and their increasing complexity, namely one layer of highly porous material, one layer of highly porous air space material, and a multi-layer structure. A porous pyramid sandwich structure was studied by Liu et al. [19] that was characterized by a good ratio of strength and stiffness to weight. Due to its good mechanical properties, such a porous material is used in applications ranging from lightweight structures to aircraft components [20].
Double-porosity materials were studied by Olny and Boutin [21] to control the absorption coefficient in the desired frequency range, in which periodic porous material at the micro level was examined using a homogenization technique and then applied to heterogeneous triple-range materials. The behavior of the specific, periodically arranged cavities with a cylindrical geometry in porous materials was investigated at the microscopic level by Roh and Yoon [22], at which the losses of thermal and viscous characters were taken into account. Lagarrigue et al. [23] came with the idea of incorporating the rigid inclusions in a porous material to be tunable and for it to be possible to improve their sound absorption properties at the low-frequency scope. Cellular materials with several types of inclusions differing in shape was studied by Groby et al. [24], while Xu et al. [25] dealt with an optimum design for the propagation of acoustics in the exact material layer inside the cavity using the bounded element method.
Numerical analysis of porous layer properties and their optimization by linking effective acoustic properties and geometry were discussed in several available studies. While Bulvert et al. [26] used a non-linear conjugate gradient algorithm for optimization, Krödel et al. [27] used Biot’s theory that confirmed a good match of a predicted sound wave speed with the experimental measures within an analysis of the acoustic response of periodic millimeter-sized microlattices immersed in water. An analytical model of obtaining the coefficient of loss of admitted sound in a cylindrical box made of porous materials was presented by Gohari et al. [28]. The measured values have shown that when the length of the porous structure is increased, the loss of sound transmission approximates that of the infinite shells. They also have found out that by changing the length of the poroelastic roller, the amount of transmitted sound was reduced. However, better sound insulation properties are obtained in the low-frequency band when the shell radius is reduced. Numerical analysis and experimental research of the propagation and loss of sound in porous materials in pipelines using regular fixed diffusers to increase transmission loss by Bragg diffraction was carried out by Jena and Qiu [29]. The most preferred method for calculating sound propagation through homogeneous sandwich materials as well as porous materials with isotropic properties in a pipe that is below the cut-off frequency is the transfer matrix method [30,31], while for simulating the behavior of complex structures and inclusions with complex shape in a wide frequency range, it is appropriate to use numerical models [32,33].
There are many sound-absorbent materials, including various plastics and porous fibers, the development of which has advanced rapidly in recent years. They are used to effectively control noise or to improve the acoustic conditions by shortening the echo time in the room [34,35,36]. The important aspects of the applicability of sound-absorbent materials are not only their effective noise absorption and insulation but also their structural stability, environment- and health-friendly properties, as well as their suitability for mass production [37,38]. These requirements caused a significant part of the research to be focused on investigating the properties of polymer composites and polycarbonate.
As the complex structures for a sound absorption application are easily manufactured by a 3D printing technique, it is very interesting to deal with these specific properties of the materials usually used within this technology. One of the most widely used plastics available in filaments for additive manufacturing is acrylonitrile butadiene styrene (ABS). However, only a few studies [39,40,41] have been focused on the investigation of the sound absorption properties of components produced from ABS material.
The main benefit of ABS as a material is its possibility to combine the toughness of the polybutadiene rubber with the rigidity and strength of acrylonitrile and styrene polymers. This material is resistant to chemical degradation either by alkaline or acidic agents. For most applications, ABS can be used between −20 to 80 °C [42]. In addition to the good mechanical properties, ABS material also shows good electrical insulating characteristics over a wide range of frequencies, even in high humidity and high temperature environments, making this material appropriate as a protecting material for electrical components such as chips and cables [43]. The next advantageous property of ABS is that it belongs to the category of thermoplastics that means that even with repeated heating and cooling, it does not degrade [44]. This property classifies material as suitable for recycling. It is an amorphous solid, which technically means that ABS hasn’t a melting point [45]. It is flammable at open flames or in case of its exposure to very high temperatures [46]. It is widely applied at daily used things and household appliances such as, e.g., knife and plier handles, for the manufacture of pipes for water treatment and distribution, for air conditioning, in the food industry, for the manufacture of furniture, etc. It is useful for the production of complex and precise shaped components such as musical instruments, automotive parts, medical devices, and others. As it is widely used in many applications, it is also worthy to discover the sound absorption properties of the structures made from this ABS plastic material to use it for such a purpose.
Generally, unperforated hard solid materials (e.g., concrete, stone, glass, and plastics) are not suitable for noise reduction. Rather, they can be used as sound reflective materials. The open-porous materials manufactured using 3D printing technology are applicable for products in the case if it is possible to ensure their both mechanical stiffness and sound absorption in practice. The goal of this work is to study various factors affecting the sound absorption performance of 3D-printed open-porous ABS materials which were produced with different geometry of pores inside of lattice metamaterials with different thicknesses and with different volume ratios. Based on the abovementioned and also the authors’ best knowledge, it can be stated that a study of such porous structures produced by the additive technology from the acrylonitrile butadiene styrene (ABS) material and the effects of several parameters (the pore shape within a structure, volume ratio Vr of the material within the sample, sample thickness t, and air space size a) on their sound absorption properties have not yet been investigated and presented from such a complex point of view.
2. Materials and Methods
2.1. Characteristics of ABS Samples and Their Production
The samples for the research have been produced from acrylonitrile butadiene styrene (ABS) material (Smart Materials 3D, Alcala la Real, Spain).
In this study, the plastic material ABSplus-P430 Ivory was used as a filament with a diameter of 1.75 mm, while the Fused Filament Fabrication (FFF) technique was employed as the additive manufacturing technology.
The main advantage of additive technology is the feasibility to manufacture complex-shaped components with cavities that is not achievable by another type of technology. Such specific materials are also used for sound absorption applications, at which the size and shape of the pores affect the properties of the material. The volume of material separating individual pores in the structure of the material is given by the volume ratio Vr that is expressed by the Equation (1) [47]:
| (1) |
where VS is the volume of material used to make the structure, and VT is the volume of the whole solid body.
Virtual models were generated in PTC Creo software (Parametric Technology Corporation Inc., Boston, MA, USA), version 6. This CAD/CAM system differs from version 5 by offering automatic generation of some types of cellular structures, which is very advantageous for creating a product for application in real practice when the component has a complex shape and it is necessary to fill its core with a light- or sound-absorbing structure. By defining the basic conditions, such as the location of the base cell, its size, location of the struts, etc., the software automatically fills the specified space with the defined structure. Hence, the design of types of structures and their geometries in the research was related to the software offer, while at the same time, the authors tried to focus on atypical and little-studied structures such as Rhomboid, Starlit, or Octagonal and compare their behavior with a simple but relatively frequently used Cartesian structure.
Due to the requirements of the testing equipment (see Section 2.2.3), the samples were designed in a cylindrical shape with an external diameter of 29 mm. A continuous layer of the ABS material of 2 mm thick formed a shell enclosing the inner lattice structure. The lattice structure in the core of every specimen was created in such a way that so-called a “basic cell” has been patterned in the radial direction and the z-axis direction, or in all three orthogonal directions along the x, y, or z axes, while the z-direction was always parallel to the axis of the cylindrical shape of the specimen. Each cell type contains not only all the outer beams (horizontal and vertical) but also the inner angular struts.
In this study, 36 types of lattice structures varied in shape, volume ratio Vr, and thickness t were experimentally tested. They were named according to their shape of an internal structure as Starlit, Rhomboid, Cartesian, and Octagonal as they are shown in Figure 1a.
Figure 1.
The examples of investigated samples: (a) different shapes of porous structures; (b) different volume ratios Vr of the Octagonal structure; (c) a set of the specimens of the Rhomboid structure with different sample thicknesses t = 1, 2, and 3 cm, and with different sample volume ratios Vr = 44, 57, and 70%.
Every shape of the specimen was made in three different volume ratios of 44, 57, and 70% (see Figure 1b), and in three different thicknesses with the values of 1, 2, and 3 cm (Figure 1c).
The choice of volume ratios in the presented research was therefore mainly connected with the possibility to define the same volume of material in the software for all 4 types of structures. The same volume ratio was determined as a basic parameter for comparing the sound absorption properties of individual structures and for evaluating the efficiency of the use of plastic material in production, and it has been controlled over the diameter of the pore-enveloping strut. The specification of the smallest volume fraction Vr = 40% was also related to the technological conditions because the production of structures with a lower volume fraction was either not possible or the samples were of poor quality. When selecting the largest considered volume fraction Vr =70%, the aspect of the practical character was also taken into account, in which the saving of material in combination with the given production technology would show not only an economic but also time and ecological effects.
The samples were 3D-printed at the orientation of the cylindrical axis z normal to the building platform xy. The next properties of the individual internal structures are presented in Table 1.
Table 1.
Characteristics of the investigated 3D-printed structures.
| Structure Type | Volume Ratio (%) |
Label | Front View | Strut Diameter (mm) |
Basic Cell Sizes x/y/z (mm) |
|---|---|---|---|---|---|
| Starlit | 44 | ST_44 |

|
1 | 9/9/8 |
| 57 | ST_57 | 1.4 | 9/9/7.5 | ||
| 70 | ST_70 | 1.8 | 9/9/8 | ||
| Rhomboid | 44 | RH_44 |

|
1 | 7/7/5.5 |
| 57 | RH_57 | 1.35 | 7/7/5 | ||
| 70 | RH_70 | 1.7 | 7/7/5 | ||
| Cartesian | 44 | CA_44 |

|
1 | 5/5/5 |
| 57 | CA_57 | 1.4 | 5/5/5 | ||
| 70 | CA_70 | 1.8 | 5/5/5 | ||
| Octagonal | 44 | OC_44 |

|
1 | 7/7/6 |
| 57 | OC_57 | 1.4 | 7/7/6 | ||
| 70 | OC_70 | 1.7 | 7/7/5.5 |
Due to the test of sound absorption properties being non-destructive, it was enough to make only one piece of every type of the specimens; that means 36 pieces of the samples with 4 types of porous structures at 3 volume ratios Vr and 3 different thicknesses t.
The 3D printer Prusa i3 Mk2 (Prusa Research a.s., Prague, Czech Republic) was used for specimen production. During printing, the material prepared in the form of a plastic fiber is unwound from a spool and is guided inside the extruder. The nozzle melts the filament (temperature of the nozzle has been 255 °C) and extrudes it onto a build platform with a temperature of 100 °C. Both the nozzle and the platform are controlled by a computer which converts the dimensions of the body into x, y, and z coordinates so that the print head moves correctly in relation to the building platform. As is usual with the FFF method, the printhead also moves over the base to “draw” the cross-sectional shape of the printed body on the base plate. The rate of the nozzle in this research was 40 mm/s at the shape circumference and 30 mm/s inside the cross-section of a sample. This thin layer of plastic cools and hardens very quickly bonded to the layer beneath it. When the layer is finished, the base is moved to make space for another layer of material. When an object is taken off the FFF printer, its support materials are usually removed if they have been used. In the case of investigated samples, no supports were used.
In contrast to the authors’ initial already published research [48], in which only 3 types of structures with one volume ratio Vr = 57% were used to assess and compare sound properties, within the presented research a different nozzle size and a different layer height of the applied material were used for the samples production. These technological conditions affect not only the quality of the finished product but also its mechanical properties [49,50]. While in the previous research, a nozzle with a diameter of 0.6 mm and a height of the applied layer of 0.3 mm was employed, in this case, the samples were made with a nozzle with a diameter of 0.4 mm and a layer height of 0.254 mm. Although the production time of the samples was extended by almost 60%, the quality of the samples (in terms of shape, purity, and compactness of the printout) has already increased at first glance.
2.2. Measurement Methodology
2.2.1. Sound Absorption Coefficient
A material’s ability to damp sound is expressed by the sound absorption coefficient that measures the fraction of incident sound energy which is absorbed on the surface of the sound-absorbing material. The sound absorption coefficient α (−) is defined by the equation [51], Equation (2):
| (2) |
where PA is the absorbed (dissipated) acoustic power and PI is the incident acoustic power. Generally, the material’s ability to absorb sound is affected by different aspects, such as the sound-absorbing material type, excitation frequency of an acoustic wave, thickness, pore geometry, air flow resistivity, density, temperature, and humidity. The airflow resistivity is defined by the ratio of the static pressure difference between two sides of the tested material to the line speed of the airflow which stably passes through the porous material. It is well known that an increase of the airflow resistivity improves the absorption performance in the whole frequency range but only until an intermediate value [52]. An overly acoustically resistant porous material exhibits low sound absorption behavior and prevents the propagation of acoustic waves into the interior of the material. Nevertheless, the smaller flow resistance of porous materials will less efficiently convert sound energy into heat which, again, leads to the low sound absorption performance. For this reason, it is necessary to ensure an optimum flow resistance of the porous material [52,53].
2.2.2. Noise Reduction Coefficient
As mentioned above, the sound absorption properties of sound-absorbing materials are strongly influenced by the excitation frequency. This phenomenon is given by the noise reduction coefficient (NRC), which is specified as the arithmetical average of measured values of the sound absorption coefficient in the central frequency bands 250, 500, 1000, and 2000 Hz [54,55], Equation (3):
| (3) |
2.2.3. Sound Absorption Performance
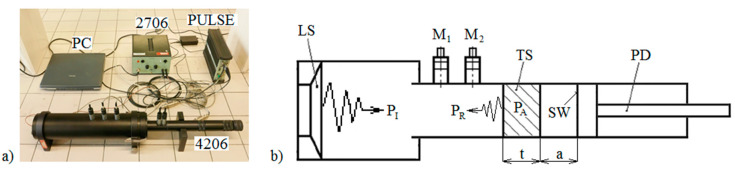
Experimental measurements of the normal incidence sound absorption coefficient of the studied 3D-printed open-porous ABS materials in the frequency range of 200–6400 Hz were performed employing a two-microphone acoustic impedance tube (BK 4206), a dynamic signal PULSE multi-analyzer (BK 3560-B-030), and a power amplifier (BK 2706). The view of the experimental setup (Brüel & Kjær, Nærum, Denmark) for measuring frequency dependencies of the sound absorption coefficient is shown in Figure 2a.
Figure 2.
View of the experimental setup for measuring frequency dependencies of the sound absorption coefficient (a) and a scheme of the two-microphone acoustic impedance tube (b). Legend of the abbreviations: a—air space size; LS—loudspeaker; M1, M2—measuring microphones; PA—absorbed acoustic power; PI—incident acoustic power; PR—reflected acoustic power; PD—piston disk; TS—Tested Sample; SW—solid wall; t—sample thickness.
Frequency dependencies of the normal incidence sound absorption coefficient of the investigated ABS specimens of a given thickness t (ranging from 1 to 3 cm) were experimentally measured for various air space sizes a (ranging from 0 to 12 cm) behind the tested samples. The air space size was set by means of the movable piston disk, as shown in Figure 2b.
Experimental measurements of the normal incidence sound absorption coefficient were performed by means of the two-microphone transfer function method [56] based on the standing wave principle. This method has been standardized by the International Organization for Standardization as ISO 10534-2. Based on this method, the normal incidence sound absorption coefficient α is given by Equation (4) [57]:
| (4) |
where r is the sound reflection factor at normal incidence that is defined as Equation (5):
| (5) |
where k is the complex wave number, x1 is the distance between the microphone M1 from the reference sample plane (x = 0), H is the complex acoustic transfer function, HI is the transfer function of the incident wave, and HR is the transfer function of the reflection wave. The transfer functions are defined by the following equations, Equations (6)–(8):
| (6) |
| (7) |
| (8) |
where x2 and is the distance between the microphone M2 from the reference sample plane (x = 0), and p1 and p2 are the complex acoustic pressures that were measured by means of the microphones M1 and M2. The complex wave number k is defined as Equation (9):
| (9) |
where k′ and k″ are the real and imaginary parts of the complex wave number that are expressed by the equations, Equations (10) and (11):
| (10) |
| (11) |
where f is the excitation frequency, c is the speed of sound, and Δn is the dimensionless quantity that is obtained from the experimentally measured acoustic pressure amplitudes in two neighboring local minima xmin (numbered n and n + 1) and the local maximum xmax (numbered n) between the local minima, Equation (12):
| (12) |
where n is the integer (i.e., n = 0, 1, 2, …).
3. Results
This section deals with various aspects that affect the sound absorption performance of the studied lattice structures made by additive technology from ABS material, which is marked as follows: Firstly, the sample specification is given by the geometry of the structure (see Table 1). Thereafter, the label of the sample is made up of three numbers. The first one defines the volume ratio Vr (in %). The second number represents the sample thickness t (in cm). Finally, the third number denotes the air space size a (in cm) behind the Tested Sample TS inside the acoustic impedance tube (see Figure 2b).
3.1. Frequency Dependencies of the Sound Absorption Coefficient
3.1.1. Influence of Pore Shape
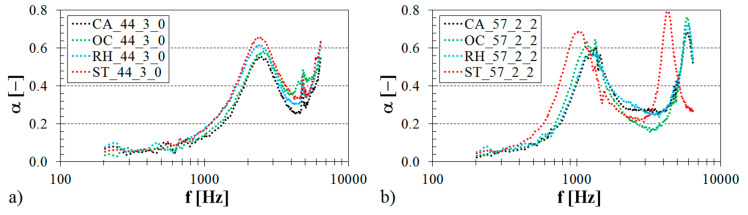
The structure type of 3D-printed ABS materials is affected by pores of various shapes and sizes and has a substantial effect on their sound absorption performance. The influence of the pore geometry on the sound absorption behavior of the open-pore ABS materials is illustrated in Figure 3.
Figure 3.
Influence of the pore geometry of the 3D-printed ABS material on the frequency dependencies of the sound absorption coefficient: (a) volume ratio Vr = 44%, sample thickness t = 3 cm, air space size a = 0 cm, (b) volume ratio Vr = 57%, sample thickness t = 2 cm, air space size a = 2 cm.
The effect of the structure type of the tested ABS samples (with Vr = 44% and t = 3 cm) fixed directly on the solid wall SW (i.e., with a = 0 cm) inside the acoustic impedance tube (see Figure 2b) is shown in Figure 3a. Similarly, the effect of the structure type on frequency dependencies of the sound absorption coefficient for the ABS samples of the same volume ratio (i.e., Vr = 57%) and the same thickness (i.e., t = 2 cm) placed at a distance of 2 cm from the solid wall is demonstrated in Figure 3b. It is evident that the effect of the structure type on the sound absorption performance was generally negligible for low-frequency acoustic waves, specifically at f < 700 Hz (see Figure 3a) and at f < 400 Hz (see Figure 3b). Furthermore, it can be seen in a wide frequency range that better sound absorption performance was noticed for the ABS samples, which were made with the Starlit structure. Conversely, the ABS samples manufactured with the Cartesian structure (see Figure 3a) are characterized by a lower ability to absorb sound compared to the other ABS structures examined. The effect of the structure type of the studied ABS materials is connected with the airflow resistivity that is the most important parameter affecting the sound absorption performance of porous materials [58]. As shown in Table 1, the Starlit structure type is specified by more complex pore geometry in comparison with the other open-porous structure types. This phenomenon is accompanied by multiple sound reflections and by higher internal friction during the acoustic wave propagation through this porous structure type. For these reasons, the Starlit structure exhibited a more efficient conversion from sound energy into heat than the other investigated open-porous structures. This effect was observed in the frequency ranges of 1.7–4.1 kHz (see Figure 3a), 0.4–1.2 kHz (see Figure 3b), and 3.3–4.0 kHz (see Figure 3b). Contrariwise, the 3D-printed ABS specimens prepared with the Cartesian structure were characterized by a lower ability to dampen sound in the frequency ranges of 1.0–6.4 kHz (see Figure 3a) and 0.8–1.2 kHz (see Figure 3b) compared to the other open-porous structure types.
3.1.2. Influence of Volume Ratio
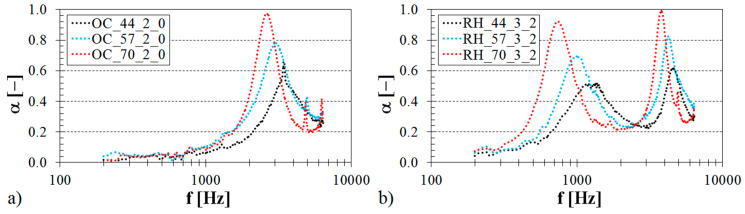
The volume ratio (or the relative density), which increases with a decrease in the pore size, generally has a big influence on the airflow resistivity [59,60] and, thus, on the sound damping properties of the examined open-porous structures. The relative density, which increases with an increase in the strut diameter (see Table 1), increases the mass and, thus, the mechanical stiffness of the tested ABS materials [61]. Generally, higher density open-porous materials have better sound absorbing properties than lower density materials with open pores [58,62,63]. The influence of the sample volume ratio on the frequency dependencies of the sound absorption coefficient for two various types of 3D-printed structures (i.e., Octagonal and Rhomboid) is demonstrated in Figure 4.
Figure 4.
Influence of the sample volume ratio on the frequency dependencies of the sound absorption coefficient for the tested ABS samples: (a) Octagonal structure, sample thickness t = 2 cm, air space size a = 0 cm; (b) Rhomboid structure, sample thickness t = 3 cm, air space size a = 2 cm.
It is visible that the sound absorption performance of the tested ABS samples generally increased with an increase in the volume ratio at low excitation frequencies. In the case of the ABS sample measuring 2 cm in the thickness (see Figure 4a), which was produced with the Octagonal structure and was fixed directly on the solid wall SW inside the impedance tube (see Figure 2b), higher values of the sound absorption coefficient were observed for the volume ratio Vr = 70% in the frequency range of 0.7–2.0 kHz. If the ABS sample of the same volume ratio measuring 3 cm in the thickness was made with the Rhomboid structure and positioned at a distance of 2 cm from the solid wall (see Figure 4b), a positive effect of the volume ratio on the sound absorption performance was observed in the frequency ranges of 200–880 Hz and 1.5–3.0 kHz. Conversely, the abovementioned ABS samples, which were produced with the smallest volume ratio (i.e., with Vr = 44%), exhibited higher values of the sound absorption coefficient in the frequency ranges of 3.9–4.8 kHz (see Figure 4a) and 1.3–2.5 kHz (see Figure 4b) compared to the same ABS samples that were produced with higher volume ratios (i.e., with Vr = 57% and Vr = 70%). It can be noticed in the case of the OC_70_2_0 sample type (see Figure 4a) that frequency bands corresponding to a given number of peaks of the sound absorption coefficient vary in their width. Generally, wider frequency bands are obtained at higher values of the sound absorption coefficient. Therefore, the first frequency band (αmax ≈ 0.97) is characterized by the broad peak compared to the second and third frequency bands (αmax ≈ 0.41) that appear narrower.
3.1.3. Influence of Material Thickness
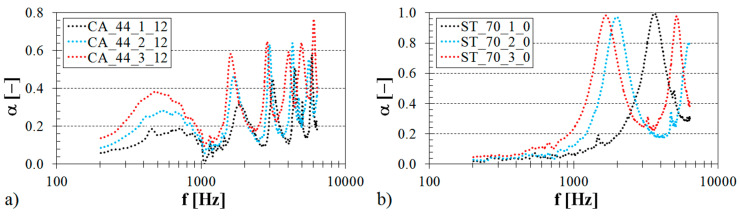
The material thickness also belongs to the important factors affecting the sound absorption performance of the investigated 3D-printed open-porous ABS samples. Figure 5 illustrates the influence of different sample thickness when the studied sample is positioned at a distance of 12 cm from the solid wall (see Figure 5a) or is mounted directly on the solid wall (see Figure 5b).
Figure 5.
Influence of the sample thickness on the frequency dependencies of the sound absorption coefficient for the tested ABS samples: (a) Cartesian structure, volume ratio Vr = 44%, air space size a = 12 cm; (b) Starlit structure, volume ratio Vr = 70%, air space size a = 0 cm.
It was found that the sound absorption performance significantly increased with an increase in the material thickness toward lower excitation frequencies. It should also be noted that frequency dependencies of thicker porous materials are generally characterized by wider frequency bands compared to thin porous materials. Therefore, the application of very thin porous materials with air-gap construction to absorb sound is suitable only for narrow frequency bands depending on the sample distance from the solid wall (more in Section 3.1.4). Nevertheless, the material thickness of 3D-printed products may affect their printing times and production costs [64,65]. Because the printing process conditions of a given open-porous structure and the ground plane dimensions (i.e., samples with an outer diameter of 29 mm) of the tested 3D-printed samples were identical, the increasing material thickness results in an increase in the printing time and the manufacturing costs of the 3D printing technology [66]. For this reason, this method is not effective to damp noise.
3.1.4. Influence of Air Space Size
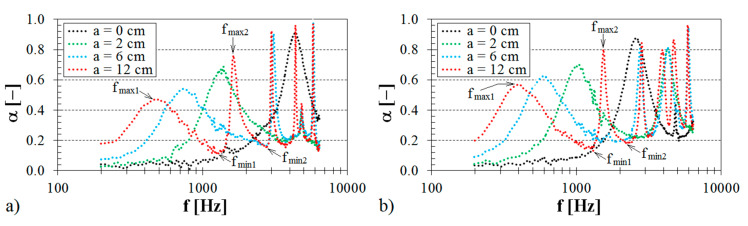
The air space size between the Tested Sample TS and the solid wall SW inside the impedance tube (see Figure 2b) is another factor which strongly affects the sound absorption performance of porous materials. Figure 6 shows the effect of the air space size on sound absorption behavior for two different ABS samples.
Figure 6.
Influence of the air space size on the frequency dependencies of the sound absorption coefficient for the tested ABS samples: (a) Rhomboid structure, volume ratio Vr = 44%, sample thickness t = 1 cm; (b) Starlit structure, volume ratio Vr = 57%, sample thickness t = 2 cm.
It is evident that the frequency dependencies of the sound absorption coefficient have oscillating waveforms with a certain number of minima and maxima of the sound absorption coefficient at the corresponding excitation frequencies fmin and fmax. This phenomenon is related to the reflections of acoustic waves from the solid wall inside the acoustic impedance tube and to the wavelength of sound λ, which is defined by the ratio of the speed of sound to the frequency [67]. The maximal acoustic pressure is reached at the solid wall surface. Conversely, the air particle velocity is equal to zero at the wall. Generally, the sound absorption maximum is reached for the maximum air particle velocity and zero acoustic pressure. For these reasons, the maximum sound absorption coefficient is obtained, when the air space size is equal to the odd multiples of ¼ wavelength [68,69] at the excitation frequencies, Equation (13):
| (13) |
where n is an integer (n = 0, 1, 2, …) and l is the sample distance from the solid wall, which is given by the formula shown in Equation (14):
| (14) |
Similarly, the minimum sound absorption coefficient is obtained, when the air space size is equal to the even multiples of ¼ wavelength at the excitation frequencies, Equation (15):
| (15) |
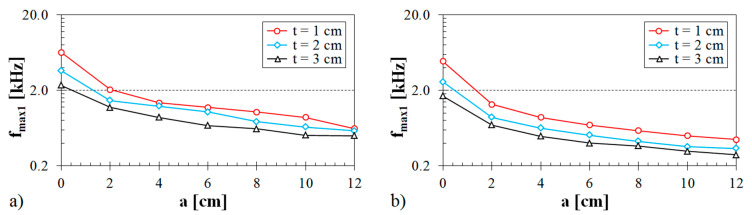
It is evident from the Equations (13) and (15) that the excitation frequencies, at which the sound absorption coefficient reaches the maximum and minimum values, decrease with an increase in the distance l and the air space size a, respectively. This phenomenon was also confirmed by the measured frequency dependencies of the sound absorption coefficient, as shown in Figure 6. Therefore, a higher air space size between the porous sample and the solid wall inside the impedance tube generally leads to improving the sound absorption behavior of porous materials in the low frequency range [68,70]. The effect of the air space size a on the primary excitation frequency fmax1, which corresponds to the primary sound absorption maxima αmax1, is depicted in Figure 7.
Figure 7.
Dependencies of the primary sound absorption maxima on the air space size at various thicknesses of the tested ABS samples: (a) Rhomboid structure, volume ratio Vr = 44%; (b) Octagonal structure, volume ratio Vr = 70%.
It can be seen that the primary excitation frequency decreased with an increase in the air space size independently of the specimen thickness. Therefore, instead of increasing the sound absorber thickness, which means adding more 3D-printed materials, increasing the air space size is more effective in terms of sound absorption.
3.1.5. Influence of Excitation Frequency
The excitation frequency of acoustic wave propagation in solids is one of the significant factors affecting the sound absorption performance of the tested 3D-printed open-porous ABS samples. As shown in Figure 3, Figure 4, Figure 5 and Figure 6, the highest values of the sound absorption coefficient were observed at certain excitation frequencies depending on the structure type, volume ratio, thickness, and air space size of the investigated 3D-printed open-porous ABS samples. The maximum values of the sound absorption coefficient αmax for each type of the ABS structure type and the corresponding excitation frequency fmax, including volume ratio, sample thickness and air space size, are shown in Table 2.
Table 2.
Maximum values of the sound absorption coefficient and their corresponding excitation frequency, volume ratio, sample thickness and air space size for the investigated ABS samples with different structure types.
| Structure Type |
αmax (−) |
fmax (Hz) |
Vr (%) |
t (cm) |
a (cm) |
|---|---|---|---|---|---|
| Cartesian | 0.999959 | 3736 | 70 | 3 | 6 |
| Octagonal | 0.999995 | 3488 | 70 | 3 | 8 |
| Rhomboid | 0.999763 | 1728 | 70 | 3 | 10 |
| Starlit | 0.999937 | 3920 | 70 | 2 | 10 |
It is obvious that the absorption maxima were generally obtained for the ABS samples that were produced with the highest volume ratio and higher sample thickness and were located at a greater distance from the solid wall inside the acoustic impedance tube. It is also evident from Figure 3, Figure 4, Figure 5 and Figure 6 that the sound absorption properties of the ABS samples were poor at low frequencies, which is a common property of porous materials [71,72].
3.2. Noise Reduction Coefficient
As stated above, the excitation frequency of acoustic wave propagation in solids has a substantial effect on the sound absorption performance. Therefore, the noise reduction coefficient, which is defined by Equation (3), was introduced in order to describe an average sound absorption performance of tested sound absorbing materials. This section deals with different factors affecting the noise reduction coefficient of the investigated 3D-printed open-porous ABS materials.
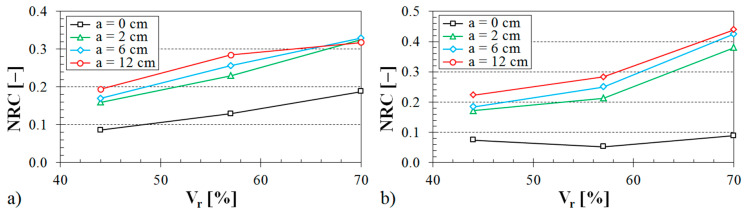
3.2.1. Influence of Air Space Size
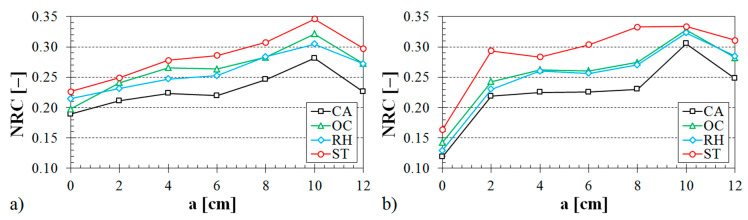
The influence of the air space size between the tested sample and the solid wall inside the impedance tube on the noise reduction coefficient is shown in Figure 8, Figure 9 and Figure 10.
Figure 8.
Influence of the 3D-printed ABS material structure on the noise reduction coefficient vs. air space size for the tested ABS samples: (a) volume ratio Vr = 44%, sample thickness t = 3 cm; (b) volume ratio Vr = 57%, sample thickness t = 2 cm.
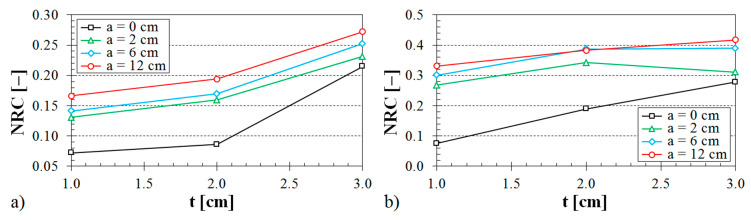
Figure 9.
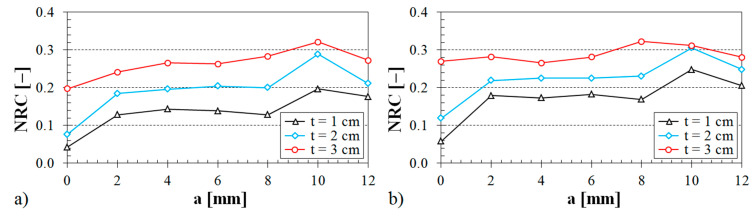
Influence of the material thickness on the noise reduction coefficient vs. air space size for the tested ABS samples: (a) Octagonal structure, volume ratio Vr = 44%; (b) Cartesian structure, volume ratio Vr = 57%.
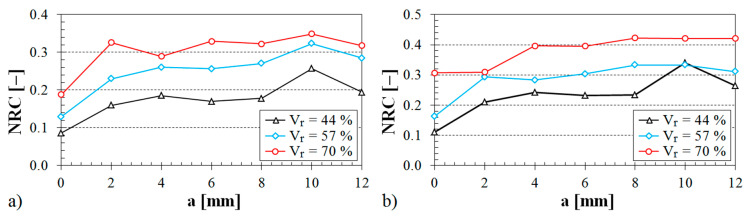
Figure 10.
Influence of the volume ratio on the noise reduction coefficient vs. air space size for the tested ABS samples: (a) Rhomboid structure, sample thickness t = 2 cm; (b) Starlit structure, sample thickness t = 1 cm.
The influence of the structure type on the sound absorption behavior is shown in Figure 8. It is obvious from this evaluation that the specimens made from the ABS material with the Starlit structure had higher values of the noise reduction coefficient independently of the air space size. Therefore, these samples made with the Starlit structure showed a better capability to dampen noise in comparison with other structure types. Conversely, the lowest values of the noise reduction coefficient were obtained for the samples that were prepared with the Cartesian structure. It was also found from the dependencies of the noise reduction coefficient on the air space size that the sample thickness (see Figure 9) and the volume ratio (see Figure 10) have a positive effect on the sound absorption behavior of the investigated ABS samples.
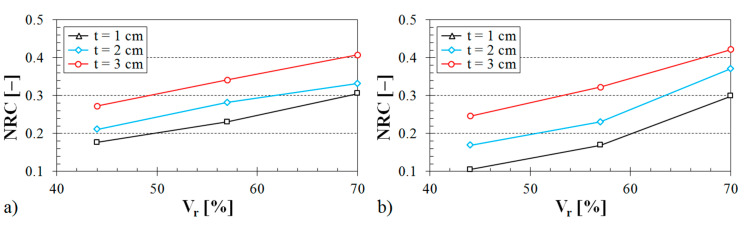
3.2.2. Influence of Material Thickness
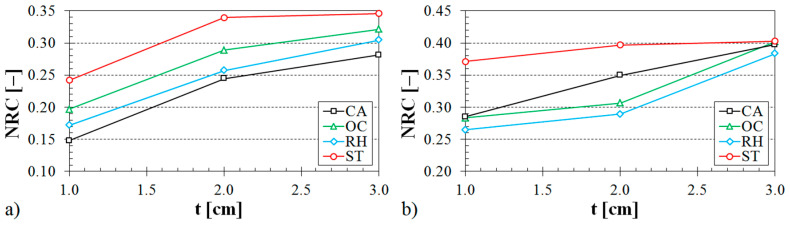
The influence of the ABS sample thickness on the noise reduction coefficient is demonstrated in Figure 11, Figure 12 and Figure 13.
Figure 11.
Influence of the 3D-printed ABS material structure on the noise reduction coefficient vs. material thickness for the investigated ABS samples: (a) volume ratio Vr = 44%, air space size a = 10 cm; (b) volume ratio Vr = 70%, air space size a = 4 cm.
Figure 12.
Influence of the air space size on the noise reduction coefficient vs. material thickness for the investigated ABS samples: (a) Rhomboid structure, volume ratio Vr = 44%; (b) Cartesian structure, volume ratio Vr = 70%.
Figure 13.
Influence of the volume ratio on the noise reduction coefficient vs. material thickness for the investigated ABS samples: (a) Octagonal structure, air space size a = 12 cm; (b) Starlit structure, air space size a = 4 cm.
It is evident (see Figure 11) that the samples made with the Starlit structure exhibited better sound absorption characteristics compared to the samples produced with Octagonal, Rhomboid, and Cartesian structures. It was also found that the noise reduction coefficient generally increased with an increase in the air space size (see Figure 12), the volume ratio (see Figure 13), and the ASB sample thickness (see Figure 11, Figure 12 and Figure 13).
3.2.3. Influence of Volume Ratio
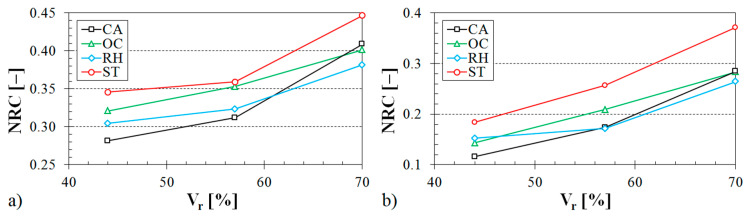
The influence of the ABS volume ratio on the noise reduction coefficient is depicted in Figure 14, Figure 15 and Figure 16.
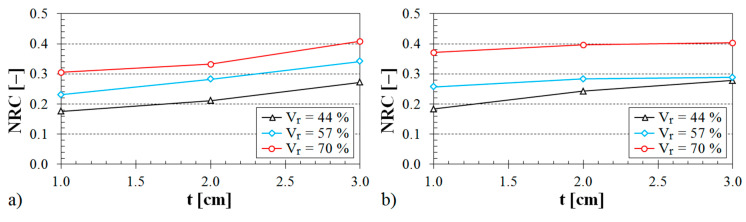
Figure 14.
Influence of the 3D-printed ABS material structure on the noise reduction coefficient vs. volume ratio for the investigated ABS samples: (a) sample thickness t = 3 cm, air space size a = 10 cm; (b) sample thickness t = 1 cm, air space size a = 4 cm.
Figure 15.
Influence of the air space size on the noise reduction coefficient vs. volume ratio for the investigated ABS samples: (a) Rhomboid structure, sample thickness t = 2 cm; (b) Starlit structure, sample thickness t = 1 cm.
Figure 16.
Influence of the sample thickness on the noise reduction coefficient vs. volume ratio for the investigated ABS samples: (a) Cartesian structure, air space size a = 8 cm; (b) Octagonal structure, air space size a = 12 cm.
It was found again that the Starlit-shaped specimens made from the ABS material had a higher capability to dampen noise in comparison with the other structure types (see Figure 14). It is also evident that the volume ratio (see Figure 14, Figure 15 and Figure 16), air space size (see Figure 15), and sample thickness (see Figure 16) had a positive effect on the noise reduction coefficient and, thus, on the sound absorption performance of the tested 3D-printed ABS materials.
4. Conclusions
The sound absorption performance of 3D-printed open-porous ABS samples, which were produced with Cartesian, Octagonal, Rhomboid, and Starlit structures, have been evaluated in this work. The investigated ABS samples were also produced with different volume ratios and thicknesses.
It can be concluded that the Starlit-shaped specimens made from the ABS material exhibited better sound absorption performance in comparison with the other structure types. This was caused by the more complex pore shapes of the Starlit structure, which led to a higher airflow resistivity during the propagation of acoustic waves through this porous structure and, subsequently, to a more efficient conversion from sound energy into heat. It was also found in this work that the sound absorption properties of the tested 3D-printed ABS specimens generally increased with an increase in the sample volume ratio and the material thickness. However, the increasing sample thickness generally results in higher manufacturing costs of the 3D-printed materials. Hence, this method is not effective for sound absorption. Therefore, it is more suitable to use open-porous sound absorbing materials with air spaces in order to improve the sound absorption performance of the ABS materials. Generally, the increasing air space size between the tested sample and the solid wall inside the impedance tube led to a shift of the primary sound absorption maxima to lower excitation frequencies. For this reason, increasing the air space size is suitable for damping of low-frequency acoustic waves. The above findings were also confirmed by the noise reduction coefficient, which expresses an average sound absorption performance of the investigated materials independently of the excitation frequency.
In future work, it is possible to develop and optimize new 3D printing open-porous materials (e.g., more complex pore shapes and advanced multilayer 3D-printed structures) in order to increase acoustic absorption efficiency in a wide frequency range.
Acknowledgments
The authors would like to thank the Ministry of Education, Science, Research, and Sport of the Slovak Republic for its direct support of this research through the projects APVV-19-0550, KEGA 007TUKE-4/2018, VEGA 1/0812/21 and KEGA 005TUKE-4/2021, as well as the European Regional Development Fund in the Research Centre of Advanced Mechatronic Systems for its financial support of this research through the project number CZ.02.1.01/0.0/0.0/16_019/0000867 within the Operational Programme Research, Development, and Education.
Author Contributions
Conceptualization, K.M. and M.V.; methodology, K.M. and M.V.; software, M.V. and K.M.; validation, P.P.M.; formal analysis, P.P.M.; investigation, M.V.; resources, J.V. and D.K.; data curation, J.V. and D.K.; writing—original draft preparation, M.V. and K.M.; writing—review and editing, D.K.; visualization, P.P.M.; supervision, M.V. and K.M.; project administration, K.M. and M.V.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education, Science, Research, and Sport of the Slovak Republic through the projects APVV-19-0550 and KEGA 007TUKE-4/2018, as well as with direct support of the European Regional Development Fund in the Research Centre of Advanced Mechatronic Systems project, project number CZ.02.1.01/0.0/0.0/16_019/0000867 within the Operational Programme Research, Development and Education.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- 1.Amares S., Sujatmika E., Hong T.W., Durairaj R., Hamid H.S.H.B. A Review: Characteristics of Noise Absorption Material. J. Phys. Conf. Ser. 2017;908:012005. doi: 10.1088/1742-6596/908/1/012005. [DOI] [Google Scholar]
- 2.Lee B.H., Cha S.W., Kang Y.J. Study of Sound Absorption and Transmission Characteristics for MCPs Foaming Rate by Batch Process. Proc. KSPE. 2004:338–342. [Google Scholar]
- 3.Lee W.K., Park B.H., Yoon H.J., Kim J.S., Maeng J.Y. The Optimization of Interior Acoustic Package of Vehicle Using the Sound Absorbing Materials. Korean Soc. Automot. Eng. 2004;2:1212–1217. [Google Scholar]
- 4.Tang S.K. Improving Traffic Noise Transmission Loss of Plenum Windows by Using Sound Scatterer Arrays. J. Acoust. Soc. Am. 2018;143:1715. doi: 10.1121/1.5035587. [DOI] [Google Scholar]
- 5.Yang M., Chen S., Fu C., Sheng P. Optimal Sound-Absorbing Structures. Mater. Horiz. 2017;4:673. doi: 10.1039/C7MH00129K. [DOI] [Google Scholar]
- 6.Allard J.F., Atalla N. Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials. 2nd ed. John Wiley & Sons; Chichester, UK: 2009. [Google Scholar]
- 7.Sun X., Jiang F., Wang J. Acoustic Properties of 316L Stainless Steel Lattice Structures Fabricated via Selective Laser Melting. Metals. 2020;10:111. doi: 10.3390/met10010111. [DOI] [Google Scholar]
- 8.Yoon W.U., Park J.H., Lee J.S., Kim Y.Y. Topology Optimization Design for Total Sound Absorption in Porous Media. Comput. Methods Appl. Mech. Eng. 2020;360:112723. doi: 10.1016/j.cma.2019.112723. [DOI] [Google Scholar]
- 9.Liu G.-S., Zhou Y., Liu M.-H., Yuan Y., Zou X.-Y., Cheng J.-C. Acoustic Waveguide with Virtual Soft Boundary Based on Metamaterials. Sci. Rep. 2020;10:981–987. doi: 10.1038/s41598-020-57986-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Assouar M.B., Senesi M., Oudich M., Ruzzene M., Hou Z. Broadband Plate-Type Acoustic Metamaterial for Low-Frequency Sound Attenuation. Appl. Phys. Lett. 2012;101:173505. doi: 10.1063/1.4764072. [DOI] [Google Scholar]
- 11.Mei J., Ma G., Yang M., Yang Z.Y., Wen W., Sheng P. Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat. Commun. 2012;3:756. doi: 10.1038/ncomms1758. [DOI] [PubMed] [Google Scholar]
- 12.Xin F., Ma X., Liu X., Zhang C. A Multiscale Theoretical Approach for the Sound Absorption of Slit-Perforated Double Porosity Materials. Compos. Struct. 2019;223:110919. doi: 10.1016/j.compstruct.2019.110919. [DOI] [Google Scholar]
- 13.Siano D., Viscardi M., Panza M.A. Automotive Materials: An Experimental Investigation of an Engine Bay Acoustic Performances. Energy Procedia. 2016;101:598–605. doi: 10.1016/j.egypro.2016.11.076. [DOI] [Google Scholar]
- 14.Vakhitova S.M., Shaehova I.F., Zharin E.I. IOP Conference Series: Materials Science and Engineering. IOP Publishing; Bristol, UK: 2016. Study of Vibro-Acoustic Properties of Composite Materials Based on Polyurethane Injection; p. 012030. [Google Scholar]
- 15.Cai X., Yang J., Hu G., Lu T. Sound Absorption by Acoustic Microlattice with Optimized Pore Configuration. J. Acoust. Soc. Am. 2018;144:EL138–EL143. doi: 10.1121/1.5051526. [DOI] [PubMed] [Google Scholar]
- 16.Deshmukh S., Ronge H., Ramamoorthy S. Design of Periodic Foam Structures for Acoustic Applications: Concept, Parametric Study and Experimental Validation. Mater. Des. 2019;175:107830. doi: 10.1016/j.matdes.2019.107830. [DOI] [Google Scholar]
- 17.Wang D.-W., Wen Z.-H., Glorieux C., Ma L. Sound Absorption of Face-Centered Cubic Sandwich Structure With Micro-Perforations. Mater. Des. 2020;186:108344. doi: 10.1016/j.matdes.2019.108344. [DOI] [Google Scholar]
- 18.Jiménez N., Romero-García V., Groby J.-P. Perfect Absorption of Sound by Rigidly-Backed Hight-Porous Materials. Acta Acust. Acust. 2018;104:396–409. [Google Scholar]
- 19.Liu J., Chen T., Zhang Y., Wen G., Qing Q., Wang H., Sedaghati R., Xie Y.M. On Sound Insulation of Pyramidal Lattice Sandwich Structure. Compos. Struct. 2019;208:385–394. doi: 10.1016/j.compstruct.2018.10.013. [DOI] [Google Scholar]
- 20.Pantazopoulos G. A Short Review on Fracture Mechanisms of Mechanical Components Operated under Industrial Process Conditions: Fractographic Analysis and Selected Prevention Strategies. Metals. 2019;9:148. doi: 10.3390/met9020148. [DOI] [Google Scholar]
- 21.Olny X., Boutin C. Acoustic Wave Propagation in Double Porosity Media. J. Acoust. Soc. Am. 2003;114:73–89. doi: 10.1121/1.1534607. [DOI] [PubMed] [Google Scholar]
- 22.Roh H.-S., Yoon S.W. Acoustic Diagnosis for Porous Medium With Circular Cylindrical Pores. J. Acoust. Soc. Am. 2004;115:1114–1124. doi: 10.1121/1.1645247. [DOI] [PubMed] [Google Scholar]
- 23.Lagarrigue C., Groby J.P., Tournat V., Dazel O., Umnova O.V. Absorption of Sound by Porous Layers with Embedded Periodic Arrays of Resonant Inclusions. J. Acoust. Soc. Am. 2013;134:4670–4680. doi: 10.1121/1.4824843. [DOI] [PubMed] [Google Scholar]
- 24.Groby J.-P., Lagarrigue C., Brouard B., Dazel O., Tournat V., Nennig B. Using Simple Shape Three-Dimensional Rigid Inclusions to Enhance Porous Layer Absorption. J. Acoust. Soc. Am. 2014;136:1139–1148. doi: 10.1121/1.4892760. [DOI] [PubMed] [Google Scholar]
- 25.Xu Y., Zhao W., Chen L., Chen H. Distribution Optimization for Acoustic Design of Porous Layer by the Boundary Element Method. Acoust. Aust. 2020;48:1–13. doi: 10.1007/s40857-020-00181-7. [DOI] [Google Scholar]
- 26.Boulvert J., Cavalieri T., Costa-Baptista J., Schwan L., Romero-García V., Gabard G., Fotsing E., Ross A., Mardjono J., Groby J.-P. Optimally Graded Porous Material for Broadband Perfect Absorption of Sound. J. Appl. Phys. 2019;126:175101. doi: 10.1063/1.5119715. [DOI] [Google Scholar]
- 27.Krödel S., Palermo A., Daraio C. Acoustic Properties of Porous Microlattices From Effective Medium to Scattering Dominated Regimes. J. Acoust. Soc. Am. 2018;144:319–329. doi: 10.1121/1.5046068. [DOI] [PubMed] [Google Scholar]
- 28.Gohari H.D., Zarastvand M., Talebitooti R. Acoustic Performance Prediction of a Multilayered Finite Cylinder Equipped with Porous Foam Media. J. Vib. Control. 2020;26:899–912. doi: 10.1177/1077546319890025. [DOI] [Google Scholar]
- 29.Jena D.P., Qiu X. Sound Transmission Loss of Porous Materials in Ducts With Embedded Periodic Scatterers. J. Acoust. Soc. Am. 2020;147:978–983. doi: 10.1121/10.0000650. [DOI] [PubMed] [Google Scholar]
- 30.Song B.H., Bolton J.S. A Transfer-Matrix Approach for Estimating the Characteristic Impedance and Wave Numbers of Limp and Rigid Porous Materials. J. Acoust. Soc. Am. 2000;107:1131–1152. doi: 10.1121/1.428404. [DOI] [PubMed] [Google Scholar]
- 31.Munjal M.L. Acoustics of Ducts and Mufflers. 2nd ed. John Wiley & Sons; New York, NY, USA: 2014. [Google Scholar]
- 32.Kang Y.J., Bolton J.S. A Finite Element Model for Sound Transmission Through Foam-Lined Double-Panel Structures. J. Acoust. Soc. Am. 1996;99:2755. doi: 10.1121/1.414856. [DOI] [Google Scholar]
- 33.Panneton R. Numerical Prediction of Sound Transmission Through Finite Multilayer Systems with Poroelastic Materials. J. Acoust. Soc. Am. 1996;100:346. doi: 10.1121/1.415956. [DOI] [Google Scholar]
- 34.Xie S., Yang S., Yang C., Wang D. Sound Absorption Performance of a Filled Honeycomb Composite Structure. Appl. Acoust. 2020;162:107202. doi: 10.1016/j.apacoust.2019.107202. [DOI] [Google Scholar]
- 35.Christensen J., Romero-García V., Pico R., Cebrecos A., De Abajo F.J.G., Mortensen N.A., Willatzen M., Sánchez-Morcillo V.J. Extraordinary Absorption of Sound in Porous Lamella-Crystals. Sci. Rep. 2014;4:1–5. doi: 10.1038/srep04674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu Z., Zhan J., Fard M., Liu Z. Acoustic Properties of Multilayer Sound Absorbers With a 3d Printed Micro-Perforated Panel. Appl. Acoust. 2017;121:25–32. doi: 10.1016/j.apacoust.2017.01.032. [DOI] [Google Scholar]
- 37.Lee J.-C., Hong Y.-S., Nan R.-G., Jang M.-K., Lee C.S., Ahn S.-H., Kang Y.-J. Soundproofing Effect of Nano Particle Reinforced Polymer Composites. J. Mech. Sci. Technol. 2008;22:1468–1474. doi: 10.1007/s12206-008-0419-4. [DOI] [Google Scholar]
- 38.MacGillivray I. Acoustic Performance of Periodic Composite Materials; Proceedings of the Australian Acoustical Society; Acoustics, Hunter Valley, Australia. 15–18 November 2015. [Google Scholar]
- 39.Stanciu M.D., Curtu I., Lica D. Evaluating the Efficiency of Recycling Composite Panels Made from ABS to Reduce the Traffic Noise; Proceedings of the 5th International Conference “Computational Mechanics and Virtual Engineering—COMEC”; University of Brasov, Brasov, Romania. 24–25 October 2013; pp. 489–492. [Google Scholar]
- 40.Stanciu M.D., Curtu I., Cosereanu C., Lica D. Soundproofing Performance Evaluation of Panels Made of Fibers of Acrylonitrile Butadiene Styrene Copolymer (ABS) Procedia Technol. 2015;19:260–267. doi: 10.1016/j.protcy.2015.02.038. [DOI] [Google Scholar]
- 41.Lee J.-W., Lee J.-C., Pandey J., Ahn S.-H., Kang Y.J. Mechanical Properties and Sound Insulation Effect of ABS/Carbon-black Composites. J. Compos. Mater. 2010;44:1701–1716. doi: 10.1177/0021998309357673. [DOI] [Google Scholar]
- 42.Adair L.C., Cook R.L. Acoustic Properties of Rho-C Rubber and ABS in the Frequency Range 100-kHz-2 MHz. J. Acoust. Soc. Am. 1973;54:1763–1765. doi: 10.1121/1.1914484. [DOI] [Google Scholar]
- 43.Mamalis A.G., Manolakos D.E., Szalay A., Pantazopoulos G. Processing of High-Temperature Superconductors at High Strain Rates. Informa UK Limited; Colechester, UK: 2019. Impact Loading of Solid/Porous Media; p. 94. [Google Scholar]
- 44.Stansbury J.W., Idacavage M.J. 3D Printing With Polymers: Challenges Among Expanding Options and Opportunities. Dent. Mater. 2016;32:54–64. doi: 10.1016/j.dental.2015.09.018. [DOI] [PubMed] [Google Scholar]
- 45.Bourell D., Pierre J., Leu M., Levy G., Rosen D., Beese A.M., Clare A. Materials for Additive Manufacturing. CIRP Ann. Manuf. Technol. 2017;66:659–681. doi: 10.1016/j.cirp.2017.05.009. [DOI] [Google Scholar]
- 46.Challis V., Xu X., Zhang L., Roberts A.P., Grotowski J.F., Sercombe T.B. High Specific Strength and Stiffness Structures Produced Using Selective Laser Melting. Mater. Des. 2014;63:783–788. doi: 10.1016/j.matdes.2014.05.064. [DOI] [Google Scholar]
- 47.Hanzl P., Zetková I., Kučerová L. Structural Changes and Microstructure of Maraging Steel Lattice Structures using Additive Manufacturing. Manuf. Technol. 2019;19:37–41. doi: 10.21062/ujep/241.2019/a/1213-2489/MT/19/1/37. [DOI] [Google Scholar]
- 48.Vašina M., Monkova K., Monka P.P., Kozak D., Tkac J. Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures. Polymers. 2020;12:1062. doi: 10.3390/polym12051062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Monkova K., Monka P., Tkac J., Torok J., Suba O., Zaludek M. Research of Young’s Modulus of the Simple Lattice Structures Made from Plastics; Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE); Institute of Electrical and Electronics Engineers (IEEE), Brussels, Belgium. 22–25 July 2019; pp. 555–558. [Google Scholar]
- 50.Pantazopoulos G. Basic Principles: Some Fundamental Concepts. J. Fail. Anal. Prev. 2015;15:335–336. doi: 10.1007/s11668-015-9952-5. [DOI] [Google Scholar]
- 51.Sgard F., Castel F., Atalla N. Use of a Hybrid Adaptive Finite Element/Modal Approach to Assess the Sound Absorption of Porous Materials With Meso-Heterogeneities. Appl. Acoust. 2011;72:157–168. doi: 10.1016/j.apacoust.2010.10.011. [DOI] [Google Scholar]
- 52.Doutres O., Atalla N., Dong K. Effect of the Microstructure Closed Pore Content on the Acoustic Behavior of Polyurethane Foams. J. Appl. Phys. 2011;110:064901. doi: 10.1063/1.3631021. [DOI] [Google Scholar]
- 53.Chen S., Jiang Y., Chen J., Wang D. The Effects of Various Additive Components on the Sound Absorption Performances of Polyurethane Foams. Adv. Mater. Sci. Eng. 2015;2015:1–9. doi: 10.1155/2015/317561. [DOI] [Google Scholar]
- 54.Buratti C. Indoor Noise Reduction Index with an Open Window (Part II) Appl. Acoust. 2006;67:383–401. doi: 10.1016/j.apacoust.2005.07.006. [DOI] [Google Scholar]
- 55.Okudaira Y., Kurihara Y., Ando H., Satoh M., Miyanami K. Sound Absorption Measurements for Evaluating Dynamic Physical Properties of a Powder Bed. Powder Technol. 1993;77:39–48. doi: 10.1016/0032-5910(93)85005-T. [DOI] [Google Scholar]
- 56.International Organization for Standardization . ISO 10534-2, Acoustics-Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes-Part 2: Transfer-Function Method. CEN, European Committee for Standardization; Brussels, Belgium: 1998. pp. 10534–10542. ISO/TC 43/SC2 Building Acoustics. [Google Scholar]
- 57.Han F.S., Seiffert G., Zhao Y.Y., Gibbs B. Acoustic Absorption Behaviour of an Open-Celled Alluminium Foam. J. Phys. D. Appl. Phys. 2003;36:294–302. doi: 10.1088/0022-3727/36/3/312. [DOI] [Google Scholar]
- 58.Yilmaz N.D., Powell N.B., Banks-Lee P., Michielsen S., Yilmaz N.D. Hemp-Fiber Based Nonwoven Composites: Effects of Alkalization on Sound Absorption Performance. Fibers Polym. 2012;13:915–922. doi: 10.1007/s12221-012-0915-0. [DOI] [Google Scholar]
- 59.Schiavi A., Guglielmone C., Miglietta P. Effect and Importance of Static-Load on Airflow Resistivity Determination and Its Consequences on Dynamic Stiffness. Appl. Acoust. 2011;72:705–710. doi: 10.1016/j.apacoust.2011.03.009. [DOI] [Google Scholar]
- 60.Tarnow V. Measured Anisotropic Air Flow Resistivity and Sound Attenuation of Glass Wool. J. Acoust. Soc. Am. 2002;111:2735–2739. doi: 10.1121/1.1476686. [DOI] [PubMed] [Google Scholar]
- 61.McRae J.D., Naguib H.E., Atalla N. Mechanical and Acoustic Performance of Compression-Molded Open-Cell Polypropylene Foams. J. Appl. Polym. Sci. 2009;116:1106–1115. doi: 10.1002/app.31581. [DOI] [Google Scholar]
- 62.Tiuc A.E., Vasile O., Usca A.D., Gabor T., Vermesan H. The Analysis of Factors That Influence the Sound Absorption Coefficient of Porous Materials. Rom. J. Acoust. Vib. 2014;11:105–108. [Google Scholar]
- 63.Zhu W.B., Chen S.M., Wang Y.B., Zhu T.T., Jiang Y. Sound Absorption Behavior of Polyurethane Foam Composites with Different Ethylene Propylene Diene Monomer Particles. Arch. Acoust. 2018;43:403–411. [Google Scholar]
- 64.Ayrilmis N., Kariz M., Kwon J.H., Manja K. Effect of Printing Layer Thickness on Water Absorption and Mechanical Properties of 3d-Printed Wood/PLA Composite Materials. Int. J. Adv. Manuf. Technol. 2019;102:2195–2200. doi: 10.1007/s00170-019-03299-9. [DOI] [Google Scholar]
- 65.Domínguez-Rodríguez G., Ku-Herrera J.J., Hernández-Pérez A. An Assessment of the Effect of Printing Orientation, Density, and Filler Pattern on the Compressive Performance of 3d Printed ABS Structures by Fuse Deposition. Int. J. Adv. Manuf. Technol. 2017;95:1685–1695. doi: 10.1007/s00170-017-1314-x. [DOI] [Google Scholar]
- 66.Baich L., Manogharan G., Marie H. Study of Infill Print Design on Production Cost-Time of 3d Printed ABS Parts. Int. J. Rapid Manuf. 2015;5:308. doi: 10.1504/IJRAPIDM.2015.074809. [DOI] [Google Scholar]
- 67.Everest F.A. Master Handbook of Acoustics. 4th ed. McGraw-Hill; New York, NY, USA: 2001. Absorption of Sound; pp. 179–233. [Google Scholar]
- 68.Nor M.J.M., Jamaludin N., Tamiri F.M. A Preliminary Study of Sound Absorption Using Multi-Layer Coconut Coir Fibers. Electron. J. Tech. Acoust. 2004;3:1–8. [Google Scholar]
- 69.Hua Q., Yang E.H. Effect of Thickness, Density and Cavity Depth on the Sound Absorption Properties of Wool Boards. Autex Res. J. 2018;18:203–208. [Google Scholar]
- 70.Lim Z., Putra A., Nor M., Yaakob M. Sound Absorption Performance of Natural Kenaf Fibres. Appl. Acoust. 2018;130:107–114. doi: 10.1016/j.apacoust.2017.09.012. [DOI] [Google Scholar]
- 71.Ismail L., Ghazali M.I., Mahzan S., Zaidi A.M.A. Sound Absorption of Arenga Pinnata Natural Fiber. World Acad. Sci. Eng. Technol. 2010;43:804–806. [Google Scholar]
- 72.Gliscinska E., Michalak M., Krucinska I. Sound Absorption Property of Nonwowen Based Composites. Autex Res. J. 2013;13:150–155. doi: 10.2478/v10304-012-0036-2. [DOI] [Google Scholar]