Evolution of Generalists by Phenotypic Plasticity

Summary

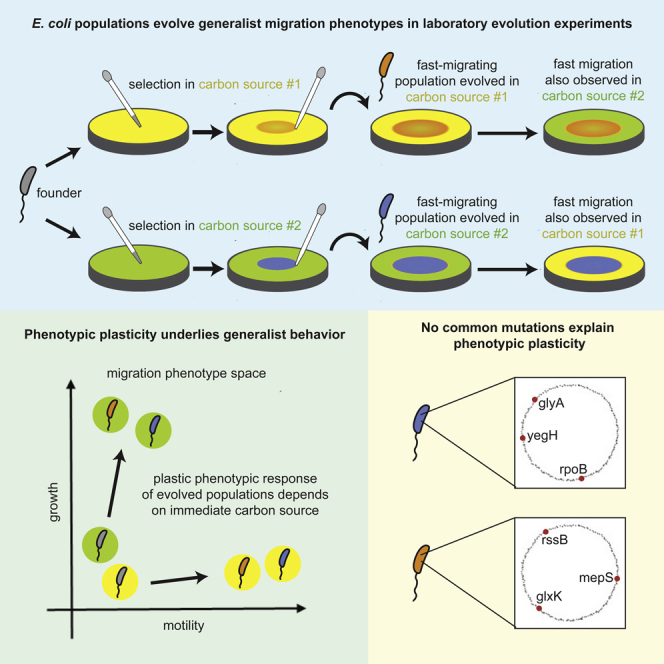
Adapting organisms face a tension between specializing their phenotypes for certain ecological tasks and developing generalist strategies that permit persistence in multiple environmental conditions. Understanding when and how generalists or specialists evolve is an important question in evolutionary dynamics. Here, we study the evolution of bacterial range expansions by selecting Escherichia coli for faster migration through porous media containing one of four different sugars supporting growth and chemotaxis. We find that selection in any one sugar drives the evolution of faster migration in all sugars. Measurements of growth and motility of all evolved lineages in all nutrient conditions reveal that the ubiquitous evolution of fast migration arises via phenotypic plasticity. Phenotypic plasticity permits evolved strains to exploit distinct strategies to achieve fast migration in each environment, irrespective of the environment in which they were evolved. Therefore, selection in a homogeneous environment drives phenotypic plasticity that improves performance in other environments.

Graphical Abstract

Highlights

• •Bacteria evolve fast migration in porous media by adapting growth and motility
• •Selection in one nutrient condition results in fast migration in other conditions
• •Fast migrating generalists evolve by plasticity in growth and motility
• •Selection in homogeneous environments can evolve generalist phenotypes

Microbiology; Evolutionary Biology; Evolutionary Mechanisms

Introduction

Organisms in nature often encounter varied environments throughout their lifetimes, each with its own demands on the phenotype. Therefore, the ability of a single genotype to thrive under different environmental conditions can be essential for a lineage's chance of long-term persistence. Organisms that can thrive in varied environments are called generalists. It is thought that generalists evolve in fluctuating environments, while fixed environments select for specialists (Kassen, 2002). In its native environment, a specialist is expected to have enhanced fitness relative to a generalist but reduced fitness in other environments (Elena and Lenski, 2003).

However, the results of experimental evolution studies show remarkably diverse outcomes. While trade-offs are sometimes observed (Cooper and Lenski, 2000), they are far from universal: studies with a constant selection environment (which are expected to produce specialists) often produce a mixture of specialists and generalists across replicate lineages (Velicer and Lenski, 1999). Additionally, trade-offs observed in experimental evolution are sometimes asymmetric: studies employing multiple selection conditions may produce specialists in one condition and generalists in another (Lee et al., 2009; Travisano, 1997). Other studies find that a majority of evolved lines are generalists, even with selection performed in a constant environment (Ostrowski et al., 2005; Fong et al., 2005).

A key question that emerges from these studies is understanding the limits and mechanisms of the evolution of phenotypic generality. Experiments suggest that generalists will only show enhanced fitness in environments that are sufficiently similar to their selection condition (Travisano et al., 1995; Travisano and Lenski, 1996). While this notion is intuitive, there are distinct avenues of phenotypic adaptation that could give rise to generalist phenotypes. An experimentally supported interrogation of the conditions under which generalists evolve, the environmental limits of their generality, as well as its underlying genotypic and phenotypic mechanisms, would shed light on how populations deploy phenotypic variation during adaptation (Pigliucci, 2001).

To address this, we selected Escherichia coli for faster migration through porous media with one of four different sugars as a carbon source and chemoattractant. We observed the evolution of generalists: selection for fast migration in any one sugar resulted in fast migration in all sugars. Because migration depends on both growth and motility, we measured these phenotypes for strains from each evolutionary history in all four nutrient conditions to investigate the evolution of migration rate generality. We found that the environment determined the phenotype more than the evolutionary history: strains from all selection conditions exhibited a distinct growth and motility phenotype for each assay condition irrespective of their evolutionary history. That is, all strains observed in a particular environment showed similar adaptation of growth and motility regardless of their selection condition. Because the evolved strains in this study exhibit different phenotypes depending on their environment and because those phenotypes are associated with faster migration, we conclude that generalists evolved in our experiment via phenotypic plasticity (Scheiner, 1993).

Results

Selection Enhances Migration of Bacterial Populations through Soft Agar

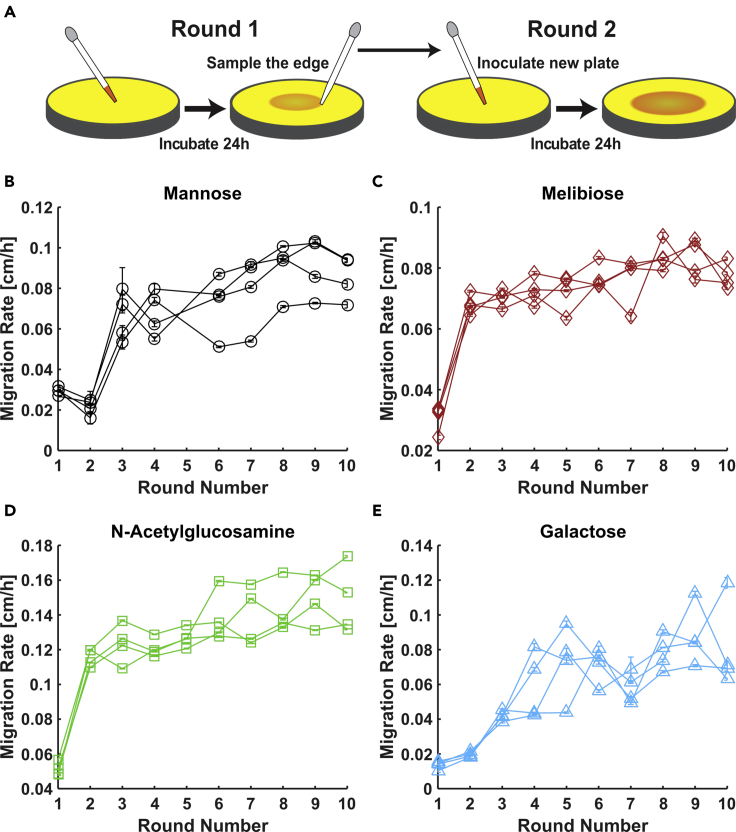
E. coli inoculated into low-viscosity agar depletes nutrients locally, as cells swim and divide in the porous, three-dimensional environment. This depletion establishes a nutrient gradient that drives chemotaxis outward and subsequent growth of the population (Adler, 1966; Wolfe and Berg, 1989). The result is a macroscopic colony that expands radially from the site of inoculation at a speed determined by growth, motility, and chemotaxis of its constituent cells (Croze et al., 2011). We performed time-lapse imaging on these colonies and observed an initial growth phase followed by radial expansion at a constant rate (Figure S1).

We performed experimental evolution by selecting E. coli for faster migration through soft agar. From a single ancestral strain (MG1655-motile, Coli Genetic Stock Center #8237), we performed selection for faster migration in M63 minimal medium with 0.2% w/v agar and one of four different sugars as carbon sources at 1 mM concentration: mannose, melibiose, N-acetylglucosamine (NAG), and galactose. After allowing a population to expand for 24 hr, we selected a small population of cells from the outermost edge of the colony and used these cells to inoculate a new low-viscosity agar plate (Figure 1A). This process of expansion and selection was repeated for ten rounds. In each condition, the sugar served as the sole energy source and chemoattractant for the expanding population. We chose these four sugars because we believed that the diverse set of genetic architectures involved in their chemotaxis, import, and metabolism could lead to diverse opportunities for genomic evolution and resultant phenotypic adaptation in each condition. All four sugars traverse the outer membrane through OmpF, but mannose and NAG use phosphotransferase systems to cross the inner membrane while melibiose and galactose rely on cation symporters MelB and GalP (Travisano and Lenski, 1996; Yazyu et al., 1984; Henderson et al., 1977). Once inside the cell, catabolism of NAG and galactose is regulated by repression from NagC and GalR/GalS (Plumbridge, 1991; Weickert and Adhya, 1993). Alternatively, melibiose catabolism is regulated by activation from MelR (Bourgerie et al., 1997) and mannose catabolism does not have a specific inducer, requiring only the global regulator cyclic AMP receptor protein to signal glucose starvation (Fraser and Yamazaki, 1980).

Figure 1.

Repeated Selection Enhances E. Coli Migration through Soft Agar in Four Nutrient Conditions

(A) Schematic of migration selection procedure. Motile E. coli is inoculated into the bulk of a soft agar plate containing growth medium. Nutrient consumption and chemotaxis drive the growing population to expand radially across the plate at a constant migration rate. After a fixed interval, cells are sampled from the edge of the expanding colony and used to inoculate a new plate.

(B–E) Migration rates as a function of round of selection for experiments conducted in 0.2% w/v agar plates containing M63 minimal medium with one of four different carbon sources at 1 mM concentration: (B) mannose, (C) melibiose, (D) N-acetylglucosamine, and (E) galactose. Four replicate experiments were carried out to 10 rounds in each condition. Migration rates are measured by time-lapse imaging of expanding colonies followed by linear fit of colony radius versus time; error bars are 95% confidence intervals on fitted rates. No rates are reported for round 5 in mannose due to failure of the imaging device. See Transparent Methods for details of selection procedure and migration rate measurement.

See also Figure S1.

Across all four conditions, we observed a dramatic enhancement of migration rates due to selection. Migration rates of all lineages in melibiose and NAG more than doubled after just one round of selection (Figures 1C and 1D), while similar improvement in mannose and galactose was achieved after two rounds of selection (Figures 1B and 1E). The reason for the small drop in migration rates between rounds 1 and 2 in mannose is not known but might be due to the different growth history of the cells used at the beginning or rounds 1 and 2 (liquid culture and agar plates, respectively). In all four conditions, migration rates continued to improve from round 2 to round 10, albeit modestly compared to the initial increase. In round 10, migration rates had increased almost threefold in mannose and NAG, 2.5-fold in melibiose, and nearly 6-fold in galactose.

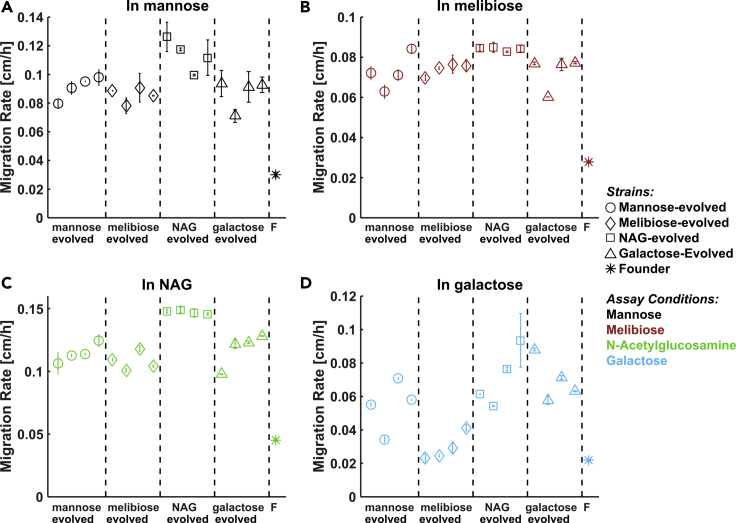
Selection for Fast Migration in One Sugar Results in Fast Migration in all Sugars

We asked whether migration rate evolution was specific to each selection condition or whether strains evolved in one sugar were adapted for fast migration in other sugars as well. Therefore, we measured the migration rates of evolved strains in all nutrient conditions. Specifically, the migration rates were measured for four independent replicate lineages from each selection condition (a total of 16 strains) in each of the four different assay conditions (mannose, melibiose, NAG, and galactose). Surprisingly, nearly all strains exhibited enhanced migration across all conditions relative to the founding strain in that condition (Figure 2). For example, a strain evolved for fast migration in NAG (squares, Figure 2) also exhibited faster migration than the ancestral strain in all three of the other sugars. Migration rates of non-native strains (that is, populations assayed in a condition different from their selection condition) were nearly always much greater than the ancestor's migration rate, often comparable to or exceeding the natively evolved populations' migration rates. The non-native populations exhibit fast migration, despite having no evolutionary history in that nutrient condition. The objective of this study therefore became to understand how selection in one nutrient environment generically gives rise to fast migration in all nutrient environments.

Figure 2.

Nutrient Generality of Migration Rate Evolution

The 16 strains isolated after 10 rounds of selection (four from each nutrient condition, Figures 1B–1E) were assayed for enhanced migration rate in each of the four nutrient conditions used for the selection experiments: (A) mannose, (B) melibiose, (C) NAG and (D) galactose. Migration rates of evolved strains are presented as mean ± standard error of two replicate plates for each strain in each condition, except as noted below. Marker shapes denote selection condition; marker colors denote assay condition (legend). Migration rates of the founding strain (F) in each condition are presented as mean ± standard error of 3–4 replicate plates in each condition. For the following exceptions, error bars are standard error on migration rate from a single plate: The rightmost NAG-evolved strain and leftmost gal-evolved strain had only one usable plate in in NAG (C). For the rightmost two galactose-evolved strains in galactose (D), rates are reproduced from round 10 of the selection experiments (Figure 1E). See also Figures S2 and S3 and Table S1.

To probe the limits of the observed phenotypic generality, we first measured the migration rates of the ancestor as well as two evolved strains from each selection condition in seven additional nutrient environments beyond the initial four: arabinose, dextrose, fructose, lactose, maltose, rhamnose, and sorbitol. Again, we found that nearly all the strains showed enhanced migration rates relative to the ancestral strain across all these conditions (Table S1). The evolved strains typically migrated 1.5- to 3-fold faster than the ancestor. We concluded that the nutrient generality of migration rate selection extends to many different carbon sources within the regime of M63 medium with 0.2% w/v agar and 1 mM sugar. In contrast, migration rates of all 16 evolved strains presented in Figure 2 did not exhibit fast migration in lysogeny broth (LB) rich medium and instead exhibited a drop in migration rate relative to the ancestor (Figure S2). For comparison, we also measured three independently evolved strains isolated after 10 rounds of selection in LB and found that they migrate around 50% faster than the ancestor (Figure S3). So, while repeated selection still enhances migration in LB, the generality of the strains evolved in minimal medium does not extend to this rich medium where chemotaxis and growth are driven by amino acids (Adler, 1966).

What Makes a Generalist?

We next set out to understand how phenotypes evolved under selection for fast migration in one sugar give rise to fast migration in other sugars. Population-level migration through soft agar depends on both growth and motility of individual cells. Therefore, selection for faster migration can be driven by enhancements to growth rate, chemotactic response, and undirected motility (Croze et al., 2011; Fraebel et al., 2017). For example, increases in running speed or tumble frequency are known to drive faster migration through soft agar (Ni et al., 2017). We therefore asked what phenotypic changes permit a lineage selected on one sugar to migrate more rapidly than the ancestral population in another sugar (Figure 2).

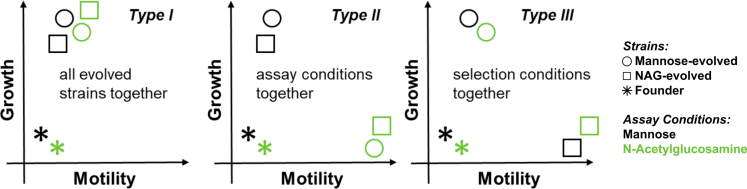
To understand why strains from distinct evolutionary histories (selection conditions) show enhanced migration across different environments (assay conditions), we considered the growth and motility of each evolved strain in each assay condition. For the present discussion, we considered growth and motility as abstract traits, but our hypotheses do not depend on the number or identity of the traits considered. In this framework, we proposed that there are three main possibilities for how the generality of fast migration could evolve (Figure 3).

Figure 3.

Hypothesized Modes of Evolution of Migration Rate Generality

We propose three distinct possibilities for the underlying phenotypic basis of the nutrient generality of migration rate adaptation presented in Figure 2. Type I (universality): All evolved strains show the same adaptation from founder across all assay conditions. There is no separation of evolved phenotypes in the two-dimensional phenotypic space of motility and growth. Type II (plasticity): Evolved strains exhibit a flexible adapted state. Evolved strains show a characteristic adaptation for each assay condition, regardless of their evolutionary history. Phenotypes separate by assay condition (marker color). Type III (degeneracy): Evolved strains display a characteristic phenotype for each evolutionary history, regardless of assay condition. Phenotypes separate by selection condition (marker shape).

Type I: Universal Adaptation

Neither the selection condition nor the assay condition has an impact on the evolved phenotype. Instead, there is a single phenotype conferring fast migration through 0.2% w/v agar and 1 mM sugar, irrespective of any differences in import, metabolism, and chemotactic affinity between different sugars. Evolved strains could achieve this phenotype across all selection conditions. Generality would then be achieved as long as evolved strains exhibit the adapted phenotype across different assay conditions. For example, the evolved strains could have achieved a growth rate adaptation that does not depend on the specific sugar, allowing them to grow rapidly (and thereby exhibit fast migration) in all 1 mM sugar assay conditions, or they could exhibit a change in run-tumble statistics which confer a migration rate advantage in soft agar. However, “type I” generality need not be this simple. The ideal phenotype could be a particular combination of growth and motility enhancements, corresponding to a distinct direction away from founder in the two-dimensional space of phenotypes. The key feature of “type I” generality is that there is no separation of evolved phenotypes by either selection condition or assay condition. Instead there is a single, universal phenotype that is achieved by all evolved strains in all conditions (Figure 3).

Type II: Phenotypic Plasticity

In each sugar, there exists a distinct growth/motility phenotype conferring fast migration. The adaptive value of growth or motility can easily depend on the assay condition. For example, in a condition that supports slow growth of the ancestral strain, increases in growth may confer a greater advantage compared to motility. These differences could also arise at the molecular level due to differences in import, metabolism, and chemotactic affinity for each sugar. In this scenario, generality would emerge if evolved strains exhibit the different adapted phenotypes for each assay condition, irrespective of their selection condition. This would mean that selection acts to put evolved populations in a plastic, adaptive state. Once in this state, cells could adapt their phenotype to the particular balance of growth and motility needed to enhance migration in different environments. We refer this mechanism for evolving generalists as “plasticity” because it requires that the same genotype (evolved strain) and exhibits distinct phenotypes (growth/motility) in different nutrient conditions. In this situation, a strain's phenotype is determined more by its assay condition than selection condition. Graphically, this would mean that the evolved phenotypes separate by assay condition (Figure 3). For example, if evolved strains across different evolutionary histories showed enhanced growth in mannose but enhanced motility in NAG, we would conclude that the nutrient generality of migration rate evolution was achieved through phenotypic plasticity.

Type III: Degeneracy

There is a degenerate set of distinct phenotypes which all confer faster migration on the evolved strains in all assay conditions. Suppose that there is a distinct method of adaptation associated with each selection condition and evolved populations exhibit these different adaptations in all assay conditions. Generality would be possible in this case as long as different growth and motility phenotypes could produce similar migration rates in a particular environment. In this sense, the evolved phenotypes would be degenerate at the level of migration rate. Graphically, this would correspond to the case where evolved phenotypes separate by selection condition (Figure 3). For example, if mannose-evolved strains enhance growth in all environments, while strains evolved in NAG enhance motility across all environments, we would classify the observed migration rate generality as “type III”.

Quantitative Relationship between Phenotypes and Migration Rates

Selection in our experiment is performed on migration rate. Therefore, to test which of these three hypotheses accounts for the evolution of generalists we observe in Figure 2 we must first relate phenotypes (growth and motility) quantitatively to the migration rate of the population. To accomplish this, we use an established reaction-diffusion formalism (Cremer et al., 2019) to describe the spatiotemporal dynamics of the chemoattractant and nutrient source and the bacterial population. The model takes the following form:

$$\frac{\partial \rho }{\partial t}=D_b{\nabla }^2\rho -\nabla \left(v\rho \right)+\frac{k_g\rho c}{K_g+c}\text{,}$$ (Equation 1)

$$\frac{\partial c}{\partial t}=D_c{\nabla }^{2}c-\frac{k_g\rho c}{Y\left(K_g+c\right)}\text{,}$$ (Equation 2)

$$\text{with }v=\chi \text{log}\left(\frac{1+c/A}{1+c/B}\right)\text{,}$$ (Equation 3)

where ρ is a field describing the bacterial density in space and time and c describes the nutrient/chemoattractant field. D_b and D_c are diffusion constants for bacteria and nutrients, respectively, and k_g is the maximum growth rate with affinity K_g and biomass yield Y. A and B are constants that determine the range of attractant concentrations over which cells respond chemotactically. χ controls the strength of the chemotactic response and can be decomposed further χ = fD_b, where D_b is the diffusion constant and f is a factor that depends on the bias of cells swimming up a gradient of attractant (Croze et al., 2011).

In the limit of a homogeneous field of nutrients (∇c = 0), the second term in Equation 1 tends to zero and we recover the familiar Fisher-Kolmogorov (FK) model. In this limit, the migration rate of the population rate is given by s_FK∝D_bk_g. At long times, when the population has consumed available nutrients at the center of the plate, scaling arguments show that the chemotactic front moves with an enhanced migration rate s_eFK∝χk_g = fD_bk_g (Cremer et al., 2019), which is larger than s_FK since f is typically greater than 1. In either case, faster growth drives faster migration by more rapidly creating a larger population to drive colony expansion.

Simulations of the model in Equations (1), (2), and (3) show that expanding colonies transition from migrating at a rate s_FK at early times to s_eFK at late times (Figure 4). Migration at a rate s_FK occurs when the initial population is diffusing but has not yet consumed enough nutrients to create a sufficiently large gradient for chemotaxis to be important. Once nutrients have been consumed locally, which takes a time approximately t_xo~Yc₀/k_g, with c₀ the initial nutrient supply, the population transitions to migrating at a rate s_eFK (Figure S4). We observe this crossover in our experiments and simulations of the model presented above (Figure 4).

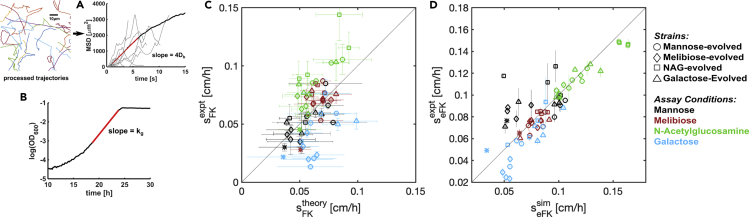
Figure 4.

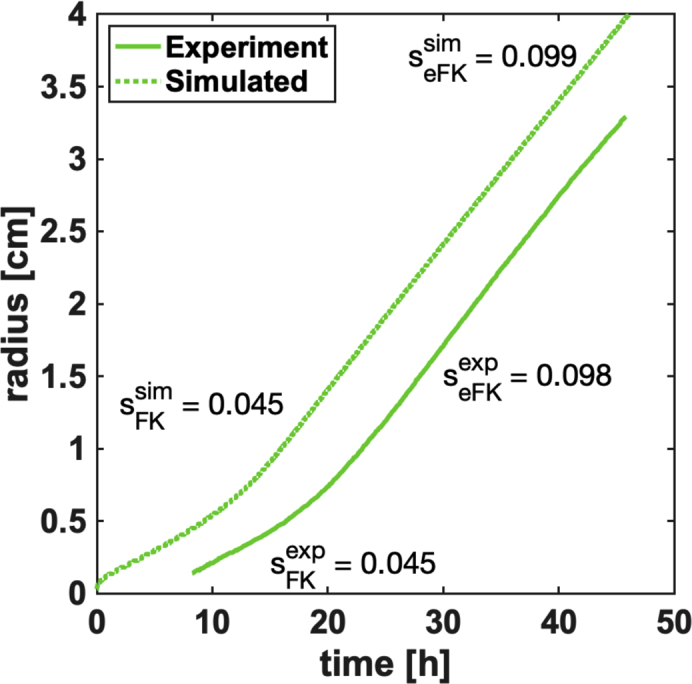
Theory-Experiment Comparison of Migrating Front Displacement in Time

Simulated and measured front position as a function of time for the founding strain in N-acetylglucosamine. The labeled rates, s_FK for the early times, and enhanced migration rates, s_eFK for the later times, are labeled for simulation (sim) and experiment (exp), respectively, in units of cm/h. For details of the simulation and parameter values see Transparent Methods. See also Figure S4.

Therefore, a population could evolve faster migration by increasing D_b, k_g, or f or any combination of these phenotypic parameters. In some conditions (e.g., galactose) where the founder initially grows slowly, the crossover time (t_xo) may approach the duration of one round of selection (24 hr). In this case, an adaptation that increases the growth rate and brings t_xo< 24 hr will result in substantially faster migration simply because the faster growth allows for an expanding population to access the migration rate s_eFK > s_FK earlier in time. In this case, large increases in the migration rate, of order f, could be observed even for only modest increases in the growth rate (k_g) and no evolutionary modification of motility (D_b and χ).

Quantifying the Impact of Evolved Phenotypes on Migration Rate

We measured phenotypic parameters for the founder and evolved strains in order to determine which of the three hypotheses in Figure 3 best explained the evolution of generalists in our experiment. We measured the growth and diffusion of the ancestor, as well as the 16 evolved strains, presented in Figure 2 in each of the four environments. These experiments were conducted in liquid minimal medium identical to the plates used for migration assays but without agar. Motility was measured by performing high-throughput single-cell tracking on populations of cells with phase contrast microscopy (Perlova et al., 2019), and diffusion constants (D_b) were inferred from the slope of the mean squared displacement across individual trajectories (Figure 5A). We note that measured diffusion constants in liquid are within approximately 10% of the diffusion constant in 0.2% w/v agar where our selection experiment took place (Croze et al., 2011). Growth was measured by monitoring the optical density of well-mixed liquid cultures, and maximum growth rates (k_g) were fitted during the exponential phase of the growth curve (Figure 5B). We assume a fixed and small K_g in all conditions (see Transparent Methods).

Figure 5.

Quantified Phenotypes Predict Front Migration Rates of Founder and Evolved Strains.

(A) Scheme for measuring bacterial diffusion constants. For each strain in each condition, thousands of individuals were recorded swimming (7856 ± 5623, mean ± standard deviation trajectories per experiment). Videos were automatically processed into trajectories, and squared displacement was calculated for each cell. Examples of single-cell squared displacement traces given in light gray. Population-level mean squared displacement (MSD, black line) was calculated by averaging over single-cell traces at each frame (see Figure S5). D_b was inferred from a linear fit to the MSD vs time (red line), assuming cells were diffusing in two dimensions.

(B) Maximum growth rates were measured by continuously measuring the optical density of well-mixed liquid cultures. k_g was fitted from the slope of log(OD₆₀₀) versus time and averaged over replicate wells. See Transparent Methods for details of both experiments.

(C) Measured s_FK migration rates for all strains in all conditions plotted against the theoretical expectation of $s_{\mathrm{FK}}=\sqrt{2D_b{k}_g}$. The black line corresponds to perfect agreement between measurement and prediction. Error bars in measured rate are standard errors on slopes fit to front position in time. Errors on predicted rates are computed via error propagation from the uncertainty in D_b and k_g from the regressions in A and B. Pearson's correlation 0.51, p value 2 × 10⁻⁵.

(D) Simulated and measured s_eFK for all stains in all conditions. Simulations are of the model in Equations (Equation 1), (Equation 2), (Equation 3) as described in Transparent Methods. Errors on predicted rates are smaller than the size of the markers. Pearson's correlation 0.83, p value 8 × 10⁻¹⁹.

See also Figure S4.

Using measured k_g and D_b parameters for all 16 strains in each of 4 conditions, we predicted the front migration rate early in the colony expansion process by computing s_FK and comparing this value to the measured early time expansion rates for 63 of 68 strain/condition combinations and found good agreement (Figure 5C). For 5 condition/strain combinations, s_FK could not reliably be determined from imaging data (see Transparent Methods). Therefore, our measurements of D_b and k_g accurately account for changes in migration rates by the evolved strains early in the colony expansion process.

Accounting for the late-time migration rates in founding and evolved strains, (s_eFK) requires measuring χ and therefore f. Measuring f in high throughput, at the single-cell level, is challenging because it requires applying controlled attractant gradients while measuring single-cell motility. We therefore inferred this parameter from our data. To accomplish this, we note that f∝s_eFK²/(D_bk_g), where s_eFK is the measured migration rate late in the colony expansion process (Figure 4). To measure f for the founding strain, we measured colony expansions for 48 hr to ensure the colony had enough time to consume the initial supply of nutrients. We measured the migration rate via regression of front position in time (Figure 4) and computed s_eFK²/(D_b^fok_g^fo). For the evolved strains, we measured s_eFK as the migration rate during the last 5 hr of expansion (during an 24 hr expansion) and inferred f using independent measurements of D_b and k_g on evolved strains.

With these inferred values of f for all strains, we paramterized the model in Equations 1, 2, and 3 for all strains in all media conditions (see Transparent Methods). We simulated front migration for all strains and measured s_eFK^sim for all strains. Figure 5D compares this simulated migration rate with our experimental observations and again shows good agreement.

In summary, high-throughput single-cell tracking allowed us to quantify the bacterial diffusion constant D_b in all 68 distinct strain/condition combinations shown in Figure 2. We combined these results with measurements of growth rate k_g and an established reaction-diffusion model to infer the impact of selection on the chemotaxis coefficient χ = fD_b. We then were able to directly compare measured front migration rates with model predictions and observed good agreement (Figures 5C and 5D).

Measured Phenotypes Suggest Generality Evolved by Plasticity

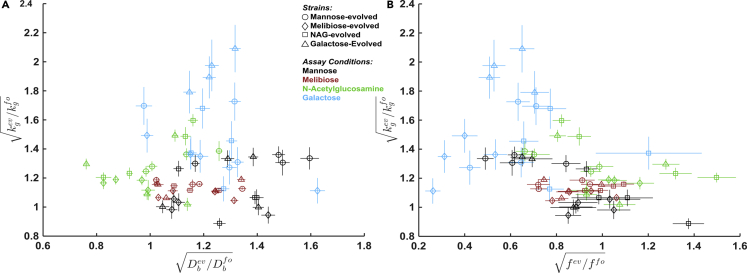
Having quantified how the evolved phenotypes impact migration rate, we could then ask which hypothesis for generality (Figure 3) is correct. Migration rate can be increased in the evolved strains by changes in f, D_b, or k_g. The contribution of any adaptation in these parameters to the evolved strains increase in migration rate relative to the founder is given by: f^ev/f^fo, D_b^ev/D_b^fo, and k_g^ev/k_g^fo. Therefore, to distinguish between the three types of generality presented in Figure 3, we examine the distributions of these quantities. Figures 6A and 6B show these quantities for all strains in all conditions.

Figure 6.

Phenotypic Adaptation Suggests Plasticity

(A) Motility and growth adaptation in liquid media of all 16 evolved strains presented in Figure 2 in four different assay conditions. The founder has a diffusion constant of 52 ± 1.3, 63 ± 1.2, 58 ± 1.1, and 56 ± 1.7 μm²s⁻¹ in mannose, melibiose, NAG, and galactose, respectively, fitted slope (MSD vs time) ± standard error after combining data from two independent experiments (Figure S6). The founder has a maximum growth rate of 0.18 ± 0.05, 0.29 ± 0.01, 0.30 ± 0.05, and 0.16 ± 0.08 hr⁻¹ in mannose, melibiose, NAG, and galactose, respectively; mean ± standard deviation of ten replicate wells spread over two independent plates. We present adaptation of diffusion constant as $\sqrt{D_b^{ev}/D_b^{fo}}$ and adaptation of maximum growth rate as $\sqrt{k_g^{ev}/k_g^{fo}}$ since these quantities contribute linearly to fractional enhancement of migration rate. Error bars are standard error calculated using error propagation.

(B) Shows changes in the chemotactic coefficient plotted versus changes in growth rate.

f^ev and f^fo denote the founder and evolved coefficients which are computed from the observed late-time migration rates and measured diffusion constants and growth rates as $f=s_{eFK}^2/\left(D_b{k}_g\right)$. The founder has an f^fo of 17 ± 1.6, 6.5 ± 0.4, 15.3 ± 1.3, and 7.5 ± 1.2 for mannose, melibiose, NAG, and galactose, respectively. Error bars are from error propagation. See Figure S6 for a plot of $\sqrt{D_b^{ev}/D_b^{fo}}$ vs $\sqrt{f^{ev}/f^{fo}}$.

See also Figures S5–S8.

A quick inspection of the evolved phenotypes suggested phenotypic plasticity. The data seemed to roughly separate by assay condition (Figures 6A and 6B). For example, strains measured in mannose typically exhibited a larger enhancement to diffusion but a more modest enhancement to growth when compared to strains measured in galactose. In addition, the increases in f appeared to concentrate in strains assayed in NAG, whereas strains assayed in galactose appeared to have reduced chemotactic capabilities irrespective of their selection condition.

We utilized a statistical approach to evaluate the significance of any separation of evolved phenotypes by selection condition and/or assay condition. Specifically, we performed analysis of variance (ANOVA) on the following linear mixed-effects model:

$$y_{ijk}=\mu +{\alpha }_i+{\beta }_j+{\gamma }_k+{\left(\alpha \beta \right)}_{ij}+{\epsilon }_{ijk}$$ (Equation 4)

This model decomposes a response variable y_ijk (k_g^ev/k_g^fo, D_b^ev/D_b^fo, or f^ev/f^fo) in terms of deviations from the global mean μ attributable to different groupings of the data. α_i is a fixed effect due to selection condition, with i indexing the four selection conditions. β_j is a fixed effect due to assay condition, with j indexing the four assay conditions. γ_k is a random effect for each of the 16 evolved strains, with k indexing the evolved strain. (αβ)_ij is an interaction term included to allow for unique effects due to particular combinations of selection and assay conditions. For example, if some strains grew particularly well in the condition they were selected for compared to the other strains, this would manifest itself as a significant interaction term. Lastly, ε_ijk is a noise term in the form of normally distributed random disturbances.

ANOVA analysis allowed us to determine which groupings, if any, displayed significant differences in the response variable. Performing ANOVA on D_b^ev/D_b^fo, we found that assay condition is the only grouping with a significant (p < 0.05) F-statistic (Table 1). That is, we rejected the null hypothesis that all the β_j are zero. We concluded that there is a significant difference between the assay conditions in the adaptation of undirected motility. To investigate which assay conditions show significant departures from the global mean and in which direction, we performed post-hoc testing via a non-parametric bootstrapping approach. This revealed that strains measured in mannose were significantly above the global mean in D_b^ev/D_b^fo, while strains measured in NAG were significantly below the mean, and strains in melibiose and galactose showed no significant change in D_b^ev/D_b^fo relative to the global mean (Figure S7).

Table 1.

Assay Condition Drives Differences in Diffusion Constant Adaptation

Source of Variance	F	p value
Selection condition (αi)	1.01	0.42
Assay condition (βj)	12.80	7.61 × 10−6
Strain (γk)	1.65	0.12
Selection condition x assay condition (αβij)	0.60	0.79

Summary statistics for ANOVA on the model presented in Equation 4 using $\sqrt{D_b^{ev}/D_b^{fo}}$ as the response variable. The F-statistic describes the ratio of between-group variability to within-group variability. Here, we only found a significant (p < 0.05) F-statistic for assay condition.

Bacterial diffusion constants are approximately related to the run speed and duration in the following way: D_b ≈ v_r²τ_r. Therefore, changes in diffusion constants can be achieved through changes in run duration and/or speed. We asked whether changes in D_b^ev/D_b^fo were achieved with a consistent microscopic strategy within each assay condition. Therefore, we investigated correlations between changes in run statistics and changes in diffusion constant across all evolved strains within each assay condition (Figure S8). We found that D_b^ev/D_b^fo was significantly correlated with a particular microscopic strategy for strains measured in each assay condition, regardless of their evolutionary history. For example, in mannose, changes in D_b were correlated with changes in τ_r but not v_r. Conversely, in NAG, changes in diffusion constant were correlated with changes in both v_r and τ_r.

Similarly, performing ANOVA with $\sqrt{k_g^{ev}/k_g^{fo}}$ as the response variable shows that, by far, the most significant effect is due to assay condition (largest F-statistic, Table 2). Post-hoc testing revealed that strains measured in galactose have above-average growth rate adaptation, while strains measured in mannose and melibiose were below average, and strains measured in NAG showed no significant change relative to the global mean (Table S2). We also found smaller but still significant (p < 0.05) effects due to selection condition and the interaction term (Table S3). Post-hoc testing on the α_i revealed only one significant coefficient: melibiose-evolved strains exhibited a below-average growth rate enhancement. For the interaction term, post-hoc showed only one significant term: an increased growth rate adaptation for strains evolved in galactose when measured in galactose (Table S4). We concluded that the assay condition is the strongest determinant of growth rates in evolved strains.

Table 2.

Assay Condition is the Main Driver of Differences in Growth Adaptation

Source of Variance	F	p value
Selection condition (αi)	7.00	0.01
Assay condition (βj)	31.86	3.10 × 10−10
Strain (γk)	1.15	0.36
Selection condition x assay condition (αβij)	4.68	3.78 × 10−4

Summary statistics for ANOVA on the model presented in Equation 4 using $\sqrt{k_g^{ev}/k_g^{fo}}$ as the response variable. The F-statistic describes the ratio of between-group variability to within-group variability. Here, we found significant F-statistics for selection condition, assay condition, and the interaction term between them. The largest F-statistic was associated with assay condition, indicating this predictor is the dominant source of variability in $\sqrt{k_g^{ev}/k_g^{fo}}$. See also Tables S2–S4.

Lastly, ANOVA with f^ev/f^fo as the response variable again showed that the most significant effect was due to assay condition (largest F-statistic, Table 3). Post-hoc testing revealed here that strains measured in NAG exhibited above-average chemotactic adaptation, while strains measured in galactose were below average, and strains measured in mannose and melibiose showed no significant change relative to the global mean (Table S5). We also found a smaller but still significant (p < 0.05) effect due to selection condition. Post-hoc testing on the α_i revealed that strains selected in NAG were above average in their chemotactic adaptation, while strains selected in mannose were below average, and strains selected in melibiose and galactose showed no significant deviation from the global mean (Table S6).

Table 3.

Assay Condition is the Main Driver of Differences in Apparent Chemotactic Adaptation

Source of Variance	F	p value
Selection condition (αi)	7.66	4.02 × 10−3
Assay condition (βj)	20.04	8.27 × 10−8
Strain (γk)	1.47	0.18
Selection condition x assay condition (αβij)	2.16	0.05

Summary statistics for ANOVA on the model presented in Equation 4 using f^ev/f^fo as the response variable. The F-statistic describes the ratio of between-group variability to within-group variability. Here, we found significant F-statistics for selection condition and assay condition. The largest F-statistic was associated with assay condition, indicating this predictor is the dominant source of variability in f^ev/f^fo. See also Tables S5 and S6.

These ANOVA analyses provided clear evidence that the evolved phenotypes presented in Figures 6A and 6B separate by assay condition. We concluded that, within each of the four environments, evolved strains exhibited similar adaptation in growth and motility, regardless of their evolutionary history. The result is consistent with “type II” generality (i.e., plasticity). Evolved strains across all selection conditions appeared to have evolved phenotypic plasticity that allowed them to enhance population-level migration by adapting cellular phenotypes to meet the unique demands of each nutrient condition.

Mutations Present in Evolved Strains Cannot Predict Phenotypes in Any Condition

We next asked whether specific mutations present in strains evolved for faster migration could explain the migration, growth, and motility phenotypes we observed. We performed whole genome sequencing on all 16 evolved strains and identified de novo mutations relative to the common ancestor present at a frequency of at least 20% (Deatherage and Barrick, 2014) (Tables S7 and S8). We identified 33 unique mutations occurring in diverse genes and pathways including biosynthesis of essential molecules, stress response, and metabolite import. We observed no single mutation common to all evolved strains, nor were any mutations common to all 4 evolved strains from any particular selection condition. However, 24 of the 33 mutations were present in more than one strain. By grouping together mutations occurring in the same gene, as well as those in adjacent intergenic regions, we identified 21 unique genes or flanking regions where mutations occurred, which we term mutational targets. Twelve of those targets were affected in multiple strains, and of those, 8 were affected across strains with different selection conditions. Unlike previous studies (Fraebel et al., 2017), we did not observe mutations with an obvious interpretation in terms of their impact on evolved phenotypes. Therefore, we took a statistical approach to interpreting the sequencing data.

Having grouped mutations by their target, we created a mutation candidacy matrix (X) which describes the presence (1) or absence (0) of each observed mutation in each strain. We then asked whether the presence or absence of these mutations could predict the migration phenotypic parameters of each strain in each condition. To do this, we performed linear regression using mutation candidacy as the predictor variables and the adaptation in either growth rate (k_g), diffusion constant (D_b), or the chemotactic coefficient (f) as the dependent variable, e.g., $\sqrt{f^{ev}/f^{fo}}={\eta }_0+X\overrightarrow{\eta }+\overrightarrow{\epsilon }$, where η₀ is an intercept, $\overrightarrow{\eta }$ is a vector of regression coefficients expressing the impact of each mutation on the response variable, and $\overrightarrow{\epsilon }$ is a noise term with zero mean and variance σ². We performed L₁-regularized regression (least absolute shrinkage and selection operator [LASSO]) to avoid overfitting (Yi and Xu, 2008; Li and Sillanpää, 2012), using leave-one-out cross-validation to determine the best value of the regularization hyperparameter. For several assay conditions, LASSO regression selected a model with only an intercept (e.g., giving $\sqrt{f^{ev}/f^{fo}}={\eta }_0+\overrightarrow{\epsilon }$), indicating that no mutation predicted the migration parameter across the set of strains. In cases where a model with non-zero $\overrightarrow{\eta }$ was selected (i.e., some mutations were identified as having predictive power), the improvement in the mean squared error (estimated using cross-validation) relative to a model with only an intercept was small, and the statistical significance of a non-zero $\overrightarrow{\eta }$ was unclear.

These observations led us to undertake a numerical investigation using surrogate data to assess the performance of our LASSO regressions (see Transparent Methods for details). The purpose of this investigation was to determine whether regressions that selected a non-zero $\overrightarrow{\eta }$ had robust out-of-sample predictive power. If not, then we would consider it unlikely that any mutation in these regressions truly predicted the migration phenotypic parameters. Briefly, we constructed surrogate data sets where the coefficients $\overrightarrow{\eta }$ were specified, and the signal-to-noise ratio was effectively modulated by specifying the number of non-zero coefficients in $\overrightarrow{\eta }$and the random noise strength σ (Figures S9B and S9C). Each data set comprised a training set and an out-of-sample test set, where the predictors in both training and test sets matched the candidacy matrix (X) in the number of observations, number of variables, and first-order statistics (presence frequency of each mutation). On each of 3 × 10⁵ instances of surrogate data sets, we performed LASSO regressions as described above and evaluated performance by computing the coefficient of determination R² using the out-of-sample data.

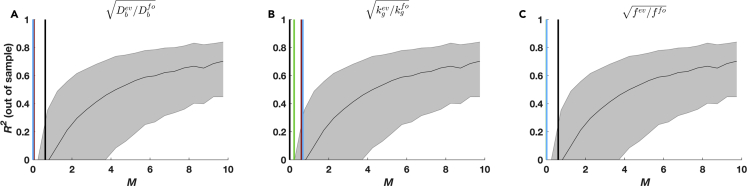
We developed a test statistic M to relate these surrogate data regressions to the real regressions on migration parameters (see Transparent Methods for details) since the true coefficient vectors $\overrightarrow{\eta }$ and noise strength σ for the regressions on real data are unknown. This statistic measured the improvement in model fits (mean squared error estimated using cross-validation) for the model selected by LASSO relative to a model with only an intercept (η₀). In the surrogate data, we observed that M correlated positively with the out-of-sample predictive power of a model inferred by LASSO, giving us a clear relationship between the test statistic and regression performance (Figures 7, S9D, and S9E). We then computed our test statistic for the real data regressions for adaptation in growth rate, diffusion constants, or chemotactic coefficients from the mutation candidacy matrix and observed small values of the test statistic M (Figure 7), indicating low predictive power is likely (out-of-sample R² ≈ 0). We concluded that, for our data, mutations are highly unlikely to predict the measured phenotypic adaptation. In sum, the presence of “individual” mutations has no predictive power of evolved phenotypes.

Figure 7.

Numerical Investigation of LASSO Regression Demonstrates Mutations Have Limited Predictive Power for Migration Phenotypes

(A–C) Relationship between the test statistic M and out-of-sample R² obtained from surrogate data regressions (see Transparent Methods), with M values from regressions on real migration phenotypic parameters overlaid. M and R² values from all surrogate data simulations are combined, binned by M, and the quartiles of R² within the bins are shown as a function of M. The same quartile curves are shown in A–C. Vertical lines indicate the M values resulting from LASSO regressions on real data for the quantities (A) $\sqrt{D_b^{ev}/D_b^{fo}}$, (B) $\sqrt{k_g^{ev}/k_g^{fo}}$, and (C) $\sqrt{f^{ev}/f^{fo}}$, , where the colors indicate the assay condition (black: mannose, red: melibiose, green: N-acetylglucosamine, blue: galactose).

See also Figure S9, Tables S7 and S8.

Discussion

The central finding of this study is the emergence of generalists when bacterial populations are selected for faster migration through a porous minimal medium environment. We found that distinct phenotypic strategies gave rise to fast migration, and, remarkably, these strategies were determined more by the immediate nutrient condition than by the evolutionary history of the strains being measured. We concluded that repeated selection in any condition drove fast migration in all conditions via distinct, plastic phenotypic responses to each nutrient condition. As a result, the fast migration in all conditions emerged via plasticity, which is a byproduct of selection for fast migration in any one condition. Therefore, in this case, plastic phenotypes evolved even in homogeneous selection conditions.

It is not yet clear why selection in a single environment results in plastic phenotypic responses to other environments that increase migration rate. Perhaps the simplest explanation is that similar physiological changes occur during evolution in all four nutrient conditions. However, the molecular mechanisms that give rise to the observed generality via phenotypic plasticity are not yet clear. Our statistical analysis of the genetic variation observed in evolved strains shows that there is no simple genetic basis for this plastic adaptive response. Given what is known about sugar uptake and metabolism in E. coli, some of our observed mutations could be targeting the uptake or metabolism of multiple sugars. For example, EnvZ regulates expression of OmpF, the outer membrane porin responsible for import of all four sugars (Mizuno and Mizushima, 1987; Travisano and Lenski, 1996). NagA is essential for metabolism of NAG but also has a role in regulating expression of the nag regulon, including nagC (Plumbridge, 1991). There is evidence that NagC is capable of repressing the mannose phosphotransferase system (PTS) system (Plumbridge, 1991) and the galactose transporter (El Qaidi et al., 2009). Therefore, the mutations we observed in nagA for two galactose-evolved strains could have an impact in mannose, NAG, and galactose environments.

The mechanistic basis for how metabolism is coupled to motility remains unclear, and elucidating this fully will be necessary to understand why evolved strains in some conditions exhibit large changes in both motility and growth (e.g., galactose). The fact that the evolved strains did not exhibit fast migration in a rich medium, where amino acids are responsible for growth and chemotaxis, is consistent with the idea that the plastic generalist adaptation observed in this study was specific to sugars. Therefore, the limits on generalist evolution due to plasticity in this system would appear to be defined by the chemical identity of the nutrient/chemoattractant. Given that we observed mutations in regulatory elements (e.g., rssB, wzzE, envZ), it is possible that the plasticity we observed in the evolved strains might be best understood at the regulatory level. In this case, the plastic response would be selected in a homogeneous environment, due to regulatory variation that results in changes in gene expression impacting motility and metabolism in other environments. Therefore, the shared molecular-level features of the evolved strains which were responsible for the phenotypic plasticity outcomes in different nutrient conditions may be explained by gene expression measurements (Huang et al., 2005).

More broadly, the smooth phenotypic variation we observed across strains and environments (Figure 6) is consistent with a complex genetic basis where the plastic response of a given genotype depends on genetic variants at a large number of loci. One possible mechanism for genetic complexity in evolved plastic responses would be phenotypic impacts from a large number of weak regulatory linkages (Gerhart and Kirschner, 2007), which is supported by genetic screens on motility (Girgis et al., 2007). The apparent smooth phenotypic variation is in contrast to phenotypic switches, where plasticity drives discrete phenotypic variation (Balaban, 2004). It would be interesting to design future experiments to determine when and why selection favors continuous or discrete plastic responses. Perhaps one way to approach this problem is to compare the present results to selection in fluctuating environments. Fluctuating selection is believed to favor the evolution of cooperative (non-linear) responses in biological systems, for example, in proteins (Stiffler et al., 2015), and one might speculate that the same could be true for phenotypic plasticity.

Since the seminal work of Baldwin and later Waddington (Baldwin, 1896; Waddington, 1953), a main focus of work on phenotypic plasticity has been to understand the relationship between plastic responses to environmental change and subsequent genetic adaptation (Ghalambor et al., 2015; Schaum and Collins, 2014; Ho and Zhang, 2018). Our results suggest another possible role of phenotypic plasticity in evolution: namely, that selection in one environment can potentiate new physiological responses to other environments resulting in the evolution of generalists even in homogeneous environmental conditions. Future work should focus on understanding why selection in one environment can elicit new phenotypic responses to other environments and the scope of phenotypic generality that can evolve by this mechanism.

Limitations of the Study

The central limitation of the present study is that it relies on a statistical argument to support the claim that generalists evolve via phenotypic plasticity. As a result, the physiological basis of the observed plastic responses is not yet known. Future work should examine the impact of selection for fast migration on gene expression profiles across all evolved lineages to discern conserved patterns of expression which could then inform more detailed mechanistic interrogation of the evolution of plasticity.

Resource Availability

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Seppe Kuehn (seppe.kuehn@gmail.com).

Materials Availability

All strains generated in this study are available upon request. No reagents were generated.

Data and Code Availability

Details of the detected mutations are shown in Table S8. Parameter values for the simulations are given in the Supplementary Information. Source code for simulations is available upon request. The accession number for the DNA sequencing data reported in this paper is NCBI: PRJNA667609.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: November 20, 2020