Abstract
Salt-bridge interactions play an important role in stabilizing many protein structures, and have been shown to be designable features for protein design. In this work, we study the effects of non-native salt-bridges on the folding of a soluble alanine-based peptide (Fs peptide), using extensive all-atom molecular dynamics simulations performed on the Folding@home distributed computing platform. Using Markov State Models (MSMs), we show how non-native salt-bridges affect the folding kinetics of Fs peptide by perturbing specific conformational states. Furthermore, we present methods for the automatic detection and analysis of such states. These results provide insight into helix folding mechanisms and useful information to guide simulation-based computational protein design.
Introduction
Protein folding results from the balance of many different molecular driving forces–hydrophobic interactions, electrostatics, van der Waals effects, salt-bridge interactions, and hydrogen bonding. A detailed understanding of the roles played by these interactions in the folding process is necessary both for a complete picture of protein folding, and for developing improved de novo protein design algorithms. Salt-bridge interactions, i.e. electrostatic interactions between oppositely charged amino acid residues, have been shown to stabilize or destabilize protein helices1–3 depending on the identity of interacting residues4 and their sequence patterning. 5 Salt-bridge interactions can be highly cooperative, 6,7 and extreme cases of such cooperativity is exploited by motor proteins to form rigid structural elements8,9. Not surprisingly, salt-bridge interactions have been targeted as highly designable features for de novo protein design, with computational algorithms utilizing a combination of information from structural databases10,11 as well as biophysical models of electrostatics.12,13.
It is only more recently that time-resolved spectroscopic studies have begun to address how different patterns of salt-bridge interactions affect protein folding kinetics.14 Using temperatrue-jump IR measurements, Meuzelaar et al. has shown that non-optimal Glu-Arg salt-bridge patterning not only destabilizes protein helices but slows folding rates by almost an order of magnitude15. At low pH (2.5) this effect is less pronounced, suggesting that non-optimal salt-bridges stabilize non-native folding intermediates, acting as kinetic traps. Tzul et al. have shown that computational optimization of surface charge-charge interactions for protein native structures results in faster folding kinetics, suggesting that electrostatic interactions normally give rise to some kinetic frustration. 16 Similarly, the Raleigh group has shown that a non-native salt-bridge likely forms in the unfolded state of NTL9, thus rationalizing the stabilizing effects of mutation K12M, which disrupts this interaction 17–19 All of the above examples raise the question of how computational algorithms might address the problem of designing non-native salt-bridge interactions that may impact kinetics as well as thermodynamics.
Here, we explore how to use atomically-detailed molecular dynamics simulations along with Markov State Model (MSM) approached to assess the kinetic and thermodynamic consequences of salt-bridge mutations on folding. Recent advances in computing platforms, such as the specialized supercomputer Anton20, the world-wide distributed computing network Folding@Home21 and GPU-accelerated MD algorithms22–24, now make possible the study of folding processes on the millisecond timescale. Complementing these advances have been the development of software platforms such as MSMBuilder25 and EMMA26 to build sophisticated kinetic network models of conformational dynamics from large-scale simulation data, and extract meaningful biophysical information to help further guide future de novo design.27
As a model system, we examine how non-native salt-bridges effect the folding of a soluble alanine-based peptide (Fs peptide). In particular, we examine variants of the Fs peptide (Ac-A5(AAARA)3A-Nme) where Arg residues have been mutated to Glu(Table 1), the folding and stability of which has been extensively studied by experiment28–31 and simulation.32. We chose this sequence because the (i, i + 5) pattern of charged residues are unable to form salt bridges in the native helical conformation, and can only form in non-native states.
Table 1:
Simulation trajectory data for Fs peptide sequence variants.
| Abbreviation | Sequence | Simulation time (µs) |
|---|---|---|
| Fs-EEE | Ace-A5AAAEAAAAEAAAAEAA-Nme | 124.6 |
| Fs-EER | Ace-A5AAAEAAAAEAAAARAA-Nme | 126.0 |
| Fs-ERE | Ace-A5AAAEAAAARAAAAEAA-Nme | 134.7 |
| Fs-ERR | Ace-A5AAAEAAAARAAAARAA-Nme | 138.5 |
| Fs-REE | Ace-A5AAARAAAAEAAAAEAA-Nme | 138.5 |
| Fs-RER | Ace-A5AAARAAAAEAAAARAA-Nme | 136.8 |
| Fs-RRE | Ace-A5AAARAAAARAAAAEAA-Nme | 139.2 |
| Fs-RRR (wild type) | Ace-A5AAARAAAARAAAARAA-Nme | 139.4 |
To achieve the statistical sampling necessary to model the complete folding reaction for multiple sequences, we use extensive all-atom molecular dynamics simulations performed on the Folding@home distributed computing platform. We analyze the data using Markov State Model (MSM) approaches, in which a unified set of metastable states is used to model the conformational dynamics of all sequences. In the following sections, we first describe our use of a recently developed variational cross-validation method33 to select a set of model parameters to build very accurate MSMs for all eight different sequences. We then present an analysis of how folding mechanisms are affected by different salt-bridge mutations. In particular, we find that a salt-bridge interactions can greatly stabilize non-native helix-bundle conformations, resulting in slower folding kinetics. Finally, towards developing tools for computational design, we present an unsupervised Bayesian method that is able to automatically identify the contacts that uniquely define the most important metastable conformational states comprising observed sequence differences. These results are steps toward automated simulation-based computational protein design.
Methods
Molecular dynamic simulations
Molecular dynamics (MD) simulations of eight Fs peptide variants were performed using GROMACS 4.5.434 on the Folding@home distributed computing platform.21. These variants consisted of all possible Arg/Glu substitutions at positions R9, R14 and R19, which we will abbreviate as Fs-EEE, Fs-EER, Fs-ERE, Fs-ERR, Fs-REE, Fs-RER, Fs-RRE and Fs-RRR (Table 1). One hundred initial starting conformations were obtained by conformational clustering of previous simulation trajectories of wild type Fs peptide (unpublished), each threaded using UCSF Chimera to generate structures for the other seven sequence variants. Explicit-solvent simulations were then performed for all sequences using the AMBER ff99SB-ildn-nmr force field35 and TIP3P water model, with 8900 atoms in a (45Å)3 periodic box. Na+ and Cl− counter ions were added at 100 mM to neutralize charge. The simulations used stochastic dynamics (Langevin) integration at 300K using a 2 fs time step. Covalent hydrogen bond lengths were constrained using LINCS, and PME electrostatics were used with a non-bonded cutoff of 9 Å. The NVT ensemble was enforced using a Berendsen thermostat.
About 130 trajectories were simulated for each variant, with an average trajectory length of about 1 µs. The complete trajectory data set for all sequences represents over a millisecond of simulation time, with about 130 µs of total simulation data per sequence.
Time structure based Independent Component Analysis (tICA)
tICA is a dimensionality reduction technique in which protein coordinates are projected to a subspace representing the degrees of freedom along which the slowest motions occur. 36,37 Thus, the tICA subspace is ideal for kinetic-based clustering of molecular conformations, for the construction of Markov State Models (see below). The tICA components (tICs) can be found as the set of uncorrelated vectors α that maximize the objective function
| (1) |
subject to the constraint that each component have unit variance (i.e. ). Here, Cτ is a time-lagged correlation matrix (TLCM) of elements , and Σ is the covariance matrix (CM) of elements . The set of tICA components α can be found variationally by solving the generalized eigenvalue problem .
Although the tICA approach is linear (i.e. the tICA components are, by definition, linear combinations of the input coordinates), it can be extended to account for nonlinearity by using the so-called “kernel trick” in which the original coordinates are projected into an even higher-dimensional basis of nonlinear functions. 38 In practice, projection to pairwise distance coordinates has been found to work very well for constructing MSMs,36 and here we similarly construct the time lagged correlation matrix (TLCM) and covariance matrix (CM) using Cα + Cβ atom pair distances for all residues. Previous studies have also shown that the TLCM is not sensitive to the lag time39, and following this work, choose τ = 5 ns as the lag time to build the TLCM. The number of tICA components used for conformational clustering is a free parameter that we select according to the results of a variational cross-validation method described below.
Markov State Models
Markov State Models (MSMs) are kinetic network models of conformational dynamics, comprising many metastable states connected by kinetic transition rates. 40 MSMs have been widely used to analyze molecular simulation data due to several key advantages. Most importantly, MSMs enable long-timescale dynamics and equilibrium properties to be modeled from ensembles of much shorter trajectories.39,41–43. When combined with adaptive sampling techniques, MSMs can also help guide simulations to achieve converged sampling.44–46 Moreover, coarse-graining of metastable states, combined with pathway flux analysis, has been used to extract a great deal of human-understandable information about molecular mechanisms of conformational change and molecular association.47–49
Theory.
MSM metastable states are defined using a discrete partitioning of the configuration space into K metastable regions, typically through the use of conformational clustering algorithms. Once metastable states are suitable defined, transition probabilties from state i to state j in time τ are estimated from transitions observed in the simulation trajectories. In the case that transitions are Markovian (a good approximation given a sufficiently long lag time τ ), the eigenvalues and eigenvectors of T(τ), the matrix of inter-state transition rates, provide a complete description of conformational dynamics. 41,50,51 Starting from an initial distribution of state populations p(0), the complete time evolution of the system is given by
| (2) |
where and are the left and right eigenvectors of T(τ), and τn are the so-called implied timescales corresponding to each eigenmode relaxation, defined as τn = −τ/(ln µn), where µn are the eigenvalues of T(τ). Equilibrium populations (the stationary state) are given by the n = 0 eigenvector , for which τ0 = ∞.
MSM construction.
We used the MSMBuilder 3.0 software package to build over 300 MSMs, each using different hyper-parameters. Hyper-parameters included the number of tICA components, the lagtime used to construct the TLCM, the number of MSM states, and the clustering method used to define MSM states. We denote these as “hyper-parameters” to distinguish them from the MSM parameters (i.e. the transition rates). Each MSM was scored using a variational cross-validation method (described below) to select the best model.
The Bayesian agglomerative clustering engine (BACE) algorithm52 was used to coarsegrain MSM microstates into macrostate models. Macrostate committor values and folding pathway fluxes were computed using Transition Path Theory (TPT), as described else-where.42,53
GMRQ scores.
In order to correctly extract useful information from the simulations, hyper-parameters need to be carefully selected to construct the most accurate MSM possible. Here, we use the recently developed GMRQ (generalized matrix Rayleigh quotient) method to select the optimized set of hyper-parameters for MSMs.33
Briefly, the objective of the GMRQ method is to find MSM hyper-parameters (metastable state definitions, lag times, etc.) such that projection of the observed dynamics to the discrete metastable state space maximizes the same objective function as the tICA method (Equation 1). In the discrete-state basis defined by the metastable state definitions, this objective function is known as a “generalized matrix Rayleigh quotient”. To avoid over-fitting to the observed transition data, a cross-validation approach is used in which a portion of the data is used to training the model, and the remaining data is used for testing the model. In the results below, we report the mean cross-validation value of the generalized matrix Rayleigh quotient (along with it’s estimated uncertainty) as the “GMRQ score”. Unlike other methods for validating MSM models (such as the Chapman-Kolmogorov test), the GMRQ method is extremely useful as it allows one to make quantitative, statistically significant comparisons across all models, even those built using different numbers of metastable states. We thus choose the model with the highest GMRQ score as the best model for subsequent analysis.
Surprisal analysis
Previously, we presented a surprisal metric based analysis to quantify differences in transition counts between two different kinetic network models.45 Here, we extend the original two-model surprisal analysis to a multi-model surprisal analysis of K different kinetic network models, each sharing the same definition of metastable states, but different numbers of observed transitions. The surprisal value si for a state i can be thought of as a relative entropy metric estimated from the observed outgoing transition counts, for the case where transition counts from all K models are combined, versus if we consider each model separately:
| (3) |
where
| (4) |
and
| (5) |
are entropies estimated from the observed transition counts. Here, is the number of transition counts from state i to state j observed for model k, is the total number of outgoing transition counts from state i in model k, and is the total number of transitions counts from state i across all models.
We have shown previously45 that the Jenson-Shannon divergence,
| (6) |
of a collection of K MSMs defined by transition matrices T(k) with stationary state populations , can be closely approximated using surprisal metrics, by giving all the models equal weight.(i.e., pk = 1/K) and assuming that the perturbations are small that the state equilibrium population are approximately equal to each other across all models(i.e., ), we had the final approximation of JSD as
| (7) |
Bayes factor analysis
In order to identify the key contacts defining each metastable state, here we develop a Bayes factor method to calculate the importance of an interresidue contact in a particular state. Consider two sets of interesidue contacts {cij} and {cij}*. The variables cij are contact indicator variables, such that cij = 1 if a contact is present between residues i and j, and t cij = 0 otherwise. We define the Bayes factor BF to be the ratio of probabilities that the structure is in state k given the set of contacts {cij} versus the set of contacts {cij}*.
| (8) |
Suppose the two sets of contacts only differ by a single contact, cmn, that is formed in the first set of contacts, and not formed in the second set. If we assume that each contact is statistically independent, such that , then cancellation of terms and application of Bayes’ Theorem results in:
| (9) |
This final form of the Bayes factor (Eq. 9) can be thought as the statistical over-representation of contact cmn in state k, and hence a measure of its importance in uniquely defining the structural features of that state. (Of course, we note that the Bayes Factor formula presented here can apply to any other structural feature as well; here we consider only inter-residue contacts.)
To compute Bayes factors in practice, we estimate probabilities from the frequencies of contacts N observed in the simulation trajectory data, using , , and setting , . In order to avoid a zero-valued denominator in the Bayes factors, unobserved contacts are given a single pseudocount, N (cim = 1|k) = 1. Since Ntotal is a very large number, this approximation does not affect the results. In our analysis below, we compute Bayes factors for contacts separated by three or more residues, |i − j| ≥ 3, and define a contact formed if the any pair of non-hydrogen atoms between two residues are closer than 4 Å.
Results
Simulation data sets
Extensive all-atom MD simulations were performed as described in Methods. Before building MSMs, we first discarded some short trajectories shorter than 10 ns. The total simulation time for each sequence used for building MSMs is around 130 µs. In the following sections, we refer to the combined data set of all sequences as the “combined” data set, and data sets containing only one sequence as “individual” data sets.
Construction of optimal Markov State Models
We tested the performance of two different clustering algorithms, k-means and k-centers, used with three different distance metrics: rmsd, dihedral-angle rmsd, and tICA distance. First, we tried to build a series of MSMs using the combined simulation data from all eight different sequences. We varied the number of tICA components, the lag time used to build the MSMs, the cluster method, and the number of microstates of the MSM. For each model, 8-fold cross-validation was used to calculate the GMRQ scores, leaving out the data of each sequence for test data to compute the GMRQ score, and using the remaining data to train the model. To avoid memory overflow from clustering such a large data set, we use one hundredth of the data for clustering, and assigned the rest of the data using the generated cluster centers.
The results of these efforts are summarized in Figure 1. The model with the highest GMRQ score is a 1200-microstate MSM built using k-means clustering over 8 tICA components and a tICA lag time of 5 ns. This model was chosen as the best model, and used for analysis in further sections. That said, several models had scores very similar to the largest score, within sampling error. A possible reason for such similarity in scores is that we are in a data-rich regime. To test this idea, we calculated 5-fold cross-validated GMRQ scores for the individual data sets corresponding to each sequence. Indeed, unlike the combined data set, the GMRQ scores of individual data sets tend to reach the maximum at less states with only a few exceptions (data not shown).
Figure 1:
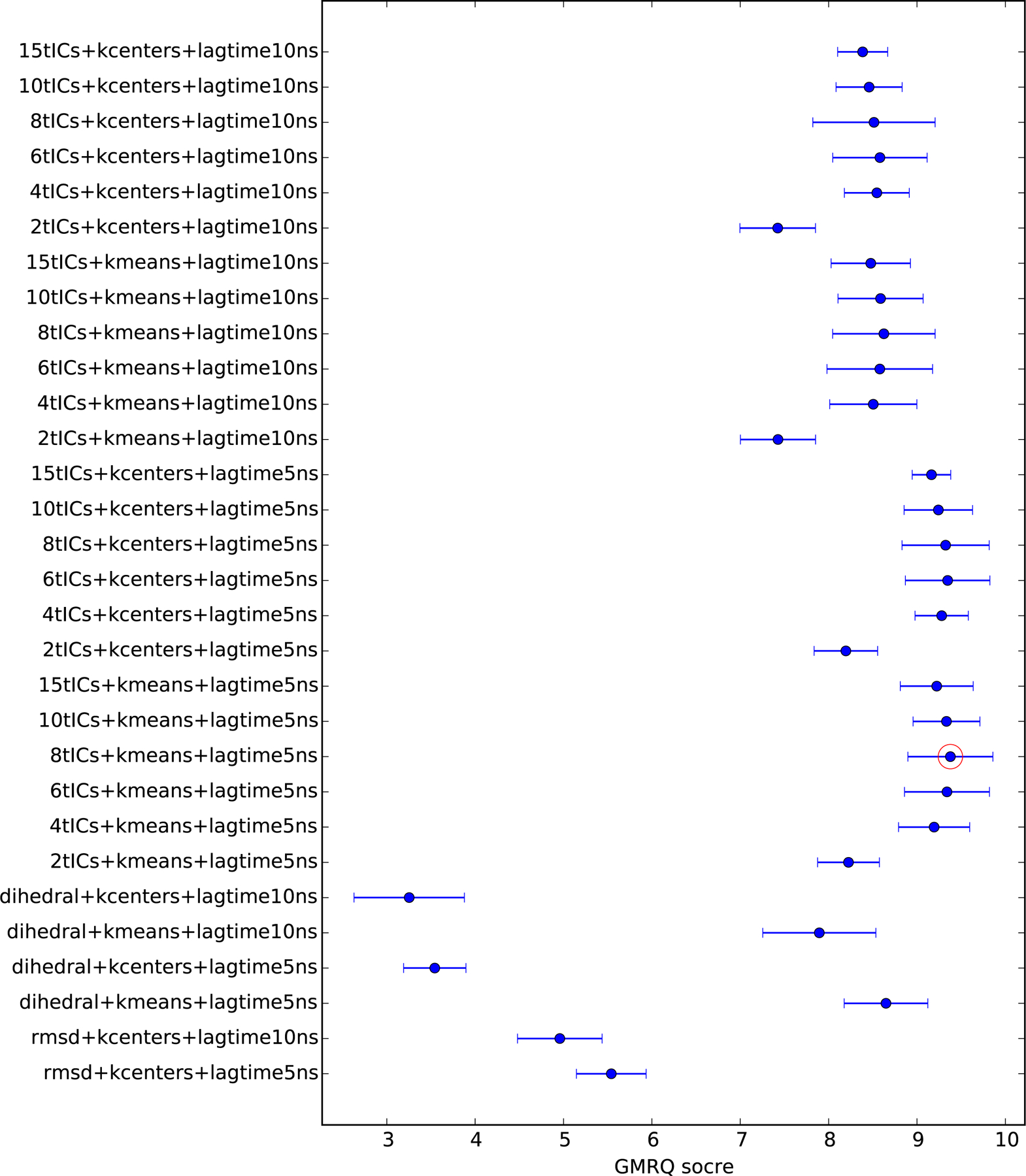
A comparison of the maximum GMRQ scores of Markov State Models built using various hyper-parameters. Error bars denote uncertainties estimated by cross-validation. Circled in red is the set of hyper-parameters yielding the highest GMRQ score, which we used henceforth for all subsequent MSM construction and analysis.
Using the optimized parameters described in previous section, a 1200-microstate MSM was constructed from all the combined data sets, with an MSM lag time of 5 ns. MSMs for each individual data set were built using the same metastable state definitions and lag times by using only the observed transition counts from each individual data set. Because the model hyper-parameters and metastable state definitions are the same, the conformational dynamics for each sequence can be directly compared.
However, because of finite sampling, and sequence-dependent differences in the free energy landscape, each individual data set does not populate the full set of 1200 microstates. Using the Bayesian agglomerative clustering engine (BACE) lumping algorithm,52 we further coarse-grained this model into a macrostate MSM having 40 states, the maximum number of states found for which all macrostates are populated by all sequences. The 40-macrostate model is a more comprehendible description of folding mechanisms, yet predicts implied timescales similar to the microstate model (see Figure 2). Chapman-Kolmogorov tests of state residence probabilities for the 40-macrostate model furthermore suggest that the macrostate model is very good (Figure S5). We also compare the implied timescales between the 40-macrostate model and 1200-microstate model built from each individual data set (Figure S4). The trend of implied timescales are very similar to each other within error bars.
Figure 2:
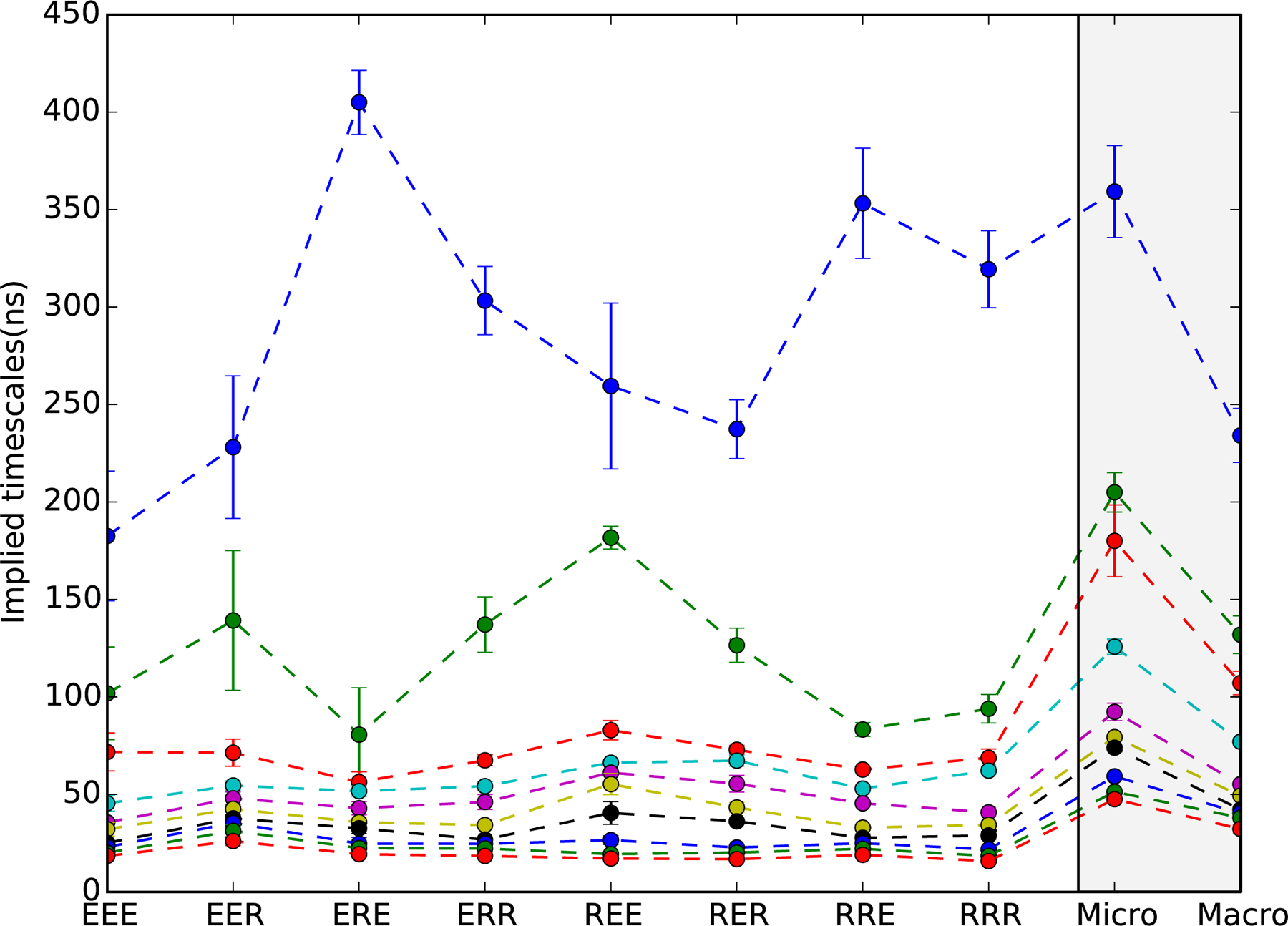
Implied timescale spectra of 40-macrostate MSMs for all eight protein sequences. Shown are the ten slowest timescales with error bars denoting uncertainties estimated from ten-fold cross-validation. Dashed lines are to guide the eye. For all sequences, the slowest timescale is well-separated from the rest, indicative of two-state helix folding. Sequences containing R14 (Fs-ERE, ERR, RRE and RRR) have slower folding times than those containing E14, with the greatest difference seen for Fs-EEE (~180 ns) versus Fs-ERE (~400 ns). On the right (gray panel) is shown a comparison of implied timescales for 1200-microstate and 40-macrostate MSMs built from the combined sequence data. Only a slight acceleration in timescales is seen in the macrostate model, indicating very modest artifacts due to coarse-graining.
We note that the number of tICA components used to build the microstate MSM strongly influences the quality of the macrostate model. Whereas clustering using only 2 tICA components (a poor model, as judged by GMRQ score) allowed us to build a 230-macrostate model in which all states are populated by all sequences, using 8 tICA components (the best model according to the GMRQ score) resulted in only 40 such states. In the former, the large number of populated macrostates is an artifact due to the overlap of metastable states when projected to only two tICA dimensions.
Non-native salt-bridges alter the folding kinetics of Fs-peptide variants
The slowest implied timescales for each individual macrostate model were computed using 10-fold cross-validation to account for uncertainty due to finite sampling. The results show that, for all sequences, the slowest relaxation timescale is clearly separated from the rest, indicating apparent two-state folding (Figure 2). We note that macrostate MSM implied timescales are accelerated compared to the implied timescales obtained for microstate MSMs. This is an expected artifact of coarse-graining, which arises because macrostate MSM eigenvectors are poorer discrete-state approximations of the true continuous-space eigenvectors. 54 To examine the severity of this coarse-graining artifact, we compare implied timescales for microstate and macrostate MSMs built from the combined data set (Figure 2, right panel). While macrostate coarse-graining decreases the number of states considerably from 1200 to 40, the slowest implied timescale only decreases from ∼360 ns to ∼240 ns, which is less than a fifth of an order of magnitude. We conclude that coarse-graining artifacts are not very severe. Regardless, each individual macrostate MSM is similarly affected by such coarse-graining artifacts, and thus remain comparable.
A comparison of macrostate MSM implied timescales for each sequence reveals a striking difference in folding rates for Fs-EEE (∼180 ns) versus Fs-ERE (∼400 ns), more than doubling the folding time due a mutation of a single residue. Even though a doubling in relaxation timescales may not appear to be a dramatic difference, our results clearly show that we can quantitatively predict such differences, which are significant within error. Indeed, the magnitude of these differences are comparable to those measured in experimental studies.15 To investigate the structural interactions responsible for this difference, we examined the projection of the trajectory data to the 2D landscape defined by the largest two tICA components, tIC1and tIC2.
tICA landscapes reveal helix-bundle “trap” states involved in the slowest relaxations
The 2D tICA projection reveals the presence of metastable states visible as distinct regions of population density, also distinguished by the locations of the 40 macrostate cluster centers, which overlap well with these regions (Figure 3). tIC1 represents the degrees of freedom over which the slowest conformational transition (i.e. folding) occurs, and indeed, native-like macrostates (helical structures) are found on the right side of of the tICA projection, while non-native structures are found on the left side. tIC2 separates two broad kinds of non-native structures; located in the lower half of the tICA projection is a collection of non-helical and helix-bundle states, while the top left is distinctly dominated by a specific helix-bundle conformation (macrostate 20). This helix-bundle state is the most distant from native helical states along the tIC1 component, indicating its importance in determining the overall folding time. It is most populated in the slowest-folding Fs-ERE system, and least populated in the fastest-folding Fs-EEE system. It is worth noting that, unlike the tICA projections, projections of simulation trajectory data to Rg (radius of gyration) vs. RMSD coordinates produces remarkably similar landscapes that provide little, if any, insight into important metastable states (Figure S1).
Figure 3:
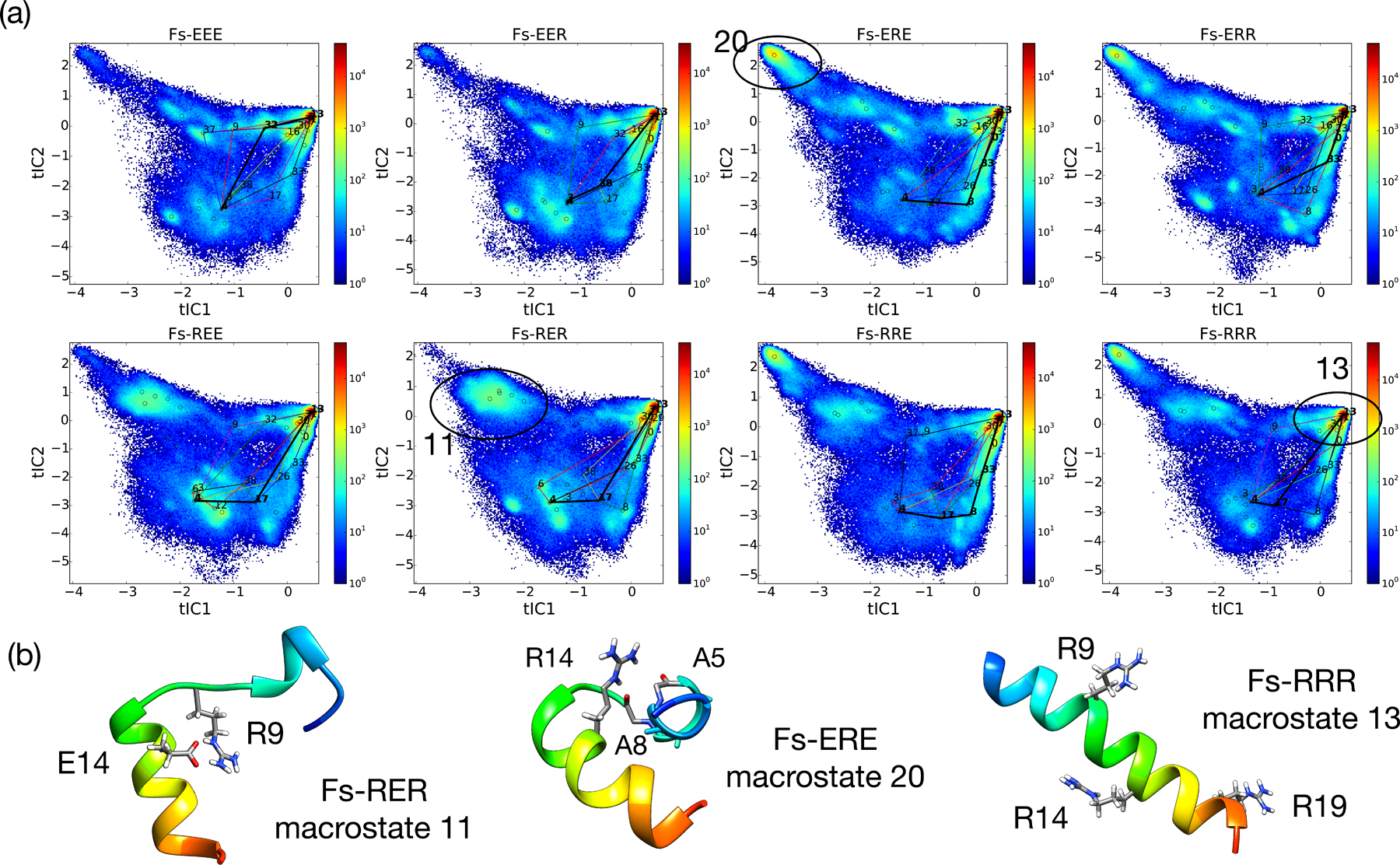
The tICA landscapes of all eight sequences reveal the importance of metastable states with non-native salt-bridges. (a) For each sequence is shown a population density heat-map of simulation snapshots projected to the 2D tICA landscape defined by components tIC1 and tIC2. Open circles denote the cluster center of each of the 40 macrostates. Superimposed on the tICA landscape are pathways showing the ten highest-flux routes from an unstructured macrostate to the native folded state, with the highest-flux path displayed using a black bold line. Macrostates that participate in these pathways are labeled by macrostate index. (b) Representative structures of key macrostates stabilized by non-native salt-bridges (macrostates 11 and 20), and the native-state macrostate 13. The corresponding regions of the tICA landscape for these macrostates are circled and labeled.
Close inspection of the helix-bundle macrostate 20 reveals the structural mechanism of stabilization for Fs-ERE: The guanidinium group on the side chain of R14 makes strong hydrogen bonding interactions with the backbone carbonyl of A8 in the turn region, as well as more transiently with the backbone carbonyl of A5, acting to cap the C-terminus of the preceding helix (Figure 3b). Comparison of the tICA landscapes and implied timescales for all eight sequences suggest that residue 14 is a “gatekeeper” residue for both structure and dynamics. The four sequences having the slowest implied timescales (see Figure 2) all have an R14 residue, whereas the fastest implied timescales are for sequences having an E14 residue. The tICA landscapes for these two groups are strikingly different with respect to macrostate 20, which is significantly populated in all sequences having an R14 residue, and nearly absent in sequences having E14 residue.
Of the sequences having an E14 residue, a further dichotomy can be established. Sequences with an R9 residue (Fs-REE and Fs-RER) have slower implied timescales than those having an E9 residue (Fs-EEE and Fs-EER). The tICA landscapes show that the former group has significant population for macrostate 11, while the latter group does not. Inspection of conformations from macrostate 11 show a structured C-terminal helix and a turn stabilized by a salt bridge between R9 and E14.
To determine the roles of particular macrostates in determining the slowest relaxations, we examined the eigenvectors ϕn of the 40-macrostate MSM transition matrix (Figure S2). For all eight sequences, the eigenvector ϕ0 corresponding to the equilibrium populations shows macrostate 13 (a folded helix) to have the largest population. The eigenvector ϕ1 corresponds to population flux on the folding timescale; positive components represent macrostates of outgoing population flux (i.e. the most important unfolded states), and negative components represent incoming flux (i.e. folded states). For all sequences, the largest negative component of ϕ1 is native macrostate 13, but the positive components differ greatly. The four slowest-folding sequences, all of which contain R14, show macrostate 20 as dominating the positive components. Thus, unlike what we would we expect with diffusive folding from multiple states, we see that the slowest folding relaxation is predominated by flux from macrostate 20, which acts a kinetic “trap” to control the folding rate. For the other four sequences (containing E14), helix-bundle states (macrostates 20 and 2) compose the main kinetic traps.
To verify that these macrostates are indeed off-pathway kinetic traps, we computed the folding flux along macrostate folding pathways using Transition Path Theory (TPT).42,53 For this anaylsis, macrostate 4 was chosen as the unfolded (source) state, as it is the macrostate with the lowest average number of helical residues as the source state; and macrostate 13 was chosen as the folded (sink) state, as it is the macrostate with the lowest conformational free energy (i.e. highest equilibrium population). The ten folding pathways with the largest folding fluxes are shown for all sequences in Figures 3 and S3. Across all eight sequences, the top pathways comprise a family of similar folding paths sharing many common intermediate states, each involving only three to five steps. A clearer picture of these pathways are shown in Figure S3, plotted as a function of the number of helical residues. None of the top ten pathways for any sequence passes through any of the “trap” macrostates, indicating that the traps must be off-pathway. The shape of the population density on the 2D tICA landscape is also consistent with this finding.
Automatic detection and analysis of metastable states most affected by mutations
A key challenge in using Markov State Model approaches for computational protein design is to develop methods by which the effects of sequence mutations on state populations and folding kinetics can be automatically detected and evaluated. In the model system studied here, we have designed sequence mutations with clear expectations about how salt-bridge properties may change. In general, though, the effects of mutations may be quite non-intuitive, and rationalizing their underlying mechanism may be difficult without help from computer algorithms.
Which conformational states have equilibrium populations that are most sensitively perturbed by mutations? To answer this, we computed the Jensen-Shannon divergence of population distributions projected onto the 2D tICA landscape defined by x = (tIC1, tIC2):
| (10) |
where is the probability density of trajectory snapshot counts Nk(x) for sequence k at position x on the tICA landscape, and pk = 1/K (K = 8 sequences).
In practice, since JSpops is calculated by partitioning the tICA landscape into discrete bins x, we plot the contribution of each bin to the Jensen Shannon divergence to visualize which conformational states show the greatest variation in equilibrium populations across all sequence mutants (Figure 4). A similar calculation of JSpops was performed whereby we calculated the contributions of each macrostate. The results show that particular MSM macrostate conformations coincide well with regions of the tICA landscape that contribute most to the JSpops. Consistent with our analysis above, the greatest contribution comes from the helix-bundle “trap” macrostate 20. Other significant macrostates, such as macrostate 11, are similarly detected in an automatic fashion.
Figure 4:
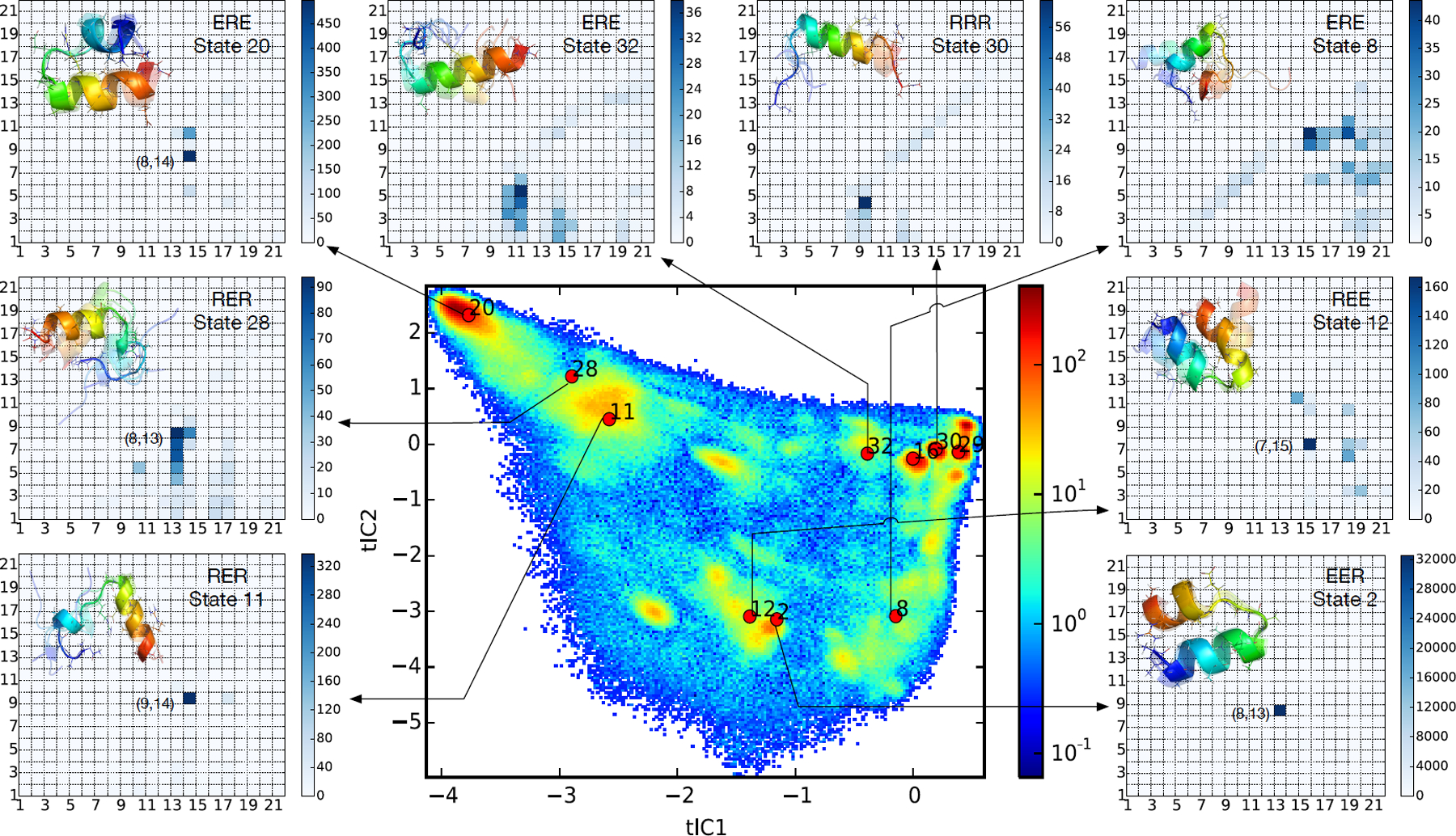
Automatic detection and analysis of important metastable states. A heat-map showing the largest contributions to JSpops clearly identifies regions of conformational space coinciding with metastable states whose populations are most affected by sequence mutations. Contact maps show computed Bayes Factors for all contacts within selected macrostates. Contacts with large Bayes Factor values are those that uniquely define each macrostate. In all cases, computed Bayes Factors recapitulate the important inter-residue contacts otherwise found by visual inspection (see Figure 3).
Bayes Factor analysis.
Once important macrostates are identified, can we automatically discern the structural features that uniquely define each macrostate conformation? To do this, we employed a Bayes Factor analysis of inter-residue contacts, as described in Methods. Shown in Figure 4 are the results of this analysis for selected macrostates (from the ten which that contribute most to JSpops). In all cases, the computed Bayes Factors recapitulate the important inter-residue contacts previously found by visual inspection. Moreover, the Bayes Factor analysis gives a quantitative ranking of the uniqueness of discovered contacts. We find that the largest Bayes Factors are for contact (8,13) in macrostate 2 and contact (8,14) in macrostate 20. The large values of the Bayes Factors for these contacts reflect how unique they are with respect to other macrostates. Mutations that specifically perturb such contacts can thus have large effects on the populations of these macrostates.
Surprisal analysis.
In previous work, we developed surprisal metrics to quantify how MSM dynamics are perturbed by sequence mutations.45 This surprisal analysis is based on the Jensen-Shannon divergence of MSM transition rates, as opposed to state populations. To examine the different kinds of information these two approaches give (i.e. JS vs. JSpops), we performed a surprisal analysis on the 40-macrostate MSM (Figure 5).
Figure 5:
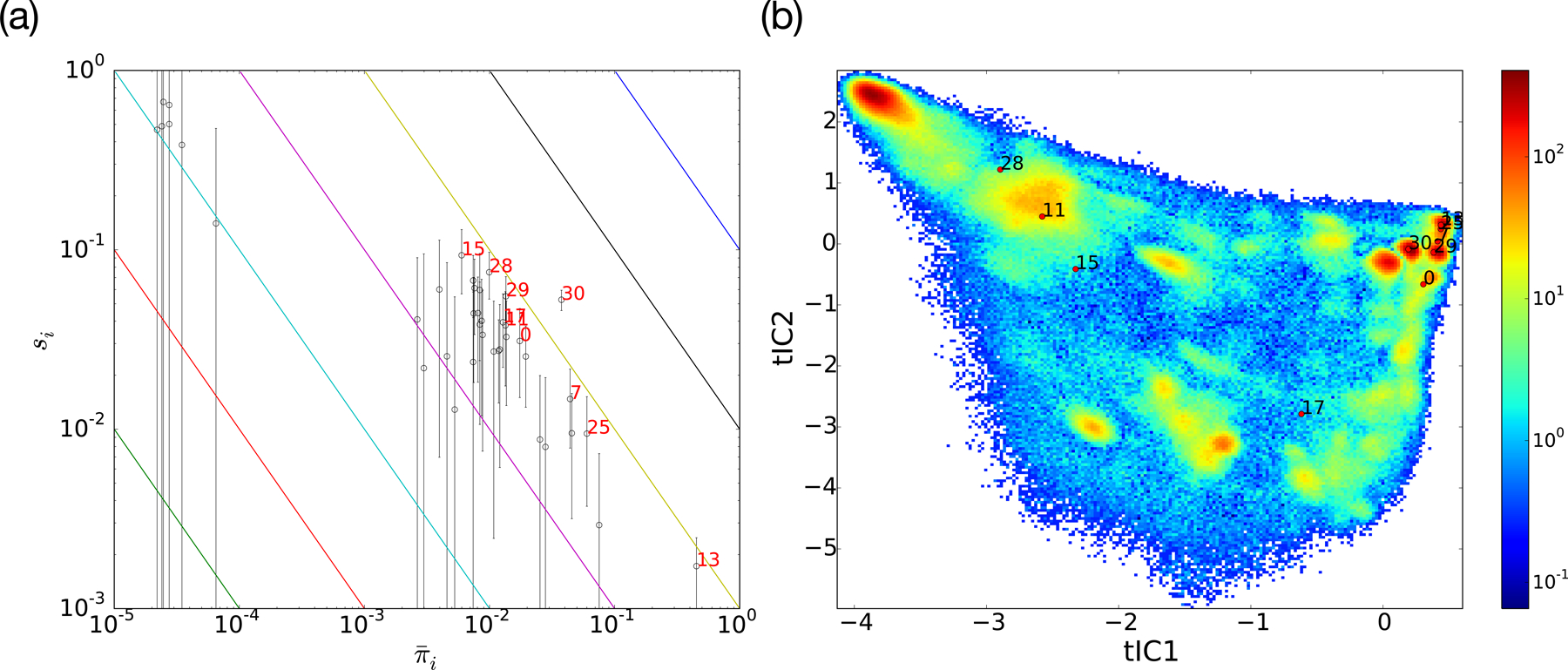
Multi-model surprisal analysis for the eight Fs peptide sequences. (a) A (log-scale) scatter plot of si versus values for each macrostate. Error bars denote estimated uncertainties in si due to finite sampling. Diagonal lines correspond to contours where the JS value is constant, with red index labels marking the ten macrostates with the largest contributions to the JS. (b) The location of these macrostates on the JSpops tICA landscape show that they tend to lie between macrostates whose equilibrium populations are sensitively perturbed by sequence mutations.
As described in Methods, the Jensen-Shannon divergence of a collection of MSMs can be estimated as a sum of contributions, , where is the average population of macrostate i across all sequences, and si is the surprisal for macrostate i (i.e. the Jensen-Shannon divergence of outgoing transition counts across all sequences). Figure 5a shows a (log-scale) scatter plot of si versus values for each macrostate, along with estimated uncertainties due to finite sampling. From this plot, it is clear that some macrostates (such as the native state, macrostate 13), while not having very surprising differences in outgoing transition rates, nevertheless contribute significantly to the JS because of their large equilibrium populations. Other, less populated macrostates, contribute to the JS due to large differences in outgoing transition rates.
We further examine the ten macrostates which contribute most to the JS by showing their locations superimposed on a tICA landscape plot of the contributions to JSpops. (Figure 5b). The plot reveals that these macrostates tend to be located between regions of high population, as one might expect for states bridging local basins on the folding landscape. Like local “transition states”, these macrostates show the largest changes in outgoing transition rates in response to sequence mutations. Particular states that contribute significantly are macrostate 30, which is located along the predominant folding pathways, and macrostate 28, which bridges the important “trap” conformations in macrostate 20 and macrostate 11. As discussed elsewhere, improved sampling of these states would help to efficiently converge the JS metric, as part of a surprisal-baed adaptive sampling algorithm.45
Discussion
The prediction of slower folding kinetics for Fs-ERE compared to Fs-EEE (or more generally, any sequence containing R14 versus those that do not) is reminiscent of experimentally observed changes in folding rates as a function of pH, which suggest that as the propensity for opposite charge-pairing increases, the folding rate becomes slower15,55,56. Recently, Chung et al. published a joint single-molecule FRET and molecular simulation study of the designed helix-bundle protein α3D, which showed a remarkable increase in folding rate at low pH; an effect which the authors could only ascribe to non-native salt bridges between helices.56 Anomalous diffusion in protein folding had previously been interpreted in terms of internal friction57,58; this study firmly establishes that non-native salt-bridges can add to internal friction by increasing the roughness of the energy landscape.
Our simulation study reaches similar conclusions about the role of salt-bridge interactions in slowing helix folding rates. Here, the microscopic detail provided by molecular simulations allow us to make additional predictions about specific non-native conformations that contribute to slower kinetics. In light of recent time-resolved IR studies of salt-bridge perturbations to helix folding15,59, our predictions about the role of non-native salt-bridges on Fs peptide should be highly testable.
We must be careful to note the usual caveats about the ability of molecular forcefields to make accurate predictions about such fine details as the populations of non-native states. That said, several factors contribute to the confidence of our predictions. First, because of the large amount of simulation data made possible by distributed computing, our predictions are not necessary limited by finite sampling effects. Second, we note that AMBER ff99SB-ildn-nmr, the force field used in this study, is highly accurate at predicting experimental NMR data, much of which include chemical shifts and coupling constants for alanine-based peptides.60 Indeed AMBER ff99SB-ildn-nmr was parameterized expressly to best reproduce NMR experimental data.35
Furthermore, the technique of using combined data to build MSMs relys on one assumption that for sequences with only small differences (only several different residues), the metastable states are the same or at least very similar to each other. It is true that different sequences will have different states if we cluster the protein folding conformation very finely and in practice, we did observe that for the 1200-micro states model, different sequence occupy different subset of the states. This is the reason that we need to coarse grain the micro states model to macro states model. Once coarse-grained, the assumption will most likely to be valid. In this work, we use BACE as the lumping method to build the macrostate model. We did not test other lumping algorithms such as the Nystrom algorithm61 which has been shown to be one the best lumping algorithms available.62
Finally, we note that Chung et al. suggest that α3D exhibits such a dramatic increase in folding rate at low pH in part because it is a protein rationally designed for high stability, not for fast folding.56 Our computational results suggest that simulation-based modeling with automated algorithms like the kind were present here could help to optimize salt-bridge interactions for both stability and folding kinetics of designed proteins such as α3D. The ability to computationally design kinetics as well as stability could be useful for controlling many properties, for example, aggregation propensity.63
Conclusion
Using variants of the Fs-peptide as a model system, we have used Markov State Model approaches to clearly show that non-native salt-bridge interactions can have significant effects on folding kinetics. Through the combined use of large-scale conformational sampling made possible by distributed computing, and tICA-based approaches to MSM construction, we have dissected the mechanism by which non-native salt-bridges can affect helix folding in exquisite detail. Across the Arg/Glu variants we examined, we find that R14 acts as a gatekeeper, controlling the formation of a helix-bundle “trap” conformation that dictates the overall folding timescale. In addition, we present a number of new analytical tools that enable the automatic detection and analysis of conformational states most sensitive to perturbation by mutations. We consider these new approaches to be progress toward simulation-based computational protein design.
Supplementary Material
Acknowledgement
The authors thank the participants of Folding@home, without whom this work would not be possible.
Footnotes
Supplemental Figures S1–S5. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- (1).Marqusee S; Robbins VH; Baldwin RL Unusually Stable Helix Formation in Short Alanine-Based Peptides. Proc. Natl. Acad. Sci. U. S. A 1989, 86, 5286–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Marqusee S; Baldwin RL Helix Stabilization by Glu-…Lys+ Salt Bridges in Short Peptides of de novo Design. Proc. Natl. Acad. Sci. U. S. A 1987, 84, 8898–8902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Kim PS; Bierzynski A; Baldwin RL A Competing Salt-Bridge Suppresses Helix Formation by the Isolated C-Peptide Carboxylate of Ribonuclease A. J. Mol. Biol 1982, 162, 187–199. [DOI] [PubMed] [Google Scholar]
- (4).Sommese RF; Sivaramakrishnan S; Baldwin RL; Spudich JA Helicity of Short E-R/K Peptides. Protein Sci 2010, 19, 2001–2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Huyghues-Despointes BM; Scholtz JM; Baldwin RL Helical Peptides with Three Pairs of Asp-Arg and Glu-Arg Residues in Different Orientations and Spacings. Protein science : a publication of the Protein Society 1993, 2, 80–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Horovitz A; Serrano L; Avron B; Bycroft M; Fersht AR Strength and co-Operativity of Contributions of Surface Salt Bridges to Protein Stability. J. Mol. Biol 1990, 216, 1031–1044. [DOI] [PubMed] [Google Scholar]
- (7).Iqbalsyah TM; Doig AJ Anticooperativity in a Glu-Lys-Glu Salt Bridge Triplet in an Isolated α-Helical Peptide ? Biochemistry 2005, 44, 10449–10456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Sivaramakrishnan S; Spink BJ; Sim AY; Doniach S; Spudich JA Dynamic Charge Interactions Create Surprising Rigidity in the ER/K α-Helical Protein Motif. Proc. Natl. Acad. Sci. U. S. A 2008, 13356–13361. [DOI] [PMC free article] [PubMed]
- (9).Sivaramakrishnan S; Sung J; Ali M; Doniach S; Flyvbjerg H; Spudich JA Combining Single-Molecule Optical Trapping and Small-Angle X-Ray Scattering Measurements to Compute the Persistence Length of a Protein ER/K α-Helix. Biophys. J 2009, 97, 2993–2999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Donald JE; Kulp DW; DeGrado WF Salt Bridges: Geometrically Specific, Designable Interactions. Proteins 2011, 79, 898–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Sarakatsannis JN; Duan Y Statistical Characterization of Salt Bridges in Proteins. Proteins 2005, 60, 732–739. [DOI] [PubMed] [Google Scholar]
- (12).Hendsch ZS; Tidor B Do Salt Bridges Stabilize Proteins? A Continuum Electrostatic Analysis. Protein science : a publication of the Protein Society 1994, 3, 211–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Gribenko AV; Patel MM; Liu J; McCallum SA; Wang C; Makhatadze GI Rational Stabilization of Enzymes by Computational Redesign of Surface Charge–Charge Interactions. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 2601–2606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Du D; Bunagan MR; Gai F The Effect of Charge-Charge Interactions on the Kinetics of α-Helix Formation? Biophys. J 2007, 93, 4076–4082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Meuzelaar H; Tros M; Huerta-Viga A; van Dijk CN; Vreede J; Woutersen S Solvent-Exposed Salt Bridges Influence the Kinetics of α-Helix Folding and Unfolding. J. Phys. Chem. Lett 2014, 5, 900–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Tzul FO; Schweiker KL; Makhatadze GI Modulation of Folding Energy Landscape by Charge-Charge Interactions: Linking Experiments with Computational Modeling. Proc. Natl. Acad. Sci. U. S. A 2015, 112, E259–E266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Cho JH; Meng W; Sato S; Kim EY; Schindelin H; Raleigh DP Energetically Significant Networks of Coupled Interactions within an Unfolded Protein. Proc. Natl. Acad. Sci. U. S. A 2014, 111, 12079–12084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Cho J-H; Raleigh DP Denatured State Effects and the Origin of Nonclassical φ Values in Protein Folding. J. Am. Chem. Soc 2006, 128, 16492–16493. [DOI] [PubMed] [Google Scholar]
- (19).Anil B; Craig-Schapiro R; Raleigh DP Design of a Hyperstable Protein by Rational Consideration of Unfolded State Interactions. J. Am. Chem. Soc 2006, 128, 3144–3145. [DOI] [PubMed] [Google Scholar]
- (20).Shaw DE; Chao JC; Eastwood MP; Gagliardo J; Grossman JP; Ho CR; Lerardi DJ; Kolossváry I; Klepeis JL; Layman T et al. Anton, a Special-Purpose Machine for Molecular Dynamics Simulation. Commun. ACM 2008, 51, 91–97. [Google Scholar]
- (21).Shirts M; Pande VS Screen Savers of the World Unite! Science 2000, 290, 1903–1904. [DOI] [PubMed] [Google Scholar]
- (22).Friedrichs MS; Eastman P; Vaidyanathan V; Houston M; Legrand S; Beberg AL; Ensign DL; Bruns CM; Pande VS Accelerating Molecular Dynamic Simulation on Graphics Processing Units. J. Comput. Chem 2009, 30, 864–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Stone JE; Hardy DJ; Ufimtsev IS; Schulten K GPU-Accelerated Molecular Modeling Coming of Age. J. Mol. Graphics Modell 2010, 29, 116–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Nguyen H; Maier J; Huang H; Perrone V; Simmerling C Folding Simulations for Proteins with Diverse Topologies are Accessible in Days with a Physics-Based Force Field and Implicit Solvent. J. Am. Chem. Soc 2014, 136, 13959–13962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Beauchamp KA; Bowman GR; Lane TJ; Maibaum L; Haque IS; Pande VS MSMBuilder2: Modeling Conformational Dynamics on the Picosecond to Millisecond Scale. J. Chem. Theory Comput 2011, 7, 3412–3419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Senne M; Trendelkamp-Schroer B; Mey ASJS; Schütte C; Noé F EMMA: A Software Package for Markov Model Building and Analysis. J. Chem. Theory Comput 2012, 8, 2223–2238. [DOI] [PubMed] [Google Scholar]
- (27).Razavi AM; Wuest WM; Voelz VA Computational Screening and Selection of Cyclic Peptide Hairpin Mimetics by Molecular Simulation and Kinetic Network Models. J. Chem. Inf. Model 2014, 54, 1425–1432. [DOI] [PubMed] [Google Scholar]
- (28).Williams S; Causgrove TP; Gilmanshin R; Fang KS; Callender RH; Woodruff WH; Dyer RB Fast Events in Protein Folding: Helix Melting and Formation in a Small Peptide. Biochemistry 1996, 35, 691–697. [DOI] [PubMed] [Google Scholar]
- (29).Thompson PA; Eaton WA; Hofrichter J Laser Temperature Jump Study of the Helix-Coil Kinetics of an Alanine Peptide Interpreted with a’Kinetic Zipper’Model. Biochemistry 1997, 36, 9200–9210. [DOI] [PubMed] [Google Scholar]
- (30).Lednev IK; Karnoup AS; Sparrow MC; Asher SA α-Helix Peptide Folding and Unfolding Activation Barriers: A Nanosecond UV Resonance Raman Study. J. Am. Chem. Soc 1999, 121, 8074–8086. [Google Scholar]
- (31).Garcia AE; Sanbonmatsu KY Alpha-Helical Stabilization by Side Chain Shielding of Backbone Hydrogen Bonds. Proc. Natl. Acad. Sci. U. S. A 2002, 99, 2782–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Sorin EJ; Pande VS Exploring the Helix-Coil Transition via All-Atom Equilibrium Ensemble Simulations. Biophys. J 2005, 88, 2472–2493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).McGibbon RT; Pande VS Variational Cross-Validation of Slow Dynamical Modes in Molecular Kinetics. J. Chem. Phys 2015, 142, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Pronk S; Pall S; Schulz R; Larsson P; Bjelkmar P; Apostolov R; Shirts MR; Smith JC; Kasson PM; van der Spoel D et al. GROMACS 4.5: a High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Li D-W; Brüschweiler R NMR-Based Protein Potentials. Angew. Chem., Int. Ed 2010, 49, 6778–6780. [DOI] [PubMed] [Google Scholar]
- (36).Schwantes CR; Pande VS Improvements in Markov State Model Construction Reveal Many Non-Native Interactions in the Folding of NTL9. J. Chem. Theory Comput 2013, 9, 2000–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Perez-Hernandez G; Paul F; Giorgino T; De Fabritiis G; Noé F Identification of Slow Molecular Order Parameters for Markov Model Construction. J. Chem. Phys 2013, 139, 015102. [DOI] [PubMed] [Google Scholar]
- (38).Schwantes CR; Pande VS Modeling Molecular Kinetics with tICA and the Kernel Trick. J. Chem. Theory Comput 2015, 11, 600–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Razavi AM; Voelz VA Kinetic Network Models of Tryptophan Mutations in β-Hairpins Reveal the Importance of Non-Native Interactions. J. Chem. Theory Comput 2015, 11, 2801–2812. [DOI] [PubMed] [Google Scholar]
- (40).Chodera JD; Noé F Markov State Models of Biomolecular Conformational Dynamics. Curr. Opin. Struct. Biol 2014, 25, 135–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Prinz J-H; Wu H; Sarich M; Keller B; Senne M; Held M; Chodera JD; Schütte C; Noé F Markov Models of Molecular Kinetics: Generation and Validation. J. Chem. Phys 2011, 134, 174105. [DOI] [PubMed] [Google Scholar]
- (42).Noé F; Schütte C; Vanden-Eijnden E; Reich L; Weikl TR Constructing the Equilibrium Ensemble of Folding Pathways from Short off-Equilibrium Simulations. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 19011–19016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Voelz VA; Bowman GR; Beauchamp K; Pande VS Molecular Simulation of ab initio Protein Folding for a Millisecond Folder NTL9(1–39). J. Am. Chem. Soc 2010, 132, 1526–1528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Bowman GR; Ensign DL; Pande VS Enhanced Modeling via Network Theory: Adaptive Sampling of Markov State Models. J. Chem. Theory Comput 2010, 6, 787–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Voelz VA; Elman B; Razavi AM; Zhou G Surprisal Metrics for Quantifying Perturbed Conformational Dynamics in Markov State Models. J. Chem. Theory Comput 2014, 10, 5716–5728. [DOI] [PubMed] [Google Scholar]
- (46).Zimmerman MI; Bowman GR FAST Conformational Searches by Balancing Exploration/Exploitation Trade-Offs. J. Chem. Theory Comput 2015, 11, 5747–5757. [DOI] [PubMed] [Google Scholar]
- (47).Kohlhoff KJ; Shukla D; Lawrenz M; Bowman GR; Konerding DE; Belov D; Altman RB; Pande VS Cloud-Based Simulations on Google Exacycle Reveal Ligand Modulation of GPCR Activation Pathways. Nat. Chem 2013, 6, 15–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Gu S; Silva D-A; Meng L; Yue A; Huang X Quantitatively Characterizing the Ligand Binding Mechanisms of Choline Binding Protein Using Markov State Model Analysis. PLoS Comput. Biol 2014, 10, e1003767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Plattner N; Noé F Protein Conformational Plasticity and Complex Ligand-Binding Kinetics Explored by Atomistic Simulations and Markov Models. Nat. Commun 2015, 6 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Chodera JD; Swope WC; Pitera JW; Dill KA Long-Time Protein Folding Dynamics from Short-Time Molecular Dynamics Simulations. Multiscale Model. Simul 2006, 5, 1214–1226. [Google Scholar]
- (51).Buchete N-V; Hummer G Coarse Master Equations for Peptide Folding Dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. [DOI] [PubMed] [Google Scholar]
- (52).Bowman GR Improved Coarse-Graining of Markov State Models via Explicit Consideration of Statistical Uncertainty. J. Chem. Phys 2012, 137, 134111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Metzner P; Schütte C; Vanden-Eijnden E Transition Path Theory for Markov Jump Processes. Multiscale Model. Simul 2009, 7, 1192–1219. [Google Scholar]
- (54).Djurdjevac N; Sarich M; Schütte C Estimating the Eigenvalue Error of Markov State Models. Multiscale Model. Simul 2012, 10, 61–81. [Google Scholar]
- (55).Gooding EA; Sharma S; Petty SA; Fouts EA; Palmer CJ; Nolan BE; Volk M pH-Dependent Helix Folding Dynamics of Poly-Glutamic Acid. Chem. Phys 2013, 422, 115–123. [Google Scholar]
- (56).Chung HS; Piana-Agostinetti S; Shaw DE; Eaton WA Structural Origin of Slow Diffusion in Protein Folding. Science 2015, 349, 1504–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Volk M; Milanesi L; Waltho JP; Hunter CA; Beddard GS The Roughness of the Protein Energy Landscape Results in Anomalous Diffusion of the Polypeptide Backbone. Phys. Chem. Chem. Phys 2014, 17, 762–782. [DOI] [PubMed] [Google Scholar]
- (58).Schulz JCF; Miettinen MS; Netz RR Unfolding and Folding Internal Friction of β-Hairpins Is Smaller than That of α-Helices. J. Phys. Chem. B 2015, 119, 4565–4574. [DOI] [PubMed] [Google Scholar]
- (59).Huerta-Viga A; Amirjalayer S; Domingos SR; Meuzelaar H; Rupenyan A; Woutersen S The Structure of Salt Bridges between Arg+ and Glu- in Peptides Investigated with 2D-IR Spectroscopy: Evidence for Two Distinct Hydrogen-Bond Geometries. J. Chem. Phys 2015, 142, 212444. [DOI] [PubMed] [Google Scholar]
- (60).Beauchamp KA; Lin Y-S; Das R; Pande VS Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements. J. Chem. Theory Comput 2012, 8, 1409–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Yao Y; Cui RZ; Bowman GR; Silva D-A; Sun J; Huang X Hierarchical Nyström Methods for Constructing Markov State Models for Conformational Dynamics. J. Chem. Phys 2013, 138, 174106. [DOI] [PubMed] [Google Scholar]
- (62).Bowman GR; Meng L; Huang X Quantitative Comparison of Alternative Methods for Coarse-Graining Biological Networks. J. Chem. Phys 2013, 139, 121905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Ahmad B; Chen Y; Lapidus LJ Aggregation of α-Synuclein is Kinetically Controlled by Intramolecular Diffusion. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 2336–2341. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


