Abstract
Differentiable rendering is a technique to connect 3D scenes with corresponding 2D images. Since it is differentiable, processes during image formation can be learned. Previous approaches to differentiable rendering focus on mesh-based representations of 3D scenes, which is inappropriate for medical applications where volumetric, voxelized models are used to represent anatomy. We propose a novel Projective Spatial Transformer module that generalizes spatial transformers to projective geometry, thus enabling differentiable volume rendering. We demonstrate the usefulness of this architecture on the example of 2D/3D registration between radiographs and CT scans. Specifically, we show that our transformer enables end-to-end learning of an image processing and projection model that approximates an image similarity function that is convex with respect to the pose parameters, and can thus be optimized effectively using conventional gradient descent. To the best of our knowledge, we are the first to describe the spatial transformers in the context of projective transmission imaging, including rendering and pose estimation. We hope that our developments will benefit related 3D research applications. The source code is available at https://github.com/gaocong13/Projective-Spatial-Transformers.
1. Introduction
Differentiable renderers that connect 3D scenes with 2D images thereof have recently received considerable attention [15,7,14] as they allow for simulating, and more importantly inverting, the physical process of image formation. Such approaches are designed for integration with gradient-based machine learning techniques including deep learning to, e.g., enable single-view 3D scene reconstruction. Previous approaches to differentiable rendering have largely focused on mesh-based representation of 3D scenes. This is because compared to say, volumetric representations, mesh parameterizations provide a good compromise between spatial resolution and data volume. Unfortunately, for most medical applications the 3D scene of interest, namely the anatomy, is acquired in volumetric representation where every voxel represents some specific physical property. Deriving mesh-based representations of anatomy from volumetric data is possible in some cases [2], but is not yet feasible nor desirable in general, since surface representations cannot account for tissue variations within one closed surface. However, solutions to the differentiable rendering problem are particularly desirable for X-ray-based imaging modalities, where 3D content is reconstructed from – or aligned to multiple 2D transmission images. This latter process is commonly referred to as 2D/3D registration and we will use it as a test-bed within this manuscript to demonstrate the value of our method.
Mathematically, the mapping from volumetric 3D scene V to projective transmission image Im can be modeled as Im = A(θ)V, where A(θ) is the system matrix that depends on pose parameter θ ∈ SE(3). In intensity-based 2D/3D registration, we seek to retrieve the pose parameter θ such that the image Im simulated from V is as similar as possible to the acquired image If:
| (1) |
where L is the similarity function. Gradient decent-based optimization methods require the gradient at every iteration. Although the mapping was constructed to be differentiable, analytic gradient computation is still impossible due to excessively large memory footprint of A for all practical problem sizes1. Traditional stochastic optimization strategies are numeric-based methods, such as CMA-ES [4]. Since the similarity functions are manually crafted, such as mutual information (MI) [16] or normalized cross correlation, these methods require an initialization which is close to the global optimum, and thus suffer from a small capture range. Recent deep learning-based methods put efforts on learning a similarity metric or regressing the pose transformation from the image observations (If, Im) to extend the capture range [19] [8] [6]. Several researchers proposed reinforcement learning paradigms to iteratively estimate a transformation [18] [11] [13]. However, these learning-based methods only trained on 2D images with no gradient connection to 3D space. Spatial transformer network (STN) [9] has been applied on 3D registration problems to estimate deformation field [12] [1]. Yan et al. proposed perspective transformer nets which applied STN for 3D volume reconstruction [26]. In this work, we propose an analytically differentiable volume renderer that follows the terminology of spatial transformer networks and extends their capabilities to spatial transformations in projective transmission imaging. Our specific contributions are:
We introduce a Projective Spatial Transformer (ProST) module that generalizes spatial transformers [9] to projective geometry. This enables volumetric rendering of transmission images that is differentiable both with respect to the input volume V as well as the pose parameters θ.
We demonstrate how ProST can be used to solve the non-convexity problem of conventional intensity-based 2D/3D registration. Specifically, we train an end-to-end deep learning model to approximate a convex loss function derived from geodesic distances between poses θ and enforce desirable pose updates via double backward functions on the computational graph.
2. Methodology
2.1. Projective Spatial Transformer (ProST)
Canonical projection geometry
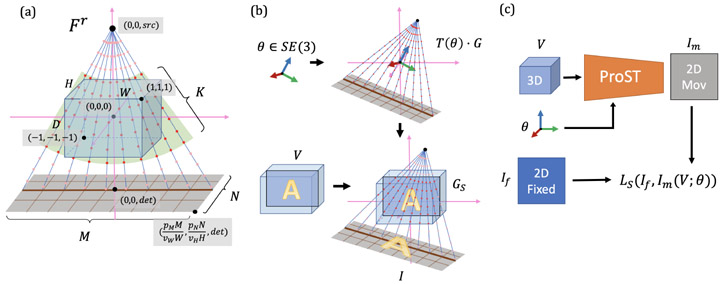
Given a volume with voxel size vD × vW × vH, we define a reference frame Fr with the origin at the center of V. We use normalized coordinates for depth (DvD), width (WvW) and height (HvH), so that the points of V are contained within the unit cube (d, w, h) ∈ [−1, 1]3. Given a camera intrinsic matrix , we denote the associated source point as (0, 0, src) in Fr. The spatial grid G of control points, shown in Fig. 1-(a), lies on M × N rays originating from this source. Because the control points in regions where no CT voxels exist will not contribute to the line integral, we cut the grid point cloud to a cone-shape structure that covers the exact volume space. Thus, each ray has K control points uniformly spaced within the volume V, so that the matrix of control points is well-defined, where each column is a control point in homogeneous coordinates. These rays describe a cone-beam geometry which intersects with the detection plane, centered on (0, 0, det) and perpendicular to the z axis with pixel size pM × pN, as determined by . The upper-right corner of the detection plane is at .
Fig. 1.
(a) Canonical projection geometry and a slice of cone-beam grid points are presented with key annotations. The green fan covers the control points which are used for further reshape. (b) Illustration of grid sampling transformer and projection. (c) Scheme of applying ProST to 2D/3D registration.
Grid sampling transformer
Our Projective Spatial Transformer (ProST) extends the canonical projection geometry by learning a transformation of the control points G. Given θ ∈ SE(3), we obtain a transformed set of control points via the affine transformation matrix T(θ):
| (2) |
as well as source point T(θ) · (0, 0, src, 1) and center of detection plane T(θ) · (0, 0, det, 1). Since these control points lie within the volume V but in between voxels, we interpolate the values GS of V at the control points:
| (3) |
where . Finally, we obtain a 2D image by integrating along each ray. This is accomplished by “collapsing” the k dimension of GS:
| (4) |
The process above takes advantage of the spatial transformer grid, which reduces the projection operation to a series of linear transformations. The intermediate variables are reasonably sized for modern computational graphics cards, and thus can be loaded as a tensor variable. We implement the grid generation function using the C++ and CUDA extension of the PyTorch framework and embed the projection operation as a PyTorch layer with tensor variables. With the help of PyTorch autograd function, this projection layer enables analytical gradient flow from the projection domain back to the spatial domain. Fig. 1 (c) shows how this scheme is applyied to 2D/3D registration. Without any learning parameters, we can perform registration with PyTorch’s powerful built-in optimizers on large-scale volume representations. Furthermore, integrating deep convolutional layers, we show that ProST makes end-to-end 2D/3D registration feasible.
2.2. Approximating Convex Image Similarity Metrics
Following [3], we formulate an intensity-based 2D/3D registration problem with a pre-operative CT volume V, Digitally Reconstructed Radiograph (DRR) projection operator P, pose parameter θ, a fixed target image If, and a similarity metric loss LS:
| (5) |
Using our projection layer P, we propose an end-to-end deep neural network architecture which will learn a convex similarity metric, aiming to extend the capture range of the initialization for 2D/3D registration. Geodesic loss, LG, which is the square of geodesic distance in SE(3), has been studied for registration problems due to its convexity [23] [17]. We take the implementation of [20] to calculate the geodesic gradient , given a sampling pose θ and a target pose θf. We then use this geodesic gradient to train our network, making our training objective exactly the same as our target task – learning a convex shape similarity metric.
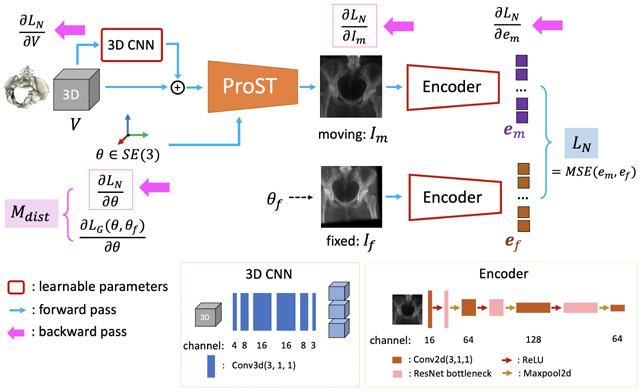
Fig. 2 shows our architecture. The input includes a 3D volume: V, a pose parameter: θ ∈ SE(3) and a fixed target image: If. All blocks which contain learnable parameters are highlighted with a red outline. The 3D CNN is a skip connection from the input volume to multi-channel expansion just to learn the residual. Projections are performed by projection layer with respect to θ, which does not have learnable parameters. The projected moving image Im and the fixed image If go through two encoders, which are the same in structure but the weights are not shared, and output embedded features em and ef. Our network similarity metric LN is the mean squared error of em and ef. We will then explain the design from training phase and application phase separately.
Fig. 2.
DeepNet Architecture. Forward pass follows the blue arrows. Backward pass follows pink arrows, where gradient input and output of ProST in Eq. 10 are highlighted with pink border.
Training phase
The goal of training is to make the gradient of our network error function w.r.t. pose parameter, , close to the geodesic gradient . The blue arrows in Fig. 2 show the forward pass in a single iteration. The output can be written as LN(ϕ; V, θ, If), where ϕ are the network parameters. We then apply back-propagation, illustrated with pink arrows in Fig. 2. This yields and . Assuming LN is the training loss, ϕ would normally be updated according to , where lr is learning rate. However, we do not update the network parameters during the backward pass. Instead we obtain the gradient and calculate a distance measure of these two gradient vectors, , which is our true network loss function during training. We perform a second forward pass, or “double backward” pass, to get for updating network parameters ϕ. To this end, we formulate the network training as the following optimization problem
| (6) |
Since the gradient direction is the most important during iteration in application phase, we design Mdist by punishing the directional difference of these two gradient vectors. Translation and rotation are formulated using Eq. 7-9
| (7) |
| (8) |
| (9) |
where the rotation vector is transformed into Rodrigues angle axis.
Application phase
During registration, we fix the network parameters ϕ and start with an initial pose θ. We can perform gradient-based optimization over θ based on the following back-propagation gradient flow
| (10) |
The network similarity is more effective when the initial pose is far away from the groundtruth, while less senstive to local textures compared to traditional image-based methods, such as Gradient-based Normalized Corss Correlation (Grad-NCC) [21]. We implement Grad-NCC as a pytorch loss function LGNCC, and combine these two methods to build an end-to-end pipeline for 2D/3D registration. We first detect the convergence of the network-based optimization process by monitoring the standard deviation (STD) of LN. After it converges, we then switch to optimize over LGNCC until final convergence.
3. Experiments
3.1. Simulation study
We define our canonical projection geometry following the intrinsic parameter of a Siemens CIOS Fusion C-Arm, which has image dimensions of 1536 × 1536, isotropic pixel spacing of 0.194 mm/pixel, a source-to-detector distance of 1020 mm. We downsample the detector dimension to be 128 × 128. We train our algorithm using 17 full body CT scans from the NIH Cancer Imaging Archive [22] and leave 1 CT for testing. The pelvis bone is segmented using an automatic method in [10]. CTs and segmentations are cropped to the pelvis cubic region and downsampled to the size of 128 × 128 × 128. The world coordinate frame origin is set at center of the processed volume, which is 400 mm above the detector plane center.
At training iteration i, we randomly sample a pair of pose parameters, (θi, ), rotation from N(0, 20) in degree, translation from N(0, 30) in mm, in all three axes. We then randomly select a CT and its segmentation, VCT and VSeg. The target fixed image is generated online from VCT and using our ProST. VSeg and θ are used as input to our network forward pass. The network is trained using SGD optimizer with a cyclic learning rate between 1e-6 and 1e-4 every 100 steps [24] and a momentum of 0.9. Batch size is chosen as 2 and we trained 100k iterations until convergence.
We performed the 2D/3D registration application by randomly choosing a pose pair from the same training distribution, (θR, ). Target fixed image is generated from the testing CT and . We then use SGD optimizer to optimize over θR with a learning rate of 0.01, momentum of 0.9 for iteration. We calculate the STD of the last 10 iterations of LN as stdLN, and set a stop criterion of stdLN < 3 × 10−3, then we switch to Gradient-NCC similarity using SGD optimizer with cyclic learning rate between 1e-3 and 3e-3, and set the stop criterion, stdLNCC < 1 × 10−5. We conduct in total of 150 simulation studies for testing our algorithm.
3.2. Real X-ray study
We collected 10 real X-ray images from a cadaver specimen. Groundtruth pose is obtained by injecting metallic BBs with 1 mm diameter into the surface of the bone and manually annotated from the X-ray images and CT scan. The pose is recovered by solving a PnP problem [5]. For each X-ray image, we randomly choose a pose parameter, rotation from N(0, 15) in degree, translation from N(0, 22.5) in mm, in all three axes. 10 registrations are performed for each image using the same pipeline, resulting in a total of 100 registrations.
4. Results
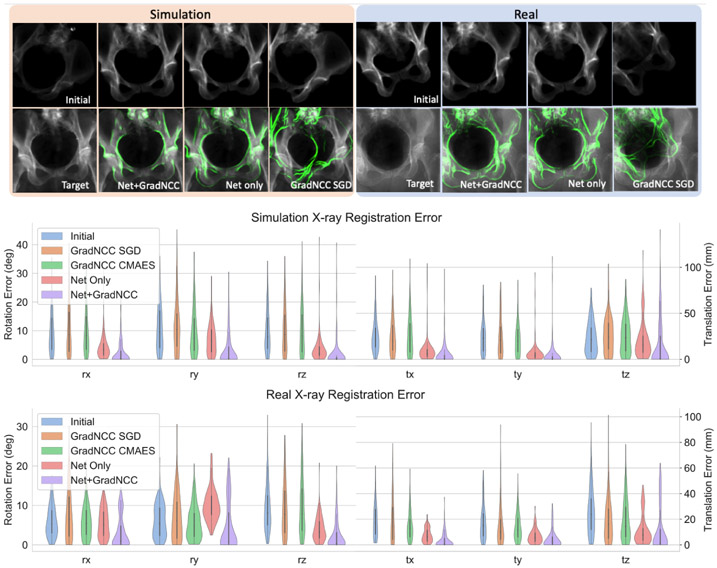
We compared the performance of four methods, which are Grad-NCC with SGD optimizer (GradNCC SGD), Grad-NCC with CMA-ES optimizer (GradNCC CMAES), Net only, and Net+GradNCC. The registration accuracy was used as the evaluation metric, where the rotation and translation errors are expressed in degree and millimeter, respectively. The coordinate frame Fr are used to define the origin and orientation of the pose. In Fig. 3, both qualitative and quantitative results on the testing data are shown. Numeric results are shown in Table 1. The Net+GradNCC works the best among comparisons in both studies.
Fig. 3.
The top row shows qualitative examples of Net+GradNCC, Net only, GradNCC only convergence overlap, for simulation and real X-ray respectively. The middle is the registration error distribution of simulation. The bottom is the distribution for real X-ray experiments. x, y and z-axis correspond to LR, IS and AP views.
Table 1.
Quantitative Results of 2D/3D Registration
| Simulation Study | Real X-ray Study | ||||
|---|---|---|---|---|---|
| Translation | Rotation | Translation | Rotation | ||
| Initialization | 41.57 ± 18.01 | 21.16 ± 9.27 | 30.50 ± 13.90 | 14.22 ± 5.56 | |
| GradNCC SGD | mean | 41.83 ± 23.08 | 21.97 ± 11.26 | 29.52 ± 20.51 | 15.76 ± 8.37 |
| median | 38.30 | 22.12 | 26.28 | 16.35 | |
| GradNCC CMAES | mean | 40.68 ± 22.04 | 20.16 ± 9.32 | 25.64 ± 12.09 | 14.31 ± 6.74 |
| median | 37.80 | 20.63 | 23.87 | 13.80 | |
| Net | mean | 13.10 ± 18.53 | 10.21 ± 7.55 | 12.14 ± 6.44 | 13.00 ± 4.42 |
| median | 9.85 | 9.47 | 11.06 | 12.61 | |
| Net+ GradNCC | mean | 7.83 ± 19.8 | 4.94 ± 8.78 | 7.02 ± 9.22 | 6.94 ± 7.47 |
| median | 0.25 | 0.27 | 2.89 | 3.76 | |
5. Discussion
We have seen from the results that our method largely increases the capture range of 2D/3D registration. Our method follows the same iterative optimization design as the intensity-based registration methods, where the only difference is that we take advantage of the great expressivity of deep network to learn a set of more complicated filters than the conventional hand-crafted ones. This potentially makes generalization easier because the mapping that our method needs to learn is simple. In the experiment, we observed that the translation along the depth direction is less accurate than other directions in both simulation and real studies, as shown in Fig. 3, which we attribute to the current design of the network architecture and will work on that as a future direction.
6. Conclusion
We propose a novel Projective Spatial Transformer module (ProST) that generalizes spatial transformers to projective geometry, which enables differentiable volume rendering. We apply this to an example application of 2D/3D registration between radiographs and CT scans with an end-to-end learning architecture that approximates convex loss function. We believe this is the first time that spatial transformers have been introduced for projective geometry and our developments will benefit related 3D research applications.
Acknowledgments
Supported by NIH R01EB023939, NIH R21EB020113, NIH R21EB028505 and Johns Hopkins University Applied Physics Laboratory internal funds.
Footnotes
It is worth mentioning that this problem can be circumvented via ray casting-based implementations if one is interested in ∂L/∂V but not in ∂L/∂θ [25].
References
- 1.Ferrante E, Oktay O, Glocker B, Milone DH: On the adaptability of unsupervised cnn-based deformable image registration to unseen image domains. In: International Workshop on Machine Learning in Medical Imaging pp. 294–302. Springer; (2018) [Google Scholar]
- 2.Gibson E, Giganti F, Hu Y, Bonmati E, Bandula S, Gurusamy K, Davidson B, Pereira SP, Clarkson MJ, Barratt DC: Automatic multi-organ segmentation on abdominal ct with dense v-networks. IEEE transactions on medical imaging 37(8), 1822–1834 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Grupp R, Unberath M, Gao C, Hegeman R, Murphy R, Alexander C, Otake Y, McArthur B, Armand M, Taylor R: Automatic annotation of hip anatomy in fluoroscopy for robust and efficient 2d/3d registration. arXiv preprint arXiv:1911.07042 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hansen N, Müller SD, Koumoutsakos P: Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (cma-es). Evolutionary computation 11(1), 1–18 (2003) [DOI] [PubMed] [Google Scholar]
- 5.Hartley R, Zisserman A: Multiple view geometry in computer vision. Cambridge university press; (2003) [Google Scholar]
- 6.Haskins G, Kruger U, Yan P: Deep learning in medical image registration: a survey. Machine Vision and Applications 31(1), 8 (2020) [Google Scholar]
- 7.Henderson P, Ferrari V: Learning single-image 3d reconstruction by generative modelling of shape, pose and shading. International Journal of Computer Vision pp. 1–20 (2019) [Google Scholar]
- 8.Hou B, Alansary A, McDonagh S, Davidson A, Rutherford M, Hajnal JV, Rueckert D, Glocker B, Kainz B: Predicting slice-to-volume transformation in presence of arbitrary subject motion In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 296–304. Springer; (2017) [Google Scholar]
- 9.Jaderberg M, Simonyan K, Zisserman A, et al. : Spatial transformer networks. In: Advances in neural information processing systems. pp. 2017–2025 (2015) [Google Scholar]
- 10.Krčah M, Székely G, Blanc R: Fully automatic and fast segmentation of the femur bone from 3d-ct images with no shape prior. In: 2011 IEEE international symposium on biomedical imaging: from nano to macro pp. 2087–2090. IEEE; (2011) [Google Scholar]
- 11.Krebs J, Mansi T, Delingette H, Zhang L, Ghesu FC, Miao S, Maier AK, Ayache N, Liao R, Kamen A: Robust non-rigid registration through agent-based action learning In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 344–352. Springer; (2017) [Google Scholar]
- 12.Kuang D, Schmah T: Faim–a convnet method for unsupervised 3d medical image registration. In: International Workshop on Machine Learning in Medical Imaging pp. 646–654. Springer; (2019) [Google Scholar]
- 13.Liao R, Miao S, de Tournemire P, Grbic S, Kamen A, Mansi T, Comaniciu D: An artificial agent for robust image registration. In: Thirty-First AAAI Conference on Artificial Intelligence (2017) [Google Scholar]
- 14.Liu S, Li T, Chen W, Li H: Soft rasterizer: A differentiable renderer for image-based 3d reasoning. In: Proceedings of the IEEE International Conference on Computer Vision. pp. 7708–7717 (2019) [Google Scholar]
- 15.Loper MM, Black MJ: Opendr: An approximate differentiable renderer In: European Conference on Computer Vision. pp. 154–169. Springer; (2014) [Google Scholar]
- 16.Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P: Multimodality image registration by maximization of mutual information. IEEE transactions on Medical Imaging 16(2), 187–198 (1997) [DOI] [PubMed] [Google Scholar]
- 17.Mahendran S, Ali H, Vidal R: 3d pose regression using convolutional neural networks. In: Proceedings of the IEEE International Conference on Computer Vision Workshops. pp. 2174–2182 (2017) [Google Scholar]
- 18.Miao S, Piat S, Fischer P, Tuysuzoglu A, Mewes P, Mansi T, Liao R: Dilated fcn for multi-agent 2d/3d medical image registration. In: Thirty-Second AAAI Conference on Artificial Intelligence (2018) [Google Scholar]
- 19.Miao S, Wang ZJ, Liao R: A cnn regression approach for real-time 2d/3d registration. IEEE transactions on medical imaging 35(5), 1352–1363 (2016) [DOI] [PubMed] [Google Scholar]
- 20.Miolane N, Mathe J, Donnat C, Jorda M, Pennec X: geomstats: a python package for riemannian geometry in machine learning. arXiv preprint arXiv:1805.08308 (2018) [Google Scholar]
- 21.Penney GP, Weese J, Little JA, Desmedt P, Hill DL, et al. : A comparison of similarity measures for use in 2-d-3-d medical image registration. IEEE transactions on medical imaging 17(4), 586–595 (1998) [DOI] [PubMed] [Google Scholar]
- 22.Roth HR, Lu L, Seff A, Cherry KM, Hoffman J, Wang S, Liu J, Turkbey E, Summers RM: A new 2.5 d representation for lymph node detection using random sets of deep convolutional neural network observations In: International conference on medical image computing and computer-assisted intervention. pp. 520–527. Springer; (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Salehi SSM, Khan S, Erdogmus D, Gholipour A: Real-time deep registration with geodesic loss. arXiv preprint arXiv:1803.05982 (2018) [Google Scholar]
- 24.Smith LN: Cyclical learning rates for training neural networks. In: 2017 IEEE Winter Conference on Applications of Computer Vision (WACV) pp. 464–472. IEEE; (2017) [Google Scholar]
- 25.Würfl T, Hoffmann M, Christlein V, Breininger K, Huang Y, Unberath M, Maier AK: Deep learning computed tomography: Learning projection-domain weights from image domain in limited angle problems. IEEE transactions on medical imaging 37(6), 1454–1463 (2018) [DOI] [PubMed] [Google Scholar]
- 26.Yan X, Yang J, Yumer E, Guo Y, Lee H: Perspective transformer nets: Learning single-view 3d object reconstruction without 3d supervision. In: Advances in neural information processing systems. pp. 1696–1704 (2016) [Google Scholar]