Count regression models for COVID-19

Abstract

At the end of 2019, the current novel coronavirus emerged as a severe acute respiratory disease that has now become a worldwide pandemic. Future generations will look back on this difficult period and see how our society as a whole united and rose to this challenge. Many reports have suggested that this new virus is becoming comparable to the Spanish flu pandemic of 1918. We provide a statistical study on the modelling and analysis of the daily incidence of COVID-19 in eighteen countries around the world. In particular, we investigate whether it is possible to fit count regression models to the number of daily new cases of COVID-19 in various countries and make short term predictions of these numbers. The results suggest that the biggest advantage of these methods is that they are simplistic and straightforward allowing us to obtain preliminary results and an overall picture of the trends in the daily confirmed cases of COVID-19 around the world. The best fitting count regression model for modelling the number of new daily COVID-19 cases of all countries analysed was shown to be a negative binomial distribution with log link function. Whilst the results cannot solely be used to determine and influence policy decisions, they provide an alternative to more specialised epidemiological models and can help to support or contradict results obtained from other analysis.

Highlights

• •COVID-19 cases for 18 countries are modelled.
• •Simple and easily interpretable models are used.
• •Predictions on number of cases are given which are robust.

1. Introduction

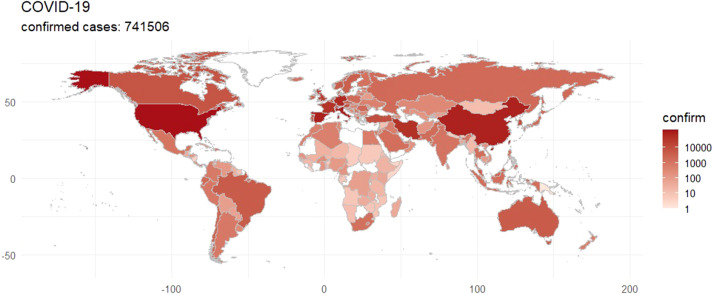
The novel coronavirus disease (COVID-19) first identified in Wuhan, the capital of Hubei, China in October 2019, is a severe acute respiratory disease that has now become a worldwide pandemic. Fig. 1 shows the extreme extent to which this pandemic has spread across the world, with the total number of confirmed global cases exceeding 700,000 as of 30th March 2020 and is still increasing exponentially. The total number of cases worldwide has already surpassed the number due to the severe acute respiratory syndrome (SARS) in the early 2000s. Many reports have suggested that this new virus is becoming comparable to the Spanish flu pandemic from 1918.

Fig. 1.

A world map of the total confirmed cases of COVID-19 as of 30th March 2020.

The most common symptoms of COVID-19 are almost identical to those of the flu - e.g. high fever, fatigue, cough and shortness of breath. Individuals have been required to self-isolate if they believe that they are exhibiting these symptoms. The most severe symptoms have been linked to pneumonia, multi-organ failure, and death. Other symptoms of COVID-19 include the loss of sense of smell (anosmia) and in some cases individuals may display no symptoms at all, but will still be carrying the virus.

The global effects of COVID-19 have led to many countries locking down their international borders, cities and towns for extended periods. For example, in China, UK, Italy, Spain, France and many others. Hence, many are fearful that another global recession is on the horizon. On the contrary, after a two month national lock-down, China has shown the world that a strict lock-down has contributed to a reduction in the number of new cases and deaths from COVID-19, with the number of new cases recently decreasing to zero.

The current literature relating to COVID-19 is limited and the majority of the known work focuses exclusively on China, where the first major outbreaks occurred. The existing research has focused on topics such as determining the population who are most at risk, the factors increasing the risk of infection, the medical properties of those who become infected, the factors that can improve clinical outcomes and reduce the spread of the virus, the biological properties of the virus, and many others. See for example [1], [2], [3], [4], [5], [6], [7], and [8].

More specifically, the literature relating to COVID-19 analysis outside of China has been limited. Since these countries are lagging behind China in terms of the overall spread of the disease, much of the literature has been focused on modelling and predicting the disease in the early stages of the outbreak — particularly the daily incidence (number of new confirmed cases per day) and the basic reproductive number. For example, in Italy [9], [10], in France [11], and in Japan [12], [13], [14]; to name but a few.

Thus far, a wide range of statistical and predictive methods have already been applied to the analysis of COVID-19 in China, for example traditional epidemic models, such as the SIR model [15], [16] and the basic reproductive number [17]; neural networks [18]; regression models [19], [20]; experimental frameworks [21]; correlation analysis [22].

From the literature, it is evident that the majority of the analyses on COVID-19 are limited to China, and a limited number of countries in Asia and Europe. These are arguably the countries that first identified known cases of COVID-19. However, we should note that since this is an ongoing situation, new research is being published daily and therefore the literature is being updated continuously. Hence, our main motivation is to provide a statistical analysis in modelling and analysing the number of confirmed cases of COVID-19 in eighteen countries around the world. The main contributions of this paper are: (i) to provide a statistical analysis of COVID-19 worldwide; (ii) to investigate whether it is possible to utilise count regression models for fitting and predicting the number of daily confirmed cases due to COVID-19 globally.

The contents of this paper are organised as follows. Section 2 describes the data used in our analysis. In Section 3, we detail the methodology and models used. Section 4 outlines the results, and provides a discussion of these results. Section 5 provides a conclusion and summary of our results.

2. Data

The data we analyse consists of the historical daily new cases due to the COVID-19 Coronavirus confirmed from eighteen different countries worldwide (China, Denmark, Estonia, France, Germany, Italy, Malaysia, Philippines, Qatar, South Korea, Sri Lanka, Sweden, Taiwan, Thailand, UAE, UK, USA, Vietnam), listed on the EU Open Data Portal from 31st December 2019 to 25th March 2020. These countries were chosen because they were the earliest countries to detect COVID infections.

The data were downloaded from the website “European Centre for Disease Prevention and Control” (ECDC) which sources its data from the WHO, and our analysis is limited to the data available at the time of writing. The eighteen countries were chosen based on their ranking in terms of the highest numbers of cases, thus we believe that the data obtained gives a satisfactory representation of the main countries affected by the virus at these times.

3. Methodology

In epidemiology and the study of infectious diseases, count-based data related to incidence are commonplace. In particular, data such as the daily incidence (number of cases) relating to an infectious disease can be modelled and predicted using a wide variety of methods, including compartmental (or deterministic) models such as the SIR and SEIR models, and stochastic models such as discrete time and continuous time Markov chains, and stochastic differential equations. In this study, we apply discrete time count regression models with the aim of modelling and predicting the daily incidence of COVID-19 across the world. Such models are preferred because they provide an appropriate, rich, and flexible modelling environment for non-negative integers. In addition, the models are robust for estimating constant relative policy effects and when implemented to policy evaluations, such models can move beyond the consideration of mean effects and determine the effect on the entire distribution of outcomes instead [23]. Poisson count regression models are part of the family of generalised linear models that are commonly used in epidemiological studies [24]. The Poisson and negative binomial regression models are widely used for modelling discrete count data where the count takes a non-negative integer with no upper limit, while the data is highly skewed. The negative binomial regression has the added advantage of being able to deal with the problem of overdispersion [25].

The four models below are due to Christou and Fokianos [26], [27], Fokianos and Fried [28], Fokianos et al. [29] and Fokianos and Tjostheim [30]. The models due to Christou and Fokianos [26] are based on the negative binomial distribution. The models due to the others are based on the Poisson distribution. Both Poisson and negative binomial distributions are commonly implemented when dealing with count data and observations occurring at a specific rate.

Let $Z_t=$ denote the number of newly confirmed cases in a country on day $t$, $t=1,\dots ,T$. In other words, $Z_t=$ the change in the cumulative confirmed cases from day $t-1$ to $t$. For each of the eighteen countries selected, the following four regression models were fitted to the corresponding daily incidence data:

• • $Z_t\mid {\mathcal{F}}_{t-1}\sim \mathrm{Poisson}\left(\alpha +\beta t\right)$, with link function $=$ ‘identity’ and distribution $=$ ‘Poisson’.
• • $Z_t\mid {\mathcal{F}}_{t-1}\sim \mathrm{Poisson}\left(exp\left(\alpha +\beta t\right)\right)$, with link function $=$ ‘log’ and distribution $=$ ‘Poisson’.
• • $Z_t\mid {\mathcal{F}}_{t-1}\sim \mathrm{NegativeBinomial}\left(\alpha +\beta t,\varphi \right)$, with link function $=$ ‘identity’ and distribution $=$ ‘negative binomial’.
• • $Z_t\mid {\mathcal{F}}_{t-1}\sim \mathrm{NegativeBinomial}\left(exp\left(\alpha +\beta t\right),\varphi \right)$, with link function $=$ ‘log’ and distribution ‘negative binomial’.

where ${\mathcal{F}}_{t-1}$ denotes the history up to day $t-1$, $\alpha$ represents the intercept parameter, and $\beta$ is the slope parameter.

Each of the four models was fitted by the method of maximum likelihood. That is, by maximising

$$L_1(\alpha ,\beta )=\prod _{t=1}^T\frac{{\left(\alpha +\beta t\right)}^{Z_t}}{Z_t!}exp\left(-\alpha -\beta t\right),$$

$$L_2(\alpha ,\beta )=\prod _{t=1}^T\frac{exp{\left(\alpha +\beta t\right)}^{Z_t}}{Z_t!}exp\left[-exp\left(\alpha +\beta t\right)\right],$$

$$L_3(\alpha ,\beta ,\varphi )=\prod _{t=1}^T\left[\left(\genfrac{}{}{0ex}{}{Z_t+\alpha +\beta t-1}{Z_t}\right){(1-\varphi )}^{\alpha +\beta t}{\varphi }^{Z_t}\right],$$

and

$$L_4(\alpha ,\beta ,\varphi )=\prod _{t=1}^T\left[\left(\genfrac{}{}{0ex}{}{Z_t+exp\left(\alpha +\beta t\right)-1}{Z_t}\right){(1-\varphi )}^{exp\left(\alpha +\beta t\right)}{\varphi }^{Z_t}\right],$$

respectively, with respect to $\alpha$, $\beta$ and $\varphi$. We shall denote the maximum likelihood estimates by $\widehat{\alpha }$, $\widehat{\beta }$ and $\widehat{\varphi }$, respectively. For a more in-depth discussion of the four regression models we refer the readers to the literature cited above. The models were fitted using the command tsglm in the R package tscount [31].

For each of the fitted models, we computed the Akaike information criterion (AIC), Bayesian information criterion (BIC) and associated $p$-values obtained by re-sampling. The AIC for the four models were computed as

$$AIC=4-2log{L}_1\left(\widehat{\alpha },\widehat{\beta }\right),$$

$$AIC=4-2log{L}_2\left(\widehat{\alpha },\widehat{\beta }\right),$$

$$AIC=6-2log{L}_3\left(\widehat{\alpha },\widehat{\beta },\widehat{\varphi }\right),$$

and

$$AIC=6-2log{L}_4\left(\widehat{\alpha },\widehat{\beta },\widehat{\varphi }\right).$$

The BIC for the four models were computed as

$$BIC=2logT-2log{L}_1\left(\widehat{\alpha },\widehat{\beta }\right),$$

$$BIC=2logT-2log{L}_2\left(\widehat{\alpha },\widehat{\beta }\right),$$

$$BIC=3logT-2log{L}_3\left(\widehat{\alpha },\widehat{\beta },\widehat{\varphi }\right),$$

and

$$BIC=3logT-2log{L}_4\left(\widehat{\alpha },\widehat{\beta },\widehat{\varphi }\right).$$

The values are given in Table 1. According to AIC and BIC values, the best model out of the four is the negative binomial model with a logarithmic link function. Table 2 gives the estimates of the intercept and slope parameters along with their corresponding standard errors for this model. Also given in Table 2 are the $p$-values quantifying the significance of the slope parameter. In line with standard significance levels, if the $p$-value is less than 0.05 then the slope estimate is deemed to be significant.

Table 1.

Values of AIC (and values of BIC in brackets) for the four models fitted to the data from 31 December 2019 to 25 March 2020.

Country	Models
	(Identity, Poisson)	(Log, Poisson)	(Identity, negative binomial)	(Log, negative binomial)
China	−99.1 (−94.1)	−100.0 (−95.0)	−123.7 (−116.3)	−138.2 (−130.8)
Denmark	−97.9 (−93.0)	−112.7 (−107.8)	−135.2 (−127.8)	−142.0 (−134.6)
Estonia	−106.3 (−101.5)	−108.7 (−103.8)	−121.0 (−113.8)	−121.3 (−114.1)
France	−99.6 (−94.6)	−100.7 (−95.8)	−111.3 (−103.9)	−141.9 (−134.5)
Germany	−96.4 (−91.5)	−114.9 (−110.0)	−114.9 (−107.5)	−139.2 (−131.8)
Italy	−110.2 (−105.3)	−114.1 (−109.2)	−123.1 (−115.7)	−132.1 (−124.7)
Malaysia	−103.6 (−98.7)	−120.5 (−115.5)	−123.1 (−115.7)	−143.0 (−135.6)
Philippines	−99.9 (−95.1)	−109.9 (−105.1)	−127.2 (−120.0)	−130.1 (−122.9)
Qatar	−96.6 (−91.7)	−107.5 (−102.7)	−107.6 (−100.4)	−114.3 (−107.0)
South Korea	−98.4 (−93.5)	−98.9 (−94.0)	−113.4 (−106.0)	−140.7 (−133.3)
Sri Lanka	−98.1 (−93.3)	−106.5 (−101.8)	−111.6 (−104.5)	−117.2 (−110.1)
Sweden	−103.6 (−98.6)	−119.8 (−114.8)	−118.3 (−110.9)	−139.8 (−132.4)
Taiwan	−110.2 (−105.3)	−122.9 (−118.0)	−121.0 (−113.7)	−128.8 (−121.5)
Thailand	−107.5 (−102.7)	−109.7 (−104.9)	−121.1 (−114.0)	−138.7 (−131.6)
United Arab Emirates	−120.3 (−115.5)	−122.9 (−118.2)	−128.3 (−121.2)	−128.4 (−121.2)
United Kingdom	−107.3 (−102.4)	−129.6 (−124.7)	−134.4 (−127.0)	−139.1 (−131.7)
United States of America	−107.9 (−102.9)	−114.7 (−109.8)	−121.7 (−114.3)	−125.5 (−118.1)
Vietnam	−97.3 (−92.4)	−100.1 (−95.3)	−136.2 (−128.9)	−139.6 (−132.4)

Table 2.

Parameter estimates and standard errors for the (log, negative binomial) model.

Country	Observations	Intercept	SE	Slope	SE	$p$-value
China	87	6.960	0.442	−0.003	0.009	0.763
Denmark	87	−4.032	1.179	0.106	0.017	0.000
Estonia	82	−6.390	1.118	0.125	0.016	0.000
France	87	−5.660	1.582	0.160	0.021	0.000
Germany	87	−7.119	2.583	0.182	0.034	0.000
Italy	87	−1.609	1.088	0.123	0.015	0.000
Malaysia	86	−6.524	11.131	0.139	0.054	0.000
Philippines	83	−9.782	18.315	0.173	0.254	0.082
Qatar	83	−3.636	1.683	0.090	0.017	0.000
South Korea	87	2.363	0.458	0.041	0.008	0.005
Sri Lanka	78	−8.422	3.753	0.141	0.018	0.000
Sweden	87	−4.795	0.849	0.120	0.012	0.000
Taiwan	85	−4.538	2.377	0.089	0.017	0.000
Thailand	80	−6.063	15.291	0.127	0.017	0.011
United Arab Emirates	81	−4.184	92.251	0.077	0.007	0.000
United Kingdom	87	−9.289	8.573	0.192	0.011	0.000
United States of America	87	−4.851	69.898	0.106	0.028	0.000
Vietnam	83	−4.519	1.810	0.084	0.019	0.000

4. Results and discussion

We applied the models specified in Section 3 and fitted them to our data on the number of new daily cases of individuals infected with COVID-19 from eighteen different countries worldwide. According to Table 2, the majority of $p$-values corresponding to the best fitting model (negative binomial model with a logarithmic link function) for each country’s data are smaller than 0.05 — indicating significance of the slope coefficient estimates at the 5 percent significance. However, a particular exception is that of China, whose $p$-value is significantly greater than 0.05. This result is, perhaps, not surprising as China was the first country to be majorly affected by COVID-19 and by the time most other countries started to see significant increases in new numbers of cases its numbers had already peaked and new cases in China were being confirmed at a slower rate.

Among the countries where the model appears to show a reasonable fit, the slope estimate was positive in all cases indicating the expected number of new cases confirmed each day is expected to increase with respect to time. In particular, the UK and Vietnam have the largest and smallest slope estimates, respectively, hence the rate of increase in new daily COVID-19 cases with time is the highest for the UK and lowest for Vietnam.

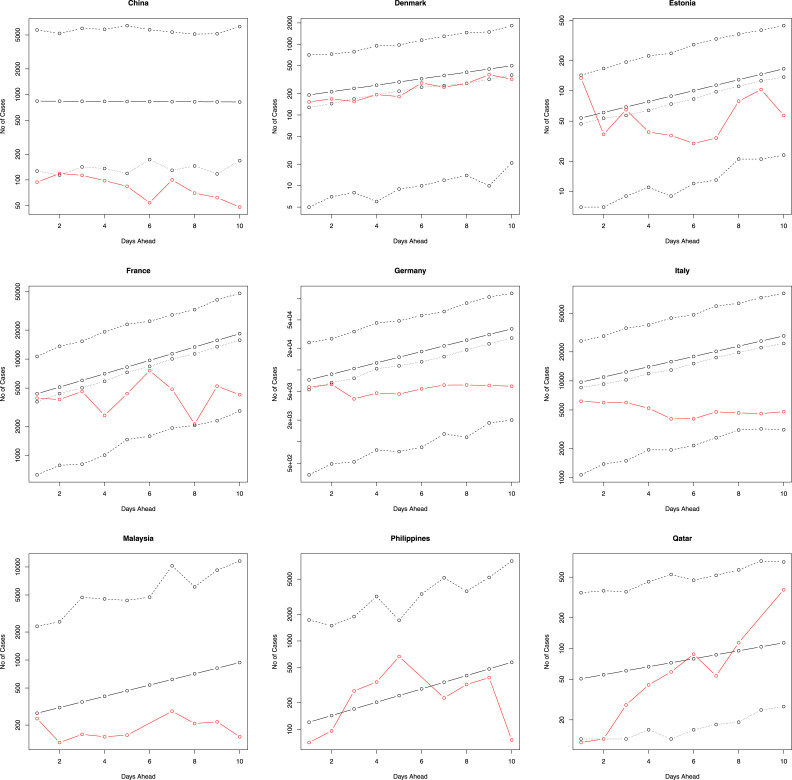
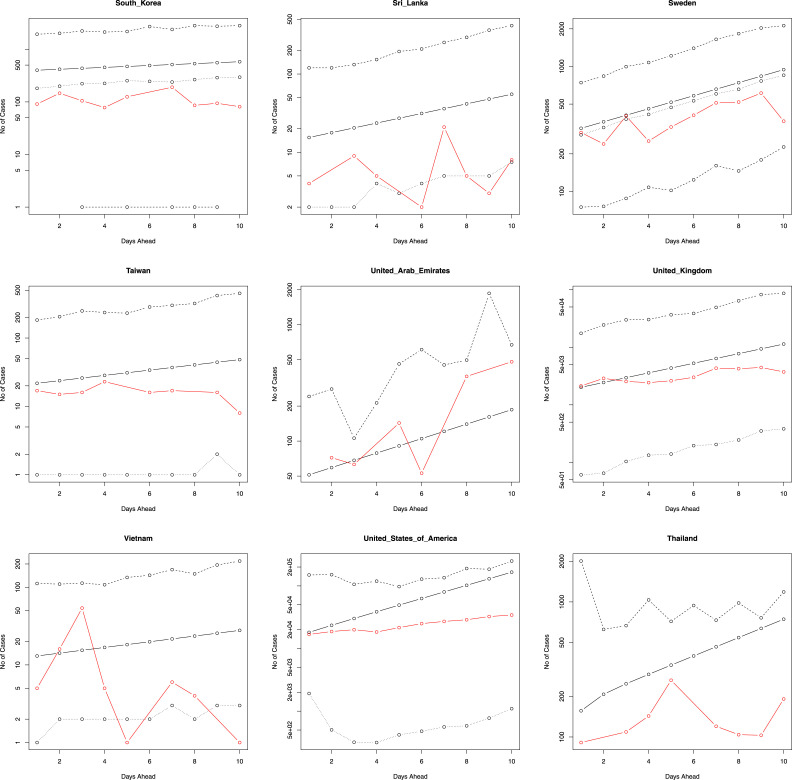
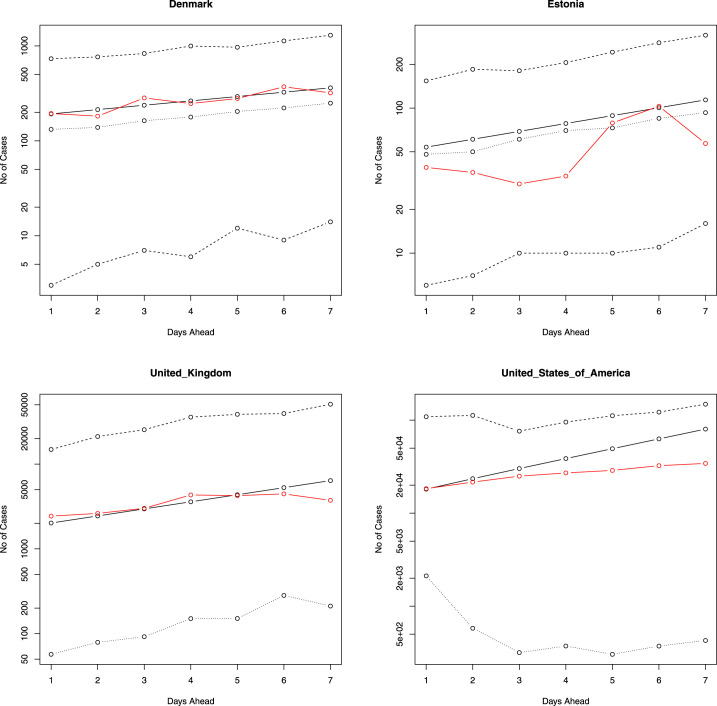
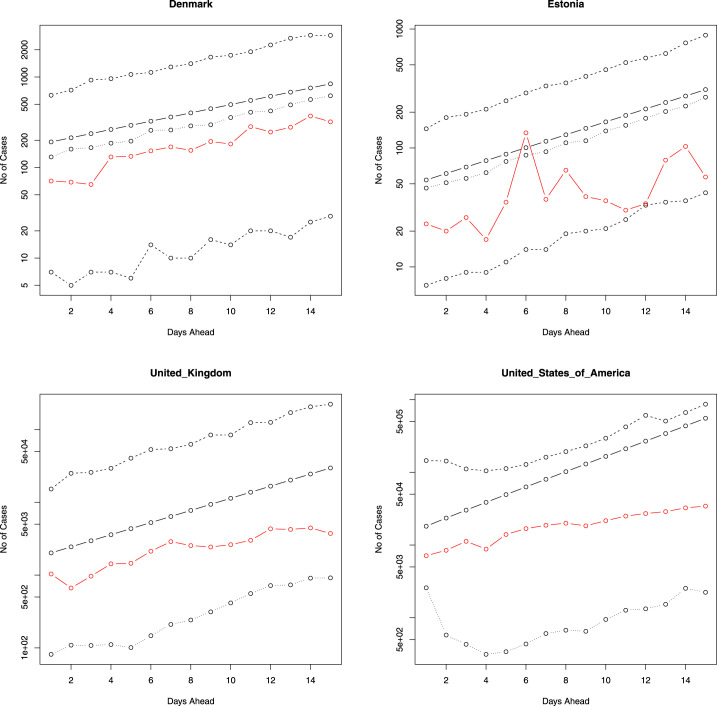
Fig. 2, Fig. 3 provide the predicted values of $Z_t$, their median and 95 percent confidence intervals for the 10 days immediately following the period that our data covers (starting from 26 March 2020). Also plotted in the figures are the actual number of newly reported cases for these 10 days. Fig. 4, Fig. 5 plot the same for four of the eighteen countries for, respectively, 7 days ahead and 15 days ahead. We have chosen four countries for limitations of space and for not being repetitive. The $y$ axes of Fig. 2, Fig. 3, Fig. 4, Fig. 5 are plotted in log scale. Because $log0$ is undefined, we have left out zeros while plotting in log scale. This means some of the plots in Fig. 2, Fig. 3, Fig. 4, Fig. 5 have fewer than five curves.

Fig. 2.

The number of new cases versus the next 10 days ahead. The solid line is the predicted number of new cases. The lines of dashes are the 95 percent confidence intervals. The line of dots is the predicted median of the number of new cases. The red line gives the actual number of new cases. The $y$ axes are in log scale.

Fig. 3.

The number of new cases versus the next 10 days ahead. The solid line is the predicted number of new cases. The lines of dashes are the 95 percent confidence intervals. The line of dots is the predicted median of the number of new cases. The red line gives the actual number of new cases. The $y$ axes are in log scale.

Fig. 4.

The number of new cases versus the next 7 days ahead. The solid line is the predicted number of new cases. The lines of dashes are the 95 percent confidence intervals. The line of dots is the predicted median of the number of new cases. The red line gives the actual number of new cases. The $y$ axes are in log scale.

Fig. 5.

The number of new cases versus the next 15 days ahead. The solid line is the predicted number of new cases. The lines of dashes are the 95 percent confidence intervals. The line of dots is the predicted median of the number of new cases. The red line gives the actual number of new cases. The $y$ axes are in log scale.

The predicted $Z_t$ values time at $t$ were computed as $\widehat{\varphi }{\left(1-\widehat{\varphi }\right)}^{-1}exp\left(\widehat{\alpha }+\widehat{\beta }t\right)$. The predicted median at time $t$, say $M\left(t\right)$, was computed as the solution of

$$\sum _{k=0}^{M\left(t\right)}\left[\left(\genfrac{}{}{0ex}{}{k+exp\left(\widehat{\alpha }+\widehat{\beta }t\right)-1}{k}\right){\left(1-\widehat{\varphi }\right)}^{exp\left(\widehat{\alpha }+\widehat{\beta }t\right)}{\left(\widehat{\varphi }\right)}^k\right]=0.5.$$

The predicted 95 percent confidence interval at time $t$, say $\left[L\left(t\right),U\left(t\right)\right]$, was computed as the solutions of

$$\sum _{k=0}^{L\left(t\right)}\left[\left(\genfrac{}{}{0ex}{}{k+exp\left(\widehat{\alpha }+\widehat{\beta }t\right)-1}{k}\right){\left(1-\widehat{\varphi }\right)}^{exp\left(\widehat{\alpha }+\widehat{\beta }t\right)}{\left(\widehat{\varphi }\right)}^k\right]=0.025$$

and

$$\sum _{k=0}^{U\left(t\right)}\left[\left(\genfrac{}{}{0ex}{}{k+exp\left(\widehat{\alpha }+\widehat{\beta }t\right)-1}{k}\right){\left(1-\widehat{\varphi }\right)}^{exp\left(\widehat{\alpha }+\widehat{\beta }t\right)}{\left(\widehat{\varphi }\right)}^k\right]=0.975.$$

The actual number of new cases falls within the 95 percent confidence intervals for each of the eighteen countries (for 7 days, 10 days and 15 days), suggesting that the fitted model is robust in spite of being simple. For some countries, such as Denmark, Malaysia, and the Philippines, the actual and predicted values are reasonably close. On the other hand, for many countries the predicted values overestimate the actual number of new cases (Estonia, France, Germany, Italy, etc.). However, in a few instances - e.g. Qatar and United Arab Emirates, the actual number of new daily cases starts to outgrow the predicted values in the latter half of the 10 days (same was observed for 7 days and 15 days). Note that these countries do not appear to share a common connection. Although the regression model accounts for the historical number of daily cases (and the average rate of new daily cases), a possible explanation why it may under or overestimates the true number of new daily cases is due to the fact that it does not take into account many other factors that can influence the spread of infectious diseases, such as the behaviour of individuals (e.g. social, travel, etc.), government action, and economic policies.

Whilst this method has its advantages of being simple, straightforward and yet robust, the results should be interpreted with caution. They allow us to capture the general trend of the new daily cases in each country and generate some basic predictions in the short term. However, arguably, this approach misses key factors that are accounted for in other types of available models. Therefore, it would not be wise to purely use the results presented here to make policy decisions, but rather these results should be used in conjunction with those from other analyses, which can help to support or contradict.

Furthermore, we do not consider here the historical daily mortality due to COVID-19 as there exist many dependent factors that should be considered when modelling these numbers. Examples include available treatments, susceptible population, hospital capacity, transmission rate, location and elevation risk, socio-economic factors and many more. This data can often be limited or hard to obtain due to restrictions such as data privacy or unreliable reporting. For further information we refer the readers to Booth and Tickle [32].

Finally, we check robustness of the (log, negative binomial) model. We fitted all four models ((identity, Poisson), (log, Poisson), (identity, negative binomial) and (log, negative binomial)) to the two halves of the data set. The first half was taken as the data from 31 December 2019 to 11 February 2020. The second half was taken as the data from 12 February 2020 to 25 March 2020. The values of AIC and BIC for the four models for each half are given in Table 3, Table 4. We see that the (log, negative binomial) model gives the smallest values for each country and for each half.

Table 3.

Values of AIC (and values of BIC in brackets) for the four models fitted to the data from 31 December 2019 to 11 February 2020.

Country	Models
	(Identity, Poisson)	(Log, Poisson)	(Identity, negative binomial)	(Log, negative binomial)
China	−52.5 (−49.0)	−53.8 (−50.2)	−57.9 (−52.6)	−60.7 (−55.4)
Denmark	−47.2 (−43.7)	−55.7 (−52.1)	−58.9 (−53.6)	−60.0 (−54.6)
Estonia	−53.8 (−50.4)	−54.1 (−50.6)	−54.2 (−49.1)	−63.6 (−58.4)
France	−49.6 (−46.0)	−50.8 (−47.2)	−60.4 (−55.1)	−61.1 (−55.7)
Germany	−49.8 (−46.3)	−59.4 (−55.9)	−61.0 (−55.6)	−62.8 (−57.5)
Italy	−53.2 (−49.6)	−54.2 (−50.7)	−54.4 (−49.1)	−58.5 (−53.2)
Malaysia	−49.7 (−46.2)	−54.2 (−50.7)	−56.9 (−51.6)	−60.3 (−55.0)
Philippines	−48.1 (−44.6)	−50.0 (−46.6)	−48.3 (−43.1)	−57.4 (−52.2)
Qatar	−46.4 (−42.9)	−47.8 (−44.4)	−48.7 (−43.5)	−62.6 (−57.4)
South Korea	−47.9 (−44.3)	−52.4 (−48.9)	−57.5 (−52.2)	−61.5 (−56.1)
Sri Lanka	−58.2 (−54.8)	−58.5 (−55.2)	−58.5 (−53.5)	−60.9 (−55.9)
Sweden	−52.5 (−48.9)	−57.0 (−53.5)	−55.2 (−49.9)	−61.5 (−56.2)
Taiwan	−53.6 (−50.1)	−57.9 (−54.4)	−60.8 (−55.6)	−63.7 (−58.5)
Thailand	−46.6 (−43.2)	−48.9 (−45.5)	−48.9 (−43.8)	−53.7 (−48.7)
United Arab Emirates	−46.3 (−42.9)	−53.2 (−49.8)	−55.7 (−50.5)	−62.2 (−57.1)
United Kingdom	−49.9 (−46.4)	−51.3 (−47.8)	−55.6 (−50.3)	−62.3 (−57.0)
United States of America	−47.3 (−43.7)	−53.7 (−50.2)	−58.9 (−53.6)	−61.2 (−55.8)
Vietnam	−50.9 (−47.4)	−53.8 (−50.4)	−55.9 (−50.7)	−57.1 (−51.9)

Table 4.

Values of AIC (and values of BIC in brackets) for the four models fitted to the data from 12 February 2020 to 25 March 2020.

Country	Models
	(Identity, Poisson)	(Log, Poisson)	(Identity, negative binomial)	(Log, negative binomial)
China	−46.8 (−43.3)	−50.9 (−47.3)	−55.3 (−50.0)	−56.2 (−50.9)
Denmark	−47.4 (−43.9)	−50.1 (−46.5)	−49.0 (−43.7)	−59.7 (−54.4)
Estonia	−50.5 (−47.1)	−58.6 (−55.2)	−59.1 (−53.9)	−63.0 (−57.9)
France	−51.7 (−48.2)	−54.7 (−51.1)	−59.4 (−54.0)	−60.7 (−55.4)
Germany	−50.3 (−46.7)	−58.5 (−55.0)	−58.6 (−53.3)	−60.6 (−55.3)
Italy	−47.6 (−44.1)	−47.8 (−44.2)	−58.8 (−53.5)	−60.7 (−55.3)
Malaysia	−52.8 (−49.3)	−53.3 (−49.8)	−55.8 (−50.6)	−58.1 (−52.8)
Philippines	−46.4 (−42.9)	−48.2 (−44.7)	−49.9 (−44.7)	−50.6 (−45.4)
Qatar	−53.9 (−50.5)	−59.5 (−56.0)	−59.4 (−54.3)	−62.8 (−57.6)
South Korea	−46.5 (−42.9)	−55.6 (−52.1)	−62.1 (−56.8)	−62.5 (−57.2)
Sri Lanka	−47.2 (−43.9)	−49.9 (−46.5)	−50.9 (−46.0)	−60.1 (−55.1)
Sweden	−49.0 (−45.5)	−49.7 (−46.2)	−54.0 (−48.6)	−57.5 (−52.2)
Taiwan	−47.3 (−43.8)	−47.9 (−44.4)	−52.8 (−47.5)	−55.9 (−50.7)
Thailand	−49.2 (−45.8)	−59.7 (−56.3)	−61.9 (−56.8)	−62.2 (−57.2)
United Arab Emirates	−47.5 (−44.1)	−51.2 (−47.8)	−56.9 (−51.8)	−63.9 (−58.8)
United Kingdom	−51.5 (−48.0)	−54.6 (−51.1)	−54.6 (−49.3)	−59.1 (−53.8)
United States of America	−50.6 (−47.0)	−51.4 (−47.9)	−54.8 (−49.5)	−55.2 (−49.9)
Vietnam	−49.4 (−45.9)	−49.9 (−46.5)	−54.8 (−49.6)	−60.1 (−54.9)

5. Conclusions

We have provided a statistical study on the modelling and analysis of the daily incidence of COVID-19 in eighteen countries around the world. In particular, we have investigated whether it is possible to fit count regression models to the number of daily new cases of COVID-19 in various countries and make short term predictions of these numbers. The results suggest that the biggest advantage of these methods is that they are simplistic and straightforward allowing us to obtain preliminary results and an overall picture of the trends in the daily confirmed cases of COVID-19 in different countries.

The best fitting count regression model for modelling the number of new daily COVID-19 cases of all countries was shown to be a negative binomial distribution with log link function. The best fitted model was robust in that the 95 percent confidence intervals for prediction contained the actual number of new cases for each country. However, the model was not able to predict the trends of new daily cases well for China. We believe that this could be related to fact that China was the first country to be significantly affected, and by the time other countries started to be affected by COVID-19, China had already reached its peak in confirmed cases and their confirmed cases dramatically declined. Given these results, this suggests that this model may be more useful for modelling the early stages of an outbreak, when the number of new cases is increasing, and, more specifically, this suggests that a count regression model is better suited for modelling new daily cases when the trend is increasing linearly, semi-exponentially, or exponentially. Among the countries that fit well with this model, the slope estimate was positive in all cases, indicating that the expected number of new cases being confirmed each day is expected to increase with respect to time. The UK and Vietnam have the largest and smallest slope estimates, respectively, hence the rate of the daily increase in COVID-19 cases is highest for the UK and lowest for Vietnam. The model is beneficial for short term predictions in order to see the short term trend and the rate of growth of new cases, when no intervention measures are taken. In addition, the results could be useful in contributing to making health policy decisions or government intervention, but more importantly, these results should be used in conjunction with the results from other mathematical models that are more specific to epidemiology.

Nevertheless, direct extensions to the current work could include modelling the daily mortality due to COVID-19. Such models could incorporate dependent factors that influence mortality rate such as available treatments, susceptible population, hospital capacity, transmission rate, location and elevation risk, socio-economic factors and many more. A further extension is to seek models that are theoretically motivated for COVID data.

CRediT authorship contribution statement

Stephen Chan: Introduction, Motivation, Data. Jeffrey Chu: Analysis, Discussion. Yuanyuan Zhang: Analysis, Discussion. Saralees Nadarajah: Methods, Fitting.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.