Abstract
The pharmacokinetics (PK) of prednisolone (PNL) exhibit nonlinearity related to plasma protein binding, tissue binding, metabolic interconversion with prednisone (PN), and renal elimination. Blood and 11 tissues were collected from male Wistar rats after steady-state (SS) infusion and after subcutaneous boluses of 50 mg/kg of PNL. Concentrations of PNL and PN were measured by liquid chromatography–tandem mass spectrometry. Plasma and tissue profiles were described using a complex physiologically based pharmacokinetics (PBPK) model. Concentrations of PN and PNL were in rapid equilibrium in plasma and tissues. The tissue partition coefficients (Kp) of PNL calculated from most subcutaneously dosed tissue and plasma areas were similar to SS infusion and in silico values. The blood-to-plasma ratio of PNL was 0.71 with similar red blood cell and unbound-plasma concentrations. Plasma protein binding (60%–90%) was related to corticosteroid-binding globulin (CBG) saturation. Tissue distribution was nonlinear. The equilibrium dissociation constant (Kd) of PNL shared by all tissues was 3.01 ng/ml, with the highest binding in muscle, followed by liver, heart, intestine, and bone and the lowest binding in skin, spleen, fat, kidney, lung, and brain. Fat and bone distribution assumed access only to interstitial space. Brain PNL concentrations (Kp = 0.05) were low owing to presumed P-glycoprotein–mediated efflux. Clearances of CBG-free PNL were 1789 from liver and 191.2 ml/h from kidney. The PN/PNL ratio was nonlinear for plasma, spleen, heart, intestine, bone, fat, and linear for the remaining tissues. Our PBPK model with multiple complexities well described the PK profiles of PNL and PN in blood, plasma, and diverse tissues.
SIGNIFICANCE STATEMENT
Because steroids, such as prednisolone and prednisone, have similar and complex pharmacokinetics properties in various species, receptors in most tissues, and multiple therapeutic and adverse actions, this physiologically based pharmacokinetics (PBPK) model may provide greater insights into the pharmacodynamic complexities of corticosteroids. The complex properties of these compounds require innovative PBPK modeling approaches that may be instructive for other therapeutic agents.
Introduction
Corticosteroids (CSs) have long been frequently and intensively used in clinical practice for various indications, such as inflammatory (e.g., rheumatoid arthritis and asthma) and autoimmune diseases (e.g., solid organ transplant rejection and systemic lupus erythematosus) owing to their potent anti-inflammatory and immunosuppressive properties (Czock et al., 2005; Rhen and Cidlowski, 2005; Bergmann et al., 2012; Kadmiel and Cidlowski, 2013). As synthetic glucocorticoids (GCs), CSs act primarily through genomic mechanisms by binding to cytosolic glucocorticoid receptors (GRs) in tissues and causing inhibition of transcriptional factors, such as nuclear factor-κB and activator protein-1, thus suppressing the activation of genes encoding various proinflammatory mediators that promote inflammation and tissue damage (Coutinho and Chapman, 2011; Oakley and Cidlowski, 2011). As a result of the ubiquitous expression of GRs across the body, the CSs show multiple organ sites of activity (both desired and undesired), of which the commonly occurring dose- and time-dependent side effects, including growth retardation, metabolic disturbances, and osteoporosis (Saag et al., 1994), often compromise the overall therapeutic effects and limit the sustained use of CSs.
Prednisolone (PNL) and prednisone (PN) are among the top widely prescribed oral CSs (Overman et al., 2013). PNL is the biologically active substance, whereas PN is both the prodrug and inactive metabolite of PNL, with their interconversion mediated by 11β-hydroxysteroid dehydrogenases (11β-HSDs) (Raza et al., 2010). The pharmacokinetics (PK) of PNL is extremely complex, with dose dependence exhibited in both animals (Frey et al., 1980; Rocci and Jusko, 1981; Boudinot and Jusko, 1986) and humans (Rose et al., 1981). PNL binds to corticosteroid-binding globulin (CBG) with high affinity and low capacity, whereas it binds to albumin with low affinity and high capacity (Rocci et al., 1980). In humans, the dose-dependent increase in plasma clearance (CL) and volume of distribution of PNL at doses over 20 mg is attributed to the saturable binding to CBG (Rose et al., 1981; Frey and Frey, 1990; Barth et al., 1992). A decreasing trend of CL and volume of distribution with dose occurred in humans at very high doses of PNL (Derendorf et al., 1985), which may be explained by saturable elimination mechanisms (e.g., saturable conversion from PNL to PN and saturable renal elimination) (Frey et al., 1980; Legler et al., 1982). The PK of PNL in rats, when calculated based on total- or free-plasma concentrations, exhibits nonlinear distribution and elimination, with decreased CL and volume of distribution at steady state (Vss) and increased free fraction with increasing doses (Boudinot et al., 1986; Boudinot and Jusko, 1986; Huang and Jusko, 1990). Capacity-limited binding to CBG alone cannot account for the decrease in CL and Vss, as these are opposite to predictions that these parameters would increase with increased availability of free drug; thus saturable elimination and tissue distribution might be involved. The tissue distribution of PNL was assessed in rabbits, and the steady-state (SS) tissue/unbound-plasma concentration ratios were linear for all the examined tissues except the liver (Khalafallah and Jusko, 1984b); consistent results were obtained using rabbit tissue slices under in vitro conditions (Khalafallah and Jusko, 1984a).
Considering their clinical importance and the fact that CSs exert their pharmacologic actions as a direct consequence of their presence in numerous target tissues (Melby, 1977), it is important to understand the whole-body disposition characteristics of PNL. This requires the direct examination of drug concentration in tissues. Physiologically based pharmacokinetics (PBPK) modeling, which is based on physiologic tissue sizes and blood/plasma flow rates, allows characterization of tissue distribution in a diverse array of situations and also offers a way to extrapolate tissue concentrations from preclinical species to humans (Gerlowski and Jain, 1983; Sager et al., 2015).
This work characterizes the diverse complexities in disposition of PNL and PN in rats using a combination of experimental, whole-body PBPK modeling, and in silico approaches.
Materials and Methods
Reagents and Chemicals.
Prednisolone hemisuccinate sodium salt, prednisolone (purity ≥99%), prednisone (purity ≥98%), liquid chromatography/mass spectrometry–grade acetonitrile, methanol and high-performance liquid chromatography–grade formic acid, and phosphoric acid were purchased from Sigma-Aldrich (St Louis, MO). Prednisolone-d8 [internal standard (IS) for prednisolone, purity ≥97.71%] and prednisone-d8 (IS for prednisone, purity ≥98%) were obtained from Toronto Research Chemicals (Toronto, ON, Canada). Milli-Q water (Millipore Corporation, Bedford, MA) was used.
Animals.
Twenty-nine healthy male Wistar rats aged 5 to 6 weeks (weighing 225–249 g) were purchased from Envigo (Chicago, IL) and housed individually in the University Laboratory Animal Facility under controlled conditions with free access to water and food. All rats were acclimated for 1 week before the experiments. The research protocol adhered to the Guide for the Care and Use of Laboratory Animals (National Research Council, 2011) and was approved by the University at Buffalo Institutional Animal Care and Use Committee.
Experimental Design.
The prednisolone dosing solution was prepared freshly as the hemisuccinate sodium salt in sterile saline and filtered through 0.22-µm filters before use. The drug was administered subcutaneously in a volume of 1 ml/kg.
PNL was first infused subcutaneously to two rats through Alzet osmotic pumps at a concentration of 336 mg/ml at a rate of 8 μl/h for 7 hours to achieve SS. Animals were then sacrificed by exsanguination. Whole blood was drained from the abdominal aorta into EDTA-containing syringes. The 0.5 ml of whole blood was aliquoted, and the remaining blood was centrifuged (2000g, 15 minutes) immediately to obtain plasma samples. Various tissues [heart, liver, spleen, lung, kidney, muscle (gastrocnemus), skin, fat, brain, bone (tibia), intestine] were collected, rinsed in ice-cold PBS, and gently blotted, weighed, and immediately frozen in liquid nitrogen.
A second group of rats were given a subcutaneous bolus dose of 50 mg/kg prednisolone and sacrificed by exsanguination at 0.25, 0.5, 1, 2, 4, 6, 8, 12, and 24 hours (n = 3 per time point). The following procedures for tissue collection were the same as those described in the infusion study. To assess the unbound concentrations of PNL and PN in plasma, an aliquot of plasma samples was subject to ultrafiltration using Centrifree micropartition devices (Millipore Corporation) with a 30-kDa molecular mass cutoff filter. Aliquots of plasma samples (1 ml) were added into the ultrafiltration devices and incubated for 30 minutes at 37°C. Then the samples were centrifuged at 2000g for 20 minutes (37°C) to obtain ultrafiltrates for measurement of free PNL plasma concentrations. Tissues were powdered under liquid nitrogen before drug extraction. All samples were stored at −80°C before further analysis.
Drug Analysis.
A liquid chromatography–tandem mass spectrometry (LC-MS/MS) method was established to simultaneously determine the concentrations of PNL and PN in each of the collected samples. The LC-MS/MS system consisted of Shimadzu (Kyoto, Japan) modules, including a binary pump, a degasser, an autosampler, an column oven, and an Applied Biosystems (Foster City, CA) PE/SCIEX API3000 mass spectrometer equipped with a turbo ion spray interface. Sample separations were achieved on a HydroBond AQ C8 reverse phase column (2.1 × 150 mm, particle size 3 µm; MAC-MOD Analytical, Inc., Chadds Ford, PA). The mobile phase consisted of eluent A [water/methanol (95:5, v/v) containing 0.1% formic acid] and eluent B [methanol containing 0.1% formic acid] and was pumped at a flow rate of 0.2 ml/min with a gradient elution. The gradient profile was: 0–0.5 minutes, 30% B; a linear increase to 70% B from 0.5 to 6.5 minutes; a linear increase to 95% B over 0.1 minutes; 95% B for 5.4 minutes; a linear decrease to 30% B over 0.1 minutes; 30% B for 3.9 minutes; and stop at 16.00 minutes. The mass spectrometer was operated in the positive ion mode for the detection of ion transitions at mass-to-charge ratio 361.2/343.2 (prednisolone), 359.3/341.3 (prednisone), 369.4/351.3 (prednisolone-d8), and 367.3/349.5 (prednisone-d8). The LC-MS/MS system was controlled by Analyst software version 1.4 (Applied Biosystems SCIEX) for data acquisition and analysis.
Linearity was achieved over a concentration range of 1–2000 ng/ml for all samples. The coefficients of variation (CV%) for intraday and interday accuracies and precisions were within ±15%. The lower limit of quantification (LLOQ) was 1 ng/ml for both PNL and PN. The recovery of the sample pretreatment method approached 100%. The PNL and PN in various matrices during freeze-thaw cycles and long-term storage at 4°C or a lower temperature were known to be stable (Difrancesco et al., 2007; Methlie et al., 2013; Yao et al., 2020).
Preparation of Plasma and Ultrafiltrate Samples.
Plasma and ultrafiltrate samples (100 µl) were spiked with 10 µl of IS working solutions (300 ng/ml) and 100 μl of 4% phosphoric acid. The mixture was vortexed for 30 seconds and centrifuged at 13,000g for 10 minutes (4°C). A 190-μl aliquot of the supernatant was then subject to solid-phase extraction (SPE) using Oasis HLB 1 cc (30 mg) cartridges (Waters Corporation, Milford, MA). Prior to extraction, each cartridge was conditioned using 1 ml of methanol and twice followed by 1 ml of water using a Vac Elut SPS24 solid-phase extraction manifold (Varian, Palo Alto, CA). The cartridges were washed twice with 500 μl of water containing 5% (v/v) methanol and eluted thrice with 500 μl of methanol. The eluates were dried under nitrogen for 30 minutes and reconstituted with 100 μl of methanol/water (30:70 v/v). The mixture was vortexed for 30 seconds and centrifuged (13,000g, 10 minutes, 4°C). Finally, 10 μl of the supernatant was injected into the LC-MS/MS for analysis.
Preparation of Whole-Blood and Tissue Samples.
The PNL and PN concentrations in whole-blood and tissue samples were pretreated using a slightly modified method. Briefly, whole-blood samples were directly homogenized at 4°C using a PRO-200 BIO-GEN homogenizer (ProScientific, Oxford, CT), and tissue samples were homogenized in PBS at a 3-fold dilution using a bullet blender (Next Advance, Inc., Troy, NY) at 4°C. Whole-blood and tissue homogenates (100 µl) were spiked with 10 µl of IS working solutions (300 ng/ml) and 980 μl of methanol. The mixture was vortexed for 30 seconds and centrifuged at 14,000g for 20 minutes (4°C). A 900-μl aliquot of the supernatant was then evaporated to dryness. The residue was reconstituted with methanol (50 μl) and vortexed twice for 30 seconds and then diluted with water (450 μl) and vortexed for another 30 seconds. A 450-μl aliquot of the mixture was acidified with 4% phosphoric acid (450 μl) and centrifuged at 13,000g for 10 minutes (4°C). An 850 μl aliquot of the supernatant was subject to SPE using preconditioned Oasis PRiME HLB 1 cc (30 mg) cartridges (Waters Corporation). The remaining SPE extraction procedures were similar to those described for the plasma samples except that the analytes were eluted 2× with 500 μl of acetonitrile/methanol (90:10, v/v). The eluates were dried under nitrogen for 30 minutes and reconstituted with 150 μl of methanol/water (30:70, v/v). The mixture was vortexed for 30 seconds and centrifuged (13,000g, 10 minutes, 4°C). Finally, 10 μl of the supernatant was injected into the LC-MS/MS for analysis.
Blood-to-Plasma Ratio (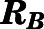 ).
).
The blood-to-plasma concentration ratio (RB) was obtained using the measured blood (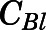 ) and plasma (
) and plasma (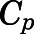 ) concentrations of PNL from the subcutaneous bolus and the subcutaneous SS infusion studies in male rats:
) concentrations of PNL from the subcutaneous bolus and the subcutaneous SS infusion studies in male rats:
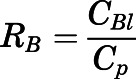 |
(1) |
The concentration of PNL in red blood cells (RBCs) was calculated according to:
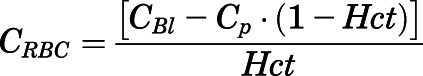 |
(2) |
in which 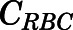 is the concentration of PNL in RBCs, and
is the concentration of PNL in RBCs, and 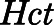 is the hematocrit of male Wistar rats (0.45) (Kampfmann et al., 2012).
is the hematocrit of male Wistar rats (0.45) (Kampfmann et al., 2012).
Correction of Tissue Concentrations.
The concentrations of PNL and PN in all measured tissues were corrected for residual blood using:
 |
(3) |
| (4) |
in which 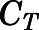 and
and 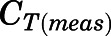 are the residual blood-corrected and measured tissue concentrations;
are the residual blood-corrected and measured tissue concentrations; 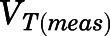 is the measured or estimated tissue volume;
is the measured or estimated tissue volume; 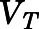 is the tissue vascular-corrected volume; and
is the tissue vascular-corrected volume; and 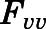 is the fractional vascular volume of blood trapped in tissues, which was obtained from the literature concentrations (Bernareggi and Rowland, 1991). The
is the fractional vascular volume of blood trapped in tissues, which was obtained from the literature concentrations (Bernareggi and Rowland, 1991). The 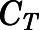 and
and 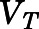 values were used for further model analysis.
values were used for further model analysis.
Tissue-to-Plasma Partition Coefficients.
The values of Kp were calculated and compared using several methods:
-
Calculation from the SS plasma (
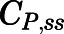 ) and tissue (
) and tissue (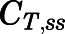 ) concentrations in the subcutaneous infusion study. For nonelimination organs:
) concentrations in the subcutaneous infusion study. For nonelimination organs: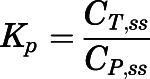
(5) For elimination organs (liver and kidney):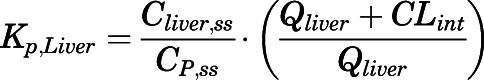
(6)
in which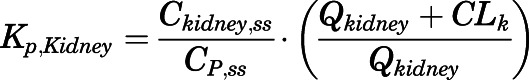
(7) 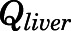 and
and 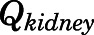 are the liver and kidney blood flows, and
are the liver and kidney blood flows, and 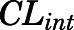 and
and 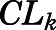 are the hepatic intrinsic and renal (metabolic) clearances.
are the hepatic intrinsic and renal (metabolic) clearances. - Apparent Kp values were calculated from the PBPK model–predicted data (detailed description will follow):
in which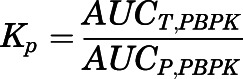
(8) 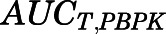 and
and 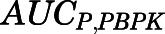 are the area under the curve (AUC) of the PBPK model–predicted tissue and plasma curves. The same correction method for liver and kidney
are the area under the curve (AUC) of the PBPK model–predicted tissue and plasma curves. The same correction method for liver and kidney 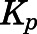 as described in eqs. 6 to 7 was applied here based on eq. 8.
as described in eqs. 6 to 7 was applied here based on eq. 8. In silico methods implemented by the GastroPlus PBPK Simulator (version 9.6.2; Simulations Plus Inc., Lancaster, CA) were also used for Kp prediction. Published methods (Poulin and Theil, 2002a,b; Berezhkovskiy, 2004; Rodgers and Rowland, 2006) for neutral compounds were used and are listed as Methods 1–3.
Plasma Protein Binding of PNL.
The concentration-dependent plasma protein binding of PNL in various species owing to saturable binding to CBG has been well investigated previously (Sandberg et al., 1957; Rocci et al., 1980; Rocci and Jusko, 1981; Boudinot and Jusko, 1984, 1986). The binding equation is:
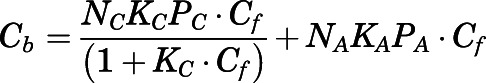 |
(9) |
in which 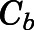 and
and 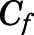 are the bound- and free-plasma PNL concentrations; N is the number of binding sites; K is the association constant; P is the plasma protein concentration; and subscripts C and A refer to CBG and albumin.
are the bound- and free-plasma PNL concentrations; N is the number of binding sites; K is the association constant; P is the plasma protein concentration; and subscripts C and A refer to CBG and albumin.
The total (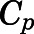 ) plasma concentrations can be described as:
) plasma concentrations can be described as:
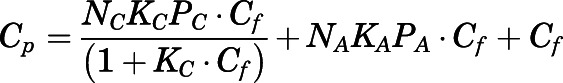 |
(10) |
Rearrangement of eq. 10 gives:
| (11) |
The CBG-free PNL plasma concentrations (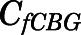 ) were determined as the sum of albumin-bound (
) were determined as the sum of albumin-bound (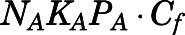 ) and free (
) and free (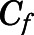 ) PNL plasma concentrations at various total- and free-drug concentrations:
) PNL plasma concentrations at various total- and free-drug concentrations:
| (12) |
Combining eqs. 11 and 12, the CBG-free plasma concentration can be calculated from total plasma concentration as:
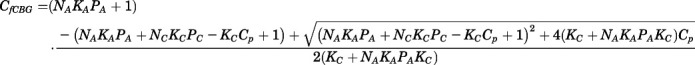 |
(13) |
Combining eqs. 10 and 12, 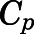 can be computed from
can be computed from 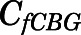 by:
by:
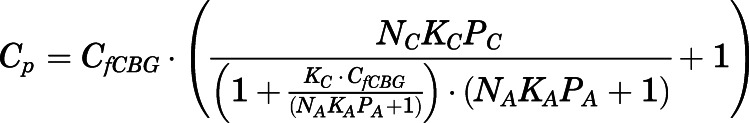 |
(14) |
Tissue Binding of PNL.
The nonlinear tissue binding of PNL was expressed by:
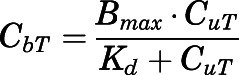 |
(15) |
in which 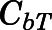 and
and 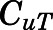 are the bound and free concentrations of PNL in tissue;
are the bound and free concentrations of PNL in tissue; 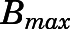 is the binding capacity of the tissue (ng/ml); and
is the binding capacity of the tissue (ng/ml); and 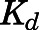 is the equilibrium dissociation constant. Therefore, total tissue concentration (
is the equilibrium dissociation constant. Therefore, total tissue concentration (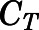 ) can be described by:
) can be described by:
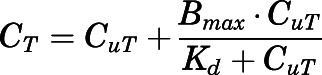 |
(16) |
Assuming only CBG-free drug has access to tissues, and tissue-free concentration (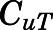 ) is the same as the CBG-free drug concentration in tissue venous plasma (
) is the same as the CBG-free drug concentration in tissue venous plasma (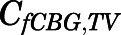 ), then the tissue-to-CBG free-plasma concentration ratio (
), then the tissue-to-CBG free-plasma concentration ratio (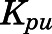 ) is given by:
) is given by:
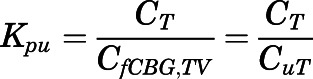 |
(17) |
Combining eqs. 16 and 17 yields:
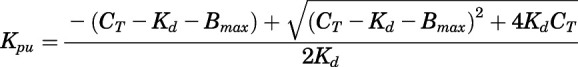 |
(18) |
PBPK Model Development and Modeling Strategy.
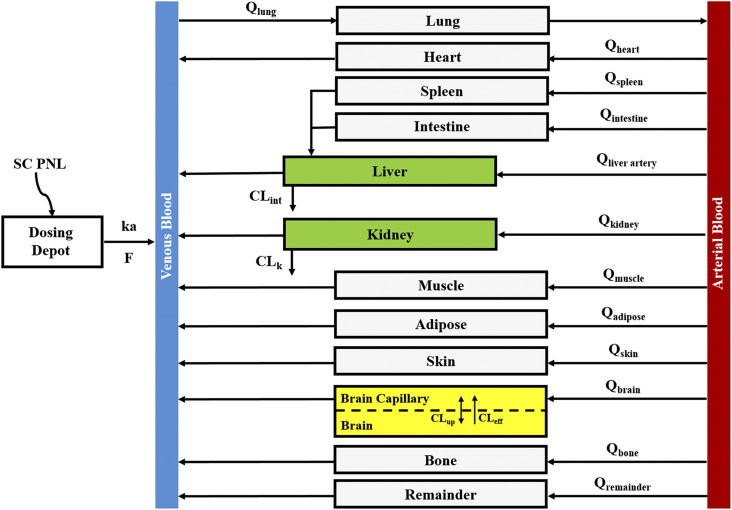
The proposed PBPK model of prednisolone (Fig. 1) consists of two plasma/blood compartments (arterial and venous plasma) and 12 tissue compartments (liver, kidney, lung, heart, spleen, intestine, muscle, fat, bone, skin, brain, and remainder). Tissues accounting for about 90% of total body weight were evaluated. Unmeasured tissues were lumped as a remainder compartment to attain whole-body mass balance. The model was based upon the following observations and assumptions: (1) tissue concentrations are considered to be in instant equilibrium with the CBG-free drug in venous plasma, which is assumed to be in equilibrium with the tissue-unbound concentration; (2) circulatory transport occurs by plasma/blood flow; (3) brain has two subcompartments (vascular and extravascular) with a presumed P-glycoprotein (P-gp)-mediated efflux process; (4) the distribution of PNL into fat and bone is limited to the interstitial space; (5) only CBG-free PNL is available for tissue distribution and elimination; (6) the elimination of PNL occurs from liver and kidney; (7) tissue binding of PNL is saturable; and (8) interconversion of PNL and PN was in continual rapid equilibrium. Physiologic parameters, including tissue weights and blood flow rates to different organs, were fixed to literature values in the PBPK model (Table 1) (Shah and Betts, 2012).
Fig. 1.
Whole-body PBPK model scheme for prednisolone and prednisone disposition in rats. Parameters and symbols are defined in the text and tables. Lines with arrows indicate blood flows and drug transport. Each box represents one tissue compartment as indicated by the label.
TABLE 1.
Physiologic parameters of tissues in 294-g male rats
| Tissue | Volume (V, ml) | Blood Flow (Q, ml/h) |
|---|---|---|
| Lung | 0.96a | 5548.6b |
| Brain | 1.41a | 123.1b |
| Brain capillary | 0.02a | |
| Heart | 0.87a | 285b |
| Intestine | 8.14b | 1047.7b |
| Spleen | 0.43a | 336.8b |
| Kidney | 1.81a | 687.1b |
| Muscle | 127.52b | 1743.1b |
| Liver | 9.94a | 1424.4c |
| Liver artery | NA | 39.8 b |
| Skin | 52.17b | 376.2b |
| Bone | 21.61b | 115.7b |
| Bone ISF | 4.02b | |
| Fat | 34.44b | 422.8b |
| Fat ISF | 5.85b | |
| Arterial blood | 5.76b | 5548.6b |
| Venous blood | 11.52b | 5548.6b |
| Remainder | 17.08c | 371.2c |
NA, not applicable.
Tissue vascular-corrected volume (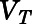 ) calculated based on experiment value using eq. 4.
) calculated based on experiment value using eq. 4.
Calculated based on the value from Shah and Betts (2012).
Calculated value assuming 1) 1 ng/ml tissue density, volume for remainder compartment = body weight – summation of volume for all measured tissues; 2) blood flow for remainder compartment = cardiac output – summation of blood flow for all measured tissues; 3) liver blood flow = summation of blood flow of liver artery, spleen, and intestine).
The model differential equations are listed below, with all initial conditions set to 0 except for the dosing depot in eq. 33.
Rates of change of drug concentration in tissues. Except for lung, liver, kidney, brain, fat, bone, arterial, and venous plasma, the mass balance in each tissue was expressed as:
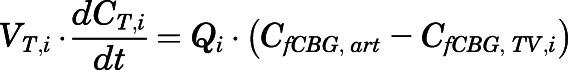 |
(19) |
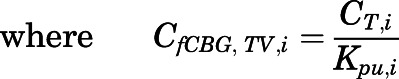 |
(20) |
in which 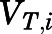 ,
, 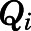 ,
,  , and
, and 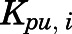 are volume, blood flow, PNL concentration, and unbound partition coefficient for tissue i;
are volume, blood flow, PNL concentration, and unbound partition coefficient for tissue i; 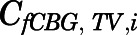 is the CBG-free venous plasma concentration leaving tissue i; and
is the CBG-free venous plasma concentration leaving tissue i; and 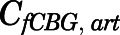 is the CBG-free PNL concentration in arterial plasma, which can be calculated from the total arterial plasma concentration (
is the CBG-free PNL concentration in arterial plasma, which can be calculated from the total arterial plasma concentration (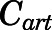 ) using eq. 13.
) using eq. 13.
Rates of change of drug concentration in the venous and arterial plasma. The total PNL concentration in venous plasma leaving tissue i (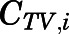 ) and entering the venous and arterial plasma pools can be computed according to eqs. 14 and 20 as:
) and entering the venous and arterial plasma pools can be computed according to eqs. 14 and 20 as:
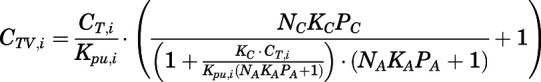 |
(21) |
Therefore, the rates of change of PNL concentration in venous and arterial plasma pools were:
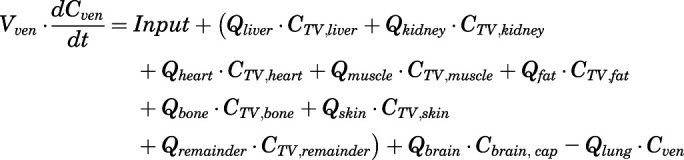 |
(22) |
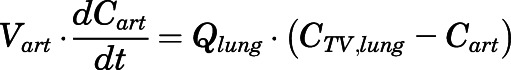 |
(23) |
Rate of change of drug concentrations in the lung can be computed as:
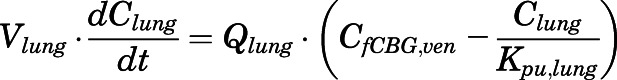 |
(24) |
in which the CBG-free venous plasma concentration of PNL (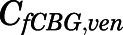 ) was computed from the total venous plasma concentration (
) was computed from the total venous plasma concentration (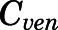 ) according to eq. 13 and
) according to eq. 13 and 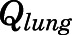 is the lung blood flow corresponding to the cardiac blood flow.
is the lung blood flow corresponding to the cardiac blood flow.
Rate of change of drug concentrations in the liver can be computed as:
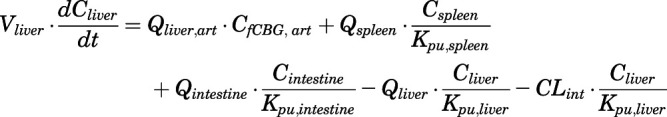 |
(25) |
in which 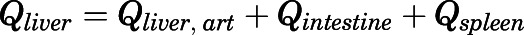 .
.
Rate of change of drug concentration in the kidney is:
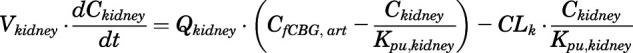 |
(26) |
Rates of change of drug concentration in bone and fat can be computed with:
 |
(27) |
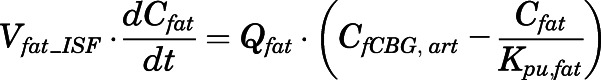 |
(28) |
in which 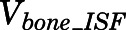 and
and 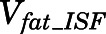 are the interstitial volumes of bone and fat.
are the interstitial volumes of bone and fat.
The measured PNL concentrations in bone (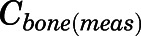 ) and fat (
) and fat (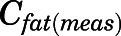 ) were modeled as:
) were modeled as:
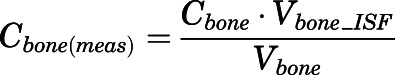 |
(29) |
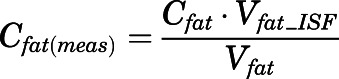 |
(30) |
Rates of change of drug concentration in brain capillary and brain can be computed as:
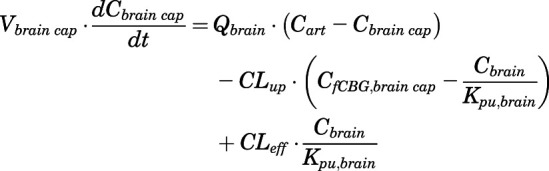 |
(31) |
 |
(32) |
in which 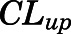 and
and 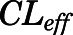 are the bidirectional uptake and unidirectional efflux clearance of PNL in brain;
are the bidirectional uptake and unidirectional efflux clearance of PNL in brain;  is the CBG-free PNL concentration in brain capillary that can be calculated from total brain capillary concentration (
is the CBG-free PNL concentration in brain capillary that can be calculated from total brain capillary concentration ( ) using eq. 13.
) using eq. 13.
The subcutaneous injection was treated as a bolus into a dosing depot (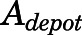 ) as described by:
) as described by:
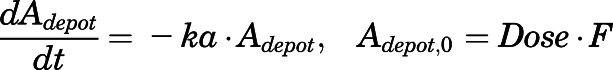 |
(33) |
in which 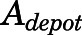 is the amount of drug to be absorbed into the venous plasma;
is the amount of drug to be absorbed into the venous plasma; 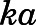 is the first-order absorption rate constant;
is the first-order absorption rate constant; 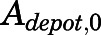 is the initial condition of
is the initial condition of 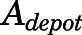 ; and F is the bioavailability of subcutaneous dose calculated to be 0.65 from literature-reported intravenous data in rats (Huang and Jusko, 1990).
; and F is the bioavailability of subcutaneous dose calculated to be 0.65 from literature-reported intravenous data in rats (Huang and Jusko, 1990).
Therefore, the Input function in eq. 22 is:
| (34) |
Given the rapid appearance of PN in plasma and tissues upon PNL administration and often parallel profiles, the interconversion between PNL and PN was assumed to be in continual rapid equilibrium. The concentration of PN in tissue i (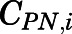 ), including lung, kidney, muscle, skin, liver, and brain, was modeled as a linear fraction of PNL concentration in the corresponding tissue (
), including lung, kidney, muscle, skin, liver, and brain, was modeled as a linear fraction of PNL concentration in the corresponding tissue (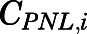 ):
):
| (35) |
in which 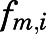 is the metabolite/drug ratio of PN/PNL for tissue i.
is the metabolite/drug ratio of PN/PNL for tissue i.
The PN concentration in arterial plasma, spleen, heart, intestine, bone, and fat was fitted to a Michaelis-Menten type equation:
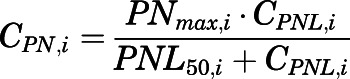 |
(36) |
in which 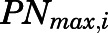 is the maximal PN concentration achievable, and
is the maximal PN concentration achievable, and 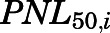 is the PNL concentration achieving 50%
is the PNL concentration achieving 50% 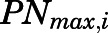 .
.
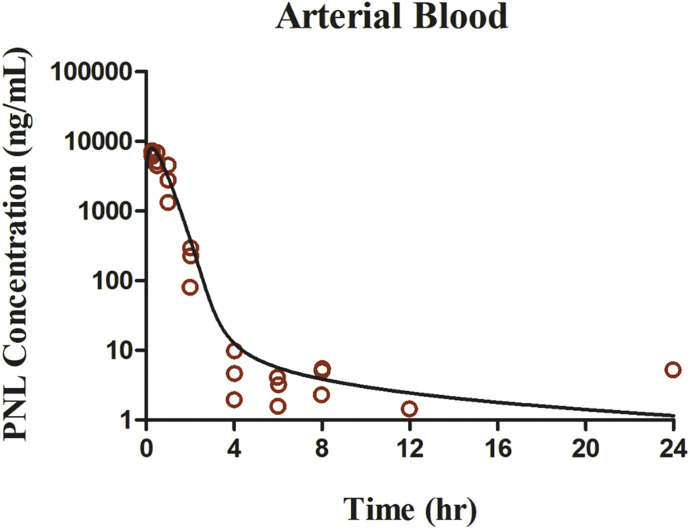
The measured PNL concentrations in arterial blood were described as:
| (37) |
in which 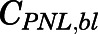 and
and 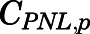 are the PNL concentrations in arterial blood and plasma.
are the PNL concentrations in arterial blood and plasma.
The relationship between systemic (CLs) and intrinsic clearances (Clint) of CBG-free PNL is:
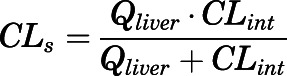 |
(38) |
A similar calculation related renal systemic clearance to kidney blood flow (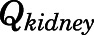 ) and renal intrinsic clearance (CLk).
) and renal intrinsic clearance (CLk).
Model Fitting.
The blood-to-plasma concentration ratio (RB) and the metabolite/drug ratio–related parameters (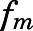 ,
, 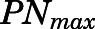 , and
, and 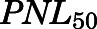 ) were estimated by Orthogonal Regression (Package “onls”) in R (version 3.4.3) according to eqs. 1, 35, and 36 and fixed in the PBPK model. Naïve-pooled plasma and tissue time-concentration data from all rats were analyzed jointly using the established PBPK model. The plasma protein binding parameters (
) were estimated by Orthogonal Regression (Package “onls”) in R (version 3.4.3) according to eqs. 1, 35, and 36 and fixed in the PBPK model. Naïve-pooled plasma and tissue time-concentration data from all rats were analyzed jointly using the established PBPK model. The plasma protein binding parameters (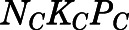 ,
, 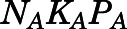 , and
, and 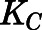 ) were fixed to literature-reported values (Boudinot and Jusko, 1986), with the estimation of the subcutaneous first-order absorption rate constant (
) were fixed to literature-reported values (Boudinot and Jusko, 1986), with the estimation of the subcutaneous first-order absorption rate constant (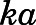 ), hepatic intrinsic (
), hepatic intrinsic (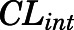 ) and renal (
) and renal (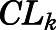 ) clearance, tissue binding parameters (
) clearance, tissue binding parameters (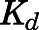 and
and 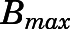 ), the bidirectional uptake (
), the bidirectional uptake (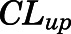 ) and unidirectional efflux (
) and unidirectional efflux (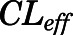 ) clearance of PNL in brain, and metabolite/drug ratio for liver (
) clearance of PNL in brain, and metabolite/drug ratio for liver (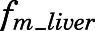 ). The whole-body PBPK-model fittings involved nonlinear regression using the maximum likelihood algorithm in ADAPT 5 (Biomedical Simulations Resource, Los Angeles, CA) (D' Argenio et al., 2009). The variance model used was:
). The whole-body PBPK-model fittings involved nonlinear regression using the maximum likelihood algorithm in ADAPT 5 (Biomedical Simulations Resource, Los Angeles, CA) (D' Argenio et al., 2009). The variance model used was:
| (39) |
in which 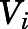 represents the variance of the ith data point;
represents the variance of the ith data point; 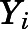 is the ith model-predicted concentration; and
is the ith model-predicted concentration; and 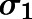 and
and 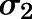 are variance model parameters. Model selection was based on the goodness-of-fit criteria, which included the Akaike Information Criterion, visual inspection of the fitted profiles, and CV% of the parameter estimates.
are variance model parameters. Model selection was based on the goodness-of-fit criteria, which included the Akaike Information Criterion, visual inspection of the fitted profiles, and CV% of the parameter estimates.
The Adapt code for the PBPK model is provided in the Supplemental Materials.
Results
Distribution of PNL between Blood Fractions.
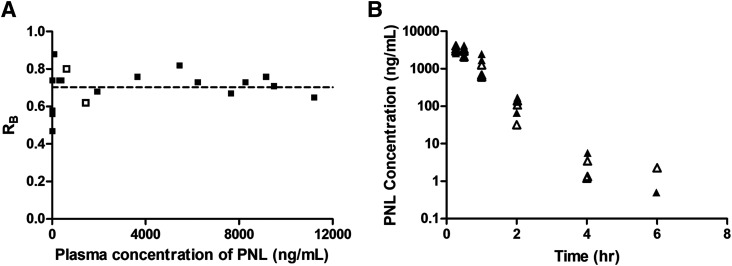
Figure 2A shows the relationship between the blood-to-plasma concentration ratio (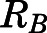 ) versus plasma concentrations of PNL from both the subcutaneous bolus and subcutaneous infusion studies. The combined average
) versus plasma concentrations of PNL from both the subcutaneous bolus and subcutaneous infusion studies. The combined average 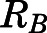 value calculated using eq. 1 was 0.703 ± 0.10 (n = 18), which was very close to the estimated
value calculated using eq. 1 was 0.703 ± 0.10 (n = 18), which was very close to the estimated 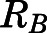 value by Orthogonal Regression (0.71, Table 3). The calculated PNL concentrations in RBCs according to eq. 2 closely match the measured free drug in plasma (Fig. 2B), indicating limited entry of PNL into RBCs.
value by Orthogonal Regression (0.71, Table 3). The calculated PNL concentrations in RBCs according to eq. 2 closely match the measured free drug in plasma (Fig. 2B), indicating limited entry of PNL into RBCs.
Fig. 2.
Blood partitioning of prednisolone. (A) Blood-to-plasma concentration ratio (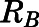 ) vs. plasma concentration of PNL from the subcutaneous bolus (closed squares) and subcutaneous infusion (open squares) studies. (B) Calculated RBCs (closed triangles) and measured free plasma (open triangles) prednisolone concentrations in rats after a single 50-mg/kg s.c. dose of PNL. The dashed line indicates the mean value of all points.
) vs. plasma concentration of PNL from the subcutaneous bolus (closed squares) and subcutaneous infusion (open squares) studies. (B) Calculated RBCs (closed triangles) and measured free plasma (open triangles) prednisolone concentrations in rats after a single 50-mg/kg s.c. dose of PNL. The dashed line indicates the mean value of all points.
TABLE 3.
PBPK model parameter estimates after a single subcutaneous dose of 50-mg/kg PNL in rats
| Parameter (Unit) | Definition | Estimate (CV%) |
|---|---|---|
| NCPC (ng/ml) | Binding capacity of CBG | 297.8 (Fixed) |
| KC (ml/ng) | Association constant of CBG | 0.0046 (Fixed) |
| NAPA (ng/ml) | Binding capacity of albumin | 164,342 (Fixed) |
| KA (ml/ng) | Association constant of albumin | 1.02 × 10−5 (Fixed) |
| Bmax1 (ng/ml) | Binding capacity of muscle | 690.5 (12.5) |
| Bmax2 (ng/ml) | Binding capacity of liver, heart, intestine, bone | 188.5 (11.6) |
| Bmax3 (ng/ml) | Binding capacity of kidney, lung, skin, spleen, fat, brain | 50.77 (10.8) |
| Kd (ng/ml) | Dissociation constant for PNL-tissue interaction | 3.01 (23.8) |
| ka (h−1) | Subcutaneous first-order absorption rate constant | 2.59 (5.1) |
| CLint (ml/h) | CBG-free hepatic intrinsic clearance | 1789 (16.3) |
| CLk (ml/h) | CBG-free renal clearance | 191.2 (40.3) |
| CLup (ml/h) | Brain bidirectional uptake clearance | 0.13 (22.6) |
| CLeff (ml/h) | Brain unidirectional efflux clearance | 4.58 (25.9) |
| fm_liver | Metabolite/drug ratio of PN/PNL for liver | 0.01 (30.1) |
| RB a | Blood-to-plasma conc. ratio | 0.71 (Fixed) |
RB was estimated by Orthogonal Regression according to eq. 1.
Plasma Protein Binding of PNL.
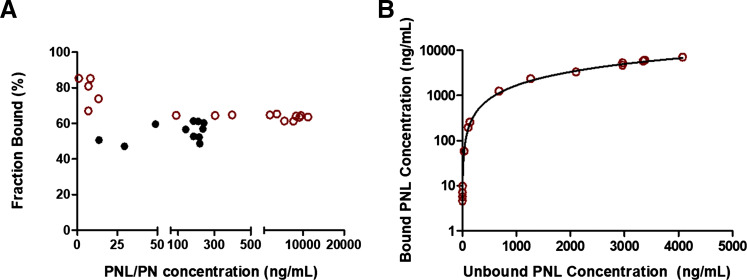
The plasma protein binding of PNL in vivo was assessed by measuring the unbound PNL concentration in plasma samples collected at each time point after subcutaneous bolus dosing using ultrafiltration. The protein binding of PNL in rats was concentration-dependent, with a lower bound fraction (60%) at higher total plasma concentrations and 90% bound at low concentrations (Fig. 3A). The protein binding parameters of PNL in rats were similar across different studies (Rocci et al., 1980; Boudinot and Jusko, 1984, 1986) and thus were applied to relate the bound and unbound PNL plasma concentrations using eq. 9. The model simulations were in very good agreement with the observed data (Fig. 3B). Therefore, these protein binding parameter values (Table 3) were fixed in the subsequent PBPK model to calculate CBG-free drug in plasma. This assumes that tissue uptake of PNL is not restricted to free drug but includes rapid dissociation from albumin. The PNL is bound to CBG with affinity that is several orders of magnitude higher than that of albumin. There is evidence that albumin-bound drug does not retard steroid diffusion into tissues owing to the rapid dissociation from albumin (Pardridge, 1981). Our previous study showed that administration of exogenous CBG significantly decreased the apparent CL and Vss of PNL. The PK of methylprednisolone (MPL), which does not bind to CBG, did not change in rats (Ko et al., 1995). Therefore, we assumed that only CBG-free drug has access to tissues and is subject to elimination in the current PBPK model. In contrast, the protein binding of PN was essentially linear with an average bound fraction of 55% (Fig. 3A), which is consistent with previous observations in rabbit and human plasma (Ferry and Wagner, 1987).
Fig. 3.
Plasma protein binding of prednisolone and prednisone. (A) Bound fractions vs. total concentrations of prednisolone and prednisone. (B) Relationship of bound vs. unbound concentrations of prednisolone. Red open circles are PNL, and black closed circles are PN data. The curve depicts model simulations using eq. 9 with protein binding parameters values listed in Table 3.
Application of Whole-Body PBPK Model.
The tissue-to-unbound-plasma concentration ratios (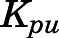 ) decreased in all tissues with CBG-free plasma concentrations obtained using eq. 13 (calculations not shown), indicating nonlinear tissue distribution. Therefore, nonlinear
) decreased in all tissues with CBG-free plasma concentrations obtained using eq. 13 (calculations not shown), indicating nonlinear tissue distribution. Therefore, nonlinear 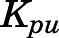 functions for each tissue were incorporated into the PBPK model in the form of eq. 18.
functions for each tissue were incorporated into the PBPK model in the form of eq. 18.
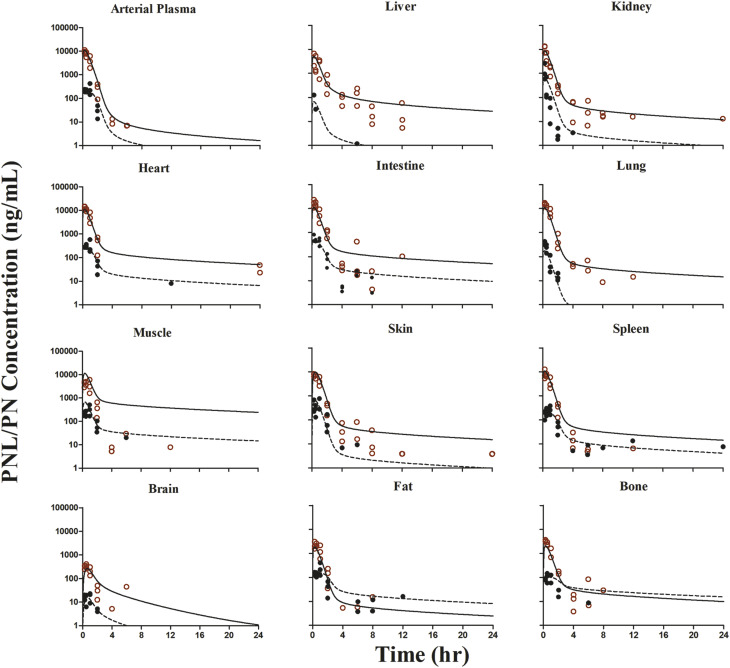
The whole-body PBPK model was applied to jointly fit the concentration-time data of PNL and PN from plasma and all tissues after subcutaneous bolus of 50 mg/kg PNL. The observed and model-predicted PK profiles are shown in Fig. 4. The observed PNL concentrations in arterial blood were fitted using eq. 37 (Fig. 5). In general, this model described all profiles reasonably well with slight overestimation for muscle around the maximum concentration. All model parameters were estimated precisely with reasonable CV% values (Table 3). The absorption of PNL after subcutaneous dosing was relatively fast, with an estimated 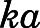 value of 2.59 hour−1 producing immediate high concentrations. The concentrations of PNL in tissues increased rapidly, indicating that PNL distributes quickly within blood and between blood and tissues upon dosing. The PNL PK profiles in most tissues exhibited similar patterns with a dominant early decline phase and a slow terminal phase. The model-estimated binding equilibrium dissociation constant (
value of 2.59 hour−1 producing immediate high concentrations. The concentrations of PNL in tissues increased rapidly, indicating that PNL distributes quickly within blood and between blood and tissues upon dosing. The PNL PK profiles in most tissues exhibited similar patterns with a dominant early decline phase and a slow terminal phase. The model-estimated binding equilibrium dissociation constant (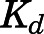 ) of PNL shared by all tissues was 3.01 ng/ml with highest binding observed in muscle (
) of PNL shared by all tissues was 3.01 ng/ml with highest binding observed in muscle (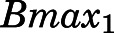 = 690.5 ng/ml), followed by liver, heart, intestine, and bone (
= 690.5 ng/ml), followed by liver, heart, intestine, and bone (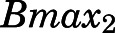 = 188.5 ng/ml) and the lowest binding observed in kidney, lung, spleen, skin, fat, and brain (
= 188.5 ng/ml) and the lowest binding observed in kidney, lung, spleen, skin, fat, and brain (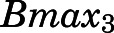 = 50.8 ng/ml). Clearances of CBG-free PNL were 1789 ml/h from liver (
= 50.8 ng/ml). Clearances of CBG-free PNL were 1789 ml/h from liver (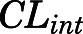 ) and 191.2 ml/h from kidney (
) and 191.2 ml/h from kidney (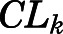 ). Low brain PNL concentrations (
). Low brain PNL concentrations (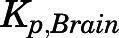 = 0.05, Table 4) in contrast to the expected high permeability (logP = 1.62) were well captured by incorporating a presumed unidirectional active efflux process (
= 0.05, Table 4) in contrast to the expected high permeability (logP = 1.62) were well captured by incorporating a presumed unidirectional active efflux process (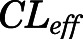 =4.58 ml/h) based upon the bidirectional uptake process (
=4.58 ml/h) based upon the bidirectional uptake process (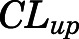 =0.13 ml/h). The much higher
=0.13 ml/h). The much higher 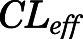 value as compared with that of
value as compared with that of 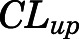 indicates that the limited brain distribution of PNL is strongly affected by the active efflux process. The PK profiles of PNL in fat and bone were reasonably characterized by assuming only the interstitial space was available for distribution.
indicates that the limited brain distribution of PNL is strongly affected by the active efflux process. The PK profiles of PNL in fat and bone were reasonably characterized by assuming only the interstitial space was available for distribution.
Fig. 4.
The prednisolone and prednisone concentration-time profiles in plasma and tissues after 50-mg/kg s.c. bolus dose of PNL in rats. Red open circles are PNL, and black closed circles are PN data. Curves depict PBPK model fittings of PNL (solid line) and PN (dashed line).
Fig. 5.
The prednisolone concentration-time profiles in blood after 50-mg/kg s.c. bolus dose of PNL in rats. Red open circles are PNL data. Curves depict PBPK model fittings.
TABLE 4.
Summary of prednisolone tissue partition coefficients by several methods
| Tissue | PBPK | Infusiona | Method 1 | Method 2 | Method 3 |
|---|---|---|---|---|---|
| Kp,Lung | 1.00 | 1.21 ± 0.47 | 0.86 | 0.7 | 0.53 |
| Kp,Brain | 0.05 | 0.03 ± 0.003 | 1.24 | 0.89 | 0.63 |
| Kp,Kidney | 1.02 | 0.22 ± 0.05 | 0.79 | 0.66 | 0.47 |
| Kp,Kidney (uncorrected) | 0.79 | 0.17 ± 0.04 | |||
| Kp,Heart | 1.17 | 0.92 ± 0.19 | 0.74 | 0.64 | 0.47 |
| Kp,Intestine | 1.17 | 1.37 ± 0.78 | NAb | NAb | NAb |
| Kp,Spleen | 1.01 | 0.47 ± 0.16 | 0.67 | 0.64 | 0.46 |
| Kp,Muscle | 1.88 | 0.32 ± 0.02 | 0.67 | 0.6 | 0.36 |
| Kp,Liver | 1.31 | 3.67 ± 0.19 | 0.77 | 0.63 | 0.48 |
| Kp,Liver (uncorrected) | 0.58 | 1.63 ± 0.08 | |||
| Kp,Skin | 1.01 | 0.57 ± 0.30 | 0.81 | 0.63 | 0.46 |
| Kp,Bone | 0.22 | 0.29 ± 0.13 | NAc | NAc | NAc |
| Kp,Fat | 0.17 | 0.14 ± 0.05 | 0.51 | 0.4 | 0.42 |
| Kp,Remainder | 1.00 (Fixed) |
NA, not applicable.
Calculated based on SS infusion study with n = 2 (S.D. provided).
Tissues associated with gastro-intestinal tract were lumped together.
Different bone marrows were listed separately in software.
Plasma and tissue PN concentrations at each time point after dosing were well characterized simply as a fraction of PNL concentration reflecting their rapid equilibrium (Fig. 4). The metabolite/drug ratio–related parameters (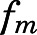 ,
, 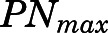 and
and 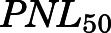 ) were fixed in the PBPK model to the estimated values from the individual organ data (Table 2). Orthogonal regression of the PN versus PNL relationships listed in Table 2 resulted in reasonable fittings but with inexplicable high relative standard error values. Using ordinary least-squares regression in Adapt yielded CV% values that were usually less than 30% but were less reliable fittings. Within the assessed concentration range, the conversion from PNL to PN, as defined by the PN/PNL ratio, exhibited saturable characteristics in plasma, heart, intestine, spleen, bone, and fat, with the lowest
) were fixed in the PBPK model to the estimated values from the individual organ data (Table 2). Orthogonal regression of the PN versus PNL relationships listed in Table 2 resulted in reasonable fittings but with inexplicable high relative standard error values. Using ordinary least-squares regression in Adapt yielded CV% values that were usually less than 30% but were less reliable fittings. Within the assessed concentration range, the conversion from PNL to PN, as defined by the PN/PNL ratio, exhibited saturable characteristics in plasma, heart, intestine, spleen, bone, and fat, with the lowest 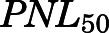 (PNL concentration at half-maximal saturation) in fat and bone and the highest in intestine. Although linear PN/PNL ratios were found for lung, kidney, muscle, skin, liver, brain, and liver, the linear ratio gave the highest
(PNL concentration at half-maximal saturation) in fat and bone and the highest in intestine. Although linear PN/PNL ratios were found for lung, kidney, muscle, skin, liver, brain, and liver, the linear ratio gave the highest 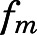 for kidney (0.076, Table 2) and the lowest for liver (0.01, Table 3).
for kidney (0.076, Table 2) and the lowest for liver (0.01, Table 3).
TABLE 2.
PN/PNL ratios as determined by Orthogonal Regression in each tissuea
| Tissue | Parameters b(RSE%) | ||
|---|---|---|---|
| PNmax (ng/ml) | PNL50 (ng/ml) | fm | |
| Fat | 166 (41.9) | 283 (202) | |
| Bone | 108 (28.4) | 314 (173) | |
| Spleen | 230 (48.2) | 794 (252) | |
| Heart | 338 (63.3) | 2575 (251) | |
| Intestine | 589 (62.8) | 3174 (231) | |
| Plasma | 249 (47.2) | 1276 (224) | |
| Kidney | 0.076 (39.5) | ||
| Lung | 0.016 (7.7) | ||
| Brain | 0.059 (26.7) | ||
| Skin | 0.064 (17.2) | ||
| Muscle | 0.060 (28.3) | ||
The PNL 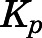 values obtained using different methods are listed in Table 4. For methods based on in vivo data, the
values obtained using different methods are listed in Table 4. For methods based on in vivo data, the 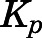 for liver and kidney were corrected for tissue elimination. The uncorrected liver and kidney
for liver and kidney were corrected for tissue elimination. The uncorrected liver and kidney 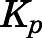 values are also listed. The time- and concentration-averaged
values are also listed. The time- and concentration-averaged 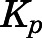 values calculated from the PBPK model–fitted AUC values were generally around 1 and similar to those obtained from the SS infusion study and the in silico methods for most tissues except for brain and liver. The
values calculated from the PBPK model–fitted AUC values were generally around 1 and similar to those obtained from the SS infusion study and the in silico methods for most tissues except for brain and liver. The 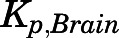 obtained by in silico methods were more than 10-fold higher than those obtained from the in vivo data. The corrected
obtained by in silico methods were more than 10-fold higher than those obtained from the in vivo data. The corrected 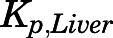 (3.67) obtained from the SS infusion study was higher than those calculated by the other methods.
(3.67) obtained from the SS infusion study was higher than those calculated by the other methods.
Discussion
The PBPK model incorporating nonlinear plasma and tissue binding well characterized the disposition characteristics of PNL and its major metabolite PN in plasma and 11 tissues of rats after SS infusion and a 50-mg/kg s.c. bolus dose of PNL. The blood partitioning of PNL (RB = 0.703/0.71) is comparable to that of dexamethasone (DEX) (RB = 0.664) (Fig. 2A) (Song et al., 2020). The RBC uptake of PNL was limited to the unbound drug in plasma (Fig. 2B), as also found in humans (Araki et al., 1966) and rabbits (Khalafallah and Jusko, 1984b). Initial modeling was attempted based on blood PNL concentrations, but fittings were much better as presented. The model thus assumes that CBG-free drug is available for distribution from both plasma and RBCs.
Moderate binding to cellular constituents may account for tissue distribution of PNL, a neutral molecule. The tissue-to-unbound-plasma concentration ratios (Kpu) declined with higher free-plasma concentrations, and the slow terminal decline of plasma and tissue concentrations required nonlinear tissue binding for best fittings. Preliminary model fittings without considering nonlinear tissue binding resulted in more rapid decline of the terminal phases in all tissues to below the LLOQ by 4 hours after dosing. The rabbit exhibited linear distribution of PNL into tissues except liver; but these studies were performed over a small range of free-plasma concentrations (66–1213 ng/ml) (Khalafallah and Jusko, 1984b).
The moderate lipid solubility (logP = 1.62) and molecular weight (360.4) allow for rapid equilibrium of PNL between blood and tissues, as indicated by the rapid increase in PNL concentrations in tissues (Figs. 4 and 5). Similar PNL profiles across tissues allowed use of one universal tissue binding equilibrium dissociation constant (Kd) and three groups of binding capacities (Bmax). The GRs, which are ubiquitously expressed in tissues and most abundant in the liver (Ballard et al., 1974), may contribute to the tissue binding of PNL. We have shown that the in vitro Kd value for the PNL-GR interaction in liver is about 61 nM (Boudinot et al., 1986). Also, 11β-HSD, which interconverts biologically active GCs (cortisol and PNL) with their inactive counterparts (cortisone and PN), may also contribute to tissue binding. There are two distinct 11β-HSD enzymes, of which 11β-HSD1 is a bidirectional enzyme but primarily an activator of GCs, whereas 11β-HSD2 unidirectionally inactivates GCs (Raza et al., 2010). The affinity constant (Kd) of the weaker binding cortisol to human 11β-HSD2 is 25–55 nM (Chapman et al., 2013). The PBPK model–estimated Kd of PNL (3.01 ng/ml = 8.4 nM) is close to this and the GR Kd value. Furthermore, using a highly purified rat plasma membrane free of CBG and GR, the presence of a GC-responsive site mediating high-affinity active uptake of PNL was demonstrated in rat liver (Lackner et al., 1998). Thus, there are several possible explanations for the nonlinear tissue distribution of PNL.
Several tissues, including brain, fat, and bone, exhibited relatively little drug uptake consistent with our finding for DEX (Song et al., 2020). PNL is a substrate for P-gp, which is highly expressed at the blood-brain barrier and hampers brain exposure of steroids (Karssen et al., 2002; Yates et al., 2003). Despite the moderate lipid solubility of PNL, the in vivo 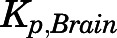 values (0.05/0.03) were much lower than in silico values and those for other tissues. This difference was accounted for in the PBPK model by incorporating P-gp–mediated active efflux in brain. Although this phenomenon may reflect lower binding in the brain, our preliminary modeling without the P-gp–mediated efflux process showed an approximate 20-fold overestimation of brain exposure even though the Bmax value was estimated to be low. This was also seen for DEX in rats (
values (0.05/0.03) were much lower than in silico values and those for other tissues. This difference was accounted for in the PBPK model by incorporating P-gp–mediated active efflux in brain. Although this phenomenon may reflect lower binding in the brain, our preliminary modeling without the P-gp–mediated efflux process showed an approximate 20-fold overestimation of brain exposure even though the Bmax value was estimated to be low. This was also seen for DEX in rats (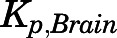 =0.06) (Song et al., 2020), another P-gp substrate (Ueda et al., 1992; Schinkel et al., 1995).
=0.06) (Song et al., 2020), another P-gp substrate (Ueda et al., 1992; Schinkel et al., 1995).
The concentrations of PNL in fat, in which drug uptake usually depends on lipid solubility, were low (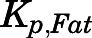 = 0.17), as was also found for DEX (
= 0.17), as was also found for DEX (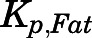 = 0.15) (Song et al., 2020). These results are in line with findings that the SS fat
= 0.15) (Song et al., 2020). These results are in line with findings that the SS fat 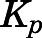 of PNL in rabbits was 0.13 (Khalafallah and Jusko, 1984b). This explains why volumes of distribution of PNL only increased modestly in obese men (Milsap et al., 1984) and rats (Nichols et al., 1989). Further, CBG is expressed in rat white adipose tissue, and the CBG layer surrounding white adipose tissue cells near the plasma membrane may act as a protective barrier limiting the access of GCs to adipocytes (del Mar Grasa et al., 2001).
of PNL in rabbits was 0.13 (Khalafallah and Jusko, 1984b). This explains why volumes of distribution of PNL only increased modestly in obese men (Milsap et al., 1984) and rats (Nichols et al., 1989). Further, CBG is expressed in rat white adipose tissue, and the CBG layer surrounding white adipose tissue cells near the plasma membrane may act as a protective barrier limiting the access of GCs to adipocytes (del Mar Grasa et al., 2001).
The relatively low concentrations of PNL in bone (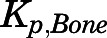 = 0.22) are consistent with observations for DEX (
= 0.22) are consistent with observations for DEX (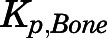 = 0.23) (Song et al., 2020). Why bone has such low values is not clear. Nevertheless, knowledge of factors responsible for steroid access to bone may be important for understanding their deleterious effects (Lukert and Raisz, 1990). The limited distribution of PNL into fat and bone was well described by assuming only interstitial space is accessible.
= 0.23) (Song et al., 2020). Why bone has such low values is not clear. Nevertheless, knowledge of factors responsible for steroid access to bone may be important for understanding their deleterious effects (Lukert and Raisz, 1990). The limited distribution of PNL into fat and bone was well described by assuming only interstitial space is accessible.
Hepatic and renal metabolism and renal excretion are responsible for PNL clearance (Caspi and Pechet, 1958; Vermeulen and Caspi, 1958; Glenn, 1959; Bailey and West, 1967; Rocci et al., 1981). The model-estimated CBG-free hepatic intrinsic clearance was high (1789 ml/h), accounting for rapid conversion of PNL to PN. Using eq. 38 and the hepatic blood flow (1424 ml/h), this converts to a systemic clearance of 793 ml/h. For kidney, the systemic clearance (CLs) is 149 ml/h. The overall systemic clearance is thus 942 ml/h, which is comparable to the value of 1129 ml/h for CBG-free PNL clearance in rats (Boudinot and Jusko, 1986; Boudinot et al., 1986). These previous studies showed similar plasma concentration profiles of PNL and PN after a 50-mg/kg i.v. dose to ours. The liver thus accounts for 90% of PNL disposition, and the kidney accounts for 10%. However, these clearance values do not account for PNL and PN interconversion because recycling augments the PNL AUC and thus underestimates the true clearance (Ebling and Jusko, 1986). There is evidence of an enterohepatic circulation (EHC) of GCs, which might partially explain their appreciable liver clearance. The intestinal absorption and biliary excretion of DEX in rats were reduced by dicyclomine, a cholinergic blocking agent, and consequently resulted in a decrease in AUC (Ogiso et al., 1985), indicating the involvement of EHC in DEX disposition. The possibility for EHC in rats might also apply to PNL (Mueller and Potter, 1981), although total radioactivity was measured in their study, which would include PNL metabolites.
As shown in Fig. 4, the appearance of PN in each tissue is very rapid upon PNL administration with similar times to reach maximum concentrations observed for both compounds. Modeling PN concentration simply as a fraction of PNL described the PN data reasonably well. This supports the assumption that the interconversion between PNL and PN is in continual rapid equilibrium. The interconversion of PNL and PN is mediated by 11β-HSDs, of which 11β-HSD1 is widely distributed with high expression in the liver and also in adipose tissue, muscle, bone, synovium, gonadal tissue, decidua, ocular tissues, and the CNS. The 11β-HSD2 is largely restricted to the mineralocorticoid-target tissues and the placenta (Raza et al., 2010). There has been evidence showing that the different tissue ratios of PN/PNL are mainly due to the tissue-specific expression and activity of 11β-HSDs (Escher et al., 1994). The conversion from PNL to PN is mediated by 11β-HSD2, and some tissues exhibit 11β-HSD2 saturation. The nonlinear PN/PNL ratio in rat plasma is consistent with observations in dogs (Frey et al., 1980) and humans (Legler et al., 1982). The 11β-HSD2 has tissue-specific distribution with highest enzyme activity in kidney (Monder, 1991; Yau et al., 1991), which may explain the appreciable and nonsaturable production of PN in kidney. Our liver concentrations of PN were very low. This could be explained by the high 11β-HSD1 expression in the liver and also agrees with findings in rats (Escher et al., 1994) that the PN/PNL ratio in liver was far lower than in other tissues. Liver perfusions were carried out in rabbits in which the extraction ratio of PNL was 50%, but no measurable PN was formed (Hale and Benet, 1991). Redistribution of PN between various tissues cannot be ruled out owing to the likely high permeability of this compound, which partly necessitated our metabolite modeling approach.
The Kp predictions using three in silico methods were similar and generally comparable to those obtained from in vivo data except for liver and brain (Table 4). The difference between liver Kp before (1.63) and after (3.67) metabolic correction can be attributed to substantial hepatic extraction of PNL and moderate partitioning. Similar findings of moderate liver partitioning were found for DEX (Kp = 5.06) (Song et al., 2020) and MPL (Kp = 13.5) (Ayyar et al., 2019). The extensive accumulation of GCs within liver may be largely attributed to the abundant expression of GRs (Ballard et al., 1974). Also, the GC importer-mediated active uptake of PNL, DEX, and MPL into highly purified rat liver plasma membranes free of CBGs and GRs (Lackner et al., 1998) may be another factor contributing to their high Kp values. However, the PBPK model–derived Kp (1.31) and the in silico Kp (0.48–0.77) for liver were 2.8- to 10-fold smaller than those obtained with the SS infusion. The plasma concentrations of PNL after the 50-mg/kg bolus s.c. dose (Fig. 4) are substantially higher than those from (1032.5 ng/ml) the infusion study. These nonlinear Kp differences agree with observations in rabbits that the tissue distribution of PNL is saturable in liver (Khalafallah and Jusko, 1984b). The in silico methods assume that tissue distribution is largely determined by neutral and phospholipid drug partitioning. They do not consider the roles of transport proteins, complex binding of drugs in liver, and active efflux in brain.
Limitations of the current study are that only one bolus dose level of PNL was used, and the subcutaneous bioavailability (F) was based on the intravenous data from another study (Huang and Jusko, 1990). However, the 50-mg/kg dose of subcutaneous PNL yielded a wide range of plasma and tissue concentrations spanning several orders of magnitude. The calculated F appeared reliable in that the same rat strain (male Wistar rats) with comparable body weights were used, and the intravenous AUC values were consistent across studies (Boudinot and Jusko, 1986; Boudinot et al., 1986; Huang and Jusko, 1990). The metabolic interconversion rates between PNL and PN were observed to be in rapid equilibrium. It would be necessary to directly give PN to assess its clearance parameters (Ebling and Jusko, 1986). Through incorporating nonlinear plasma and tissue binding, the current PBPK model was able to reasonably capture the PK profiles of PNL and PN in all tissues. Although the late low concentrations of PNL in muscle were overpredicted, these values are complicated by being close to the LLOQ of 1 ng/ml, account for less than 0.1% of early concentrations, and are the latest values in individual animals after subcutaneous dosing and subject to diverse sources of variation. The similarity of PNL and PN profiles across tissues supports the general behavior of all tissues as modeled.
The metabolic and pharmacokinetic properties of PNL and PN are generally similar in rat and human, making this PBPK model applicable to human and perhaps other species. In particular, as described for humans in the Introduction, this includes nonlinear binding to CBG in plasma, reversible metabolism with PNL dominating over PN in a similar ratio in plasma, metabolism by liver and kidney, involvement of CYP3A in liver (Pichard et al., 1992; Penzak et al., 2005), and 11β-HSDs in various tissues, a similar apparent Vss/body weight in rat (1.31 l/kg) (Huang and Jusko, 1990) and human (1.04 l/kg) (Czock et al., 2005) implying similar tissue binding. There is also similar binding to glucocorticoid receptors in both species. Differences would include metabolic rates and possible EHC only in the rat. Because corticosteroids generally have similar PK properties in various species, receptors in most tissues, and multiple therapeutic and adverse actions, this PBPK model may provide greater insights into their pharmacodynamic complexities.
Acknowledgments
We appreciate the assistance of Donna Ruszaj in setting up the LC-MS/MS assay.
Abbreviations
- AUC
area under the curve
- 11β-HSD
11β-hydroxysteroid dehydrogenase
- CBG
corticosteroid-binding globulin
- CL
clearance
- CS
corticosteroid
- CV%
coefficients of variation
- DEX
dexamethasone
- EHC
enterohepatic circulation
- GR
glucocorticoid receptor
- IS
internal standard
- LC-MS/MS
liquid chromatography–tandem mass spectrometry
- LLOQ
lower limit of quantification
- MPL
methylprednisolone
- PBPK
physiologically based pharmacokinetics
- P-gp
P-glycoprotein
- PK
pharmacokinetics
- PN
prednisone
- PNL
prednisolone
- RBC
red blood cell
- SPE
solid-phase extraction
- SS
steady state
- Vss
volume of distribution at SS
Authorship Contributions
Participated in research design: Li, DuBois, Jusko.
Conducted experiments: Li, DuBois.
Performed data analysis: Li, Jusko.
Wrote or contributed to the writing of the manuscript: Li, DuBois, Almon, Jusko.
Footnotes
This work was supported by National Institutes of Health National Institute of General Medical Sciences [Grant R35-GM131800].
 This article has supplemental material available at jpet.aspetjournals.org.
This article has supplemental material available at jpet.aspetjournals.org.
References
- Araki Y, Yokota O, Kato T, Kashima M, Miyazaki T. (1966) Dynamics of synthetic corticosteroids in man, in Steroid Dynamics (Pincus P, Nakao JTT. eds) pp 463–480, Academic Press, New York. [Google Scholar]
- Ayyar VS, Song D, DuBois DC, Almon RR, Jusko WJ. (2019) Modeling corticosteroid pharmacokinetics and pharmacodynamics, part I: determination and prediction of dexamethasone and methylprednisolone tissue binding in the rat. J Pharmacol Exp Ther 370:318–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey E, West HF. (1967) Prednisolone metabolism and rheumatoid arthritis. Lancet 2:1231–1232. [DOI] [PubMed] [Google Scholar]
- Ballard PL, Baxter JD, Higgins SJ, Rousseau GG, Tomkins GM. (1974) General presence of glucocorticoid receptors in mammalian tissues. Endocrinology 94:998–1002. [DOI] [PubMed] [Google Scholar]
- Barth J, Damoiseaux M, Möllmann H, Brandis KH, Hochhaus G, Derendorf H. (1992) Pharmacokinetics and pharmacodynamics of prednisolone after intravenous and oral administration. Int J Clin Pharmacol Ther Toxicol 30:317–324. [PubMed] [Google Scholar]
- Berezhkovskiy LM. (2004) Volume of distribution at steady state for a linear pharmacokinetic system with peripheral elimination. J Pharm Sci 93:1628–1640. [DOI] [PubMed] [Google Scholar]
- Bergmann TK, Barraclough KA, Lee KJ, Staatz CE. (2012) Clinical pharmacokinetics and pharmacodynamics of prednisolone and prednisone in solid organ transplantation. Clin Pharmacokinet 51:711–741. [DOI] [PubMed] [Google Scholar]
- Bernareggi A, Rowland M. (1991) Physiologic modeling of cyclosporin kinetics in rat and man. J Pharmacokinet Biopharm 19:21–50. [DOI] [PubMed] [Google Scholar]
- Boudinot FD, D’Ambrosio R, Jusko WJ. (1986) Receptor-mediated pharmacodynamics of prednisolone in the rat. J Pharmacokinet Biopharm 14:469–493. [DOI] [PubMed] [Google Scholar]
- Boudinot FD, Jusko WJ. (1984) Plasma protein binding interaction of prednisone and prednisolone. J Steroid Biochem 21:337–339. [DOI] [PubMed] [Google Scholar]
- Boudinot FD, Jusko WJ. (1986) Dose-dependent pharmacokinetics of prednisolone in normal and adrenalectomized rats. J Pharmacokinet Biopharm 14:453–467. [DOI] [PubMed] [Google Scholar]
- Caspi E, Pechet MM. (1958) Metabolism of 1-dehydrosteroids in man. I. Isolation of six urinary products after the administration of prednisolone. J Biol Chem 230:843–851. [PubMed] [Google Scholar]
- Chapman K, Holmes M, Seckl J. (2013) 11β-hydroxysteroid dehydrogenases: intracellular gate-keepers of tissue glucocorticoid action. Physiol Rev 93:1139–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutinho AE, Chapman KE. (2011) The anti-inflammatory and immunosuppressive effects of glucocorticoids, recent developments and mechanistic insights. Mol Cell Endocrinol 335:2–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czock D, Keller F, Rasche FM, Häussler U. (2005) Pharmacokinetics and pharmacodynamics of systemically administered glucocorticoids. Clin Pharmacokinet 44:61–98. [DOI] [PubMed] [Google Scholar]
- D’ Argenio D, Schumitzky A, Wang X. (2009) Adapt 5 user’s guide: pharmacokinetic/pharmacodynamic systems analysis software, BMSR, University of Southern California, Los Angeles, CA. [Google Scholar]
- del Mar Grasa M, Cabot C, Adán C, de Matteis R, Esteve M, Cinti S, Fernández JA, López, Remesar X, Alemany A. (2001) Corticosteroid-binding globulin synthesis and distribution in rat white adipose tissue. Mol Cell Biochem 228:25–31. [DOI] [PubMed] [Google Scholar]
- Derendorf H, Rohdewald P, Möllmann H, Rehder J, Barth J, Neveling D. (1985) Pharmacokinetics of prednisolone after high doses of prednisolone hemisuccinate. Biopharm Drug Dispos 6:423–432. [DOI] [PubMed] [Google Scholar]
- Difrancesco R, Frerichs V, Donnelly J, Hagler C, Hochreiter J, Tornatore KM. (2007) Simultaneous determination of cortisol, dexamethasone, methylprednisolone, prednisone, prednisolone, mycophenolic acid and mycophenolic acid glucuronide in human plasma utilizing liquid chromatography-tandem mass spectrometry. J Chromatogr B Analyt Technol Biomed Life Sci 859:42–51. [DOI] [PubMed] [Google Scholar]
- Ebling WF, Jusko WJ. (1986) The determination of essential clearance, volume, and residence time parameters of recirculating metabolic systems: the reversible metabolism of methylprednisolone and methylprednisone in rabbits. J Pharmacokinet Biopharm 14:557–599. [DOI] [PubMed] [Google Scholar]
- Escher G, Frey FJ, Frey BM. (1994) 11 beta-Hydroxysteroid dehydrogenase accounts for low prednisolone/prednisone ratios in the kidney. Endocrinology 135:101–106. [DOI] [PubMed] [Google Scholar]
- Ferry JJ, Wagner JG. (1987) The nonlinear pharmacokinetics of prednisone and prednisolone. II. Plasma protein binding of prednisone and prednisolone in rabbit and human plasma. Biopharm Drug Dispos 8:261–272. [DOI] [PubMed] [Google Scholar]
- Frey BM, Frey FJ. (1990) Clinical pharmacokinetics of prednisone and prednisolone. Clin Pharmacokinet 19:126–146. [DOI] [PubMed] [Google Scholar]
- Frey FJ, Frey BM, Greither A, Benet LZ. (1980) Prednisolone clearance at steady state in dogs. J Pharmacol Exp Ther 215:287–291. [PubMed] [Google Scholar]
- Gerlowski LE, Jain RK. (1983) Physiologically based pharmacokinetic modeling: principles and applications. J Pharm Sci 72:1103–1127. [DOI] [PubMed] [Google Scholar]
- Glenn EM. (1959) In vitro and in vivo metabolism of prednisolone: studies concerning its biological effectiveness. Endocrinology 64:373–378. [DOI] [PubMed] [Google Scholar]
- Hale VG, Benet LZ. (1991) Prednisolone and prednisone exhibit linear extraction in the perfused rabbit liver. Drug Metab Dispos 19:87–93. [PubMed] [Google Scholar]
- Huang ML, Jusko WJ. (1990) Nonlinear pharmacokinetics and interconversion of prednisolone and prednisone in rats. J Pharmacokinet Biopharm 18:401–421. [DOI] [PubMed] [Google Scholar]
- Kadmiel M, Cidlowski JA. (2013) Glucocorticoid receptor signaling in health and disease. Trends Pharmacol Sci 34:518–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kampfmann I, Bauer N, Johannes S, Moritz A. (2012) Differences in hematologic variables in rats of the same strain but different origin. Vet Clin Pathol 41:228–234. [DOI] [PubMed] [Google Scholar]
- Karssen AM, Meijer OC, van der Sandt IC, De Boer AG, De Lange EC, De Kloet ER. (2002) The role of the efflux transporter P-glycoprotein in brain penetration of prednisolone. J Endocrinol 175:251–260. [DOI] [PubMed] [Google Scholar]
- Khalafallah N, Jusko WJ. (1984a) Determination and prediction of tissue binding of prednisolone in the rabbit. J Pharm Sci 73:362–366. [DOI] [PubMed] [Google Scholar]
- Khalafallah N, Jusko WJ. (1984b) Tissue distribution of prednisolone in the rabbit. J Pharmacol Exp Ther 229:719–725. [PubMed] [Google Scholar]
- Ko HC, Almon RR, Jusko WJ. (1995) Effect of corticosteroid binding globulin on the pharmacokinetics of prednisolone in rats. Pharm Res 12:902–904. [DOI] [PubMed] [Google Scholar]
- Lackner C, Daufeldt S, Wildt L, Alléra A. (1998) Glucocorticoid-recognizing and -effector sites in rat liver plasma membrane. Kinetics of corticosterone uptake by isolated membrane vesicles. III. Specificity and stereospecificity. J Steroid Biochem Mol Biol 64:69–82. [DOI] [PubMed] [Google Scholar]
- Legler UF, Frey FJ, Benet LZ. (1982) Prednisolone clearance at steady state in man. J Clin Endocrinol Metab 55:762–767. [DOI] [PubMed] [Google Scholar]
- Lukert BP, Raisz LG. (1990) Glucocorticoid-induced osteoporosis: pathogenesis and management. Ann Intern Med 112:352–364. [DOI] [PubMed] [Google Scholar]
- Melby JC. (1977) Clinical pharmacology of systemic corticosteroids. Annu Rev Pharmacol Toxicol 17:511–527. [DOI] [PubMed] [Google Scholar]
- Methlie P, Hustad SS, Kellmann R, Almås B, Erichsen MM, Husebye E, Løvås K. (2013) Multisteroid LC-MS/MS assay for glucocorticoids and androgens, and its application in Addison’s disease. Endocr Connect 2:125–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milsap RL, Plaisance KI, Jusko WJ. (1984) Prednisolone disposition in obese men. Clin Pharmacol Ther 36:824–831. [DOI] [PubMed] [Google Scholar]
- Monder C. (1991) Heterogeneity of 11 beta-hydroxysteroid dehydrogenase in rat tissues. J Steroid Biochem Mol Biol 40:533–536. [DOI] [PubMed] [Google Scholar]
- Mueller UW, Potter JM. (1981) Enterohepatic circulation of prednisolone in rats. Res Commun Chem Pathol Pharmacol 32:195–206. [PubMed] [Google Scholar]
- National Research Council (2011) Guide for the Care and Use of Laboratory Animals, National Academies Press, Washington, DC. [Google Scholar]
- Nichols AI, D’Ambrosio R, Pyszczynski NA, Jusko WJ. (1989) Pharmacokinetics and pharmacodynamics of prednisolone in obese rats. J Pharmacol Exp Ther 250:963–970. [PubMed] [Google Scholar]
- Oakley RH, Cidlowski JA. (2011) Cellular processing of the glucocorticoid receptor gene and protein: new mechanisms for generating tissue-specific actions of glucocorticoids. J Biol Chem 286:3177–3184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogiso T, Iwaki M, Ohtori A. (1985) Effect of dicyclomine on intestinal absorption, disposition and biliary excretion of dexamethasone. J Pharmacobiodyn 8:41–49. [DOI] [PubMed] [Google Scholar]
- Overman RA, Yeh JY, Deal CL. (2013) Prevalence of oral glucocorticoid usage in the United States: a general population perspective. Arthritis Care Res (Hoboken) 65:294–298. [DOI] [PubMed] [Google Scholar]
- Pardridge WM. (1981) Transport of protein-bound hormones into tissues in vivo. Endocr Rev 2:103–123. [DOI] [PubMed] [Google Scholar]
- Penzak SR, Formentini E, Alfaro RM, Long M, Natarajan V, Kovacs J. (2005) Prednisolone pharmacokinetics in the presence and absence of ritonavir after oral prednisone administration to healthy volunteers. J Acquir Immune Defic Syndr 40:573–580. [DOI] [PubMed] [Google Scholar]
- Pichard L, Fabre I, Daujat M, Domergue J, Joyeux H, Maurel P. (1992) Effect of corticosteroids on the expression of cytochromes P450 and on cyclosporin A oxidase activity in primary cultures of human hepatocytes. Mol Pharmacol 41:1047–1055. [PubMed] [Google Scholar]
- Poulin P, Theil FP. (2002a) Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci 91:129–156. [DOI] [PubMed] [Google Scholar]
- Poulin P, Theil FP. (2002b) Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J Pharm Sci 91:1358–1370. [DOI] [PubMed] [Google Scholar]
- Raza K, Hardy R, Cooper MS. (2010) The 11beta-hydroxysteroid dehydrogenase enzymes--arbiters of the effects of glucocorticoids in synovium and bone. Rheumatology (Oxford) 49:2016–2023. [DOI] [PubMed] [Google Scholar]
- Rhen T, Cidlowski JA. (2005) Antiinflammatory action of glucocorticoids--new mechanisms for old drugs. N Engl J Med 353:1711–1723. [DOI] [PubMed] [Google Scholar]
- Rocci ML, Jr., Johnson NF, Jusko WJ. (1980) Serum protein binding of prednisolone in four species. J Pharm Sci 69:977–978. [DOI] [PubMed] [Google Scholar]
- Rocci ML, Jr., Jusko WJ. (1981) Dose-dependent protein binding and disposition of prednisolone in rabbits. J Pharm Sci 70:1201–1204. [DOI] [PubMed] [Google Scholar]
- Rocci ML, Jr., Szefler SJ, Acara M, Jusko WJ. (1981) Prednisolone metabolism and excretion in the isolated perfused rat kidney. Drug Metab Dispos 9:177–182. [PubMed] [Google Scholar]
- Rodgers T, Rowland M. (2006) Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci 95:1238–1257. [DOI] [PubMed] [Google Scholar]
- Rose JQ, Yurchak AM, Jusko WJ. (1981) Dose dependent pharmacokinetics of prednisone and prednisolone in man. J Pharmacokinet Biopharm 9:389–417. [DOI] [PubMed] [Google Scholar]
- Saag KG, Koehnke R, Caldwell JR, Brasington R, Burmeister LF, Zimmerman B, Kohler JA, Furst DE. (1994) Low dose long-term corticosteroid therapy in rheumatoid arthritis: an analysis of serious adverse events. Am J Med 96:115–123. [DOI] [PubMed] [Google Scholar]
- Sager JE, Yu J, Ragueneau-Majlessi I, Isoherranen N. (2015) Physiologically based pharmacokinetic (PBPK) modeling and simulation approaches: a systematic review of published models, applications, and model verification. Drug Metab Dispos 43:1823–1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandberg AA, Slaunwhite WR, Jr., Antoniades HN. (1957) The binding of steroids and steroid conjugates to human plasma proteins. Recent Prog Horm Res 13:209–260, NaN–267. [PubMed] [Google Scholar]
- Schinkel AH, Wagenaar E, van Deemter L, Mol CA, Borst P. (1995) Absence of the mdr1a P-Glycoprotein in mice affects tissue distribution and pharmacokinetics of dexamethasone, digoxin, and cyclosporin A. J Clin Invest 96:1698–1705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah DK, Betts AM. (2012) Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn 39:67–86. [DOI] [PubMed] [Google Scholar]
- Song D, Sun L, DuBois DC, Almon RR, Meng S, Jusko WJ. (2020) Physiologically based pharmacokinetics of dexamethasone in rats. Drug Metab Dispos 48:811–818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueda K, Okamura N, Hirai M, Tanigawara Y, Saeki T, Kioka N, Komano T, Hori R. (1992) Human P-glycoprotein transports cortisol, aldosterone, and dexamethasone, but not progesterone. J Biol Chem 267:24248–24252. [PubMed] [Google Scholar]
- Vermeulen A, Caspi E. (1958) The metabolism of prednisolone by homogenates of rat liver. J Biol Chem 233:54–56. [PubMed] [Google Scholar]
- Yao Q, Guo Y, Xue J, Kong D, Li J, Tian X, Hao C, Zhou T. (2020) Development and validation of a LC-MS/MS method for simultaneous determination of six glucocorticoids and its application to a pharmacokinetic study in nude mice. J Pharm Biomed Anal 179:112980. [DOI] [PubMed] [Google Scholar]
- Yates CR, Chang C, Kearbey JD, Yasuda K, Schuetz EG, Miller DD, Dalton JT, Swaan PW. (2003) Structural determinants of P-glycoprotein-mediated transport of glucocorticoids. Pharm Res 20:1794–1803. [DOI] [PubMed] [Google Scholar]
- Yau JL, Van Haarst AD, Moisan MP, Fleming S, Edwards CR, Seckl JR. (1991) 11 beta-Hydroxysteroid dehydrogenase mRNA expression in rat kidney. Am J Physiol 260:F764–F767. [DOI] [PubMed] [Google Scholar]