One-dimensional spatial patterning along mitotic chromosomes: A mechanical basis for macroscopic morphogenesis

Significance

Spatial patterns are a prominent and interesting feature of both biological and physical systems. We have discovered that mammalian mitotic chromosomes, which comprise two closely associated sister chromatids, exhibit two interesting spatial patterns. In one pattern, the structural axis of each chromatid acquires sequential partial helices of alternating handedness. In the other, an array of evenly spaced bridges links these two axes. Development of any spatial pattern requires communication within the system. We present a constellation of observations suggesting that these patterns are related and are promoted by a mechanical mechanism in which the communication required for development of patterns arises from redistribution of mechanical stress. Models involving bonded chromatin/axis bilayers and Kirchhoff–Love theory for elastic rods are discussed.

Abstract

Spatial patterns are ubiquitous in both physical and biological systems. We have recently discovered that mitotic chromosomes sequentially acquire two interesting morphological patterns along their structural axes [L. Chu et al., Mol. Cell, 10.1016/j.molcel.2020.07.002 (2020)]. First, axes of closely conjoined sister chromosomes acquire regular undulations comprising nearly planar arrays of sequential half-helices of similar size and alternating handedness, accompanied by periodic kinks. This pattern, which persists through all later stages, provides a case of the geometric form known as a “perversion.” Next, as sister chromosomes become distinct parallel units, their individual axes become linked by bridges, which are themselves miniature axes. These bridges are dramatically evenly spaced. Together, these effects comprise a unique instance of spatial patterning in a subcellular biological system. We present evidence that axis undulations and bridge arrays arise by a single continuous mechanically promoted progression, driven by stress within the chromosome axes. We further suggest that, after sister individualization, this same stress also promotes chromosome compaction by rendering the axes susceptible to the requisite molecular remodeling. Thus, by this scenario, the continuous presence of mechanical stress within the chromosome axes could potentially underlie the entire morphogenetic chromosomal program. Direct analogies with meiotic chromosomes suggest that the same effects could underlie interactions between homologous chromosomes as required for gametogenesis. Possible mechanical bases for generation of axis stress and resultant deformations are discussed. Together, these findings provide a perspective on the macroscopic changes of organized chromosomes.

During the mitotic cell cycle, duplicated chromosome copies (“sister chromatids”) segregate to two daughter cells, thereby ensuring cellular inheritance. In preparation for this segregation, chromosomes become discrete, organized units and then undergo two sequential transitions (1). First, sister chromatids undergo side-by-side separation. Second, the resulting pair of parallel sister chromatids progressively compact, becoming shorter, fatter, and denser, so as to allow their clean separation to opposite poles of the mitotic spindle.

Morphological events of this period have been elucidated in some detail (e.g., refs. 1 and 2). Each sister unit is organized into a linear array of chromatin loops that emanates from within a complex structural meshwork of protein/protein/DNA/DNA interactions referred to here as the “axis” (refs. 2–6 and Fig. 1A). Sister linear loop/axis arrays are cooriented. When organized chromosomes first emerge (at “prophase”), the two arrays are intimately associated such that they comprise a single morphological unit (Fig. 1 B, Left). They then individualize by lateral splitting, at the chromatin and axis levels (Fig. 1 B, Right). This splitting transition is accompanied by the appearance of interaxis bridges (Fig. 1 B, Right), which lie along the sisters’ shared axis interface (SI Appendix, Fig. S1A). Compositional analysis suggests that these bridges are themselves “miniature axes.” From this newly individualized state, chromosomes then progressively compact, apparently in large part via restructuring of their loop/axis arrays. Bridges are present throughout this period. One important role is to provide mechanical stability to the sister couple through the turbulence of internal compaction forces and from external forces due to concomitant alignment of chromosomes on the mitotic spindle.

Fig. 1.

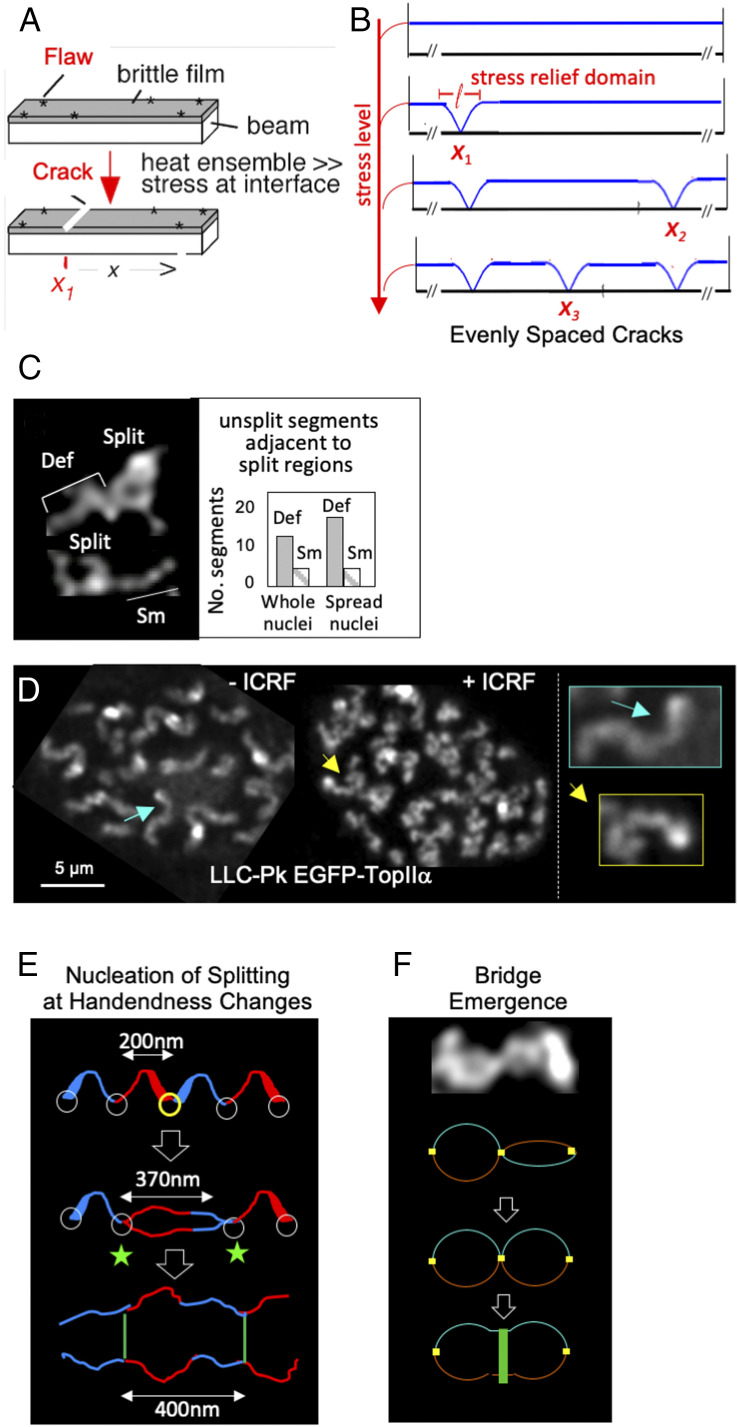
Two spatial patterns emerge in succession along mitotic chromosomes by a proposed single continuous stress-promoted process. (A) Each mitotic chromatid is organized as a linear array of loops that emanate from a complex axis meshwork. At prophase, prior to sister individualization, the two arrays are closely conjoined into a single morphological unit. Arrows indicate that the paths of the centroids of the chromatin and axis signals (defined as in B) were determined. In each case, the shape was sliced along its length and the centroid of each slice determined and assembled into the corresponding path. The tendency for helicity along the path and the handedness of that helicity were then determined (details in ref. 2). (B) Images of DNA (DAPI) or chromatin (H2B-mCherry) and TopIIα axis signals for a prophase chromosome comprising a closely conjoined pair of sister chromatids (Left) and postprophase chromosome in which sisters are individualized (Right) (details in Materials and Methods). (C and D) Examples of undulating axis paths along unsplit prophase chromosomes (C) and individual chromatids of split postprophase chromosomes (D). (C) Centroid paths of the conjoined axes (red/blue) of two prophase chromosome segments; the centroid path of the chromatin shape (green/white) is also shown for the segment at Left. (D) Centroid paths of the axes of single chromatids (one of two sister chromatids) from two different postprophase chromosomes. (Top) Centroids are superimposed on thresholded Pymol images of the axis shapes. (Bottom) Different views of the axis paths illustrating regular changes in helical handedness (red/blue); regular kinks that often occur at positions of handedness changes (white dots) and the tendency for successive segments to be rotated (twisted) relative to one another (brackets) are shown. (E) Chromosomes with individualized sisters exhibit separated parallel axes with undulating paths that are linked by “miniaxis” bridges. Bridges (turquoise dots) are visible by the eye in the primary image (Left) and also definable as peaks of intensity along a line between the sister chromatids (yellow arrows). Positions with respect to axis paths (Right) are defined by superimposition of paths on thresholded Pymol images of axis shapes (Middle). (F) Sister chromatid axis separation occurs via evenly spaced bubbles with evenly spaced interaxis bridges emerging from the short unsplit regions between bubbles (examples in G). (G) The sequence of prophase events that give rise to spatially patterned (regular) axis deformations and then spatially patterned (evenly spaced) bridges is proposed to involve a single continuous process promoted by mechanical stress within the axes. (Scale bar: 1 µm.) B, Right and C–G adapted from ref. 2, with permission from Elsevier.

This morphological pathway also involves two interesting chromosomal patterns, both of which involve the chromosome axes (2). First, axes are not straight. Instead, they exhibit a series of regular deformations. Visual inspection of intensity-weighted centroids reveals a consensus path that overall tends to be nearly planar and includes 1) a sequential array of ∼200-nm half-helical segments of alternating handedness (red and blue) and 2) a regular array of kinks (white dots) that often occur at the positions of handedness changes and frequently involve rotation of adjacent segments (Fig. 1 C and D). The same path also directly visible in the overall shape of the axis compartment (Fig. 1D overlays). The presence of alternating helical handedness comprises a unique subcellular example of a geometric feature known as a “perversion.” This deformed axis path arises prior to sister individualization and remains present, while also being highly dynamic, during ensuing compaction and alignment on the spindle.

Second, splitting of sister chromatid axes occurs by formation of close-packed, regularly sized (∼370-nm) bubbles (Fig. 1 F and G). Interaxis bridges then emerge at the short unsplit regions between this regular array of bubbles (Fig. 1 F and G). As a result, adjacent bridges are very evenly spaced, at ∼400-nm separation. Regularity of spacing can be defined by the shape parameter of the best-fit gamma distribution of component distances, where ν = 1 corresponds to an exponential distribution, while higher values correspond to deviations toward evenness. For interbridge distances, the shape parameter for the best-fit gamma distribution is 6 to 10 (ref. 2 and SI Appendix, Fig. S1B).

In biological systems, such patterns often arise by biochemical processes, with communication provided by molecular diffusion in Turing-derived “reaction-diffusion” mechanisms (e.g., refs. 7–9). In contrast, in physical systems, patterns arise by mechanical effects. The key central feature of patterning is a requirement for communication, e.g., along a chromosome. In a reaction–diffusion process, changes are the result of cyclic biochemical changes, and communication is provided by diffusion. In a mechanical process, changes are driven by active imposition of forces against resistance from the system, resulting in accumulation of stress. Stress is a high-energy state. Patterns arise as changes that reduce that energy (and thus stress). In this case, communication is provided by the intrinsic tendency for changes in stress to redistribute through the system to give a minimal energy state. A mechanical process has also been proposed to occur in a biological system, to underlie even spacing of DNA recombination (cross-over) events along meiotic chromosomes (10).

The present study further analyzes the axis patterns observed along mitotic chromosomes. We describe a mechanical hypothesis in which internal stress is actively generated within the chromosomes and progressively promotes the entire sequence of prophase axis changes: deformation of unsplit axes; emergence of evenly spaced bubbles of sister axis splitting and their targeting by deformation patterns; evolution bridges from the array of bubbles; and, finally, after the sister individualization transition, the destabilized state created by internal stress renders the axes susceptible to the molecular events responsible for axis restructuring for chromosome compaction. Among other implications, this synthesis provides a functional rationale for the existence of deformed axis paths, whose relevance to morphogenesis has previously been unclear. We also note that analogous mechanical effects may play important roles also for meiotic interhomolog interactions (Discussion).

We also note that mitotic (and meiotic) chromosomes are particularly suitable objects for mechanical effects. They are organized and mechanically coherent (3, 11, 12). Their two component compartments, the axis and the chromatin loop matrix (above and Fig. 1A), are both complex meshworks of protein/protein and protein/DNA interactions plus DNA/DNA catenations between topologically closed chromatin domains. Such a meshwork should be capable of accumulating and transducing mechanical stress (e.g., refs. 4–6 and 13). Because of their DNA component, both compartments are significantly elastic; however, axes are substantially stiffer than the (softer) chromatin (3, 6, 11, 12). In fact, modulations of chromatin are already known to mediate mechanical effects. Like any polymer, chromatin tends to resist confinement from internal or external constraints. Such confinement results in so-called “chromatin pressure” in which, effectively, the chromatin tends to push on the constraints (14).

Correspondingly, the presence of such constraints implies the presence of mechanical stress within the chromatin due to the tendency for chromatin expansion. That stress can promote important changes (e.g., refs. 1 and 10). Participation of axes in mechanically promoted internal chromosome dynamics, while clearly possible, has not been widely considered previously for mitotic chromosomes (but see ref. 10).

The primary purpose of this paper is to report observations on the behavior of mitotic chromosomes as they evolve toward their final separation at anaphase. However, in doing so, we have also speculated on mechanical aspects underlying the observed behaviors that we believe to be essential factors of the phenomena. Overall, the presented findings provide a perspective from which to analyze mitotic (and potentially also meiotic) chromosome morphogenesis.

Results

Regular Axis Deformations Result from the Presence of Actively Induced Internal Mechanical Stress.

Several lines of evidence suggest that chromosome axis paths are deformed due to the presence and effects of internal mechanical stress, rather than arising as passive architectural features.

The regularity seen for undulations along chromosome axes is a defining characteristic of instabilities of mechanical origin, where it reflects the intrinsic consequence of stress redistribution.

Axis deformations become progressively more pronounced as prophase progresses. The same basic features occur both early and late. However, earlier forms exhibit less-frequent handedness changes and less-dramatic kinking as compared to the later forms as described in the Introduction and ref. 2. Such effects are expected for a process involving progressive accumulation and redistribution of mechanical stress.

Mechanical stress arises because an imposed force is resisted/constrained by internal features of the object. The observed axis path, if described as a spatial curve, exhibits signs of three-dimensional constraints imposed on its curvature and torsion that could reflect the presence of stress. Although segments of the path have helicity, the curvature vector is restricted from making a full turn, as opposed to the case of general helix. Torsion is restricted as well. Neighboring segments have alternating handedness, with the torsion vector making less than 2π rotations in alternating directions (example in SI Appendix, Fig. S2). Assuming that segments correspond to roughly 1π rotations of the torsion vector, the axis path is defined as a half-helix with multiple perversions separating segments with opposite helicity. The above-described constraints imply a tendency for planarity of the axis path and a tendency for strong curvature/kinking at positions of handedness changes, both of which are observed for experimental axis paths (e.g., Fig. 1 C and D).

A change in helical handedness is a geometric feature known as a perversion, first famously described by Darwin for plant tendrils (as analyzed in ref. 15) and observed for macromolecules (reviewed in ref. 16), in animal gut (17), along the Escherichia coli nucleoid (18), and in diverse physical systems (e.g., SI Appendix, Fig. S3). The current findings provide a case of perversions identified in a eukaryotic subcellular system. Perversions of plant tendrils and in animal gut have been demonstrated to arise by mechanical processes (15, 17), as do the perversions obtained in experimental physical systems and mathematically simulated cases (discussion in How Does Mechanical Stress Arise within Chromosome Axes). These analogies encourage the idea of a mechanical origin in the present case.

Stress-Promoted Axis Splitting Promotes Emergence of Evenly Spaced Bubbles.

Mechanical stress within an object can give rise not only to regular, dynamically adjustable deformations (Regular Axis Deformations Result from the Presence of Actively Induced Internal Mechanical Stress) but also to arrays of discrete changes, which also will tend to be evenly spaced (Fig. 2 A and B and ref. 10). In such a case, stress promotes local changes at weak points within the object (“flaws”; Fig. 2A). The result is a local reduction in stress. However, this change automatically tends to redistribute outward, giving a surrounding “domain of stress relief” (“l” in Fig. 2B). In a complex object, this domain will be “self-limiting” because the change in stress is progressively absorbed by the system as it spreads. If multiple stress-promoted changes occur, sequential events tend to “fill in the holes” between the stress relief domains created by prior events. The result is a tendency for an array of evenly spaced local changes and their accompanying stress relief domains (Fig. 2B).

Fig. 2.

Stress-promoted emergence of evenly spaced bridges between sister chromatid axes. (A and B) A physical system that illustrates how local events can arise with even spacing along a linear object as driven by mechanical stress. (A) A beam is coated by a thin brittle film that contains flaws (weak points). Upon heating of the ensemble, differential expansion of the beam relative to the film creates stress at the beam/film interface, ultimately provoking formation of cracks across the beam, which occur at flaw sites. (B) Each stress-promoted local change results in local relief of stress (10). This effect redistributes outward, dissipating with distance, giving a surrounding domain of reduced stress. Successive local changes will tend to occur outside of the stress relief domains created by previous events, giving even spacing. Adapted with permission from ref. 10. Copyright (2004) National Academy of Sciences, U.S.A. (C and D) Evidence that axis deformation (and thus stress within axes) drives axis splitting is provided by morphological analysis of chromosomes in prophase nuclei. (C) In nuclei that are undergoing the splitting transition, unsplit regions can be defined as either less or more deformed (smooth “Sm” or deformed “Def”) (2). In some regions, split regions (bubbles) appear adjacent to unsplit regions. In such cases, the majority of those unsplit regions are deformed (Def) rather than smooth (Sm), as seen in two different types of chromosome preparations (fixed whole nuclei or spread samples). (D) Nuclei that are just about to undergo the splitting transition (midprophase) are exposed to the TopIIα inhibitor ICRF (Right) or not (Left) and then further incubated. In the treated nucleus, axes fail to split and become hyperdeformed (details in SI Appendix, Fig. S4). (E) Stress-promoted axis splitting is proposed to be nucleated at the sites of handedness changes/kinks, which will be weak points along the axis (Top). Given the known average dimensions of half-helical segments and resultant bubbles, this scenario explains why bubbles are ∼370 nm in size and ensuing bridges are separated by ∼400 nm. For clarity, handedness assignments are shown to be maintained after splitting but, in reality, are dynamically adjusted (2). (F) Adjacent bubbles of axis splitting tend to be rotated relative to one another, raising the possibility that stress stored in this configuration could help to promote the emergence of bridges at the corresponding site.

Emergence of evenly spaced arrays of axis splitting bubbles matches the progression of events. Stress would accumulate within the chromosomes, resulting in more deformed axis paths. At a certain point, that stress would nucleate a local axis split, with resultant local relief of stress, which would redistribute outward, giving a bubble of splitting corresponding to a domain of stress relief. Multiple such events would fill in the holes to give a regular array of bubbles. Since bridges emerge at the short segments between adjacent bubbles, this process would also underlie the even spacing of bridges.

In accord with this possibility, bubbles are quite regular in size, at ∼370 nm (2). This is expected if bubbles are stress-relief domains because the sizes of such domains will be specified by the basic properties of the object, which tend to be the same along its length.

Additional evidence suggests that emergence of bubbles is driven by stress within the axes (as manifested in the deformed axis path; Regular Axis Deformations Result from the Presence of Actively Induced Internal Mechanical Stress). 1) When a bubble occurs adjacent to an unsplit region, the unsplit region tends to be “more deformed,” as expected if overall deformation (and thus constrained writhe) accumulates and then provokes splitting (Fig. 2C). 2) If splitting is blocked by inhibition of the main axis component TopIIα, axes become hyperdeformed (Fig. 2D and SI Appendix, Fig. S4). This effect suggests that, in the normal situation, splitting alleviates deformation (and thus stress). It also provides further evidence for progressive accumulation of deformation (stress) during prophase (Regular Axis Deformations Result from the Presence of Actively Induced Internal Mechanical Stress). 3) Formation of split axes is accompanied by a decrease in axis curvature. Since axis deformation is a manifestation of internal stress, a decrease in curvature is expected if the level of stress is reduced. If bubble formation is driven by stress within the axes, it will result in a decreased level of stress. 4) Imposed helicity (writhe) along unsplit axes has the intrinsic potential to drive axis splitting. Split axes will tend to be thinner, and thus more able to absorb deformations, than their unsplit counterparts. The level of stress will thereby be decreased, thus promoting splitting. 5) Onset of axis splitting is triggered by onset of release of intersister linkages at the chromatin and axis levels (1). This molecular change will directly reduce the level of stress within the axis required to promote splitting, to a level below an appropriate critical threshold. In addition, loss of these linkages allows expansion of the chromatin, which will tend push sister chromatin units apart (1). This intersister pushing effect at the chromatin level should work synergistically with axis stress to enable “sister axis splitting.”

Axis Deformations Target and Delimit Bubble Formation, Thereby Defining the Specific Positions of Bridges.

Half-helical segments have an average contour length of ∼200 nm (the Introduction and ref. 2). Bubbles are ∼370 nm in length and ensuing adjacent bridges are separated by ∼400 nm (Fig. 1F). Thus, each bubble and each pair of adjacent bridges corresponds, on average, to two half-helical segments of ∼200 nm. In addition, experimentally, ∼50% of bridge/axis junctions occur at positions of handedness changes (2). These findings point to a direct relationship between axis deformations and bubbles/bridges.

By the scenario described in the previous section, bubble emergence should be nucleated at weak points (flaws) along the axes. Such weak points will be a direct consequence of stress-promoted deformation. Specifically, they should occur at the sites of handedness changes and/or kinks (which often occur at positions of handedness changes) because these are the points of greatest discontinuity, and thus greatest strain (19), along the axes. If axis splitting is nucleated at the position of a handedness change (Fig. 2E), a resulting ∼370-nm bubble will extend for ∼200 nm in either direction and thus across one half-helical segment of each handedness (Fig. 2E). Moreover, the bubble spreading will terminate at the junctions of those segments with their adjacent flanking segments (Fig. 2E). Those termination positions will also be positions of handedness changes/kinks and also will be the sites of bridge emergence (in accord with observation). Delimitation of bubble spreading at sites of handedness changes is also a predicted effect of the mechanical scenario: being flaws, these positions will tend to differentially absorb the redistributing reduction in stress, thereby blocking its spreading. Taken together, these considerations would suggest that the sizes of bubbles, and thus the distance between bridges, are determined by the periodicity of axis deformations. Put another way, the energy landscape created by stress-induced axis deformations both targets nucleation of bubbles to sites of handedness changes/kinks and delimits their spreading to these same positions.

These considerations further imply that evenly spaced bridges emerge from an array of flaws which themselves already tend to exhibit regular spacing. The distribution of distances between the midpoints of half-helical segments has a best-fit gamma shape parameter of ν = 2.5 while, bridges are much more evenly spaced (gamma distribution shape parameter ν = 6 to 10) (2). Thus, as described previously (20), regular spacing of precursor flaw sites can sharpen the patterning process at the bubble/bridge stage, resulting in more even spacing of bridges than would have occurred if flaws were randomly spaced.

Residual axis stress may promote bridge emergence per se.

Finally, after bubble formation, residual stress within the axes could help to promote bridge emergence per se. Adjacent bubbles tend to be rotated relative to one another (Figs. 1G and 2F and ref. 2). Such rotation is consistent with the presence of residual writhe/twist within the small unsplit axis positions between bubbles. If emergence of bridges at these positions were accompanied by untwisting, it could be driven by that residual stress (Fig. 2F).

Stress within the Axis Could Promote Postprophase Chromosome Compaction.

The parallel, cooriented sister linear loop/axis arrays of mitotic chromosomes shorten progressively along their lengths, as a central feature of chromosome compaction (2). As illustrated in Fig. 1 B, Right and D and E, throughout this process, chromosome axes exhibit undulating paths with half-helices of alternating handedness and accompanying kinks, implying the presence of mechanical stress within the axes. Evenly spaced interaxis bridges are also stably present but decrease in number in proportion to decreasing axis length (2). These and other effects suggest that postprophase chromosome axes undergo simple linear shortening by restructuring of the basic loop/axis array (e.g., by a decrease in the number of major loops and a corresponding increase in loop size) (2). Such restructuring, including concomitant loss of bridges, would be facilitated by destabilization of the basic linear loop/axis array, which is an expected effect of the presence of stress within the axis meshwork. Thus, mechanical stress within the axis would not only govern axis splitting and formation and positioning of evenly spaced bridges but could then also drive chromosome compaction, by rendering axis structure more susceptible to the requisite molecular changes. This scenario is circumstantially supported by the finding that exact axis path conformations fluctuate dynamically, over timescales of 15 s or less (2), as could be expected for adjustments driven by the attempt to minimize internal stress.

How Does Mechanical Stress Arise within Chromosome Axes?

A specific mechanical basis for the deformations seen along mitotic chromosome axes remains to be elucidated. However, several points are of note.

The observed axis deformations have much in common with instability modes observed in slender rod-shaped entities on which twist is imposed, classically described by Kirchhoff and Love (21, 22). The most familiar examples are rods whose ends are displacement constrained but are subject to axial torques which generate a state of uniform twist. The rod becomes unstable when it becomes overstressed exceeding a critical limit. Writhing modes emerge, the simplest being a helical mode comprising a combination of uniform twist and bending. Many previous cases of perversions, real and theoretical (including the case of DNA supercoiling), have been explained or modeled in this context. Moreover, resultant morphologies can be quite similar to those observed for mitotic chromosomes and include cases of multiple, as well as single, perversions (SI Appendix, Figs. S3 and S5).

A helical shape can also be a natural consequence of an internal growth process such as in the constrained growth of vine tendrils (15). Such growth processes take place incrementally at a scale that is much smaller than the wavelength of the helix. In the case of Darwin’s pea plant tendrils, when both ends are attached to fixed objects, the resulting constraint on twist can lead to perversions which disrupt otherwise regular helical-shape development. This change in behavior is stress-driven due to the fact that, by resisting continuing twist due to growth, the end constraint builds up overall torque along the tendril, which in turn promotes the perversion. Put another way: as the tendril increases in length, that increase is accommodated by helicity, and because the ends are fixed to give a topological constraint, that helicity must include equivalent levels of right- and left-handedness.

Another system displaying dramatic curvature switches, which may have more in common with what is described here, is provided by prestretched bimaterial elastomer rod-like strips (19, 23). In this system, two slender elastomer strips are prestretched to different levels and then bonded together. The overall stretch is then gradually reduced by allowing the constrained ends to approach each other. The straight configuration becomes unstable and transitions first to a helix and then to a pattern of short full-helical segments of alternating handedness. The deformation events of this bilayer are driven by the nonuniform stress distribution set up by the differing levels of prestretch. Differential behaviors of bonded bilayers have also been described to explain perversions that arise during folding of the gut (17) and the cerebral cortex (24).

Importantly, however, in these and other analyzed cases of which we are aware, the two ends of the deforming filament are constrained. In the present case, specific tethering of mitotic chromosome telomeres to the nuclear periphery has been reported only at the anaphase/G1 transition (25). Thus, although other types of constraints have not been excluded, there is no known reason to think that the ends of the chromosome are constrained, nor that forces are imposed at the ends of the chromosome. Thus, it appears that forces must arise internally to the chromosomes and, most importantly, must give deformations that are not relieved, e.g., by rotation of the chromosome axis along its length, as would be the case for internally generated twisting along a free elastic rod.

In principle, for mitotic chromosomes, axis stress could arise by molecularly driven transformations within either (or both) of the two compartments, i.e., the axis or the chromatin matrix that protrudes from that axis.

Transformations within the axis might generate helical writhe either directly, e.g., by incorporation of a toroidal molecule (26, 27), or indirectly, by conversion of twist to writhe (as for elastic rods). For example, in the former case, deformation of axes into a writhed conformation might result from installation of molecules that have an intrinsic tendency for a toroidal (helical) shape, as proposed by Gibcus et al. (26), who suggested that condensin II, which is required for helicity, might create that shape by depositing HEAT-repeat subunits along the axes.

Alternatively (or in addition), stress might arise within the axes due to changes that occur only within the chromatin matrix. For example, if the chromatin of the matrix expands, differentially as compared to the axis, a tendency for “pushing” of adjacent loops against one another could promote bending, twisting, and local instability (10). A tendency for expansion is known to be present during the period when perversions and bridges emerge and is expected to contribute to separation of sister chromatids at the axis level and also at the chromatin level (1).

In any scenario, it also necessary to explain the two fundamental features of axis deformations: planarity and perversion (which is limited approximately to alternating half-helices). Planarity arises because axis bending is constrained to occur prominently in the visual loop/axis plane, rather than in the perpendicular plane. This bias could reflect the fact that bending in the perpendicular plane will result in compression of the chromatin loops, which is intrinsically unfavorable (SI Appendix, Fig. S6 and ref. 14). Other interesting possible effects are suggested by considering the loop/axis array as a bonded bilayer, analogous to the artificial system of refs. 19 and 23. For example, axis twisting might be constrained from occurring through more than half a helical turn due to bonding with the chromatin-matrix meshwork, which, while compliant on a small length scale, could resist major deformation. In accord with this idea, dramatic axis undulations are mirrored in more modest changes in the chromatin matrix, as seen in both the overall shape (Fig. 1 B, Left; compare chromatin and axis) and the chromatin centroid paths, which tend to occur “up and down” in the same plane as that defined by the loop/axis relationship (Fig. 1 C, Top Left, white and green versus blue and red). Also, in this same general context, the striking departure from uniform helicity along the axis of the chromosomes might be due to the strongly nonuniformly circumferential distribution of the chromatin, which results in low bending stiffness in one direction (in the visual loop/axis plane) and high stiffness perpendicular to that plane (where bending requires chromatin-loop compression) (SI Appendix, Fig. S6). With internal stress generated by different time-dependent evolutional processes in the chromatin and axis compartments, it is possible that a more-or-less uniform helical-deformation pattern will transition to one with perversions, not due to end-constraint but due to the ease of bending in directions of low bending stiffness. To our knowledge, this aspect has never been investigated for torsional rod instabilities. Moreover, analogous effects can be envisioned if stress is generated by chromatin expansion rather than by direct (torsional) stress along the axes. We also note that we have not considered any possible role for transient lateral association of chromosomes along the inner surface of the nuclear periphery during the period when perversions first emerge (midprophase) (1) or other in vivo factors as yet unknown.

Discussion

The presented findings consider in detail the nature, origin(s), and relationships between the two spatial patterns recently identified for organized mitotic chromosome axes. The constellation of observed effects suggests that both patterns are driven by mechanical stress within the chromosome axes and that the two patterns are directly related.

Axis stress first results in sequential ∼200-nm segments of alternating handedness (perversions) with accompanying kinks. Then, as enabled by loss of sister cohesion/catenation linkages, axis stress promotes the formation of closely packed, evenly spaced bubbles of axis splitting, thereby determining their even spacing. Moreover, the pattern of axis deformations also targets bubble nucleation to, and delimits bubble spreading at, resultant weak points (flaws). These effects define the positions of the bridges that ultimately emerge at interbubble regions. Axial stress might also promote bridge emergence per se.

The presence of axis deformations, and thus axis stress, after bridge emergence and throughout the period of chromosome compaction, also raises the possibility that this stress creates an unstable, high-energy state that sensitizes the axes to the molecular events of axis restructuring as required for progressive mitotic chromosome compaction.

At the most general level, the presented findings are consonant with the fact that organized chromosomes are physically coherent objects with defined macroscopic mechanical properties. The overall significance of these findings is that the molecular events involved in chromosome morphogenesis appear to be directed by the energy landscapes created by stress within the chromosome axes, with communication over diverse length scales provided by redistribution of stress and with feedback between molecular changes and resultant stress patterns.

These observations also suggest an answer to a basic mystery: it has been unclear why chromosome axes exhibit perversions and kinks. These deformations are not required topologically for organization, lateral separation, or progressive shortening of the chromosomes, all of which could be accomplished by perfectly straight axes (2). We can now understand that these deformations are manifestations of internal mechanical stress within the axes and that this stress, including the specific pattern of resultant deformations, mediates the two major processes involved in progression of chromosomes after they first appear as discrete objects. At the sister-splitting transition, axis stress promotes not only axis splitting but also concomitant bridge emergence and, most importantly, ensures the even spacing of bridges at ∼400-nm separation along the chromosomes. Bridges play an essential role in stabilizing the coaligned sister couple against disruptive internal forces from compaction and disruptive external forces from the mitotic spindle, and even spacing of bridges, at an appropriate length scale, is required to maintain regular sister coalignment (further discussion in ref. 2). Thereafter, mechanical stress along the axes, as manifested in deformations, can be expected to sensitize the loop/axis arrays to the molecular changes required for axis restructuring.

Interestingly, evenly spaced bridges have been observed to occur between axes of homologous maternal and paternal chromosomes (homologs) during meiosis (28). These bridges, like their mitotic counterparts, include both DNA/chromatin and structural components (notably cohesin-related Spo76/Pds5), and the two types of bridges are strikingly morphologically similar. The meiotic program is characterized by a prolonged prophase that precedes the first round of chromosome segregation and is specifically devoted to pairing and recombination between homologs, each of which comprises a pair of closely conjoined sisters. Bridges occur transiently during this period, between the axes of homologs that have been brought into distance coalignment, and they mediate a complex set of coordinate transitions that include movement of recombination complexes from on-axis to between-axis positions and nucleation of closer axis juxtaposition via installation of the synaptonemal complex (28). It will not be surprising if the principles that underlie emergence of mitotic intersister bridges also apply to these apparent meiotic counterparts (10, 29).

The presented findings also lead us to speculate on mechanical aspects underlying the observed behaviors that appear to be essential factors in the described phenomena. In particular, we are intrigued by consideration of loop/axis arrays as bonded bilayers, comprising mechanically linked axis meshwork and chromatin-meshwork compartments. We are particularly interested in the ideas that 1) stress might arise internally within the axes due to transformations within the axis compartment which tend to promote writhe, 2) constraints on curvature and handendess lead to a nearly planar array of perversions with associated bends, and 3) these constraints are provided by the non-radially symmetric disposition of the chromatin compartment relative to the axis compartment. We recognize that these speculations are of a qualitative nature, but we believe they provide a rich lode for further research.

In summary, the presented findings provide a perspective from which to analyze macroscopic morphogenetic events along mitotic (and meiotic) chromosomes.

Materials and Methods

Chromosome Imaging and Analysis.

Images in Fig. 1 B, Left are from muntjac DM87-fixed whole cells; DNA was stained by DAPI, and the axis was stained using fluorescent anti-TopIIα antibodies. Images in Fig. 1 B, Right are from living pig LLC-Pk cells expressing EGFP-TopIIα and histone H2B-mCherry. Images and centroid paths in Fig. 1 B, Right and C, D, and G are taken from ref. 2. Cell lines and methodologies for all images and for centroid analyses in Fig. 1 are described in detail in ref. 2. Images in Fig. 2C and D and SI Appendix, Fig. S4 were obtained from, respectively, muntjac DM87-fixed whole cells and living pig LLC-Pk EGFP-TopIIα cells. Cell lines, sample preparation, and imaging methodologies for these experiments were all exactly as described in ref. 1.

Data Availability.

All data, codes, and materials are available as described in the article and SI Appendix.