Physics successfully implements Lagrange multiplier optimization

Significance

All through human civilization, optimization has played a major role, from aerodynamics to airline scheduling, delivery routing, and telecommunications decoding. Optimization is receiving increasing attention, since it is central to today’s artificial intelligence. All of these optimization problems are among the hardest for human or machine to solve. It has been overlooked that physics itself does optimization in the normal evolution of dynamical systems, such as seeking out the minimum energy state. We show that among such physics principles, the idea of minimum power dissipation, also called the Principle of Minimum Entropy Generation, appears to be the most useful, since it can be readily implemented in electrical or optical circuits.

Abstract

Optimization is a major part of human effort. While being mathematical, optimization is also built into physics. For example, physics has the Principle of Least Action; the Principle of Minimum Power Dissipation, also called Minimum Entropy Generation; and the Variational Principle. Physics also has Physical Annealing, which, of course, preceded computational Simulated Annealing. Physics has the Adiabatic Principle, which, in its quantum form, is called Quantum Annealing. Thus, physical machines can solve the mathematical problem of optimization, including constraints. Binary constraints can be built into the physical optimization. In that case, the machines are digital in the same sense that a flip–flop is digital. A wide variety of machines have had recent success at optimizing the Ising magnetic energy. We demonstrate in this paper that almost all those machines perform optimization according to the Principle of Minimum Power Dissipation as put forth by Onsager. Further, we show that this optimization is in fact equivalent to Lagrange multiplier optimization for constrained problems. We find that the physical gain coefficients that drive those systems actually play the role of the corresponding Lagrange multipliers.

Optimization is ubiquitous in today’s world. Everyday applications of optimization range from aerodynamic design of vehicles and physical stress optimization of bridges to airline crew scheduling and delivery truck routing. Furthermore, optimization is also indispensable in machine learning, reinforcement learning, computer vision, and speech processing. Given the preponderance of massive datasets and computations today, there has been a surge of activity in the design of hardware accelerators for neural-network training and inference (1).

We ask whether physics can address optimization? There are a number of physical principles that drive dynamical systems toward an extremum. These are the Principle of Least Action; the Principle of Minimum Power Dissipation (also called Minimum Entropy Generation); the Variational Principle; Physical Annealing, which preceded computational Simulated Annealing; and the Adiabatic Principle (which, in its quantum form, is called Quantum Annealing).

In due course, we may learn how to use each of these principles to perform optimization. Let us consider the Principle of Minimum Power Dissipation in dissipative physical systems, such as resistive electrical circuits. It was shown by Onsager (2) that the equations of linear systems, like resistor networks, can be reexpressed as the minimization principle of a power dissipation function $f\left(i_1,i_2,\dots ,i_n\right)$ for currents $i_n$ in various branches of the resistor network. By reexpressing a merit function in terms of power dissipation, the circuit itself will find the minimum of the merit function, or minimum power dissipation. Optimization is generally accompanied by constraints. For example, perhaps the constraint is that the final answers must be restricted to be $\pm 1$. Such a digitally constrained optimization produces answers compatible with any digital computer.

A series of physics-based Ising solvers have been created in the physics and engineering community. The Ising challenge is to find the minimum energy configuration of a large set of magnets. This is very hard even when the magnets are restricted to only two orientations, North Pole up or down (3). Our main insights in this paper are that most of these Ising solvers use hardware based on the Principle of Minimum Power Dissipation and that almost all of them implement the well-known Lagrange multipliers method for constrained optimization.

An early work was by Yamamoto and coworkers in ref. 4, and this was followed by further work from their group (5–8) and other groups (9–15). These entropy-generating machines range from coupled optical parametric oscillators to resistor–inductor–capacitor electrical circuits, coupled exciton–polaritons, and silicon photonic-coupler arrays. These types of machines have the advantage that they solve digital problems orders of magnitude faster, and in a more energy-efficient manner, than conventional digital chips that are limited by latency and the energy cost (8).

Within the framework of these dissipative machines, constraints can be readily included. In effect, these machines perform constrained optimization equivalent to the technique of Lagrange multipliers. We illustrate this connection by surveying seven published physically distinct machines and showing that each minimizes power dissipation in its own way, subject to constraints; in fact, they perform Lagrange multiplier optimization.

In effect, physical machines perform local steepest descent in the power-dissipation rate. They can become stuck in local optima. At the very least, they perform a rapid search for local optima, thus reducing the search space for the global optimum. These machines are also adaptable toward advanced techniques for approaching a global optimum.

At this point, we note that there are several other streams of work on physical optimization in the literature that we shall not be dealing with in this paper. These works include a variety of Lagrange-like continuous-time solvers (16, 17), Memcomputing methods (18), Reservoir Computing (19, 20), adiabatic solvers using Kerr nonlinear oscillators (21), and probabilistic bit logic (22). A brief discussion of adiabatic Kerr oscillator systems (21) is presented in SI Appendix, section 4.

The paper is organized as follows. In Section 1, we recognize that physics performs optimization through its various principles. Then, we concentrate on the Principle of Minimum Power Dissipation. In Section 2, we give an overview of the minimum power-dissipation optimization solvers in the literature and show how they incorporate constraints. Section 3 has a quick tutorial on the method of Lagrange multipliers. Section 4 studies five published solvers in detail and shows that they all follow some form of Lagrange multiplier dynamics. In Section 5, we look at those published physics-based solvers that are less obviously connected to Lagrange multipliers. Section 6 presents the applications of these solvers to perform linear regression in statistics. Finally, in Section 7, we conclude and discuss the consequences of this ability to implement physics-based Lagrange multiplier optimization for areas such as machine learning.

1. Optimization in Physics

We survey the minimization principles of physics and the important optimization algorithms derived from them. The aim is to design physical optimization machines that converge to the global optimum, or a good local optimum, irrespective of the initial point for the search.

1.A. The Principle of Least Action.

The Principle of Least Action is the most fundamental principle in physics. Newton’s Laws of Mechanics, Maxwell’s Equations of Electromagnetism, Schrödinger’s Equation in Quantum Mechanics, and Quantum Field Theory can all be interpreted as minimizing a quantity called Action. For the special case of light propagation, this reduces to the Principle of Least Time, as shown in Fig. 1.

Fig. 1.

The Principle of Least Time, a subset of the Principle of Least Action. The actual path that light takes to travel from point A to point B is the one that takes the least time to traverse. Recording the correct path entails a small energy cost consistent with the Landauer Limit.

A conservative system without friction or losses evolves according to the Principle of Least Action. The fundamental equations of physics are reversible. A consequence of this reversibility is the Liouville Theorem, which states that volumes in phase space are left unchanged as the system evolves.

Contrary-wise, in both a computer and an optimization solver, the goal is to have a specific solution that occupies a smaller zone in the search space than the initial state, incurring an entropy cost first specified by Landauer and Bennett. Thus, some degree of irreversibility, or energy cost, is needed, specified by the number of digits in the answer in the Landauer–Bennett analysis. An algorithm has to be designed and programmed into the reversible system to effect the reduction in entropy needed to solve the optimization problem.

The reduction in entropy implies an energy cost but not necessarily a requirement for continuous power dissipation. We look forward to computer science breakthroughs that would allow the Principle of Least Action to address unsolved problems. An alternative approach to computing would involve physical systems that continuously dissipate power, aiding in the contraction of phase space toward a final solution. This brings us to the Principle of Least Power Dissipation.

1.B. The Principle of Least Power Dissipation.

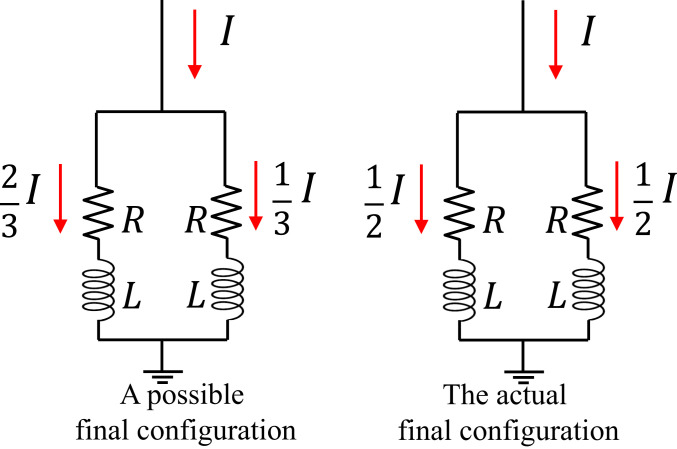
If we consider systems that continuously dissipate power, we are led to a second optimization principle in physics, the Principle of Least Entropy Generation or Least Power Dissipation. This principle states that any physical system will evolve into a steady-state configuration that minimizes the rate of power dissipation given the constraints (such as fixed thermodynamic forces, voltage sources, or input power) that are imposed on the system. An early version of this statement is provided by Onsager in his celebrated papers on the reciprocal relations (2). This was followed by further foundational work on this principle by Prigogine (23) and de Groot (24). This principle is readily seen in action in electrical circuits and is illustrated in Fig. 2. We shall frequently use this principle, as formulated by Onsager, in the rest of the paper.

Fig. 2.

The Principle of Least Power Dissipation. In a parallel connection, the current distributes itself in a manner that minimizes the power dissipation, subject to the constraint of fixed input current $I$.

1.C. Physical Annealing; Energy Minimization.

This technique is widely used in materials science and metallurgy and involves the slow cooling of a system starting from a high temperature. As the cooling proceeds, the system tries to maintain thermodynamic equilibrium by reorganizing itself into the lowest energy minimum in its phase space. Energy fluctuations due to finite temperatures help the system escape from local optima as shown in Fig. 3. This procedure leads to global optima when the temperature reaches zero in theory, but the temperature has to be lowered prohibitively slowly for this to happen.

Fig. 3.

Physical Annealing involves the slow cooling down of a system. The system performs gradient descent in configuration space with occasional jumps activated by finite temperature. If the cooling is done slowly enough, the system ends up in the ground state of configuration space.

1.D. Adiabatic Method.

The Adiabatic Method, illustrated in Fig. 4, involves the slow transformation of a system from initial conditions that are easily constructed to final conditions that capture the difficult problem at hand.

Fig. 4.

A system initialized in the ground state of a simple Hamiltonian continues to stay in the ground state as long as the Hamiltonian is changed slowly enough.

More specifically, to solve the Ising problem, one initializes the system of spins in the ground state of a simple Hamiltonian and then transforms this Hamiltonian into the Ising problem by slowly varying some system parameters. If the parameters are varied slowly enough, the system stays in the instantaneous ground state throughout and the problem gets solved. In a quantum mechanical system, this is sometimes called “quantum annealing.” Several proposals and demonstrations, including the well-known D-Wave machine (25), utilize this algorithm.

The slow rate of variation of the Hamiltonian parameters is determined by the minimum energy spacing between the instantaneous ground state and first excited state that occurs as we move from the initial Hamiltonian to the final one. The smaller the gap is, the slower the rate at which we need to perform the variation to successfully solve the problem. It has been shown that the gap can become exponentially small in the worst case, implying that this algorithm takes exponential time in the worst case for nondeterministic polynomial time (NP)-hard problems.

1.E. Minimum Power Dissipation in Multioscillator Arrays.

Multioscillator Arrays subject to Parametric Gain were introduced in refs. 4 and 5 for solving Ising problems. This can be regarded as a subset of the Principle of Minimum Power Dissipation, which always requires an input power constraint to avoid the null solution. In this case, gain acts as a constraint for minimum power dissipation, and the oscillator array must arrange itself to dissipate the least power subject to that constraint. If the oscillator array is bistable, this problem becomes analogous to the magnetic Ising problem. This mechanism will be the main point of Section 2.

2. Coupled Multioscillator Array Ising Solvers

The motivation for “Coupled Multioscillator Array Ising Solvers” is best explained using concepts from laser physics. As a laser is slowly turned on, spontaneous emission from the laser-gain medium couples into the various cavity modes and begins to become amplified. The different cavity modes have different loss coefficients due to their differing spatial profiles. As the laser pump/gain increases, the least-loss cavity mode grows faster than the others, and the gain is clamped by saturation. This picture can be incomplete since further nonlinear evolution among all of the modes can occur.

Coupled Multioscillator Array Ising machines try to map the power losses of the optimization machine to the magnetic energies of the Ising problem. If the mapping is correct, the lowest power configuration will match the energetic ground state of the Ising problem. This is illustrated in Fig. 5. The system evolves toward a state of minimum power dissipation, or minimum entropy generation, subject to the constraint of gain being present.

Fig. 5.

A lossy multioscillator system is provided with gain. The x axis is a list of all of the available modes in the system, whereas the y axis plots the loss coefficient of each mode. Gain is provided to the system and is gradually increased. As in single-mode lasers, the lowest loss mode, illustrated by the blue dot, grows exponentially, saturating the gain. Above the threshold, we can expect further nonlinear evolution among the modes so as to minimize power dissipation.

The archetypal solver in this class consists of a network of interconnected oscillators driven by phase-dependent parametric gain. Parametric gain amplifies only the cosine quadrature and causes the electric field to lie along the $\pm$Real Axis in the complex plane. The phase of the electric field (0 or $\pi$) can be used to represent $\pm$spin in the Ising problem. The resistive interconnections between the oscillators are designed to favor ferromagnetic or antiferromagnetic “spin–spin” interactions by the Principle of Minimum Power Dissipation, subject to parametric (phase-dependent) gain as the power input.

The gain input is very important to the Principle of Minimum Power Dissipation. If there were no power input, all of the currents and voltages would be zero, and the minimum power dissipated would be zero. In the case of the Coupled Multioscillator circuit, the power input is produced through a gain mechanism, or a gain module. The constraint could be the voltage input to the gain module. However, if the gain were to be too small, it might not exceed the corresponding circuit losses, and the current and voltage would remain near zero. If the pump gain is then gradually ramped up, the oscillatory mode requiring the least threshold gain begins oscillating. Upon reaching the threshold gain, a nontrivial current distribution of the Couple Multioscillator circuit will emerge. As the gain exceeds the required threshold, there will be further nonlinear evolution among the modes so as to minimize power dissipation. The final-state “spin” configuration, dissipating the lowest power, is reported as the desired optimum.

With Minimum Power Dissipation, as with most optimization schemes, it is difficult to guarantee a global optimum.

In optimization, each constraint contributes a Lagrange multiplier. We will show that the gains of the oscillators are the Lagrange multipliers of the constrained system. In Section 3, we provide a brief tutorial on Lagrange multiplier optimization.

3. Lagrange Multiplier Optimization Tutorial

The method of Lagrange multipliers is a very well-known procedure for solving constrained optimization problems in which the optimal point ${\mathit{x}}^{*}\equiv \left(x,y\right)$ in multidimensional space locally optimizes the merit function $f\left(\mathit{x}\right)$ subject to the constraint $g\left(\mathit{x}\right)=0$. The optimal point has the property that the slope of the merit function is zero as infinitesimal steps are taken away from ${\mathit{x}}^{*}$, as taught in calculus. However, these deviations are restricted to the constraint curve, as shown in Fig. 6. The isocontours of the function $f\left(\mathit{x}\right)$ increase until they are limited by, and just touch, the constraint curve $g\left(\mathit{x}\right)=0$ at the point ${\mathit{x}}^{*}$.

Fig. 6.

Maximization of function $f\left(x,y\right)$ subject to the constraint $g\left(x,y\right)=0$. At the constrained local optimum, the gradients of $f$ and $g$, namely $\nabla f\left(x,y\right)$ and $\nabla g\left(x,y\right)$, are parallel.

At the point of touching, ${\mathit{x}}^{*}$, the gradients of $f$ and $g$ are parallel to each other:

$$\nabla f\left({\mathit{x}}^{*}\right)={\lambda }^{*}\nabla g\left({\mathit{x}}^{*}\right).$$ [1]

The proportionality constant ${\lambda }^{*}$ is called the Lagrange multiplier corresponding to the constraint $g\left(\mathit{x}\right)=0$.

When we have multiple constraints $g_1,\dots ,g_p$, we expand Eq. 1 as follows:

$$\nabla f\left({\mathit{x}}^{*}\right)=\sum _{i=1}^p{\lambda }_i^{*}\nabla g_i\left({\mathit{x}}^{*}\right),$$ [2]

where the gradient vector $\nabla$ represents $n$ equations, accompanied by the $p$ constraint equations $g_i\left(\mathit{x}\right)=0$, resulting in $n+p$ equations. These equations solve for the $n$ components in the vector ${\mathit{x}}^{*}$ and the $p$ unknown Lagrange multipliers ${\lambda }_i^{*}$. That would be $n+p$ equations for $n+p$ unknowns.

Motivated by Eq. 2, we introduce a Lagrange function $L\left(\mathit{x},\mathit{\lambda }\right)$ defined as follows:

$$L\left(\mathit{x},\mathit{\lambda }\right)=f\left(\mathit{x}\right)+\sum _{i=1}^p{\lambda }_i{g}_i\left(\mathit{x}\right),$$ [3]

which can be optimized by gradient descent or other methods to solve for ${\mathit{x}}^{*}$ and ${\mathit{\lambda }}^{*}$. The theory of Lagrange multipliers, and the popular “Augmented Lagrange Method of Multipliers” algorithm used to solve for locally optimal $\left({\mathit{x}}^{*},{\mathit{\lambda }}^{*}\right)$, are discussed in great detail in refs. 26 and 27. A gist of the main points is presented in SI Appendix, sections 1–3.

For the case of the Ising problem, the objective function is given by $f\left(\mathit{\mu }\right)={\sum }_{i,j}{J}_{ij}{\mathit{\mu }}_{\mathbf{i}}\cdot {\mathit{\mu }}_{\mathbf{j}}$, where $f\left(\mathit{\mu }\right)$ is the magnetic Ising Energy and ${\mathit{\mu }}_{\mathbf{i}}$ is the $i$th magnetic moment vector. For the optimization method represented in this paper, we need a circuit or other physical system whose power dissipation is also $f\left(\mathit{x}\right)={\sum }_{i,j}{J}_{ij}{x}_i{x}_j$, but now $f\left(\mathit{x}\right)$ is power dissipation, not energy; $x_i$ is a variable that represents voltage, or current or electric field; and the $J_{ij}$ are not magnetic energy but rather dissipative coupling elements. The correspondence is between magnetic spins quantized along the z axis, ${\mu }_{zi}=\pm 1$ and the circuit variable $x_i=\pm 1$.

While “energy” and “power dissipation” are represented by different units, we nonetheless need to establish a correspondence between them. For every optimization problem, there is a challenge of finding a physical system whose power-dissipation function represents the desired equivalent optimization function.

If the Ising problem has $n$ spins, there are also $p=n$ constraints, one for each of the spins. A sufficient constraint is $g_i\left(\mathit{x}\right)=1-x_i^2=0$. More complicated nonlinear constraints can be envisioned, but $\left(1-x_i^2\right)$ could represent the first two terms in a more complicated constraint Taylor expansion.

Therefore, a sufficient Lagrange function for the Ising problem, with digital constraints, is given by

$$L\left(\mathit{x},\mathit{\lambda }\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{x}_i{x}_j+\sum _{i=1}^n{\lambda }_i\left(1-x_i^2\right)$$

where ${\lambda }_i$ is the Lagrange multiplier associated with the corresponding constraint. We shall see in Section 4 that most analog algorithms that have been proposed for the Ising problem in the literature actually tend to optimize some version of the above Lagrange function.

4. The Physical Ising Solvers

We now discuss some physical methods proposed in the literature and show how each scheme implements the method of Lagrange multipliers. They all obtain good performance on the Gset benchmark problem set (28), and many of them demonstrate better performance than the heuristic algorithm, Breakout Local Search (29). The main result of our work is the realization that the gains used in all these physical methods are in fact Lagrange multipliers.

The available physical solvers in the literature, we entitle as follows: Optical Parametric Oscillators [4.A], Coupled Radio Oscillators on the Real Axis [4.B], Coupled Laser Cavities Using Multicore Fibers [4.C], Coupled Radio Oscillators on the Unit Circle [4.D], and Coupled Polariton Condensates [4.E]. In Section 5, we discuss schemes that might be variants of minimum power dissipation: Iterative Analog Matrix Multipliers [5.A] and Leleu Mathematical Ising Solver [5.B]. In SI Appendix, section 4, we discuss “Adiabatic Coupled Radio Oscillators” (21), which seems unconnected with minimum power dissipation.

Optical Parametric Oscillators, Coupled Radio Oscillators on the Real Axis, and Coupled Radio Oscillators on the Unit Circle use only one gain for all of the oscillators, which is equivalent to imposing only one constraint, while Coupled Laser Cavities Using Multicore Fibers, Coupled Polariton Condensates, and Iterative Analog Matrix Multipliers use different gains for each spin and correctly capture the $n$ constraints of the Ising problem.

4.A. Optical Parametric Oscillators.

4.A.1. Overview.

An early optical machine for solving the Ising problem was presented by Yamamoto and coworkers (4, 30). Their system consists of several pulses of light circulating in an optical-fiber loop, with the phase of each light pulse representing an Ising spin. In parametric oscillators, gain occurs at half the pump frequency. If the gain overcomes the intrinsic losses of the fiber, the optical pulse builds up. Parametric amplification provides phase-dependent gain. It restricts the oscillatory phase to the Real Axis of the complex plane. This leads to bistability along the positive or negative real axis, allowing the optical pulses to mimic the bistability of magnets.

In the Ising problem, there is magnetic coupling between spins. The corresponding coupling between optical pulses is achieved by specified interactions between the optical pulses. In Yamamoto and coworkers’ approach (30), one pulse $i$ is first plucked out by an optical gate, amplitude modulated by the proper connection weight specified in the $J_{ij}$ Ising Hamiltonian, and then reinjected and superposed onto the other optical pulse $j$, producing constructive or destructive interference, representing ferromagnetic or antiferromagnetic coupling.

By providing saturation to the pulse amplitudes, the optical pulses will finally settle down, each to one of the two bistable states. We will find that the pulse-amplitude configuration evolves exactly according to the Principle of Minimum Power Dissipation. If the magnetic dipole solutions in the Ising problem are constrained to $\pm 1$, then each constraint is associated with a Lagrange multiplier. Surprisingly, we find that each Lagrange multiplier turns out to be equal to the gain or loss associated with the corresponding oscillator.

4.A.2. Lagrange multipliers as gain coefficients.

Yamamoto and coworkers (5) analyze their parametric oscillator system using slowly varying coupled wave equations for the circulating optical modes. We now show that the coupled wave equation approach reduces to an extremum of their system “power dissipation.” The coupled-wave equation for the slowly varying amplitude $c_i$ of the in-phase electric field cosine component of the $i$th optical pulse (representing magnetic spin in an Ising system) is as follows:

$$\frac{d{c}_i}{dt}=\left(-{\alpha }_i+{\gamma }_i\right)c_i-\sum _{j=1,j\ne i}^n{J}_{ij}{c}_j$$ [4]

where the weights, $J_{ij}$, are the dissipative coupling rate constants. (The $J_{ij}$ arise from constructive and destructive interference and can be positive or negative. where $=\pm 1$ is the corresponding weight in the binary Ising problem.) ${\gamma }_i$ represents the parametric gain (1/sec) supplied to the $i$th pulse, and ${\alpha }_i$ is the corresponding loss (1/sec). We shall henceforth use normalized, dimensionless $c_i$ in the rest of the paper. The normalization electric field is that which produces an energy of 1/2 joule in the normalization volume, while for voltages, the normalization voltage is that which produces an energy of 1/2 joule in the linear capacitor. For clarity of discussion, we dropped the cubic terms in Eq. 4 that Yamamoto and coworkers (5) originally had. A discussion of these terms in given in SI Appendix, section 3.

Owing to the nature of parametric amplification, the quadrature sine components $s_i$ of the electric fields die out rapidly. The normalized power dissipation, $h$ (in watts divided by one joule), including the negative dissipation associated with gain can be written:

$$h\left(\mathit{c},\mathit{\gamma }\right)=\sum _{i=1}^n{\alpha }_i{c}_i^2-\sum _{i=1}^n{\gamma }_i{c}_i^2+\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j$$ [5]

where the electric field cosine amplitudes $c_i$ are rendered dimensionless. If we minimize the power dissipation $h\left(\mathit{c}\right)$ without invoking any constraints, that is, with ${\gamma }_i=0$, the amplitudes $c_i$ simply go to zero.

If the gain ${\gamma }_i$ is large enough, some of the amplitudes might go to infinity. To avoid this, we employ the $n$ constraint functions $g_i\left(c_i\right)=\left(1-c_i^2\right)=0$, which enforce a digital $c_i=\pm 1$ outcome. Adding the constraint function to the power dissipation yields the Lagrange function, L (in units of watts divided by one joule), (which includes the constraint functions times the respective Lagrange multipliers):

$$L\left(\mathit{c},\mathit{\gamma }\right)=\sum _{i=1}^n{\alpha }_i{c}_i^2-\sum _{i=1}^n{\gamma }_i\left(c_i^2-1\right)+\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j$$ [6]

The unconstrained Eq. 5 and the constrained Eq. 6 differ only in the ($-1$) added to the ${\gamma }_i$ term, which effectively constrains the amplitudes and prevents them from diverging to $\infty$. Eq. 6 is the Lagrange function given at the end of Section 3. Surprisingly, the gains ${\gamma }_i$ emerge to play the role of Lagrange multipliers. This means that each mode, represented by the subscripts in $c_i$, must adjust to a particular gain ${\gamma }_i$ such that power dissipation is minimized. Minimization of the Lagrange function (Eq. 6) provides the final steady state of the system dynamics. In fact, the right-hand side of Eq. 4 is the gradient of Eq. 6, demonstrating that the dynamical system performs gradient descent on the Lagrange function. If the circuit or optical system is designed to dissipate power in a mathematical form that matches the Ising magnetic energy, then the system will seek out a local optimum of the Ising energy.

Such a physical system, constrained to $c_i=\pm 1$, is digital in the same sense as a flip–flop circuit, but unlike the von Neumann computer, the inputs are resistor weights for power dissipation. Nonetheless, a physical system can evolve directly, without the need for shuttling information back and forth as in a von Neumann computer, providing faster answers. Without the communications overhead but with the higher operation speed, the energy dissipated to arrive at the final answer will be less, despite the circuit being required to generate entropy during its evolution toward the final state.

To achieve minimum power dissipation, the amplitudes $c_i$ and the Lagrange multipliers ${\gamma }_i$ must all be simultaneously optimized using the Lagrange function as discussed in Section 4.E. While a circuit will evolve toward optimal amplitudes $c_i$, the gains ${\gamma }_i$ must arise from a separate active circuit. Ideally, the active circuit that controls the Lagrange multiplier gains ${\gamma }_i$ would have its power dissipation included with the main circuit. A more common method is to provide gain that follows a heuristic rule. For example, Yamamoto and coworkers (5) follow the heuristic rule ${\gamma }_i=a+bt$. It is not yet clear whether the heuristic-based approach toward gain evolution will be equally effective as using the complete Lagrange method in Section 4.E and lumping together all main circuit and feedback components and minimizing the total power dissipation.

We conclude this subsection by noting that the Lagrange function, Eq. 6, corresponds to the following merit function, the normalized power dissipation, $f$ (in watts divided by one joule), and constraints:

$$\begin{array}{l}\hfill f\left(\mathit{c}\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j+\sum _{i=1}^n{\alpha }_i{c}_i^2\\ \hfill g_i\left(c_i\right)=\left(1-c_i^2\right)=0,\text{for}\hspace{0.17em}i=\mathrm{1,2},\dots ,n.\end{array}$$

4.B. Coupled Radio Oscillators on the Real Axis.

4.B.1. Overview.

A coupled inductor–capacitor (LC) oscillator system with parametric amplification was analyzed in the circuit simulator, SPICE, by Xiao (9). This is analogous to the optical Yamamoto system, but this system consists of a network of radio frequency LC oscillators coupled to one another through resistive connections. The LC oscillators contain linear inductors but nonlinear capacitors, which provide the parametric gain. The parallel or cross-connect resistive connections between the oscillators are designed to implement the ferromagnetic or antiferromagnetic couplings $J_{ij}$ between magnetic dipole moments ${\mu }_i$ as shown in Fig. 7. The corresponding phase of the voltage amplitude $V_i$, 0 or $\pi$, determines the sign of magnetic dipole moment ${\mu }_i$.

Fig. 7.

Coupled LC oscillator circuit for two coupled magnets. The oscillation of the LC oscillators represents the magnetic moments, while the parallel or antiparallel cross-connections represent ferromagnetic or antiferromagnetic coupling, respectively. The nonlinear capacitors are pumped by $V\left(2{\omega }_0\right)$ at frequency $2{\omega }_0$, providing parametric gain at ${\omega }_0$.

The nonlinear capacitors are pumped by voltage $V\left(2{\omega }_0\right)$ at frequency $2{\omega }_0$, where the LC oscillator natural frequency is ${\omega }_0$. Second harmonic pumping leads to parametric amplification in the oscillators. As in the optical case, parametric amplification induces gain ${\gamma }_i$ in the Real Axis quadrature and imposes phase bistability on the oscillators.

Ideally, an active circuit would control the Lagrange multiplier gains ${\gamma }_i$, and the gain control circuit would have its power dissipation included with the main circuit. A more common approach is to provide gain that follows a heuristic rule. Xiao (9) linearly ramps up the gain as in Optical Parametric Oscillators. Again, as in the previous case, a mechanism is needed to prevent the parametric gain from producing infinite amplitude signals. Zener diodes are used to restrict the amplitudes to finite saturation values. With the diodes in place, the circuit settles into a voltage phase configuration, 0 or $\pi$, that minimizes net power dissipation for a given pump gain.

4.B.2. Lagrange function and Lagrange multipliers.

The evolution of the oscillator capacitor voltages was derived from Kirchhoff’s laws by Xiao (9). The slowly varying amplitude approximation on the cosine component of these voltages, $c_i$, produces the following equation for the ith oscillator:

$$\frac{d{c}_i}{dt}=\left(\sum _{j=1,j\ne i}^n{J}_{ij}{c}_j\right)-\alpha c_i+\gamma c_i$$ [7]

where the $c_i$ are the peak voltage amplitudes; $R_c$ is the resistance of the coupling resistors; the cross-couplings $J_{ij}$ are assigned values ; $C_0$ is the linear part of the capacitance in each oscillator; $n$ is the number of oscillators; ${\omega }_0$ is the natural frequency of the oscillators; the parametric gain constant $\gamma ={\omega }_0\left|\mathrm{\Delta }C\right|/4C_0$, where $\left|\mathrm{\Delta }C\right|$ is the capacitance modulation at the second harmonic; and the decay constant $\alpha =\left(n-1\right)/\left(4R_c{C}_0\right)$. In this simplified model, all decay constants $\alpha$ are taken as equal, and, moreover, each oscillator experiences exactly the same parametric gain $\gamma$, conditions that can be relaxed if needed.

We note that Eq. 7 performs gradient descent on the net power-dissipation function:

$$h\left(\mathit{c},\gamma \right)=-\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j+\sum _{i=1}^n\alpha c_i^2-\sum _{i=1}^n\gamma c_i^2$$ [8]

where h, L, f are the power-dissipation functions in watts divided by one joule. This is very similar to Section 4.A. The first two terms on the right-hand side together represent the dissipative losses in the coupling resistors, while the third term is the negative of the gain provided to the system of oscillators.

Next, we obtain the following Lagrange function through the same replacement of $\left(-c_i^2\right)$ with $\left(1-c_i^2\right)$ that we performed in Section 4.A:

$$L\left(\mathit{c},\gamma \right)=-\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j+\sum _{i=1}^n\alpha c_i^2-\sum _{i=1}^n\gamma \left(c_i^2-1\right)$$ [9]

where the $c_i$ are normalized to the voltage that produces an energy of 1/2 joule on the capacitor $C_0$. The above Lagrange function corresponds to Lagrange multiplier optimization using the following merit function and constraints:

$$f\left(\mathit{c}\right)=-\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{c}_i{c}_j+\sum _{i=1}^n\alpha c_i^2,g\left(\mathit{c}\right)=\sum _{i=1}^n\left(1-c_i^2\right)=0$$

Again, we see that the gain coefficient $\gamma$ is the Lagrange multiplier of the constraint $g=0$.

4.B.3. Time dynamics and iterative optimization of the Lagrange function.

Although the extremum of Eq. 9 represents the final evolved state of the physical system and represents an optimization outcome, it would be interesting to examine the time evolution toward the optimal state. We shall show in this subsection that iterative optimization of the Lagrange function in time reproduces the slowly varying time dynamics of the circuit. Each iteration is assumed to take time $\mathrm{\Delta }t$. In each iteration, the voltage amplitude $c_i$ takes a step antiparallel to the gradient of the Lagrange function:

$$c_i\left(t+\mathrm{\Delta }t\right)=c_i\left(t\right)-\kappa \mathrm{\Delta }t\frac{\partial }{\partial c_i}L\left(\mathit{c},\gamma \right),$$ [10]

where the minus sign on the right-hand side drives the system toward minimum power dissipation. The proportionality constant $\kappa$ controls the size of each iterative step; it also calibrates the dimensional units between power dissipation and voltage amplitude. (Since $c_i$ is voltage amplitude, $\kappa$ has units of reciprocal capacitance.) Converting Eq. 10 to continuous time,

$$\frac{d{c}_i}{dt}=-\kappa \frac{\partial }{\partial c_i}L\left(\mathit{c},\gamma \right),$$ [11]

where the ${\gamma }_j$ play the role of Lagrange multipliers, and the $g_j=0$ are the constraints. Substituting $L\left(\mathit{c},\gamma \right)$ from Eq. 9 into Eq. 11, we get

$$\frac{d{c}_i}{dt}=2\kappa \left(\left(\sum _{j=1,j\ne i}^n{J}_{ij}{c}_j\right)-\alpha c_i+\gamma c_i\right)$$ [12]

The constant $\kappa$ can be absorbed into the units of time to reproduce Eq. 7, the slowly varying amplitude approximation for the coupled radio oscillators. Thus, in this case and many of the others (except Section 4.E), the slowly varying time dynamics can be reproduced from iterative optimization steps on the Lagrange function.

4.C. Coupled Laser Cavities Using Multicore Fibers.

4.C.1. Overview.

The Ising solver designed by Babaeian et al. (10) makes use of coupled laser modes in a multicore optical fiber. Polarized light in each core of the optical fiber corresponds to each magnetic moment in the Ising problem. The number of cores is equal to the number of magnets in the given Ising instance. The right-hand and left-hand circular polarization of the laser light in each core represent the two polarities (up and down) of the corresponding magnet. The mutual coherence of the various cores is maintained by injecting seed light from a master laser.

The coupling between the fiber cores is achieved through amplitude mixing of the laser modes by Spatial Light Modulators at one end of the multicore fiber (10). These Spatial Light Modulators couple light amplitude from the $i$th core to the $j$th core according to the prescribed connection weight $J_{ij}$.

4.C.2. Equations and comparison with Lagrange multipliers.

As in prior physical examples, the dynamics can be expressed using slowly varying equations for the polarization modes of the $i$th core, $E_{iL}$ and $E_{iR}$, where the two electric-field amplitudes are in-phase temporally, are positive real, but have different polarization. They are

$$\begin{array}{ll}\hfill \frac{d}{dt}{E}_{iL}& =-{\alpha }_i{E}_{iL}+{\gamma }_i{E}_{iL}+\frac{1}{2}\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_{jR}-E_{jL}\right),\hfill \\ \hfill \frac{d}{dt}{E}_{iR}& =-{\alpha }_i{E}_{iR}+{\gamma }_i{E}_{iR}-\frac{1}{2}\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_{jR}-E_{jL}\right),\hfill \end{array}$$

where ${\alpha }_i$ is the decay rate in the $i$th core, and ${\gamma }_i$ is the gain in the $i$th core. The third term on the right-hand side represents the coupling between the $j$th and $i$th cores that is provided by the Spatial Light Modulators. They next define the degree of polarization as ${\mu }_i\equiv E_{iL}-E_{iR}$. Subtracting the two equations above, we obtain the following evolution equation for ${\mu }_i$:

$$\frac{d}{dt}{\mu }_i=-{\alpha }_i{\mu }_i+{\gamma }_i{\mu }_i+\sum _{j=1,j\ne i}^n{J}_{ij}{\mu }_j$$ [13]

where the electric fields are properly dimensionless and normalized as in Section 4.A. The power dissipation is proportional to $|E_{iL}{|}^2+|E_{iR}{|}^2$. However, this can also be written $|E_{iL}-E_{iR}{|}^2+|E_{iL}+E_{iR}{|}^2=|{\mu }_i{|}^2+|E_{iL}+E_{iR}{|}^2$. $|E_{iL}+E_{iR}{|}^2$ can be regarded as relatively constant as energy switches back and forth between right and left circular polarization. Then, power dissipation $h\left(\mathit{\mu }\right)$ would be most influenced by quadratic terms in $\mathit{\mu }$:

$$h\left(\mathit{\mu },\mathit{\gamma }\right)=\sum _{i=1}^n{\alpha }_i{\mu }_i^2+\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{\mu }_i{\mu }_j-\sum _{i=1}^n{\gamma }_i{\mu }_i^2.$$

As before, we add the $n$ digital constraints $g_i\left({\mu }_i\right)=1-{\mu }_i^2=0$, where ${\mu }_i=\pm 1$ represents fully left or right circular polarization, and obtain the Lagrange function:

$$L\left(\mathit{\mu },\mathit{\gamma }\right)=\sum _{i=1}^n{\alpha }_i{\mu }_i^2+\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{\mu }_i{\mu }_j-\sum _{i=1}^n{\gamma }_i\left({\mu }_i^2-1\right).$$ [14]

Once again, the gains ${\gamma }_i$ play the role of Lagrange multipliers. Thus, a minimization of the power dissipation, subject to the optical gain ${\gamma }_i$, solves the Ising problem defined by the same $J_{ij}$ couplings. In fact, the right-hand side of Eq. 13 is the gradient of Eq. 14, demonstrating that the dynamical system performs gradient descent on the Lagrange function.

The merit and constraint functions in the Lagrange function above are

$$\begin{array}{l}\hfill f\left(\mathit{\mu }\right)=\sum _{i=1}^n{\alpha }_i{\mu }_i^2+\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{\mu }_i{\mu }_j\\ \hfill g_i\left({\mu }_i\right)=\left(1-{\mu }_i^2\right)=0,\text{for}\hspace{0.17em}i=\mathrm{1,2},\dots ,n.\end{array}$$

4.D. Coupled Electrical Oscillators on the Unit Circle.

4.D.1. Overview.

We now consider a network of nonlinear, amplitude-stable electrical oscillators designed by Wang and Roychowdhury (11) to represent an Ising system for which we seek a digital solution with each dipole ${\mu }_{iz}=\pm 1$ along the z axis in the magnetic dipole space. Wang and Roychowdhury provide a dissipative system of LC oscillators with oscillation amplitude clamped and oscillation phase ${\varphi }_i=0$ or $\pi$ revealing the preferred magnetic dipole orientation ${\mu }_{iz}=\pm 1$. It is noteworthy that Roychowdhury goes beyond Ising machines and constructs general digital logic gates using these amplitude-stable oscillators in ref. 31.

In their construction, Wang and Roychowdhury (11) use nonlinear elements that behave like negative resistors at low-voltage amplitudes but as saturating resistance at high-voltage amplitudes. This produces amplitude-stable oscillators. In addition, Wang and Roychowdhury (11) provide a second harmonic pump and use a form of parametric amplification (referred to as subharmonic injection locking in ref. 11) to obtain bistability with respect to phase.

With the amplitudes being essentially clamped, it is the readout of these phase shifts, 0 or $\pi$, that provides the magnetic dipole orientation ${\mu }_{iz}=\pm 1$. One key difference between this system and Yamamoto’s system is that the latter had fast phase dynamics and slow amplitude dynamics, while Roychowdhury’s system has the reverse.

4.D.2. Equations and comparison with Lagrange multipliers.

Wang and Roychowdhury (11) derived the dynamics of their amplitude-stable oscillator network using perturbation concepts developed in ref. 32. While a circuit diagram is not shown, ref. 11 invokes the following dynamical equation for the phases of their electrical oscillators:

$$\frac{d{\varphi }_i}{dt}=-\left(\sum _{j=1,j\ne i}^n{J}_{ij}\sin \left({\varphi }_i\left(t\right)-{\varphi }_j\left(t\right)\right)\right)-{\lambda }_i\sin \left(2{\varphi }_i\left(t\right)\right),$$ [15]

where $R_c$ is a coupling resistance in their system, ${\varphi }_i$ is the phase of the $i$th oscillator, and the ${\lambda }_i$ are decay parameters that dictate how fast the phase angles settle toward their steady-state values.

We now show that Eq. 15 can be reproduced by iteratively minimizing the power dissipation in their system. Power dissipation across a resistor $R_c$ is ${\left(V_1-V_2\right)}^2/R_c$, where $\left(V_1-V_2\right)$ is the voltage difference. Since $V_1$ and $V_2$ are sinusoidal, the power dissipation consists of constant terms and a cross-term of the form

$$f\left({\varphi }_1,{\varphi }_2\right)=\frac{|V{|}^2\cos \left({\varphi }_1-{\varphi }_2\right)}{R_c},$$

where $f\left({\varphi }_1,{\varphi }_2\right)$ is the power dissipated in the resistors. Magnetic dipole orientation parallel or antiparallel is represented by whether ${\varphi }_1-{\varphi }_2=0$ or $\pi$, respectively. We may choose an origin for angle space at $\varphi =0$, which implies ${\varphi }_i=0$ or $\pi$. This can be implemented as

$$g_i\left({\varphi }_i\right)=\left(\cos \left(2{\varphi }_i\right)-1\right)=0.$$

Combining the power dissipated in the resistors with the constraint function $g_i\left({\varphi }_i\right)=0$, we obtain a Lagrange function:

$$L\left(\mathit{\varphi },\mathit{\lambda }\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\cos \left({\varphi }_i-{\varphi }_j\right)+\sum _{i=1}^n{\lambda }_i\left(\cos \left(2{\varphi }_i\right)-1\right)$$ [16]

where ${\lambda }_i$ is the Lagrange multiplier corresponding to the phase-angle constraint, and $J_{ij}$ are resistive coupling rate constants. The right-hand side of Eq. 15 is the gradient of Eq. 16, demonstrating that the dynamical system performs gradient descent on the Lagrange function.

The Lagrange function above is isomorphic with the general form in Section 3. The effective merit function $f$ and constraints $g_i$ in this correspondence are

$$\begin{array}{l}\hfill f\left(\mathit{\varphi }\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\cos \left({\varphi }_i-{\varphi }_j\right)\\ \hfill g_i\left({\varphi }_i\right)=\left(\cos \left(2{\varphi }_i\right)-1\right)=0,\text{for}\hspace{0.17em}i=\mathrm{1,2},\dots ,n.\end{array}$$

4.E. Coupled Polariton Condensates.

4.E.1. Overview.

Kalinin and Berloff (12) proposed a system consisting of coupled polariton condensates to minimize the XY Hamiltonian. The XY Hamiltonian is a two-dimensional version of the Ising Hamiltonian and is given by

$$H\left(\mathit{\mu }\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{\mathit{\mu }}_{\mathbf{i}}\cdot {\mathit{\mu }}_{\mathit{j}}$$

where the ${\mathit{\mu }}_{\mathbf{i}}$ represents the magnetic moment vector of the $i$th spin restricted to the spin-space XY plane.

Kalinin and Berloff (12) pump a grid of coupled semiconductor microcavities with laser beams and observe the formation of strongly coupled exciton–photon states called polaritons. For our purposes, the polaritonic nomenclature is irrelevant. For us, these are simply coupled electromagnetic cavities that operate by the Principle of Minimum Power Dissipation similar to the previous cases. The complex electromagnetic amplitude in the $i$th microcavity can be written $E_i=c_i+\text{j}{s}_i$, where $c_i$ and $s_i$ represent the cosine and sine quadrature components of $E_i$, and j is the unit imaginary. $c_i$ is mapped to the X-component of the magnetic dipole vector, and $s_i$ to the Y-component. The electromagnetic microcavity system settles into a state of minimum power dissipation as the laser pump and optical gain are ramped up to compensate for the intrinsic cavity losses. The phase angles in the complex plane of the final electromagnetic modes are then reported as the corresponding $\mathit{\mu }$-magnetic moment angles in the XY plane.

Since the electromagnetic cavities experience phase-independent gain, this system does not seek phase bistability. We are actually searching for the magnetic dipole vector angles in the XY plane that minimize the corresponding XY magnetic energy.

4.E.2. Lagrange function and Lagrange multipliers.

Ref. 12 uses “Ginzburg–Landau” equations to analyze their system, resulting in equations for the complex amplitudes ${\mathrm{\Psi }}_i$ of the polariton wavefunctions. However, the ${\mathrm{\Psi }}_i$ are actually the complex electric-field amplitudes $E_i$ (properly dimensionless and normalized as in Section 4.A) of the $i$th cavity. The electric-field amplitudes satisfy the slowly varying amplitude equation:

$$\frac{d{E}_i}{dt}=\left({\gamma }_i-{\alpha }_i-\beta |E_i{|}^2\right)E_i-iU|E_i{|}^2{E}_i-\sum _{j=1,j\ne i}^n{J}_{ij}{E}_j$$ [17]

where ${\gamma }_i$ is optical gain, ${\alpha }_i$ is linear optical loss, $\beta$ is nonlinear attenuation, $U$ is nonlinear phase shift, and $J_{ij}$ are dissipative coupling rate constants. We note that both the amplitudes and phases of the electromagnetic modes are coupled to each other and evolve on comparable timescales. This is in contrast to ref. 11, where the main dynamics were embedded in phase—amplitude was fast and almost fixed—or, conversely (9), where the dynamics were embedded in amplitude—phase was fast and almost fixed.

We show next that the method of ref. 12 is essentially the method of Lagrange multipliers with an added “rotation.” The power-dissipation rate is

$$\begin{array}{ll}\hfill h\left(\mathit{E}\right)& =-\frac{d}{dt}\sum _{i=1}^n{\left(\frac{E_i^{*}}{2}+\frac{E_i}{2}\right)}^2\hfill \\ \hfill & =\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_i^{*}{E}_j+E_i{E}_j^{*}\right)+\sum _{i=1}^n\beta |E_i{|}^4\hfill \\ \hfill & \hspace{1em}+\sum _{i=1}^n{\alpha }_i|E_i{|}^2-\sum _{i=1}^n{\gamma }_i|E_i{|}^2.\hfill \end{array}$$

If we add a saturation constraint, $g_i\left(E_i\right)=\left(1-|E_i{|}^2\right)=0$, then by analogy to the previous sections, ${\gamma }_i$ is reinterpreted as a Lagrange multiplier:

$$\begin{array}{cc}\hfill L\left(\mathit{E},\mathit{\gamma }\right)& =\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_i^{*}{E}_j+E_i{E}_j^{*}\right)+\sum _{i=1}^n\beta |E_i{|}^4\hfill \\ \hfill & \hspace{1em}+\sum _{i=1}^n{\alpha }_i|E_i{|}^2-\sum _{i=1}^n{\gamma }_i\left(|E_i{|}^2-1\right)\hfill \end{array}$$ [18]

where $L$ is the Lagrange function and h, L, f are the normalized power-dissipation functions (in watts divided by one joule). Thus, the scheme of coupled polaritonic resonators operates to find the state of minimum power dissipation in steady state, similar to the previous cases.

Dynamical Eq. 17 performs gradient descent on the Lagrange function Eq. 18 in conjunction with a rotation about the origin, $iU$. This rotation term, $iU$, is not captured by the Lagrange multiplier interpretation. It could, however, be useful in developing more sophisticated algorithms than the method of Lagrange multipliers, and we discuss this prospect in Section 5.B, where a system with a more general “rotation” term is discussed.

4.E.3. Iterative evolution of Lagrange multipliers.

In the method of Lagrange multipliers, the merit-function Eq. 18 is used to optimize not only the electric-field amplitudes $E_i$ but also the Lagrange multipliers ${\gamma }_i$. The papers of the previous sections used simple heuristics to adjust their gains/decay constants, which we have shown to be Lagrange multipliers. Kalinin and Berloff (12) employ the Lagrange function itself to adjust the gains, as in the complete Lagrange method discussed next.

We introduce the full method of Lagrange multipliers by briefly shifting back to the notation of Section 3. The full Lagrange method finds the optimal ${\mathit{x}}^{*}$ and ${\mathit{\lambda }}^{*}$ by performing gradient descent of $L$ in $\mathit{x}$ and gradient ascent of $L$ in $\mathit{\lambda }$. The reason for ascent in $\mathit{\lambda }$ rather than descent is to more strictly penalize deviations from the constraint. This leads to the iterations

$$x_i\left(t+\mathrm{\Delta }t\right)=x_i\left(t\right)-\kappa \mathrm{\Delta }t\frac{\partial }{\partial x_i}L\left(\mathit{x},\mathit{\lambda }\right),$$ [19]

$${\lambda }_i\left(t+\mathrm{\Delta }t\right)={\lambda }_i\left(t\right)+{\kappa }^{\prime }\mathrm{\Delta }t\frac{\partial }{\partial {\lambda }_i}L\left(\mathit{x},\mathit{\lambda }\right),$$ [20]

where $\kappa$ and ${\kappa }^{\prime }$ are suitably chosen step sizes.

With our identification that the Lagrange multipliers $\lambda$ are the same as the gains $\gamma$, we plug the Lagrange function Eq. 18 into the second iterative equation and take the limit $\mathrm{\Delta }t\to 0$. We obtain the following dynamical equation for the gains ${\gamma }_i$:

$$\frac{d{\gamma }_i}{dt}={\kappa }^{\prime }\left(1-|E_i{|}^2\right).$$ [21]

This iterative evolution of the Lagrange multipliers is indeed what Kalinin and Berloff (12) employ in their coupled polariton system.

To Eq. 21, we must add the iterative evolution of the field variables $x_i$:

$$\frac{d{x}_i}{dt}=-\kappa \frac{\partial }{\partial x_i}L\left(\mathit{x},\mathit{\lambda }\right).$$ [22]

Eqs. 21 and 22 represent the full iterative evolution, but in some of the earlier subsections, ${\gamma }_i\left(t\right)$ was assigned a heuristic time dependence.

We conclude this subsection by splitting the Lagrange function into the effective merit function $f$ and the constraint function $g_i$. The extra “phase rotation” U is not captured by this interpretation.

$$\begin{array}{ll}\hfill f\left(E_1,\dots ,E_n\right)& =\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_i^{*}{E}_j+E_i{E}_j^{*}\right)+\sum _{i=1}^n\beta |E_i{|}^4\hfill \\ \hfill & \hspace{1em}+\sum _{i=1}^n{\alpha }_i|E_i{|}^2\hfill \\ \hfill & \hspace{1em}{g}_i\left(E_i\right)=\left(1-|E_i{|}^2\right)=0,\text{for}\hspace{0.17em}i=\mathrm{1,2},\dots ,n.\hfill \end{array}$$

4.F. General Conclusions from Coupled Multioscillator Array Ising Solvers.

1) Physical systems minimize the power-dissipation rate subject to input constraints of voltage, amplitude, gain, etc. 2) These systems actually perform Lagrange multiplier optimization with the gain ${\gamma }_i$ playing the role of multiplier for the $i$th digital constraint. 3) Under the digital constraint, amplitudes $c_i=\pm 1$ or phases ${\varphi }_i=0$ or $\pi$, power-dissipation minimization schemes are actually binary, similar to a flip–flop. 4) In many of the studied cases, the system time dependence follows gradient descent on the power-dissipation function as the system approaches a power-dissipation minimum. In one of the cases (Section 4.E), there was a rotation superimposed on this gradient descent.

5. Other Methods in the Literature

We now look at other methods in the literature that do not explicitly implement the method of Lagrange multipliers but nevertheless end up with dynamics that resemble it to varying extents. All of these methods offer operation regimes where the dynamics is not analogous to Lagrange multiplier optimization, and we believe it is an interesting avenue of future work to study the capabilities of these regimes.

5.A. Iterative Analog Matrix Multipliers.

Soljacic and coworkers (13) developed an iterative procedure consisting of repeated matrix multiplication to solve the Ising problem. Their algorithm was implemented on a photonic circuit that utilized on-chip optical matrix multiplication units composed of Mach–Zehnder interferometers that were first introduced for matrix algebra by Zeilinger and coworkers in ref. 33. Soljacic and coworkers (13) showed that their algorithm performed optimization on an effective merit function that is demonstrated to be a Lagrange function in SI Appendix, section 5.

We use our insights from the previous sections to implement a simplified iterative optimization using an optical matrix multiplier. A block diagram of such a scheme is shown in Fig. 8. Let the multiple magnetic moment configuration of the Ising problem be represented as a vector of electric-field amplitudes, $E_i$, of the spatially separated optical modes. Each mode-field amplitude represents the value of each magnetic moment. In each iteration, the optical modes are fed into the optical circuit, which performs matrix multiplication, and the resulting output optical modes are then fed back to the optical circuit input for the next iteration. Optical gain or some other type of gain sustains the successive iterations.

Fig. 8.

An optical circuit performing iterative multiplications converges on a solution of the Ising problem. Optical pulses are fed as input from the left-hand side at the beginning of each iteration, pass through the matrix multiplication unit, and are passed back from the outputs to the inputs for the next iteration. Distributed optical gain sustains the iterations.

We wish to design the matrix multiplication unit such that it has the following power-dissipation function:

$$\begin{array}{ll}\hfill h\left(\mathit{E}\right)& =\sum _{i=1}^n{\alpha }_i|E_i{|}^2-\sum _{i=1}^n{\gamma }_i|E_i{|}^2+\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_i^{*}{E}_j\right.\hfill \\ \hfill & \hspace{1em}\left.+E_i{E}_j^{*}\right)\hfill \end{array}$$

The Lagrange function, including a binary constraint, $|E_i{|}^2=1$, is given by

$$\begin{array}{ll}\hfill L\left(\mathit{E},\mathit{\gamma }\right)& =\sum _{i=1}^n{\alpha }_i|E_i{|}^2-\sum _{i=1}^n{\gamma }_i\left(|E_i{|}^2-1\right)+\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\hfill \\ \hfill & \hspace{1em}\times \left(E_i^{*}{E}_j+E_i{E}_j^{*}\right)\hfill \end{array}$$ [23]

where the $J_{ij}$ is the dissipative loss rate constant associated with electric-field interference between optical modes in the Mach–Zehnder interferometers, and ${\gamma }_i$ is the optical gain.

The iterative multiplicative procedure that evolves the electric fields toward the minimum of the Lagrange function Eq. 23 is given by

$$\begin{array}{cc}\hfill E_i\left(t+1\right)-E_i\left(t\right)& =-\kappa \mathrm{\Delta }t\frac{\partial }{\partial E_i}\left(\sum _{i=1}^n{\alpha }_i|E_i\left(t\right){|}^2\right.\hfill \\ \hfill & \hspace{1em}+\sum _{i=1}^n{\gamma }_i\left(1-|E_i\left(t\right){|}^2\right)\hfill \\ \hfill & \hspace{1em}+\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}\left(E_i^{*}\left(t\right)E_j\left(t\right)\right.\hfill \\ \hfill & \hspace{1em}\left.\left.+E_i\left(t\right)E_j^{*}\left(t\right)\right)\right),\hfill \end{array}$$

where $\kappa$ is a constant step size with the appropriate units, and each iteration involves taking steps in $E_i$ proportional to the gradient $\partial /\partial E_i$ of the Lagrange function. ($\partial /\partial E_i$ represents differentiation with respect to the two quadratures.) Simplifying and sending all of the terms involving time step $t$ to one side, we get

$$\begin{array}{ll}\hfill E_i\left(t+1\right)& =\sum _{j=1}^n\left(\left(1+2\kappa \mathrm{\Delta }t{\gamma }_i-2\kappa \mathrm{\Delta }t{\alpha }_i\right){\delta }_{ij}\right.\hfill \\ \hfill & \hspace{1em}\left.-2\kappa \mathrm{\Delta }t{J}_{ij}\left(1-{\delta }_{ij}\right)\right)E_j\left(t\right)\hfill \end{array}$$ [24]

where ${\delta }_{ij}$ is the Kronecker delta (1 only if $i=j$). The Mach–Zehnder interferometers should be tuned to the matrix $\left[\left(1+2\kappa \mathrm{\Delta }t{\gamma }_i-2\kappa \mathrm{\Delta }t{\alpha }_i\right){\delta }_{ij}-2\kappa \mathrm{\Delta }t{J}_{ij}\left(1-{\delta }_{ij}\right)\right]$. Thus, we have an iterative matrix multiplier scheme that minimizes the Lagrange function of the Ising problem. In effect, a lump of dissipative optical circuitry, compensated by optical gain, will, in a series of iterations, settle into a solution of the Ising problem.

The simple system above differs from that of Soljacic and coworkers (13) in that their method has added noise and nonlinear thresholding in each iteration. A detailed description of their approach is presented in SI Appendix, section 5.

5.B. Leleu Mathematical Ising Solver.

Leleu et al. (8) proposed a modified version of the Yamamoto’s Ising machine (5) that significantly resembles the Lagrange method while incorporating important new features. To understand the similarities and differences between Leleu’s method and that of Lagrange multipliers, we recall the Lagrange function for the Ising problem that we encountered in Section 4:

$$L\left(\mathit{x},\mathit{\gamma }\right)=\sum _{i=1}^n\sum _{j=1,j\ne i}^n{J}_{ij}{x}_i{x}_j+\sum _{i=1}^n{\alpha }_i{x}_i^2+\sum _{i=1}^n{\gamma }_i\left(1-x_i^2\right)$$ [25]

In the above, $x_i$ are the optimization variables, $J_{ij}$ is the interaction matrix, ${\gamma }_i$ is the gain provided to the $i$th variable, and ${\alpha }_i$ is the loss experienced by the $i$th variable. To find a local optimum $\left({\mathit{x}}^{*},{\mathit{\gamma }}^{*}\right)$ that satisfies the constraints, one performs gradient descent on the Lagrange function in the $\mathit{x}$ variables and gradient ascent in the $\mathit{\gamma }$ variables, as discussed in Section 4.E, Eqs. 19 and 20. Substituting Eq. 25 into them and taking the limit of $\mathrm{\Delta }t\to 0$, we get

$$\frac{d{x}_i}{dt}=2\kappa \left(\left(-{\alpha }_i+{\gamma }_i\right)x_i-\sum _{j=1,j\ne i}^n{J}_{ij}{x}_j\right)$$ [26]

$$\frac{d{\gamma }_i}{dt}={\kappa }^{\prime }\left(1-x_i^2\right).$$ [27]

On the other hand, Leleu et al. (8) propose the following system:

$$\frac{d{x}_i}{dt}=\left(-\alpha +\gamma \right)x_i+e_i\sum _{j=1,j\ne i}^n{J}_{ij}{x}_j$$ [28]

$$\frac{d{e}_i}{dt}=\beta \left(1-x_i^2\right)e_i,$$ [29]

where the $x_i$ are the optimization variables, $\alpha$ is the loss experienced by each variable, $\gamma$ is a common gain supplied to each variable, $\beta$ is a positive parameter, and the $e_i$ are error coefficients that capture how far away each $x_i$ is from its saturation amplitude. Leleu et al. also had cubic terms in $x_i$ in ref. 8, and a discussion of these terms is given in SI Appendix, section 3.

It is clear that there are significant similarities between Leleu’s system and the Lagrange multiplier system. The optimization variables in both systems experience linear losses and gains and have interaction terms that capture the Ising interaction. Both systems have auxiliary variables that are varied according to how far away each degree of freedom is from its preferred saturation amplitude. However, the similarities end here.

A major differentiation in Leleu’s system is that $e_i$ multiplies the Ising interaction felt by the $i$th variable, resulting in $e_i{J}_{ij}$. The complementary coefficient is $e_j{J}_{ij}$. Consequently, Leleu’s equations implement asymmetric interactions $e_i{J}_{ij}\ne e_j{J}_{ij}$ between vector components $x_i$ and $x_j$. The inclusion of asymmetry seems to be important because Leleu’s system achieves excellent performance on the Gset problem set, as demonstrated in ref. 8.

We obtain some intuition about this system by splitting the asymmetric term $e_i{J}_{ij}$ into a symmetric and antisymmetric part. This follows from the fact that any matrix $A$ can be written as the sum of a symmetric matrix, $\left(A+A^T\right)/2$, and an antisymmetric matrix, $\left(A-A^T\right)/2$. The symmetric part leads to gradient descent dynamics similar to all of the systems in The Physical Ising Solvers. The antisymmetric part causes a energy-conserving “rotary” motion in the vector space of $x_i$.

The secret of Leleu et al.’s (8) improved performance seems to lie in this antisymmetric part. The dynamical freedom associated with asymmetry might provide a fruitful future research direction in optimization and deserves further study to ascertain its power.

6. Applications in Linear Algebra and Statistics

We have seen that minimum power-dissipation solvers can address the Ising problem and similar problems like the traveling salesman problem. In this section, we provide yet another application of minimum power-dissipation solvers to an optimization problem that appears frequently in statistics, namely curve fitting. In particular, we note that the problem of linear least-squares regression, linear curve fitting with a quadratic merit function, resembles the Ising problem. In fact, the electrical circuit example we presented in Section 4.B can be applied to linear regression. We present such a circuit in this section. Our circuit provides a digital answer but requires a series of binary resistance values, that is, $\dots ,2R_0,R_0,0.5R_0,\dots$, to represent arbitrary binary statistical input observations.

The objective of linear least-squares regression is to fit a linear function to a given set of data $\left\{\left({\mathit{x}}_{\mathbf{1}},y_1\right),\left({\mathit{x}}_{\mathbf{2}},y_2\right),\left({\mathit{x}}_{\mathbf{3}},y_3\right),\dots ,\left({\mathit{x}}_{\mathit{n}},y_n\right)\right\}$. The ${\mathit{x}}_{\mathit{i}}$ are input vectors of dimension $d$, while the $y_i$ are the observed outputs that we want our regression to capture. The linear function that is being fit is of the form $y\left(\mathit{a}\right)={\sum }_{i=1}^d{w}_i{a}_i$, where $\mathit{a}$ is a feature vector of length $d$, and $\mathit{w}$ is a vector of unknown weights. The vector $\mathit{w}$ is calculated by minimizing the sum of the squared errors it causes when used on an actual dataset:

$${\mathit{w}}^{*}=\text{arg}\hspace{0.17em}\underset{\mathit{w}}{min}\sum _{i=1}^n{\left[\left(\sum _{j=1}^d{w}_j{x}_{ij}\right)-y_i\right]}^2,$$

where $x_{ij}$ is the $j$th component of the vector ${\mathit{x}}_{\mathit{i}}$. This functional form is identical to the Ising Hamiltonian, and we may construct an Ising circuit with $J_{ij}={\sum }_{k=1}^n{x}_{ki}{x}_{kj}$, with the weights $\mathit{w}$ acting like the unknown magnetic moments. There is an effective magnetic field in the problem $h_i=-2{\sum }_{j=1}^n{x}_{ji}{y}_j$. A simple circuit that solves this problem for $d=2$ (each instance has two features) is provided in Fig. 9. This circuit provides weights to 2-bit precision.

Fig. 9.

A 2-bit, linear regression circuit to find the best two curve-fitting weights $w_d$, using the Principle of Minimum Power Dissipation.

The oscillators on the left-hand side of Fig. 9 represent the $2^0$ and $2^1$ bits of the first weight, while the oscillators on the other side represent the second weight.

The cross-resistance $R$ that one would need to represent the $J_{ij}$ that connects the $i$th and $j$th oscillators is calculated as

$$\frac{1}{R}=\frac{b_1}{R_{-1}}+\frac{b_0}{R_0}+\frac{b_{-1}}{R_1},$$

where $R_m=2^m{R}_0$ is a binary hierarchy of resistances based on a reference resistor $R_0$, and $b_m$ are the bits of $J_{ij}$: $J_{ij}=b_1\times 2^1+b_0\times 2^0+b_{-1}\times 2^{-1}$. This represents $J_{ij}$ to 3-bit precision using resistors that span a dynamic range $2^2=4$. Further, the sign of the coupling is allotted according to whether the resistors $R$ are parallel-connected or cross-connected. In operation, the resistors $R$ would be externally programmed to the correct binary values, with many more bits than 3-bit precision, as given by the matrix product $J_{ij}={\sum }_{k=1}^n{x}_{ki}{x}_{kj}$.

We have just solved the regression problem of the form $\mathit{X}\mathit{w}=\mathit{y}$, where matrix $\mathit{X}$ and vector $\mathit{y}$ were known measurements and the corresponding best weight vector $\mathit{w}$ for fitting was the unknown. We conclude by noting that this same procedure can be adopted to solve linear systems of equations of the form $\mathit{X}\mathit{w}=\mathit{y}$.

7. Discussion and Conclusion

Physics obeys a number of optimization principles such as the Principle of Least Action, the Principle of Minimum Power Dissipation (also called Minimum Entropy Generation), the Variational Principle, Physical Annealing, and the Adiabatic Principle (which, in its quantum form, is called Quantum Annealing).

Optimization is important in diverse fields, ranging from scheduling and routing in operations research to protein folding in biology, portfolio optimization in finance, and energy minimization in physics. In this article, we made the observation that physics has optimization principles at its heart and that they can be exploited to design fast, low-power digital solvers that avoid the limits of standard computational paradigms. Nature thus provides us with a means to solve optimization problems in all of these areas, including engineering, artificial intelligence, machine learning (backpropagation), Control Theory, and reinforcement learning.

We reviewed seven physical machines that purported to solve the Ising problem and found that six of the seven were performing Lagrange multiplier optimization; further, they also obey the Principle of Minimized Power Dissipation (always subject to a power-input constraint). This means that by appropriate choice of parameter values, these physical solvers can be used to perform Lagrange multiplier optimization orders of magnitude faster and with lower power than conventional digital computers. This performance advantage can be utilized for optimization in machine-learning applications where energy and time considerations are critical.

The following questions arise: What are the action items? What is the most promising near term application? All of the hardware approaches seem to work comparably well. The easiest to implement would be the electrical oscillator circuits, although the optical oscillator arrays can be compact and very fast. Electrically, there would two integrated circuits, the oscillator array, and the connecting resistors that would need to be reprogrammed for different problems. The action item could be to design the first chip consisting of about 1,000 oscillators and a second chip that would consist of the appropriate coupling resistor array for a specific optimization problem. The resistors should be in an addressable binary hierarchy so that any desired resistance value can be programmed in by switches, within the number of bits accuracy. It is possible to imagine solving a new Ising problem every millisecond by reprogramming the resistor chip.

On the software side, a compiler would need to be developed to go from an unsolved optimization problem to the resistor array that matches that desired goal. If the merit function were mildly nonlinear, we believe that the Principle of Minimum Power Dissipation would still hold, but there has been less background science justifying that claim.

With regard to the most promising near-term application, it might be in Control Theory or in reinforcement learning in self-driving vehicles, where rapid answers are required, at modest power dissipation.

The act of computation can be regarded as a search among many possible answers. Finally, the circuit converges to a final correct configuration. Thus the initial conditions may include a huge phase-space volume of $2^n$ possible solutions, ultimately transitioning into a final configuration representing a small- or modest-sized binary number. This type of computing implies a substantial entropy reduction. This led to Landauer’s admonition that computation costs $kn\log 2$ of entropy decrease and $kTn\log 2$ of energy, for a final answer with $n$ binary digits.

By the Second Law of Thermodynamics, such an entropy reduction must be accompanied by an entropy increase elsewhere. In Landauer’s viewpoint, the energy and entropy limit of computing was associated with the final acting of writing out the answer in $n$ bits, assuming the rest of the computer was reversible. In practice, technology consumes $\sim$10⁴ times more than the Landauer limit, owing to the insensitivity of the transistors operating at $\sim$1 V, when they could be operating at $\sim$10 mV.

In the continuously dissipative circuits we have described here, the energy consumed would be infinite if we waited long enough for the system to reach the final optimal state. If we terminate the powering of our optimizer systems after they reach the desired final-state answer, the energy consumed becomes finite. By operating at voltage $<$1 V and by powering off after the desired answer is achieved, our continuously dissipating Lagrange optimizers could actually be closer to the Landauer limit than a conventional computer.

A controversial point relates to the quality of solutions that are obtained for NP-hard problems. The physical systems we are proposing evolve by steepest descent toward a local optimum, not a global optimum. Nonetheless, many of the authors of the seven physical systems presented here have claimed to find better local optima than their competitors, due to special adjustments in their methods. Undoubtedly, some improvements are possible, but none of the seven papers reviewed here claims to always find the one global optimum, which would be NP-hard (34).

We have shown that a number of physical systems that perform optimization are acting through the Principle of Minimum Power Dissipation, although other physics principles could also fulfill this goal. As the systems evolve toward an extremum, they perform Lagrange function optimization where the Lagrange multipliers are given by the gain or loss coefficients that keep the machine running. Thus, nature provides us with a series of physical optimization machines that are much faster and possibly more energy-efficient than conventional computers.

Data Availability.

All study data are included in the article and SI Appendix.