Significance
Dual-comb spectroscopy has emerged a powerful technique of Fourier transform spectroscopy without moving parts. Broad spectra can be acquired with a single photodetector in any spectral range where laser frequency combs are available. Because the technique is multiplex, systematic effects are minimized and a great consistency of the spectra can be achieved. We show that dual-comb spectroscopy can be implemented with photon-counting instrumentation and work at power levels one-billion-fold weaker than those usually employed. Our demonstration opens many scenarios for applications of this powerful spectroscopic technique.
Keywords: frequency comb, precision spectroscopy, laser spectroscopy, interference, photon counting
Abstract
We probe complex optical spectra at high resolution over a broad span in almost complete darkness. Using a single photon-counting detector at light power levels that are a billion times weaker than commonly employed, we observe interferences in the counting statistics with two separate mode-locked femtosecond lasers of slightly different repetition frequencies, each emitting a comb of evenly spaced spectral lines over a wide spectral span. Unique advantages of the emerging technique of dual-comb spectroscopy, such as multiplex data acquisition with many comb lines, potential very high resolution, and calibration of the frequency scale with an atomic clock, can thus be maintained for scenarios where only few detectable photons can be expected. Prospects include spectroscopy of weak scattered light over long distances, fluorescence spectroscopy of single trapped atoms or molecules, or studies in the extreme-ultraviolet or even soft–X-ray region with comb sources of low photon yield. Our approach defies intuitive interpretations in a picture of photons that exist before detection.
We demonstrate broadband dual-comb spectroscopy with two femtosecond laser frequency combs even when the lasers are so strongly attenuated that only low photon-count rates can be obtained. The detection rates are so low that it is extremely unlikely that two photons, one from each source, are present in the detection path at the same time.
Dual-comb spectroscopy with two mode-locked lasers of slightly different repetition frequencies is emerging as a powerful tool for broadband spectroscopy with high precision (1). This unique technique of multiplex spectroscopy over broad spectral bandwidths does not require any moving parts, it works with a single fast photodetector, and it can be performed in any spectral region where comb sources are available, from submillimeter waves to the extreme ultraviolet (UV).
A variety of laser sources have been successfully harnessed, including fiber lasers (2) with optional nonlinear frequency conversion (3), semiconductor lasers (4, 5), electrooptic modulators (6), or Kerr-comb microresonators (7, 8). Samples have been probed via absorption, dispersion (2, 3), fluorescence (9), or polarization (10), and cavity enhancement (11) is possible, demonstrating a convincing potential for spectral diagnostics in fundamental and applied science. With two-photon excitation (9), coherent Raman effects (12), or photon echoes (13), even nonlinear dual-comb spectroscopy has become possible.
Compared to state-of-the-art broadband spectrometers, dual-comb interferometers show two key assets for spectral measurements. First, the frequency scale of the spectra can be calibrated within the accuracy of an atomic clock. Second, the instrumental line-shape can remain negligible for transitions broadened by Doppler or collisional effects in gas-phase species. Furthermore, Doppler-free spectroscopy has been demonstrated (9), raising the question of the fundamental limits in frequency accuracy of the technique.
The principle of a dual-comb spectrometer is easily described in terms of classical electromagnetic waves. Each laser emits a large number of precisely equally spaced spectral comb lines (14). Pairs of comb lines, one from each laser source, interfere at a fast photodetector, so that a comb of radio-frequency beat notes appears in the detector signal, where it is accessible to digital signal processing. Any optical spectral structure introduced by a sample is transformed to a corresponding structure in the radio-frequency spectrum. Optical resonance frequencies in a sample are effectively slowed down by a large factor equal to the repetition frequency divided by the difference in repetition frequencies.
Here we demonstrate dual-comb spectroscopy at such low light levels that only one photon-counting click is detected on average during the time of 1,000 laser pulses. The statistics of the detected photons carries the information about the two femtosecond lasers with their hundreds of thousands of comb lines and about the sample with its possibly highly complex optical spectrum. Dual-comb spectroscopy can thus be extended to counterintuitive situations where only very low photon-count rates are available from the sources or the sample, opening a new realm to precise broadband multiplexed spectroscopy. Naturally, such scenarios imply long observation times. While photon-counting instrumentation could potentially be implemented with other techniques of broadband frequency-comb spectroscopy, dual-comb spectroscopy maintains its unique advantages as a time-domain method without moving parts. This includes in particular the lack of geometric limitations, so that arbitrary resolutions and spectral bandwidths are becoming potentially feasible.
Results
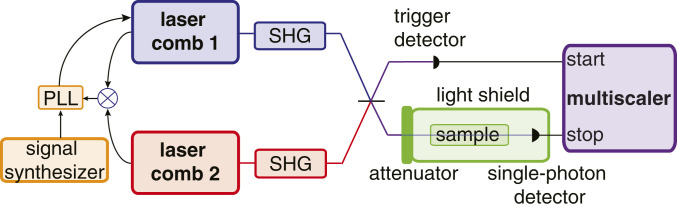
For the proof-of-principle experiments reported here (Fig. 1 and Materials and Methods), two essentially free-running mode-locked erbium-doped fiber femtosecond lasers with second-harmonic generation to 780 nm are used. Their repetition frequency is about 100 MHz, corresponding to a period of 10 ns, and the difference in repetition frequencies is maintained at a chosen value between 10 and 300 Hz using a slow feedback loop. The beams of the two lasers are combined on a pellicle beamsplitter. One output of the interferometer is strongly attenuated to the picowatt or femtowatt range as detailed below. A solid étalon with silvered end faces and a free spectral range of 500 GHz is used as a sample. The photons are counted on a single-photon detector and the counts are acquired as a function of time by a multiscaler. To obtain a dual-comb single-photon interferogram that approaches its classical counterpart, many photon clicks have to be accumulated. Here we use a simple yet limited approach which consists of triggering the data acquisition using the central fringe, detected with a standard fast silicon photodiode, at the second output of the interferometer and in accumulating many scans that add up the clicks for each time delay per increments of 800 ps.
Fig. 1.
Sketch of the experimental setup for photon-counting dual-comb spectroscopy. Two femtosecond laser oscillators, labeled laser comb 1 and laser comb 2, have a stabilized difference Δfrep in repetition frequencies. Their frequency-doubled beams with a spectrum centered at 780 nm (384 THz), are combined on a beamsplitter. The fringes at one output of the interferometer provide a trigger signal. The second output of the interferometer is strongly attenuated to a flux of photons lower than 3 × 106 photons per s−1, implying that the mean interval between photons is always more than 100-fold longer than the transit time of a photon in the interferometer. The photon clicks are counted by a single-photon detector and accumulated as a function of arrival time after the trigger by a multiscaler.
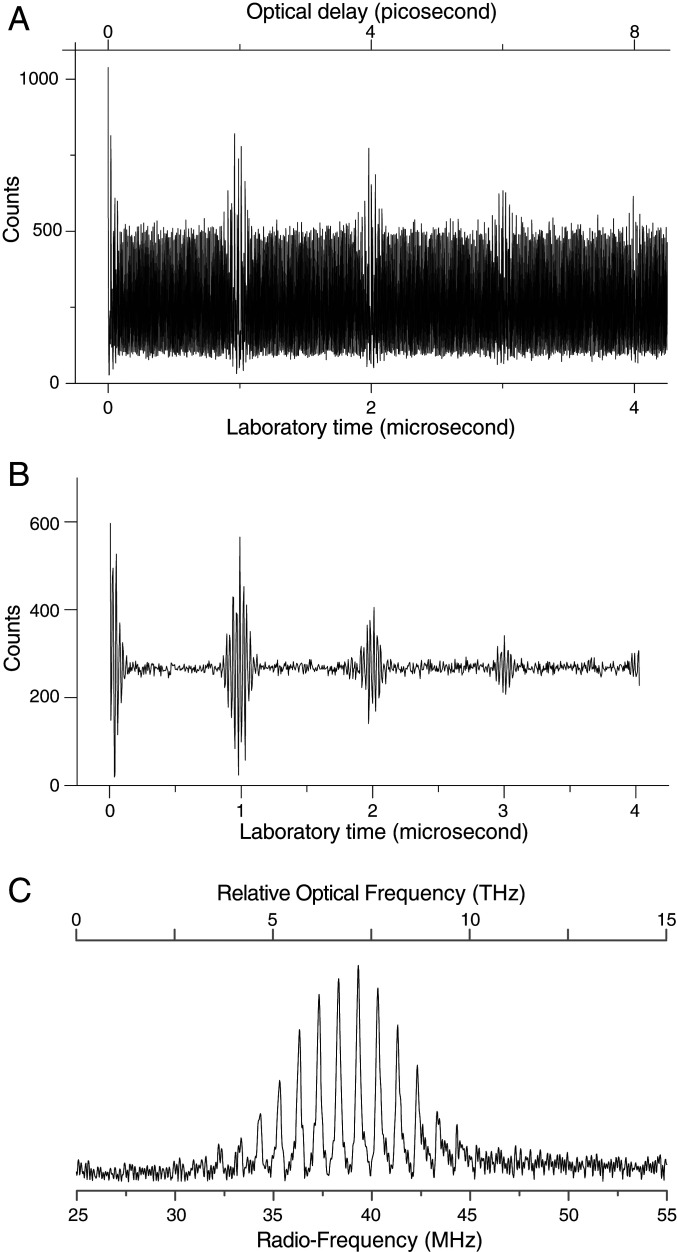
The interferogram shown in Fig. 2A (see also Materials and Methods) has been recorded at an average rate of one photon click every 368 ns, corresponding to an average power at the detector of 1.1 × 10−12 W. A total of 1.4 × 106 clicks are detected in 1.2 × 105 scans, of 4.25 µs each, in a total experimental time of 10 min. The interferogram shows a noninterferential background, which is usually electronically filtered out in dual-comb spectroscopy and that we numerically filter in Fig. 2B. Superimposed on the background signal, five bursts with good modulation contrast are discernible. They correspond to the interference pattern at the output of the Fabry–Pérot étalon. The Fourier transform of the interferogram reveals the spectrum of the étalon (Fig. 2C), down-converted in the radio-frequency region. In the optical region, the spectrum spans about 7 THz.
Fig. 2.
Experimental dual-comb interferogram and spectrum at a detected photon rate 2.7 × 106 photons per s−1. (A) The raw interferogram sampled at a rate of 0.8 ns (lower x scale: laboratory time) comprises a background part, unmodulated by the interference. The periodic interference signatures of a Fabry–Pérot étalon appear with a high contrast even at an optical delay of 8 ps (upper x scale: optical delays). (B) The interferogram of A is numerically filtered to highlight better the photon-counting interference signal. (C) The Fourier transform of a photon-counting interferogram (including A) reveals the evenly spaced transmission lines of the étalon, over a broad spectral span of several terahertz in the optical domain.
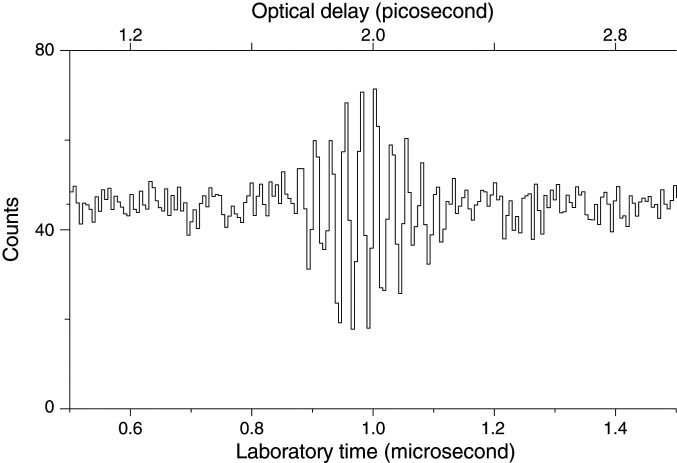
Lower light levels are reachable. An interferogram of the same Fabry–Pérot étalon is recorded (Fig. 3 and SI Appendix, Fig. S1A) at an average power as low as 20 × 10−15 W. This corresponds to an average rate of one photon click every 21 µs, or one photon during the time of 2,000 pulse pairs, or 0.14 photon click per interferometric scan of 3.0 µs. The Fourier transform of the interferogram properly reproduces the spectrum of the étalon (SI Appendix, Fig. S1B). The signal-to-noise ratio in our low-resolution proof-of-principle spectra (Fig. 2C and SI Appendix, Fig. S1B) is dominated by shot noise. For longer accumulation times and higher resolution, technical limitations such as the relative drift of the carrier-envelope frequencies of the free-running lasers take over. Since the dark count rate of the detector is much smaller than the signal count, detector noise can be neglected. In experiments of dual-comb spectroscopy, the average power at the detector is usually on the order of a few tens of microwatts. We thus achieve a billion-fold decrease of the light level using single-photon counting technology.
Fig. 3.
Photon-counting interference signal (with numerical filtering) when, on average, one photon is detected every 21 µs. For this interferogram, the average power on the detector is one-billion-fold lower than in usual dual-comb spectroscopy experiments.
Discussion
Single-photon interference fringes have long been observed in Young’s double-slit experiment or with a Michelson/Mach–Zehnder interferometer (15) and have continuously attracted interest, as exemplified by a recent demonstration with a frequency comb (16). In such a situation, it is possible to imagine that a photon from a defined source can follow two different quantum paths, which interfere constructively or destructively at the detector. Feynman famously called such interference “the only mystery” in quantum physics (17). For our dual-comb interferometry with two separate laser sources, one has to abandon the concept that a photon exists before detection. The photon is defined by the detection event. To predict the probability of such an event, one has to sum the probability amplitudes from any quantum paths that can contribute to this detector click.
The possibility of observing interference effects by detecting single photons from two mutually coherent continuous-wave single-mode laser sources was first demonstrated in 1967 (18). The experiments presented here extend this phenomenon to the much more complex scenario of two mode-locked femtosecond lasers and broadband spectroscopy.
One might argue that no dual-comb interferences can be expected with single-photon clicks from two femtosecond lasers, since the arrival time of a photon makes it possible to determine which of the two lasers has emitted the photon. To counter this argument, it is useful to look at dual-comb spectroscopy in the time domain. A single short pulse that interacts with narrow spectral resonances of a sample acquires a temporal tail, such as the free induction decay field due to molecular resonances. This tail carries most of the spectral information and is read out interferometrically in Fourier transform spectroscopy or dual-comb spectroscopy. As long as the temporal separation of two pulses does not exceed the coherence time of the sample, a photon click cannot be uniquely assigned to one particular laser, and interference between two photon paths originating from different sources becomes possible.
The proof-of-concept described here, although fully demonstrative of dual-comb spectroscopy at photon-counting ultralow intensities, is technically limited by our elementary experimental implementation. For interferometry, the mutual coherence of the two laser sources has to be maintained during the entire recording time. Sophisticated electronic stabilization techniques have been developed to maintain mutual coherence of two femtosecond lasers over periods of seconds. Recently, our group has demonstrated a feed-forward dual-comb spectrometer with extended mutual coherence enabling direct time-domain averaging over more than 30 min (2). This latter development has actually motivated the present proof-of-principle as it enables the straightforward use of single-photon counting instrumentation with dual-comb spectroscopy by permitting direct accumulation of photon clicks over extended time period. Now that the feasibility of photon-counting dual-comb interferometry is established, forthcoming investigations will harness feed-forward stabilization to enable scientific applications through long term averaging. With further system development, a new spectroscopic tool may become available for studying fundamental optical processes at the level of single photons and single emitters.
Aside from its conceptual interest, the demonstration of dual-comb spectroscopy at the single-photon level opens up new applications, which perhaps would not have suggested themselves intuitively. Precise multimodal broadband spectroscopy can now be envisioned with light passing through strongly absorbing or scattering media or traveling over long distances. For remote sensing, dual-comb spectroscopy might provide spectra even in the limit of photon-level backscattering, adding to the power of atmospheric light detection and ranging (LIDAR) measurements. Dual-comb spectroscopy will become possible with comb generators that emit only at very low power, such as in the soft–X-ray region or in the extreme UV range. Even photon-level high-harmonic generation at or near solid surfaces (19, 20) could provide suitable comb sources. Frequency down- and up-conversion will enable dual-comb spectroscopy with comb generators of high repetition frequency in spectral regions such as the mid- and far-infrared even at their low photon yields. Finally, broadband dual-comb action spectroscopy has previously been demonstrated (9, 12), e.g., via excitation of fluorescence in first proof-of-principle experiments of nonlinear Doppler-free detection (9). With the expanded opportunities offered by photon-counting technology, fluorescence detection at the single-photon level will permit linear or nonlinear dual-comb spectroscopy of rarefied or microscopic samples, down to individual atoms, ions, or molecules. This may benefit many areas of science and technology, such as condensed-phase spectroscopy of nanoscopic samples, down to single molecules (21–24). In precision spectroscopy and frequency metrology, stringent tests of quantum molecular theory (25) will be improved by accurate measurements of the shapes and positions of the spectral lines of trapped single emitters, over a broad spectral bandwidth.
The experiments that we present toward dual-comb spectroscopy rely on first-order interference, which is robust against attenuation. More sophisticated but also more delicate approaches to spectroscopy may become possible by exploiting higher-order correlations and the photon entanglement that can be created with quantum optical frequency combs (26).
Materials and Methods
Detailed Experimental Setup.
Two amplified erbium-doped fiber mode-locked lasers (Fig. 1) emit pulses at a repetition frequency of about frep = 100 MHz and an average power of 220 mW. Their spectrum is centered at 1,560 nm (192 THz). They are frequency doubled to generate a spectrum centered at 780 nm (384 THz), with an average power of 50 mW. The pulse duration is about 90 fs. In the experiments reported here, we mainly rely on the passive mechanical stability of the lasers. The temperatures of the two lasers are controlled with Peltier elements and this enables coarse setting of the repetition frequency. Only the difference of the repetition frequencies is actively stabilized to a frequency-synthesized signal generator, at a value Δfrep chosen between 10 and 300 Hz, with the help of a slow digital phase-locked loop. The error signal from the phase-locked loop is used to adjust the voltage for a fiber-stretching piezoelectric element inside one of the lasers, so that the difference in pulse repetition frequencies can be maintained at the chosen value. The repetition frequency of the other laser and the carrier-envelope frequencies of the two lasers are left unstabilized. Regardless of the fluctuations, not stabilizing the difference in carrier-envelope frequencies to a well-chosen value fundamentally limits the capabilities of time-domain accumulation of the interferometric signal, as an arbitrary value of this difference implies that the time-domain interferometric signal does not periodically recur.
The beams of the two frequency-doubled femtosecond lasers are superimposed with a pellicle beamsplitter. One output of the beamsplitter is sent, after suitable attenuation, to a fast silicon photodiode. When the pulses of the two femtosecond lasers overlap in time, a strong interference signal is produced. Its central fringe is used to generate the trigger signal, which starts the photon counting by a multiscaler. The second output beam is used for photon-counting dual-comb spectroscopy. To avoid aliasing in the dual-comb spectra at the chosen repetition rate difference of 200 Hz, the frequency-doubled laser beams are first sent through a bandpass filter, which slightly narrows the spectrum to a full width at half maximum of about 5 THz. After attenuation to a flux between 104 to 3 × 106 photon counts per second, the light passes through a sample. In this simple proof-of-concept, a solid étalon with silvered end faces and a free spectral range of 500 GHz is used as sample. The beam is then directed to a fiber-coupled single-photon detector of low dark-count rate. A suitable light shield protects the detector input from ambient stray light. After the multiscaler receives a trigger “start” signal, any single-photon signals received by the “stop” input are counted according to their arrival time in time bins with increments of 800 ps.
Detailed Recording Conditions.
In the recording leading to the data shown in Fig. 2A, a total of 1,406,790 photon clicks have been counted over 121,894 sweeps of 5,312 time bins of 0.8 ns each. The duration of one sweep is 4.25 µs and the total measurement time is 0.52 s. The cycling time of a sweep is 1/Δfrep = 1/(200 Hz) = 5 ms; therefore, the entire time for the experiment is 10 min. Unfortunately, insufficient stability of the difference of laser repetition rates is so far preventing the averaging of such interferograms over times longer than a few minutes, except for the central fringe pattern and the first three or four subsequent interference bursts produced by the étalon. Nevertheless, the clear interference contrast unambiguously demonstrates that dual-comb interferograms can be accumulated by photon counting even at very low light levels. On average, 11.5 clicks per sweep of 4.25 µs are measured. The detected photon rate is therefore 2.72 × 106 photon per second. On average, 1 photon click every 368 ns is detected, whereas the transit time of a photon from the sources to the detector is about 3 ns. The photons have a wavelength of 780 nm. The average power corresponding to the detected interferogram is 690 fW. The efficiency of the detector is 60% and the detector dead time after a count is 43 ns, which brings the power falling onto the detector to 1.15 × 10−12 W. The interferogram extends to 10,000 time bins and it is completed with zeros up to 60,000 samples in order to interpolate the spectrum, as is common practice in Fourier transform spectroscopy. A magnitude Fourier transform is computed. The resulting radio-frequency spectrum of the étalon shown in Fig. 2C has a resolution of 125 kHz. In dual-comb spectroscopy, the optical frequencies are down-converted to the radio-frequency domain by a factor Δfrep/frep. A resolution of 125 kHz in the radio-frequency domain corresponds, in the optical domain, to a resolution of 125 kHz × 100 MHz/200 Hz, that is 62.5 GHz. The central optical frequency in the spectrum is about 384 THz. In this experiment, absolute calibration of the frequency scale is not achieved, as the carrier-envelope offset frequencies of the lasers are not measured. State-of-the art dual-comb setups, though, enable absolute frequency calibration (2, 3, 9) and we will implement this functionality together with long coherence times (2) in future work. For now, we only display the relative optical scale in the upper x axis of Fig. 2C.
At low light level, the cumulated photon count over 3,750 time bins of 0.8 ns each is shown in Fig. 3 and SI Appendix, Fig. S1A. A total of 168,703 photon clicks have been counted over 1,190,033 sweeps, each lasting 3.0 µs. On average 0.14 clicks are captured per sweep of 3.0 µs. The total acquisition time is 3.57 s while, owing to the interferogram cycling time, the experiment lasts 1 h and 39 min. The detected photon rate is 47,254 photon s−1. In other words, on average, one photon click is detected every 21 µs. The average power corresponding to the detected interferogram is 1.2 × 10−14 W = 12 fW. Accounting for the detector efficiency, the power falling onto the detector is 2 × 10−14 W. An interferogram extended to 4,376 time bins is completed with fivefold more zeros than actual samples for spectral interpolation and it is Fourier transformed to reveal the spectrum shown in SI Appendix, Fig. S1B with a radio-frequency resolution of 285 kHz, corresponding to 143 GHz in the optical domain. The spectrum in SI Appendix, Fig. S1B appears centered at a different radio frequency than that of Fig. 2C because of drifts, and the absence of control, of the carrier-envelope offset frequencies of the lasers. It is however centered at the same optical frequency as that of Fig. 2C.
Supplementary Material
Acknowledgments
We are grateful to Anton Scheich for the design and implementation of locking electronics. Work performed within the frame of the Munich Center for Quantum Science and Technology funded by the Deutsche Forschungsgemeinschaft (German Research Foundation) under Germany’s Excellence Strategy–EXC-2111–390814868. Support by the Carl-Friedrich von Siemens Foundation is acknowledged.
Footnotes
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2010878117/-/DCSupplemental.
Data Availability.
Raw experimental data have been deposited in Edmond, the Open Access Max Planck Research Data Repository at https://dx.doi.org/10.17617/3.49.
References
- 1.Picqué N., Hänsch T. W., Frequency comb spectroscopy. Nat. Photonics 13, 146–157 (2019). [Google Scholar]
- 2.Chen Z., Yan M., Hänsch T. W., Picqué N., A phase-stable dual-comb interferometer. Nat. Commun. 9, 3035 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ycas G.et al., High-coherence mid-infrared dual-comb spectroscopy spanning 2.6 to 5.2 mum. Nat. Photonics 12, 202–208 (2018). [Google Scholar]
- 4.Villares G., Hugi A., Blaser S., Faist J., Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nat. Commun. 5, 5192 (2014). [DOI] [PubMed] [Google Scholar]
- 5.Link S. M., Maas D. J. H. C., Waldburger D., Keller U., Dual-comb spectroscopy of water vapor with a free-running semiconductor disk laser. Science 356, 1164–1168 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Millot G.et al., Frequency-agile dual-comb spectroscopy. Nat. Photonics 10, 27–30 (2016). [Google Scholar]
- 7.Suh M.-G., Yang Q.-F., Yang K. Y., Yi X., Vahala K. J., Microresonator soliton dual-comb spectroscopy. Science 354, 600–603 (2016). [DOI] [PubMed] [Google Scholar]
- 8.Dutt A.et al., On-chip dual-comb source for spectroscopy. Sci. Adv. 4, e1701858 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meek S. A., Hipke A., Guelachvili G., Hänsch T. W., Picqué N., Doppler-free Fourier transform spectroscopy. Opt. Lett. 43, 162–165 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Minamikawa T.et al., Dual-comb spectroscopic ellipsometry. Nat. Commun. 8, 610 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bernhardt B.et al., Cavity-enhanced dual-comb spectroscopy. Nat. Photonics 4, 55–57 (2010). [Google Scholar]
- 12.Ideguchi T.et al., Coherent Raman spectro-imaging with laser frequency combs. Nature 502, 355–358 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Lomsadze B., Cundiff S. T., Frequency combs enable rapid and high-resolution multidimensional coherent spectroscopy. Science 357, 1389–1391 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Hänsch T. W., Nobel lecture: Passion for precision. Rev. Mod. Phys. 78, 1297–1309 (2006). [Google Scholar]
- 15.Grangier P., Roger G., Aspect A., Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences. Europhys. Lett. 1, 173–179 (1986). [Google Scholar]
- 16.Lee S. K., Han N. S., Yoon T. H., Cho M., Frequency comb single-photon interferometry. Commun. Phys. 1, 51 (2018). [Google Scholar]
- 17.Feynman R., Leighton R., Sands M., The Feynman Lectures on Physics, Volume III: Quantum Mechanics, (New Millennium Education, Basic Books, New York, 2011). [Google Scholar]
- 18.Pfleegor R. L., Mandel L., Interference of independent photon beams. Phys. Rev. 159, 1084–1088 (1967). [Google Scholar]
- 19.Sivis M.et al., Tailored semiconductors for high-harmonic optoelectronics. Science 357, 303–306 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Ghimire S., Reis D. A., High-harmonic generation from solids. Nat. Phys. 15, 10–16 (2019). [Google Scholar]
- 21.Korlacki R., Steiner M., Qian H., Hartschuh A., Meixner A. J., Optical Fourier transform spectroscopy of single-walled carbon nanotubes and single molecules. ChemPhysChem 8, 1049–1055 (2007). [DOI] [PubMed] [Google Scholar]
- 22.Piatkowski L., Gellings E., van Hulst N. F., Broadband single-molecule excitation spectroscopy. Nat. Commun. 7, 10411 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maser A., Gmeiner B., Utikal T., Götzinger S., Sandoghdar V., Few-photon coherent nonlinear optics with a single molecule. Nat. Photonics 10, 450–453 (2016). [Google Scholar]
- 24.Thyrhaug E.et al., Single-molecule excitation-emission spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 116, 4064–4069 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hölsch N., et al., Benchmarking theory with an improved measurement of the ionization and dissociation energies of H2. Phys. Rev. Lett. 122, 103002 (2019). [DOI] [PubMed] [Google Scholar]
- 26.Kues M.et al., Quantum optical microcombs. Nat. Photonics 13, 170–179 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Raw experimental data have been deposited in Edmond, the Open Access Max Planck Research Data Repository at https://dx.doi.org/10.17617/3.49.