Statistical Properties of Stepped Wedge Cluster-Randomized Trials in Infectious Disease Outbreaks

Abstract

Randomized controlled trials are crucial for the evaluation of interventions such as vaccinations, but the design and analysis of these studies during infectious disease outbreaks is complicated by statistical, ethical, and logistical factors. Attempts to resolve these complexities have led to the proposal of a variety of trial designs, including individual randomization and several types of cluster randomization designs: parallel-arm, ring vaccination, and stepped wedge designs. Because of the strong time trends present in infectious disease incidence, however, methods generally used to analyze stepped wedge trials might not perform well in these settings. Using simulated outbreaks, we evaluated various designs and analysis methods, including recently proposed methods for analyzing stepped wedge trials, to determine the statistical properties of these methods. While new methods for analyzing stepped wedge trials can provide some improvement over previous methods, we find that they still lag behind parallel-arm cluster-randomized trials and individually randomized trials in achieving adequate power to detect intervention effects. We also find that these methods are highly sensitive to the weighting of effect estimates across time periods. Despite the value of new methods, stepped wedge trials still have statistical disadvantages compared with other trial designs in epidemic settings.

Abbreviations

CRT

cluster-randomized trial

IRT

individually randomized trial

MEM

mixed effects model

MEM-CP

mixed effects model–cluster period

NPWP

nonparametric within-period

PH

proportional hazards

R₀

basic reproduction number

SC

synthetic control

SWT

stepped wedge cluster-randomized trial

VE

vaccine efficacy

Randomized controlled trials are crucial to evaluating interventions, including vaccines and other preventive measures, during infectious disease outbreaks. Epidemic settings and vaccine studies, however, pose statistical, logistical, and ethical challenges that make randomized trials more difficult to design, conduct, and analyze (1). Statistically, trials must account for the interference between individuals and define explicitly whether they identify the direct or indirect effects of the vaccine, as well as handle a high degree of spatiotemporal variation, uncertain incidence rates, and the potential for mild or asymptomatic infections (2–4). Logistically, trials must be able to be implemented in the context of ongoing epidemiologic work in outbreaks and account for the timeline of production of the vaccine and the speed at which it can be rolled out to affected communities (3, 5, 6). Ethically, vaccine trials face complex considerations of the overall value of the trial as well as the risks and benefits to participants and individuals in communities with participants (7, 8).

Cluster-randomized trials (CRTs) have recently become more common in infectious disease settings. These designs are well-suited to capture indirect effects (e.g., the effects of herd immunity) and, in some situations, might be logistically easier to implement or more acceptable to participating communities (3, 7, 9). More complex CRT designs have also been proposed for vaccine trials in outbreak settings. These include the ring vaccination design that was used in the 2015 Ebola outbreak in Guinea (10) as well as the stepped wedge cluster-randomized trial (SWT) design, which has been proposed in various outbreak settings, including the Ebola outbreak in Sierra Leone (11). SWTs might be more acceptable to communities enrolling in trials because there is no placebo group, and they might align well with a phased rollout necessitated by implementation challenges (12, 13).

There are, however, tradeoffs to these designs. They are not designed to identify direct effects of intervention (7). In addition, CRTs and SWTs generally have lower power to detect treatment effects and thus require a larger sample size than individually randomized trials (IRTs) (9, 14, 15). They also might exhibit biases due to imbalance between clusters, especially with the high incidence heterogeneity of outbreaks, and they have less flexibility to adapt the design or increase sample size (3, 9, 11, 16). To better understand the statistical properties of these designs, we can evaluate their performance on simulated outbreaks (17). Bellan et al. (14) found that SWTs had much lower power than IRTs in simulations of the waning Ebola outbreak. Hitchings et al. (15) used simulated outbreaks to examine the tradeoff between capturing indirect vaccine effects and reduced power between parallel-arm CRTs and IRTs.

SWTs in particular are highly susceptible to misspecification and can produce biased results when time trends and time-intervention interactions are not modeled correctly (18, 19). Type I error of hypothesis tests can be preserved by using permutation-based inference, but this generally results in reduced power (20–22). New methods for analyzing SWTs have recently been proposed that preserve type I error but might have more precision and higher power than permutation tests based on misspecified mixed effects models (MEM). These can be purely “vertical” methods that avoid the need to model time trends, such as the nonparametric within-period (NPWP) method (23), the design-based approach (24), and the synthetic control (SC)-based approach (22), or “horizontal” methods that compare within-cluster differences between 2 time points across clusters (22). The properties of these analysis methods have been studied in various theoretical and simulation-based contexts but not specifically for infectious disease outbreaks and not in a context that compares them with IRT and CRT designs.

Understanding the statistical properties of various trial designs for infectious disease outbreaks is a key part of planning for vaccine studies. Vaccine studies in outbreak settings, as currently with coronavirus disease 2019, should take into consideration these properties, along with feasibility and ethical considerations, in the design phase. To be ethical, a randomized trial should have a clear analysis plan that will result in a statistically valid estimate of the effect and is adequately powered to detect a meaningful effect size in a reasonable amount of time. By considering the properties of various SWT analysis methods and comparing these with IRT and CRT methods, this article contributes to the appropriate design of future trials conducted during epidemics.

METHODS

Outbreak and trial simulation

We simulated outbreaks using a model developed by Hitchings et al. (15). This model simulates a main population, in which an epidemic progresses, and the study population, which is composed of many smaller communities. Infections are imported from the main population into the study population, where the outbreak spreads within the communities, but, for our simulation, not between communities.

The model and parameters are described in more detail by Hitchings et al. (15). We used the infectious period distribution (gamma distributed with a mean of 5.0 days and a standard deviation of 4.7 days), community size (uniformly distributed from 80 to 120 persons), within-community probability of a contact between 2 individuals (0.15), and percentage of a community enrolled in the trial (50%) used in those simulations. In our model, the infectious period corresponds approximately with reported timing of the peak viral load for severe acute respiratory syndrome coronavirus-2 infection (25). The community size and contact rates are highly dependent on context but might be reasonable if most transmissions are from very close contacts. To reduce the number of communities with no cases, we increased the expected number of importations into a community to 2 over the course of the study. We assumed that the incubation period and latent period were the same for each individual, independently generated from a gamma distribution with shape parameter 5.807 and scale parameter 0.948, for a mean incubation period of 5.51 days, as has been estimated for coronavirus disease 2019 (26). We enrolled 40 communities into the trial 56 days after the start of the epidemic in the main population and conducted follow-up for 308 days. Finally, we considered 4 values of basic reproduction number (R₀) for the outbreak: R₀ = 1.34, 1.93, 2.47, and 2.97, by varying the transmission rate constant parameter in the model.

On top of this outbreak, we simulated 3 types of randomized trials: an IRT, a CRT, and a SWT. The IRT and CRT were conducted as described by Hitchings et al. (15). In all designs, on day 56, half of the individuals in each study cluster who had not yet been infected were enrolled into the trial, and these individuals were followed for 308 days. In the IRT, half of these individuals in each cluster were assigned to vaccination and the other half to control; the vaccination occurred immediately upon enrollment. In the CRT, half of the clusters were assigned to vaccination and the other half to control; all enrolled individuals in a cluster received the treatment for that cluster immediately upon enrollment. In the SWT, all clusters began in the control arm. In design SWT-A, 4 clusters crossed over to the vaccination arm every 28 days, beginning on day 84. In design SWT-B, 1 cluster crossed over to the vaccination arm every 7 days, beginning on day 84. So the period lengths differed for SWT-A (28 days) and SWT-B (7 days). We considered 3 values of the direct vaccine efficacy (VE): 0, 0.6, and 0.8. In both of the nonzero cases, the vaccine is leaky, conferring a constant reduction in the probability of infection acquisition per contact across all vaccinated individuals. For each combination of R₀, VE, and trial type, we conducted 1,000 simulations and analyzed the results.

Analysis methods

The results from the IRT and CRT designs were analyzed as described by Hitchings et al. (15), using the time to symptom onset for each enrolled individual. For the IRT, statistical analysis was conducted using a Cox proportional hazards (PH) analysis, stratified by community. For the CRT, statistical analysis was conducted using a Cox PH model with a gamma-distributed shared frailty to account for clustering by community. In both of these analyses, individuals who have not experienced symptom onset by the end of follow-up are censored.

The results from the 2 SWT designs were analyzed using a variety of methods. A PH approach used the time to symptom onset to estimate a hazard ratio, like the approaches used for the IRT and CRT designs. The other approaches use the proportion of individuals with symptom onset in each cluster in each period to estimate a risk or odds ratio; this has the advantage of being less sensitive to consistent determination of the date of symptom onset but might have less power than methods using the time to event. The methods used were:

• SWT-PH: Cox PH analysis with a time-varying intervention covariate and a gamma-distributed shared frailty to account for clustering by community (14, 27).

• MEM: MEM with a fixed effect of time and a normally distributed random effect for cluster, with a logit link (28).

• MEM-cluster period (CP): MEM with a fixed effect of time and independent normally distributed random effects for cluster and cluster period, with a logit link (29).

• Two vertical nonparametric within-period methods, both with a log link (23):

  • ∘ NPWP-1: equally weighting period-specific NPWP estimates across periods.

  • ∘ NPWP-2: weighting period-specific NPWP estimates by the total number of cases in that period.

• Four vertical synthetic control methods, all with a log link (22):

  • ∘ SC-1: equally weighting clusters within each period and equally weighting period-specific SC estimates across periods.

  • ∘ SC-2: equally weighting clusters within each period and weighting period-specific SC estimates by the total number of cases in that period.

  • ∘ SC-Wt-1: weighting clusters within each period by the inverse mean square prediction error of the SC fit and equally weighting period-specific SC estimates across periods.

  • ∘ SC-Wt-2: weighting clusters within each period by the inverse mean square prediction error of the SC fit and weighting period-specific SC estimates by the total number of cases in that period.

We did not consider the horizontal crossover method because it is not well suited to capture indirect effects and is highly sensitive to time trends (22). While time to infection might be more representative (than time to symptom onset) of the underlying transmission dynamics, it is difficult to observe, so we considered the more reasonable study outcome of time to symptom onset. It is assumed in this model that symptom onset and beginning of infectiousness are the same and that an individual will not be reinfected after symptom onset. To account for the delay in symptom onset (and thus the delayed effect of the intervention), we removed the first period on intervention for each cluster from all SWT analyses. For the time-to-event analyses, we removed any infections that occur within the first 6 days (the average incubation time) of trial enrollment or of beginning the intervention.

For NPWP and SC, we took the log risk ratio of the mean intervention cluster outcome compared with the mean control (or synthetic control) cluster outcome within each period. For periods with zero cases among either the control clusters or intervention clusters, we added one-half case and one-half noncase to each arm so that a period-specific effect estimate could be computed. Failure to do so results in noncomputable effect estimates. Periods with zero cases in both arms do not contribute to the effect estimate. For hypothesis testing, we used asymptotic inference for MEM and MEM-CP and permutation inference for SWT-PH, NPWP, and SC (20–22). Permutation inference was not done for the MEM and MEM-CP methods because of the high computational burden of these methods. All code is available at https://github.com/leekshaffer/SW-CRT-outbreak.

RESULTS

VE estimates and power by analysis method

Figure 1 shows the median and first and third quartiles of the VE estimates, calculated as 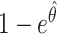, where 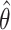is the estimated hazard ratio (IRT, CRT, and SWT-PH), odds ratio (SWT MEM and MEM-CP), or risk ratio (SWT NPWP and SC) across 1,000 simulations. We show main results for R₀ = 2.47 and direct VE = 0.6 for the IRT, CRT, and SWT-A (Figure 1A) and SWT-B (Figure 1B) designs. Note that while these effect measures are not equivalent, they are approximately equal under the rare disease assumption given that the incidence rate is low in each cluster period (1).

Figure 1.

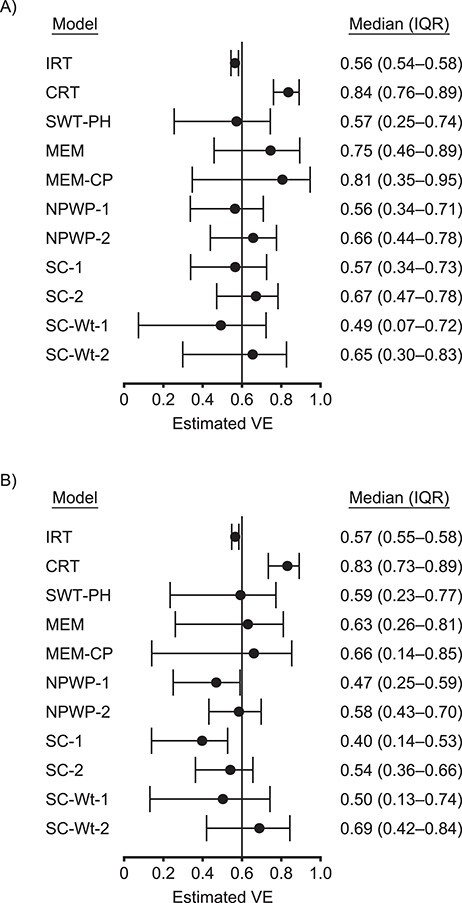
Estimates by model for an analysis of vaccine efficacy (VE) in an outbreak setting. Median and interquartile range (IQR) of VE estimates for direct VE of 0.6 (vertical line) and a basic reproduction number, R₀, of 2.47 for individually randomized trial (IRT) analyzed with stratified Cox model, cluster-randomized trial (CRT) analyzed with a Cox model with a gamma-distributed shared frailty, and stepped wedge trials with 4 clusters crossing over every 28 days (SWT-A) (A) and with 1 cluster crossing over every 7 days (SWT-B) (B) analyzed by a Cox model with a gamma-distributed shared frailty (SWT-PH), mixed effects model (MEM), mixed effects model with cluster-period random effect (MEM-CP), nonparametric within-period method equally weighted across periods (NPWP-1) and weighted across periods by total case count (NPWP-2), and synthetic control method equally weighted across clusters and periods (SC-1), equally weighted across clusters and weighted across periods by total case count (SC-2), weighted across clusters by inverse mean square prediction error and equally weighted across periods (SC-Wt-1), and weighted across clusters by inverse mean square prediction error and across periods by total case count (SC-Wt-2).

These results demonstrate that the IRT has the least variability among estimates and is centered near the true direct VE. Because the control individuals in the IRT benefit from the indirect effect of being in the same cluster as vaccinated individuals, the estimated VE is slightly below the true direct VE. The CRT estimates a higher effectiveness; it captures some indirect effects but with higher variability. The SWT results are very dependent on the analysis method chosen, but all have higher variability than the CRT results and have a lower median estimate. Among SWT results, a higher effect is estimated when weighting across periods by the total number of cases in a given period than when weighting equally. A higher effect is generally also estimated for SWT-A than for SWT-B, except for SWT-PH, which has comparable medians between the 2 SWT designs.

Figure 2 shows the empirical power (Figure 2A, VE = 0.6) and empirical type I error (Figure 2B, VE = 0) for asymptotic inference for the IRT, CRT, MEM, and MEM-CP analyses and permutation inference for the SWT-PH, NPWP, and SC analyses. As seen in other settings, the asymptotic inference for MEM and MEM-CP leads to greatly inflated type I error (over 25%) and is omitted from the figure (14, 20, 22); while not shown, the asymptotic inference for SWT-PH leads to inflated error similar to that for MEM. The permutation inference for SWT-PH, NPWP, and SC has greatly reduced power compared with the IRT and CRT methods, with less than 50% power to detect a true direct vaccine effect of 0.6 compared with over 90% for the CRT and nearly 100% for the IRT. The NPWP-2 method achieves greater power in SWT-B than in SWT-A, but this is not the case for NPWP-1. SC-1 and SC-2 perform comparably to NPWP-1 and NPWP-2, respectively, but the SC-Wt methods have noticeably lower power. SWT-PH performs similarly to NPWP-1 and SC-1, which is not as high as NPWP-2 and SC-2.

Figure 2.

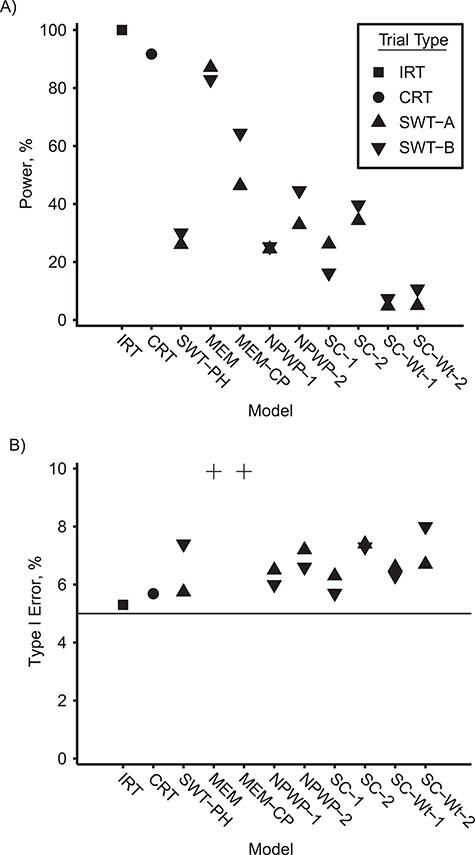
Power and type I error by model for an analysis of vaccine efficacy in an outbreak setting. Empirical power for direct vaccine effect of 0.6 (A) and empirical type I error for direct vaccine effect of 0 (B) with a basic reproduction number, R₀, of 2.47 for individually randomized trial analyzed with stratified Cox model (IRT), cluster-randomized trial analyzed with a Cox model with a gamma-distributed shared frailty (CRT), and stepped wedge trials with 4 clusters crossing over every 28 days (SWT-A) and with 1 cluster crossing over every 7 days (SWT-B) analyzed by a Cox model with a gamma-distributed shared frailty (SWT-PH), mixed effects model (MEM), mixed effects model with cluster-period random effect (MEM-CP), nonparametric within-period method equally weighted across periods (NPWP-1) and weighted across periods by total case count (NPWP-2), and synthetic control method equally weighted across clusters and periods (SC-1), equally weighted across clusters and weighted across periods by total case count (SC-2), weighted across clusters by inverse mean square prediction error and equally weighted across periods (SC-Wt-1), and weighted across clusters by inverse mean square prediction error and across periods by total case count (SC-Wt-2). Four type I error values greater than 10% are denoted by “+” in (B): SWT-A MEM (72%), SWT-B MEM (72%), SWT-A MEM-CP (28%), and SWT-B MEM-CP (52%). The horizontal line in (B) denotes the nominal type I error of 5%.

VE estimates and power by R₀

Figure 3 demonstrates the effect of R₀ on the median VE estimate (Figure 3A) and empirical power (Figure 3B) among these methods for the true direct VE = 0.6. Figure 4 shows the same results for true direct VE = 0.8. For comparison, Figure 5 shows the same results for the null setting where the true direct VE = 0. For both nonzero VE values, as R₀ increases, both the estimated VE and the power of all of the SWT-A and SWT-B methods decrease. The same trend occurs for the CRT, although it maintains nearly 100% power when VE = 0.8 for all R₀ values considered here. The IRT approach maintains its estimate and power throughout. The SWT methods decrease much more quickly than the CRT method, although there is no noticeable difference in this regard among the various SWT methods. For higher R₀ values, the epidemic is passing so quickly through the communities that many communities have already experienced the epidemic before crossing over to the intervention, thus reducing the power of the SWT methods to detect effects. Throughout, the various SWT methods perform similarly. While these figures display only SWT-PH, NPWP-2, and SC-2, the same trends held for NPWP-1 and SC-1. Similar trends, but with lower power throughout, held for SC-Wt-1 and SC-Wt-2.

Figure 3.

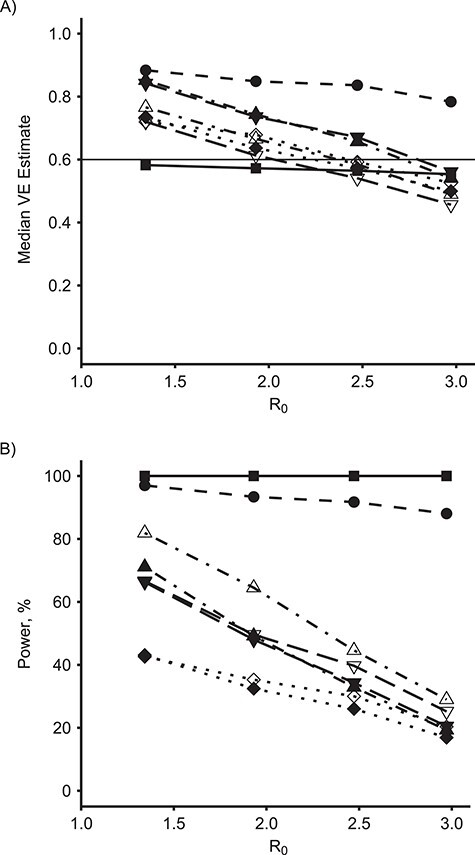
Estimates and power by basic reproduction number, R₀, and model for an analysis of vaccine efficacy (VE) in an outbreak setting for direct VE of 0.6. Median VE estimate (A) and empirical power (B) for direct VE of 0.6 (horizontal line in (A)) versus R₀, for individually randomized trial (IRT) analyzed with stratified Cox model (squares, solid line), cluster-randomized trial (CRT) analyzed with a Cox model with a gamma-distributed shared frailty (circles, dashed line), and stepped wedge trials (SWT-PH) with 4 clusters crossing over every 28 days (SWT-A, filled points) and with 1 cluster crossing over every 7 days (SWT-B, unfilled points) analyzed by a Cox model with a gamma-distributed shared frailty (diamonds, dotted line), nonparametric within-period method weighted across periods by total case count (NPWP-2; upward triangle, dash-dotted line), and synthetic control method equally weighted across clusters and weighted across periods by total case count (SC-2; downward triangle, long-dash line).

Figure 4.

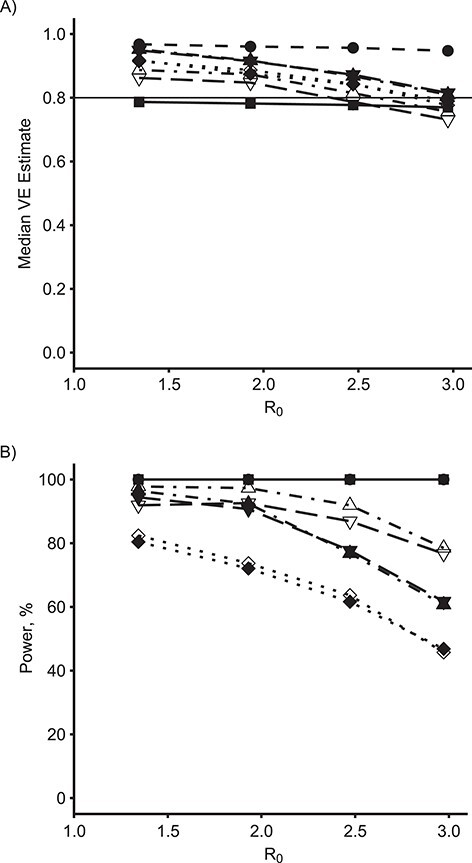
Estimates and power by basic reproduction number, R₀, and model for an analysis of vaccine efficacy (VE) in an outbreak setting for direct VE of 0.8. Median VE estimate (A) and empirical power (B) for direct VE of 0.8 (horizontal line in (A)) versus R₀, for individually randomized trial (IRT) analyzed with stratified Cox model (squares, solid line), cluster-randomized trial (CRT) analyzed with a Cox model with a gamma-distributed shared frailty (circles, dashed line), and stepped wedge trials with 4 clusters crossing over every 28 days (SWT-A, filled points) and with 1 cluster crossing over every 7 days (SWT-B, unfilled points) analyzed by a Cox model with a gamma-distributed shared frailty (SWT-PH; diamonds, dotted line), nonparametric within-period method weighted across periods by total case count (NPWP-2; upward triangle, dash-dotted line), and synthetic control method equally weighted across clusters and weighted across periods by total case count (SC-2; downward triangle, long-dash line).

Figure 5.

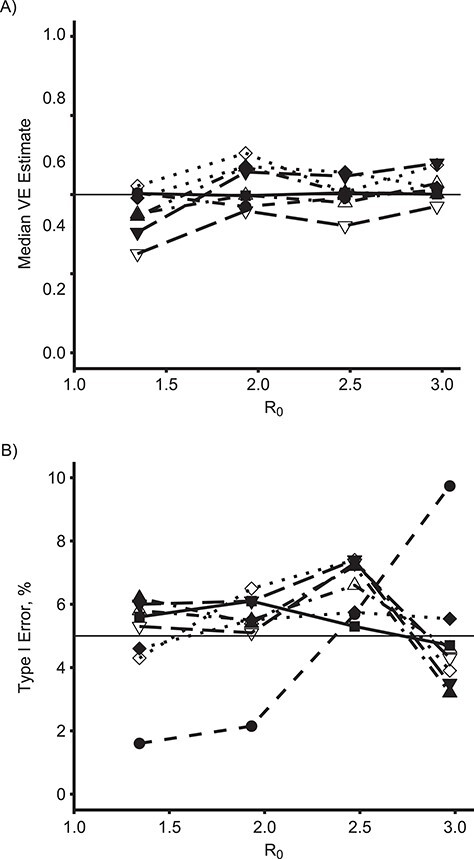
Estimates and type I error by basic reproduction number, R₀, and model for an analysis of vaccine efficacy (VE) in an outbreak setting for direct VE of 0. Median VE estimate (A) and empirical type I error (B) for direct VE of 0 (horizontal line in (A)) versus R₀, for individually randomized trial (IRT) analyzed with stratified Cox model (squares, solid line), cluster-randomized trial (CRT) analyzed with a Cox model with a gamma-distributed shared frailty (circles, dashed line), and stepped wedge trials with 4 clusters crossing over every 28 days (SWT-A, filled points) and with 1 cluster crossing over every 7 days (SWT-B, unfilled points) analyzed by a Cox model with a gamma-distributed shared frailty (SWT-PH; diamonds, dotted line), nonparametric within-period method weighted across periods by total case count (NPWP-2; upward triangle, dash-dotted line), and synthetic control method equally weighted across clusters and weighted across periods by total case count (SC-2; downward triangle, long-dash line). The horizontal line in (B) denotes the nominal type I error of 5%.

Time-varying vaccine effects and weighting of vertical SWT methods

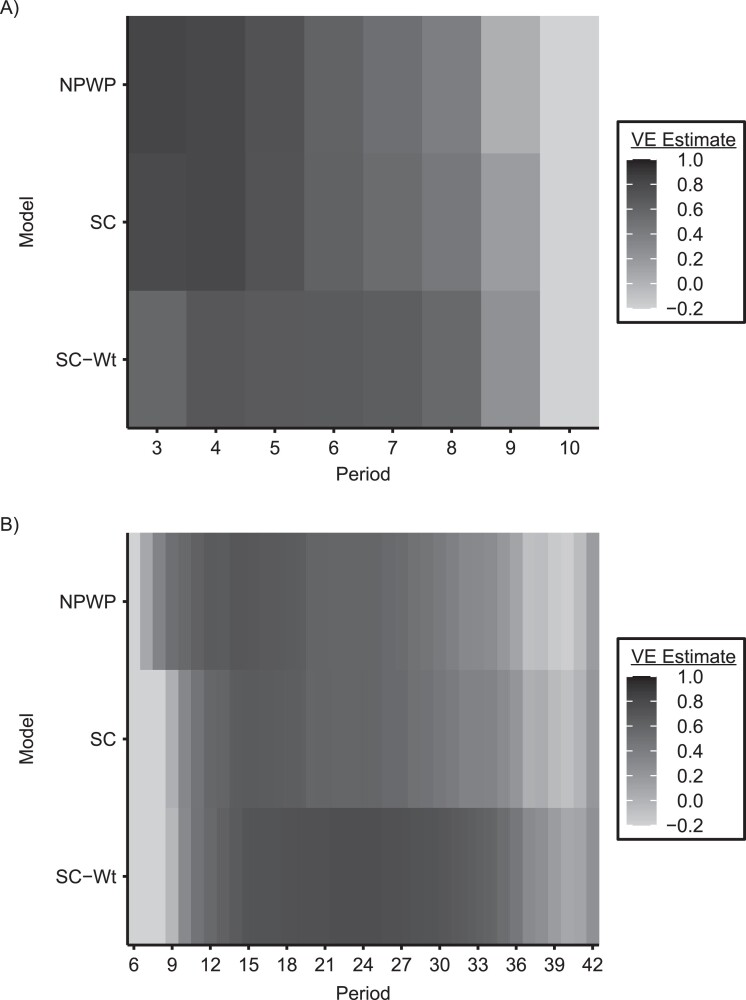
The vertical methods for analysis of SWTs allow the investigator to specify the weighting across periods and, to some extent, clusters in the study. These choices can have a substantial effect on the overall estimated effect, as well as the power of the analysis. Figure 6 displays the estimated period-specific treatment effect (on the VE scale) for SWT-A (Figure 6A) and SWT-B (Figure 6B), analyzed by NPWP, SC, and SC-Wt. In both panels, for all 3 methods, there is a clear trend of maximum effect estimate early in the trial (although not at the very beginning for SWT-B) and a declining effect as the trial continues. For SWT-B, the negative effect estimates early in the trial are likely due to the very small number of clusters on intervention at that point, which can lead to a few simulations with a high number of early cases in those clusters having a big effect on the averages presented here. Later in the trial, clusters that were on control throughout are more likely to have exhausted the susceptible population than clusters already intervened-upon, leading to lower incidence in the control clusters than the intervention clusters at that point.

Figure 6.

Period-specific estimates by period and model for an analysis of vaccine efficacy (VE) in an outbreak setting. Average period-specific VE estimate by period for stepped wedge trials with 4 clusters crossing over every 28 days (SWT-A) (A) and 1 cluster crossing over every 7 days (SWT-B) (B) with VE = 0.6 and a basic reproduction number, R₀, of 2.47, analyzed by nonparametric within-period method (NPWP), synthetic control (SC) method weighted equally across clusters, and SC method weighted across clusters by inverse mean square prediction error (SC-Wt). Values less than −0.2 are truncated to −0.2 for legibility.

DISCUSSION

The statistical performance of the SWT analysis methods considered here in simulated outbreaks highlights the drawbacks of the SWT design for the assessment of vaccines and other preventive measures during infectious disease outbreaks. Because of the high spatiotemporal variance of outbreaks, asymptotic inference on MEM or PH models of SWTs might have greatly inflated type I error. This is especially true when the outbreak has a high R₀, resulting in rapid spread within communities. And while permutation inference of purely vertical analysis methods (like the NPWP method and SC methods) or of PH models can preserve type I error, they have greatly reduced power compared with analysis methods for other trial designs.

The time trend in the number of intervention and control clusters removes the overall exchangeability of the intervention and control groups in an SWT and results in time-dependent cluster-level intervention effects. The flattening of the epidemic curve due to the intervention leads to an apparent decreased effectiveness of the intervention in later periods—the intervention clusters still have more remaining susceptible individuals than the control clusters. The existence of a contrast is also dependent on the timing of the crossovers relative to the outbreak onset. If the crossovers occur too early, before the onset, then there will be few events in the control condition. If the crossovers occur too late, after the outbreaks have passed, then there will be few events in the intervention condition. Either result will reduce power and lead to potential bias from the handling of cluster periods with zero cases. These timing effects weaken a key advantage of randomization: that it ensures comparability between the 2 groups (3).

Results of an SWT will thus be inherently limited by the duration and timing of the trial, decreasing the generalizability of these results. Additionally, the results of these vertical analysis methods are very dependent on the weighting scheme used to combine period-specific estimates and on the period length. It might be difficult to select the optimal weighting method a priori because it likely depends on the temporal variation of incidence in the setting under study, leading to more researcher degrees of freedom in the analysis. While the design might provide useful information on the relative effects of intervening at different points in the outbreak, it provides less clear evidence on the overall efficacy of the intervention, and the generalizability of the results might suffer. More research is needed to understand the trends in the estimated effect and power to detect an effect as the timing and duration of a CRT or SWT vary.

The NPWP and SC methods also allow investigators to consider VE on other scales, such as the risk difference scale (22, 23). These results might be of interest to policy makers and might be better suited to settings with very few outcomes in the intervention arm. In particular, when the VE is close to 1, and thus few cases are likely to occur in the intervention arm, the log-link methods used here to handle zero-case periods might bias the results toward the null, and another approach should be used.

These simulated results focus narrowly on the statistical properties of the design. The ethical concerns, including the effect on trial participants and the speed with which a conclusion is reached, are also crucial considerations (3, 7, 30, 31). In addition, the logistics of implementing the intervention might limit the choices available to trial designers. However, these issues might be better solved with risk prioritization in IRT or parallel-arm CRT designs rather than SWTs (14, 30, 31). All of these factors should be considered and appropriately weighed when designing a trial.

Further research is needed to clarify the relative advantages of various designs and analysis methods when a trial starts at different points relative to the outbreak curve. In addition, future work could consider methods to determine the relative benefits of beginning and ending interventions at different points. The stepped wedge design could be useful for that purpose, given that it can provide information on the time trends in intervention effectiveness, but other designs might be valuable for this purpose as well.

In conclusion, we have shown in simulated outbreaks that, while permutation inference on proportional hazards models and vertical methods to analyze SWTs can preserve type I error and provide valid effect estimates, they are less powerful than parallel-arm CRT designs, which are themselves less powerful than IRT designs. Given the primary purpose of a randomized trial to demonstrate efficacy of the intervention, SWTs have serious statistical disadvantages compared with these other 2 designs for evaluating vaccines during infectious disease outbreaks.