Abstract
The V(DD)J recombination is currently viewed as an aberrant and inconsequential variant of the canonical V(D)J recombination. Moreover, since the classical 12/23 rule for the V(D)J recombination fails to explain the V(DD)J recombination, the molecular mechanism of tandem D-D fusions has remained unknown since they were discovered three decades ago. Revealing this mechanism is a biomedically important goal since tandem fusions contribute to broadly neutralizing antibodies with ultralong CDR3s. We reveal previously overlooked cryptic nonamers in the recombination signal sequences of human IGHD genes and demonstrate that these nonamers explain the vast majority of tandem fusions in human repertoires. We further reveal large clonal lineages formed by tandem fusions in antigen-stimulated immunosequencing data sets, suggesting that such data sets contain many more tandem fusions than previously thought and that about a quarter of large clonal lineages with unusually long CDR3s are generated through tandem fusions. Finally, we developed the SEARCH-D algorithm for identifying D genes in mammalian genomes and applied it to the recently completed Vertebrate Genomes Project assemblies, nearly doubling the number of mammalian species with known D genes. Our analysis revealed cryptic nonamers in RSSs of many mammalian genomes, thus demonstrating that the V(DD)J recombination is not a “bug” but an important feature preserved throughout mammalian evolution.
The VDJ recombination of the IGH locus is guided by the recombination signal sequences (RSSs) that flank immunoglobulin genes. Each RSS consists of a conserved heptamer followed by a nonconserved spacer (12-nt-long 12-spacer in IGHD genes and 23-nt-long 23-spacer in IGHV and IGHJ genes) and a conserved nonamer. Each IGHV gene has a 23-spacer in its “right” RSS, each IGHJ gene has a 23-spacer in its “left” RSS, and each IGHD gene is flanked by the left and right RSSs, each containing a 12-spacer (Fig. 1A).
Figure 1.
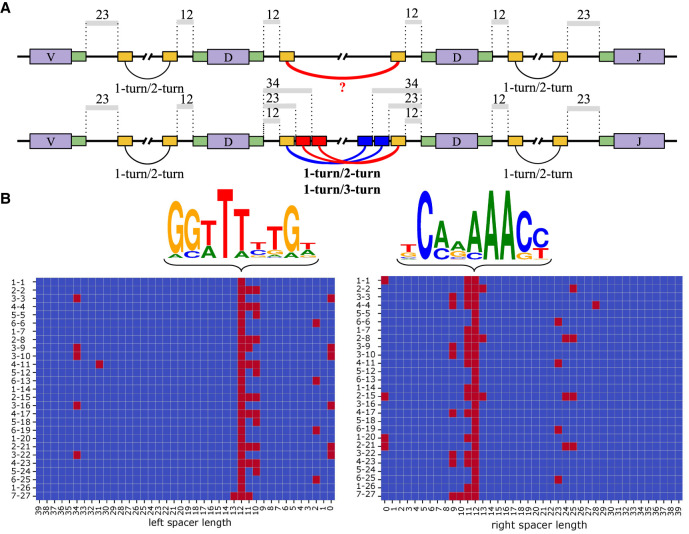
Cryptic nonamers explain V(DD)J recombination via the 1-turn/2-turn and 1-turn/3-turn mechanisms. (A) Canonical heptamers and nonamers in RSSs are shown by green and yellow rectangles, respectively. The 12/23 rule (1-turn/2-turn) explains the V-D and D-J recombination but fails to explain the D-D recombination using canonical nonamers (upper row). Cryptic nonamers (shown as red and blue rectangles) enable both the canonical 12/23 rule and the alternative 12/34 mechanism (1-turn/3-turn) and explain the V(DD)J recombination (lower row). (B) The left and right figures correspond to nonamers in the left and right RSSs. Sequence logos for canonical nonamers with 12-spacers for the human IGHD genes. Cryptic nonamers (with spacers shorter than 40 nt) in the RSSs of all 27 human D genes. D genes are shown on the left and are ordered according to the order in the IGHD locus. Canonical and cryptic nonamers (with likelihoods exceeding minLikelihood) are shown as red cells.
During the VDJ recombination, the 12-spacer in an RSS for a D gene and the 23-spacer in an RSS for a V/J gene are bound by the RAG protein complex that catalyzes recombination between these genes (McBlane et al. 1995). This interaction of 12- and 23–spacers represents the critical control point in V(D)J recombination and is called the 12/23 rule (Tonegawa 1983; van Gent et al. 1996; Hiom and Gellert 1998). Since the DNA helix makes a full turn each 10 ± 2 nt (Levitt 1978), the 12/23 rule explains recombination of V-D and D-J genes using the correspondence between one and two turns of DNA helix during VDJ recombination.
Meek et al. (1989) showed that spacers might vary in length by 1 and even 2 nucleotides without losing the ability to recombine. Ramsden et al. (1996) conducted experimental analysis of many more spacer lengths to answer the question whether the 12/23 rule can be extended to a 12/N pattern for N ≠ 22–24. It turned out 12/34 is the only other pattern that also enables the V(D)J recombination (albeit with smaller efficiency). Since a 34-nt-long spacer (referred to as 34-spacer) corresponds to three turns of a DNA helix, Ramsden et al. (1996) concluded that the protein complex can enable V(D)J recombination only if the heptamer and nonamer are separated by spacers according to the helical phase. We thus refer to 12/23 and 12/34 recombinations as 1-turn/2-turn and 1-turn/3-turn.
Although the 12/23 rule explains the mechanism of VDJ recombination, tandem V(DD)J recombination (also known as tandem fusion) represents an exception to this rule (Parkinson et al. 2015). The question about the molecular mechanism leading to tandem fusions of D genes has remained opened since the discovery of tandem fusions thirty years ago (Meek et al. 1989). Moreover, it remains unclear why some pairs of D genes form tandem fusions, but others do not.
These questions are important since tandem fusions often result in long (at least 24 amino acids long) and ultralong CDR3s (at least 28 amino acids long) as defined by Briney et al. (2012b). These CDR3s are sufficiently longer than typical CDR3s with average length of 16 amino acids: there are only 3.5% (0.4%) B cells with long (ultralong) CDR3s in the naive B cell population (Briney et al. 2012b). Since long CDR3s, although rare, are selected to target conserved epitopes in deep and obscured regions of the HIV-1 envelope, they are found in broadly neutralizing antibodies (bnAbs) against HIV-1 (Burton et al. 2012; Yu and Guan 2014). Thus, it is important to evaluate how tandem fusions contribute to long CDR3s and elucidate the molecular mechanism of their formation.
Previous attempts to analyze V(DD)J recombination faced the challenge of generating a large data set of tandem fusions since there was no software for identifying tandem fusions in immunosequencing data sets. Yu and Guan (2014) noted that it is a computational challenge to accurately identify tandem fusions in highly mutated memory B cells. As a result, the extent of contribution of tandem fusions to long CDR3s in antigen-stimulated antibody repertoires remains largely unknown. For example, since the bnAbs exhibit extensive hypermutation that make it virtually impossible to accurately match the germline D gene segments, Yu and Guan (2014) provided only one example of a bnAb formed by a tandem fusion. Also, even though Janeway's Immunobiology (Murphy et al. 2016) acknowledges that V(DD)J recombination is the major mechanism accounting for unusually long CDR3 loops, previous studies of tandem fusions (Briney et al. 2012a; Larimore et al. 2012; Safonova and Pevzner 2019a) were largely limited to naive repertoires due to difficulties of identifying tandem fusions in antigen-stimulated repertoires.
We identify previously overlooked cryptic nonamers with 23- and 34-spacers in RSSs of immunoglobulin D genes and analyze their associations with the tandem fusions of these genes revealed by the recently developed IgScout tool (Safonova and Pevzner 2019a) for identifying tandem fusions. We formulate a Cryptic Nonamers Hypothesis that tandem fusions are explained by these cryptic nonamers and test this hypothesis using multiple statistical tests that return P-values as low as 10−13. Our analysis reveals that cryptic nonamers enable tandem fusions via the canonical 1-turn/2-turn recombinations, complemented by the alternative (albeit less frequent) 1-turn/3-turn recombinations (Fig. 1A).
Results
Identifying tandem fusions in immunosequencing data sets
We analyzed three immunosequencing data sets described in Supplemental Table S1 and referred to as ALLERGY, INTESTINAL, and MOUSE data sets. To reveal tandem fusions, we launched the IgScout tool (Safonova and Pevzner 2019a) on these data sets. In the case of the ALLERGY data set (Levin et al. 2017), IgScout with a stringent parameter k–mer–size = 15 identified 1715 distinct CDR3s formed by tandem fusions (estimated false discovery rate 0.8%). IgScout computes the usage of each D gene (denoted as usage[D]) and tandem usage of each pair of genes D and D* (denoted as usage[D, D*]). A D gene is called commonly used if its usage exceeds minUsage (the default value is 2%). For each pair of genes D and D*, we compute the tandem coefficient coeff(D, D*), defined as usage(D, D*) divided by usage(D) × usage(D*). Genes D and D* are called coupled if coeff(D, D*) exceeds a threshold minCoefficient (the default value 1.3).
Canonical and cryptic nonamers in RSSs of human IGHD genes
We analyzed the RSSs of all human IGHD genes in the reference human genome (version GRCh38.p13). We distinguish between the right RSS (following a D gene in the reference genome) and the left RSS (preceding a D gene in the reference genome). Given an RSS of an IGHD gene, we refer to the nonamer with 12-spacer in this RSS as the canonical nonamer.
We extracted all canonical nonamers from the right RSSs and computed their 4 × 9 profile matrix ProfileRIGHT (with pseudocounts) and their consensus TCAAAAACC (Fig. 1B). Nagawa et al. (1998) demonstrated that changing nucleotides AAA at positions 5–7 significantly reduces the frequency of V(D)J recombinations. To penalize nonamers that differ from AAA at positions 5–7, we assigned smaller pseudocounts 0.001 to these three positions and larger pseudocounts 1 to the other six positions while computing the profile. We refer to the positions in the profile matrix with information content above 0.75 as conserved positions (positions 2–3 and 5–9 for the canonical nonamers from the right RSSs) and define the conserved consensus –CA–AAACC as the consensus on these positions only.
The same procedure was applied to nonamers from the left RSSs resulting in the matrix ProfileLEFT, consensus GGTTTTTGT and the conserved consensus GGTTT–TG–. Similarly, we assigned pseudocounts 0.001 to conserved positions 3–5 corresponding to nucleotide TTT and pseudocounts 1 to the other six positions. The probability Prob(Consensus|Profile) that Profile generates the consensus string (referred to as Consensus) is 0.042 for the right nonamer (for Profile = ProfileRIGHT) and 0.058 for the left nonamer (for Profile = ProfileLEFT) (Fig. 1B).
Given a nonamer Pattern, we define its likelihood as Prob(Pattern|Profile)/Prob(Consensus|Profile). The likelihoods of the canonical nonamers in the RSSs of the IGHD genes vary by three orders of magnitude from 3 × 10−3 to 1. However, it is known that nonamers with even smaller likelihoods may also trigger the standard V(D)J recombination process (Lewis et al. 1997; Nagawa et al. 1998). For example, Nagawa et al. (1998) demonstrated that a nonamer ACAAAGACC (that is quite different from the consensus nonamer TCAAAAACC) with likelihood 7 × 10−6 can trigger V(D)J recombination via the conventional 12/23 rule, albeit with reduced efficiency. We thus classify a nonamer (with an arbitrary spacer) as cryptic if its likelihood exceeds a likelihood threshold minLikelihood. We set an even less stringent default value minLikelihood = 2 × 10−6 than the likelihood of ACAAAGACC analyzed by Nagawa et al. (1998). Only 3% (5%) of randomly generated nonamers are classified as cryptic for ProfileRIGHT (ProfileLEFT) for the default threshold.
Figure 1B shows all cryptic nonamers (with spacers of length below 40 nt) as red cells in the 27 × 40 matrices for the left and right RSS of all 27 human D genes. If cryptic nonamers represented nonconsequential statistical artifacts, we would expect them to be somewhat randomly distributed through these matrices. However, Figure 1B reveals a highly nonrandom distribution of cryptic nonamers. Below, we analyze this distribution and demonstrate that cryptic nonamers “explain” tandem fusions.
The Cryptic Nonamers Hypothesis
Briney et al. (2012a) showed that the order of D genes in tandem CDR3s follows the order of D genes in the immunoglobulin locus; that is, genes D and D* can form a tandem fusion only if D precedes D* in the immunoglobulin locus. The canonical 12/23 rule implies that a cryptic nonamer with a spacer of length 23 ± 1 in the right RSS of a gene D can recombine with the conventional nonamer (with a spacer of length 12 ± 1) in the left RSS of a gene D* that follows D in the IGH locus (Fig. 1A). Such cryptic nonamer can potentially explain a V(DD*)J recombination as an unusual three-step process that includes a standard D*-J recombination event, a nonstandard D-D* recombination event, and a standard D*-V recombination event that all use the canonical 12/23 rule. The alternative 12/34 mechanism implies that such V(DD*)J recombination can also be explained by a cryptic nonamer with a spacer of length 34 ± 1 in the right RSS of a gene D. The Cryptic Nonamers Hypothesis states (1) that a cryptic nonamer in the right RSS of a gene D (with 23-spacer or 34-spacer) enables tandem fusions of a gene D with each gene D* that follows D in the IGH locus and that (2) a cryptic nonamer in the left RSS of a gene D* (with 23-spacer or 34-spacer) enables tandem fusions of each gene D (that precedes D*) with D* (Fig. 1A).
The gene D2-15 has a cryptic nonamer aCTgCAAAC in the right RSS with a 24-spacer that coincides with the canonical consensus nonamer -CA-AAACC in four out of seven conserved positions (shown by uppercase letters). Such cryptic nonamers are known to enable the standard V(D)J recombination, albeit with reduced efficiency as compared to conventional nonamers with 12-spacers (Nagawa et al. 1998). We refer to the right (left) RSS of gene D2-15 as 2-15R (2-15L). According to the Cryptic Nonamers Hypothesis, this nonamer enables (D2-15, D*) fusions using the conventional nonamers with 12-spacer in the left RSSs of a gene D* that follow D2-15 in the IGH locus. Indeed, D2-15 forms tandem fusions with: D3-16 (27 tandem fusions, tandem coefficient 3.5); D4-17 (28, 6.0); D6-19 (58, 3.5); D1-20 (8, 17.6); D2-21 (37, 4.2); D3-22 (92, 2.5); D4-23 (4, 2.1); D5-24 (5, 2.0); and D1-26 (7, 2.2).
As another example, the gene D3-16 has a cryptic nonamer GGTTTccCc with a 34-spacer in the left RSS that coincides with the canonical conserved consensus nonamer GGTTT-G- in five out of six conserved positions (shown by uppercase letters). According to the Cryptic Nonamers Hypothesis, this nonamer enables (D*, D3–16) fusions using conventional nonamers in the right RSSs of D genes that precede D3–16 in the IGH locus. Indeed, the genes that precede D3–16 in the IGH locus form many tandem fusions with D3–16: D2–2 (7 tandem fusions, tandem coefficient 6.0); D3–3 (7, 1.0); D6–6 (13, 16.2); D1–7 (3, 14.7); D2–8 (4, 3.7); D3–9 (8, 1.9); D3–10 (17, 2.0); D5–12 (13, 9.3); and D2–15 (27, 3.5).
Of course, the described cryptic nonamers in the RSSs of D2-15 and D3-16 may merely represent computational artifacts rather than a proof of the Cryptic Nonamers Hypothesis. Below, we provide statistical evidence in favor of this hypothesis that comes from three angles: the highly nonrandom distribution of spacers of cryptic nonamers in human RSSs; evolutionary conservation of cryptic nonamers with 23- and 34-spacers across many mammalian species; and the good correlation between the cryptic nonamers and the highly nonrandom structure of the fusion graph.
Fusion graph and fusion matrix
Given a subset of D genes, the fusion graph is a directed graph where each vertex corresponds to a gene in this subset. Genes D and D* are connected by a directed edge (D, D*) if D precedes D* in the IGH locus and genes D and D* are coupled. The fusion matrix is defined as the adjacency matrix of the fusion graph.
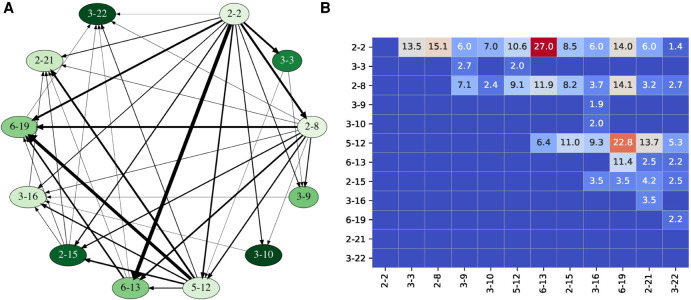
In the case when IgScout identifies very few tandem CDR3s formed by a pair of D genes, it is unclear whether these genes indeed have an ability to form tandem fusion or whether their tandem fusions represent false positives (Safonova and Pevzner 2019a). To minimize the influence of false positives reported by IgScout, we limit attention to commonly used D genes. There are 12 such D genes: D2–2, D3–3, D2–8, D3–9, D3–10, D5–12, D6–13, D2–15, D3–16, D6–19, D2–21, and D3–22. Figure 2 presents the fusion graph with 39 edges on these 12 vertices (Fig. 2A) as well as the fusion matrix (Fig. 2B).
Figure 2.
Fusion graph and fusion matrix for 12 D genes with at least 2% usage computed for the ALLERGY data set. (A) Vertices of the fusion graph are arranged clockwise along the circle according to the order in the IGHD locus, from D2-2 to D3-22. Vertices are colored according to the usage of the corresponding D genes: from pale (D2-8, usage 2.0%) to dark (D3-10, usage 15.5%). Each directed edge connects a vertex D with a vertex D*, where D* follows D in the IGHD locus. The width of an edge (D, D*) is proportional to coeff(D, D*). Only edges corresponding to coupled D genes are shown. (B) The matrix on the right shows values of coeff(D, D*) for fusions of the selected twelve commonly used IGHD genes, where genes D and D* correspond to rows and columns, respectively. Cells are colored according to the values of tandem coefficients: from low (dark blue) through medium (pale) to high (dark red).
Correlations between cryptic nonamers and edges of the fusion graph
Figure 2 reveals that the most-used genes D3-10 (usage 15.5%) and D2-15 (usage 14.2%) do not form tandem fusions with each other. However, this pattern is easy to explain in the framework of the Cryptic Nonamers Hypothesis since there are no cryptic nonamers in RSSs 3-10R and 2-15L among nonamers with all possible spacers of length 0 ≤ i < 40. We refer to a nonamer as turning if its spacer falls in the range 0–2 bp (0–turn spacer), 11–13 bp (1–turn spacer), 21–25 bp (2–turn spacer), and 34 bp (3–turn spacer).
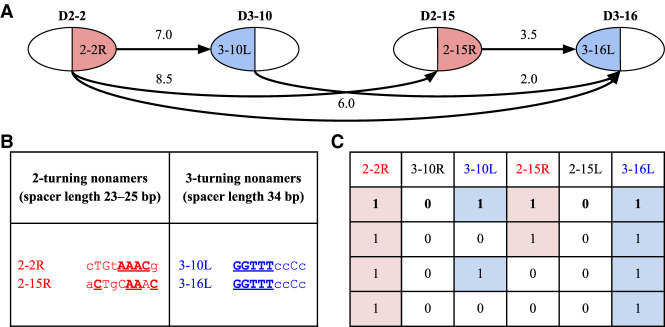
On the other hand, moderately used genes D2–2 (usage 2.1%) and D3–16 (usage 3.2%) form tandem fusion (D2–2, D3–16) with a large tandem coefficient coeff(D2–2, D3–16) = 6.0. Gene D2–2 further forms fusions with D3–10, D2–15, and D3–16, gene D3–10 does not form fusions with D2–15 but forms fusions with D3–16, and gene D2–15 forms fusions with D3-16. This intricate pattern can be explained by the Cryptic Nonamers Hypothesis if there exist 2- or 3-turning cryptic nonamers in 2–2R and 3–16L but no 2- or 3–turning cryptic nonamers in 3–10R and 2–15L (2- or 3-turning cryptic nonamers may or may not exist in 3–10L and 2–15R to explain the fusion graph on these four vertices) (Fig. 3A). It turned out that indeed there are turning cryptic nonamers in 2–2R and 3–16L and no cryptic nonamers (among all 40 positions that we consider) in 3-10R and 2-15L (Fig. 3B). Cryptic nonamers in 2-2R and 3-16L are the 2- and 3–turning, respectively.
Figure 3.
Fusion graph on genes D2–2, D3–10, D2–15, and D3–16 (A), cryptic nonamers in RSSs of these genes that explain this graph (B), and four optimal configurations for this graph (C). (A) Fusion graph on genes D2–2, D3–10, D2–15, and D3–16. Each cryptic nonamer is shown as either a blue left half-vertex or a red right half-vertex of the corresponding vertex in the fusion graph. Edges represent tandem fusions and are labeled with the tandem coefficient for the corresponding fusion. The edge between D3–10 and D2–15 is not shown since these genes do not form tandem fusions. (B) The table shows that all cryptic nonamers in RSSs of genes D2-2, D3-10, D2-15, and D3–16, found among the top 12 nonamers, correspond to 2- and 3-turning nonamers; 2- and 3-turning cryptic nonamers explain all edges of the fusion graph and do not “trigger” any other edges. Conserved positions in these nonamers are shown by uppercase letters. Positions coinciding with the consensus sequence of the canonical nonamers are bolded and underlined. (C) The table shows four optimal configurations of cryptic RSSs (i.e., configurations explaining all edges of the fusion graph) for the fusion graph on genes D2-2, D3-10, D2-15, and D3-16. Each configuration is shown as a binary vector, where 1 (0) means that the corresponding cryptic nonamer forms (does not form) tandem fusions.
Generating a ranked list of cryptic nonamers
After excluding the left RSS of D2-2 and the right RSS of D3-16 (that do not contribute to the formation of tandem fusions between the selected four D genes), we are left with six RSSs: right RSS of D2-2, D3-10, and D2-15, and left RSS of D3-10, D2-15, and D3-16. To analyze cryptic nonamers in these six RSSs, we arrange all nonamers for all spacer length 0 ≤ i < 40 in the decreasing order of their likelihoods. Since the canonical nonamer motifs are self-overlapping, the shadow nonamers of canonical nonamers (i.e., nonamers positioned within 1–2 nt from the canonical nonamers with 12-spacers) tend to have relatively high likelihoods. We thus remove a nonamer from the ranked list if it is positioned within 1–2 nt from a higher-ranked nonamer in the list. Since the canonical nonamers typically have high likelihoods, their shadows are sometimes even larger than 1–2 nt. We thus assume that the shadow of a canonical nonamers with 12-spacer spans spacers of length from 9 to 13.
In addition to the six canonical nonamers with 12-spacers in these RSSs that dominate the resulting ranked list (with likelihoods varying from 0.003 to 1), we analyzed six more cryptic nonamers with the highest likelihoods in these regions among nonamers with all possible spacers. All these highest-ranked cryptic nonamers represent turning nonamers with spacers corresponding to 0, 2, or 3 turns of the DNA helix (Fig. 3B). The likelihoods of these nonamers vary from 7 × 10−6 to 4 × 10−4. Although these likelihoods are rather low, some canonical nonamers with standard 12-spacers also have rather low likelihoods; for example, the nonamer GGTTTGAAG of the second most used gene D3–22 (usage 15.3%) has likelihood of only 3 × 10−3. The P-value that all top six cryptic nonamers are turning is 0.2576= 0.0003 since only nine out of 35 (25.7%) possible spacers (from 0 to 39, excluding the 9–13 shadow for canonical nonamers) correspond to 0-, 2-, and 3-turning cryptic nonamers.
Configurations
For a four-vertex fusion graph corresponding to four considered D genes, there are 4 × 2–2 = 6 RSSs that may contribute to tandem fusions of these genes (we ignore cryptic nonamers in 2-2L and 3-16R since they have no effect on the edges of the fusion graph) depending on whether there exists a cryptic nonamer in the corresponding RSS. It results in 26= 64 possible configurations, each configuration represented by a binary 6-mer vector. It turned out that only four out of 64 configurations “explain” all edges of the fusion graph shown in Figure 3A and do not create any false edges (P-value = 4/64 = 0.0625). These four configurations are formed by 6-mer vectors with 1s at positions 2–2R and 3–16L (Fig. 3C). Cryptic nonamers in RSSs 3–10L and 2–15R are present in the first of the four optimal configurations shown in Figure 3C.
Of course, this statistical analysis needs to be extended from just four D genes to all 12 commonly used human D genes. Below, we demonstrate that all cryptic nonamers in these twelve D genes represent turning nonamers (P-value = 10−13) and that these turning nonamers “explain” the structure of the fusion graph (P-value = 0.0003).
Cryptic nonamers in RSSs of D genes
We are interested in 11 right RSSs (for all 12 commonly used D genes but the last one) and 11 left RSSs (for all 12 of these D genes but the first one). In addition to the 22 canonical nonamers with 12-spacers in these RSSs (with likelihoods varying from 3 × 10−3 to 1), we analyzed 22 more cryptic nonamers with the highest likelihoods in these RSSs among nonamers with all possible spacers. We arrange all nonamers for spacer length 0 ≤ i < 40 in the decreasing order of their likelihoods and remove shadow nonamers from the resulting ranked list as described above. As expected, 22 canonical nonamers with 12-spacers dominate the ranked list. The next 22 highest-ranked cryptic nonamers in this list represent turning nonamers with spacers corresponding to 0, 2, or 3 turns of the DNA helix (Fig. 4A). The likelihoods of these nonamers vary from 2 × 10−6 to 4 × 10−4 (minLikelihood threshold = 1.9 × 10−6). The P–value that top 10 + 7+5 = 22 cryptic nonamers are turning is 0.25722= 10−13 since only 25.7% of all possible spacers (from 0 to 39) correspond to 0-, 2-, and 3-turning nonamers, respectively.
Figure 4.
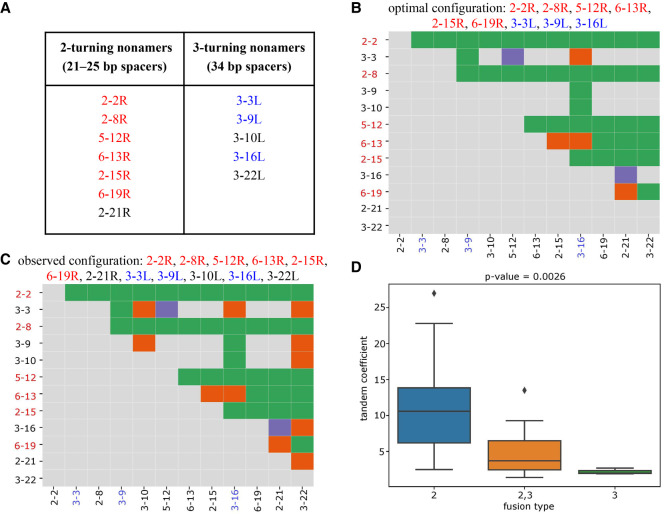
RSSs with cryptic nonamers corresponding to 2- and 3-turn spacers explain the fusion graph in Figure 2A. (A) 2- and 3-turning nonamers that “explain” the fusion graph in Figure 2A are highlighted in red and blue, respectively. (B,C) The fusion matrices with each cell classified as explained (green), unexplained (purple), or false (orange) based on the optimal configuration with nine (6 left + 3 right) cryptic nonamers (B) and the observed configuration with 12 (7 left + 5 right) cryptic nonamers (C). A D gene on the y-axis (x-axis) is colored red (blue) if its right (left) RSS contributes to the optimal configuration. (D) Each tandem fusion in Figure 2 is classified by the number of turns in cryptic nonamers that can explain it. For example, the fusion (D2-2, D3-3) can be explained by both 2–turning and 3–turning nonamers and thus is classified as “2,3 fusion type.” In total, we generate three groups: “2” (fusions are explained by the 2–turning nonamers), “2,3” (fusions are explained either by the 2-turning or by the 3–turning nonamers), and “3” (fusions are explained by the 3-turning nonamers) with average values of tandem coefficients 10.7, 5.0, and 2.2, respectively. The y-axis shows tandem coefficients of tandem fusions. Group “2” has higher values of tandem coefficients that groups “2,3” and “3” (P-value = 0.0026 according to the one-way ANOVA test [Heiman 2001]).
Many of the 10 0-turning nonamers come from the same RSSs as 7 + 5 = 12 2–turning and 3–turning nonamers, a possible indication that they may play a similar role to the 2-turning cryptic nonamers in the canonical 12/23 rule and the 3-turning cryptic nonamers in the alternative 12/34 mechanism. However, since there are no experimental data suggesting that the 0/12 pattern enables V(D)J recombination and since it is unclear whether it is consistent with the structure of the RAG-RSS complex (Ru et al. 2015), we ignore 0-turning nonamers and instead investigate how well the remaining 12 cryptic nonamers (corresponding to 2-turns and 3-turns of a DNA helix) explain the fusion graph. The list of 12 2– and 3–turning nonamers is provided in Supplemental Table S2.
2- and 3-turning cryptic nonamers explain the fusion graph
As discussed above, all edges of the fusion graph on four genes (D2–2, D3–10, D2–15, and D3–16) are explained by the assumption that there are cryptic nonamers in 2–2R and 3–16L and no cryptic nonamers in 3–10R and 2–15L. For a graph on 12 vertices, there are 12 × 2 – 2 = 22 possible choices of whether there exists a cryptic nonamer in the corresponding 22 RSSs (we ignore the left RSS of the first commonly used D gene and the right RSS of the last commonly used D gene), resulting in 222 possible configurations. Each such configuration results in explained edges, unexplained edges, and false edges in the fusion graph. We score each configuration as follows:
For example, Figure 4B illustrates that the fusion graph in Figure 2A has 37 explained, two unexplained, and four false edges for a configuration 2–2R, 2–8R, 5–12R, 6–13R, 2–15R, 6–19R, 3–3L, 3–9L, and 3–16L with score 37–2–4 = 31. Our goal is to find maximum-scoring configurations among all 222 configurations. It turned out that eight configurations have the maximum score 31 for the fusion graph (found by exhaustive search), all configurations formed by 22-mer vectors with 1s at positions 2–2R, 2–8R, 5–12R, 6–13R, 2–15R, 6–19R, 3–9L, and 3–16L (Supplemental Table S3). One more nonamer 3–3L is present in four out of eight optimal configurations. The optimal configuration shown in the top row of Supplemental Table S3 is formed by nine cryptic nonamers 2–2R, 2–8R, 5–12R, 6–13R, 2–15R, 6–19R, 3–3L, 3–9L, and 3–16L, and all these nonamers are present in the list of 12 cryptic nonamers in Figure 4A. The low P-value of this event (P–value = 0.0004) provides additional statistical support for the hypothesis that 2-turning and 3-turning cryptic nonamers enable tandem fusions.
Supplemental Figure S1 shows the distribution of scores of all 222 configurations. The 12 2- and 3–turning cryptic nonamers in Figure 4A (2–2R, 2–8R, 5–12R, 6–13R, 2–15R, 6–19R, 2–21R, 3–3L, 3–9L, 3–10L, 3–16L, and 3–22L) result in a configuration with score 24. Since there are only 1440 configurations with scores at least 24, the P-value of the configuration formed by these 12 nonamers is 1440/222= 0.0003. Even if we limit attention only to configurations with twelve 1s (C22,12 = 646,646 such configurations), only 238 of them have scores at least 24, resulting in a similar P-value 0.0004.
Although the 2- and 3-turning cryptic nonamers explain the vast majority of edges in the fusion graph (Fig. 4C), some edges remain unexplained. We note that even “ideal” heptamers and nonamers in an RSS do not guarantee that this RSS contributes to V(D)J recombinations, let alone V(DD)J recombinations (Supplemental Methods, “Analyzing correlation between the usage of D genes and the likelihoods of heptamers/nonamers in their RSSs”; Supplemental Figs. S3, S4). Indeed, although the spacer sequence is often viewed as nonconserved, mutations in this sequence are known to affect the efficiency of V(D)J recombination (Lee et al. 2003). We thus argue that the low P–value of the configuration formed by 2- and 3-turning nonamers provides a strong support for the Cryptic Nonamers Hypothesis even though it results in a (small) number of false and unexplained edges in the fusion graph.
Our analysis confirms that 34-spacers have reduced activity (as reported by Ramsden et al. 1996; Kim and Oettinger 1998) as compared to 12- and 23-spacers. Figure 4D illustrates that the 2-turning nonamers are associated with higher values of tandem coefficients than the 3-turning nonamers (P-value = 0.0026). The 3-turning nonamers alone explain only three tandem fusions—(D3-3, D3-9), (D3-9, D3-19), and (D3-10, D3-16)—describing 2.7%, 1.9%, and 2% of tandem CDR3s, respectively.
Tandem CDR3s in antigen-stimulated repertoires
To analyze tandem fusions in functional antibody repertoires, we applied IgScout to the INTESTINAL data set (Magri et al. 2017) and identified 72 distinct tandem CDR3s with false discovery rates 12.5%. Although the small number of identified tandem fusions and high false discovery rate make this data set not ideal for analyzing tandem fusions, Figure 5 illustrates two clonal trees that originated from tandem fusions—one of them (Fig. 5A) was automatically derived by IgScout with the default k-mer-size parameter (k-mer-size = 11) and another (Fig. 5B) was semimanually reconstructed by lowering the default k-mer-size parameter.
Figure 5.
Clonal trees derived from V(DD)J recombinations in the INTESTINAL data set. Two large clonal trees derived from tandem fusions of D2-15 with D5-24 (A) and D2-2 with D2-15 (B) genes in the INTESTINAL data set. Genes D2-15 (AGGATATTGTAGTGGTGGTAGCTGCTACTCC), D5-24 (GTAGAGATGGCTACAATTAC), and D2-2*01 (AGGATATTGTAGTAGTACCAGCTGCTATGCC) have length 31, 20, and 31 nt, respectively (substrings occurring in CDR3s are underlined). A clonal tree for each clonal lineage was constructed using the IgEvolution tool (Safonova and Pevzner 2019b) applied to all reads from these lineages. These clonal lineages originated from a V(DD)J recombination that resulted in long CDR3s of length 72 and 78 nt, respectively. For the tree in B, we showed 20 out of 131 CDR3s. Blue, orange, and green vertices represent sequences of IgA memory, IgA plasma, and IgM plasma B cells, respectively. Violet vertices represent sequences found in both plasma and memory B cells. Alignments of CDR3s corresponding to the lineages are shown below the trees: green/red substrings correspond to fragments of D2-15/D5-24 genes in A and D2-2/D2-15 in B, respectively. Somatic hypermutations in green and red substrings are shown in blue. Plus and minus signs before each sequence in the alignment of the CDR3s in A indicates whether IgScout identified it as a tandem CDR3 or not (with the default k-mer-size parameter). CDR3s in B were semimanually annotated, as IgScout (with the default k-mer-size parameter) failed to identify them as tandem.
Figure 5 illustrates that some of the identified tandem CDR3s correspond to large clonal lineages that were subjected to selection. The alignment of all CDR3 from each clonal lineage reveals that highly mutated tandem CDR3s are often difficult to classify as tandem, thus demonstrating that IgScout has a high false negative rate in the case of highly mutated antigen-stimulated repertoires for the parameter k-mer-size = 11.
We classify a clonal tree (lineage) as large if it contains at least minLineageSize sequences (the default value minLineageSize = 30). IgEvolution (Safonova and Pevzner 2019b) constructed 157 large clonal trees with long CDR3s in the INTESTINAL data set (Supplemental Fig. S2). We classify a clonal tree as tandem if IgScout classifies CDR3 in one of its vertices as a tandem fusion. IgScout classified 22 out of 157 (14%) large clonal trees with long CDR3s as tandem for the k-mer-size = 11 parameter. The percentage of long CDR3 resulting from tandem fusions in naive data sets (among all long CDR3s) is only ≈1% (Safonova and Pevzner 2019a), an order of magnitude smaller than the percentage of large tandem clonal trees with long CDR3s in antigen-stimulated repertoires. This large increase indicates that tandem fusions may play an important role in immune response.
Since IgScout has a high false negative rate (estimated at 39% for the clonal tree on the top in Fig. 5), there may be even more tandem clonal trees that IgScout missed; for example, decreasing the default k-mer-size parameter to a less stringent k-mer-size = 10 reduces the false negative rate but increases the false discovery rate from 12.5% to 29%. IgScout with k-mer-size = 10 identified 40 out of 157 (25%) large tandem clonal trees with long CDR3s.
Analyzing mammalian IGHD genes
Since the highly repetitive IGH locus is difficult to assemble (Watson et al. 2013), there are very few high-quality assemblies of this locus across mammalian species. Moreover, it is unclear how to infer short D genes (that are highly variable across mammalian species) even in the case when the IGH locus is well assembled (Merelli et al. 2010). For example, the alpaca IGH locus was assembled using cosmid libraries and physical mapping (Achour et al. 2008), but D genes in this locus were annotated using a heuristic that undoubtedly generates some false positives and false negatives. We thus addressed the problem of identifying the contig(s) containing IGHD genes in mammalian assemblies and predicting D genes in these contigs.
We analyzed 17 mammalian species with high-quality draft assemblies recently generated by the Vertebrate Genome Project (VGP; https://vgp.github.io/genomeark/) (Rhie et al. 2020) and searched for a contig that contains all IGHD genes in each of these assemblies (see Methods). To analyze these contigs, we developed a SEARCH-D algorithm for de novo finding of IGHD genes and benchmarked it on the known human, mouse, rat, and cow IGHD genes (see Methods).
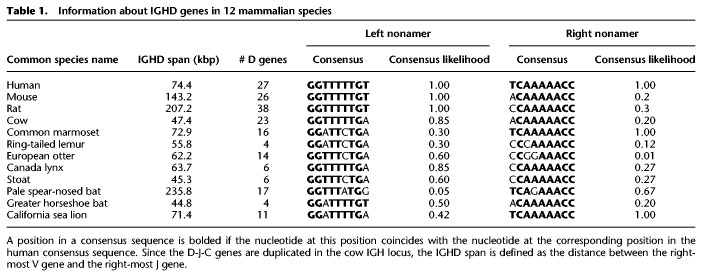
Since VGP assemblies remain fragmented, we did not find contigs that contain all IGHD genes in six out of 17 assemblies (Supplemental Table S4) and thus removed them from further consideration. We further applied SEARCH-D to the 11 remaining assemblies. To minimize the influence of possible misassemblies and false negatives of the SEARCH-D algorithm, we excluded the vaquita and Eurasian red squirrel genomes from further consideration since we identified a very low number of D genes (only three) in these two genomes. To minimize the influence of false positives of the SEARCH-D algorithm, we also excluded the gray squirrel genome from further consideration since the nonamer consensus likelihood for the RSSs in this genome was an order of magnitude smaller than for all other genomes. Table 1 summarizes information about the identified IGHD genes across the eight remaining VGP genomes as well as all genomes with previously sequenced IGHD locus (human, mouse, rat, and cow) and more than 20 identified IGHD genes. Sequences of found IGHD genes are listed in Supplemental Table S5.
Table 1.
Information about IGHD genes in 12 mammalian species
Analyzing cryptic nonamers in RSS of the IGHD genes across mammalian species
Since the consensus of canonical nonamers with 12-spacers is rather conserved across mammalian species (Table 1), we used the ProfileLEFT and ProfileRIGHT matrices (computed for the canonical human nonamers with 12-spacers) to analyze cryptic nonamers in eight mammalian species. For each D gene in each species, we analyze its left and right RSSs and compute the likelihood of each of 40 cryptic nonamers in this RSS as before (for spacers varying in length from 0 to 39 nt). For each species, we sort all nonamers from all D genes in the descending order of their likelihoods (across all RSSs), remove shadow nonamers, and analyze the top nonamers in the resulting ranked list with likelihood exceeding motifScore = 5 × 10−6. We increased the motifScore threshold as compared to the default value motifScore = 2 × 10−6 because ProfileLEFT and ProfileRIGHT, derived from the human genes, imperfectly represent nonamers in RSSs of nonhuman D genes. After removing canonical 1-turning nonamers, we analyze the remaining cryptic nonamers and compute the percentage of turning cryptic nonamers among them.
If turning cryptic nonamers represented computational artifacts rather than functional elements, we would expect that this percentage to be close to the fraction of 0-, 2-, and 3-turning nonamers among all analyzed nonamers (25.7%). It is important to keep in mind that cryptic nonamers in nonhuman species were identified based on the profile matrices derived from human conventional nonamers with 12-spacers. In the case of species with significantly different nonamers, this procedure may lead to false negatives in identifying cryptic nonamers. Nevertheless, we compared the fraction of turning cryptic nonamers in the resulting list with what is expected by chance (25.7%). For example, eight out of 15 (53%) cryptic nonamers for common marmoset (after removing shadow nonamers) represent 2- and 3-turning cryptic nonamers.
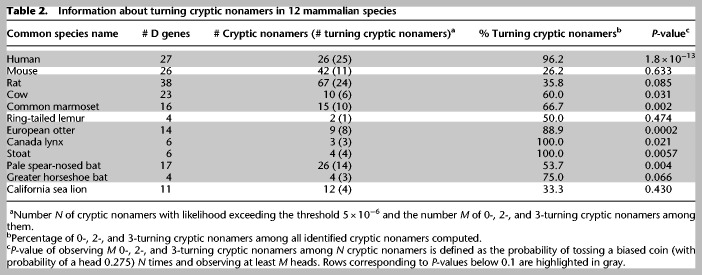
Table 2 shows that the percentage of 0-, 2-, and 3-turning cryptic nonamers exceeds 25.7% in all species, even though the increase is small for mouse and California sea lion. We note that the D gene usage is extremely biased in mice (with a single D gene responsible for over 80% usage and only two other genes with bias exceeding 2%), making it difficult to analyze tandem fusions in mice (see Supplemental Methods, “Challenge of analyzing tandem fusions in mouse Rep-Seq data sets”).
Table 2.
Information about turning cryptic nonamers in 12 mammalian species
Table 2 illustrates that, with the exception of mouse (P-value = 0.633), ring-tailed lemur (P-value = 0.474), and California sea lion (P-value = 0.430), P-values for other nine species do not exceed 0.1 (varying from 1.8 × 10−13 for human to 0.085 for rat), providing an additional support for the Cryptic Nonamers Hypothesis and suggesting that turning cryptic nonamers represent an evolutionarily conserved mechanism for generating antibodies with long CDR3s.
Tandem duplications in the IGHD locus
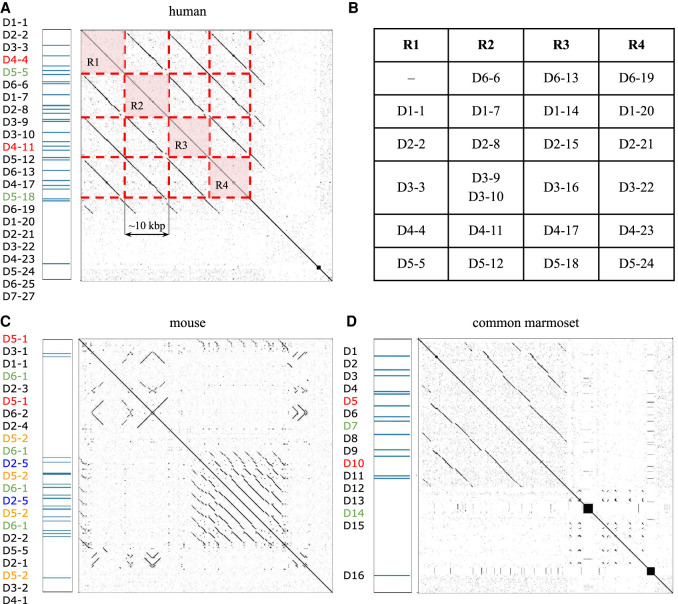
To understand the origin of cryptic turning nonamers, we analyze the repeat structure of the IGHD loci across multiple mammalian species listed in Table 1. Figure 6A presents the dot plot of the human IGHD region that reveals an ≈40-kbp-long tandem repeat R1-R2-R3-R4 of multiplicity four covering 24 out of 27 D genes. D genes in a single unit of this tandem repeat can be described by a pattern “D6-*, D1-*, D2-*, D3-*, D4-*, D5-*”, where Di-* is a D gene from the ith family (Fig. 6B). Copies R1 and R2 have small differences from the pattern: while R1 does not contain a gene from the D6 family, R2 contains duplicated genes D3-9 and D3-10 from the D3 family. Safonova and Pevzner (2019a) showed that these two D genes can be processed as a single D gene during the VDJ recombination, resulting in an ultralong CDR3. Figure 6, C and D, reveals similar structures of IGHD loci in the genomes of mouse and common marmoset, respectively.
Figure 6.
Tandem repeats in IGHD locus of human (A,B), mouse (C), and common marmoset (D) IGHD loci. Duplicated and identical IGHD genes are shown by the same (nonblack) color. Dot plots were generated by the Gepard tool (Krumsiek et al. 2007). (A) The dot plot shows that the 56-kbp-long human IGHD locus contains a tandem repeat R1-R2-R3-R4 covering 24 out of 27 IGHD genes. Positions of 27 IGHD genes are shown on the left. (B) The structure of units R1–R4. (C) For better resolution, we show only a 97-kbp-long fragment of the 1.1-Mbp-long mouse IGHD loci that covers 22 out of 26 IGHD genes. The shown fragment does not cover genes IGHD4–1, IGHD5–2, and IGHD1–3 that precede the first occurrence of IGHD5-1 (the first gene in the dot plot) and a copy of gene IGHD4-1 that follows IGHD4-1 (the last gene in the dot plot). (D) A dot plot shows the 47-kbp-long IGHD locus of the common marmoset.
In total, large tandem duplications contribute to the IGHD loci of eight out of 12 analyzed mammalian species: human, mouse, rat, cow, common marmoset, European otter, pale spear-nosed bat, and California sea lion. These species are characterized by a revlatively large number of identified IGHD genes, varying from 11 to 38. Figure 6 and Supplemental Figure S5 illustrate that most D genes in these species are concentrated in tandem repeats. However, units forming these tandem repeats are unique for a species, suggesting that tandem duplications of IGHD genes emerged independently in various mammalian lineages to increase the combinatorial diversity of V(D)J recombinations. Supplemental Figure S6 illustrates that nonamers at turning positions are more conserved than nonamers at nonturning positions, suggesting that nonamers corresponding to turning spacers may be subjected to selective pressure.
Four remaining species without tandem duplications in the IGHD loci (ring-tailed lemur, Canada lynx, stoat, and greater horseshoe bat) are characterized by a lower number of IGHD genes, varying from 4 to 6.
Discussion
Although the 12/23 rule explains the molecular mechanism of the standard V(D)J recombination, the mechanism of the V(DD)J recombination has remained unknown since tandem fusions were hypothesized in 1982 (Kurosawa and Tonegawa 1982) and experimentally confirmed in 1989 (Meek et al. 1989). Although recent studies demonstrated that tandem fusions represent a stable feature of antibody repertoires (Briney et al. 2012a; Safonova and Pevzner 2019a), their role in immune response remained unclear. Moreover, while some immunologists view V(DD)J recombination as the major mechanism for generating long CDR3s (Yu and Guan 2014), others consider it as simply a “bug” in the 12/23 rule or even an artifact (Corbett et al. 1997; Watson et al. 2006). We demonstrate that the V(DD)J recombination is not a “bug” but an important feature of immune response resulting in long CDR3s that contribute to large clonal lineages in antigen-stimulated repertoires.
In T cells, rather common tandem fusions occur in 2% of all recombinations (note that there are only two TRBD genes and three TRDD genes). Liu et al. (2014) demonstrated that tandem fusions of D genes in T cells are governed by the 12/23 rule and involve nonamers corresponding to 23-spacers in D genes (in addition to the conventional 12-spacers). Ma et al. (2016) demonstrated that the 12/23 rule also explains unusual VJ recombinations in T cells using nonamers corresponding to 12-spacers in V and J genes (in addition to the conventional 23-spacers). Our Cryptic Nonamers Hypothesis postulates that a similar 12/23 mechanism, complemented by the 12/34 mechanism, leads to tandem fusions in B cells. The likelihoods of the cryptic nonamers that support our Cryptic Nonamers Hypothesis in B cells are an order of magnitude higher than the likelihoods of nonamers (like AGAAACACT) that were shown to contribute to tandem fusions in T cells (Liu et al. 2014). This observation alleviates a concern that 2- and 3-turning cryptic nonamers may be too diverged (as compared to conventional 1-turning nonamers) to contribute to the RAG-RSS complex.
Kim and Oettinger (1998) demonstrated that two genes with 12-spacers can also be recombined by RAG proteins, albeit with low efficiency. However, the 12/12 mechanism cannot possibly explain tandem fusions since many D genes (even if each of them has a high usage) do not generate tandem fusions with each other. For example, genes D3-10 and D3-22, with the highest usage in CDR3s (average usage exceeds 15%), do not contribute to tandem fusions (Safonova and Pevzner 2019a).
Rommel et al. (2017) demonstrated that RAG proteins can perform insertions and deletions of fragments of the IGH locus flanked by RSSs with various orientations. However, this observation cannot serve as an alternative explanation of tandem fusions since Safonova and Pevzner (2019a) demonstrated the presence of inter-D insertions separating fragments of D genes in tandem CDR3s, indicating activity of the TdT protein. This proves that tandem fusions result from the V(DD)J recombination process.
We showed that tandem fusions in human B cells are governed by the standard 12/23 rule (through 2–turning cryptic nonamers) accompanied by the nonconventional yet experimentally verified 12/34 mechanism (involving 3–turning cryptic nonamers). We further developed and benchmarked the SEARCH-D algorithm for predicting D genes in assembled mammalian genomes. Using SEARCH-D, we revealed a statistically significant overrepresentation of turning cryptic nonamers across multiple mammalian species, suggesting that tandem fusions represent an evolutionarily conserved mechanism for generating antibodies with long CDR3s.
Methods
Identifying tandem fusions
We processed each Rep-Seq data set using the DiversityAnalyzer tool (Shlemov et al. 2017) to extract CDR3s and applied the IgScout tool (Safonova and Pevzner 2019a) to identify tandem CDR3s among all CDR3s. For each sequence in the Rep-Seq data set, DiversityAnalyzer also identified the V and J genes that gave rise to this sequence.
Constructing clonal trees
We classify two CDR3s as similar if they have the same length l and the Hamming distance between them falls below 0.1 × l. We launched the IgEvolution tool (Safonova and Pevzner 2019b) that groups all sequences with identical V and J genes and similar CDR3s into a single clonal lineage. For each clonal lineage, IgEvolution constructs a weighted graph with vertices corresponding to sequences in this clonal lineage. The weight of an edge in this graph is defined as the Hamming distance between the corresponding sequences. A clonal tree is constructed as a minimum spanning tree in this graph. The root of this clonal tree is selected as a sequence with the minimum number of differences from the closest germline V and J genes. Finally, we transform this (undirected) tree into a directed tree by orienting all edges from the root toward the leaves. In the INTESTINAL data set, we additionally combined Rep-Seq data sets corresponding to the same donor before constructing the clonal tree.
Analyzing the immunoglobulin loci in whole-genome assemblies
A contig in an assembly is classified as an IGH-contig if it aligns to at least one of the human IGHV, IGHJ, and IGHC genes. To identify all IGH-contigs in a draft assembly, we align all human immunoglobulin IGHV, IGHJ, and IGHC genes against all contigs in this assembly using Bowtie 2 (Langmead and Salzberg 2012). An IGH-contig is classified as an IGHD-contig if its prefix aligns to an IGHV gene and its suffix aligns to an IGHJ gene (or if this condition holds for the reverse-complement of this contig). Since the IGHD genes are located between the IGHV and IGHJ genes, we assume that an IGHD-contig contains all IGHD genes. We define the IGHD span as the distance from the end of the last V gene to the start of the first J gene in an IGHD-contig. For example, the IGHD span in the common marmoset genome is 72.9 kbp.
We searched for IGHD-contigs in 17 mammalian genomes assembled by the Vertebrate Genome Project (VGP; https://vgp.github.io/genomeark/) (Rhie et al. 2020). For 11 out of these species, we found a single contig that spans both IGHV and IGHJ genes and thus entirely covers all IGHD genes (Supplemental Table S4).
SEARCH-D algorithm: searching for IGHD genes in the IGHD-contigs
We analyzed all heptamers and canonical nonamers in the left and right RSSs of 27 human, 26 mouse, 38 rat, and 23 cow IGHD genes found in the reference IGHD loci of the corresponding species. For (more conserved) heptamers, we generated the set Heptamersleft (Heptamersright) of all 28 (30) distinct heptamers occurring in the left (right) RSSs of these four species. For (less conserved) nonamers, we computed the profile matrix of all canonical nonamers in the left RSSs of these species and the profile matrix of all canonical nonamers in the right RSSs of these species (as described in Results).
We classify a substring of an IGHD-contig as a putative left (putative right) heptamer if it coincides with a heptamer in Heptamersleft (Heptamersright). This procedure identifies 404 (350) putative left (right) heptamers in the IGHD contig of the common marmoset genome. We classify a putative left and a putative right heptamer as paired if the distance between them does not exceed the parameter maxDistance with the default value 40 nt (only seven D genes in the human, mouse, rat, and cow genomes have length exceeding 40 nt). We refer to a segment between the paired left and right putative heptamers as a D-gene candidate. There are 158 D-gene candidates in the common marmoset genome, but many of them likely represent false positives. To filter out false positives, we identified all canonical left and right nonamers with 12-spacers and computed their likelihoods using the corresponding profile matrices. If the likelihood of the left nonamer exceeds leftmin and the likelihood of the right nonamer exceeds rightmin, we report the corresponding D-gene candidate as an identified D gene if it has at least one open reading frame without stop codons. This algorithm, that we refer to as SEARCH-D, identified 16 D genes in the common marmoset genome. Below, we describe selection of parameters leftmin and rightmin.
Benchmarking SEARCH-D algorithm
To select the default leftmin (rightmin) threshold, we computed the distribution LP (RP) as likelihoods of all left (right) nonamers (computed using the corresponding left [right] profile). We set leftmin (rightmin) to the qth quantile of the distribution LP (RP), where q is a parameter. For each parameter q from 0 to 100, we launched SEARCH-D to predict human, mouse, rat, and cow IGHD genes based on their reference IGHD loci and computed sensitivity and precision values for the parameter q varying from 0 to 100. To optimize both sensitivity and precision, we computed their product. Since q = 30 maximizes the product of sensitivity and precision in all four species (Supplemental Fig. S7), we used the 30th quantile of LP and RP distributions as the default leftmin and rightmin thresholds. SEARCH-D with q = 30 identified 24 out of 27 human D genes with seven false positives, 10 out 26 mouse D genes (six false positives), 25 out of 38 rat D genes (five false positives), and eight out of 23 cow D genes (16 false positives). Large false positive and false negative rates of SEARCH-D illustrate the difficulties in identifying D genes even in well-assembled genomes and emphasize the need for more advanced machine learning methods for D gene identification. The only other tool for inferring D genes is the RSSsite tool that, however, was designed for RSS identification rather than D gene prediction (Merelli et al. 2010). RSSsite predicted 195, 831, 1983, and 480 RSSs with 12-spacers in human, mouse, rat, and cow IGHD loci, respectively. It results in a high false positive rate since it is not clear how to reliably identify D genes from the RSSsite output.
Software availability
SEARCH-D is available as Supplemental Code and at GitHub (https://github.com/Immunotools/SEARCH-D).
Competing interest statement
The authors declare no competing interests.
Supplementary Material
Acknowledgments
The work of Y.S. was supported by the American Association of Immunologists, AAI Intersect Fellowship 2019. The work of P.A.P. and Y.S. was supported by the National Institutes of Health 2-P41-GM103484PP and by National Science Foundation 2032783 grants.
Author contributions: Y.S. and P.A.P. conceived the study, developed the approach, designed the computational experiments, and wrote the manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.259598.119.
References
- Achour I, Cavelier P, Tichit M, Bouchier C, Lafaye P, Rougeon F. 2008. Tetrameric and homodimeric camelid igGs originate from the same IgH locus. J Immunology 181: 2001–2009. 10.4049/jimmunol.181.3.2001 [DOI] [PubMed] [Google Scholar]
- Briney BS, Willis JR, Hicar MD, Thomas JW, Crowe JE. 2012a. Frequency and genetic characterization of V(DD)J recombinants in the human peripheral blood antibody repertoire. Immunology 137: 56–64. 10.1111/j.1365-2567.2012.03605.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briney BS, Willis JR, Crowe JE Jr. 2012b. Human peripheral blood antibodies with long HCDR3s are established primarily at original recombination using a limited subset of germline genes. PLoS One 7: e36750 10.1371/journal.pone.0036750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton DR, Poignard P, Stanfield RL, Wilson IA. 2012. Broadly neutralizing antibodies present new prospects to counter highly antigenically diverse viruses. Science 337: 183–186. 10.1126/science.1225416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett SJ, Tomlinson IM, Sonnhammer EL, Buck D, Winter G. 1997. Sequence of the human immunoglobulin diversity (D) segment locus: A systematic analysis provides no evidence for the use of DIR segments, inverted D segments, “minor” D segments or D-D recombination. J Mol Biol 270: 587–597. 10.1006/jmbi.1997.1141 [DOI] [PubMed] [Google Scholar]
- Heiman GW. 2001. Understanding research methods and statistics: an integrated introduction for psychology, 2nd ed Houghton Mifflin, Boston. [Google Scholar]
- Hiom K, Gellert M. 1998. Assembly of a 12/23 paired signal complex: A critical control point in V(D)J recombination. Mol Cell 1: 1011–1019. 10.1016/S1097-2765(00)80101-X [DOI] [PubMed] [Google Scholar]
- Kim DR, Oettinger MA. 1998. Functional analysis of coordinated cleavage in V(D)J recombination. Mol Cell Biol 18: 4679–4688. 10.1128/MCB.18.8.4679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumsiek J, Arnold R, Rattei T. 2007. Gepard: a rapid and sensitive tool for creating dotplots on genome scale. Bioinformatics 23: 1026–1028. 10.1093/bioinformatics/btm039 [DOI] [PubMed] [Google Scholar]
- Kurosawa Y, Tonegawa S. 1982. Organization, structure, and assembly of immunoglobulin heavy chain diversity DNA segments. J Exp Med 155: 201–218. 10.1084/jem.155.1.201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Salzberg SL. 2012. Fast gapped-read alignment with Bowtie 2. Nat Methods 9: 357–359. 10.1038/nmeth.1923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larimore K, McCormick MW, Robins HS, Greenberg PD. 2012. Shaping of human germline IgH repertoires revealed by deep sequencing. J Immunol 189: 3221–3230. 10.4049/jimmunol.1201303 [DOI] [PubMed] [Google Scholar]
- Lee AI, Fugmann SD, Cowell LG, Ptaszek LM, Kelsoe G, Schatz DG. 2003. A functional analysis of the spacer of V(D)J recombination signal sequences. PLoS Biol 1: e1 10.1371/journal.pbio.0000001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin M, Levander F, Palmason R, Greiff L, Ohlin M. 2017. Antibody-encoding repertoires of bone marrow and peripheral blood-a focus on IgE. J Allergy Clin Immunol 139: 1026–1030. 10.1016/j.jaci.2016.06.040 [DOI] [PubMed] [Google Scholar]
- Levitt M. 1978. How many base-pairs per turn does DNA have in solution and in chromatin? Some theoretical calculations. Proc Natl Acad Sci 75: 640–644. 10.1073/pnas.75.2.640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis SM, Agard E, Suh S, Czyzyk L. 1997. Cryptic signals and the fidelity of V(D)J joining. Mol Cell Biol 17: 3125–3136. 10.1128/MCB.17.6.3125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P, Liu D, Yang X, Gao J, Chen Y, Xiao X, Liu F, Zou J, Wu J, Ma J, et al. 2014. Characterization of human αβTCR repertoire and discovery of D-D fusion in TCRβ chains. Protein Cell 5: 603–615. 10.1007/s13238-014-0060-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Yang L, Shi B, He X, Peng A, Li Y, Zhang T, Sun S, Ma R, Yao X. 2016. Analyzing the CDR3 repertoire with respect to TCR—beta chain V-D-J and V-J rearrangements in peripheral T cells using HTS. Sci Rep 6: 29544 10.1038/srep29544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magri G, Comerma L, Pybus M, Sintes J, Lligé D, Segura-Garzón D, Bascones S, Yeste A, Grasset EK, Gutzeit C, et al. 2017. Human secretory IgM emerges from plasma cells clonally related to gut memory B cells and targets highly diverse commensals. Immunity 47: 118–134.e8. 10.1016/j.immuni.2017.06.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McBlane JF, van Gent D, Ramsden DA, Romeo C, Cuomo CA, Gellert M, Oettinger MA. 1995. Cleavage at a V(D)J recombination signal requires only RAG1 and RAG2 proteins and occurs in two steps. Cell 83: 387–395. 10.1016/0092-8674(95)90116-7 [DOI] [PubMed] [Google Scholar]
- Meek KD, Hasemann CA, Capra DJ. 1989. Novel rearrangements at the immunoglobulin D locus. Inversions and fusions add to IgH somatic diversity. J Exp Med 170: 39–57. 10.1084/jem.170.1.39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merelli I, Guffanti A, Fabbri M, Cocito A, Furia L, Grazini U, Bonnal RJ, Milanesi L, McBlane F. 2010. RSSsite: a reference database and prediction tool for the identification of cryptic recombination signal sequences in human and murine genomes. Nucleic Acids Res 38: W262–W267. 10.1093/nar/gkq391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Travers P, Walport M, Janeway C. 2016. Immunobiology, 9th ed. Garland Science, New York. [Google Scholar]
- Nagawa F, Ishiguro KI, Tsuboi A, Yoshida T, Ishikawa A, Takemori T, Otsuka AJ, Sakano H. 1998. Footprint analysis of the RAG protein recombination signal sequence complex for V(D)J type recombination. Mol Cell Biol 18: 655–663. 10.1128/MCB.18.1.655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkinson NJ, Roddis M, Ferneyhough B, Zhang G, Marsden AJ, Maslau S, Sanchez-Pearson Y, Barthlott T, Humphreys IR, Ladell K, et al. 2015. Violation of the 12/23 rule of genomic V(D)J recombination is common in lymphocytes. Genome Res 25: 226–234. 10.1101/gr.179770.114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsden DA, McBlane JF, van Gent DC, Gellert M. 1996. Distinct DNA sequence and structure requirements for the two steps of V(D)J recombination signal cleavage. EMBO J 15: 3197–3206. 10.1002/j.1460-2075.1996.tb00682.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhie A, McCarthy SA, Fedrigo O, Damas J, Formenti G, Koren S, Uliano-Silva M, Chow W, Fungtammasan A, Gedman GL, et al. 2020. Towards complete and error-free genome assemblies of all vertebrate species. bioRxiv 10.1101/110833 [DOI] [PMC free article] [PubMed]
- Rommel PC, Oliveira TY, Nussenzweig MC, Robbiani DF. 2017. RAG1/2 induces genomic insertions by mobilizing DNA into RAG1/2-independent breaks. J Exp Med 214: 815–831. 10.1084/jem.20161638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ru H, Chambers MG, Fu TM, Tong AB, Liao M, Wu H. 2015. Molecular mechanism of V(D)J recombination from synaptic RAG1-RAG2 complex structures. Cell 163: 1138–1152. 10.1016/j.cell.2015.10.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safonova Y, Pevzner PA. 2019a. De novo inference of diversity genes and analysis of non-canonical V(DD)J recombination in immunoglobulins. Front Immunol 10: 987 10.3389/fimmu.2019.00987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safonova Y, Pevzner PA. 2019b. IgEvolution: clonal analysis of antibody repertoires. bioRxiv 10.1101/725424 [DOI]
- Shlemov A, Bankevich S, Bzikadze A, Turchaninova MA, Safonova Y, Pevzner PA. 2017. Reconstructing antibody repertoires from error-prone immunosequencing reads. J Immunol 199: 3369–3380. 10.4049/jimmunol.1700485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tonegawa S. 1983. Somatic generation of antibody diversity. Nature 302: 575–581. 10.1038/302575a0 [DOI] [PubMed] [Google Scholar]
- van Gent D, Ramsden D, Gellert M. 1996. The RAG1 and RAG2 proteins establish the 12/23 rule in V(D)J recombination. Cell 85: 107–113. 10.1016/S0092-8674(00)81086-7 [DOI] [PubMed] [Google Scholar]
- Watson LC, Moffatt-Blue CS, McDonald RZ, Kompfner E, Ait-Azzouzene D, Nemazee D, Theofilopoulos AN, Kono DH, Feeney AJ. 2006. Paucity of V-D-D-J rearrangements and VH replacement events in lupus prone and nonautoimmune TdT−/− and TdT+/+ mice. J Immunol 177: 1120–1128. 10.4049/jimmunol.177.2.1120 [DOI] [PubMed] [Google Scholar]
- Watson CT, Steinberg KM, Huddleston J, Warren RL, Malig M, Schein J, Willsey AJ, Joy JB, Scott JK, Graves TA, et al. 2013. Complete haplotype sequence of the human immunoglobulin heavy-chain variable, diversity, and joining genes and characterization of allelic and copy-number variation. AJHG 92: 530–546. 10.1016/j.ajhg.2013.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu L, Guan Y. 2014. Immunologic basis for long HCDR3s in broadly neutralizing antibodies against HIV-1. Front Immunol 5: 250 10.3389/fimmu.2014.00250 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.