Abstract
Recent studies have postulated that the human motor control system recruits groups of muscles through low-dimensional motor commands, or muscle synergies. This scheme simplifies the neural control problem associated with the high-dimensional structure of the neuromuscular system. Several lines of evidence have suggested that neurological injuries, such as stroke or cerebral palsy, may reduce the dimensions that are available to the motor control system, and these altered dimensions or synergies are thought to contribute to impaired walking patterns. However, no study has investigated whether impaired low-dimensional control spaces necessarily lead to impaired walking patterns. In this study, using a two-dimensional model of walking, we developed a synergy-based control framework that can simulate the dynamics of walking. The simulation analysis showed that a synergy-based control scheme can produce well-coordinated movements of walking matching unimpaired gait. However, when the dimensions available to the controller were reduced, the simplified emergent pattern deviated from unimpaired gait. A system with two synergies, similar to those seen after neurological injury, could not produce an unimpaired walking pattern. These findings provide further evidence that altered muscle synergies can contribute to impaired gait patterns and may need to be directly addressed to improve gait after neurological injury.
Keywords: Muscle Synergy, Forward Dynamic Simulation, Altered Synergy, Impaired Motor Control, Direct Collocation, Optimal Control
1. Introduction
Locomotion is a complex motor task which requires precise coordination of highly nonlinear and redundant musculotendinous units. The redundancy of the musculotendinous units, where the number of muscles crossing each joint exceeds the kinematic degrees of freedom, provides a flexible but intricate mechanism for controlling the human body. Prior research analyzing muscle activity with surface electromyography (EMG) recordings suggests that the human central nervous system may reduce motor control complexity by recruiting muscles through individual motor commands sent to weighted groups of muscles (Ivanenko, et al., 2005; Tresch, et al., 1999; Davis & Vaughan, 1993). This results in a low dimensional control space that may be represented by a small set of muscle synergies. In this manuscript, a muscle synergy (sometimes called module or motor primitive) is defined as a weighted group of muscles that are activated together during functional motor tasks. The complex muscle activation patterns during walking, and their variability across walking speeds, can be accounted for by independent control of muscle synergies (Cappellini, et al., 2006). Muscle synergies can be identified by applying various factorization techniques to EMG data (e.g., factor analysis, independent component analysis, and nonnegative matrix factorization). The muscle synergies identified during walking have relatively consistent muscle organizations and activation patterns regardless of the technique used (Tresch, et al., 2006), and appear to be organized around functional motor tasks of walking (e.g., body support and forward propulsion) (Ting & Macpherson, 2005; Neptune, et al., 2009).
Several research studies have reported that four to six functionally relevant muscle synergies are needed to describe muscle activity during unimpaired walking (Clark, et al., 2010; Ivanenko, et al., 2006; Cappellini, et al., 2006). Motor control complexity increases during human development (Dominici, et al., 2011), and may be reduced following a neurological injury (Ivanenko, et al., 2013). Individuals who have impaired walking due to a stroke (Clark, et al., 2010), incomplete spinal cord injury (Fox, et al., 2013) or cerebral palsy (Steele, et al., 2015) recruit fewer muscle synergies compared to unimpaired individuals. Often, in individuals who have had a stroke, the impaired synergies resemble merging of specific unimpaired synergies (Clark, et al., 2010). Similar conclusions have been drawn for upper-extremity movements after stroke (Cheung, et al., 2012; Roh, et al., 2015). Altered synergies have been hypothesized to contribute to not only impaired movement, but also the increased muscle activity and greater energetic costs commonly observed among individuals with neuromuscular disorders compared to unimpaired individuals (Rose, et al., 1990; Steele, et al., 2017; Kramer, et al., 2016; van der Krogt, et al., 2012).
Using computer simulations of musculoskeletal models, previous studies have provided evidence that synergy-based control can produce well-coordinated steady-state forward walking (Neptune, et al., 2009; Allen & Neptune, 2012; Sartori, et al., 2013). Synergy-based control has been previously used to incorporate subject-specific motor impairments in control to simulate impaired walking patterns (Meyer, et al., 2016; Walter, et al., 2014). However, whether altered synergies, such as those commonly observed after neurological injury, can control unimpaired gait remains unknown. The answer to this question can provide useful insight into the neurological complexity required for walking. Specifically, the ability of a simulation to achieve unimpaired gait using “impaired” synergies may suggest that unimpaired gait is feasible despite the neurological injury and may be obtained through targeted treatments such as strength training or orthopaedic surgery. However, the impaired synergies may require greater muscle activity or energetic cost to achieve this unimpaired gait pattern. Alternatively, failure to achieve an unimpaired gait with impaired synergies would suggest that altered motor control enforces fundamental constraints or reflects compensatory strategies that underlie impaired gait. These constraints or compensations must be acknowledged and addressed in the treatment of non-neurological issues to achieve unimpaired walking.
In the present study, we combined muscle synergy theory with musculoskeletal simulation and optimal control theory to develop a synergy-based controller that can simulate the forward dynamics of walking. Muscle synergies were identified by applying factorization techniques to model-based muscle excitations. Each synergy was then controlled through a low-dimensional set of motor commands computed by a synergy-based controller. Unlike previous studies (Neptune, et al., 2009; Sartori, et al., 2013) that assumed a fixed number of synergies, this research examined multiple potential synergy solutions to determine whether a given number of synergies could achieve unimpaired gait. This research aimed to use synergy-based control to (a) investigate whether an unimpaired gait can be achieved from low-dimensional control spaces represented by altered muscle synergies, (b) analyze the kinematics and muscle activities resulting from synergy-based control, and (c) evaluate the effort required by the resulting gait pattern to examine how muscle recruitment may change with synergy-based control, and whether these changes contribute to a less-efficient gait pattern. Addressing these aims will enhance our understanding about the impacts of altered synergies from neurological injuries on impaired gait, and the implications of these synergies on treatment planning.
2. METHODS
2.1. Musculoskeletal model
A dynamic model of human walking in the sagittal plane, similar to the planar model of Geyer and Herr (2010), was implemented in MATLAB (Mathworks, Inc) (Fig. 1). The model consisted of seven rigid body segments connected to each other via hinge joints. The segments included an upper-extremity segment (i.e., head, arm, and trunk), two thighs, two shanks, and two feet. This model had nine kinematic degrees-of-freedom (DOF) and was actuated with eight Hill-type musculotendinous units per leg. The musculotendinous units were designed to mimic the rectus femoris (RF), hip flexors (iliopsoas, HFL), gluteus maximums (GLU), vastus medialis (VAS), biarticular hamstrings (HAM), gastrocnemius (GAS), tibialis anterior (TA), and soleus (SOL). The musculotendinous unit model and its parameters, including musculotendinous path and moment arm curves, muscle activation time constants, maximum isometric force, tendon slack length, optimal fiber length, and maximum shortening velocity of all muscles except RF, were based on Geyer & Herr (2010). Similar to (Dorn, et al., 2015), we added RF to Geyer and Herr’s model to include the dynamics of a hip and knee biarticular muscle.
Figure 1:
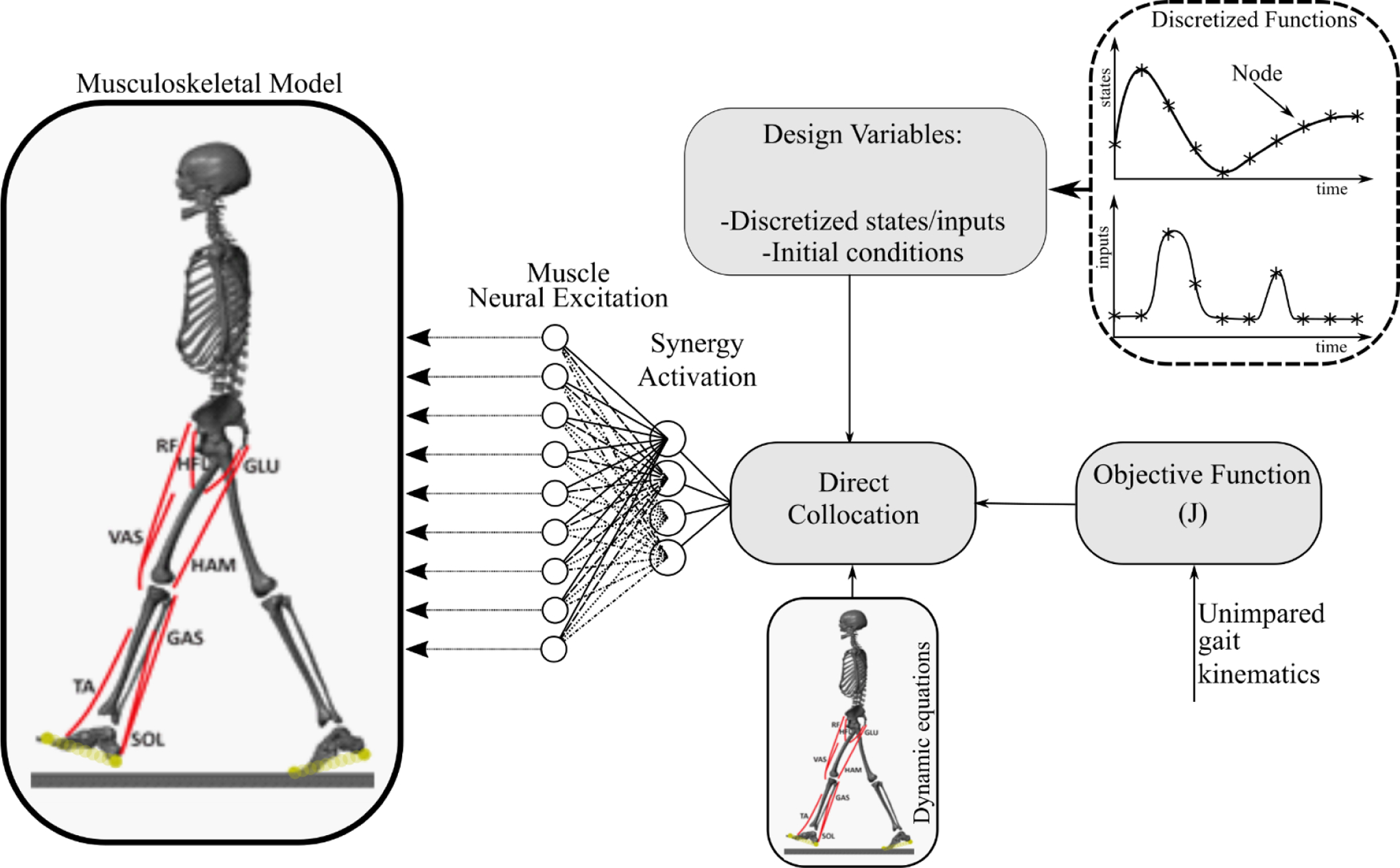
The two-dimensional sagittal-plane musculoskeletal model and the synergy-based control framework. The musculoskeletal model included flexion and extension of hip, knee, and ankle of each leg, and horizontal and vertical translations and rotation of trunk. The model had nine kinematic degrees-of-freedom (DOFs) and eight muscles per leg. The synergy-based control applied a direct collocation algorithm to find the optimal synergy activation profiles and gait dynamics. All state and input variables including synergy activations and kinematics, and the dynamic equations of motion were discretized via a 51-node temporal grid for half a gait cycle. These variables were subsequently optimized such that both the differences between simulated and experimental kinematics, and the neural excitation effort over the gait cycle were minimized. Individual muscle excitations were calculated by adding the contribution of each synergy to that specific muscle.
To simulate foot-ground interaction, the model incorporated ten elements, with continuous coulomb friction (Brown & McPhee, 2016) evenly distributed along the foot. This differs from Geyer and Herr’s model that used two nonlinear viscoelastic spherical contact elements. The normal force between the foot and ground was calculated based on the Hunt-Crossley model described in Geyer & Herr (2010); however, the stiffness in this equation, through trial and error, was changed to 848,500 N/m to avoid unrealistically bouncy foot movements and sharp peaks in ground reaction forces in the simulations (Dorn, et al., 2015).
2.2. Neuromuscular controller
Direct collocation (DC) was employed to track joint trajectories of an unimpaired, bilateral symmetric gait cycle (Ackermann & Van den Bogert, 2010). Briefly, DC converts the trajectory tracking problem to a nonlinear program by discretizing the states (18 generalized coordinates and velocities corresponding to kinematic DOFs, 16 muscle contractile element lengths, 16 muscle activations) and inputs (16 neural excitations), and transcribing dynamic equations of motion to algebraic constraints using the implicit Euler method by means of a 51-node temporal grid for half a gait cycle (assumed symmetry). Since unimpaired gait is symmetric, assuming symmetry reduced simulation complexity without loss of fidelity. The dynamic equations of motion of the musculoskeletal model were generated using the symbolic modeling engine MapleSim (Maplesoft, Inc). The discretized motor control inputs and states, and the initial joint angles and angular velocities were optimized using an interior point optimization (IPOPT) solver in MATLAB, such that the difference between simulated and desired kinematics and the neural excitation effort were minimized. The IPOPT solver is well suited for solving large-scale nonlinear optimization problems (Wächter & Biegler, 2006). The neural excitation effort was defined as the summation of neural excitations squared over a full gait cycle (Ackermann & Van den Bogert, 2010). This measure was used to quantify and compare the required neural excitation of the emergent gait patterns. The desired kinematics consisted of the sagittal plane trajectories of hip, knee, and ankle angles, and trunk rotational and translational movements. Thus, the cost function was defined as:
| (1) |
where u are neural excitations, θ and θdesired are the kinematic state variables and their desired trajectories, respectively, and i and j are the indices for individual muscles and kinematic state variables. The parameter w is a weighting factor whose value was set to 1000 to weigh the tracking term against the physiological term in the cost function, and was manually tuned to find acceptable joint trajectories and control profiles (Umberger, 2010).
We performed tracking simulations with two different motor control strategies: (1) individual muscle control, in which motor control inputs were sent to each muscle independently, and (2) synergy-based control, in which muscles were controlled via low-dimensional signals (i.e., synergy activations). In synergy-based control, two sets of simulations with fixed and flexible synergies were performed. In synergy-based control with fixed synergies, the muscles in each synergy were activated together with a fixed ratio (i.e., synergy weights), and their synergy activation profiles were optimized. While in synergy-based control with flexible synergies, the synergy weights were also allowed to deviate from the original weights during the optimizations. In this simulation, the deviation from the original synergy weights was penalized by including a lightly weighted error term (i.e., the difference between the original and flexible synergy weights) in the cost function. In the synergy-based control simulations, the desired kinematics trajectories were set to those derived from the individual muscle control simulations. This ensured that the simulation results were comparable between individual and synergy-based control. The root-mean-square of tracking error (RMSE) was used to compare the emergent simulated kinematics, and to verify whether the low-dimensional control spaces represented by altered synergies could produce an unimpaired gait. Figure 2 summarizes the procedures used in this study for developing synergy-based controllers to simulate unimpaired gait.
Figure 2:
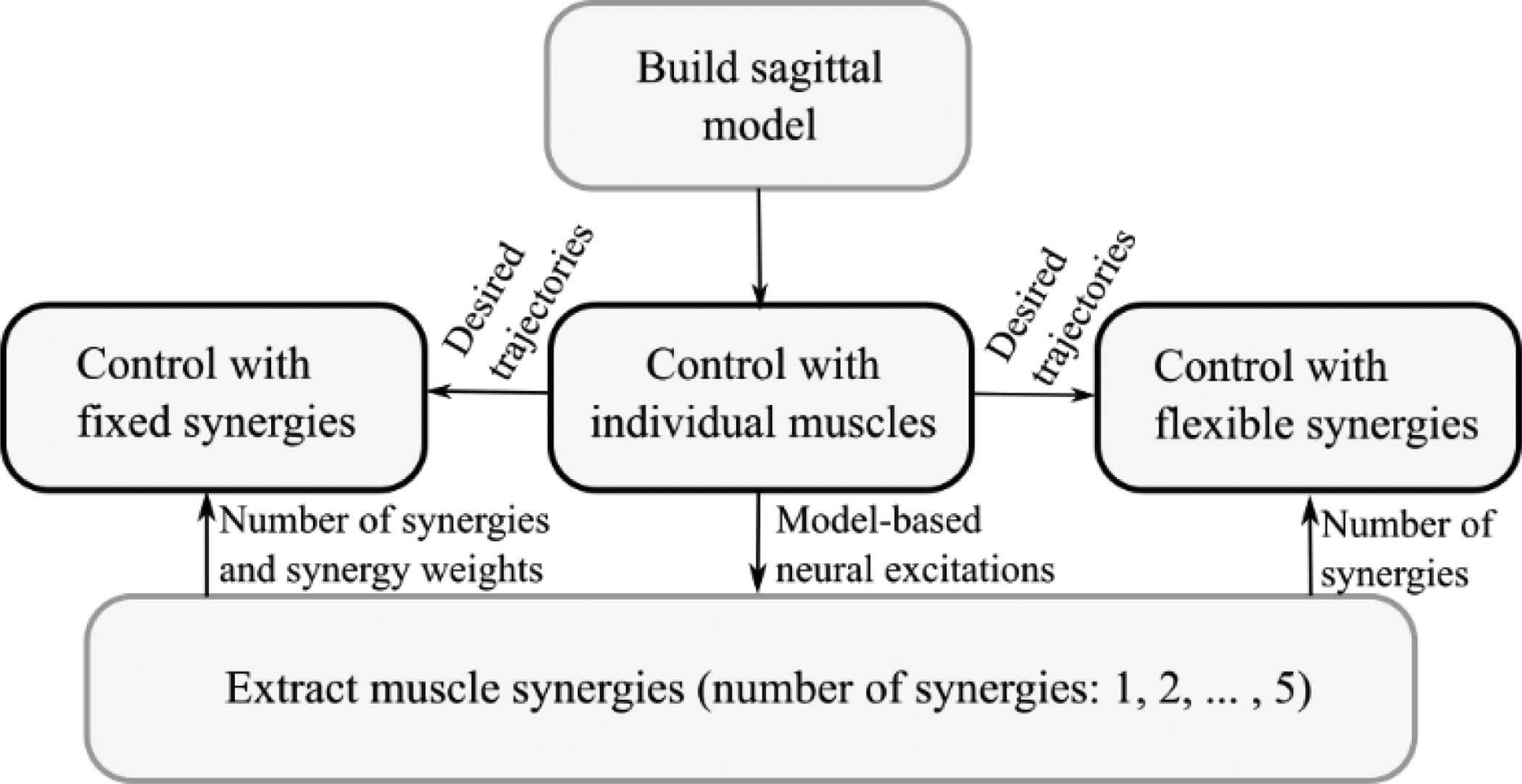
Study design and sequence of methods used in this research. First, we implemented a sagittal-plane model of walking and then performed individual muscle control to simulate an unimpaired gait and compute the model-based neural excitations. The NNMF algorithm was used to extract muscle synergies from the model-based neural excitations. These synergies were used in the synergy-based controllers to simulate the unimpaired gait pattern predicted by individual muscle control. In control with fixed synergies, both the number of synergies and their weights were embedded in the controller, while in control with flexible synergies, only the number of synergies was used.
2.3. Non-negative matrix factorization
Muscle synergies used for the synergy-based control simulations were identified by applying a non-negative matrix factorization (NNMF, Lee & Seung, 1999) algorithm to model-based neural excitations (u) from the tracking simulation with individual muscle control in MATLAB. The NNMF algorithm computes the fixed ratios with which muscles are activated in each synergy (W), and the temporal synergy activations (C) such that the excitations u = W × C + error. Here, W is m × n matrix where m and n are respectively the number of muscles and synergies, and C is an n × t matrix where t represents the number of sample points in a full gait cycle. Thus, each column of W represents the relative weighting of individual muscles in each synergy, and each row of C represents the activation levels of the specific synergies over the full gait cycle. The NNMF algorithm was repeated with random initial guesses, and the result with the minimum error was selected. The NNMF algorithm in MATLAB was configured to use the multiplicative update algorithm, where the maximum number of iteration was 5000, the termination tolerance on change of size of the residual and relative change in elements of W and C were 10−7, and NNMF was repeated with 500 random initial guesses. The total variance accounted for (tVAF) by n synergies was defined by tVAFn = 1 − (W × C − u)2/ u2. We repeated this analysis by incrementally increasing the number of synergies from two to five. These synergies were consecutively included in the synergy-based controller to investigate the impacts of reduced synergies on gait patterns.
2.4. Experimental data
Two separate studies were used to evaluate simulate kinematics and EMG activations. The average kinematics of eight healthy subjects were used from a prior study that measured kinematics using a marker-based motion capture system (Liu, Anderson, Schwartz, & Delp, 2008). Muscle excitation patterns were evaluated by comparing to the on-off activation patterns during unimpaired gait as reported in Winter (1987). The muscles were assumed to be “on” during walking when their EMG activity was above the 15% threshold of their maximum activity over the gait cycle.
3. RESULTS
The kinematics predicted by individual muscle control closely matched those observed in unimpaired gait. The average RMSE of hip, knee, and ankle kinematics compared to experimental data were 3.1°, 2.0°, and 2.1°, respectively over a gait cycle (Fig. 3, left). Simulated model-based neural excitations were consistent with on-off activity of muscles from EMG data during unimpaired gait (Fig. 3, right). In the simulations, RF was negligibly active, and the HFL was activated earlier than expected from experimental EMG recordings.
Figure 3:
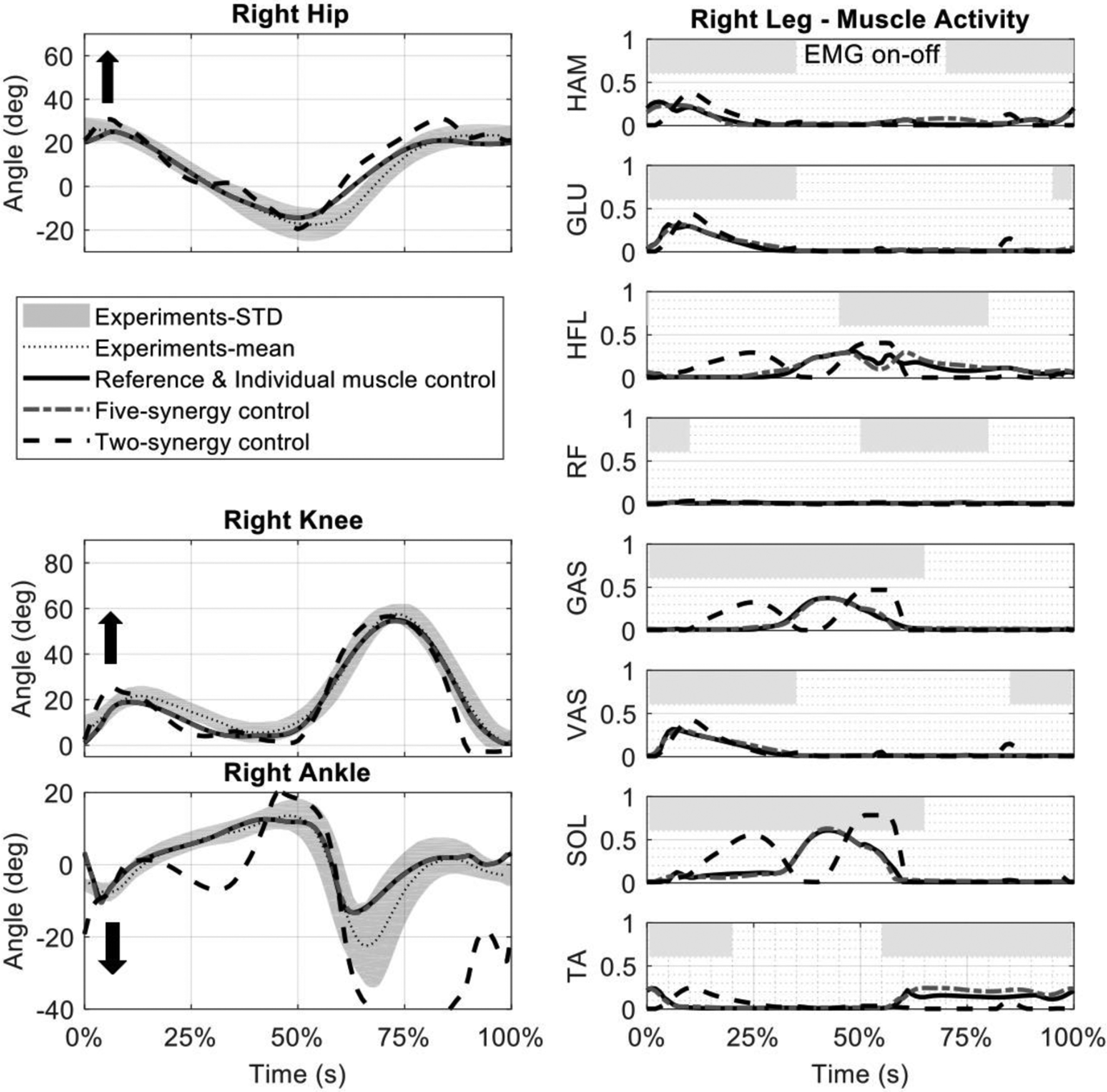
(left) Simulated kinematics with individual-muscle and fixed synergy-based control against experimental unimpaired kinematics. A controller with five muscle synergies closely tracked unimpaired gait kinematics while there were significant deviations from unimpaired kinematics in control with two synergies. The kinematics with both individual muscle control and five-synergy control are shown and are on top of each other. (right) Muscle neural excitations demonstrate similar activity to experimental periods of muscle activity (gray bars (Winter, 1987)).
The muscle synergies extracted by the NNMF algorithm from the model-based neural excitations had a total variance accounted for (tVAF) greater than 0.97 when three or more synergies were identified (0.98 and 0.99 for four and five synergies, respectively) and 0.87 when two muscle synergies were identified (Fig. 4b). The VAFs of individual muscle were greater than 0.80 for all muscles in five, four, and three synergies solutions. The two synergy solution described over 0.80 of VAF for all muscles except for TA, which dropped to 0.30. In the five-synergy solution (first column in Fig. 4a), the first synergy (ankle plantarflexor: SOL and GAS), second synergy (hip and knee extensors: VAS, GLU, and SOL), third synergy (hip flexor: HFL), fourth synergy (ankle dorsiflexor-hip flexor: TA, HFL), and fifth synergy (hip extensor: HAM, GLU) accounted for 0.60, 0.16, 0.16, 0.11, and 0.10 of the total variation in individual muscle excitations, respectively. In the four-synergy solution, the ankle dorsiflexor-hip flexor synergy merged with the hip flexor and the hip extensor synergies, and in the three-synergy solution, the three aforementioned synergies formed one combined synergy (second and third columns in Fig. 4a). The independent burst of synergy activation during late swing and early stance disappeared in the two-synergy solution, resulting in lower tVAF.
Figure 4:
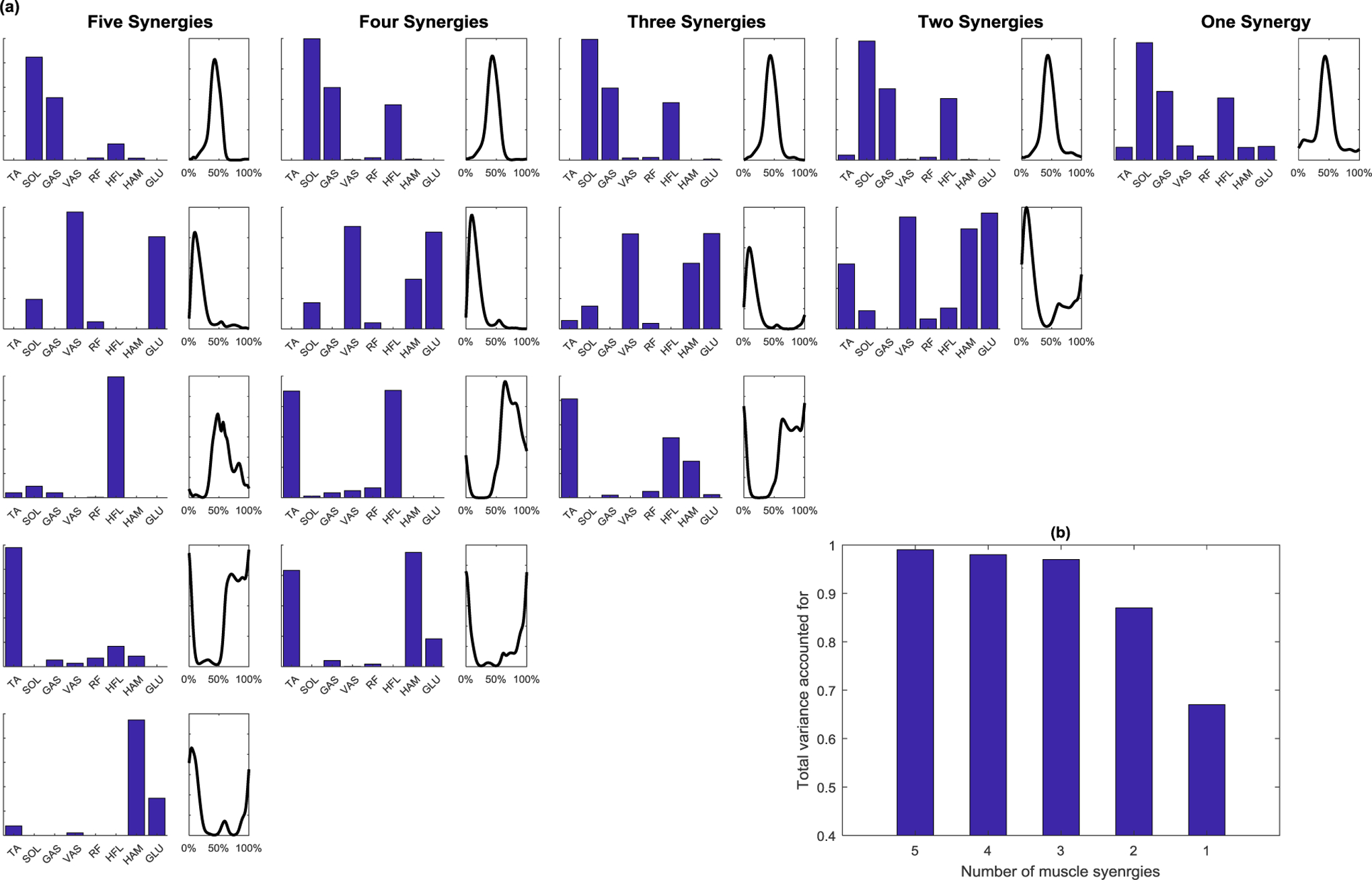
(a) Muscle synergy weights and activations with different number of synergies from individual muscle control. The number of synergies identified by NNMF for five to one are depicted from left to right. Muscle synergies were identified by applying NNMF to the neural excitations computed by individual muscle control. The bar plots on the left of each column represent the muscle weights within each synergy, and the waveform on the right is the synergy activation. (b) The total variance accounted for (tVAF) was greater than 0.95 for three or more synergies.
Compared to synergy-based control with five fixed synergies, the tracking performance of control with two fixed synergies was significantly degraded. The RMSE of hip, knee, and ankle kinematics between individual muscle and two-synergy control were 4.9°, 5.8°, and 21.8°, while they were 0.1°, 0.2°, and 0.2° between individual muscle and five-synergy control, respectively. With the fixed two-synergy control, the hip flexion and ankle dorsiflexion angles were outside of 1SD of unimpaired gait for 30% and 60% of gait cycle, respectively. The neural excitation effort for fixed two-synergy control was increased by 50% compared to five-synergy control (Fig. 3). The neural excitation effort of SOL and GAS had large increases of 98% and 93%, while TA had a reduction of 71%.
The simulated kinematics with the flexible two-synergy control showed improvement in tracking compared to the original fixed two-synergy control (RMSE of hip 6.5%, knee 1.3%, and ankle 15.7% were reduced compared to the original two-synergy control); however, the ankle still failed to track the unimpaired trajectory (Fig. 5). The flexible synergy weights adjusted such that, in the extensor synergy, the weight of TA notably increased while VAS and HAM decreased, and synergy activation during stance phase increased (Fig. 6). A small increase of synergy activation during swing reduced the ankle tracking error while the total muscle excitation effort increased.
Figure 5:
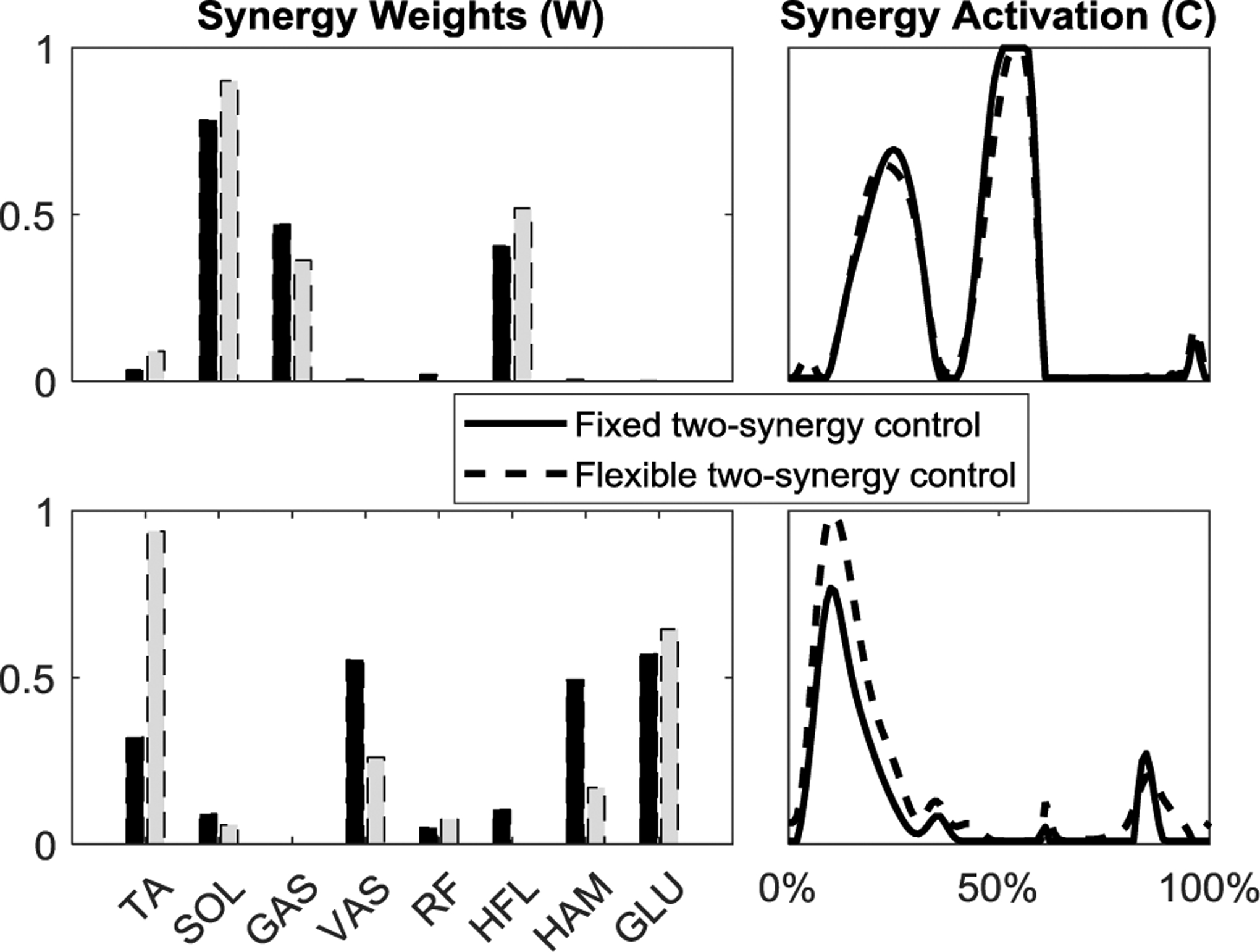
Comparison of synergy weights and activations between the original fixed two-synergy control and when the synergy weights were optimized in the flexible two-synergy control.
Figure 6:
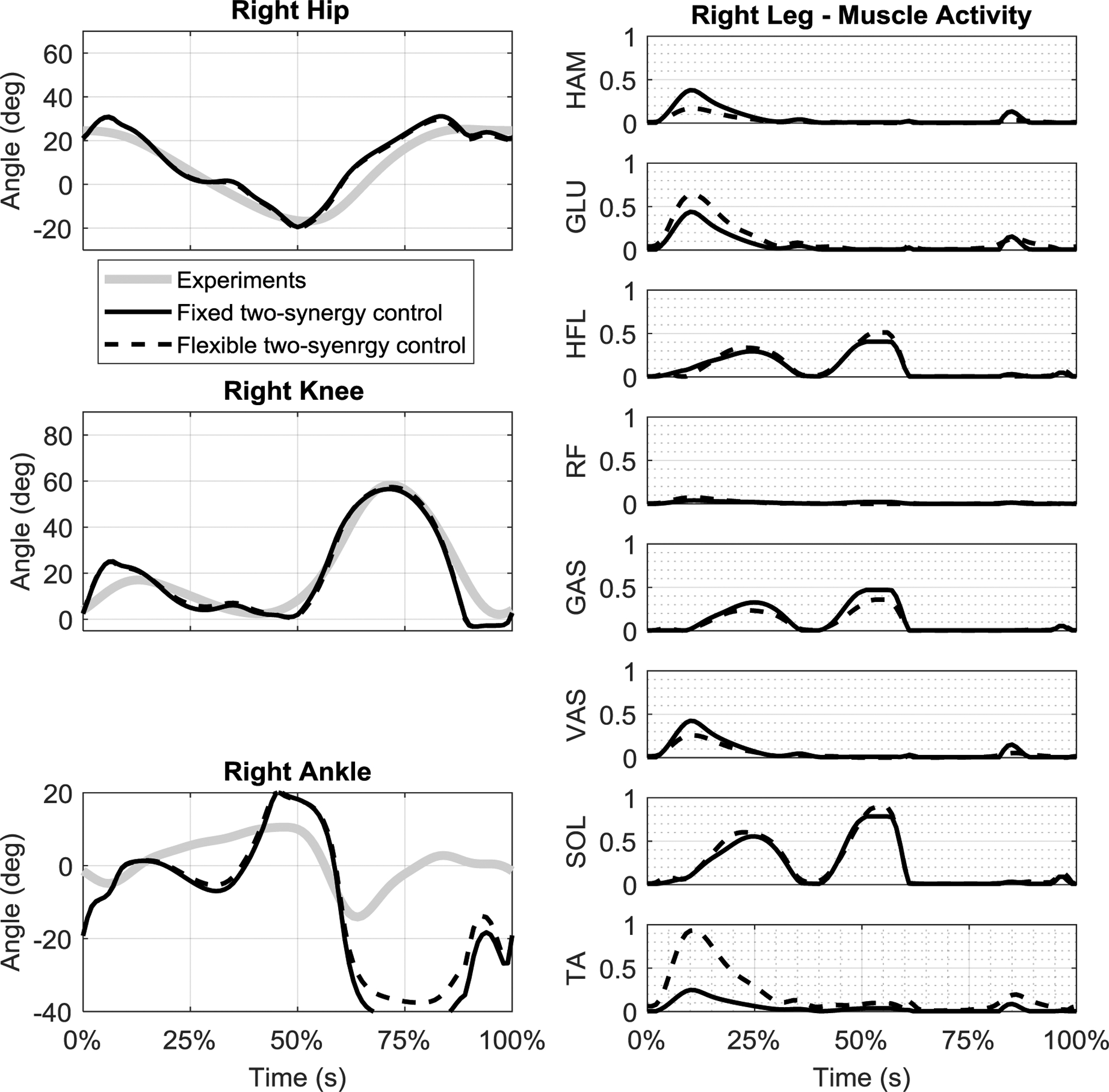
(left) comparison of kinematics and (right) muscle activities between the synergy-based control with the original fixed two synergies identified with NNMF algorithm and the flexible two synergies.
The simulation results showed that synergy activation and muscle neural excitation patterns change during control with a reduced number of synergies, and they may not match the synergy activation patterns computed by NNMF from model-based neural excitations of unimpaired gait. The optimal synergy activations predicted by the five-synergy control with fixed synergies were highly correlated with those extracted using NNMF algorithm from model-based neural excitations of tracking an unimpaired gait (average Pearson correlation coefficient, p = 0.96). However, there was less correlation between the synergy activations of the two-synergy control and the NNMF-identified two-synergy solution from unimpaired gait. In the two-synergy control, the optimal synergy activation corresponding to the flexor synergy (SOL, GAST, and HFL) had two consecutive bursts that may separately correspond to ankle plantar flexor and hip flexor synergies. Similarly, the optimal activation of the extensor synergy (TA, VAST, HAM, and GLU) had a large burst of synergy activations in stance and a small burst later in swing that may correspond to the hip and knee extensors and ankle dorsiflexion synergies, respectively.
4. DISCUSSION
This study demonstrated that impaired motor control, modeled as a reduced number of synergies, could not accurately track an unimpaired gait pattern. This finding can be used to inform our understanding of how altered synergies may contribute to impaired gait after neurologic injury with implications for treatment planning. For example, these results suggest that treatments that target only orthopaedic problems without considering underlying neurological capacity are unlikely to succeed in producing unimpaired post-treatment gait patterns. Recent research has indicated that there are minimal changes in synergies after orthopaedic surgery and other treatments common in cerebral palsy. These treatments also have inconsistent outcomes between individuals (Hicks, et al., 2011). These unsatisfactory outcomes may be tied to the underlying neuromuscular control strategy that is not addressed by surgical intervention. This simulation framework may provide new tools to identify and optimize individualized treatments targeted at the neurological impairment to improve walking ability.
The simulation results of control with two synergies demonstrated that, with this reduced control space, the synergy-based controller failed to accurately track unimpaired gait kinematics, especially at the ankle, and had inferior tracking performance compared to control with five fixed synergies (Fig. 3). This observation suggests that even if the motor system can optimize the neural commands based on the confined control space, there would be no command that can achieve an unimpaired gait in the two synergies control space. To further test the robustness of this conclusion, we also conducted a post-hoc analysis to test additional sets of synergies within the two synergies control space. Specifically, we removed the lightly-weighted error term on synergy weights from the objective function with flexible synergies and initiated the optimization with different sets of random synergy weights. Despite expanding our search space with these changes, we still found the two-synergy solution could not track unimpaired kinematics and converged to similar synergy weights and activation profiles. Interestingly, the weights of the two synergy solution were also similar to prior experimental analyses of synergies from rhythmic-stepping in infants, children with cerebral palsy, and adult stroke survivors (Dominici, et al., 2011; Steele, et al., 2015; Clark, et al., 2010). It is plausible that the objective of the human control system is not to create an “unimpaired gait”, but rather to minimize some physiological cost. Further research might explore the optimality of the simulated walking patterns with altered synergies in terms of energy consumption and predict patterns that minimize this cost for subject-specific muscle synergies.
The neural excitation effort of tracking unimpaired kinematics in the reduced control space represented by two synergies was largely increased compared to the control space represented by five synergies or by individual muscles. This may provide an explanation on why it is more difficult to achieve an unimpaired gait following a neurological injury, and also accords with earlier observations, which showed that energy cost tends to be larger for individuals with a neuromuscular disorder such as CP (Rose, et al., 1990; Steele, et al., 2017) or stroke (Kramer, et al., 2016), or with functional weakness, which may be a consequence of poor motor control (van der Krogt, et al., 2012). However, additional analyses that also incorporate other factors such as weakness or poor balance are needed to understand the mechanisms with which impaired neuromuscular control impacts metabolic energy consumption.
The simulation with flexible synergies aimed to investigate the effect of muscle synergy reorganization and neuroplasticity in an impaired low-dimensional control space on tracking performance and walking patterns. Previous studies evaluating EMGs during walking observed that the muscle activity patterns and the synergy weights could be changed when the biomechanical demands of walking were altered (e.g., walking with added trunk load or with a weight support system) (McGowan, et al., 2010; McGowan, et al., 2008). By allowing the synergy weights in the flexible two-synergy control to change, we deviated from the typical definition of muscle synergy and shifted towards other studies that allow some flexibility in synergy structure and weights (Ivanenko, et al., 2005). However, the simulation results further support the conjecture that there were no muscle synergy configurations within this lower dimensional control space that could accurately track the unimpaired gait kinematics.
It is important to note the limitations of the methods of this research when interpreting the simulation results. The musculoskeletal model represents the dynamics of walking in the sagittal plane and neglects the contributions of muscle forces to the frontal and transverse planes. Thus, this model cannot capture motor control strategies used by the central nervous system to stabilize the body in three-dimensions. While two synergies were unable to accurately track unimpaired gait with this simplified model, if greater complexity were added (e.g., more muscles or 3D-kinematics) then three or more synergies may also struggle to accurately track unimpaired gait. We also assumed symmetry between the right and left legs, which may not be a valid assumption for individuals with unilateral cerebral palsy or stroke. Determining whether applying impaired synergies for one leg prevents unimpaired walking kinematics remains unknown. The muscle synergies used in this research were identified by applying NNMF to the model-based neural excitations predicted by individual muscle control for tracking the kinematics of an unimpaired gait. The identified model-based synergy activations and weights were relatively similar to those identified from EMG in prior studies (Clark, et al., 2010; Ivanenko, et al., 2006), suggesting the sagittal-plane walking model can simulate the neural control requirements of support and progression during gait. Other factors that may contribute to impaired gait, such as weakness, spasticity, or poor balance were not included in this study to focus on the impacts of altered synergies. Examining the impacts of these factors in combination with altered synergies may provide greater insight into the mechanisms contributing to impaired gait and increased energetic cost for individuals with neuromuscular disorders.
In this investigation, we examined whether unimpaired gait kinematics can be achieved from lower dimensional control spaces that are commonly observed after neurological injuries. In accordance with previous studies (Neptune, et al., 2009; Sartori, et al., 2013), the present results demonstrated that synergy-based control could produce well-coordinated forward walking. However, lower-dimensional control spaces represented with altered muscle synergies could not track an unimpaired gait, and resulted in elevated neural exertion levels. This finding suggests that if synergies are an underlying neural control mechanism, gait may be impaired due to the reduction of the number of synergies available to the neuromuscular system. Treatments that target the underlying neurological capacity to increase the number and complexity of muscles synergies may be required to improve an individual’s walking pattern. For example, the flexible synergy controller used in this research could be applied to identify rehabilitation targets that are customized to an individual’s unique gait pattern and control strategy. Alternatively, if synergies are challenging to alter, simulation could be used to help identify and guide optimal walking patterns for an individual’s neurological capacity. Determining the plasticity of synergies and potential changes in gait with targeted treatment remain open and important areas for future research.
Acknowledgments
This work was supported by the National Institute of Neurological Disorders & Stroke, NIH R01NS091056 in collaboration with Gillette Children’s Specialty Healthcare.
Footnotes
Conflict of interest statement
There is no conflict of interest regarding the publication of this manuscript.
References
- Ackermann M & Van den Bogert AJ, 2010. Optimality principles for model-based prediction of human gait. Journal of biomechanics, 43(6), pp. 1055–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen JL & Neptune RR, 2012. Three-dimensional modular control of human walking. Journal of biomechanics, 45(12), pp. 2157–2163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown P & McPhee J, 2016. A continuous velocity-based friction model for dynamics and control with physically meaningful parameters. ASME Journal of Computational and Nonlinear Dynamics, 11(5), pp. 054502–6. [Google Scholar]
- Cappellini G, Ivanenko YP, Poppele RE & Lacquaniti F, 2006. Motor patterns in human walking and running. Journal of neurophysiology, 95(6), pp. 3426–3437. [DOI] [PubMed] [Google Scholar]
- Cheung VC et al. , 2012. Muscle synergy patterns as physiological markers of motor cortical damage. Proceedings of the National Academy of Sciences, 109(36), pp. 14652–14656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark DJ et al. , 2010. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. Journal of neurophysiology, 103(2), pp. 844–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis BL & Vaughan CL, 1993. Phasic behavior of EMG signals during gait: Use of multivariate statistics. Journal of Electromyography and Kinesiology, 3(1), pp. 51–60. [DOI] [PubMed] [Google Scholar]
- Dominici N et al. , 2011. Locomotor primitives in newborn babies and their development. Science, 334(6058), pp. 997–999. [DOI] [PubMed] [Google Scholar]
- Dorn TW, Wang JM, Hicks JL & Delp SL, 2015. Predictive simulation generates human adaptations during loaded and inclined walking. PloS one, 10(4), p. e0121407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox EJ et al. , 2013. Modular control of varied locomotor tasks in children with incomplete spinal cord injuries. Journal of neurophysiology, 110(6), pp. 1415–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geyer H & Herr H, 2010. A Muscle-Reflex Model That Encodes Principles of Legged Mechanics Produces Human Walking Dynamics and Muscle Activities. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 18(3), pp. 263–273. [DOI] [PubMed] [Google Scholar]
- Hicks JL, Delp SL & Schwartz MH, 2011. Can biomechanical variables predict improvement in crouch gait?. Gait & posture, 34(2), pp. 197–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP et al. , 2005. Coordination of locomotion with voluntary movements in humans. Journal of Neuroscience, 25(31), pp. 7238–7253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP et al. , 2013. Plasticity and modular control of locomotor patterns in neurological disorders with motor deficits. Frontiers in computational neuroscience, Volume 7, p. 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE & Lacquaniti F, 2006. Motor control programs and walking. The Neuroscientist, 12(4), pp. 339–348. [DOI] [PubMed] [Google Scholar]
- Kramer S, Johnson L, Bernhardt J & Cumming T, 2016. Energy expenditure and cost during walking after stroke: a systematic review. Archives of physical medicine and rehabilitation, 497(4), pp. 619–632. [DOI] [PubMed] [Google Scholar]
- Lee DD & Seung HS, 1999. Learning the parts of objects by non-negative matrix factorization. Nature, 401(6755), p. 788. [DOI] [PubMed] [Google Scholar]
- Liu MQ, Anderson FC, Schwartz MH & Delp SL, 2008. Muscle contributions to support and progression over a range of walking speeds. Journal of biomechanics, 41(15), pp. 3243–3252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGowan CP, Neptune RR, Clark DJ & Kautz SA, 2010. Modular control of human walking: adaptations to altered mechanical demands. Journal of biomechanics, 43(3), pp. 412–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGowan CP, Neptune RR & Kram R, 2008. Independent effects of weight and mass on plantar flexor activity during walking: implications for their contributions to body support and forward propulsion. Journal of applied physiology, 105(2), pp. 486–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer AJ et al. , 2016. Muscle synergies facilitate computational prediction of subject-specific walking motions. Frontiers in bioengineering and biotechnology, Volume 4, p. 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neptune RR, Clark DJ & Kautz SA, 2009. Modular control of human walking: a simulation study. Journal of biomechanics, 42(9), pp. 1282–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roh J, Rymer WZ & Beer RF, 2015. Evidence for altered upper extremity muscle synergies in chronic stroke survivors with mild and moderate impairment. Frontiers in human neuroscience, 9(6). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose J et al. , 1990. Energy expenditure index of walking for normal children and for children with cerebral palsy. Developmental Medicine & Child Neurology, 32(4), pp. 333–340. [DOI] [PubMed] [Google Scholar]
- Sartori M, Gizzi L, Lloyd DG & Farina D, 2013. A musculoskeletal model of human locomotion driven by a low dimensional set of impulsive excitation primitives. Frontiers in computational neuroscience, Volume 7, p. 79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele KM, Rozumalski A & Schwartz MH, 2015. Muscle synergies and complexity of neuromuscular control during gait in cerebral palsy. Developmental Medicine & Child Neurology, 57(12), pp. 1176–1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele KM, Shuman BR & Schwartz MH, 2017. Crouch severity is a poor predictor of elevated oxygen consumption in cerebral palsy. Journal of biomechanics, Volume 60, pp. 170–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting LH & Macpherson JM, 2005. A limited set of muscle synergies for force control during a postural task. Journal of neurophysiology, 93(1), pp. 609–613. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Cheung VC & d’Avella A, 2006. Matrix factorization algorithms for the identification of muscle synergies: evaluation on simulated and experimental data sets. Journal of neurophysiology, 98(4), pp. 2199–2212. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Saltiel P & Bizzi E, 1999. The construction of movement by the spinal cord. Nature neuroscience, 2(2), pp. 162–167. [DOI] [PubMed] [Google Scholar]
- Umberger BR, 2010. Stance and swing phase costs in human walking. Journal of the Royal Society Interface, 7(50), pp. 1329–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Krogt MM, Delp SL & Schwartz MH, 2012. How robust is human gait to muscle weakness?. Gait & posture, 36(1), pp. 113–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wächter A & Biegler LT, 2006. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical programming, 106(1), pp. 25–57. [Google Scholar]
- Walter JP et al. , 2014. Muscle synergies may improve optimization prediction of knee contact forces during walking. Journal of biomechanical engineering, 136(2), p. 021031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter DA, 1987. The biomechanics and motor control of human gait. s.l.:University of Waterloo Press. [Google Scholar]


