Hemodynamic and morphological characteristics of a growing cerebral aneurysm

Abstract

The growth of cerebral aneurysms is linked to local hemodynamic conditions, but the driving mechanisms of the growth are poorly understood. The goal of this study was to examine the association between intraaneurysmal hemodynamic features and areas of aneurysm growth, to present the key hemodynamic parameters essential for an accurate prediction of the growth, and to gain a deeper understanding of the underlying mechanisms. Patient-specific images of a growing cerebral aneurysm in 3 different growth stages acquired over a period of 40 months were segmented and reconstructed. A unique aspect of this patient-specific case study was that while one side of the aneurysm stayed stable, the other side continued to grow. This unique case enabled the authors to examine their aims in the same patient with parent and daughter arteries under the same inlet flow conditions. Pulsatile flow in the aneurysm models was simulated using computational fluid dynamics and was validated with in vitro experiments using particle image velocimetry measurements. The authors’ detailed analysis of intrasaccular hemodynamics linked the growing regions of aneurysms to flow instabilities and complex vortex structures. Extremely low velocities were observed at or around the center of the unstable vortex structure, which matched well with the growing regions of the studied cerebral aneurysm. Furthermore, the authors observed that the aneurysm wall regions with a growth greater than 0.5 mm coincided with wall regions of lower (< 0.5 Pa) time-averaged wall shear stress (TAWSS), lower instantaneous (< 0.5 Pa) wall shear stress (WSS), and high (> 0.1) oscillatory shear index (OSI). To determine which set of parameters can best identify growing and nongrowing aneurysms, the authors performed statistical analysis for consecutive stages of the growing CA. The results demonstrated that the combination of TAWSS and the distance from the center of the vortical structure has the highest sensitivity and positive predictive value, and relatively high specificity and negative predictive value. These findings suggest that an unstable, recirculating flow structure within the aneurysm sac created in the region adjacent to the aneurysm wall with low TAWSS may be introduced as an accurate criterion to explain the hemodynamic conditions predisposing the aneurysm to growth. The authors’ findings are based on one patient’s data set, but the study lays out the justification for future large-scale verification. The authors’ findings can assist clinicians in differentiating stable and growing aneurysms during preinterventional planning.

THE growth of a cerebral aneurysm (CA) has been known as a key indicator of aneurysm rupture,^{2,5,7,9,20,41} and growth has previously been connected to hemodynamic characteristics.^{2,3,5,7,9,17,23,26,28,36,41} However, the mechanisms underlying aneurysm growth are not completely understood. In the present study, we attempted to evaluate the precise association of hemodynamics with growing regions of the aneurysm by analyzing clinical images of a growing CA at 3 stages of growth (over a period of 40 months) in a specific patient. In addition, we aimed to determine the role of hemodynamic characteristics in the aneurysm growth near the aneurysm wall and intrasaccular region. Understanding the linkage of hemodynamic features to aneurysm growth may provide new criteria predisposing the aneurysm to growth.

Primarily, wall shear stress (WSS) has been reported as an important contributor to aneurysm growth due to its direct effects on the physiology of endothelial cells (ECs).^3,17,36,37 The dysfunction of ECs has been linked to vessel wall remodeling.^3,17,36 Boussel et al.³ and Tanoue et al.³⁶ observed extremely low WSS in the growing regions of the CA in their studies on 7 and 2 patient cases, respectively. Liu et al.¹⁷ investigated the hemodynamic features of 3 large internal carotid artery aneurysms prior to rupture and reported that the best indicators of fatal rupture were low WSS, a higher aspect ratio, and an irregular shape. On the other hand, Ramachandran et al.²³ reported in their study of 178 patients harboring 198 unruptured CAs that low WSS did not statistically significantly differentiate between the stable and unstable aneurysms. Based on their study of 33 unruptured intracranial aneurysms, Sforza et al.²⁸ suggested that concentrated inflow streams blown into complex intrasaccular flow patterns, inducing non-uniform WSS distributions, could represent the characteristics of a hemodynamic environment that predisposes the aneurysm to growth. Moreover, the authors proposed that other hemodynamic parameters, including time-averaged wall shear stress (TAWSS), vorticity, flow structure, and oscillatory shear index (OSI), in addition to WSS, could be used to identify growing aneurysms. However, the role of these parameters in aneurysm growth has not been completely clarified. Taken together, the previous studies were unable to identify the exact mechanisms driving aneurysm growth, in part due to the lack of patient-specific data describing consecutive stages of aneurysm progression.^{3,17,23,28,36} Exploring the key hemodynamic features predisposing an aneurysm to growth can provide a clear understanding of the mechanisms underlying aneurysm growth and determine precise criteria to predict the risk of aneurysm evolution.

In this study, we compared patient-specific CA models corresponding to 3 distinct stages of aneurysm growth in one patient. Our goal was to elucidate the mechanisms underpinning CA growth and identify reliable criteria for predicting regions of aneurysm growth. A massively parallel computational fluid dynamics (CFD) code was applied to simulate the local hemodynamic features (including flow pattern, vorticity, WSS, TAWSS, and OSI) in the CA models. We analyzed the link between the local hemodynamics and aneurysm growth regions. Simulated hemodynamic flow patterns were also validated by particle image velocimetry (PIV) measurements of flow in physical versions of the studied models.

Methods

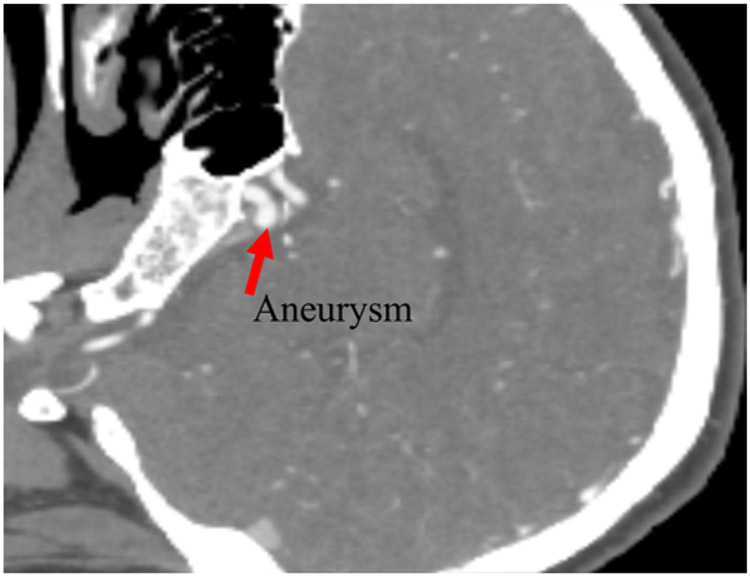
Computed tomography angiography was performed in a 49-year-old female patient with an unruptured CA. The CA, a centered aneurysm, was located in the internal carotid terminus (Fig. 1). The images obtained at the first examination correspond to the early stage in this study. A second scan was obtained 445 days after the initial scan (mid stage), and a third scan was obtained 759 days after the second scan (late stage; Supplemental Appendix).

FIG. 1.

CT angiogram showing the aneurysm in the early stage.

Aneurysm and Computational Modeling

The CTA data sets corresponding to the 3 stages were segmented, and the computational meshes representing the 3D topology were created using Materialise Mimics image processing software (Materialise). To quantify morphological changes between two consecutive stages of CA growth, a part-comparison analysis was conducted using the mesh software Materialise 3-matic (Materialise).

CFD Simulations Using HARVEY

An in-house developed massively parallel CFD code, HARVEY, was used to simulate hemodynamics in the 3 computational models.^19,25,24,32 The hemodynamics solver HARVEY uses an implementation of the lattice Boltzmann method (LBM) to solve the Navier-Stokes equations governing fluid flows in complex 3D geometries.^3,17,36 Discretizing space and velocity with a fixed Cartesian lattice, LBM models the fluid with a particle distribution function $f_i(\overrightarrow{x},t)$, which denotes the probability of finding a particle at time t and lattice point $\overrightarrow{x}$ with the discrete velocity ${\overrightarrow{c}}_i$. The lattice Boltzmann equation governs the time evolution of f:

$$\begin{gathered} f_i(\overrightarrow{x}+{\overrightarrow{c}}_i\delta t,t+\delta t)-f_i(\overrightarrow{x},t)= \\ -\omega (f_i(\overrightarrow{x},t)-f_i^{eq}(\overrightarrow{x},t)). \end{gathered}$$

The local equilibrium $f_i^{eq}(\overrightarrow{x},t)$ is the second-order expansion of the local Maxwellian-Boltzmann distribution.³ HARVEY’s implementation of LBM makes use of the standard D3Q19 velocity discretization and the single relaxation time (or BGK) collision kernel ω. A no-slip boundary condition is enforced on rigid vessel walls by the halfway bounce-back method, while finite difference boundary conditions are used at the inlets and outlets.³⁶ The convergence of the velocity solution was achieved in HARVEY with 40-μm resolution. To compute the WSS vector $\widehat{\tau }$, the stress tensor σ_αβ, is computed from the non-equilibrium distribution:

$$f_i^{neq}(\overrightarrow{x},t)=(fi(\overrightarrow{x},t)-f_i^{eq}(\overrightarrow{x},t)).$$

Using the approach from Matyka et al.,¹⁹ the outward normal vector $\widehat{n}$ is estimated, and the WSS vector components are computed as ${\tau }_a={\sigma }_{\alpha \beta }{\widehat{n}}_{\beta }-({\widehat{n}}_{\beta }{\sigma }_{\gamma \beta }{\widehat{n}}_{\gamma }){\widehat{n}}_{\alpha }$. Additional details about the HARVEY implementation, parallelization, and scaling may be found in the articles by Randles et al.^24,25 TAWSS and OSI are defined as:²¹

$$\begin{gathered} TAWSS=\frac{1}{T}{\int }_0^T\mid \overrightarrow{{\tau }_w}\mid dt \\ OSI=\frac{1}{2}\left(1-\frac{\mid {\int }_0^T{\overrightarrow{\tau }}_{w}dt\mid }{{\int }_0^T\mid {\overrightarrow{\tau }}_w\mid dt}\right) \end{gathered}$$

where $\overrightarrow{{\tau }_w}$ represents the instantaneous WSS vector and T is the period of the cardiac cycle.

Data Analysis

In-house MATLAB codes (release R2017a, The MathWorks Inc.) were applied to determine the statistical significance of the correlations (via sensitivity analysis) between hemodynamic factors and the morphological changes (growth rates) between the two consecutive growth stages.

Boundary Conditions

Simulations were performed under pulsatile inflow conditions. A modified internal carotid artery velocity waveform, obtained from Ford et al.,¹⁵ was applied at the inlet of the parent artery, and pulsatile inflow continued for 5 cardiac cycles (i.e., approximately 5 seconds). The inlet waveform had an average flow rate of 3 mL/sec. Zero pressure was assigned at the outlets. The inflow and outflow zones were defined at a distance away from the ostium of the aneurysm. Blood was assumed to be an incompressible Newtonian fluid.^{3,6,13,17,18,21,23,28,31,34,36}

Statistical Analysis of Computational Results

Statistical analysis was performed on the computational data from simulations to draw the criteria for classifying an aneurysm as growing or stable. This was performed in 2 stages: 1) determination of the cutoff value for which the distance from the vortex center to the aneurysm surface (denoted as R) had the maximum correlation with growth; and 2) identification of which set of parameters had the strongest prediction of aneurysm growth. In the first stage, we determined the cutoff value for distances between the aneurysm surface points and the vortex center, within which a high correlation existed between the growth rate and the distance to the vortex center. The location of the vortex in the intrasaccular region adjacent to the area of aneurysm growth was extracted precisely, and the distance of any point on the aneurysm surface to the vortex center was calculated. We used the Spearman rank-order correlation test to investigate the relationship between different hemodynamic parameters and the regions of growth. A nonparametric analysis was used because there was no underlying assumption of a linear relationship between the data sets. The growth data were iteratively split into 2 groups based on the calculated distance cutoff. At each iteration, the Spearman correlation coefficient was calculated. The cutoff maximizing the correlation coefficient was selected as our prediction criterion. Using the early- to mid-stage diastole data set at diastole as our training data, the cutoff was found to be 2.7 mm with a correlation coefficient of 0.86 (p < 0.0001). In the second stage, we used the mid- to late-stage data set as our test data to perform statistical analysis in order to identify the strongest predictor parameter or combination of parameters for regions of aneurysm growth. We have broadened the range of geometric changes (0.5 mm to 1.65 mm) between mid and late stages to investigate whether our developed predictive criteria (WSS < 0.5 pa ^{3,17,23,28,36} TAWSS < 0.5,²⁸ vorticity <0.1 sec⁻¹,¹⁷ and OSI > 0.1)²⁸ and the distances from the vortex center (denoted by R) (< 2.7 mm) accurately identify the growing regions of the aneurysm. The surface of the aneurysm was discretized into regular patches (approximately 6000) with a size of 0.2 mm corresponding to 50 ECs. The growth rate and hemodynamic parameters for each patch were calculated as the mean overall surface points inside that patch. Then, true positive, true negative, false positive, and false negative were calculated for entire patches over the surface of the mid-stage aneurysm. True positive indicates the number of patches on the surface of the CA that reflect a growth larger than 0.5 mm when predictive criteria are present. False positive indicates the number of points on the surface of the CA that signify a growth less than 0.5 mm when predictive criteria are present. True negative indicates the number of points on the surface of the CA that signify a growth less than 0.5 mm when the predictive criteria are not present. False negative indicates the number of points on the surface of the CA that reflect a growth larger than 0.5 mm when the predictive criteria are not present. We then computed the specificity, sensitivity, positive predictive value (PPV), and negative predictive value (NPV) of hemodynamic parameters versus growth between the mid and late stages over the entire surface of the mid-stage aneurysm. Sensitivity is defined as 100 × true positive/(true positive + false negative); specificity is 100 × true negative/(true negative + false positive); PPV is 100 × true positive/(true positive + false positive); and NPV is 100 × true negative/(true negative + false negative). In this study, sensitivity refers to the ability of a test to correctly classify the conditions identifying an aneurysm as growing, and specificity refers to the ability to correctly classify the conditions identifying an aneurysm as not growing.

Results

Anatomical Variations

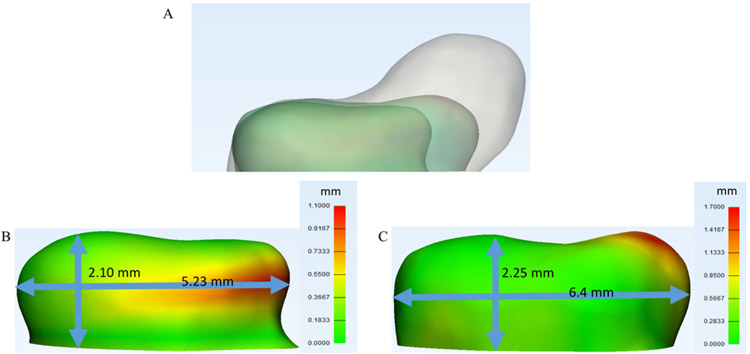
Anatomical variations between the 3 investigated aneurysm models are illustrated in Fig. 2A. The variations among geometries were also quantified by calculating displacements between the early and mid stages, as well as between the mid and late stages (Fig. 2B and C). In Fig. 2, it is evident that the aneurysm grew the most on the right portion of the dome (from the reader’s perspective).

FIG. 2.

A: Illustration of the anatomical variations between the 3 investigated aneurysm models. B and C: Displacement maps between early and mid stages (B) and mid and late stages (C).

Validation Results

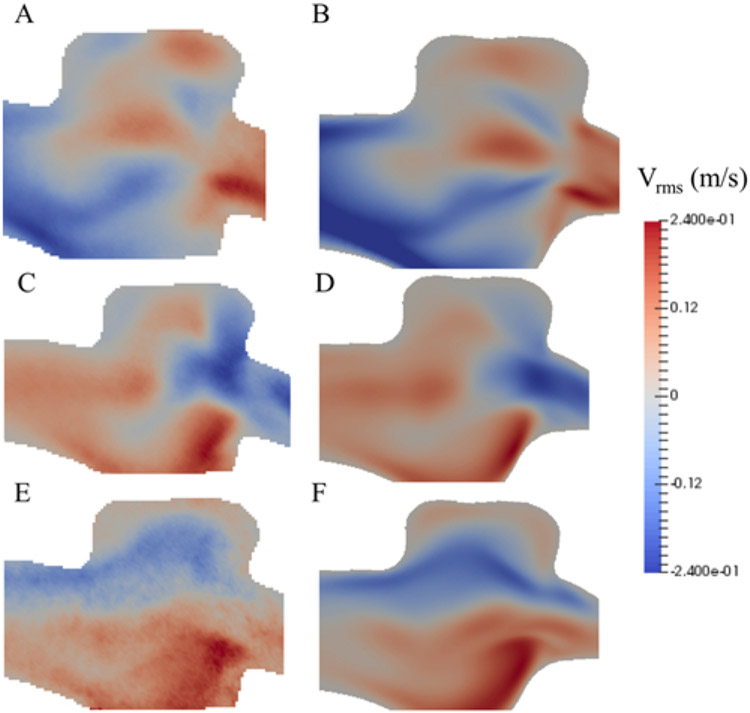
The CFD results obtained from HARVEY were compared with the velocities measured by PIV for the purpose of validation. The flow distributions and velocities obtained from both techniques agreed well, for all 3 stages, under steady-state conditions. Figure 3 represents the comparison between the velocity vector distribution along the center plane of the aneurysm measured by PIV and the CFD simulation.

FIG. 3.

Velocity vector distribution along the center plane of the aneurysm, in the X, Y, and Z directions for the early stage obtained from HARVEY (B, D, and F) and measured by PIV (A, C, and E). V_rms = root mean square velocity magnitude.

Pulsatile Flow Results

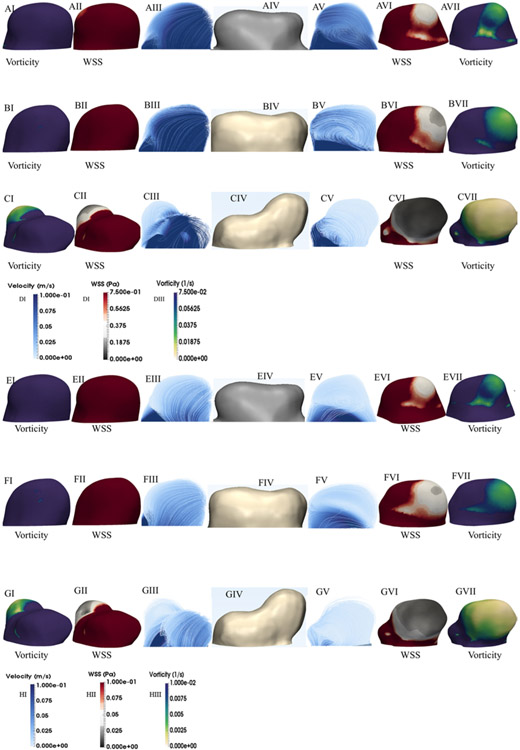
Examination of the flow patterns within the aneurysm revealed the existence of vortical structures, with high flow instability within the aneurysm sac and in the region adjacent to the growing area of the CA (Fig. 4A-C and E-G). The images on the left represent the relatively stable area of the aneurysm, while the images on the right represent the region of aneurysm growth. Figures 2 and 4 show that the center of the vortex structure corresponds to the area of the CA with the highest growth rate. It is evident from Fig. 4AV-4EV, 4BV-4FV, and 4CV-4GV that during a cardiac cycle, the flow pattern exhibits recirculation within the aneurysm sac; formed vortex structures move, do not persist, and change in size and shape. In addition, the minimum values for both vorticity and WSS occur at the area of recirculation (Fig. 4A-G). Furthermore, the flow impingement zone is narrow in all aneurysm growth stages, particularly at systole. The flow impingement zone is associated with the region of elevated WSS because of the inflow stream.

FIG. 4.

A–C: Flow pattern, WSS, and vorticity distribution at systole for the early (A), mid (B), and late (C) stages. The left side demonstrates the nongrowing side of the aneurysm, while the right side corresponds to the growing side of the aneurysm. Note that the first column from left and right show vorticity, the second from left and right show the WSS, and third columns from both directions show the flow pattern. E–G: Flow pattern, WSS, and vorticity distribution at diastole for the early (E), mid (F), and late (G) stages. D and H: Color bars of velocity, WSS, and vorticity at systole and diastole, respectively.

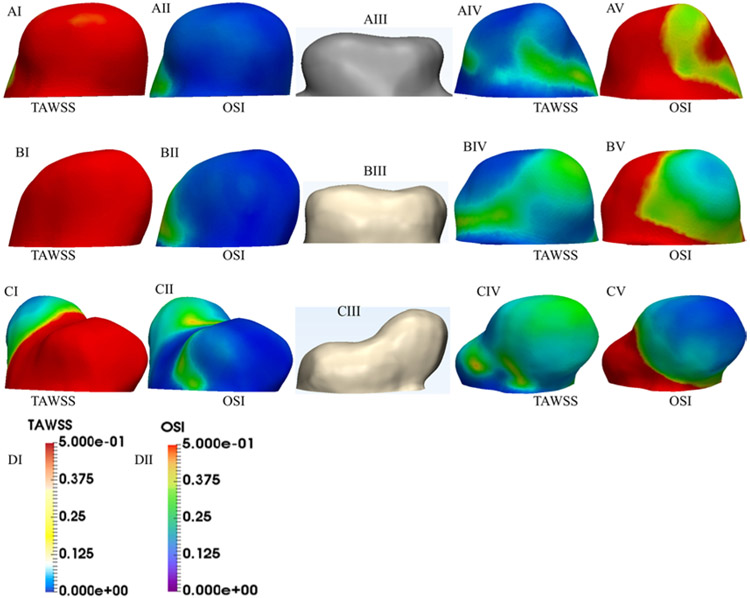
The distributions of TAWSS and OSI are indicated in Fig. 5. OSI is a dimensionless parameter that characterizes the oscillations in WSS direction over a cardiac cycle. OSI has been widely used to identify the regions experiencing flow separation, which leads to the creation of a recirculation zone.^18,28 The areas of high OSI and lower TAWSS values are consistent with the recirculation areas corresponding to the aneurysm growth zone.

FIG. 5.

A–C: TAWSS and OSI distributions for the early (A), mid (B), and late (C) stages, respectively. The first column from left and second from right show TAWSS, and the second column from left and first from right show the OSI. D: Color bars of TAWSS and OSI.

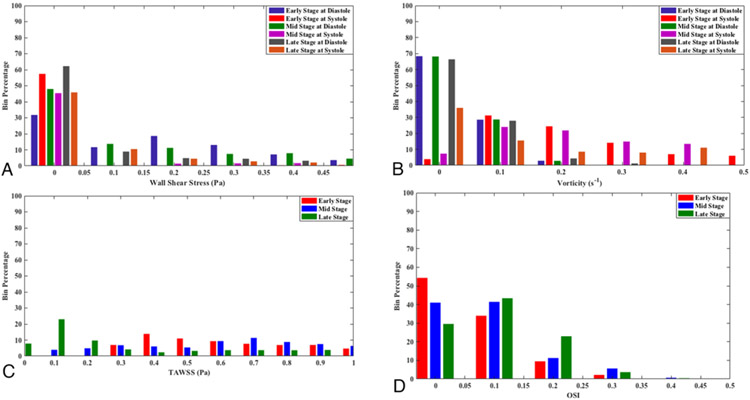
Figure 6 presents the bin percentage (i.e., the ratio of data points in each bin to total number of data points) of the WSS, vorticity, TAWSS, and OSI. Earlier studies suggested that aneurysm growth occurs in regions of abnormally low WSS (0 < WSS < 0.5 Pa).^3,17,28,36 This range is used to show the WSS and vorticity data. In all 3 stages of growth, large areas of the aneurysm experience low WSS and vorticity magnitude, particularly at diastole. The bin percentages of TAWSS and OSI indicate that the low TAWSS and high OSI areas at the late stage are significantly larger than in the early and mid stages.

FIG. 6.

Bin percentages of WSS (A), vorticity (B), TAWSS (C), and OSI (D).

Statistical Analysis Results

Based on the results shown in Figs. 2,4, and 5, it is clear that the near aneurysm wall/intrasaccular hemodynamic features exhibit different distributions in the growing and stable sides of the CA. In this part, we applied statistical analysis to determine which hemodynamic parameter(s) can be used as the best prediction index for aneurysm growth. The mean specificity, sensitivity, PPV, and NPV for hemodynamic parameters (WSS, TAWSS, OSI, vorticity, and R) are demonstrated in Table 1. To establish new strong criteria to accurately predict the aneurysm growth, we examined whether any combination of TAWSS/WSS/OSI/vorticity and R can help to improve the statistical results. Table 1 demonstrates that the combination of TAWSS and R can stand as a new criterion for identifying a growing aneurysm.

TABLE 1.

Statistical analysis between growth and hemodynamic features in the growing regions of the mid-stage model

Hemodynamic Feature	Sensitivity	Specificity	PPV	NPV
R	80.14	56.86	60.39	70.26
TAWSS	70.77	90.17	85.98	75.33
TAWSS & R*	80.58	86.68	86.86	73.30
OSI	41.79	65.11	53.11	48.13
OSI & R	73.94	68.56	64.93	67.41
TAWSS, OSI, & R	71.76	89.83	87.61	65.86
WSS (at systole)	29.05	97.60	90.97	59.78
R & WSS (at systole)	64.71	97.29	93.93	69.94
WSS (at diastole)	94.99	28.84	24.99	95.06
R & WSS (at diastole)	73.59	85.69	68.34	95.16
Vorticity (at systole)	53.01	89.36	79.50	64.78
R & vorticity (at systole)	72.87	88.88	86.21	68.69
Vorticity (at diastole)	98.46	16.25	22.85	97.57
R & vorticity (at diastole)	77.79	75.66	66.66	97.78

The mean magnitudes of the analysis parameters are presented; R indicates the distance from the vortex center to the aneurysm surface at diastole. Values are percentages.

^*Given its high sensitivity, PPV, specificity, and NPV, this combination may be applied as the best identification metrics for aneurysm growth.

Discussion

The main purpose of this study was to introduce new criteria in predisposing the aneurysm to growth. We investigated the mechanisms underpinning the growth in patient-specific CA models corresponding to 3 stages of CA growth (over a period of 40 months) in one patient. The CFD simulations with HARVEY were utilized to study the hemodynamics in consecutive stages of a growing CA. Aneurysms are classified as growing if an increase in size (displacement) larger than 0.5 mm can be measured in any direction on at least 5% of the aneurysm points from the initial examination; aneurysms are classified as stable if they do not enlarge more than 0.5 mm for at least 9 months.²⁸ We classified our aneurysm as growing (Fig. 2B and C), since it exhibited an increase in size larger than 0.5 mm between two consecutive examinations (the second scan 445 days after the initial and the third scan 759 days after the second scan).

Wall shear stress has been shown to be the primary measure of the wall/flow interaction in the arterial network and the principal physiological stimulus to ECs, which are linked to arterial wall remodeling.^{1-3,5-7,9-11,16,17,27,30,33,36,38,41} sforza et al.²⁸ Suggested that both intrasaccular flow characteristics and wall/flow interactions may be associated with aneurysm growth. Cebral et al.⁴ showed that local flow conditions have an important influence on the local evolution and remodeling of the aneurysm wall. Cebral et al. also reported that rupture sites are characterized by thin wall regions and low WSS values. Among the intrasaccular flow characteristics, a recirculation flow structure, where the blood flow velocity is low, has also been identified as a risk factor for aneurysm growth.^4,8,36 Several in vitro studies have reported that exposing ECs to slow circulating flow (abnormally low WSS) caused the absence of cell alignment, EC loss, and thrombus formation, which is linked to aneurysm wall digestion and favors aneurysm rupture.^{12,14,22,24,28,29,35,39,40,42} Despite these findings, the association between the recirculation area and growing regions of the aneurysm is not yet completely understood.

In the present study, we focused on both the near aneurysm wall/intrasaccular hemodynamic characteristics (recirculation zone, flow instability, impingement area) and the hemodynamic characteristics associated with the aneurysm wall/intrasaccular flow interactions (WSS, TAWSS, OSI, and vorticity). Our results (Fig. 4) indicated that the WSS and OSI distributions are in agreement with those of previous studies^3,17,28,36 that reported larger areas of low WSS and higher values of OSI in areas of aneurysm growth compared with in the stable areas. The impingement regions were smaller in growing areas of the CA than in stable regions, which is consistent with the finding of Cebral and Raschi.⁵ On the other hand, our results showed that flow complexity and instability occurred in the regions adjacent to the aneurysm wall in the growing areas of the CA (Fig. 4). The recirculation area corresponding to the area with a growth greater than 0.5 mm was consistent with regions of low TAWSS, WSS, and vorticity, and high OSI (Figs. 4 and 5).

To identify hemodynamic parameter(s) displaying statistically significant consistency with growing regions of the aneurysm, we performed statistical analysis. Our statistical analysis demonstrated that the combination of TAWSS and the distance from the center of recirculation area may be applied as the best identification metrics for aneurysm growth (Table 1) because this combination has the highest sensitivity and PPV, and relatively high specificity and NPV. The exposure of ECs to recirculating flow, with low TAWSS (< 0.5 Pa), has been previously reported to be damaging in vitro.^{11,29,33,35,39} Therefore, an unstable, recirculating flow structure within the aneurysm sac created in the region adjacent to the aneurysm wall with low TAWSS may be introduced as an accurate criterion to explain the hemodynamic conditions predisposing the aneurysm to growth. More importantly, this can be used to predict the risk of growth.

Typically, the geometric changes are based on measuring the size on a slicing plane.^3,28 Such analysis can miss 3D topographical changes that occur during the unpredictable aneurysm growth. Therefore, we employed a technique to measure the morphological changes in 3 dimensions, which is more complete and accurate than previous methods. To this end, we used a part-comparison analysis method from Mimics to quantify the morphological variations between two consecutive stages of aneurysm growth. The analysis computes the local Hausdorff distance showing the local morphological differences between the two 3D geometries. Our analysis showed that the aneurysm growth occurred in volume and neck diameter, highlighting the importance of our technique in quantifying the anatomical variations.

Limitations of the Study

There are several assumptions applied in the present study. As non-Newtonian effects have been shown to be negligible in aneurysm flow simulations due to high shear rates,^{4,17,21,28,34-36} blood is modeled as a Newtonian fluid. The usual assumption of a rigid wall is applied for the arterial wall.^{4,17,28,35,36} It has been shown that results of flow instabilities are not affected by the rigid wall assumption in the aneurysm.³⁹ Zero pressure is specified at the outlets. A potential limitation is that only one patient data set is used. To generalize the conclusions drawn from our observations of a single aneurysm case, our study will be extended to further cases in the future. Here, we identified predictive criteria for aneurysm growth and laid out the justification for future large-scale verification. Aneurysm growth may be associated with different kinds of flow conditions in different aneurysms; for instance, the flow conditions influence the remodeling of the aneurysm wall in several different ways. Further studies are required to completely understand how the flow condition is associated with aneurysm growth in different aneurysms. As a patient-specific measured waveform was unavailable, we used a conventional velocity waveform (applied at the inlet of the parent artery) from a patient similar to our studied case with a CA located in the internal carotid artery.¹⁵ To relieve the inconsistencies in the creation of geometric models from medical images, which could affect the accuracy of aneurysm growth measurements, we segmented the CTA data sets corresponding to the 3 stages using Mimics software. Mimics was also used to create the computational meshes representing the 3D topology. Using Mimics could deduct the errors caused by manual segmentations. Moreover, morphological changes between two consecutive stages of CA growth were quantified using a part-comparison analysis, which was conducted using Materialise 3-matic software. The 3D models corresponding to two consecutive stages of CA growth (early and mid stages as well as mid and late stages) were overlaid using global registration to exclude differences due to different patient positioning. The present investigation has attempted to elucidate the link between the hemodynamic features and regions of growth in a growing CA where a patient-specific study is applied to reconstruct the aneurysm growth models. Our results for local hemodynamic features at 3 stages of CA growth indicated that the high-frequency velocity fluctuations, vortices, and instabilities, and low TAWSS can form a condition to predispose the aneurysm to growth.

Conclusions

Three patient-specific CA models for 3 stages of aneurysm growth were compared in one patient. The models were reconstructed based on the data from a patient-specific study. Thus, the classification of growing versus stable regions of the aneurysm is unique and accurate. Our study provides fundamental knowledge on hemodynamic conditions that may prompt aneurysm progression. Our precise analysis establishes new predictive criteria that can be used as a potential tool to differentiate stable from growing regions of the aneurysm during preinterventional planning.

ABBREVIATIONS

CA

cerebral aneurysm

CFD

computational fluid dynamics

EC

endothelial cell

LBM

lattice Boltzmann method

NPV

negative predictive value

OSI

oscillatory shear index

PIV

particle image velocimetry

PPV

positive predictive value

TAWSS

time-averaged WSS

WSS

wall shear stress