Extended Capture Range of Rigid 2D/3D Registration by Estimating Riemannian Pose Gradients

Abstract

Traditional intensity-based 2D/3D registration requires near-perfect initialization in order for image similarity metrics to yield meaningful updates of X-ray pose and reduce the likelihood of getting trapped in a local minimum. The conventional approaches strongly depend on image appearance rather than content, and therefore, fail in revealing large pose offsets that substantially alter the appearance of the same structure. We complement traditional similarity metrics with a convolutional neural network-based (CNN-based) registration solution that captures large-range pose relations by extracting both local and contextual information, yielding meaningful X-ray pose updates without the need for accurate initialization. To register a 2D X-ray image and a 3D CT scan, our CNN accepts a target X-ray image and a digitally reconstructed radiograph at the current pose estimate as input and iteratively outputs pose updates in the direction of the pose gradient on the Riemannian Manifold. Our approach integrates seamlessly with conventional image-based registration frameworks, where long-range relations are captured primarily by our CNN-based method while short-range offsets are recovered accurately with an image similarity-based method. On both synthetic and real X-ray images of the human pelvis, we demonstrate that the proposed method can successfully recover large rotational and translational offsets, irrespective of initialization.

1. Introduction

The localization of patient anatomy during surgical procedures is an integral part of navigation for computer-assisted surgical interventions. Traditional navigation systems use specialized sensors and fiducial objects to recover the pose of patient anatomy [28,17,25], which are often invasive, sensitive to occlusion, and complicate surgical workflows.

Fluoroscopic imaging provides an alternative method for navigation and localization. Fluoroscopy is widely used during surgery and is not sensitive to the limitations imposed by other surgical navigation sensors. Therefore, a 2D/3D registration between the intra-operative 2D X-ray imaging system and a 3D CT volume may be used to perform navigation [19]. Such tracking approaches based on 2D/3D registration find applications in a wide spectrum of surgical interventions including orthopedics [29,23,10], trauma [8] and spine surgery [14]

1.1. Background

The two main variants of 2D/3D registration are split between intensity-based and feature-based approaches. Feature-based approaches require manual or automated segmentation or feature extraction in both of the imaging modalities and are optimized in a point-to-point, etc. fashion [24]. The accuracy of the feature-based methods directly relies on the accuracy of the feature extraction pipeline.

Intensity-based approaches, on the other hand, directly use the information contained in pixels of 2D images and voxels of 3D volumes. A typical intensity-based registration technique iteratively optimizes the similarity measure between simulated X-ray images known as digitally reconstructed radiographs (DRRs) that are generated by forward projecting the pre-operative 3D volume, and the real X-ray image [15]. The optimization problem for registering a single view image is described as:

$$\underset{{}_{\theta \in SE(3)}}{\min }\mathcal{S}(I,\mathcal{P}(\theta ;V))+\mathcal{R}(\theta )$$ (1)

In Eq. 1, I denotes the 2D fluoroscopic image, V the preoperative 3D model, θ the pose of the volume with respect to the projective coordinate frame, $\mathcal{P}$ the projection operator used to create DRRs, $\mathcal{S}$ the similarity metric used to compare DRRs and I, and $\mathcal{R}$ the regularization over the plausible poses.

1.2. Related work

A reasonable initial pose estimate is required for any intensity-based registration to find the true pose. A common technique used for initialization is to annotate corresponding anatomical landmarks in the 2D and 3D images and solve the PnP problem [19,3]. Another technique requires a user to manually adjust an object’s pose and visually compare the estimated DRR to the intraoperative 2D image. These methods are time-consuming and challenging for inexperienced users, which makes them impractical during surgery. Alternatively, some restrictions may be imposed on plausible poses to significantly reduce, or eliminate, the number of landmarks required for initialization [19]. SLAM-based inside-out tracking solutions were suggested to provide re-initialization in 2D/3D registration settings. These group of methods only provide relative pose updates and do not contribute to the estimation of the absolute pose between the 2D and 3D data [7,11].

In [10], a single-landmark was used to initialize the registration of a 2D anterior-posterior (AP) view of the pelvis, and further views were initialized by restricting any additional C-arm movement to orbital rotations. However, for certain applications, such as the chiseling of bone at near-lateral views, it is not feasible to impose such restrictions on the initial view or C-arm movements.

Several works attempted to solve the ill-posed 2D/3D registration problem using convolutional neural networks (CNN). An early work by Miao et al. directly regressed the pose between simulated radiographs and X-ray images using CNNs [20]. Recent works combined the geometric principles from multi-view geometry and the semantic information extracted from CNNs to improve the capture range of 2D/3D registration. In [2,3,6], distinct anatomical landmarks were extracted from 2D X-ray images using CNNs and were matched with their corresponding locations on the 3D data. These 2D/3D correspondences were then used to estimate the relative projection matrix in a least-squares fashion. Similarly, a multi-view CNN-based registration approach used CNNs for correspondence establishment and triangulation between multiple X-ray images and a single 3D CT [16].

To overcome current shortcomings, we propose a novel CNN-based approach that is capable of learning large scale pose updates between a 2D X-ray image and the corresponding 3D CT volume. For large offsets, the network effectively learns the pose adjustment process that a human could conduct to initialize an intensity-based optimization. When close to the ground truth pose, updates will be derived by a classic intensity-based method for fine adjustments. Our proposed method exhibits a substantially extended capture range compared to conventional image-based registration [10,19]. Although similar effort to achieve robustness to poor initialization is made in [14] by using a multi-start optimization strategy within an intensity-based registration framework, their method was limited to level-check in spine surgery and the 2D radiographs acquired using a portable X-ray unit have a large field-of-view of the anatomy which is not suitable for interventions where only local radiographs is available (for example, those using mobile C-arms).

2. Methods

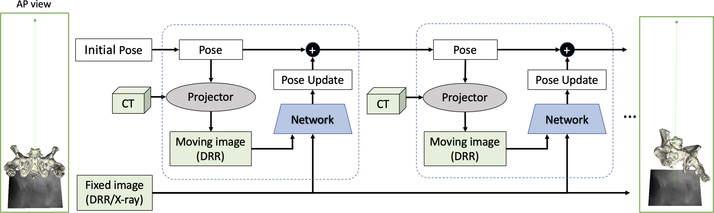
Similar to previous approaches, we employ an iterative strategy to sequentially approach the correct relative pose. In each iteration, a DRR is rendered from CT using the current pose estimate and compared to the fixed, target X-ray image using a CNN (Fig. 1). The network is trained to predict the relative 3D pose between the two 2D input fluoroscopy images using an untangled representation of 3D location and 3D orientation. While the proposed approach still requires the selection of a starting pose, the selection thereof is no longer critical because the image similarity metric estimated by our CNN approximates the geodesic distance between the respective image poses, which in theory, makes the registration problem globally convex (Sec. 2.1).

Fig.1.

Context-based registration workflow in an iterative scheme. The registration pipeline initiates with a fixed 2-D image, a 3-D CT, and a pose guess. The anterior-posterior pose of the anatomy is used for all images as an initial guess. The pose of the X-ray camera is updated in each iteration and forward projected to generate the moving image as part of the input of the network.

2.1. Image similarity, the Riemannian manifold, and geodesic gradients

Among the biggest challenges in 2D/3D image registration is the question of how to properly model the similarity between two images. This is because pose updates of iterative registration algorithms are generally derived from the gradient of the selected image similarity function. Conventional image similarity metrics, such as cross correlation [10] or normalized gradient information [1], only evaluate local intensity patterns that may agree in some areas while being substantially different in others. Since the changes in transmission image appearance can be substantial even for small pose differences, the aforementioned property of conventional image-based similarity metrics gives rise to a highly non-convex optimization landscape that is characterized by many local minima even far from the ground truth. It would be appealing to express 2D image similarity as the relative pose difference between the two viewpoints. Expressed in terms of the Riemannian tangent space, this image similarity metric defined over viewpoints is convex and thus effectively overcomes the aforementioned challenges. Given SE(3) as Special Euclidean Group in 3D space, the distance between two rigid-body poses $T=\exp (\widehat{p})\in SE(3)$ and $T^{\prime }=\exp \left({\widehat{p}}^{\prime }\right)\in SE(3)$ can be defined as the gradient of the geodesic distance on the Riemannian manifold as [21,12]:

$$g\left(p,p^{\prime }\right)=\nabla \mathrm{dist}\left(p,p^{\prime }\right)=-2{\log }_{p^{\prime }}(p),$$ (2)

where ${\log }_{p^{\prime }}(.)$ denotes the Riemannian logarithm at p′; $\widehat{p}$ and ${\widehat{p}}^{\prime }$ are the elements of the Lie algebra se(3), the tangent space to SE(3); $\left(p,p^{\prime }\right)\in {ℝ}^6$ are the twist coordinates. The geodesic gradient g(p, p′) indicates the direction of update from one viewpoint to the other, considering the structure of SE(3). It is the generalization of straight lines of Euclidean geometry on Riemannian manifolds. We refer to [22] for a more detailed description and use the implementation provided in [21] for the experiments reported here.

In the case of 2D/3D image registration, only the pose of the moving DRR is known while the pose of the fixed, target X-ray image must be recovered and is thus unknown a priori. This means that Eq. 2 cannot be computed in practice to evaluate image similarity. However, if many images of similar 3D scenes with accurate viewpoint pose information are available then this image similarity function can be approximated with a CNN that processes both 2D images. Given two images I and $\widehat{I}$ with viewpoints p and $\widehat{p}$, respectively, we seek to learn the parameters θ of a CNN $f(I,\widehat{I},\theta )$ such that

$$f(I,\widehat{I},\theta )=g(p,\widehat{p})+ϵ,$$ (3)

where ϵ is an irreducible error.

2.2. Network structure

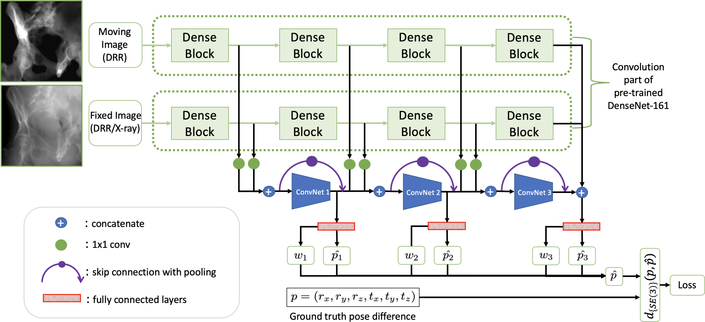
We design a CNN architecture that takes two images of the same size as an input and predicts the gradient of the geodesic distance on the Riemannian manifold between the respective viewpoints, as per Sec. 2.1. An overview of the architecture is provided in Fig. 2. The images first pass through the convolutional part of a Siamese DenseNet-161 [13] pre-trained on ImageNet [5].

Fig.2.

A high-level overview of the proposed network architecture. The input images include a fixed, target image and a moving DRR image that is generated based on the current pose estimate of each iteration. To train the network, both input images are synthetically generated DRR images with precisely known camera poses with respect to the 3D CT volume. p represents the pose difference between the two image viewpoints in twist form, which establishes the target of the network. The relative pose ${\widehat{p}}_i$ and respective ”certainty” w_i is estimated at three different depths i in our CNN to capture both global and local information.

Feature maps of deeper layers are widely assumed to contain higher-level semantic information, while most information on spatial configuration and local image appearance is lost; yet, local features are likely informative for predicting pose updates as relative image poses get closer. We hypothesize that both – global and local – representations carry information that is relevant for regressing relative pose solely based on image content. Therefore, we 1) extract feature maps of both images at three different depths i of DenseNet, 2) concatenate them, and 3) pass them through additional CNNs and fully connected layers to individually estimate the geodesic gradient ${\widehat{p}}_i$. During inference, it is unclear which of these three estimates ${\widehat{p}}_i$ will be most appropriate at any given scenario and we surrender this importance weighting task to the CNN itself. This is realized by simultaneously regressing a weight w_i corresponding to the geodesic gradient prediction ${\widehat{p}}_i$ at the respective depth i. After applying softmax to the weights w_i for normalization, the final output of the CNN ${\widehat{p}}_i={\sum }_{i=1}^3{w}_i\cdot {\widehat{p}}_i$ is evaluated end-to-end together with the other three predictions.

During experimentation, we found that rotational pose changes were captured quite well while purely translational displacements could not be recovered accurately. Following [18], we replace all convolution layers after feature extraction from DenseNet by coordinate convolution (CoordConv) layers [18], which gives convolution filters access to the input image coordinate by appending a normalized coordinate channel to the respective feature representation.

We use the proposed method [10] as an effective initialization strategy to quickly approach the desired X-ray camera pose from an arbitrary initialization but then rely on a recent image-based method [10] to fine-tune the final pose once after convergence. Once the gradient update is below a certain threshold that is comparable with the capture range of the image-based registration method, we surrender to purely image-based registration to achieve very high accuracy.

3. Experiments and Results

3.1. Datasets

We select 7 high-resolution CT volumes from the NIH Cancer Imaging Archive [4] as the basis for our synthetic dataset and split data on the CT level into 5 volumes for training, 1 for validation, and 1 for testing. For each CT volume, a total of 4311 synthetic DRR images were generated from different positions (randomly sampling poses with rotations in LAO/RAO ∈ [−40°, 40°] and CRAN/CAUD ∈ [−20, 20], and translations of ±75mm in all directions). DRRs and corresponding ground truth poses are generated using DeepDRR [27,26].

During training, we then sample two DRRs generated from the same 3D CT volume with random and different perspectives and optimize the parameters of our network to regress the geodesic gradient that represents the relative pose difference. We use the open-source geomstats package to perform all calculations pertaining to the Riemannian tangent space[21]. Each image input to the model is log-corrected followed by Contrast Limited Adaptive Histogram Equalization and Gaussian filter to blur out high-frequency signal. Images are then normalized within [−1, 1] and a maximum 40% random contrast and intensity to increase the robustness of generalization on real X-ray data. The training was performed on a single Nvidia Quadro P6000 GPU. Batch size used for training was 16; the learning rate starts from 1e-6, and decreases to 30% after every 30,000 iterations.

3.2. Registration of simulated X-ray images

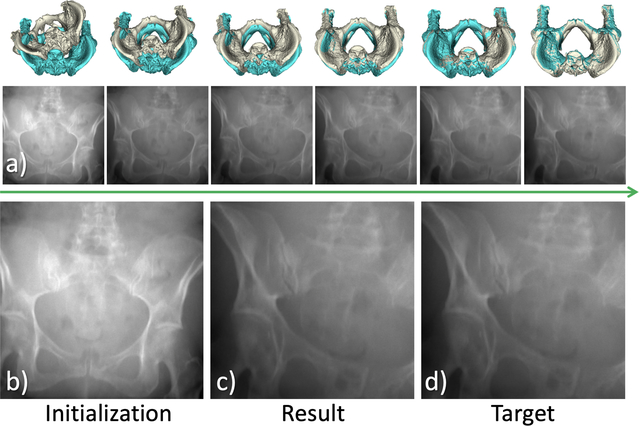
While the registration is conducted in its iterative scheme, as long as the gradients are driving in a coherent direction, we allow the network to predict gradients with minor errors during the intermediate steps to compensate small errors and make our registration method robust. An example is shown in Fig. 3.

Fig.3.

Example of pose update and registration on synthetic data. In (a), intermediate DRRs are rendered from initialization towards the final estimation. In (b-d) the initial DRR in AP view, the final predicted DRR view, and the target image are shown respectively.

In Table. 1 we present the rotational and translational misalignment errors for the 196 synthetic test cases with known ground truth. Violin plot of distribution for the misalignment with three methods are attached in the supplementary material. We compare the final pose of our CNN-based registration to intensity-based registration using the covariance matrix adaptation evolution strategy (CMA-ES) [10]; both initialized at AP View. Among all the 196 test cases, 15 cases failed due to their non-typical appearance which were not seen in the images of the training set. Only the numerical comparison of the 181 success case using our method with the other two approaches is included in Table 1. Since the testing images mostly have large offset from the AP view (initialization), the image-based registration method fails in all tested cases and results are trapped in local minima near the initialization.

Table 1.

Comparison of the the rotational and translational misalignment errors of the proposed sequential, contextual registration with standard image-based registration on simulated images. All methods are initialized at AP view.

	Contextual Registration		Image-based Registration		Sequential Registration
	Rotation	Translation	Rotation	Translation	Rotation	Translation
Mean	4.80	75.6	17.4	258	0.12	1.58
Standard deviation	2.80	60.4	5.38	81.2	0.08	0.89
Median	4.23	62.2	17.8	265	0.10	1.39
Minimum	1.01	10.9	1.72	37.5	0.01	0.29
Maximum	11.6	342	26.0	385	0.35	3.93

3.3. Registration results on real X-ray images

The registration of a real X-ray image to pre-operative CT is more complicated than simulated images. The X-ray images were acquired from a Siemens CIOS Fusion C-arm. To reduce ambiguity caused by the relative motion between different rigid and non-rigid anatomies from pre-operative CT to intra-operative X-ray, we used the segmentation of the pelvis in CT in the image-based registration method. Although following the same pre-processing scheme as we did on simulated image during training, the domain shifting still deteriorates the context-based prediction compared with simulated data. As a result, only 8 out of 22 tested real X-ray converge in our experiment. Once converged, the accuracy of the algorithm could reach the level of typical image-based method. The overall statistics of all 22 tested real X-ray images are shown in Table 2.

Table 2.

Comparison of the the rotational and translational misalignment errors of the proposed sequential, contextual registration with standard image-based registration on real X-ray images. All methods are initialized at AP view.

	Contextual Registration		Image-based Registration		Sequential Registration
	Rotation	Translation	Rotation	Translation	Rotation	Translation
Mean	11.5	61.7	14.3	200	6.95	39.4
Standard deviation	6.16	27.4	8.46	118	5.13	34.1
Median	12.3	60.0	11.9	171	8.13	43.2
Minimum	1.48	16.4	4.15	61.5	0.25	1.17
Maximum	24.4	113	35.5	473	14.7	104

4. Discussion and Conclusion

Our method is not compared with other CNN-based prior work because we consider our work sufficiently different from the prior works. [20] only demonstrates successful pose regression for artificial, metallic, objects. The use of the sum-of-squared distances similarity loss during training most likely does not generalize to natural anatomical objects. [2,3,6] all rely on manually identified anatomically relevant landmarks in 3D. [16] requires multiple views - the method proposed in this paper is compatible with applications limited to single views.

Our method largely increases the capture range of the 2D/3D registration algorithm as shown in Table 1, and indicates robustness against arbitrary view initialization. The proposed sequential registration strategy benefits from both the effective global search of the learning-based approaches as well as the accurate local search of the image-based methods, which jointly overcome the limitation of previous methods.

Currently, our pipeline combines pose update proposals obtained from three learning-based sub-networks. Upon convergence, the recovered poses are reasonably close to the desired target view. This learning-based architecture is capable of integrating pose updates provided by an intensity-based registration algorithm, the corresponding weight of which could be learned end-to-end. Since such algorithm cannot provide an estimate of the geodesic gradient, careful design of the overall loss function is necessary in a future work. A prospective cadaver study would allow implantation of radiopaque fiducial markers that can provide accurate ground truth, enabling these investigations and retraining of the CNN on real data.

In conclusion, we have shown that our CNN model is capable of learning pose relations in the presence of large rigid body distances. This is achieved by approximating a globally convex similarity metric in our CNN-based registration pipeline. The proposed network regresses a geodesic loss function over SE(3) and produces promising results on the simulated X-ray images.

While our solution produces updates along the correct direction when tested on real data, the performance is compromised, particularly if tools and implants are present in the field of view. As the next step, we plan on more carefully analyzing the performance and failure modes of our method on clinical data. Improving generalization of our method to clinical X-rays is of highest importance. While pre-processing or style-transfer may be feasible, unsupervised domain adaptation or retraining on small clinical datasets that could be annotated using approach similar to [9] can also be considered.