Abstract
Ca2+ spikes initiated in the distal trunk of layer 5 pyramidal cells (PCs) underlie nonlinear dynamic changes in the gain of cellular response, critical for top-down control of cortical processing. Detailed models with many compartments and dozens of ionic channels can account for this Ca2+ spike-dependent gain and associated critical frequency. However, current models do not account for all known Ca2+-dependent features. Previous attempts to include more features have required increasing complexity, limiting their interpretability and utility for studying large population dynamics. We overcome these limitations in a minimal two-compartment biophysical model. In our model, a basal-dendrites/somatic compartment included fast-inactivating Na+ and delayed-rectifier K+ conductances, while an apical-dendrites/trunk compartment included persistent Na+, hyperpolarization-activated cation (Ih), slow-inactivating K+, muscarinic K+, and Ca2+ L-type. The model replicated the Ca2+ spike morphology and its critical frequency plus three other defining features of layer 5 PC synaptic integration: linear frequency-current relationships, back-propagation-activated Ca2+ spike firing, and a shift in the critical frequency by blocking Ih. Simulating 1000 synchronized layer 5 PCs, we reproduced the current source density patterns evoked by Ca2+ spikes and describe resulting medial-frontal EEG on a male macaque monkey. We reproduced changes in the current source density when Ih was blocked. Thus, a two-compartment model with five crucial ionic currents in the apical dendrites reproduces all features of these neurons. We discuss the utility of this minimal model to study the microcircuitry of agranular areas of the frontal lobe involved in cognitive control and responsible for event-related potentials, such as the error-related negativity.
SIGNIFICANCE STATEMENT A minimal model of layer 5 pyramidal cells replicates all known features crucial for distal synaptic integration in these neurons. By redistributing voltage-gated and returning transmembrane currents in the model, we establish a theoretical framework for the investigation of cortical microcircuit contribution to intracranial local field potentials and EEG. This tractable model will enable biophysical evaluation of multiscale electrophysiological signatures and computational investigation of cortical processing.
Keywords: biophysical modeling, cognitive control, cortical microcircuitry, EEG, LFP sources, pyramidal cells
Introduction
The arrival times to cortical lamina of sensory inputs, efferent copies, and task rules in agranular frontal cortex are critical in cognitive control (Cohen, 2014; Sajad et al., 2019; Subramanian et al., 2019). Regulated by local inhibitory neurons, signaling from these pathways converges on the opposite poles of layer 5 (L5) pyramidal cells (PCs), the basal dendrites/soma and apical dendrites, in which coincident arrivals are robustly encoded (Larkum, 2013; Cohen, 2014). One well-characterized cognitive control function is error monitoring by the medial frontal cortex (Stuphorn et al., 2000; Sajad et al., 2019), which is indexed by an error-related negativity (ERN) in scalp potentials (Gehring et al., 1993). L5-PCs display distributions of voltage-gated channels that together with returning currents form small dipolar configurations (Einevoll et al., 2013; Reimann et al., 2013). Local synchronization of these miniaturized dipoles arranged in parallel by their elongated trunks produces electric potentials that can be measured both intracranially and on the scalp (i.e., the EEG) (Riera et al., 2012). Therefore, models of the L5-PC are necessary to translate between neural spiking, event-related local field potentials (LFPs), and the scalp ERN reflections during performance monitoring.
L5-PCs exhibit two excitability zones, affording the integration of signals across cortical lamina. One deep excitability zone, at the axon hillock, produces Na+ action potentials (Na+-APs), and another more superficial, in the distal trunk, produces Ca2+ spikes (Amitai et al., 1993; Yuste et al., 1994; Schiller et al., 1997; Larkum and Zhu, 2002). The coincidence of an Na+-AP with an apical dendritic excitatory postsynaptic potential produces additional Na+-APs via a back-propagation-activated Ca2+ spike, “BAC firing” (Larkum et al., 1999b). Na+-APs show a linear frequency-current (f-I) relation with different sensitivities at the two excitability zones (Larkum et al., 2004). Dendritic Ca2+ spikes generated by strong inputs show a sustained depolarization (Larkum et al., 2001) that produces high-frequency Na+-APs (Schwindt and Crill, 1999; Williams and Stuart, 1999; Larkum et al., 2001). L5-PCs exhibit a critical frequency (CF) between 60 and 200 Hz for eliciting Ca2+ spikes (Larkum et al., 1999a) via somatic stimulation, which is sensitive to the hyperpolarization-activated cation current, Ih, in apical dendrites (Berger et al., 2001).
Previous simplified biophysical models explained some key features, that is, the I-f curves (Larkum et al., 2004) and the back-propagating AP-activated Ca2+ spike (BAC) firing (Chua et al., 2015; Yi et al., 2017). More complex biophysical models accounted for some combinations of the three major features: the BAC firing (Rapp et al., 1996; Schaefer et al., 2003; Hay et al., 2011; Bahl et al., 2012; Almog and Korngreen, 2014; Mäki-Marttunen et al., 2018), the f-I curves (Hay et al., 2011; Bahl et al., 2012; Mäki-Marttunen et al., 2018), and the CF of Ca2+ spikes (Schaefer et al., 2003; Hay et al., 2011; Bahl et al., 2012; Almog and Korngreen, 2014). However, single-cell models with many compartments and ionic channels are computationally expensive to use in large-scale simulations of neocortical networks. Furthermore, fitting these complex models to LFP/EEG data are impractical, limiting interpretability and scalability to studies in system neuroscience. Only one previous model replicated realistic [Ca2+] dynamics in the distal trunk during Ca2+ spikes (Mäki-Marttunen et al., 2018). Furthermore, no previous model has reported an Ih shift on the CF, the current source density (CSD) patterns associated with dendritic Ca2+ spikes evoked by somatic stimulation of PCs above the CF, and the effect of blocking Ih on these patterns (Suzuki and Larkum, 2017).
We describe the simplest possible, to our knowledge, biophysical model (2 compartments, 7 ionic conductances) of L5-PCs accounting for all these features. In particular, it reproduced Ca2+ dynamics above the CF and explained the shift produced by Ih. The model replicates CSD patterns obtained from synchronized Ca2+ spikes of 1000 L5-PCs because of supra-CF somatic stimulation. In addition, our model predicts a positive scalp potential linked to Ca2+ spikes in macaque monkeys as previously reported in rats (Suzuki and Larkum, 2017). Therefore, this minimal L5-PC model will be crucial for the interpretation of the ERN cortical microcircuit (Sajad et al., 2019).
Materials and Methods
L5-PC minimal model
We modeled the L5-PC as a two-compartment neuron, with a compartment representing the basal dendrites/soma and another compartment representing its distal trunk (Ca2+ spike initiation zone) and the apical dendrites. The trunk is represented by a transfer resistance () between the two compartments (Fig. 1A). The basal-dendrites/soma compartment includes the classic Hodgkin-Huxley fast-inactivating sodium () and potassium delayed rectifier () currents (Hodgkin and Huxley, 1952). The apical-dendrites/trunk compartment includes persistent Na+ current () (Magistretti and Alonso, 1999), Ca2+ L-type current () (Lytton and Sejnowski, 1991), hyperpolarization-activated nonspecific cation current () (Kole et al., 2006), muscarinic K+ current () (Adams et al., 1982), and the slow-inactivating potassium current () (Korngreen and Sakmann, 2000). The membrane potentials of the two compartments are given by the following coupled differential equations:
| (1) |
| (2) |
where subscripts s and d denote the basal-dendrites/soma and apical dendrites/trunk compartments, respectively. , , , and () represent the membrane potential, membrane capacitance, leak current, and injected current for the i-th compartment, respectively (Table 1, parameters). and denote the Weiner fluctuations of the basal-dendritic/somatic and apical-dendritic/trunk membrane potential, respectively. We assumed and in all simulations unless otherwise specified. The ionic currents are modeled using the Hodgkin-Huxley formalism in which:
| (3) |
where, is the maximal conductance of the k-th ionic channel; and are its activation and inactivation gating variables (Table 2, ionic current kinetics); and are their respective exponents; and is the equilibrium potential of the k-th ion. The leak current was modeled by . All the equilibrium potentials are considered constant, except for the equilibrium potential of Ca2+, which depends on the intracellular Ca2+ concentration () through the Nernst equation. Because of ionic diffusion, we treat [Ca2+] as a stochastic variable. Therefore, we added a Wiener noise to Equation 4 using the approach described in a previous study (Riera et al., 2011), with .
Figure 1.
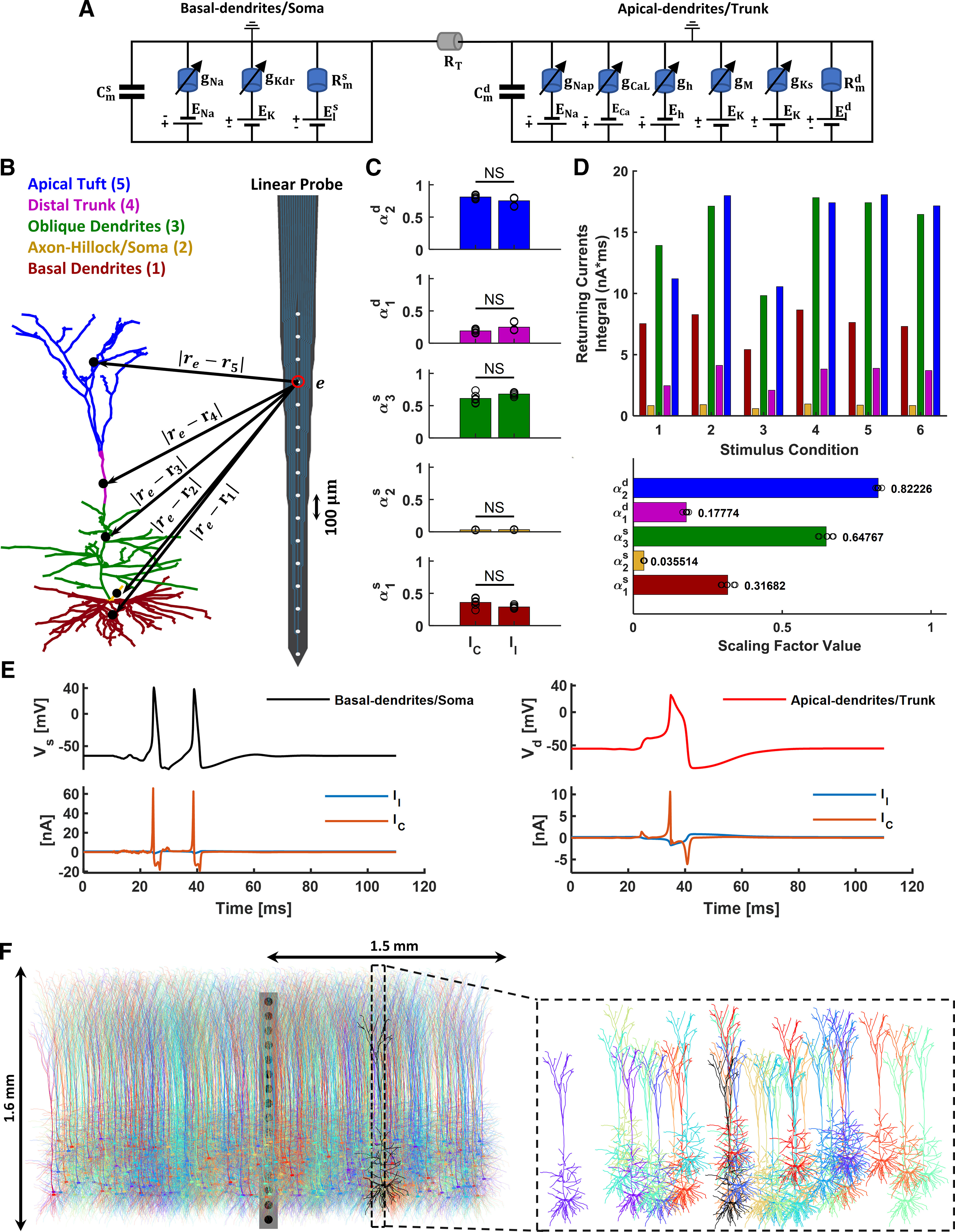
Illustration of the biophysical model, LFP estimation, and simulated neocortical column. A, Equivalent circuit of the two-compartment biophysical model. The first and second portions of the circuit represent the basal-dendrites/soma and apical-dendrites/trunk compartments, respectively. The lengthy trunk is represented by the transfer resistance () between the compartments. Each ionic channel (k-th) is represented by an electromotive force (i.e., the ion equilibrium potential) and a voltage-dependent conductance in parallel. B, Illustration of the forward-modeling used for LFP estimation from the two-compartmental model of L5-PCs. To compute the transmembrane currents, the cell was divided into five current source/sink regions (indicated in colors). The position of the point source/sink representing the mass center for each compartment of a neuron is given by the parameter . The position of an electrode in the probe is given by the parameter . The cell morphology was obtained from Hay et al. (2011); (ModelDB, accession #139653, “cell #1”). The linear probe sketch was adapted from an image of the NeuroNexus A1x16 probe. C, Estimated scaling factors of the capacitive (IC) and leak (Il) currents of each neuronal region for six stimulus conditions (black circles): 1. Suprathreshold somatic current pulse. 2. Suprathreshold EPSP-like distal dendritic current injection. 3. Subthreshold EPSP-like distal dendritic current injection. 4. Suprathreshold somatic current pulse followed by subthreshold EPSP-like distal dendritic current injection. 5. Brief train of suprathreshold somatic current pulses at 120 Hz. 6. Noisy supra-CF somatic current pulse. We found no significant difference in the values of () and () across stimulus conditions for either or (all p values > 0.05, Wilcoxon signed-rank test, n = 6 conditions), or between the values of and (all p values > 0.05, Wilcoxon signed-rank test). D, Top, Integral of the returning current traces for each neuron region for the six stimulus conditions. Bottom, Estimated scaling factors of the returning currents for the six stimulus conditions (black circles). Mean values are reported next to the bars. C, D, Simulations were performed using the Hay et al. (2011) model (ModelDB, accession #139653, “cell #1”) in LFPy (Lindén et al., 2014), which builds on NEURON (Hines et al., 2009). E, Membrane potential (top) and leak/capacitive current traces (bottom) of the basal-dendrites/soma (left) and apical-dendrites/trunk (right) compartments of our two-compartment L5-PC model for stimulus condition 6. Leak (Il) and capacitive (IC) current traces are shown in blue and orange, respectively. F, 2D representation of the simulated cortical column formed by a collection of 1000 L5-PCs (“cell #1” in Hay et al., 2011). The simulated cortical column had a diameter of 3 mm and a total depth of 1.6 mm. The somas were distributed randomly in the tangential dimension of L5. The mean (SD) depth of the neurons was 1.04 (0.22) mm from the pia matter. The expanded plot, at the right, visualizes the variation in the spatial distribution of L5-PCs in the column.
Table 1.
Parameters used for the simulationsa
| () | () | (x, y) | |
|---|---|---|---|
| Somatic compartment (Larkum et al., 2004) | |||
| Na | 18 | 50 | (3, 1) |
| Kdr | 5 | −85 | (0, 4) |
| Leak | −31.5 | (0, 0) | |
| Dendritic compartment (Larkum et al., 2004) | |||
| Nap | 0.022 | 50 | (3, 1) |
| CaL | 3.85 | (2, 0) | |
| h | 0.865 | −45 | (1, 0) |
| M | 1 | −85 | (1, 0) |
| Ks | 28 | −85 | (2, 1) |
| Leak | −48.1 | (0, 0) | |
| (Larkum et al., 2004) | |||
aThe first column indicates the ionic channels per compartment. The second and third columns show the maximum conductance and equilibrium potential for each ionic channel, respectively. The exponents of the activation (x) and inactivation (y) gating are indicated in the fourth column. Electrotonic parameters (capacitances/resistances) are also shown.
Table 2.
The gating kinetics for each ionic channel
| Ionic current | Gating variables |
|---|---|
|
|
|
|
|
|
|
|
|
|
, for , otherwise |
|
|
|
|
|
|
|
The intracellular Ca2+ concentration dynamics is given by the following:
| (4) |
where is the dendritic resting potential, is the intracellular Ca2+ concentration at rest, and is the decay time constant of the intracellular Ca2+ concentration because of active transport (Schaefer et al., 2003). is the depth of the submembrane Ca2+ shell, is the Faraday's constant, and is the unit conversion constant for (mA). The surface area of the apical-dendrites/trunk compartment was calculated based on the values given by Larkum et al. (2004) for parameters and . represents the fraction of free Ca2+ (not buffered), which was adjusted to reproduce experimental data for in the distal trunk (Larkum et al., 1999a). The basal intracellular Ca2+ was set at its typical physiological value nm.
f-I relation
We create the f-I curves by injecting a noisy staircase current into either compartment and calculating the somatic firing rate for each current step. The noisy input current was an Ornstein-Uhlenbeck process (Larkum et al., 2004) as follows:
| (5) |
where is the injected current at the i-th compartment with mean , compartment-dependent SD and time correlation length . is a random number generated at each time point from a Gaussian distribution with mean = 0 and SD = 1. We set as in the experimental study (Larkum et al., 2004), and , the time increment, equal to the integration time step. The mean increased over time between 0.2 and 0.75 nA as a staircase function with steps of every 2 s.
Modeling a population of L5-PCs
In addition to reproducing all main features of PC reported from intracellular recording studies, we validated its usefulness to model large-scale extracellular electric potentials (e.g., LFP) generated by cortical microcircuits. To that end, we simulated a neocortical column comprised of 1000 L5-PCs. For now, they were not connected to each other. Nevertheless, this approach allowed us to determine the transmembrane active (i.e., voltage-gated) and returning ionic current densities and laminar LFP associated with synchronized apical dendritic L5-PC Ca2+ spikes. The laminar LFPs and CSD patterns were compared with those obtained by Suzuki and Larkum (2017).
Calculating the LFPs
We calculate the LFP from the transmembrane currents generated by a collection of neurons using the point source approximation (Holt and Koch, 1999), which assumes that the transmembrane currents through a compartment can be approximated as a single monopolar source/sink placed in an extracellular medium at the center of the compartment. To compute the transmembrane currents, we divided each compartment into regions (Fig. 1B). This approach permits the spatial separation of active ionic and passive returning (i.e., capacitive and leak) currents. The basal-dendrites/soma compartment was modeled by three regions: the basal dendrites, the axon hillock/soma, and the oblique dendrites. The apical-dendrites/trunk compartment was modeled by two regions: the distal trunk (including the main bifurcation point) and the tufted apical dendrites. Each region was represented by a single monopolar current source/sink. The ionic and capacitive/leak currents are distributed between these regions as follows:
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where , , , , and are the total transmembrane currents (Fig. 1B) of the basal dendrites (1), axon hillock/soma (2), oblique dendrites (3), distal trunk (4), and the tufted apical dendrites (5) regions, respectively. and are the somatic and dendritic capacitive currents, respectively; and are equal to . The distribution of ionic currents in these five regions was determined by taking into consideration physiological/morphologic characteristics and modeling results.
First, to distribute the capacitive and leak currents in the five regions, we performed a series of simulations using the detailed Hay et al. (2011) model (available on ModelBD) (Hines et al., 2004), accession #139653, “cell #1” (parameters from Hay et al., 2011, their Table 3), in which we calculated the leak and capacitive currents associated with the five neuronal regions in the detailed morphology (Fig. 1B) for six general stimulus conditions. The stimulus conditions considered were as follows: (1) suprathreshold somatic current pulse (similar to stimulus used in Fig. 3C); (2) suprathreshold EPSP-like distal dendritic current injection (similar to stimulus in Fig. 3E); (3) subthreshold EPSP-like distal dendritic current injection (similar to stimulus in Fig. 3B); (4) suprathreshold somatic current pulse followed by subthreshold EPSP-like distal dendritic current injection (similar to stimulus in Fig. 3D); (5) brief train of suprathreshold somatic current pulses at 120 Hz (similar to stimulus in Fig. 4A); and (6) noisy supra-CF somatic current pulse (similar to stimulus used in Fig. 5).
Figure 3.
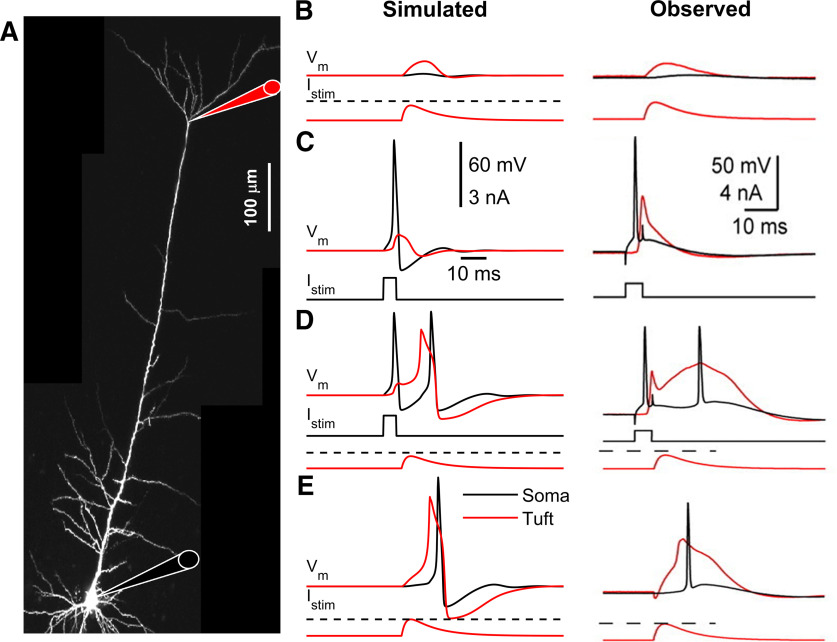
Back-propagating AP-activated Ca2+ spike firing. A, Micrograph of a L5-PC with recording locations at the soma (black) and distal trunk (red) indicated with a schematic pipette. B, Simulated (left) and observed (right) (Schaefer et al., 2003) subthreshold current injected into the apical dendrites creates only subthreshold somatic and dendritic depolarization. C, Simulated and observed suprathreshold somatic current pulse elicits an Na+-AP that propagates back to the apical dendrites creating a dendritic depolarization but no dendritic Ca2+ spike. D, Simulated and observed combined somatic and tuft stimulation evokes an Na+-AP, a dendritic Ca2+ spike, and another somatic Na+-AP following the onset of the dendritic Ca2+ spike. E, Simulated and observed suprathreshold stimulation of distal apical dendrites evokes a dendritic Ca2+ spike. C, Scales are common for all simulated (left) and observed (right) results. Red represents apical-dendrites/trunk. Black represents basal-dendrites/soma. Dashed line indicates dendritic threshold. For visualization, the ∼10 mV shift in membrane resting potential from the somatic to the apical-dendrites/trunk compartment was removed.
Figure 4.
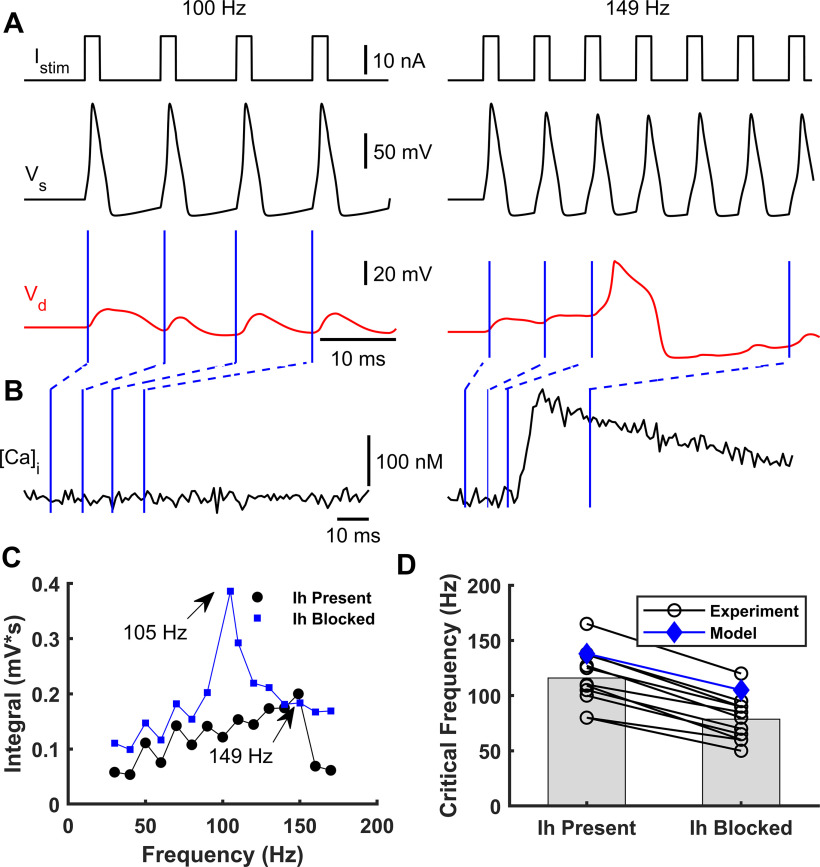
Effect of somatic stimulation frequency on dendritic Ca2+ spike occurrence. A, A simulated train of brief suprathreshold pulses at frequencies of 100 Hz (left) and 149 Hz (right) (top) was injected into soma eliciting a train of Na+-APs (black, below). Only the 149 Hz train evoked a dendritic Ca2+ spike (red, bottom). B, Intracellular dendritic Ca2+ concentration during somatic stimulation at 100 Hz (left) and 149 Hz (right), respectively. Blue lines indicate the Ca2+ concentration at each time instant of the dendritic voltage traces indicated in A. C, Integrated area below the dendritic voltage traces as a function of the Na+-AP frequency with (blue) and without (black) the Ih current. CFs of 105 Hz and 149 Hz were obtained when Ih was present and absent, respectively. D, Observed shift in CF after blocking Ih for 11 cells (black circles, numerically estimated from Berger et al., 2003) and simulated with the model (blue diamonds).
Figure 5.
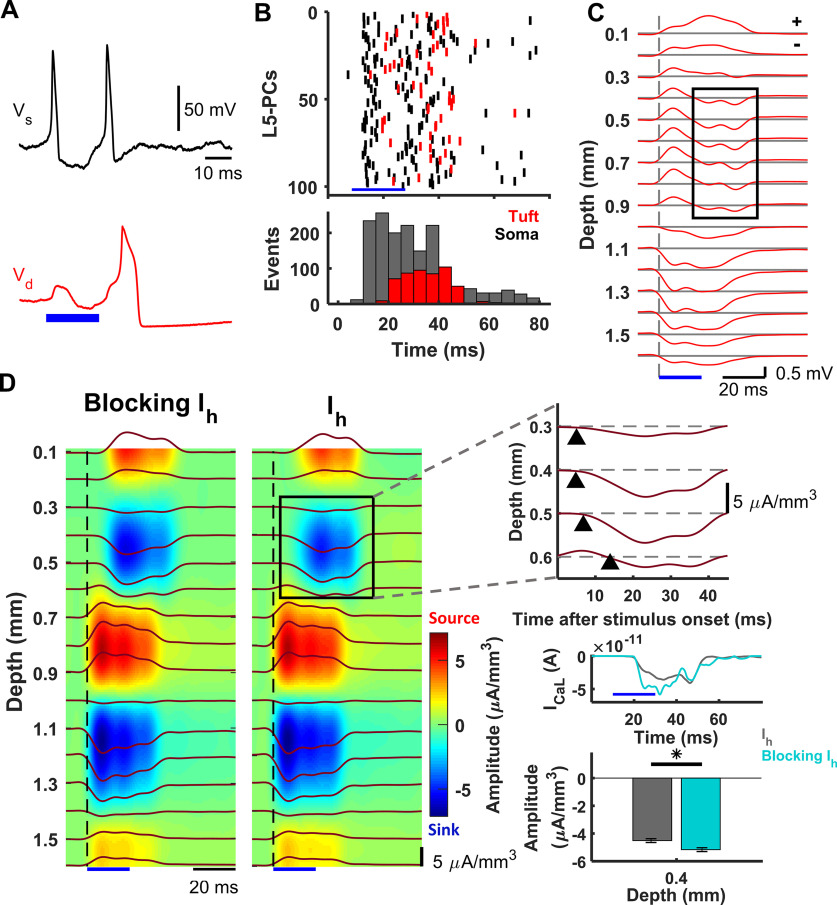
LFP and CSD derived from dendritic Ca2+ spikes in a collection of L5-PCs. A, Basal-dendritic/somatic (black, Vs) and apical-dendritic/trunk (red, Vd) simulated responses of a collection of 1000 L5-PCs to suprathreshold somatic stimulation above the CF. B, Raster plots (top) and poststimulus time histogram (bottom) of 100 randomly selected L5-PCs (top) showing spike times of Na+-APs (black) and Ca2+ spikes (red). The total number of Na+-AP and Ca2+ spike events every 5 ms is shown (bar plots, bottom). C, LFPs evoked by supra-CF stimulation of the collection of L5-PCs calculated on an array of 16 microelectrodes (100 µm separation). Voltage traces at each depth are averaged over 10 simulated trials, each randomly affected by system noises in the membrane potentials and the calcium concentrations. Black rectangle represents the delayed sink associated with the dendritic Ca2+ spike. The symbols '+' and '−' in the top-right corner of the panel indicate positive and negative potentials relative to the horizontal gray lines, respectively. D, CSD analysis of the evoked LFPs averaged over 10 trials without (left) and with (right) the Ih current. Blue represents sinks. Red represents sources. Top right, Expansion of the selected area to reveal the delayed sink associated with the Ca2+ spikes arising earliest 0.4 mm below the pia matter. Middle right, Plots averaged current in the trunk of the L5-PCs, showing an amplitude increase ∼15-25 ms after stimulation when Ih was absent. Bottom right, Comparison of the average with SEM of the amplitude of this current sink with and without the Ih current, which was significantly different (p = 0.002, Wilcoxon signed-rank test, N = 10 trials). *p < 0.05. Blue bar in all the plots represents the time window for the supra-CF stimulation.
Simulations were performed using LFPy (Lindén et al., 2014), which builds on NEURON (version 7.7) (Hines et al., 2009).
We computed the area under the current traces for each region and stimulus condition. Because we were interested in estimating the proportion of the leak/capacitive current through each region, we grouped these currents into those that contribute to the basal/oblique/soma/axon hillock area and to the distal trunk/tuft area. Accordingly, we estimated the proportion of the capacitive/leak current through each region as follows:
with ; ; ; ; ; and . and denote the areas under the total captative () and leak () current traces for the i-th neuronal region, respectively (i.e., basal dendrites, axon hillock/soma, oblique dendrites, distal trunk, and apical tuft; Fig. 1B). and represent the percentage of the capacitive/leak currents that goes to the i-th neuronal region, with respect to the total current of the basal/oblique/soma/axon hillock area and the distal trunk/tuft area, respectively. The normalization by the total areas, and , is necessary because our two-compartment neuronal model generates the total capacitive/leak currents in each compartment: basal-dendrites/soma and apical-dendrites/trunk. According to our model, the capacitive and leak currents are different in each compartment (Fig. 1E).
Figure 1C shows the estimated values of and for all stimulus conditions for each neuronal region. We found no significant difference between the values of and across stimulus conditions (all p values > 0.05, Wilcoxon signed-rank test, n = 6 conditions), or between the values of and (all p values >0.05, Wilcoxon signed-rank test). These results indicate that the capacitive and leak currents can be distributed equally, using the same scaling factors, in our 5-regions model to calculate the LFPs. Finally, the scaling factors of the returning currents (sum of the leak and capacitive currents) can be estimated as follows:
where is the area under the total returning current trace () of the i-th neuronal region; ; and . Figure 1D illustrates the integral of the returning currents through each neuronal region (top) and the values of scaling factors (bottom) for the six stimulus conditions. The values of and used in Equations 6–10 are reported in Figure 1D (bottom).
Second, we distributed the ionic currents based on their distribution in L5-PCs. We separated the current into its contribution by the basal and oblique dendrites, setting = 0.5. These regions occupy a larger area with an overall higher density of channels than the axon hillock (Ramaswamy and Markram, 2015). In the axon hillock/soma, we included the Na+ current because its density in this area is at least 50-fold higher than at proximal dendrites (Ramaswamy and Markram, 2015). The and currents were incorporated in the main bifurcation point of the trunk since this region is the Ca2+ spike excitability zone (Larkum et al., 1999b). The Ih current was added to the apical tuft compartment because of its high density in this region (Kole et al., 2006) and critical influence on synaptically evoked activity in the distal apical dendritic arbor (Harnett et al., 2015). The (Schwindt and Crill, 1995) and IM (Hay et al., 2011) currents were also included in this area because of their role in the amplification/attenuation of synaptic currents. A more detailed rationale is provided in Results.
We compute the LFPs at 16 equally spaced vertically aligned points to simulate the linear microelectrode array (Michigan probe) used by Suzuki and Larkum (2017). As in their study, the interelectrode distance (h) was 100 μm. Motivated by their stimulation protocol with the right-angled prism, we consider that the linear probe was located at the center of a cylindrical neocortical column of 3 mm in diameter, and with constant and isotropic electrical conductivity (i.e., average across layers; Fig. 1F) (Goto et al., 2010). Given the maximal current produced by individual PCs, 1000 L5-PCs were required to generate CSD amplitudes in the range reported by Suzuki and Larkum (2017). The electric potential at electrode position is given (Nicholson and Llinas, 1971) as follows:
| (11) |
where is the transmembrane current generated by the point source of the neuron ; , , and are the coordinates of the point source of the network neuron , and is the volume of the cortical column. Nn = 1000 and Ns = 5 represent the total number of neurons in the network and the total number of regions in each neuron, respectively. The , coordinates of the neurons in the simulated neocortical column were generated randomly from a uniform distribution. The coordinate of the axon hillock/soma point source/sink of the network neurons was also generated randomly from a uniform distribution with values between 1.025 mm and 1.450 mm below the pia matter (Suzuki and Larkum, 2017). The location of the basal dendrites, trunk main bifurcation point, and apical dendrite point sources were calculated relative to the location of the neurons' axon hillock. The basal dendrite point source was always 0.15 mm below the axon hillock, the main bifurcation point of the trunk was always 0.89 mm above the axon hillock (Ledergerber and Larkum, 2010, their Fig. 12), and the apical dendrite point source was 0.15 mm above the trunk main bifurcation point. The position of the oblique dendrites, representing part of the somatic returning currents, was generated randomly with values between 0.7 and 1 mm from the cortical surface. The proposed distribution of point sources for dendrites was inspired by morphologic data of L5-PCs (Mohan et al., 2015). To instantiate variability in the timing of L5-PC Na+-APs and Ca2+ spikes, we considered and in Equations 1 and 2, respectively.
CSD analysis
We estimated the CSD patterns evoked by the simulated LFPs using the spline inverse CSD method (spline iCSD) (Pettersen et al., 2006). The iCSD methods are based on the inversion of the solutions of the electrostatics forward problem and assume cylindrical confined and symmetric CSDs. Specifically, the spline iCSD method assumes a continuously varying CSD along the recording electrodes, which is calculated by interpolating a set of cubic splines, requiring the CSD and its first and second derivatives in the vertical direction to be continuous (Pettersen et al., 2006). It also considers a homogeneous disk distribution in the in-plane (x, y) directions. As described in the previous section, a homogeneous and isotropic volume conductor with extracellular conductivity of was used. Based on L5-PC density and the CSD peak amplitudes in Suzuki and Larkum (2017), the diameter of the cylindrical source model was set to 3 mm. The estimated CSD based on the simulated LFPs was convolved with a Gaussian filter of σ = 0.1 mm to produce a spatially smoothed CSD estimate.
Forward model of electroencephalogram
Data were collected from 1 male bonnet macaque (Macaca radiata, ∼8.5 kg) that was cared for in accordance with the United States Department of Agriculture and Public Health Service Policies on Human Care and Use of Laboratory Animals. All procedures were performed with supervision and approval from the Vanderbilt Institutional Animal Care and Use Committee. Anatomic images were acquired with a Philips Intera Achieva 3 tesla scanner using SENSE Flex-S surface coils placed above and below the head. T1-weighted gradient-echo structural images were obtained with a 3D turbo field echo anatomic sequence (TR = 8.729 ms; 130 slices, 0.70 mm thickness). Segmentations of the scalp and skull were performed in SPM12 (Penny et al., 2007) and segmentation of the brain in BrainSuite (Shattuck et al., 2001).
To compare estimated with observed EEG potentials described previously (Godlove et al., 2014; Sajad et al., 2019), we positioned the simulated population of PCs in a cortical column within the supplementary eye field (SEF), an agranular area on the dorsomedial convexity in macaques (Fig. 6B). The monkey's head was modeled as an isotropic and piecewise homogeneous volume conductor (Fig. 6A). The positions of the EEG electrodes were defined using an algorithm that automatically estimates the international 10-10 scalp coordinates of the EEG electrodes on the scalp's surface of the subject (Giacometti et al., 2014) (Fig. 6A). The conductivities used for the brain (σbr), skull (σsk), and scalp (σsc) were 0.323, 0.43 (Lee et al., 2015), and 0.0063 S/m (Lee et al., 2015), respectively.
Figure 6.
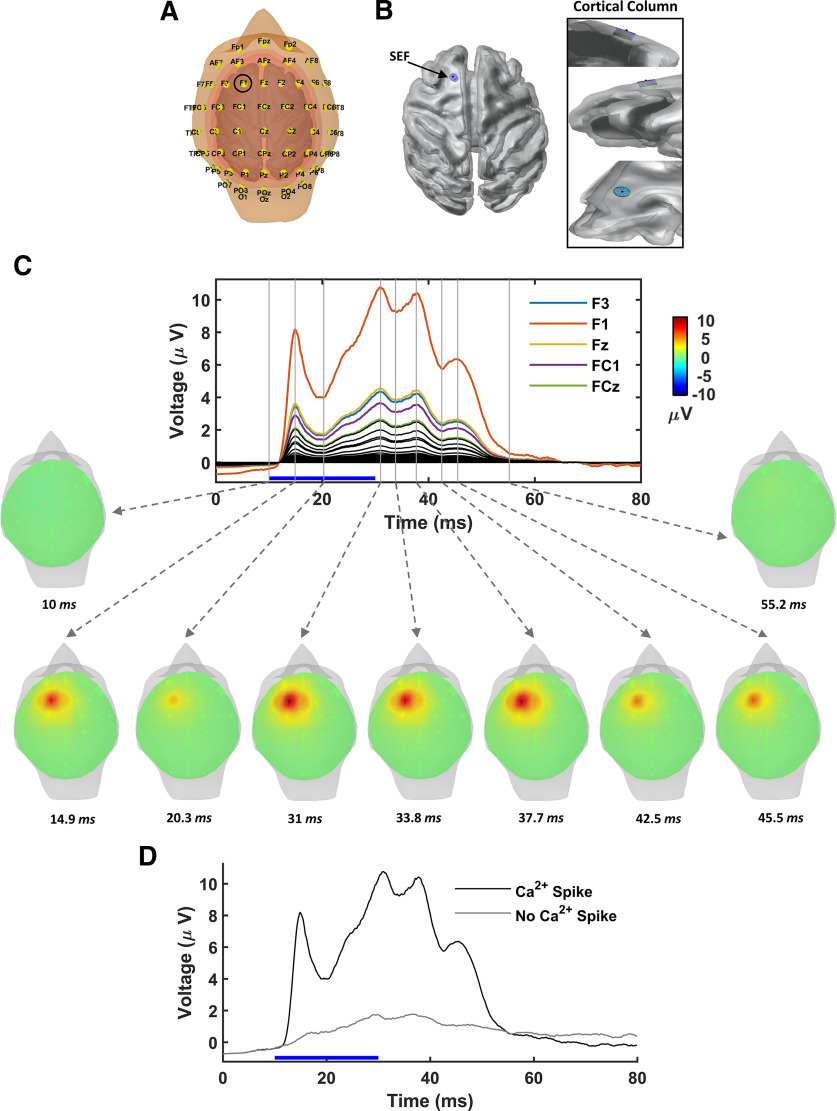
Large-scale EEG signatures of subcellular dendritic Ca2+ spikes generated by a collection of L5-PCs located in SEF. A, Monkey's head model with EEG electrodes positioned according to the international 10-10 system. Tissue compartments are indicated in different colors. B, Location of the simulated functional cortical column in the SEF. Right, Expanded view of the functional cortical column from different perspectives. C, Top, EEG potentials at each electrode resulting from brief supra-CF stimulation (blue horizontal bar) of the collection of L5-PCs simulating optogenetic stimulation in Suzuki and Larkum (2017). Scalp potentials at each electrode contact are averaged over 10 simulated trials, each randomly affected by system noises in the membrane potentials and the calcium concentrations. Bottom, Topographical voltage maps illustrated for indicated times (gray vertical attached to dashed arrows). D, EEG potential sampled by electrode F1 (circled A), which is the closest electrode to the functional cortical column. Samples are shown with (black) and without (gray) discernible Ca2+ spikes.
In general, the scalp potential at any position produced by a continuous field of microscopic electrical sources inside the brain R can be represented by an inhomogeneous Fredholm integral equation of the second kind (Riera et al., 2012) as follows:
| (12) |
| (13) |
| (14) |
where represents the secondary currents defined for each elemental volumetric shell (i.e., a surface of thickness ). denotes the conductivity of the k-th compartment (i.e., brain, skull, scalp), and is the normal vector to the surface at location . defines the location of the c-th compartment of the i-th neuron. The theoretical framework and numerical strategies used to compute the surface potentials can be found in Hämäläinen and Sarvas (1989).
Simulations and code accessibility
All simulations, except those using the Hay et al. (2011) model, were performed in MATLAB (R2018b, The MathWorks) with custom-written scripts. The model equations are solved using the SDETools toolbox for the numerical solution of stochastic differential equations (https://github.com/horchler/SDETools), with a time-step of 1 μs. All simulation parameters are listed in Table 1 with ionic channel kinetics in Table 2. To calculate the CSD, we created customized scripts that use the functions provided in the CSDplotter toolbox (https://github.com/espenhgn/CSDplotter), which implements the iCSD methods described by Pettersen et al. (2006). The MATLAB scripts of the model implementation as well as for the LFPs and CSD calculations are publicly available (https://github.com/beaherrera/2-compartments_L5-PC_model) under the GPL-3.0 license.
A version of the boundary element method for neuronal microscopic monopolar current sources used to solve the EEG forward problem was implemented in MATLAB based on the deflation method (Hämäläinen and Sarvas, 1989) (code available on request from J.J.R.). The plots of the monkey's head model and the EEG topographical maps were generated in Brainstorm (Tadel et al., 2011).
Results
Model testing approach
Traditionally, parameter estimation of L5-PC biophysical models is performed using quantitative strategies aimed at numerically minimizing model prediction errors while reproducing transmembrane potential traces in specific experimental paradigms. In some cases, the data are used to fit channel kinetics (Rapp et al., 1996); whereas in others (Hay et al., 2011; Bahl et al., 2012; Almog and Korngreen, 2014; Chua et al., 2015; Mäki-Marttunen et al., 2018), conductance ranges are fitted with generic optimization methods, based on known channel kinetics. However, such a quantitative approach is very challenging if biophysical models are used to simultaneously fit data from multiple experimental paradigms. In such cases, a qualitative trial/error approach based on electrophysiological knowledge about the effect that each ion channel produces on the data are more effective (Schaefer et al., 2003; Larkum et al., 2004; Yi et al., 2017). We will use the qualitative trial/error approach as a satisfying strategy to reproduce the six features of L5-PCs observed in various experimental paradigms (Table 3) without a meticulous quantitative description of the Na+-APs and Ca2+ spikes. We also used previously known channel kinetics. The rationale used to determine ionic distributions and conductances is now explained.
Table 3.
Summary of previous/current biophysical models used to describe the principal features of L5-PCsa
| Study | Compartments | Ions | Platform | Features explained |
|---|---|---|---|---|
| Rapp et al., 1996 | >>1000 | 2: 2/c; Total >>2000 | NEURON | BAC firing |
| Larkum et al., 2004 | 2 | 2: 1/c, +IF model; Total = 2 | Not reported | f-I curves |
| Schaefer et al., 2003 | 8 | 7: 6/c; Total = 48 | NEURON | BAC firing; CF |
| Hay et al., 2011 | 196 sections; 1018 segments | 8: 9/c S(1); 7/c AD(561); 1/c BD(454); Total = 4390 | NEURON | BAC firing; CF; f-I curves |
| Bahl et al., 2012 | 5 sections; 14 segments | 8: 1/c Ah(5); 5/c S(1); 1/c BD(1), 4/c AD(7); Total = 39 | NEURON | BAC firing; f-I curves |
| Almog and Korngreen, 2014 | 153 sections; 663 segments | 8: 8/c; Total = 5304 | NEURON | BAC firing; CF |
| Chua et al., 2015 | 3 | 1: 1/c AD, + IF model; Total = 1 | NEST | BAC firing |
| Yi et al., 2017 | 2 | 3: 2/c S(1), 1/c AD(1); Total = 3 | MATLAB | f-I curves |
| Mäki-Marttunen et al., 2018 | 4 sections; 20 segments | 10: 9/c S(1), 1/c BD(1); 7/c AD(5), 7/c T(2); Total = 59 | NEURON | BAC firing; f-I curves; [Ca2+]i |
| Current study | 2 | 7: 2/c BD/S(1), 5/c; AD/T(1); Total = 7 | MATLAB | BAC firing; CF; f-I curves; [Ca2+]i; Ih effect; CSD maps |
aThe first, second, third, and fourth columns show the study, number of compartments, number of ionic channels, and the platform used to create the simulated data for each study. The fifth column lists the features that were explained by each study. The column “Ions” provides the following information: , where and are the number of ionic species considered and the number of ionic channels per compartment, respectively. In some cases, the number of ionic channels per compartment depends on the regions of the neuron considered. IF, Integrated and fire model; S, soma; AD, apical dendrites; BD, basal dendrites; T, trunk; Ah, axon hillock.
Ion channels for each compartment were selected based on experimental findings and modeling studies. According to estimation by Hay et al. (2011), the transient-Na (Nat)/Nap ratio was ∼20,400 pS/µm2/17.2 pS/µm2 for the soma of L5-PCs; hence, the effect of cation influx into the soma of L5-PCS because of the Nap channel must be minimal. It has been suggested that the Nat channel is uniformly distributed along the somato-dendritic axis (Stuart and Sakmann, 1994), playing a role in AP back-propagation. However, a more recent numerical estimation by Hay et al. (2011) suggests that its distribution from the soma to the apical dendrite may decrease in density sharply, from 20,400 pS/µm2 for the soma to 107 pS/µm2 for the apical dendrites, which is in agreement with two following theoretical studies (Bahl et al., 2012; Almog and Korngreen, 2014). The Nat channels also decrease in density quickly from soma to basal dendrites (Nevian et al., 2007); therefore, it was not included in the basal compartment for the genesis of the LFP. The high density of Nat channels in the axon hillock determines its integration properties (low threshold) and plays a role in the AP frequency. The density of Nat channels decreases sharply along the hillock-proximal-dendrites axis (Hu et al., 2009; Fleidervish et al., 2010). For that reason, we included Na+ voltage-gated channels only in the hillock while generating the LFPs.
Previous studies (Lytton and Sejnowski, 1991; Larkum et al., 2004; Yamada et al., 2004; Hay et al., 2011; Mäki-Marttunen et al., 2018) reported the need for the after-hyperpolarization current (SK-type) to reproduce the f-I relationship shown experimentally by the L5-PCs. Many other biophysical models have included it to describe somatic firing properties in these cells. Including SK channels implies a need for voltage-gated Ca2+ channel, as well as other intracellular sources for cytosolic Ca2+ (e.g., ryanodine-receptor, IP3-receptors, and mitochondrion). R-type Ca2+ channels, together with all high voltage-activated (HVA) Ca2+ channels, have been associated with AP firing properties (Almog and Korngreen, 2009). However, Bahl et al. (2012) reproduced the f-I relationship without this current. Similarly, we could describe the f-I relationship without an after-hyperpolarization current, by just using the classical fast inactivating Na+ and K+ delayed rectifier channels (Hodgkin and Huxley, 1952), which exhibits a longer refractory period. We were less interested in any differences in Na+ spike waveform because of Na-K dynamics since our focus was on the f-I relationship for regular spiking cells (Guan et al., 2015).
On the other hand, the (Almog and Korngreen, 2009; Pérez-Garci et al., 2013), the (Schwindt and Crill, 1995; Crill, 1996), and the (Harnett et al., 2013) currents were inserted in the dendritic compartment to approximate the characteristic shape of dendritic Ca2+ spikes and their associated properties. L-type Ca2+ channels are the most relevant component in the electrogenesis of Ca2+ spikes, which are highly localized in the distal trunk (Reuveni et al., 1993; Pérez-Garci et al., 2013). In our model, defined the amplitude of the initial depolarization phase and, together with the , the plateau-like depolarization characteristic of these spikes. was also essential for the CF effect. A regenerative role in the apical tuft of Nap channels has been suggested in the past (Schwindt and Crill, 1995; Fleidervish and Gutnick, 1996; Mittmann et al., 1997). Our compartmentalization of Nap (tuft) and L-type Ca2+ (distal trunk) active currents was based on these findings and effective for the genesis of LFP.
Low voltage-activated (LVA) Ca2+ channels were not included in the dendrites because of their very low density (Tarasenko et al., 1998; Zhu, 2000). Several LVA and HVA Ca2+ channels are localized in dendritic spines, which play a role in synaptic plasticity (Leresche and Lambert, 2017). However, blocking all types of HVA/LVA Ca2+ channels in the tuft with Cd2+ and Ni2+ has no effect on NMDA spike amplitude or threshold (Larkum et al., 2009). Hence, a distal apical dendritic compartment was not included in our model.
Communication between the distal tuft and the trunk can be nonlinearly regulated by two types of highly compartmentalized voltage-gated potassium channels (Korngreen and Sakmann, 2000; Schaefer et al., 2007; Harnett et al., 2013): the transient Kt (also known as IA) type and the sustained IDR-Like (also known as Ks/Kp) type. The expression of these two channels monotonically decreases from the soma to the apical dendrites (Korngreen and Sakmann, 2000; Schaefer et al., 2007). However, without an outward current in the apical-dendrites/trunk compartment, Ca2+ spikes would not terminate. Therefore, we included the Ks current, with kinetics reported as in Korngreen and Sakmann (2000), which ensured a longer Ca2+ spike because of its slow inactivation. We included this particular outward current only in the distal trunk compartment to model the LFP because of the sharp decrease in its expression along the soma-dendritic axis reported by Schaefer et al. (2007). defined the amplitude of the after-hyperpolarization phase of the Ca2+ spikes.
Ih expression increases substantially from the soma to the apical tuft (Kole et al., 2006). Hence, because of their low density, Ih channels were not included in the basal-dendrites/soma compartment (Lörincz et al., 2002). In apical dendrites although Ih channels not only increase resting membrane potential (Berger et al., 2001), they also regulate neuronal excitability (Harnett et al., 2015), impair temporal summation of synaptic inputs (Berger et al., 2003), and facilitate dendritic frequency tuning (Ulrich, 2002). Additionally, Ness et al. (2018) demonstrated the direct link of LFP low-frequency oscillations to Ih channels using the theoretical framework proposed by Hay et al. (2011). Moreover, this current plays a significant role in BAC firing modulation and synaptic integration, as well as in the reported changes in both the CF for Ca2+ spike generation (Berger et al., 2003) and the CSD pattern evoked by dendritic Ca2+ spikes (Suzuki and Larkum, 2017).
Saganich et al. (2001) demonstrated that IM channels are expressed in L5-PCs. Previous models (Hay et al., 2011; Mäki-Marttunen et al., 2018) included this channel in the apical dendrites and tuft only, not in the soma, to replicate the BAC firing feature of L5-PCs. In our model, the M-current was needed for the Ca2+ spike repolarization phase when staircase input currents were applied to the apical dendrites. Without this current, the dendritic membrane potential could not complete the repolarization phase. The voltage dependence of the channel kinetics at the apica-dendrites/trunk compartment was shifted by 8 mV to account for the shift in the resting membrane potential.
We tested our L5-PC biophysical model in two steps. We first show that the minimal model reproduces all known Ca2+-dependent synaptic facilitation features. We next assess further capabilities of the model by reproducing the LFPs and large-scale scalp EEG signatures associated with Ca2+ spikes evoked by the synchronized activation of a population of L5-PCs in a neocortical column using a somatic current stimulation that exceeded the CF.
Reproducing the main biophysical features in L5-PCs
f-I relationship
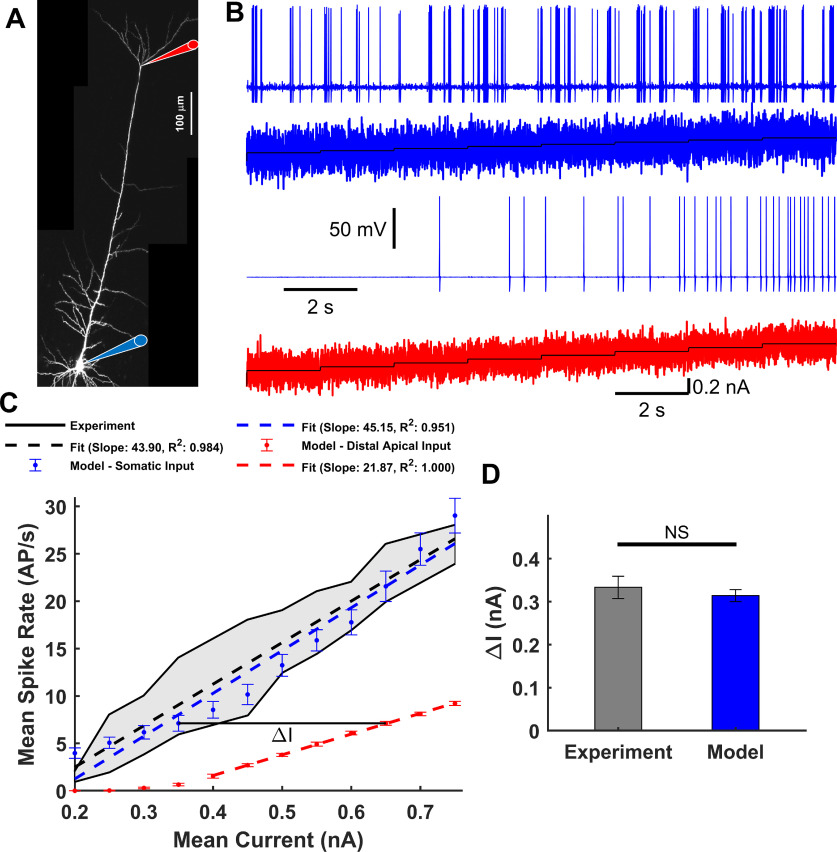
We first show that our model predicts the f-I relationship previously reported for L5-PCs when either the soma or the distal trunk region is stimulated (Fig. 2A) (Larkum et al., 2004). We injected, into the soma or the distal trunk, a staircase incrementing noisy input current generated using the Ornstein–Uhlenbeck method (see Materials and Methods), with SD = 0.2 nA or SD = 0.09 nA, respectively. Figure 2B shows the Na+-AP response (top, blue) to the somatic input current (second panel, blue). The mean somatic Na+-AP frequency was computed for each current step. Mean and SEM over 50 simulations were estimated (Fig. 2C). Overall, the model predicted a linear f-I relationship for the somatic input current (goodness-of-fit R2 = 0.959) that overlapped measurements from two studies (Fig. 2C) (Larkum et al., 2004; Bahl et al., 2012). Figure 2B also shows the somatic Na+-AP response (third panel, blue) to the dendritic input current (bottom, red). The model predicted a perfect linear f-I relationship for dendritic input current (Fig. 2C, goodness-of-fit R2 = 1.00). In agreement with experimental data (Larkum et al., 2004), current injections at the trunk must be ∼300 pA larger than that needed at the soma to produce the same Na+-AP frequency in these L5-PCs. This effect was quantified using parameter ΔI, which was calculated for all somatic Na+-AP rates from simulated (N = 6, ΔI = 0.3142 ± 0.0140 nA) and experimental (N = 6, ΔI = 0.3333 ± 0.0258 nA) data (Fig. 2D). This difference was statistically insignificant (t(5) = 2.0789, p = 0.0922, two-tailed paired t test). Thus, our model replicates the experimental f-I relationships, but it predicted a threshold for somatic Na+-AP initiation of ∼0.35 nA at trunk current injection sites, which was smaller than the ∼0.5 nA reported experimentally. This inconsistency can be explained by the difference in the injection site along the trunk of the actual L5-PCs used in the experiments (Larkum et al., 2004). Current injections at sites distant to the trunk bifurcation require larger amplitudes because the density of Ca2+ L-type channels may be lower. We modeled current injection at the level of the bifurcation, which reduced the threshold required to achieve somatic Na+-AP firing.
Figure 2.
f-I relationship. A, Micrograph of an L5-PC with recording locations at the soma (blue) and distal trunk (red) indicated with diagram pipettes. B, Somatic Na+-AP responses (first and third panels) to the staircase incremented noisy input current (second and fourth panels) injected into the soma (blue) and distal trunk (red). C, Observed (black) (Larkum et al., 2004; Bahl et al., 2012) Na+-AP firing frequency as a function of the mean input current. Gray fill represents the range of observed values. Simulated mean and SEM spike rate over 50 trials for each current step in the soma (blue) or distal trunk (red) compartment. Superimposed are observed (black dashed) and simulated (blue and red dashed) linear regressions. D, Current differences (ΔI) between the f-I curves for somatic and distal trunk stimulation to produce the same Na+-AP firing frequency. No significant differences were found between the observed ΔI, numerically estimated from Larkum et al. (2004) and that predicted by the model (t(5) = 2.0789, p = 0.0922, paired two-tailed t test).
BAC firing
Next, we examined how our L5-PC model integrates inputs into the distal trunk and soma (Fig. 3A). First, we stimulated the distal trunk with a subthreshold current generated from a double-exponential function of the form with and , and an amplitude of 0.29 nA. In agreement with experimental studies (Larkum et al., 1999b; Schaefer et al., 2003), only a small somatic and apical-dendritic/trunk depolarization was evoked by this current injection (Fig. 3B). Second, we simulated injection of a near-threshold current pulse (duration: 5 ms, amplitude: 1 nA) into the soma, which elicited an Na+-AP that propagated back to the apical-dendrites/trunk compartment creating dendritic depolarization but no Ca2+ spike (Fig. 3C). Third, we simulated combined stimulation with a somatic current pulse followed 1 ms later by subthreshold current at the trunk. This resulted in the generation of an Na+-AP, a dendritic Ca2+ spike, and another somatic Na+-AP following the dendritic Ca2+ spike (Fig. 3D). Finally, we verified that we could evoke dendritic Ca2+ spikes by suprathreshold current injections to the trunk (Fig. 3E). Each simulated stimulation condition produced polarizations that recapitulated experimental observations.
CF for Ca2+ spike generation
We next investigated the influence of the frequency of brief somatic current stimulation on the occurrence of Ca2+ spikes. We simulated somatic stimulation with trains of brief suprathreshold pulses (2 ms) at different frequencies, eliciting trains of somatic Na+-APs. As previously reported (Larkum et al., 1999a; Berger et al., 2003), only stimulation trains above a CF (149 Hz in the model) evoked Ca2+ spikes. Figure 4A illustrates the somatic and apical-dendritic/trunk responses to somatic stimulation below and at the CF. Figure 4B shows the simulated intracellular Ca2+ concentration dynamics for both stimulation paradigms, which resemble experimental data (Larkum et al., 1999a).
We also studied how the CF varied in the presence or absence of the Ih current in the distal apical dendrites. We simulated a L5-PC without Ih current at the apical-dendrites/trunk compartment responding to the same trains of suprathreshold currents at the soma with different frequencies. To quantify the CF, we measured the area below the dendritic voltage traces, shifting them to remove the prestimulation baseline, and plotted them as a function of AP frequency. When the Ih current was blocked relative to present, the CF was lower by ∼40 Hz (Fig. 4C). Furthermore, we compared the CF values with and without the Ih current predicted by our model with those predicted by experimental data from 11 L5-PCs (Berger et al., 2003) (Fig. 4D). In both the observed and simulated data, the CF is reduced by at least 30-40 Hz when the Ih current is blocked. The CFs predicted by our model are slightly higher than the observed CFs, but they fell within the observed range.
Reproducing Ca2+ spike-dependent LFPs
To examine the capabilities of this minimal L5-PC model, we tested whether nonsynaptic events, such as Ca2+ spikes, can be detected in the evoked LFPs as reported by Suzuki and Larkum (2017). To that end, we simulated a collection of 1000 model L5-PCs (Fig. 1F). The somas of the modeled L5-PCs were randomly distributed in-depth with a uniform probability between 1.025 and 1.450 mm. The experimental paradigm achieved simultaneous stimulation of the soma of L5-PCs using optogenetics (Suzuki and Larkum, 2017). Therefore, no synaptic connections were necessary for our simulations. Modeled L5-PCs were stimulated with a 20 ms duration current pulse () with stochastic amplitude at a mean level sufficient to generate Na+-AP trains at a frequency above the CF. The mean input current was strong enough to generate somatic Na+-AP trains and evoke dendritic Ca2+ spikes (Fig. 5A). for this simulation. Figure 5B shows the raster plots and associated poststimulus time histograms of 100 randomly selected simulated L5-PCs (top), with the timing for typical Na+-APs and Ca2+ spikes. After the somatic stimulation ceased, somatic Na+-APs persisted because of the nonlinear changes in the somatic-dendritic gain.
Figure 5C illustrates the averaged LFPs across cortical depth, evoked by 10 trials of simulated stimulation. A strong early negative LFP component was observed in lower layers (1.0-1.6 mm), in each of the trials, accompanied by a relatively strong positive LFP component in the upper layers. We also detected a late negative LFP component in the middle-upper layers (0.4-0.9 mm) around the onset of the Ca2+ spikes (Fig. 5B,C). CSD analysis of the simulated evoked LFPs showed an early strong sink 1.0-1.3 mm below the pia matter, which was accompanied by two sources: one stronger at 0.7-0.9 mm and another weaker at 1.4-1.6 mm (Fig. 5D, Ih panel). According to our model, the sink was caused by large inward currents at the level of the axon hillock/soma because of the induced Na+-APs. The two sources were caused by a combination of and the returning capacitive/leak outward currents through the oblique dendrites and the basal dendrites. The CSD analysis also revealed a 10–20 ms delayed sink after stimulation onset, originating ∼0.4 mm below the pia matter and propagating both upward and downward (Fig. 5D, Ih panel, and expanded plot). The sink was accompanied by a very superficial (0.1-0.2 mm) source, also delayed (Fig. 5D, Ih panel). This late sink appeared during the same interval in which the collection of L5-PCs generated more Ca2+ spikes (Fig. 5B, bottom). Hence, we believe it was caused by the inward current.
According to our model, the superficial sources resulted from a combination of IM, IKs, and the returning capacitive/leak outward currents through the apical dendrites. Because of its reversal potential, the cation current Ih could be either a source or a sink during a Ca2+ spike at a very superficial level. The CSD analysis revealed the presence of a sink/source current density distribution (Fig. 5D) similar to that reported by Suzuki and Larkum (2017). Because we did not include synaptic connectivity, the above results suggest that the late sink is associated with the dendritic Ca2+ spikes.
As an additional test of our model, we investigated the influence of the Ih current on the source-sink pattern generated by the dendritic Ca2+ spikes. We simply repeated the simulations without the Ih current in the apical-dendrites/trunk compartment (Fig. 5D, blocking Ih). In agreement with the experimental data (Suzuki and Larkum, 2017), we found a significant increase in the amplitude of the delayed sink in the middle-upper layers (p = 0.002, Wilcoxon signed-rank test, N = 10 trials). In the model, we also found that fewer Ca2+ spikes were produced (t(18) = −10.9723, , two-tailed unpaired t test, N = 10 trials) when Ih is present () than when this current was absent (). The Ih current makes the apical dendrites more depolarized. Hence, we would expect that, for the same somatic stimulation, more Ca2+ spikes will occur when Ih is present compared with when the channel is blocked. However, the Ih current also increases the electrotonic distance between the distal apical dendritic region and the soma (Berger et al., 2001, 2003) requiring larger somatic inputs to generate Ca2+ spikes. Evidence of this is the decrease in the CF for Ca2+ spike initiation after blocking this channel (Berger et al., 2003), which our model replicates. Contrary to the experimental results, our model also predicted an increase in the source near to the pia surface. The iCSD calculation uses the “method of the image” to account for a jump in conductivity at the cortical surface. This method depends on the actual conductivity values in the cortex and that of the substance used to keep the craniotomy moisturized (e.g., CSF or oil). CSF was used in the case of Suzuki and Larkum (2017). However, information about the actual conductivities used in the iCSD method was not provided in their paper. In our simulations, we used an infinite homogeneous volume conductor model; hence, CSD maps near the cortical surface might be affected by assumptions used in the source analysis. The Ih current was crucial to produce a shifted resting membrane potential of 10 mV in the apical-dendrites/trunk compartment, which disappeared when Ih was absent. As the trunk resting membrane potential became more negative, the effect of was larger 15-25 ms after stimulation (Fig. 5D), producing a deeper, delayed sink during Ca2+ spiking at the level of the L5-PC trunk.
Ca2+ spike-dependent scalp EEG signatures in macaque
To demonstrate the utility of this minimal model of L5-PC, we estimated the electrical potentials measured by contacts arranged in a 10-10 system applied to the macaque head (Fig. 6A) that are evoked by the activation of 1000 simulated L5-PCs in a cortical column occupying 1.6 mm in depth and 3 mm in diameter (Fig. 1F). To compare with previous results and use realistic anatomic information (Godlove et al., 2014; Sajad et al., 2019), we positioned the simulated column in the SEF in one hemisphere of a macaque monkey cerebral cortex (Fig. 6B). Each L5-PC was oriented perpendicular to the cortical surface.
Figure 6C shows the simulated EEG potentials sampled at all electrodes plus the topographical EEG maps at selected times. The simulated L5-PC Ca2+ spikes produced a positive scalp potential reaching maximal amplitude ∼10 ms after the dendritic Ca2+ spikes (Fig. 5B). Additional dynamics were observed in the simulated EEG after the PC stimulation was removed. Furthermore, when the population of L5-PCs was stimulated with a current that does not initiate discernible dendritic Ca2+ spikes, the amplitude of the scalp potential was substantially smaller (Fig. 6D).
These results correspond closely to the scalp potentials detected by Suzuki and Larkum (2017) in rats with and without discernible Ca2+ spikes. Our simulations show a positive peak before the onset of the dendritic Ca2+ spikes, likely related to Na+-AP firing that was smaller in Suzuki and Larkum (2017). We believe this peak is caused by the high synchronization of Na+-APs in our simulations, even in the presence of noise, which must be physiologically blurred in Suzuki and Larkum (2017) by in vivo excitatory/inhibitory ongoing network activity.
Discussion
Synaptic integration in apical dendrites of L5-PCs is facilitated by unique characteristics of these neurons: (1) different sensitivity of f-I curves for the soma and distal trunk, (2) amplification of coincident apical dendritic inputs by BAC firing, (3) a CF for eliciting Ca2+ spikes in the distal trunk, and (4) strengthening NMDA synaptic efficacy by Ca2+ spike-dependent magnesium release and the subsequent increases in in apical dendritic spines. Biophysical models with different level of complexity have been proposed to account for particular L5-PC features (Rapp et al., 1996; Larkum et al., 2004; Chua et al., 2015; Yi et al., 2017) or combinations of features (Schaefer et al., 2003; Hay et al., 2011; Bahl et al., 2012; Almog and Korngreen, 2014; Mäki-Marttunen et al., 2018). Models explaining combinations of features required many compartments to capture realistic L5-PC morphology and more than four ionic channels per compartment (Table 3). Such complexity substantially increases computational cost and time, challenging their use in large-scale simulations of collections of L5-PCs. Fitting these complex models to LFP/EEG data will imply the use of large computational resources and advanced optimization strategies, which will limit applications to study the brain at the system level. For simplified models of PCs, we propose a new strategy to distribute ionic and returning currents in distinct neuronal regions. In this strategy, ionic currents are placed according to experimental findings, and returning currents are distributed using numerically estimated scaling coefficients, an approach motivated by a type of 3/2 power law for intracellular impedances. The scaling factor proposed in this paper should not be used for other types of PCs. Also, to our knowledge, no previous model has reported the shift in the CF because of the influence of Ih, or explained the CSD patterns associated with dendritic Ca2+ spikes evoked by supra-CF somatic stimulation, or accounted for the effect of blocking Ih (Suzuki and Larkum, 2017). We proposed a two-compartment model of L5-PCs with seven ion channels that explain qualitatively all the above-mentioned features.
Layer 2/3 PCs versus L5-PCs
Our model does not apply to L2/3 PCs. Although they share many electrophysiological properties with L5-PCs, L2/3-PCs have distinct features that differentiate their role in the cortical microcircuit (Larkum et al., 2007). As L5-PCs, L2/3-PCs have two excitability zones: the axon initial segment and the apical dendrites. Large and regenerative dendritic potentials are also evoked by back-propagating APs above a CF. Moreover, as in L5-PCs (Pérez-Garci et al., 2006), GABAergic inhibitory inputs to the apical dendrites cause long-lasting reduction of dendritic activity. However, L2/3-PCs do not show a prolonged dendritic depolarization, thus having less influence on Na+-AP output. In addition, L2/3-PCs of rodents show a low density of Ih channels (Larkum et al., 2007); whereas, in humans, their density is similar to L5-PCs (Kalmbach et al., 2018).
Functional implications: microcircuitry underlying cognitive control
Cognitive control involves the suppression of automatic or impulsive behavior for successful goal-directed behavior. Some models of cognitive control formalize this function as the coactivation of two conflicting action plans, which need to be resolved for correct performance (Botvinick et al., 2001). Coincidence detection can also support error detection, a mismatch (or conflict) between task goals and actual behavior; and prediction error, a mismatch between expected and experienced outcomes (Alexander and Brown, 2011; Cohen, 2014). Human and macaque electrophysiology experiments have characterized scalp potentials associated with these cognitive functions (Gehring et al., 1993): N2 component for conflict detection and ERN for error detection. While the N2 and ERN are indices of cognitive control, studying signal processing at the microcircuit level is essential to understanding definite mechanisms (Cohen, 2017). Our biophysical model offers a powerful tool to test different hypotheses and instantiate circuit models motivated by recent research sampling neural spiking and LFP across frontal cortical layers (Chandrasekaran et al., 2017; Bastos et al., 2018; Sajad et al., 2019).
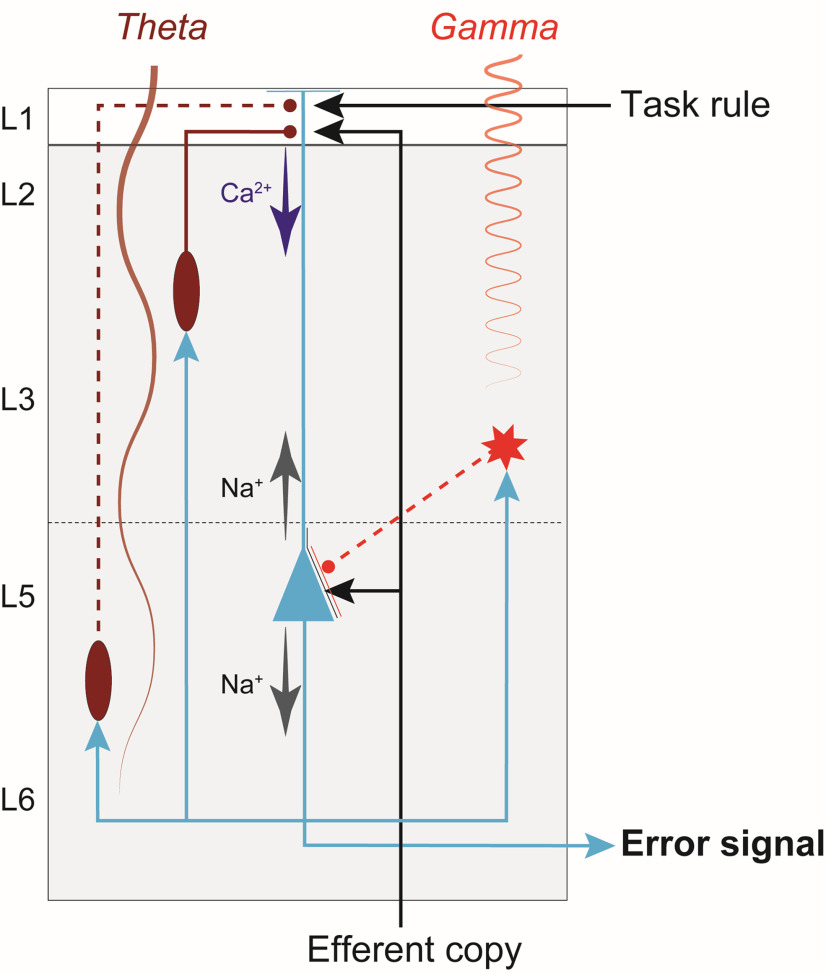
Recent models have proposed that conflict detection can be achieved by the detection of coincident synaptic inputs in the mPFC (Alexander and Brown, 2011; Cohen, 2014; Dembrow et al., 2015). L5-PCs can provide the neural substrate for the coincidence detection as they have large dendritic trees that allow for integration across inputs from cognitive, limbic, and motor structures (Huerta and Kaas, 1990; London and Häusser, 2005; Morecraft et al., 2012). Recently, we found that, following errors in the stop-signal task, error-related neural spiking in SEF was first observed in putative PCs in L5 and lower-L3 (Sajad et al., 2019) simultaneous with current sinks in the superficial layers where these neurons extend their dendrites (Sajad et al., 2017), similar to those associated to Ca2+ spikes. Figure 7 diagrams our conjecture on the role of L5-PCs in error detection in agranular cortex guided by the knowledge of the microcircuitry and known anatomic connections. L5-PCs can detect the coincidence of an efferent copy of the motor command from the mediodorsal thalamus and the task rule from PFC (Sajad et al., 2019). A mismatch between the two signals can result in spiking activity that can project extrinsically to other structures (Barbas, 2015) and intrinsically to other neurons in the microcircuit (Douglas et al., 1995; Haeusler and Maass, 2007; Kajikawa and Schroeder, 2011). L5-PCs are densely interconnected with each other (data not shown), resulting in rapid synchronous excitation of a large number of L5-PCs on receiving input currents (Hempel et al., 2000; Wang et al., 2006; Morecraft et al., 2012). L5-PCs are also connected to inhibitory interneurons, which control this excitation. Noteworthy, recent evidence suggests inhibitory neurons in agranular cortex support more intralaminar than interlaminar connections (Kätzel et al., 2011; Beul and Hilgetag, 2015). Hence, the interlaminar inhibitory projections depicted in Figure 7 represent inhibitory influences that are likely mediated by additional PCs and interneurons in L3 and L5 (data not shown).
Figure 7.
Cortical microcircuit for coincidence detection underlying cognitive control. The simplified diagram of circuitry embedding a L5-PC (blue) in agranular cortex with soma (triangle) located in L5, dendrites that extend up to L1, and axons (blue arrows) that project both intrinsically, innervating inhibitory neurons (red) and other pyramidal neurons (data not shown) in the microcircuit, and extrinsically, innervating other brain areas. This figure illustrates how dendritic dynamics can contribute to an error signal. An efferent copy of a motor command is delivered through a feedforward thalamic pathway, terminating on the L5-PC soma and apical dendrites. A task rule signal from PFC is delivered through a feedback pathway, terminating on the L5-PC apical dendrites. The soma of a L5-PC (blue triangle) generates Na+-APs that propagate intracortically to Martinotti cells (ovals) and other inhibitory interneurons (star). The Martinotti cells terminate on the L5-PC apical dendrites, while the other interneuron terminates on the soma. Because inhibitory neurons in agranular cortex largely make intralaminar projections, the interlaminar inhibitory projections depicted here (dashed red lines) represent connections that are likely mediated by additional PCs and interneurons in L3 and L5 (data not shown). The dynamics of this connectivity induces Ca2+ spikes, which amplify the coincidence of the efferent copy and the task rule to generate an error signal. These neuronal events are signaled by the generation of theta band LFP from deeper layers and gamma band LFP from superficial layers (indicated by labeled oscillations).
We hypothesize that differences in the theta-band resonance recently reported in the SEF during a saccade countermanding paradigm (Doubnia et al., 2019) is caused by an excitatory influence on L5-PC apical dendrites coming from the dlPFC, representing a learned task rule. Theta-band resonance in L5-PCs has also been linked to GABA-based synaptic activity from parvalbumin interneurons, mediated by the Ih current. This can be caused by sustained dendritic depolarizations via activation of Ih by hyperpolarizing inputs into the apical dendrites (Stark et al., 2013). Parvalbumin interneurons are homogeneously expressed in all layers of SEF (Godlove et al., 2014). However, the inhibitory sources underlying theta-band resonance are yet to be elucidated, as Cohen (2014) related it to somatostatin interneurons. On the other hand, ACh release in the PFC from basal forebrain has been linked to attentional performance (Parikh et al., 2007) and suggested to participate in the push-pull basal ganglia mechanisms supporting reactive and planned eye movements (Sajad et al., 2019). Evoked transient increases in ACh activity produce prolonged dendritic depolarizations in L5-PCs by the selective reduction of the voltage-gated potassium current IM (McCormick and Prince, 1985). The presence of both Ih and IM channels in L5-PCs has been linked to a suprathreshold theta-band resonance (Schmidt et al., 2017). Inhibition of L5-PCs by interneurons in the upper layers has been associated with the generation of gamma oscillations (Buzsáki and Wang, 2012; Bastos et al., 2018). These oscillations result in EEG polarizations in the gamma and theta rhythms, one of the hallmarks of error and conflict detection (Tallon-Baudry and Bertrand, 1999; Cohen and Donner, 2013).
While Figure 7 provides one explanation for signal flow within the microcircuit, it is far from complete and includes untested assumptions. For instance, the location where inputs to L5-PCs converge and the mechanism integrating these signals at the biophysical level remains technically challenging to study (Stuart and Spruston, 2015). The biophysical model proposed in the current study provides an essential tool for further testing and refining competing hypotheses. Future work needs also the development of similar biophysical models for L2/3-PCs and other neurons in the microcircuitry.
A necessary step toward understanding the origin of the ERN
The proposed model will be useful for another research goal of developing a forward model of the ERN component. Clearly, the EEG arises from the activity of neurons in the brain tissue, but the detailed relationship to activity within the neocortex remains unclear (Riera et al., 2012; Einevoll et al., 2013). Recently, we have shown that error-related neuronal spiking in the upper layers, but not lower layers, of monkey SEF predicts the magnitude of the ERN (Sajad et al., 2019). Also, recent work recording from single neurons in humans has shown coupling between error neuron activity and intracranial EEG (Fu et al., 2019). Because of their fast dynamics, only bursts of APs from a large population of neurons can influence the EEG (Buzsáki et al., 2012); however, postsynaptic Ca2+ spikes can be observed in EEG as they are slower events. To our knowledge, we are the first to simulate EEG polarizations resulting from L5-PC Ca2+ spikes using a realistic monkey head model. Establishing a link between specific microcircuit motifs and fluctuations in the EEG can render event-related potentials more effective markers of specific cortical processes and stronger diagnostic tools for patients with compromised cognitive control functions.
Footnotes
This work was supported by FIU SEED Grant Wallace Coulter Foundation to B.H. and J.J.R.; R01-EY019882 to J.D.S., G.F.W., B.H., and J.J.R.; and Robin and Richard Patton through the E. Bronson Ingram Chair in Neuroscience to J.D.S. We thank Michelle Schall and Arash Moshkforoush for helpful discussions and comments on the manuscript. Guided by the reviewers of the manuscript, our strategy for the LFP/EEG estimation improved from a qualitative to quantitative perspective.
The authors declare no competing financial interests.
References
- Adams PR, Brown DA, Constanti A (1982) M‐currents and other potassium currents in bullfrog sympathetic neurones. J Physiol 330:537–572. 10.1113/jphysiol.1982.sp014357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander WH, Brown JW (2011) Medial prefrontal cortex as an action-outcome predictor. Nat Neurosci 14:1338–1344. 10.1038/nn.2921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almog M, Korngreen A (2009) Characterization of voltage-gated Ca2+ conductances in layer 5 neocortical pyramidal neurons from rats. PLoS One 4:e4841. 10.1371/journal.pone.0004841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almog M, Korngreen A (2014) A quantitative description of dendritic conductances and its application to dendritic excitation in layer 5 pyramidal neurons. J Neurosci 34:182–196. 10.1523/JNEUROSCI.2896-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amitai Y, Friedman A, Gutnick MJ, Connors BW (1993) Regenerative activity in apical dendrites of pyramidal cells in neocortex. Cereb Cortex 3:26–38. 10.1093/cercor/3.1.26 [DOI] [PubMed] [Google Scholar]
- Bahl A, Stemmler MB, Herz AV, Roth A (2012) Automated optimization of a reduced layer 5 pyramidal cell model based on experimental data. J Neurosci Methods 210:22–34. 10.1016/j.jneumeth.2012.04.006 [DOI] [PubMed] [Google Scholar]
- Barbas H. (2015) General cortical and special prefrontal connections: principles from structure to function. Annu Rev Neurosci 38:269–289. 10.1146/annurev-neuro-071714-033936 [DOI] [PubMed] [Google Scholar]
- Bastos AM, Loonis R, Kornblith S, Lundqvist M, Miller EK (2018) Laminar recordings in frontal cortex suggest distinct layers for maintenance and control of working memory. Proc Natl Acad Sci USA 115:1117–1122. 10.1073/pnas.1710323115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger T, Larkum ME, Lüscher HR (2001) High Ih channel density in the distal apical dendrite of layer V pyramidal cells increases bidirectional attenuation of EPSPs. J Neurophysiol 85:855–868. 10.1152/jn.2001.85.2.855 [DOI] [PubMed] [Google Scholar]
- Berger T, Senn W, Lüscher HR (2003) Hyperpolarization-activated current Ih disconnects somatic and dendritic spike initiation zones in layer V pyramidal neurons. J Neurophysiol 90:2428–2437. 10.1152/jn.00377.2003 [DOI] [PubMed] [Google Scholar]
- Beul SF, Hilgetag CC (2015) Towards a “canonical” agranular cortical microcircuit. Front Neuroanat 8:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Carter CS, Braver TS, Barch DM, Cohen JD (2001) Conflict monitoring and cognitive control. Psychol Rev 108:624–652. 10.1037/0033-295x.108.3.624 [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Anastassiou CA, Koch C (2012) The origin of extracellular fields and currents: EEG, ECoG, LFP and spikes. Nat Rev Neurosci 13:407–420. 10.1038/nrn3241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, Wang XJ (2012) Mechanisms of gamma oscillations. Annu Rev Neurosci 35:203–225. 10.1146/annurev-neuro-062111-150444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran C, Peixoto D, Newsome WT, Shenoy KV (2017) Laminar differences in decision-related neural activity in dorsal premotor cortex. Nat Commun 8:16 10.1038/s41467-017-00715-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua Y, Morrison A, Helias M (2015) Modeling the calcium spike as a threshold triggered fixed waveform for synchronous inputs in the fluctuation regime. Front Comput Neurosci 9:1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX. (2014) A neural microcircuit for cognitive conflict detection and signaling. Trends Neurosci 37:480–490. 10.1016/j.tins.2014.06.004 [DOI] [PubMed] [Google Scholar]
- Cohen MX. (2017) Where does EEG come from and what does it mean? Trends Neurosci 40:208–218. 10.1016/j.tins.2017.02.004 [DOI] [PubMed] [Google Scholar]
- Cohen MX, Donner TH (2013) Midfrontal conflict-related theta-band power reflects neural oscillations that predict behavior. J Neurophysiol 110:2752–2763. 10.1152/jn.00479.2013 [DOI] [PubMed] [Google Scholar]
- Crill WE. (1996) Persistent sodium current in mammalian central neurons. Annu Rev Physiol 58:349–362. 10.1146/annurev.ph.58.030196.002025 [DOI] [PubMed] [Google Scholar]
- Dembrow NC, Zemelman BV, Johnston D (2015) Temporal dynamics of l5 dendrites in medial prefrontal cortex regulate integration versus coincidence detection of afferent inputs. J Neurosci 35:4501–4514. 10.1523/JNEUROSCI.4673-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doubnia R, Sajad A, Herrera B, Schall J, Riera J, Woodman G (2019) Microcircuitry of agranular frontal cortex: laminar phase-amplitude coupling for cognitive control. In: Neuroscience Meeting Planner (Program 081.12). Chicago: Society for Neuroscience. [Google Scholar]
- Douglas RJ, Koch C, Mahowald M, Martin KA, Suarez HH (1995) Recurrent excitation in neocortical circuits. Science 269:981–985. 10.1126/science.7638624 [DOI] [PubMed] [Google Scholar]
- Einevoll GT, Kayser C, Logothetis NK, Panzeri S (2013) Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat Rev Neurosci 14:770–785. 10.1038/nrn3599 [DOI] [PubMed] [Google Scholar]
- Fleidervish IA, Gutnick MJ (1996) Kinetics of slow inactivation of persistent sodium current in layer V neurons of mouse neocortical slices. J Neurophysiol 76:2125–2130. 10.1152/jn.1996.76.3.2125 [DOI] [PubMed] [Google Scholar]
- Fleidervish IA, Lasser-Ross N, Gutnick MJ, Ross WN (2010) Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nat Neurosci 13:852–860. 10.1038/nn.2574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Z, Wu DA, Ross I, Chung JM, Mamelak AN, Adolphs R, Rutishauser U (2019) Single-neuron correlates of error monitoring and post-error adjustments in human medial frontal cortex. Neuron 101:165–177.e5. 10.1016/j.neuron.2018.11.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gehring WJ, Goss B, Coles MG, Meyer DE, Donchin E (1993) A neural system for error detection and compensation. Psychol Sci 4:385–390. 10.1111/j.1467-9280.1993.tb00586.x [DOI] [Google Scholar]
- Giacometti P, Perdue KL, Diamond SG (2014) Algorithm to find high density EEG scalp coordinates and analysis of their correspondence to structural and functional regions of the brain. J Neurosci Methods 229:84–96. 10.1016/j.jneumeth.2014.04.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godlove DC, Maier A, Woodman GF, Schall JD (2014) Microcircuitry of agranular frontal cortex: testing the generality of the canonical cortical microcircuit. J Neurosci 34:5355–5369. 10.1523/JNEUROSCI.5127-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goto T, Hatanaka R, Ogawa T, Sumiyoshi A, Riera J, Kawashima R (2010) An evaluation of the conductivity profile in the somatosensory barrel cortex of Wistar rats. J Neurophysiol 104:3388–3412. 10.1152/jn.00122.2010 [DOI] [PubMed] [Google Scholar]
- Guan D, Armstrong WE, Foehring RC (2015) Electrophysiological properties of genetically identified subtypes of layer 5 neocortical pyramidal neurons: Ca2+ dependence and differential modulation by norepinephrine. J Neurophysiol 113:2014–2032. 10.1152/jn.00524.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haeusler S, Maass W (2007) A statistical analysis of information-processing properties of lamina-specific cortical microcircuit models. Cereb Cortex 17:149–162. 10.1093/cercor/bhj132 [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Sarvas J (1989) Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans Biomed Eng 36:165–171. 10.1109/10.16463 [DOI] [PubMed] [Google Scholar]
- Harnett MT, Xu NL, Magee JC, Williams SR (2013) Potassium channels control the interaction between active dendritic integration compartments in layer 5 cortical pyramidal neurons. Neuron 79:516–529. 10.1016/j.neuron.2013.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett MT, Magee JC, Williams SR (2015) Distribution and function of HCN channels in the apical dendritic tuft of neocortical pyramidal neurons. J Neurosci 35:1024–1037. 10.1523/JNEUROSCI.2813-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay E, Hill S, Schürmann F, Markram H, Segev I (2011) Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Comput Biol 7:e1002107. 10.1371/journal.pcbi.1002107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hempel CM, Hartman KH, Wang XJ, Turrigiano GG, Nelson SB (2000) Multiple forms of short-term plasticity at excitatory synapses in rat medial prefrontal cortex. J Neurophysiol 83:3031–3041. 10.1152/jn.2000.83.5.3031 [DOI] [PubMed] [Google Scholar]
- Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM (2004) ModelDB: a Database to support computational neuroscience. J Comput Neurosci 17:7–11. 10.1023/B:JCNS.0000023869.22017.2e [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Davison AP, Muller E (2009) NEURON and Python. Front Neuroinform 3:1. 10.3389/neuro.11.001.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117:500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt GR, Koch C (1999) Electrical interactions via the extracellular potential near cell bodies. J Comput Neurosci 6:169–184. 10.1023/a:1008832702585 [DOI] [PubMed] [Google Scholar]
- Hu W, Tian C, Li T, Yang M, Hou H, Shu Y (2009) Distinct contributions of Nav1.6 and Nav1.2 in action potential initiation and back-propagation. Nat Neurosci 12:996–1002. 10.1038/nn.2359 [DOI] [PubMed] [Google Scholar]
- Huerta MF, Kaas JH (1990) Supplementary eye field as defined by intracortical microstimulation: connections in macaques. J Comp Neurol 293:299–330. 10.1002/cne.902930211 [DOI] [PubMed] [Google Scholar]
- Kajikawa Y, Schroeder CE (2011) How local is the local field potential? Neuron 72:847–858. 10.1016/j.neuron.2011.09.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalmbach BE, Buchin A, Long B, Close J, Nandi A, Miller JA, Bakken TE, Hodge RD, Chong P, de Frates R, Dai K, Maltzer Z, Nicovich PR, Keene CD, Silbergeld DL, Gwinn RP, Cobbs C, Ko AL, Ojemann JG, Koch C, et al. (2018) h-Channels contribute to divergent intrinsic membrane properties of supragranular pyramidal neurons in human versus mouse cerebral cortex. Neuron 100:1194–1208.e5. 10.1016/j.neuron.2018.10.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kätzel D, Zemelman BV, Buetfering C, Wölfel M, Miesenböck G (2011) The columnar and laminar organization of inhibitory connections to neocortical excitatory cells. Nat Neurosci 14:100–109. 10.1038/nn.2687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kole MH, Hallermann S, Stuart GJ (2006) Single Ih channels in pyramidal neuron dendrites: properties, distribution, and impact on action potential output. J Neurosci 26:1677–1687. 10.1523/JNEUROSCI.3664-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korngreen A, Sakmann B (2000) Voltage-gated K+ channels in layer 5 neocortical pyramidal neurones from young rats: subtypes and gradients. J Physiol 525:621–639. 10.1111/j.1469-7793.2000.00621.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. (2013) A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends Neurosci 36:141–151. 10.1016/j.tins.2012.11.006 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ (2002) Signaling of layer 1 and whisker-evoked Ca2+ and Na+ action potentials in distal and terminal dendrites of rat neocortical pyramidal neurons in vitro and in vivo. J Neurosci 22:6991–7005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Kaiser KM, Sakmann B (1999a) Calcium electrogenesis in distal apical dendrites of layer 5 pyramidal cells at a critical frequency of back-propagating action potentials. Proc Natl Acad Sci USA 96:14600–14604. 10.1073/pnas.96.25.14600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ, Sakmann B (1999b) A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398:338–341. 10.1038/18686 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ, Sakmann B (2001) Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J Physiol 533:447–466. 10.1111/j.1469-7793.2001.0447a.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Senn W, Lüscher HR (2004) Top-down dendritic input increases the gain of layer 5 pyramidal neurons. Cereb Cortex 14:1059–1070. 10.1093/cercor/bhh065 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Waters J, Sakmann B, Helmchen F (2007) Dendritic spikes in apical dendrites of neocortical layer 2/3 pyramidal neurons. J Neurosci 27:8999–9008. 10.1523/JNEUROSCI.1717-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Nevian T, Sandler M, Polsky A, Schiller J (2009) Supplementary synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325:756–760. 10.1126/science.1171958 [DOI] [PubMed] [Google Scholar]
- Ledergerber D, Larkum ME (2010) Properties of layer 6 pyramidal neuron apical dendrites. J Neurosci 30:13031–13044. 10.1523/JNEUROSCI.2254-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WH, Lisanby SH, Laine AF, Peterchev AV (2015) Electric field model of transcranial electric stimulation in nonhuman primates: correspondence to individual motor threshold. IEEE Trans Biomed Eng 62:2095–2105. 10.1109/TBME.2015.2425406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leresche N, Lambert RC (2017) T-type calcium channels in synaptic plasticity. Channels (Austin) 11:121–139. 10.1080/19336950.2016.1238992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindén H, Hagen E, Lęski S, Norheim ES, Pettersen KH, Einevoll GT (2014) LFPy: a tool for biophysical simulation of extracellular potentials generated by detailed model neurons. Front Neuroinform 7:41. 10.3389/fninf.2013.00041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- London M, Häusser M (2005) Dendritic computation. Annu Rev Neurosci 28:503–532. 10.1146/annurev.neuro.28.061604.135703 [DOI] [PubMed] [Google Scholar]
- Lörincz A, Notomi T, Tamás G, Shigemoto R, Nusser Z (2002) Polarized and compartment-dependent distribution of HCN1 in pyramidal cell dendrites. Nat Neurosci 5:1185–1193. 10.1038/nn962 [DOI] [PubMed] [Google Scholar]
- Lytton W, Sejnowski TJ (1991) Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J Neurophysiol 66:1059–1079. 10.1152/jn.1991.66.3.1059 [DOI] [PubMed] [Google Scholar]
- Magistretti J, Alonso A (1999) Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer II principal neurons: a whole-cell and single-channel study. J Gen Physiol 114:491–509. 10.1085/jgp.114.4.491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäki-Marttunen T, Halnes G, Devor A, Metzner C, Dale AM, Andreassen OA, Einevoll GT (2018) A stepwise neuron model fitting procedure designed for recordings with high spatial resolution: application to layer 5 pyramidal cells. J Neurosci Methods 293:264–283. 10.1016/j.jneumeth.2017.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA (1985) Two types of muscarinic response to acetylcholine in mammalian cortical neurons. Proc Natl Acad Sci USA 82:6344–6348. 10.1073/pnas.82.18.6344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittmann T, Linton SM, Schwindt P, Crill W (1997) Evidence for persistent Na+ current in apical dendrites of rat neocortical neurons from imaging of Na+-sensitive dye. J Neurophysiol 78:1188–1192. 10.1152/jn.1997.78.2.1188 [DOI] [PubMed] [Google Scholar]
- Mohan H, Verhoog MB, Doreswamy KK, Eyal G, Aardse R, Lodder BN, Goriounova NA, Asamoah B, Brakspear AB, Groot C, Van Der Sluis S, Testa-Silva G, Obermayer J, Boudewijns ZS, Narayanan RT, Baayen JC, Segev I, Mansvelder HD, De Kock CP (2015) Dendritic and axonal architecture of individual pyramidal neurons across layers of adult human neocortex. Cereb Cortex 25:4839–4853. 10.1093/cercor/bhv188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morecraft RJ, Stilwell-Morecraft KS, Cipolloni PB, Ge J, McNeal DW, Pandya DN (2012) Cytoarchitecture and cortical connections of the anterior cingulate and adjacent somatomotor fields in the rhesus monkey. Brain Res Bull 87:457–497. 10.1016/j.brainresbull.2011.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ness TV, Remme MW, Einevoll GT (2018) h-Type membrane current shapes the local field potential from populations of pyramidal neurons. J Neurosci 38:6011–6024. 10.1523/JNEUROSCI.3278-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevian T, Larkum ME, Polsky A, Schiller J (2007) Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat Neurosci 10:206–214. 10.1038/nn1826 [DOI] [PubMed] [Google Scholar]
- Nicholson C, Llinas R (1971) Field potentials in the alligator cerebellum and theory of their relationship to Purkinje cell dendritic spikes. J Neurophysiol 34:509–531. 10.1152/jn.1971.34.4.509 [DOI] [PubMed] [Google Scholar]
- Parikh V, Kozak R, Martinez V, Sarter M (2007) Prefrontal acetylcholine release controls cue detection on multiple timescales. Neuron 56:141–154. 10.1016/j.neuron.2007.08.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny W, Friston K, Ashburner J, Kiebel S, Nichols T (2007) Statistical parametric mapping: the analysis of functional brain images. Amsterdam: Elsevier. [Google Scholar]
- Pérez-Garci E, Gassmann M, Bettler B, Larkum ME (2006) The GABAB1b isoform mediates long-lasting inhibition of dendritic Ca2+ spikes in layer 5 somatosensory pyramidal neurons. Neuron 50:603–616. 10.1016/j.neuron.2006.04.019 [DOI] [PubMed] [Google Scholar]
- Pérez-Garci E, Larkum ME, Nevian T (2013) Inhibition of dendritic Ca2+ spikes by GABAB receptors in cortical pyramidal neurons is mediated by a direct Gi/o-βγ-subunit interaction with Cav1 channels. J Physiol 591:1599–1612. 10.1113/jphysiol.2012.245464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen KH, Devor A, Ulbert I, Dale AM, Einevoll GT (2006) Current-source density estimation based on inversion of electrostatic forward solution: effects of finite extent of neuronal activity and conductivity discontinuities. J Neurosci Methods 154:116–133. 10.1016/j.jneumeth.2005.12.005 [DOI] [PubMed] [Google Scholar]
- Ramaswamy S, Markram H (2015) Anatomy and physiology of the thick-tufted layer 5 pyramidal neuron. Front Cell Neurosci 9:1–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapp M, Yarom Y, Segev I (1996) Modeling back propagating action potential in weakly excitable dendrites of neocortical pyramidal cells. Proc Natl Acad Sci USA 93:11985–11990. 10.1073/pnas.93.21.11985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimann MW, Anastassiou CA, Perin R, Hill SL, Markram H, Koch C (2013) A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron 79:375–390. 10.1016/j.neuron.2013.05.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuveni I, Friedman A, Amitai Y, Gutnick MJ (1993) Stepwise repolarization from Ca2+ plateaus in neocortical pyramidal cells: evidence for nonhomogeneous distribution of HVA Ca2+ channels in dendrites. J Neurosci 13:4609–4621. 10.1523/JNEUROSCI.13-11-04609.1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riera J, Hatanaka R, Uchida T, Ozaki T, Kawashima R (2011) Quantifying the uncertainty of spontaneous Ca2+ oscillations in astrocytes: particulars of Alzheimer's disease. Biophys J 101:554–564. 10.1016/j.bpj.2011.06.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riera JJ, Ogawa T, Goto T, Sumiyoshi A, Nonaka H, Evans A, Miyakawa H, Kawashima R (2012) Pitfalls in the dipolar model for the neocortical EEG sources. J Neurophysiol 108:956–975. 10.1152/jn.00098.2011 [DOI] [PubMed] [Google Scholar]
- Saganich MJ, Machado E, Rudy B (2001) Differential expression of genes encoding subthreshold-operating voltage-gated K+ channels in brain. J Neurosci 21:4609–4624. 10.1523/JNEUROSCI.21-13-04609.2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajad A, Godlove D, Schall J (2017) Microcircuitry of performance monitoring. bioRxiv 187989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajad A, Godlove DC, Schall JD (2019) Cortical microcircuitry of performance monitoring. Nat Neurosci 22:265–274. 10.1038/s41593-018-0309-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer AT, Helmstaedter M, Schmitt AC, Bar-Yehuda D, Almog M, Ben-Porat H, Sakmann B, Korngreen A (2007) Dendritic voltage-gated K+ conductance gradient in pyramidal neurones of neocortical layer 5B from rats. J Physiol 579:737–752. 10.1113/jphysiol.2006.122564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer AT, Larkum ME, Sakmann B, Roth A (2003) Coincidence detection in pyramidal neurons is tuned by their dendritic branching pattern. J Neurophysiol 89:3143–3154. 10.1152/jn.00046.2003 [DOI] [PubMed] [Google Scholar]
- Schiller J, Schiller Y, Stuart G, Sakmann B (1997) Calcium action potentials restricted to distal apical dendrites of rat neocortical pyramidal neurons. J Physiol 505:605–616. 10.1111/j.1469-7793.1997.605ba.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt SL, Dorsett CR, Iyengar AK, Fröhlich F (2017) Interaction of intrinsic and synaptic currents mediate network resonance driven by layer V pyramidal cells. Cereb Cortex 27:4396–4410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwindt PC, Crill WE (1995) Amplification of synaptic current by persistent sodium conductance in apical dendrite of neocortical neurons. J Neurophysiol 74:2220–2224. 10.1152/jn.1995.74.5.2220 [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Crill W (1999) Mechanisms underlying burst and regular spiking evoked by dendritic depolarization in layer 5 cortical pyramidal neurons. J Neurophysiol 81:1341–1354. 10.1152/jn.1999.81.3.1341 [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM (2001) Magnetic resonance image tissue classification using a partial volume model. Neuroimage 13:856–876. 10.1006/nimg.2000.0730 [DOI] [PubMed] [Google Scholar]
- Stark E, Eichler R, Roux L, Fujisawa S, Rotstein HG, Buzsáki G (2013) Inhibition-Induced theta resonance in cortical circuits. Neuron 80:1263–1276. 10.1016/j.neuron.2013.09.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart GJ, Sakmann B (1994) Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature 367:69–72. 10.1038/367069a0 [DOI] [PubMed] [Google Scholar]
- Stuart GJ, Spruston N (2015) Dendritic integration: 60 years of progress. Nat Neurosci 18:1713–1721. 10.1038/nn.4157 [DOI] [PubMed] [Google Scholar]
- Stuphorn V, Taylor TL, Schall JD (2000) Performance monitoring by the supplementary eye field. Nature 408:857–860. 10.1038/35048576 [DOI] [PubMed] [Google Scholar]
- Subramanian D, Alers A, Sommer MA (2019) Corollary discharge for action and cognition. Biol Psychiatry Cogn Neurosci Neuroimaging 4:782–790. 10.1016/j.bpsc.2019.05.010 [DOI] [PubMed] [Google Scholar]
- Suzuki M, Larkum ME (2017) Dendritic calcium spikes are clearly detectable at the cortical surface. Nat Commun 8:11 10.1038/s41467-017-00282-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tadel F, Baillet S, Mosher JC, Pantazis D, Leahy RM (2011) Brainstorm: a user-friendly application for MEG/EEG analysis. Comput Intell Neurosci 2011:879716. 10.1155/2011/879716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O (1999) Oscillatory gamma activity in humans and its role in object representation. Trends Cogn Sci 3:151–162. [DOI] [PubMed] [Google Scholar]
- Tarasenko AN, Isaev DS, Eremin AV, Kostyuk PG (1998) Developmental changes in the expression of low-voltage-activated Ca2+ channels in rat visual cortical neurones. J Physiol 509:385–394. 10.1111/j.1469-7793.1998.385bn.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich D. (2002) Dendritic resonance in rat neocortical pyramidal cells. J Neurophysiol 87:2753–2759. 10.1152/jn.2002.87.6.2753 [DOI] [PubMed] [Google Scholar]
- Wang Y, Markram H, Goodman PH, Berger TK, Ma J, Goldman-Rakic PS (2006) Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat Neurosci 9:534–542. 10.1038/nn1670 [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ (1999) Mechanisms and consequences of action potential burst firing in rat neocortical pyramidal neurons. J Physiol 521:467–482. 10.1111/j.1469-7793.1999.00467.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada SI, Takechi H, Kanchiku I, Kita T, Kato N (2004) Small-Conductance Ca2+-Dependent K+ Channels Are the Target of Spike-Induced Ca2+ Release in a Feedback Regulation of Pyramidal Cell Excitability. J Neurophysiol 91:2322–2329. [DOI] [PubMed] [Google Scholar]
- Yi G, Wang J, Wei X, Deng B (2017) Action potential initiation in a two-compartment model of pyramidal neuron mediated by dendritic Ca2+ spike. Sci Rep 7:16 10.1038/srep45684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuste R, Gutnick MJ, Saar D, Delaney KR, Tank DW (1994) Ca2+ accumulations in dendrites of neocortical pyramidal neurons: an apical band and evidence for two functional compartments. Neuron 13:23–43. 10.1016/0896-6273(94)90457-X [DOI] [PubMed] [Google Scholar]
- Zhu JJ. (2000) Maturation of layer 5 neocortical pyramidal neurons: amplifying salient layer 1 and layer 4 inputs by Ca2+ action potentials in adult rat tuft dendrites. J Physiol 526:571–587. 10.1111/j.1469-7793.2000.00571.x [DOI] [PMC free article] [PubMed] [Google Scholar]