A Hybrid Machine Learning Approach to Localizing the Origin of Ventricular Tachycardia Using 12-Lead Electrocardiograms

Abstract

Background:

Machine learning models may help localize the site of origin of ventricular tachycardia (VT) using 12-lead electrocardiograms. However, population-based models suffer from inter-subject anatomical variations within ECG data, while patient-specific models face the open challenge of what pacing data to collect for training.

Methods:

This study presents and validates the first hybrid model that combines population and patient-specific machine learning for rapid “computer-guided pace-mapping”. A population-based deep learning model was first trained offline to disentangle inter-subject variations and regionalize the site of VT origin. Given a new patient with a target VT, an on-line patient-specific model -- after being initialized by the population-based prediction -- was then built in real time by actively suggesting where to pace next and improving the prediction with each added pacing data, progressively guiding pace-mapping towards the site of VT origin.

Results:

The population model was trained on pace-mapping data from 38 patients and the patient-specific model was subsequently tuned on one patient. The resulting hybrid model was tested on a separate cohort of eight patients in localizing 1) 193 LV endocardial pacing sites, and 2) nine VTs with clinically determined exit sites. The hybrid model achieved a localization error of 5.3 ± 2.6 mm using 5.4 ± 2.5 pacing sites in localizing LV pacing sites, achieving a significantly higher accuracy with a significantly smaller amount of training sites in comparison to models without active guidance.

Conclusion:

The presented hybrid model has the potential to assist rapid pace-mapping of interventional targets in VT.

Introduction

Monomorphic ventricular tachycardia (VT), a heart arrhythmia in which abnormal electrical activity causes accelerated and irregular heartbeats, is primarily classified into two groups, idiopathic and structural. Idiopathic VT, referring to the absence of structural heart issues, is typically associated with less severe symptoms, such as palpations, and poses small risk for sudden cardiac death (SCD) [1]. Structural VT, conversely, stems from structural heart disease, such as myocardial scar tissue isthmuses, and can be the source of sustained VT. Sustained VTs can lead to ventricular fibrillation (VF) and harbors a serious risk for SCD [1]. This progression of VT to VF contributes to approximately 350,000 sudden cardiac deaths each year in the United States [2] and 4.2 million deaths globally [3]. To enable interventional electrophysiologists to concentrate on a specific region of the heart in cases of diagnosed VT, it is important to localize the sites of origins of VTs: in focal VT, this corresponds to the site where the ventricular activation starts; in reentrant VT, this corresponds to the site at which the slow conduction of a surviving channel inside the myocardial scar exits from the scar, also known as the “exit site” of VT [1, 4]. These exit sites can be blocked off through catheter ablation procedures shown to effectively alleviate or prevent the occurrence of VT [1]. Identifying exit site locations efficiently and accurately to minimize damage to healthy tissue is an important problem to which modern computational techniques can be applied.

The 12-lead electrocardiogram (ECG) is a useful tool to localize the sites of origins of monomorphic VTs because the QRS morphology on ECG, to a large extent, is determined by the site of origin of ventricular activation [5]. The associated accuracy however is limited by inter-subject variations in ECG arising from factors such as geometrical relationship between the heart and the chest wall, the anatomical and conduction characteristics of the heart, and the structural remodeling of the myocardium [4], [5]. Therefore, when VT is not sustained or tolerated sufficiently for activation mapping, pace-mapping in conjunction with substrate mapping is often utilized. Pace-mapping with substrate mapping is the practice of matching QRS complexes found through electrical stimulation of various sites on the heart with the recorded VT substrate for replicated morphologies [4]. This practice is of a “trial-and-error” nature guided by rapid qualitative interpretation of the ECG by clinicians, which can be time consuming and challenging.

To improve the existing practice of using QRS complexes on 12-lead ECGS to predict the site of VT origin, advances in modern machine learning and deep learning can be leveraged. Recent works in this direction can be loosely categorized into two groups. On one hand, methods such as template matching [6], linear and nonlinear regression [7], support vector machine [8], and deep neural networks [9], [10] have been trained using paced ECG data with known pacing-sites collected from a cohort of patients. These population-based approaches can be directly applicable to a new patient without prior pace-mapping data from the specific patient. Their accuracy, however, is fundamentally limited by the large inter-subject anatomical and physiological variations. This challenge is further exacerbated by the difficulty of acquiring the large amount of paced ECG data that is necessary for a machine learning model to be invariant to such variations. Until now, the accuracy of reported population-based models is limited to an average distance error of over 12-mm in localizing the 3D coordinate of a pacing site on the LV endocardium [7], [9].

On the other hand, the potential of localizing the site of VT origin in a patient-specific fashion has been considered, utilizing models such as linear regression [6], support vector regression [11], and convolutional neural networks [12]. These patient-specific approaches avoid the challenge of inter-subject variations and, if successfully trained, may potentially be able to provide a higher accuracy than their population-based counterparts. They however require the collection of training data, in the form of ECG data paced at different sites in a patient’s heart, before the model can be used for predictions for the same patient. Avoiding excessive pace-mapping and minimizing the necessary number of training data remain a critically unresolved challenge in building these patient-specific models.

In this paper, we present a novel hybrid model for “computer-guided pace-mapping” that includes two modules: 1) an off-line population-based deep learning model that provides an initial regionalization of the site of VT origin, and 2) an on-line patient-specific model that, after being initialized by the population predictions, in real-time actively prompts the clinician where to pace next and progressively improves the prediction of the origin of VT using each added pacing data. To our knowledge, this is the first hybrid approach that fully combines the advantage of population-based predictions (i.e., the ability to predict without patient-specific data) and patient-specific predictions (i.e., the ability to improve prediction accuracy: the population-based deep learning model leverages our most recent work to disentangle inter-subject variations when learning to localize the sites of VT origins from ECG data, improving the initial localization accuracy compared to its counterparts that do not explicitly address such heterogeneity in population data [10]; the patient-specific model is equipped with a strategy of “active guidance” that is able to provide real-time guidance to clinicians regarding where to pace next in order to minimize the amount of pace-mapping necessary before localizing the site of VT origins. The code for our model implementations and experiments is available here: https://github.com/qu-gg/vt-localization.

We evaluated the hybrid model in a complete prediction workflow for “computer-guided pace-mapping” in localizing the site of VT on the left ventricular endocardium surface, using the retrospective pace-mapping data from 47 patients [6], [7]. Specifically, paced 12-lead ECG data and the associated pacing sites from a cohort of 38 patients were used to train the population-based deep learning model offline. The patient-specific model, integrated with the trained population model, was then tuned on another patient for hyperparameters. The completed hybrid model was tested on a separate cohort of eight patients in localizing 1) 193 LV endocardial pacing sites with exactly-known sites of pacing, and 2) nine VTs in seven patients with clinically-determined VT exit sites. In all cases, we emulated how the presented hybrid model progressively guided the pace-mapping towards the target site using retrospective pace-mapping data. The results demonstrated the potential of the presented hybrid model to assist rapid localization of interventional targets for VT.

Methods

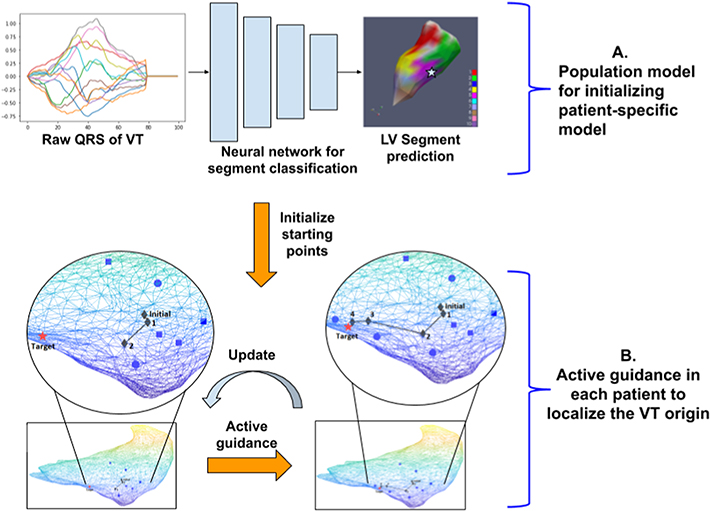
Fig. 1 outlines the overall workflow of the presented hybrid model when applied to assist pace-mapping procedures. Given the QRS trace of a 12-lead ECG of a target VT on a new patient, the population-based deep neural network first regionalizes the site of the VT origin into one of seven left-ventricular (LV) segments (Fig. 1A). Using a small number of pace-mapping data collected within the predicted region, a patient-specific model is initialized. It then enters a process iterating between suggesting where to pace next and using the added pacing data to improve the prediction. This process repeats until the QRS morphology of the newly predicted site matches that of the VT, either quantitatively or determined by the clinician (Fig. 1B). Below we describe in detail the two key modules of the hybrid model.

Figure 1:

Overview of the hybrid model. A: Population-based deep neural network uses 12-lead QRS traces to regionalize the origin of ventricular activation in5to seven LV endocardial segments. B: Patient-specific regression iterates between actively suggesting pacing sites for training and improving using the newly added pacing data, until satisfying convergence criteria.

Population-based deep learning of VT origin by disentangling inter-subject variations

The first module of the presented hybrid model is a population-based deep learning model that uses the raw trace of the QRS complex to regionalize the site of VT origin into one of seven LV segments. As illustrated in Fig. 2A, the seven-segment definition adopts a lower-resolution representation of the 17-segment LV division following the American Heart Association standard: the rationale of using a lower-resolution is that the goal of population-based prediction, given the inter-subject variations, is for an initialization rather than precise localization of the VT origin.

Figure 2:

Illustration of data processing and labeling. (A): ‘Bull’s eye view’ schematics of the seven-segment division of the left ventricle. (B): An example of ECG traces for extracting pace-captured QRS complexes, and the final input data to the population-based model.

Since ECG data are associated with a wide range of anatomical and physiological factors that vary across individuals, we leverage the expressive representation learning capacity of a deep network to disentangle such factors of variation when distilling the latent ECG representation specific to the location of the VT origin.

Variational autoencoders (VAE) for learning disentangled representations

We use a variational autoencoder (VAE) for unsupervised disentangling of independent generative factors from raw QRS complex. VAEs are deep latent-variable models with an encoding-decoding architecture, where the encoder network learns the posterior distribution of the latent representation of the data, and the decoder network learns the likelihood function that generates data from the latent representation. In this paper, we use an encoder consisting of 1D convolutional neural networks (CNN) to extract the feature from the input QRS traces, followed by linear layers to obtain the mean and variance of a multivariate Gaussian distribution of the latent variables. The CNN decoder then starts with a sample from the latent Gaussian density, with a final transpose convolution to output the signal matching the dimension of the input QRS complex without any non-linear activation. The parameters of the encoder and decoder network are optimized by maximizing the evidence lower bound of (ELBO) the marginal likelihood [13] on the training QRS data without any associated labels.

Fine-tuning for classification

To further distill the latent QRS representation specific to the origin of ventricular activation, the VAE encoder is fine-tuned with a supervised loss using the segment label from which the ventricular activation originated. In specific, we introduce additional fully-connected linear layers that take a sample of the VAE-encoded latent distribution and output a seven-dimensional output corresponding to seven LV segments, on which a soft-max function is applied for supervised classification loss. This loss is backpropagated to fine tune both the VAE encoder and the fully-connected layers, which gives the population model that will be used to provide the initial regionalization of the origin of ventricular activation given a testing 12-lead QRS complex of a new patient.

Patient-specific localization of VT origin with actively-guided pace-mapping

The second module of the presented hybrid model is an actively-guided patient-specific model that uses the 120-ms integral of the QRS complex from the 12-lead ECG to pinpoint the (x, y, z) coordinate of the site of VT origin. The coordinates are defined in the electroanatomic mapping system in which pace-mapping will be performed, such that the model prediction can be directly incorporated into the pace-mapping procedure without additional need of registration. As illustrated in Fig. 1B, this actively-guided patient-specific model is initialized by predictions provided by the population-based deep network, and works by iterating between suggesting the next sites of pace-mapping and updating the model with the newly added pace-mapping data, progressively improving the localization of the site of the origin of VT until reaching the termination criterion.

Base regression model

The base regression approach in the patient-specific model is support vector regression (SVR) with a radial basis function (RBF) kernel that independently predict the x, y, and z coordinate. A hyperparameter C controls the tradeoff between the ability of the model to fit the training data and generalize to unseen data, and will be empirically tuned on experimental data before being applied to a separate cohort of test patients.

Active guidance strategy

The goal of active guidance is to intelligently suggest sites where additional pacing data will yield a maximum gain in the prediction accuracy of SVR, such that redundancy in training samples and the number of pace-mapping sites can be minimized.

For a balanced exploitation and exploration of the pacing space, we suggest two additional sites for pacing at each iteration. First, we exploit the predictive power of the model by simply taking the current model prediction as the next suggested pacing site. Second, we explore the unknown space of the model by focusing on the area which the current model is the least certain about. Inspired by the strategy of “Query By Committee” used in active learning [14], we determine the region with the highest prediction error by the training site with the highest localization error: in each iteration of active guidance for each pacing site in the training data, one SVR model for coordinate regression is built using the rest of the training samples and applied to the left-out sample. A rank-ordered list is obtained regarding how accurately each of the left-out sites can be predicted, indicating how well each site is represented in the current training data. From this list, the site with the highest prediction error will be chosen as the next site to pace near.

As such, in each iteration of actively-guided pace-mapping, two new pacing sites will be suggested to the clinicians. In the case that the two suggested sites are within 5-mm (approximate diameter of typical ablation lesion) with each other, only the model-predicted site will be suggested.

Initialization, termination, and hyperparameters

The patient-specific model is initialized with n_init number of pacing sites from the segment predicted by the population-based model. As the actively-guided patient-specific modeling iterates, CCs between new QRS complex obtained at each newly predicted site and that of the target VT are examined at each of the 12 leads: the process will terminate if the CC is higher than a predefined threshold CC_match in 12 out of 12 ECG leads (12/12 match). The effect of different hyperparameters within the patient-specific model will be experimentally analyzed.

Results

Study population & electrophysiology study and ablation

The training cohort was adopted from [6] and included 38 sequentially consenting patients with recurrent scar-related VT undergoing catheter ablation. The test cohort was adopted from [15] and included a separate cohort of nine patients with scar-related VT referred for catheter ablation. All participating patients gave written informed consent, and the protocol was approved by the institutional research ethics board.

In both cohorts, ablation was performed using standard endocardial techniques. VT was induced by programmed stimulation from the right ventricular apex or outflow tract. 3D electroanatomic maps were acquired by the Carto XP or Carto 3 system (Biosense Webster, Diamond Bar, CA, USA). Point-by-point endocardial mapping was performed using a multielectrode mapping catheter or an irrigated 3.5-mm tip deflectable electrode catheter (Navistar Pentaray or Thermocool Smart-Touch SF, Biosense Webster, Inc., Irvine, CA, USA) during sinus or paced rhythm. Pacing was performed with stable catheter position at multiple endocardial sites at minimum pacing output that ensured consistent focal myocardial capture.

Data acquisition and data processing

In 18 patients of the training cohort, 120-lead ECG recordings were acquired using disposable electrode strips (FoxMed, Idstein, Germany) on a 128-channel acquisition system (Mar 6, BioSemi, Amsterdam, the Netherlands), from which 12-lead ECG were derived [6]. In 20 patients of the training cohort, 12-lead ECGs were acquired via the CardioLab system (GE Inc.), sampled at 1000 Hz with 16-bit resolution, and recorded for 15 seconds. In the test cohort, eight ECG leads (I, II, V1-V6) were acquired using the CardioLab system at 1000 Hz, from which 12-lead ECG were calculated.

In both cohorts, the (x, y, z) coordinate of the pacing site for each paced ECG were exported from the electroanatomic mapping system. In seven out of the nine patients in the test cohort, exit sites were successfully localized for nine VTs on the electroanatomic map by clinical investigators who were blinded to the predicted site of origin. The site of earliest myocardial activation was identified for these nine VTs using activation and entrainment mapping, supplemented by pace-mapping at the scar margin.

All ECG data were processed for noise removal and baseline correction using an open-source software [9]. As illustrated in Fig. 2B, QRS complexes were manually extracted to avoid motion artifacts, ectopic beats, and non-capture beats. Each QRS complex was down-sampled to 256 Hz in frequency and padded with zeros to a uniform length of 100 per complex. From the training cohort, paced 12-lead ECG data from 1012 distinct pacing sites were extracted. Considering beat-to-beat variations, multiple beats were extracted from each paced ECG recording, generating in-total 16848 QRS complexes, each concatenated into a 1200×1 vector. Each QRS complex was associated with a label of one of the seven LV segments as described in [6]. From the test cohort, paced 12-lead ECG from 216 distinct pacing sites and 12-lead ECG acquired during nine induced VTs were extracted. Each QRS complex was associated with a label of LV segments, as well as a label of the (x, y, z) coordinate of the pacing site or VT exit site exported from the electroanatomic mapping system. Owing to the nature of the presented hybrid model, there is no need to register these patient-specific coordinates to a common space.

Results of the population model

Model architecture and training

We compare three alternative models for the population-based prediction:

• Linear regression (LR): As a baseline, we considered a linear regression model that utilized 120-ms time-integral of each of the 12-lead QRS complex as the predictors, as described in [6].

• CNN: Given the success of supervised CNNs in a wide variety of tasks, we also considered a supervised CNN model that consisted of four convolution blocks for feature extraction, followed by two fully connected layers. Each convolution block consisted of a 1D convolution layer, batch normalization layer, dropout layer, and ReLU as an activation function. The kernel size in these four convolution layers was 7, 5, 3, and 3 respectively, all with a stride length of 1. These convolutional layers delivered a feature dimension of 3840, which was passed onto fully connected layers (with dropout and batch normalization layer) to output a final prediction of seven dimensions and wrapped with a soft-max function for the supervised loss.

• CNN-VAE (presented): The encoder of the presented CNN-VAE consisted of a similar CNN architecture (kernel size of four convolution layers was, respectively, 10, 10, 10, and 13, all with a stride length of 2) to the supervised CNN, followed by two linear layers to obtain the expectation and variance of the latent Gaussian distribution, each with an output dimension of 100. The CNN decoder started with a sample from the latent distribution as the input. It consisted of three convolution blocks with transpose convolution (with a kernel size of 13, 9, 10, and 10 respectively, and a stride length of 1, 1, 2, and 2 respectively), batch normalization, and ReLU activation. For the supervised fine-tuning, two additional linear layers (output of seven dimensions representing seven LV segments) were used before the soft-max classification loss.

During training, the training data was split into training (11719 beats from 28 patients) and validation (2440 beats from 5 patients) sets. Hyper-parameters for all models, such as learning rate, were tuned based on the performance of the network on the validation set. The dropout, with probability = 0.5, was used during fine-tuning. All models were implemented using deep learning framework PyTorch.

During testing, the trained population model was applied to multiple beats of QRS traces corresponding to each VT or test pacing site. The majority predictions were then determined as the initial regionalization of the origin of ventricular activation, with which the accuracy of the population model was evaluated and the patient-specific model was initialized.

Evaluation metrics

We evaluated the performance of the segment classification by the percentage that the model 1) predicted the true segment as the most likely prediction (top-1 exact), and 2) predicted either the true segment or an immediate neighbor of the true segment as the most likely prediction (top-1 adjacent).

We evaluated the model performance in two scenarios. First, we tested the model in localizing a total of 216 pacing sites on the nine patients in the test cohort. This had the advantage that the location of origin (pacing sites) was exactly known, although it may be different from the intended use of the model in VT. We then tested the model in localizing the site of origin for nine VTs on seven patients within the test cohort. This directly tested the intended use of the presented model, although the exit site of the VT was clinically determined and maybe associated with error itself.

Results

Table 1 summarizes the accuracy of the presented population model in comparison to the alternative models in localizing, respectively, pacing sites and the origin of VT. In general, deep neural networks provided an improved accuracy over QRS-integral based regression. In localizing pacing sites, the presented CNN-VAE outperformed the other models in “top-1 exact” metric. The difference between “top-1 exact” and “top-1 adjacent” showed that, in all models, approximately 40% of the pacing sites were located immediately adjacent to the true segment. In VT, performance of the other two models decreased significantly, most likely owing to the difference in ECG data between VT (test) and paced rhythms (training). In comparison, the presented CNN-VAE maintained a similar performance, and significantly outperformed the other models in both metrics. In eight out of the nine VTs, the presented CNN- VAE was able to localize the VT origin either in the true segment (5/9, 55.6%) or immediately next to the true segment (3/9, 33.3%).

Table 1:

Accuracy (in %) of population-based models in localizing the site of pacing or VT origin into one of seven LV segments. Best performance in each metric is in bold.

Model	Localizing pacing sites (n= 192)		Localizing the origin of VT(n= 9)
	Top-1 exact	Top-1 adjacent	Top-1 exact	Top-1 adjacent
LR	42.0	84.0	33.3	66.7
CNN	50.0	93.7	33.3	77.8
CNN-VAE	52.6	91.1	55.6	88.9

Results of the hybrid model

Model architecture and training

To evaluate the presented hybrid model, we compared alternative approaches with differences in two main aspects:

• Initial conditions: To evaluate the benefit of integrating population model, we compared two different strategies for initializing the patient-specific model: random initialization (Random Init), vs. initialization within the segment predicted by the population model (Population Init).

• Active guidance: To evaluate the benefit of active guidance, we compared two different strategies for incrementally adding pacing sites to update the patient-specific model: random pacing (No Guidance), vs. actively-guided pacing (Active Guidance).

The combination of the above two factors gave us a total of four modeling strategies, where “Population Init + Active Guidance” being the presented hybrid-modeling strategy.

The hyperparameter C for SVR was tuned on one patient (23 pacing sites) in the test cohort and set to a value of 50. This value was then used in all models for localizing 1) 193 pacing sites on the remaining eight patients, and 2) the origins of nine clinical VTs in a subset of seven patients.

Emulation of clinical procedures

Retrospective evaluation of the presented hybrid model is challenging as paced ECG data may not be available at the exact model-suggested sites, and certain levels of approximation were needed in order to emulate how the model may actively guide pace-mapping. To initialize the patient-specific model, n_init number of pacing sites were randomly selected either from all available pacing sites (Random Init), or from the segment predicted by the population model (Population Init). To incrementally add pacing data to train the model, new pacing sites were either randomly selected from the remaining available pacing sites (No Guidance), or selected from the remaining available pacing sites that were the closest to model-suggested sites (Active Guidance). In the latter, if no available pace-mapping site was within 15-mm of the suggested sites, the emulation was terminated prematurely. A successful termination for all models was when the CC between the newly-collected QRS complex and the target QRS complex was over a pre-defined threshold C_match on 12 out of 12 ECG leads (12/12 match).

Emulation was performed for all four models on 193 paced ECG data and nine VT ECG data using n_init = 4, and C_match = 0.9. 15 runs of each model were tested considering the effect of random initialization. Note that the performance of active guidance would be restricted by the retrospective nature of the testing: 1) since each added training site was selected from existing data closest to the model-suggested sites, the added training data would be suboptimal in comparison to actual model suggestions; and 2) in cases of premature termination, the obtained results would not reflect what the presented model could have achieved if training data at suggested sites were available. To address the second restriction, we examined model results both in all 193 cases, and in a common subset where the presented hybrid model was able to complete its active guidance without premature termination.

Results on localizing pacing sites

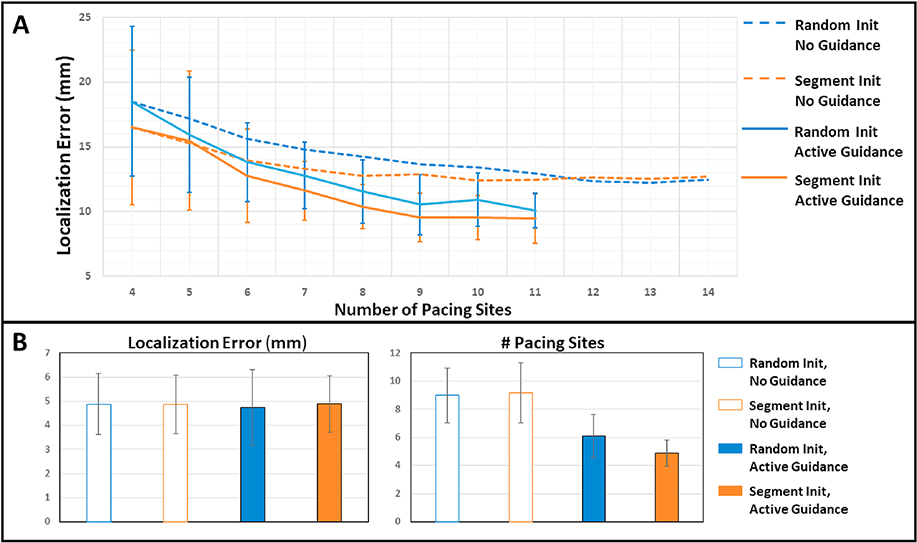
Fig. 3A summarizes the results of the four alternative modeling strategies in localizing pacing sites in the test cohort. All models started with the entire set of 193 pacing sites to localize. As each model progressed, different cases were terminated either successfully, or prematurely in models equipped with active guidance. The average localization error (in mm) from each model showed the progression of model prediction errors – calculated from a mixture of terminated and in-progression cases – as additional pace-mapping data were collected. As shown, initialization within population-based predictions (orange) in general improved the localization accuracy of the model in comparison to random initialization (blue), although this advantage was slowly diminished when no guidance was used for adding training sites (dashed line). In comparison, the use of active guidance (solid lines) not only substantially accelerated the drop of localization error but also, when combined with population-based initialization (orange solid), delivered the best reduction of prediction errors with the minimum number of training sites.

Figure 3:

Results of the hybrid model in comparison to alternative models in localizing 192 pacing sites. A: Decrease of average localization errors with each added training site. B: Final localization accuracy (left) and the number of training sites used (right) obtained from successfully-terminated cases. Because all successfully-terminated cases found 12/12 match in QRS to the target, the final accuracy as expected was similar among models. The number of pacing sites used was significantly lower using active guidance (p < 0.0001, paired t-tests).

Fig. 3B summarizes the final localization accuracy and the number of used training sites for each model on its respective successfully-terminated cases. As expected, because all successfully-terminated cases found sites with 12/12 match to the target, there was no significant difference in the final accuracy among the four models (p = 0.20, one-way ANOVA). To achieve this level of accuracy, the presented hybrid model needed only 4.9 ± 1.9 training pacing sites, significantly lower (p < 0.0001, paired t-tests) than an average of 9.0 ± 3.9 and 9.2 ± 4.3 pacing sites by the two models with no active guidance.

Because active-guidance models had to be terminated prematurely if no training data was near model-suggested sites, Fig. 4A–B summarizes the performance of the presented model on the subset of cases where it was able to complete. In addition to the two models without active guidance, we added comparison to SVR models 1) using all the available pacing sites and 2) using pacing sites selected within a 25-mm radius within the target site (black dashed line). As shown in Fig.4B, the final accuracy of the presented model, 5.4 ± 2.7 mm using a total of only 5.6 ± 2.7 pacing sites, was significantly lower than what random initialization without active guidance was able to achieve (7.5 ± 4.4 mm, p < 0.001, paired t-test) using 10.8 ± 5.7 sites, and what population-based initialization without active guidance was able to achieve (6.4 ± 3.7 mm, p = 0.009, paired t-test) using 8.2 ± 5.4 sites. This verified our hypothesis that the presented hybrid model was able to significantly improve localization accuracy using a significantly smaller amount of pacing sites (p<0.0001, paired t-tests), owing to a significantly larger reduction of prediction error with each added site (2.2 ± 3.4 mm by the presented model vs. 1.3 ± 3.9 and 0.5 ± 3.0 by the two models without active guidance, p<0.03, paired t-tests).

Figure 4:

Results of the hybrid model in comparison to alternative models on a common subset where the hybrid model was able to complete active guidance. A: Decrease of average localization errors with each added training pacing site. B: Final localization accuracy (left), the number of training sites (middle), and reduction of error per step (right). Without premature termination, the presented model was able to obtain a significantly higher localization accuracy (p < 0.009, paired t-tests) with a significantly smaller number of pacing data (p < 0.0001, paired t-tests) and a significantly higher reduction of prediction error per step (p < 0.03, paired t-tests).

Furthermore, the accuracy of the hybrid model was higher than what can be achieved using all available pacing sites (7.5 ± 4.4 mm with 24.3 ± 8.1 sites) and what can be achieved using pacing sites intentionally selected to be within a 25-mm radius of the target site (6.0 ± 2.4 mm with 12.5 ± 2.1 sites). Without being forced to terminate early due to sparse retrospective data, this set of results provided a closer approximation of the performance of the presented method.

Fig. 5 provides two examples of how the prediction of the patient-specific model (black diamonds) progressed towards the target site (red star), using incrementally added pacing sites (blue dots) as suggested by the model. Fig. 5A gave an example where the 12/12-matched pacing site was localized within a 2.3-mm distance using eight pacing sites. Fig. 5B gave an example where the active guidance, despite relatively remote initialization points (blue square), showed a clear progression towards the target site. It however had to be terminated after seven actively-suggested sites, since no existing pacing sites (black dots) were within 15-mm of the model-suggested site. At the time of termination, the localization error was 17-mm, which artificially inflated the error of the presented model.

Figure 5:

Examples of actively-guided pace-mapping. A: The presented model was able to progress towards the target site (12/12 match) using four pacing sites after initialization: achieving a final localization error = 2.3 mm using a total of eight training sites. B: The presented model showed a clear progression towards the target site despite a far initialization. It however was terminated prematurely because no existing paced data (black dots) was available within 15-mm of model-suggested sites (black dimond, step 7), resulting in a localization error of 17-mm at the time of termiation.

Results on localizing the origins of VTs

Due to the small sample size, restrictions from the retrospective data became more evident in localizing the origin of VT: the presented model was not able to complete its active guidance in any of the nine VTs, all due to the absence of available training sites within a reasonable radius of model-suggested sites. Fig. 6 summarizes the results of the presented model on each VT at the time of premature termination, including detailed progression of model predictions (black diamonds), training sites used (blue squares and dots), and quantitative numbers on the initial localization error versus final localization error at the time of termination.

Figure 6:

Results in localizing the exit site of clinical VTs, following the same visualization scheme as in Figure 5. A-E: the model was well initialized, although within 1–2 steps it exhausted available training data near target sites and had to be terminated. F-G: the model was initialized further from the target, although it showed a clear progression towards the target but was terminated when no training sites were within 15-mm radius of model-suggested sites. H-I: the model was initialized far from the target and, due to the lack of training data, was not able to progress away from the initialization.

As shown, in all cases, training data available around the VT exit site were sparse. Fig. 6A–E show examples where the presented method was well initialized, although within 1–2 steps of active guidance it has exhausted all the available training sites near the target site and had to be terminated prematurely. Fig6. F–G are examples where the population-based initialization (blue square) was relatively further from the VT exit site, despite which the model showed a clear progression of predictions towards the target. In nine and two steps, respectively, the model ran out of available training data within a reasonable distance from the last suggested site and had to be terminated. In these seven cases, the localization error was on averaged reduced by 2.5 ± 3.0 mm using 2.4 ± 2.9 pacing sites, demonstrating an evident progression of localization accuracy despite early termination. Fig. 6H–I are two examples where the initialization was relatively far from the target and, because no training sites were available within model-suggested sites, the model was not able to progress away from the initialization towards the target.

Because no 12/12 match was found due to sparse training data, the final accuracy here did not represent the actual accuracy that could be obtained by the presented hybrid model. The results, however, did suggest the ability of the presented model to progress towards the target sites using intelligently-selected training sites, as what was observed in the paced data.

Discussion

Effect of retrospective emulation of active guidance

A main restriction in evaluating the presented hybrid model was the retrospective nature of the clinical data, which were relatively sparse with an average distance of 10–15 mm among available pacing sites in each heart. This issue was especially significant in localizing the origins of VTs. Instead of being able to collect paced ECG data at the actual sites suggested by the model, we had to resort to ECG data at the pacing site nearest to the suggested site. This not only introduced suboptimal training sites than the model suggestions, but also resulted in premature termination of many test cases where no existing pacing sites could be found within a 15-mm radius of the suggested sites despite a clear progression of the model prediction towards the target site (Fig. 4B and Fig. 5). This may have negatively biased the reported accuracy of the presented hybrid model.

Furthermore, among existing pacing sites in the experimental data, many had zero or a small number of neighbors. In these cases, even if active guidance did progress towards the target site, it would have to be terminated prematurely due to the lack of available training data. To test the effect of including/excluding these points as target sites, we compared the performance of the presented model as we excluded target sites that had 0, 1, or 2 neighbors within a 15-mm radius. As expected, as more of these “isolated” pacing sites were removed from target sites, the percentage of cases successfully terminating active guidance increased (from 8% to 27%) and the performance of the final localization accuracy increased (from 4.8 ± 2.8 mm to 4.6 ± 2.4 mm). Regardless, throughout all settings, the presented hybrid model always outperformed the other three models in delivering the lowest localization error with the smallest amount of training pacing sites.

Effect of model hyperparameters

The hyperparameters associated with the population-based deep network was tuned on a separate training cohort. The hyperparameter C in the SVR was tuned on one separate patient in the test cohort and set to a value of 50. Fig. 7A shows how the final localization accuracy of the presented method would change on the rest of the eight patients with respect to the value of C: a large value of C would overfit the model, while a small value of C led to a poor fitting. The value of 50 obtained on the one “calibration” patient, as shown in Fig. 7A, applied well to the rest of the test patients. Since both C and the hyperparameters for the deep network were tuned on patients separated from the test subjects, it provided a reliable evaluation of the generalization ability of the presented hybrid model in new patients.

Figure 7:

Effects of hyperparameters. A: The effect of hyperparameter in the SVR on the accuracy of the hybrid model. B: The effect of initial pacing sites on the accuracy (blue) and the number of training sites (orange) needed in the presented patient-specific model.

The active guidance strategy included two additional hyperparameters related to initialization and termination of the procedure. Fig. 7B shows how the overall accuracy (blue) and the number of training sites needed (orange) of the presented method changed with respect to the number of initial training points.

As expected, as more initial points were introduced, the final accuracy of the model was increased, at the expense of requiring more training pacing sites. The decision on the number of initial sites should depend on clinical need. For instance, if an average of 5-mm localization error is a desired clinical target, an initial number of four pacing sites would be sufficient.

The termination criterion used in this paper was 12/12 match as defined by a CC_match > 0.9 between the prediction and target QRS. Intuitively, as we make this criterion more or less strict, we will achieve, respectively, a higher or lower localization accuracy with the need of a higher or lower number of pacing sites. This criterion thus could be adjusted based on clinical needs of precision vs. efficiency in localizing the interventional targets.

Limitations and future works

This study can be improved in several directions. First, this paper considered only ventricular activation originating from the LV endocardium, although the underpinning methodology is generally applicable to sites of origins in other regions of the heart. The main challenge of this extension is the availability of pace-mapping data for training the population model: in the case that such data are not available in a clinical setting, exploiting simulated ECG data and transferring the learned knowledge to clinical data may be a promising option [11].

The patient-specific model considered in the presented hybrid model, following [15], used a simple time-integral of the QRS complex as input predictors. Investigation of richer QRS features, such as a vector of incremental QRS integrals [11], may further increase the performance of the presented model. Similarly, it was noted in recent work [15] that there exists an optimal combination of leads for predicting the origin of VT to reduce the redundancy within input data. These aspects will be investigated in future work.

The presented active guidance strategy exploits the current model predictions and explores regions where the current model is the least accurate about. A potential alternative solution is to reformulate the problem at hand such that we search over an input space of 3D coordinate in order to maximize the similarity between the ECG of a target site and that of any given 3D coordinate. This will allow incorporation of region of dense scar that is not considered in the presented strategy of active guidance. Gaussian-processed based Bayesian optimization provides an elegant solution to this problem, which is being investigated as an immediate extension of the presented work.

Only a small number of clinical VTs were tested in this paper, mainly due to the difficulty of obtaining clinically-determined labels for the 3D coordinate of the VT exit site. Furthermore, the exit sites of the nine VTs considered were distributed in only four segments. This skewed label distribution may bias the observed performance of the population models. Finally, for a given pacing site or VT origin, the morphology of QRS varies from beat to beat. In this study, we applied the population model to multiple ECG beats from the same pacing site / VT exit and used the majority prediction as the segment prediction. The patient-specific model was then tested on one sample beat that corresponded to the majority prediction. In the future, the effect of beat-to-beat variations on the presented hybrid model need to be tested by applying the hybrid model on multiple beats originated from the same origin of ventricular activation.

Conclusions

We present a hybrid model for computer-guided pace-mapping that relies on a population-based deep neural network for initialization, followed by an active patient-specific model that intelligently suggests the next pacing sites and guide clinicians progressively towards a target site using a minimum number of pacing data for training. The performance of the hybrid model was retrospectively evaluated on a test cohort of patients separated from the training cohort, demonstrating the ability of the model in accurately localizing the origin of ventricular activation a small number of pace-mapping data for training.

Highlights.

• A novel hybrid model that combines the advantage of population-based deep learning (can be applied to a new patient without prior training data on the patient) and patient-specific model (higher accuracy for a specific patient without the challenge of inter-subject variations).

• A novel population model that disentangles inter-subject variations when learning to localize the sites of origins of ventricular activation from ECG data.

• A novel patient-specific model that actively suggests where to pace in order to best improve the model prediction using a minimum number of pacing data for training.

• A complete workflow based on the hybrid model, evaluated in clinical data from patients with ventricular tachycardia.

• A novel emulation strategy to test how the hybrid model may guide pace-mapping in retrospective data.